 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simulation of conformality of ALD growth inside lateral channels: comparison between a diffusion–reaction model and a ballistic transport–reaction model†
Jänis
Järvilehto
 *,
Jorge A.
Velasco
*,
Jorge A.
Velasco
 ,
Jihong
Yim
,
Jihong
Yim
 ,
Christine
Gonsalves
,
Christine
Gonsalves
 and
Riikka L.
Puurunen
and
Riikka L.
Puurunen
 *
*
Department of Chemical and Metallurgical Engineering, School of Chemical Engineering, Aalto University, P.O. Box 16100, FI-00076 AALTO, Finland. E-mail: janis.jarvilehto@aalto.fi; riikka.puurunen@aalto.fi
First published on 10th August 2023
Abstract
Atomic layer deposition (ALD) has found significant use in the coating of high-aspect-ratio (HAR) structures. Approaches to model ALD film conformality in HAR structures can generally be classified into diffusion–reaction (DR) models, ballistic transport–reaction (BTR) models and Monte Carlo simulations. This work compares saturation profiles obtained using a DR model and a BTR model. The saturation profiles were compared qualitatively and quantitatively in terms of half-coverage penetration depth, slope at half-coverage penetration depth and adsorption front broadness. The results showed qualitative agreement between the models, except for a section of elevated surface coverage at the end of the structure, ‘trunk’, observed in the BTR model. Quantitatively, the BTR model produced deeper penetration into the structure, lower absolute values of the slope at half-coverage penetration depth and broader adsorption fronts compared to the DR model. These differences affect the values obtained when extracting kinetic parameters from the saturation profiles.
1 Introduction
Atomic layer deposition (ALD) has had a significant impact on the semiconductor industry due to its ability to deposit films of controllable, constant thickness inside narrow structures with challenging aspect ratios.1–4 Other ALD applications involving high-aspect-ratio (HAR) structures include composite materials for energy storage devices5 and preparation of heterogenous catalysts.6 Furthermore, HAR test structures can be used to study the reaction kinetics of an ALD process.1,7Saturation profiles plot the surface coverage inside a HAR structure as a function of the distance from the structure entrance (i.e. penetration depth).8,9 Parameters, such as the half-coverage penetration depth and the slope at half-coverage penetration depth can be extracted from the saturation profiles to enable quantitative comparison.8,9 In addition, as long as certain assumptions are valid, the slope at half-coverage penetration depth can be used to determine the lumped sticking coefficient, a kinetic parameter of the reaction.7
Models developed for the simulation of conformality in HAR structures can be categorized,10,11 based on how they treat particle transport, into diffusion–reaction (DR) models,12–20 ballistic transport–reaction (BTR) models10,21,22 and Monte Carlo simulations.23–25 Additionally, models based on the Boltzmann equation have been developed.26,27Fig. 1 illustrates particle transport in a DR model and a BTR model. DR models (Fig. 1a), also sometimes referred to as continuum (or continuous) models,11,20,28–30 solve particle transport using a diffusion equation.11,28 In BTR models (Fig. 1b), particle fluxes are calculated between discretization segments on the structure surface using view factors derived from the structure geometry.28 The assumption of ballistic transport is valid only in Knudsen diffusion conditions, i.e. when the particles interact with the structure and not with other particles in the gas phase.28 A previous work30 has compared a DR model and BTR model in the context of low-pressure chemical vapor deposition (LPCVD).
The goal of this work was to compare, both qualitatively and quantitatively, two fundamentally different models, a DR model and a BTR model, to describe the evolution of ALD film conformality in microchannels. The comparison is limited to Knudsen diffusion conditions, because this is where one of the models (BTR model) is valid. We will show that, while the model predictions are qualitatively largely similar, quantitative differences exist, which will lead to different interpretations when extracting kinetic information from the saturation profiles.
2 Model description
In this work, the DR model12 (DReaM-ALD31) will be referred to as Model A, while the Markov chain based BTR model10 (Machball32) will be called Model B. Furthermore, this work will refer to the ALD counter-reactants as Reactant A and Reactant B, with Reactant A being the metal precursor of the process, denoted by subscript ‘A’. The parameters describing the inert carrier gas will carry the ‘I’ subscript (in line with ref. 9 and 31), as opposed to ‘B’ used in the original description of the diffusion–reaction model.12 A brief description of each model will be given next. More in-depth explanations of the diffusion–reaction model can be found in the original work,12 as well as more recently elsewhere.9 Model B will be introduced in the context of a single reaction pathway with no possibility of reactant recombination. The full description of Model B is presented in the original work.10 Both models assume immediate thermalization of the reactant molecules, i.e. the molecules enter the structure at surface temperature, as opposed to heating up when they reach the structure surface.2.1 Model A: diffusion–reaction model
The DR model by Ylilammi et al.12 assumes constant concentration of Reactant A along the height and width of the channel. Thus, the one-dimensional diffusion equation can be used to model reactant molecule transport:12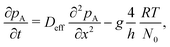 | (1) |
 | (2) |
 | (3) |
 | (4) |
Here, pA0 is the partial pressure of Reactant A at the channel entrance (Pa) (i.e. pA(0,t)). In turn, xs is the distance the gas front has travelled at time t (m), approximated from the diffusion length:12,28
 | (5) |
 | (6) |
Here, c is the sticking coefficient (−) and Q is collision rate at unit pressure (m−2 s−1 Pa−1):12
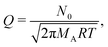 | (7) |
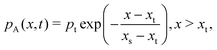 | (8) |
 | (9) |
The Langmuir model of adsorption is used to determine how the fractional surface coverage θ (−) evolves over time:12
 | (10) |
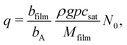 | (11) |
| g = fads − fdes. | (12) |
Here, the rate of adsorption is:12
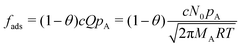 | (13) |
| fdes = qθPd, | (14) |
 | (15) |
Alternatively, eqn (15) can be expressed as
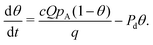 | (16) |
In Model A, the analytical approximation of the partial pressure of Reactant A (eqn (4) and (8)) is inserted in the adsorption model (eqn (15)), which is then solved numerically. In the original work,12 the numerical solution was obtained using the 4th order Runge–Kutta method. However, the implementation of Model A used in this work, DReaM-ALD,31 utilized MATLAB's built-in ODE23 differential equation solver instead. Both solvers have been shown to produce similar saturation profiles.9
2.2 Model B: ballistic Markov chain model
The ballistic Markov chain model developed by Yanguas-Gil and Elam10,32 (Model B) uses a stochastic method to determine reactant molecule transport inside the structure. In ballistic models, reactant molecule transport is expressed in terms of particle fluxes between discretization segments.10,37 The particle flux reaching segment i can be expressed as:10,37 | (17) |
The particle flux reaching segment i per unit surface area per unit time ϕi (m−2 s−1), multiplied by the segment's surface area Si (m2), is equal to the sum of particles arriving from the other segments in the structure (qij(1 − βj)Sjϕj) and from the structure entrance (q0iS0ϕ0). The particle flux originating from segment j is determined by multiplying the particle flux per surface area arriving at segment j, ϕj, by the surface area of segment j, Sj, and the view factor between segments j and i, qji (−), as well as the probability that the particle did not react at segment j, (1 − βj), where βj is the local reaction probability at segment j (−). Similarly, the particle flux originating from the entrance of the structure is calculated by multiplying the particle flux per entry area, ϕ0 (m−2 s−1), by the entry area, S0 (m2), and by the view factor from the structure entrance to segment i, q0i (−). The view factors indicate the probability of transmission from a specific segment to another and are determined from the structure geometry.10,37
In principle, the model can be used with structures of any three-dimensional geometry, provided their surfaces can be discretized into segments and the view factors between these segments can be determined. The channel examined in this work was constructed by dividing the channel side walls (upper and lower walls in Fig. 1) into vertical discretization segments, with the entrance and end wall (left and right side in Fig. 1, respectively) represented by a single segment each.10,32
Once the structure geometry has been defined, the model solves reactant molecule transport as a Markov chain.10 In a Markov chain, the probability of an event (i.e. a gas molecule interacting with a specific part of the structure) is only dependent on the outcome of the previous event (i.e. where the molecule previously collided with the structure).10,38 These events can be seen as transitions between states, where each state represents the conditions a molecule is in.10 For example, a molecule could be located at segment i and transition to segment j by colliding with the structure wall.10 Other state transitions include reacting at the segment or exiting the structure.10 In Model B, the probabilities between these state transitions (δ → γ) are defined in a transition probability matrix Pδγ (−), consisting of the following probabilities (excluding recombination):10
 | (18) |
Here, Pij is the transmission probability matrix (−), Pi0 is the reemission probability matrix (−) and PiFi is the reaction probability matrix (−). The relationship between the molecule state and the transition probabilities can be summarized as:10
 | (19) |
Here, the probability of a reactant molecule existing in state γ after m collisions, pγ(m) (−), is determined by the probability of the reactant molecule existing previously in state δ, pδ(m − 1), multiplied by the probability of the reactant molecule transitioning from state δ to γ, Pδγ.
In the case of irreversible adsorption with a single reaction pathway, the evolution of surface coverage depends on the incident flux ϕis0, multiplied by the local reaction probability βi(θi):10
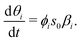 | (20) |
Here, s0 is the average area of a surface reaction site (m2), which is the inverse of the adsorption capacity at saturation q in Model A:
 | (21) |
As the adsorption is saturating and irreversible, the local reaction probability at each discretization segment βi (−) is dependent on the specific discretization segment's current surface coverage θi (−):10
| βi = β0(1 − θi), | (22) |
If we define Pi as the probability of a reactant molecule adsorbing in segment i (−), a balance equation can be formulated:10
 | (23) |
Combining eqn (20) and (23), we obtain:10
 | (24) |
This equation is solved numerically with an adaptive time step, which is based on the change in surface coverage after each step.10
3 Simulation details
3.1 Saturation profile terminology and analysis
The saturation profiles presented in this work follow the classification proposed in ref. 8. The amount of film grown is expressed as surface coverage θ, indicated on the vertical axis. On the horizontal axis, the distance from the channel entrance is indicated either as dimensionless distance![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = x/H (−) (Type I normalized saturation profile), or normalized distance ξ = x/L (−) (Type II normalized saturation profile). Here, H is the channel height (m) and L is the channel length (m).
= x/H (−) (Type I normalized saturation profile), or normalized distance ξ = x/L (−) (Type II normalized saturation profile). Here, H is the channel height (m) and L is the channel length (m).
The half-coverage penetration depth ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.5 was determined using two points from each saturation profile: the first point from the channel entrance where θ ≤ 0.5, and the point prior to it. These points were interpolated to θ = 0.5 to obtain the half-coverage penetration depth, as well as the slope at half-coverage penetration depth. The method has been described elsewhere9 in detail. Absolute values were calculated for the slope to ease comparison, as the slope is typically negative.
θ=0.5 was determined using two points from each saturation profile: the first point from the channel entrance where θ ≤ 0.5, and the point prior to it. These points were interpolated to θ = 0.5 to obtain the half-coverage penetration depth, as well as the slope at half-coverage penetration depth. The method has been described elsewhere9 in detail. Absolute values were calculated for the slope to ease comparison, as the slope is typically negative.
As a further point of comparison, the broadness of the adsorption front, ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.1 −
θ=0.1 − ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.9, was measured. The adsorption front broadness was defined as the dimensionless distance between the first point where θ < 0.9 and the first point where θ < 0.1, measured from the channel entrance. Saturation profiles, where the surface coverage was below one at the channel entrance, or where the surface coverage did not decrease below 0.1, were excluded from the comparison.
θ=0.9, was measured. The adsorption front broadness was defined as the dimensionless distance between the first point where θ < 0.9 and the first point where θ < 0.1, measured from the channel entrance. Saturation profiles, where the surface coverage was below one at the channel entrance, or where the surface coverage did not decrease below 0.1, were excluded from the comparison.
3.2 Selection of parameters
The trimethylaluminum (TMA)–water ALD process to grow aluminum oxide8,39 was used as a starting point for the selection of the simulation parameters, similarly as in ref. 9 and 12. The molar mass of Reactant A MA was selected to be 0.1 kg mol−1, which is in the same order of magnitude as TMA. The molar mass of the inert carrier gas MI was selected based on the commonly used nitrogen as 0.028 kg mol−1. Similarly, the molecular diameters dA = 0.6 nm and dI = 0.4 nm were chosen based on approximations12 of TMA and nitrogen gas, respectively. The molar mass of the deposited film Mfilm was 0.05 kg mol−1 and the film density ρ was 3500 kg m−3, which are in the same order of magnitude as the respective values for aluminum oxide.40 The number of metal atoms in a reactant molecule bA and molecular unit of film bfilm were set to one. The saturated adsorption capacity q was 4 nm−2, which is in the same order of magnitude as indicated by the growth-per-cycle observed in the TMA–water process.39,41 An equivalent value of 0.25 nm2 for the average surface site area s0 was determined using eqn (21). The temperature T was selected to be in a range typical for ALD,11 with a baseline value of 573.15 K.A channel height H of 0.5 μm was selected based on the dimensions commonly used in PillarHall™ lateral HAR test structures.8,12,42,43 The channel width W was arbitrarily set to 0.01 m, to be orders of magnitude larger than the channel height. The length of the channel L was selected to be 500 μm, which gives a sufficiently high aspect ratio (AR = L/H) of 1000 to obtain visible adsorption fronts for most of the simulations.
A proper resolution for the simulations was determined through preliminary simulations, where the number of discretization points ϕp (Model A) or discretization segments ϕs (Model B) was varied. To account for varying channel lengths, the resolution was defined relative to the channel aspect ratio. For example, the aspect ratio of a channel of L = 500 μm and H = 0.5 μm is (500 μm)/(0.5 μm) = 1000 (−). When the relative number of discretization points ϕp is four, the number of discretization points used is 4 × 1000 = 4000 (−). A summary of the studied resolutions is given in Table 1.
| Relative no. of discretization points ϕp or segments ϕs (−) | No. of discretization points or segments (−) | |
|---|---|---|
| L = 500 μm | L = 1000 μm | |
| 0.0625 | 62.5 | 125 |
| 0.25 | 250 | 500 |
| 1.00 | 1000 | 2000 |
| 4.00 | 4000 | 8000 |
| 16.0 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
A range of values was selected for the sticking coefficient c to cover the upper and lower extremes (0.00001 to 1), with a baseline value of 0.001. Similarly, the exposure duration tend ranged through multiple orders of magnitude: 0.01 to 100 s, with a baseline value of 1 s.
As Model B is only applicable in Knudsen diffusion conditions (Kn ≫ 1), the initial partial pressure of Reactant A pA0 had to be sufficiently low. Therefore, the initial partial pressure of Reactant A was set to 10 Pa. As the partial pressure of the inert carrier gas pI is not included in Model B, it was set to zero in Model A. Similarly, the desorption probability Pd was set to 0.0001 s−1 in Model A, which renders desorption insignificant to the obtained saturation profile. The simulation parameters are summarized in Table 2. The selected simulation parameters resulted in Knudsen numbers ranging from ∼99 to ∼62000 and the Thiele modulus ranged from ∼2.7 to ∼870. The Knudsen number and Thiele modulus were calculated as described in ref. 9.
| Case | Symbol | Value | Unit | |
|---|---|---|---|---|
| Model A | Model B | |||
| a The following simulation parameters are denoted by different symbols compared to when Model A was first presented:12pI was denoted as pB, MI was denoted as MB, Mfilm was denoted as M, tend was denoted as tp and dI was denoted as dB. b In Model B, the channel height H and length L are considered only through the aspect ratio AR = L/H. c L was varied in the preliminary simulations to find a suitable resolution as indicated in Table 1. d The adsorption capacity at saturation q and the average surface site area s0 are inversely related (eqn (21)). e In this work, ϕp and ϕs are defined as the ratio of the number of discretization points or segments, respectively, to the aspect ratio of the channel. As such, they should not be confused with the usage in the Machball model,10 where ϕ denotes particle flux per unit surface area per time. | ||||
| I | T | T | 373.15, 473.15, 573.15, 673.15, 773.15 | K |
| II | p A0 | p | 1, 2.5, 5, 10, 20 | Pa |
| p I | — | 0 | Pa | |
| III | M A | m | 0.05, 0.1, 0.15, 0.2, 0.25 | kg mol−1 |
| M I | — | 0.028 | kg mol−1 | |
| M film | — | 0.05 | kg mol−1 | |
| IV | H | —b | 0.125, 0.25, 0.5, 1, 2 | μm |
| W | — | 0.01 | m | |
| L | —b | 500c | μm | |
| V | t end | t c | 0.01, 0.1, 1, 10, 100 | s |
| VI | c | β 0 | 1, 0.1, 0.01, 0.001, 0.0001, 0.00001 | — |
| P d | — | 0.0001 | — | |
| VII | q | — | 0.5, 1, 2, 4, 8 | nm−2 |
| VII | — | s 0 | 2, 1, 0.5, 0.25, 0.125 | nm2 |
| ρ | — | 3500 | kg m−3 | |
| b A | — | 1 | — | |
| b film | — | 1 | — | |
| d A | — | 0.6 | nm | |
| d I | — | 0.4 | nm | |
| ϕ p | — | 2 | — | |
| — | ϕ s | 4 | — | |
| VIII | p A0 | p | 0.08, 0.4, 2, 10, 50 | Pa |
| VIII | t end | t c | 125, 25, 5, 1, 0.2 | s |
4 Results
4.1 Effect of the simulation resolution
The number of discretization points (Model A) and discretization segments (Model B) was varied to determine a suitable resolution for the simulations. Fig. 2 shows how the resolution affects the resulting saturation profile in channels with different lengths. In Model A, increasing the number of discretization points merely increases the saturation profile roundness. In contrast, the saturation profiles generated using Model B show a change in shape and penetration depth when the number of discretization segments is changed: as the number of discretization segments is increased, the surface coverage at the end of the channel is reduced and the penetration depth decreases. Additionally, the adsorption front becomes more steep. Once the relative number of discretization segments is increased beyond one (i.e. one discretization segment per dimensionless distance unit of channel length), the saturation profiles stabilize. For the comparison of the saturation profiles produced by the models, an intentionally high resolution was selected to ensure consistent results. The relative number of discretization points was selected to be two for the simulations performed using Model A. For Model B, the relative number of discretization segments was selected to be four. | ||
| Fig. 2 Series of saturation profiles obtained with varying numbers of (a) and (c) discretization points (Model A) and (b) and (d) discretization segments (Model B). The legends indicate the resolution as the number of discretization points or segments relative to the channel length in dimensionless distance units. In panel (a), a set of insets shows the shape of the saturation profile in the highlighted area for two relative numbers of discretization points: (upper inset) 0.0625 and (lower inset) 1.00. The channel length L was (a) and (b) 500 μm and (c) and (d) 1000 μm. The other simulation parameters were as in the baseline values indicated in Table 2. Table 1 shows the absolute number of discretization points or segments used in the simulations. | ||
4.2 Comparison of saturation profiles
The series of simulated saturation profiles is presented in Fig. 3, while the half-coverage penetration depth and the absolute value of the slope at half-coverage penetration depth extracted from each saturation profile are shown in Fig. 4. When the temperature was increased (Fig. 3a and 4a), the penetration depth of the film decreased, while the shape of the saturation profile remained similar. An increase in initial partial pressure of Reactant A (Fig. 3b and 4b) caused the film to penetrate deeper into the structure and, in Model B, led to an increase in coverage at the end of the channel. Increasing the molar mass of Reactant A (Fig. 3c and 4c) decreased the penetration depth, with the decrease in penetration depth tapering off as the molar mass was increased. The higher the aspect ratio of the channel (Fig. 3d), the lower the penetration depth was, relative to the total length of the channel. Longer exposure durations (Fig. 3e and 4e) led to deeper penetration depths in both models, compared to shorter exposure durations. In Model B, the channel was covered with a uniform film at an exposure duration of t = 10 s, which was not sufficient to coat the entire channel in Model A. In both models, increasing the sticking coefficient (Fig. 3f and 4f) resulted in an increase in the absolute value of the slope at half-coverage penetration depth. Decreasing the adsorption capacity at saturation (Model A) or increasing the average surface site area (Model B) (Fig. 3g and 4g) generated deeper penetration and increased the coverage at the end of the channel in Model B. The increase in penetration depth with decreasing adsorption capacity at saturation observed in Model A is consistent with a previous work.9 Finally, varying the initial partial pressure of Reactant A and the exposure duration, while keeping the exposure constant (Fig. 3h), had no impact on the resulting saturation profile in either model. | ||
| Fig. 3 Series of saturation profiles that shows the effect of (a) temperature T (K), (b) initial partial pressure of Reactant A pA0 (Pa), (c) molar mass of Reactant A MA (kg mol−1), (d) channel aspect ratio L/H (−), (e) exposure duration tend (s), (f) sticking coefficient c (−), (g) surface site area s0 (nm2) and adsorption capacity at saturation q (nm−2), and (h) constant dose with varying initial partial pressure of Reactant A pA0 and exposure duration tend. In each panel, the left graph shows results for the diffusion–reaction model (Model A), while the right graph shows the saturation profiles obtained using the ballistic transport–reaction model (Model B). See Table 2 for a summary of the simulation parameters, the corresponding symbols used in each model, as well as the variation of the adsorption capacity at saturation q in panel (g). Note that panel (d) has normalized distance on the horizontal axis, as opposed to dimensionless distance in the other panels. | ||
 | ||
Fig. 4 Comparison of the parameters extracted from each series of simulations as a function of the varied simulation parameter. Each panel shows how (left) the half-coverage penetration depth ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.5 and (right) the absolute value of the slope at half-coverage penetration depth (Δθ/Δ θ=0.5 and (right) the absolute value of the slope at half-coverage penetration depth (Δθ/Δ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) )θ=0.5 changes as the simulation parameter indicated on the horizontal axis is varied. The simulation parameters are summarized in Table 2. Saturation profiles, where the surface coverage at the channel entrance was less than one, or where the surface coverage was equal to one throughout the channel, were excluded from parameter extraction. )θ=0.5 changes as the simulation parameter indicated on the horizontal axis is varied. The simulation parameters are summarized in Table 2. Saturation profiles, where the surface coverage at the channel entrance was less than one, or where the surface coverage was equal to one throughout the channel, were excluded from parameter extraction. | ||
Fig. 5 shows the adsorption front broadness measured from the series of saturation profiles. Increasing the temperature (Fig. 5a) had no effect in Model A, while the adsorption front broadness decreased slightly in Model B. An increase in initial partial pressure of Reactant A (Fig. 5b) led to no change in Model A, while an increase in adsorption front broadness was observed in Model B. When the molar mass of Reactant A was increased (Fig. 5c), the adsorption front broadness was not affected in Model A. In Model B, the adsorption front broadness decreased and appeared to plateau. The aspect ratio of the channel (Fig. 5d) did not affect the adsorption front broadness in either model. The variation in exposure duration (Fig. 5e) produced few saturation profiles, from which the adsorption front broadness could be determined. Between the two valid saturation profiles obtained from Model A, no change in adsorption front broadness could be observed. Increasing the sticking coefficient (Fig. 5f) caused the adsorption front broadness to decrease sharply and then plateau in both models. When the average surface site area was increased (Model B) (Fig. 5g), i.e. the adsorption capacity at saturation was decreased (Model A), the adsorption front broadness remained unaffected in Model A, while it increased in Model B. The series of constant exposure by variation of the initial partial pressure of Reactant A and the exposure duration (Fig. 5h) produced identical saturation profiles in both models.
 | ||
| Fig. 5 Comparison of the adsorption front broadness measured from each series of simulations as a function of the varied simulation parameter, indicated on the horizontal axis of each graph. The adsorption front broadness was determined by measuring the distance between the first point from the channel entrance where the surface coverage θ < 0.9 and the first point where θ < 0.1. If the surface coverage was below one at the beginning of the channel or did not fall below 0.1 in the rest of the channel, the saturation profile was excluded from the broadness measurements. The simulation parameters are summarized in Table 2. | ||
Fig. 6 compares the half-coverage penetration depth, the absolute value of the slope at half-coverage penetration depth and the adsorption front broadness observed throughout the series of simulations. Model B yielded systematically larger penetration depths (Fig. 6a) and broader adsorption fronts (Fig. 6c) than Model A. The highest deviation in half-coverage penetration depth between the models was observed when the average surface site area was increased (Fig. 6a and 4g), while the models were closest at low partial pressures of Reactant A (Fig. 6a and 4b). Varying most of the simulation parameters had little impact on the slope at half-coverage penetration depth, with the exception of the sticking coefficient, which led to an increase in the absolute value of the slope as it was increased (Fig. 6b and 4f). Similarly, the broadness of the adsorption front was influenced most by the sticking coefficient in both models (Fig. 6c and 5f). In Model A, the other varied parameters had no impact on adsorption front broadness (Fig. 6c). In contrast, Model B showed variation in adsorption front broadness in all cases, especially when the partial pressure of Reactant A and average surface site area were varied (Fig. 6c, 5b and 5g).
 | ||
Fig. 6 Parity plots comparing the (a) half-coverage penetration depth ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.5, (b) absolute value of slope at half-coverage penetration depth (Δθ/Δ θ=0.5, (b) absolute value of slope at half-coverage penetration depth (Δθ/Δ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) )θ=0.5 and (c) adsorption front broadness )θ=0.5 and (c) adsorption front broadness ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.1 − θ=0.1 − ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.9 observed in Model A and Model B. The legend shows which simulation parameter was varied for each plotted value. On the grey dashed line, the results from both models would be identical. The simulation parameters are summarized in Table 2. θ=0.9 observed in Model A and Model B. The legend shows which simulation parameter was varied for each plotted value. On the grey dashed line, the results from both models would be identical. The simulation parameters are summarized in Table 2. | ||
5 Discussion
This section comments on the general trends observed in the results and provides reasoning for the resolution-dependent behaviour of Model B. Additionally, the inclusion of the end wall in the structure geometry and its effect on the shape of the simulated saturation profile is discussed.5.1 Similarities and differences between the models' output
Model A and Model B produced qualitatively similar trends in terms of half-coverage penetration depth when the simulation parameters were varied (Fig. 3 and 4). For example, an increase in temperature resulted in a slight decrease in half-coverage penetration depth (Fig. 3a and 4a). However, Model B showed systematically deeper penetration into the structure than Model A (Fig. 4 and 6). The relative difference in half-coverage penetration depth ranged from ∼38% higher in Model B compared to Model A (pA = 1 Pa, Fig. 4b and c = 0.00001, Fig. 4f) to ∼57% higher in Model B compared to Model A (s0 = 1 nm2, Fig. 4g). On average, the half-coverage penetration depth was ∼48% higher in Model B compared to Model A. This systematic difference is consistent with an earlier comparison30 of a DR model and BTR model, which operated in the context of LPCVD and studied the relationship between the film thickness at the channel end and the outer, exposed surface (i.e. the step coverage). In the earlier comparison,30 the BTR model gave a systematically higher step coverage compared to the DR model.On average, the absolute value of the slope at half-coverage penetration depth was ∼2.0 times higher in Model A compared to Model B. In the series of simulated saturation profiles, the most agreement between Model A and Model B, in terms of slope, was at pA = 1 Pa (Fig. 4b), where the absolute value of the slope was ∼1.6 times higher in Model A compared to Model B. The models agreed the least at c = 1 (Fig. 4f), where the absolute value of the slope at half-coverage penetration depth was ∼4.2 times higher in Model A compared to Model B. Overall, varying the sticking coefficient had the most extreme effect on the slope at half-coverage penetration depth for both models. When the sticking coefficient was increased (Fig. 3f), the absolute value of the slope at half-coverage penetration depth increased (Fig. 4f), with the saturation profiles produced by both models pivoting around a fixed point. Varying the sticking coefficient (Fig. 4f), produced a broader range in the absolute value of the slope in Model A (∼0.0031 to ∼0.30) compared to Model B (∼0.0051 to ∼0.071).
The broadness of the adsorption front remained mostly constant throughout the simulations in Model A, while Model B produced more variation in broadness (Fig. 5). The adsorption front broadness in Model B was, on average, ∼2.8 times the respective value given by Model A (Fig. 5). The series where the sticking coefficient was varied produced the greatest difference in adsorption front broadness between Model A and Model B: when c = 1, the adsorption front broadness in Model B was equal to ∼19 times the respective value in Model A (Fig. 5f). If the sticking coefficient series is excluded from the examined saturation profiles, the adsorption front broadness in Model B is, on average, ∼2.0 times higher than the value obtained from Model A. As varying the sticking coefficient also had the highest impact on the absolute value of the slope at half-coverage penetration depth, the results suggest that the measured slope and the broadness of the adsorption front correlate to some degree.
While the saturation profiles produced by both models were generally similar in shape, Model B produced a section of increasing coverage at the closed end of the channel, which we call a trunk in this work. The shape of the saturation profiles was especially sensitive to variation of the sticking coefficient, with the adsorption front turning steeper and approaching the shape of a step function as the sticking coefficient was increased (Fig. 3f). In Model B, increasing the sticking coefficient also increased the height of the trunk. Furthermore, in Model B, the whole trunk section (i.e. from the saturation profile's minimum coverage to the end of the channel) was elevated as the adsorption front approached the end of the channel.
5.2 Resolution and end wall effect in Model B
In Model B, the number of discretization segments was found to affect the saturation profiles. Increasing the number of discretization segments decreased the penetration depth of the profiles, up to a ratio of approximately one discretization segment per aspect ratio unit, beyond which the profiles stabilized (Fig. 2b and d).This change in penetration depth is explained by how Model B treats particle transport as probabilistic transitions between discretized segments of the channel. In Model B, the probability distribution of the potential target discretization segments for a given molecule to travel to is determined by the view factors between the departure segment and each target discretization segment.10,37 These view factors follow a cosine distribution with the maximum probability of transmission being along the surface normal n (−) of the departure segment.10,37
Fig. 7 illustrates how the angle between the surface normal and the connecting line between neighboring discretization segments Ω (−) (i.e. the normal angle) behaves as the channel aspect ratio and discretization resolution are varied. As the aspect ratio of the channel is increased (Fig. 7b), or the number of segments is decreased, the normal angle increases. An increase in the normal angle, in turn, decreases the view factor between the segments, causing the view factor distribution of a given channel wall segment to narrow. Conversely, increasing the resolution (Fig. 7c) broadens the view factor distribution, which leads to an increase in the number of potential target discretization segments for the molecule to travel to. A visual representation of the view factors can be found in the ESI† (Section 2). Furthermore, when the resolution is low, a molecule advancing the length of a single discretization segment has a more pronounced effect on the saturation profile, compared to when the resolution is high, as the resolution directly affects the length of each discretization segment on the channel wall.
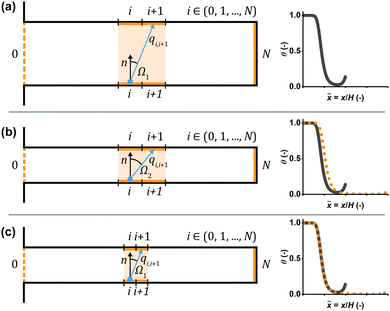 | ||
| Fig. 7 Schematics depicting the normal angle in microchannels of varying aspect ratios discretized with varying resolutions, as well as the resulting saturation profiles. Three situations are shown: (a) reference case, (b) case with higher aspect ratio and the same number of segments as in the reference case and (c) case with higher aspect ratio and the same resolution as in the reference case. The left column shows schematics depicting how the channel aspect ratio and discretization resolution affect the normal angle Ω between neighboring discretization segments (i and i + 1, highlighted in orange). The blue arrow marks the trajectory of the molecule, while the surface normal n is marked by a black arrow. In the right column, the resulting saturation profiles (orange dotted line in panels (b) and (c)) are illustrated in comparison to the reference case (grey solid line). If the aspect ratio is increased without increasing the number of discretization segments (panel (b)), the resolution decreases and the normal angle increases, compared to the reference case (panel (a)): Ω1 < Ω2. As a result, the resulting saturation profile (orange dotted line in panel (b)) does not align with the reference case (grey solid line). If the aspect ratio is increased and the resolution is maintained (panel (c)), the normal angle remains similar to the reference case (panel (a)). Here, the resulting saturation profile (orange dotted line in panel (c)) aligns with the reference case (grey solid line). The saturation profiles were produced using the baseline parameters shown in Table 2, except (a) ϕs = 0.250, (b) ϕs = 0.125, L = 1000 μm and (c) ϕs = 0.250, L = 1000 μm. An intentionally low resolution was used to make the difference in saturation profiles more clearly visible. Note that, as the channel aspect ratio is varied, the length of the saturation profile in dimensionless distance units varies as well. Therefore, the trunk is not visible in the longer saturation profiles (orange dotted line in panels (b) and (c)). | ||
With a higher resolution and a higher number of potential target discretization segments, the molecule has to interact with a higher number of segments to penetrate the structure to a given depth, compared to a lower resolution with fewer potential target discretization segments from each channel wall segment. Given that each collision with a bare or partially covered segment entails the possibility of adsorption, a high number of segments will curb the probability of a molecule reaching a given penetration depth. A high number of collisions with bare or partially covered segments (i.e. a broad view factor distribution) also produces narrower adsorption fronts, as the propagation of gas molecules in the channel is more dependent on the local degree of surface coverage, compared to a case with few collisions (i.e. a narrow view factor distribution).
Model B produced a region of increasing surface coverage at the channel end, a trunk, which was not observed in Model A. This is explained by the fact that the end wall of the channel is included in the modelled structure in Model B, while in Model A, it is not. As the molecules approach the closed end of the channel, the normal angle towards the end wall decreases, which increases its probability as a destination segment. The view factor of the end wall is further increased by its larger solid angle,37,44 in comparison to the channel side wall segments.10 As a result of the relatively high view factor of the end wall, reactant molecules are likely to collide with it, and either adsorb directly on the end wall or continue to the discretization segments in its vincinity. As the molecules are not able to propagate past the end wall, they cumulate in the channel end area, forming the trunk shape. A trunk shape has previously been produced by a Monte Carlo model,45 in the context of plasma-assisted ALD. However, to the best of our knowledge, the trunk has not been reported experimentally yet. Further examination of the trunk in channel and hole structures is presented in the ESI† (Section 1).
6 Conclusions
This work provided a qualitative and quantitative comparison of a diffusion–reaction model (DR model, Model A) and a ballistic transport–reaction model (BTR model, Model B) for ALD conformality simulation. The models were used to generate series of saturation profiles based on identical simulation parameters, with one simulation parameter varied in each series. The parameter values were chosen so that the Knudsen number was Kn ≫ 1, i.e. free molecular flow, as this is where the BTR model is valid. These saturation profiles were compared qualitatively, and quantitatively in terms of half-coverage penetration depth, slope at half-coverage penetration depth and adsorption front broadness.Qualitatively, the DR model and the BTR model resulted in similar trends of ALD film conformality in each series of parameter variation. For example, in both models, increasing the partial pressure of Reactant A caused the film to penetrate further into the structure, while an increase in the Reactant A molar mass decreased penetration depth. Increasing the temperature caused the half-coverage penetration depth to decrease. Furthermore, an increase in the sticking coefficient resulted in steeper adsorption fronts in both models. However, the BTR model produced an elevated section at the channel end, i.e. a trunk, which was not present in the DR model. This lack of a trunk in the DR model is explained by the fact that, in contrast to the BTR model, the DR model does not account for the end wall of the channel. The trunk observed in the BTR model is likely the result of Reactant A molecules accumulating at the channel end.
Quantitatively, the half-coverage penetration depth, as well as the slope at half-coverage penetration depth, were extracted from the saturation profiles and compared. The half-coverage penetration depth was systematically higher in the BTR model—on average, by ∼48% compared to the DR model. In contrast, the absolute value of the slope at half-coverage penetration depth was consistently higher in the DR model, reaching ∼1.6 to ∼4.2 times the respective value in the BTR model. These gentler slopes observed in the BTR model are connected to the broader adsorption fronts it produces. The adsorption fronts obtained from the BTR model were generally approximately twice as broad, compared to the DR model, if the sticking coefficient is constant. When the sticking coefficient was varied, the adsorption front broadness observed in the BTR model exceeded the DR model by a factor of up to ∼19.
In the BTR model, the number of discretization segments was found to significantly influence the shape and penetration depth of the saturation profile, depending on the aspect ratio of the channel. When the resolution (i.e. the number of discretization segments per channel aspect ratio unit) was increased, the penetration depth decreased. Beyond a resolution of one discretization segment per aspect ratio unit, the saturation profiles stabilized. This behaviour is explained by the geometry involved in the calculation of the view factors between discretization segments, which determine molecule transport inside the channel. The authors recommend to allocate at least two discretization segments per channel aspect ratio unit in future simulations with the BTR model.
This work showed that the choice of model has a significant impact on the quantitative characteristics obtained in conformality simulations. When fitting experimental data, the back-extracted kinetic parameters will be influenced by the selected model. For example, when the steepness of the adsorption front is used to determine the sticking coefficient of the process,7 the two models used in this work would lead to different results.
Author contributions
The manuscript was composed by J. J. Most of the thickness profiles obtained from the Ylilammi et al.12 diffusion–reaction model (Model A) were simulated by J. A. V. using a code based on the work by Verkama and Puurunen.31 The saturation profiles obtained from the Yanguas-Gil and Elam10 ballistic transport–reaction model (Model B) were simulated by J. J. using the implementation by Yanguas-Gil and Elam.32 The simulation parameters were selected by J. A. V., J. J. and R. L. P. The half-coverage penetration depth and slope at half-coverage penetration depth were determined by J. A. V. for results from Model A and J. J. for results from Model B. The adsorption front broadness was measured by J. J. for results from both Model A and Model B. The figures were created by J. J. An initial comparison of Model A and Model B with original simulations was made by J. Y. under supervision of R. L. P. The work was initiated and supervised by R. L. P. All authors discussed the results and contributed to the final manuscript.List of symbols
| AR | Aspect ratio (−) |
| b A | Number of metal atoms in one Reactant A molecule (−) |
| b film | Number of metal atoms in formula unit of film (−) |
| c | Sticking coefficient (−) |
| d A | Diameter of Reactant A molecule (m) |
| d I | Diameter of inert carrier gas molecule (m) |
| D | Apparent longitudal diffusion constant (m2 s−1) |
| D A | Gas-phase diffusion coefficient of Reactant A (m2 s−1) |
| D eff | Effective diffusion coefficient (m2 s−1) |
| D Kn | Knudsen diffusion coefficient (m2 s−1) |
| f ads | Adsorption rate (m−2 s−1) |
| f des | Desorption rate (m−2 s−1) |
| g | Net adsorption rate (m−2 s−1) |
| gpc sat | Saturation growth per cycle (m) |
| h | Hydraulic diameter of the channel (m) |
| H | Channel height (m) |
| i,j | Discretization segments (−) |
| Kn | Knudsen number (−) |
| L | Channel length (m) |
| m | Number of particle collisions (−) |
| M A | Molar mass of Reactant A (kg mol−1) |
| M film | Molar mass of the deposited film (kg mol−1) |
| M I | Molar mass of inert carrier gas (kg mol−1) |
| n | Surface normal (−) |
| N | Number of discretization segments (−) |
| N 0 | Avogadro's constant (mol−1) |
| p | Pressure (Pa) |
| p A | Partial pressure of Reactant A (Pa) |
| p A0 | Partial pressure of Reactant A at the channel entrance (Pa) |
| p I | Partial pressure of inert carrier gas (Pa) |
| p γ | Probability of particle existing in state γ (−) |
| P i | Probability of a particle adsorbing at segment i (−) |
| P d | Desorption probability (s−1) |
| P ij | Transmission probability matrix (−) |
| P i0 | Reemission probability matrix (−) |
| P iF i | Reaction probability matrix (−) |
| P δγ | Transition probability matrix (−) |
| q | Adsorption capacity at saturation (nm−2) |
| q ij | View factor from segment i to segment j (−) |
| q 0i | View factor from structure entrance to segment i (−) |
| Q | Collision rate at unit pressure (m−2 s−1 Pa−1) |
| R | Molar gas constant (J K−1 mol−1) |
| s 0 | Average surface site area (m2) |
| S i | Surface area of segment i (m2) |
| S 0 | Entry area (m2) |
| t | Time (s) |
| t c | Exposure duration (s) |
| t end | Exposure duration (s) |
| T | Temperature (K) |
| W | Channel width (m) |
| x | Distance from the channel entrance (m) |
| x s | Distance the gas front has travelled at time t (m) |
| x t | Limit of linear approximation (m) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif)
| Dimensionless distance (−) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) θ=0.5
θ=0.5
| Half-coverage penetration depth (−) |
| β i | Local reaction probability at segment i (−) |
| β 0 | Bare reaction probability (−) |
| γ,δ | Particle states |
| θ | Fractional surface coverage (−) |
| θ i | Fractional surface coverage at segment i (−) |
| ξ | Normalized distance (−) |
| ρ | Mass density of film (kg m−3) |
| ϕ i | Particle flux reaching segment i per unit surface area per unit time (m−2 s−1) |
| ϕ p | Number of discretization points per channel aspect ratio unit (−) |
| ϕ s | Number of discretization segments per channel aspect ratio unit (−) |
| ϕ 0 | Particle flux per entry area (m−2 s−1) |
| Ω | Normal angle (−) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was financially supported by the Academy of Finland (ALDI consortium, decision no. 331082 and COOLCAT consortium, decision no. 329978) and by Prof. Puurunen's starting grant at Aalto University. Emma Verkama implemented the Ylilammi et al.12 diffusion–reaction model as a MATLAB script.31 Aleksi Heikkinen initiated the use of the ballistic transport–reaction model by Yanguas-Gil and Elam10,32 as a summer student in Puurunen's research group. Angel Yanguas-Gil's help in getting the group started with Machball is gratefully acknowledged; likewise is Andreas Werbrouck's peer feedback on the submitted preprint. J. J. thanks Aada Illikainen for the discussions on mathematical notation conventions. This work was presented as a talk at the AVS 23rd International Conference on Atomic Layer Deposition (ALD 2023) in Bellevue, Washington, Jul 23–26, 2023. Earlier versions of this work have been presented as a talk at the ALD 2021 conference (online) by Yim et al.46 and as a poster at the ALD 2022 conference, Belgium, by Velasco et al.47 We acknowledge the computational resources provided by the Aalto Science-IT project.References
- J. R. van Ommen, A. Goulas and R. L. Puurunen, Atomic Layer Deposition, Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, Inc, 2021 Search PubMed.
- S. M. George, Chem. Rev., 2010, 110, 111–131 CrossRef CAS PubMed.
- C. S. Hwang and C. Y. Yoo, Atomic Layer Deposition for Semiconductors, Springer, New York, New York, NY, 2013 Search PubMed.
- N. Biyikli and A. Haider, Semicond. Sci. Technol., 2017, 32, 093002 CrossRef.
- O. Tiurin and Y. Ein-Eli, Adv. Mater. Interfaces, 2019, 6, 1901455 CrossRef CAS.
- B. J. O'Neill, D. H. Jackson, J. Lee, C. Canlas, P. C. Stair, C. L. Marshall, J. W. Elam, T. F. Kuech, J. A. Dumesic and G. W. Huber, ACS Catal., 2015, 5, 1804–1825 CrossRef.
- K. Arts, V. Vandalon, R. L. Puurunen, M. Utriainen, F. Gao, W. M. M. E. Kessels and H. C. M. Knoops, J. Vac. Sci. Technol., A, 2019, 37, 030908 CrossRef.
- J. Yim, O. M. E. Ylivaara, M. Ylilammi, V. Korpelainen, E. Haimi, E. Verkama, M. Utriainen and R. L. Puurunen, Phys. Chem. Chem. Phys., 2020, 22, 23107–23120 RSC.
- J. Yim, E. Verkama, J. A. Velasco, K. Arts and R. L. Puurunen, Phys. Chem. Chem. Phys., 2022, 24, 8645–8660 RSC.
- A. Yanguas-Gil and J. W. Elam, Theor. Chem. Acc., 2014, 133, 1465 Search PubMed.
- V. Cremers, R. L. Puurunen and J. Dendooven, Appl. Phys. Rev., 2019, 6, 021302 Search PubMed.
- M. Ylilammi, O. M. E. Ylivaara and R. L. Puurunen, J. Appl. Phys., 2018, 123, 205301 CrossRef.
- A. Yanguas-Gil and J. W. Elam, ECS Trans., 2011, 41, 169–174 CrossRef CAS.
- A. Yanguas-Gil and J. W. Elam, Chem. Vap. Deposition, 2012, 18, 46–52 CrossRef CAS.
- A. Yanguas-Gil and J. W. Elam, J. Vac. Sci. Technol., A, 2012, 30, 01A159 CrossRef.
- A. J. Gayle, Z. J. Berquist, Y. Chen, A. J. Hill, J. Y. Hoffman, A. R. Bielinski, A. Lenert and N. P. Dasgupta, Chem. Mater., 2021, 33, 5572–5583 CrossRef CAS.
- T. Keuter, N. H. Menzler, G. Mauer, F. Vondahlen, R. Vaßen and H. P. Buchkremer, J. Vac. Sci. Technol., A, 2015, 33, 01A104 CrossRef.
- N. Heikkinen, J. Lehtonen, L. Keskiväli, J. Yim, S. Shetty, Y. Ge, M. Reinikainen and M. Putkonen, Phys. Chem. Chem. Phys., 2022, 24, 20506–20516 RSC.
- D. Kane, R. Davis and R. Vanfleet, J. Vac. Sci. Technol., A, 2019, 37, 030907 CrossRef.
- W. Szmyt, C. Guerra-Nuñez, L. Huber, C. Dransfeld and I. Utke, Chem. Mater., 2022, 34, 203–216 CrossRef CAS.
- J. Dendooven, D. Deduytsche, J. Musschoot, R. L. Vanmeirhaeghe and C. Detavernier, J. Electrochem. Soc., 2009, 156, P63–P67 CrossRef CAS.
- R. A. Adomaitis, Chem. Vap. Deposition, 2011, 17, 353–365 CrossRef CAS.
- M. C. Schwille, J. Barth, T. Schössler, F. Schön, J. W. Bartha and M. Oettel, Modelling Simul. Mater. Sci. Eng., 2017, 25, 035008 CrossRef.
- J. W. Elam, D. Routkevitch, P. P. Mardilovich and S. M. George, Chem. Mater., 2003, 15, 3507–3517 CrossRef CAS.
- V. Cremers, F. Geenen, C. Detavernier and J. Dendooven, J. Vac. Sci. Technol., A, 2017, 35, 01B115 CrossRef.
- M. K. Gobbert, V. Prasad and T. S. Cale, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2002, 20, 1031–1043 CrossRef CAS.
- M. K. Gobbert, V. Prasad and T. S. Cale, Thin Solid Films, 2002, 410, 129–141 CrossRef CAS.
- A. Yanguas-Gil, Growth and Transport in Nanostructured Materials: Reactive Transport in PVD, CVD, and ALD, Springer Nature, Cham, 2017 Search PubMed.
- T. S. Cale, G. B. Raupp and T. H. Gandy, J. Appl. Phys., 1990, 68, 3645–3652 CrossRef CAS.
- M. K. Jain, T. S. Cale and T. H. Gandy, J. Electrochem. Soc., 1993, 140, 242–247 CrossRef CAS.
- E. Verkama and R. L. Puurunen, DReaM-ALD (v1.0.0), https://github.com/Aalto-Puurunen/dream-ald, DOI:10.5281/zenodo.7759195, 2023.
- A. Yanguas-Gil and J. W. Elam, Machball (0.2.0), https://github.com/aldsim/machball, 2020 Search PubMed.
- P. Poodt, A. Mameli, J. Schulpen, W. M. M. E. Kessels and F. Roozeboom, J. Vac. Sci. Technol., A, 2017, 35, 021502 CrossRef.
- C. Bosanquet, British TA Report BR-507, 1944 Search PubMed.
- W. G. Pollard and R. D. Present, Phys. Rev., 1948, 73, 762–774 CrossRef CAS.
- M. Knudsen, Ann. Phys., 1909, 333, 75–130 CrossRef.
- T. S. Cale and G. B. Raupp, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 1990, 8, 1242–1248 CrossRef.
- S. Brooks, A. Gelman, G. L. Jones and X.-L. Meng, Handbook of Markov Chain Monte Carlo, CRC Press LLC, Boca Raton, FL, 2011 Search PubMed.
- R. L. Puurunen, J. Appl. Phys., 2005, 97, 121301 CrossRef.
- Knovel Critical Tables, 2nd edn, https://app.knovel.com/hotlink/toc/id:kpKCTE000X/knovel-critical-tables/knovel-critical-tables (accessed August 2023).
- R. L. Puurunen, Appl. Surf. Sci., 2005, 245, 6–10 CrossRef CAS.
- F. Gao, S. Arpiainen and R. L. Puurunen, J. Vac. Sci. Technol., A, 2015, 33, 010601 CrossRef.
- PillarHall, http://pillarhall.com/ (accessed 20.4.2023).
- R. Feres and G. Yablonsky, Chem. Eng. Sci., 2004, 59, 1541–1556 CrossRef CAS.
- H. C. M. Knoops, E. Langereis, M. C. M. van de Sanden and W. M. M. Kessels, J. Electrochem. Soc., 2010, 157, G241–G249 CrossRef CAS.
- J. Yim, E. Verkama and R. L. Puurunen, oral presentation at AVS 21st International Conference on Atomic Layer Deposition, Online, June 27-30, 2021.
- J. A. Velasco, J. Järvilehto, J. Yim, C. Gonsalves, E. Verkama and R. L. Puurunen, poster at AVS 22nd International Conference on Atomic Layer Deposition, Ghent, Belgium, June 26-29, 2022.
Footnote |
| † Electronic supplementary information (ESI) available: Extended information related to discussion section. See DOI: https://doi.org/10.1039/d3cp01829f |
| This journal is © the Owner Societies 2023 |

