 Open Access Article
Open Access ArticleEffects of vacancies on the thermal conductivity of Si nanowires
Marc
Túnica
 ab,
Paolo Sebastiano
Floris
ab,
Paolo Sebastiano
Floris
 a,
Pol
Torres
a,
Pol
Torres
 ac and
Riccardo
Rurali
ac and
Riccardo
Rurali
 *a
*a
aInstitut de Ciència de Materials de Barcelona (ICMAB-CSIC), Campus de Bellaterra, 08193 Bellaterra, Barcelona, Spain. E-mail: rrurali@icmab.es
bLaboratoire de Physique des Solides, Université Paris-Saclay, CNRS, Orsay 91405, France
cEurecat, Centre Tecnològic de Catalunya, Unit of Applied Artificial Intelligence, Av. Universitat Autònoma, 23, 08290 Cerdanyola del Vallès, Spain
First published on 10th July 2023
Abstract
Point defects can be used to tailor the properties of semiconductors, but can also have undesired effects on electronic and thermal transport, particularly in ultrascaled nanostructures, such as nanowires. Here we use all-atom molecular dynamics to study the effect that different concentrations and spatial distributions of vacancies have on the thermal conductivity of Si nanowires, overcoming the limitations of previous studies. Although vacancies are not as effective as the nanovoids found in e.g. porous Si, they can still reduce the thermal conductivity in ultrathin Si nanowires by more than a factor of two, when found in concentrations smaller than 1%. We also present arguments against the so-called self-purification mechanism, which is sometimes suggested to take place and proposes that vacancies have no influence on transport phenomena in nanowires.
1 Introduction
Semiconductors are privileged materials for electronic applications, because their resistivities can be varied by design with great control. The most efficient way to tune the carrier density is incorporating substitutional impurities, i.e. dopants, in the lattice.1 Dopants are added on purpose to provide free carriers, but at the same time, especially in reduced dimensionality systems such as nanowires (NWs),2,3 they act as scattering centers,4–8 decreasing the mobility and limiting the performance of devices. Intrinsic defects, such as vacancies and self-interstitials, are lattice defects that do not need external impurities to be involved.9,10 Contrary to dopants, their presence is usually detrimental to the performances of electron devices (though important exceptions exist, see e.g. ref. 11 and 12): they can introduce deep levels in the bandgap that act as traps and they scatter carriers. The presence of vacancies, in particular, is often unavoidable. Vacancies can form as the result of an imperfect synthesis or when the annealing stage that follows ion implantation, if this technique is used to dope the material, cannot fully recover the perfect lattice structure. While there is extensive literature on the formation and effect of vacancies in bulk materials,9 they have been seldom studied in nanoscale systems. The general argument is that vacancies, similarly to other point defects,4,13–17 prefer to sit next to the surface, where the lattice strain is more easily released. However, at variance with extrinsic impurities, when vacancies reach the surface they “annihilate”. This would lead to a “self-purification” effect that makes the presence of vacancies negligible or, at most, of little importance.This simplified picture, however, has been questioned by the experimental results of Murphy et al.,18 who introduced vacancies in Si NWs by Ga+ ion-irradiation. The vacancies created were stable and their effect on phonon transport could be measured. In particular, they demonstrated that the effect of tensile strain on the thermal conductivity was greatly amplified by the presence of these lattice defects. Absence of self-purification was also reported in a theoretical study of Ge nanocrystals, where vacancies were predicted to be stable and to have a bulk-like behavior, without interacting strongly with the surface.19
Despite the interest that thermal transport in Si NWs has attracted,20–22 the role of vacancies has been overlooked. The effect of vacancies on the thermal conductivity of bulk Si was previously studied theoretically by different groups.23,24 The results are similar and feature a non-linear reduction of the thermal conductivity for an increasing concentration of vacancies. Interestingly, Wang et al.23 considered both vacancies and nanovoids – like those of porous Si samples25,26 – and found that the latter are much more effective in reducing the thermal conductivity. The effect of vacancies on the thermal conductivity of Si NWs was studied by Gholipour Shahraki and Zeinali using reverse nonequilibrium molecular dynamics,27 but their computational cell only allowed for a separation of 11 nm between the hot and the cold reservoir, and thus their results are likely to be severely affected by boundary scattering. Additionally, they obtained quite different results using the Tersoff28 and the Stillinger–Weber29 interatomic potential, finding a non-linear and a linear dependence of the thermal conductivity on the vacancy concentration, respectively. As none of these potentials was specifically parameterized to account for the vibrational or heat transport properties of Si, it is difficult to tell which of these results is more reliable (though the linear dependence seems to contradict the results obtained with analogous calculations in bulk Si23,24). Similar calculations were carried out by Meem et al.30 The separation between thermostats is in this case even shorter, amounting to only ∼7 nm. Furthermore, they considered a very unusual and unrealistic distribution of vacancies, obtained by removing Si atoms along a line parallel to the wire axis.
In this paper we try to overcome the limitations of these studies by using the phonon optimized potential (POP) of Rohskopf and coworkers,31 which was specifically reparameterized to carefully reproduce the vibrational properties of Si. Importantly, this potential was also fitted against higher-order interatomic force constants (IFCs), those that determine phonon lifetimes, and thermal conductivity is in very good agreement with density-functional theory (DFT) results.31 Also, we use computational cells of at least ∼90 nm and study the convergence of the thermal conductivity with the cell size, spanning lengths as large as 180 nm. As a preliminary step, we perform DFT calculations to study the dependence of the vacancy formation energy as a function of the radial coordinate, in order to assess the feasibility of surface segregation that could lead to the self-purification mechanism discussed above.
2 Computational methods
For the density-functional theory (DFT) calculations we use the Siesta code,32,33 an optimized double-ζ polarized basis set34 and norm-conserving pseudopotentials.35 Monovacancies are studied in 1 × 1 × 3 supercells of a NW unit cell, sampling the Brillouin zone with the Γ point only, given the large size of the lattice vector along the periodic direction, i.e. ∼3 nm. We carried out structural relaxations with the conjugate gradient method until all the forces were lower than 0.01 eV Å−1. The molecular dynamics (MD) calculations are performed with the LAMMPS package.36 Interatomic forces are accounted for by means of the Phonon Optimized Potential (POP) of Rohskopf and coworkers,31 who reparameterized a bond-order potential of the Tersoff type28 in order to improve the description of the vibrational properties. This interatomic potential yields both phonon dispersion and thermal conductivities that are in excellent agreement with those obtained with DFT.31 Si NWs are cut from the bulk, taking the axis to be along the 〈111〉 crystal direction. We considered diameters of 2.5 nm and 5 nm for the Siesta and LAMMPS calculations. In the case of DFT, the surface dangling bonds are passivated with H atoms to prevent reconstructions and electronic surface states.37The thermal conductivity is computed by means of approach-to-equilibrium molecular dynamics (AEMD). This method consists in designing given initial nonequilibrium temperature conditions and then studying how the system reaches equilibrium once all constraints are released. In this work, we first carry out a thermalization step where we define two regions of equal size, which are equilibrated at two different temperatures, T1 and T2. During the next step the two regions are allowed to gradually return to the equilibrium temperature, (T1 + T2)/2. At this point, it is possible to calculate the lattice thermal diffusivity by fitting the temperature difference ΔT(t) = 〈T1〉 − 〈T2〉 (where ΔT(t) denotes the time dependence of this quantity and the brackets denote an ensemble average) with a series of exponential functions that represent the solution to the Fourier equation of heat transport.
In this work we have set T1 = 400 K and T2 = 200 K; once a step-like temperature profile is established, we start the approach to the equilibrium step in the NVE ensemble. The thermal equilibrium corresponds to the temperature Teq = 300 K (assuming that the system is spatially uniform with respect to the direction of heat transfer, which is the case in this work) and thus the thermal conductivity that we calculate is κ(Teq). We consider the z-axis as the direction of heat transfer, and therefore the temperature difference between the two regions can be expressed as
 | (1) |
 , Lz is the length of the nanowire,
, Lz is the length of the nanowire, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) z is thermal diffusivity and
z is thermal diffusivity and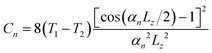 | (2) |
The lattice thermal conductivity is then obtained from
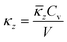 | (3) |
![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) , defined as the ratio between the simulation temperature and TD. The limit for the summation in eqn (1) is set to n = 20, which is more than sufficient to get converged thermal conductivities.38
, defined as the ratio between the simulation temperature and TD. The limit for the summation in eqn (1) is set to n = 20, which is more than sufficient to get converged thermal conductivities.38
3 Results and discussion
In order to assess the tendency to segregate towards the surface, we have mapped the formation energy39 of monovacancies as a function of their radial coordinate. The nearsightedness of classical interatomic potentials, like the one here used for our MD computational experiments, could in principle lead to an underestimation of surface segregation. Therefore, to avoid these possible shortcomings, we have carried out these calculations within a fully quantum mechanical framework, using DFT. We followed two inequivalent paths going from the center of the NW to the surface. As can be seen in Fig. 1, we find that the formation energy is essentially unchanged with respect to the reference value, when the vacancy is at the center of the NW, for r < 7 Å. Then it moderately decreases (r∼ 7.5 Å) and only when it reaches a surface or subsurface location, we obtained a more pronounced variation. These values suggest that a vacancy in the innermost part of the NW is rather stable and does not seem likely to diffuse toward the surface. Additionally, to jump between the neighboring lattice sites, whose formation energies are tracked in Fig. 1, vacancies must also overcome a diffusion barrier that is expected to be sizeable. A quantitative characterization of the diffusivity of vacancies in Si NWs would require computing the potential energy surface (PES) and then using techniques such as the nudged elastic band (NEB) method to estimate the diffusion barrier, goals that are beyond the scope of this work. Nevertheless, our results qualitatively corroborate the experimental observations of Murphy et al.,18 who observed that vacancies in Si NWs are stable and have a measurable effect on the transport properties. It should also be noted that, due to the comparatively larger computational cost of DFT calculations, this study was performed in an ultrathin NW of only 2.5 nm of diameter. Although Si NWs of similar thickness have been reported experimentally,40–42 larger diameters of the order of several tens of nm are much more common. Therefore, the segregation effects that we obtain have to be considered an overestimation of the expected behavior in thicker Si NWs, because of their lower surface-to-bulk ratio.After assessing the relative stability of vacancies at different radial coordinates, we carried out a series of MD computational experiments to study to what extent they can alter the thermal conductivity in Si NWs. We first study a radially uniform distribution of vacancies. Due to the inherently random nature of defect formation, for each target concentration we generate four independent distributions and averaged the corresponding thermal conductivities. Notice that, for each of these samples with the same nominal concentration, the actual number of vacancies in general differ a little from one sample to the other, because of the probabilistic rule assumed to create the defects. As these variations are smaller, we plotted the data as a function of the average concentration.
The thermal conductivity obtained derives from different contributions: phonon–phonon collisions, boundary scattering due to radial confinement and boundary scattering due to the finite length of the NW. While the first two are physical contributions that need to be accounted for, the last is normally considered as a computational artifact, because realistic NWs are much longer that the samples used in atomistic simulations. A common way to get rid of this last term is based on Matthiessen's rule, which assumes that the different scattering mechanisms act independently and that scattering rates are additive. It consists in repeating the calculation of the thermal conductivity in increasingly long simulation cells, plotting κ−1(L−1z) and taking the limit for L−1z → 0, i.e. Lz → ∞. The results of these calculations are shown in Fig. 2(a), where we report the averaged thermal conductivities, κ(Lz), for four different values of Lz and five different concentrations of vacancies, c, plus the pristine Si NW for comparison. At all length scales the larger values of c result in higher thermal resistivities (i.e., κ−1), an indication that vacancies act as scattering centers of propagating heat-carrying phonons. From the same set of simulations we can plot the thermal conductivity accumulation function, defined as the ratio κ(Lz)/κ∞, κ∞ being the extrapolated value of the thermal conductivity for an infinitely long NW of the same diameter. The results, displayed in Fig. 2(b), show that as the vacancy concentration increases, the relative contribution of phonons with long mean free path (mpf) also decreases. The extrapolated values of κ∞ as a function of c are shown in Fig. 2(c). In this concentration range the decrease of the thermal conductivity can be fitted with an exponential decay of the type κprist∞e−c/α, where κprist∞ is the thermal conductivity of a pristine Si NW, extrapolated for L → ∞. As it can be seen, modest concentrations of vacancies yield a considerable reduction of the thermal conductivity, e.g. for c = 0.5%, κ is almost halved. Larger defect concentrations were not considered because of their little significance in experiments and also because the system becomes numerically more difficult to handle, with a non negligible probability for clusters of atoms to leave the surface of the NW, resulting in severe instabilities. Notice that our results are valid for small concentrations of vacancies. At larger concentrations, the aggregation of vacancies leading to the formation of divacancies or small cluster – which has been shown to be energetically favoured43 – cannot be neglected. This limit, where nanovoids form, has been previously addressed in detail by studies focused on porous Si NWs.25,44
When we have discussed the segregation energy diagram of Fig. 1 we concluded that a scenario where vacancies diffuse to the surface and then annihilate, leaving behind at most some kind of surface roughness, does not appear to be very likely on the basis of total energy considerations. Therefore, the absence of vacancies in Si NWs cannot be taken for granted. However, in the immediacy of the surface there exists a non-negligible segregation tendency (see the values of Eform for r > 7.5 Å in Fig. 1) and, although they must overcome some diffusion barriers, vacancies are indeed expected to move outward. If vacancies in the innermost part of the NW are not mobile and only those very close to the surface can segregate (and then annihilate), one can figure a situation where an outer ring, close to the surface, is fully depleted of vacancies, which are only present in the inside of the NW.
To address this scenario, we computed the thermal conductivity of different nonuniform distributions of vacancies. We considered a fixed number of vacancies, those that if uniformly distributed would result in a concentration of 0.5%, and constructed the following distributions: (a) all vacancies lie inside a cylinder of radius 5, 10, and 15 Å; (b) all vacancies lie within a ring of thickness 5, 10, 15, and 20 Å, centered at r = 12.5 Å; (c) vacancies follow a Gaussian distribution with maximum at the NW center and full width half maximum (FWHM) equal to 2.35, 25.90, and 40.03 Å. Additionally, despite its scarce experimental relevance, we also considered the case where all vacancies lie outside a cylinder of radius 5, 10, and 15 Å. The calculated thermal conductivity, plotted as a function of the cross-section of the defective region, S, is shown in Fig. 3. As it can be seen, the hard-wall confinement within a given radius or the Gaussian distribution behave qualitatively in the same way: as S increases, κ decreases because the concentration in the defective region decreases as well. Similar results are obtained with the rather artificial distribution where vacancies are confined within an annulus with average radius, r = 12.5 Å. On the other hand, when vacancies are forced to lie next to the surface, we obtain larger values of κ, indicating that vacancies are much more effective in scattering phonons when they are concentrated in the innermost part of the NW or, at least, sufficiently far from the surface, as suggested by the results of the annulus distribution that exhibit a qualitatively similar behavior. In the case of surface vacancies, we found that the dependence of κ on S can also be predicted by computing the total thermal resistance as the parallel of the resistance of a pristine, Rpure, and a defective NW, Rd, i.e. R−1tot = R−1pure + R−1d. The thermal conductivity obtained in this way is displayed as a continuous green line in Fig. 3.
These results agree with previous reports based on nonequilibrium Green's functions (NEGF) where the scattering of individual vacancies was addressed.45 Vacancies in the innermost part of the NW were found to be more effective in reducing the conductance, despite the lower degree of structural distortion associated, than vacancies next to the NW surface. Similar conclusions were reached by the one-dimensional distribution of vacancies considered in ref. 30.
Our preliminary DFT calculations indicated that surface segregation of vacancies in Si NWs does not seem likely and thus self-purification should not be a mechanism at play. Corroborating these conclusions in a dynamical calculation, and seeing if they hold at finite temperature as well, is not feasible, because diffusion typically takes place over timescales that are much longer than those that can be spanned with MD. Also, we found that diffusion barriers are overestimated, if compared to DFT, by the interatomic potential here employed. Yet, we have verified that vacancies do not migrate during one of our typical runs to calculate the thermal conductivity to ensure the robustness of our computed values. To this end we have monitored the position of the vacancies in the case of a uniform distribution in a NW 90 nm long, in a 1.5 ns NVT MD run at 300 K. This, for the reasons discussed above, has a significance that is more numerical (i.e., the samples are stable and the vacancy distribution does change significantly during the simulation) than physical. In Fig. 4 we track the position of the Si atoms with less than four neighbors, which indirectly indicate the presence of a nearby vacancy. As can be seen in Fig. 4, the average distance of the under-coordinated Si atoms from the NW center, |r|, remains essentially unaltered throughout the dynamics. Despite some fluctuations, particularly in the beginning where possibly the system was not yet well equilibrated, there is no trend indicating any kind of migration of the vacancies toward the surface. These results indicate that in our computational experiments, the vacancy distributions are rather stable and are not altered significantly, let alone surface segregation, which is not observed.
4 Conclusions
In summary, we have studied the effect of vacancies on the thermal conductivity of Si NWs. We have shown that moderate concentrations of vacancies, e.g. c ∼ 0.75%, are very effective in scattering phonons and thus reducing the thermal conductivity. When looking at nonuniform radial distributions, we found that vacancies that are mostly located in the innermost part of the NW are much more effective in reducing the thermal conductivity. These calculations are based on a newly developed bond-order potential that has been specifically developed to account for the vibrational properties of Si and that predicts its bulk thermal conductivity with an accuracy comparable to DFT calculations. Finally, we presented qualitative arguments that suggest that, in agreement with experimental results, vacancies in ultrathin NWs are not expected to diffuse to the surface. Consequently, the mechanism of self-purification, wherein vacancies reach the surface and annihilate, is unlikely to occur, at least under close-to-equilibrium conditions. These findings underscore the need to assess the impact of the presence of monovacancies on electronic and thermal transport in nanostructured Si.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the European Commission through the Marie Skłodowska-Curie projects HORATES (GA-955837), by MCIN/AEI/10.13039/501100011033 under grant PID2020-119777GB-I00, and the Severo Ochoa Centres of Excellence Program under grant CEX2019-000917-S, and by the Generalitat de Catalunya under grant no. 2021 SGR 01519. Calculations were performed at the Centro de Supercomputación de Galicia (CESGA) within action FI-2022-1-0018 of the Red Española de Supercomputación (RES). We thank Antonio Cappai and Miguel Rubí for useful discussions.References
- R. S. Muller and T. I. Kamins, Device Electronics for Integrated Circuirs, John Wiley & Sons, Hoboken, NJ, 1986 Search PubMed.
- W. Lu and C. M. Lieber, J. Phys. D: Appl. Phys., 2006, 39, R387–R406 CrossRef CAS.
- R. Rurali, Rev. Mod. Phys., 2010, 82, 427–449 CrossRef CAS.
- M. V. Fernández-Serra, C. Adessi and X. Blase, Phys. Rev. Lett., 2006, 96, 166805 CrossRef PubMed.
- M.-V. Fernández-Serra, C. Adessi and X. Blase, Nano Lett., 2006, 6, 2674–2678 CrossRef PubMed.
- T. Markussen, R. Rurali, M. Brandbyge and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245313 CrossRef.
- T. Markussen, R. Rurali, A.-P. Jauho and M. Brandbyge, Phys. Rev. Lett., 2007, 99, 076803 CrossRef PubMed.
- R. Rurali, T. Markussen, J. Suñe, M. Brandbyge and A.-P. Jauho, Nano Lett., 2008, 8, 2825–2828 CrossRef CAS PubMed.
- P. M. Fahey, P. B. Griffin and J. D. Plummer, Rev. Mod. Phys., 1989, 61, 289–384 CrossRef CAS.
- H. J. Queisser and E. E. Haller, Science, 1998, 281, 945–950 CrossRef CAS PubMed.
- J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. V. de Walle and D. D. Awschalom, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 8513–8518 CrossRef CAS PubMed.
- M. Ai, J.-W. Zhang, Y.-W. Wu, L. Pan, C. Shi and J.-J. Zou, Chem. – Asian J., 2020, 15, 3599–3619 CrossRef CAS PubMed.
- H. Peelaers, B. Partoens and F. Peeters, Nano Lett., 2006, 6, 2781–2784 CrossRef CAS PubMed.
- N. Fukata, S. Ishida, S. Yokono, R. Takiguchi, J. Chen, T. Sekiguchi and K. Murakami, Nano Lett., 2011, 11, 651–656 CrossRef CAS PubMed.
- M. Amato, M. Palummo and S. Ossicini, Phys. Status Solidi B, 2010, 247, 2096 CrossRef CAS.
- M. Galicka, R. Buczko and P. Kacman, J. Phys. Chem. C, 2013, 117, 20361–20370 CrossRef CAS.
- M. Amato, S. Ossicini, E. Canadell and R. Rurali, Nano Lett., 2019, 19, 866–876 CrossRef CAS PubMed.
- K. F. Murphy, B. Piccione, M. B. Zanjani, J. R. Lukes and D. S. Gianola, Nano Lett., 2014, 14, 3785–3792 CrossRef CAS PubMed.
- K. Bayus, O. Paz and S. P. Beckman, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155409 CrossRef.
- S. G. Volz and G. Chen, Appl. Phys. Lett., 1999, 75, 2056–2058 CrossRef CAS.
- D. Li, Y. Wu, P. Kim, L. Shi, P. Yang and A. Majumdar, Appl. Phys. Lett., 2003, 83, 2934–2936 CrossRef CAS.
- M. Hu, K. P. Giapis, J. V. Goicochea, X. Zhang and D. Poulikakos, Nano Lett., 2011, 11, 618–623 CrossRef CAS PubMed.
- T. Wang, G. K. H. Madsen and A. Hartmaier, Modell. Simul. Mater. Sci. Eng., 2014, 22, 035011 CrossRef CAS.
- Y. Lee, S. Lee and G. S. Hwang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 125202 CrossRef.
- X. Cartoixà, R. Dettori, C. Melis, L. Colombo and R. Rurali, Appl. Phys. Lett., 2016, 109, 013107 CrossRef.
- S. A. Hosseini, A. Davies, I. Dickey, N. Neophytou, P. A. Greaney and L. de Sousa Oliveira, Mater. Today Phys., 2022, 27, 100719 CrossRef CAS.
- M. Gholipour Shahraki and Z. Zeinali, J. Phys. Chem. Solids, 2015, 85, 233–238 CrossRef CAS.
- J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566–5568 CrossRef PubMed.
- F. H. Stillinger and T. A. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 5262–5271 CrossRef CAS PubMed.
- A. U. H. Meem, O. Chowdhury and A. M. Morshed, Micro Nano Lett., 2018, 13, 1146–1150 CrossRef CAS.
- A. Rohskopf, H. R. Seyf, K. Gordiz, T. Tadano and A. Henry, npj Comput. Mater., 2017, 3, 27 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- E. Artacho, E. Anglada, O. Diéguez, J. D. Gale, A. García, J. Junquera, R. M. Martin, P. Ordejón, J. M. Pruneda, D. Sánchez-Portal and J. M. Soler, J. Phys.: Condens. Matter, 2008, 20, 064208 CrossRef PubMed.
- E. Anglada, J. M. Soler, J. Junquera and E. Artacho, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 205101 CrossRef.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- R. Rurali, A. Poissier and N. Lorente, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 165324 CrossRef.
- C. Melis, R. Dettori, S. Vandermeulen and L. Colombo, Eur. Phys. J. B, 2014, 87, 96 CrossRef.
- R. Rurali and X. Cartoixà, Nano Lett., 2009, 9, 975–979 CrossRef CAS PubMed.
- A. M. Morales and C. M. Lieber, Science, 1998, 279, 208–211 CrossRef CAS PubMed.
- D. D. D. Ma, C. S. Lee, F. C. K. Au, S. Y. Tong and S. T. Lee, Science, 2003, 299, 1874–1877 CrossRef CAS PubMed.
- T. W. Nam and J. C. Grossman, Nano Lett., 2023, 23, 2347–2353 CrossRef CAS PubMed.
- A. Bongiorno and L. Colombo, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 8767–8769 CrossRef CAS.
- P. Ferrando-Villalba, L. D’Ortenzi, G. G. Dalkiranis, E. Cara, A. F. Lopeandia, L. Abad, R. Rurali, X. Cartoixà, N. De Leo, Z. Saghi, M. Jacob, N. Gambacorti, L. Boarino and J. Rodríguez-Viejo, Sci. Rep., 2018, 8, 12796 CrossRef CAS PubMed.
- K. Yamamoto, H. Ishii, N. Kobayashi and K. Hirose, Appl. Phys. Express, 2011, 4, 085001 CrossRef.
| This journal is © the Owner Societies 2023 |




