 Open Access Article
Open Access ArticleHow does thickness affect magnetic coupling in Ti-based MXenes†
Néstor
García-Romeral
 ,
Ángel
Morales-García
,
Ángel
Morales-García
 ,
Francesc
Viñes
,
Francesc
Viñes
 ,
Ibério de P. R.
Moreira
,
Ibério de P. R.
Moreira
 and
Francesc
Illas
and
Francesc
Illas
 *
*
Departament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, c/Martí i Franquès 1-11, 08028 Barcelona, Spain. E-mail: francesc.illas@ub.edu
First published on 7th June 2023
Abstract
The magnetic nature of Ti2C, Ti3C2, and Ti4C3 MXenes is determined from periodic calculations within density functional theory and using the generalized gradient approximation based PBE functional, the PBE0 and HSE06 hybrids, and the on-site Hubbard corrected PBE+U one, in all cases using a very tight numerical setup. The results show that all functionals consistently predict a magnetic ground state for all MXenes, with spin densities mainly located at the Ti surface atoms. The analysis of solutions corresponding to different spin orderings consistently show that all functionals predict an antiferromagnetic conducting ground state with the two ferromagnetic outer (surface) Ti layers being antiferromagnetically coupled. A physically meaningful spin model is proposed, consistent with the analysis of the chemical bond, with closed shell, diamagnetic, Ti2+ like ions in inner layers and surface paramagnetic Ti+ like centers with one unpaired electron per magnetic center. From a Heisenberg spin model, the relevant isotropic magnetic coupling constants are extracted from an appropriate mapping of total energy differences per formula unit to the expected energy values of the spin Hamiltonian. While the numerical values of the magnetic coupling constants largely depend on the used functional, the nearest neighbor intralayer coupling is found to be always ferromagnetic, and constitutes the dominant interaction, although two other non-negligible interlayer antiferromagnetic terms are involved, implying that the spin description cannot be reduced to NN interaction only. The influence of the MXene thickness is noticeable for the dominant ferromagnetic interaction, increasing its value with the MXene width. However, the interlayer interactions are essentially due to the covalency effects observed in all metallic solutions which, as expected, decay with distance. Within the PBE+U approach, a U value of 5 eV is found to closely simulate the results from hybrid functionals for Ti2C and less accurately for Ti3C2 and Ti4C3.
1. Introduction
Since the discovery of graphene back in 2004,1 the number of two-dimensional (2D) materials has rapidly grown with a parallel increase in possible applications.2 Among these, a new family of 2D transition metal carbides, nitrides, and carbonitrides, generally known as MXenes,3,4 has attracted considerable attention because of their broad range of applications.5–7 MXenes are represented by the Mn+1XnTx general formula where M is an early transition metal, X is either C or N, and Tx stands for chemical groups attached to MXenes surfaces due to synthetic conditions, usually referred to as functionalization, and with 1 ≤ n ≤ 3 determining the MXene thickness. At variance to van der Waals layered systems, MXenes are genuine 2D materials that are generally obtained by chemically removing the A element from MAX phases, a family of layered materials where M and X are as defined above and A is a p-group element.3–5 The chemical etching of the MAX precursor leads to MXenes with the surface covered by different adsorbates, most often OH, H, O, or F, as aforementioned, denoted as Tx.3,8 Nonetheless, new experimental techniques have been described to efficiently remove the Tx groups,5,6 resulting in pristine MXene surfaces with the general formula Mn+1Xn. Due to their wide variety of compositions, MXenes exhibit a broad range of properties and applications which can be tuned by choosing appropriate composition, thickness, and/or functionalization. Many applications of MXenes are related to different types of devices such as electrochemical capacitors and their use as alkali-ion batteries,9–11 lubrication, bio- and gas-sensors, and also increasingly in chemistry and catalysis.12–14There is general consensus that functionalized MXenes exhibit a closed-shell type electronic structure and, hence, do not display magnetic properties.15 However, a different situation emerges when considering bare MXenes.16 For instance, in agreement with previous works,17,18 but using a very tight setup that leads to numerically converged results up to 1 meV with three different density functionals and an appropriate spin Heisenberg Hamiltonian, we have recently reported that Ti2C has a magnetic ground state involving antiferromagnetic coupling of the two ferromagnetic metallic layers.19 In this study, the low-lying electronic states of Ti2C were also mapped into a Heisenberg spin Hamiltonian with the three relevant isotropic magnetic coupling constants extracted from appropriate total energy per formula unit differences for the corresponding magnetic solutions to those involving the expected value of the spin Hamiltonian for the corresponding solutions. Now, the fact that MXenes are layered materials raises the question of what the influence of the number of layers on the magnetic properties is. In the case of the Ti3C2 MXene, the first synthesized member of the family,3 there are indications that it also displays a magnetic ground state.20,21 In addition, a recent study has also experimentally and theoretically studied the Ti3C2 ground state and found the co-existence of two different magnetic phases, ferromagnetic (FM) and antiferromagnetic (AFM), at room temperature.22 Even if some authors considered the existence of different possible spin solutions,23,24 a detailed study of the nature of bonding in the system and all possible magnetic states and spin orders using accurate density functionals, and appropriate mapping of the electronic states energies per formula unit into a physically meaningful Heisenberg spin Hamiltonian is still lacking and urgently needed. A similar situation is found for Ti4C3,15 for which the information is even more limited. In any case, all mentioned studies consistently report that only the Ti surface atoms have a significant net atomic spin density, which, in the case of Ti3C2 and Ti4C3, implies that Ti atoms in the inner layers are of different nature and have residual spin density only (i.e., are diamagnetic) which, again, poses the question of the influence of the MXene thickness on the magnetic interactions and the corresponding isotropic magnetic couplings.
The present work is aimed at providing an accurate and systematic description of the chemical bonding and magnetic coupling in Ti2C, Ti3C2, and Ti4C3 MXenes using the same quantum mechanically grounded electronic structure methods. An additional goal is to provide mapping of the different magnetic solutions into a Heisenberg spin Hamiltonian compatible with the quantum mechanical description of the electronic structure. This will ultimately establish the influence of the number of atomic layers on the magnetic properties and chemical bonds of these paradigmatic MXenes.
2. MXene models and computational details
The electronic structure of this family of MXenes has been studied in the framework of density functional theory (DFT) using three different exchange–correlation functionals of increasing complexity. These include the broadly used Generalized Gradient Approximation (GGA) based Perdew–Burke–Ernzerhof (PBE)25 functional, the hybrid PBE026,27 including a 25% of non-local Fock exchange, and the range separated HSE0628 hybrid functional including also a 25% of Fock exchange and a range separation for the non-local exchange with a screening parameter, ω, of 0.2 Å−1. The choice of these functionals, all derived from the PBE one, allows one to separately investigate the physics included in each model. This is necessary since PBE tends to excessively delocalize the electron density leading to incorrect description of many magnetic systems and to largely underestimate the band gap of semiconducting and insulating materials.29 Because of its popularity in rather accurately describing materials for which GGA functionals fail, we also explore the PBE+U approach30 that includes an on-site Hubbard-like two-electron repulsion term that penalizes doubly occupancy of the orbitals to which U acts upon, most often the first series of transition metal 3d or rare earth 4f levels. However, the choice of the U parameter is a delicate issue since it is not clear that the U parameters broadly used in the literature, mainly for oxides,31–33 are appropriate to describe the electronic structure of MXenes with a variety of occupations of d orbitals. To provide reliable information, we investigate in detail how the relative stability of the ground state and the magnetic interactions depends on the U parameter, and study whether a given U value mimics the results obtained by means of the more accurate PBE0 or HSE06 hybrid functionals.We also stress the fact that the whole study relies on a non-relativistic approach to describe the electronic structure of the systems and on using a single spin polarized Slater determinant description of the electron density to solve the corresponding Kohn–Sham equations. Hence, in order to describe the magnetic interactions, we rely on the mapping between the energy of different spin unrestricted electronic solutions and the Heisenberg spin Hamiltonian including two-body isotropic interactions between selected nearby paramagnetic centers located on the outer Ti+ layers as discussed below.
For each of the considered MXenes, a series of periodic DFT calculations are carried out to investigate the nature of the non-spin-polarized and several spin-polarized solutions. All calculations are performed with the Vienna ab initio simulation package (VASP)34 and a strict numerical setup, described below, to provide a numerically converged solution within 1 meV for the total energy. To study the different possible spin solutions, including the non-spin-polarized one (or diamagnetic), a first set of calculations with the PBE functional is carried out to obtain the minimum energy structure and the corresponding optimized parameters for the FM and non-magnetic (NM) solutions. For these calculations, a p(1 × 1) unit cell is used for each of the three scrutinized MXenes, see Fig. 1. The unit cell includes a 15 Å vacuum width in the z direction (perpendicular to the surface) to appropriately represent these 2D materials as well as to avoid any interaction between the artificially periodically repeated replicas. In all cases, a 700 eV kinetic energy cut-off is used for the Plane Wave (PW) basis set used to expand the electron density with the Kohn–Sham formalism, and the Projector-Augmented Wave (PAW) method is selected to account for the interaction between the valence and the core electron densities.35 A Monkhorst–Pack grid of 13 × 13 × 1 special k-points is used to carry out the numerical integrations in the reciprocal space. To guarantee the convergence of the self-consistent field procedure, all calculations were carried out using the Methfessel–Paxton smearing method with a width of 0.01 eV for partial occupancies. Upon convergence, the smearing was removed, and all total energy values were then extrapolated to 0 K. The geometry optimizations are considered converged when the forces acting on the nuclei are all below 0.01 eV Å−1 and a 10−6 eV threshold was chosen as the electronic convergence criterion.
In the second set of calculations, the total energy of the p(2 × 1) supercells was evaluated at the PBE geometry for the different corresponding spin solutions, in principle, to different ordering of spins localized in metal atoms. The energy difference between the different magnetic solutions is very small and there is evidence that the differences in the optimized structure for the different solutions are negligible.19 This may not be the case for the NM solution lying higher in energy. Therefore, for each MXene, the total energy of each different solution was computed with the PBE, PBE0, and HSE06 functionals at the PBE non-spin-polarized and spin-polarized optimized structures. In order to study the chemical bonds, a topological analysis of the charge density based on the Bader analysis36 has been performed for each Ti2C, Ti3C2, and Ti4C3 magnetic solution obtained with the three density functionals. The Bader charges were computed using the VASP-linked code provided by Henkelman et al.37 For the reader, the inputs used for VASP calculations are available in the ESI.†
3. Spin model and magnetic coupling
A thorough analysis of the calculations, described in detail in the next sections, indicates that, for all the explored solutions, the spin density is mainly located on the surface Ti atoms and is consistent with a model involving one unpaired electron per Ti atom. Note also that, due to periodic symmetry constraints, the only possible solutions for the p(1 × 1) unit cells are the non-spin-polarized—NM, diamagnetic solution—the FM one, with parallel spins mainly localized in the Ti surface atoms, and the AFM1 one, with antiparallel spins in the two surface Ti atoms of the unit cell. To explore additional spin orderings, a p(2 × 1) supercell is used where two new possible spin orderings are possible. These are the AFM2 and AFM3 (Néel-like) schematically shown in Fig. 2. To avoid numerical noise, the FM and AFM1 solutions were also obtained for the p(2 × 1) supercell.Following Moreira and Illas work,38 it is now possible to map the DFT solutions into an appropriate Heisenberg spin Hamiltonian such as the one described in eqn (1), which considers three different isotropic two body interactions (JinterNN, JintraNN, and JinterNNN) and the spin operator, Si, as described in Fig. 3.
 | (1.) |
 | ||
| Fig. 3 Spin exchange paths for the magnetic coupling parameters, JinterNN, JintraNN, and JinterNNN for p(2 × 2) (a) Ti2C, (b) Ti3C2, and (c) Ti4C3, as defined in the text. | ||
Using this form of the spin Hamiltonian, Jαi > 0 represents a ferromagnetic interaction between the corresponding magnetic centers. Other interlayer coupling constants can be considered but, from a simple distance analysis, it is expected that these would have a minor effect and that the present JinterNN, JintraNN, and JinterNNN interactions provide a consistent description of the magnetic behavior or the systems. The mapping idea between the energies of the magnetic solutions and the defined spin Hamiltonian is very simple and implies obtaining the expected energy value of Hspin in eqn (1) corresponding to each of the different spin solutions and to make it equal to the DFT value for that solution. The expected values of each solution can be easily derived following the procedure outlined by Rivero, Moreira, and Illas.39 We note here that this procedure is different from the one often used in molecular systems where the mapping involves eigenvalues of the spin Hamiltonian and calculated values for the appropriate spin eigenstates of the molecular system.40 In the framework of DFT, this type of mapping faces problems as it is not always possible to represent an appropriate spin state—e.g. an open-shell singlet—with a single Kohn–Sham determinant which implies the use of broken symmetry solutions.41 The procedure described above is general and can be applied to both molecular and periodic systems. For additional details, the reader is referred to specialized literature.38,42
The expected values of the different spin solutions for Ti2C have been reported recently and we do not find it necessary to reproduce them here. Following the same procedure,38,39,42 the expected values of the different spin solutions per formula unit for Ti3C2 are as follows:
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 | (6) |
 | (7) |
 | (8) |
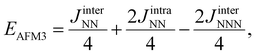 | (9) |
4. Results and discussion
As already commented, the main goal of the present work is to analyze the influence of the MXene thickness on their electronic structure and chemical bonding, and how it affects the relative stability of the low-lying electronic states that differ in spin ordering. Therefore, for completeness, the results for Ti2C already reported in previous work19 are included in the forthcoming discussion.4.1. Structural analysis
For the p(1 × 1) unit cells shown in Fig. 1, the relevant structural parameters of Ti2C, Ti3C2, and Ti4C3 are reported in Table 1. This includes the distances between Ti and C atoms (dTi–C) and the lattice parameters (a0) predicted by the PBE functional for the NM and FM solutions. For each MXene, Table 1 also includes the PBE0 and HSE06 energy difference between the FM and NM solutions; this is a quite large value of roughly 0.5 eV per formula unit (significantly larger than the corresponding PBE values listed in Table S1 of the ESI†), a clear indication that the electronic structure of these materials cannot be accurately represented by a NM solution even if the crystal structure is not very sensitive to this issue as commented below. Note that Fig. 1 clearly displays the ABC stacking inherited from the MAX phase. An alternative ABA stacking has been predicted by Gouveia et al.43 which, for some MXenes, is the preferred structure. Nevertheless, the present study focuses on the ABC stacking only.For the three MXenes, the dTi–C and a0 values for the FM and NM structures are nearly identical as expected and values are in line with previous results. For instance, Naguib et al.3 reported for the first time the experimental formation of 2D nanocrystals of Ti3C2 and carried out a series of, presumably non-spin polarized, DFT calculations using the PBE functional aimed at predicting a0; they simulated the XRD diffractograms of the bare geometry-optimized structure of Ti3C2 and compared it to the experimental ones concluding that the similarity between them supports their predicted a0 value of 3.05 Å. This is close to the present value of 3.10 Å for both solutions and to the previous results of 3.0744 and 3.09 Å23 for the non-spin-polarized solution as predicted with the Wu–Cohen45 and PBE functionals, respectively, and also to the 3.10 Å value reported for the PBE spin-polarized one. Recently, the experimental Ti3C2 lattice parameter has been reported with a value of 3.07 Å.46 Hence, the Ti3C2 optimized lattice parameters for both FM and NM solutions are in good agreement with the experimental and theoretically predicted ones, which provides support to the rest of the values in Table 1. In fact, the Ti4C3 lattice parameter predicted by other authors also with the PBE functional, 3.0744 and 3.10 Å,23 nicely match the values in Table 1. Here, there is a small difference of 0.02 Å between the optimized a0 for the NM and FM structures. Even if the differences are small, the analysis of the different magnetic solutions is carried out from the structure corresponding to the FM solutions and expanded to a p(2 × 1) supercell so as to carry out the set of calculations of the considered possible spin orderings.
4.2. Ground state analysis, spin solutions, and net charges
The results in Table 1 indicate that Ti2C, Ti3C2, and Ti4C3 MXenes exhibit a magnetic ground state with the NM solution lying significantly above in energy for both tested hybrid density functionals whereas the PBE energy differences between the FM and NM solutions, EFM–NM, for each structure and MXene are gathered in Table S1 of the ESI.† As expected, the EFM–NM at the same structure is affected by the density functional by differently stabilizing the FM configuration with respect to the NM one. Hence, the PBE0 calculated EFM–NM is larger than the HSE06 one. Nevertheless, for the three MXenes, the PBE0 and HSE06 calculated EFM–NM values are of the same order of magnitude and significantly larger than the corresponding PBE values—i.e. PBE leads to much closer values between spin-polarized and non-magnetic solutions.Once the magnetic nature of the electronic ground states of the three bare MXenes has been irrevocably established, we focus now on the FM, AFM1, AFM2, and AFM3 spin-polarized solutions obtained from the p(2 × 1) supercell as indicated in Fig. 2. For the three MXenes, Table 2 reports the energy of each solution relative to the FM one (ΔEAFMi–FM) obtained with both hybrid functionals with the corresponding PBE values reported in Table S2 of the ESI.† Energy differences are considered meaningful when are larger than 1 meV and a solution is considered magnetic when the calculated spin density per Ti atom is larger than 0.1 unpaired electrons in absolute value. Values from Table 2 show systematically that the AFM1 solution is always more stable than the FM, AFM2, and AFM3 ones for the three MXenes with the last two magnetic solutions lying above the FM solution. This implies that, for the three MXene, the AFM1 solution is in the electronic ground state. It is worth noting that, in all cases, the spin inversions needed to build the AFM2 and AFM3 spin orders from the FM imply a quite high energy penalization.
Next, we comment on the nature of the chemical bond by focusing on the Bader charges calculated with the PBE0 and HSE06 hybrid density functionals which are summarized in Table 3; for inclusiveness the PBE Bader charges are reported in Table S3 of the ESI.† The first point to highlight is that, as expected, the calculated Bader charge on each atom and MXene is not affected by the spin inversions introduced in going from the FM solution to the AFMs ones thus revealing a clear separation between the spin and the spatial part of the solution and supporting the choice of a Heisenberg Hamiltonian to describe the magnetic interactions in these systems. The second point to note is that the Bader charges on the Ti surface atoms are not significantly affected by the MXene width and the same holds for the Bader charges on the C surface atoms, only slightly decreasing with increasing the MXene thickness. In addition, for Ti3C2 and Ti4C3, the Bader charges on the Ti and C atoms in the inner atomic layers are larger than those in the more external ones. The results show that all functionals consistently predict a magnetic ground state for all MXenes with spin densities mainly located in the Ti surface atoms, as detailed in a separate section. This is likely to be related to the high reactivity of the outer metallic layers, involving only partially oxidized undercoordinated atoms. It is worth pointing out that PBE0 and HSE06 calculated Bader charges for each MXene are nearly identical. Finally, the picture of the chemical bond is completed by the calculated Density of States (DOS) with HSE06 available in the ESI† (Fig. S1–S3). For all magnetic solutions and all MXenes considered in the present work, the analysis of DOS shows the absence of a gap at the Fermi energy level, implying that these bare systems are metallic. From the atom and orbital projected DOS (Fig. S4 and S5 of the ESI†), the bands crossed by the Fermi level have large contributions from Ti atoms, the surface Ti atoms being those with larger contribution which, for Ti2C and Ti3C2, is simply due to their larger content in the unit cell. This picture, complemented with the spin density analysis (see Section 4.5) is consistent with an interpretation far away from that corresponding to the formal oxidation state, and involving C2− anions with a closed shell electronic configuration, Ti2+ cations in the inner layers also in a formal closed-shell s2d0 atomic configuration, and surface paramagnetic Ti+ cations with one unpaired electron per magnetic center in a formal s2d1 atomic configuration. Similar values are found for all explored magnetic solutions. Note, in addition, that these MXenes can be regarded as two-dimensional versions of Transition Metal Carbides (TMCs),47 known for displaying a complex bond, admixing features from ionic, covalent, and metallic bonds,48 and the oxidation state treatment model has to be taken as a way to understand magnetism in such compounds. This is clear when analyzing the coordination of the atoms involved. The surface Ti atoms have incomplete coordination leading to Ti+ ions in Ti2C and in the outer Ti layers of Ti3C2 and Ti4C3. However, Ti atoms in the inner layers of Ti3C2 and Ti4C3, which are absent in Ti2C, have complete octahedral coordination (see Fig. S6, ESI†).
| MXene | Ti2C | Ti3C2 | Ti4C3 | |||
|---|---|---|---|---|---|---|
| Functional | PBE0 | HSE06 | PBE0 | HSE06 | PBE0 | HSE06 |
Q
FMsurface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
1.3 | 1.3 | 1.4 | 1.4 | 1.4 | 1.4 |
Q
FMinner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 1.8 | 1.8 | 1.8 | 1.8 |
Q
FMinner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
— | — | — | — | −2.0 | −2.0 |
Q
FMsurface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
−2.6 | −2.6 | −2.3 | −2.3 | −2.2 | −2.2 |
Q
AFM1surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
1.3 | 1.3 | 1.4 | 1.4 | 1.4 | 1.4 |
Q
AFM1inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 1.8 | 1.8 | 1.8 | 1.8 |
Q
AFM1inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
— | — | — | — | −2.0 | −2.0 |
Q
AFM1surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
−2.6 | −2.6 | −2.3 | −2.3 | −2.2 | −2.2 |
Q
AFM2surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
1.3 | 1.3 | 1.4 | 1.4 | 1.4 | 1.4 |
Q
AFM2inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 1.8 | 1.8 | 1.8 | 1.8 |
Q
AFM2inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
— | — | — | — | −2.0 | −2.0 |
Q
AFM2surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
−2.6 | −2.6 | −2.3 | −2.3 | −2.2 | −2.2 |
Q
AFM3surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
1.3 | 1.3 | 1.4 | 1.4 | 1.4 | 1.4 |
Q
AFM3inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 1.8 | 1.8 | 1.8 | 1.8 |
Q
AFM3inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
— | — | — | — | −2.0 | −2.0 |
Q
AFM3surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
|
−2.6 | −2.6 | −2.3 | −2.3 | −2.2 | −2.2 |
4.3. Magnetic coupling parameters
Once the suitability of the Heisenberg Hamiltonian for the description of the magnetic interactions has been established, the JinterNN, JintraNN, and JinterNNN isotropic magnetic coupling parameters of the spin Heisenberg Hamiltonian in eqn (1) are calculated from the total energy difference of FM and AFM solutions per formula unit using the appropriate mapping for each MXene as in eqn (2)–(9). The spin exchange parameters obtained with the PBE0 and HSE06 functionals are summarized in Table 4 whereas the PBE values are reported in Table S4 of the ESI.† Results in Table 4 consistently show that, for the three MXenes, the JintraNN term is the largest, and thus, the dominant one. Moreover, the positive sign of JintraNN implies that the intralayer magnetic interaction is FM. However, the other two spin exchange parameters are not negligible and, interestingly, exhibit negative values meaning that, in their ground state, the magnetic layers are antiferromagnetically coupled. Also, the magnitude of JinterNNN indicates that the description of the magnetic coupling of these materials cannot be reduced to a NN Hamiltonian only. This is noticeable, especially in the case of Ti4C3, since non-negligible interactions involve magnetic center atoms that are above 7 Å apart from each other. To summarize, the ground state of the three MXenes studied in the present work have ferromagnetic layers antiferromagnetically coupled.As the thickness of the MXene increases, the absolute value of JintraNN and JinterNN increases, i.e., moving from Ti2C to Ti3C2, and to Ti4C3 the HSE06 JintraNN monotonically increases from 92.9 through 103.2 to 138.9 meV while the JinterNN and JinterNNN follow a different trend as their absolute values increase and decrease along the series (see Table 4). It is worth mentioning here that the choice of the functional has a marked influence on the calculated values although the qualitative description is maintained. In all cases, the HSE06 functional provides smaller, in absolute value, magnetic coupling constants than the PBE0 ones. In the absence of experimental values, the predictions from PBE0 and HSE06 values must be taken as a reasonable range.
As a final comment on the overall behavior of JintraNN, JinterNN and JinterNNN, we remark the fact that all the structures exhibit paramagnetic ions in surface layers but these are in direct contact in Ti2C, whereas in Ti3C2 and Ti4C3 a diamagnetic layer is present. This structural difference establishes a clear difference between Ti2C and the rest of the thicker layers that will affect their magnetic properties since the overlap between localized orbitals leads to magnetic interactions, usually antiferromagnetic in nature due to superexchange, which always decay with distance. Hence, interlayer magnetic interactions in the systems are expected to decay whereas the intralayer are expected to maintain their sign and magnitude as far as the structure of the external layers are maintained. The strong interlayer antiferromagnetic interactions observed can be justified by the metallic nature of the systems and the strong covalent and ionic contributions to the binding in the system as described below. This interlayer interaction can be justified by analyzing the DOS plots from Fig. S7 (ESI†) in which Ti+ d1 occupied orbitals of the outer layers show a large dispersion around the Fermi energy thus suggesting that covalent interactions between paramagnetic and diamagnetic in the structure. At this point it is important to stress the fact that Ti2C shows important differences in their structures compared to Ti3C2 and Ti4C3. In fact, Ti2C shows only two paramagnetic outer layers whereas Ti3C2 and Ti4C3 show one or two intercalated diamagnetic inner layers leading to different paths for magnetic interactions. In Ti2C, the observed strong ferromagnetic intralayer and strong antiferromagnetic interlayer interactions seem to be mostly due to covalent interactions between C2− and Ti+ ions in close contact. In contrast, in Ti3C2 and Ti4C3 the interlayer magnetic interactions are mediated by diamagnetic Ti2+ and C2− layers and clearly decrease with distance whereas the intralayer interactions are of the same magnitude as in Ti2C as long as the structure of these layers is maintained.
4.4. The effect of the on-site Hubbard potential
To assess the performance of the PBE+U approach, for each MXene, the energy of each magnetic solution relative to the FM one, ΔEAFMi–FM, has been obtained with values for the U parameter varying from 1 to 8 eV. Fig. 4 reports a plot of the ΔEAFMi–FM values as a function of U while the raw values are gathered in Table S5 of the ESI.† For the three studied MXenes, the ΔEAFMi–FM vary with respect to the U parameter in a quite smooth way for U values below 5 eV and then abruptly from 5 to 8 eV. Interestingly, U = 5 eV provides ΔEAFM1–FM values close to the ones provided by the hybrid functionals, especially for Ti2C and Ti3C2 HSE06 values and for Ti4C3 PBE0. In addition, the PBE+U with U = 5 eV also matches the HSE06 ΔEAFM2–FM and ΔEAFM3–FM AFM solutions for Ti2C. Nevertheless, upon increasing the MXene thickness, the PBE+U results become less reliable. In fact, regarding the relative energy stability of the AFM2 and AFM3 magnetic states deviating up to 200 meV from the values calculated with the hybrid functional. However, it is worth pointing out that in general, the PBE+U method consistently situates the AFM1 solution energy level below the FM one, except for Ti2C with U = 8 eV, and the AFM2 and AFM3 energy levels above the FM one, except for Ti2C with U > 7 eV, matching the essential description obtained with the hybrid functionals. The effect of the U parameter on the PBE+U calculated spin densities is discussed in the next section.The PBE+U magnetic coupling interactions of Ti2C, Ti3C2, and Ti4C3 are calculated from the AFM1, AFM2, and AFM3 energies relatives to the FM one for each U parameter and using eqn (2)–(9). Fig. 5 presents a plot of the different magnetic coupling parameters as a function of U with the corresponding values gathered in Table S6 of the ESI.† Not surprisingly, the calculated J values largely depend on the U value with those corresponding to U = 5 eV providing J values close to those obtained with the hybrid functionals for the Ti2C, and somewhat poorer for the Ti3C2 and Ti4C3 MXene. This is because the thicker MXenes contain two different types of Ti atoms with different occupation of the d shells, a feature that is difficult to describe with a single U value. Furthermore, the PBE+U calculated J values also vary with the MXene thickness. As the MXene width increases, the difference between the PBE+U and hybrid values of the dominant term, JintraNN, increases, up to ∼65 meV for Ti4C3. On the other hand, the PBE+U method essentially provides the same take-home message as the hybrid functionals, the JintraNN is the positive dominant term and the other two parameters are negative and not negligible, leading to the same definite conclusion that the ground state of the three MXenes is the antiferromagnetic coupling of two ferromagnetic layers. However, one must advert that the strong dependence of the J values with U makes this approach unreliable unless obtaining a U value able to mimic results from hybrid functionals.
 | ||
| Fig. 5 Magnetic coupling constants (JinterNN, JintraNN, and JinterNNN, all in meV) for (a) Ti2C, (b) Ti3C2, and (c) Ti4C3 as obtained from calculations with the PBE+U functional as a function of U (in eV) and using the equations derived from the mapping approach as in eqn (2–9). For completeness, the PBE0 and HSE06 values are also represented. The solid/dashed/dotted lines correspond to PBE+U/PBE0/HSE06 functionals, respectively. The blue/orange/brown lines correspond to AFM1-FM, AFM2-FM, and AFM3-FM energy differences, respectively. | ||
4.5. Spin density analysis
The magnitude of the calculated spin densities deserves some attention even if this is not an experimental measurable quantity and the calculated values largely depend on computational details such as the choice of the atomic volumes. With the necessary caution, we now discuss the relevant results in the literature for Ti3C2 and Ti4C3 as those for Ti2C have been discussed at length in a recent work. Some studies report Ti3C2 to have a magnetic ground state with a total net spin density per unit cell of ∼1.7, 1.87, 1.93,49,50 2.20, and 3.0421 a.u., which provides a measure of unpaired electrons per unit cell or, equivalently, one unpaired electron per Ti atom, thus justifying the Heisenberg Hamiltonian model chosen in this work. It is worth noting that a value of 1.7 was obtained using the HSE06 functional while the three intermediate values correspond to calculations with PBE and the last one to PBE+U with U = 2 eV, a value that, according to the results in the previous section, is likely to be far from being accurate, since a U = 5 eV value is required to reproduce the hybrid results for Ti2C. However, even if this value improves the description of spin density and magnetic coupling constants for Ti3C2 and Ti4C3, it is clear that using a single U value may not be appropriate to account for the two different kinds of Ti atoms, namely Ti+ and Ti2+, present in these materials, each with different occupations of the d shell.The present values for Ti3C2 FM solution for the p(1 × 1) unit cell are of 1.7, 2.14, and 2.13 unpaired electrons for PBE, PBE0, and HSE06, respectively. The PBE value of total spin density agrees with the HSE06 value reported by Xie et al.,15 however, the present hybrid values are 0.4 unpaired electrons higher. It is possible that these differences are rooted in the use of a different basis set, with Xie et al.15 using a kinetic energy cutoff of 580 eV, 120 eV lower than our value. Regarding the atomic spin densities, for the FM solution, values of 0.51 and 0.28 for the Ti surface atoms have been reported with PBE,21,49,50 while PBE+U with U = 2 eV predicts values of 0.41. In all cases, the inner Ti atoms are predicted to exhibit a residual spin density only with PBE values of 0.0321 and 0.02,49,50 and PBE+U with U = 2 eV of 0.0521 per Ti atom. It is worth noting that surface Ti spin densities of 0.28 and 0.41 unpaired electrons from ref. 21 using PBE and PBE+U largely differ, as expected, from the ones reported in Table 5 from calculations with PBE0 and HSE06. From Table 5 it also appears that all functionals systematically predict that the C atomic spin density is also residual, in consequence, the significative spin density is located mainly in the Ti surface atoms, a statement that applies to all explored magnetic solutions and to all functionals, including PBE. From previous studies, exploring diverse spin polarized solutions and reporting Ti3C2 to exhibit an AFM ground state, only Shein et al.23 provide PBE estimates of the Ti spin density of 0.74 per Ti surface atoms with residual spin densities of 0.05 only for the Ti inner atoms only close to those reported in Table S7 of the ESI;† with those predicted by HSE06 in close agreement to values in Table 5.
| Ti2Ca | Ti3C2 | Ti4C3 | ||||
|---|---|---|---|---|---|---|
| PBE0 | HSE06 | PBE0 | HSE06 | PBE0 | HSE06 | |
| a Values from ref. 19 are included for completeness. | ||||||
| S FMTot | 3.85 | 3.85 | 4.17 | 4.58 | 5.01 | 5.00 |
S
FMsurface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
0.55 | 0.55 | 0.62 | 0.67 | 0.78 | 0.78 |
S
FMinner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 0.04 | 0.07 | 0.04 | 0.04 |
| S FMC | −0.07 | −0.07 | −0.07 | −0.07 | −0.08 | −0.08 |
S
AFM1surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
0.72 | 0.72 | 0.81 | 0.80 | 0.86 | 0.85 |
S
AFM1inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 0.00 | 0.00 | 0.15 | 0.14 |
S
AFM2surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
0.33 | 0.32 | 0.25 | 0.25 | 0.21 | 0.22 |
S
AFM2inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 0.00 | 0.00 | 0.01 | 0.01 |
S
AFM3surface![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
0.35 | 0.34 | 0.24 | 0.23 | 0.25 | 0.24 |
S
AFM3inner![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti Ti
|
— | — | 0.00 | 0.00 | 0.02 | 0.02 |
Regarding Ti4C3, a few studies have predicted it to have a magnetic ground state with spin densities of 2.0015 and 1.9249,50 unpaired electrons per unit cell using HSE06 and PBE functionals, respectively, with reported atomic spin densities of 0.51 per Ti surface atoms and of 0.03 unpaired electrons per Ti inner atoms.49,50 These values are in agreement with the present total net spin densities for the p(1 × 1) unit-cell of FM solution of Ti4C3 of 1.91, 2.51, and 2.51 per unit cell as obtained from PBE, PBE0, and HSE06 respectively. Again, the PBE total spin density closely matches the HSE06 reported by Xie et al.15 placing our PBE0 and HSE06 values 0.5 unpaired electrons above which is rooted in the aforementioned different use of cutoff energy. One can see that using both hybrid functionals, the total spin density increases up to 2.51, significantly larger than the one obtained with a GGA functional due to the excessive delocalization of the electron density. Lastly, following the trend reported for Ti2C and Ti3C2, the C and Ti inner atomic spin densities of Ti4C4 are residual implying that the spin density is mainly located on the Ti surface atoms. The spin densities obtained with the largely used PBE+U method deserve further analysis. To this end, Fig. S8 in the ESI† reports the total and Ti surface atomic spin densities as a function of the U. Overall, all spin densities increase in absolute value as U increases. Interestingly, for U = 5 eV both spin densities and energy differences are close to the results from hybrid functionals.
Finally, one must highlight, that for the AFM2 and AFM3 solutions of Ti3C2 and Ti4C3, the Ti surface atomic spin densities are smaller than the ones for the more stable AFM1 and FM solutions. This fact is rooted in the metallic nature of these solutions and the large energy penalty necessary to invert spins in the Ti surface atom layers to build the AFM2 and AFM3 solutions which appear higher in energy; this evidences a clear competition between chemical bonding and magnetic interactions.
5. Conclusions
A systematic study has been presented aimed at describing the influence of MXene thickness on the magnetic properties and chemical bonding along the Ti2C, Ti3C2, and Ti4C3 series. To account for the well-known influence of the exchange correlation on the calculated magnetic couplings,29,38 the PBE functional, two different hybrids (HSE06 and PBE0) derived from PBE, and the broadly used PBE+U functionals are employed; in the latter by using a broad range of U values so as to determine the one that mimics the results of the more accurate hybrid functionals. In all cases, a tight setup is used to provide numerically converged results up to 1 meV.The PBE calculated lattice parameters are in good agreement with the available literature and the effect of spin polarization on the structural parameters is negligible. All functionals, regardless of the tested U parameter in the case of PBE+U, consistently provide the same conclusion regarding the magnetic properties of these systems, and the three MXenes have a magnetic ground state. In addition, the magnetic moments estimated from spin densities show that, for the three MXenes, these are mainly located at the Ti surface atoms leaving a residual spin density for the inner Ti and C atoms.
The analysis of the low-lying spin polarized solutions shows that all functionals consistently predict an AFM ground state with the atoms on the two outer metallic layers being ferromagnetically coupled and these two layers antiferromagnetically coupled. Nevertheless, the energy differences between the different solutions show a clear dependence on the functional with PBE0 providing the largest ones. Due to the lack of available experimental values, the results obtained with hybrid functionals are expected to provide an accurate prediction as well as a benchmark for future magnetic studies of these systems.
The analysis of the spin densities and Bader charges predicted with the two hybrid functionals, is consistent with a situation involving one unpaired electron per magnetic center. This picture, complemented with the spin density analysis, would agree with a model involving closed shell C2− ions in an octahedral environment, diamagnetic Ti2+ ions in inner layers in a s2d0 configuration and surface paramagnetic Ti+ ions with one unpaired electron per center in a s2d1 configuration with similar values for all magnetic orderings. This picture, far from the total ionic limit corresponding to the formal charges, is consistent with the mixed covalent-ionic-metallic character of the bulk TMCs. This picture also explains the high reactivity of the outer metallic layers, involving only partially oxidized undercoordinated atoms.
The information extracted from the analysis of the chemical bond is used to build an appropriate spin Heisenberg Hamiltonian where the energy differences between the low-lying solutions is mapped to the difference in expected values of the spin Hamiltonian for the same solutions, which allows a direct extraction of the isotropic magnetic coupling constants. As expected, these parameters are also sensitive to the employed functional, and those arising from the hybrid ones are expected to provide a reasonable and realistic range. Despite the numerical dependence of the magnetic coupling constants with the functional, both hybrid functionals predict that JintraNN is the positive dominant interaction although the other two couplings are noticeable and of opposite sign. In fact, the magnitude of JinterNNN indicates that the magnetic description cannot be reduced to a NN model only. In Ti2C, the observed strong ferromagnetic intralayer and strong antiferromagnetic interlayer interactions seem to be mostly due to covalent interactions between C2− and Ti+ ions in close contact. In contrast, in Ti3C2 and Ti4C3 the interlayer magnetic interactions are mediated by diamagnetic Ti2+ and C2− layers and clearly decrease with distance whereas the intralayer interactions are of the same magnitude as in Ti2C as far as the structure of these layers are maintained. For the PBE+U functional a value of U = 5 eV is found to closely mimic the results from hybrid functionals for Ti2C although some important deviations are found for Ti3C2 and Ti4C3 due to the fact that two different Ti ions, namely surface Ti+ and inner Ti2+ ions, are present in these structures. Finally, we note that the described structural, electronic, and magnetic properties can be affected by applying an external pressure as shown for a series of M2C MXenes.51
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Spanish Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación (AEI) MCIN/AEI/10.13039/501100011033 through grants PID2020-115293RJ-I00, PID2021-126076NB-I00, TED2021-129506B-C22, la Unidad de Excelencia María de Maeztu CEX2021-001202-M granted to the ITQCUB and, in part, from COST Action CA18234 and Generalitat de Catalunya 2021SGR00079 and 2021SGR00354 grants. The Red Española de Supercomputación (RES) and Consorci de Serveis Universitaris de Catalunya (CSUC) are also acknowledged for the generous computational resources. N. G.-R. is indebted to Generalitat the Catalunya for a predoctoral contract with reference 2022 FISDU 00106. F. V. is thankful for the ICREA Academia Award 2023 Ref. Ac2216561.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field in Atomically Thin Carbon Films, Science, 2004, 306, 666–669 CrossRef CAS.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, 2D materials and van der Waals heterostructures, Science, 2016, 353, aac9439 CrossRef CAS.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Two-Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS.
- Y. Gogotsi and B. Anasori, The Rise of MXenes, ACS Nano, 2019, 13, 8491–8494 CrossRef CAS.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, 2D Metal Carbides and Nitrides (MXenes) for Energy Storage, Nat. Rev. Mater., 2017, I, 16098 CrossRef.
- B. Anasori and Y. Gogotsi, 2D Metal Carbides and Nitrides (MXenes), ed. B. Anisori and Y. Gogotsi, Springer, 1st edn, 2019 Search PubMed.
- Á. Morales-García, F. Calle-Vallejo and F. Illas, MXenes: New Horizons in Catalysis, ACS Catal., 2020, 10, 13487–13503 CrossRef.
- A. VahidMohammadi, J. Rosen and Y. Gogotsi, The World of Two-Dimensional Carbides and Nitrides (MXenes), Science, 2021, 372, 1165 CrossRef.
- F. Bu, M. M. Zagho, Y. Ibrahim, B. Ma, A. Elzatahry and D. Zhao, Porous MXenes: Synthesis, Structures, and Applications, Nano Today, 2020, 30, 100803 CrossRef CAS.
- Q. Tang, Z. Zhou and P. Shen, Are MXenes Promising Anode Materials for Li Ion Batteries? Computational Studies on Electronic Properties and Li Storage Capability of Ti3C2 and Ti3C2X2 (X = F, OH) Monolayer, J. Am. Chem. Soc., 2012, 134, 16909–16916 CrossRef CAS.
- Y. Yang, J. Chen, J. Tang, F. Xing and M. Yao, Investigation on the Structure-Performance Correlation of TiC MXenes as Cathode Catalysts for LiO2 Batteries, J. Phys. Chem. C, 2021, 125, 21453–21459 CrossRef CAS.
- J. D. Gouveia, Á. Morales-García, F. Viñes, F. Illas and J. R. B. Gomes, MXenes as Promising Catalysts for Water Dissociation, Appl. Catal., B, 2020, 260, 118191 CrossRef CAS.
- I. Ihsanullah, MXenes (Two-Dimensional Metal Carbides) as Emerging Nanomaterials for Water Purification: Progress, Challenges and Prospects, J. Chem. Eng., 2020, 388, 124340 CrossRef CAS.
- L. Verger, V. Natu, M. Carey and M. W. Barsoum, MXenes: An Introduction of Their Synthesis, Select Properties, and Applications, Trends Chem., 2019, 1, 656–669 CrossRef CAS.
- Y. Xie and P. R. C. Kent, Hybrid Density Functional Study of Structural And Electronic Properties Of Functionalized Tin+1Xn (X = C, N) Monolayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235441 CrossRef.
- M. Khazaei, A. Ranjbar, M. Arai, T. Sasaki and S. Yunoki, Electronic Properties and Applications of MXenes: A Theoretical Review, J. Mater. Chem. C, 2017, 5, 2488–2503 RSC.
- P. Lv, Y. L. Li and J. F. Wang, Monolayer Ti2C MXene: Manipulating Magnetic Properties and Electronic Structures by an Electric Field, Phys. Chem. Chem. Phys., 2020, 22, 11266–11272 RSC.
- B. Akgenc, E. Vatansever and F. Ersan, Tuning of electronic structure, magnetic phase, and transition temperature in two-dimensional Cr-based Janus MXenes, Phys. Rev. Mater., 2021, 5, 083403 CrossRef CAS.
- N. García-Romeral, Á. Morales-García, F. Viñes, I. de P. R. Moreira and F. Illas, A Theoretical Analysis of Magnetic Coupling in the Ti2C bare MXene, J. Phys. Chem. C, 2023, 127, 3706–3714 CrossRef PubMed.
- S. Zhao, W. Kang and J. Xue, MXene Nanoribbons, J. Mater. Chem. C, 2015, 3, 879–888 RSC.
- J. Fatheema, M. Fatima, N. B. Monir, S. A. Khan and S. Rizwan, A Comprehensive Computational and Experimental Analysis of Stable Ferromagnetism in Layered 2D Nb-Doped Ti3C2 MXene, Phys. E, 2020, 124, 114253 CrossRef CAS.
- M. Iqbal, J. Fatheema, Q. Noor, M. Rani, M. Mumtaz, R. Zheng, S. A. Khan and S. Rizwan, Co-existence of Novel Ferromagnetic/Anti-ferromagnetic Phases in Two-dimensional Ti3C2 MXene, Mater. Today Chem., 2020, 16, 100271 CrossRef CAS.
- I. R. Shein and A. L. Ivanovskii, Graphene-like Titanium Carbides and Nitrides Tin+1Cn, Tin+1Nn (n = 1, 2, and 3) from De-intercalated MAX Phases: First-Principles Probing of their Structural, Electronic Properties and Relative Stability, Comput. Mater. Sci., 2012, 65, 104–114 CrossRef CAS.
- F. Wu, K. Luo, C. Huang, W. Wu, P. Meng, Y. Liu and E. Kan, Theoretical Understanding of Magnetic and Electronic Structures of Ti3C2 Monolayer and Its Derivatives, Solid State Commun., 2015, 222, 9–13 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale For Mixing Exact Exchange With Density Functional Approximations, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, Chem. Phys., 2003, 118, 8207–8215 CAS.
- I. D. P. R. Moreira, F. Illas and R. L. Martin, Effect of Fock Exchange on the Electronic Structure and Magnetic Coupling in NiO, Phys. Rev. B, 2002, 65, 155102 CrossRef.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, First-Principles Calculations of the Electronic Structure and Spectra of Strongly Correlated systems: the LDA + U Method, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef CAS.
- Z. Zhenpeng Hu and H. Metiu, Choice of U for DFT+U Calculations for Titanium Oxides, J. Phys. Chem. C, 2011, 115, 5841–5845 CrossRef.
- C. Loschen, J. Carrasco, K. M. Neyman and F. Illas, First-Principles LDA + U and GGA + U Study of Cerium Oxides: Dependence on the Effective U Parameter, Phys. Rev. B, 2007, 75, 035115 CrossRef.
- M. Nolan, S. Grigoleit, D. C. Sayle, S. C. Parker and G. W. Watson, Density Functional Theory Studies of the Structure and Electronic Structure of Pure and Defective Low Index Surfaces of Ceria, Surf. Sci., 2005, 576, 217–229 CrossRef CAS.
- G. Kresse and J. Furthmuller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using A Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, C. J. Först and J. Schimpl, The Projector Augmented Wave Method: Ab-Initio Molecular Dynamics with Full Wave Functions, Bull. Mater. Sci., 2002, 26, 33–41 CrossRef.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Condens. Matter. Phys., 2009, 21, 084204 CrossRef CAS.
- I. D. P. R. Moreira and F. Illas, A Unified View of the Theoretical Description of Magnetic Coupling in Molecular Chemistry and Solid State Physics, Phys. Chem. Chem. Phys., 2006, 8, 1645–1659 RSC.
- P. Rivero, I. D. P. R. Moreira and F. Illas, Spin Hamiltonian effective parameters from periodic electronic structure calculations, J. Phys.: Conf. Ser., 2008, 117, 012025 CrossRef.
- F. Illas, I. D. P. R. Moreira, C. de Graaf and V. Barone, Magnetic coupling in biradicals, binuclear complexes and wide gap insulators: A survey of ab initio wave function and density functional theory approaches, Theor. Chem. Acc., 2000, 104, 265–272 Search PubMed.
- R. Caballol, O. Castell, F. Illas, J. P. Malrieu and I. D. P. R. Moreira, Remarks on the proper use of the broken symmetry approach to magnetic coupling, J. Phys. Chem. A, 1997, 101, 7860–7866 CrossRef CAS.
- S. N. Datta, C. O. Trindle and F. Illas, Theoretical and Computational Aspects of Magnetic Organic Molecules, Imperial College Press, World Scientific Publishing, London, 2014 Search PubMed.
- J. D. Gouveia, F. Viñes, F. Illas and J. R. B. Gomes, MXenes atomic layer stacking phase transitions and their chemical activity consequences, Phys. Rev. Mater., 2020, 4, 054003 CrossRef CAS.
- M. Kurtoglu, M. Naguib, Y. Gogotsi and M. W. Barsoum, First Principles Study of Two-Dimensional Early Transition Metal Carbides, MRS Commun., 2012, 2, 133–137 CrossRef CAS.
- Z. Wu and R. E. Cohen, More accurate generalized gradient approximation for solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- V. Kamysbayev, A. S. Filatov, H. Hu, X. Rui, F. Lagunas, D. Wang, R. F. Klie and D. V. Talapin, Covalent surface modifications and superconductivity of two-dimensional metal carbide MXenes, Science, 2020, 369, 979–983 CrossRef CAS.
- Á. Morales-García, M. Mayans-Llorach, F. Viñes and F. Illas, Thickness biased capture of CO2 on carbide MXenes, Phys. Chem. Chem. Phys., 2019, 21, 23136–23142 RSC.
- F. Viñes, C. Sousa, P. Liu, J. A. Rodriguez and F. Illas, A systematic density functional theory study of the electronic structure of bulk and (001) surface of transition-metals carbides, J. Chem. Phys., 2005, 122, 174709 CrossRef.
- H. Haastrup, M. Strange, M. Pandey, T. Deilmann, P. S. Schmidt, N. F. Hinsche, M. N. Gjerding, D. Torelli, P. M. Larsen, A. C. Riis-Jensen, J. Gath, K. W. Jacobsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals, 2D Mater., 2018, 5, 042002 CrossRef.
- M. N. Gjerding, A. Taghizadeh, A. Rasmussen, S. Ali, F. Bertoldo, T. Deilmann, N. R. Knøsgaard, M. Kruse, A. H. Larsen, S. Manti, T. G. Pedersen, T. Skovhus, M. K. Svendsen, J. J. Mortensen, T. Olsen and K. S. Thygesen, Recent progress of the Computational 2D Materials Database (C2DB), 2D Mater., 2021, 8, 044002 CrossRef CAS.
- S. Zhao, W. Kang and J. Xue, Manipulation of Electronic and Magnetic Properties of M2C (M = Hf, Nb, Sc, Ta, Ti, V, Zr) Monolayer by Applying Mechanical Strains, Appl. Phys. Lett., 2014, 104, 133106 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01617j |
| This journal is © the Owner Societies 2023 |



