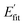¹²CO₂ transition frequencies with kHz-accuracy by saturation spectroscopy in the 1.99–2.09 μm region

Abstract

Saturation spectroscopy has been used to determine the absolute frequencies of 107 ro-vibrational transitions of the two strongest ¹²CO₂ bands of the 2 μm region. The considered 20012-00001 and 20013-00001 bands are of importance for the CO₂ monitoring in our atmosphere. Lamb dips were measured using a cavity ring-down spectrometer linked to an optical frequency comb referenced to a GPS-disciplined Rb oscillator or to an ultra-stable optical frequency. The comb-coherence transfer (CCT) technique was applied to obtain a RF tunable narrow-line comb-disciplined laser source using an external cavity diode laser and a simple electro-optic modulator. This setup allows obtaining transition frequency measurements with kHz-level accuracy. The resulting accurate values of the energy levels of the 20012 and 20013 vibrational states are reproduced with a (1σ)-rms of about 1 kHz using the standard polynomial model. The two upper vibrational states appear thus to be highly isolated except for a local perturbation of the 20012 state leading to an energy shift of 15 kHz at J = 43. A recommended list of 145 transition frequencies with kHz accuracy is obtained providing secondary frequency standards across the 1.99–2.09 μm range. The reported frequencies will be valuable to constrain the zero-pressure frequencies of the considered transitions in ¹²CO₂ retrieval from atmospheric spectra.

---

1. Introduction

Carbon dioxide, CO₂, is the most important anthropogenic greenhouse gas and several satellite missions like GOSAT, GOSAT-2 (JAXA), OCO-2 (NASA), TanSat (CAS), and the upcoming MicroCarb (CNES) and CO2M (ESA) missions, as well as ground-based networks like TCCON,¹ are dedicated to the monitoring of its column-averaged dry-air mole fraction in the Earth's atmosphere. These missions are increasingly demanding in terms of high quality spectroscopic data for the CO₂ absorption bands in the 1.6 and 2.0 μm regions used for these measurements. In the former spectral region, numerous line profile studies^2–6 as well as highly accurate frequency measurements^7–14 have been reported so far. In particular, transition frequencies with kHz-accuracy were determined both in the Doppler limited regime^8,9,12,13 and in the saturation regime.^10,14

The 2 μm region is dominated by the 20013-00001 and 20012-00001 bands of ¹²CO₂ centered at 2.06 and 2.01 μm, respectively (Fig. 1). Here we adopt the HITRAN convention for the vibrational labelling (so-called AFGL notation) described in Rothman and Young.¹⁵ These bands have been the subject of several spectroscopic studies using Fourier transform spectroscopy (FTS),^16–23 laser diode absorption spectroscopy^24–29 and cavity ring down spectroscopy (CRDS).^30–32 In particular, the latter CRDS studies were dedicated to accurate measurements of the line profiles broadened by air (and their temperature dependence) in support of missions devoted to CO₂ atmospheric retrieval. Regarding transition frequencies, to the best of our knowledge, only the very recent (zero-pressure) frequencies reported with 100 kHz accuracy for four lines of CO₂ in air measured by CRDS were referenced to an absolute frequency standard.³² Let us also mention that the absolute positions of five lines of the 21113-01101 band were reported with 300 kHz accuracy in the 2.09 μm spectral region.³³ However, these latter measurements were performed only at 13.3 mbar (of pure CO₂) and transition frequencies (i.e. line centre at zero-pressure) could not be provided.

Fig. 1 Overview of the 20012-00001 and 20013-00001 bands of ¹²CO₂ as provided by the HITRAN database. Transitions presently measured by saturation spectroscopy are highlighted (red open circles).

We report here the frequencies of most of the strongest transitions of the 20013-00001 and 20012-00001 bands with kHz-level accuracy. This provides a series of secondary frequency standards with kHz-level uncertainties across the wide 4788–5015 cm⁻¹ frequency range (i.e. 1994–2089 nm) where frequency standards are scarce.⁷ Carbon dioxide, a non-toxic and easy-to-manipulate gas with regularly spaced strong (up to 10⁻²¹ cm molecule⁻¹) transitions, is particularly well adapted for that purpose. The achieved uncertainty will be valuable for fixing the positions at pressure equal to zero in the multi-spectrum fit procedures used to analyze spectra of CO₂ diluted in air, allowing for the improvement of the other line profile parameters, especially the pressure shift coefficients (see e.g. Mondelain et al.⁴). The obtained frequency values will be also valuable for spectra calibration purposes as for instance for frequency referencing differential absorption LIDAR (LIght Detecting And Ranging) dedicated to CO₂ measurements.³⁴ Finally, transition frequencies measured at the kHz level can also be used to increase the accuracy of several other transition frequencies through the application of the Ritz principle or effective Hamiltonian models.³⁵

Regarding the experiment, in order to circumvent the Doppler line broadening, the measurements were performed by CRDS in saturation regime.³⁶ The CRDS technique is well-adapted for Lamb-dip frequency measurements thanks to the narrow (kHz level) resonances of the high-finesse optical cavities and the high intracavity power.^37,38 After a description of the experimental set-up and recorded transitions (Part 2), we will detail the data analysis and error budget (Part 3). The spectroscopic constants of the two bands studied will be derived from a fit of the measured upper energy levels and the final set of recommended position values will be compared to available literature data in Part 4, before the concluding remarks (Part 5).

2. Experimental set-up and recorded transitions

Measurements were performed with an improved version of the comb-referenced cavity ring down spectrometer described in Mondelain et al.³² and shown in Fig. 2. This spectrometer is based on an extended cavity diode laser (ECDL) (New Focus; Model TLB 6736) covering the 1975–2075 nm range. A large part (90%) of the emitted laser power is coupled to a temperature regulated high finesse cavity (HFC) described in Vasilchenko et al.³⁹via an acousto-optic modulator (AOM) (to produce the ring down (RD) events) and an electro-optic modulator (EOM) to correct for laser jitter and phase noise (DC to >40 MHz correction bandwidth) as explained below. The 45 cm-long high finesse cavity is made of two high reflectivity mirrors (from Layertec, with a reflection coefficient R > 99.99% over the 1950–2250 nm range). Periodic resonances between the laser light and the cavity modes are achieved by applying a voltage triangular ramp on the PZT tube on which the output cavity mirror is mounted. At resonance, the AOM (model ACM-1002AA1 from IntraAction Corp.) is used to switch off the injection of photons in the cavity and generate a RD event detected by an extended InGaAs PIN photodiode (G12183 series from Hamamatsu). Typical RD times of the evacuated cell are τ = 55 μs at 4875 cm⁻¹ and 48 μs at 4953 cm⁻¹.

Fig. 2 Scheme of the experimental set-up. OFC: optical frequency comb, AOM: acousto-optic modulator, EOM: electro-optic modulator, ECDL: external cavity diode laser, SSBM: single sideband modulator, TDFA: thulium doped fiber amplifier, PD: photo-diode. B(ν) and δν represent the beat note frequency and its noise, respectively.

In our previous works,^4,32,39 a beat note (BN) signal, between the laser source and the closest tooth of a frequency comb (FC), was used to accurately determine the absolute frequency of the laser source, limited by a laser line width of a few hundred kHz. Here, this signal is used to transfer the coherence of the comb to a fraction of the ECDL output using the feed-forward technique, described in Votava et al.⁴⁰ and in Gotti et al.,⁴¹ providing a driftless and spectrally narrower source directly tunable using a RF synthesizer. In more detail, the BN signal is first low-pass filtered (BLP-150+ from Mini-Circuits; 150 MHz cut-off) to select only the BN with the closest comb tooth, amplified with a series of three amplifiers (ZFL500LN+ from Mini-Circuits; 28 dB of gain), and then separated with a power splitter (PSC-2-1 from Mini-Circuits; 0.1 to 400 MHz). The first output channel is digitized by a fast acquisition card (250 MHz-16 bits, by GAGE) which gives the BN frequency, f_BN, after Fourier transform of this signal and a peak determination procedure over the 0 to 125 MHz RF range at a 350 Hz repetition rate with a 15 kHz resolution. The BN linewidth is a combination of comb tooth and ECDL linewidths (which dominates) and is typically 200 kHz FWHM. This BN frequency measurement, previously used for frequency calibration, is only used here to stabilize the ECDL frequency around f_BN = 55 MHz via the Current modulation input of the controller. The second output channel is mixed with a signal from a RF synthesizer (SMA100B from Rohde&Schwarz; 8 kHz–20 GHz) in a single-sideband modulator (TRF370417 50 MHz to 6 GHz Quadrature Modulator from Texas Instruments), then amplified to feed the RF input of the EOM (MPZ-LN-10 from iXBlue; electro-optical bandwidth >10 GHz; central wavelength: 1550 nm). This latter generates a corrected and an uncorrected sideband in addition to the carrier frequency with the following frequencies:

ν_carrier = nf_rep + f_CEO + sign f_BN (1)

ν_{sideband_nc} = nf_rep + f_CEO + sign f_BN − sign(f_synth − f_BN) (2)

ν_{sideband_c} = nf_rep + f_CEO + sign f_BN + sign(f_synth − f_BN) (3)

where f_rep = 250 MHz and f_CEO = −20 MHz are the repetition rate and the carrier-envelope offset of the FC referenced to a 10 MHz rubidium frequency standard (Model PRS 10 from SRS) (hereafter called RF lock) which is phase-locked to a GPS timing receiver. n is the comb tooth number determined with a commercial wavelength meter (HighFinesse WS7-60 IR-II). Sign is equal to + or − and corresponds to the sign of the BN. f_synth is the frequency generated by the RF synthesizer to add a programmable shift to f_BN (which is kept close to 55 MHz). Note that, as indicated in Tables 1 and 2, part of the measurements were performed with the comb optically locked via an intra-cavity EOM to an ultra-stable optical frequency (known with accuracy at the 10⁻¹⁶ level) at 1542 nm (∼194 417 936 MHz) (hereafter called optical lock). This frequency standard is transferred to our laboratory from the LNE-SYRTE in Paris over about 1000 km through a dedicated line of the RENATER academic fiber network thanks to the French Equipex project REFIMEVE+.⁴²

Table 1 Frequencies of the transitions of the 20013-00001 band of ¹²CO₂ determined in this work with their final uncertainties (see text and Table 3). The frequencies are given after correction of the 90 Hz second-order Doppler shift. RF and Opt correspond to the RF lock and optical lock (see text for details), respectively

Assig.	Freq. (kHz)	Pres. (Pa)	# of spectra	Lock	Final unc. (kHz)
P16	145 119 049 920.6	0.13	3	RF	3.0
P14	145 169 371 981.4	0.13	6	RF	3.4
P12	145 219 201 993.0	0.13	9	RF	3.5
P10	145 268 542 644.7	0.07	8	RF	3.4
P8	145 317 396 075.5	0.07	7	RF	3.6
P6	145 365 763 879.6	0.14	9	RF	3.2
P4	145 413 647 096.5	0.03	10	Opt.	3.1
P2	145 461 046 214.5	1.20	9	RF	3.4
R0	145 531 236 890.1	2.00	21	RF	3.4
R2	145 577 424 223.3	0.73	6	RF	3.1
R4	145 623 124 768.3	0.03	10	Opt.	2.9
R6	145 668 336 501.3	0.03	10	Opt.	3.0
R8	145 713 056 851.0	0.03	9	Opt.	2.9
R10	145 757 282 685.6	0.03	6	Opt.	3.4
R12	145 801 010 333.2	0.03	10	Opt.	3.0
R14	145 844 235 571.7	0.03	10	Opt.	2.9
R16	145 886 953 640.9	0.03	10	Opt.	2.9
R18	145 929 159 249.7	0.03	10	Opt.	3.0
R20	145 970 846 578.6	0.03	10	Opt.	2.9
R22	146 012 009 289.8	0.03	11	Opt.	2.9
R24	146 052 640 536.8	0.04	10	Opt.	2.9
R26	146 092 732 967.0	0.07	10	Opt.	3.1
R28	146 132 278 738.5	0.07	10	Opt.	3.0
R30	146 171 269 531.1	0.12	30	Opt.	3.3
R32	146 209 696 545.2	0.12	20	Opt.	3.1
R34	146 247 550 532.3	0.12	20	Opt.	3.0
R36	146 284 821 792.1	0.16	168	Opt.	2.9
R38	146 321 500 193.2	0.18	21	Opt.	3.0
R40	146 357 575 182.8	0.19	16	Opt.	2.9
R42	146 393 035 800.0	0.20	10	Opt.	3.0
R44	146 427 870 697.5	0.16	10	Opt.	3.0
R46	146 462 068 137.7	0.16	10	Opt.	2.9
R48	146 495 616 036.8	0.16	10	Opt.	3.0
R50	146 528 501 949.4	1.41	20	Opt. & RF	3.2
R52	146 560 713 096.8	2.67	6	RF	3.3
R54	146 592 236 384.6	2.67	9	RF	3.5
R56	146 623 058 410.3	2.67	9	RF	3.2
R58	146 653 165 481.7	6.67	9	RF	3.8
R60	146 682 543 621.6	13.33	9	RF	3.4
R62	146 711 178 600.3	13.33	10	RF	3.4
R64	146 739 055 925.1	20	10	RF	7.7
R66	146 766 160 861.4	16.29	18	RF	6.5
R68	146 792 478 469.7	26.66	10	RF	14.6

---

Table 2 Same as Table 1 for the 20012-00001 band of ¹²CO₂

Assig.	Freq. (kHz)	Pres. (Pa)	# of spectra	Lock	Final unc. (kHz)
P74	146 911 623 361.5	20	10	RF	8.7
P72	146 989 515 840.3	13.33	10	RF	4.0
P70	147 066 640 733.3	13.33	10	RF	3.5
P68	147 142 980 565.8	6.67	10	RF	3.5
P66	147 218 521 294.3	6.67	18	RF	3.4
P64	147 293 251 422.9	6.67	12	RF	3.7
P62	147 367 161 400.9	6.67	9	RF	3.3
P60	147 440 243 211.6	6.67	10	RF	3.3
P58	147 512 490 048.1	6.67	10	RF	3.3
P56	147 583 896 096.4	6.67	10	RF	3.3
P54	147 654 456 358.4	6.66	10	RF	3.3
P52	147 724 166 519.3	0.07	10	RF	3.0
P50	147 793 022 842.6	0.03	10	RF	3.1
P48	147 861 022 080.7	0.03	10	RF	3.0
P46	147 928 161 407.1	0.03	10	RF	3.1
P44	147 994 438 380.1	0.03	10	Opt.	3.3
P42	148 059 850 796.9	0.03	10	Opt.	3.0
P40	148 124 396 819.3	0.03	10	Opt.	2.9
P38	148 188 074 787.2	0.03	10	Opt.	2.9
P36	148 250 883 255.1	0.03	9	Opt.	2.8
P34	148 312 820 947.2	0.03	10	Opt.	2.9
P32	148 373 886 735.5	0.03	10	Opt.	2.9
P30	148 434 079 613.5	0.03	10	Opt.	2.9
P28	148 493 398 682.7	0.03	10	Opt.	3.9
P26	148 551 843 131.1	0.03	10	Opt.	2.9
P24	148 609 412 204.0	0.03	10	Opt.	3.0
P22	148 666 105 210.8	0.02	13	RF	3.1
P20	148 721 921 498.3	0.02	10	RF	3.0
P18	148 776 860 436.3	0.02	10	RF	3.0
P16	148 830 921 417.8	0.02	10	RF	3.0
P14	148 884 103 839.8	0.02	10	RF	3.2
P12	148 936 407 097.7	0.02	3	RF	3.1
P10	148 987 830 579.6	0.02	20	RF	3.6
P8	149 038 373 657.5	0.03	14	Opt.	2.9
P6	149 088 035 683.0	0.03	10	Opt.	2.9
P4	149 136 815 987.3	0.03	7	Opt.	2.9
P2	149 184 713 867.3	0.03	10	Opt.	3.0
R0	149 254 904 543.6	0.03	10	Opt.	3.1
R2	149 300 593 110.5	0.03	8	Opt.	2.9
R4	149 345 396 570.0	0.03	10	Opt.	2.9
R6	149 389 314 083.5	0.03	10	Opt.	2.9
R8	149 432 344 784.5	0.02	20	RF	3.1
R10	149 474 487 792.4	0.02	5	RF	3.1
R12	149 515 742 194.7	0.02	10	RF	3.0
R14	149 556 107 069.8	0.01	16	RF	3.2
R16	149 595 581 482.8	0.01	9	RF	3.1
R18	149 634 164 511.2	0.01	6	RF	3.0
R20	149 671 855 220.4	0.01	10	RF	3.1
R22	149 708 652 707.4	0.01	5	RF	2.9
R24	149 744 556 091.7	0.01	9	RF	3.1
R26	149 779 564 532.6	0.01	9	RF	3.2
R28	149 813 677 243.6	0.01	10	RF	3.1
R30	149 846 893 508.5	0.01	10	RF	3.1
R32	149 879 212 692.8	0.01	10	RF	3.0
R34	149 910 634 270.4	0.01	10	RF	3.0
R36	149 941 157 834.1	0.01	9	RF	3.3
R38	149 970 783 128.6	0.01	10	RF	3.1
R40	149 999 510 067.7	0.01	9	RF	3.2
R42	150 027 338 777.9	0.01	10	RF	3.2
R44	150 054 269 570.1	0.01	9	RF	3.2
R46	150 080 303 113.5	0.01	10	RF	3.3
R48	150 105 440 317.6	0.01	10	RF	3.1
R50	150 129 682 483.6	0.01	9	RF	3.2

---

As can be seen from eqn (3), the BN frequency is eliminated for the corrected sideband frequency. This means that the jitter and also higher frequency phase noise of the laser source (i.e. the ECDL) is suppressed for this sideband making it a frequency-shifted clone of a comb tooth, with the programmable offset given by f_synth. This clone possesses the comb tooth linewidth which is typically 100 kHz and 5 kHz for the RF and optical locks, respectively instead of a few hundred kHz (at a 1 ms time scale) for the ECDL emission width. On the other hand, eqn (2) shows that for the uncorrected frequency we have two times the BN frequency, leading to a broadening of this sideband relative to the carrier. Due to the different linewidths, only the corrected sideband is efficiently injected at a passage through cavity resonance. This allows to easily track the dithering cavity length (via the PZT-mounted mirror) to keep it centered around the corrected sideband and not around the carrier or the uncorrected sideband.

The output of the EOM is then amplified by a cw-Thulium-doped fiber amplifier (CTFA-PB-PM-20-BW4 from Keopsys; central wavelength: 2004 nm; saturated output power: 17 to 40 dBm) before passing through the AOM and the high finesse cavity. The RF signal (94.15 MHz) applied to the AOM is generated by a direct digital synthesizer (DDS) referenced to the 10 MHz rubidium frequency standard as well as the RF synthesizer. Note that the laser frequency in the cavity has to be corrected from the AOM frequency used here in its order −1. The feed-forward “correction” is optimized by placing an optical delay line (i.e. a 5 m long optical fiber) before the EOM.

Note that in the previous works^40,41 a telecom dual Mach-Zehnder modulator (MZM) was used. Unfortunately, this optical component is not available in the 2 μm spectral range, leading us to use an EOM. This latter has the drawback of having both sidebands and the carrier sent in the HFC instead of only one sideband for the MZM (the carrier and the other sideband being suppressed in this case). This leads to potential frequency crossing between the corrected sideband and the carrier and other sidebands, since the latter become resonant with the HFC if they are separated by a multiple of the free spectral range, complicating the (large) tuning. Note that even if the operating wavelength of the EOM is 1.55 μm, it works in the 2 μm region only with small additional losses which illustrates the large spectral coverage of this optical component. Unfortunately, integrated MZM devices do not appear to be so versatile.

Spectra are acquired step by step by changing f_synth which can be tuned in our setup between 2 and 6 GHz (due to technical limitation of our RF electronics). In the case of Lamb dip acquisitions, each spectrum corresponds to a scan over 4 MHz with spectral steps of 20 kHz. At each spectral step, 150 or 200 RD events are averaged. The scan duration is about 5 minutes.

The HFC is filled by a flow of pure CO₂ (from Air Liquide; 99.995% of purity). The pressure inside the cell is measured thanks to a MKS Baratron 626B absolute pressure transducer (1.33 mbar full scale; 0.25% uncertainty of reading) and controlled with an electro-valve (2871 series from Burkert; 0.3 mm orifice dia.) and homemade PID software. The temperature of the sounded gas is measured with an accuracy of 0.04 K and the temperature homogeneity of the gas in the HFC is better than 0.05 K (see Vasilchenko et al.³⁹ for the details).

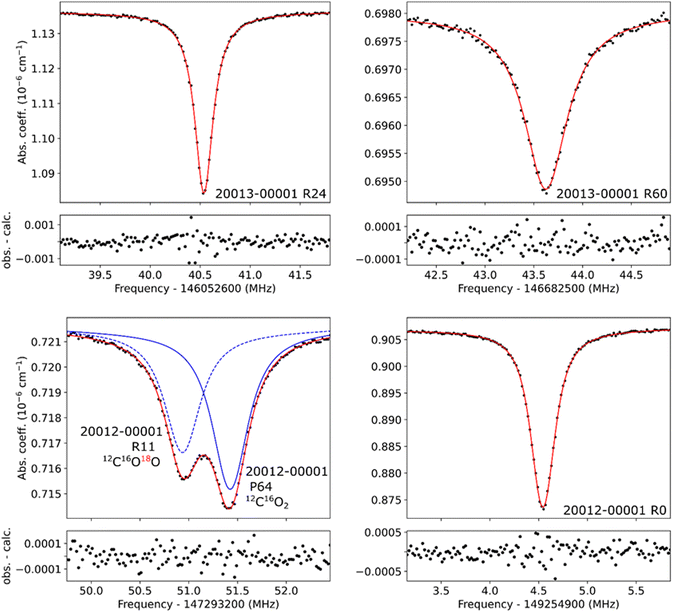
In this work, 63 transitions up to J′′ = 74 and 43 transitions up to J′′ = 70 have been studied from Lamb dip spectra for the 20012-00001 and 20013-00001 band, respectively. The measured transitions are highlighted in Fig. 1. Several examples of Lamb dips spectra are presented in Fig. 3.

Fig. 3 Examples of Lamb dips (dotted points) for the R(24) (upper left panel) and R(60) (upper right panel) transitions of the 20013-00001 band of ¹²CO₂, and the P(64) (lower left panel) and R(0) (lower right panel) transitions of the 20012-00001 band of ¹²CO₂. The frequency step is 20 kHz and the indicative pressure values P_CO2 are about 0.04, 13, 7 and 0.03 Pa, respectively. Note that for the P(64) transition, an additional Lamb dip is visible, due to the R(11) transition of the 20012-00001 band for the ¹²C¹⁶O¹⁸O isotopologue. The fits using a Voigt profile (red solid line) are also shown on the figure as well as the residuals (obs.–calc.) plotted on the small panels below each graph.

3. Data analysis and error budget

A. Data analysis

As already reported^37,40,43,44 in the case of a saturated line profile, the ring down signals are no more a purely decreasing exponential with time. In Giusfredi et al.,³⁷ a non-exponential model was proposed to fit the ring down events and to obtain more reliable Lamb dip profiles. However, in the studies dedicated to transition frequency retrievals from Lamb dips, a simple exponential treatment is generally adopted^10,12,38,45 arguing that this should not bias the determination of the center frequency of the absorption line due to the symmetry of the saturation spectrum.

The four examples of Lamb dips displayed on Fig. 3 result from the RD fit with a purely exponential function. The Lamb dip profiles are then fitted with a Voigt function for which the Lorentzian widths as well as the dip amplitude and a second order polynomial baseline are free to float. This results in residuals at the noise level (lower panels of Fig. 3). Typical fitted values of Lorentzian widths are between 130 and 250 kHz (FWHM). Interestingly, no Gaussian contribution was necessary for the Lamb dips recorded for the 20013-00001 band while for the 20012-00001 band, a Gaussian contribution with a typical width of 110 kHz (FWHM) had to be added. Fig. 3 illustrates the very good quality factor (QF defined as the ratio of the change of absorption of the dip to the rms of the residuals) that can be achieved with a value close to 200 for the R(0) transition, as well as the pressure broadening which was observed for the higher J transitions such as R(60) for which a larger pressure value was used. The lower left panel shows an interesting feature with two Lamb dips accidentally close to each other, one corresponding to the P(64) transition of the 20012-00001 band of ¹²CO₂, as expected, and the second one to the R(11) transition for the same band but for the ¹²C¹⁶O¹⁸O isotopologue (the assignment of the P(64) 20012-00001 dip of ¹²CO₂ was established using combination difference relation – see below). The frequency of the R(11) transition of the ¹²C¹⁶O¹⁸O isotopologue is also reported in the ESI,† as well as for the P(12) transition of the same isotopologue.

For each transition, 10 spectra are generally recorded showing a statistical dispersion on the line centers below 2 kHz for all the transitions with J′′ ≤ 70 for the 20012-00001 band and J′′ ≤ 62 for the 20013-00001 band. Tables 1 and 2 list the studied transitions with their measured frequencies, estimated final uncertainties and the number of recorded spectra for each of them, as well as the indicative pressure value.

B. Error budget

The different sources of uncertainties on the zero-pressure line frequencies reported in Tables 1 and 2 are discussed below and summarized in Table 3.

Table 3 Uncertainty budget of the low pressure transition frequencies reported in Table 1 for the 20013-00001 band and in Table 2 for the 20012-00001 band. The Freq. shift column corresponds to the correction applied to the measured frequencies

Source of uncertainty	Freq. shift (kHz)	Uncertainty (kHz)
Notes.a For all the transitions with J ≤ 70 for the 20012-00001 band and with J ≤ 62 for the 20013-00001 band.b For 102 over 107 transitions.
Statistics		<2.0^a
RF comb lock		0.73
Optical comb lock		<0.001
1st order Doppler shift		0.6
2nd order Doppler shift	0.09	<0.001
AC and DC Stark shift		<0.01
Power shift		2
Pressure shift		<1^b
RD treatment		2
Total	0.09	<4

---

According to eqn (3), the frequency of the laser light injected in the cavity only depends on f_rep, f_CEO, f_synth and f_AOM. All these frequencies are referenced to a 10 MHz Rb frequency standard (Model PRS 10 from SRS) which is phase-locked to a GPS timing receiver leading to a (short-term and long-term) stability better than 5 × 10⁻¹². This leads to negligible uncertainties on the four frequencies but as f_rep has to be multiplied by the tooth number (between ∼581 200 and 587 700 in our studied range) when the comb is RF locked, it leads to uncertainties between 726 and 734 Hz. Note that for the optical lock the reference frequency is known with a relative accuracy at the 10⁻¹⁶ level, reducing drastically the uncertainty on the corrected side-band frequency. To check the impact of the RF and optical locks, we recorded 36 spectra of the P(12) transition in the 20012-00001 band with the comb optically-locked followed by 46 spectra with the comb RF-locked. We observe a decrease of 760 Hz of the mean frequency value in the RF-lock case compared to the optical lock case (with standard error of the mean of 138 and 130 Hz, respectively). This difference is close to the estimated uncertainty of the RF-lock. Additionally, due to a narrower source linewidth and improved cavity injection, the QF of the Lamb dip is improved with the optical lock from 175 to 253 in average.

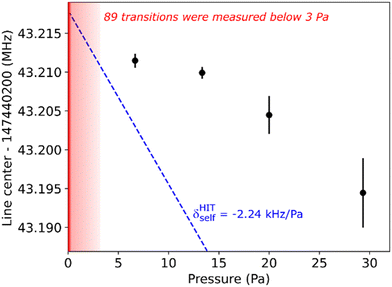
The possible impact of the pressure shift on the Lamp dip center values has to be considered as it might affect the frequency at zero-pressure. For this purpose, we measured several Lamb dip spectra for the weak P(60) transition in the 20012-00001 band at pressure values of about 7, 13, 20 and ∼30 Pa (Note that most of our measurements rely on spectra recorded at much lower pressure, below 1 Pa – see Tables 1 and 2). The pressure dependence of the Lamb dip centers averaged over all the spectra at a given pressure are plotted on Fig. 4. As expected from Fig. 2 (case a) of Alekseev et al.⁴⁶ and from Fig. 2 of Bagaev et al.⁴⁷ (or identically Fig. 4.35 of Letokhov⁴⁸), a non-linear dependence of the pressure shift with the pressure is observed. This is due to the transition from the low pressure regime towards the usual high pressure collisional regime. As a result, the pressure shift is observed to evolve from a value of ∼−0.23 kHz Pa⁻¹ (or −7.8 × 10⁻⁴ cm⁻¹ atm⁻¹) at very low pressure to an high pressure value which has a 10 times larger amplitude (−2.24 kHz Pa⁻¹ or −7.57 × 10⁻³ cm⁻¹ atm⁻¹) according to HITRAN2020.⁴⁹ This variation is similar to that reported in Tan et al.¹⁴ for the P(10) transition of the 30012-00001 band of ¹²CO₂: a pressure shift of −0.35 ± 0.08 kHz Pa⁻¹ was measured below 4 Pa, i.e. a four times smaller than the −1.7 kHz Pa⁻¹ pressure shift coefficient recommended in the HITRAN database. The uncertainty due to the pressure shift was estimated by fitting a second order polynomial function to the data points of Fig. 4. Thanks to the very low pressures adopted for most of the Lamb dip measurements (Tables 1 and 2), the pressure shift has a negligible contribution (<1 kHz) for most of the transitions. Note that if the usual pressure shift values are used to get zero-pressure frequencies from measurements in the low pressure regime,^8,12 errors could be introduced.

Fig. 4 Pressure dependence of the Lamb dip center for the P(60) transition of the 20012-00001 band of ¹²CO₂. The dashed blue line represents the self-pressure shift coefficient reported in HITRAN2020 for the same transition.

Another source of uncertainty in our experimental set-up could be due to the Doppler frequency shift, induced by the moving speed of the output mirror mounted on the piezo-actuator and accumulated during the recorded light decays. To quantify this possible bias we have slightly modified the acquisition software and the set-up to distinguish between the RD events obtained for the increasing part of the triangular voltage function applied to the piezo actuator (RD_i) and those obtained for the decreasing part (RD_d). As shown on Fig. 5, a shift between the Lamb dips retrieved from RD_i and RD_d is clearly visible. For the triangular function parameters applied during all the measurements, the observed shift is typically equal to 80 kHz. A bias could occur if the number of RD_i and RD_d differs. From several Lamb dip spectra, differences of a few percent can be observed between the number of RD_i and RD_d. This leads to a small bias between the “true” frequency and the one retrieved when all RDs are considered. From these measurements, an estimated uncertainty of 0.6 kHz due to this 1^st order Doppler shift effect is adopted in the budget error.

Fig. 5 Example of Lamb dips for the P(32) transition of the 20012-00001 band. The Lamb dips are obtained from the RDs corresponding to the increasing (dashed line) and decreasing (dotted line) part of the triangular voltage function applied to the piezo actuator on which the output mirror is mounted. Note the shift of 77 kHz between the two Lamb dips due to the 1^st order Doppler effect. The red solid line corresponds to the Lamb dip retrieved from all the RD events.

Measured absolute frequencies have to be corrected from the 2^nd order Doppler shift by ³⁶ with c the speed of light in vacuum, k_B the Boltzmann constant, T the gas temperature in K and m the molecular mass of ¹²C¹⁶O₂. The correction that we applied to the measured frequencies is between 90.5 and 93.5 Hz depending on the transition with an uncertainty of ∼15 mHz due to the gas temperature uncertainty.

The AC Stark shift due to the intracavity optical field, as well as the DC Stark shift which could be due to the static charge buildup on the cavity mirrors, have to be considered.^12,43 Based on the isotropic, [small alpha, Greek, tilde], and anisotropic, Δ[small alpha, Greek, tilde], polarizabilities of the CO₂ molecule in its ground state and excited vibrational states,⁵⁰ we obtain the DC Stark shift from eqn (1) of Cai et al.⁵¹ and the AC Stark shift from .⁵² The calculated impact on the measured frequencies is at the Hz level (taking a static field strength of 30 kV m⁻¹ as in Reed et al.¹² and an intracavity optical field strength of 19.6 kV m⁻¹), so completely negligible.

In addition, we investigated experimentally the potential shift due to intra-cavity power by recording series of Lamb dip spectra for the P(40) transition of the 20012-00001 band with four levels of RD threshold corresponding to different intra-cavity power at the RD starting point (between 0.15 and 0.45 W). A maximum variation of ∼2 kHz is observed between the four data points. This value is consistent with what is obtained by adopting different thresholds in the analysis of the RDs. The same analysis on other recorded dips shows a similar behavior. Thus we observe a positive systematic shift of the center frequency as a function of power whose physical mechanism is not clear. An uncertainty of 2 kHz due to this power shift is thus integrated in the budget error for all the transitions.

As a test of the impact of our modeling of the RD signal with a standard exponential function, we considered a treatment using a non-linear exponential function in order to take into account the fact that, in a not too high saturation regime and at low pressure, the absorption coefficient depends on the light intensity in the form:³⁷

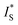where α_cav is the empty-cavity loss, α_gas is the unsaturated molecular absorption and is the saturation intensity. The non-linear exponential function was calculated in a recursive manner and led to residuals of the RD fit at the noise level. Due to correlations, the obtained parameters were very noisy if floated all together. Fixing α_cav which can reasonably be expected to be constant over the range of a given spectrum, has led to frequency variations on the order of 2 kHz when fitting the obtained as compared to the frequency values reported here using a purely exponential fit. The origin of these variations needs further investigations. An additional uncertainty of 2 kHz was thus added for all the transitions to take into account the impact of the ring-down treatment.

4. Spectroscopic analysis and comparison to literature

For an isolated vibrational state, the energy values of the rotational levels can be reproduced with the standard expression:

E(J) = G_v + B_vJ(J + 1) − D_vJ²(J + 1) + H_vJ³(J + 1)³ + L_vJ⁴(J + 1)⁴ + M_vJ⁵(J + 1)⁵ + N_vJ⁶(J + 1)⁶ + O_vJ⁷(J + 1)⁷ +… (5)

where G_v is the vibrational term and B_v…O_v are the rotational and centrifugal distortion constants. The experimental value of the energy of the upper rotational levels in the 20012 and 20013 vibrational states was obtained by adding the lower state energy values to the measured transition frequencies. The ¹²CO₂ ground state rotational constants determined in Wu et al.¹⁰ with a very high accuracy were used to calculate the ground state energy levels. The spectroscopic constants of the 20012 and 20013 upper states were derived from a fit of the obtained upper state energy values. (Note that each energy level has generally two experimental determinations from the R(J − 1) and P(J + 1) transitions). Applying Eq. (5) of Wu et al.¹⁰ to the transitions measured in this work for the 20012-00001 and 20013-00001 bands and fixing the B′′, D′′, H′′ and L′′ constants to the values reported in the Table 2 of Wu et al.,¹⁰ we are able to reproduce our experimental ground combination differences at the kHz level (mean difference of 1.0 kHz; 1σ-standard deviation of 1.2 kHz), confirming the constants of Wu et al.¹⁰ up to J = 63. Energy levels up to J ≤ 63 were thus included in our fit. The fitted spectroscopic constants listed in Table 4 allow reproducing the energy levels of the 20012 and 20013 states with a (meas. – calc.) standard deviation of 1.1 kHz and 0.8 kHz, respectively.

Table 4 Ro-vibrational constants (in MHz) of the 20012 and 20013 vibrational states of ¹²CO₂. The fit was limited to J ≤ 63 excluding the perturbed J = 43 and 45 energy levels of the 20012 state (see text). N_fit and N_meas represent the number of levels included in the fit and measured, respectively

Parameter (MHz)	20012	20013
G	1.492317285961(5) × 10^8	1.455079611574(3) × 10^8
B	1.1587981508(6) × 10^4	1.1637877181(4) × 10^4
D	4.08036(2) × 10^−3	5.45134(1) × 10^−3
H	2.187(3) × 10^−8	1.818(1) × 10^−8
L	1.4(2) × 10^−13	−3.2(5) × 10^−14
M	1.38(9) × 10^−16	−2.5(1) × 10^−17
N	−2.1(2) × 10^−20	9.8(10) × 10^−22
O	3.1(1) × 10^−24
N fit /N meas	54/63	40/43
rms (Hz)	1100	808

---

The residuals of the fit plotted in Fig. 6 indicate that the J = 43 and 45 rotational energy levels of the 20012 state (excluded from the fit) are affected by a local resonance interaction around J = 43. The very small energy perturbation on the order of 15 kHz at J = 43 is confirmed by the very close value of the residuals obtained from the P(44) and R(42) Lamb dip centers. By consideration of the theoretical calculations of the ¹²CO₂ spectrum by the Ames group⁵³ and in the Carbon Dioxide Spectroscopic Databank (CDSD),³⁵ the perturber state could be identified as the 04411 vibrational state. Both calculations predict that the rotational levels of the 20012 and 04411 exhibit an energy crossing with an energy separation of only 0.15 cm⁻¹ at J = 43. The 20012 J = 43 energy level being larger than its 04411 counterpart, the perturbation leads to a shift to higher energy of the 20012 J = 43 level, in agreement with experiment. Note that the energy separation between the next J = 45 level is predicted to be significantly larger (0.47 cm⁻¹) and of opposite sign, in agreement with the observation of a more reduced and negative shift of the 20012 J = 45 level from its unperturbed position (about −3 kHz). We present in Fig. 7, the spectrum of the 20012-00001 and 04411-00001 bands as provided by the CDSD and Ames line lists. According to these calculations, the evidenced interaction leads to a weak intensity transfer from the 20012-00001 band to the dark 04411-00001 band around J = 43. Both calculations indicate that the strongest 04411-00001 lines, P(44) and R(42), have a predicted intensity of a few 10⁻²⁸ cm molecule⁻¹ which makes them detectable by high sensitivity CRDS [see e.g. Čermák et al.⁵⁴ and Karlovets et al.⁵⁵]. These intensity values are six orders of magnitude smaller than the intensity of the corresponding 20012-00001 lines, illustrating the weakness of the evidenced interaction. Let us note that the level of convergence of the Ames calculations and the accuracy of the CDSD calculations are not sufficient to account for the 15 kHz (or 5 × 10⁻⁷ cm⁻¹) perturbation of the 20012 J = 43 level but the very faint interaction evidenced by our measurements is convincingly revealed by the intensity transfer predicted by both calculations. Although the Ames and CDSD intensities of the 04411-00001 extra lines differ by up to 50%, the agreement of the CDSD and Ames predictions obtained with quite different theoretical approaches is remarkable (Fig. 7). Finally, let us mention that the 20012 and 04411 states belong to the same P = 2V₁ + V₂ + 3V₃ = 7 polyad (V₁, V₂, and V₃ are the quantum numbers of the harmonic oscillators). The interaction mechanism is thus a Δl₂ = 4 intrapolyad interaction accounted for by the effective Hamiltonian model used for the CDSD (In fact, the original version of the CDSD⁵⁶ was restricted to Δl₂ < 4 bands but the Δl₂ = 4 bands were added in the updated version adopted for the HITRAN2020 line list).

Fig. 6 Difference between the measured rotational energy levels, and the values fitted using Eq. (5), , for the 20013 and 20012 vibrational states (upper and lower panel, respectively). Red triangles and black dots correspond to energy levels obtained from P- and R-transitions, respectively. The dashed zones correspond to J values excluded from the fit.

Fig. 7 The 20012-00001 and the 04411-00001 bands of ¹²CO₂ as provided by the CDSD³⁵ and Ames⁵³ databases. The 04411-00001 lines are induced by an intensity transfer from the 20012-00001 band for upper J values around 43.

From a detailed consideration of the 20012-00001 residuals presented in Fig. 6, it appears that residuals associated to P(J + 1) transitions are in general larger than those of the R(J − 1) transitions reaching the same J upper level. With an average difference of about 1 kHz and a similar value for the standard deviation, the effect is small. Nevertheless, it seems to reveal some small deviations between the R(J − 1)–P(J + 1) ground state combination differences (GSCD) obtained from the measured frequencies and those calculated using the ground state spectroscopic constants adopted from Wu et al.¹⁰ Consequently, together with literature data, the present measurements might be valuable to slightly refine the ground state spectroscopic constants of ¹²CO₂.

As main output of the present study, we provide as ESI,† a recommended list of accurate ¹²CO₂ transition frequencies for the 20012-00001 and 20013-00001 bands. It was obtained as follows.

(i) for upper state J values smaller than 63 (e.g. P(64)–R(62) transitions), the recommended frequencies are values calculated using the spectroscopic constants of Table 4, except for the P(44), P(46), R(42) and R(44) perturbed transitions of the 20012-00001 band for which experimental values were kept.

(ii) for J values larger than 63, experimental values are available only for R(64)–R(68) of the 20013-00001 band and P(64)–P(74) of the 20012-00001 band. The experimental values were kept and complemented with their GSCD counterpart allowing extending the set of accurate frequencies beyond the observations. Finally, the recommended list, including 145 accurate transition frequencies is obtained while 107 transition frequencies were measured. This set of secondary reference standards with kHz-accuracy samples regularly the large 4788–5015 cm⁻¹ interval (from 1994 to 2089 nm). The uncertainty attached to the recommended transition frequencies derived from the fitted spectroscopic constants was obtained as the square root of the quadratic sum of the RMS of the fit, indicated in Table 4 for the statistical error, and of the other sources of uncertainties reported in Table 3.

The recommended frequencies can be used for comparison with literature data (Fig. 8). We will consider the position values included in CDSD³⁵ as reproduced in the HITRAN2020 database⁴⁹ and measurements by Fourier transform spectroscopy (FTS) by Benner et al.¹⁶ and Toth et al.,²¹ hereafter called Benner2016 and Toth2008, respectively. For both FTS datasets, the transition frequencies are values calculated from spectroscopic constants fitted on the corresponding FTS measurements.

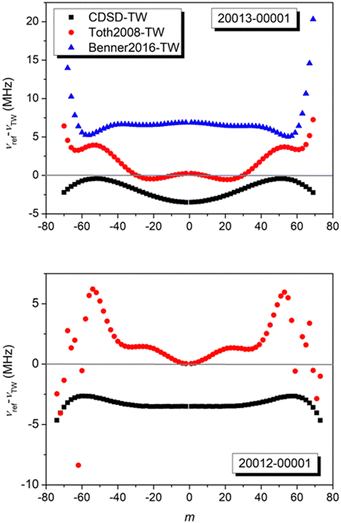Fig. 8 Comparison between the transition frequencies reported in HITRAN2020,⁴⁹ derived from CDSD, Toth2008²¹ and Benner2016¹⁶ with values obtained in this work (TW) versus m for the 20012-00001 and 20013-00001 bands. Note the different scale of the y-axis.

Overall, the deviations range between −4 and 7 MHz with a strong m dependence for Toth2008 (m is defined as m = −J and m = J + 1 for P- and R-branch transitions, respectively). In his publication, Toth estimated the frequency uncertainties to 1.5 MHz and 15 MHz for the strong lines and the weak high J lines of strong bands, respectively. This is mostly consistent with the observations if we consider as strong lines those with |m| < 35.

A quite constant difference of about 6 MHz is observed for the FTS data of Benner2016, up to J values of about 60. Benner et al. reported their positions of the 20013-00001 band with uncertainties <1 × 10⁻⁶ cm⁻¹ (30 kHz) for 0 ≤ J ≤ 40, <1 × 10⁻⁵ cm⁻¹ for 40 < J ≤ 60 and <1 × 10⁻⁴ cm⁻¹ for 60 < J ≤ 80. These values correspond to the statistical error obtained from the fit of the theoretical quantum mechanical formulae and do not include systematic errors. The evidenced 6 MHz shift (about 2 × 10⁻⁴ cm⁻¹) thus measures the error of the frequency axis calibration of the used FTS spectra.

The CDSD positions (adopted in HITRAN2020) are systematically lower than our values for both bands. The CDSD deviations show weak m dependence with an amplitude limited to 3.5 MHz even for high J values, which is largely below the 300 MHz uncertainty attached to the considered positions in the HITRAN2020 database.

Finally, when comparing the four frequency values reported in Mondelain et al.³² to this work, differences between 6 to 150 kHz are found, in agreement with the 90 kHz 1σ-uncertainty of this reference.

5. Conclusion

Frequencies of 107 transitions have been determined by saturation spectroscopy for the two strongest bands of ¹²CO₂ in the 2 μm region which are of particular importance for remote sensing retrievals. Compared to the most accurate literature data, the achieved kHz-accuracy represents a gain of three orders of magnitude. These measurements, which are the first ones of the considered bands referenced to absolute frequency reference standard, were performed by recording series of Lamb dip spectra with a comb-referenced cavity ring down spectrometer and applying the feed-forward technique via an electro-optic modulator to transfer the coherence of an optical comb tooth to an extended cavity laser source. The amplitude of the self-pressure shift of the Lamb-dip was evaluated for the P(60) transition of the 20012-00001 band and found significantly smaller than its usual value at higher pressure. The sub-Pa pressure values adopted for the recordings made the Lamb dip pressure shifts totally negligible in our experimental conditions.

The fitted values of the spectroscopic constants of the 20012 and 20013 vibrational states allow reproducing their rotational energy levels (for J ≤ 63) with an RMS deviation of 1.1 and 0.8 kHz, respectively, the ground state spectroscopic constants being constrained to the values reported by Wu et al.¹⁰ A 15 kHz shift of the J = 43 level of the 20012 state from its unperturbed energy value reveals a very faint interaction with a dark state. On the basis of Ames⁵³ and CDSD³⁵ theoretical calculations of the ¹²CO₂ absorption spectrum, the perturber could be identified as the 04411 dark state. Interestingly, the measured 15 kHz energy shift is beyond the accuracy of both calculations but the existence of the coupling between the 20012 and 04411 states is theoretically predicted and shows up as an intensity transfer to the 04411-00001 band around the J = 43 value of the energy crossing between the 20012 and 04411 states. Note that the predicted intensity of the 04411-00001 extra lines are more than six orders of magnitude smaller than those of the 20012-00001.

Combining frequencies calculated from the determined spectroscopic constants, measurements and GSCD relations, a recommended list of 145 transition frequencies spanning the large 1.99–2.09 μm interval (4788–5015 cm⁻¹) is provided. Most of these frequencies are given with a combined standard uncertainty on the order of 4 kHz that we believe to be conservative. They will be valuable as secondary reference standards for a number of atmospheric remote sensing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is funded by the European Space Agency (ESA) through the contract No. 4000132228/20/I-NS with DLR (Deutsches Zentrum fuer Luft- und Raumfahrt) entitled Improved Spectroscopy for Carbon Dioxide, Oxygen, and Water Vapour Satellite Measurements for which the authors are sub-contractants. The authors are grateful to Equipex REFIMEVE+ (ANR-11-EQPX-0039) for the ultra-stable reference frequency delivered. F. Gibert from LMD and P. Cacciani from PhLAM are acknowledged for lending the Thulium doped fiber amplifier and the external cavity diode laser, respectively. The work was also supported by the joint Slovak-Czech-French Danube Region project (DS-FR-19-0050), and by the Slovak Research and Development Agency (contract number APVV-19-0386). P.C. thanks CNRS for a one-month support at LIPhy-Grenoble. DM wants to thank A. Ross from ILM and J.-M. Hartmann from LMD for fruitful discussions on global fit of effective Hamiltonians and on pressure shifts with Lamb dips, respectively. We are indebted to X. Huang (NASA-Ames) for useful discussions about the identification of the 04411 state as perturber of the 20012 state.

References

1. D. Wunch, G. C. Toon, J. F. L. Blavier, R. A. Washenfelder, J. Notholt, B. J. Connor, D. W. T. Griffith, V. Sherlock and P. O. Wennberg, The Total Carbon Column Observing Network, Philos. Trans. R. Soc., A, 2011, 369, 2087–2112.
2. V. M. Devi, D. C. Benner, K. Sung, L. R. Brown, T. J. Crawford, C. E. Miller, B. J. Drouin, V. H. Payne, S. Yu, M. A. H. Smith, A. W. Mantz and R. R. Gamache, Line parameters including temperature dependences of self- and air-broadened line shapes of ¹²C¹⁶O₂: 1.6 μm region, J. Quant. Spectrosc. Radiat. Transfer, 2016, 177, 117–144.
3. M. Birk, C. Röske and G. Wagner, High accuracy CO₂ Fourier transform measurements in the range 6000–7000 cm⁻¹, J. Quant. Spectrosc. Radiat. Transfer, 2021, 272, 107791.
4. D. Mondelain, A. Campargue, H. Fleurbaey, S. Kassi and S. Vasilchenko, CRDS measurements of air-broadened lines in the 1.6 μm band of ¹²CO₂: line shape parameters with their temperature dependence, J. Quant. Spectrosc. Radiat. Transfer, 2022, 288, 108267.
5. D. A. Long, S. Wójtewicz, C. E. Miller and J. T. Hodges, Frequency-agile, rapid scanning cavity ring-down spectroscopy (FARS-CRDS) measurements of the (30012) ← (00001) near-infrared carbon dioxide band, J. Quant. Spectrosc. Radiat. Transfer, 2015, 161, 35–40.
6. R. Guo, J. Teng, H. Dong, T. Zhang, D. Li and D. Wang, Line parameters of the P-branch of (30012) ← (00001) ¹²C¹⁶O₂ band measured by comb-assisted, PoundDrever-Hall locked cavity ring-down spectrometer, J. Quant. Spectrosc. Radiat. Transfer, 2021, 264, 107555.
7. D. A. Long, G.-W. Truong, J. T. Hodges and C. E. Miller, Absolute ¹²C¹⁶O₂ transition frequencies at the kHz-level from 1.6 to 7.8 μm, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 112–115.
8. Z. D. Reed, B. J. Drouin, D. A. Long and J. T. Hodges, Molecular transition frequencies of CO₂ near 1.6 μm with kHz-level uncertainties, J. Quant. Spectrosc. Radiat. Transfer, 2021, 271, 107681.
9. Z. D. Reed, B. J. Drouin and J. T. Hodges, Inclusion of the recoil shift in Doppler-broadened measurements of CO₂ transition frequencies, J. Quant. Spectrosc. Radiat. Transfer, 2021, 275, 107885.
10. H. Wu, C.-L. Hu, J. Wang, Y. R. Sun, Y. Tan, A.-W. Liu and S.-M. Hu, A well-isolated vibrational state of CO₂ verified by near-infrared saturated spectroscopy with kHz accuracy, Phys. Chem. Chem. Phys., 2020, 22, 2841–2848.
11. J. Burkart, T. Sala, D. Romanini, M. Marangoni, A. Campargue and S. Kassi, Communication: saturated CO₂ absorption near 1.6 μm for kilohertz-accuracy transition frequencies, J. Chem. Phys., 2015, 142, 191103.
12. Z. D. Reed, D. A. Long, H. Fleurbaey and J. T. Hodges, SI-traceable molecular transition frequency measurements at the 10⁻¹² relative uncertainty level, Optica, 2020, 7, 1209–1220.
13. G.-W. Truong, D. A. Long, A. Cygan, D. Lisak, R. D. Zee and J. T. Hodges, Comb-linked, cavity ring-down spectroscopy for measurements of molecular transition frequencies at the kHz-level, J. Chem. Phys., 2013, 138, 094201.
14. Y. Tan, Y. R. Xu, T. P. Hua, A. W. Liu, J. Wang, Y. R. Sun and S.-M. Hu, Cavity-enhanced saturated absorption spectroscopy of the (30012)–(00001) band of ¹²C¹⁶O₂, J. Chem. Phys., 2022, 156, 044201.
15. L. S. Rothman and L. D. Young, Infrared energy levels and intensities of carbon dioxide-II, J. Quant. Spectrosc. Radiat. Transfer, 1981, 25, 505.
16. D. C. Benner, V. M. Devi, K. Sung, L. R. Brown, C. E. Miller, V. H. Payne, B. J. Drouin, S. Yu, T. J. Crawford, A. W. Mantz, M. A. H. Smith and R. R. Gamache, Line parameters including temperature dependences of air- and self-broadened line shapes of ¹²C¹⁶O₂: 2.06 μm region, J. Mol. Spectrosc., 2016, 326, 21–47.
17. R. A. Toth, L. R. Brown, C. E. Miller, V. M. Devi and D. C. Benner, Line strengths of ¹²C¹⁶O₂: 4550–7000 cm⁻¹, J. Mol. Spectrosc., 2006, 239, 221–242.
18. R. A. Toth, L. R. Brown, C. E. Miller, V. M. Devi and D. C. Benner, Self-broadened widths and shifts of ¹²C¹⁶O₂: 4750–7000 cm⁻¹, J. Mol. Spectrosc., 2006, 239, 243–271.
19. R. A. Toth, C. E. Miller, V. M. Devi, D. C. Benner and L. R. Brown, Air-broadened half width and pressure shift coefficients of ¹²C¹⁶O₂ bands: 4750–7000 cm⁻¹, J. Mol. Spectrosc., 2007, 246, 133–157.
20. R. A. Toth, C. E. Miller, L. R. Brown, V. M. Devi and D. C. Benner, Line positions and strengths of ¹⁶O¹²C¹⁸O, ¹⁸O¹²C¹⁸O and ¹⁷O¹²C¹⁸O between 2200 and 7000 cm⁻¹, J. Mol. Spectrosc., 2007, 243, 43–61.
21. R. A. Toth, L. R. Brown, C. E. Miller, V. M. Devi and D. C. Benner, Spectroscopic database of CO₂ line parameters: 4300–7000 cm⁻¹, J. Quant. Spectrosc. Radiat. Transfer, 2008, 109, 906–921.
22. C. B. Suarez and F. P. J. Valero, Temperature dependence of self-broadened halfwidths of CO₂, J. Quant. Spectrosc. Radiat. Transfer, 1990, 43, 327–334.
23. L. Régalia-Jarlot, V. Zénninari, B. Parvitte, A. Grossel, X. Thomas, P. Heyden von der and G. Durry, A complete study of the line intensities of four bands of CO₂ around 1.6 and 2.0 μm: a comparison between Fourier transform and diode laser measurements, J. Quant. Spectrosc. Radiat. Transfer, 2006, 101, 325–338.
24. L. Joly, F. Gibert, B. Grouiez, A. Grossel, B. Parvitte, G. Durry and V. Zénninari, A complete study of CO₂ line parameters around 4845 cm⁻¹ for lidar applications, J. Quant. Spectrosc. Radiat. Transfer, 2008, 109, 426–434.
25. L. Joly, F. Marnas, F. Gibert, D. Bruneau, B. Grouiez, P. H. Flamant, G. Durry, N. Dumelie, B. Parvitte and V. Zéninari, Laser diode absorption spectroscopy for accurate CO₂ line parameters at 2 μm: consequences for space-based DIAL measurements and potential biases, Appl. Opt., 2009, 48, 5475–5483.
26. J. S. Li, G. Durry, J. Cousin, L. Joly, B. Parvitte, P. H. Flamant, F. Gibert and V. Zéninari, Tunable diode laser measurement of pressure-induced shift coefficients of CO₂ around 2.05 μm for lidar applications, J. Quant. Spectrosc. Radiat. Transfer, 2011, 112, 1411–1419.
27. J. S. Li, G. Durry, J. Cousin, L. Joly, B. Parvitte and V. Zénninari, Self-induced pressure shift and temperature dependence measurements of CO₂ at 2.05 μm with a tunable diode laser spectrometer, Spectrochim. Acta, Part A, 2012, 85, 74–78.
28. L. E. Christensen, G. D. Spiers, R. T. Menzies and J. C. Jacob, Tunable laser spectroscopy of CO₂ near 2.05 μm: atmospheric retrieval biases due to neglecting line-mixing, J. Quant. Spectrosc. Radiat. Transfer, 2012, 113, 739–748.
29. G. Casa, R. Wehr, A. Castrillo, E. Fasci and L. Gianfrani, The line shape problem in the near-infrared spectrum of self-colliding CO₂ molecules: experimental investigation and test of semiclassical models, J. Chem. Phys., 2009, 130, 184306.
30. T. Q. Bui, D. A. Long, A. Cygan, V. T. Sironneau, D. W. Hogan, P. M. Rupasinghe, R. Ciuryło, D. Lisak and M. Okumura, Observations of Dicke narrowing and speed dependence in air-broadened CO₂ lineshapes near 2.06 μm, J. Chem. Phys., 2014, 141, 174301.
31. H. Fleurbaey, H. Yi, E. M. Adkins, A. J. Fleisher and J. T. Hodges, Cavity ring-down spectroscopy of CO₂ near λ = 2.06 μm: accurate transition intensities for the Orbiting Carbon Observatory-2 (OCO-2) “strong band”, J. Quant. Spectrosc. Radiat. Transfer, 2020, 252, 107104.
32. D. Mondelain, A. Campargue, H. Fleurbaey, S. Kassi and S. Vasilchenko, Line shape parameters of air-broadened ¹²CO₂ transitions in the 2.0 μm region, with their temperature dependence, J. Quant. Spectrosc. Radiat. Transfer, 2023, 298, 108485.
33. D. Gatti, N. Coluccelli, A. Gambetta, A. Di Lieto, M. Tonelli, G. Galzerano, P. Laporta and M. Marangoni, Absolute frequency spectroscopy of CO₂ lines at around 2.09 μm by combined use of an Er: fiber comb and a Ho: YLF amplifier, Opt. Lett., 2011, 36, 3921–3923.
34. F. Gibert, D. Edouart, P. Monnier, C. Cénac, J. López and J. Collignan, A wind, temperature, H₂O and CO₂ scanning lidars mobile observatory to study surface-atmosphere interaction, Application in temperate and semi-arid region, European Lidar Conference (ELC2021), 2021, Granada, Spain.
35. S. A. Tashkun, V. I. Perevalov, R. R. Gamache and J. Lamouroux, CDSD-296, high-resolution carbon dioxide spectroscopic databank: an update, J. Quant. Spectrosc. Radiat. Transfer, 2019, 228, 124–131.
36. W. Demtröder, Laser Spectroscopy: Experimental Techniques, Springer, 4th edn, 2008, vol. 2.
37. G. Giusfredi, S. Bartalini, S. Borri, P. Cancio, I. Galli, D. Mazzotti and P. De, Natale, Saturated-absorption cavity ring-down spectroscopy, Phys. Rev. Lett., 2010, 104, 1–4.
38. J. Wang, Y. R. Sun, L.-G. Tao, A.-W. Liu, T.-P. Hua, F. Meng and S.-M. Hu, Comb-locked cavity ring-down saturation spectroscopy, Rev. Sci. Instrum., 2017, 88, 043108.
39. S. Vasilchenko, T. Delahaye, S. Kassi, A. Campargue, R. Armante, H. Tran and D. Mondelain, Temperature dependence of the absorption of the R (6) manifold of the 2ν₃ band of methane in air in support of the MERLIN mission, J. Quant. Spectrosc. Radiat. Transfer, 2023, 298, 108483.
40. O. Votava, S. Kassi, A. Campargue and D. Romanini, Comb coherence-transfer and cavity ring-down saturation spectroscopy around 1.65 μm: kHz-accurate frequencies of transitions in the 2ν₃ band of ¹²CH₄, Phys. Chem. Chem. Phys., 2022, 24, 4157–4173.
41. R. Gotti, M. Prevedelli, S. Kassi, M. Marangoni and D. Romanini, Feed-forward coherent link from a comb to a diode laser: application to widely tunable cavity ring-down spectroscopy, J. Chem. Phys., 2018, 148, 054202.
42. https://www.refimeve.fr/index.php/en/ .
43. J. Burkart, Optical feedback frequency-stabilized cavity ring-down spectroscopy – Highly coherent near-infrared laser sources and metrological applications in molecular absorption spectroscopy, PhD thesis, 2015.
44. D. Romanini, P. Dupré and R. Jost, Non-linear effects by continuous wave cavity ringdown spectroscopy in jet-cooled NO₂, Vib. Spectrosc., 1999, 19, 93–106.
45. S. Kassi, T. Stoltmann, M. Casado, M. Daëron and A. Campargue, Lamb dip CRDS of highly saturated transitions of water near 1.4 μm, J. Chem. Phys., 2018, 148, 054201.
46. V. A. Alekseev, T. L. Andreeva and I. I. Sobelman, Contribution to the theory of nonlinear power resonances in gas lasers, Sov. Phys.-JETP, 1973, 37, 413–418.
47. S. Bagaev, E. Baklanov and V. Chebotaev, Anomalous decrease of the shift of the center of the Lamb dip in low-pressure molecular gases, Sov. J. Exp. Theor. Phys. Lett., 1972, 16, 243.
48. V. S. Letokhov, Saturation spectroscopy, in High-Resolution Laser Spectroscopy. Topics in Applied Physics, ed. K. Shimoda, Springer, Berlin, Heidelberg, 1976, vol. 13.
49. I. E. Gordon, L. S. Rothman, R. J. Hargreaves, R. Hashemi, E. V. Karlovets, F. M. Skinner, E. K. Conway, C. Hill, R. V. Kochanov, Y. Tan, P. Wcisło, A. A. Finenko, K. Nelson, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, A. Coustenis, B. J. Drouin, J.-M. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, E. J. Mlawer, A. V. Nikitin, V. I. Perevalov, M. Rotger, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, E. M. Adkins, A. Baker, A. Barbe, E. Canè, A. G. Császár, A. Dudaryonok, O. Egorov, A. J. Fleisher, H. Fleurbaey, A. Foltynowicz, T. Furtenbacher, J. J. Harrison, J.-M. Hartmann, V.-M. Horneman, X. Huang, T. Karman, J. Karns, S. Kassi, I. Kleiner, V. Kofman, F. Kwabia-Tchana, N. N. Lavrentieva, T. J. Lee, D. A. Long, A. A. Lukashevskaya, O. M. Lyulin, V. Y. Makhnev, W. Matt, S. T. Massie, M. Melosso, S. N. Mikhailenko, D. Mondelain, H. S. P. Müller, O. V. Naumenko, A. Perrin, O. L. Polyansky, E. Raddaoui, P. L. Raston, Z. D. Reed, M. Rey, C. Richard, R. Tóbiás, I. Sadiek, D. W. Schwenke, E. Starikova, K. Sung, F. Tamassia, S. A. Tashkun, J. Vander Auwera, I. A. Vasilenko, A. A. Vigasin, G. L. Villanueva, B. Vispoel B, G. Wagner, A. Yachmenev and S. N. Yurchenko, The HITRAN2020 molecular spectroscopic database, J. Quant. Spectrosc. Radiat. Transfer, 2022, 277, 107949.
50. C. Boulet, Personnal communication.
51. W. Q. Cai, T. E. Gough, X. J. Gu, N. R. Isenor and G. Scoles, Polarizability of CO₂ studies in molecular beam laser Stark spectroscopy, Phys. Rev. Lett., 1987, 36, 4722.
52. L. A. Rahn, R. L. Farrow, M. Koszykowski and P. Mattern, Observation of an Optical Stark Effect on Vibrational and Rotational Transitions, Phys. Rev. Lett., 1980, 45, 620.
53. X. Huang, D. W. Schwenke, R. S. Freedman and T. J. Lee, Ames-2016 line lists for 13 isotopologues of CO₂: updates, consistency, and remaining issues, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 224–241.
54. P. Čermák, E. V. Karlovets, D. Mondelain, S. Kassi, V. I. Perevalov and A. Campargue, High sensitivity CRDS of CO₂ in the 1.74 μm transparency window. A validation test for the spectroscopic databases, J. Quant. Spectrosc. Radiat. Transfer, 2018, 207, 95–103.
55. E. V. Karlovets, S. Kassi and A. Campargue, High sensitivity CRDS of CO₂ in the 1.18 μm transparency window. Validation tests of current spectroscopic databases, J. Quant. Spectrosc. Radiat. Transfer, 2020, 247, 106942.
56. S. A. Tashkun, V. I. Perevalov, R. R. Gamache and J. Lamouroux, CDSD-296, high resolution carbon dioxide spectroscopic databank: version for atmospheric applications, J. Quant. Spectrosc. Radiat. Transfer, 2015, 152, 45–73.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01603j

‡ LIPhy, Bat. E, 140 rue de la Physique, 38400 Saint-Martin d’Hères, France.

---