 Open Access Article
Open Access ArticleThe Rydberg 3p multiplet structure of the fenchone C band absorption
Ivan
Powis
 * and
Dhirendra P.
Singh†
* and
Dhirendra P.
Singh†

School of Chemistry, The University of Nottingham, University Park, Nottingham NG7 2RD, UK. E-mail: ivan.powis@nottingham.ac.uk; Tel: +44 115 9513467
First published on 1st June 2023
Abstract
The vibrationally structured 3pz Rydberg excitation is identified and assigned in the VUV absorption spectrum of fenchone with an origin at 6.31 eV, below the prominent 6.4 eV ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) (nominally 3p) band onset. This feature cannot, however, be observed in (2+1) REMPI spectra, as its relative excitation cross-section is much reduced in a two-photon transition. The 3py and 3px excitation thresholds, found to differ by only 10–30 meV, lie around 6.4 eV corresponding to the first intense
(nominally 3p) band onset. This feature cannot, however, be observed in (2+1) REMPI spectra, as its relative excitation cross-section is much reduced in a two-photon transition. The 3py and 3px excitation thresholds, found to differ by only 10–30 meV, lie around 6.4 eV corresponding to the first intense ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band peak in both VUV and REMPI spectra. Calculations of vertical and adiabatic Rydberg excitation energies, photon absorption cross-sections, and vibrational profiles are used to support these interpretations.
band peak in both VUV and REMPI spectra. Calculations of vertical and adiabatic Rydberg excitation energies, photon absorption cross-sections, and vibrational profiles are used to support these interpretations.
The chiral terpenoid fenchone (C10H16O) has commonly been used as a benchmark system in a range of chiroptical studies spanning both gas and liquid phases. These include optical rotation (OR),1,2 electronic circular dichroism (ECD),3,4 vibrational circular dichroism (VCD),5 Raman optical activity (ROA),6 photoelectron circular dichroism (PECD),7–10 photoexcitation circular dichroism (PXECD),11 and strong field-driven optical processes.12 A major attraction of fenchone for such studies lies in its conformationally rigid bicyclic ring structure (see Scheme 1), which facilitates rigorous theory-experiment comparisons in these conformationally sensitive phenomena by simply eliminating uncertainties associated with potentially ill-defined conformer populations obtained under typical experimental circumstances.
Recently, fenchone has become established as the prototypical molecule for the introduction and study of laser-driven PECD phenomena, in particular those using resonance enhanced multiphoton ionization (REMPI-PECD).13–24 Just as in single photon PECD phenomena, photoelectron angular distributions that are forward/backward asymmetric with respect to the propagation direction of a circularly polarized laser beam are observed. These arise from pure electric dipole interaction of the ionizing photon with the molecular target, resulting in very strong chiral asymmetry factors that may range up to several tens per cent. The additional target anisotropy induced by the photoexcitation of the intermediate state before its ionization is, however, expected to produce an even more richly structured, informative angular distribution.25
In this context an additional incentive promoting the prominent adoption of fenchone lies in its Rydberg excitation spectrum, starting a little above 200 nm.3 The low n = 3 Rydberg states then make readily accessible intermediates in REMPI ionization schemes using convenient laboratory UV laser sources. A number of REMPI-PECD studies using fenchone have explicitly sought insight into the role played by these Rydberg intermediates, primarily by comparing excitation through different bands of the Rydberg spectrum.15–17 Comparisons with different laser pulse durations further reveal that excitation through the 3p states can be subject to internal conversion to a 3s Rydberg state preceding the ionization step,15–18 while the implied rapid non-adiabatic dynamics results in different ion vibrational distributions with a corresponding influence upon the PECD asymmetry being observed.17 Direct time-resolved REMPI-PECD experiments with a delayed pump-probe have demonstrated additional ultrafast relaxation processes and rotational dephasing of the intermediate alignment that may occur prior to ionization of the intermediate.19,20
Theoretical studies of fenchone (2+1) REMPI-PECD26 indicate that very different photoelectron distributions are to be expected from excitation via each of the 3p substates (even neglecting intermediate dynamics within the intermediate state) due to state-specific alignment and ionization dynamics. Conversely, appreciation of the practical importance of intermediate state alignment and dynamics highlights the need for precise knowledge concerning the intermediate vibronic state excited (or of the wavepacket composition in short pulse experiments) not only for fundamental understanding, but also for ensuring reproducibility in those REMPI-PECD experiments that aim for the quantitative determination of enantiomeric excess.21–24
However, as noted by Pulm et al.3 in their seminal study of the VUV absorption by fenchone, the individual 3p multiplet states appear not to be resolved. Currently, the exact composition of 3pα=x,y,z state populations within an experimentally excited manifold is considered to be uncertain. The purpose of this communication is to re-examine recent experimental spectra and, aided by new calculations, to better identify the 3p absorption band composition.
We start by reviewing the spectroscopy of the Rydberg excitation. Fig. 1 shows the comparison between a recent gas phase absorption spectrum of fenchone, recorded with the VUV Fourier Transform (FT) absorption spectrometer on the DESIRS beamline at Synchrotron Soleil, and a (2+1) REMPI spectrum, recorded using 1.3 ps duration UV laser pulses.27 In agreement with the much earlier absorption spectrum3 one observes two structured bands, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) , in the region of interest which are assigned to excitation of, respectively, the 3s and 3p Rydberg states, but with the vibrational structure now better resolved.
, in the region of interest which are assigned to excitation of, respectively, the 3s and 3p Rydberg states, but with the vibrational structure now better resolved.
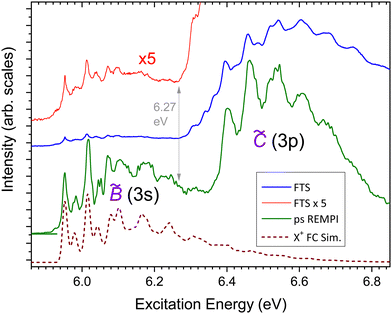 | ||
Fig. 1 The VUV ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) bands of fenchone: a comparison of the VUV FT spectrum and picosecond pulse laser (2+1) REMPI spectrum (both from ref. 27). Also shown is a 10 K Franck-Condon vibrational simulation of the bands of fenchone: a comparison of the VUV FT spectrum and picosecond pulse laser (2+1) REMPI spectrum (both from ref. 27). Also shown is a 10 K Franck-Condon vibrational simulation of the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) + cation spectrum (B3LYP/cc-pVTZ harmonic analysis, convolved with 120 cm−1 FWHM Gaussian function) with its origin set at the experimental 3s Rydberg origin, 5.952 eV.31 + cation spectrum (B3LYP/cc-pVTZ harmonic analysis, convolved with 120 cm−1 FWHM Gaussian function) with its origin set at the experimental 3s Rydberg origin, 5.952 eV.31 | ||
While the single-photon VUV absorption and two-photon REMPI spectra in Fig. 1 are overall very similar, differences are nevertheless evident. The estimated instrumental resolution for both recordings is ∼20 cm-1 but the FT spectrum was recorded using a room temperature sample cell, while the REMPI experiment was performed with a cooled molecular beam inlet. This may perhaps be seen in better definition of the vibrational peaks in the REMPI spectrum. A more immediately striking difference, however, is the relative weakness of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) band excitation in the FT spectrum compared to that in the (2+1) REMPI spectrum. This has been explained by the change of 3s transition strength, relative to that of the 3p excitations predicted by the calculated one-photon oscillator strengths and two-photon cross-sections.27,28
band excitation in the FT spectrum compared to that in the (2+1) REMPI spectrum. This has been explained by the change of 3s transition strength, relative to that of the 3p excitations predicted by the calculated one-photon oscillator strengths and two-photon cross-sections.27,28
Another feature that has not previously been remarked is the clear step-onset at 6.27 eV evident in the FT-VUV absorption spectrum (especially obvious with ×5 magnification) and that is not mirrored in the REMPI spectrum. Furthermore, the FT-VUV spectrum additionally displays distinct shoulders below the first intense ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band peak at 6.4 eV, again not noticeable in the REMPI spectrum. An expanded view of this region of the FT spectrum is provided in Fig. 2 and the vibrational structure is explored by comparison with a Franck-Condon vibrational simulation. Specifically, we here choose to use the
band peak at 6.4 eV, again not noticeable in the REMPI spectrum. An expanded view of this region of the FT spectrum is provided in Fig. 2 and the vibrational structure is explored by comparison with a Franck-Condon vibrational simulation. Specifically, we here choose to use the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) + cation simulated spectrum. This serves as a generic template for excitation into any Rydberg state, insofar as these states can be assumed to share the ground state cation structure as a common molecular core with only weak interaction with the outer Rydberg electron. Hence, we for now avoid making any prior assumption about the specific states. (Simulations for the individual Rydberg states and the cation
+ cation simulated spectrum. This serves as a generic template for excitation into any Rydberg state, insofar as these states can be assumed to share the ground state cation structure as a common molecular core with only weak interaction with the outer Rydberg electron. Hence, we for now avoid making any prior assumption about the specific states. (Simulations for the individual Rydberg states and the cation ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) + can be compared in Fig. 9 of ref. 27 and detailed vibrational analysis of the 3s band, using higher resolution ns REMPI data and a specific 3s state FC simulation, may also be found there. One may, however, anticipate that the
+ can be compared in Fig. 9 of ref. 27 and detailed vibrational analysis of the 3s band, using higher resolution ns REMPI data and a specific 3s state FC simulation, may also be found there. One may, however, anticipate that the ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) + ion core model is most challenged by the anticipated greater core penetration of the 3s Rydberg orbital. Nevertheless, at the more modest resolution of the jet-cooled ps REMPI
+ ion core model is most challenged by the anticipated greater core penetration of the 3s Rydberg orbital. Nevertheless, at the more modest resolution of the jet-cooled ps REMPI ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) band spectrum, the 10K
band spectrum, the 10K ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) + FC simulation can be seen in Fig. 1 to maintain good agreement with the experimental 3s spectrum.)
+ FC simulation can be seen in Fig. 1 to maintain good agreement with the experimental 3s spectrum.)
 | ||
Fig. 2 Expanded view of the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band region of the FT spectrum (effusive sample cell, room temperature).27 Also shown are copies of a simulated 290K Franck-Condon band region of the FT spectrum (effusive sample cell, room temperature).27 Also shown are copies of a simulated 290K Franck-Condon ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) + cation spectrum (B3LYP/cc-pVTZ harmonic analysis, convolved with 120 cm−1 FWHM Gaussian function) with their origin set at 6.308 eV and 6.397 eV. Along the top are marked the positions of the calculated CCSD/cc-pVDZ + R adiabatic excitations (Table 2), offset by −0.027 eV required to exactly align the 3s calculation with the experimental 3s origin (2.952 eV). Relative intensities of the FC simulation plots are arbitrarily chosen. + cation spectrum (B3LYP/cc-pVTZ harmonic analysis, convolved with 120 cm−1 FWHM Gaussian function) with their origin set at 6.308 eV and 6.397 eV. Along the top are marked the positions of the calculated CCSD/cc-pVDZ + R adiabatic excitations (Table 2), offset by −0.027 eV required to exactly align the 3s calculation with the experimental 3s origin (2.952 eV). Relative intensities of the FC simulation plots are arbitrarily chosen. | ||
In Fig. 2 a first such generic Rydberg FC simulation is plotted with its origin set to match the first prominent feature, 6.4 eV, in the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band. This can be seen to already offer a good reproduction of the
band. This can be seen to already offer a good reproduction of the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band spectrum above 6.4 eV. A second instance of the FC simulation is plotted to best align with the additional features noted in the FT spectrum below 6.4 eV, and it may be seen that this does then suggest that the shoulders at 6.31, 6.34, and 6.37 eV may originate from a Rydberg state with an origin around 6.31 eV. There is some evidence that the hot-band structure may contribute to the intensity between 6.27 eV and 6.31 eV although this is not apparent in the FC simulation.27
band spectrum above 6.4 eV. A second instance of the FC simulation is plotted to best align with the additional features noted in the FT spectrum below 6.4 eV, and it may be seen that this does then suggest that the shoulders at 6.31, 6.34, and 6.37 eV may originate from a Rydberg state with an origin around 6.31 eV. There is some evidence that the hot-band structure may contribute to the intensity between 6.27 eV and 6.31 eV although this is not apparent in the FC simulation.27
To gain more guidance, new calculations for the vertical and adiabatic excitation energies of the 3s and 3p Rydberg states were undertaken. The 3p multiplet states are labelled according to the local C2v geometry of the carbonyl group, as proposed by Pulm et al.,3 where 3pz lies parallel to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, 3px is normal to the C1–C2(
O bond, 3px is normal to the C1–C2(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–C3 plane and 3py lies in that plane. These designations are completely unambiguous when viewing the excited Rydberg orbitals obtained by a simple CIS calculation (that omits any correlation treatment). On the other hand, at this elementary level the predicted excitation energies exhibit errors of 2 eV compared to the experiment and it is evident that a treatment for electron correlation needs to be incorporated into the calculations. Table 1 includes results obtained by TD-DFT (with the CAM-B3LYP functional) and coupled cluster (CC) methods. Other calculations offering intermediate level treatments of electron correlation—CC2, ADC(2), ADC(3)—were made but only the latter are included in Table 1 as they all still exhibit absolute errors for the Rydberg energies of 0.5 eV or more. In this context, the performance of the much more economical TD-DFT method is notable.
O)–C3 plane and 3py lies in that plane. These designations are completely unambiguous when viewing the excited Rydberg orbitals obtained by a simple CIS calculation (that omits any correlation treatment). On the other hand, at this elementary level the predicted excitation energies exhibit errors of 2 eV compared to the experiment and it is evident that a treatment for electron correlation needs to be incorporated into the calculations. Table 1 includes results obtained by TD-DFT (with the CAM-B3LYP functional) and coupled cluster (CC) methods. Other calculations offering intermediate level treatments of electron correlation—CC2, ADC(2), ADC(3)—were made but only the latter are included in Table 1 as they all still exhibit absolute errors for the Rydberg energies of 0.5 eV or more. In this context, the performance of the much more economical TD-DFT method is notable.
| Methoda | TD-DFT (CAM-B3LYP) | ADC(3) | CCSD | CCSD(T) | CCSD | ||
|---|---|---|---|---|---|---|---|
| Transition | Verticalb | Adiabaticc | Verticalb | Adiabaticc | |||
| Basis | tAug-cc-Pvdz | cc-pVDZ + Rd | cc-pVDZ + Rd | ||||
| a Excited state CCSD calculations were performed using the EOM formalism implemented in Q-Chem 5.4. The ADC(3) calculation also used Q-Chem. TD-DFT calculations were made using Q-Chem and Dalton 2018 with the CAM-B3LYP functional. b Vertical transition energies calculated from the MP2/6-31G** optimised ground state geometry. c Adiabatic excitations estimated as ΔESCF values. Excited state energies were found by single point EOM-CCSD/cc-pVDZ + R or TD-DFT calculations made at the optimized excited state geometries found by TD-DFT (CAM-B3LYP)/cc-pVDZ + R calculations. For internal consistency the ground state geometry was calculated using the same density functional and basis set, again followed by a single point CCSD or TD-DFT calculation for its energy. No correction has been applied for zero-point energy difference. d The non-standard cc-pVDZ + R basis uses atom-centred cc-pVDZ functions with the addition of a set of diffuse hydrogenic-like functions29 (here ranging to n = 5.5 for s, p, d and n = 4.5 for f) which are located at the molecular centre-of-mass. e The numbers appearing in parentheses have had a constant offset (indicated in the bottom row) applied, bringing the calculated result for the 3s excitation into agreement with the experimental 3s origin value of 5.952 eV.31 | |||||||
| π* | 4.22 | 4.24 | — | 4.30 | 4.28 | 4.01 | — |
| 3s | 6.30 | 6.29 | 6.04 (5.95) | 6.55 (5.95) | 6.21 (5.95) | 6.03 (5.95) | 5.98 (5.95) |
| 3pz | 6.72 | 6.71 | 6.44 (6.35) | 6.91 (6.31) | 6.56 (6.30) | 6.38 (6.30) | 6.33 (6.31) |
| 3py | 6.75 | 6.75 | 6.47 (6.39) | 6.99 (6.39) | 6.64 (6.38) | 6.46 (6.38) | 6.39 (6.37) |
| 3px | 6.80 | 6.78 | 6.52 (6.43) | 7.01 (6.42) | 6.66 (6.40) | 6.49 (6.41) | 6.43 (6.40) |
| 3s origin offsete | −0.085 | −0.594 | −0.256 | −0.075 | −0.027 | ||
The first two columns of Table 1 provide a basis set comparison using TD-DFT (CAM-B3LYP) vertical excitation energies. The first set employs a conventional cc-pVDZ basis, augmented by 3 levels of diffuse functions on each atom (tAug-cc-pVDZ); the second uses the un-augmented cc-pVDZ atom-centred basis, but with a single set of s,p,d,f diffuse functions ranging up to n = 5.5 placed at the molecular centre of mass (designated cc-pVDZ + R).29 We have benchmarked the performance of cc-pVDZ + R in calculations made for similar terpene molecules.30 Relative to triple- or double-augmented atomic bases, the same, or better accuracy, is obtained with considerable savings—over 50% fewer basis functions. This provides invaluable economy in processor requirements for the poorly scaling coupled cluster calculations and is adopted for the remaining calculations reported in Table 1.
The ADC(3), CCSD & CCSD(T) vertical transition energies, and ΔESCF CCSD adiabatic energies (Table 1) all indicate very similar spacing between the 3s and 3pα substates. Because of the very similar electronic structure anticipated for the Rydberg states it is plausible to assume that the intrinsic error for a given model chemistry may be effectively constant between the Rydberg states. Furthermore, in the case of the vertical transition energies, the very similar FC profiles for each Rydberg state suggest that the offset between adiabatic and vertical excitation energies will also be approximately constant, and this may be estimated, e.g. from Fig. 1 or 2, to be ∼0.065 eV. Therefore for each calculation model we have estimated a “best” adiabatic excitation energy by the subtraction of a constant determined so as to bring the 3s excitation into agreement with the experimental 5.952 eV 3s origin,31 as shown in the respective columns of Table 1. In the case of the CCSD ΔESCF adiabatic results this offset is just −27 meV, in fact comparable to the estimated neglect of the zero point energy difference between ground and Rydberg states. The CCSD ΔESCF results, including this 27 meV correction, are marked along the top axis in Fig. 2.
The coupled cluster results in Table 1 provide a very strong indication that the three distinct shoulders observed from 6.31–6.37 eV in the FT spectrum can be assigned to the 3pz Rydberg state. Further support comes from calculated optical transition strengths listed in Table 2 and elsewhere.27,28 The reliability and absolute accuracy of one-photon electronic oscillator strengths obtained by quantum chemical calculations has not, in contrast to calculated excitation energies, been systematically established for systems the size of fenchone and which have multiple close lying excited states.32 For example, a simple mapping of the numerical 3s and 3p electronic oscillator strengths (Table 2) onto full rovibronic band profiles would suggest a much larger ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) to
to ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) band relative intensity ratio than is experimentally observed in the one-photon FT spectrum (Fig. 1). Nonetheless, making only semi-quantitative use of these particular results, one sees that while the 3pz VUV single-photon absorption is relatively favourable, its excitation in a two-photon transition would be strongly disfavoured, accounting for the failure to detect comparable 3pz excitation in the REMPI spectrum.
band relative intensity ratio than is experimentally observed in the one-photon FT spectrum (Fig. 1). Nonetheless, making only semi-quantitative use of these particular results, one sees that while the 3pz VUV single-photon absorption is relatively favourable, its excitation in a two-photon transition would be strongly disfavoured, accounting for the failure to detect comparable 3pz excitation in the REMPI spectrum.
| Excited state | |||||
|---|---|---|---|---|---|
| Calculation | π* | 3s | 3pz | 3py | 3px |
| a Taken from ref. 26 | |||||
| 1-photon oscillator strength, f, × 102 | |||||
| CAM-B3LYP/tAug-cc-pVDZ | 0.001 | 0.030 | 2.260 | 1.394 | 0.413 |
| CAM-B3LYP/cc-pVDZ + R | 0.001 | 0.038 | 2.299 | 1.339 | 0.508 |
| ADC(3)/cc-pVDZ + R | 0.002 | 0.162 | 2.238 | 1.451 | 0.643 |
| CCSD/cc-pVDZ + R | 0.001 | 0.055 | 1.924 | 0.765 | 0.894 |
| 2-photon cross-section, σ(2)lin. (a.u) | |||||
| CAM-B3LYP/tAug-cc-pVDZ | 0.03 | 61.3 | 14.2 | 143.0 | 58.5 |
| CAM-B3LYP/cc-pVDZ + R | 0.02 | 61.9 | 14.9 | 138.0 | 71.8 |
| CCSD/cc-pVDZ + R | 0.06 | 77.4 | 14.0 | 106.5 | 177.0 |
| CCSD/Ryd-TZa | 0.06 | 94.9 | 20.6 | 131.9 | 253.6 |
| C/L polarization ratio | |||||
| CAM-B3LYP/tAug-cc-pVDZ | 1 | 1.48 | 1.48 | 0.40 | 0.36 |
| CAM-B3LYP/cc-pVDZ + R | 0.36 | 1.47 | 1.47 | 0.41 | 0.35 |
| CCSD/cc-pVDZ + R | 1.03 | 1.47 | 1.49 | 0.39 | 0.28 |
| CCSD/Ryd-TZa | 0.33 | 1.49 | 1.47 | 0.42 | 0.27 |
The REMPI C/L dichroism measurements reported in ref. 27 shed further light on the identity of the contributing states at different excitation energies. The circular:linear polarization ratio of the (2+1) REMPI signal was measured as ∼0.4 across the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band region above 6.4 eV, under conditions where the laser intensity dependence varies as I2. As this is usually taken to indicate saturation of the one-photon ionization step, the experimental (2+1) REMPI signal polarization ratio may be directly compared to theoretical two-photon absorption cross section ratios (Table 2). Hence, it is seen that the experimental
band region above 6.4 eV, under conditions where the laser intensity dependence varies as I2. As this is usually taken to indicate saturation of the one-photon ionization step, the experimental (2+1) REMPI signal polarization ratio may be directly compared to theoretical two-photon absorption cross section ratios (Table 2). Hence, it is seen that the experimental ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band C/L ratio is in excellent agreement with that predicted for 3py and/or 3px excitations. Conversely, any significant contribution from resonant ionization via the 3s and/or 3pz intermediate states may be discounted in this region since these states would contribute towards a much elevated C/L ratio. Below 6.4 eV, the experimental C/L ratio does indeed rise rapidly towards the value of 1.5 predicted for the 3s state at the
band C/L ratio is in excellent agreement with that predicted for 3py and/or 3px excitations. Conversely, any significant contribution from resonant ionization via the 3s and/or 3pz intermediate states may be discounted in this region since these states would contribute towards a much elevated C/L ratio. Below 6.4 eV, the experimental C/L ratio does indeed rise rapidly towards the value of 1.5 predicted for the 3s state at the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) band maximum.27
band maximum.27
This leaves an open question surrounding the specifics of the 3py and 3px contributions to the REMPI ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band spectrum. Fig. 3 shows an expanded region taken from higher resolution jet-cooled (2+1) REMPI spectra recorded using a narrow linewidth, ns pulse laser.15,16 It is once again clear that the features assigned to the 3pz excitation in the VUV absorption are missing in a REMPI spectrum. Included in the figure are two state-specific FC simulations for the 3py & 3px excitations.27 Neither alone appears to adequately account for the density of the near-threshold vibronic structure in the experimental spectrum, so we consider commensurate excitation of both. However, the relative peak intensities in the experimental spectrum may not be fully reliable since while ion fragmentation was noted as occurring under the chosen experimental conditions, only the parent ion yield channel was actively monitored in the REMPI scan.15,33 Consequently, we do not attempt to find a unique best-fit for the two simulations, but rather identify and choose origins for the two to match well the experimental peak positions. The comparison with experiments presented in Fig. 3 has chosen origins of 6.393 eV (3px) and 6.403 eV (3py). Keeping these same origins but exchanging them between the 3px and 3py simulations produces a similarly successful looking theory-experiment comparison of the vibrational structure. While, therefore, a definitive judgement regarding the relative energetic ordering of the 3py and 3px state cannot be reached based on the current high resolution evidence, there is a clear indication that the energy separation may be as little as ∼10 meV, smaller even than the 20–30 meV predicted by the coupled cluster calculations (Table 1).
band spectrum. Fig. 3 shows an expanded region taken from higher resolution jet-cooled (2+1) REMPI spectra recorded using a narrow linewidth, ns pulse laser.15,16 It is once again clear that the features assigned to the 3pz excitation in the VUV absorption are missing in a REMPI spectrum. Included in the figure are two state-specific FC simulations for the 3py & 3px excitations.27 Neither alone appears to adequately account for the density of the near-threshold vibronic structure in the experimental spectrum, so we consider commensurate excitation of both. However, the relative peak intensities in the experimental spectrum may not be fully reliable since while ion fragmentation was noted as occurring under the chosen experimental conditions, only the parent ion yield channel was actively monitored in the REMPI scan.15,33 Consequently, we do not attempt to find a unique best-fit for the two simulations, but rather identify and choose origins for the two to match well the experimental peak positions. The comparison with experiments presented in Fig. 3 has chosen origins of 6.393 eV (3px) and 6.403 eV (3py). Keeping these same origins but exchanging them between the 3px and 3py simulations produces a similarly successful looking theory-experiment comparison of the vibrational structure. While, therefore, a definitive judgement regarding the relative energetic ordering of the 3py and 3px state cannot be reached based on the current high resolution evidence, there is a clear indication that the energy separation may be as little as ∼10 meV, smaller even than the 20–30 meV predicted by the coupled cluster calculations (Table 1).
 | ||
Fig. 3 An expanded view around the 6.4 eV ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band onset in the ns laser (2+1) REMPI spectrum of jet cooled fenchone taken from ref. 15,16 and comparison with FC simulated spectra27 (75 K, FWHM of 15 cm−1) for the 3py and 3px Rydberg states. Their origins have been selected to lie at 6.403 and 6.393 eV, respectively, for this illustration. band onset in the ns laser (2+1) REMPI spectrum of jet cooled fenchone taken from ref. 15,16 and comparison with FC simulated spectra27 (75 K, FWHM of 15 cm−1) for the 3py and 3px Rydberg states. Their origins have been selected to lie at 6.403 and 6.393 eV, respectively, for this illustration. | ||
A weak feature at 6.377 eV, visible in Fig. 3, was previously noted and suggested to be the origin of a 3p state.16 While agreeing with the calculated 3py origin (coupled cluster results, Table 1) this is not fully consistent with the origins just deduced at 6.39/6.40 eV using the FC vibrational simulations.
In conclusion, we have identified the origin of the 3pz state to be at 6.31 eV in the VUV absorption, significantly below the first prominent ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band peak seen at 6.4 eV. However, this state is not seen in the REMPI spectra due to a much weaker 2-photon transition strength relative to the 3py and 3px states and so becomes effectively a “dark” state in such spectra. Consequently, the manifold of states populated within the
band peak seen at 6.4 eV. However, this state is not seen in the REMPI spectra due to a much weaker 2-photon transition strength relative to the 3py and 3px states and so becomes effectively a “dark” state in such spectra. Consequently, the manifold of states populated within the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band in a (2+1) REMPI excitation is expected to consist of predominantly 3px and 3py states, these having nearly identical origins matching with the experimentally observed REMPI
band in a (2+1) REMPI excitation is expected to consist of predominantly 3px and 3py states, these having nearly identical origins matching with the experimentally observed REMPI ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) band origin of 6.4 eV. A major caveat must, however, be issued in that all modelling and discussion has been presented in the adiabatic limit. The available high resolution analysis (Fig. 3) is ambiguous concerning the relative ordering of 3px and 3py states, but in all cases the absolute separation energy is small (10–30 meV). It is already clear from the experimentally observed internal conversion to the 3s state that there is some non-adiabatic interaction within the 3p manifold. Moreover, the very close proximity of the 3px and 3py potentials suggests that there will be a likelihood of non-adiabatic coupling between at least these two states.
band origin of 6.4 eV. A major caveat must, however, be issued in that all modelling and discussion has been presented in the adiabatic limit. The available high resolution analysis (Fig. 3) is ambiguous concerning the relative ordering of 3px and 3py states, but in all cases the absolute separation energy is small (10–30 meV). It is already clear from the experimentally observed internal conversion to the 3s state that there is some non-adiabatic interaction within the 3p manifold. Moreover, the very close proximity of the 3px and 3py potentials suggests that there will be a likelihood of non-adiabatic coupling between at least these two states.
Understanding the composition, and complexity, of the excited state manifold will ultimately be important for a quantitative modelling of MP-PECD asymmetries as these depend on alignment, ionization cross-sections, and internal dynamics of the initially populated intermediate states. These considerations and requirements are underscored for the closely related technique of photoelectron elliptical dichroism24,28 (PEELD). Here, a high repetition rate fs laser source has its ellipticity continuously modulated while the photoelectron angular distribution is monitored, generating a distinctive chiral “signature”. Although the electron chiral asymmetry is expected to scale with ionizing photon ellipticity, of potentially greater significance for observations are polarization induced changes within the manifold of short-pulse excited Rydbergs. State-specific variations in the circular:linear multiphoton cross-section ratios may be as much as ±50% (see Table 2). Cycling the ellipticity of a two-photon pump laser could thus be expected to correspondingly modulate the relative populations of intermediates within the manifold of the excited states. Combined with the polarization induced state-specific modulation of a given intermediate's alignment and molecule-frame photoionization anisotropies, the complexity of behaviour observed experimentally can be readily anticipated.28
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge the provision of resources by the University of Nottingham High Performance Computing Facility and are grateful to Bang Huynh for support implementing the CCSD(T) calculations on the Nottingham Computational Chemistry cluster. Barratt Park and Tim Schäfer are thanked for helpful discussions and for making available their ns REMPI spectra of fenchone in digital form. Their help and support in confirming calibration details and generally preparing the spectra is also much appreciated. Finally, we thank James O. F. Thompson and Katharine Reid for their help and support in this project.References
- B. Mennucci, J. Tomasi, R. Cammi, J. R. Cheeseman, M. J. Frisch, F. J. Devlin, S. Gabriel and P. J. Stephens, J. Phys. Chem. A, 2002, 106, 6102–6113 CrossRef CAS.
- T. Muller, K. B. Wiberg and P. H. Vaccaro, J. Phys. Chem. A, 2000, 104, 5959–5968 CrossRef.
- F. Pulm, J. Schramm, J. Hormes, S. Grimme and S. D. Peyerimhoff, Chem. Phys., 1997, 224, 143–155 CrossRef CAS.
- F. Pulm, J. Schramm, H. Lagier and J. Hormes, Enantiomer, 1998, 3, 315–322 CAS.
- G. Longhi, R. Gangemi, F. Lebon, E. Castiglioni, S. Abbate, V. M. Pultz and D. A. Lightner, J. Phys. Chem. A, 2004, 108, 5338–5352 CrossRef CAS.
- P. L. Polavarapu, C. L. Covington, K. Chruszcz-Lipska, G. Zajac and M. Baranska, J. Raman Spectrosc., 2017, 48, 305–313 CrossRef CAS.
- V. Ulrich, S. Barth, S. Joshi, U. Hergenhahn, E. A. Mikajlo, C. J. Harding and I. Powis, J. Phys. Chem. A, 2008, 112, 3544–3549 CrossRef CAS PubMed.
- L. Nahon, L. Nag, G. A. Garcia, I. Myrgorodska, U. Meierhenrich, S. Beaulieu, V. Wanie, V. Blanchet, R. Géneaux and I. Powis, Phys. Chem. Chem. Phys., 2016, 18, 12696–12706 RSC.
- M. N. Pohl, S. Malerz, F. Trinter, C. Lee, C. Kolbeck, I. Wilkinson, S. Thurmer, D. M. Neumark, L. Nahon, I. Powis, G. Meijer, B. Winter and U. Hergenhahn, Phys. Chem. Chem. Phys., 2022, 24, 8081–8092 RSC.
- D. Faccialà, M. Devetta, S. Beauvarlet, N. Besley, F. Calegari, C. Callegari, D. Catone, E. Cinquanta, A. G. Ciriolo, L. Colaizzi, M. Coreno, G. Crippa, G. D. Ninno, M. D. Fraia, M. Galli, G. A. Garcia, Y. Mairesse, M. Negro, O. Plekan, P. P. Geetha, K. C. Prince, A. Pusala, S. Stagira, S. Turchini, K. Ueda, D. You, N. Zema, V. Blanchet, L. Nahon, I. Powis and C. Vozzi, Phys. Rev. X, 2023, 13, 011044 Search PubMed.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Geneaux, A. G. Harvey, F. Legare, Z. Masin, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484 Search PubMed.
- R. Cireasa, A. E. Boguslavskiy, B. Pons, M. C. H. Wong, D. Descamps, S. Petit, H. Ruf, N. Thire, A. Ferre, J. Suarez, J. Higuet, B. E. Schmidt, A. F. Alharbi, F. Legare, V. Blanchet, B. Fabre, S. Patchkovskii, O. Smirnova, Y. Mairesse and V. R. Bhardwaj, Nat. Phys., 2015, 11, 654 Search PubMed -+.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Q. Liang, J. Kohler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS.
- C. Lux, M. Wollenhaupt, C. Sarpe and T. Baumert, Chem. Phys. Chem., 2015, 16, 115–137 CrossRef CAS.
- A. Kastner, G. Koumarianou, P. Glodic, P. C. Samartzis, N. Ladda, S. T. Ranecky, T. Ring, S. Vasudevan, C. Witte, H. Braun, H.-G. Lee, A. Senftleben, R. Berger, G. B. Park, T. Schäfer and T. Baumert, Phys. Chem. Chem. Phys., 2020, 22, 7404–7411 RSC.
- A. Kastner, T. Ring, B. C. Kruger, G. B. Park, T. Schafer, A. Senftleben and T. Baumert, J. Chem. Phys., 2017, 147, 013926 CrossRef.
- D. P. Singh, J. O. F. Thompson, K. L. Reid and I. Powis, J. Phys. Chem. Lett., 2021, 12, 11438–11443 CrossRef CAS PubMed.
- H.-G. Lee, S. T. Ranecky, S. Vasudevan, N. Ladda, T. Rosen, S. Das, J. Ghosh, H. Braun, D. M. Reich, A. Senftleben and T. Baumert, Phys. Chem. Chem. Phys., 2022, 24, 27483–27494 RSC.
- A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Legare, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchett, J. Phys. Chem. Lett., 2016, 7, 4514–4519 CrossRef CAS.
- S. Beaulieu, A. Comby, B. Fabre, D. Descamps, A. Ferré, G. Garcia, R. Géneaux, F. Légaré, L. Nahon, S. Petit, T. Ruchon, B. Pons, V. Blanchet and Y. Mairesse, Faraday Discuss., 2016, 194, 325–348 RSC.
- M. M. Rafiee Fanood, N. B. Ram, C. S. Lehmann, I. Powis and M. H. M. Janssen, Nat. Commun., 2015, 6, 7511 CrossRef PubMed.
- A. Kastner, C. Lux, T. Ring, S. Zullighoven, C. Sarpe, A. Senftleben and T. Baumert, Chem. Phys. Chem., 2016, 17, 1119–1122 CrossRef CAS.
- J. Miles, D. Fernandes, A. Young, C. M. M. Bond, S. W. Crane, O. Ghafur, D. Townsend, J. Sá and J. B. Greenwood, Anal. Chim. Acta, 2017, 984, 134–139 CrossRef CAS PubMed.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Nat. Commun., 2018, 9, 5212 CrossRef CAS PubMed.
- M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2014, 16, 856–871 RSC.
- R. E. Goetz, T. A. Isaev, B. Nikoobakht, R. Berger and C. P. Koch, J. Chem. Phys., 2017, 146, 024306 CrossRef CAS PubMed.
- D. P. Singh, N. D. Oliveira, G. Garcia, A. Vredenborg and I. Powis, Chem. Phys. Chem., 2020, 21, 2468–2483 CrossRef CAS PubMed.
- S. Beauvarlet, E. Bloch, D. Rajak, D. Descamps, B. Fabre, S. Petit, B. Pons, Y. Mairesse and V. Blanchet, Phys. Chem. Chem. Phys., 2022, 24, 6415–6427 RSC.
- K. Kaufmann, W. Baumeister and M. Jungen, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 2223–2240 CrossRef CAS.
- H. Ganjitabar, D. P. Singh, R. Chapman, A. Gardner, R. S. Minns, I. Powis, K. L. Reid and A. Vredenborg, Mol. Phys., 2020, 119, e1808907 CrossRef.
- T. J. Cornish and T. Baer, J. Am. Chem. Soc., 1988, 110, 6287–6291 CrossRef CAS.
- A. Chrayteh, A. Blondel, P. F. Loos and D. Jacquemin, J. Chem. Theory Comput., 2021, 17, 416–438 CrossRef CAS PubMed.
- G. B. Park, personal communication, 2019.
Footnote |
| † Current address: IMEC, Kapeldreef 75, 3001 Leuven, Belgium. |
| This journal is © the Owner Societies 2023 |

