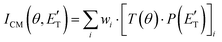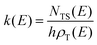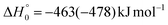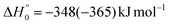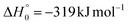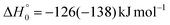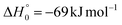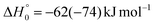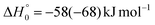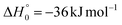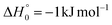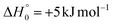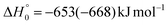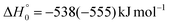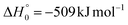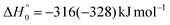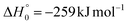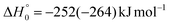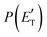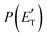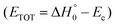A combined crossed molecular beam and theorerical study of the O(³P,¹D) + acrylonitrile (CH₂CHCN) reactions and implications for combustion and extraterrestrial environments

Abstract

Acrylonitrile (CH₂CHCN) is ubiquitous in space (molecular clouds, solar-type star forming regions, and circumstellar envelopes) and is also abundant in the upper atmosphere of Titan. The reaction O(³P) + CH₂CHCN can be of relevance in the chemistry of the interstellar medium because of the abundance of atomic oxygen. The oxidation of acrylonitrile is also important in combustion as the thermal decomposition of pyrrolic and pyridinic structures present in fuel-bound nitrogen generates many nitrogen-bearing compounds, including acrylonitrile. Despite its relevance, limited information exists on this reaction. We report a combined experimental and theoretical investigation of the reactions of acrylonitrile with both ground ³P and excited ¹D atomic oxygen. From product angular and time-of-flight distributions in crossed molecular beam experiments with mass spectrometric detection at a collision energy, E_c, of 31.4 kJ mol⁻¹, we have identified the primary reaction products and determined their branching fractions (BFs). Theoretical calculations of the relevant triplet and singlet potential energy surfaces (PESs) were performed to interpret the experimental results and elucidate the reaction mechanism. Adiabatic statistical calculations of product BFs for the decomposition of the main triplet and singlet intermediates have been carried out. Combining the experimental and theoretical results, we conclude that the O(³P) reaction leads to two main product channels: (i) CH₂CNH (ketenimine) + CO (dominant with a BF of 0.87 ± 0.05), formed via efficient intersystem crossing from the entrance triplet PES to the underlying singlet PES, and (ii) HCOCHCN + H (minor, with a BF of 0.13 ± 0.05), occurring adiabatically on the triplet PES. Our study suggests the inclusion of this reaction as a possible destruction pathway of CH₂CHCN and a possible formation route of CH₂CNH in the interstellar medium. The O(¹D) + CH₂CHCN reaction mainly leads to the formation of CH₂CNH + CO adiabatically on the singlet PES. This result can improve models related to the chemistry of interstellar ice and cometary comas, where O(¹D) reactions can play a role. Overall, our results are expected to be useful for improving the models of combustion and extraterrestrial environments.

---

1. Introduction

The oxidative processes of acrylonitrile, CH₂CHCN, are of considerable importance in a variety of fields, ranging from astrochemistry to combustion.^1–3 Acrylonitrile (also called cyanoethene or vinyl cyanide) is widespread in textile and plastics industries, with countless applications. The polymerization of acrylonitrile results in the formation of polyacrylonitrile (PAN), the precursor of acrylic and carbon fibers; furthermore, its combination with other repeat units, such as styrene and 1,3-butadiene, is the basis for the synthesis of many copolymers, such as SAN (styrene acrylonitrile), ABS (acrylonitrile butadiene styrene), and ASA (acrylonitrile styrene acrylate).^4,5 Acrylonitrile is also classified as a “volatile organic compound” (VOC) and it has hazardous properties, including toxicity and carcinogenicity.⁶ Therefore, the regulation on the emission of this compound into the atmosphere is very strict and many efforts have been made to optimize sustainable methods to convert acrylonitrile into clean species. Thermal combustion at temperatures higher than 850 °C results in the emission of secondary pollutants (nitrogen oxides, NO_x),⁷ while selective catalytic combustion (SCC), which is characterized by an operating temperature of 300–500 K, has a lower environmental impact.^8–12 Moreover, the inclusion of the oxidation process of acrylonitrile in models that simulate the combustion of coal and other low-rank fossil fuels is important to account for dangerous emissions. This is because the nitrogen content of many fuels is essentially ascribed to the presence of pyrrolic and pyridinic structures,^13–15 but their thermal decomposition generates many nitrogen-bearing compounds, including acrylonitrile,^16–19 that can undergo subsequent oxidation to NO_x.²⁰ For the above reasons, it is worth investigating the reactions of acrylonitrile with common oxidant species in combustion, including atomic oxygen.

In addition, the O(³P) + acrylonitrile reaction can also be relevant in the chemistry of the interstellar medium (ISM), with acrylonitrile being the first molecule with a C=C double bond detected in the ISM via its rotational transition at 1372 MHz (2₁₁–2₁₂),^21,22 and atomic oxygen being quite abundant in various regions of the ISM (where it represents the third most abundant element after H and He). After its first detection in Sagittarius (Sgr) B2,²¹ acrylonitrile has been identified in a variety of interstellar environments, such as the hot molecular core Sgr B2(N),^23,24 Orion-KL,²⁵ the TMC-1 dark cloud,²⁶ the circumstellar envelope of the C-rich star IRC + 10216,²⁷ and the L1544 prototypical prestellar core,²⁸ as well as in Titan's atmosphere.^29–35 Additionally, atomic oxygen in its first electronically excited state, O(¹D), can play a role in the chemistry of extraterrestrial environments, and several reactions involving O(¹D) have been considered in the chemistry of cometary comae³⁶ and of interstellar ice.³⁷ Therefore, the study of the reaction of acrylonitrile with oxygen atoms can contribute to enrich current astrochemical models, as was done previously in our group with the CN(X²Σ⁺) + CH₂CHCN³⁸ and N(²D) + CH₂CHCN reactions.³⁹

Despite its possible relevance, the O(³P) + CH₂CHCN reaction has been the subject of only one kinetic study and one theoretical investigation so far. The rate constant at 298 K and 1.2–1.7 Torr was determined to be (4.9 ± 1.0) × 10⁻¹³ cm³ molecule⁻¹ s⁻¹ by Upadhyaya et al. in a fast-flow experiment with a derived activation energy of 7.1 kJ mol⁻¹.⁴⁰ The authors suggested that the reaction occurs via electrophilic addition of the oxygen atom to the C=C double bond, resulting in the formation of a resonantly stabilized intermediate OCH₂CHCN, which can be cyclized to cyanoethyleneoxide.⁴⁰ The same conclusion was reached by Kimber et al.⁴¹ by experimentally studying the heterogeneous reaction between oxygen atoms and acrylonitrile on highly oriented pyrolytic graphite (HOPG) kept at 14–100 K. The experimental rate constant⁴⁰ was corroborated by theoretical computations carried out by Sun et al.⁴² using a statistical approach on the calculated triplet potential energy surface (PES) (k_tot = 1.79 × 10⁻¹³ cm³ mol⁻¹ s⁻¹ at 298 K and at a pressure of 1.2 Torr of Ar). Branching fractions (BFs) for addition and abstraction channels on the adiabatic triplet PES were estimated as a function of temperature and pressure. The dominant product channel was predicted to be H + HCOCHCN (BF ∼ 0.75), followed by CH₂O + HCCN (BF ∼ 0.25), while other channels became significant only with temperature rising above 500 K.⁴² In this theoretical study, intersystem-crossing (ISC) to the underlying singlet PES was not considered, even though it is well known that ISC is quite common in most reactions involving unsaturated hydrocarbons and O(³P).^43–49 To improve current combustion and astrochemical models, it is important to explore the role of ISC and its effect on the product branching fractions.

Here, we report the first investigation of the dynamics of the O(³P,¹D) + acrylonitrile reactions using the crossed-molecular beam (CMB) scattering technique with mass spectrometric (MS) detection and time-of-flight (TOF) analysis, which is arguably the most powerful method to reveal the primary products and determine their BFs for elementary multichannel reactions (see ref. 50, 51, and references therein). The experimental work has been complemented by theoretical calculations of the triplet/singlet PESs and statistical RRKM/ME (Rice–Ramsperger–Kassel–Marcus/Master equation) computations of the product BFs as a function of temperature, considering separately the triplet and the singlet PESs.

The paper is organized as follows. In Section 2 the experimental technique is presented, while in Section 3 the computational method is described. Section 4 presents the experimental and theoretical results, while the discussion is presented in Section 5. Finally, Section 6 is about the implications of the findings on extraterrestrial environments and Section 7 provides a summary and conclusions.

2. Experimental method

The dynamics of the O(³P) + CH₂CHCN reaction was investigated by exploiting the CMB technique based on an apparatus equipped with a rotatable electron-impact quadrupole MS detector and TOF analysis system. The basis of the method and the technical specifications of our apparatus have been extensively described elsewhere.^50–55 Briefly, two supersonic beams of the reactants were crossed at the angle γ = 90° inside a scattering chamber kept at a base pressure of 2 × 10⁻⁷ hPa, which increased up to 1 × 10⁻⁶ hPa under the operating conditions. The aim of identifying the primary reaction products is supported by the “single-collision conditions” of the experiment. The scattered products at the collision center enter a triply differentially pumped, ultra-high vacuum (UHV) chamber; in the inner region of this chamber, ionization takes place through an electron impact ionizer, featuring tunable electron energy; the ions are then selected by a quadrupole mass filter and collected in a Daly-type detector.⁵⁶ The detector angular resolution for a point collision zone is about 1°.

The intensity of the products as a function of the laboratory (LAB) scattering angle Θ, namely, the product angular distribution N(Θ), is recorded using a mass spectrometer that can be rotated in the collision plane, around an axis orthogonal to the plane containing the colliding beams and passing through their intersection axis. During the angular distribution measurements, the molecular beam is modulated at 160 Hz using a tuning fork chopper for background subtraction. The distribution of the products as a function of time (or velocity) is obtained by setting the detector at selected angles and employing the pseudo-random TOF technique based on a pseudo-random wheel containing four identical sequences of 127 open/closed elements, spinning at 328.1 Hz (corresponding to a dwell time of 6 μs/channel) in front of the entrance of the detector.

The supersonic oxygen beam was generated using a radio-frequency (RF) discharge beam source^57–59 in which 85 mbar of a diluted gas mixture of (5%) He/O₂ was discharged at 300 W of RF power, through a 0.48 mm diameter water-cooled quartz nozzle followed by a 0.8 mm diameter boron nitride skimmer and a further collimating aperture. The resulting beam was characterized by a predominance (≥90%) of atomic oxygen in its ground electronic state (³P), with a small fraction (≤10%) of atomic oxygen in its first electronically excited state (¹D).⁵⁷ The supersonic beam of acrylonitrile was produced using the neat species. Commercial acrylonitrile (CH₂CHCN, Merck 99% purity, containing 35–45 ppm of mequinol, C₇H₈O₂, as inhibitor) was stored inside a reservoir kept at 20 °C; 87 torr, corresponding to the vapor pressure of liquid acrylonitrile at the temperature of the container, undergo an expansion through a 0.1 mm diameter stainless steel (S.S.) nozzle, followed by a 0.8 mm S. S. skimmer, and a further collimating aperture. The peak velocity of the resulting atomic and molecular beams, as obtained from single-shot TOF analysis, was 2162 m s⁻¹ with a speed ratio of 4.4 and 663 m s⁻¹ with a speed ratio of 3.8, respectively. The resulting collision energy, E_c, was 31.4 kJ mol⁻¹ and the center-of-mass angle, Θ_CM, was 45°.

In order to gain a detailed understanding of the reaction dynamics with a quantitative and physical interpretation of the scattering event, it is necessary to move from the LAB reference frame to the center-of-mass (CM) one.^51–54 The LAB number density, N_LAB(Θ), and the CM flux, I_CM(θ,u), are related through the equation: 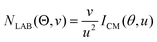(where v and u are the velocity in the LAB and in the CM frame, respectively, and the term v/u² is the transformation Jacobian).⁶⁰ Because of the finite resolution of the experimental conditions, the CM flux, which can be factorized into the product of the angular (T(θ)) and translational energy 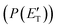distributions, is derived through a forward convolution fit of the total product LAB angular and TOF distributions at a certain mass to charge (m/z) ratio value^50,51 according to the relation:

with the parameter w_i representing the relative contribution of the integral cross section of the ith channel.

3. Computational methods

3.1 Quantum chemical calculations

The theoretical investigation of the reactions between O(³P,¹D) and acrylonitrile was performed adopting a well-established computational strategy previously used for the investigation of many other bimolecular reactions.^61–65 In particular, both the triplet and the singlet PESs were characterized by locating the lowest stationary points using density functional theory (DFT), with the hybrid B3LYP functional^66,67 in conjunction with the correlation consistent valence polarized set aug-cc-pVTZ.^68–70 Harmonic vibrational frequencies were computed at the same level of theory, in order to check the nature of the stationary points, i.e., minimum if all the frequencies are real, while a saddle point if there is one, and only one, imaginary frequency. Intrinsic reaction coordinate (IRC) calculations^71,72 were performed in order to ensure the correct assignment of the identified transition states. The more accurate coupled cluster theory, including single and double excitations as well as a perturbative estimate of connected triples [CCSD(T)],^73–75 was used in conjunction with the same basis set aug-cc-pVTZ to calculate the energy of each stationary point. Both B3LYP and CCSD(T) energies were corrected to 0 K by adding the zero-point energy correction computed using the scaled harmonic vibrational frequencies evaluated at the B3LYP/aug-cc-pVTZ level.

Following a computational strategy already used by some of the present authors for different reactions involving atomic oxygen,^{43,46,47,76–78} more accurate calculations for the stationary points involved in the main reaction channels were performed at the CCSD(T) level corrected with a density fitted (DF) MP2 extrapolation to the complete basis set (CBS) and with corrections for core electrons excitations. In particular, we computed the energies as:

E = E(CCSD(T)/aug-cc-pVTZ) + [E(CCSD(T,core)/cc-pVTZ) − E(CCSD(T)/cc-pVTZ)] + [E(DF-MP2/CBS)-E(DF-MP2/aug-cc-pVTZ)]

where E(DF-MP2/CBS) is defined as:

E(DF-MP2/CBS) = E[(DF-MP2)/aug-cc-pVQZ)] + 0.5772 × [E(DF-MP2/aug-cc-pVQZ) − E(DF-MP2/aug-cc-pVTZ)]

The E(DF-MP2/CBS) extrapolation was performed using Martin's two parameter scheme⁷⁹ and the related energies were used for the kinetic investigation described below. All calculations were performed using Gaussian 09⁸⁰ and Molpro^81,82 while the analysis of the vibrational frequencies was performed using AVOGADRO.^83,84 For the investigation of the singlet PES, the energy of O(¹D) was estimated by adding an experimental separation O(³P)–O(¹D) of 190 kJ mol⁻¹ to the energy of O(³P) at all levels of calculation. Since the accuracy of our best computed values should not be smaller than the “chemical accuracy” of 1 kcal mol⁻¹, we rounded all the reported energies to 1 kJ mol⁻¹.

3.2 RRKM calculations of the product branching fractions

RRKM calculations were carried out on the two separated PESs to derive the BFs of the products for the O(³P,¹D) + CH₂CHCN reactions separately on the triplet and singlet PESs, that is, the extent of ISC was not evaluated theoretically. In detail, RRKM calculations were performed using a code developed by our group for this purpose.^85–88 At a specific total energy, the microcanonical rate constant k(E) for a specific reaction is given by the following expression:
where N(E) denotes the sum of states in the transition state at energy E, ρ(E) is the reactant density of states at the energy E, and h is Planck's constant. N(E) is obtained by integrating the relevant density of states up to energy E, using the rigid rotor/harmonic oscillator model. Tunneling effects are included in the present RRKM calculations using the imaginary vibrational frequency of the transition states and calculating the tunneling probability for the corresponding Eckart barrier. For the cases where no clear transition state barrier was found, the corresponding microcanonical rate constants were obtained through the variational RRKM approach, evaluating k(E) at various points along the reaction coordinate and choosing the point which minimizes the rate constant, in accordance with the variational approach (variational transition state theory-VTST).⁸⁹ For the dissociation steps in which no intermediates point were available, due to difficulties in the electronic structure calculations, the products at infinite separation were taken into account as possible “transition states”. In this way it was possible to avoid problems arising from the different number of degrees of freedom between the reactants and the transition state by not including the 2D part of the overall rotation in the RRKM treatment of the reactants (leaving only the “prolate” 1D contribution). After the calculation of all microcanonical rate constants, a Markov (stochastic) matrix was set up for all intermediates and final channels of the reaction containing all product BFs derived from the rate constants, separately on the triplet PES and the singlet PES. k(E) was subsequently Boltzmann averaged for each temperature of interest to yield k(T).

4. Results

According to our electronic structure calculations, there are many possible open reactive channels (for the complete list, see the ESI†) which can originate from the triplet and singlet PESs, of which the most relevant ones are:

O(^3P) + CH2CHCN	→ ^1CH3CN + CO		(1a)
	→ ^1CH2CNH + CO		(1b)
	→ ^1OCCHCN + H2		(1c)
	→ ^2CH2CN + HCO		(1d)
	→ ^2COCN + ^2CH3		(1e)
	→ ^2HCOCHCN + H		(1f)
	→ ^1CH2O + ^3HCCN		(1g)
	→ ^2CH2COCN + H		(1h)
	→ ^2CH2CH + ^2NCO		(1i)
	→ ^1OCHCN + ^3CH2		(1j)
O(^1D) + CH2CHCN	→ ^1CH3CN + CO		(2a)
	→ ^1CH2CNH + CO		(2b)
	→ ^1OCCHCN + H2		(2c)
	→ ^2CH2CN + HCO		(2d)
	→ ^2COCN + ^2CH3		(2e)
	→ ^2HCOCHCN + H		(2f)

The enthalpies of reaction reported are those calculated in the present work at the CCSD(T)/aug-cc-pVTZ level and at the CCSD(T)/CBS level (values in parentheses) (only for the most relevant channels). Regarding the O(³P) + acrylonitrile reaction, channels (1g)–(1j) correlate adiabatically with the triplet PES, while channels (1a)–(1e) are expected to occur on the singlet PES after ISC. Channel (1f) can occur both adiabatically on the triplet PES and via ISC to the singlet PES. All the channels (2a)–(2f) of the O(¹D) + acrylonitrile reaction correlate adiabatically with the singlet PES.

4.1. Experimental results: LAB product angular and TOF distributions

Experimentally, reactive scattering signals were detected at m/z = 68 (C₃H₂NO⁺), 67 (C₃HNO⁺), 66 (C₃NO⁺), 41 (C₂H₃N⁺), 40 (C₂H₂N⁺), 39 (C₂HN⁺), and 29 (HCO⁺) with relative intensities of 0.08, 0.56, 0.04, 0.16, 1.00, 0.64, and 0.34, respectively, at Θ = 44° (which is very close to the CM angle of 45°), when using an electron energy of 28 eV. Due to considerations regarding the signal-to-noise (S/N) ratio, product LAB angular distributions, N(Θ), and TOF distributions, N(Θ, t), were measured in detail only for m/z = 67 and m/z = 40, and they are shown in Fig. 1 and 2, respectively. The angular distribution at m/z = 67 was obtained by counting the reactive signal for 50 s per angle during each angular scan (total five scans), while the accumulation time for the TOF spectra at Θ = 44° and 32° was 150 and 240 minutes, respectively. It should be noted that while measurements at m/z = 67 could be performed using both hard (70 eV) and soft (28 eV) electron ionization, measurements at m/z = 40 needed to be performed using soft ionization to suppress/mitigate the problem of dissociative ionization of interfering species.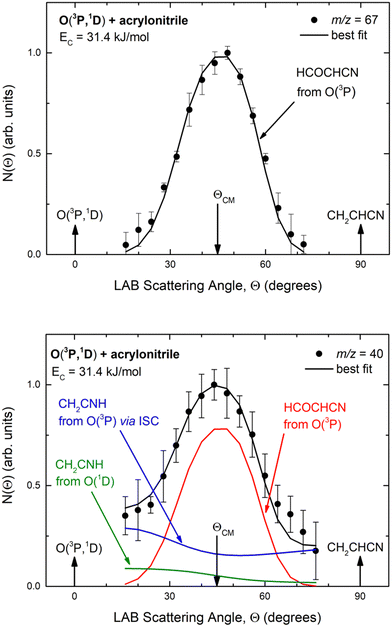

Fig. 1 LAB angular distribution of (top) the HCOCHCN product (from channel (1f)) detected at m/z = 67 (C₃HNO⁺), and (bottom) of the HCOCHCN and CH₂CNH products detected at m/z = 40 (C₂H₂N⁺) for the O(³P,¹D) + acrylonitrile reactions at E_c = 31.4 kJ mol⁻¹. The filled circles are the experimental data (with ±1σ error bars indicated), while the heavy solid black curve represents the calculated total distribution when using the best-fit functions shown in Fig. 4. (bottom): The red, blue, and green solid curves (bottom panel) represent the separate contributions of the HCOCHCN and CH₂CNH products from channel (1f), (1b), and (2b), respectively, to the calculated total LAB angular distribution. The black curve of HCOCHCN from O(³P) in the top panel corresponds to the red curve in the bottom panel.

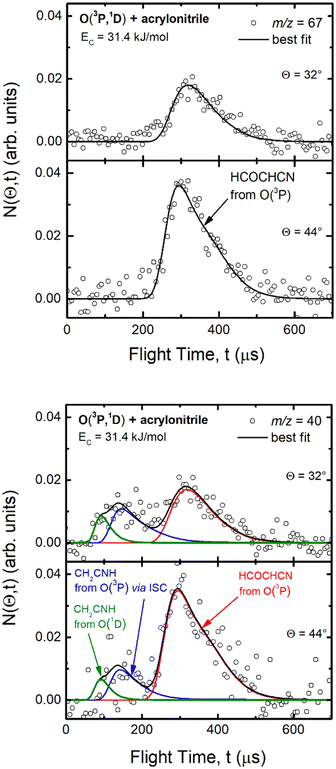Fig. 2 Time-of-flight distributions at the indicated LAB angles of (top) the HCOCHCN product detected at m/z = 67 (C₃HNO⁺), and (bottom) the HCOCHCN and CH₂CNH products detected at m/z = 40 (C₂H₂N⁺) for the O(³P,¹D) + acrylonitrile reactions at E_c = 31.4 kJ mol⁻¹. The empty circles are experimental data, while the solid black curve represents the calculated (total) distribution when using the best-fit functions shown in Fig. 4. (bottom): The red, blue, and green solid curves represent the separate contributions of the indicated products to the calculated global TOF distribution. The black curve of HCOCHCN from O(³P) in the top panel corresponds to the red curve in the bottom panel.

As discussed below, from the experimental data we have characterized channels (1f), (1b), and (2b) by measuring angular and TOF distributions at m/z = 67 and 40, respectively and we have determined their relative yields (BFs).

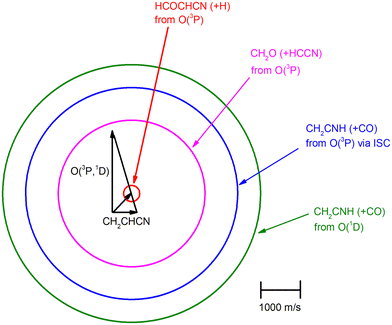
The velocity vector (so-called “Newton”) diagram of the experiment is depicted in Fig. 3, where only the limiting circles of the observed products are indicated. The circle associated to the CH₂O (+ HCCN) product from the O(³P) reaction (channel (1g)) was also added to the Newton diagram because it will be useful for the discussion of the results.

Fig. 3 Velocity vector (Newton) diagram of the experiment. The radius of each circle represents the maximum velocity that the indicated products HCOCHCN, CH₂CNH, and CH₂O can attain in the CM system if all available energy is channeled into product recoil energy (see text).

4.1.1 The m/z = 67 data: H-displacement channel. The signals at m/z = 68, 67, and 66 correspond to the parent ion (m/z = 68) of the heavy coproduct (C₃H₂NO) of the H-displacement channel (1f) and to its daughter ion after loss, due to dissociative ionization, of one (m/z = 67) or two (m/z = 66) H atoms, respectively. Even though the HCOCHCN-forming channel correlates adiabatically with both the triplet and singlet PES we can confidently associate the signal at m/z = 68, 67, and 66 mainly to the HOCHCN product formed by the O(³P) + acrylonitrile reaction (channel (1f)) (see further below). We have already studied numerous systems involving oxygen atoms and unsaturated hydrocarbons, such as O(³P) + ethylene,⁹⁰ O(³P) + benzene,⁴⁸ O(³P) + pyridine,⁴⁹ and O(³P) + cyanoacetylene,⁹¹ characterized by an entrance potential energy barrier on the triplet PES comparable to or higher than that of the title reaction, where the O(³P) reaction dynamics has been disentangled from that of O(¹D). So, in the present system also, the reaction of O(³P) (that represents ∼90% of our atomic oxygen beam⁵⁷) is expected to contribute significantly to the measured reactive signal. Obviously, an additional contribution related to the HCOCHCN product of the O(¹D) + acrylonitrile reaction (channel (2f)) could also be invoked to explain the signal registered at m/z = 68, 67, and 66. However, as will be shown later (see Section 4.3), the theoretical predictions of the BFs on the singlet PES clearly indicate a very small contribution of the HCOCHCN + H reactive channel (BF = 1.2% at the collision energy of the experiment). Therefore, we can reasonably neglect, within our experimental sensitivity (i.e., BF ≤ 2–3%), the reactive channel (2f). The contribution of HCOCHCN from O(³P) via ISC is very hard to evaluate, and, therefore, it was not considered. On the other hand, the signal at m/z = 67 could also be associated to the parent ion of OCCHCN (cyanoketene), the coproduct of H₂ from channels (1c)/(2c) that, in principle, could also lose a hydrogen atom in a dissociative ionization process and then also contribute to the signal at m/z = 66. However, a close examination of the data at m/z = 67 (obtained using 70 eV electron energy, because there were no advantages in using soft ionization) reveals the presence of only the H-displacement channel (1f). In fact, as can be seen in Fig. 1(top) the angular distribution at m/z = 67 is bell-shaped and fairly narrow; it ranges from 15° to 75° and peaks around the CM angle. The corresponding TOF spectrum (see Fig. 2(top)) exhibits a single, well-defined peak at around 320 μs. This data could well be fitted with only one set of CM functions (see Fig. 4), corresponding to the H-displacement channel (1f) leading to the formation of HCOCHCN + H products. Indeed, the experimental distributions reflect a very small Newton circle within which the HCOCHCN product is constrained to be scattered (see Fig. 3).

Fig. 4 Best-fit product angular, T(θ), (left) and translational energy, , (right) distributions in the CM reference system for the O(³P,¹D) + acrylonitrile reactions. The shaded areas represent the error bars determined for the best-fit CM functions. The vertical arrow in the graphs of indicates the total energy for the corresponding reactive channel.

4.1.2. The m/z = 40 data: the CH₂CNH (ketenimine) + CO reactive channel. As can be seen in Fig. 1(bottom), in contrast to the m/z = 67 angular distribution (Fig. 1(top)), the angular distribution at m/z = 40 is characterized by a prominent peak centered at around Θ_CM = 45°, superimposed on two additional wings. The central peak corresponds to a daughter ion of the HCOCHCN product coming from the H-displacement channel (1f), whose presence is also evident from the slow broad peak in the corresponding m/z = 40 TOF spectra (see Fig. 2 (bottom)), which is identical to that observed at m/z = 67 (Fig. 2 (top)). The two additional wings in the angular distribution and the fast peak in the TOF spectra at m/z = 40 can be fitted by invoking two other reactive contributions associated with the CO-forming channels (1b) and (2b), observed via the daughter ion C₂NH₂⁺ of ketenimine (CH₂CNH). The assignment of the signal registered at m/z = 40 to ketenimine was made on the basis of the topology of the singlet PES and considering the RRKM/ME predictions of product BFs on the singlet PES (see below). In principle, the data registered at m/z = 40 could also be fitted using a single contribution associated to the CH₂CNH product obtained from the O(³P) + acrylonitrile reaction via ISC from the triplet to the singlet PES, thus overlooking the reactive channel (2b). Nevertheless, in this case, the reaction of O(¹D), which theoretical RRKM/ME calculations predicted to lead essentially to the formation of CH₂CNH + CO (BF = 94.8% at E_c = 31.4 kJ mol⁻¹; see further below, Section 4.3), was not neglected for two main reasons. The first one is that, as will be outlined in Section 5.3., the related system O(³P) + C₂H₄⁹⁰ is characterized by a potential energy surface similar to that of O(³P) + acrylonitrile, with an entrance potential energy barrier that is only ∼4 kJ mol⁻¹ (at CCSD(T)/aug-cc-pVTZ level) greater than that of O(³P) + acrylonitrile (12 kJ mol⁻¹vs. 8 kJ mol⁻¹) and a comparable rate constant (k_298 K = 7.3 × 10⁻¹³ cm³ mol⁻¹ s⁻¹ for the O(³P) + C₂H₄ reaction⁹² and k_298 K = 4.9 × 10⁻¹³ cm³ mol⁻¹ s⁻¹ for the O(³P) + CH₂CHCN reaction⁴⁰). For the system involving ethylene, pulsed CMB studies at E_c = 6 kcal mol⁻¹ and 3 kcal mol⁻¹ with VUV photoionization detection^93,94 revealed that the contribution of O(¹D) cannot be neglected and its role was also confirmed in the CMB experiment performed at E_c = 35.1 kJ mol⁻¹ by our research group.⁹⁰ The second reason is that the system involving atomic oxygen and cyanoacetylene (another nitrile molecule, with gross formula HC₃N), recently studied by our research group at E_c = 31.1 kJ mol⁻¹,⁹¹ characterized by an entrance energy barrier on the triplet PES similar to that of O(³P) + acrylonitrile (9 kJ mol⁻¹vs. 7 kJ mol⁻¹, at CBS level), had shown unambiguous evidence of the O(¹D) reaction in the TOF spectra of the HCCN coproduct of CO registered at the daughter ion m/z = 38. So, it is reasonable to state that, in the present experimental investigation also, the O(¹D) + acrylonitrile reaction contributes to the total reactive signal registered at m/z = 40. Therefore, in order to correctly account for the contribution of CH₂CNH formed adiabatically on the singlet PES to the signal recorded at m/z = 40, we have taken the O(³P,¹D) + cyanoacetylene reactions⁹¹ as reference because the two systems, having a comparable entrance potential energy barrier on the triplet PES and having been studied at nearly equal collision energy, have been investigated by using an oxygen beam generated under the same conditions (in the experimental study of the O(³P,¹D) + ethylene reactions the diameter of the nozzle was different) and because the reaction pathway under analysis is the same, i.e., a CO-forming channel (in the experiment involving ethylene, however, the CO-forming channel was not observed to occur^90,93,94).

Analyzing the TOF spectra, it should be noted that the fingerprint of the CH₂CNH + CO channel from the reaction of O(³P) and O(¹D) is clearer at Θ = 32° than at the angle Θ = 44° (that is, very near to the center of mass angle of 45°), because at Θ_CM the relative contribution of the heavy coproduct of the H-displacement channel (1f) is strongly amplified for kinematic reasons (by the CM → LAB transformation Jacobian⁶⁰), being scattered over a much narrower LAB angular range (see the Newton diagram in Fig. 3). The fact that the angular distribution of CH₂CNH (formed in channels (1b) and (2b)) is much wider than that of HCOCHCN (formed in channel (1f)), as well as that the TOF peaks associated with the two contributions of CH₂CNH are much faster than those associated with HCOCHCN, is due to two reasons: (i) the main one is that the CH₂CHCN product is scattered over a much larger angular range (see the Newton circles in Fig. 3) compared to the HCOCHCN product because CO (the coproduct of CH₂CNH) is much heavier than H (the coproduct of HCOCHCN); (ii) in addition, channels (1b) and (2b) are much more exothermic than channel (1f) (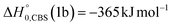, 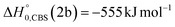vs.).

4.1.3. Other possible minor product channels. Dissociative ionization processes of the product with gross formula C₃H₂NO (m/z = 68), corresponding to the heavy coproduct of the H-displacement channel (1f), can also affect the signal registered at m/z = 41, 40, 39, and 29 by generating various fragments with the same m/z of the products at these masses. Furthermore, the elastically/inelastically scattered CH₂CHCN reactant beam could also dissociate in the electron impact ionizer into species with m/z = 40 and 39, thus contributing to the overall signal at these masses. So, in order to minimize these effects, while maintaining an acceptable S/N ratio, the measurements at m/z = 41, 40, 39, and 29 were performed with 28 eV electron energy which was sufficient to suppress most of the dissociative ionization effects. In particular, while m/z = 41 is unambiguously associated with the parent ion of the heavy coproducts (CH₃CN or CH₂CNH) resulting from the CO-forming channels (1a)/(2a) and (1b)/(2b), m/z = 40 could correspond to both the parent ion of the cofragment (CH₂CN) of the HCO radical channels (1d)/(2d) and the daughter ion of the CH₃CN (acetonitrile)/CH₂CNH (ketenimine) product(s). So, in principle, from the comparison between the angular distributions recorded at the two m/z values, one could disentangle the dynamics of the two reactive pathways, if present. Unfortunately, due to the low S/N at m/z = 41, we have been able to register angular and TOF distributions only at m/z = 40; however, as we will discuss below, because of the topology of the singlet PES and the statistical estimates of BFs, we can assert with reasonable certainty that the signal at m/z = 40 is representative of only channels (1b)/(2b), and that the HCO channels (1d)/(2d) are therefore negligible.

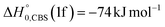In order to characterize channel (1g) (CH₂O + HCCN), we attempted to measure the angular distribution at m/z = 30, corresponding to the parent ion of formaldehyde (CH₂O), but there was no detectable signal; at the same time, the angular distribution at m/z = 39, corresponding to the parent ion of HCCN (the coproduct of formaldehyde), resulted to be perfectly superimposable (within the error bars) to the angular distribution measured at m/z = 67: therefore, the signal at m/z = 39 can only be associated to a fragment of the heavy coproduct of the H-displacement channel, whose dynamics was already characterized from measurements at m/z = 67.

Formaldehyde could also undergo dissociative ionization to HCO⁺ (m/z = 29), which could also be the parent ion of the HCO product of channels (1d)/(2d). However, our attempt to measure reliable angular and TOF distributions at m/z = 29 failed because the S/N ratio was too low due to the unfavorable kinematics and the high inherent detector background at m/z = 28 connected with residual CO in the HUV chamber of the MS detector, that significantly affects m/z = 29 also because of the natural isotopic abundance of ¹³C. Furthermore, we could not subtract the contribution associated with the elastically/inelastically scattered acrylonitrile beam, that still dissociates in the ionizer to a fragment with m/z = 28 (that influences also the signal at m/z = 29 due to ¹³C). So, we must rely on the RRKM statistical estimates of the BFs in order to learn if channels (1g) and (1d)/(2d) are both present or not and what eventually is their relative importance to the collision energy of the experiment (see below).

Regarding channel (1e)/(2e) (COCN + CH₃), there was no signal at m/z = 15 (CH₃⁺). Hence, we can rule out, within our sensitivity (i.e., BF ≤ 2–3%), the occurrence of reactive channels (1e)/(2e).

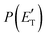4.1.4. Best-fit T(θ) and functions and reaction mechanism. Quantitative information on the reaction dynamics is obtained by moving from the LAB frame to the CM frame and analyzing the product angular, T(θ), and translational energy, 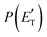, distributions, into which the total CM product flux can be factorized (see Section 2). The black solid curves superimposed on the experimental results in Fig. 1 and 2 are the total calculated LAB angular and TOF distributions (at the indicated m/z) when using the best-fit CM functions T(θ) and 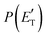depicted in Fig. 4, for the contributing reaction channels. The partial contributions at a given m/z value are indicated with color coded lines.

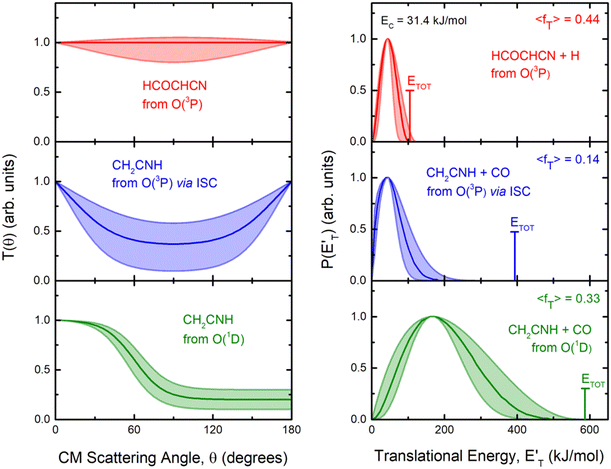
By examining the best-fit T(θ) and 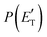functions for the main competing channels (1f), (1b), and (2b) shown in Fig. 4, we can note that the two best-fit T(θ) functions related to the channels of the O(³P) + acrylonitrile reaction are backward–forward symmetric; however, while the CM angular distribution of the HCOCHCN radical is found to be isotropic, i.e., constant within the error bars in the whole CM angular range (θ = 0°–180°), the T(θ) of ketenimine is fairly polarized at the poles (θ = 0° and θ = 180°). These characteristics are consistent with the occurrence of a long-lived complex mechanism (i.e., the intermediate complex lifetime is longer than 5–6 rotational periods).^95–97 The different degree of polarization of the two T(θ) functions can be rationalized in terms of the different partitioning of the total angular momentum for the two different product channels.^95–98 In fact, the total momentum conservation law can be written in the form J_i= L_i+ j_i= J_f= L_f+ j_f, with J_i, L_i, j_i, J_fL_f, and j_f, being the initial and final total, orbital, and rotational angular momenta, respectively. We remind that j_i can usually be neglected in a crossed molecular beam experiment because the supersonic expansion causes a strong rotational cooling of the molecular reactant. For the H-displacement channel, it is expected to have j_f ≫ L_f because L is directly proportional to the reduced mass μ of the products, and is therefore small as μ is small (L = μvb, where b is the exit impact parameter); so, from the total momentum conservation law, one has L_f ≪ L_i, for the H-displacement channel and the products can be scattered isotropically, which implies a high rotational excitation of the molecular product HCOCHCN.⁹⁹ In contrast, when L_f ≅ L_i (as for the CO-forming channel) (and therefore j_f is small), and the plane of the relative velocity vector 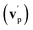of the products is the same of that of the reagents (v_r), the T(θ) function is backward–forward symmetric with a maximum at θ = 0° and θ = 180°.^95–99 Regarding the O(¹D) + CH₂CHCN reaction, the T(θ) function for the CO-forming channel (2b) was found to be strongly forward biased, as in the case of the O(¹D) + HCCCN (cyanoacetylene) reaction,⁹¹ indicating an osculating complex mechanism.⁹⁷

Regarding the product translational energy distributions, the 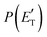functions of the two reactive channels of the O(³P) + acrylonitrile reaction exhibit a peak well away from zero (at ∼44 kJ mol⁻¹ for both channels), an indication that the two reactive channels have a sizeable exit potential energy barrier. The 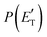of channel (1f) extends up to the total available energy 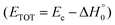of the channel and the average product translational energy, defined as 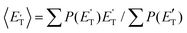, is 47 kJ mol⁻¹ which corresponds to a fraction, 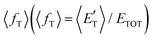, of the total available energy released in translation of 0.44. This means that the energy of the products is partitioned nearly equally between the translational and internal (ro-vibrational) degrees of freedom. In contrast, the 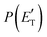of channel (1b) has a cut-off at about 190 kJ mol⁻¹, which is much less than the total energy available for the reaction channel (1b) (∼396 kJ mol⁻¹, which is the energy calculated at the CCSD(T)/CBS level of theory), and the molecular product (CH₂CNH) is highly internal excited, with 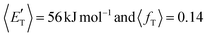. This indicates that about 85% of the total available energy is channeled into internal ro-vibrational excitation of the CH₂CNH and CO products. Notably, as will be shown in Section 4.2, the peaking of the 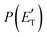for the CH₂CNH + CO channel is in line with the high (about 130 kJ mol⁻¹ with respect to products) exit barrier for this channel (see Fig. 6), and much less with the very high (340 kJ mol⁻¹ with respect to products) exit barrier to the competing, more exothermic, isomeric channel (1a) (CH₃CN + CO), which, because of the very high transition state ¹TS4 (from ¹MIN3), is not expected to have a large BF, despite being more exothermic than channel (1b), as discussed further below. Finally, the 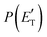distribution of the CH₂CNH-forming channel (2b) peaks very far away from zero, at 167 kJ mol⁻¹, and dies off at ∼490 kJ mol⁻¹, which is less than the total energy available for the reaction channel (2b) (∼586 kJ mol⁻¹). The corresponding average product translational energy and the fraction of the total energy channeled into translation are 195 kJ mol⁻¹ and 0.33, respectively.

4.1.5. Product branching fractions and extent of intersystem crossing. Following the derivation of the best-fit CM angular and translational energy distribution functions, we have used the method outlined by Schmoltner et al.¹⁰⁰ and applied by us in numerous previous CMB studies of bimolecular reactions,^48,49,91 to determine the experimental BFs. The ionization cross-sections have been evaluated using the procedure of Fitch and Sauter.¹⁰¹ The estimated product BFs are reported in Table 1. As can be seen from Table 1 the predominant channel is the one leading to CH₂CNH + CO on the singlet PES (channel (1b)), reached via ISC from the triplet to the underlying singlet PES, with its relative yield being 55%. The second most abundant channel is CH₂CNH + CO (channel (2b)) from the O(¹D) + acrylonitrile reaction (BF = 37%), while the H-displacement channel (1f) (HCOCHCN + H), occurring adiabatically on the triplet PES, is minor with a BF = 8%.

Table 1 Experimental branching fractions (%) obtained for the O(³P,¹D) + acrylonitrile reactions at E_c = 31.4 kJ mol⁻¹ (global and for the O(³P) + acrylonitrile reaction)

Reactants	Primary products	PES involved	Global BFs	BFs for the O(^3P) + CH2CHCN reaction
O(^3P) + CH2CHCN	HCOCHCN + H	Triplet	8 ± 3%	13 ± 5%
	CH2CNH + CO	Singlet via ISC	55 ± 17%	87 ± 5%
O(^1D) + CH2CHCN	CH2CNH + CO	Singlet	37 ± 13%	—

---

The BFs for the O(³P) + acrylonitrile reaction reported in the last column of Table 1 are obtained from the global BFs (second last column of Table 1) by normalizing the sum of BFs of the two O(³P) channels to unity. The derived BFs for the O(³P) + acrylonitrile reaction indicate a very strong preference for formation of CH₂CNH + CO (BF = 87%), while the competing HCOCHCN + H-displacement channel has BF = 13%. Uncertainties in the derived BFs vary from about ±30% to ±40% and are indicated in Table 1.

Because the calculated yield of the H channel from the singlet PES is almost negligible (BF = 1.2%, see Section 4.3), we can conclude that the extent of ISC in the O(³P) + CH₂CHCN reactions at E_c = 31.4 kJ mol⁻¹ is, therefore, about 87%.

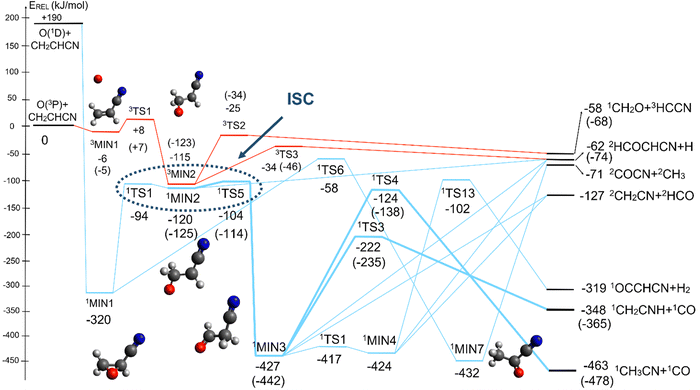
4.2 Triplet and singlet OCH₂CHCN potential energy surfaces

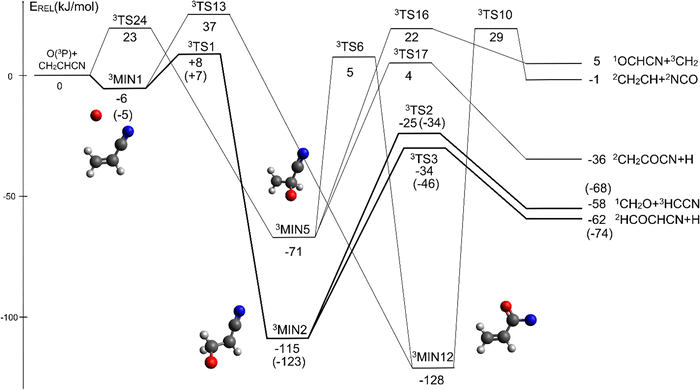
The overall triplet/singlet PES obtained theoretically for the reactions O(³P,¹D) + CH₂CHCN shows 12 different minima and 34 possible transition states. A total number of 13 possible product channels, energetically located below the experimental collision energy, can be formed. For the sake of clarity, in Fig. 5 we have reported a simplified version of the triplet PES, considering only the main channels, leading to appreciable values of product BFs, with the energies reported at the CCSD(T)/aug-cc-pVTZ level of theory. The energies computed at the CCSD(T)/CBS level of theory for the most relevant channels are given in parentheses. A global overview of the triplet PES including all possible isomerization processes of the intermediates, together with all the energetically accessible product channels, is reported in Fig. S1 of the ESI.†

Fig. 5 Schematic representation of the simplified triplet potential energy surface for the O(³P) + acrylonitrile reaction with energies evaluated at the CCSD(T)/aug-cc-pVTZ level of theory; the energies computed at the CCSD(T)/CBS level of theory are reported in parentheses for the most relevant channels (see text).

The reaction of O(³P) with CH₂CHCN starts with the initial formation of the weakly bound van der Waals (vdW) adduct ³MIN1, where the oxygen atom interacts with the acrylonitrile molecule at long distances, larger than 3 Å. The so formed weakly bound complex is located 6 (5) kJ mol⁻¹ below the reactant energy asymptote. A potential energy barrier (³TS1), whose relative energy is +8 (+7) kJ mol⁻¹, must be overcome in order to form the intermediate ³MIN2, located 115 (123) kJ mol⁻¹ below the reactant energy asymptote, in which a new C1–O bond is formed. Addition on C1 is the most favorable site of attack of O(³P).

Once formed, MIN2 can dissociate to form HCOCHCN + H (channel (1f)), the most exothermic channel on the triplet PES, through an exit barrier (³TS3) of 81 kJ mol⁻¹ (77 kJ mol⁻¹ at the CBS level) from ³MIN2, that is of 28 kJ mol⁻¹ (at the CBS level) with respect to products (see Fig. 5). The related transition state ³TS3 clearly shows the breaking of the C1-H bond, with a bond distance of 1.831 Å (see Fig. S6 in the ESI†). In addition, the fission of the C1–C2 σ bond allows the formation of formaldehyde (CH₂O), together with the ³HCCN (cyanomethylene) coproduct (channel (1g)). Also in this case, an exit barrier (³TS2) of 90 (89) kJ mol⁻¹ from ³MIN2 (that is, + 33 (34) kJ mol⁻¹ with respect to the product asymptote), is present and the related transition state, ³TS2, shows a C1–C2 distance of 2.108 Å (see Fig. S6 in the ESI†). Alternatively, the oxygen atom can add to the C3 atom of the CN group of the acrylonitrile molecule, leading to the formation of ³MIN12 via³TS13 (located 37 kJ mol⁻¹ above the reactants) (see Fig. 5). The breaking of the C2–C3 bond in ³MIN12 would lead to formation of CH₂CH (vinyl) + NCO (channel (1i)), via the transition state ³TS10 located 29 kJ mol⁻¹ above the energy of the reactants. However, because of the high energy of ³TS13 and ³TS10, this pathway is expected to contribute negligibly to the product yield under our experimental conditions.

A different reaction mechanism is represented by the attack of O(³P) on the C2 of the acrylonitrile molecule. In this case the related transition state (³TS24) is located 23 kJ mol⁻¹ above the energy of the reactants (see Fig. 5). Once formed, the intermediate ³MIN5, which shows a relative energy of −71 kJ mol⁻¹, can isomerize to the above ³MIN12, through a barrier (³TS6) of 76 kJ mol⁻¹. Alternatively, a hydrogen elimination process can take place from ³MIN5, leading to the formation of CH₂COCN + H (channel (1h)), through a barrier of 75 kJ mol⁻¹, located 4 kJ mol⁻¹ above the reactants and represented by the transition state ³TS17. Also in this case, the fission of the C1–C2 σ bond is possible, leading to the formation of a slightly endothermic (by 5 kJ mol⁻¹) ³CH₂ + ¹OCHCN product channel (1j). However, channels (1j), (1h), and (1i) are expected, on energetic grounds, to be minor at E_c = 31.4 kJ mol⁻¹ because of the high barriers involved, and only the channels (1f) and (1g) are likely significant on the triplet PES.

The singlet PES shows 13 different minima and 21 possible transition states, leading to 18 energetically possible products at the experimental collision energy. Following the same approach described for the triplet PES, in Fig. 6 we have reported a simplified version of the singlet PES, while a global picture is portrayed in Fig. S2 of the ESI.† In Fig. 6 the singlet PES is reported in blue lines, with energies evaluated at the CCSD(T)/aug-cc-pVTZ level of theory for all stationary points and at the CCSD(T)/CBS level of theory (values in parentheses) for the main reactive channels. In the same figure, the most relevant stationary points of the triplet PES are also reported in red, together with the qualitative indication (dashed ellipse) of the region of ISC between the triplet/singlet PESs. The energy of all identified stationary points, including the possible products, in the singlet PES is referred to the reactants O(³P) + CH₂CHCN.

Fig. 6 Schematic representation of the simplified singlet potential energy surface (in blue) for the O(³P,¹D) + acrylonitrile reactions with energy evaluated at the CCSD(T)/aug-cc-pVTZ level of theory and at the CCSD(T)/CBS level of theory (data in parentheses) for the most relevant channels (see text). In both cases the zero of the energy is represented by the O(³P) + CH₂CHCN reactants. A simplified representation of the two most important channels of the triplet PES (in red) is also reported, together with a possible identification of the region of ISC (blue dashed ellipse).

The barrierless addition of O(¹D) to the acrylonitrile molecule leads to the formation of the cyclic intermediate ¹MIN1, located 320 kJ mol⁻¹ below the O(³P) reactant energy asymptote. ¹MIN1, by migration of a hydrogen atom from the C2 to the C1 carbon, together with the breaking of the O–C1 bond, can lead to the formation of the intermediate ¹MIN7, located 432 kJ mol⁻¹ below the reactant energy asymptote. The related transition state (¹TS6) shows a relative energy of −58 kJ mol⁻¹ with respect to reactants.

The breaking of the C1–C2 σ bond in ¹MIN7 can lead to the formation of COCN + CH₃ (channel (2e)) through a barrierless process. ¹MIN1 can also isomerize to the ¹MIN2 intermediate, by overcoming a barrier (¹TS1) of 214 (211) kJ mol⁻¹ from ¹MIN1. It should be noted that ¹MIN2 can be reached also from a nonadiabatic transition (ISC) from the triplet to the singlet PES, because of the closeness in energy of ³MIN2 and ¹MIN2 (see Fig. 6). Once formed, ¹MIN2 can rapidly undergo two different competitive processes. The migration of a hydrogen atom via the transition state ¹TS5 from the C1 to the C2 carbon atom of ¹MIN2 leads to formation of a very stable intermediate ¹MIN3 (located at −427 (−442) kJ mol⁻¹ with respect to the reactants). Competitively, a barrierless H-displacement process is possible, leading to the formation of the HCOCHCN + H products (channels (1f)/2(f)). Two main products can be formed starting from ¹MIN3. The breaking of the C1–C2 bond, together with the migration of the H atom from C1 to the N atom of the CH₂CN moiety, leads to the formation of CH₂CNH (ketenimine) + CO (channels (1b)/(2b)), through an exit barrier, represented by ¹TS3, located −222 kJ mol⁻¹ below the reactant energy asymptote (−235 kJ mol⁻¹ at the CBS level), of 126 (130) kJ mol⁻¹ (with respect to products), showing a global channel exothermicity of 348 (365) kJ mol⁻¹. This is the lowest energy pathway to products on the singlet PES. Alternatively, a barrier (¹TS4, located at −124 (−138) kJ mol⁻¹) of 303 (304) kJ mol⁻¹ (from ¹MIN3) must be overcome in order to have the C1–C2 hydrogen migration, together with the fission of the C1–C2 σ bond, allowing the formation of the CH₃CN + CO isomeric product channel ((1a)/(2a)), which is the most exothermic of all channels 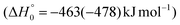. However, the very high energy of the transition state ¹TS4 (98 (97) kJ mol⁻¹ higher than ¹TS3) should make channels (1a)/(2a) much less likely than channels (1b)/(2b). Competitively, ¹MIN3 can also undergo isomerization. The rotation around the C1–C2 bond leads to the formation of the intermediate ¹MIN4, located 424 kJ mol⁻¹ below the reactant energy asymptote. The barrierless C1–C2 σ bond breaking in ¹MIN4 can allow the formation of CH₂CN + HCO (channels (1d)/(2d)) 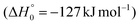. In addition, together with the barrierless formation of H + HCOCHCN (channels (1f)/(2f)), ¹MIN4 can also lead, via¹TS13, to the formation of ¹OCCHCN + H₂ (channels (1c)/(2c)) 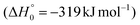. Again, channels (1d)/(2d) and (1c)/(2c) are expected, on energetic grounds, to be less favorable than channel (1b)/(2b) (see Fig. 6).

It is interesting to compare the theoretical data of the energies for the different stationary points for the main reactive channels obtained at the CCSD(T) level with those obtained when using the aug-cc-pVTZ basis set and the complete basis set (CBS) algorithm presented in Section 3.1. Some differences can be appreciated and, in particular, the global exothermicity values evaluated with the CBS method are lower than the respective aug-cc-pVTZ values. In general, all stationary points at the CBS level appear to be lower in energy, with respect to those at the aug-cc-pVTZ level, by about 8–16 kJ mol⁻¹. It is noteworthy that the most significant variations in energy are related to some of the stationary points identified in the singlet PES. The main reason of the discrepancies is the multi-reference character of the intermediates and stationary points, evaluated through the T1 factor, which assumes values of 0.023, 0.030, 0.014 and 0.016 for ³MIN2, ³TS2, ¹MIN3 and ¹TS3, respectively. As already suggested,⁴⁶ one of the main processes showing a strong multireference character is the isomerization of the oxiranyl singlet intermediate to aldehydes, similar to the case of the isomerization of ¹MIN1 to ¹MIN2 and ¹MIN3. In this case, multireference calculations would be the best solution to provide accurate energy values. In the present work, as a consequence of the topology of the PES, no particular deviations in the values of the final BFs (see below) were experienced when using CCSD(T) and CCSD(T)-CBS values. Therefore, it is possible to conclude that the calculations performed at the CCSD(T) level of theory afford, for our purpose, a good estimation of the energy of the stationary points.

The geometry of the most relevant stationary points for both PESs (including intermediates, transition states and products) is reported in Fig. S6–S8 in the ESI.†

4.3 Statistical branching fractions

The kinetic calculations were performed using the energies obtained from the CCSD(T)/CBS extrapolations. These calculations (see Section 3.2) were performed at four different temperatures (10 K, 100 K, 200 K, and 298 K (room temperature)), as well as at the collision energy of the present CMB experiment.

According to the present RRKM calculations, the main reaction channel on the computed triplet PES is the H-displacement channel (1f) starting from intermediate ³MIN2, leading to the formation of HCOCHCN + H, with a value of BF, at the E_c of the experiment, of 62.4%, while the fission of the C–C bond followed by the formation of CH₂O (formaldehyde) + ³HCCN represents the second most favorable channel ((1g)), with BF = 37.6% (see Table 2). Due to the presence of high barriers, whose energy lies above the reactant energy asymptote, the other reaction pathways identified on the triplet PES (see Fig. 5), leading to the formation of ¹OCHCN + ³CH₂ (channel (1j)), CH₂CH + NCO (channel (1i)), and CH₂COCN + H (channel (1h)), appear to have no contribution to the value of the global branching fractions (see Table 2). On the other hand, as can be seen from Table 3, according to the present RRKM analysis, the main reaction channel on the singlet PES is, by far, the molecular channel leading to formation of CH₂CNH (ketenimine) + CO (channel (2b)), with BF = 94.8% at the experimental collision energy. The second and the third most abundant channels are associated with the formation of CH₃CN + CO (channel (2a)) and HCOCHCN + H (channel (2f)) with BFs of only 2.5% and 1.2%, respectively. At the experimental E_c, the formation of CO accounts for 97.3% of the total reactive flux on the singlet PES. Finally, on this PES, the fourth most abundant channel is formation of CH₃ + COCN (channel (2e)), with BF = 1.1%, while the formation of HCO + CH₂CN (channel (2d)) and OCCHCN + H₂ (channel (2c)) accounts for only 0.3% and 0.03%, respectively, of the total reactive flux.

Table 2 Product branching fractions (%) for the reaction channels identified on the triplet PES for the O(³P) + acrylonitrile reaction calculated at four different temperatures and at the E_c of the CMB experiment

Reaction channel	Products	10 K	100 K	200 K	298 K	E c = 31.4 kJ mol^−1
1j	^1OCHCN + ^3CH2	∼0.0%	∼0.0%	∼0.0%	∼0.0%	∼0.0%
1i	CH2CH + NCO	∼0.0%	∼0.0%	∼0.0%	∼0.0%	∼0.0%
1h	CH2COCN + H	∼0.0%	∼0.0%	∼0.0%	∼0.0%	∼0.0%
1g	^1CH2O + ^3HCCN	23.6%	25.3%	27.6%	30.2%	37.6%
1f	HCOCHCN + H	76.4%	74.7%	72.4%	69.8%	62.4%

---

Table 3 Product branching fractions (%) for the reaction channels identified in the singlet PES for the O(¹D) + acrylonitrile reaction calculated at four different temperatures and at the E_c of the CMB experiment

Reaction channel	Products	10 K	100 K	200 K	298 K	E c = 31.4 kJ mol^−1
2f	HCOCHCN + H	0.6%	0.6%	0.7%	0.8%	1.2%
2e	COCN + CH3	0.4%	0.5%	0.6%	0.7%	1.1%
2d	CH2CN + HCO	0.2%	0.2%	0.2%	0.2%	0.3%
2c	OCCHCN + H2	∼0.0%	∼0.0%	∼0.0%	∼0.0%	0.03%
2b	^1CH2CNH + CO	97.6%	97.4%	97.0%	96.6%	94.8%
2a	^1CH3CN + CO	1.2%	1.2%	1.4%	1.6%	2.5%

---

If we analyze the variation of the BFs with temperature (see Table 3), we note that on the singlet PES, the decrease in temperature leads to a mild increase in the BF of the dominant, spin-forbidden, channel (2b) (CH₂CN + CO) from 94.8% at 31.4 kJ mol⁻¹ (experimental E_c) to 97.6% at 10 K, while the branching fraction of the second and the third most important channels ((2a) and (2f)) decreases from 1.2% and 2.5% to 0.6% and 1.2%, respectively. Analogously, on the triplet PES (see Table 2), the main channel (1f) HCOCHCN + H increases with decreasing energy (in the same energy range) from 62.4% to 76.4%, while in contrast the less exothermic CH₂O + HCCN channel (1g) decreases from 37.6% to 23.6%.

Overall, the results in Tables 2 and 3, reporting the values of the distinct BFs on the triplet and singlet PES, respectively, at different temperatures, show that there is little dependence of the BFs on the energy (temperature) available to the system. Since in this work the extent of ISC has not been evaluated theoretically, we will use the experimental BFs to estimate the extent of ISC in the reaction by comparing the experimental BFs with the statistically predicted BFs, separately on the triplet PES and on the singlet PES.

5. Discussion

5.1 Dynamics of the O(³P) + acrylonitrile reaction

The treatment of the experimental and theoretical results in an integrated way allows us to provide a detailed description of the dynamics of the title reactions.

Regarding the O(³P) + acrylonitrile reaction, the possibility to fit the angular and TOF distributions at m/z = 67 with a single set of CM functions characterized, in particular, by a 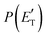peaking at 44 kJ mol⁻¹, allows us to ascertain the presence of channel (1f) occurring on the triplet PES with an exit energy barrier that is theoretically predicted to be 28 kJ mol⁻¹ (with respect to products) and rule out (within our sensitivity) the barrierless pathways to the same products from the singlet PES via ISC. These findings are corroborated by the statistical estimates of the BFs at the collision energy of the experiment, which have revealed that, among the various H-displacement channels, the most important is the one leading to H + HCOCHCN (channel (1f)) on the triplet PES with a BF = 62.4%, having its analogue on the singlet PES a BF of 1.2% and the others negligible BFs (see Tables 2 and 3). It should be noted that the isotropic CM angular distribution of the HCOCHCN product is perfectly in line with the considerable stability (about −120 kJ mol⁻¹) of ³MIN2 on the triplet PES that can be defined as a long-lived complex at E_c = 31.4 kJ mol⁻¹. Furthermore, the absence of clear traces of the H₂-elimination channel in the experimental data registered at m/z = 67 is consistent with the low yield of this channel statistically calculated on the singlet PES at the collision energy of the experiment (BF = 0.03%) (see Table 3).

It is noteworthy that the RRKM calculations on the triplet PES have predicted a yield of 37.6% for the CH₂O-forming channel (Table 2); however, despite this fact, we have ruled out this channel from an experimental point of view due to the absence of reactive signals at m/z = 30 and the total overlap (within the error bars) of the angular distribution recorded at m/z = 39, corresponding to the coproduct of formaldehyde (HCCN), with that obtained at m/z = 67. This apparent contradiction, instead, supports our hypothesis of considering, in the fitting of the two wings of the angular distribution and the fast peak of the TOF spectra at m/z = 40, not only the contribution resulting from CH₂CNH formed adiabatically on the singlet PES, but also a contribution associated to the O(³P) + acrylonitrile reaction, that can lead to the formation of CH₂CNH via ISC from the triplet to the singlet PES. As a matter of fact, having succeeded in revealing the presence of the HCOCHN + H reactive pathway of the O(³P) + acrylonitrile reaction, if the ketenimine product was formed only from the O(¹D) + acrylonitrile reaction, our experimental sensitivity would have been sufficient to detect (despite the less favorable kinematics) CH₂O (or HCCN) also, which was predicted to have a BF of ∼38% through statistical computations, as was carried out in other systems in the past.^43,45,76 So, considering that 87% of the reactive flux (see Table 1) related to the O(³P) + acrylonitrile reaction is channeled into the singlet PES (via ISC) leading to CH₂CNH + CO, the relative yield of the CH₂O + HCCN reactive channel, that correlates only with the triplet PES, will be a fraction of the minor H-displacement channel (BF = 13%). Furthermore, the intensity of formaldehyde (and, to a lesser extent, of HCCN) in the LAB frame is strongly reduced because of the unfavorable CM → LAB Jacobian transformation.⁶⁰ These two combined factors make the sensitivity of the experimental method insufficient to speculate on the CH₂O + HCCN channel.

Although the theoretical calculations did not consider the evaluation of the nonadiabatic effect of ISC, its importance in the dynamics of the title reaction is appreciable, as suggested by the experimental results. As a matter of fact, experimentally, the main reaction channel of the O(³P) + acrylonitrile reaction was found to be CH₂CNH + CO (channel (1b)), which was accessible only after ISC from the triplet to the singlet PES, with a BF = 87% (see Table 1). The attribution of the experimental signal registered at m/z = 40 to ketenimine (formed by also the O(¹D) + acrylonitrile reaction) was supported by two pieces of theoretical evidence: (i) the relatively small BFs for the CH₂CN + HCO (BF = 0.3%) and CH₃CN + CO (BF = 2.5%) channels, with respect to the channel that involves ketenimine (BF = 94.8%) on the singlet PES and (ii) the presence, for the CH₂CNH + CO channel (channel (1b)), of a potential energy barrier that must be overcome to reach the transition state ¹TS3 from ¹MIN3 which is much lower (205 vs. 303 kJ mol⁻¹) than that involving ¹TS4 and leading to the formation of CH₃CN + CO (channel (1a)) products. Notably, the possibility of disentangling the two isomeric products with a gross formula C₂H₃N from the CM functions used to obtain the best-fit of the experimental data is inhibited due to the fact that both functions are in principle consistent with the micro-mechanism and the energetics of the two channels. In fact, the backward–forward symmetric T(θ) distribution is consistent with the occurrence of a long lived complex, that is, ¹MIN3 which is common between the two reactive pathways. Then, the fitting is not sensitive to the different exothermicity of CH₂CNH + CO and CH₃CN + CO channels because the CM translational energy distribution 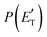dies off at about 190 kJ mol⁻¹, a value which is much lower than the total energy of both reactive channels (E_TOT CBS = 509 kJ mol⁻¹ for CH₃CN + CO and E_TOT CBS = 396 kJ mol⁻¹ for CO + CH₂CNH) (see Fig. 4). However, the fact that the peak of 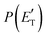is much closer to the height of the exit barrier of the CH₂CNH channel than to that of the CH₃CN channel (130 kJ mol⁻¹vs. 340 kJ mol⁻¹) is an indication that the observed reaction dynamics align more closely with the ketenimine channel. Moreover, we would like to point out that a CO-forming channel (³CH₂CHN + CO) can occur adiabatically on the triplet PES from the O(³P) reaction, as can be seen from the complete PES scheme reported in Fig. S1 of the ESI.† However, in order to form these products, the ³MIN3 intermediate has to be reached while its formation is precluded by the presence of high barriers, located above the energy of the reactants (³TS24 and ³TS34 are +23 kJ mol⁻¹ and +37 kJ mol⁻¹ above the reactant energy asymptote, respectively). This leads to a negligible contribution of the ³CH₂CHN + CO product channel to the global branching fractions.

The CH₂CH + NCO and OCHCN + CH₂ channels ((1i) and (1j), respectively) have been included in the simplified triplet PES (Fig. 5) for completeness, but they are negligible due to the presence of high energy barriers, as demonstrated by their calculated BFs that are close to zero (see Tables 2 and 3). Finally, the relatively low BF of the COCN + CH₃ channel on the singlet PES (BF = 1.1%) is in line with the experimental outcome (absence of a signal at m/z = 15 (CH₃⁺)) that has excluded the occurrence of this reactive pathway (that, in principle, could have derived from also the O(¹D) + acrylonitrile reaction).

It is interesting to note that the yields of the various reaction channels obtained from our RRKM/ME calculations on the triplet PES vary with temperature (see Table 2). Indeed, although the HCOCHCN + H channel is always the preferential route (its BF increases from 62.4% at E_c = 31.4 kJ mol⁻¹ up to 76.4% at 10 K), its relative importance with respect to the CH₂O + HCCN channel increases as the collision energy (or temperature) decreases, with the ratio [yield HCOCHCN + H]/[yield CH₂O + HCCN] being 1.7 at E_c = 31.4 kJ mol⁻¹ and 3.2 at 10 K.

If we compare the above results with the theoretical results of Sun et al.,⁴² some differences are present in the values of the product BFs, even though the trends are similar. In fact, Sun et al.⁴² estimated that at 298 K and 10⁻⁷ Torr (i.e., under single-collision conditions), the ratio [yield HCOCHCN + H]/[yield CH₂O + HCCN] is more or less the same as that at 1.2 Torr, that is, about 3. This could be compared to our predicted ratio of 69.8/30.2 = 2.3 (see Table 2). However, it should be noted that Sun et al., having neglected the singlet PES and the intersystem crossing, did not predict the occurrence of the spin-forbidden ¹CH₂CNH + CO channel, which, according to the present results, has a BF that is about seven times larger than that of the adiabatic H-forming channel at E_c= 31.3 kJ mol⁻¹ (see Table 1).

5.2 Dynamics of the O(¹D) + acrylonitrile reaction

Regarding the O(¹D) + acrylonitrile reaction, the attribution of the signal registered at m/z = 40 to the ketenimine product (channel (2b)) was made on the basis of the topology of the singlet PES and the statistical RRKM/ME estimates of product BFs, as described in the previous section on the dynamics of the O(³P) + acrylonitrile reaction.

The best-fit CM angular distribution for the CH₂CNH + CO channel (2b) is characterized by a noticeable forward bias, that reflects the occurrence of an osculating complex mechanism. In fact, the electronic energy of O(¹D) (the O(³P)–O(¹D) energy separation is ∼190 kJ mol⁻¹) is channeled into the internal energy of the intermediate ¹MIN3, which is formed via the isomerization of the cyclic intermediate ¹MIN1 obtained through the barrierless addition of O(¹D) to acrylonitrile. The high internal energy content of ¹MIN3 reduces its lifetime, τ, making it shorter than its rotational period (τ_r). By using the approximate osculating model of chemical reactions,^95,97,98 it is possible to estimate that τ/τ_r is smaller than unity, with the backward–forward asymmetry of the T(θ) being equal to 0.2.

Analyzing the CM translational energy distribution for the CH₂CNH + CO channel (2b), it should be noted that the peaking of the 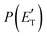function (at ∼167 kJ mol⁻¹) is consistent with the high exit energy barrier that separates the products and ¹TS3, which is theoretically predicted to be 128 kJ mol⁻¹. However, the peak of the best-fit CM 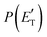for channel (2b) is substantially shifted toward higher energy compared to that of the CH₂CNH + CO channel (1b) resulting from the O(³P) + acrylonitrile reaction, despite the intermediate (¹MIN3), the transition state (¹TS3), and the exit potential energy barrier (128 kJ mol⁻¹) being the same. This could be rationalized with two different explanations: (i) the electronic energy of O(¹D) is largely channeled into product translational motion, much more so than in the O(³P) + acrylonitrile reaction, and/or (ii) in the O(¹D) + acrylonitrile reaction, the energy randomization of the intermediate is not complete because of its short lifetime.

The description of the dynamics of the O(¹D) + acrylonitrile reaction is totally in line with that of the O(¹D) + cyanoacetylene reaction,⁹¹ based on the analogy between the two systems which has been justified and described in Section 4.1.2. In the present system, however, the ratio between the sum of the relative yields of the O(³P) reaction channels ((1b) and (1f)) and the yield of the O(¹D) reaction channel (2b) was found to be [yield O(³P) reaction]/[yield O(¹D) reaction] = 0.63/0.37 (= 1.7), which is higher than that found in the system involving cyanoacetylene (the ratio was [yield O(³P) reaction]/[yield O(¹D) reaction] = 0.38/0.62 (= 0.6)).⁹¹ The higher reactivity of O(³P) when reacting with acrylonitrile compared to the system involving cyanoacetylene is a direct consequence of the lower entrance potential energy barrier on the triplet PES, which was calculated to be 7 kJ mol⁻¹ (at the CCSD(T)/CBS level of theory) for the O(³P) + acrylonitrile reaction and 9 kJ mol⁻¹ (at the CCSD(T)/CBS level of theory) for the O(³P) + cyanoacetylene reaction.⁹¹

5.3 Comparison with the O(³P) + ethylene (CH₂CH₂) and O(³P) + propene (CH₂CHCH₃) reactions

The interpretation of the results of this work can be enriched by comparison with the related O(³P) + C₂H₄ and O(³P) + C₃H₆ reactions that have been studied in our laboratory at a comparable collision energy.^{43,90,102,103} From a chemical point of view, ethylene and propene can be considered analogous to an acrylonitrile molecule where the CN group is substituted with H and CH₃, respectively. The role of substituents in determining a change in the reactivity of the species is of utmost importance in the development of realistic models and, in this case, we can rationalize the effect of a nitrile group in place of one of the four hydrogen atoms of ethylene and of the methyl group of propene. To make a consistent experimental comparison between the three systems, we focus only on the reaction involving O(³P). The topology of the triplet/singlet PESs of the three systems presents many similarities but a substantial difference arises in the topology of their singlet PESs. In particular, in the case of the reactions involving acrylonitrile, the hydrogen atom bound to the CO unit of ¹MIN3 (see Fig. 6) can migrate to the other two carbon atoms and to the nitrogen atom, leading to the formation of CH₃CN + CO and CH₂CNH + CO, respectively. The first pathway has a barrier (¹TS4) at −138 kJ mol⁻¹ (that is, 304 kJ mol⁻¹ above ¹MIN3), while the second one is characterized by a transition state (¹TS3) at −235 kJ mol⁻¹ (that is, located 207 kJ mol⁻¹ above ¹MIN3) (see Fig. 6 and also Fig. S6 in the ESI† for the structure of ¹TS4 and ¹TS3). In contrast, in the case of ethylene and propene, if we consider the evolution of the CH₃CHO (for the O(³P) + ethylene reaction) and CH₃CH₂CHO (for the O(³P) + propene reaction) intermediates, which are the equivalent to ¹MIN3 of the OCH₂CHCN system, the only possibility is the migration of the H atom from the terminal carbon atom to the directly bound carbon atom with very large potential energy barriers toward CO elimination and formation of CH₄ + CO (in O(³P) + ethylene) and of C₂H₆ + CO (in O(³P) + propene). This results in the predominance of the HCO-forming channels in these two O(³P) + alkene reactions and the absence of the CO-forming channels on the singlet PES. So, the presence of an additional, energetically favored reactive pathway, following H migration to the N atom of acrylonitrile on the singlet PES after ISC, is the main difference between the three systems that justifies the significant prevalence of the CH₂CNH + CO channel over the CH₂CN + HCO channel in the O(³P) + acrylonitrile reaction (see Table 3). The extent of ISC is inferred to be largest (87%) in O(³P) + acrylonitrile, while it is lower (50%) in O(³P) + ethylene, and even lower (20%) in O(³P) + propene. Finally, the easy channeling of the reactive flux, via ISC, toward the CH₂CNH + CO products explains why, in the O(³P) + CH₂CHCN reaction, the CH₂O + HCCN, OCCH₂CN + H, CH₂CN + HCO, and OCCHCN + H₂ channels are negligible (see Table 3), in contrast, for instance, to the equivalent channels in the O(³P) + C₂H₄ reaction.^90,102,103

6. Implications for extraterrestrial environments

The main result of our combined experimental and theoretical study is that the channel leading to the formation of ketenimine (CH₂CNH) + CO from the O(³P) + acrylonitrile reaction is by far the dominant reaction pathway. Since the reaction is characterized by an entrance potential energy barrier of 7 kJ mol⁻¹ (at CCSD(T)/CBS level), in line with a rate constant of (4.9 ± 1.0) × 10⁻¹³ cm³ molecule⁻¹ s⁻¹ at 298 K,⁴⁰ it can play a significant role only in warm extraterrestrial environments, such as the Sagittarius B2(N) hot molecular core,^23,24 the circumstellar envelope of C-rich star IRC + 10216,²⁷ or, possibly, the upper atmosphere of Titan.^29–35,104

Ketenimine and acrylonitrile have both been detected toward the Sagittarius B2(N) hot core (see Introduction) in comparable abundance. Ketenimine abundance has been estimated to be a hundredth of that of its constitutional isomer acetonitrile (CH₃CN).¹⁰⁵ Quan and Herbst¹⁰⁶ were able to reproduce the abundance of ketenimine by assuming that it is formed from the electron ion recombination of CH₃CNH⁺ in competition with the formation of CH₃CN and CH₂CN. There is experimental evidence that electron–ion recombination of CH₃CNH⁺ predominantly preserves the heavy atom skeleton¹⁰⁷ while recent theoretical estimates have actually found that the formation of ketenimine is the dominant channel by far.¹⁰⁸ The present reaction adds to the list of ketenimine formation routes especially in those regions where atomic oxygen and acrylonitrile are both abundant, as the O-rich Sagittarius B2(N) hot core. Ketenimine is neglected in the most common astrochemical databases, such as KIDA¹⁰⁹ and UMIST,¹¹⁰ that also overlook the reaction between acrylonitrile and oxygen atoms. To improve the accuracy of current astrochemical models, we recommend including the O(³P) + acrylonitrile reaction both as a possible destruction pathway of CH₂CHCN and a possible formation route of CH₂CNH.

Furthermore, the same conclusions can be extended to the O(¹D) + acrylonitrile reaction because our theoretically predicted BF of the CH₂CNH + CO channel on the singlet PES is very high (BF > 90%, see Table 3) at all the investigated temperatures. O(¹D) is extremely reactive and its bimolecular reactions have been invoked to explain the formation of complex species on the icy mantle of interstellar grains³⁷ or in the comas of comets.³⁶

In conclusion, the present work can enrich our knowledge of the gas-phase chemistry of nitrile compounds and imines that are key intermediates in the formation of many species with biological potential, such as nucleobases and amino acids.¹¹¹

7. Conclusions

We have reported a combined CMB and theoretical study of the O(³P,¹D) + acrylonitrile reactions that are processes of considerable relevance in combustion systems as well as in a variety of extraterrestrial environments (from Sagittarius B2(N) hot molecular cores^23,24 to Titan's atmosphere^29–35,104). We have determined that the O(³P) + acrylonitrile reaction exhibits two main product channels, among a large variety of possible open channels. Specifically, at a collision energy of 31.4 kJ mol⁻¹, it was found that the main reaction channel is the one leading to the formation of spin-forbidden CH₂CNH (ketenimine) + CO products (BF = 0.87 ± 0.05), which are formed via efficient intersystem crossing from the entrance triplet PES to the underlying singlet PES, while the spin-allowed H + HCOCHCN product channel, occurring adiabatically on the triplet PES, is minor (BF = 0.13 ± 0.05). The theoretical results have indicated that the dominant reaction mechanism is addition of atomic oxygen to the C1 carbon of the double bond, occurring after overcoming an entrance potential energy barrier of 7 kJ mol⁻¹ (at CCSD(T)/CBS level), and this makes this reaction not only relevant in combustion environments, but also in warm extraterrestrial environments, where it could represent an efficient mechanism of formation of ketenimine. Notably, the BF of the CH₂CNH + CO channel actually increases with decreasing temperature (Table 3), as expected, because the probability of ISC increases with decreasing temperature (i.e., with increasing lifetime of the initial triplet diradical intermediate, which facilitates the possibility of ISC).¹¹² We note that the main product of the title reaction, ketenimine, has been detected toward the same star-forming region of acrylonitrile as in Sagittarius B2(N) hot core. ^23,24,105 Ketenimine is often neglected by modelers, with respect to its more abundant isomer CH₃CN, and also the reaction between O(³P) and acrylonitrile is overlooked in models. This study leads us to propose the inclusion of the O(³P) + acrylonitrile reaction both as a possible destruction pathway of CH₂CHCN and a possible formation route of CH₂CNH.

We have also characterized the dynamics of the O(¹D) + acrylonitrile reaction that mainly leads to the formation of CH₂CNH + CO adiabatically on the singlet PES. This can improve models related to the chemistry of interstellar ice³⁷ and cometary comas,³⁶ where O(¹D) reactions are believed to play an important role. We remind that nitriles and imines are key intermediates in the formation of species with biological potential, such as nucleobases and amino acids.¹¹¹ Finally, the results of this study are expected to be also useful for improving combustion models involving the oxidation of acrylonitrile.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the Italian MUR (Ministero dell’Università e della Ricerca) for “PRIN 2017” funds, project “Modeling and Analysis of carbon nanoparticles for innovative applications Generated dIrectly and Collected DUring combuSTion (MAGIC DUST)”, grant number 2017PJ5XXX. This work was also supported by the Italian Space Agency (ASI, DC-VUM-2017-034, grant no. 2019-3 U.0 Life in Space). We also acknowledge the support from Italian MUR, University of Perugia within the program “Department of Excellence-2018-2022-Project AMIS”, and “Dipartimento di Ingegneria Civile ed Ambientale” (DICA) of the University of Perugia for allocated computing time within the project “Dipartimenti di Eccellenza 2018–2022”. P. L. thanks the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 811312 for the project “Astro-Chemical Origins” (ACO).

References

1. A. Belloche, H. S. P. Müller, K. M. Menten, P. Schilke and C. Comito, Astron. Astrophys., 2013, 559, A47 (187 pp).
2. R. Zhang, D. Shi, N. Liu, B. Chen, L. Wu, L. Wu and W. Yang, Catal. Today, 2015, 258, 17–27.
3. P. Wyman, V. Crook, J. Ebdon, B. Hunt and P. Joseph, Polym. Int., 2006, 55, 764–771.
4. R. Zhang, N. Liu, Z. Lei and B. Chen, Chem. Rev., 2016, 116, 3658–3721.
5. L. T. Groet, Encyclopedia of Chemical Technology, Wiley, New York, 3rd edn, 1978.
6. S. P. Felter and J. S. Dollarhide, Regul. Toxicol. Pharm., 1997, 26, 281–287.
7. D. R. van der Vaart, W. M. Vatvuk and A. H. Wehe, J. Air Waste Manage. Assoc., 1991, 41, 92–98.
8. T. Namba, S. Masukawa, J. Uchisawa and A. Obuchi, Catal. Lett., 2004, 93, 195–201.
9. N. Liu, D. Shi, R. Zhang, Y. Li and B. Chen, Catal. Today, 2019, 332, 201–213.
10. A. Gervasini, G. C. Vezzoli and V. Ragani, Catal. Today, 1996, 29, 449–455.
11. S. Y. Li, S. L. Li and B. L. Li, React. Kinet. Catal. Lett., 1997, 62, 89–95.
12. T. Namba, S. Masukawa, A. Ogata, J. Uchisawa and A. Obuci, Appl. Catal., B, 2005, 61, 288–296.
13. L. R. Snyder, Anal. Chem., 1969, 41, 314–323.
14. C. F. Brandenburg and D. R. Latham, J. Chem. Eng. Data, 1968, 13, 391–394.
15. S. Wallace, K. D. Bartle and D. L. Perry, Fuel, 1989, 68, 1450–1455.
16. J. C. Mackie, M. B. Colket III and P. F. Nelson, J. Phys. Chem., 1990, 94, 4099–4106.
17. A. Lifshitz, C. Tamburu and A. Suslensky, J. Phys. Chem., 1989, 93, 5802–5808.
18. N. R. Hore and D. K. Russell, J. Chem. Soc., Perkin Trans., 1998, 2, 269–276.
19. A. Terentis, A. Doughty and J. C. Mackie, J. Phys. Chem., 1992, 96, 10334–10339.
20. B. J. Finlayson-Pitts and J. N. Pitts Jr, Atmospheric Chemistry – Fundamentals and Experimental Techniques, Wiley, New York, 1986.
21. F. F. Gardner and G. Winnewisser, Astrophys. J., 1975, 195, L127–L130.
22. M. C. L. Gerry, K. Yamada and G. Winnewisser, J. Phys. Chem. Ref. Data, 1979, 8, 107.
23. A. Nummelin and P. Bergman, Astron. Astrophys., 1999, 341, L59–L62.
24. H. S. Müller, A. Belloche, K. M. Menten, C. Comito and P. Schilke, J. Mol. Spectrosc., 2008, 251, 319–325.
25. A. López, B. Tercero, Z. Kisiel, A. M. Daly, C. Bermúdez, H. Calcutt, N. Marcelino, S. Viti, B. J. Drouin, I. R. Medvedev, C. F. Neese, L. Pszczólkowski, J. L. Alonso and J. Cernicharo, Astron. Astrophys., 2014, 572, A44 (39 pp).
26. H. E. Matthews and T. J. Sears, Astrophys. J., 1983, 272, 149–153.
27. M. Agúndez, J. P. Fonfría, J. Cernicharo, J. R. Pardo and M. Guélin, Astron. Astrophys., 2008, 479, 493–501.
28. C. Vastel, J. C. Loison, V. Wakelam and B. Lefloch, Astron. Astrophys., 2019, 625, A91 (19 pp).
29. J. Cui, R. Yelle, V. Vuitton, J. Waite, W. Kasprzak, D. Gell, H. Niemann, I. Müller-Wodarg, N. Borggren and G. Fletcher, et al. , Icarus, 2009, 200, 581–615.
30. V. Vuitton, R. V. Yelle and M. J. McEwan, Icarus, 2007, 191, 722–742.
31. B. A. Magee, J. H. Waite, K. E. Mandt, J. Westlake, J. Bell and D. A. Gell, Planet. Space Sci., 2009, 57, 1895–1916.
32. B. Bézard, R. V. Yelle and C. A. Nixon, in Titan: Interior, Surface, Atmosphere, and Space Environment, ed. I. Müller-Wodarg, C. A. Griffith, E. Lellouch, T. E. Cravens, Cambridge Planetary Science, Cambridge University Press, 2014, vol. 5, pp. 158–189.
33. M. Y. Palmer, M. A. Cordiner, C. A. Nixon, S. B. Charnley, N. A. Teanby, Z. Kisiel, P. G. J. Irwin and M. J. Mumma, Sci. Adv., 2017, 3, e1700022.
34. J. C.-Y. Lai, M. A. Cordiner, C. A. Nixon, R. K. Achterberg, E. M. Molter, N. A. Teanby, M. Y. Palmer, S. B. Charnley, J. E. Lindberg, Z. Kisiel, M. J. Mumma and P. G. J. Irwin, Astron. J., 2017, 154, 206 (10 pp).
35. M. A. Cordiner, N. A. Teanby, C. A. Nixon, V. Vuitton, A. E. Thelen and S. B. Charnley, Astron. J., 2019, 158, 76 (14 pp).
36. M. A. Cordiner and S. B. Charnley, MNRAS, 2021, 504, 5401–5408.
37. J. B. Bergner, K. I. Öberg and M. Rajappan, Astophys. J., 2019, 874, 115 (16 pp).
38. D. Marchione, L. Mancini, P. Liang, G. Vanuzzo, F. Pirani, D. Skouteris, M. Rosi, P. Casavecchia and N. Balucani, J. Phys. Chem. A, 2022, 126, 3569–3582.
39. G. Vanuzzo, D. Marchione, L. Mancini, P. Liang, G. Pannacci, P. Recio, Y. Tan, M. Rosi, D. Skouteris, P. Casavecchia and N. Balucani, J. Phys. Chem. A, 2022, 126, 6110–6123.
40. H. P. Upadhyaya, P. D. Naik, U. B. Pavanaja, A. Kumar, R. K. Vatsa, A. V. Sapre and J. P. Mittal, Chem. Phys. Lett., 1997, 274, 383–389.
41. H. J. Kimber, J. Toscano and S. D. Price, Mon. Notices Royal Astron. Soc., 2018, 476, 5332–5340.
42. J. Sun, W. Wu, Y. Zhang, Y. Tang, H. Yi, J. Lu and R. Wang, Comput. Theor. Chem., 2015, 1052, 17–25.
43. F. Leonori, N. Balucani, V. Nevrly, A. Bergeat, S. Falcinelli, G. Vanuzzo, P. Casavecchia and C. Cavallotti, J. Phys. Chem. C, 2015, 119, 14632–14652.
44. G. Vanuzzo, N. Balucani, F. Leonori, D. Stranges, V. Nevrly, S. Falcinelli, A. Bergeat, P. Casavecchia and C. Cavallotti, J. Phys. Chem. A, 2016, 120, 4603–4618.
45. A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, P. Casavecchia, L. Pratali Maffei and C. Cavallotti, J. Phys. Chem. A, 2019, 123, 9934–9956.
46. A. Caracciolo, G. Vanuzzo, N. Balucani, D. Stranges, S. Tanteri, C. Cavallotti and P. Casavecchia, Chin. J. Chem. Phys., 2019, 32, 113–122.
47. C. Cavallotti, C. De Falco, L. Pratali Maffei, A. Caracciolo, G. Vanuzzo, N. Balucani and P. Casavecchia, J. Phys. Chem. Lett., 2020, 11, 9621–9628.
48. G. Vanuzzo, A. Caracciolo, T. K. Minton, N. Balucani, P. Casavecchia, C. de Falco, A. Baggioli and C. Cavallotti, J. Phys. Chem. A, 2021, 125, 8434–8453.
49. P. Recio, S. Alessandrini, G. Vanuzzo, G. Pannacci, A. Baggioli, D. Marchione, A. Caracciolo, V. J. Murray, P. Casavecchia, N. Balucani, C. Cavallotti, C. Puzzarini and V. Barone, Nat. Chem., 2022, 14, 1405–1412.
50. P. Casavecchia, F. Leonori and N. Balucani, Int. Rev. Phys. Chem., 2015, 34, 161–204.
51. P. Casavecchia, F. Leonori, N. Balucani, R. Petrucci, G. Capozza and E. Segoloni, Phys. Chem. Chem. Phys., 2009, 11, 46–65.
52. Y. T. Lee, Science, 1987, 236, 793–798.
53. P. Casavecchia, Rep. Prog. Phys., 2000, 63, 355–414.
54. P. Casavecchia, K. Liu and X. Yang, in Reactive Scattering: Reactions in Three Dimensions. In Tutorials in Molecular Reaction Dynamics, ed. M. Brouard, C. Vallance, Royal Society of Chemistry, Cambridge, UK, 2010, ch. VI.
55. M. Alagia, N. Balucani, P. Casavecchia, D. Stranges and G. G. Volpi, J. Chem. Soc., Faraday Trans., 1995, 91, 575–596.
56. N. R. Daly, Rev. Sci. Instrum., 1960, 31, 264–267.
57. M. Alagia, V. Aquilanti, D. Ascenzi, N. Balucani, D. Cappelletti, L. Cartechini, P. Casavecchia, F. Pirani, G. Sanchini and G. G. Volpi, Isr. J. Chem., 1997, 37, 329–342.
58. F. Leonori, K. M. Hickson, S. D. Le Picard, X. Wang, R. Petrucci, P. Foggi, N. Balucani and P. Casavecchia, Mol. Phys., 2010, 108, 1097–1113.
59. S. J. Sibener, R. J. Buss, C. Y. Ng and Y. T. Lee, Rev. Sci. Instrum., 1980, 51, 167–182.
60. Y. T. Lee, Reactive Scattering I: Nonoptical Methods, in Atomic and Molecular Beam Methods, ed. G. Scoles, Oxford University Press, New York, USA, 1987, vol. 1, pp. 553–568.
61. F. Leonori, R. Petrucci, N. Balucani, P. Casavecchia, M. Rosi, C. Berteloite, S. D. Le Picard, A. Canosa and I. R. Sims, Phys. Chem. Chem. Phys., 2009, 11, 4701–4706.
62. C. Sleiman, G. El Dib, M. Rosi, D. Skouteris, N. Balucani and A. Canosa, Phys. Chem. Chem. Phys., 2018, 20, 5478–5489.
63. C. Berteloite, S. D. Le Picard, I. R. Sims, M. Rosi, F. Leonori, R. Petrucci, N. Balucani, X. Wang and P. Casavecchia, Phys. Chem. Chem. Phys., 2011, 13, 8485–8501.
64. N. Balucani, A. Bergeat, L. Cartechini, G. G. Volpi, P. Casavecchia, D. Skouteris and M. Rosi, J. Phys. Chem. A, 2009, 113, 11138–11152.
65. N. Balucani, M. Alagia, L. Cartechini, P. Casavecchia, G. G. Volpi, K. Sato, T. Takayanagi and Y. Kurosaki, J. Am. Chem. Soc., 2000, 122, 4443–4450.
66. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
67. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
68. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023.
69. D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358–1371.
70. R. A. Kendall, T. H. Dunning Jr. and J. R. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
71. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
72. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
73. R. J. Bartlett, Annu. Rev. Phys. Chem., 1981, 32, 359–401.
74. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
75. J. Olsen, P. Jorgensen, H. Koch, A. Balkova and R. J. Bartlett, J. Chem. Phys., 1996, 104, 8007–8015.
76. C. Cavallotti, F. Leonori, N. Balucani, V. Nevrly, A. Bergeat, S. Falcinelli, G. Vanuzzo and P. Casavecchia, J. Phys. Chem. Lett., 2014, 5, 4213–4218.
77. I. Gimondi, C. Cavallotti, G. Vanuzzo, N. Balucani and P. Casavecchia, J. Phys. Chem. A, 2016, 120, 4619–4633.
78. C. Cavallotti, A. Della Libera, C.-W. Zhou, P. Recio, A. Caracciolo, N. Balucani and P. Casavecchia, Faraday Discuss., 2022, 238, 161–182.
79. J. M. L. Martin, Chem. Phys. Lett., 1996, 259, 669–678.
80. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, rev. A.02, Gaussian, Inc., Wallingford, CT, 2009.
81. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253.
82. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin, et al. , J. Chem. Phys., 2020, 152, 144107 (24 pp).
83. Avogadro: an open-source molecular builder and visualization tool. Ver. 1.2.0. https://avogadro.cc/.
84. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminform., 2012, 4, 17.
85. D. Skouteris, N. Balucani, C. Ceccarelli, F. Vazart, C. Puzzarini, V. Barone, C. Codella and B. Lefloch, Astrophys. J., 2018, 854, 135 (10 pp).
86. N. Balucani, L. Cartechini, M. Alagia, P. Casavecchia and G. G. Volpi, J. Phys. Chem. A, 2000, 104, 5655–5659.
87. N. Balucani, F. Leonori, R. Petrucci, M. Stazi, D. Skouteris, M. Rosi and P. Casavecchia, Faraday Discuss., 2010, 147, 189–216.
88. N. Balucani, D. Skouteris, F. Leonori, R. Petrucci, M. Hamberg, W. D. Geppert, P. Casavecchia and M. Rosi, J. Phys. Chem. A, 2012, 116, 10467–10479.
89. S. J. Klippenstein, J. Chem. Phys., 1992, 96, 367–371.
90. B. Fu, Y.-C. Han, J. M. Bowman, F. Leonori, N. Balucani, L. Angelucci, A. Occhiogrosso, R. Petrucci and P. Casavecchia, J. Chem. Phys., 2012, 137, 22A532 (22 pp).
91. P. Liang, E. V. F. de Aragão, G. Pannacci, G. Vanuzzo, A. Giustini, D. Marchione, P. Recio, F. Ferlin, D. Stranges and N. Faginas Lago, et al. , J. Phys. Chem. A, 2023, 127, 685–703.
92. D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, T. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 ; and references therein.
93. S.-H. Lee, W. J. Huang and W. K. Chen, Chem. Phys. Lett., 2007, 446, 276–280.
94. S.-H. Lee, W. K. Chen and W. J. Huang, J. Chem. Phys., 2009, 130, 054301.
95. W. B. Miller, S. A. Safron and D. R. Herschbach, Discuss. Faraday Soc., 1967, 44, 108–122.
96. J. I. Steinfeld, G. A. Fisk, J. D. McDonald and D. R. Herschbach, et al. , Discuss. Faraday Soc., 1967, 44, 226–240.
97. R. D. Levine and R. B. Bernstein, Molecular reaction dynamics and chemical reactivity, Oxford University Press, New York, 1987.
98. G. A. Fisk, J. D. McDonald and D. R. Herschbach, Discuss. Faraday Soc., 1967, 44, 228–229.
99. D. R. Herschbach, Adv. Chem. Phys., 1966, 10, 319–393.
100. A. M. Schmoltner, P. M. Chu and Y. T. Lee, J. Chem. Phys., 1989, 91, 5365–5373.
101. W. L. Fitch and A. D. Sauter, Anal. Chem., 1983, 55, 832–835.
102. B. Fu, Y.-C. Han, J. M. Bowman, L. Angelucci, N. Balucani, F. Leonori and P. Casavecchia, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9733–9738.
103. N. Balucani, F. Leonori, P. Casavecchia, B. Fu and J. M. Bowman, J. Phys. Chem. A, 2015, 119, 12498–12511.
104. H. R. Martens, D. B. Reisenfeld, J. D. Williams, R. E. Johnson and H. D. Smith, Geophys. Res. Lett., 2008, 35, L20103 (4pp).
105. F. J. Lovas, J. M. Hollis, A. J. Remijan and P. R. Jewell, Astrophys. J., 2006, 645, L137–L140.
106. D. Quan and E. Herbst, Astron. Astrophys., 2007, 474, 521–527.
107. E. Vigren, M. Kamińska, M. Hamberg, V. Zhaunerchyk, R. D. Thomas, M. Danielsson, J. Semaniak, P. U. Andersson, M. Larsson and W. D. Geppert, Phys. Chem. Chem. Phys., 2008, 10, 4014–4019.
108. L. Giani, C. Ceccarelli, L. Mancini, E. Bianchi, F. Pirani, M. Rosi and N. Balucani, Interstellar methyl cyanide and methanol connection: the revised CH₃CN gas-phase chemical network, MNRAS.
109. V. Wakelam, E. Herbst, J. C. Loison, I. W. M. Smith, V. Chandrasekaran, B. Pavone, N. G. Adams, M. C. Bacchus-Montabonel and A. Bergeat, et al. , Astrophys. J., Suppl. Ser., 2012, 199, 21 (10 pp).
110. J. Woodall, M. Agúndez, A. J. Markwick-Kemper and T. J. Millar, Astron. Astrophys., 2007, 466, 1197–1204.
111. D. E. Woon, Astrophys. J., 2002, 571, L177–L180.
112. H. Pan, K. Liu, A. Caracciolo and P. Casavecchia, Chem. Soc. Rev., 2017, 46, 7517–7547.

---

Footnote

† Electronic supplementary information (ESI) available: List of all possible reaction channels of the O(³P,¹D) + acrylonitrile reactions, with reaction enthalpies. Detailed global triplet and singlet PESs, with reaction enthalpies and barrier heights (kJ mol⁻¹, 0 K) computed at the CCSD(T)/aug-cc-pVTZ level of theory, considering the geometries obtained at the B3LYP/aug-cc-pVTZ level, for dissociation and isomerization processes for the O(³P,¹D) + CH₂CHCN reactions. Energies at the CCSD(T)/CBS level of theory for the most relevant reaction channels are reported (in parentheses) only in Fig. 5 of the main text. See DOI: https://doi.org/10.1039/d3cp01558k

---