An ab initio study of the photodissociation of CH₂I and CH₂I⁺

Abstract

Photodissociation of the CH₂I radical and the CH₂I⁺ cation is studied by means of high-level ab initio calculations, including spin–orbit effects. Potential-energy curves (PEC) along the dissociating bond distances involved in some fragmentation pathways of these species are computed for the ground and several excited electronic states. Based on the PECs obtained, the possible photodissociation mechanisms are analyzed and suggested. Significant differences are found between the fragmentation dynamics of the neutral radical and that of the cation. While a relatively simple dissociation dynamics is predicted for CH₂I, more complex fragmentation mechanisms involving internal conversion and couplings between different excited electronic states are expected for CH₂I⁺. The species studied here are relevant to atmospheric chemistry, and the present work can help to understand better how their photodissociation may affect chemical processes in the atmosphere.

---

1. Introduction

The photochemistry of radicals and reactive intermediates is of particular importance in atmospheric and interstellar chemistry.¹ In this sense, reactive intermediates of the family of halocarbocations play an important role in gas phase reactions, among them reacting with ozone to produce carbon monoxide, forming adducts with N- and O-containing molecules, or producing the functionalization of aromatic molecules.^2,3 In the present work, we explore the photodissociation dynamics of the CH₂I radical and the related CH₂I⁺ halocarbocation. Such species contribute to the rich atmospheric chemistry of iodine, particularly related to the oxidizing power of the atmosphere and to the formation of ultrafine aerosol particles.^4,5 The CH₂I radical can be produced through different reactions starting from either CH₂I₂ or CH₃I,

CH₂I₂ → CH₂I + I, (1)

CH₂I₂ +R → CH₂I + IR, (2)

CH₃I + R → CH₂I + HR, (3)

were R can be OH, F or Cl. The CH₂I⁺ cation is generated by further removing an electron from CH₂I.

The equilibrium geometry of the CH₂I radical in the ground electronic state has been charaterized as planar or quasi-planar. It is noted that rather few theoretical studies have been reported on both CH₂I and CH₂I⁺. One likely reason is that these two systems, and particularly CH₂I⁺, are computationally very demanding. Among the works reported in the literature is the investigation of the formation of CH₂I upon photodissociation of CH₂I₂ in acetonitrile solution, by means of ab initio molecular dynamics simulations.⁶ In that work, the equilibrium geometry of CH₂I in the ground state, as well as vertical excitation energies between the ground and several excited states of the radical, were computed. Equilibrium geometries in the ground state, along with vibrational frequencies, ab initio energies and enthalpies of formation were also calculated for several halomethanes and halomethyl radicals, among them CH₂I.⁷ More recently, potential-energy curves (PEC) along the C–I bond distance were reported for the ground electronic state of CH₂I, and for the ground and first excited electronic states of CH₂I⁺.⁸

The experimental works reported in the literature on CH₂I and CH₂I⁺ are more abundant than the theoretical ones. Vibrational frequencies of several normal modes of CH₂I in the ground electronic state were measured using infrared spectroscopy.^9–11 Hyperfine microwave and millimiter-wave spectra of CH₂I in the ground vibrational state were measured,¹² providing structural and electronic properties of the radical. Photoelectron spectra of CH₂I were obtained, from which vertical ionization and adiabatic ionization energies,^13,14 as well as the vibrational frequency of the C–I stretching mode (ν₃),¹⁴ were determined. In a photoion-photoelectron coincidence study the CH₂I⁺ cation was detected for the first time.¹⁵ Later on, the vibrational and electronic structure of CH₂I⁺ was explored by means of fluorescence excitation and emission spectroscopy.¹⁶ In recent photoion-photoelectron coincidence spectra obtained with synchroton radiation, the VUV photoionozation of CH₂I was investigated.⁸ The kinetics of the reaction of CH₂I with O₂ was also explored by measuring the reaction rate constant at different atmospheric temperatures.¹⁷ In the present work the structure of the electronic states of CH₂I and CH₂I⁺ is investigated in order to understand their photodissociation dynamics along some of their fragmentation pathways. Specifically, the fragmentation pathways studied are:

CH₂I → CH₂ + I (4)

CH₂I⁺ → (CH₂ + I)⁺ (5)

CH₂I⁺ → HCI⁺ + H. (6)

The above dissociation pathways have been investigated by means of multireference configuration interaction (MRCI) ab initio calculations including spin–orbit effects. In the case of pathway (5) the notation (CH₂ + I)⁺ denotes that the charge can be located in any of the two fragments, i.e., the product fragments can be both CH₂⁺ + I and CH₂ + I⁺. The PECs of the ground and several excited electronic states along the corresponding dissociation coordinate of the three pathways have been calculated. As already mentioned, pathways (4) and (5) were previously investigated in ref. 8 by computing the PECs of the ground electronic state of pathway (4), and of the ground and first excited states of pathway (5), along a range of distances R_C–I ≤ 3.5 Å, that is, essentially restricted to the interaction region of the curves. In the present work, the study of pathways (4) and (5) is extended to a lager number of excited states, and also to larger R_C–I distances in the asymptotic region.

Pathways (4)–(6) are all of atmospheric relevance. In particular, pathway (4) may constribute to increase the budget of atomic I in different regions of the atmosphere. It is well known that atomic halogens (X = Cl, Br, I) are among the main causes of depletion of ozone (X + O₃ → XO + O₂) in the stratosphere and troposphere.^18,19 While CH₃I formed by the marine biological activity is one of the main sources of atomic iodine in the atmosphere,^18,19 pathways (4) and (5) may also be a relevant contribution in the atmospheric regions where radiation is abundant enough. Pathway (6) is also interesting because it produces another iodocarbon radical species that can be an intermediate in several atmospheric chemical processes and cycles. Thus, this work intends to elucidate how photodissociation of the CH₂I and CH₂I⁺ species takes place through different pathways and by which mechanisms, which can help to understand better how it may affect the atmospheric chemistry.

The article is organized as follows. In Section 2 the methodology applied is described. In Section 3 the results are presented and discussed. Finally, some conclusions are drawn in Section 4.

2. Methodology

The potential energy curves of the ground and several excited electronic states have been computed at MRCI level,^20,21 including spin–orbit effects, for the C–I and C–H streching coordinates associated with dissociation through pathways (4)–(6). For each value of the corresponding dissociation coordinate, a relaxed scan, i.e. a geometry optimization on all the remaining coordinates of the radical or cation, was carried out in the ground state. The geometry optimizations were performed at CASPT2 level²² to describe properly the breaking of the different bonds, since mono-reference methods usually fail to describe this type of processes. In order to compare with the CASPT2 results, equilibrium geometries at CCSD(T) level were also obtained.

The MRCI calculations were performed over the optimized geometries obtained at CASPT2 level, in order to build up the PECs of the different electronic states. The orbitals and references used in the MRCI calculations were obtained by previous state-averaged CASSCF²³ calculations. For each relaxed geometry along the dissociation coordinate, the state-averaged CASSCF calculations considered an active space of thirteen electrons in eleven orbitals (eight a′ and three a′′ in C_s symmetry). In order to obtain a good description of the relative energy between the neutral radical and the cation, the ground state of the radical species was included in the state average together with ten singlet states (five A′ and five A′′) and twelve triplet states (six A′ and six A′′) of the cation. Thus, considering the resulting state-averaged optimized orbitals, twenty two electronic states of the cation plus the ground state of the neutral species were included in the calculations at the MRCI level. The spin–orbit matrix, built up with ten singlet and twelve triplet states, was calculated using the Breit-Pauli operator.²⁴ All the calculations were carried out with the MOLPRO package²⁵ using the full-electron ANO-RCC basis set.²⁶ The Douglas-Kroll Hamiltonian was employed in order to describe properly the relativistic effects on the inner electrons of the iodine atom.

Finally, a harmonic frequency calculation of both radical and cation was performed at their respective equilibrium position in order to obtain a estimation of the vibrational zero point energy (ZPE) and frequencies at CCSD(T) level of theory.

3. Results and discussion

3.1 Geometrical and energy properties

The equilibrium geometries were optimized in the ground electronic state for CH₂I and CH₂I⁺ at CASPT2 and CCSD(T) levels of theory. The distances and angles obtained are collected in Table 1, and they are found to be very similar. Fig. 1 displays the equilibrium geometries optimized at CCSD(T) level for the two species. In Table 1 these values are also compared with those alculated in previous works for CH₂I. Very good agreement is found between the present and the previously computed equilibrium geometries.

Table 1 Calculated equilibrium geometries (at CASPT2 and CCSD(T) (in parenthesis) levels), harmonic frequencies, and harmonic zero-point energies (at CCSD(T) level) of the electronic ground states of CH₂I and CH₂I⁺, and comparison with theoretical and experimental data from ref. 6, 7 and 9

	CH2I (this work) CASPT2 (CCSD(T))	CH2I^+ (this work) CASPT2 (CCSD(T))	CH2I (theory^a^b and experiment^c)
a Calculated with density functional theory using a B-LYP functional (ref. 6). b Calculated at quadratic configuration interaction singles and doubles/6-311G(d,p), QCISD/6-311G(d,p), level (ref. 7). c Experimental data (ref. 9).
r CI (Å)	2.031 (2.042)	1.921 (1.949)	2.066^a, 2.049^b
r CH (Å)	1.074 (1.077)	1.083 (1.085)	1.083^a, 1.081^b
	122.8 (123.0)	120.7 (121.0)	123.8^a, 122.9^b
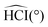
	118.6 (118.5)	119.65 (119.5)	118.1^a, 118.55^b
ω 1 (cm^−1) (B1)	222	763	21^b, 375^c
ω 2 (cm^−1) (A1)	632	880	591^b, 611^c
ω 3 (cm^−1) (B2)	849	981	835^b
ω 4 (cm^−1) (A1)	1371	1415	1336^b, 1330^c
ω 5 (cm^−1) (A1)	3170	3119	3047^b, 3050^c
ω 6 (cm^−1) (B2)	3320	3260	3188^b
ZPE (cm^−1)	4781	5210	4509^b

---

Fig. 1 Distances (in Å) and angles (in degree) associated with the equilibrium geometries optimized at CCSD(T) level in the ground electronic state for CH₂I and CH₂I⁺.

Vibrational harmonic frequencies of the different modes, as well as zero-point energies (ZPE) were computed at CCSD(T) level, and are shown in Table 1 for CH₂I and CH₂I⁺. They are also compared with the harmonic frequencies and the ZPE value calculated earlier for CH₂I, and with the available experimental frequencies for CH₂I. Again, the agreement is good between the current and previosuly calculated frequencies and ZPE values, being the present results somewhat larger.

Calculated vertical excitation energies from the ground to several excited states of both CH₂I and CH₂I⁺ are collected in Table 2, and the dipole moments associated with the transitions in CH₂I are shown in Table 3. As seen from Table 3, the first, third, and fourth excited states are those with the largest oscillator strength, although higher excited states (like states 9–12) also exhibit a remarkable dipole moment. Vertical excitation energies corresponding to the first excited states of CH₂I were reported in ref. 6 without considering spin–orbit coupling effects. Such energies are significantly lower than the present ones.

Table 2 Computed vertical excitation energies (VEEs) for several spin–orbit states of CH₂I and CH₂I⁺ with respect to the minimum of their respective ground states X̃²B₁ and X̃¹A₁. For the neutral radical, all spin–orbit states are doubly degenerated. For the cation, the symmetry of the total electronic wavefunction with respect to the plane of the molecule is also shown. The calculated ionization potential of CH₂I⁺ is 8.334 eV

CH2I		CH2I^+
State	VEE (eV)	State	VEE (eV)	State	VEE (eV)
X̃	—	X̃ (A′)	—	20 (A′′)	7.0964
1	3.6303	1 (A′′)	1.8645	21 (A′)	7.1375
2	3.9544	2 (A′)	1.8654	22 (A′)	7.1446
3	4.8003	3 (A′′)	1.9385	23 (A′′)	7.5425
4	4.9969	4 (A′)	2.0183	24 (A′)	7.6272
5	5.1261	5 (A′)	2.7727	25 (A′′)	7.8002
6	5.3482	6 (A′′)	2.7902	26 (A′)	7.8173
7	5.7829	7 (A′′)	2.7972	27 (A′)	7.9117
8	5.8577	8 (A′)	4.8152	28 (A′′)	7.9266
9	6.1675	9 (A′′)	5.3204	29 (A′′)	8.6946
10	6.4176	10 (A′)	5.3237	30 (A′′)	9.0532
11	6.8079	11 (A′)	5.4183	31 (A′′)	9.0675
12	7.7297	12 (A′′)	5.6327	32 (A′)	9.0810
13	7.7427	13 (A′′)	5.6456	33 (A′′)	9.1298
14	8.1671	14 (A′)	5.6726	34 (A′)	9.1990
		15 (A′′)	6.0698	35 (A′′)	9.2293
		16 (A′)	6.3514	36 (A′′)	9.4577
		17 (A′)	6.9759	37 (A′)	9.4615
		18 (A′′)	7.0721	38 (A′′)	9.4692
		19 (A′)	7.0913	39 (A′)	9.7544

---

Table 3 Transition dipole moments for excitation from the ground to several excited electronic states of CH₂I

State	TDMx (Debye)	TDMy (Debye)	TDMz (Debye)
1	0	0	0.625
2	0.026	0.100	0.059
3	0.012	0.015	0.663
4	0.012	0.040	1.456
5	0	0	0.110
6	0.060	0.067	0
7	0.221	0.074	0.036
8	0.027	0.058	0.084
9	0.012	0.063	0.128
10	0.438	0.133	0.105
11	0.126	0.187	0.251
12	0.111	0.616	0.034
13	0	0.057	0.010
14	0.059	0.023	0

---

Ionization energies for the 0–0 vibronic transitions in the C–I stretching mode for the eight first electronic states of CH₂I⁺ from the ground state of CH₂I, were calculated and compared with the experimental values in ref. 8. All the absolute values of the computed energies were lower than the experimental ones by a nearly constant amount of about 0.5 eV. Table 4 collects the calculated ionization energies, the energies corrected by adding the above constant amount of energy, and the experimental ionization energies for comparison. The discrepancy between the calculated and experimental energies is essentially due to the one-dimensional (1D) model used to calculate the ground vibrational levels involved in the vibronic transitions, which neglects the zero-point energy of all the remaining modes except the C–I stretch one. Once the calculated energies were shifted by this constant amount, agreement with the experimental energies was found to be practically quantitative. This means that the energy separation between the minima of the PECs of the ground electronic state of CH₂I and of the ground and first excited electronic states of CH₂I⁺ is calculated very accurately. And these energy separations remain essentially the same when adding the calculated 1D vibrational energies, which are very similar for the different excited states of CH₂I⁺ (see Table 4). The essential reason of the good agreement between the calculated and the experimental ionization energies is that we are using a high-level, highly correlated MRCI method to calculate the PECs that includes all the electrons and the spin–orbit coupling. For the same reason, the vertical excitation energies of Table 2 are expected to be as accurate as the energy separations between the minima of the ground state of CH₂I and of the ground and first excited states of CH₂I⁺.

Table 4 Calculated ionization energies (IE) for the 0–0 vibronic transitions of the C–I stretching mode for the eight first electronic states of CH₂I⁺ with respect to the ground electronic state CH₂I(X̃²B₁). The computed ionization energies corrected by adding a constant amount of 0.504 eV are also shown and compared to the experimental energies from ref. 8

State	Calculated IE (eV)	Corrected IE (eV)	Experimental IE (eV)
X̃ (A′)	7.830	8.334	8.334
1 (A′′)	9.577	10.081	10.04
2 (A′)	9.579	10.083
3 (A′′)	9.605	10.109	10.10
4 (A′)	9.772	10.276	10.22
5 (A′)	10.320	10.824	10.79
6 (A′′)	10.338	10.842	10.84
7 (A′′)	10.348	10.853

---

3.2 Potential energy curves of the fragmentation pathways

The existence of different types of bonds in small organic molecules and radicals makes possible the occurrence of several fragmentation pathways, which produce a variety of different fragments following specific photodissociation dynamics. This has been shown by investigating the photofragmentation of two relatively small radical molecules like ethyl (C_βH₃–C_αH₂)^27–30 and vinyl (C_βH₂=C_αH),³¹ through the dissociation pathways involving breaking of the C_α–H, C_β–H or C–C bonds. A similar situation is found in the CH₂I radical and the CH₂I⁺ cation. In the following, the PECs associated with the fragmentation pathways (4)–(6) are analyzed in order to elucidate the possible dissociation mechanisms involved.

Upon excitation of the molecular species from the ground electronic state to the different excited states, the dynamical mechanisms expected to occur are typically of two types. When the molecule is excited to a bound electronic state where fragmentation of the system is not possible, the usual mechanism is a nonradiative gradual relaxation to lower states (and eventually to the ground one) known as internal conversion. If excitation populates repulsive, dissociative electronic states, then the molecule will fragment along a specific bond. A combination of the above two mechanims may also happen when a bound state is initially excited, and this state is nonadiabatically or spin–orbit coupled to a dissociative state. In this case, an initial relaxation by internal conversion may be followed by dissociation of the system when population is nonadiabatically transferred from the bound to the repulsive state.

In Fig. 2 the PECs of both CH₂I (lower black curves) and CH₂I⁺ (upper red curves) are shown along the C–I bond distance. While calculations were carried out up to larger distances, Fig. 2 only shows the range up to R_C–I = 3.5 Å in order to present a view in more detail of the interaction region of the PECs. An interesting feature is the large density of states found, particularly for the cation above 12 eV.

Fig. 2 Adiabatic potential energy curves of the ground and excited electronic states of CH₂I (lower black curves) and CH₂I⁺ (upper red curves) along the C–I bond distance up to 3.5 Å.

The figure displays the relative position of the potential curves of the neutral and cationic species. A large separation of 8.334 eV, which would correspond to the adiabatic ionization potential of CH₂I (accounting for both the radical and cation ZPEs), is found between the ground state of CH₂I and the ground state of CH₂I⁺, which implies high ionization energies of more than 8 and 10 eV to reach the ground and first excited electronic states of CH₂I⁺, respectively.⁸ The energy separation between the asymptotes of the curves of the neutral and cationic species is even larger.

The shape of the PECs of CH₂I and CH₂I⁺ is also quite different. The neutral species exhibits a clearly bound ground state with a well of 2.71 eV, a first excited state with a rather shallow well, and a second excited state with a small well and a low exit barrier to dissociation. In particular, the structure found in the second excited state around 2.25 Å corresponds to a double avoided crossing. The first avoided crossing arises from the nonadiabatic coupling between the spin-free 2² A′ (bound) and 3² A′ (dissociative) states. Both of them are also coupled by the spin–orbit coupling. In addition, the spin-free 1⁴ A′′ dissociative state is also coupled by the spin–orbit coupling with the above two states, giving rise to the structure of the exit barrier displayed in by the second excited state. Higher excited states calculated are unbound, dissociative ones. On the contrary, the cationic species exhibits a ground state and a large number of excited states as bound ones with typically deep wells, up to energies of about 14 eV. For higher energies several states with shallow wells and low exit barriers appear, and only above nearly 16 eV purely dissociative states are found. The dissociation energy of 5.11 eV of the C–I bond of the cation is considerably larger than in the neutral radical, and the equilibrium position reduces from 2.05 Å to 1.95 Å, a clear indication of the formation of a double bond between the carbon and iodine atoms. Actually, the occupation of orbitals indeed confirms that the π bonding orbital is doubly occupied, leading to a stable closed-shell molecule.

The above structure of the electronic PECs of CH₂I and CH₂I⁺ along the C–I coordinate determines their photodissociation dynamics behavior. In the case of CH₂I, dissociation is favored by relatively low energy transitions (>4 eV) to the first and second excited states, due to their shallow wells and low exit barrier of the latter state. For excitation energies >5 eV the higher dissociative excited states can be accessed, leading also to dissociation into CH₂ + I fragments. The CH₂I PECs of Fig. 2 display two groups of curves separated at R_C–I = 3.5 Å by about 1 eV, which is the splitting between the ground I(²P_3/2) and the excited I(²P_1/2) spin–orbit states of atomic iodine. Thus, depending on the excitation energy, it is possible to access dissociative PECs that will produce either I(²P_3/2) or I(²P_1/2) fragments. This point will be addressed in more detail later.

The PECs found for CH₂I⁺ indicate that fragmentation dynamics in the cation is much more unlikely. Indeed, since all the electronic states of CH₂I⁺ are bound across a large range of energies, excitation to those states will not produce dissociation, and only nonradiative relaxation through internal conversion to the lower electronic states, eventually leading to the ground state, will be possible. Excitation to the dissociative states located above 14 eV that would produce fragmentation of the cation would require very large excitation energies. It is noted that, in contrast with the curves of CH₂I, at R_C–I = 3.5 Å the PECs of the cation still do not display energy separations that could be assigned to the spin–orbit splitting of iodine, as would be expected. This point will be discussed in more detail below.

A more detailed view of the PECs associated with CH₂I along the C–I bond coordinate is displayed in Fig. 3 by extending the C–I bond distance up to R_C–I = 5 Å, where the curves typically exhibit an asymptotic behavior. It is noted that Fig. 3 shows a larger number of electronic PECs of the CH₂I radical than Fig. 2. Specifically, the CH₂I PECs with asymptotes above 4 eV were suppressed in Fig. 2 to avoid too much overlap with the PECs of CH₂I⁺ that would cause congestion of Fig. 2. The asymptotes of the different potential curves have been labeled by identifying the different electronic states of the CH₂ and I product fragments. The PECs of Fig. 3 correlate with CH₂ fragments produced in the states X̃, ã, b̃, and c̃, in combination with both I(²P_3/2) and I(²P_1/2) fragments, except in the case of CH₂(c̃), for which the only curve correlating with CH₂(c̃) + I(²P_3/2) is shown in Fig. 3. Splitting of the asymptotes associated with the same electronic state of the CH₂ fragment due to the two spin–orbit states of the I fragment is clearly displayed in the figure.

Fig. 3 Adiabatic potential energy curves of the ground and excited electronic states of CH₂I along the C–I bond distance up to 5 Å.

Fig. 3 shows in more detail that, as already mentioned, the ground and the two first excited states are the only bound low-energy electronic states. However, both the first and the second excited states exhibit very shallow wells, followed by such a low exit barrier in the case of the second excited state (easy to overcome), that they are expected to behave rather as dissociative states instead of as bound ones. A similar situation is found at high energies for the two curves correlating with CH₂(ã) + I(²P_1/2) and CH₂(c̃) + I(²P_3/2). The PEC producing CH₂(ã) also exhibits a very shallow well and a very low exit barrier to dissociation, similarly to the second excited state, while the highest PEC producing CH₂(c̃) displays a shallow well with no barrier, same as the first excited state. These two electronic states are also expected to behave essentially as dissociative states. The remaining PECs of Fig. 3 correspond to purely dissociative states. The implication of the above results is that excitation from the ground state at energies above ∼2.8 eV promotes the radical to states which are dissociative in practice, producing fragmentation into CH₂ and I, following a rather simple direct dissociation dynamics. Mechanisms of internal conversion appear rather unlikely to occur in any of the excited states. Interestingly, it is noted that due to the relatively high density of states above 4 eV, excitation above this energy is expected to populate several excited states, then producing fragments in different electronic states with rather broad, delocalized translational energy distributions.

Regarding the cation, Fig. 4 displays the PECs associated with fragmentation pathway (5), along the C–I bond distance. Before discussing the photodissociation dynamics on these PECs, a few remarks should be made. In the calculations involving this pathway the C–I distance has been extended up to R_C–I = 10 Å to ensure that the true asymptotic region of the curves was reached. In contrast to the PECs of pathway (4) (see Fig. 3) where the asymptotic behavior is typically reached at R_C–I = 5 Å, the curves of Fig. 4 interact more strongly between themselves, and thus their asymptotic behavior appears at larger distances. In addition, the fact that pathway (5) can produce CH₂⁺ + I and CH₂ + I⁺ fragments, implies a larger density of electronic states and PECs, which in turn also contributes to a stronger interaction between them. The situation becomes more complicated because the ionization potentials of CH₂ (10.396 eV) and I (10.451 eV) are very similar,³² as well as the spin–orbit splittings of I and I⁺ are. As a result of all the above, the different curves are mixed together in the asymptotic region at close energy positions, and it is not possible to identify the spin–orbit splittings between them that would lead to an unambiguous assignment of the different curves, and of the electronic states in which their corresponding fragments are produced. This is why an asymptotic assignment of the fragments similar to that of Fig. 3 could not be carried out for the curves of Fig. 4.

Fig. 4 Adiabatic potential energy curves of the ground and excited electronic states along the C–I bond distance up to 10 Å for the CH₂I⁺ → (CH₂ + I)⁺ fragmentation pathways, where (CH₂ + I)⁺ denotes that the charge can be in any of the two fragments, and that this pathway can produce both CH₂⁺ + I and CH₂ + I⁺. Note that in contrast to Fig. 2, the zero of energy is set up at the ground state minimum.

Among the excited state PECs of Fig. 4 it is possible to establish three different groups according to their energy position and density of states. A first group would be composed of the first excited states with an energy minimum below 3 eV. A relatively low density of states is found in this energy region. Their corresponding PECs are bound, with relatively deep wells, and without exit barriers. Thus, after excitation to any of these electronic states at energies below ∼3.5 eV, the dominant mechanism expected is relaxation through internal conversion to the lower electronic states.

At energies in the range 3.5–6 eV a second group of excited states can be distinguished, composed also of typically bound PECs with shallower wells and without exit barriers. In this energy region the density of states is significantly higher than below 3.5 eV. Due to the energy location of the asymptotes of these states the dynamics upon excitation will be different depending on the excitation energy. For excitation energies <5 eV dissociation is not possible, and only relaxation by internal conversion is expected. For excitation in the range 5–6 eV fragmentation of CH₂I⁺ can now occur in combination with internal conversion.

For excitation energies above 6 eV a third group of excited states would consist of bound states with shallow wells and low exit barriers in some cases along with purely repulsive states. Similarly as in Fig. 3, some of the states with low exit barriers are expected to behave in practice as dissociative states. Thus, for this group of states we change to a regime of photodissociation where the dynamics will be dominated by the fragmentation of the cation. Fig. 2 indicates that access to these states would require high excitation energies of about 14 eV (∼ 89 nm).

It is noted that the threshold photoelectron spectrum (TPES) of CH₂I was measured up to energies of 12 eV by ionizing the CH₂I radical using synchrotron radiation.⁸ Within this range of energy, essentially only the bound electronic states of CH₂I⁺ corresponding to the first, low-energy group are accessed. As a result of the bound nature of the electronic states excited, the TPES displayed a progression of vibrational bands. In future experiments with synchrotron radiation, the photoelectron spectrum could be measured probing energies >12 eV, and reaching the higher-energy states of the second and third groups of CH₂I⁺. Fig. 2 and 4 indicate that the nature and shape of these electronic states change with respect to the first group, because the density of states increases (increasing the couplings between them), shallow wells and low exit barriers appear in the bound states, and several of the states become repulsive. As discussed above, dissociation of CH₂I⁺ is predicted to coexist with the mechanism of internal conversion, which would lead to a TPES signal rather different than that found for <12 eV. Thus, the PECs of Fig. 2 and 4 could help to understand the TPES signal measured for energies >12 eV in future experiments with synchrotron radiation.

At this point it is interesting to compare briefly the dissociation of the C–I bond in the neutral species and in the cation through pathways (4) and (5), respectively. As already mentioned, the repulsive nature of all the PECs of Fig. 3 implies that fragmentation of the C–I bond will occur at all excitation energies in CH₂I. In CH₂I⁺, however, depending on the excitation energy we may have relaxation by internal conversion without fragmenation (at low energies), C–I bond dissociation (at very high energies), or a combination of these two mechanisms (at middle energies). When there is a high density of excited states, nonadiabatic and spin–orbit couplings between the different states are expected to occur, that will favor population transfer between them. The high density of states is also likely to favor the simultaneous population of several electronic states in a range of excitation energies. The consequence is the occurrence of complex fragmentation mechanisms on different electronic PECs, producing fragments in a variety of final electronic states. The above is predicted to occur in both CH₂I and CH₂I⁺, although to a larger extent in the cation, since the density of states is higher than in CH₂I. This combined with the addition of the internal conversion mechanism (not present in CH₂I) makes the photodissociation dynamics of pathway (5) more complex than that of pathway (4).

The PECs associated with the other fragmentation pathway of CH₂I⁺ studied here, that along one of the C–H bond distances, are shown in Fig. 5. Likewise the PECs of pathway (5), the curves of Fig. 5 display a high density of states, and we can also distinguish at least two groups of excited states. The first group would consist of low-energy excited states with a minimum near 2 or 3 eV, while the second group would be composed of high-energy states with a minimum near or above 5 eV. There are, however, several significant differences between these PECs and those of Fig. 4. One of them is that all the potential curves of pathway (6) correspond to bound electronic states, even at high energies as nearly 10 eV, with the absence of dissociative states. Another difference is that most of the curves of Fig. 5 exhibit exit barriers to dissociation, which in general are low. Such barriers are present in the very first excited states. A third interesting difference is that the energy separation between the groups of low- and high-energy excited states is substantially larger than in Fig. 4. In addition, the energy spreading of the asymptotes of the PECs of Fig. 5 is much larger (in the range 5–10 eV) than in Fig. 4 (in the range 5–8 eV), which is expected to have a different reflection in the product fragment distributions of pathways (5) and (6). Interaction between the electronic PECs of Fig. 5 appears to be clearly weaker than in Fig. 4, and the asymptotic regime is reached at substantially shorter distances.

Fig. 5 Adiabatic potential energy curves of the ground and excited electronic states along the C–H bond distance for the CH₂I⁺ → HCI⁺ + H fragmentation pathway.

The above features of the PECs will determine the photodissociation dynamics behavior of this fragmentation pathway. Upon excitation from the ground state below 5 eV to the excited states correlating with HCI⁺(i) + H (i = X̃, Ã, B̃), relaxation by internal conversion to the lower electronic states appears to be the most likely mechanism. For excitation energies slightly above 5 eV, after internal conversion to the two first excited states, a slow dissociation mechanism mediated by tunneling through the exit barriers of those states may compete to some extent with a further internal conversion to the ground state.

For excitation energies above 6 eV the density of the high-energy states of the second group increases remarkably, and at some energies probably several electronic states will be populated. Internal conversion is still predicted to be an important mechanism, particularly for excitation between 5 and 7 eV. However, similarly to the case of pathway (5), the nonadiabatic couplings expected to occur between the different excited states and the numerous exit barriers present in the PECs, are likely to favor fragmentation of the cation following a complex dissociation dynamics on several PECs, producing HCI⁺ and H fragments in different final electronic states.

4. Conclusions

Photodissociation of the CH₂I radical and CH₂I⁺ cation is investigated by means of high-level multireference configuration interaction ab initio calculations. Spin–orbit effects have been included in the calculations. More specifically, the fragmentation pathway CH₂I → CH₂ + I of the neutral species and the pathways CH₂I⁺ → (CH₂ + I)⁺ and CH₂I⁺ → HCI⁺ + H of the cation have been studied. Potential energy curves associated with the ground and several excited electronic states along the dissociating bond distance corresponding to each pathway are calculated. The potential-energy curves obtained for the different dissociation pathways are analyzed in order to elucidate the possible photofragmentation dynamics mechanisms.

In the case of CH₂I, the excited state dynamics along the C–I bond is determined by states that are dissociative or behave as such in practice. Thus, the dominant dynamical mechanism is predicted to be dissociation of the radical. The dynamical behavior of CH₂I⁺ along the C–I bond is, however, more complex. A remarkably higher density of states and potential energy curves is found as a result that both CH₂⁺ + I and CH₂ + I⁺ fragments are possible for this dissociation pathway. The electronic spectrum of excited states consists of low- and middle-energy bound states, and high-energy essentially dissociative states. Thus, depending on the excitation energy, the dynamics will combine mechanisms of relaxation to lower states through internal conversion with fragmentation of the C–I bond. In the case of the second pathway of CH₂I⁺ along the C–H coordinate, the potential-energy curves show some similarities (high density of states) and some differences with the curves along the C–I bond distance. The main difference is that along the C–H distance all the curves are bound, with absence of dissociative states. As a result, internal conversion is expected to be the dominant mechanism at relatively low excitation energies, while a combination of internal conversion and C–H fragmentation is predicted for higher energies.

Due to the high density of states found in general for the three fragmentation pathways, but particularly for those of CH₂I⁺, population of several electronic states is likely to occur upon excitation in a large range of energies. This fact, along with the nonadiabatic couplings expected to take place between different excited states in the three pathways, are predicted to favor the occurence of complex fragmentation mechanisms on several electronic potential-energy curves, producing fragments in different final electronic states and with a rather broad distribution of translational energies. Experimental confirmation of the present findings should be very interesting.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This research has been carried out within the Unidad Asociada Química Física Molecular between the Departamento de Química Física of Universidad Complutense de Madrid and CSIC. This work was funded by the Ministerio de Ciencia e Innovación (MICINN, Spain), grant no. PGC2018-096444-B-I00, PID2019-107115GB-C21, PID2021-122549NB-C21, PID2021-122796NB-I00, and PID2021-122839NB-I00. A. B. acknowledges funding from the I-COOP program from CSIC, grant no. COOPB20364, which made possible a research stay at Instituto de Física Fundamental, CSIC. This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 872081, and from the COST Action CA21101 (COSY). The Centro de Supercomputación de Galicia (CESGA, Spain) is acknowledged for the use of its resources.

References

1. R. A. Moss, M. Platz, M. Joneset al., Reactive Intermediate Chemistry, Wiley Online Library, 2004.
2. R. A. J. O'Hair and S. Gronert, Int. J. Mass. Spectrum, 2000, 195, 303–317.
3. A. E. Sorrilha, L. S. Santos, F. C. Gozzo, R. Sparrapan, R. Augusti and M. N. Eberlin, J. Phys. Chem. A, 2004, 108, 7009–7020.
4. J. L. Jiménez, et al. , J. Geophys, Res., 2003, 108(D10), 4318.
5. A. Sáiz-López, J. M. C. Plane, A. R. Baker, L. J. Carpenter, R. von Glasow, J. C. Gómez Martín, G. McFiggans and R. W. Saunders, Chem. Rev., 2012, 112, 1773–1804.
6. M. Odelius, M. Kadi, J. Davidsson and A. N. Tarnovsky, J. Chem. Phys., 2004, 121, 2208–2214.
7. P. Marshall, G. Srinivas and M. A. Schwartz, J. Phys. Chem. A, 2005, 109, 6371–6379.
8. D. V. Chicharro, H. R. Hrodmarsson, A. Bouallagui, A. Zanchet, J.-C. Loison, G. A. García, A. García-Vela, L. Bañares and S. Marggi Poullain, J. Phys. Chem. A, 2021, 125, 6122–6130.
9. E. E. Rogers, S. Abramowitz, M. E. Jacox and D. E. Milligan, J. Chem. Phys., 1970, 52, 2198.
10. D. W. Smith and L. Andrews, J. Chem. Phys., 1973, 58, 5222–5229.
11. S. L. Baughcum and S. R. Leone, J. Chem. Phys., 1980, 72, 6531–6545.
12. S. Bailleux, P. Kania, J. Skrinsky, T. Okabayashi, M. Tanimoto, S. Matsumoto and H. Ozeki, J. Phys. Chem. A, 2010, 114, 4776–4784.
13. L. Andrews, J. M. Dyke, N. Jonathan, N. Keddar and A. Morris, J. Phys. Chem., 1984, 88, 1950–1954.
14. B. Sztáray, K. Voronova, K. G. Torma, K. J. Covert, A. Bodi, P. Hemberger, T. Gerber and D. L. Osborn, J. Chem. Phys., 2017, 147, 013944.
15. B. P. Tsal, T. Baer, A. S. Werner and S. F. Lin, J. Phys. Chem., 1975, 79, 570–574.
16. C. Tao, C. Mukarakate, Y. Mishchenko, D. Brusse and A. S. Reid, J. Phys. Chem. A, 2007, 111, 10562–10566.
17. A. J. Eskola, D. Wojcik-Pastuszka, E. Ratajczak and R. S. Timonen, Phys. Chem. Chem. Phys., 2006, 8, 1416–1424.
18. W. R. Simpson, S. S. Brown, A. Saiz-Lopez, J. A. Thornton and R. von Glasow, Chem. Rev., 2015, 115, 4035–4062.
19. M. A. Navarro, E. L. Atlas, A. Saiz-Lopez and U. Donets, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13789–13793.
20. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
21. P. J. Knowles and H.-J. Werner, Theor. Chim. Acta, 1992, 84, 95.
22. H.-J. Werner, Mol. Phys., 1996, 89, 645.
23. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053.
24. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
25. H.-J. Werner, P. J. Knowles, R. Lindh, M. Schütz, P. Celani, T. Korona, F. R. Manby, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012, a package of ab initio programs, see https://www.molpro.net.
26. B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858.
27. D. V. Chicharro, S. Marggi Poullain, A. Zanchet, A. Bouallagui, A. García-Vela, M. L. Senent, L. Rubio-Lago and L. Bañares, Chem. Sci., 2019, 10, 6494–6502.
28. S. Marggi Poullain, D. V. Chicharro, A. Zanchet, L. Rubio-Lago, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2019, 21, 23017–23025.
29. D. V. Chicharro, A. Zanchet, A. Bouallagui, L. Rubio-Lago, A. García-Vela, L. Bañares and S. Marggi Poullain, Phys. Chem. Chem. Phys., 2021, 23, 2458–2468.
30. S. Marggi Poullain, L. Rubio-Lago, D. V. Chicharro, A. Bouallagui, A. Zanchet, O. Yazidi, A. García-Vela and L. Bañares, Mol. Phys., 2022, 120(1–2), e1984598.
31. A. Bouallagui, A. Zanchet, L. Bañares and A. García-Vela, Phys. Chem. Chem. Phys., 2022, 24, 7387–7395.
32. https://www.nist.gov/pml/electron-impact-cross-sections-ionization-and-excitation-database .

---