Open Access Article
Open Access ArticleAdsorption of HCN on cosmic silicates: a periodic quantum mechanical study†
Niccolò Banconeab,
Stefano Pantaleone a,
Piero Ugliengo
a,
Piero Ugliengo a,
Albert Rimola
a,
Albert Rimola *b and
Marta Corno
*b and
Marta Corno *a
*a
aDipartimento di Chimica and NIS – Nanostructured Interfaces and Surfaces – Centre, Università degli Studi di Torino, via P. Giuria 7, 10125, Torino, Italy. E-mail: marta.corno@unito.it; Tel: +39-0116702439
bDepartament de Química, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain. E-mail: albert.rimola@uab.cat; Tel: +34-935812164
First published on 26th September 2023
Abstract
Hydrogen cyanide (HCN) represents a small but widely distributed fraction of the interstellar molecules, and it has been observed in all the environments characterizing the formation of a new planetary system. HCN can polymerize to form biomolecules, including adenine (H5C5N5), and it has drawn attention as a possible precursor of several building blocks of life due to the presence of its polymerization products in meteorites, comets and other asteroidal bodies. To elucidate the potential catalytic role that cosmic silicates have played in these processes, we have investigated, at DFT-PBE level inclusive of a posteriori dispersion correction, the energetic and spectroscopic features of the adsorption of HCN molecules on the most relevant crystalline surfaces of the mineral forsterite (Mg2SiO4), a common silicate constituent of the interstellar core grains and planetary rocky bodies. The results reveal that HCN adsorbs both in molecular and dissociative ways, within a wide range of adsorption energies (−29.4 to −466.4 kJ mol−1). Thermodynamic and kinetic results show that dissociative adsorption is dominant already at low temperatures, a fact particularly relevant at the protoplanetary conditions (i.e., the latest stages in the star system formation process). The simulated spectroscopic features of the studied adducts show a wide range of different degrees of perturbation of C–H and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds. This finding agrees with previous experimental works, and our results confirm that a complex chemistry is observed when this astrochemically-relevant molecule interacts with Mg2SiO4, which may be associated with a considerable potential reactivity towards the formation of relevant prebiotic compounds.
N bonds. This finding agrees with previous experimental works, and our results confirm that a complex chemistry is observed when this astrochemically-relevant molecule interacts with Mg2SiO4, which may be associated with a considerable potential reactivity towards the formation of relevant prebiotic compounds.
Introduction
HCN has been identified in many different astrophysical environments, including protostellar hot cores/corinos,1–4 proto-planetary disks,5–8 comets,9,10 carbonaceous chondrites,11 planetary atmospheres,12–14 and diffuse and dense clouds.15,16 Its ability to polymerize is known since the 60's of the last century17 and its products, including adenine (H5C5N5), have been identified in meteorite fragments.18 HCN polymers are thought to contribute to the dark/brown color observed on the exterior of comets Halley and P/Stephan–Oterma and the observed 2.2 and 4.4 μm bands have been assigned to C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching modes.19,20 The same hypothesis was also proposed for the absorption lines detected on the saturn's satellite Iapetus, the rings of uranus and some asteroids of the solar system.20 In addition, some assumptions postulate the presence of HCN polymers on titan, saturn and jupiter.21,22 These premises led to the study of HCN reactivity under different conditions with the aim of identifying plausible pathways for its polymerization in interstellar and prebiotic conditions.17,23–29 Possible HCN-derived prebiotic compounds are not observed in pristine and cold interstellar regions such as giant molecular clouds (GMCs) where temperatures are around 10 K.30 Instead, they are observed in rather more evolved environments such as those listed above, where the conditions are less inert due to higher temperatures, reaching 150–300 K, and to a higher exposition to radiative energy inputs.18–22 The presence of HCN and its prebiotic derivatives on larger celestial bodies may then be ascribable to catalytic processes taking place during later stages in planetary system formations (e.g., in protoplanetary disks or on planetesimals) or on formed celestial bodies like asteroids, comets, meteorites, planets and satellites.18–22
N stretching modes.19,20 The same hypothesis was also proposed for the absorption lines detected on the saturn's satellite Iapetus, the rings of uranus and some asteroids of the solar system.20 In addition, some assumptions postulate the presence of HCN polymers on titan, saturn and jupiter.21,22 These premises led to the study of HCN reactivity under different conditions with the aim of identifying plausible pathways for its polymerization in interstellar and prebiotic conditions.17,23–29 Possible HCN-derived prebiotic compounds are not observed in pristine and cold interstellar regions such as giant molecular clouds (GMCs) where temperatures are around 10 K.30 Instead, they are observed in rather more evolved environments such as those listed above, where the conditions are less inert due to higher temperatures, reaching 150–300 K, and to a higher exposition to radiative energy inputs.18–22 The presence of HCN and its prebiotic derivatives on larger celestial bodies may then be ascribable to catalytic processes taking place during later stages in planetary system formations (e.g., in protoplanetary disks or on planetesimals) or on formed celestial bodies like asteroids, comets, meteorites, planets and satellites.18–22
Indeed, it has been demonstrated that gas-phase pathways are unfavoured due to high energetic barriers hindering the reaction already at its first steps, thus making it unfeasible in GMCs, where temperatures are in the order of 10 K and external energy inputs are missing.30 In fact, a number of studies report that the key step for triggering the polymerization of HCN to adenine and nucleobases is the deprotonation of one molecule to form the nucleophilic CN−.17,27,29 Studies in the condensed phase, indeed, show that the polymerization is more favoured in basic water solutions and at solid catalytic surfaces, where basic catalysts facilitate proton transfer mechanisms.17,29,31,32
In this regard, cosmic silicates (ubiquitously present in different astrophysical environments) can be possible candidates as solid-state catalysts for the HCN polymerization. This is due to the basic behaviour of exposed O2− anions,33 which are expected to deprotonate adsorbed HCN molecules and provide the reactive CN−. These minerals represent a fundamental fraction of the mineral phase of solid astronomical bodies such as dust grains,34 meteorites,35 cometary grains,36 and rocky planets, and have been considered as solid-state matter relevant in the synthesis of cosmic molecules. The study from an atomistic point of view can provide fundamental insights on their physico-chemical features, and on the interaction and reactivity with gas-phase molecules. In that respect, quantum mechanical simulations are a powerful tool to investigate olivines (one of the most abundant families of cosmic silicates),37–41 allowing to reproduce harsh environments, too. Indeed, Mg-pure olivines (i.e., Mg2SiO4, forsterite) have been adopted as model materials in both experimental and theoretical studies, focusing, in particular, on the interaction of molecules of astronomical and prebiotic interest with amorphous and crystalline Mg2SiO4 surfaces.33,42–62
A very recent work by Santalucia et al. reported the results of HCN adsorption and reactivity on crystalline Mg2SiO4 surfaces.31 The authors characterized the HCN/surface interactions and the products that result from the HCN polymerization on a laboratory scale by means of IR spectroscopy and ESI(-)/HRMS, in a first attempt of exploring the interaction of HCN with Mg2SiO4.
To the best of our knowledge, an ab initio study on this topic is still lacking. Because of that, in the present work, the interaction of HCN molecules on Mg2SiO4 forsterite surfaces has been explored by means of density functional theory (DFT) simulations. Although the amorphous phase is dominant in many cosmic rocky bodies,63 modelling the adsorption of HCN on different exposed crystalline surfaces of forsterite (i.e., six faces at 0 K40), surely provides relevant insights on the intrinsic adsorption properties derived from HCN/Mg2SiO4 interactions. The aim of this work is, thus, to propose a reliable theoretical background on the adsorption of HCN molecules on cosmic silicate surface models to elucidate the role of HCN as a prebiotic precursor and to investigate how cosmic silicates could have participated in reactions of prebiotic interest.
Computational details
All calculations were performed with the CRYSTAL17 code,64 which implements Hartree–Fock and DFT methods for periodic systems by adopting localized Gaussian Type Orbitals (GTOs). The PBE Hamiltonian65 was adopted for geometry optimization and frequency calculations of all the structures. To take into account dispersive forces, all calculations include the Grimme's empirical dispersion D266 in its revised version D*(N),67,68 specifically customized for Mg2+ cations. H, C and N atoms were described with the Ahlrichs-VTZ69 basis sets augmented with polarization functions whilst for forsterite atoms the smaller basis set proposed by Bruno et al. was adopted,40 that is, 8-511G* for Mg, 8-6311G* for Si, and 8-411G* for O. The exponents (in Bohr−2) of the most diffuse sp shells are 0.68 and 0.22 (Mg), 0.32 and 0.13 (Si), and 0.59 and 0.25 (O). The exponents of the d shells are 0.5 (Mg), 0.6 (Si), and 0.5 (O) (the full basis sets are available in the ESI†). The accuracy in the evaluation of the Coulomb integrals were controlled by adopting the default threshold parameters in CRYSTAL17. The default DFT grid was adopted to ensure a satisfactory accuracy in the numerical integrated electron charge density, in accordance with Bruno et al.40 The number of k points to sample the Brillouin zone was set to 5 for all the calculations, with the only exception of the adduct of HCN on the (010) surface, where a 2 × 2 supercell model was adopted and for which the number of k points was lowered to 4. Geometry optimizations were performed by adopting the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.70–73 The Bruno et al. bulk structure40 was used as initial guess and both the atomic positions and the cell parameters were optimized at PBE-D*(N) level. Slabs and HCN adducts were optimized by keeping the cell parameters fixed at the bulk optimized values. When possible, symmetry was exploited to speed up the calculation. The relative stability of each surface was evaluated by computing its surface energy (ES) as:where Eslab and Ebulk are the unit cell absolute energies of the slab and the bulk, respectively. The factor 4 considers the stoichiometric ratio 4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 between the slabs and the bulk. For a more detailed discussion on the computation of surface energies, the reader can refer to ref. 74 For each optimized HCN/surface adduct, the adsorption energy (ΔEads) of the adsorbed molecules was computed as:
1 between the slabs and the bulk. For a more detailed discussion on the computation of surface energies, the reader can refer to ref. 74 For each optimized HCN/surface adduct, the adsorption energy (ΔEads) of the adsorbed molecules was computed as:| ΔEads = Eadd − (Emol + Eslab) |
| ΔHads(0) = ΔEads + ΔZPE |
To facilitate comparison with the experiments, all the computed C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and C–H stretching frequencies were corrected for a scaling factor s to partially recover the systematic error associated with the PBE-D*(N) method. s was obtained as the ratio between the experimental79 and the computed frequency of an isolated HCN molecule, that is:
N and C–H stretching frequencies were corrected for a scaling factor s to partially recover the systematic error associated with the PBE-D*(N) method. s was obtained as the ratio between the experimental79 and the computed frequency of an isolated HCN molecule, that is:
The energy barriers for the dissociation of an adsorbed HCN molecule were computed by localizing the transition states (TSs) related to the proton transfer from the C atom of HCN to the closest O atom of the surface silicate. The distinguished reaction coordinate (DRC)80 was adopted to localize the TSs. Activation and reaction enthalpies were computed by applying the zero-point and the thermal corrections to the potential energy variations:
| ΔH = ΔE + ΔZPE + ΔET |
where N≠(E–E0) is the sum of states for the TS (where the integration range expands to energies below the barrier and not just above it), ρ(E) is the density of states of reactants (i.e., the number of states per unit of energy, in quantum mechanics the degeneracy g(E)), and h the Planck constant. The sum of states of the TS can be expressed as an integral of its density of states over the translational energy of the reaction coordinate ξ≠. Tunneling effects are included by introducing the transmission probability T(ξ≠) inside the integral. In a final step, microcanonical k(E) can be converted into canonical k(T) by populating the energy levels according to the Boltzmann distribution, P(E):
for the calculation of the transmission probability T(ξ≠), the asymmetric Eckart potential has been used:85,86
with a = 2(α1ζ)1/2(α1−1/2 + α2−1/2)−1, b = 2[(ζ − 1)α1 + α2]1/2(α1−1/2 + α2−1/2)−1, α1 = 2πV1/hν≠, α2 = 2πV2/hν≠, ζ = E/V1, V1 being the barrier from TS to reactants, V2 the barrier from TS to products and ν≠ the absolute value of the frequency associated with the TS. For the cases with α1 ≫ 1, such as the (010) A, (120) B, and (101) B, the symmetrical Eckart's approach was employed. Finally, we highlight that the RRKM was developed for gas-phase processes. To adapt this theory to solid state processes only the vibrational degrees of freedom of all the species were taken into account, thus leaving aside the translational and rotational ones, since they are to be disregarded in solid state systems. Results are, in the end, equivalent to rate constants obtained with the Eyring's transition state theory accounting for only vibrational partition functions.
Results and discussion
Modelling of Mg2SiO4 surfaces and theoretical characterization
Forsterite (Mg2SiO4) is the Mg end-member of olivines and its bulky structure presents an orthorhombic lattice (a ≠ b ≠ c, α = β = γ = 90.0°). It belongs to the Pbnm space group, although sometimes it is reported as Pnma space group; the only difference consists in the reference assigned to the basis vectors of the lattice, namely, in Pbnm the lattice parameters are |a| = x, |b| = y, |c| = z, while according to the Pnma convention they are |a| = z, |b| = x, |c| = y. For our scope, this choice has no implications, and we consider the Pbnm space group.The bulk structure presents a distorted hexagonally close-packed array of O2− anions. Si4+ cations occupy one-eighth of the available tetrahedral interstices (SiO4 units) while Mg2+ cations occupy one-half of the octahedral sites (MgO6 units), resulting in the displacement of O2− anions and a variation of the Mg–O distance, about 2.05–2.21 Å.87,88 The octahedral sites accommodating Mg2+ cations are usually referred to as M1 and M2 sites, M1 being more distorted and compact than M2, and forming edge-sharing chains of Mg2+ cations along the c axis (see Fig. 1).
 | ||
| Fig. 1 Left: Forsterite bulk unit cell (cell borders are in black). Right: Wulff's construction of a forsterite nanocrystal using the computed ES values of this work at PBE-D*(N) level. | ||
In this work, both atomic positions and cell parameters of the forsterite bulk have been optimized at the PBE-D*(N) level and compared with the values calculated by Bruno et al. at the B3LYP level. The results are reported in Table 1, together with a comparison with the experimental data of Bostrom.89 In a previous work by De la Pierre et al.90 it was reported that the PBE functional overestimates the structural parameters of forsterite, even more than the B3LYP. The PBE-D*(N), instead, describes the b and c parameters better than the dispersion-uncorrected B3LYP ones, resulting in a cell volume closer to the experimental result. This is due to the contribution of the D*(N) correction, stabilizing compact structures.
From the optimized Mg2SiO4 bulk structure, seven periodic 2D slabs of Miller indices (010), (120), (101), (001), (111), (021) and (110) were cut out (shown in Fig. 2) from the optimized bulk structure. All the considered slabs exhibit zero dipole moment across the non-periodic dimension (z)91 also keeping the SiO4 units intact. The geometry optimization of the 2D slabs was performed by keeping the cell parameters fixed at the bulk values to enforce the rigidity of the real material. The seven slabs have been characterized by computing their surface energy (ES) and morphological relevant index (MRI, expressed as the percentage ratio between the unit area of a single surface and the total area of the crystal). The equilibrium shape at 0 K of a forsterite nano-crystal was obtained by applying the Wulff's theorem92 (see Table 2 and Fig. 1). Our ES values computed at PBE-D*(N) are all lower than those computed by Zamirri et al. at B3LYP-D*,53 with an average percentage deviation of −7.3%. This is likely due to the different scheme we used for the dispersion correction. In particular, the D*(N) scheme adopts smaller C6 coefficients for Mg with respect to the D* (see ref. 66–68 for more details), the latter determining an overstabilization of the bulk and, thus, higher ES values. Despite this, the relative ES stability order is the same when computed with the two methods, that is: (010) < (120) < (101) < (001) < (111) < (021) < (110). The PBE-D*(N) MRI values do not appreciably deviate from the B3LYP-D* ones and the overall crystal shape is very similar. It results that the (120) face, despite being energetically less stable than the (010), is the most extended facet. It is worth mentioning that the (110) face does not appear in the Wulff's structure at any level of theory, and, for this reason, it is not considered in this work.
| (hkl) | Cell parameters | ES | MRI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | γ | A | This work | Zamirria | %Δ | This work | Zamirria | Δ | |
| a Zamirri et al.53 | ||||||||||
| (010) | 4.801 | 6.008 | 90.0 | 28.84 | 1.38 | 1.44 | −3.9 | 21.3 | 23.7 | −2.4 |
| (120) | 6.008 | 14.017 | 90.0 | 84.21 | 1.52 | 1.68 | −9.4 | 33.0 | 29.6 | 3.4 |
| (101) | 7.691 | 10.212 | 90.0 | 78.53 | 1.78 | 1.96 | −9.2 | 21.8 | 20.6 | 1.2 |
| (001) | 4.801 | 10.212 | 90.0 | 49.03 | 1.85 | 1.98 | −6.6 | 15.5 | 19.7 | −4.2 |
| (111) | 7.691 | 11.284 | 105.4 | 83.67 | 1.99 | 2.19 | −8.9 | 3.3 | 2.4 | 0.9 |
| (021) | 4.801 | 15.769 | 90.0 | 75.71 | 2.06 | 2.24 | −7.9 | 5.1 | 3.5 | 1.6 |
| (110) | 6.008 | 11.284 | 90.0 | 67.79 | 2.34 | 2.46 | −4.9 | 0.0 | 0.0 | 0.0 |
Interestingly, and as already pointed out by Zamirri et al., more compact and regular surfaces (such as the (010) and the (001) ones) possess smaller surface areas, and, accordingly, a minor number of Mg2+ sites available for adsorption. In contrast, the most irregular surfaces (such as the (120), (111) and (101) ones) show a larger number of available adsorption sites. The large ES value shown by the (021) surface is probably due to the highly uncoordinated Mg2+ cation. King et al.49 reported that the strength of the interaction of water molecules with forsterite is highly influenced by the degree of coordination of the available adsorption sites. According to that, it is then reasonable to expect stronger interactions on low-coordinated exposed Mg2+ cations like the A sites of the (021) surface (see Fig. 2).
HCN adsorption on the forsterite surfaces
The electrostatic potential maps (EPMs) superimposed to the ground state electron density were plotted for each forsterite surface model, as well as for HCN. Fig. 3 shows that, expectedly, HCN presents a clear dipole moment (experimental: 2.98 Debye, computed at PBE-D*(N) level: 2.9 Debye), the H and N atoms determining the zone of positive and negative potentials, respectively. As regards the surfaces, the outermost Mg2+ cations define the positive regions of electrostatic potential, while the outermost O atoms the negative potentials. Accordingly, Signorile et al.33 pointed out that the exposed Mg2+ cations have a Lewis acid character while the exposed O2− anions behave like Lewis bases. Therefore, the HCN adsorption was modelled considering the electrostatic potential complementarity rule, that is, by pointing the N-end of HCN towards an available Mg2+ of the surface at a starting distance of about 2.0 Å. Moreover, HCN molecules were placed both on the top and on the bottom of the slabs to exploit the inversion operator during geometry optimizations to ensure zero dipole moment across the slab.By proceeding this way, 16 different single adsorption complexes have been obtained with the six forsterite surfaces. Each adduct is named according to the surface Miller indices together with the adsorbing Mg2+ cation label; for instance, (010) A represents the adduct obtained by placing HCN on the Mg2+ A site of the (010) surface (see Fig. 2). Table 3 reports the dispersion-corrected adsorption energy (ΔEads), the dispersion- and BSSE75–77-corrected adsorption energy (ΔEads,disp), and the adsorption enthalpy at 0 K (ΔHads(0)) of each optimized adduct. We point out that not always was possible to formally compute the BSSE, especially for the dissociative adsorption cases, where the proton is transferred to the surface (see Fig. 4). Nevertheless, a linear dependence (R2 = 0.81, see Fig. S1, ESI†) between the adsorption energies and the corresponding BSSE values was obtained by plotting 13 representative points which have been used to extrapolate the BSSE values for those cases in which it was not possible to explicitly apply the counterpoise correction. Inter-cell lateral interactions between adsorbed molecules represent a spurious contribution to the ΔEads due to the periodic approach. Indeed, when the computed lateral interaction absolute value (|ΔEL|) results higher than 3.0 kJ mol−1, supercell models are adopted to decrease the |ΔEL| contribution. This was done in 7 (out of 16) adsorption cases by doubling the unit cell along the a direction (i.e., a 2 × 1 supercell), with the only exception of the (010) A case, where it was necessary to extend the cell along both a and b directions (i.e., a 2 × 2 supercell). For some dissociative cases (namely, (101) C, (001) A, (021) A, B1 and C) the instability of the SCF when computing the almost broken HCN in the absence of the surface, did not allow us to isolate the ΔEL contribution.
| (hkl) | Site | Type | ΔEads,disp | ΔD*(N) | ΔEads | ΔHads(0) |
|---|---|---|---|---|---|---|
| (010) | A | M | −134.9 | −17.2 | −101.0 | −96.9 |
| (120) | A | M | −165.0 | −15.2 | −127.7 | −119.9 |
| B | M | −60.8 | −14.3 | −29.4 | −21.0 | |
| C | M | −104.8 | −19.6 | −63.1 | −52.1 | |
| (101) | A | D | −219.4 | −18.4 | −174.5 | −163.9 |
| B | M | −106.1 | −18.2 | −68.6 | −61.8 | |
| C | D | −226.6 | −22.3 | −181.2 | −171.9 | |
| (001) | A | D | −273.3 | −17.4 | −223.7 | −202.4 |
| B | M | −114.2 | −20.1 | −77.4 | −58.8 | |
| (111) | A | M | −155.4 | −19.6 | −105.4 | −96.6 |
| B | D | −272.9 | −22.1 | −223.3 | −207.8 | |
| D | M | −271.0 | −19.1 | −221.5 | −194.7 | |
| (021) | A | D | −540.9 | −24.2 | −466.4 | −447.8 |
| B1 | D | −187.5 | −20.1 | −145.8 | −133.9 | |
| B2 | D | −175.8 | −16.9 | −135.0 | −123.9 | |
| C | D | −186.4 | −19.2 | −143.7 | −137.0 |
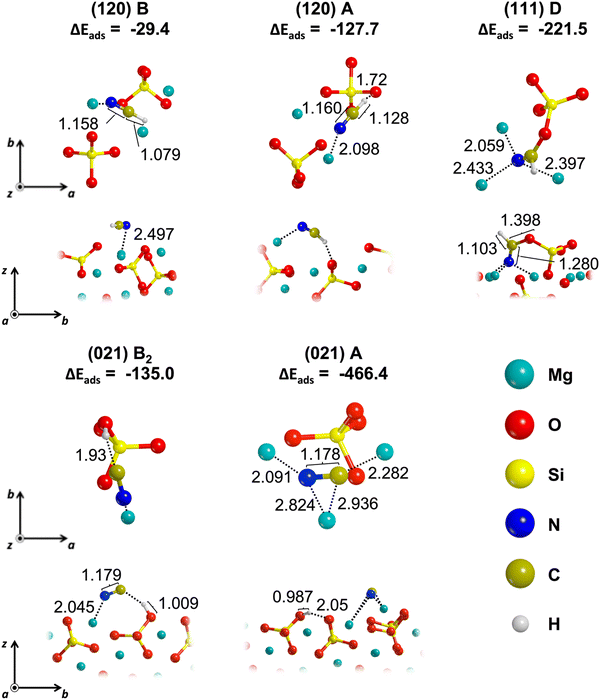
In 8 out of the 16 optimized adsorption complexes, HCN is molecularly adsorbed (i.e., non-dissociative adsorption), interacting with one or more Mg2+ cations through the N-end and, in most cases, the proton establishing hydrogen bonds (H-bonds) with surface O atoms, in consistency with the electrostatic potential features. The ΔEads values for these cases span from −29.4 to −127.7 kJ mol−1. In one case (the (111) D complex), HCN is chemisorbed by forming a C–O chemical bond between the C atom of HCN and the O atom of an exposed silicate (see Fig. 4). Even if the molecule does not dissociate, the computed adsorption energy results to be relatively high (ΔEads = −221.5 kJ mol−1) due to the new covalent bond formation.
In the remaining 8 cases, HCN adsorbs in a dissociative way, i.e. it deprotonates upon adsorption, transferring the proton to an available surface O atom. Dissociated adducts present larger ΔEads values than the molecular ones (spanning the −135.0 to −466.4 kJ mol−1 range). Some of these dissociated structures show the newly formed CN− anion to interact with the surface through a Mg–N dative covalent bond and a C⋯HO H-bond, with ΔEads values being between −135.0 and −223.3 kJ mol−1. In other cases, the CN− anion prefers to establish additional interactions with surface Mg2+ cations, involving simultaneously different Mg–N and Mg–C dative bonds, thus presenting larger ΔEads values (between −181.2 and −466.4 kJ mol−1). For these cases, the C⋯HO H-bonds are not formed, but the newly formed Si-OH groups establish H-bonds with other surface O atoms. One of the most representative cases is the (021) A (see Fig. 4), where CN− strongly bridges three Mg2+cations. This structure presents the largest ΔEads value (ΔEads = −466.4 kJ mol−1). This is due to three main features: (i) the low stability of the surface (ES = 2.06 J m−2), which renders the outermost atoms very reactive enhancing their adsorbent properties (see Fig. 4 and Fig. S14, ESI†), (ii) the simultaneous three CN–Mg interactions and (iii) the formation of a strong H-bond between the surface SiOH group and an exposed surface O atom.
A linear plot between the ΔEads values and the Mg–N/Mg–C distances is not possible, especially for the dissociated cases, due to the variety in the number of Mg/CN interactions. A more reliable descriptor to rationalize the energetics of the HCN adsorption is the contribution of dispersion forces to ΔEads and the surfaces stability, as discussed in the next section.
Role of dispersion and surface stability
Here we discuss the relationships between the stability of the surfaces and the HCN/surface dispersion-based interactions to further rationalize the computed ΔEads values.The surface stability (see values in Table 2 and Fig. 5B) is quantified by the surface energy (ES), which in turn is partly determined by the amount of coordinatively unsaturated Mg2+ ions, in such a way that, the higher the surface energy, the less stable (and consequently the more reactive) the surface. The relative surface stabilities (see above) allow explaining the spontaneous HCN dissociation upon adsorption in the four less stable surfaces, namely, (101), (001), (111), (021). For these cases, the exposed O2− anions present an enhanced basicity that induces HCN deprotonation, due to the surface instability.33 Despite this consistency, by comparing Fig. 5A (the average of the calculated |ΔEads| values for each surface) and Fig. 5B (the ES values for each surface), it is difficult to find a clear quantitative correlation, even if the trend of the two charts is somehow similar. This is because the overall surface stability of a specific slab depends on many variables (e.g., the degree of unsaturation of the Mg2+ cations, the exposure to the surface of the O2− anions), conditioning the HCN/surface interactions.
 | ||
| Fig. 5 (A) Average of the calculated |ΔEads| values based on all the adsorptions on each forsterite surface. (B) Calculated surface energies (ES) for each surface (see Table 2). (C) Correlation between calculated averaged-|ΔEads| values with the corresponding percentage dispersion contributions, provided by the D*(N) term. | ||
As for dispersive forces, Fig. 5C reports the |ΔEads| values as a function of the dispersion contribution (disp.%) showing higher |ΔEads| values corresponding to lower percentages of dispersive contributions. The two quantities can be well correlated (R2 = 0.96) by a non-linear plot given by a power function of the disp.% contribution. This trend suggests that molecular adsorptions (which in turn are those presenting the less favourable ΔEads values) are usually more dominated by weak dispersive forces (48.8% < disp. < 8.1%). On the other hand, dissociative adsorptions are governed by covalent/ionic forces (12.5% < disp. < 5.2%) such as Mg–N and Mg–C dative covalent bonds and strong H-bonds.
Dissociation of molecularly adsorbed HCN molecules
As mentioned in the Introduction, the prebiotic polymerization of HCN is strongly hindered in the gas phase under interstellar conditions,30 while it is more facilitated in the condensed phase, in the presence of a basic catalyst and at higher temperatures.17,29,31,32 Since the formation of CN− anions is considered as the real trigger to the reaction, we explored the deprotonation channels of molecularly adsorbed HCN in case that a kinetic energy barrier is present. The reactants (namely, the molecular adsorption complexes), the TSs and the products of proton transfers from HCN to the closest outermost O2− anion of forsterite (see Fig. 6 as a test case) were localized for 5 (out of 8) non-dissociative cases. For the remaining three cases, we could not localize minima on the potential energy surface corresponding to stable deprotonated structures and every deprotonated initial guess showed the proton going back to covalently bound the CN−.Table 4 reports the relevant thermodynamic and kinetic parameters (i.e., activation barriers, reaction energies, and kinetic and equilibrium constants) of the dissociation process for the 5 cases, considering different temperatures (10, 50, 150, 200 and 300 K). We report the values at these temperatures as representative of different astrophysical environments: 10 K as the typical temperature of dark clouds, 50 and 150 K for hot cores/corinos and outer regions of proto-planetary disks and 200 and 300 K as temperatures of planetary atmospheres and those to which the system is exposed in the case of asteroids and comets when passing close to stars.
| Case | t.k. param. | Temp. (K) | ||||
|---|---|---|---|---|---|---|
| 10 | 50 | 150 | 200 | 300 | ||
| (010) A | ΔH* | 6.1 | 6.1 | 6.3 | 6.6 | 7.2 |
| ΔG* | 6.1 | 6.2 | 6.2 | 6.1 | 5.8 | |
| ΔH‡ | 64.5 | 64.4 | 63.9 | 63.6 | 62.9 | |
| ΔG‡ | 64.5 | 64.5 | 64.9 | 65.3 | 66.3 | |
| k full | 1.1 × 10−45 | 5.0 × 10−34 | 2.3 × 10−10 | 6.3 × 10−05 | 2.2 × 1001 | |
| K eq | 7.6 × 10−33 | 3.6 × 10−07 | 6.9 × 10−03 | 2.5 × 10−02 | 9.8 × 10−02 | |
| (120) B | ΔH* | −152.4 | −153.4 | −156.4 | −157.0 | −157.6 |
| ΔG* | −152.3 | −151.5 | −145.5 | −141.8 | −134.0 | |
| ΔH‡ | 27.0 | 26.3 | 23.9 | 23.0 | 20.9 | |
| ΔG‡ | 27.1 | 27.8 | 32.3 | 35.2 | 41.8 | |
| k full | 1.2 × 10−58 | 3.9 × 10−23 | 1.1 × 1000 | 7.5 × 1002 | 5.3 × 1005 | |
| K eq | 4.0 × 10265 | 2.1 × 10158 | 4.5 × 1050 | 1.0 × 1037 | 2.1 × 1023 | |
| (120) C | ΔH* | −7.6 | −7.8 | −8.1 | −8.2 | −8.5 |
| ΔG* | −7.6 | −7.4 | −6.9 | −6.5 | −6.0 | |
| ΔH‡ | 2.5 | 2.2 | 0.7 | −0.1 | −2.0 | |
| ΔG‡ | 2.5 | 2.7 | 4.7 | 6.2 | 9.7 | |
| k full | 2.6 × 1009 | 5.1 × 1010 | 3.1 × 1011 | 4.5 × 1011 | 6.6 × 1011 | |
| K eq | 6.5 × 1039 | 6.4 × 1007 | 1.9 × 1002 | 37.0 | 7.0 | |
| (101) B | ΔH* | 22.9 | 23.0 | 23.9 | 24.4 | 25.2 |
| ΔG* | 22.9 | 22.8 | 22.0 | 21.3 | 19.5 | |
| ΔH‡ | 17.6 | 17.6 | 16.9 | 16.4 | 15.3 | |
| ΔG‡ | 17.6 | 17.3 | 17.6 | 17.9 | 19.0 | |
| k full | 5.0 × 10−04 | 2.8 × 10−01 | 1.6 × 1004 | 9.1 × 1005 | 1.2 × 1008 | |
| K eq | 3.6 × 10−120 | 1.5 × 10−24 | 2.2 × 10−08 | 2.8 × 10−06 | 4.0 × 10−04 | |
| (111) A | ΔH* | −13.8 | −14.2 | −13.8 | −13.2 | −12.2 |
| ΔG* | −13.8 | −13.6 | −12.3 | −11.9 | −11.5 | |
| ΔH‡ | 14.8 | 14.5 | 13.5 | 12.9 | 11.5 | |
| ΔG‡ | 14.8 | 14.9 | 16.3 | 17.3 | 19.7 | |
| k full | 1.3 × 1002 | 3.9 × 1003 | 7.2 × 1005 | 9.3 × 1006 | 3.4 × 1008 | |
| K eq | 1.8 × 1072 | 1.6 × 1014 | 2.0 × 1004 | 1.3 × 1003 | 1.0 × 1002 | |
Three out of 5 cases (namely, (120) B, (120) C, and (111) A) present exergonic reactions, while the other two (namely, (010) A and (101) B) are endergonic. It follows that equilibrium constants (Keq) for the former are >0 at every considered temperature while the opposite occurs for the latter. For all the cases the decrease of the activation enthalpy with temperature is eroded by the entropic effects. The same happens to the reaction enthalpies: the spontaneity of the exergonic dissociations on the (120) B, (120) C and (111) A cases decreases as the temperature increases, while the (010) A and (101) B adducts (those with positive free energy reactions) follow the opposite trend. Nevertheless, no inversion of stability is observed in any case.
The (120) B is a special case, because the dissociation of the adsorbed molecule leads to a considerably favourable reaction energy (ΔH*(10 K) = −152.4 kJ mol−1) and to strong entropic effects. This is due to a rearrangement of the CN− anion on the surface (see Fig. S19, ESI†), where the CN− species bridges between two Mg2+ cations, thus forming a strong interaction with the surface. The high stabilization can be explained when considering the non-dissociated starting structure (see Fig. 4), where the HCN weakly interacts with only one surface Mg2+ without forming appreciable H-bonds with O2− anions. This initial structure is the adduct with the least favourable adsorption energy (ΔEads = −29.4 kJ mol−1) so that, upon dissociation, the system gains large stabilization.
Kinetic constants have been computed through the RRKM scheme, taking into account tunnelling effects (see Fig. 7). In Table S1 (ESI†) the comparison between the kinetic constants with (kfull) and without accounting for tunnelling (kclass) is reported in detail. In general, tunnelling starts to be relevant at 150 K for almost all cases and become dominant as the temperature decreases, increasing the reaction rate of several orders of magnitude at T ≤ 50 K.
At 10 K, the deprotonated forms of cases (120) C and (111) A are both thermodynamically and kinetically favoured. If we also consider the barrier-less dissociative adsorption previously discussed, 10 out of the total 16 adsorption cases confirm that the deprotonated form of HCN is more abundant in the ISM than HCN. If we consider the latest stages of a planetary system formation (proto-planetary disks, planetesimals, comets, asteroids, and satellites) only two cases are thermodynamically unfavoured, i.e. (010) A and (101) B, while all the others result in the deprotonation of HCN.
The results exposed up to now refer to HCN-forsterite systems, that is, only the crystalline pure Mg-silicate is considered. If we consider interstellar dust grains, the crystalline phase is thought to constitute only around 5% of the silicates in the grain cores, the amorphous phase being dominant.63 Even if the crystalline phase tends to become dominant during a planetary systems formation,93 it surely represents just a fraction of the silicates in the environments we have considered. Amorphous silicates differ from the crystalline one in the basicity of the exposed O2−, which are averagely more basic in the former than in the latter.33 This is due to the formation of MgO polymers in the amorphous phase, whose exposed O2− are more basic than those belonging to SiO44− units.94 If we consider the high degree of deprotonation in the HCN-forsterite system, we can then suppose that amorphous silicates and MgO would deprotonate adsorbed HCN even more efficiently. This would lead to a greater quantity of CN− and, thus, to a more efficient catalysis towards the HCN polymerization. Indeed, it was experimentally observed by Santalucia et al.31 that the reactivity of HCN on these materials increases in the order: forsterite → amorphous silicate → MgO.
IR spectral features of adsorbed HCN molecules
The vibrational frequencies were computed for all the adsorption complexes, including the dissociated ones. The scaled stretching frequencies of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and C–H have been compared with those computed for the HCN molecule in the gas phase to evaluate the perturbation of these chemical bonds upon HCN adsorption (see Tables S2–S4, ESI† for full details about bond distances and corresponding frequencies).
N and C–H have been compared with those computed for the HCN molecule in the gas phase to evaluate the perturbation of these chemical bonds upon HCN adsorption (see Tables S2–S4, ESI† for full details about bond distances and corresponding frequencies).
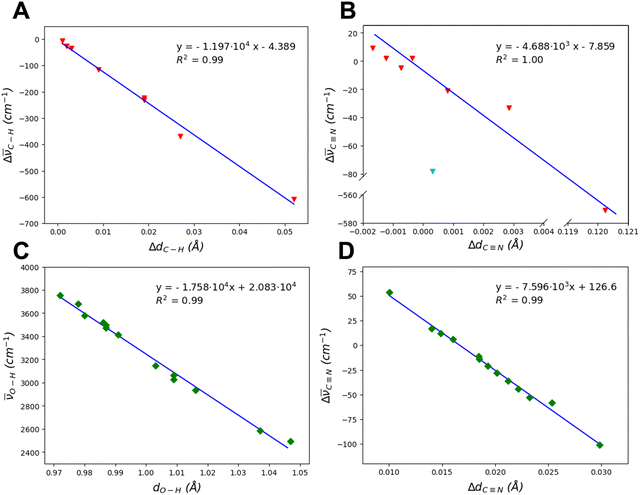
Fig. 8A and B plot the variation of the C–H and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond lengths against the corresponding frequency shift values with respect the gas-phase molecule. The correlation is very good, with the only exception of the C
N bond lengths against the corresponding frequency shift values with respect the gas-phase molecule. The correlation is very good, with the only exception of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond in (120) A. This adduct (see Fig. 4) presents high bathochromic shifts (Δ
N bond in (120) A. This adduct (see Fig. 4) presents high bathochromic shifts (Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N = −78 cm−1 and Δ
N = −78 cm−1 and Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C–H = −609 cm−1, see Table S2, ESI†) correlated to the strong interactions due to the adsorption, i.e. short O⋯HC and Mg–N distance (1.721 and 2.098 Å, respectively). As expected, the adducts presenting the largest adsorption energies are the most perturbed by the adsorption and, accordingly, those with the largest frequency shifts. Thus, the strong interaction with the surface and, in the specific, the electron donation from the lone pair on the N to the Mg2+ cations (dative Mg–N bond) cause a weaking of the CN bond. As regards the C–H bond, its vibrational perturbation is generally driven by the H donation towards surface O atoms. However, there is no direct correlation between the Mg–N distances and Δ
C–H = −609 cm−1, see Table S2, ESI†) correlated to the strong interactions due to the adsorption, i.e. short O⋯HC and Mg–N distance (1.721 and 2.098 Å, respectively). As expected, the adducts presenting the largest adsorption energies are the most perturbed by the adsorption and, accordingly, those with the largest frequency shifts. Thus, the strong interaction with the surface and, in the specific, the electron donation from the lone pair on the N to the Mg2+ cations (dative Mg–N bond) cause a weaking of the CN bond. As regards the C–H bond, its vibrational perturbation is generally driven by the H donation towards surface O atoms. However, there is no direct correlation between the Mg–N distances and Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and between O⋯HC distances and Δ
N and between O⋯HC distances and Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C–H, due to the variable number of simultaneous Mg–N and O⋯HC interactions occurring in the different adsorption complexes.
C–H, due to the variable number of simultaneous Mg–N and O⋯HC interactions occurring in the different adsorption complexes.
For the dissociative cases, the O–H bond lengths and stretching frequencies follow a good correlation as well, as shown in Fig. 8C. As expected, larger shifts are observed when the newly formed SiOH group establishes H-bonds with the C atom of CN− rather than with another surface O atom. This is consistent with the fact that CN− carries a negative net charge and that it has more mobility with respect to bulky silicates, thus maximizing the efficiency of the H-bond interaction. Nevertheless, this trend is not followed when CN− is strongly bound by more than one Mg2+, as they compensate its negative charge and prevent its displacement towards the silanol ((111) B case, see Table 5, class IV, and Fig. S12, ESI†). The CN distances and the stretching frequency shifts (see Fig. 8D) show a good correlation as well. In these cases, however, we observe both bathochromic and hypsochromic shifts with respect to the HCN molecule, which depend on the adsorption modes between the CN− and the surface.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and C–H bonds, together with the Mg–N and Mg–C distances and the H-bonds distances given either by molecular HCN or by silanols formed upon dissociation
N and C–H bonds, together with the Mg–N and Mg–C distances and the H-bonds distances given either by molecular HCN or by silanols formed upon dissociation
Basing on the common structural and spectroscopic features, the HCN/surface interactions can be grouped in 8 different adsorption complex classes, which are described in Table 5. Classes I, II, and III include different situations of molecular adsorption. In class I the appreciable H-bond donations occurring between HCN and the O atoms of the surface cause an appreciable activation of the C–H bond (Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C–H = −609 to −116 cm−1) together with bathochromic shifts of the C
C–H = −609 to −116 cm−1) together with bathochromic shifts of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching frequencies (Δ
N stretching frequencies (Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N = −78 to −5 cm−1). In class II the H⋯O–Si donation is less appreciable or even null: weaker effects on the C–H bond and slight hypsochromic shifts of the C
N = −78 to −5 cm−1). In class II the H⋯O–Si donation is less appreciable or even null: weaker effects on the C–H bond and slight hypsochromic shifts of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N frequency are observed (Δ
N frequency are observed (Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C–H = −35 to −6 cm−1, Δ
C–H = −35 to −6 cm−1, Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N = 2–9 cm−1). Class III only includes the (111) D case, where the new C–O bond formation implies a change of hybridization of the C atom and a decrease in the bond order of the CN. It follows that important bathochromic shifts of both the CH and the CN frequency are observed (Δ
N = 2–9 cm−1). Class III only includes the (111) D case, where the new C–O bond formation implies a change of hybridization of the C atom and a decrease in the bond order of the CN. It follows that important bathochromic shifts of both the CH and the CN frequency are observed (Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C–H = −369 cm−1, Δ
C–H = −369 cm−1, Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N = −571 cm−1).
N = −571 cm−1).
Classes IV to VIII include dissociative adsorptions. The largest bathochromic shifts are observed when the C atom of CN− works as H-bond acceptor from the new formed silanols. This is the case for classes IV, V and VI, for which the bathochromic shifts of the CN stretching frequencies span from −101 to −11 cm−1. A minor effect to these red-shifts can also be ascribed to σ-donations occurring from the bonding molecular orbitals (MOs) 2π HOMO−1 (E = −0.539 eV) of the CN− to the empty s orbitals of the exposed Mg2+. In classes VII and VIII, instead, the CN− does not interact with exposed silanols but it maximizes the number of dative bonds with exposed Mg2+ cations. In fact, class VII involves a bridged Mg–CN–Mg motif resulting in hypsochromic shifts for CN (Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N = 6–54 cm−1), which can be attributed to the interaction between the electric field of the surface and the dipole moment of the molecule (Stark effect)95–97 and, in a minor extent, to the depopulation of the HOMO (E = 0.650 eV) of CN− by σ-donation to the empty s-orbitals of Mg2+. This class is the one that better fits the 2130 cm−1 signal observed by Santalucia et al.31 at 150 K, which the authors attribute to deprotonated CN− anions adsorbed on forsterite surfaces. Lastly, in class VIII a triple Mg–CN interaction results in a weak bathochromic shift (Δ
N = 6–54 cm−1), which can be attributed to the interaction between the electric field of the surface and the dipole moment of the molecule (Stark effect)95–97 and, in a minor extent, to the depopulation of the HOMO (E = 0.650 eV) of CN− by σ-donation to the empty s-orbitals of Mg2+. This class is the one that better fits the 2130 cm−1 signal observed by Santalucia et al.31 at 150 K, which the authors attribute to deprotonated CN− anions adsorbed on forsterite surfaces. Lastly, in class VIII a triple Mg–CN interaction results in a weak bathochromic shift (Δ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) C
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N = −14 cm−1), likely due to a balance between the opposite blue-shifting contribution of the Stark effect and the red-shifting σ-donation from the HOMO−1 orbital of CN− to the empty s-orbitals of Mg2+.
N = −14 cm−1), likely due to a balance between the opposite blue-shifting contribution of the Stark effect and the red-shifting σ-donation from the HOMO−1 orbital of CN− to the empty s-orbitals of Mg2+.
Conclusions
In this work, the adsorption of hydrogen cyanide (HCN) on different silicate forsterite (Mg2SiO4) surfaces (i.e., the crystalline slab models of the (010), (120), (101), (001), (111) and (021) surfaces) has been investigated by means of periodic DFT simulations.The interaction of HCN molecules with the forsterite surfaces resulted in 16 different adducts. Adsorption at 0 K can take place either in molecular (8 cases) and dissociative (8 cases) ways, the latter providing more favourable adsorption energies (−135.0 kJ mol−1 > ΔEads > −466.4 kJ mol−1) than the former (−29.4 kJ mol−1 > ΔEads > −221.5 kJ mol−1).
Dissociation reactions from molecularly adsorbed complexes have been studied by localizing the transition states of the proton transfer from HCN to nearby surface O atoms. Out of 8 non-dissociated initial systems, 3 have been found to result in stable dissociated structures through exergonic processes. Activation barriers and reaction thermodynamic parameters, as well as kinetic and equilibrium constants for the deprotonation have been computed at T = 10, 50, 150, 200 and 300 K. It resulted that at the temperatures typical of dark clouds (10 K) the majority of HCN–forsterite complexes results in the deprotonation of the molecule. At the conditions proper of outer proto-planetary disks (50–150 K) and of small celestial bodies (T = 200–300 K) this tendency is even enhanced, an important implication for HCN reactivity, which is considered a fundamental outcome of the present research. Ongoing work is devoted to study the HCN polymerization towards adenine.
Finally, a spectroscopic vibrational analysis has been performed, focusing on the stretching frequencies of the C–H, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N and O–H bonds. Good correlations have been observed between the bond lengths and the corresponding stretching frequencies, hence providing a way to determine the degree of perturbation of the C–H and C
N and O–H bonds. Good correlations have been observed between the bond lengths and the corresponding stretching frequencies, hence providing a way to determine the degree of perturbation of the C–H and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds of HCN upon adsorption, which is an indicator for the subsequent polymerization. In particular, the C
N bonds of HCN upon adsorption, which is an indicator for the subsequent polymerization. In particular, the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N frequencies undergo both bathochromic and hypsochromic shifts due to adsorption, depending on the type and number of simultaneous interactions occurring with surface Mg2+ cations and the strength of the H-bonds formed. More specifically, it was observed that Mg–N, NC−⋯HO–Si, and lateral Mg–C
N frequencies undergo both bathochromic and hypsochromic shifts due to adsorption, depending on the type and number of simultaneous interactions occurring with surface Mg2+ cations and the strength of the H-bonds formed. More specifically, it was observed that Mg–N, NC−⋯HO–Si, and lateral Mg–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N interactions contribute to bathochromic shifts of the C
N interactions contribute to bathochromic shifts of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bonds, while bridged Mg–CN–Mg motifs cause hypsochromic shifts.
N bonds, while bridged Mg–CN–Mg motifs cause hypsochromic shifts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding within the European Union's Horizon 2020 research and innovation program from the European Research Council (ERC) for the project “Quantum Chemistry on Interstellar Grains” (Quantumgrain), grant agreement No. 865657, and from the Marie Sklodowska-Curie for the project “Astro-Chemical Origins” (ACO), grant agreement No. 811312. The Italian Space Agency for co-funding the Life in Space Project (ASI N. 2019-3-U.O), the Italian MUR (PRIN 2020, Astrochemistry beyond the second period elements, Prot. 2020AFB3FX) are also acknowledged for financial support. This research is also funded by MICINN (project PID2021-126427NB-I00). This research acknowledges support from the Project CH4.0 under the MIUR program “Dipartimento di Eccellenza 2023-2027”.References
- A. M. S. Boonman, R. Stark, F. F. S. van der Tak, E. F. van Dishoeck, P. B. van der Wal, F. Schafer, G. de Lange and W. M. Laauwen, Highly abundant HCN in the inner hot envelope of GL 2591: probing the birth of a hot core?, Astrophys. J., 2001, 553, L63–L67 CrossRef.
- H.-C. Huang, Y.-J. Kuan, S. B. Charnley, N. Hirano, S. Takakuwa and T. L. Bourke, Organic molecules in the hot corinos and circumstellar disks of IRAS 16293-2422, Adv. Space Res., 2005, 36, 146–155 CrossRef CAS.
- T. S. Rice, E. A. Bergin, J. K. Jørgensen and S. F. Wampfler, Exploring the origins of Earth's nitrogen: Astronomical observations of nitrogen-bearing organics in protostellar environments, Astrophys. J., 2018, 866, 156 CrossRef.
- M. N. Drozdovskaya, E. F. van Dishoeck, M. Rubin, J. K. Jørgensen and K. Altwegg, Ingredients for solar-like systems: protostar IRAS 16293-2422 B versus comet 67P/Churyumov–Gerasimenko, Mon. Not. R. Astron. Soc., 2019, 490, 50–79 CrossRef CAS.
- A. Dutrey, S. Guilloteau and M. Guelin, Chemistry of protosolar-like nebulae: The molecular content of the DM Tau and GG Tau disks, Astron. Astrophys., 1997, 317, L55–L58 CAS.
- W.-F. Thi, G.-J. van Zadelhoff and E. F. van Dishoeck, Organic molecules in protoplanetary disks around T Tauri and Herbig Ae stars, Astron. Astrophys., 2004, 425, 955–972 CrossRef CAS.
- J. B. Bergner, K. I. Öberg, E. A. Bergin, R. A. Loomis, J. Pegues and C. Qi, A Survey of C2H, HCN, and C18O in Protoplanetary Disks, Astrophys. J., 2019, 876, 25 CrossRef CAS.
- V. V. Guzmán, J. B. Bergner, C. J. Law, K. I. Öberg, C. Walsh, G. Cataldi, Y. Aikawa, E. A. Bergin, I. Czekala, J. Huang, S. M. Andrews, R. A. Loomis, K. Zhang, R. Le Gal, F. Alarcón, J. D. Ilee, R. Teague, L. I. Cleeves, D. J. Wilner, F. Long, K. R. Schwarz, A. D. Bosman, L. M. Pérez, F. Ménard and Y. Liu, Molecules with ALMA at Planet-forming Scales (MAPS). VI. Distribution of the Small Organics HCN, C2H, and H2CO, Astrophys. J., Suppl. Ser., 2021, 257, 6 CrossRef.
- E. S. Wirström, M. S. Lerner, P. Källström, A. Levinsson, A. Olivefors and E. Tegehall, HCN observations of comets C/2013 R1 (Lovejoy) and C/2014 Q2 (Lovejoy), Astron. Astrophys., 2016, 588, A72 CrossRef.
- W. F. Huebner, L. E. Snyder and D. Buhl, HCN radio emission from Comet Kohoutek (1973f), Icarus, 1974, 23, 580–584 CrossRef CAS.
- S. Pizzarello, Hydrogen Cyanide in the Murchison Meteorite, Astrophys. J., 2012, 754, L27 CrossRef.
- L. Tanguy, B. Bézard, A. Marten, D. Gautier, E. Gérard, G. Paubert and A. Lecacheux, Stratospheric profile of HCN on Titan from millimeter observations, Icarus, 1990, 85, 43–57 CrossRef CAS.
- M. Rengel, D. Shulyak, P. Hartogh, H. Sagawa, R. Moreno, C. Jarchow and D. Breitschwerdt, Ground-based HCN submillimetre measurements in Titan's atmosphere: an intercomparison with Herschel observations, Astron. Astrophys., 2022, 658, A88 CrossRef CAS.
- R. J. de Kok, N. A. Teanby, L. Maltagliati, P. G. J. Irwin and S. Vinatier, HCN ice in Titan's high-altitude southern polar cloud, Nature, 2014, 514, 65–67 CrossRef CAS PubMed.
- H. Liszt and R. Lucas, Comparative chemistry of diffuse clouds - II. CN, HCN, HNC, CH3CN & N2H+, Astron. Astrophys., 2001, 370, 576–585 CrossRef CAS.
- T. Hirota, S. Yamamoto, H. Mikami and M. Ohishi, Abundances of HCN and HNC in Dark Cloud Cores, Astrophys. J., 1998, 503, 717–728 CrossRef CAS.
- J. Oró, Mechanism of Synthesis of Adenine from Hydrogen Cyanide under Possible Primitive Earth Conditions, Nature, 1961, 191, 1193–1194 CrossRef PubMed.
- Z. Martins, O. Botta, M. L. Fogel, M. A. Sephton, D. P. Glavin, J. S. Watson, J. P. Dworkin, A. W. Schwartz and P. Ehrenfreund, Extraterrestrial Nucleobases in the Murchison Meteorite, Origins Life Evol. Biospheres, 2009, 30, 214 Search PubMed.
- C. N. Matthews and R. Ludicky, ESLAB Symposium on the Exploration of Halley's Comet, 1986, vol. 250 Search PubMed.
- D. P. Cruikshank, L. J. Allamandola, W. K. Hartmann, D. J. Tholen, R. H. Brown, C. N. Matthews and J. F. Bell, Solid C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bearing material on outer solar system bodies, Icarus, 1991, 94, 345–353 CrossRef CAS PubMed.
N bearing material on outer solar system bodies, Icarus, 1991, 94, 345–353 CrossRef CAS PubMed. - C. N. Matthews, Heteropolypeptides on Titan?, Origins Life, 1982, 12, 281–283 CrossRef CAS PubMed.
- C. N. Matthews, Hydrogen cyanide polymers: from laboratory to space, Planet. Space Sci., 1995, 43, 1365–1370 CrossRef CAS.
- R. A. Sanchez, J. P. Ferbis and L. E. Orgel, Studies in Prebiodc Synthesis: II. Synthesis of purine precursors and amino acids from aqueous hydrogen cyanide, J. Mol. Biol., 1967, 30, 223–253 CAS.
- M. K. Yim and J. C. Choe, Dimerization of HCN in the gas phase: a theoretical mechanistic study, Chem. Phys. Lett., 2012, 538, 24–28 CrossRef CAS.
- S. H. Jung and J. C. Choe, Mechanisms of prebiotic adenine synthesis from HCN by oligomerization in the gas phase, Astrobiology, 2013, 13, 465–475 CrossRef CAS PubMed.
- B. Fábián, M. Szőri and P. Jedlovszky, Floating Patches of HCN at the Surface of Their Aqueous Solutions – Can They Make “HCN World” Plausible?, J. Phys. Chem. C, 2014, 118, 21469–21482 CrossRef.
- H. Sandstrom and M. Rahm, The Beginning of HCN Polymerization: Iminoacetonitrile Formation and Its Implications in Astrochemical Environments, ACS Earth Space Chem., 2021, 5, 2152–2159 CrossRef PubMed.
- J. C. Choe, Water-assisted Dimerization of Hydrogen Cyanide: A Computational Study, Bull. Korean Chem. Soc., 2017, 38, 1531–1533 CrossRef CAS.
- O. Kikuchi, T. Watanabe, Y. Satoh and Y. Inadomi, Ab initio GB study of prebiotic synthesis of purine precursors from aqueous hydrogen cyanide: dimerization reaction of HCN in aqueous solution, THEOCHEM, 2000, 507, 53–62 CrossRef CAS.
- I. W. M. Smith, D. Talbi and E. Herbst, The production of HCN dimer and more complex oligomers in dense interstellar clouds, Astron. Astrophys., 2001, 369, 611–615 CrossRef CAS.
- R. Santalucia, M. Pazzi, F. Bonino, M. Signorile, D. Scarano, P. Ugliengo, G. Spoto and L. Mino, From gaseous HCN to nucleobases at the cosmic silicate dust surface: an experimental insight into the onset of prebiotic chemistry in space, Phys. Chem. Chem. Phys., 2022, 24, 7224–7230 RSC.
- J. C. Choe, Dimerization of HCN in Interstellar Icy Grain Mantles: A DFT Study, Bull. Korean Chem. Soc., 2019, 40, 205–206 CrossRef CAS.
- M. Signorile, L. Zamirri, A. Tsuchiyama, P. Ugliengo, F. Bonino and G. Martra, On the Surface Acid–Base Properties of Amorphous and Crystalline Mg2SiO4 as Probed by Adsorbed CO, CO2, and CD3CN, ACS Earth Space Chem., 2020, 4, 345–354 CrossRef CAS.
- T. Henning, Cosmic Silicates, Annu. Rev. Astron. Astrophys., 2010, 48, 21–46 CrossRef CAS.
- P. R. Buseck and H. Xin Hua, Matrices of carbonaceous chondrite meteorites, Annu. Rev. Earth Planet. Sci., 1993, 21, 255–305 CrossRef CAS.
- A. H. Delsemme, S. K. Runcorn, G. Turner and M. M. Woolfson, The chemistry of comets, Philos. Trans. R. Soc., A, 1988, 325, 509–523 CrossRef CAS.
- A. M. Walker, S. M. Woodley, B. Slater and K. Wright, A computational study of magnesium point defects and diffusion in forsterite, Phys. Earth Planet. Inter., 2009, 172, 20–27 CrossRef CAS.
- G. Ottonello, B. Civalleri, J. Ganguly, M. Vetuschi Zuccolini and Y. Noel, Thermophysical properties of the α–β–γ polymorphs of Mg2SiO4: a computational study, Phys. Chem. Miner., 2009, 36, 87–106 CrossRef CAS.
- J. Navarro-Ruiz, P. Ugliengo, A. Rimola and M. Sodupe, B3LYP Periodic Study of the Physicochemical Properties of the Nonpolar (010) Mg-Pure and Fe-Containing Olivine Surfaces, J. Phys. Chem. A, 2014, 118, 5866–5875 CrossRef CAS PubMed.
- M. Bruno, F. R. Massaro, M. Prencipe, R. Demichelis, M. De La Pierre and F. Nestola, Ab initio calculations of the main crystal surfaces of forsterite (Mg2SiO4): a preliminary study to understand the nature of geochemical processes at the olivine interface, J. Phys. Chem. C, 2014, 118, 2498–2506 CrossRef CAS.
- R. Demichelis, M. Bruno, F. R. Massaro, M. Prencipe, M. De La Pierre and F. Nestola, First-principle modelling of forsterite surface properties: Accuracy of methods and basis sets, J. Comput. Chem., 2015, 36, 1439–1445 CrossRef CAS PubMed.
- J. Navarro-Ruiz, M. Sodupe, P. Ugliengo and A. Rimola, Interstellar H adsorption and H2 formation on the crystalline (010) forsterite surface: a B3LYP-D2* periodic study, Phys. Chem. Chem. Phys., 2014, 16, 17447–17457 RSC.
- J. Navarro-Ruiz, J. Á. Martínez-González, M. Sodupe, P. Ugliengo and A. Rimola, Relevance of silicate surface morphology in interstellar H2 formation. Insights from quantum chemical calculations, Mon. Not. R. Astron. Soc., 2015, 453, 914–924 CrossRef CAS.
- S. Garcia-Gil, D. Teillet-Billy, N. Rougeau and V. Sidis, H Atom Adsorption on a Silicate Surface: The (010) Surface of Forsterite, J. Phys. Chem. C, 2013, 117, 12612–12621 CrossRef CAS.
- T. Suhasaria, J. D. Thrower and H. Zacharias, Thermal desorption of astrophysically relevant molecules from forsterite(010), Mon. Not. R. Astron. Soc., 2017, 472, 389–399 CrossRef CAS.
- G. Molpeceres, A. Rimola, C. Ceccarelli, J. Kästner, P. Ugliengo and B. Maté, Silicate-mediated interstellar water formation: a theoretical study, Mon. Not. R. Astron. Soc., 2019, 482, 5389–5400 CrossRef CAS PubMed.
- T. Liu, S. S. Gautam, L. L. Daemen, A. I. Kolesnikov, L. M. Anovitz, M. Hartl and D. R. Cole, Vibrational Behavior of Water Adsorbed on Forsterite (Mg2SiO4) Surfaces, ACS Earth Space Chem., 2020, 4, 1050–1063 CrossRef CAS.
- R. S. Smith, Z. Li, Z. Dohnálek and B. D. Kay, Adsorption, Desorption, and Displacement Kinetics of H2O and CO2 on Forsterite, Mg2SiO4(011), J. Phys. Chem. C, 2014, 118, 29091–29100 CrossRef CAS.
- H. E. King, M. Stimpfl, P. Deymier, M. J. Drake, C. R. A. Catlow, A. Putnis and N. H. de Leeuw, Computer simulations of water interactions with low-coordinated forsterite surface sites: Implications for the origin of water in the inner solar system, Earth Planet. Sci. Lett., 2010, 300, 11–18 CrossRef CAS.
- T. P. M. Goumans, C. R. A. Catlow, W. A. Brown, J. Kästner and P. Sherwood, An embedded cluster study of the formation of water on interstellar dust grains, Phys. Chem. Chem. Phys., 2009, 11, 5431–5436 RSC.
- N. H. de Leeuw, S. C. Parker, C. R. A. Catlow and G. D. Price, Modelling the effect of water on the surface structure and stability of forsterite, Phys. Chem. Miner., 2000, 27, 332–341 CrossRef CAS.
- K. Muralidharan, P. Deymier, M. Stimpfl, N. H. de Leeuw and M. J. Drake, Origin of water in the inner Solar System: A kinetic Monte Carlo study of water adsorption on forsterite, Icarus, 2008, 198, 400–407 CrossRef.
- L. Zamirri, M. Corno, A. Rimola and P. Ugliengo, Forsterite Surfaces as Models of Interstellar Core Dust Grains: Computational Study of Carbon Monoxide Adsorption, ACS Earth Space Chem., 2017, 1, 384–398 CrossRef CAS.
- L. Zamirri, S. Pantaleone and P. Ugliengo, Carbon monoxide adsorption at forsterite surfaces as models of interstellar dust grains: An unexpected bathochromic (red) shift of the CO stretching frequency, J. Chem. Phys., 2019, 150, 064702 CrossRef PubMed.
- A. Rimola, J. M. Trigo-Rodríguez and Z. Martins, Interaction of organic compounds with chondritic silicate surfaces. Atomistic insights from quantum chemical periodic simulations, Phys. Chem. Chem. Phys., 2017, 19, 18217–18231 RSC.
- A. M. Asaduzzaman, T. J. Zega, S. Laref, K. Runge, P. A. Deymier and K. Muralidharan, A computational investigation of adsorption of organics on mineral surfaces: Implications for organics delivery in the early solar system, Earth Planet. Sci. Lett., 2014, 408, 355–361 CrossRef CAS.
- E. Escamilla-Roa and C. I. Sainz-Díaz, Amorphous Ammonia–Water Ice Deposited onto Silicate Grain: Effect on Growth of Mantles Ice on Interstellar and Interplanetary Dust, J. Phys. Chem. C, 2014, 118, 3554–3563 CrossRef CAS.
- T. Suhasaria, J. D. Thrower and H. Zacharias, Thermal desorption of ammonia from crystalline forsterite surfaces, Mon. Not. R. Astron. Soc., 2015, 454, 3317–3327 CrossRef CAS.
- M. A. Corazzi, D. Fedele, G. Poggiali and J. R. Brucato, Photoprocessing of formamide ice: route towards prebiotic chemistry in space, Astron. Astrophys., 2020, 636, A63 CrossRef CAS.
- E. Escamilla-Roa and F. Moreno, Adsorption of glycine by cometary dust: Astrobiological implications, Planet. Space Sci., 2012, 70, 1–9 CrossRef CAS.
- E. Escamilla-Roa and F. Moreno, Adsorption of glycine on cometary dust grains: II—Effect of amorphous water ice, Planet. Space Sci., 2013, 75, 1–10 CrossRef CAS.
- E. Escamilla-Roa and C. I. Sainz-Díaz, Effect of Amorphous Ammonia–Water Ice onto Adsorption of Glycine on Cometary Dust Grain and IR Spectroscopy, J. Phys. Chem. C, 2014, 118, 26080–26090 CrossRef CAS.
- A. Li and B. T. Draine, On ultrasmall silicate grains in the diffuse interstellar medium, Astrophys. J., 2001, 550, L213 CrossRef CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima and S. Salustro, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- M. Cutini, L. Maschio and P. Ugliengo, Exfoliation energy of layered materials by DFT-D: Beware of dispersion!, J. Chem. Theory Comput., 2020, 16, 5244–5252 CrossRef CAS PubMed.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, B3LYP augmented with an empirical dispersion term (B3LYP-D*) as applied to molecular crystals, CrystEngComm, 2008, 10, 405–410 RSC.
- A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- C. G. Broyden, The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef.
- R. Fletcher, A new approach to variable metric algorithms, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, A family of variable-metric methods derived by variational means, Math. Comput., 1970, 24, 23–26 CrossRef.
- D. F. Shanno, Conditioning of quasi-Newton methods for function minimization, Math. Comput., 1970, 24, 647–656 CrossRef.
- M. Corno and P. Ugliengo, Surface modeling of ceramic biomaterials, in Encyclopedia of Nanotechnology, ed. B. Bhushan, Springer Science + Business Media, 2015, pp. 1–13 Search PubMed.
- H. B. Jansen and P. Ros, Non-empirical molecular orbital calculations on the protonation of carbon monoxide, Chem. Phys. Lett., 1969, 3, 140–143 CrossRef CAS.
- B. Liu and A. D. McLean, Accurate calculation of the attractive interaction of two ground state helium atoms, J. Chem. Phys., 1973, 59, 4557–4558 CrossRef CAS.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- D. A. Williams, The interstellar medium: an overview, Solid State Astrochem., 2003, 1–20 Search PubMed.
- K. Nakamoto, Handbook of Vibrational Spectroscopy, John Wiley & Sons, Ltd, 2006 Search PubMed.
- C. M. Zicovich-Wilson, M. L. San Román and A. Ramírez-Solís, Mechanism of F- elimination from zeolitic D4R units: A periodic B3LYP study on the octadecasil zeolite, J. Phys. Chem. C, 2010, 114, 2989–2995 CrossRef CAS.
- R. A. Marcus and O. K. Rice, The Kinetics of the Recombination of Methyl Radicals and Iodine Atoms, J. Phys. Chem., 1951, 55, 894–908 CrossRef CAS.
- R. A. Marcus, Unimolecular Dissociations and Free Radical Recombination Reactions, J. Chem. Phys., 1952, 20, 359–364 CrossRef CAS.
- H. M. Rosenstock, M. B. Wallenstein, A. L. Wahrhaftig and H. Eyring, Absolute Rate Theory for Isolated Systems and the Mass Spectra of Polyatomic Molecules, Proc. Natl. Acad. Sci. U. S. A., 1952, 38, 667–678 CrossRef CAS PubMed.
- T. Baer and W. L. Hase, Unimolecular Reaction Dynamics: Theory and Experiments, Oxford University Press, USA, 1996 Search PubMed.
- C. Eckart, The penetration of a potential barrier by electrons, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- H. S. Johnston and J. Heicklen, Tunnelling corrections for unsymmetrical Eckart potential energy barriers, J. Phys. Chem., 1962, 66, 532–533 CrossRef.
- J. R. Smyth and R. M. Hazen, The crystal structures of forsterite and hortonolite at several temperatures up to 900 C, Am. Mineral. J. Earth Planet. Mater., 1973, 58, 588–593 CAS.
- G. W. Watson, P. M. Oliver and S. C. Parker, Computer simulation of the structure and stability of forsterite surfaces, Phys. Chem. Miner., 1997, 25, 70–78 CrossRef CAS.
- D. Bostroem, Single-crystal X-ray diffraction studies of synthetic Ni-Mg olivine solid solutions, Am. Mineral., 1987, 72, 965–972 CAS.
- M. De La Pierre, R. Orlando, L. Maschio, K. Doll, P. Ugliengo and R. Dovesi, Performance of six functionals (LDA, PBE, PBESOL, B3LYP, PBE0, and WC1LYP) in the simulation of vibrational and dielectric properties of crystalline compounds. The case of forsterite Mg2SiO4, J. Comput. Chem., 2011, 32, 1775–1784 CrossRef CAS PubMed.
- P. W. Tasker, The stability of ionic crystal surfaces, J. Phys. C-Solid State Phys., 1979, 12, 4977 CrossRef CAS.
- G. Wulff, Xxv. zur frage der geschwindigkeit des wachsthums und der auflösung der krystallflächen, Z. Kristallogr. - Cryst. Mater., 1901, 34, 449–530 CrossRef CAS.
- A. Natta, L. Testi, N. Calvet, T. Henning, R. Waters and D. Wilner, in Protostars and Planets V, ed. D. Jewitt and K. Keil, University of Arizona Press, Tucson, 2007, pp. 767–781 Search PubMed.
- L. Zamirri, A. Macià Escatllar, J. Mariñoso Guiu, P. Ugliengo and S. T. Bromley, What Can Infrared Spectra Tell Us about the Crystallinity of Nanosized Interstellar Silicate Dust Grains?, ACS Earth Space Chem., 2019, 3, 2323–2338 CrossRef CAS.
- G. Pacchioni, G. Cogliandro and P. S. Bagus, Characterization of oxide surfaces by infrared spectroscopy of adsorbed carbon monoxide: a theoretical investigation of the frequency shift of CO on MgO and NiO, Surf. Sci., 1991, 255, 344–354 CrossRef CAS.
- G. Pacchioni, A. M. Ferrari and P. S. Bagus, Cluster and band structure ab initio calculations on the adsorption of CO on acid sites of the TiO2 (110) surface, Surf. Sci., 1996, 350, 159–175 CrossRef CAS.
- L. Mino, A. M. Ferrari, V. Lacivita, G. Spoto, S. Bordiga and A. Zecchina, CO Adsorption on Anatase Nanocrystals: A Combined Experimental and Periodic DFT Study, J. Phys. Chem. C, 2011, 115, 7694–7700 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01459b |
| This journal is © the Owner Societies 2023 |


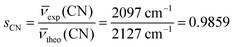











![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N