Open Access Article
Open Access ArticleTetracoordinate Co(II) complexes with semi-coordination as stable single-ion magnets for deposition on graphene†
Jorge Navarro
Giraldo
 a,
Jakub
Hrubý‡
a,
Jakub
Hrubý‡
 a,
Šárka
Vavrečková§
ab,
Ondřej F.
Fellner
a,
Šárka
Vavrečková§
ab,
Ondřej F.
Fellner
 c,
Lubomír
Havlíček
c,
Lubomír
Havlíček
 ad,
DaVonne
Henry
e,
Shehan
de Silva
e,
Radovan
Herchel
ad,
DaVonne
Henry
e,
Shehan
de Silva
e,
Radovan
Herchel
 c,
Miroslav
Bartoš
a,
Ivan
Šalitroš
c,
Miroslav
Bartoš
a,
Ivan
Šalitroš
 af,
Vinicius T.
Santana
a,
Paola
Barbara
af,
Vinicius T.
Santana
a,
Paola
Barbara
 e,
Ivan
Nemec
e,
Ivan
Nemec
 *ac and
Petr
Neugebauer
*ac and
Petr
Neugebauer
 *a
*a
aCentral European Institute of Technology, CEITEC BUT, Purkyňova 656/123, 61200 Brno, Czech Republic. E-mail: ivan.nemec@ceitec.vutbr.cz; petr.neugebauer@ceitec.vutbr.cz
bInstitute of Physical Engineering, Faculty of Mechanical Engineering, Brno University of Technology, Technická 2, 61669 Brno, Czech Republic
cDepartment of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, 77147 Olomouc, Czech Republic
dInstitute of Physics of Materials, Czech Academy of Sciences, Žižkova 22, 61662 Brno, Czech Republic
eDepartment of Physics, Georgetown University, Washington, DC, USA
fDepartment of Inorganic Chemistry, Faculty of Chemical and Food Technology, Slovak University of Technology in Bratislava, Bratislava SK-81237, Slovakia
First published on 17th October 2023
Abstract
We present a theoretical and experimental study of two tetracoordinate Co(II)-based complexes with semi-coordination interactions, i.e., non-covalent interactions involving the central atom. We argue that such interactions enhance the thermal and structural stability of the compounds, making them appropriate for deposition on substrates, as demonstrated by their successful deposition on graphene. DC magnetometry and high-frequency electron spin resonance (HF-ESR) experiments revealed an axial magnetic anisotropy and weak intermolecular antiferromagnetic coupling in both compounds, supported by theoretical predictions from complete active space self-consistent field calculations complemented by N-electron valence state second-order perturbation theory (CASSCF-NEVPT2), and broken-symmetry density functional theory (BS-DFT). AC magnetometry demonstrated that the compounds are field-induced single-ion magnets (SIMs) at applied static magnetic fields, with slow relaxation of magnetization governed by a combination of quantum tunneling, Orbach, and direct relaxation mechanisms. The structural stability under ambient conditions and after deposition was confirmed by X-ray photoelectron spectroscopy (XPS) and Raman spectroscopy. Theoretical modeling by DFT of different configurations of these systems on graphene revealed n-type doping of graphene originating from electron transfer from the deposited molecules, confirmed by electrical transport measurements and Raman spectroscopy.
1 Introduction
Hybrid materials combining single-molecule magnets (SMMs) and solid-state materials are attractive candidates for next-generation technologies, such as high-density magnetic memory devices,1 qubits,2 and spintronic devices.3–5 The solid-state substrate, having metallic, semi-metallic, or insulating character, provides a platform for the deposition of SMMs in the form of thin films, allowing addressing or manipulation of the molecular magnetic and electric properties.4,6,7 For their successful deposition, the molecular compounds must present an increased chemical, structural, and thermal stability that guarantees the preservation of their magnetic properties during and after the deposition process,4 which often involves their sublimation at high temperatures and under high-vacuum conditions. These features pose considerable challenges to the design of sublimable SMMs, such that the number of demonstrated complexes suitable for deposition and spintronic applications remains small.4Co(II)-based coordination compounds often exhibit interesting magnetic properties emerging from a large spin–orbit coupling (SOC) inducing very large magnetic anisotropies in certain ligand field symmetries. For the preparation of SMMs, or their analogs with only one paramagnetic center, single-ion magnets (SIMs), it is important for the molecule to possess a large and preferably axial type of magnetic anisotropy (D < 0), which is usually observed for low coordinate Co(II) complexes such as dicoordinate,8 tetracoordinate,9–13 pentacoordinate,14–20 but also hexacoordinate with trigonal ligand field symmetry.21–27 To date, the most extensively investigated group of Co(II) SIMs consists of tetracoordinate complexes.28,29 Within this class, the most intriguing results have been observed for SIMs that exhibit slow relaxation of magnetization in zero external magnetic fields, commonly known as zero-field SIMs (ZF-SIMs). There are only two groups of tetracoordinate Co(II) ZF-SIMs: those composed of monodentate ligands with S, Se, or Te donor atoms,30–32 and those formed by bidentate ligands that create acute bite angles.33–37 Our previous investigations strongly suggest avoiding the use of monodentate ligands in complexes intended for thermal depositions. Recently, we attempted to deposit two different types of tetracoordinate Co(II) complexes on various substrates, but found that the stability of the complex molecules during deposition was problematic under ambient conditions.38 Even the use of a protective atmosphere was not sufficient to deposit intact tetracoordinate Co(II) molecules.39 To enhance the stability of the Co(II) complexes intended for depositions we opted to use bidentate ligands instead of monodentate ligands. We decided to use bidentate Schiff base ligands which are well known for forming mononuclear Co(II) complexes exhibiting field-induced or zero-field slow relaxation of magnetization. Furthermore, we modified the Schiff base ligands by adding a 2-pyridyl substituent to ensure the high stability of the molecular complexes. This provides an additional nitrogen atom that is sterically hindered from forming a regular coordination bond with the metal atom. However, it can form a non-covalent interaction with the adjacent metal center. As we recently proposed,40 non-covalent interactions between the donor atoms possessing free electron pairs such as N or O, and metal atoms can enhance the stability of the molecular complex without affecting the magnetic anisotropy of the metal centers significantly. Therefore, for depositions, we decided to utilize Co(II) compounds with a specific class of Schiff base ligands derived from the condensation of aromatic 2-hydroxo-benzaldehydes and 2-amino-6-picoline. The crystal structure of the Co(II) compound with the Hsalapi ligand (Hsalapi = 2-methyl-6-(2′-oxybenzylideneamino)pyridin) was reported previously.41 In its crystal structure (Cambridge Structural Database code MIFWUU),42 we see that two deprotonated salapi− ligands coordinate the Co(II) atom in a bidentate manner giving rise to the [Co(salapi)2] molecule (Fig. 1). Remarkably, the pyridine nitrogen atoms point towards the metal center, but the Co⋯N distances are relatively long (2.625(14) and 2.708(14) Å). Thus, from the perspective of structural coordination chemistry, these contacts could be classified as semi-coordinative because of their non-covalent nature and major electrostatic contribution.43–48
In this work, we opted to investigate whether the [Co(salapi)2] (hereafter 1) and structurally related [Co(me-salapi)2] (hereafter 2, Hme-salapi = 2-methyl-6-(2′-oxy-4′-methyl-benzylideneamino)pyridin) molecules can be magnetically considered to be tetracoordinate despite having relatively short Co⋯N non-covalent interactions. Furthermore, we investigated whether the Co⋯N interactions are stabilizing structures of molecules in 1 and 2 sufficiently enough for their utilization in depositions by wet chemistry and thermal sublimation. In this case, we performed molecular deposition on commercially available single-layer graphene.49 Graphene offers interesting properties such as high electron mobility, spin transport, mechanical strength, and thermal conductivity.50–53 Furthermore, in our vision, graphene serves as a good substrate for deposition when nanostructured into a quantum dot, which could be used as a bolometer for in situ spectroscopy of deposited compounds.54,55 Graphene could also be used for the electrical addressing of SMMs, as it can be shaped and utilized for graphene transistors56 that are commercially available nowadays.
Herein, we report on the synthesis, crystal structure, magnetic properties, and characterization of compounds 1 and 2 along with a theoretical study of their semi-coordination aspects, magnetic properties, and intermolecular exchange interactions. Direct current (DC) magnetometry and HF-ESR measurements demonstrated that the compounds present an axial magnetic anisotropy and a weak intermolecular antiferromagnetic exchange interaction, corroborated by broken-symmetry DFT (BS-DFT) calculations; while alternating current (AC) magnetometry showed that both compounds behave as field-induced SIMs. We also carried out a successful deposition of 1 and 2 on graphene and compared the results to a bulk reference. Raman spectroscopy, X-ray photoelectron spectroscopy (XPS), atomic force microscopy (AFM), and electrical transport measurements were used as characterization techniques supporting the theoretical predictions of molecular adsorption performed by DFT.
2 Materials and methods
Detailed information on the sample preparation, elemental analysis, characterization by infrared spectroscopy and X-ray diffraction (XRD), DC and AC magnetometry, electrical transport, and HF-ESR measurements is found in the ESI.†2.1 Deposited samples
For both deposition processes (drop-cast and thermal sublimation) a chemical vapour deposition (CVD) grown monolayer graphene on a Si/SiO2 substrate was used (300 nm thickness of SiO2, Si (100), p-doped, 1–10 Ω cm from Graphenea, San Sebastian, Spain). The drop-cast sample was prepared by dissolving the bulk compound 1 or 2 in acetone (99%, Penta, Czech Republic) to make a final solution with a 1 mM concentration. The actual drop-casting was conducted in ambient conditions as 40 μL was drop-cast onto graphene. For the thermal sublimation, we used a home-built high-vacuum sublimation chamber equipped with a quartz crucible heated by a ceramic heater (BACH RC, Seefeld, Germany) with a thermocouple in thermal contact with the heater. The base chamber pressure during the sublimation was 1 × 10−6 mbar. The sublimations for 1 and 2 were performed at 270 and 283, respectively. The bulk powder from the crucible after sublimation was taken for further analysis. Optical images were acquired on a confocal Raman microscope WITec Alpha300 R+ (WITec, Ulm, Germany). All topography images and profiles were obtained with the scanning probe microscope Dimension Icon (Bruker, Billerica, USA) in tapping mode. X-ray photoelectron (XPS) measurements were carried out with Kratos Axis Supra (Kratos Analytical, Manchester, United Kingdom).2.2 Computational details
The zero-field splitting (ZFS) terms were computed using Gaussian-basis DFT in the ORCA 4.2.1 and 5.0 electronic structure packages,57,58 using the state average-CASSCF,59 complemented by NEVPT2.60,61 The input coordinates for the calculations were obtained from experimentally determined molecular structures refined by Hirshfeld atom refinement62 incorporated in Olex2 (ver. 1.5).47 The basis sets for the ZFS calculations were used as follows: def2-SVP for hydrogen and carbon atoms, triple-ζ def2-TZVP for the remaining atoms.63 The calculation costs were decreased by using the def2/J and def2-TZVP/C auxiliary basis sets64,65 together with the chain-of-spheres (RIJCOSX)66,67 approximation to the exact exchange as implemented in ORCA. The active space was defined by seven electrons in five d-orbitals of Co(II) (CAS(7,5)), and all possible multiplets, 10 quartets, and 40 doublets, were involved in the calculations. The ligand field parameters were obtained using the ab initio ligand field theory (AILFT) calculations.68BS-DFT calculations in ORCA 5.0 were carried out to estimate the isotropic exchange interaction. Two DFT hybrid functionals, B3LYP69–71 and PBE0,72 were selected based on their good performance on previously studied coordination compounds.73–78 Moreover, the calculations were performed with Ahlrichs triple-ζ basis sets def2-TZVP and also with their relativistic analogs ZORA-def2-TZVP.63 Furthermore, the non-local density-dependent dispersion correction to DFT was accounted for in two ways, as non-self-consistent (DFT-NL) and as self-consistent (DFT-SCNL) implementation.79,80
The quantum theory of atoms in molecules81 (QT-AIM) calculations were performed using ORCA 4.2.1, employing single-point DFT calculations utilizing the B3LYP functional and bases as described above (def2-TZVP). Then, the wavefunctions were used for the QT-AIM calculations using the Multiwfn program.82,83 ELF calculations for Co(II) complexes, which visualize electron pairs, were compared to those for diamagnetic Zn(II) analogues, revealing no significant differences.
Molecular adsorption on graphene was calculated using plane-wave DFT performed on the Vienna Ab-Initio Simulation Package (VASP)84–87 version 5.4.4, which uses a plane-wave basis for the Kohn–Sham orbitals, the Projector Augmented Wave method,87,88 and pseudopotentials. The exchange–correlation was accounted for by the PBE functional,89,90 with van der Waals corrections included by the D3 method with Becke–Johnson damping.91,92 Collinear spin polarization and electric dipole corrections93,94 were also included. In all calculations, the kinetic energy cut-off for the plane waves was 520 eV, and the cut-off energy of the plane wave representation of the augmentation charges was 644.9 eV. The threshold for electronic self-consistency loops was 10−6 eV, and ionic relaxation was performed until residual forces on each ion were below 0.02 eV Å−1, unless stated otherwise.
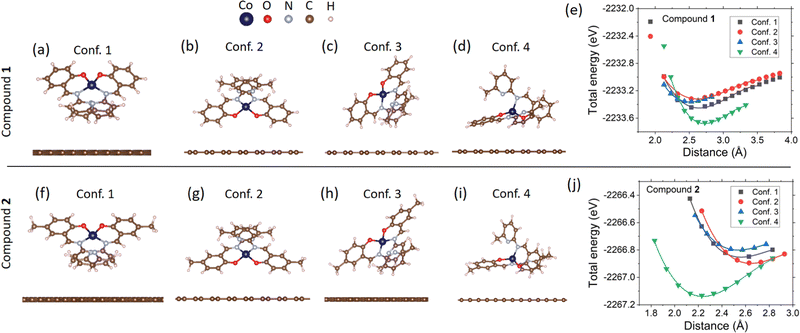
For calculations of the ground-state energy, ionic relaxation of isolated molecules, and ionic relaxation of the molecules on graphene, the reciprocal space was sampled using only one point at the Brillouin zone center (Γ-point calculation). For charge density calculations, a Γ-centered 2 × 2 × 1 Monkhorst–Pack mesh95 was used to sample the Brillouin zone of all configurations. The obtained charge densities were used and kept constant in the density of states calculations, where the reciprocal space was sampled with a Γ-centered 4 × 4 × 1 Monkhorst–Pack mesh. Reciprocal space integration used Gaussian smearing of k-points equal to 0.1 eV. To generate the partial density of states (Fig. 7a), and the planar average of the charge density difference (Fig. 7b, c and ESI† Fig. S41, S42), we used the VASPKIT code.96 We used the VESTA software97 to plot Fig. 6a–d, f–i, 7b, c and ESI† Fig. S40–S42.
To model the monolayer graphene substrate, we first performed ionic relaxation of the 10 × 10 graphene superlattice by plane-wave DFT until the interatomic forces were below 0.001 eV Å−1. (1 × 1 corresponds to a graphene unit cell containing two carbon atoms with an interatomic distance of 1.424 Å.) During the relaxation, the supercell's volume was kept constant, and the ionic positions were relaxed within the graphene's plane. The molecules were modeled taking as a basis their XRD structure. Then, ionic relaxation of the isolated molecules (gas phase) was performed using a parallelepiped unit cell of dimensions 24.67 × 24.67 × 30 Å3 (ESI† Fig. S40). To simulate molecular adsorption on graphene, four different configurations (orientations) of each molecular complex were placed on the 10 × 10 graphene substrate. A supercell height of 30 Å in the direction perpendicular to the graphene plane (z direction), guaranteed at least a 15 Å vacuum above the molecule on the substrate, minimizing the interaction between supercells in the z direction. Electric dipole corrections along the z direction were applied to reduce this interaction further. The supercell size and shape were kept the same in all calculations.
3 Results and discussion
3.1 Synthesis and structure
Compounds 1 and 2 can be prepared using the previously reported procedure.41 However, we synthesized both compounds by in situ reaction of 2-amino-6-methylpyridine, salicylaldehyde (or 5- methylsalicylaldehyd for preparation of 2), CoCl2·6H2O and triethylamine in methanolic solution (molar ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, Fig. 1). The mixture was refluxed after the addition of all reagents and then filtered. Red-orange crystals suitable for single-crystal XRD were obtained by slow diffusion of Et2 O into the solution. The purity of both compounds was confirmed by elemental analysis and powder XRD experiments (ESI† Fig. S1). The thermal stability was investigated using thermogravimetric analysis (ESI† Fig. S2 and S3), and it was revealed that compounds 1 and 2 are stable up to 290 and 310 °C, respectively, and with melting temperatures 263–265 and 301 °C, respectively.
2, Fig. 1). The mixture was refluxed after the addition of all reagents and then filtered. Red-orange crystals suitable for single-crystal XRD were obtained by slow diffusion of Et2 O into the solution. The purity of both compounds was confirmed by elemental analysis and powder XRD experiments (ESI† Fig. S1). The thermal stability was investigated using thermogravimetric analysis (ESI† Fig. S2 and S3), and it was revealed that compounds 1 and 2 are stable up to 290 and 310 °C, respectively, and with melting temperatures 263–265 and 301 °C, respectively.
Compounds 1 and 2 adopt very similar crystal structures although they are not isostructural. 1 crystallizes in the monoclinic I2/a space group, whereas 2 in the orthorhombic Pbcn space group. The basic crystallographic and refinement data are summarized in the ESI† Table S1. Both crystal structures consist solely of the molecular complex (Fig. 2a and ESI† Fig. S4, S5). In both structures, the cobalt atom sits at a two-fold rotational axis, and thus only half of the complex molecule is symmetrically independent. Two bidentate ligands coordinate the central Co(II) atom, each by one phenolate oxygen atom (dCo1–O1 = 1.9527(16) Å and 1.9613(7) Å in 1 and 2, respectively) and by an imine nitrogen atom (N1 in Fig. 2a, dCo1–N1 = 1.9913(18) Å and 1.9923(9) Å in 1 and 2, respectively). The Co⋯N distance of the pyridine nitrogen atoms (N2) is longer: 2.6908(19) Å and 2.6951(9) Å in 1 and 2, respectively, therefore, both 1 and 2 can be formally considered to be tetracoordinate. According to the SHAPE algorithm and continuous shape measurements (CSMs), the shape of the coordination polyhedron corresponds to a distorted tetrahedron (CSMs(Td): 2.857 and 2.531, respectively), however, distortion from the see-saw geometry is relatively small: (CSMs(C2v): 3.800 and 4.723, respectively, ESI† Table S2). The complex molecules form extensive networks of π–π aromatic stacking interactions organized in supramolecular layers parallel to (00l) planes (in 1) or chains along the c-axis (in 2, ESI† Fig. S4 and S5).
To investigate the nature of the Co⋯N interaction we utilized the topological analysis of electron density by QT-AIM. Firstly, we performed single-point DFT calculations using the coordinates of the complex molecules 1 and 2 obtained from XRD experiments. To ensure reliable positions of the hydrogen atoms we applied the Hirshfeld atom refinement for both structures (for details see the ESI† Section S1). Then, we performed topological analysis of the electron density (ρ(r)) using Multiwfn software.82,83 As a result, we did not find any bond critical point (BCP) between the Co1 and N2 atoms, as seen from the Laplacian of electron density (∇2ρ(r), ESI† Fig. S6). This can be attributed to the orientation of the pyridyl moiety, which modulated the topology of ∇2ρ(r) between the Co and N atoms, preventing the formation of bond path or BCP (ESI† Fig. S6). Next, we analyzed this interaction using the non-covalent interaction (NCI) method.98 This method utilizes the analysis of ρ(r) using the reduced density gradient function to distinguish between attractive and repulsive non-covalent interactions by determining the sign of the eigenvalue of the electron density Hessian matrix, defined as λ2. We visualized the interactions within molecules using VMD software99 (Fig. 2b). The Co⋯N interaction was found to be a combination of steric effect (repulsion between the neighboring nitrogen atoms, red color) and attraction between the pair of the Co and N atoms (blue color). To better visualize this interaction, we also computed the electron localization function (ELF), which depicts the probability of finding an electron pair in multielectronic systems.100,101Fig. 2c shows that the pyridine electron pair is well localized, pointing towards the more electropositive cobalt atom (ESI† Fig. S6). In summary, despite the absence of BCP, we show that the Co⋯N interaction exhibits an attractive non-covalent character due to the interaction between the pyridyl electron pair and the cobalt atom. Therefore, we classify this interaction as semi-coordination.44
3.2 Magnetic properties and HF-ESR
We employed magnetometry to perform DC magnetic measurements, including temperature- (2–300 K) and field- (0–7 T at 2 K) dependence of the magnetic moment (Fig. 3a and ESI† Fig. S27). The crystal structures of 1 and 2 consist of isolated complexes that interact through π–π stacking interactions, which are well-known non-covalent magnetic exchange pathways.102 To appropriately analyze the magnetic data, we first performed theoretical calculations. We selected dimeric structural fragments (Fig. 3d) and conducted BS-DFT calculations following the procedure of Section 2.2 to estimate the isotropic exchange of the spin Hamiltonian defined as Ĥ = −JŜ1·Ŝ2, with Ŝ1 and Ŝ2 corresponding to the spin operator of each molecule in the dimer. The comparison of the energy difference between the high-spin (HS, S1↑⋯S2↑) and broken-symmetry spin states (BS, S1↑⋯S2↓), Δ = εBS − εHS, was utilized to calculate J according to the formulas of Ruiz103 and Yamaguchi:104 | (1) |
 | ||
| Fig. 3 (a) Temperature dependence of μeff/μB acquired for 1 in the range from 2 K to 300 K with an external magnetic field 0.1 T, and the isothermal magnetization data measured at 2 K shown in the inset. The empty circles represent experimental data, while the red lines represent fittings to eqn (2)–(4). (b) Frequency dependence of the HF-ESR spectra of compound 1 at 7.4 K. (c) Temperature dependence of the HF-ESR spectra of compound 1 at 119.97 GHz. The parameters in the simulated spectra (with offset for more clarity) were D = −20 cm−1, gx = 2.20, gy = 2.15, gz = 2.40, E/D = 0.122, and J = −0.3 cm−1. Green stars correspond to thermally-activated transitions ascribed to the excited S = 1/2 doublet, black crosses indicate an ESR signal from an impurity in the sample holder's mirror, and red dots indicate a spurious signal not considered in the simulation. (d) The outcome of the BS-DFT calculations for 1 with visualization of the spin density isosurface. (e) Visualization of the D-tensor axes overlayed over the molecular structure of 1. (f) AILFT-calculated d-orbital splitting (left) and ligand field terms (right). | ||
All approaches predicted a weak antiferromagnetic coupling within the dimer for compounds 1 and 2 using all tested functionals and bases (see the ESI,† Tables S8 and S9); for example, using the functional B3LYP + NL we find JY = −0.247 cm−1 and −0.268 cm−1 for 1 and 2, respectively. A slightly stronger antiferromagnetic exchange was predicted for 2, which is consistent with its shorter C⋯C and C⋯N distances between the π–π stacked ligands of the neighboring molecules compared to those in compound 1. The magnetic exchange interaction between neighboring molecules is expected to be weak due to the relatively large Co⋯Co distances being 5.94479(9) and 5.82467(7) Å in compounds 1 and 2, respectively.
Since the magnetic measurements for both compounds were very similar, we provided a more detailed description of the properties of 1. The effective magnetic moment μeff/μB measured for 1, where μB is the Bohr magneton, adopts a value of 4.3 at room temperature, which is consistent with a large contribution of SOC. Thus, the Landé g-factor (giso = 2.20) is larger than that of the free electron (g = 2.0023). The μeff/μB values stayed approximately constant down to 30 K, where we observed a drop starting from 4.1 to 3.7 at 2 K suggesting the presence of intermolecular magnetic exchange interactions or ZFS. Since we did not observe maxima in the susceptibility curve (χ = f(T)), we may conclude that the intermolecular magnetic interactions among molecules are weak. Nevertheless, we were unable to fit the magnetic data in the absence of exchange coupling, and due to this fact as well as taking into account the results of BS-DFT calculations, we applied a spin Hamiltonian including axial (D) and rhombic (E) single-ion ZFS terms and exchange coupling for the supramolecular dimer:
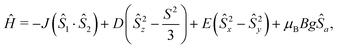 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, sin
ϕ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, cos
ϕ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), where θ and ϕ are the polar and azimuthal angles of the field. The molar magnetization in the a-direction of the magnetic field was numerically calculated from the partition function, Z, built from the energy levels of the spin Hamiltonian as follows:
θ), where θ and ϕ are the polar and azimuthal angles of the field. The molar magnetization in the a-direction of the magnetic field was numerically calculated from the partition function, Z, built from the energy levels of the spin Hamiltonian as follows: | (3) |
 | (4) |
The experimental magnetic data were fitted using EasySpin,105 analyzing both temperature- and field-dependent measurements simultaneously. The best fit was obtained with the following sets of parameters: for 1, J = −0.19 cm−1, giso = 2.272, D = −15.3 cm−1 and E/D = 0.012; for 2, J = −0.27 cm−1, giso = 2.213, D = −17.5 cm−1 and E/D = 0.044 (Fig. 3a and ESI† Fig. S27). This confirmed the presence of a relatively large and axial magnetic anisotropy.
ZFS was studied theoretically using the procedure outlined in Section 2.2, using ORCA 5.0. The calculations indicate that the 4F atomic term is split into seven ligand field multiplets as expected due to the low symmetry of the coordination polyhedron in 1 and 2. Additionally, the energy of the first excited state is above 1000 cm−1, making the spin Hamiltonian formalism suitable for analyzing magnetic data.106 The splitting of the d-orbitals reflects the distorted tetrahedral geometry with the lowest dx2–y2 orbital. The configuration of the d-orbitals is for both complexes as follows: dx2–y22, dz22, dxy1, dxz1, dyz1 (ESI† Fig. S21 and S22). In this configuration, the energy of the first excitation between the d-orbitals with the same |ml| value (dx2–y22 → dxy1, |ml| = 2) is smaller than the first excitation with Δ|ml| = 1 (dz22 → dxz1). This indicates a relatively large and axial magnetic anisotropy.23 CASSCF-NEVPT2 calculations of the ZFS parameters confirmed this assumption: D = −25.3 cm−1 and E/D = 0.084 for 1; D = −28.3 cm−1 and E/D = 0.107 for 2 (ESI† Tables S10 and S11). The obtained ZFS parameters were markedly different from those obtained by magnetometry. Therefore, we investigated if the used basis sets can help to diminish the difference between the calculated and experimentally derived ZFS parameters. We included relativistic effects by introducing relativistic analogs of Ahlrichs double- and triple-ζ basis sets (ZORA-def2-SVP for hydrogen and carbon atoms). The calculated D values were slightly lower than those resulting from non-relativistic calculations, but their absolute values are still significantly larger than those derived from magnetometry (ESI† Tables S10 and S11).
We investigated the impact of the pyridine nitrogen atoms on the electronic structure and magnetic anisotropy of compounds 1 and 2 by replacing the 6-methyl-pyridine groups with phenyl rings. Using DFT calculations (B3LYP and def2-SVP in ORCA 5.0) we optimized the positions of these new groups while keeping the positions of other atoms fixed, resulting in the 1′ and 2′ input structures. This method allowed us to maintain the ligand field strength and symmetry from the regular donor atoms ({NO}2) while eliminating any influence of the pyridine nitrogen atoms. The CASSCF-NEVPT2 calculations for 1 and 2 yielded very similar ligand field term structures as in 1 and 2. However, the energy of the lowest quartet was found to be lower in 1 and 2 compared to 1 and 2 (ESI† Fig. S23–S25). The resulting ZFS parameters are different from those obtained for 1 and 2; the |D| values were found to be larger (−40.3 cm−1 for 1 and −38.1 cm−1 for 2) while the E/D values were significantly lower (E/D = 0.055 in 1, 0.039 in 2).
Thus, the anisotropy of 1 and 2 is larger and less rhombic than calculated for 1 and 2. The larger |D| values can be explained by the d-orbital splitting. Despite having the same splitting pattern and similar orbital energies as 1 and 2, the observed changes in 1 and 2 are most pronounced for the dxy orbital, which experiences the greatest decrease in energy (ESI† Fig. S25). This aligns with the orientation of this orbital in relation to the position of the pyridyl rings. In 1 and 2, the pyridyl nitrogen atoms point towards the lobes of the dxy orbital (ESI† Fig. S25). However, in 1 and 2, the orientation of the orbital remains unchanged even without the pyridyl nitrogen atoms. It is worth noting that the decrease of the dxy energy is larger in 2 than in 1 which correlates with the shorter Co⋯N distance (and thus larger destabilization of dxy) in 2 (2.6592(9) Å) than in 1 (2.6901(11) Å). As a result, the lower energy of the dxy orbital leads to a smaller dx2–y22 → dxy1 excitation, resulting in larger |D| values. In summary, the CASSCF-NEVPT2 calculations revealed that while the interaction between the Co(II) atom and pyridyl nitrogen atoms does not induce significant changes in the overall ligand field, the interaction between the dxy orbital and lone pairs of the nitrogen atoms produce smaller |D| values in complexes with the Co⋯N interactions.
The magnetization blocking barriers in 1 and 2 were calculated using the SINGLE_ANISO module107 incorporated in ORCA 5.0.58 The results strongly indicate that quantum tunneling is the dominant relaxation process since the matrix element of the transversal magnetic moment between the ground states with opposite magnetizations is greater than 0.1 (0.23 for 1, 0.18 for 2, ESI† Fig. S26). Therefore, it is expected that 1 and 2 will behave as field-induced SIMs. Notably, changing the basis from non-relativistic to relativistic (def2-TZVP vs. ZORA-def2-TZVP) did not affect the matrix elements of any of the calculated magnetic moments (ESI† Fig. S26).
Further analysis of the magnetic properties of 1 was performed by HF-ESR. Although measurements were taken on compounds 1 and 2 both in powder form and deposited on graphene, only the powder spectra of 1 showed satisfactory results. HF-ESR measurements on the deposited compounds on graphene did not show a clear signal due to the low deposited amounts, as evidenced in the ESI† Fig. S30 for compound 1. Fig. 3b and c show the HF-ESR powder spectra of 1 at different frequencies and temperatures, respectively. (HF-ESR spectra at other frequencies are shown in the ESI† Fig. S28.) From the temperature-dependent spectra, we observed strong thermally-activated transitions ascribed to the S = 1/2 doublet, indicated by green stars in the spectra, confirming that the ground state has spin 3/2, and thus D is negative. Nevertheless, transitions between the ground-state S = 3/2 and the excited state S = 1/2 were not observed in the energy range accessible in our experiments. Therefore, we set a bound for the ZFS such that the mentioned transition does not appear in the simulated spectrum, being equal to |D| > 600 GHz = 20 cm−1. Simulations with the parameters gx = 2.20, gy = 2.15, gz = 2.40, D = −20 cm−1, E/D = 0.122, and an exchange term J = −0.3 cm−1 reproduce most of the spectral features successfully and suggest intermolecular antiferromagnetic coupling, in agreement with BS-DFT calculations (JY = −0.247 cm−1, B3LYP-NL method), and similar to the one found by DC magnetometry (J = −0.19 cm−1). The ZFS parameters g-factors are in agreement with the ones calculated for 1 in bulk configuration by CASSCF-NEVPT2, as shown in Section 3.4 and Table 3. Although weak, the exchange coupling has a noticeable effect on the HF-ESR spectra, since it is responsible for the emergence of a second peak in the low magnetic field region (the first two peaks in the simulated spectra of Fig. 3b). The separation between those peaks indicates the strength of the exchange coupling, such that at J = 0 there is only one peak in the low magnetic field region. Of the spectral features not captured in the simulation, the ones indicated by black crosses correspond to a signal coming from the mirror in the sample holder, while for the ones indicated by red dots, we do not have a conclusive explanation. From the simulations, we can infer that they do not come from plausible values of the spin Hamiltonian parameters for compound 1.
To probe the slow relaxation of magnetization behavior in 1 and 2, the AC susceptibility was measured at low temperatures (see the ESI† Section S7 for a detailed experimental description of AC susceptibility measurements and data analysis). At 2 K, a static magnetic field (BDC) scan revealed the absence of an out-of-phase signal χ′′ at BDC = 0 T for both compounds (ESI† Tables S13, S21 and Fig. S31, S35), which is a consequence of fast relaxation of magnetization resulting from the quantum tunneling (QT) effect induced by hyperfine interactions with nuclear spins. However, the applied BDC field suppressed the tunneling, allowing us to map the AC susceptibility and find the optimal BDC field for further temperature-dependent dynamic magnetic investigations. The frequency-dependent in-phase χ′′ and out-of-phase χ′′ components of the AC susceptibility were satisfactorily fitted to the extended one-set Debye model (ESI† eqn. (S1), (S2), Tables S13, S21 and Fig. S31, S35), by which the isothermal χT and adiabatic χS susceptibilities along with the relaxation time τ (Fig. 4a) and its distribution parameter α were determined at given BDC fields.
The global relaxation rate τ−1 is usually described by Orbach, Raman, direct, and QT relaxation processes as follows:
 | (5) |
At very low temperatures (i.e. at 2 K), the Raman, direct or QT terms of eqn (5) usually participate in the relaxation of magnetization; therefore, the τ vs. BDC dependencies for both compounds were analyzed with the respective combinations of direct & QT or direct & Raman mechanisms. No combination of these mechanisms was appropriate for the τ vs. BDC analysis of 1 (ESI† Fig. S31d and Table S16), while a combination of direct & Raman processes gave satisfactory results in the low field region 0–0.1 T of 2 (ESI† Fig. S35d and Table S24).
The longest relaxation times were observed at BDC = 0.06 T for 1 and BDC = 0.09 T for 2 (Fig. 4a) and these static fields were used for further temperature-dependent dynamic magnetic studies. Additionally, slightly higher static fields (BDC = 0.09 T for 1 and BDC = 0.125 T for 2) were used to record the same acquisition of dynamic magnetic measurements upon the change of temperature, enabling a comprehensive analysis of the slow relaxation of magnetization in both investigated SIMs (vide infra). Frequency-dependent in-phase (χ′) and out-of-phase (χ′′) components of the magnetic susceptibility measured as a function of the frequency of an alternating magnetic field, BAC, for a set of temperatures (1.9–4.9 K for 1 and 1.9–4.1 K for 2; ESI† Fig. S32, S33, S36, S37 and Tables S14, S15, S22, S23) suggest a single relaxation channel. The out-of-phase components χ′′ for 1 and 2 show the maximum shift from 69 Hz (at 1.9 K and 0.06 T, τ ≈ 2.3 ms) and from 106 Hz (at 1.9 K and 0.09 T, τ ≈ 1.5 ms), respectively, towards higher frequencies upon a temperature increase (ESI† Tables S14, S15, S22 and S23). This indicates a typical feature of SMMs – the maxima of χ′′ are frequency and temperature dependent, and the relaxation time τ shortens as the temperature increases. The temperature-dependent AC susceptibility measurements were fitted using an extended one-set Debye model (ESI† eqn (S1) and (S2)), which enabled us to obtain the relaxation time τ at the corresponding temperatures and static magnetic fields. The analysis of temperature dependencies lnτ vs. 1/T at a given BDC was carried out with respect to various combinations of relaxation processes involved in the following relaxation equation:
 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1/T functions at two static BDC fields. Thus, two ln
τ vs. 1/T functions at two static BDC fields. Thus, two ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1/T dependencies recorded at 0.06 and 0.08 T for 1 and at 0.09 and 0.125 T for 2 were simultaneously analyzed using combinations of various relaxation mechanisms. The most accurate fits involve the combination of Orbach, direct, and QT processes for each compound (Fig. 4b, c and ESI† Tables S19, S27). The Orbach energy barriers (Ueff) and relaxation time at infinite temperature (τ0) are comparable to the previously reported tetracoordinated Co(II) field-induced SIMs with a similar degree of tetrahedral distortion and magnetic anisotropy (see the ESI† Table S28 for a comparison with similar compounds in other studies). Furthermore, the obtained relaxation parameters suggest that the presence of methyl substituents introduced on the tridentate Schiff base ligand accelerates the slow relaxation of magnetization governed via QT and Orbach relaxation, while the direct relaxation seems to be unaffected by such subtle structural variation. Table 1 summarizes the main results from the AC susceptibility analysis.
τ vs. 1/T dependencies recorded at 0.06 and 0.08 T for 1 and at 0.09 and 0.125 T for 2 were simultaneously analyzed using combinations of various relaxation mechanisms. The most accurate fits involve the combination of Orbach, direct, and QT processes for each compound (Fig. 4b, c and ESI† Tables S19, S27). The Orbach energy barriers (Ueff) and relaxation time at infinite temperature (τ0) are comparable to the previously reported tetracoordinated Co(II) field-induced SIMs with a similar degree of tetrahedral distortion and magnetic anisotropy (see the ESI† Table S28 for a comparison with similar compounds in other studies). Furthermore, the obtained relaxation parameters suggest that the presence of methyl substituents introduced on the tridentate Schiff base ligand accelerates the slow relaxation of magnetization governed via QT and Orbach relaxation, while the direct relaxation seems to be unaffected by such subtle structural variation. Table 1 summarizes the main results from the AC susceptibility analysis.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1/T at the corresponding BDC fields. Comprehensive fitting analysis of ln
τ vs. 1/T at the corresponding BDC fields. Comprehensive fitting analysis of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. 1/T involves simultaneous fittings at two BDC fields
τ vs. 1/T involves simultaneous fittings at two BDC fields
| Compound, Model | U (K) | τ 0 (ns) | τ QTM (ms) | a (Tm K s)−1 |
|---|---|---|---|---|
| m | ||||
| a For data in the range 3.5–4.7 K. b At 0.06 T and 0.08 T. c For data in the range 3.3–4.1 K. d At 0.09 T and 0.125 T. | ||||
| 1, Orbacha at 0.06 T | 40 | 12 | — | — |
| — | ||||
| 1, Orbacha at 0.08 T | 40 | 11 | — | — |
| — | ||||
| 1, Orbach & direct & QTb | 48.2 | 2.0 | 2 | 4 × 104 |
| 4 (fixed) | ||||
| 2, Orbachc at 0.09 T | 38 | 4 | — | — |
| — | ||||
| 2, Orbachc at 0.125 T | 36 | 8 | — | — |
| — | ||||
| 2, Orbach & direct & QTd | 41 | 2.2 | 1.3 | 4 × 104 |
| 4 (fixed) | ||||
3.3 Deposition and charge transfer
Depositions on CVD graphene on Si/SiO2 by drop-cast and thermal sublimation were performed to test the stability of both compounds. Optical images of deposited compounds 1 and 2 can be seen in Fig. 5a and Fig. S7, S14 (ESI†). The topography of both samples was investigated by AFM (Fig. 5(b, c) and Fig. S7, S14, ESI†), revealing that drop-cast depositions led to the formation of crystals a few micrometers high, while thermal sublimation resulted in islands with heights up to 150 nm for 1 (Fig. 5c), and 50 nm for 2 (ESI† Fig. S13). Raman spectroscopy and XPS confirmed that the chemical identity of the molecules was preserved upon the deposition by both drop-cast and thermal sublimation, a detailed comparison of XPS and Raman spectroscopy on the deposited samples with a bulk reference is found in the ESI† Sections S3 and S4. Raman spectra revealed a consistent shift of graphene's 2D peak (∼2690 cm−1) towards lower energy values after the deposition of both compounds (Fig. 5d and ESI† Fig. S8, S15), which, considering that graphene was initially p-doped due to the contact with impurities under ambient conditions, suggests n-doping of graphene arising from electron transfer from the compounds.108,109 n-Doping was further confirmed in transport measurements on samples deposited on graphene field-effect transistors (GFETs). To assess the charge transfer characteristics, 1 and 2 were drop-cast onto GFETs, following the procedure in the ESI† Section S8. The conductance through the devices was monitored as the gate voltage was varied from zero to 100 V, as shown in Fig. 5e and Fig. S39 (ESI†). As fabricated, the charge neutrality point (conductivity minimum) of the devices was approximately 95 V. With 2 deposited, the charge neutrality point shifted by −23 V, indicating significant electron transfer to the graphene. Charge transfer was less apparent in devices coated with 1 (ESI† Fig. S39). The charge transfer effect may be much weaker with 1, or a lower coverage of the devices may have muted the effect.3.4 Theoretical calculations of molecular deposition and their magnetic properties
To simulate the molecular adsorption on graphene, we followed the procedure described in Section 2.2. For each molecular complex, we considered four different molecule orientations relative to the graphene substrate, based on the possible enhancement of hydrogen–carbon and carbon–carbon interactions between the molecule and substrate, as shown in Fig. 6a–d and f–i. Then, the molecules in each configuration were placed on top of the substrate, such that the ground state energy of the whole system was calculated, but without performing ionic relaxation. By varying the relative distance between the molecule and substrate, we generated the energy profiles in Fig. 6e and j for each configuration. The presence of energy minima in the profiles confirms that there is an attractive interaction between the molecule and substrate, which allows estimating the equilibrium distance of each system. We performed a third-degree polynomial fit to each curve to estimate the equilibrium distances, deq, and the results are found in Table 2. The distance between molecule and substrate was defined as the distance between the closest H atom to the graphene plane. We found that the equilibrium distances are in the range 2.50–2.72 Å for 1, and 2.24–2.65 Å for 2.| System | d eq (Å) | E bin (eV) | d Co1–N1 (Å) | d Co1–N2 (Å) | d Co1–O1 (Å) | ΔEHOMO–LUMO (eV) | Δq (e−) | μ (μB) |
|---|---|---|---|---|---|---|---|---|
| 1 XRD (exp.) | — | — | 1.991 | 2.691 | 1.953 | 0.64 | — | 3.000 |
| 1 Isolated, DFT relax. | — | — | 1.954 | 2.860 | 1.918 | 0.85 | — | 3.000 |
| 1 Conf. 1 | 2.61 | −0.83 | 1.955 | 2.856 | 1.917 | 0.76 | 0.065 | 3.078 |
| 1 Conf. 2 | 2.59 | −0.70 | 1.957 | 2.858 | 1.917 | 0.73 | 0.003 | 3.006 |
| 1 Conf. 3 | 2.50 | −0.73 | 1.955 | 2.816 | 1.917 | 0.76 | 0.056 | 3.075 |
| 1 Conf. 4 | 2.72 | −1.08 | 1.955 | 2.811 | 1.919 | 0.74 | 0.016 | 3.020 |
| 2 XRD (exp.) | — | — | 1.992 | 2.695 | 1.961 | 0.65 | — | 3.000 |
| 2 Isolated, DFT relax. | — | — | 1.954 | 2.776 | 1.918 | 0.84 | — | 3.000 |
| 2 Conf. 1 | 2.56 | −0.90 | 1.955 | 2.768 | 1.921 | 0.75 | 0.084 | 3.099 |
| 2 Conf. 2 | 2.65 | −0.92 | 1.955 | 2.782 | 1.917 | 0.74 | 0.014 | 3.020 |
| 2 Conf. 3 | 2.54 | −0.80 | 1.954 | 2.772 | 1.917 | 0.76 | 0.078 | 3.095 |
| 2 Conf. 4 | 2.24 | −1.15 | 1.957 | 2.768 | 1.921 | 0.73 | 0.033 | 3.045 |
To determine the binding energies and equilibrium geometries of the molecules on graphene, we positioned the molecule in each configuration at the equilibrium distance and performed ionic relaxation of all ions (molecule and substrate) by plane-wave DFT. After obtaining the relaxed structure, we took the resulting molecule and substrate separately and computed a DFT self-consistent cycle for each of them to obtain the total energy of the individual systems. In this procedure, the binding energies were computed as
| Ebin = Emol+subs − Emol − Esubs, | (7) |
We now study the changes in the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO, respectively) after deposition. In the bulk structure and isolated, DFT-relaxed molecules, the HOMO–LUMO gap (ΔEHOMO–LUMO) was obtained from the total density of states (DOS), while in the molecule + substrate system, it was obtained from the partial density of states (PDOS), selecting only the molecule's electronic orbitals. Fig. 7a shows a comparison between the DOS of 1 in the bulk structure and the PDOS of graphene and molecule in Conf. 1 after deposition (ESI† Fig. S43 and S43 show the PDOS of all systems). The results of the HOMO–LUMO gap, shown in Table 2, indicate a noticeable change in the quantity in all considered systems. In particular, graphene affects the HOMO–LUMO gap of the deposited molecules, decreasing it by around 0.1 eV, considering that the initial system for plane-wave DFT calculations of molecular adsorption was the isolated, DFT relaxed molecules, which have a HOMO–LUMO gap of 0.85 eV and 0.84 eV for 1 and 2, respectively. In Fig. 7a, we observe a depopulation of the molecules HOMO after deposition, leading to a population of graphene conduction bands and consequently, to n-doping of graphene. This is consistent in all studied configurations of both molecular complexes, as shown in the ESI† Fig. S43 and S44. Transport measurements (Fig. 5e and Fig. S39, ESI†) and Raman spectroscopy (Fig. 5d and ESI† Fig. S8, S15) confirmed electron transfer from the molecule to graphene, leading to n-doping of graphene.
To obtain a better understanding of the electron transfer behavior between the molecule and substrate, we performed Bader charge analysis81 as implemented by Henkelman et al.110,111 The results, shown in Table 2 for each configuration, indicate a consistent electron transfer from molecule to substrate, in agreement with the results from DOS analysis. Although such electron transfer is below 0.1 e−, it is observed that it has a direct effect in increasing the total magnetization of the system, compared to a value of 3.00 μB for isolated molecules, corresponding to three unpaired electrons of Co(II). The increase in magnetization is consistent with electron transfer from the molecule's HOMO to graphene, which has spin-down polarization as observed in Fig. 7a, and consequently, increasing the spin polarization of the molecules charge density (difference between spin up and spin down charge densities).
To analyze further the charge transfer behavior, we computed the charge density difference, defined as
| Δρ = ρmol+subs − ρmol − ρsubs, | (8) |
We focus now on the ZFS terms and g-factors of the deposited structures, as calculated by CASSCF-NEVPT2 in ORCA 4.2.1. The results are summarized in Table 2. In all systems, we obtained a negative D, in agreement with DC magnetometry and HF-ESR measurements. Additionally, the calculations suggest an anisotropy of the g-factors before and after adsorption. Overall, a discrepancy between the calculated parameters for the bulk structures and the deposited configurations is found, which is more evident in the ZFS terms D and E. This result is a direct consequence of the geometrical changes in the molecule in the gas phase after DFT relaxation. Furthermore, the parameters of the isolated and adsorbed molecules are practically the same in both compounds due to the negligible geometrical change after deposition.
| System | D (cm−1) | E/D | g x | g y | g z | g iso |
|---|---|---|---|---|---|---|
| a CASSCF-NEVPT2 def2-TZVP method in ORCA 5.0. b CASSCF-NEVPT2 def2-TZVP method in ORCA 4.2.1. | ||||||
| 1 XRD (exp.)a | −25.3 | 0.084 | 2.185 | 2.126 | 2.462 | 2.258 |
| 1 Isolatedb | −18.5 | 0.009 | 2.139 | 2.141 | 2.368 | 2.216 |
| 1 Conf. 1 | −18.5 | 0.011 | 2.139 | 2.142 | 2.368 | 2.216 |
| 1 Conf. 2b | −18.6 | 0.014 | 2.139 | 2.143 | 2.370 | 2.217 |
| 1 Conf. 3b | −18.4 | 0.010 | 2.139 | 2.141 | 2.367 | 2.216 |
| 1 Conf. 4 | −18.4 | 0.016 | 2.139 | 2.144 | 2.368 | 2.217 |
| 1 HF-ESR | <−20 | 0.122 | 2.20 | 2.15 | 2.40 | 2.25 |
| 1 DC magn | −15.3 | 0.012 | — | — | — | 2.272 |
| 2 XRD (exp.)a | −28.3 | 0.107 | 2.201 | 2.119 | 2.501 | 2.274 |
| 2 Isolatedb | −18.2 | 0.040 | 2.129 | 2.152 | 2.364 | 2.215 |
| 2 Conf. 1 | −18.9 | 0.030 | 2.131 | 2.151 | 2.373 | 2.218 |
| 2 Conf. 2b | −18.5 | 0.033 | 2.131 | 2.151 | 2.368 | 2.217 |
| 2 Conf. 3b | −18.4 | 0.038 | 2.129 | 2.152 | 2.367 | 2.216 |
| 2 Conf. 4 | −19.2 | 0.034 | 2.131 | 2.152 | 2.378 | 2.220 |
| 2 DC magn. | −17.5 | 0.044 | — | — | — | 2.213 |
4 Conclusions and outlook
We have presented a theoretical and experimental study on the structure, stability, magnetic properties, and deposition properties on graphene of compounds 1 and 2. DFT calculations and analysis of the topology of the electron density by QT-AIM confirmed that the Co center and the pyridyne nitrogens N2 interact through attractive non-covalent interactions, thus exhibiting a semi-coordination character. We claim that such interaction is the source of the stability of the complexes under ambient conditions and after deposition on graphene, as confirmed by XPS and Raman spectroscopy. DC magnetometry showed that the compounds present an axial magnetic anisotropy, with an axial ZFS term of D = − 15.3 cm−1 and − 17.5 cm−1 for 1 and 2, respectively, while HF-ESR set the bound |D| > 20 cm−1 on compound 1. Both experimental methods confirm a weak intermolecular antiferromagnetic exchange interaction, in agreement with BS-DFT predictions. Dynamic magnetic investigations confirmed that the compounds are field-induced SIMs with maximum relaxation times of 2.3 ms (at 0.06 T, 1.9 K) and 1.5 ms (at 0.09 T, 1.9 K) for 1 and 2, respectively. Theoretical modeling of the compounds on graphene by DFT shows an attractive interaction between them with a relatively small binding energy, with the highest one (in absolute value) corresponding to −1.15 eV per molecule for compound 2 in Conf. 4. DOS and charge transfer analysis revealed an electron transfer from the molecule's HOMO to graphene, confirmed by transport measurements on GFETs and Raman spectroscopy, which increases the molecules’ magnetic moment due to an increase in their spin density. This suggests the possibility of tuning the molecule's magnetic moment by electrostatic gating of the graphene substrate, which could be done by depositing them directly onto graphene quantum dot bolometers,54,55 taking advantage of their high sensitivity that enables an in situ spectroscopic investigation.Author contributions
Writing original draft preparation, plane-wave DFT, CASSCF-NEVPT2 calculations, J. N. G.; writing original draft preparation, XPS, depositions, J. H.; AFM, Raman, and depositions, Š. V.; chemical synthesis and analytical characterization of ligand and complex, O. F. F.; DC magnetometry experiments and preliminary analysis, L. H.; deposition on GFETs, transport measurements, D. H.; GFETs fabrication, S. d. S.; BS-DFT, CASSCF-NEVPT2 calculations, R. H.; graphene sample preparation, M. B.; AC magnetometry analysis, writing original draft preparation, I. Š.; HF-ESR experiments and analysis, V. T. S.; transport measurements, GFETs fabrication, supervision, P. B.; XRD analysis, DFT-topology and ELF calculations, DC magnetometry analysis, writing review and editing, I. N.; supervision, P. N. All authors have agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the projects and grant agencies that supported this work. O. F. F., R. H., and I. N. acknowledge support from the Grant Agency of the Czech Republic (GAČR 23-07175S); J. N. G. acknowledges the Grant Agency of the Czech Republic (GAČR 23-05578S), a student grant of the Brno University of Technology (CEITEC-J-21-7508), and the Brno PhD Talent Scholarship – Funded by the Brno City Municipality; J. N. G., J. H., and L. H. acknowledge the MEYS CR INTER-EXCELLENCE Programme (grant LTAUSA19060); O. F. F. acknowledges Palacky University's student grant DSGC-2021-0032 financed from the funds of the Operational Program Research, Development and Education under the project “Improving schematics of Doctoral student grant competition and their pilot implementation”, Reg. No. CZ.02.2.69/0.0/0.0/19_ 073/0016713; M. B. acknowledges funding from the ESF under the project CZ.02.2.69/0.0/0.0/20_079/0017436; I. Š. acknowledges the grants from Slovak grant agencies DS-FR-22-0010, APVV-22-0172, APVV-19-0087, VEGA 1/0029/22; V. T. S. acknowledges funding from the EXPRO grant of the Grant Agency of the Czech Republic (GAČR 21-20716X); P. N. acknowledges the ERC Starting Grant (No. 714850) under the European Unions Horizon 2020 Research and Innovation Program. J. N. G., J. H., Š. V., and L. H. gratefully acknowledge the CzechNanoLab Research Infrastructure supported by MEYS CR (LM2018110). This article was written thanks to generous support through the Operational Program Integrated Infrastructure for the project: “Strategic research in the field of SMART monitoring, treatment and preventive protection against coronavirus (SARS-CoV-2)”, Project No. 313011ASS8, co-financed by the European Regional Development Fund.Notes and references
- D. Tanaka, N. Aketa, H. Tanaka, S. Horike, M. Fukumori, T. Tamaki, T. Inose, T. Akai, H. Toyama, O. Sakata, H. Tajiri and T. Ogawa, Dalton Trans., 2019, 48, 7074–7079 RSC.
- A. Ardavan, O. Rival, J. J. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed.
- M. Urdampilleta, S. Klyatskaya, J. P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506 CrossRef CAS PubMed.
- E. Coronado, Nat. Rev. Mat., 2020, 5, 87–104 CrossRef.
- J. Dugay, M. Aarts, M. Gimenez-Marqués, T. Kozlova, H. W. Zandbergen, E. Coronado and H. S. Van Der Zant, Nano Lett., 2017, 17, 186–193 CrossRef CAS PubMed.
- T. S. Rahman, R. S. Berkley, Z. Hooshmand, T. Jiang, D. Le and A. F. Hebard, J. Phys. Chem. C, 2020, 124, 28186–28200 CrossRef.
- R. J. Holmberg and M. Murugesu, J. Mater. Chem. C, 2015, 3, 11986–11998 RSC.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. Van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319 CrossRef CAS PubMed.
- F. Yang, Q. Zhou, Y. Zhang, G. Zeng, G. Li, Z. Shi, B. Wang and S. Feng, Chem. Commun., 2013, 49, 5289–5291 RSC.
- T. Wu, Y. Q. Zhai, Y. F. Deng, W. P. Chen, T. Zhang and Y. Z. Zheng, Dalton Trans., 2019, 48, 15419–15426 RSC.
- M. Böhme, S. Ziegenbalg, A. Aliabadi, A. Schnegg, H. Görls and W. Plass, Dalton Trans., 2018, 47, 10861–10873 RSC.
- S. Vaidya, P. Shukla, S. Tripathi, E. Rivière, T. Mallah, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2018, 57, 3371–3386 CrossRef CAS PubMed.
- Y. Q. Zhai, Y. F. Deng and Y. Z. Zheng, Dalton Trans., 2018, 47, 8874–8878 RSC.
- T. Jurca, A. Farghal, P. H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814–15817 CrossRef CAS PubMed.
- I. Nemec, H. Liu, R. Herchel, X. Zhang and Z. Trávnícek, Synth. Met., 2016, 215, 158–163 CrossRef CAS.
- R. Ruamps, L. J. Batchelor, R. Guillot, G. Zakhia, A. L. Barra, W. Wernsdorfer, N. Guihéry and T. Mallah, Chem. Sci., 2014, 5, 3418–3424 RSC.
- D. Schweinfurth, J. Krzystek, M. Atanasov, J. Klein, S. Hohloch, J. Telser, S. Demeshko, F. Meyer, F. Neese and B. Sarkar, Inorg. Chem., 2017, 56, 5253–5265 CrossRef CAS PubMed.
- D. Schweinfurth, M. G. Sommer, M. Atanasov, S. Demeshko, S. Hohloch, F. Meyer, F. Neese and B. Sarkar, J. Am. Chem. Soc., 2015, 137, 1993–2005 CrossRef CAS PubMed.
- F. El-Khatib, B. Cahier, F. Shao, M. López-Jordà, R. Guillot, E. Rivière, H. Hafez, Z. Saad, J. J. Girerd, N. Guihéry and T. Mallah, Inorg. Chem., 2017, 56, 4601–4608 CrossRef PubMed.
- J. Juráková, J. Dubnická Midlíková, J. Hrubý, A. Kliuikov, V. T. Santana, J. Pavlik, J. Moncol, E.
![[C with combining breve]](https://www.rsc.org/images/entities/char_0043_0306.gif) ižmár, M. Orlita, I. Mohelský, P. Neugebauer, D. Gentili, M. Cavallini and I. Šalitroš, Inorg. Chem. Front., 2022, 9, 1179–1194 RSC.
ižmár, M. Orlita, I. Mohelský, P. Neugebauer, D. Gentili, M. Cavallini and I. Šalitroš, Inorg. Chem. Front., 2022, 9, 1179–1194 RSC. - V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795 CrossRef CAS PubMed.
- A. A. Pavlov, Y. V. Nelyubina, S. V. Kats, L. V. Penkova, N. N. Efimov, A. O. Dmitrienko, A. V. Vologzhanina, A. S. Belov, Y. Z. Voloshin and V. V. Novikov, J. Phys. Chem. Lett., 2016, 7, 4111–4116 CrossRef CAS PubMed.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef CAS PubMed.
- T. J. Ozumerzifon, I. Bhowmick, W. C. Spaller, A. K. Rappé and M. P. Shores, Chem. Commun., 2017, 53, 4211–4214 RSC.
- B. Yao, Y. F. Deng, T. Li, J. Xiong, B. W. Wang, Z. Zheng and Y. Z. Zhang, Inorg. Chem., 2018, 57, 14047–14051 CrossRef CAS PubMed.
- Y. Y. Zhu, C. Cui, Y. Q. Zhang, J. H. Jia, X. Guo, C. Gao, K. Qian, S. D. Jiang, B. W. Wang, Z. M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806 RSC.
- B. Yao, M. K. Singh, Y. F. Deng, Y. N. Wang, K. R. Dunbar and Y. Z. Zhang, Inorg. Chem., 2020, 59, 8505–8513 CrossRef CAS PubMed.
- J. M. Frost, K. L. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC.
- J. Juráková and I. Šalitroš, Monatsh. Chem., 2022, 153, 1001–1036 CrossRef PubMed.
- J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734 CrossRef CAS PubMed.
- E. A. Suturina, J. Nehrkorn, J. M. Zadrozny, J. Liu, M. Atanasov, T. Weyhermüller, D. Maganas, S. Hill, A. Schnegg, E. Bill, J. R. Long and F. Neese, Inorg. Chem., 2017, 56, 3102–3118 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209–217 CrossRef CAS.
- S. Vaidya, S. Tewary, S. K. Singh, S. K. Langley, K. S. Murray, Y. Lan, W. Wernsdorfer, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2016, 55, 9564–9578 CrossRef CAS PubMed.
- M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716–10721 CrossRef CAS PubMed.
- Y. Rechkemmer, F. D. Breitgoff, M. Van Der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. Van Slageren, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- S. Ziegenbalg, D. Hornig, H. Görls and W. Plass, Inorg. Chem., 2016, 55, 4047–4058 CrossRef CAS PubMed.
- X. N. Yao, M. W. Yang, J. Xiong, J. J. Liu, C. Gao, Y. S. Meng, S. D. Jiang, B. W. Wang and S. Gao, Inorg. Chem. Front., 2017, 4, 701–705 RSC.
- J. Hrubý, Š. Vavre
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ková, L. Masaryk, A. Sojka, J. Navarro-Giraldo, M. Bartoš, R. Herchel, J. Moncol, I. Nemec and P. Neugebauer, Molecules, 2020, 25, 5021 CrossRef PubMed.
ková, L. Masaryk, A. Sojka, J. Navarro-Giraldo, M. Bartoš, R. Herchel, J. Moncol, I. Nemec and P. Neugebauer, Molecules, 2020, 25, 5021 CrossRef PubMed. - J. Hrubý, D. Dvo
![[r with combining breve]](https://www.rsc.org/images/entities/char_0072_0306.gif) ák, L. Squillantini, M. Mannini, J. Van Slageren, R. Herchel, I. Nemec and P. Neugebauer, Dalton Trans., 2020, 49, 11697–11707 RSC.
ák, L. Squillantini, M. Mannini, J. Van Slageren, R. Herchel, I. Nemec and P. Neugebauer, Dalton Trans., 2020, 49, 11697–11707 RSC. - I. Nemec, O. F. Fellner, L. Havlí
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ek and R. Herchel, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C344 Search PubMed.
ek and R. Herchel, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77, C344 Search PubMed. - L. Xu, Y. V. Mironov, X. Qi and S. J. Kim, J. Struct. Chem., 2006, 47, 998–1001 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr. B, 2016, 72, 171–179 CrossRef CAS PubMed.
- Z. M. Efimenko, A. S. Novikov, D. M. Ivanov, A. V. Piskunov, A. A. Vereshchagin, O. V. Levin, N. A. Bokach and V. Y. Kukushkin, Inorg. Chem., 2020, 2316–2327 CrossRef CAS PubMed.
- I. V. Ananyev, N. A. Bokach and V. Y. Kukushkinc, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 436–449 CrossRef CAS PubMed.
- L. J. Bourhis, O. V. Dolomanov, R. J. Gildea, J. A. Howard and H. Puschmann, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 59–75 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- X. Du, I. Skachko, E. Y. Andrei and A. Barker, Nat. Nanotechnol., 2008, 3, 491–495 CrossRef CAS PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- J. H. Seol, I. Jo, A. L. Moore, L. Lindsay, Z. H. Aitken, M. T. Pettes, X. Li, Z. Yao, R. Huang, D. Broido, N. Mingo, R. S. Ruoff and L. Shi, Science, 2010, 328, 213–216 CrossRef CAS PubMed.
- P. Neugebauer, M. Orlita, C. Faugeras, A. L. Barra and M. Potemski, Phys. Rev. Lett., 2009, 103, 136403 CrossRef CAS PubMed.
- A. El Fatimy, R. L. Myers-Ward, A. K. Boyd, K. M. Daniels, D. K. Gaskill and P. Barbara, Nat. Nanotechnol., 2016, 11, 335–338 CrossRef CAS PubMed.
- L. S. Marie, A. El Fatimy, J. Hrubý, I. Nemec, J. Hunt, R. Myers-Ward, D. K. Gaskill, M. Kruskopf, Y. Yang, R. Elmquist, R. Marx, J. van Slageren, P. Neugebauer and P. Barbara, J. Phys. Mater., 2020, 3, 014013 CrossRef.
- B. Zhan, C. Li, J. Yang, G. Jenkins, W. Huang and X. Dong, Small, 2014, 10, 4042–4065 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, e1327 CrossRef.
- F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12, e1606 CrossRef.
- P. Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- F. Kleemiss, O. V. Dolomanov, M. Bodensteiner, N. Peyerimhoff, L. Midgley, L. J. Bourhis, A. Genoni, L. A. Malaspina, D. Jayatilaka, J. L. Spencer, F. White, B. Grundkötter-Stock, S. Steinhauer, D. Lentz, H. Puschmann and S. Grabowsky, Chem. Sci., 2021, 12, 1675–1692 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- Molecular Electronic Structures of Transition Metal Complexes II, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 143 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. M. Hossain, S. Kamilya, S. Ghosh, R. Herchel, M. A. Kiskin, S. Mehta and A. Mondal, Cryst. Growth Des., 2023, 11, 42 Search PubMed.
- L. Havlí
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ek, R. Herchel, I. Nemec and P. Neugebauer, Polyhedron, 2022, 223, 115962 CrossRef.
ek, R. Herchel, I. Nemec and P. Neugebauer, Polyhedron, 2022, 223, 115962 CrossRef. - A. N. Gusev, I. Nemec, R. Herchel, Y. I. Baluda, M. A. Kryukova, N. N. Efimov, M. A. Kiskin and W. Linert, Polyhedron, 2021, 196, 115017 CrossRef CAS.
- A. Bhanja, L. Smythe, R. Herchel, I. Nemec, M. Murrie and D. Ray, Dalton Trans., 2021, 50, 5023–5035 RSC.
- B. Rybní
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) ková, J. Kuchár, P. Antal and R. Herchel, Inorg. Chim. Acta, 2020, 509, 119689 CrossRef.
ková, J. Kuchár, P. Antal and R. Herchel, Inorg. Chim. Acta, 2020, 509, 119689 CrossRef. - I. Šalitroš, R. Herchel, O. Fuhr, R. González-Prieto and M. Ruben, Inorg. Chem., 2019, 58, 4310–4319 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1994 Search PubMed.
- T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Computational Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154709 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080 CrossRef CAS PubMed.
- G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- T. Lu and F. W. Chen, Acta Phys. Chim. Sin., 2011, 27, 2786–2792 CAS.
- Y. H. Chi, J. M. Shi, H. N. Li, W. Wei, E. Cottrill, N. Pan, H. Chen, Y. Liang, L. Yu, Y. Q. Zhang and C. Hou, Dalton Trans., 2013, 42, 15559–15569 RSC.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS.
- T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- E. Y. Misochko, A. V. Akimov, D. V. Korchagin, J. Nehrkorn, M. Ozerov, A. V. Palii, J. M. Clemente-Juan and S. M. Aldoshin, Inorg. Chem., 2019, 58, 16434–16444 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 64112 CrossRef CAS PubMed.
- J. Yan, Y. Zhang, P. Kim and A. Pinczuk, Phys. Rev. Lett., 2007, 98, 166802 CrossRef PubMed.
- A. C. Ferrari and D. M. Basko, Nat. Nanotechnol., 2013, 8, 235–246 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01426f |
| ‡ Present address: National High Magnetic Field Laboratory, Florida State University, 1800 E. Paul Dirac Drive Tallahassee, FL 32310, USA. |
| § Present address: Institute of Applied Physics, Abbe Center of Photonics, Friedrich Schiller University, Albert-Einstein-Str. 15, 07745 Jena, Germany. |
| This journal is © the Owner Societies 2023 |