Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
pH dependence of the assembly mechanism and properties of poly(L-lysine) and poly(L-glutamic acid) complexes†‡
Tuuva
Kastinen
 abc,
Dawid
Lupa
abc,
Dawid
Lupa
 de,
Piotr
Bonarek
de,
Piotr
Bonarek
 f,
Dmitrii
Fedorov
f,
Dmitrii
Fedorov
 cg,
Maria
Morga
cg,
Maria
Morga
 d,
Markus B.
Linder
d,
Markus B.
Linder
 cg,
Jodie L.
Lutkenhaus
cg,
Jodie L.
Lutkenhaus
 hi,
Piotr
Batys
hi,
Piotr
Batys
 *d and
Maria
Sammalkorpi
*d and
Maria
Sammalkorpi
 *acg
*acg
aDepartment of Chemistry and Materials Science, Aalto University, P.O. Box 16100, 00076 Aalto, Finland
bFaculty of Engineering and Natural Sciences, Chemistry & Advanced Materials, Tampere University, P.O. Box 541, 33014 Tampere University, Finland
cAcademy of Finland Center of Excellence in Life-Inspired Hybrid Materials (LIBER), Aalto University, P.O. Box 16100, 00076 Aalto, Finland. E-mail: maria.sammalkorpi@aalto.fi
dJerzy Haber Institute of Catalysis and Surface Chemistry, Polish Academy of Sciences, Niezapominajek 8, PL-30239 Krakow, Poland. E-mail: piotr.batys@ikifp.edu.pl
eJagiellonian University, Faculty of Physics, Astronomy, and Applied Computer Science, M. Smoluchowski Institute of Physics, Łojasiewicza 11, 30-348 Kraków, Poland
fDepartment of Physical Biochemistry, Faculty of Biochemistry, Biophysics and Biotechnology, Jagiellonian University, Gronostajowa 7, 30-387 Krakow, Poland
gDepartment of Bioproducts and Biosystems, Aalto University, P.O. Box 16100, 00076 Aalto, Finland
hArtie McFerrin Department of Chemical Engineering, Texas A&M University, College Station, Texas 77840, USA
iDepartment of Materials Science and Engineering, Texas A&M University, College Station, Texas 77840, USA
First published on 15th June 2023
Abstract
We show by extensive experimental characterization combined with molecular simulations that pH has a major impact on the assembly mechanism and properties of poly(L-lysine) (PLL) and poly(L-glutamic acid) (PGA) complexes. A combination of dynamic light scattering (DLS) and laser Doppler velocimetry (LDV) is used to assess the complexation, charge state, and other physical characteristics of the complexes, isothermal titration calorimetry (ITC) is used to examine the complexation thermodynamics, and circular dichroism (CD) is used to extract the polypeptides’ secondary structure. For enhanced analysis and interpretation of the data, analytical ultracentrifugation (AUC) is used to define the precise molecular weights and solution association of the peptides. Molecular dynamics simulations reveal the associated intra- and intermolecular binding changes in terms of intrinsic vs. extrinsic charge compensation, the role of hydrogen bonding, and secondary structure changes, aiding in the interpretation of the experimental data. We combine the data to reveal the pH dependency of PLL/PGA complexation and the associated molecular level mechanisms. This work shows that not only pH provides a means to control complex formation but also that the associated changes in the secondary structure and binding conformation can be systematically used to control materials assembly. This gives access to rational design of peptide materials via pH control.
1. Introduction
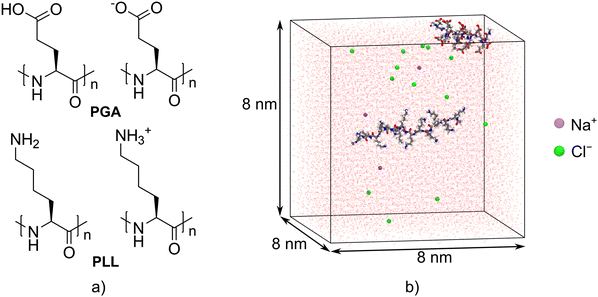
Polypeptides have attractive features, such as biocompatibility, biodegradability, and non-toxicity, which makes them ideal materials for a wide range of technological and scientific fields, e.g. pharmaceutics, tissue engineering, and biotechnology.1 Polypeptides are also stimuli-responsive, which enables the manipulation of their physical and chemical properties by adjusting external conditions, such as light, temperature, redox properties, and pH.2 In particular, the pH-responsivity of polypeptides has been exploited in designing tumor-targeting drug and gene delivery systems,3,4 antimicrobial materials,5–7 hydrogels,8 and wound dressings.9Anionic poly(L-glutamic acid) (PGA) and cationic poly(L-lysine) (PLL, see Fig. 1a) are ideal model polymers to probe pH-induced conformational changes of polypeptides and proteins.10 Due to ionizable functional groups in their side chains, i.e. carboxylic acid groups in PGA and amino groups in PLL, these polypeptides will become charged at certain pH values. The pKa values for PLL and PGA are 9.8511 and 4.3,12 respectively. As a consequence, pH affects the polypeptide's secondary structure. For instance, previous studies employing circular dichroism (CD),13–16 Fourier-transform infrared spectroscopy,15 and UV resonance Raman spectroscopy17 have shown that the secondary structures of PGA and PLL transfer from a random coil to helix when the pH is either decreased or increased from neutral states, respectively. The formation of β-sheet structures within PGA and PLL has also been reported.18–20
The relationship between the secondary structure and the pH has also been investigated for supramolecular polypeptide assemblies. Similar to single component PGA and PLL solutions, the characteristics of PLL/PGA multilayer films and also their complexes in solution have been shown to be strongly influenced by pH changes. Relative β-sheet and α-helix contents in both solution and films increase and decrease, respectively, with the increasing pH.20 For multilayers, the deposition pH and resulting secondary structures of polypeptides impact the thickness of the films. For example, films built under neutral pH conditions (pH of 6.4 and 7.4) have a higher β-sheet content and are notably thinner than those built at either acidic or basic pH, where one of the peptides is partially charged and the α-helix content is higher.16,20,21 In addition, the assembly pH affects the stability of PLL/PGA films in the culture medium.21
Alongside experimental characterization, atomistic molecular dynamics (MD) simulations can be employed to gain molecular-level understanding of the conformational characteristics of charged polypeptides22–25 and their complexes.26–28 For example, the role of chirality in PLL/PGA complexation has been investigated with standard MD26,27 and Replica Exchange with Solute Scaling MD methods.27 MD simulations have also been used to investigate the driving force for complexation of PGA and PLL.28 While these computational studies have exploited the secondary structures in complexes of the fully charged PGA and PLL models, they have not considered the pH sensitivity of their interactions and complexation, i.e. possible effects of different ionization degrees (IDs).
Despite PLL and PGA being a very interesting and widely studied polyelectrolyte pair due to their potential in biomedical applications, most prior studies focus on conditions corresponding to a specific pH. Additionally, comparison of the pH dependency in PLL and PGA complexation response based on separate studies is extremely challenging due to, e.g. differing polypeptide molar mass or ionic strength which both influence complexation. The current literature has a clear gap in data, which allows obtaining a broad picture of the pH dependency of PLL and PGA complexation. Additionally, investigation of the complexation process itself, especially its initial stage, remains lacking. It is also not clear how the complexation process influences the polypeptide secondary structure.
Here, we investigate the effect of pH on complex formation and properties, as well as the secondary structure changes in systems consisting of oppositely charged PLL and PGA, with a comprehensive set of experimental techniques and MD simulations. The experiments have been conducted varying both pH and PLL to PGA molar ratios, which enables observation of changes in the assembly and secondary structure during the complexation. To obtain a broad view on the complexation mechanism, we apply isothermal titration calorimetry (ITC), laser Doppler velocimetry (LDV), CD, and other techniques. It is notable that the complexes may be kinetically trapped,29 and hence the characterization and conclusions focus on initial complexation. Together, experiment and MD simulations show connections between the molecular-level information of polypeptide secondary structures, interactions in complexation, and pH-dependent control of PLL and PGA assemblies.
2. Materials and methods
2.1. Materials
Pure, crystalline poly(L-lysine) hydrobromide, poly(L-glutamic acid) sodium salt, and NaCl were commercial products of Sigma Aldrich. According to the supplier, the number-averaged molecular weight lies within the range of 150–300 kDa and 50–100 kDa for PLL and PGA, respectively. NaOH and HCl were analytical grade products of Avantor Performance Materials Poland S.A. All reagents were used as received. Pure water of 18.2 MΩ resistivity was obtained using Milli-Q Elix & Simplicity 185 purification system from Millipore SAS Molsheim, France. Immediately before use, all electrolyte solutions (HCl, NaOH, and NaCl) were filtered using a 0.2 μm Whatman syringe filter.2.2. Analytical ultracentrifugation (AUC)
Sedimentation velocity and sedimentation equilibrium experiments were performed using a Beckman Coulter Optima Analytical Ultracentrifuge. An-60 Ti rotor and standard 12 mm epon centerpieces were used for both experiments. All measurements were done at a temperature of 293 K and in 0.2 M NaCl in order to screen electrostatic repulsions between molecules.Sedimentation velocity data were collected at 50 000 rpm. PGA and PLL were measured in absorbance mode at a wavelength of 230 nm and at a peptide concentration of 220 mg L−1. Data analysis was carried out by both Sedfit30 and Ultrascan31 analysis software.
Sedimentation equilibrium experiments were performed at three speeds: 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 25
000, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 30
000, and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. The absorbance mode, wavelength of 230 nm, and concentration of 220 mg L−1 were used for both PGA and PLL samples. The obtained data were analyzed by Sedphat30 software. Detailed information about experimental design and data analysis procedures can be found in our previous article.32
000 rpm. The absorbance mode, wavelength of 230 nm, and concentration of 220 mg L−1 were used for both PGA and PLL samples. The obtained data were analyzed by Sedphat30 software. Detailed information about experimental design and data analysis procedures can be found in our previous article.32
2.3. Light scattering methods
Diffusion coefficients and electrophoretic mobilities of PLL, PGA, and their complexes were determined using dynamic light scattering (DLS) and LDV, respectively. These measurements were performed simultaneously using Malvern Zetasizer Nano ZS apparatus equipped with a 633 nm laser with 4 mW power. The concentration of PLL or PGA in the single component solutions was equal to 100 mg L−1.Each experimental point acquired using DLS and LDV methods was an average of five independent measurements with 20 fast runs (2 s of data acquisition) per measurement. The fast run procedure was applied to minimize the time needed to acquire the DLS/LDV signal. This was achieved by equilibrating both PLL and PGA solutions and measurement cells at 298 K and analyzing the sample without its equilibration in the apparatus chamber. This allowed us to reduce the time between sample preparation and first measurement run to ca. 10 s.
To study the PLL/PGA complex formation in a systematic way, binary mixtures with different molar ratios of PLL/PGA were prepared through the addition of an appropriate volume of PLL solution (1000 mg L−1) to a fixed volume of PGA solution (100 mg L−1). Prior to mixing the PLL and PGA solutions, their pH was adjusted to a given value by the addition of an appropriate volume of NaOH or HCl solutions. Samples prepared in this way were analyzed using DLS and LDV methods according to the procedures described above. The molar ratio of polypeptides was determined on a monomer basis. Experiments were performed at a constant temperature of 298 K.
2.4. Circular dichroism
CD spectra were obtained using a JASCO J-710 spectropolarimeter at 298 K in the range of 190–250 nm. A quartz cuvette with an optical path length of 0.2, 1, or 5 mm was used. The parameters used for spectroscopy were as follows: a scanning speed of 100 nm min−1, a data pitch of 1 nm, and a bandwidth of 2 nm. Each spectrum was a result of three averaged scans. The final spectra were obtained by subtracting the buffer spectrum. Absorption signals were recalculated from the photomultiplier tube voltage using the manufacturer software.Typically, 0.1 mg g−1 PGA solution was titrated with 1 mg g−1 PLL solution. Aliquots were added using an automatic pipette in steps of around 0.01 mg g−1, until the polymer complexation made no further signal recording possible. At pH 3.0 the inverted system was used, and the 0.02 mg g−1 PLL solution was titrated with 0.1 mg g−1 PGA solution. The signal was recalculated in terms of the difference in molar extinction coefficients Δε taking the light path length and the total amino acid residue concentrations into account.
2.5. Isothermal titration calorimetry
All ITC analyses were performed at 298 K using a VP-ITC instrument (MicroCal, Northampton, MA, USA). The polymer solutions (PLL and PGA) were prepared in 10 mM NaCl solution, and their pH was adjusted to a given value by the addition of an appropriate volume of NaOH or HCl solutions. All solutions were degassed for 5 min under vacuum before the experiments. Typically, 10 μL aliquots of 1 mg g−1 PLL solution were added as 25–30 injections into a calorimeter cell of 1435.5 μL volume filled with 0.1 mg g−1 PGA solution. The volume of the first injection was 4 μL. The injection speed was 0.5 μL s−1, and the interval between injections was 3.5 minutes. To ensure appropriate mixing after each injection, a constant stirring speed of 300 rpm was maintained throughout the experiment. Data analysis was performed using MicroCal Origin scientific plotting software. Measurements were performed at least in duplicate.2.6. Molecular dynamics simulations
All-atom MD simulations of the PLL/PGA systems were carried out with the GROMACS 2020.3 software.33 Both PGA and PLL chains (with L isomer configurations) consisted of 15 repeating units, and their N- and C-termini were end-capped with acetyl and N-methyl amine groups, respectively. This chain length was chosen because prior characterization work19 indicated that this length is long enough to accurately capture pH dependent secondary structure changes on these peptides as individual chains. The final geometries obtained from the MD simulations of ref. 19 were used as the initial structures of the polypeptides. The initial configurations of PLL/PGA systems were constructed by inserting one PGA chain and one PLL chain in a random but not overlapping location in 8 × 8 × 8 nm3 cubic simulation boxes (Fig. 1b). Seven systems differing in their ionization degrees (ID) were considered to mimic the experimental pH values: (i) fully charged PGA and PLL (ID = 1 for both), (ii) fully charged PGA and the neutral (ID = 0, i.e. pH 12) or partially charged PLL (ID = 0.33, 0.66, range overlapping pH 10 in the experiments), and (iii) the fully charged PLL together with the neutral (ID = 0, i.e. pH 3) or partially charged PGA (ID = 0.33, 0.66, i.e. pH 4 and pH 6.2).In recent years, constant-pH MD methods have been developed for an accurate description of the changes in the amino acid protonation states caused by pH.34–36 While they had been successfully tested for proteins, nucleic acids, and small peptides,37,38 the notable increase in the computational effort compared to the standard MD simulations made the constant-pH methods at the time unfeasible for this work. A very recently developed constant-pH implementation35,36 has allowed the simulation of larger systems with improved accuracy and sampling on time scales up to standard MD simulations,39 which make it an interesting tool for future polypeptide studies. However, additional torsional potential parameterization needs to be considered when using it.35
The explicit TIP3 water model40 was used for solvating the systems. Any net charge in the system was neutralized by adding a suitable amount of Na+ and Cl− ions to achieve the salt concentration of 0.01 M. For each PLL/PGA system, independent simulation runs corresponding to three different randomly generated starting configurations were used.
The AMBER99SB*-ILDNP force field41 was used because it reliably predicts pH-induced changes in the secondary structures of PGA and PLL in agreement with experiments.19 Periodic boundary conditions were applied in all directions. The van der Waals interactions were modelled using the Lennard-Jones potential with a 1.0 nm cutoff. The long-range dispersion corrections for energy and pressure were applied. The particle mesh Ewald method with a Fourier grid spacing of 0.16 nm was used for describing the long-range electrostatic interactions. The simulations were carried out at 298 K, which was controlled by the V-rescale thermostat42 with a coupling constant of 0.1 ps. The pressure was set at 1 bar and controlled by the Parrinello–Rahman barostat43 with a coupling constant of 2 ps. The LINCS44 and SETTLE45 algorithms were used to constrain all the bonds of the polypeptides and water molecules, respectively, to be able to use the time step of 2 fs.
The systems were first energy-minimized with the steepest descent algorithm, after which an initial equilibration in the NVT ensemble with the polypeptides restrained in position for 100 ps was performed. This was followed by an NPT ensemble simulation with equal polypeptide position restraints for 20 ns. In these, the purpose was to equilibrate the water and counter ions around polypeptides. Finally, unrestrained 800 ns long NPT ensemble production runs were carried out. Based on previous work,19 this time period was assessed to be long enough to exceed the equilibration time for the secondary structures of polypeptides. For the systems where one of the polypeptides was neutral, 400 ns production runs were carried out, as no complex formation occurred. Trajectory frames were saved at 10 ps frequency. For all production runs, the last 200 ns were used for analysis. The results presented correspond to an average resulting from three different initial configurations. For assessing secondary structure evolution and equilibration, the full 800 ns (or 400 ns) trajectories were considered. The DSSP program46,47 was used for classifying secondary structures. The VMD 1.9.3 software48 was used for the visualization of molecules.
3. Results and discussion
3.1. Bulk characteristics of PLL and PGA
First, we examined the bulk physicochemical properties of the single polypeptide molecules as a function of pH using DLS, LDV, and AUC techniques. The target here is to obtain a relatively complete physicochemical characterization of the peptides in solution to understand their charge state and other solution characteristics guiding assembly to materials. We note that complementing the characterization discussed below, the changes in secondary structure of single PLL and PGA chains as a function of pH have been reported in ref. 19. | (1) |
To ensure that the recorded DLS signal is not altered by interactions between alike polypeptides, the concentration range corresponding to a stable signal was determined. The dependency of the hydrodynamic diameter dH of the polypeptides on the solution concentration (40–400 mg L−1) is presented in Fig. S1a (ESI‡). The dH of PLL remains stable within the concentration range 50–300 mg L−1, with an average value of 22 nm. Fig. S1b (ESI‡) shows that similar to dH of PLL, dH of PGA remains stable within the concentration range 50–350 mg L−1, with an average value of 12 nm. Based on the concentration ranges of stable dH, the sample concentration of 200 mg L−1 for both PLL and PGA was used in further study.
Next, the dependence of the diffusion coefficients D of PLL and PGA molecules on pH for ionic strength I = 10−2 M NaCl at different pH conditions was determined, see Table 1. The average diffusion coefficient of a PLL molecule was equal to 2.1 ± 0.3 × 10−7 cm2 s−1 in the pH range of 3–10. At pH 12, the diffusion coefficient dramatically decreased, which is an indication of PLL aggregation due to the deprotonation of the NH3+ groups. For PGA molecules, the average diffusion coefficient was equal to 3.8 ± 0.8 × 10−7 cm2 s−1 within the pH range of 4–12. However, due to the protonation of the carboxylate groups, aggregation is observed at pH 3.
| pH | D × 10−7 [cm2 s−1] | d H [nm] | μ e [μm cm V−1 s−1] | ζ [mV] | N c | α |
|---|---|---|---|---|---|---|
| a Aggregation occurs; monomer molar mass for PLL M1PLL= 209 Da, monomer molar mass for PGA M1PGA= 152 Da. | ||||||
| PLL | ||||||
| 3.0 | 2.1 ± 0.4 | 23 ± 5 | 4.2 ± 0.3 | 65 ± 4 | 50 | 0.085 |
| 4.0 | 2.2 ± 0.4 | 22 ± 4 | 3.5 ± 0.6 | 58 ± 4 | 40 | 0.068 |
| 6.2 | 2.0 ± 0.3 | 24 ± 3 | 3.8 ± 0.3 | 67 ± 5 | 48 | 0.082 |
| 10.0 | 2.1 ± 0.8 | 23 ± 8 | 2.3 ± 0.2 | 34 ± 4 | 28 | 0.048 |
| 12.0a | — | — | — | 1.0 ± 4 | 1 | — |
| PGA | ||||||
| 3.0a | — | — | −0.6 ± 0.1 | −12 ± 4 | — | — |
| 4.0 | 4.1 ± 0.3 | 12 ± 3 | −1.8 ± 0.2 | −34 ± 5 | 11 | 0.028 |
| 6.2 | 4.9 ± 0.3 | 10 ± 3 | −2.7 ± 0.3 | −52 ± 4 | 14 | 0.035 |
| 10.0 | 3.1 ± 0.4 | 16 ± 4 | −3.9 ± 0.3 | −71 ± 4 | 33 | 0.083 |
| 12.0 | 3.0 ± 0.8 | 15 ± 3 | −4.1 ± 0.3 | −76 ± 4 | 32 | 0.081 |
Next, we turn to the LDV technique. LDV allows the determination of the electrophoretic mobility and, in consequence, the zeta potential as a function of pH. The data also give the isoelectric point (IEP) of the polypeptides. The electrophoretic mobility μe of PLL and PGA molecules (200 mg L−1) was measured directly using the LDV technique. The corresponding zeta potentials ζ were calculated from the Henry model, see Table 1. For PLL molecules, the zeta potential decreases from ca. 65 ± 4 at pH 3 to 1.0 ± 4 mV at pH 12, indicating the zero net charge point (IEP) of PLL molecules at the latter pH value. In contrast, the PGA zeta potential decreased from −12 ± 4 mV at pH 3 to −76 ± 4 mV at pH 12. Interestingly, the isoelectric point of PGA was not observed in the examined pH range. We note that the pH adjustment changes the ionic strength from the preparation solution value of 0.01 M NaCl to a maximum value of 0.011 M; the effect of this change in zeta potential calculation is significantly smaller than the standard deviation.
The DLS and LDV data together allow for the calculation of the number of uncompensated (electrokinetic) charges, as well as the effective ionization degree of the polypeptides. The results indicate that the number of uncompensated (electrokinetic) charges Nc and ionization degree α increase for PGA and decrease for PLL with increasing pH. For clarity, the calculated values of Nc and α for PLL and PGA molecules are presented in Table 1.
In summary, the above results on single peptides in solution suggest that the formation, properties, and structure of PLL/PGA complexes and the assembly of the peptides can be expected to be highly pH-dependent as electrostatic interactions are likely to be significant contributors to the total interaction energy.
The collected data demonstrate significant dispersity of both polypeptides in terms of molecular weight. The PGA sample shows multiple species in the 20–150 kDa Mw range (Fig. 2 and Fig. S2, ESI‡). Based on the data, the Mw of PGA was 57 kDa. The PLL sample shows three main populations with Mw of 35, 60, and 110 kDa. The Mw of PLL calculated based on these three main population peaks was 84 kDa. Similar results were obtained by Sedfit analysis (Fig. S3, ESI‡). Quality assessment of the Ultrascan fitting can be found in the ESI‡ (Fig. S4).
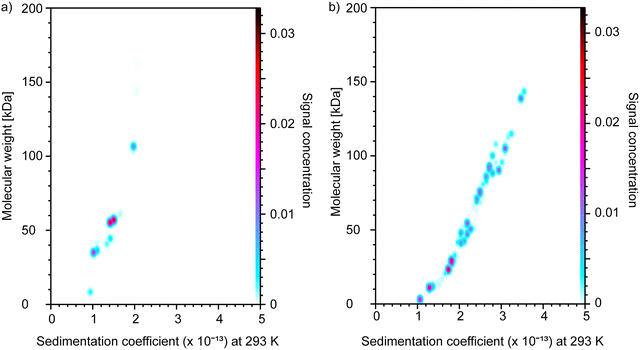 | ||
| Fig. 2 The pseudo 3D distribution in terms of sedimentation coefficient vs. molecular weight of (a) PLL and (b) PGA as determined by the AUC technique. | ||
Data obtained by sedimentation equilibrium were fit to one-, two-, and three-species models to extract weight-average molecular weights of PLL and PGA. As expected, based on the dispersity of the samples visible already in the sedimentation velocity data, the one-species model resulted in a bad fit. A better fit was obtained using a two-species model (Fig. S5, ESI‡). As no significant improvement in fit was achieved using the three-species model, the two-species model was implemented for further analysis. The obtained weight-averaged molecular weights by sedimentation equilibrium were 81 kDa for PLL and 40 kDa for PGA. These latter values were used in further analysis.
3.2. Investigation of PLL/PGA complex formation
The mixing of PLL and PGA solutions at different pH values can result in either formation of complexes, coacervates, or soluble peptide chains in a clear solution.52 The single peptide characterization allows for the postulation of charge-state dependent complexation and assembly ranges. However, examination of single peptides does not address the effect of other interactions on complexation or the resulting stoichiometry. Additionally, effects of association on complex shape and secondary structure of the peptides remain unresolved. To obtain an understanding of these factors, we mapped the pH dependency of the PLL/PGA mixtures corresponding to the initial complexation both experimentally and via MD simulations. Although the chosen experimental approaches show a temporally stable baseline and signal, the formed complexes or the coacervate phase structure may nevertheless be kinetically trapped.29 This limits the validity of the examination of the PLL/PGA complexes to initial assembly throughout the work.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as used in MD simulations.
1, as used in MD simulations.
 | ||
| Fig. 3 Hydrodynamic diameter dH and zeta potential ζ dependency of PLL and PGA mixtures on the molar ratio of PLL to PGA rPLL/PGA. At the top, the mean hydrodynamic diameter dHvs. rPLL/PGA at pH (a) 4, (b) 6.2, and (c) 10. The solid line is a non-linear fit to the measurement data (for details, see the ESI‡). The dashed line corresponds to the theoretical estimate of the hydrodynamic diameter of PLL/PGA complex dHc, following eqn (2). At the bottom, the mean zeta potential ζ at pH (d) 4, (e) 6.2, and (f) 10. The dashed and dotted lines correspond to the molar fraction weighted theoretical estimates of zeta potential calculated according to eqn (S5) (R1 experimental regime) and eqn (S6) (R2 experimental regime), respectively (ESI‡). The black solid line is the prediction by the “No interaction” model, eqn (S7) (ESI‡). Ionic strength I = 0.01 M NaCl and T = 298 K. The corresponding data for pH 3 and 12 are given in the ESI,‡ Fig. S7. | ||
The results in Fig. 3a–c and Fig. S7 (ESI‡) for dH indicate that PLL/PGA complexation can be considered in terms of the pH conditions promoting complexation (complex-promoting) or preventing complexation (complex-preventing). This is reflected in the difference in dH response vs. rPLL/PGA dependence when varying pH. For the conditions where pH promotes complexation, i.e. pH 6.2 and 10, an abrupt increase in the hydrodynamic diameter is observed with increasing rPLL/PGA. The experimental data can be fitted using a logistic regression curve (see the ESI‡ for details). The largest dH values that reach hundreds of nanometers are observed for pH 6.2 and 10, at which both of polypeptides are charged, as seen in Fig. 3b and c. This phenomenon results from the further aggregation of the complexes. In contrast to this, for pH values of 3, 4, and 12, dH increases exponentially with rPLL/PGA, with maximum values of ca. 35, 50, and 60 nm, respectively (Fig. 3a and Fig. S7, ESI‡).
It is enlightening to compare the actual measured hydrodynamic diameter to theoretical estimates that involve simplifying assumptions. Assuming that the (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) stoichiometry suggested by pH-metric titration dominates in complex formation, and that the molecules in the complex adopt elongated conformations that can be described by a cylinder (assumption valid for elongated macroions such as PLL22), a theoretical estimate of the hydrodynamic diameter for the PLL/PGA complex can be calculated from the following dependence:53
1) stoichiometry suggested by pH-metric titration dominates in complex formation, and that the molecules in the complex adopt elongated conformations that can be described by a cylinder (assumption valid for elongated macroions such as PLL22), a theoretical estimate of the hydrodynamic diameter for the PLL/PGA complex can be calculated from the following dependence:53
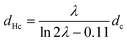 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PLL/PGA complex an estimate of hydrodynamic diameter dHc = 22 nm (plotted in Fig. 3 as a reference line). For pH conditions promoting complexation, this estimate of the dHc results in a value matching the experimentally measured hydrodynamic diameter of an individual PLL. This can be explained by interactions between PLL and PGA increasing dHc, the increase being dominated by aggregation. The above comparison with the theoretical estimate based on molecules with an elongated form, and the actual measured dHc systematically exceeding the estimate in value indicate that first, the molecules are likely to retain their elongated form in the complex but second, also that the experimentally measured hydrodynamic diameter value for the complex can be treated as an indicator of ongoing aggregation in the system. However, due to the limited resolution of DLS, the data can be considered only semiquantitatively. The secondary structure changes identified later in this work are likely to contribute to the aggregation.
1 PLL/PGA complex an estimate of hydrodynamic diameter dHc = 22 nm (plotted in Fig. 3 as a reference line). For pH conditions promoting complexation, this estimate of the dHc results in a value matching the experimentally measured hydrodynamic diameter of an individual PLL. This can be explained by interactions between PLL and PGA increasing dHc, the increase being dominated by aggregation. The above comparison with the theoretical estimate based on molecules with an elongated form, and the actual measured dHc systematically exceeding the estimate in value indicate that first, the molecules are likely to retain their elongated form in the complex but second, also that the experimentally measured hydrodynamic diameter value for the complex can be treated as an indicator of ongoing aggregation in the system. However, due to the limited resolution of DLS, the data can be considered only semiquantitatively. The secondary structure changes identified later in this work are likely to contribute to the aggregation.
Furthermore, for pH 6.2 and 10, the hydrodynamic diameter determined for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry (rPLL/PGA = 1) is in accordance with the theoretically estimated value of 22 nm, supporting the assumptions made in the theoretical estimate (elongation of the peptides). The same mass density in a spherical volume leads to a diameter
1 stoichiometry (rPLL/PGA = 1) is in accordance with the theoretically estimated value of 22 nm, supporting the assumptions made in the theoretical estimate (elongation of the peptides). The same mass density in a spherical volume leads to a diameter
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, one obtains ds = 6.5 nm, which is significantly smaller than the dH value derived from DLS. The result clearly indicates that also the complex has an elongated shape that is characteristic for both PLL and PGA.
1 stoichiometry, one obtains ds = 6.5 nm, which is significantly smaller than the dH value derived from DLS. The result clearly indicates that also the complex has an elongated shape that is characteristic for both PLL and PGA.
At conditions where pH prevents complexation, the error bars in dHc are relatively high and direct explanation of the obtained results is not feasible. At pH 3 and 12, the dHc determined experimentally matches with the theoretical reference value of dHc (within the error estimate) which suggests that the peptides do not aggregate further than what would be the estimated size of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PLL/PGA complex, i.e. complex formation cannot be concluded. Although at pH 4 the measured dH exceeds slightly the theoretical 22 nm reference value, complex formation at pH 4 based on this data remains ambiguous, compared to pH 6.2 and 10. It is noteworthy that the observed increase in dH with rPLL/PGA does not result from increasing concentration of the analyzed sample, see Fig. S1 (ESI‡). However, the limited resolution of DLS in resolving the occurrence of a binary system could contribute to the observed trend in both hydrodynamic diameter and error with increasing rPLL/PGA. However, our semiquantitative data indicate clearly that fast aggregation of the as-formed complexes takes place under pH-promoting complexation conditions, e.g. pH 6.2 and 10 here. This is visible as an abrupt increase in hydrodynamic diameter with a molar ratio of PLL to PGA.
1 PLL/PGA complex, i.e. complex formation cannot be concluded. Although at pH 4 the measured dH exceeds slightly the theoretical 22 nm reference value, complex formation at pH 4 based on this data remains ambiguous, compared to pH 6.2 and 10. It is noteworthy that the observed increase in dH with rPLL/PGA does not result from increasing concentration of the analyzed sample, see Fig. S1 (ESI‡). However, the limited resolution of DLS in resolving the occurrence of a binary system could contribute to the observed trend in both hydrodynamic diameter and error with increasing rPLL/PGA. However, our semiquantitative data indicate clearly that fast aggregation of the as-formed complexes takes place under pH-promoting complexation conditions, e.g. pH 6.2 and 10 here. This is visible as an abrupt increase in hydrodynamic diameter with a molar ratio of PLL to PGA.
Compared to DLS, LDV can be expected to provide more quantitative information on pH dependent complexation as the electrophoretic mobility of aggregated molecules should be significantly lower than individual molecules and PLL/PGA as a complex. The LDV results are shown in Fig. 3d, e and Fig. S7 (ESI‡). The zeta potential ζ of the PLL/PGA system increases with rPLL/PGA regardless of pH. Initially, for smaller molar ratios, excess PGA in the system increases the zeta potential moderately with rPLL/PGA indicating either the formation of a complex or averaging of the signal due to the addition of positively charged (pH 3, 4, 6.2, and 10) or almost neutral (pH 12) PLL molecules. The zeta potential increased more abruptly for lower values of rPLL/PGA, attaining a maximum increase rate in close proximity to rPLL/PGA = 1. This implies that the LDV method tracks changes in electrophoretic mobility resulting from the addition of even small amounts of oppositely charged polypeptide. The observed changes of ζ with rPLL/PGA follow the logistic curve, which describes the zeta potential of the complex, ζc using a fitting procedure described in detail in the ESI.‡
The value of ζc was found to be dependent on pH, attaining a value of 21, 18, −3, −35, and −62 mV for pH values of 3, 4, 6.2, 10 and 12, respectively. The observed changes of ζc with increasing pH are in qualitative accordance with the dependencies of zeta potential of PLL and PGA.19 The comparison of experimental data acquired using the LDV method with the two-stage and no-interaction models (see the ESI‡ for further details of the models, Fig. 3d and e) suggest that the interaction between PLL and PGA occurs for pH values of 4, 6.2, and 10, whereas for pH values of 3 or 12 complexes are not formed. The agreement between the experimental data and first and second stages of two-stage models, i.e. R1 and R2 is satisfactory under pH-promoting complex formation conditions, especially for smaller values of PLL/PGA molar ratio. This suggests that the main contribution to the formation of PLL/PGA complexes are electrostatic interactions, as the linearized dependency captures the zeta potential response. This linear response can be expected to arise from discrete ion pairs between the polypeptides. At pH 12, the experimental measurement data and the “no-interaction” model prediction are in relatively good agreement which indicates suppression of complexation, see Fig. S7 (ESI‡). On the other hand, for pH 3, only the R2 model agrees with the experimental data. This is probably due to the much higher mobility of the charged PLL molecules in an electric field which dominates the LDV signal over the almost neutral PGA.
Interesting results were obtained at a pH of 6.2. At this pH both PLL and PGA are strongly charged, and the resulting complexes are almost neutral (ζc = −4 mV). One should thus expect fast solution aggregation of the complexes, confirmed by the DLS experiments (Fig. 3b) which revealed the highest aggregation affinity at pH 6.2 with hydrodynamic diameters reaching 720 nm. Similar observations were made for pH 10; however, the aggregates are much smaller (250 nm). For pH 10, the measured ζc is −35 mV. No aggregation should be observed at this pH as the absolute value of zeta potential is higher than 30 mV.54 However, this rule of thumb takes into account only electrostatic repulsion and does not provide any insight into attractive interactions such as van der Waals forces and/or hydrogen bonding. The observed aggregation response at pH 10 thus suggests that some attractive, non-electrostatic interactions are responsible for the relatively fast aggregation of complexes. Additionally, based on the zeta potential values in Table 1, at pH 6.2 and 10 different PLL/PGA charge stoichiometries, close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively, can be expected.
2, respectively, can be expected.
 | ||
| Fig. 4 Changes in CD spectra of PLL/PGA systems during titrations of 1 mg g−1 PLL into 0.1 mg g−1 PGA solution at pH (a) 4, (b) 6.2, and (c) 10. The insets show the spectra of single component solutions (PGA – black line, PLL – red line). The corresponding data for pH 3 and 12 are in the ESI,‡ Fig. S8. Spectra of PLL/PGA complexes obtained as the difference between the PLL/PGA systems and the single component solutions at pH 6.2 and 10 are presented in (d). Ionic strength I = 0.01 M NaCl and T = 298 K. | ||
The secondary structure of both polypeptides is pH dependent through the degree of ionization. For pH 6.2, we observe a spectrum characteristic for the random coil structure (inset in Fig. 4b) for the single component solutions of both PGA and PLL. As suggested by the zeta potential measurements, both peptides at this pH are strongly charged. Further pH-mediated charge neutralization leads to a random coil to α-helix transition. In consequence, the CD spectra typical for the α-helix are observed at pH below 4 and above 10 for PGA and PLL, respectively (insets in Fig. 4a and c and Fig. S8, ESI‡). Significant changes in the measured spectra during titrations were observed in every pH. The isodichroic point indicates that only two states are present during the titration at every pH except at pH 4. At pH 3 and 12, the isodichroic points are similar for both the inset data and the titration, which indicates that no significant changes in the polypeptide secondary structure takes place with the titrations (Fig. S8, ESI‡). In turn, the isodichroic point at pH 10 and 6.2 changes, which points to significant changes in the secondary structure of the peptides during titrations. Notably, the peptides form complexes at these pH values; the data strongly suggests that almost all added PLL molecules form complexes with PGA, which is in line with the DLS and LDV measurements.
The CD spectra corresponding to the complexes can be extracted by subtracting the spectra of the unbound fraction of PGA from the total. The spectra of the complexes resulting from this subtraction at pH 10 and 6.2 are presented in Fig. 4d. At both pH values, these spectra differ from those of free polymers and indicate a significant secondary structure change. The presence of two extrema in pH 6.2, a maximum at 195 nm and a minimum at about 217 nm points, are characteristic for β-sheet formation. However, their amplitudes are lower than expected. This can be explained by only a fraction of polymers in the complex folding into a β-sheet structure. At pH 10, the observed minimum shows a bathochromic shift, which suggests the presence of a small fraction of α-helixes in the complex. This could result from the intramolecular hydrogen bonds, creating α-helixes before complexation, being not disrupted upon complexation.55 Similar evidence of a small amount of α-helical structure retained upon complexation has also been observed in the previous FTIR analysis of the PLL/PGA films.20,21
The CD measurements also enable simultaneous monitoring of the absorbance of the samples. As visible aggregates formed in part of titrations, the sample absorption analysis was performed at a wavelength of 250 nm. PLL and PGA do not absorb at this wavelength, so the increase of signal at this band results from light scattering. The dependency of light scattering vs. molar ratio is presented in Fig. S9 (ESI‡). No light scattering was observed at pH 3 and 12, which suggests that no aggregation of the peptides occurs, in agreement with the DLS and LDV measurements. In other pH values, the scattering is significant, with the highest scattering at pH 4.
 | ||
| Fig. 5 Molar enthalpy Q vs. molar ratio of PLL to PGA rPLL/PGA obtained from ITC as integrated data over complexation at different pH values. The corresponding raw ITC titration data is presented in Fig. S10 (ESI‡). Ionic strength I = 0.01 M NaCl and T = 298 K. | ||
The titrations performed at pH 3 and 12 do not have a significant signal characterizing them. This indicates that PLL and PGA do not interact, which is consistent with the observations via CD, DLS, and LDV methods. At pH 4 and 10, quantitative analysis is not possible due to the lack of an adequate model to describe the observed process in detail. However, at pH 4 PGA is partially charged, and at pH 10 PLL is partially charged, see Table 1 for the LDV data. The exothermic response visible in ITC can therefore be related to the changes in the protonation states during assembly. For weak polyelectrolytes, these shifts in pKa can be observed with complex formation.56
At pH 10, ITC reveals initially an exothermic process, with intensity decreasing monotonically during the titration. At rPLL/PGA of 0.5, the signal becomes endothermic and decreases to zero above the stoichiometry of 0.8. A similar exothermic signal, as observed here for the initial titration stage, was previously reported for poly(L-histidine)/PGA complexation.57 The origin of the response was related to poly(L-histidine) being close to its pKa value, i.e., small changes in pH (caused by the complexation) change the polypeptide's charge significantly. Also here, PLL is close to its pKa at pH 10, and the shift in pKa can be expected to be responsible for the initial exothermic signal. Interestingly, at pH values close to the pKa of PGA, this effect is not observed, potentially due to the significantly higher enthalpy of amine group protonation than carboxylic group deprotonation.58 The second stage, i.e., endothermic part, can be related with changes in the conformation and/or further aggregation of molecules.59 A similar two-stage response has previously been observed for β-lactoglobulin/total acacia gum complexation, where the first “structuring” stage was driven by enthalpy and the second one by entropy.59
At pH 4, the initial injections did not generate a significant heat effect. However, closer inspection of the peaks on the thermogram (Fig. S10b, ESI‡) reveals that this results from compensation of exo- and endothermic processes. After injection, the power signal initially increases above the base signal which indicates an endothermic process. Then the signal decreases sharply as the exothermic process begins to dominate. This two-phase time dependent power change is observed only at pH 4. This titration pattern is probably also due to changes in the degree of protonation of PGA during complexation. At pH 6.2, the measured process is endothermic and the signal decreases close to zero after exceeding 0.3 stoichiometry. Notably saturation is achieved at all examined pHs, i.e. further addition of PLL does not cause significant heat effects.
The pH-dependent variation observed in the ITC measurements here indicates a multi-step association process between PLL and PGA. However, for pH 6.2, the data could be quantitatively interpreted based on prior work,60 assuming a single-step process. This results in obtained apparent parameters of stoichiometry 0.318 ± 0.001, ΔH = 1940 ± 18 kJ mol−1, TΔS = 1990 kJ mol−1, and ΔG = −52.3 kJ mol−1 at pH 6.2. Here, the one binding site model that predicted a binding stoichiometry of circa 0.3 indicates that, on average, one PLL molecule binds three PGA molecules. The results from AUC showed that PLL had twice the Mw of PGA and as the polymer monomers have similar molar masses, PLL chains here can be assumed to have an average length twice that of the PGA chains. Additionally, PGA at pH 6.2 is partially charged. Assuming charge pairing as the main factor of molecular recognition, the expected stoichiometry is below 0.5. The lower value measured here may also be due to aggregation or peptide dispersity, as suggested by the AUC measurements.
In previous studies, in analysis of thermodynamic interactions between opposite charge polyelectrolytes (including PLL/PGA at pH 7.0), the determined enthalpy has also been generally positive. Specifically, enthalpy values of +3.8 ± 1.0 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 and +1.9 kJ mol−1
58 and +1.9 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 56 per monomer were determined for the PLL/PGA pair based on single-step or two-step mechanism of interaction in analysis. The enthalpy per monomer here is approximately +3 kJ mol−1 which is in line with the above values. The analysis using a two-step binding process assumed that polypeptides first pair and after which complex coacervation occurs. This second stage is not visible in our calorimetric measurements. However, the data of ref. 56 corresponds to (D,L)PGA, whereas our experiments were performed for pure (L)PGA. Notably, one can expect the polypeptide chirality to affect the state of polyelectrolyte complexes: for example, the presence of at least one racemic polypeptide has been reported to lead to fluid complexes with a random coil structure, while corresponding pairs of pure chiral polypeptides formed fibrillar solids with a β-sheet structure.26 Hence, differences in the thermodynamics of the complex formation can be attributed to possible chirality induced variation in the secondary structure of the complexes.
56 per monomer were determined for the PLL/PGA pair based on single-step or two-step mechanism of interaction in analysis. The enthalpy per monomer here is approximately +3 kJ mol−1 which is in line with the above values. The analysis using a two-step binding process assumed that polypeptides first pair and after which complex coacervation occurs. This second stage is not visible in our calorimetric measurements. However, the data of ref. 56 corresponds to (D,L)PGA, whereas our experiments were performed for pure (L)PGA. Notably, one can expect the polypeptide chirality to affect the state of polyelectrolyte complexes: for example, the presence of at least one racemic polypeptide has been reported to lead to fluid complexes with a random coil structure, while corresponding pairs of pure chiral polypeptides formed fibrillar solids with a β-sheet structure.26 Hence, differences in the thermodynamics of the complex formation can be attributed to possible chirality induced variation in the secondary structure of the complexes.
The complexation enthalpy findings are also consistent with data from Langevin dynamic simulations,61 which show that complexation interactions are endothermic and driven by the entropy from counterion release at low ionic strength. On the other hand, the recent work by Chen et al.62 also points out that the solvent entropic contributions omitted in coarse-grained modelling can be a major driving force in complexation. Overall, the experimental data indicate that the trends with respect to complexation seem to be somewhat asymmetric with regards to pH. This difference could be due to the non-electrostatic intermolecular interactions, such as the formation of hydrogen bonds.63
The simulations show that secondary structures in the PLL/PGA systems are clearly affected by the ID of the individual polypeptides. The secondary structures and conformations predicted as a function of the ID are presented in Fig. 6. The time evolution of the secondary structure of PLL/PGA systems are collected to Tables S3 and S4 (ESI‡). For the systems with fully charged PGA (basic pH conditions, Fig. 6a), the overall helical content decreases as PLL elongates with the increasing ID due to the repulsion between its charged side chains. This leads to increased β-structure content, as partially or fully charged PLL forms β-sheets with PGA. However, in the systems with the fully charged PLL (acidic pH conditions, Fig. 6b), a very prominent helical content is predicted at the ID 0.33 of PGA, while only a moderate β-structure content is predicted when PGA is partially charged. In other words, no β-sheets are formed between the polypeptides until PGA is fully charged. The same trends can also be observed from Ramachandran plots (Fig. S11 and S12, ESI‡), which show clear differences in the distributions of backbone configurations corresponding to β-sheets and α-helices as a function of the ID.
These observations for secondary structure changes in the PLL/PGA systems from simulations are in agreement with CD measurements. Notably, the CD spectrum for the mixture at pH 4 showed an α-helix formation for PGA; the MD data here point toward partial helix formation. Also the finding is consistent with the previous MD and replica exchange simulations, where β-sheets have been observed to form between the fully charged PGA and PLL chains.26,27 Further examination of polypeptide structure changes as a function of ID was done by calculating their radii of gyration Rg. The structure of the fully charged PLL is slightly affected by changing the ID of PGA, as seen by the decrease of the Rg of PLL (Fig. S13, ESI‡). Opposed to this, the fully charged PGA is unaffected by the conformational changes of PLL. Indeed, this variation in the secondary structure of the complex at different pH values was suggested by the CD measurements, see Fig. 4(d). The MD results here show how the response could emerge and provide a qualitative assessment of the peptide fraction undergoing the secondary structure changes.
For additional insight into the intermolecular interactions, we next analyzed hydrogen bonding in the PLL/PGA systems. The average number of intermolecular hydrogen bonds between PGA and PLL per repeating unit increases with the ID one of the polypeptides (Fig. 7). In the systems with fully charged PGA, the increase in intermolecular hydrogen bonding between the polypeptides correlates well with β-sheet formation (Fig. 6a). This was indicated also by the CD experiments (Fig. 4d). For the systems with the fully charged PLL, the number of the intermolecular hydrogen bonds increase with the ID, as well. However, this is not due to the β-sheet formation between the polypeptide backbones, as almost none is formed with the partially charged PGA (Fig. 6b), but mainly due to hydrogen bonding between the side chains of PGA and PLL (Fig. S14, ESI‡). Similarly, for the systems of fully charged PGA, more intermolecular hydrogen bonds are formed between the side chains than the backbones when PLL is partially charged. In total, the helix-coil transformation of the polypeptides leads to a decreased number of the intramolecular hydrogen bonds. The intramolecular hydrogen bonds and the polypeptide secondary structure have a similar relationship also for individual PGA and PLL molecules.19 Overall, the different trends in hydrogen bonding between the systems of fully charged PGA (corresponding to pH > 7) and fully charged PLL (pH < 7) could explain the asymmetric complexation with regards to pH observed in the experiments. Related to this, ref. 63 discusses non-electrostatic interactions in pH-sensitive complexes.
To study the influence of the ID on the electrostatic interactions between PGA and PLL, we determined the intrinsic and extrinsic ion pairing68 in the PLL/PGA systems (Fig. S15, ESI‡). The analysis is based on cut-off distances defined by the first minimum in the corresponding radial distribution function graph (Fig. S16–S19, ESI‡). Intrinsic ion pairs are form between the charge groups of oppositely charged polypeptides while the charge groups left unbound are compensated by small counterions forming extrinsic ion pairs. As expected based on the lack of complexation both in simulations and experiments, the data of Fig. S15 (ESI‡) shows that no intrinsic ion pairs form when one of the polypeptides is neutral. On the other hand, fully charged polypeptide in solution forms extrinsic ion pairs together with the counter ions. Increasing the number of charge groups in the oppositely charged polypeptide leads to an increase in the number of intrinsic ion pairs between it and the fully charged polypeptide. This will lead to the decrease in the number of extrinsic ion pairs. It is worth noting that the presence of excess salt changes the response, with excess ions promoting extrinsic charge compensation.69
4. Conclusions
Solution pH governs the assembly of polypeptides and is thus an important control factor for designing polypeptide materials. We examined here the solution characteristics and complexation of PLL and PGA at varying pH values. Overall, the results showed that peptide charge is the most important factor in complexation of PLL and PGA. We reported that complexation took place in the pH range of 4 to 10, which corresponds to the case of one of the polypeptides being at least partially charged. The complexed peptides adopted elongated assembly shapes, with molar fractions of the peptides governing assembly charge. Assembly occurred via pairwise ion pairing between the charged amino acids of the peptides. Less intuitive are the secondary structure changes that occur via a combination of pH changes and complexation, as supported by the CD results and MD simulations. Here, we concluded that the secondary structures of the PLL/PGA systems were dictated by the polypeptide charge state. In the pH range of 4 to 10, where polypeptides were at least partially charged, clear changes in the secondary structures were observed upon complexation, while in the other cases, the polypeptide secondary structures remained unchanged.The significance of this work is that the systematic physicochemical characterization of the pH dependency of PLL and PGA in solution and of PLL/PGA complexation shows the dominant role of charge interactions in complexation and the systematic tunability by secondary structure changes, as well as the multistep character of the thermodynamics of assembly. This work provides not only guidelines for designing PLL/PGA complexes but also more generally polypeptide materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Science Centre, Poland (grant no. 2018/31/D/ST5/01866) (P. Ba.), the Academy of Finland through its Centres of Excellence Programme (2022-2029, LIBER) under project no. 346111 (M. S.) and 346105 (M. L.) and project no. 309324 (M. S.), Novo Nordisk Foundation under project no. NNF22OC0074060 (M. S.), Finnish Cultural Foundation (T. K.), and U.S. National Science Foundation under grant no. 1905732 (J. L. L.). We are grateful for the support by FinnCERES Materials Bioeconomy Ecosystem. M. Morga thanks the European Union Erasmus+ programme (project no. 2019-1-PL01-KA103-061592) for providing financial support for the mobility and training in Aalto University, Finland. Computational resources by CSC IT Centre for Finland, Poland's high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH), grant no. PLG/2023/016229, and RAMI – RawMatters Finland Infrastructure are also gratefully acknowledged.References
- C. Ge, H. Ye, F. Wu, J. Zhu, Z. Song, Y. Liu and L. Yin, J. Mater. Chem. B, 2020, 8, 6530–6547 RSC.
- C. Dharmayanti, T. A. Gillam, M. Klingler-Hoffmann, H. Albrecht and A. Blencowe, Strategies for the development of pH-responsive synthetic polypeptides and polymer-peptide hybrids: Recent advancements, Polymers, 2021, 13, 1–17 CrossRef PubMed.
- K. A. Black, D. Priftis, S. L. Perry, J. Yip, W. Y. Byun and M. Tirrell, Protein encapsulation via polypeptide complex coacervation, ACS Macro Lett., 2014, 3, 1088–1091 CrossRef CAS PubMed.
- K. Ryu, M. K. Lee, J. Park and T. Il Kim, PH-Responsive Charge-Conversional Poly(ethylene imine)-Poly(L-lysine)-Poly(L-glutamic acid) with Self-Assembly and Endosome Buffering Ability for Gene Delivery Systems, ACS Appl. Bio Mater., 2018, 1, 1496–1504 CrossRef CAS PubMed.
- M. Xiong, Y. Bao, X. Xu, H. Wang, Z. Han, Z. Wang, Y. Liu, S. Huang, Z. Song, J. Chen, R. M. Peek, L. Yin, L. F. Chen and J. Cheng, Selective killing of Helicobacter pylori with pH-responsive helix–coil conformation transitionable antimicrobial polypeptides, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12675–12680 CrossRef CAS PubMed.
- S. Zheng, Y. Guan, H. Yu, G. Huang and C. Zheng, Poly-L-lysine-coated PLGA/poly(amino acid)-modified hydroxyapatite porous scaffolds as efficient tissue engineering scaffolds for cell adhesion, proliferation, and differentiation, New J. Chem., 2019, 43, 9989–10002 RSC.
- M. Oćwieja, A. Popov, Z. Adamczyk, M. Morga, A. Ramanaviciene and A. Ramanavicius, Deposition of silver nanoparticles from suspensions containing tannic acid, Colloids Surf., A, 2015, 477, 70–76 CrossRef.
- S. Zhao, H. Zhu, Z. Chen, S. Shuai, N. Zhang, Y. Liu, Z. Rao, Y. Li, C. Zhao, K. Zhou, W. Ge and J. Hao, Preparation and properties of a temperature- and pH- responsive polypeptide hydrogel, Mater. Res. Express, 2019, 6, 085711 CrossRef CAS.
- L. Zhang, Y. Ma, X. Pan, S. Chen, H. Zhuang and S. Wang, A composite hydrogel of chitosan/heparin/poly (γ-glutamic acid) loaded with superoxide dismutase for wound healing, Carbohydr. Polym., 2018, 180, 168–174 CrossRef CAS PubMed.
- T. Makovec, Poly-L-glutamic acid and poly-L-lysine: model substances for studying secondary structures of proteins, Biochem. Mol. Biol. Educ., 2000, 28, 244–247 CAS.
- A. Dos, V. Schimming, S. Tosoni and H. H. Limbach, Acid-base interactions and secondary structures of poly-L-lysine probed by15N and13C solid state NMR and ab initio model calculations, J. Phys. Chem. B, 2008, 112, 15604–15615 CrossRef CAS PubMed.
- M. Nagasawa and A. Holtzer, The Helix-Coil Transition in Solutions of Polyglutamic Acid, J. Am. Chem. Soc., 1964, 86, 538–543 CrossRef CAS.
- Y. P. Myer, The pH-Induced Helix-Coil Transition of Poly-L-lysine and Poly-L-glutamic Acid and the 238-mn Dichroic Band, Macromolecules, 1969, 2, 624–628 CrossRef CAS.
- K. Inoue, N. Baden and M. Terazima, Diffusion coefficient and the secondary structure of poly-L-glutamic acid in aqueous solution, J. Phys. Chem. B, 2005, 109, 22623–22628 CrossRef CAS.
- T. Kimura, S. Takahashi, S. Akiyama, T. Uzawa, K. Ishimori and I. Morishima, Direct observation of the multistep helix formation of poly-L-glutamic acids, J. Am. Chem. Soc., 2002, 124, 11596–11597 CrossRef CAS PubMed.
- D. T. Haynie, S. Balkundi, N. Palath, K. Chakravarthula and K. Dave, Polypeptide multilayer films: Role of molecular structure and charge, Langmuir, 2004, 20, 4540–4547 CrossRef CAS PubMed.
- S. Song and S. A. Asher, UV Resonance Raman Studies of Peptide Conformation in Poly(L-lysine), Poly(L-glutamic acid), and Model Complexes: The Basis for Protein Secondary Structure Determinations, J. Am. Chem. Soc., 1989, 111, 4295–4305 CrossRef CAS.
- J. J. Grigsby, H. W. Blanch and J. M. Prausnitz, Effect of secondary structure on the potential of mean force for poly-L-lysine in the α-helix and β-sheet conformations, Biophys. Chem., 2002, 99, 107–116 CrossRef CAS PubMed.
- P. Batys, M. Morga, P. Bonarek and M. Sammalkorpi, pH-Induced Changes in Polypeptide Conformation: Force-Field Comparison with Experimental Validation, J. Phys. Chem. B, 2020, 124, 2961–2972 CrossRef CAS PubMed.
- F. Boulmedais, M. Bozonnet, P. Schwinté, J. C. Voegel and P. Schaaf, Multilayered polypeptide films: Secondary structures and effect of various stresses, Langmuir, 2003, 19, 9873–9882 CrossRef CAS.
- L. Richert, Y. Arntz, P. Schaaf, J.-C. Voegel and C. Picart, pH dependent growth of poly(L-lysine)/poly(L-glutamic) acid multilayer films and their cell adhesion properties, Surf. Sci., 2004, 570, 13–29 CrossRef CAS.
- Z. Adamczyk, M. Morga, D. Kosior and P. Batys, Conformations of Poly-l-lysine Molecules in Electrolyte Solutions: Modeling and Experimental Measurements, J. Phys. Chem. C, 2018, 122, 23180–23190 CrossRef CAS.
- J. Heyda and J. Dzubiella, Ion-specific counterion condensation on charged peptides: Poisson-Boltzmann vs. atomistic simulations, Soft Matter, 2012, 8, 9338–9344 RSC.
- Z. Adamczyk, P. Batys, W. Płaziński, M. Morga, D. Lupa and A. Michna, Macroion molecule properties from slender body hydrodynamics, Polym. Adv. Technol., 2021, pat.5319 Search PubMed.
- A. L. Harmat, M. Morga, J. L. Lutkenhaus, P. Batys and M. Sammalkorpi, Molecular mechanisms of pH-tunable stability and surface coverage of polypeptide films, Appl. Surf. Sci., 2023, 615, 156331 CrossRef CAS.
- S. L. Perry, L. Leon, K. Q. Hoffmann, M. J. Kade, D. Priftis, K. A. Black, D. Wong, R. A. Klein, C. F. Pierce, K. O. Margossian, J. K. Whitmer, J. Qin, J. J. de Pablo and M. Tirrell, Chirality-selected phase behaviour in ionic polypeptide complexes, Nat. Commun., 2015, 6, 6052 CrossRef CAS PubMed.
- K. Q. Hoffmann, S. L. Perry, L. Leon, D. Priftis, M. Tirrell and J. J. de Pablo, A molecular view of the role of chirality in charge-driven polypeptide complexation, Soft Matter, 2015, 11, 1525–1538 RSC.
- A. N. Singh and A. Yethiraj, Driving Force for the Complexation of Charged Polypeptides, J. Phys. Chem. B, 2020, 124, 1285–1292 CrossRef CAS PubMed.
- S. Manoj Lalwani, C. I. Eneh and J. L. Lutkenhaus, Phys. Chem. Chem. Phys., 2020, 22, 24157–24177 RSC.
- P. Schuck, On the analysis of protein self-association by sedimentation velocity analytical ultracentrifugation, Anal. Biochem., 2003, 320, 104–124 CrossRef CAS PubMed.
- D. J. Scott, S. E. Harding and A. J. Rowe, Analytical Ultracentrifugation, Royal Society of Chemistry, 2007, pp. 210–230 Search PubMed.
- D. Fedorov, P. Batys, D. B. Hayes, M. Sammalkorpi and M. B. Linder, Analyzing the weak dimerization of a cellulose binding module by analytical ultracentrifugation, Int. J. Biol. Macromol., 2020, 163, 1995–2004 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- P. Dobrev, S. P. B. Vemulapalli, N. Nath, C. Griesinger and H. Grubmüller, Probing the Accuracy of Explicit Solvent Constant pH Molecular Dynamics Simulations for Peptides, J. Chem. Theory Comput., 2020, 16, 2561–2569 CrossRef CAS PubMed.
- P. Buslaev, N. Aho, A. Jansen, P. Bauer, B. Hess and G. Groenhof, Best Practices in Constant pH MD Simulations: Accuracy and Sampling, J. Chem. Theory Comput., 2022, 18, 6134–6147 CrossRef CAS PubMed.
- N. Aho, P. Buslaev, A. Jansen, P. Bauer, G. Groenhof and B. Hess, Scalable Constant pH Molecular Dynamics in GROMACS, J. Chem. Theory Comput., 2022, 18, 6148–6160 CrossRef CAS PubMed.
- G. B. Goh, B. S. Hulbert, H. Zhou and C. L. Brooks, Constant pH molecular dynamics of proteins in explicit solvent with proton tautomerism, Proteins: Struct., Funct., Bioinf., 2014, 82, 1319–1331 CrossRef CAS PubMed.
- P. Dobrev, S. Donnini, G. Groenhof and H. Grubmüller, Accurate three states model for amino acids with two chemically coupled titrating sites in explicit solvent atomistic constant pH simulations and pKa calculations, J. Chem. Theory Comput., 2017, 13, 147–160 CrossRef CAS PubMed.
- M. G. Chiariello, F. Grünewald, R. Zarmiento-Garcia and S. J. Marrink, pH-Dependent Conformational Switch Impacts Stability of the PsbS Dimer, J. Phys. Chem. Lett., 2023, 14, 905–911 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- A. E. Aliev, M. Kulke, H. S. Khaneja, V. Chudasama, T. D. Sheppard and R. M. Lanigan, Motional timescale predictions by molecular dynamics simulations: Case study using proline and hydroxyproline sidechain dynamics, Proteins: Struct., Funct., Bioinf., 2014, 82, 195–215 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- R. P. Joosten, T. A. H. te Beek, E. Krieger, M. L. Hekkelman, R. W. W. Hooft, R. Schneider, C. Sander and G. Vriend, A series of PDB related databases for everyday needs, Nucleic Acids Res., 2011, 39, D411–D419 CrossRef CAS PubMed.
- W. Kabsch and C. Sander, Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features, Biopolymers, 1983, 22, 2577–2637 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- K. L. Chen, S. E. Mylon and M. Elimelech, Aggregation Kinetics of Alginate-Coated Hematite Nanoparticles in Monovalent and Divalent Electrolytes, Environ. Sci. Technol., 2006, 40, 1516–1523 CrossRef CAS PubMed.
- M. Kobayashi, F. Juillerat, P. Galletto, P. Bowen and M. Borkovec, Aggregation and Charging of Colloidal Silica Particles:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Effect of Particle Size, Langmuir, 2005, 21, 5761–5769 CrossRef CAS PubMed.
Effect of Particle Size, Langmuir, 2005, 21, 5761–5769 CrossRef CAS PubMed. - S. E. Mylon, K. L. Chen and M. Elimelech, Influence of Natural Organic Matter and Ionic Composition on the Kinetics and Structure of Hematite Colloid Aggregation:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Implications to Iron Depletion in Estuaries, Langmuir, 2004, 20, 9000–9006 CrossRef CAS PubMed.
Implications to Iron Depletion in Estuaries, Langmuir, 2004, 20, 9000–9006 CrossRef CAS PubMed. - M. Tirrell, Polyelectrolyte Complexes: Fluid or Solid?, ACS Cent. Sci., 2018, 4, 532–533 CrossRef CAS PubMed.
- H. Brenner, Int. J. Multiphase Flow, 1974, 1, 195–341 CrossRef.
- S. Bhattacharjee, DLS and zeta potential - What they are and what they are not?, J. Controlled Release, 2016, 235, 337–351 CrossRef CAS PubMed.
- D. Priftis, L. Leon, Z. Song, S. L. Perry, K. O. Margossian, A. Tropnikova, J. Cheng and M. Tirrell, Self-Assembly of α-Helical Polypeptides Driven by Complex Coacervation, Angew. Chem., Int. Ed., 2015, 54, 11128–11132, DOI:10.1002/anie.201504861.
- J. Choi and M. F. Rubner, Influence of the Degree of Ionization on Weak Polyelectrolyte Multilayer Assembly, Macromolecules, 2005, 38(1), 116–124, DOI:10.1021/ma048596o.
- D. Priftis, N. Laugel and M. Tirrell, Thermodynamic characterization of polypeptide complex coacervation, Langmuir, 2012, 28, 15947–15957 CrossRef CAS PubMed.
- O. Bastiansen, J. J. Christensen, L. D. Hansen and R. M. Izatt, Handbook of Proton Ionization Heats and Related Thermodynamic Quantities, J. Wiley and Sons, New York, 1976. 269 Seiten, Preis: $28.50., Ber. Bunsenges. Phys. Chem. DOI:10.1002/bbpc.19770810517.
- L. Aberkane, J. Jasniewski, C. Gaiani, J. Scher and C. Sanchez, Thermodynamic characterization of acacia gum-β-Lactoglobulin Complex Coacervation, Langmuir, 2010, 26, 12523–12533 CrossRef CAS PubMed.
- V. Petrauskas, E. Maximowitsch and D. Matulis, Thermodynamics of Ion Pair Formations Between Charged Poly(Amino Acid)s, J. Phys. Chem. B, 2015, 119, 12164–12171 CrossRef CAS PubMed.
- Z. Ou and M. Muthukumar, Entropy and enthalpy of polyelectrolyte complexation: Langevin dynamics simulations, J. Chem. Phys., 2006, 124, 163308 CrossRef PubMed.
- S. Chen and Z. G. Wang, Driving force and pathway in polyelectrolyte complex coacervation, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2209975119 CrossRef CAS PubMed.
- L. Li, S. Srivastava, S. Meng, J. M. Ting and M. V. Tirrell, Effects of Non-Electrostatic Intermolecular Interactions on the Phase Behavior of pH-Sensitive Polyelectrolyte Complexes, Macromolecules, 2020, 53, 7835–7844 CrossRef CAS.
- J. Fu and J. B. Schlenoff, Driving Forces for Oppositely Charged Polyion Association in Aqueous Solutions: Enthalpic, Entropic, but Not Electrostatic, J. Am. Chem. Soc., 2016, 138, 980–990 CrossRef CAS PubMed.
- H. S. Antila, M. Härkönen and M. Sammalkorpi, Chemistry specificity of DNA–polycation complex salt response: a simulation study of DNA, polylysine and polyethyleneimine, Phys. Chem. Chem. Phys., 2015, 17, 5279–5289 RSC.
- P. Batys, S. Kivistö, S. M. Lalwani, J. L. Lutkenhaus and M. Sammalkorpi, Comparing water-mediated hydrogen-bonding in different polyelectrolyte complexes, Soft Matter, 2019, 15, 7823–7831 RSC.
- D. Priftis and M. Tirrell, Phase behaviour and complex coacervation of aqueous polypeptide solutions, Soft Matter, 2012, 8, 9396–9405 RSC.
- Y. Zhang, P. Batys, J. T. O’Neal, F. Li, M. Sammalkorpi and J. L. Lutkenhaus, Molecular Origin of the Glass Transition in Polyelectrolyte Assemblies, ACS Cent. Sci., 2018, 4, 638–644 CrossRef CAS PubMed.
- H. S. Antila and M. Sammalkorpi, Polyelectrolyte decomplexation via addition of salt: Charge correlation driven zipper, J. Phys. Chem. B, 2014, 118, 3226–3234 CrossRef CAS PubMed.
Footnotes |
| † Data associated with the simulations available. See DOI: https://doi.org/10.23729/d8429313-6786-4a4c-9405-0301eac5fc43 |
| ‡ Electronic supplementary information (ESI) available: The dependence of the hydrodynamic diameter of polypeptides; analysis of sedimentation velocity and sedimentation equilibrium measurements; pH-metric titration; curve fitting procedures for DLS and LDV experiments; DLS, LDV, and CD results at pH 3.0 and 12.0; the changes in light scattering vs. molar ratio determined using CD; raw ITC titration data; evolution of the secondary structures of the PLL/PGA systems; Ramachandran plots for the PLL/PGA systems; radius of gyration as a function of the ID; number of intermolecular hydrogen bonds as a function of the ID; number of the intrinsic and extrinsic ion pairs as a function of the ID; radial distribution functions and cumulative number graphs for the intrinsic and extrinsic ion pairs. See DOI: https://doi.org/10.1039/d3cp01421e |
| This journal is © the Owner Societies 2023 |