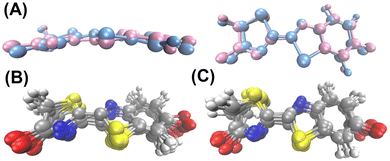The protein environment restricts the intramolecular charge transfer character of the luciferine/luciferase complex

Abstract

The electronic characterization of the luciferine/luciferase complex is fundamental to tune its photophysical properties and develop more efficient devices based on this luminiscent system. Here, we apply molecular dynamics simulations, hybrid quantum mechanics/molecular mechanics (QM/MM) calculations and transition density analysis to compute the absorption and emission spectra of luciferine/luciferase and analyze the nature of the relevant electronic state and its behaviour with the intramolecular and intermolecular degrees of freedom. It is found that the torsional motion of the chromophore is hampered by the presence of the enzyme, reducing the intramolecular charge transfer nature of the absorbing and emitting state. In addition, such a reduced charge transfer character does not correlate in a strong way neither with the intramolecular motion of the chromophore nor with the chromophore/amino-acid distances. However, the presence of a polar environment around the oxygen atom of the thiazole ring of the oxyluciferin, coming from both the protein and the solvent, enhances the charge transfer character of the emitting state.

---

1 Introduction

D-Luciferin/lucierase bioluminescent properties were first analysed by Harvey¹ in 1917 and the first crystalline structure was reported by Bitler and McElroy in 1957 by studying the North American firefly Photinus pyralis.² Since then, many other species of insects presenting this chromophore/enzyme bioluminescent system have been found.^3–16 The mechanism of the bioluminescent reaction (see Fig. 1) has been thoroughly studied and many of its intermediates have been experimentally corroborated. In a first step, the chromophore is adenylated by reacting with adenosine triphosphate (ATP) via a S_N2 nucleophilic displacement.^17,18 Consecutively, the luciferyl adenylate reacts with an oxygen molecule following a multi-step mechanism to produce oxyluciferin (OLU) in an electronically excited state,^18–25 which is able to emit light in the visible region.

Fig. 1 Schematic representation of the bioluminescent reaction of D-luciferin and the fragments of the oxyluciferin chromophore. The benzothiazole (btz) fragment is represented in blue and the thiazole (tz) one in pink. The SCCS dihedral angle is highlighted in orange.

The firefly's bioluminiscent complex has been exploited in a wide range of applications: the detection of ATP concentrations both in extracellular²⁶ and intracellular media leading to the monitoring of mitochondrial functioning²⁷ and cancer detection;^28–31 the study of different agents on cell proliferation and cytotoxycity;³² the detection of contamination of sterilized environments,^33,34 including hospitals and food;³⁵ bioimaging for, among many others, the analysis of reporter genes,^36,37 cell tracking, the study of neurodegenerative diseases,^38–43 and the analysis of protein–protein interactions via both bioluminescence resonance energy transfer (BRET)^44,45 and luciferease complementation imaging (LCI).^46–48

Despite the extensive research developed on the topic,^16,49–52 many of the factors that affect the emission mechanism and the nature of the emitting electronic state of the chromophore are still unclear. Recent computational work has characterized the emitting state as a partial intramolecular charge transfer character state.⁵³ In addition, previous studies^54,55 have pointed out the relevance of the torsion of the molecule around the SCCS dihedral angle (see Fig. 1) on the electronic properties of the chromophore and the possible generation of a twisted intramolecular CT state able to emit in the red region. Although, computational research discarded this twisted intramolecular CT state mechanism,^56,57 these works were performed without taking into account neither the environment nor the dynamic effects. Therefore, and even though the consensus is that the molecule emits in a planar conformation,⁵² it is fundamental to characterise the electronic properties with respect to the torsion in the biological media in order to understand the emission photophysics of the chromophore. In the present work, the absorption and emission spectrum of the OLU/luciferase complex is computationally investigated by means of molecular dynamics (MD) simulations and hybrid Quantum Mechanics/Molecular Mechanics (QM/MM) calculations. The CT character of the absorbing and emitting excited state is quantitatively investigated by an analysis of the transition density, which is not basis set dependent and, thus, more robust than previous analysis based on, for example, Mulliken population analysis.⁵⁶ In addition, the effect of the intramolecular torsion and the presence of the protein and solvent environments on the CT state is discussed. It is found that the enzyme restricts the intramolecular motion of the chromophore, avoiding the formation of an electronic state with strong CT character.

2 Computational details

2.1 Static potential energy rigid scan

The OLU species emits light from an electronic state which has been classified by computational methods as a state with partial intramolecular CT character.⁵³ The torsional motion around the SCCS dihedral angle (see Fig. 1), leading to a breakdown of the planarity of the molecule, could be relevant in the photophysics since the distortion of the geometry could significantly affect the electronic delocalization of the chromophore. Therefore, the effect of this intramolecular degree of freedom on the electronic structure of OLU is analyzed here in detail. As a first approach, a rigid scan around the SCCS dihedral angle was carried out for OLU in vacuum, along which the energies of the S₀ and S₁ states were computed at the time-dependent density functional theory (TD-DFT) using different functionals and the 6-311G(2d,p)^58–60 basis set. Specifically, the B3LYP,^61–63 CAM-B3LYP,⁶⁴ M062X,⁶⁵ PBE0⁶⁶ and ωB97XD⁶⁷ functionals were employed to evaluate their performance. For these calculations the Gaussian 16⁶⁸ software was used. In addition, the transition density matrix was analysed by the TheoDORE software⁶⁹ to quantify the CT character of the S₁ state along the torsion. The use of this methodology complements the analysis performed on previous works,⁵⁶ where the CT character was discussed based on Mulliken population analysis. These calculations for a simplified model were then employed to rationalise the results obtained for the more complex situation, where the chromophore is embedded in the protein environment and conformational sampling is introduced by dynamics simulations, as explained below.

2.2 Molecular dynamics simulations

In this work MD simulations of the complex oxyluciferin/luciferase were carried out. Two different approaches to compute the potential energy along the dynamics on the S₀ and S₁ states were considered. In the simplest one, the interatomic interactions were computed by means of a force field (FF). In the more accurate approach, some of the conformations sampled from the classical trajectory were selected as initial conditions to evolve hybrid QM/MM MD simulations to obtain a better structure of the chromophore, which is the only part of the system included in the QM region. For each of the simulations, a few snapshots were selected and single point QM/MM calculations were performed on top of them to compute the absorption and emission spectra and characterize the electronic states involved. Moreover, and even thought there is still some debate about the emitting species of the system,⁵² it is in general a good approximation to use the OLU mono-anion in its keto form as chromophore in the model since it is the direct product of the bioluminescence reaction and has been found to be one of the emitting species.^70–72

2.2.1 System setup. The OLU/luciferase complex was built from the X-ray diffraction structure file of the Japanese firefly luciferase (PDB ID: 2D1R⁷³), Luciola cruciata, with PyMol.⁷⁴ The adenosine monophosphate (AMP) residue was removed and the system was solvated using the tleap module of AmberTools20⁷⁵ with TIP3P⁷⁶ water molecules within a truncated octahedral box, ensuring a solvent shell of at least 12 Å from any solute molecule. This solvation process led to the inclusion of three and one initial water molecules inside the cavity of the protein for the S₀ and S₁ classical trajectories, although during the dynamics more water molecules diffused inside it. Moreover, no extra ions were required since the charge of the protein compensates for the negative charge of the OLU. The enzyme was described using the ff19SB⁷⁷ force field, whereas the General Amber Force Field (GAFF)⁷⁸ was used to describe the dihedral and improper torsions and Lennard-Jones parameters of the chromophore selected by means of the Antechamber parmchk2 module of the AmberTools20. The rest of the bonded parameters for OLU, that is, the bond and bond angle parameters for both the S₀ and S₁ electronic states, were obtained from QM calculations. Equilibrium distances and angles were obtained from a geometry optimization whereas force constants were calculated by means of the Seminario method.⁷⁹ Specifically, the optimized geometries for S₀ and S₁ and the Hessian matrices were obtained using the Gaussian16⁶⁸ software by means of DFT and TD-DFT in vacuo calculations, respectively, where the B3LYP^61–63/6-311G(2d,p)^58–60 level of theory was employed for both the S₀ and S₁ minimum-energy geometries. In the case of the S₁ optimization, the TD-DFT calculation took into account 10 roots. Moreover, the electrostatic charges were computed by using the Merz–Singh–Kollman scheme⁸⁰ at the B3LYP/6-311G(2d,p) level of theory, according to previous studies.^53,81,82 While it is true that some parameterization effort has been previously done for an OLU analogue,⁸³ this was only carried out for the electronic ground state. However, our parameters, which are listed in Tables S1–S6 of the ESI,† not only aim at describing the electronic ground state but also the first excited state. Additionally, another system was built from the same PDB file in which the AMP monoanion was kept in other to study if its presence affects the emission spectrum of the OLU chromophore. In this case, the previously discussed S₁ parameters for the chromophore were used, while the AMP was described by the GAFF together with the Merz–Singh–Kollman electrostatic charges computed at the B3LYP/6-31G*^58,84–87 level of theory.

2.2.2 Classical molecular dynamics. After setting up the solvated OLU/luciferase complex, classical MD simulations were performed for both the S₀ and S₁ states of the chromophore. The same computational protocol was used for the two simulations. First, the system was minimized for 5000 steps by means of the steepest descent algorithm, and for additional 5000 steps using the conjugate gradient algorithm. Then, it was progressively heated for 500 ps from 0 to 300 K in the NVT ensemble using a 2 fs timestep. An additional simulation was evolved at 300 K for another 500 ps in the same ensemble. The temperature was controlled by means of the Langevin thermostat⁸⁸ with a 2.0 ps⁻¹ of collision frequency. Afterwards, a production of 100 ns with a 2 fs timestep and within the NPT ensemble was performed. The temperature was also controlled by means of the Langevin thermostat with a 1.0 ps⁻¹ of collision frequency, while pressure was set to be 1.0 bar and controlled by means of the Monte Carlo barostat.⁸⁹ The particle-mesh Ewald⁹⁰ method was used with a grid spacing of 1.0 Å, and the nonbonded interactions were computed with a cutoff of 9 Å and a switching distance of 7 Å. The bonds involving hydrogen atoms were constrained using the SHAKE⁹¹ algorithm. Moreover, this simulation was extended to 500 ns in order to see whether the chromophore is able to rotate inside the cavity of the protein or not. In the case of the S₁ system with AMP inside the cavity, after the minimization and thermalization processes, 200 ns of production were run. These simulations were carried out using the previously described computational protocol.

From each of the 100 ns simulations in the S₀ and S₁ electronic states, 200 time-equidistant snapshots were extracted from the last 75 ns in order to prepare the Gaussian09 QM/MM input files for the calculation of the absorption and emission spectra. The MoBioTools software⁹² was used to automatize the preparation of the QM/MM input files, which considered 10 excited states (for the absorption spectrum) at the TD-B3LYP/6-311G(2d,p) level of theory. In the case of the emission spectrum, only the lowest-energy electronic transition was considered since the bioluminescence occurs from the S₁ state. The vertical energies were convoluted with Gaussian functions of full width at half maximum of 0.1 eV to obtain the absorption and emission spectra. For the emission spectrum computed from the 200 ns S₁ trajectory of the system with AMP inside the cavity, other 200 time-equidistant snapshots were extracted from the last 100 ns in order to prepare the Gaussian09 input files following the same procedure described before.

2.2.3 Hybrid QM/MM molecular dynamics. From the classical S₀ and S₁ trajectories 100 time-equidistant geometries, together with their respective velocities, were extracted to be used as initial conditions for 100 QM/MM MD simulations in each electronic state. Ideally, one long QM/MM MD simulation should be performed for each of the electronic states, from which the snapshots could be selected to compute the spectra. However, running such long simulations at QM/MM level is not computationally feasible. Instead, an accurate conformational sampling of the chromophore is obtained by propagating short QM/MM trajectories, starting from geometries extracted from the classical MD, well separated in time (every ns), in order to also guarantee a statiscally-accurate thermal distribution of the solvent molecules interacting with the chromophore. Thus, these QM/MM simulations can be compared with the force field based simulations to evaluate the performance of the GAFF torsion parameters against the QM/MM potential. Each of these snapshots were processed with the recently developed tools included in the COBRAMM 2 software^93,94 in order to define three different regions for the simulation: (i) the high layer, composed by the chromophore and treated with the CAM-B3LYP⁶⁴/6-31+G(d)^{58,84–87,95,96} level of theory (with 3 roots in the case of the S₁ simulation); (ii) the medium layer, formed by the protein and the water molecules within 4 Å from the chromophore treated classically; and (iii) the low layer, including the rest of the water molecules and frozen during the simulation. All the QM/MM dynamics were run with COBRAMM 2,^93,94 using its interfaces with Gaussian16 and AMBER20 suites to calculate QM and MM energies and gradients and the internal routines to build QM/MM potentials and gradients within the electrostatic embedding scheme, and to propagate the adiabatic dynamics on S₀ and S₁ with the velocity-Verlet algorithm.

The protein and the water molecules were described, respectively, by the previously used ff19SB and TIP3P force fields. The 200 trajectories (100 in the S₀ and 100 in the S₁ states) were run for 200 fs in the microcanonical ensemble (NVE) without periodic boundary conditions, which are not available in COBRAMM 2.0. For this reason, the atoms of the low layer were frozen during the QM/MM MD simulations. The time step was set to 1 fs, the cutoff for the non-bonded interactions was 10 Å, and positions and velocities of the atoms involved in X–H bonds in the medium layer were constrained with the RATTLE algorithm⁹⁷ to get a good conservation of the total energy.⁹⁸ The last step of these trajectories in the S₀ and S₁ states was used to compute the absorption and emission spectra, respectively. The preparation of the Gaussian09⁶⁸ input files was again performed by means of the MoBioTools software.⁹²

2.3. Analysis of the electronic properties

The electronically excited states, computed by QM/MM based on the snapshots of the S₀ and S₁ states taken from the classical and QM/MM MD trajectories, were analyzed by means of the TheoDORE⁶⁹ software. Specifically, the intramolecular CT number, computed from the one-electron transition density matrix between the ground state and the S₁ state (for more details, refer to ref. 69), was calculated by dividing the chromophore into two fragments: the thiazole (tz) and benzothiazole (btz) moeities, represented in Fig. 1. In addition, the absorption and emission spectra were computed by considering snapshots for which the SCCS dihedral angle lie within a particular range. Moreover, the variation of the CT number with the dihedral angle was analyzed and compared with the results obtained from the static scan of OLU in vacuum to assess the effect of the protein environment.

The QM/MM trajectory on the S₀ surface was also employed to compute the binding free energy of OLU to the enzyme by means of the one-average molecular-mechanics generalized Born surface-area (1A-MM-GBSA) approach^99,100 by using the MMPBSA.py tool.¹⁰¹ In addition, the binding free energy was decomposed into amino acid contributions by selecting only the residues located within a sphere of 5.0 Å radius from the OLU chromophore for at least 1% of the simulation time, following a similar procedure employed in a previous work.¹⁰² The residue ARG339 was also included in the analysis since it presents a positive charge and, therefore, can interact strongly with OLU. Moreover, a visual inspection of the dynamics showed that ARG339 was close to the chromophore in some of the snapshots with large CT values. A total of 16 residues were considered in the per-residue decomposition of the free binding energy. In addition, this analysis was also performed for the S₁ classical trajectories without and with the AMP contained in the cavity. Moreover, the location of the OLU inside the cavity for the QM/MM trajectory on the S₀ surface was analysed by a root mean square deviation (RMSD) and divided accordingly in 3 clusters using the K-means clustering algorithm¹⁰³ randomizing the initial set of points implemented in the cpptraj module of AmberTools20.⁷⁵

3 Results and discussion

In this work, the influence of intramolecular and intermolecular degrees of freedom on the electronic properties of the chromophore is computationally assessed. Specifically, the variation of the excitation energies, absorption and emission intensities, and CT character with the SCCS dihedral angle is analyzed. This is done by comparing the results obtained from the classical and QM/MM MD trajectories with the static potential energy scan. Regarding the impact of the intermolecular degrees of freedom, the protein residues that are more relevant in the OLU/enzyme interaction are identified and, then, a correlation between the distance between those residues and the chromophore with the CT character of the emitting state is evaluated. In the following, first, the results from the static scan are presented, followed by the discussion based on the analyses of the dynamic simulations.

3.1 Static scan around the C–C bond

The energy change of the OLU anion with the SCCS torsion have been computed by means of TD-DFT calculations using five different functionals, namely, B3LYP, CAM-B3LYP, M06-2X, PBE0 and ωB97XD, and the 6-311G(2d,p) basis set. The energy scans shown in Fig. 2 show that the S₀ surface presents two minima in the two planar situations (0 and 180° respectively) and two maxima when the benzothiazole and thiazole fragments are perpendicular to one another (90 and 270° respectively). However, the S₁ surface presents two additional minima, corresponding to the maxima of the ground state, and four maxima in total at 40, 130, 230 and 320°. Even though all the functionals present a similar behaviour, B3LYP and PBE0 show an abnormally pronounced energy decrease in the S₁ minima corresponding to the perpendicular fragments situations. This could be due to the fact that these functionals do not include long-range (LR) corrections, leading to a wrong description of CT states.¹⁰⁴ The other three functionals, which do include LR corrections, do show a smoother shape of the S₁ potential curve around the energy minima. Previous high-level wavefunction-based calculations also showed such a smooth shape of the potential.⁵⁶ Therefore, one can conclude that a LR corrected functional is needed to properly describe the shape of the potential energy curve. Thus, CAM-B3LYP was the functional selected to carry out the QM/MM MD trajectories and it is the scan that will be discussed below.

Fig. 2 S₀ (blue) and the S₁ (pink) rigid potential energy curves calculated with the functionals: (A) B3LYP, (B) CAM-B3LYP, (C) M06-2X, (D) PBE0 and (E) ωB97XD. The up x-axis shows the angle difference with respect to the planar energy minimum found at a SCCS angle of 180°.

In addition to the energies of the S₀ and S₁ states along the scan, the oscillator strength and the CT character of the S₀ → S₁ transition have been computed. As it can be observed in Fig. 3(A), the oscillator strength (f) presents two maxima and two minima corresponding, respectively, to the planar and perpendicular geometrical situations. This means that a break of the planarity of the chromophore reduces the probability of the transition to take place. This correlates well with the CT number, which increases its value when the planarity of the molecule is broken, reaching its maximum value at 90 and 270°. Both results can be rationalized by looking at the molecular orbitals involved in the electronic transition in the planar and perpendicular cases (see Fig. 3(B)). When both fragments are in the same plane (SCCS angle of 180°), the HOMO and LUMO orbitals are delocalized on the two fragments, a fact which favours the overlap of the initial and final wavefunctions and, thus, increases the transition dipole moment and the oscillator strength. Moreover, since both orbitals are delocalized over the whole molecule, the CT from one fragment to the other is not important and the CT number is small. On the flip side, when the fragments are perpendicular to each other, the HOMO is completely localized in the benzothiazole fragment, while the LUMO is localized in the thiazole one. Therefore, the overlap between the initial and final wavefunctions vanishes and the oscillator strength becomes very small. Furthermore, the CT increases since the initial and final positions of the electron are located in different fragments. In summary, the potential energy scan suggests a red shift of the absorption and emission energies when the chromophore leaves the planarity during the dynamics since the energy of the ground state increases, while the energy of the first excited state is nearly constant around both the ground and excited-state minima. In addition to the red shift, the torsional motion of OLU around the C–C single bond should also induce a decrease of the intensity of the spectra and an increase of the CT character of the S₁ state. In the following, the dynamics simulations will be analysed to see whether the expected trend predicted by the static simple model is satisfied or not.

Fig. 3 (A) Variation of the oscillator strength (orange) and CT number (green) for the S₀ → S₁ electronic transition along the dihedral angle calculated with the CAM-B3LYP functional. The up x-axis shows the angle difference with respect to the energy minimum. (B) HOMO and LUMO orbitals for the planar and perpendicular geometrical situations.

3.2 Absorption and emission spectra from the classical trajectories

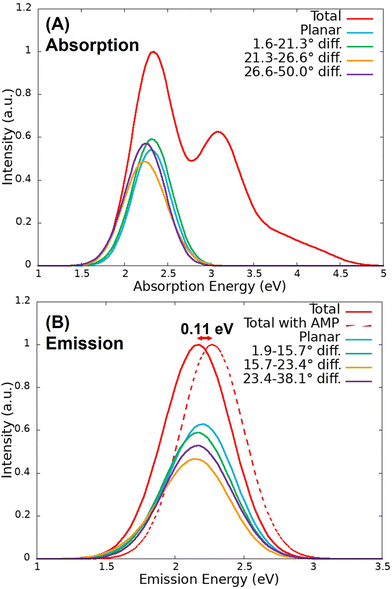
The QM/MM vertical excitation energies of the 200 equidistant snapshots taken from the S₀ and S₁ classical trajectories were convoluted to obtain the absorption and emission spectra, represented in Fig. 4. In the case of the absorption band, two peaks can be observed at 2.34 eV (530 nm) and 3.08 eV (403 nm), which correspond with the S₀ → S₁ and S₀ → S₃ electronic transitions, respectively. The emission peak was found at 2.16 eV (574 nm), in very good agreement with the experimental value (560 nm⁷³). Therefore, the methodology consisting of classical MD followed by QM/MM vertical energy calculations provides accurate results in terms of energy. Moreover, as it can be observed in Fig. 4(B), the inclusion of AMP in the model induces a slight blue shift of the emission spectrum of 0.11 eV, which is within the DFT error. This proves that the inclusion of the AMP inside the protein does not affect much the electronic properties of the system.

Fig. 4 (A) Absorption and (B) emission spectra computed from the classical trajectories, together with their respective contributions from the S₀ → S₁ band depending on the SCCS dihedral angle. Additionally, the emission spectra obtained from the classical MD with the AMP inside the cavity is shown with a dashed line.

The S₀ → S₁ contribution of the absorption spectra and the emission spectra were decomposed into bands where the chromophore presents different dihedral angles. In particular, the bands have been analysed by classifying the 200 sampled snapshots in 10 groups of 20 geometries according to the dihedral angle difference with respect to planarity (180°). Each group of snapshots contains 20 geometries to ensure that all the divisions are equally statistically meaningful, since the population of planar geometries is larger than the ones with distorted angles.

However, since the 140 geometries corresponding to the dihedral angles difference between 1.6 and 21.3°, in the case of the S₀ trajectory, and between 1.9 and 15.7°, in the case of the S₁ trajectory, resulted in very similar bands, they have been represented together taking into account the number of geometries so that the relative intensity of each group is comparable. The same figure without combining geometries is presented in Fig. S2 of the ESI.† As it can be observed in Fig. 4, there is a very small red shift for the absorption and emission bands when the chromophore goes from the planar to the bent configuration. In the case of the absorption spectrum, the planar contribution of the band peaks at 2.31 eV, while the two non-planar contributions peak at 2.24 and 2.23 eV, respectively. In the case of emission, the planar contribution of the band peaks at 2.17 eV, while the two contributions from the most rotated dihedral angle peak at 2.14 and 2.16 eV. As seen in the static scan for the chromophore in vacuum (Fig. 2), the red shift is important only when the deviation from planarity is large (more than 50°), reaching values for the SCCS angle smaller than 130° and larger than 230° degrees. Such a large deviations are not reached during the classical MD trajectories.

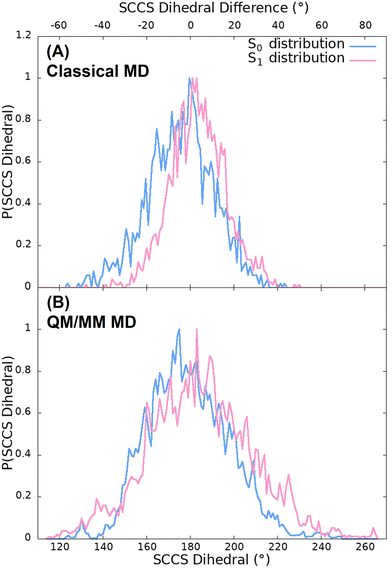
Fig. 5(A) shows the probability distribution of the dihedral angle for the classical trajectories. As it can be seen, the population of dihedral angle deviations from planarity larger than 50°, for both the S₀ and S₁ trajectories, is insignificant. Moreover, this small deviations from planarity not only happen for the 100 ns classical simulations but also for the 500 ns trajectories as it can be observed in Fig. S3 (ESI†). It is because of this that a very small red shift is observed in the spectra. Moreover, the distribution of the classical trajectory on the ground state (with a full width at half maxima (FWHM) of 36°) is wider than that of the excited state (with a FWHM of 29°). These differences between both states arise from the stretching and bending force field parameters and the atomic charges since the torsional and non-bonding parameters are the same for both simulations, as they were directly taken from the GAFF. Furthermore, this situation does not coincide with the expected behaviour attending to the static scan represented in Fig. 2 since the energy barrier of the first excited state is lower than that of the ground state. This could indicate that the force field employed to describe the motion of the chromophore is not adequate and a more accurate description could be needed. For this reason, we improved the quality of the analysis by performing QM/MM simulations in the S₀ and S₁ states of OLU.

Fig. 5 Probability distributions of the SCCS dihedral angles for the S₀ (blue) and the S₁ (pink) trajectories evolved at (A) classical and (B) QM/MM level. The up x-axis shows the angle difference with respect to the energy minimum.

3.3 Absorption and emission spectra from the QM/MM trajectories

The absorption and emission spectra were obtained from the QM/MM vertical energies of the last snapshot of the 100 QM/MM trajectories evolved on the S₀ and S₁ surfaces, respectively. As it can be observed in Fig. 6(A), the absorption spectrum presents two peaks at 2.48 eV (500 nm) and 3.32 eV (373 nm) corresponding again to the S₀ → S₁ and S₀ → S₃ electronic transitions, respectively. These energies are blue shifted with respect to those obtained from the classical trajectory (2.34 and 3.08 eV). Moreover, the relative intensity of the second peak is lower than that of the spectrum computed from the classical trajectory. In the case of the emission spectrum of Fig. 6(B), the peak appears at 2.17 eV (571 nm), 3 nm above the value of the spectrum from the classical trajectory and 11 nm above the experimental value (560 nm). Therefore, once more, the agreement with the experiment is very good.

Fig. 6 (A) Absorption and (B) emission spectra computed from the QM/MM trajectories, together with their respective contributions from different SCCS dihedral angles.

The effect of the torsion around the SCCS dihedral angle has been analysed by decomposing the S₀ → S₁ band of the absorption spectrum and the emission spectrum by dividing the 100 sampled geometries in 5 groups according to the dihedral angle difference with respect to the planar case of 180° (each group containing 20 geometries). In this case, only the 60 geometries corresponding to the dihedral angle difference between 4.5 and 23.5°, in the case of the S₀ trajectories, and the 40 geometries that present dihedral angles difference between 5.5 and 20.5°, in the case of the S₁ trajectories, have been represented together since they present very similar bands (again each contribution has been scaled considering the number of geometries so that the intensities of each group is comparable). As it can be observed in Fig. 6, the absorption band is red shifted when the chromophore is distorted from the planar configuration, while for the emission band the red shift only appears for very distorted configurations. In fact, small distortions of 5 to 21° induce a blue shift, probably due to the effect of other factors. In addition, the torsional motion also induces a decrease in the absorption and emission intensity (hypochromism), an effect that is expected looking at the behaviour of the oscillator strength along the static scan.

The spectra shown in Fig. 6 suggest, thus, that the OLU/luciferase complex follows the expected trend when the dihedral angle is strongly distorted, that is, the energy is red shifted and the intensity is reduced when the torsion increases. This can be rationalize when looking at the dihedral angle distribution obtained from the QM/MM dynamics displayed in Fig. 5(B). The distributions for both ground and excited states (with a FWHM of 43 and 49° for the S₀ and S₁, respectively) are broader than those of the classical trajectories, reaching values that differ from the planar geometry by more than 50°. According to the static scan (Fig. 3), this is the necessary angle difference to have a significant red shift and hypochromism in the spectra. Moreover, the width of the S₁ distribution is slightly larger than the one of the S₀ distribution, in consonance with the shape of the potential energy curves shown in Fig. 2. Summarizing, although the QM/MM vertical energy calculations based on both classical and QM/MM trajectories provide emission spectra that compare well with the experimental data, it seems that the classical trajectories underestimate the vibrational torsion of OLU, resulting in narrow angle distributions, as reported by Cerezo et al.⁸³ Therefore, even if energetically accurate, the classical MD protocol alone would produce a not accurate enough conformational distribution of the chromophore in the biological environment, which can be then reached once the molecule is allowed to move in a QM/MM potential.

3.4 Effect of the intramolecular and intermolecular degrees of freedom on the CT character

In the previous section it has been shown that the torsional motion of the chromophore when it is embedded in the protein is large enough to induce a red shift of the absorption and emission spectra with respect to the planar geometry. Now, we will analyse how the CT number changes with respect of the variation of the dihedral angle. According to Fig. 3, the distortion from the planarity should increase the CT character of the bright state. The snapshots extracted from the trajectories were grouped in 10 (classical trajectory) and in 5 (QM/MM trajectory) ensembles according to the dihedral angle difference with respect to planarity (180°), such that each ensemble contains 20 geometries. Then, the average CT number and their corresponding standard deviation for each ensemble was computed and the result is displayed in Fig. 7. As it is shown, the average CT number does not present significant oscillations when the SCCS angle difference increases, not even for the emission spectrum at QM/MM level for which angle differences larger than 50° are reached during the dynamics. Such a constant behaviour of the CT number can be due the combination of two factors. First, the torsional motion is not large enough to have a significant increase of the CT character. As shown in Fig. 3(A), although a distortion of 50° already enhances the CT character of the excited state, such a large distortion is achieved only for a few snapshots in the QM/MM trajectory (Fig. 5(B)). Second, even for these largely distorted geometries there might exist some other degrees of freedom that counteract the effect of having a large torsional angle. It is important to notice in Fig. 7 that the standard deviation of the CT number is larger for the QM/MM trajectory than for the classical one because the dihedral angle intervals employed to have the same number of snapshots in each interval is wider for the QM/MM analysis than for the classical one. This larger angle interval contains larger molecular distortions and, therefore, stronger CT number oscillations.

Fig. 7 Variation of the CT number with the the SCCS dihedral angle difference from planarity for the (A) absorption and (B) emission spectra computed from snapshots taken from the classical (orange) and QM/MM (green) trajectories.

The relevance of other intramolecular degrees of freedom was analyzed by a structural analysis. Specifically, the 20 geometries of the chromophore with both the smallest and largest CT number values were separately gathered in clusters, for which the centroids (representative structures) were obtained. These geometrical configurations were extracted from the S₀ QM/MM dynamics, which is the one that presents the most important CT oscillations as shown in Fig. 7. The centroid geometries for each of the clusters are represented without the enzymatic environment in Fig. 8(A) and with it in Fig. S4 (ESI†), and the ensemble of all the 20 geometries per cluster in Fig. 8(B and C). As it can be seen, no significant differences are observed between the representative structures with the smallest and largest CT number. In fact, the root mean square deviation (RMSD) between the geometries of each cluster and its centroid (0.41 ± 0.16 Å and 0.41 ± 0.17 Å for the cluster with the smallest and largest CT values, respectively) is larger than the RMSD between both centroid structures (0.33 Å), which means that the conformational change within each cluster is larger than the variations between them. In addition, the polar environment of the OLU for the small and large CT number clusters was analysed around the oxygen atoms of the thiazole (O^tz) and benzothiazole (O^btz) fragments. As previously demonstrated,²⁵ the solvation of the O^btz is larger than that of the O^tz, as it can be observed in Fig. S5 (ESI†), where the radial distribution functions between the two oxygen atoms of the chromophore and the oxygen atom of the water molecules are plotted. Moreover, it is shown that the cluster with the largest CT number values presents a larger solvation for both oxygen atoms. When looking at the number of hydrogen bonds, considering a donor–acceptor distance and an angle cutoffs of 3 Å and 150°, respectively, listed in Table S7 (ESI†), it is observed that hydrogen bonding between water and the chromophore is less important in the cases of the smallest CT number cluster. Contrary, the number of hydrogen bonds between the protein and the chromophore is very similar for both clusters. However, in the case of the smallest CT number cluster the water molecules are only present around the O^btz, while for the largest CT number cluster they surround both O atoms. When the effect of the whole environment, the water molecules and the protein, is considered, it can be concluded that the cluster of geometries with the largest CT number presents a higher number of hydrogen bonds, mainly around the thiazole oxygen atom. This result is coherent with the electron transfer direction during the excitation, which happens from the benzothiazole to the thiazole moiety. A large positive charge around the thiazole fragment due to the presence of hydrogen atoms interacting with the oxygen atom of OLU stabilize the CT state. In summary, the CT character of the electronic transition cannot be rationalize in terms of a set of intramolecular degrees of freedom, but it correlates well with the solvation of the oxygen atom of the thiazole moiety.

Fig. 8 (A) Centroid geometries of the two clusters with the 20 snapshots with smallest (blue) and largest (pink) CT number values extracted from the QM/MM trajectory of the S₀ state. Clusters of the 20 geometries with (B) smallest and (C) largest CT number values.

An additional analysis to investigate the OLU/protein intermolecular degrees of freedom is performed. In particular, the OLU/enzyme binding free energy was computed for the QM/MM S₀ dynamics by means of the 1A-MM-GBSA approach.^99,100 Then, the binding free energy was decomposed into amino acids contributions. In order to reduce the computational effort, the decomposition was performed for the 15 residues that are located at shortest distances from OLU along the dynamics. In addition, the ARG339 residue was also included in the analysis because it bears a positive charge that brings it to be close to the chromophore along the trajectory, as visible during a 3D visual analysis of the dynamics, and we thus hypothesize a potential strong interaction between OLU and ARG339.

Fig. 9 shows the binding free energy per residue and the electrostatic contribution, which should be the most relevant one for CT since in the electrostatic-embedding QM/MM vertical energy calculations only the point charges of the environment polarize the QM region by electrostatic interactions. As it can be observed, all the total binding free energies (in absolute value) are bellow −4 kcal mol⁻¹ and in most of the cases the electrostatic contribution is the most important one to the total energy, with the exception of the residues PHE249, GLY341, LEU344 and THR345. Moreover, the residue ARG339 presents a very strong electrostatic interaction, as expected due to its positive charge and proximity to the chromophore. Additionally, similar analysis was performed on the S₁ classical trajectories with and without the AMP co-factor in order to elucidate whether the surrounding environment is the same and how the binding free energy per residue is affected. As it can be observed in Fig. S6 (ESI†), more than half of the interacting residues are the same in both dynamics. However, the trajectory that includes AMP shows more residues present for at least 1% of the simulation time, which could mean that the presence of the co-factor induces some flexibility in the cavity and allows the interaction with more residues. However, as discussed above, the presence of these new additional residues interacting with OLU does not significantly influence the emission spectrum.

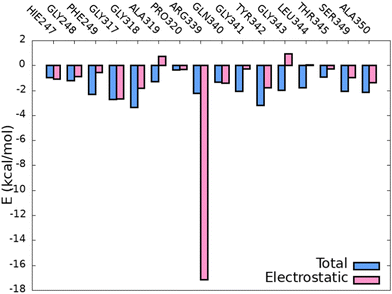Fig. 9 Total (blue) and electrostatic (pink) binding free energy of the chromophore with the closest residues of the protein along the S₀ QM/MM selected snapshots.

Once the most relevant protein residues have been identified, a potential correlation between their motion and the CT character of OLU was analysed. Fig. 10(A) shows the variation of the CT number with the distance between the centers of mass of OLU and of each of the 16 residues for the 100 snapshots of the S₀ QM/MM trajectory. As it can be seen, the CT number does not depend on any of the distances since all the positions of the surrounding amino-acids of the protein present a very wide range of CT numbers. However, Fig. 10(A) also shows that the position of some amino-acids is clustered into two or three regions defined by the distance from OLU. Previously, different positions of the chromophore were found for different protein species.¹⁰⁵ This finding indicates that the location of the chromophore inside the enzyme could be relevant to determine its electronic properties. In order to analyze further a possible relation between the position of the amino-acids and the CT of the excited state of OLU the following analysis was performed. First, the RMSD of the chromophore inside the cavity was computed and, second, a clustering analysis based on the RMSD on the selected snapshots of the trajectory was performed. Fig. 10(B) shows the result of the RMSD analysis and the separation in three different clusters, which are represented in Fig. S7 (ESI†). Moreover, colours in Fig. 10(A) represent whether the chromophore belongs to cluster 1, 2 or 3 for each analysed structure. In can be observed that for some amino-acids, such as HIE247, GLY317, GLN340 and THR345, the distance to OLU does not depend on the cluster, while for others, for example, PRO320, ARG339 and ALA350, the clusters are well separated in terms of the distance to the chromophore. However, the different clusters do not provide different CT numbers. Specifically, the average CT numbers are 0.555 ± 0.087, 0.541 ± 0.085 and 0.559 ± 0.054 for clusters 1 to 3, respectively. In addition, when a similar analysis is performed for the previously mentioned clusters formed by the smallest and largest CT numbers, shown in Fig. S8 of the ESI,† it can be observed that the smallest and largest values of CT are present for the same wide range of distances. Therefore, after a detailed analysis, we can exclude any dependency between the CT character of the emitting states of OLU and its position inside the cavity of the protein.

Fig. 10 (A) CT number variation with the distance between the centers of mass of the chromophore and different amino-acids along the 100 S₀ QM/MM MD selected snapshots. (B) Root mean squared deviation of the OLU inside the cavity. For both representations colours blue, green and orange represent clusters 1 to 3.

4 Conclusions

The intensive research on the OLU/luciferase complex performed along the last decades has shown that this biological system can be exploited in a wide range of applications. A deep knowledge of the photophysics of the chromophore/enzyme complex will allow the tuning of its properties, leading to the development of more efficient devices with enhanced properties. The CT character of the emitting electronic state is one of the key features of the complex since it is intimately related to the emission intensity. However, a clear consensus about the nature of this electronic state was not achieved yet. Here, we quantitatively characterized the bright state involved in both the absorption and emission spectra in terms of energy and CT character by combining MD simulations, hybrid QM/MM calculations, and transition density analysis. These results are compared with a simplified static model of OLU in vacuum, for which the electronic properties are computed along the SCCS torsion.

The static calculations of the chromophore in vacuum predicts a red shift of the absorption and emission spectra when the molecule is distorted from the planar configuration. Moreover, such a distortion also induces the enhancement of the CT character and the reduction of the absorption and emission intensities. The spectra computed by QM/MM vertical energy calculations, based on snapshots sampled by classical MD, show a good agreement with the experiment. However, an energy dependency with the torsional angle was not found, since classical trajectories are not able to sample a wide range of torsional angles, which would be needed to obtain a remarkable red shift. However, when the conformational sampling is performed propagating the dynamics along the QM/MM potential energy surfaces, the torsional angle distributions are slightly broader and the absorption and emission spectra shows the expected red shift for large deviations from the planarity.

The variation of the CT number with the SCCS dihedral angle, based on both classical and QM/MM dynamics simulations, was also investigated. However, a clear trend was not found because the interactions with the protein preclude large geometrical distortions of OLU. Nevertheless, further analyses including additional intramolecular and intermolecular degrees of freedom were performed. A clustering classification of the snapshots according to their CT number concluded that there is not correlation between the CT character of the chromophore and its intramolecular motion when OLU is embedded in the enzyme. Thus, the intermolecular OLU/protein and OLU/water degrees of freedom were also explored. Specifically, the protein residues that contribute the most to the binding free energy were identified. Then, a possible correlation between the motion of these residues and the position of the chromophore inside the cavity with the CT character of the chromophore was searched. However, once again, a clear dependency of the CT number with the OLU/residue distance was not found. Nevertheless, when the solvation sphere around the chromophore was analyzed, it was found that the presence of polar groups from the protein or water molecules interacting by hydrogen bonding with the oxygen atom of the thiazole moiety enhances the CT character of the electronic transition. Based on our analyses, we can conclude that protein mutations that introduces flexibility in the protein, allowing for a larger degree of mobility of the chromophore, or increases the solvation of the chromophore will induce an enhancement of the CT character and a reduction of the emission intensity. In the same way, if the mutation leads a more rigid protein scaffold or a more non-polar environment the CT nature will be reduced, increasing the emission intensity.

Author contributions

HMF: data curation, formal analysis, investigation, validation, visualization, writing – original draft, writing – review and editing. DA: supervision, writing – review and editing. MG and JJN: conceptualization, funding acquisition, project administration, resources, supervision, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM) and CINECA. We also thank the support of the Spanish Ministry of Science and Innovation through the project PID2020-117806GA-I00 funded by MCIN/AEI/10.13039/501100011033, the Comunidad de Madrid through the Attraction of Talent Program (Grant ref 2018-T1/BMD-10261) and the Universidad Autónoma de Madrid through the Ayudas para el Fomento de la Investigación en Estudios de Máster program and the predoctoral Contract Formación de Personal Investigador (FPI-UAM). The work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme and the CINECA computing center. D.A. and M.G thank funding from the European Union's Horizon 2020 research and innovation program under the H2020-NMBP-TO-IND-2018-2020/DT-NMBP-09-2018 grant agreement No. 814492 (SIMDOME).

References

1. E. N. Harvey, Am. J. Physiol., 1917, 42, 342–348.
2. B. Bitler and W. D. McElroy, Arch. Biochem. Biophys., 1957, 72, 358–368.
3. J. H. Devine, G. D. Kutuzova, V. A. Green, N. N. Ugarova and T. O. Baldwin, Biochim. Biophys. Acta, Gene Struct. Expression, 1993, 1173, 121–132.
4. H. Tatsumi, N. Kajiyama and E. Nakano, Biochim. Biophys. Acta, Gene Struct. Expression, 1992, 1131, 161–165.
5. M. Tsutomu, T. Hiroki and N. Eiichi, Gene, 1989, 77, 265–270.
6. H. Tatsumi, T. Masuda, N. Kajiyama and E. Nakano, J. Biolumin. Chemilumin., 1989, 3, 75–78.
7. Y. Oba, N. Mori, M. Yoshida and S. Inouye, Biochem., 2010, 49, 10788–10795.
8. B. R. Branchini, T. L. Southworth, J. P. DeAngelis, A. Roda and E. Michelini, Comp. Biochem. Physiol., Part B: Biochem. Mol. Biol., 2006, 145, 159–167.
9. Y. S. Choi, K. S. Lee, J. S. Bae, K. M. Lee, S. R. Kim, I. Kim, S. M. Lee, H. D. Sohn and B. R. Jin, Comp. Biochem. Physiol., Part B: Biochem. Mol. Biol., 2002, 132, 661–670.
10. Y. S. Choi, J. S. Bae, K. S. Lee, S. R. Kim, I. Kim, J. G. Kim, K. Y. Kim, S. E. Kim, H. Suzuki, S. M. Lee, H. D. Sohn and B. R. Jin, Comp. Biochem. Physiol., Part B: Biochem. Mol. Biol., 2003, 134, 199–214.
11. Y. Ohmiya, N. Ohba, H. Toh and F. I. Tsuji, Photochem. Photobiol., 1995, 62, 309–313.
12. G. B. Sala-Newby, C. M. Thomson and A. K. Campbell, Biochem. J., 1996, 313, 761–767.
13. B. Said Alipour, S. Hosseinkhani, M. Nikkhah, H. Naderi-Manesh, M. J. Chaichi and S. K. Osaloo, Biochem. Biophys. Res. Commun., 2004, 325, 215–222.
14. J. C. Day, M. J. Chaichi, I. Najafil and A. S. Whiteley, J. Insect Sci., 2006, 6, 37.
15. K. S. Lee, H. J. Park, J. S. Bae, T. W. Goo, I. Kim, H. D. Sohn and B. R. Jin, J. Biotechnol., 2001, 92, 9–19.
16. Z. M. Kaskova, A. S. Tsarkova and I. V. Yampolsky, Chem. Soc. Rev., 2016, 45, 6048–6077.
17. A. Dukhovich, A. Sillero and M. A. G. Sillero, FEBS Lett., 1996, 395, 188–190.
18. S. M. Marques and J. C. E. D. Silva, IUBMB Life, 2009, 61, 6–17.
19. B. R. Branchini, C. E. Behney, T. L. Southworth, D. M. Fontaine, A. M. Gulick, D. J. Vinyard and G. W. Brudvig, J. Am. Chem. Soc., 2015, 137, 7592–7595.
20. M. Yu and Y. Liu, Molecules, 2021, 26, 4222.
21. R. Berraud-Pache, R. Lindh and I. Navizet, J. Phys. Chem. B, 2018, 122, 5173–5182.
22. G. Orlova, J. D. Goddard and L. Y. Brovko, J. Am. Chem. Soc., 2003, 125, 6962–6971.
23. L. Yue, Y. J. Liu and W. H. Fang, J. Am. Chem. Soc., 2012, 134, 11632–11639.
24. L. P. D. Silva, A. J. M. Santos and J. C. E. D. Silva, J. Phys. Chem. A, 2013, 117, 94–100.
25. C. I. Song and Y. M. Rhee, J. Am. Chem. Soc., 2011, 133, 12040–12049.
26. E. H. Abraham, A. Y. Salikhova and E. B. Hug, Drug Dev. Res., 2003, 59, 152–160.
27. I. R. Lanza and K. S. Nair, Methods Enzymol., 2009, 457, 349–372.
28. X. Chen, Y. Qian and S. Wu, Free Radical Biol. Med., 2015, 79, 253–263.
29. D. Senyilmaz and A. A. Teleman, F1000Prime Rep., 2015, 7, 41.
30. P. E. Andreotti, I. A. Cree, C. M. Kurbacher, D. M. Hartmann, D. Linder, G. Harel, I. Gleiberman, P. A. Caruso, S. H. Ricks and M. Untch, Cancer Res., 1995, 55, 5276–5282.
31. S. Glaysher and I. A. Cree, in Cell Sensitivity Assays: The ATP-based Tumor Chemosensitivity Assay, ed. I. A. Cree, Humana Press, Totowa, NJ, 2011, pp. 247–257.
32. M. Guardigli, A. Lundin and A. Roda, Chemiluminescence and Bioluminescence: Past, Present and Future, Royal Society of Chemistry, 2010, pp. 143–190.
33. K. M. Björkman and D. M. Karl, J. Microbiol. Methods, 2001, 47, 159–167.
34. Y. S. Huang, Y. C. Chen, M. L. Chen, A. Cheng, I. C. Hung, J. T. Wang, W. H. Sheng and S. C. Chang, Am. J. Infect. Control, 2015, 43, 882–886.
35. G. Shama and D. J. Malik, Int. J. Hyg. Environ. Health, 2013, 216, 115–125.
36. P. Ray and S. S. Gambhir, Methods Mol. Biol., 2007, 411, 131–144.
37. J. Brogan, F. Li, W. Li, Z. He, Q. Huang and C. Y. Li, Radiat. Res., 2012, 177, 508–513.
38. Z. Wang and E. S. Yeung, Pure Appl. Chem., 2001, 73, 1599–1611.
39. W. C. Hsu, M. N. Nenov, A. Shavkunov, N. Panova, M. Zhan and F. Laezza, PLoS One, 2015, 10, e0117246.
40. S. A. Aelvoet, A. Ibrahimi, F. Macchi, R. Gijsbers, C. V. D. Haute, Z. Debyser and V. Baekelandt, J. Neurosci., 2014, 34, 16518–16532.
41. J. C. Watts, K. Giles, A. Oehler, L. Middleton, D. T. Dexter, S. M. Gentleman, S. J. DeArmond and S. B. Prusiner, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19555–19560.
42. J. C. Watts, C. Condello, J. Stöhr, A. Oehler, J. Lee, S. J. DeArmond, L. Lannfelt, M. Ingelsson, K. Giles and S. B. Prusiner, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10323–10328.
43. J. Stöhr, C. Condello, J. C. Watts, L. Bloch, A. Oehler, M. Nick, S. J. DeArmond, K. Giles, W. F. DeGrado and S. B. Prusiner, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10329–10334.
44. G. Borghei and E. A. Hall, Analyst, 2014, 139, 4185–4192.
45. P. Iglesias and J. A. Costoya, Biosens. Bioelectron., 2009, 24, 3126–3130.
46. T. Azad, A. Tashakor and S. Hosseinkhani, Anal. Bioanal. Chem., 2014, 406, 5541–5560.
47. M. Awais and T. Ozawa, Mol. BioSyst., 2011, 7, 1376–1387.
48. A. K. M. Kafi, M. Hattori and T. Ozawa, Nano LIFE, 2010, 01, 79–87.
49. N. N. Ugarova and L. Y. Brovko, J. Lumin., 2002, 17, 321–330.
50. A. Fleiss and K. S. Sarkisyan, Curr. Genet., 2019, 65, 877–882.
51. C. Carrasco-López, N. M. Lui, S. Schramm and P. Naumov, Nat. Rev. Chem., 2021, 5, 4–20.
52. M. B. Al-Handawi, S. Polavaram, A. Kurlevskaya, P. Commins, S. Schramm, C. Carrasco-López, N. M. Lui, K. M. Solntsev, S. P. Laptenok, I. Navizet and P. Naumov, Chem. Rev., 2022, 122, 13207–13234.
53. C. García-Iriepa, M. Zemmouche, M. Ponce-Vargas and I. Navizet, Phys. Chem. Chem. Phys., 2019, 21, 4613–4623.
54. B. R. Branchini, R. A. Magyar, M. H. Murtiashaw, S. M. Anderson, L. C. Helgerson and M. Zimmer, Biochem., 1999, 38, 13223–13230.
55. T. Nakatsu, S. Ichiyama, J. Hiratake, A. Saldanha, N. Kobashi, K. Sakata and H. Kato, Nature, 2006, 440, 372–376.
56. N. Nakatani, J. Y. Hasegawa and H. Nakatsuji, J. Am. Chem. Soc., 2007, 129, 8756–8765.
57. Y. Tianxiao and J. D. Goddard, J. Phys. Chem. A, 2007, 111, 4489–4497.
58. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
59. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
60. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
61. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
62. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
63. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
64. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
65. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
66. C. Adamo and V. Barone, Chem. Phys., 1999, 110, 6158.
67. J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
68. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
69. F. Plasser, J. Chem. Phys., 2020, 152, 084108.
70. S. F. Chen, Y. J. Liu, I. Navizet, N. Ferré, W. H. Fang and R. Lindh, J. Chem. Theory Comput., 2011, 7, 798–803.
71. Y.-Y. Cheng and Y.-J. Liu, J. Chem. Theory Comput., 2015, 11, 5360–5370.
72. L. P. Da Silva and J. C. Esteves Da Silva, J. Chem. Theory Comput., 2011, 7, 809–817.
73. T. Nakatsu, S. Ichiyama, J. Hiratake, A. Saldanha, N. Kobashi, K. Sakata and H. Kato, Nature, 2006, 440, 372–376.
74. L. Schrödinger and W. DeLano, PyMOL, http://www.pymol.org/pymol.
75. D. Case, H. Aktulga, K. Belfon, I. Ben-Shalom, S. Brozell, D. Cerutti, T. C. III, G. Cisneros, V. Cruzeiro, T. Darden, R. Duke, G. Giambasu, M. Gilson, H. Gohlke, A. Goetz, R. Harris, S. Izadi, S. Izmailov, C. Jin, K. Kasavajhala, M. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. OHearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. Simmerling, N. Skrynnikov, J. Smith, J. Swails, R. Walker, J. Wang, H. Wei, R. Wolf, X. Wu, Y. Xue, D. York, S. Zhao and P. Kollman, AMBER 2020, University of California, San Francisco.
76. W. Jorgensen, J. Chandrasekhar, J. Madura, R. Impey and M. Klein, J. Chem. Phys., 1983, 79, 926–935.
77. C. Tian, K. Kasavajhala, K. A. Belfon, L. Raguette, H. Huang, A. N. Migues, J. Bickel, Y. Wang, J. Pincay and Q. Wu, et al. , J. Chem. Theory Comput., 2019, 16, 528–552.
78. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
79. J. M. Seminario, Int. J. Quantum Chem., 1996, 60, 1271–1277.
80. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145.
81. R. Berraud-Pache and I. Navizet, Phys. Chem. Chem. Phys., 2016, 18, 27460–27467.
82. C. García-Iriepa, P. Gosset, R. Berraud-Pache, M. Zemmouche, G. Taupier, K. D. Dorkenoo, P. Didier, J. Léonard, N. Ferré and I. Navizet, J. Chem. Theory Comput., 2018, 14, 2117–2126.
83. J. Cerezo, C. Garca-Iriepa, F. Santoro, I. Navizet and G. Prampolini, Phys. Chem. Chem. Phys., 2023, 25, 5007–5020.
84. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
85. M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803.
86. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
87. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
88. T. Schneider and E. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 1302.
89. N. Metropolis and S. Ulam, J. Am. Stat. Assoc., 1949, 44, 335–341.
90. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
91. S. Miyamoto and P. Kollman, J. Comput. Chem., 1992, 13, 952–962.
92. G. Cárdenas, J. Lucia-Tamudo, H. Mateo-delaFuente, V. F. Palmisano, N. Anguita-Ortiz, L. Ruano, A. Pérez-Barcia, S. Díaz-Tendero, M. Mandado and J. J. Nogueira, J. Comput. Chem., 2023, 44, 516–533.
93. O. Weingart, A. Nenov, P. Altoè, I. Rivalta, J. Segarra-Martí, I. Dokukina and M. Garavelli, J. Mol. Model., 2018, 24, 1–30.
94. D. Avagliano, M. Bonfanti, A. Nenov and M. Garavelli, J. Comput. Chem., 2022, 43, 1641–1655.
95. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
96. G. W. Spitznagel, T. Clark, P. V. R. Schleyer and W. J. Hehre, J. Comput. Chem., 1987, 8, 1109–1116.
97. H. C. Andersen, J. Comput. Phys., 1983, 52, 24–34.
98. D. Avagliano, M. Bonfanti, M. Garavelli and L. González, J. Chem. Theory Comput., 2021, 17, 4639–4647.
99. J. Srinivasan, J. Miller, P. A. Kollman and D. A. Case, J. Biomol. Struct. Dyn., 1998, 16, 671–682.
100. P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan and W. Wang, et al. , Acc. Chem. Res., 2000, 33, 889–897.
101. B. R. Miller III, T. D. McGee Jr, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, J. Chem. Theory Comput., 2012, 8, 3314–3321.
102. V. F. Palmisano, C. Gómez-Rodellar, H. Pollak, G. Cárdenas, B. Corry, S. Faraji and J. J. Nogueira, Phys. Chem. Chem. Phys., 2021, 23, 3552–3564.
103. J. Hartigan, Clustering Algorithms, John Wiley and Sons, New York, 1975.
104. M. J. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Chem. Phys., 2008, 128, 044118.
105. C. Carrasco-López, J. C. Ferreira, N. M. Lui, S. Schramm, R. Berraud-Pache, I. Navizet, S. Panjikar, P. Naumov and W. M. Rabeh, Life Sci. Alliance, 2018, 1, e201800072.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01387a

---