Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Alkane-based eutectic phase change materials doped with carbon nanomaterials†
Mikołaj
Więckowski
 *ab,
Marek
Królikowski
*ab,
Marek
Królikowski
 b,
Łukasz
Scheller
c and
Marzena
Dzida
b,
Łukasz
Scheller
c and
Marzena
Dzida
 c
c
aDoctoral School of Warsaw University of Technology, Politechniki 1, 00-664 Warsaw, Poland. E-mail: mikolaj.wieckowski.dokt@pw.edu.pl
bDepartment of Physical Chemistry, Faculty of Chemistry, Warsaw University of Technology, Noakowskiego 3, 00-664 Warsaw, Poland
cInstitute of Chemistry, University of Silesia in Katowice, Szkolna 9, 40-006 Katowice, Poland
First published on 19th June 2023
Abstract
Cold thermal energy storage is an issue of increasing importance on a global scale particularly in the format of passive thermal protection. This study presents three eutectic Phase Change Materials (ePCMs) composed of n-alkanes, which provide passive temperature control (their operation is automatically induced by exceeding the limit temperature without the need for a control system) around 4 °C (277.2 ± 2 K) and are chemically neutral. The solid–liquid equilibrium (SLE) in the following binary systems was investigated: {n-tetradecane + n-heptadecane}, {n-tetradecane + n-nonadecane}, {n-tetradecane + n-heneicosane}, allowing the determination of two ePCMs with enthalpies close to 220 J g−1 and one significantly lower (155.5 J g−1). Moreover, two solid–liquid–liquid equilibrium (SLLE) phase diagrams were determined for systems: {n-tetradecane + 1,6-hexanediol} and {n-tetradecane + 1,12-dodecanediol}. In addition, the work provides a systematic analysis of the problem of designing ePCMs with specific properties and the aspects that need to be considered. The possibility of predicting the parameters of eutectic mixtures using the UNIFAC (Do) equation and the equation of ideal solubility was verified. A method for predicting the enthalpy of melting of eutectic was also proposed and confronted with the results of DSC analysis. Thermodynamic studies have been supplemented with measurements and correlation of experimental data of ePCMs density and dynamic viscosity as a function of temperature. The final issue is the improvement of the thermal conductivity of paraffins by the addition of nanomaterials such as Single Wall Carbon Nanotubes (SWCNTs), Expandable Graphite (GIC) or Expanded Graphite (EG). The possibility of forming a long-lasting composite material composed of ePCMs and 1 wt% of SWCNTs with a thermal conductivity significantly higher compared to pure ePCMs has been proven via stability testing under operating conditions.
1. Introduction
After previous energy crises in the 1970s and 1980s caused by turmoil in the oil markets, the time of the energy crisis related to gas supply constraints has arrived.1 Under these circumstances, we note that countries are paying particular attention to diversifying their fuel suppliers and deepening their energy independence. Considering the climate changes that have been taking place in recent times, it is important to look for solutions that provide low temperature conditions at a low cost. The energy consumption of compressor refrigerators (which are the main refrigeration technology) is directly dependent on the temperature of the heat receiver, so care must be taken to ensure good heat exchange at the condenser. However, given the diurnal variation in temperature, energy savings can be achieved by using thermal energy stores that produce cold during the night and use it during the day.2Phase-change materials, PCMs, are either effective thermal energy stores (both heat and cold) or passive temperature controllers (as they stabilize the temperature without human intervention or control). When discharging PCMs, there is no threat of significant overcooling below the material's melting point when cooling products, nor is there any risk of burns when heating, as the temperature of the medium does not significantly exceed the crystallisation temperature. For this reason, PCMs, in comparison to other thermal energy storage (TES) systems, can be used without concerns for the protection of materials that are sensitive to minute changes in temperature; however, to ensure this protection, it is necessary to select a PCM with the desired conversion temperature. For this purpose, research is being conducted on eutectic phase change materials (ePCMs), which allow the use of compounds from a group with desirable properties while having an unfavourable melting temperature.
As paraffins in the role of PCMs are characterised by an almost 100% efficiency with simultaneously practically unlimited service time, they represent environmentally friendly and efficient accumulators of thermal energy. It is also important to note their high availability and low cost due to the large scale of production in petroleum refining processes. Companies currently supplying PCMs in bulk quantities to the Chinese market offer the reagents investigated in this paper at prices ranging from $2 to $15 per kilogram, which, considering the long lifetime, seems beneficial. The main advantages of long-chain alkanes include their chemical inactivity and ease of crystallisation resulting in negligible sub-cooling while having a very high latent heat value. In the case of long-chain n-alkanes, the energetic effect of crystallisation is related to a lowering of the system entropy as a result of the formation of a highly organised crystalline structure resulting from weak but multiplied van der Waals interactions and dihydrogen bonds (C–H⋯H–C).3
In order not to lose the high enthalpy of fusion at the ePCM formation stage, it is necessary to select components with positive interactions resulting in a positive mixing enthalpy value. Blending two alkanes together results in a negligibly small negative deviation from ideality due to entropic effects. In order to obtain positive deviations, an alkane can be combined with, for example, an alcohol or carboxylic acid, and such systems have been quite intensively studied.4–6 In contrast, a poorly explored niche so far are diols and in particular, due to their lower propensity to undercool, α,ω-diols.7–9 The presence of two hydroxyl groups at the terminal positions of α,ω-diols gives them the possibility of energetically favourable packing of the crystal lattice using strong hydrogen interactions resulting in a much higher energy effect of the phase transformation than for an alkane of similar size. Considering the favourable effect of positive deviations on latent heat, in the present work an ePCMs composed of an alkane and an α,ω-diols was attempted in addition to the two-alkane systems.
The main problem observed with organic PCMs is their low thermal conductivity resulting in the inertia of the heat stores and temperature stabilizers made from them. The default solution is to increase the heat transfer surface area and therefore to use various types of metal ribbed heat exchangers10,11 or to place PCM in porous materials with high thermal conductivity.12–15 Among the most extensively studied additives with high thermal conductivity are carbon nanotubes (CNTs) whose small addition in the form of a suspension (nanofluid) repeatedly improves thermal properties with negligible degradation of the stored heat density.16–18 Alternatively, the investigated nanomaterial is expanded graphite (EG), whose production by expansion (thermal decomposition) of exfoliated graphite (expandable graphite) is much simpler, resulting in its lower price.19–21 In addition to thermal conductivity, the key properties of functional materials are the values of their physicochemical parameters such as density (which reflects energy storage density) and viscosity (crucial for hydraulic transport processes and reducing the inertia of phase transformations). The coefficients of thermal expansion, determined from the mathematical description, allow the design of suitable vessels resistant to unsealing.
Considering the practical nature of the undertaken research, it seems important to propose theoretical methods for selecting PCMs with the expected properties. For this reason, the appropriateness of using selected mathematical models for estimating the composition and melting enthalpy of eutectic with the expected melting point was experimentally verified.
2. Materials and methods
2.1. Chemicals and materials
The reagents used in this study were applied without additional purification and the purity grades were assumed according to the specifications declared by the supplier (Table 1). Alkanes and diols exhibited a narrow melting point range (below 0.3 K) and a water content of no greater than 1000 ppm for diols and less than 20 ppm for alkanes. Expandable graphite (Graphite intercalation compound, GIC) was expanded by heating it at 520 K under nitrogen flow for 30 min resulting in expanded graphite, EG.22| Compound, abbreviation | M (g mol−1) | CAS number | Supplier | Mass fraction purity |
|---|---|---|---|---|
| n-Tetradecane, C14 | 198.39 | 629-59-4 | Alfa Aesar | 0.99 |
| n-Heptadecane, C17 | 240.47 | 629-78-7 | Alfa Aesar | 0.99 |
| n-Nonadecane, C19 | 268.52 | 629-92-5 | Sigma-Aldrich | 0.99 |
| n-Heneicosane, C21 | 296.58 | 629-94-7 | Fluka | 0.99 |
| 1,6-Hexanediol | 118.17 | 629-11-8 | Aldrich | 0.99 |
| 1,12-Dodecanediol | 202.33 | 5675-51-4 | Acros organics | 0.98 |
| Single-wall carbon nanotubes, SWCNTs | — | — | OCSiAl | 0.994 (in dry matter) |
| Expandable graphite, GIC | — | — | Aldrich | 0.995 |
2.2. Solid–liquid phase equilibrium measurements
The course of the liquidus curves was determined using a highly accurate dynamic (synthetic) method, in which the sample is subjected to slow heating (slower than 2 K h−1) and the temperature at which the last fragment of the second phase (solid or liquid) disappears is recorded. The investigated samples were prepared by weighing the components on an analytical scale with an accuracy of 1 × 10−4 g (u(x) = 5 × 10−4) and then sealed in a vessel containing a stirring bar. The temperature of the system, measured using a calibrated P 750 (DOSTMANN electronic GmbH) thermometer, had an error of no more than u(T) = 0.05 K. A detailed description of the method can be found in our previous works.6,23,242.3. Differential scanning calorimetry, DSC
Values for the heat effects of phase transitions (ΔH) and the temperatures of polymorphic transformations were determined using differential scanning calorimetry, DSC. A DSC 1 STARe (Mettler Toledo) calorimeter operating in a heat-flux mode with liquid nitrogen cooling system had been adjusted prior to measurements using a series of high-purity compounds according to the procedure described in our previous work.6 The standard error of the onset temperature u(T) = 0.4 K and the relative error of the heat effects ur(ΔH) = 0.03 were determined for measurements carried out with a heating rate of 2 K min−1 or 5 K min−1, as indicated by the thermograms. For the study of mixtures, samples of approximately 2 mL were first prepared by weighing the components with a composition accuracy of u(x) = 5 × 10−4, followed by melting and thorough mixing. In liquid form, about 10 mg of the mixture was weighed out with an accuracy of 2 × 10−5 g and sealed in a tight aluminium vessel under ambient atmosphere.| Compound | T fus/K | ΔfusH/kJ mol−1 | T tr/K | ΔtrH/kJ mol−1 |
|---|---|---|---|---|
| Uncertainties are:a Dynamic method: u(T) = 0.05 K, u(p) = 5 kPa.b DSC: u(T) = 0.4 K, ur(ΔfusH) = 0.03. DSC thermograms are available in ESI. | ||||
| C146 | 279.15a, 278.4b, 278.733 | 44.7b, 45.0734 | — | — |
| C17 | 295.30a, 295.4b, 295.133 | 39.9b, 39.4,26 38.7,6 40.1734 | 284.6b, 284.2735 | 10.7b, 10.9435 |
| C19 | 305.14a, 305.3b, 304.7536 | 44.7b, 42.7,26 47.434 | 296.1b, 294.826 | 12.9b, 12.7,26 13.7537 |
| C21 | 313.57a, 313.6b, 313.6036 | 45.8b, 46.626 | 305.6b, 304.326 | 16.1b, 15.726 |
| 1,6-Hexanediol8 | 315.18a, 315.3b, 31533 | 26.1b, 25.538 | — | — |
| 1,12-Dodecanediol8 | 353.35a, 353.5b, 352.3532 | 52.8b, 51.239 | — | — |
2.4. Density and viscosity measurements
Density measurements of eutectic mixtures (EM) in the liquid phase were carried out using an Anton Paar GmbH DMA 4500 M oscillating densimeter (Graz, Austria) with two built-in Pt 100 thermometers providing a temperature uncertainty of u(T) = 0.01 K. The experiments were carried out at atmospheric pressure p = 100 kPa, with u(p) = 5 kPa. The precision of the instrument, taking into account correction for viscosity, is 1 × 10−5 g cm−3, while considering the calibration performed using standards provided by the supplier and the purity of the reagents used in the tests, the relative error of the density is ur(ρ) = 0.001.25 Viscosity was measured using a DVNext-LV cone/plate rheometer from AMETEK Brookfield (Middleboro, USA) with a relative uncertainty of dynamic viscosity of ur(η) = 0.03. Viscosity error was determined using standards: APN26E and APN75 from Paragon Scientific Ltd and n-tetradecane (Alfa Aesar, purity >99%). All measurements were carried out at an atmospheric pressure of p = 100 kPa, (u(p) = 5 kPa) and the temperature uncertainty is u(T) = 0.1 K. In both cases, samples prepared according to the procedure described for DSC were examined.2.5. Composite stability examination
Composite systems consisting of solid carbon material and ePCM were prepared by weighing a presumed portion of the powder (SWCNT, GIC or EG) on an analytical scale and then filling with ePCM previously prepared according to the same procedure as described for DSC measurements. Samples containing a (C14 + C17) EM with SWCNTs (0.1%, 0.3%, 0.5% and 1% by weight), GICs (10% and 75% by weight) and EG (0.5%, 5%, 10% by weight) were prepared. Prior to testing, the samples were vacuumed to remove air from the porous materials and then, after sealing, homogenised in an ultrasonic cleaner at 298.2 K for one hour. The propensity of the melted systems to sediment under isothermal conditions was tested first. Samples were placed in a thermostat at 298.2 K for 50 days after which the photographs were taken. Then, after re-homogenisation, the vessels were subjected to a series of 1000 temperature cycles to assess the stability of the suspensions during PCM operation. Samples were cooled to 269.2 K, held at this temperature for 10 min and then heated to 283.2 K and also held for 10 min. During the measurement the temperature of the water bath in which the samples were immersed was recorded. The full description of experiment with the apparatus scheme was published in our previous publication.8 The appearance of the composites after 1000 cycles.2.6. Thermal conductivity
The liquid-phase thermal conductivity (λ) was measured by transient hot-wire method according to the ASTM D7896-19 standard using a THW-L2 thermal conductivity meter (Thermtest Inc., Canada). Samples of approximately 30 mL were prepared by weighing an ePCM and carbonaceous materials on an analytical scale (according to the same procedure as above). Prior to measurement, the samples were placed in a vacuum chamber at 338.2 K to remove air and then homogenised in an ultrasonic bath at 338.2 K for one hour. Composite systems containing SWCNTs at 1 wt% and EGs at 10 wt%, as well as ePCM without additives, were investigated to compare the change in thermal conductivity of the ePCM. A detailed description of the measurement methodology is included in our previous publication.83. Results and discussion
3.1 Solid–liquid phase equilibrium
The results of the solid–liquid phase equilibrium (SLE) measurements using the dynamic method are summarized in numerical form in Table 3 and presented graphically as dots in Fig. 1–3.| x 1 | T/K | x 1 | T/K | x 1 | T/K |
|---|---|---|---|---|---|
| Standard uncertainties are: u(x) = 5 × 10−4, u(T) = 0.05 K, u(p) = 5 kPa. | |||||
| {C14 (1) + C17 (2)} | {C14 (1) + C19 (2)} | {C14 (1) + C21 (2)} | |||
| 0.0000 | 295.30 | 0.0000 | 305.14 | 0.0000 | 313.57 |
| 0.0350 | 294.69 | 0.1209 | 303.10 | 0.0427 | 312.82 |
| 0.0664 | 294.15 | 0.2149 | 301.16 | 0.1085 | 311.50 |
| 0.1164 | 293.31 | 0.2768 | 299.86 | 0.1469 | 310.92 |
| 0.1638 | 292.45 | 0.3441 | 298.41 | 0.1852 | 310.15 |
| 0.2142 | 291.54 | 0.4022 | 297.01 | 0.2204 | 309.45 |
| 0.2600 | 290.62 | 0.4563 | 295.65 | 0.2376 | 309.14 |
| 0.3027 | 289.71 | 0.4688 | 295.14 | 0.2636 | 308.64 |
| 0.3488 | 288.67 | 0.4743 | 294.98 | 0.2894 | 307.98 |
| 0.4002 | 287.55 | 0.4949 | 294.40 | 0.3210 | 307.45 |
| 0.4358 | 286.68 | 0.5133 | 294.07 | 0.3602 | 306.54 |
| 0.4709 | 285.76 | 0.5229 | 293.98 | 0.3862 | 305.83 |
| 0.5068 | 284.76 | 0.5625 | 293.06 | 0.4154 | 305.36 |
| 0.5456 | 283.75 | 0.6115 | 291.64 | 0.4485 | 304.61 |
| 0.5885 | 282.56 | 0.6560 | 290.29 | 0.4634 | 304.41 |
| 0.6310 | 281.30 | 0.6940 | 289.03 | 0.5185 | 303.22 |
| 0.6687 | 280.37 | 0.7267 | 287.78 | 0.5575 | 302.31 |
| 0.7079 | 279.16 | 0.7714 | 285.78 | 0.5952 | 301.38 |
| 0.7559 | 277.86 | 0.8097 | 283.76 | 0.6337 | 300.25 |
| 0.7975 | 276.73 | 0.8409 | 281.94 | 0.6583 | 299.55 |
| 0.8245 | 276.24 | 0.8784 | 279.02 | 0.6815 | 298.81 |
| 0.8389 | 276.56 | 0.8893 | 277.94 | 0.7089 | 297.79 |
| 0.8588 | 276.89 | 0.9042 | 277.57 | 0.7427 | 296.42 |
| 0.9034 | 277.58 | 0.9174 | 277.80 | 0.7745 | 295.05 |
| 0.9369 | 278.09 | 0.9340 | 278.01 | 0.7969 | 294.01 |
| 0.9623 | 278.52 | 0.9538 | 278.32 | 0.8168 | 292.95 |
| 0.9850 | 278.85 | 1.0000 | 279.15 | 0.8343 | 291.90 |
| 1.0000 | 279.15 | 0.8533 | 290.66 | ||
| 0.8707 | 289.36 | ||||
| 0.8898 | 287.78 | ||||
| 0.9044 | 286.37 | ||||
| 0.9181 | 284.84 | ||||
| 0.9394 | 281.94 | ||||
| 0.9431 | 281.20 | ||||
| 0.9481 | 280.30 | ||||
| 0.9516 | 279.65 | ||||
| 0.9554 | 278.86 | ||||
| 0.9576 | 278.56 | ||||
| 0.9628 | 278.62 | ||||
| 0.9692 | 278.76 | ||||
| 0.9772 | 278.83 | ||||
| 0.9833 | 278.97 | ||||
| 0.9930 | 279.08 | ||||
| 1.0000 | 279.15 | ||||
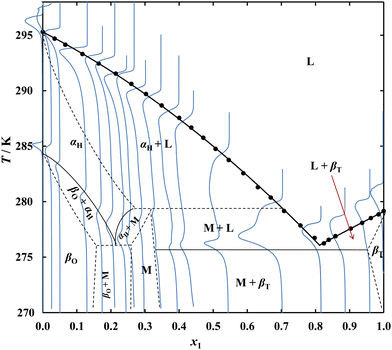
SLE measurements for the system {C14 (1) + C17 (2)} gave a liquidus curve representing a simple eutectic with a single monotonicity change point corresponding to the eutectic point. In the case of the {C14 (1) + C19 (2)} and {C14 (1) + C21 (2)} systems, in addition to the minimum, an inflection in the solubility line of the odd n-alkanes was observed. In the {C14 (1) + C21 (2)} system, the temperature of inflection (305.6 K) corresponds to the C21 polymorphic transition, suggesting that a pure alkane, rather than its solid solution, is present in equilibrium with the saturated solution. The {C14 (1) + C19 (2)} system, containing alkanes with a smaller chain length difference, despite the different crystal structure showed a slight decrease in the C19 solid–solid phase transition temperature, which is 296.1 K for pure C19 and is observed at 294.4 K on the liquidus. The dependence of the polymorphic transition temperature on the composition of the system shows that the solid phase present in equilibrium with the saturated solution is not pure C19, but its solid solution. The minor difference in the length of the n-alkanes leads, in the case of the {C14 (1) + C17 (2)} system, to a complete lack of inflection on the C17 liquidus despite the existing polymorphic transformation of pure C17 at 284.5 K and suggests the presence of a solid solution in this system over a significant range of concentration. In order to confirm the hypothesis, it was necessary to investigate the thermal effects accompanying the heating of samples with different ratios of C14 to odd n-alkanes.
The DSC thermograms plotted in blue on the phase diagrams confirm the composition dependency of the polymorphic transformation temperature and the melting temperature of the eutectic, while the small values of the thermal effects of these transformations do not allow a complete phase diagram to be explicitly determined using DSC. The continuous black lines represent relationships resulting from the DSC, while the dashed lines show the probable course of the boundaries of occurrence of the individual phases. The proposed phase diagram is consistent with studies carried out for the similar system {C16 + C17},26,27 in which all the phases: βT (triclinic of C14 and C16), αH (hexagonal of C17 occurring at higher temperatures) and βO (orthorhombic of C17 at temperatures below the polymorphic transition temperature)28 form solid solutions in specific concentration ranges. The results of the DSC analysis of the remaining systems give no reason to suspect the presence of solid solutions in significant molar fraction ranges, and confirm the formation of simple eutectic systems by pairs of even alkanes with odd ones at a difference in aliphatic chain length of more than 3 carbon atoms.
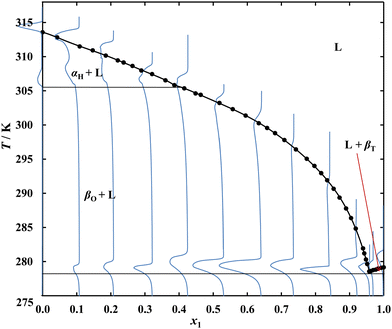
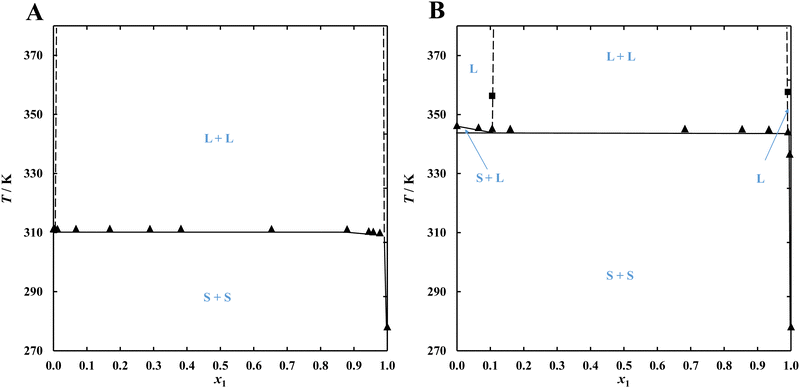
Phase equilibrium investigations in alkane-diol systems (Table 4) revealed a very broad liquid–liquid equilibrium region that, in the case of the {C14 (1) + 1,6-hexanediol (2)} system, covered the entire range of tested compositions, and for the {C14 (1) + 1,12-dodecanediol (2)} system covered molar fractions x1 from 0.1 to 0.99 (Fig. 4).
| x 1 | T SLE/K | T LLE/K | x 1 | T SLE/K | T LLE/K |
|---|---|---|---|---|---|
| Standard uncertainties are: u(x) = 5 × 10−4, u(T) = 0.05 K, u(p) = 5 kPa. | |||||
| {C14 (1) + 1,6-hexanediol (2)} | {C14 (1) + 1,12-dodecanediol (2)} | ||||
| 0.0000 | 315.18 | 0.0000 | 353.35 | ||
| 0.0118 | 315.06 | >365 | 0.0646 | 352.62 | |
| 0.0672 | 315.09 | >365 | 0.1054 | 352.23 | 356.32 |
| 0.1686 | 315.11 | >365 | 0.1595 | 352.12 | >365 |
| 0.2888 | 315.10 | >365 | 0.6825 | 352.12 | >365 |
| 0.3817 | 315.11 | >365 | 0.8538 | 352.03 | >365 |
| 0.6529 | 315.04 | >365 | 0.9338 | 351.90 | >365 |
| 0.0013 | 315.14 | >365 | 0.9911 | 351.03 | 357.65 |
| 0.0027 | 315.08 | >365 | 0.9962 | 342.78 | |
| 0.0048 | 315.12 | >365 | 1.0000 | 279.15 | |
| 0.8796 | 314.96 | >365 | |||
| 0.9444 | 314.23 | >365 | |||
| 0.9577 | 314.05 | >365 | |||
| 0.9774 | 313.69 | >365 | |||
| 1.0000 | 279.15 | ||||
The observed results are a consequence of very significant positive deviations from ideal behaviour leading to a miscibility gap in the liquid phase. Achieving the eutectic point requires the use of either a geminal, vicinal or very long α,ω-diol as well as a monohydroxy alcohol, which in contrast have lower enthalpies of melting and a higher propensity to overcool.
All liquidus curves were correlated using the NRTL equation (Fig. 5) and compared with the prediction using the ideal solubility equation and the modified (Dortmund) UNIFAC equation (UNIFAC (Do)). The used values of the surface and volumetric parameters R and Q are included in Table S1 in ESI.† In each case, small positive deviations from ideality are visible and the curves predicted by both equations are equivalent.
The consistency of the UNIFAC (Do) results and ideal solubility is due to UNIFAC model's omission of interactions between CH3 and CH2 groups belonging to the same CH2 main group. In a situation when the residual part of the calculated activity coefficient is equal to zero, deviations from ideality are influenced only by the combinatorial term. However, the geometric similarity of the CH2 and CH3 groups in most of the composition range (through γ = 1) reduces the equation form to ideal solubility. The negligible effect of the difference in the surface parameters (Q) is noticeable only for γ2 values near the eutectic composition.
In all systems except {C14 (1) + C17 (2)}, where the error due to the formation of a solid solution is noticeable, it is unnecessary to determine the eutectic point experimentally in order to use as an ePCM (Table 5).
3.2. Latent heat examination
The results of the thermal analysis of n-alkanes are presented in Fig. S1–S4 in ESI.† The polymorphic transformation of C21, in comparison with the other investigated odd alkanes, occurs in a wider temperature range (the peak is broadened and uneven), which results in a less visible change in the monotonicity of the liquidus and blurred thermograms plotted on the phase diagram (Fig. 3). The temperature and transformation enthalpies of the pure components obtained in this work are compared with literature values in Table 2, while the properties of the obtained ePCMs are summarised in Table 6.| Abbreviation | System | x 1 | T fus, Tonsetfus/K | ΔfusH/J g−1 |
|---|---|---|---|---|
| Uncertainties are: u(x1) = 5 × 10−4, u(p) = 5 kPa.a Dynamic method: u(T) = 0.05 K.b DSC: u(Tonsetfus) = 0.4 K, ur(ΔfusH) = 0.03. | ||||
| (C14 + C17) EM | {C14 (1) + C17 (2)} | 0.8149 | 275.91a, 275.6b | 155.5b |
| (C14 + C19) EM | {C14 (1) + C19 (2)} | 0.8963 | 277.28a, 276.2b | 217.4b |
| (C14 + C21) EM | {C14 (1) + C21 (2)} | 0.9574 | 278.56a, 277.6b | 221.9b |
The eutectic compositions determined from the SLE experimental data were used to prepare the samples for DSC analysis, the thermograms of which, together with a full description, are presented in ESI,† in Fig. S5–S7. Among the ePCMs studied, the (C14 + C17) EM has the lowest latent heat value (Fig. 6), which is a direct result of the solid solutions presence in this system (Fig. 1).
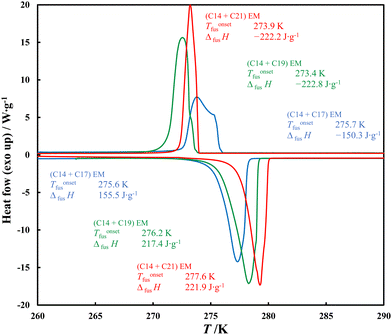 | ||
| Fig. 6 Comparison of ePCM melting and solidification DSC thermograms recorded under ambient pressure and with the heating rate 2 K min−1. | ||
According to the phase diagram presented in Fig. 1, in contrast to the other two ePCMs, the solid (C14 + C17) EM is not composed of crystals of the individual components, but of their solid solutions. As crystal lattice of the solid solution has a higher entropy than that of the pure alkane, its formation during crystallisation results in a minor entropy difference with respect to the liquid solution (ΔfusS). The difference in ordering in the solid phases implies the melting enthalpy value of the eutectic mixture according to the relation for the isobaric process: ΔfusH = T·ΔfusS and results in a minor amount of heat that such an ePCM can store.
Knowing the composition and the melting temperature of the eutectic mixture (from experiment or predictive calculations), it is possible to predict the thermal effect associated with its melting. The following equation, taking into account the temperature dependence of the enthalpy of melting of the components, is most commonly found in the literature.29,30
 | (1) |
 and
and  – respectively, the specific heat capacity of the liquid and solid phases of component i. In order for the above equation to be applicable to compounds exhibiting a polymorphic transition, it should be supplemented with the expression ΔtrHi/Ttr. In recent publications, the authors propose to perform an entropy balance starting with crystals of the two components with a eutectic ratio and ending with the molten mixture at the same, eutectic temperature.30 This approach takes into account the entropy of mixing of the ideal solution, but requires knowledge of the Cp of the liquid eutectic mixture (or the application of mixing rules for the regular solution) and is not an intuitive way to include imperfections in the system. According to the above, and bearing in mind that the total enthalpy change does not depend on the path of the transformation, we propose an enthalpy balance based on the thermodynamic cycle described in ESI,† and summarized as follows.
– respectively, the specific heat capacity of the liquid and solid phases of component i. In order for the above equation to be applicable to compounds exhibiting a polymorphic transition, it should be supplemented with the expression ΔtrHi/Ttr. In recent publications, the authors propose to perform an entropy balance starting with crystals of the two components with a eutectic ratio and ending with the molten mixture at the same, eutectic temperature.30 This approach takes into account the entropy of mixing of the ideal solution, but requires knowledge of the Cp of the liquid eutectic mixture (or the application of mixing rules for the regular solution) and is not an intuitive way to include imperfections in the system. According to the above, and bearing in mind that the total enthalpy change does not depend on the path of the transformation, we propose an enthalpy balance based on the thermodynamic cycle described in ESI,† and summarized as follows. | (2) |
 of the two polymorphic forms.
of the two polymorphic forms.
Only in the case of the {C14 + C17} system there is noticeable difference between the calculated and experimental values that exceeds the measurement error, and this is a further confirmation of the presence of solid solutions in this system (Fig. 7). In all cases, the actual values of melting enthalpy are lower than the calculated ones, indicating very small negative values of the excess enthalpy of mixing (ΔHE).
 | ||
Fig. 7 Experimental enthalpy as a function of fusion temperature of n-alkanes: ■ – C14,  – C17 – C17  – C19, – C19,  – C21, and eutectic mixtures: – C21, and eutectic mixtures:  – (C14 + C17) EM, – (C14 + C17) EM,  – (C14 + C19) EM, – (C14 + C19) EM,  – (C14 + C21) EM. Points marked as open symbols represent data calculated using eqn (2). – (C14 + C21) EM. Points marked as open symbols represent data calculated using eqn (2). | ||
3.3. Density and viscosity
The density (ρ) of the EMs has been measured in the temperature range from 283.15 to 353.15 K and for all samples it reaches similar values, typical of paraffins, i.e. 0.76 g cm−3 at 298.15 K. While the density of pure n-alkanes increases with an increase in molecular weight, the density of their eutectic mixtures drops with the difference in length of the aliphatic chains, i.e. the (C14 + C17) EM has the highest density and the (C14 + C21) EM exhibits the lowest. This relationship is a direct result of the C14 content of the investigated mixtures (Fig. 8). | ||
Fig. 8 Density (ρ) of EMs as a function of temperature:  – (C14 + C17) EM, – (C14 + C17) EM,  – (C14 + C19) EM, – (C14 + C19) EM, 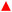 – (C14 + C21) EM in comparison with ■ – C14 density. Points correspond with experimental values, solid lines – correlation with eqn (3). The parameters of the equation used are given in Table 9. – (C14 + C21) EM in comparison with ■ – C14 density. Points correspond with experimental values, solid lines – correlation with eqn (3). The parameters of the equation used are given in Table 9. | ||
The experimental points included in Table 7 were correlated using eqn (3), the parameters of which are included in Table 9.
| ρ = ρ0·e−αp(T−T0), T0 = 298.15 K | (3) |
| T/K | ρ/g cm−3 | ||
|---|---|---|---|
| {C14 (1) + C17 (2)} | {C14 (1) + C17 (2)} | {C14 (1) + C17 (2)} | |
| Standard uncertainties are: u(T) = 0.01 K, u(p) = 5 kPa, u(x1) = 5 × 10−4; relative standard uncertainty of density is ur(ρ) = 0.001. | |||
| x 1 | 0.8149 | 0.8963 | 0.9574 |
| 283.15 | 0.7731 | 0.7729 | 0.7717 |
| 288.15 | 0.7696 | 0.7694 | 0.7682 |
| 293.15 | 0.7661 | 0.7659 | 0.7647 |
| 298.15 | 0.7626 | 0.7624 | 0.7611 |
| 303.15 | 0.7590 | 0.7588 | 0.7576 |
| 308.15 | 0.7555 | 0.7553 | 0.7541 |
| 313.15 | 0.7520 | 0.7518 | 0.7505 |
| 318.15 | 0.7485 | 0.7483 | 0.7470 |
| 323.15 | 0.7450 | 0.7448 | 0.7435 |
| 328.15 | 0.7415 | 0.7413 | 0.7400 |
| 333.15 | 0.7379 | 0.7377 | 0.7364 |
| 338.15 | 0.7344 | 0.7342 | 0.7329 |
| 343.15 | 0.7309 | 0.7307 | 0.7293 |
| 348.15 | 0.7273 | 0.7271 | 0.7258 |
| 353.15 | 0.7238 | 0.7236 | 0.7222 |
The relationships observed for the density measurements, are also fulfilled by the dynamic viscosity (η) of the tested ePCMs presented in Fig. 9 and Table 8. The highest viscosity is exhibited by the (C14 + C17) EM and the lowest viscosity by (C14 + C21) EM, while the viscosity of pure C14 is lower than that of the above mixtures (black squares in the Fig. 9). The above differences are not significant from a practical point of view, but they allow the properties of other mixtures consisting of n-alkanes to be predicted.
| T/K | η/mPa s | ||
|---|---|---|---|
| {C14 (1) + C17 (2)} | {C14 (1) + C17 (2)} | {C14 (1) + C17 (2)} | |
| Standard uncertainties are: u(T) = 0.1 K, u(p) = 5 kPa, u(x1) = 5 × 10−4; relative standard uncertainty for viscosity is ur(η) = 0.03. | |||
| x 1 | 0.8149 | 0.8963 | 0.9574 |
| 288.2 | 2.89 | 2.87 | 2.68 |
| 298.2 | 2.30 | 2.28 | 2.20 |
| 308.2 | 1.87 | 1.84 | 1.76 |
| 318.2 | 1.57 | 1.53 | 1.47 |
| 328.2 | 1.34 | 1.31 | 1.28 |
| 338.2 | 1.15 | 1.12 | 1.08 |
| 348.2 | 0.98 | 0.95 | 0.93 |
 | ||
Fig. 9 Dynamic viscosity (η) of EMs as a function of temperature:  – (C14 + C17) EM, – (C14 + C17) EM,  – (C14 + C19) EM, – (C14 + C19) EM,  – (C14 + C21) EM in comparison with ■ – C14 viscosity. Points correspond with experimental values, solid lines – correlation with eqn (4). The parameters of the equation used are given in Table 9. – (C14 + C21) EM in comparison with ■ – C14 viscosity. Points correspond with experimental values, solid lines – correlation with eqn (4). The parameters of the equation used are given in Table 9. | ||
The experimental data of dynamic viscosity were correlated using the following two-parameter De Guzman–Andrade equation.31
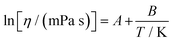 | (4) |
3.4. Carbon doped PCMs
In order to improve the thermal conductivity of paraffins, an attempt has been made to create composite materials in which a lightweight material with a high thermal conductivity value is suspended in the PCM. Predominant among such are carbon nanomaterials having structured graphene planes. In order for the vibrations of the carbon network to be able to transmit energy over long distances, carbon nanotubes with a high length-to-diameter ratio were chosen. Nanofluids based on SWCNTs are frequently studied in the literature, while their dominant disadvantage is their price. A cheaper alternative seems to be EG, which can be easily produced on a large scale. Due to the very similar properties of all blends, (C14 + C17) EM was chosen to study composite systems. The macroscopic stability of the proposed nanofluids was first investigated. Mixtures containing different mass percentages of SWCNTs (0.1%, 0.3%, 0.5%, 1.0%), GIC (10% and 75%) and EG (0.5%, 5.0%, 10%) were maintained at 298.2 K after preparation according to the procedure described above.Table 10 contains the observations made before and after 50 days of testing. All nanofluids containing SWCNTs showed stability during the experiment. The GICs started to sediment almost immediately, only the use of a solid material as high as the liquid column guarantees the stability of the material. A more developed surface area and a lower density of EG allows the material to be stable under isothermal conditions using no less than 10 wt% EG, samples with a lower content are characterised by EG floating to the liquid surface. The appearance of the samples before testing (A), after 50 days at 298.2 K (B) and after 1000 cycles of melting and crystallisation (C) is illustrated in Fig. 10.
| SWCNTs | GIC | EG | Fig. 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 wt% | 0.3 wt% | 0.5 wt% | 1.0 wt% | 10 wt% | 75 wt% | 0.5 wt% | 5.0 wt% | 10 wt% | ||
| Isothermal at 298.2 K for 50 days | st. | st. | st. | st. | ↓ | st. | ↑↓ | ↑↓ | st. | B |
| After 20 cycles of melting and crystallization | ↑ | ↑ | st. | st. | ↓ | st. | ↑↓ | ↑↓ | st. | — |
| After 1000 cycles of melting and crystallization | ↑↓ | ↑↓ | st. | st. | ↓ | st. | ↑↓ | ↑↓ | ↑↓ | C |
 | ||
| Fig. 10 Samples of (C14 + C17) EM with carbon additives: A – after homogenization, B – after 50 days at 298.2 K, C – after 1000 cycles of melting and crystallisation. | ||
Another aspect investigated was the stability of the nanofluids under PCM operating conditions, i.e. at cyclically varying temperatures. The same samples after 1000 cycles of melting and crystallisation showed the stability of the SWCNTs nanofluids with a content above 0.5 wt%, and at lower concentrations solids were observed to float to the liquid surface. For the GICs, no differences were observed compared to isothermal conditions, and for all samples containing EG, complete separation of the carbonaceous material from the liquid was observed. The observations are only valid for the situation where free space is present above the mixture, while this is a necessary condition to protect against the negative effects of thermal expansion.
Considering the inhomogeneous nature of the suspensions, it is not possible to take a representative sample for DSC analysis after the composites stability testing. Therefore, only the liquid fraction of samples was taken to evaluate the stability of the thermal effect. On the example of the composite containing 1 wt% of SWCNTs, it was found that there was no influence of the series of 1000 melting and crystallization on the temperature and thermal effect of the transition. The differences in measured values do not exceed the error of the measurement method. No influence of variable parameters on the studied system results from the inert nature of alkanes, which are thermally stable in the studied temperature range and do not react with the added carbon materials. In addition, both SWCNTs and EG show chemical passivity towards most materials.
The suspensions containing 1 wt% SWCNTs and 10 wt% EG were selected out for thermal conductivity measurements and compared with (C14 + C17) EM. For all samples, the thermal conductivity at higher temperature takes on lower values and for EM these values are comparable to those of C14 (λC14 = 0.137 W (m K)−1 at 298.2 K and λC14 = 0.130 W (m K)−1 at 338.2 K).32
An addition of SWCNTs at an amount as low as 1% increases the thermal conductivity by about 50%, while achieving the same effect with EG probably requires the use of around 6–8 wt%, since a 10% addition results in an increase of no more than 100% (Fig. 11). Apart from the matter of the costs of using these additives, an important aspect is the reduction of the heat storage density, which will be decreased to an imperceptible extent with a content of 1% SWCNTs (Table 11).
 | ||
| Fig. 11 Thermal conductivity (λ) of (C14 + C17) EM, with addition of 1 wt% SWCNTs and with 10 wt% of EG at T = 298.2 K (blue) and T = 338.2 K (red) and under ambient pressure. | ||
4. Conclusions
In the present work, three binary ePCMs containing a n-tetradecane and an odd n-alkane with melting points around 4 °C (277.2 ± 2 K) are proposed. The melting temperatures are suitable for their use in the thermal stabilisation of sensitive materials such as tissues, foods and drugs. The heat storage density, and therefore the amount of heat that can be absorbed before the temperature of the material rises, exceeds 200 J g−1 in two cases. The formation of ePCMs allows the melting temperature to be adjusted while maintaining a high latent heat: (C14 + C19) EM has an enthalpy of melting of 217.4 J g−1 at Tfus = 276.2 K, while in comparison, C14 with a similar melting point (Tfus = 278.4 K) has a latent heat of 225.3 J g−1. Among the three examined systems, only {C14 (1) + C17 (2)} forms a solid solution, which is due to the small difference in length of the aliphatic chains and therefore negatively affects the heat of fusion of such a mixture, which is 155.5 J g−1. Thus, when designing an ePCM, it is necessary to take into account the possibility of various processes occurring in the solid phase causing modification of its physical properties and failure to fulfil the model assumptions.While relying on the favourable effects of the existence of positive deviations from ideality in the designed ePCMs, it must be borne in mind that very significant deviations lead to the occurrence of a miscibility gap in the liquid phase, making it impossible to obtain the expected eutectic. Accordingly, the attempt to form ePCMs from n-alkanes and α,ω-diols (both groups are distinguished by a very high latent heat value) failed due to the miscibility gap in the liquid phase occurring over a wide range of compositions.
The application of carbon nanomaterials like SWCNTs allows for a significant improvement in the conductivity of ePCMs, which is a prerequisite to ensure efficient response to temperature changes. SWCNTs suspensions in alkanes are stable under isothermal conditions at nanomaterial contents as low as 0.1 wt%, while the negative effect of cyclic melting and crystallisation on the stability of nanofluids ceases to be noticeable at SWCNTs contents above 0.5 wt%. The flame retardant properties of GICs unfortunately do not cooperate with the possibility of using expandable graphite as a heat transfer medium due to the large density difference. The stability of such a material is only possible after the formation of a paste in which the GIC is saturated with PCM. The behaviour of nanofluids with EG is similar, as the low density of porous EG causes it to flow onto the surface of the molten PCM. Of the additives tested, SWCNTs have the highest ability to increase thermal conductivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Polish Ministry of Education and Science from the budget for science in the years 2019-2022, as a research project under the “Diamond Grant” program [grant number DI 2018 015148].References
- E. D. Coyle and R. A. Simmons, Understanding the Global Energy Crisis, Purdue University Press, West Lafayette, Indiana, 2014 Search PubMed.
- G. Li and X. Zheng, Thermal energy storage system integration forms for a sustainable future, Renewable Sustainable Energy Rev., 2016, 62, 736–757 CrossRef.
- J. Echeverria, G. Aullón, D. Danovich, S. Shaik and S. Alvarez, Dihydrogen contacts in alkanes are subtle but not faint, Nat. Chem., 2011, 3, 323–330 CrossRef CAS PubMed.
- P. Singh, R. K. Sharma, A. K. Ansu, R. Goyal, A. Sarı and V. V. Tyagi, A comprehensive review on development of eutectic organic phase change materials and their composites for low and medium range thermal energy storage applications, Sol. Energy Mater. Sol. Cells, 2021, 223, 110955 CrossRef CAS.
- N. Philip, G. Raam Dheep and A. Sreekumar, Cold thermal energy storage with lauryl alcohol and cetyl alcohol eutectic mixture: thermophysical studies and experimental investigation, J. Energy Storage, 2020, 27, 101060 CrossRef.
- M. Więckowski and M. Królikowski, Designing and Characterization of Low-Temperature Eutectic Phase Change Materials Based on Alkanes, J. Chem. Eng. Data, 2022, 67, 727–738 CrossRef.
- L. Han, G. Ma, S. Xie, J. Sun, Y. Jia and Y. Jing, Thermal properties and stabilities of the eutectic mixture: 1,6-hexanediol/lauric acid as a phase change material for thermal energy storage, Appl. Therm. Eng., 2017, 116, 153–159 CrossRef CAS.
- M. Więckowski, M. Królikowski, M. Żywólko, Ł. Scheller and M. Dzida, Examination of Eutectic Phase Change Materials Composed of Diols and Ionic Liquids, J. Mol. Liq., 2023, 379, 121660 CrossRef.
- C. Rathgeber, H. Schmit and S. Hiebler, 2nd International Conference on Sustainable Energy Storage, Dublin, 2013 Search PubMed.
- N. I. Ibrahim, F. A. Al-Sulaiman, S. Rahman, B. S. Yilbas and A. Z. Sahin, Heat transfer enhancement of phase change materials for thermal energy storage applications: a critical review, Renewable Sustainable Energy Rev., 2017, 74, 26–50 CrossRef CAS.
- L. Fan and J. M. Khodadadi, Thermal conductivity enhancement of phase change materials for thermal energy storage: a review, Renewable Sustainable Energy Rev., 2011, 15, 24–46 CrossRef CAS.
- D. G. Atinafu, W. Dong, X. Huang, H. Gao and G. Wang, Introduction of organic-organic eutectic PCM in mesoporous N-doped carbons for enhanced thermal conductivity and energy storage capacity, Appl. Energy, 2018, 211, 1203–1215 CrossRef CAS.
- S. C. Pinto, N. H. C. S. Silva, R. J. B. Pinto, C. S. R. Freire, I. Duarte, R. Vicente, M. Vesenjak and P. A. A. P. Marques, Multifunctional hybrid structures made of open-cell aluminum foam impregnated with cellulose/graphene nanocomposites, Carbohydr. Polym., 2020, 238, 116197 CrossRef CAS PubMed.
- T. X. Li, D. L. Wu, F. He and R. Z. Wang, Experimental investigation on copper foam/hydrated salt composite phase change material for thermal energy storage, Int. J. Heat Mass Transfer, 2017, 115, 148–157 CrossRef CAS.
- H. F. Abbasov, The Effective Thermal Conductivity of Composite Phase Change Materials with Open-Cellular Metal Foams, Int. J. Thermophys., 2020, 41, 164 CrossRef CAS.
- J. Wang, H. Xie, Z. Xin, Y. Li and L. Chen, Enhancing thermal conductivity of palmitic acid based phase change materials with carbon nanotubes as fillers, Sol. Energy, 2010, 84, 339–344 CrossRef CAS.
- X. Zhu, L. Han, Y. Lu, F. Wei and X. Jia, Geometry-induced thermal storage enhancement of shape-stabilized phase change materials based on oriented carbon nanotubes, Appl. Energy, 2019, 254, 113688 CrossRef CAS.
- N. A. Habib, A. J. Ali, M. T. Chaichan and M. Kareem, Carbon nanotubes/paraffin wax nanocomposite for improving the performance of a solar air heating system, Therm. Sci. Eng. Prog., 2021, 23, 100877 CrossRef CAS.
- S. Liu, L. Han, S. Xie, Y. Jia, J. Sun, Y. Jing and Q. Zhang, A novel medium-temperature form-stable phase change material based on dicarboxylic acid eutectic mixture/expanded graphite composites, Sol. Energy, 2017, 143, 22–30 CrossRef CAS.
- X. Yang, Y. Yuan, N. Zhang, X. Cao and C. Liu, Preparation and properties of myristic-palmitic-stearic acid/expanded graphite composites as phase change materials for energy storage, Sol. Energy, 2014, 99, 259–266 CrossRef CAS.
- B. Eanest Jebasingh and A. Valan Arasu, A comprehensive review on latent heat and thermal conductivity of nanoparticle dispersed phase change material for low-temperature applications, Energy Storage Mater., 2020, 24, 52–74 CrossRef.
- W. W. Focke, H. Badenhorst, W. Mhike, H. J. Kruger and D. Lombaard, Characterization of commercial expandable graphite fire retardants, Thermochim. Acta, 2014, 584, 8–16 CrossRef CAS.
- U. Domanska, Vapour-liquid-solid equilibrium of eicosanoic acid in one- and two-component solvents, Fluid Phase Equilib., 1986, 26, 201–220 CrossRef CAS.
- U. Domańska, M. Więckowski and P. Okuniewska, Designing eutectic mixtures for the extraction of 2-phenylethanol (PEA) from aqueous phase, Fluid Phase Equilib., 2017, 447, 84–94 CrossRef.
- R. D. Chirico, M. Frenkel, J. W. Magee, V. Diky, C. D. Muzny, A. F. Kazakov, K. Kroenlein, I. Abdulagatov, G. R. Hardin, W. E. Acree, J. F. Brenneke, P. L. Brown, P. T. Cummings, T. W. De Loos, D. G. Friend, A. R. H. Goodwin, L. D. Hansen, W. M. Haynes, N. Koga, A. Mandelis, K. N. Marsh, P. M. Mathias, C. McCabe, J. P. O’Connell, A. Pádua, V. Rives, C. Schick, J. P. M. Trusler, S. Vyazovkin, R. D. Weir and J. Wu, Improvement of quality in publication of experimental thermophysical property data: challenges, assessment tools, global implementation, and online support, J. Chem. Eng. Data, 2013, 58, 2699–2716 CrossRef CAS.
- D. Mondieig, F. Rajabalee, V. Metivaud, H. A. J. Oonk and M. A. Cuevas-Diarte, n-Alkane Binary Molecular Alloys, Chem. Mater., 2004, 16, 786–798 CrossRef CAS.
- J. Sui, S. Q. Zhang, M. Zhai, F. Tian, J. Zhang and X. Z. Lan, Polymorphism of a hexadecane-heptadecane binary system in nanopores, RSC Adv., 2017, 7, 10737–10747 RSC.
- M. G. Broadhurst, An analysis of the solid phase behavior of the normal paraffins, J. Res. Natl. Bur. Stand., Sect. A, 1962, 66A, 241–249 CrossRef.
- Y. Yanping, T. Wenquan, C. Xiaoling and B. Li, Theoretic Prediction of Melting Temperature and Latent Heat for a Fatty Acid Eutectic Mixture, J. Chem. Eng. Data, 2011, 2889–2891 CrossRef.
- S. Kahwaji and M. A. White, Prediction of the properties of eutectic fatty acid phase change materials, Thermochim. Acta, 2018, 660, 94–100 CrossRef CAS.
- E. N. da and C. Andrade, The Viscosity of Liquids, Nature, 1930, 125, 309–310 Search PubMed.
- Design Institute for Physical Properties Sponsored by AIChE, DIPPR Project 801, DIPPR/AIChE, 2005.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899 (retrieved June 15, 2023) Search PubMed.
- E. S. Domalski and E. D. Hearing, Heat Capacities and Entropies of Organic Compounds in the Condensed Phase. Volume III, J. Phys. Chem. Ref. Data, 1996,(25), 1–525 CrossRef CAS.
- J. F. Messerly, G. B. Guthrie, S. S. Todd and H. L. Finke, Low-Temperature Thermal Data For Pentane, n-Heptadecane, and n-Octadecane. Revised Thermodynamic Functions For The n-Alkanes, C5–C18, J. Chem. Eng. Data, 1967, 12, 338–346 CrossRef CAS.
- U. Domańska and J. A. González, Thermodynamics of branched alcohols: II. Solid–liquid equilibria for systems containing tert-butanol and long-chain n-alkanes. Experimental results and comparison with DISQUAC predictions, Fluid Phase Equilib., 1998, 147, 251–270 CrossRef.
- P. Barbillon, L. Schuffenecker, J. Dellacherie, D. Balesdent and M. Dirande, Variation d’enthalpie subie de 260–340 K par les n-paraffines, comprises entre l’octadécane (n-C18) et l’hexacosane (n-C26), J. Chim. Phys. Phys.-Chim. Biol., 1991, 88, 91–113 CrossRef CAS.
- P. J. Gardner and K. S. Hussain, The standard enthalpies of formation of some aliphatic diols, J. Chem. Thermodyn., 1972, 4, 819–827 CrossRef CAS.
- P. Umnahanant, S. Kweskin, G. Nichols, M. J. Dunn, H. Smart-Ebinne and J. S. Chickos, Vaporization enthalpies of the α,ω-alkanediols by correlation gas chromatography, J. Chem. Eng. Data, 2006, 51, 2246–2254 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01377d |
| This journal is © the Owner Societies 2023 |