Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
In-depth magnetometry and EPR analysis of the spin structure of human-liver ferritin: from DC to 9 GHz†
Lucia
Bossoni‡
 a,
Jacqueline A.
Labra-Muñoz‡
a,
Jacqueline A.
Labra-Muñoz‡
 bc,
Herre S. J.
van der Zant
bc,
Herre S. J.
van der Zant
 c,
Vera
Čaluković
b,
Anton
Lefering
d,
Ramon
Egli
c,
Vera
Čaluković
b,
Anton
Lefering
d,
Ramon
Egli
 *e and
Martina
Huber
*e and
Martina
Huber
 *b
*b
aC. J. Gorter Center for High Field MRI, Department of Radiology, Leiden University Medical Center, The Netherlands
bDepartment of Physics, Huygens-Kamerlingh Onnes Laboratory, Leiden University, 2300 RA Leiden, The Netherlands. E-mail: huber@physics.leidenuniv.nl
cKavli Institute of Nanoscience, Delft University of Technology, 2628 CJ Delft, The Netherlands
dRST-FAME, Delft University of Technology, Delft, The Netherlands
eGeoSphere Austria, Department of Geophysics, Howe Warte 38, 1190 Vienna, Austria. E-mail: ramon.egli@geosphere.at
First published on 9th October 2023
Abstract
Ferritin, the major iron storage protein in organisms, stores iron in the form of iron oxyhydroxide most likely involving phosphorous as a constituent, the mineral form of which is not well understood. Therefore, the question of how the ca. 2000 iron atoms in the ferritin core are magnetically coupled is still largely open. The ferritin core, with a diameter of 5–8 nm, is encapsulated in a protein shell that also catalyzes the uptake of iron and protects the core from outside interactions. Neurodegenerative disease is associated with iron imbalance, generating specific interest in the magnetic properties of ferritin. Here we present 9 GHz continuous wave EPR and a comprehensive set of magnetometry techniques including isothermal remanent magnetization (IRM) and AC susceptibility to elucidate the magnetic properties of the core of human liver ferritin. For the analysis of the magnetometry data, a new microscopic model of the ferritin-core spin structure is derived, showing that magnetic moment is generated by surface-spin canting, rather than defects. The analysis explicitly includes the distribution of magnetic parameters, such as the distribution of the magnetic moment. This microscopic model explains some of the inconsistencies resulting from previous analysis approaches. The main findings are a mean magnetic moment of 337μB with a standard deviation of 0.947μB. In contrast to previous reports, only a relatively small contribution of paramagnetic and ferrimagnetic phases is found, in the order of maximally 3%. For EPR, the over 30 mT wide signal of the ferritin core is analyzed using the model of the giant spin system [Fittipaldi et al., Phys. Chem. Chem. Phys., 2016, 18, 3591–3597]. Two components are needed minimally, and the broadening of these components suggests a broad distribution of the magnetic resonance parameters, the zero-field splitting, D, and the spin quantum number, S. We compare parameters from EPR and magnetometry and find that EPR is particularly sensitive to the surface spins of the core, revealing the potential to use EPR as a diagnostic for surface-spin disorder.
1 Introduction
Ferritin, has fascinated scientists for decades. This ubiquitous iron-storage protein is made of a protein shell enclosing a core of bioavailable iron mineral.1 The mammalian apoferritin shell contains two distinct polypeptide subunits: a heavy (21 kDa) and a light (19 kDa) chain.2 These self-assemble into a 24-mer spherical structure which, depending on the organism and the specific organ it is found in, can have different heavy- vs. light-chain ratios. While the heavy chain has a ferroxidase activity and protects cells from redox-active iron by rapid uptake of Fe(II) and catalytic oxidation to Fe(III), the light chain promotes the nucleation and storage of iron as a biomineral.3 The inner and outer dimensions of the protein shell are ∼7–8 nm and ∼12 nm, respectively. The biomineral inside the ferritin hollow cavity has received the attention of the biomedical community, because of a link between the protective function of ferritin against cellular iron toxicity4 and altered core composition in the brain of patients with neurodegenerative diseases.5,6 From a physics standpoint, ferritin is also relevant in the fundamental study of nanoparticle properties. Through the biochemical machinery of iron incorporation and the protective protein shell, the composition, spin configuration, and size of the core are well-controlled and protected from post-assembly modification, factors that sometimes are difficult to control in man-made iron nanoparticles. Furthermore, the apoferritin shell prevents contact between the cores, eliminating magnetic exchange interactions.Here, we focus on the magnetic properties of ferritin, which are an indicator for the spin structure and composition of the ferritin core. The magnetic properties of ferritin nanoparticles, for example their saturation magnetization, are directly linked to the relaxation rates of ferritin-rich tissue. As such, the magnetism of the protein influences the contrast of R2 and R2*-weighted MRI images.7–9
In the past decades, ‘bulk’ magnetometry techniques have been used to characterize the magnetic and mineral state of ferritin,10,11 along with spectroscopy techniques such as Mössbauer spectroscopy,11,12 electron paramagnetic resonance (EPR),13,14 nuclear magnetic resonance (NMR),15–17 as well as electron and X-ray microscopy techniques,18,19 and diamond-based quantum spin relaxometry to study the ferritin room temperature magnetic properties.20 Electron paramagnetic resonance (EPR), sometimes also referred to by the more general term electron magnetic resonance (EMR), has also been applied to ferritin,13,14,21–25 in spite of intrinsic challenges related to extreme spectral broadening.
It is generally agreed upon that the ferritin core is predominantly composed of a mineral resembling ferrihydrite,26 a poorly crystalline ferric oxyhydroxide. While some studies suggested a multiphase core composition,6,27,28 this hypothesis is not supported by NMR,16 magnetooptical measurements,17 electron energy-loss spectroscopy,29 and only partially by muon spin rotation. On the other hand, there is a general consensus on the following properties: (1) iron-spins in the cores are antiferromagnetically (AF) coupled, (2) the cores possess a spontaneous magnetic moment of the order of ∼300μB, (3) the magnetic moments becomes blocked below Tb ≈ 12 K over the typical time span of magnetometric measurements, and (4) ferritin is superparamagnetic above Tb.13,14,21,24 However, several questions remain still unanswered: for instance, the origin of the spontaneous magnetic moment of the cores has been generically attributed to randomly distributed defects in the AF lattice,10,30,31 but the nature and location of these defects (e.g., in the bulk or at the surface) remain ambiguous.32–34 The magnetic moment might also arise from core alteration, as it has been postulated in the case of ferrihydrite, which becomes partially ferrimagnetic during its transformation to hematite.35 The maghemite-like ferrimagnetic phase resulting from this alteration process might explain the postulated low-coercivity phase in ferritin.27 The apparent multiphase nature of ferritin might also originate from the interaction between different units within the core,26,36 or between core and surface spins.13 Such interactions can explain spin glass-like signatures such as shifted field-cooled hysteresis loops.37 Finally, the absence of a spin-flop transition in fields up to 50 T,38 which is incompatible with the reported exchange and anisotropy fields of ferritin, questions the definition of anisotropy energy and energy barriers in AF nanoparticles.39
Several limitations concur to our presently incomplete picture of the magnetic properties of ferritin. Interpretations of magnetometry and spectral techniques are intrinsically non-unique, therefore relying on models that require some a-priori knowledge of the spin structure of ferritin cores. Furthermore, most if not all magnetic parameters of ferritin are broadly distributed.40 This can lead to erroneous conclusions if such broad distributions are replaced with mean values without considering possible correlations. Furthermore, broad parameter distributions make model fits very sensitive to initial assumptions and measurement noise, as seen with the multiple approaches used to model the superparamagnetic and linear contributions to in-field magnetization curves.10,30,32,39,41 Finally, magnetometric and spectral techniques have been rarely combined,34 despite the intrinsic advantages of using complemental information to better constrain existing models.
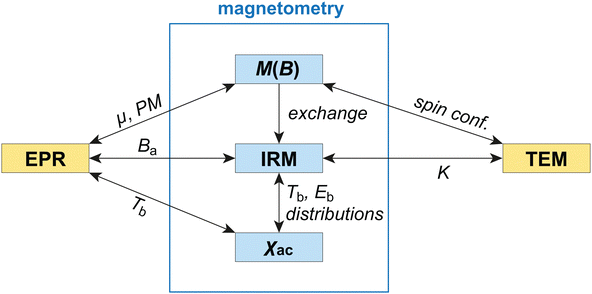
In this work, we focus on the EPR and magnetometric properties of human-liver ferritin (HuLiFt) and address some of the issues mentioned above. Using these techniques, we explore the spin dynamics over a broad frequency range that includes DC (magnetization) to sub-kHz (AC-susceptibility) and microwave (9 GHz, EPR) measurements. The present work not only combines different methods, but also different fields of research, such as magnetism and, due to the mineral core of ferritin and the widespread occurrence of ferrihydrite in nature, geological aspects. We unified different naming conventions used for the characterization of magnetic materials using a single symbol for each quantity, except the magnetic moment, for which m is used in the case of magnetometric measurements and μ in the EPR context (see the list of symbols given in the ESI†).
Most EPR studies have been performed at 9 GHz on horse-spleen ferritin.13,14,21,23,24 The broad superparamagnetic signal located at g′ = 2 was associated with antiferromagnetically coupled Fe(III) ions in the ferritin cores, while a weak signal near g′ = 4.3 was attributed to a small number of mononuclear Fe(III) centers showing typical paramagnetic behaviour.13,21,23 A few EPR studies have been performed on human ferritin, specifically from human spleens,14,24 proposing that the broad EPR signal results from two overlapping broad contributions, a very anisotropic one at lower fields, and an isotropic one around g′ = 2. Interestingly, in ref. 24 the 35 GHz data show the lower field EPR component of horse-spleen ferritin has a much lower intensity than its counterpart in human-spleen ferritin, however, the paper does not comment on this difference.
The EPR lineshape of superparamagnetic nanoparticles have been addressed using qualitative descriptions, such as the one by Noginova et al.42 based on surface quantum effects, according to which the EPR intensity is proportional to exp(−μB/kBT). Previously, Usselman et al.43 used two different models to simulate temperature-dependent lineshape trends of iron oxide nanoparticles mineralized in Listeria innocua protein cages. The first model44,45 provides a qualitative description of the lineshape dependence on temperature46 and frequency,47 assuming an ensemble of non-interacting single-domain particles, whose magnetization dynamics is described by the Landau–Lifshitz equation.45 The second model48 calculates the moment-distribution function by considering superparamagnetic fluctuations and ensemble broadening due to a distribution of anisotropy axes.48 Other models include an improved static model to describe the decrease in the magnetic anisotropy as temperature increases.49 However, these models do not reproduce all features of the measured EPR spectra.
Here, we use a quantum mechanical model50,51 to analyze 9 GHz EPR spectra of ferritin in solution, rather than in the freeze dried state, to exclude ferritin–ferritin interactions. Our analysis reveals multiple EPR spectral components resulting from the distributed nature of moment and anisotropy field distributions.
Magnetic simulations of equilibrium magnetization curves are used to understand the origin of the magnetic moment of ferritin cores. The theory behind these simulations is described in Section 3 and its application in Sections 4.2–4.5. Using these simulations and the measurement of isothermal remanent magnetization, we developed a new approach for the determination of the anisotropy field, magnetic moment, and blocking temperature distributions, as well as the relations existing between these parameters and between magnetometric and EPR measurements.
Our results can be explained by a simple model of AF nanoparticles whose magnetic moment is generated by surface-spin canting, rather than defects. This model explains the lack of a spin-flop transition below ∼50 T. We also observe minor (<3%) contributions to the anisotropy field distribution that are compatible with a ferrimagnetic phase and a phase with very large anisotropy, respectively. Finally, we show that EPR is particularly sensitive to surface spins.
2 Materials and methods
2.1 Properties and characterization of the human-liver ferritin
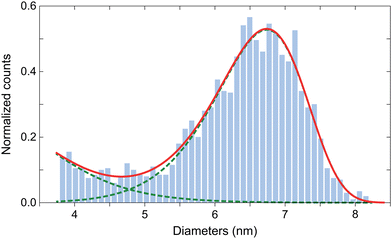
Commercial human-liver ferritin (HuLiFt) was obtained from LEE Biosolutions (Cat. No. 270-40, Lot 08E1805) and used without further purification. The protein concentration was 3.6 mg ml−1 with >95% purity as assessed by SDS-PAGE, Coomassie blue and Prussian blue stains (see ESI† for details). The protein loading factor was determined by inductively coupled plasma mass spectrometry (ICP-MS), yielding 1967 ± 78 iron atoms per ferritin. The size distribution of ferritin cores was obtained from transmission electron microscopy (TEM) images (Fig. S1, ESI†), using automatic circle detection based on the MATLAB function regionprops. The analysis of 2100 particles showed that core sizes strongly deviate from a unimodal lognormal-like distribution (Fig. 1). The main peak of the core size distribution is well approximated by a Weibull distribution with a mean of 6.5 nm and a median of 6.6 nm. An excess of small sizes with respect to the Weibull fit is observed below 4.5 nm and might represent incomplete fragmented cores.2.2 Magnetometry
The ferritin solution as purchased, i.e. without adding glycerol, see materials, was immersed into liquid nitrogen and subsequently freeze-dried over ∼48 hours. For further details and sample handling see also [ref. 52]. The obtained powder sample was pressed into a gel capsule and loaded into a Quantum Design MPMS-XL SQUID magnetometer mounting the reciprocating sample option (RSO, noise floor: 1 pA m2). First, the magnetic moment in a 5 mT field was measured as a function of temperature after cooling to 5 K in zero field (zero-field-cooled, ZFC) and in 5 mT (field-cooled, FC), respectively. Then, the field-induced magnetization was measured at 5 K and 150 K (complete hysteresis loops) and in the 5–250 K range (initial magnetization curves). Low-field AC susceptibility was measured after ZFC to 20 K in a 5 mT DC field with superimposed longitudinal AC field of 0.38 mT amplitude and frequencies ν = 0.113, 0.669, 4.481, 29.99, 59.9 Hz. Only the in-phase AC susceptibility was processed, as the quadrature component was too noisy. ZFC and FC hysteresis loops were measured at 5 K and 25 K in order to detect the presence of an exchange field. Finally, high-resolution isothermal remanent magnetization (IRM) curves were acquired from 0 to 5 T in steps comprised between 1 and 200 mT, at 3, 5, 9, 11, 13, 17, and 20 K. Each point Mr(B) of a IRM curve is obtained by ramping the field from 0 to B and then back to 0, with no overshoot. Repeated measurements were acquired to ensure reproducibility and enhance the signal-to-noise ratio (SNR): a SNR ≥100 is ideally needed over the field range containing relevant coercivity contributions. All measurements are expressed as mass magnetization obtained by dividing the magnetic moment by the sample mass. All data analyses were carried out in Matlab2016a and Mathematica 12 using built-in non-linear minimization routines.2.3 Electron paramagnetic resonance
In order to avoid ferritin-ferritin interactions that might occur in the freeze-dried samples14,21,23 we used the buffered ferritin solution for EPR measurements. For this purpose, 100 μL of the ferritin solution with 20% glycerol (vol/vol) solution were transferred into a 4 mm outer diameter EPR tube. The tube was then immediately frozen in liquid nitrogen. Continuous wave (CW) EPR measurements were performed with a 9 GHz ELEXSYS E680 EPR spectrometer (Bruker, Rheinstetten, Germany), equipped with a rectangular cavity. The spectra were recorded with 20 mW power, 90 kHz modulation frequency, and 29.46 Gpp field modulation amplitude at temperatures comprised between 5 and 210 K. The accumulation time was 11.2 min per spectrum. A helium flux cryostat was used to control the temperature. Temperatures were taken from the readout of the Oxford temperature unit connected to a thermocouple placed beneath the sample. Measurement of the buffered suspension instead of freeze-dried powders produces a lower EPR signal intensity; however, signal quality was still sufficient for further processing.Simulations of measured spectra have been conducted with the EasySpin package (5.2.4) using a Matlab (R2019a) script. Spectra between 5 and 15 K were not analyzed because it was not possible to accurately discriminate the broad signal from background noise. Final simulations have been performed with two components. The parameters D and Hstrain (Gaussian broadening) were adjusted independently for each component and each temperature, along with the relative contributions of the two components and the pepper routine parameters of the EasySin package, after choosing S = 10 and g = 2.01 as fixed parameters for both components. The sensitivity of the model to the parameters D and Hstrain was tested by changing, for example, D of one component and leaving all other parameters unchanged, until a visible lineshape alteration was detected (see section “Sensitivity of EPR parameters” in the ESI†).
3 Theoretical background of magnetometry analysis
In the following, we discuss different models of the spin structure of ferritin cores and the implications they have on magnetometry and EPR results.Starting from models proposed in the literature and our measurements we derive a new model for the spin structure of ferritin. First, we analyze the implications of polyphase ferritin cores for the interpretation of magnetometry results, showing that individual phases coexisting in the same core cannot be discriminated by isothermal magnetic measurements. Next, we use these findings to discuss possible spin structures that are compatible with equilibrium magnetization curves, showing that spin canting is needed to explain the ferritin-core susceptibility at lower field and the lack of a spin-flop transition. The universal relation between mean magnetic moment and number of Fe atoms in ferritin and ferrihydrite nanoparticles further confirms these findings. Finally, magnetometric parameters are discussed in relation to the energy barrier that needs to be overcome to switch the magnetic moment of ferritin cores, showing that the expression Eb = KV is valid also in the case of AF nanoparticles, and that a wide distribution of anisotropy fields can be a consequence of the fact that Ba, the anisotropy field, is inversely proportional to m, the magnetic moment.
3.1 Magnetic phases proposed for ferritin in the literature
The use of TEM X-ray Adsorption Near Edge Spectroscopy (XANES) and Small-Angle X-ray Scattering (SAXS) for probing the composition of ferritin cores (i.e., the proportion of Fe and O atoms), and of Electron Energy-Loss Spectroscopy (EELS) for probing the oxidation state of Fe ions suggests a polyphase structure6,27,28 made mainly of ferrihydrite (Fh) or a phosphorous-rich phase whose structure is similar to that of ferrihydrite,17 with minor hematite (α-Fe2O3), magnetite (Fe3O4), and wüstite (FeO) contributions.28 In the human brain, these secondary contributions tend to increase with age and in patients with neurological diseases.6 Spatial EELS analyses suggest that magnetite is concentrated at the core surface.28 On the other hand, other studies based on magnetooptical measurements suggest a single-phase core structure.The hypothetical polyphase nature of ferritin cores might be the result of Fh alteration or variable iron storage mechanisms. Fh is known to form an ordered ferrimagnetic structure during aging,35 as intermediate product on the pathway to full conversion to hematite. The conversion rate of synthetic Fh is very slow at room temperature, but it is greatly enhanced in the presence of ligands.53 Heating during sample preparation might therefore be an issue for the assessment of ferritin core composition. On the other hand, a 3D morphology study suggests that ferritin cores are composed of up to eight regions with disordered surfaces, consistent with the eight channels in the protein shell that deliver iron to the central cavity.26 Disordered surfaces are magnetically distinct from the bulk and can therefore be considered as an additional phase.
Ferritin-core phases identified so far are characterized by different forms of magnetic order, including AF (Fh, FeO), canted AF (hematite), ferrimagnetic (magnetite), and speromagnetic (surfaces). However, if these phases coexist within the same core units, exchange coupling is expected to produce a collective spin behavior that is not equivalent to the superposition of bulk-phase properties. Magnetometry data might still suggest a polyphase composition, for instance through a bimodal magnetic moment or energy-barrier distribution.27,36 In our case, the existence of multiple magnetic phases is supported by IRM acquisition curves (see Sections 4 and 5).
Magnetic evidences used so far in support of significant contributions from phases other than Fh depend heavily on the way energy barrier and magnetic moment distributions are measured and modelled. For instance, the energy barrier distribution obtained from magnetic viscosity measurements is bimodal,36 while the same distribution derived from quadrature AC susceptibility data is strictly unimodal.54 The case of the magnetic moment distribution is even more ambiguous, as the fit of equilibrium magnetization curves with two superparamagnetic components with distinct single-valued magnetic moments, as proposed by Brem et al.,27 is a valid alternative to the distributed moment model described in the Results section. Evidently, the additional degree of freedom of the two-component model enables better fits to the data. Nevertheless, as we demonstrate further below, this interpretation is incompatible with the IRM results obtained in the present study and therefore discarded.
3.2 The magnetic signature of idealized spin structures
Consider a collinear two-sublattice AF particle with sublattice magnetization M0 and exchange constants Aa, Ab, and Aab. In the case of slightly uncompensated sublattices, the two sublattice magnetizations are given by Mb = M0 and Ma = (1 + α)M0, respectively, where α > −1 is the fraction of excess moment in one sublattice. This creates a net spontaneous magnetic moment muc = αM0V in a particle with volume V. In the following, it is assumed that muc is rigidly coupled to the sublattice magnetizations, due to the strong AF coupling,55,56 so that any change of the magnetic moment is produced by the uniform rotation of all spins in both sublattices. Furthermore, particles possess a positive uniaxial magnetic anisotropy57 with anisotropy constant K and easy axis parallel to the unit vector e = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,0,cos
ϕ,0,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), so that
ϕ), so that 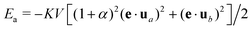 is the anisotropy energy corresponding to sublattice magnetizations parallel to the unit vectors ua and ub, respectively.58 In the absence of external fields, the total energy is minimized when the sublattice magnetizations are exactly antiparallel and oriented along the easy axis. The application of a field B rotates the lattice magnetizations away from the easy axis and introduces an induced spin canting (Fig. S23, ESI†). Following Bogdanov et al.,58 we define the spin canting angle −π/2 ≤ ε ≤ π/2, such that ua,b = ±p
is the anisotropy energy corresponding to sublattice magnetizations parallel to the unit vectors ua and ub, respectively.58 In the absence of external fields, the total energy is minimized when the sublattice magnetizations are exactly antiparallel and oriented along the easy axis. The application of a field B rotates the lattice magnetizations away from the easy axis and introduces an induced spin canting (Fig. S23, ESI†). Following Bogdanov et al.,58 we define the spin canting angle −π/2 ≤ ε ≤ π/2, such that ua,b = ±p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε + n
ε + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε, where p is the so-called Néel unit vector parallel to the staggered magnetization direction ua − ub, and n⊥p is the unit vector parallel to the canting magnetization direction ua + ub. In a spherical coordinate system with B‖ẑ, p = (sin
ε, where p is the so-called Néel unit vector parallel to the staggered magnetization direction ua − ub, and n⊥p is the unit vector parallel to the canting magnetization direction ua + ub. In a spherical coordinate system with B‖ẑ, p = (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ,sin
ψ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ,cos
ψ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and n = n1
θ) and n = n1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ + n2
λ + n2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ with n1 = (ẑ × p) × p parallel to the plane spanned by B and e, n2 = ẑ × p⊥z, 0 ≤ θ ≤ π, and −π ≤ ψ, λ ≤ π. In this case, the total energy E per unit of volume of a particle with the above properties is given by
λ with n1 = (ẑ × p) × p parallel to the plane spanned by B and e, n2 = ẑ × p⊥z, 0 ≤ θ ≤ π, and −π ≤ ψ, λ ≤ π. In this case, the total energy E per unit of volume of a particle with the above properties is given by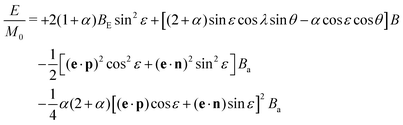 | (1) |
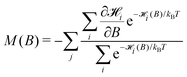 | (2) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) . In the classical case where the magnetic moments can take any orientation,
. In the classical case where the magnetic moments can take any orientation, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = E(θ,ψ,λ,ε) and ∂i
= E(θ,ψ,λ,ε) and ∂i![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) /∂B = −M0Vζ, with
/∂B = −M0Vζ, withζ = α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − (2 + α)sin θ − (2 + α)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ λ | (3) |
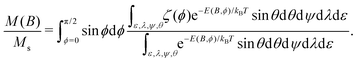 | (4) |
Numerical evaluations of eqn (4) are extremely time consuming, due to the five-fold integrals: on a PC, a single equilibrium magnetization calculation takes ∼7 min using an optimized method (ESI:† Equilibrium magnetization models). Simulations of M(B) at 50 K using BE ≈ 320 T for ferritin,56 show that the equilibrium magnetization is governed by two regimes (Fig. 2). In small fields, thermal fluctuations, which act on each degree of freedom, induce a small spin-canting angle that adds a random canting moment mc perpendicular to the uncompensated moment muc. If muc = 0, the random canting moment generates a low-field susceptibility χlf = χ⊥/3, where χ⊥ = M0/BE is the bulk perpendicular susceptibility of the AF lattice. In larger fields, the canting moment gets progressively aligned with the field, producing a transition to the high-field regime given by M = χ⊥B (Fig. 2b). If αmncBE ≫ kBT, the uncompensated moment is much larger than the canting moment, and the low-field magnetization converges to the Langevin model prediction, with χlf = Msmuc/kBT, regardless of single particle anisotropy. At larger fields, anisotropy decreases the equilibrium magnetization, because of the competition between field and easy axis alignment (dashed lines, Fig. 2a). The same result has been obtained previously59,60 for non-interacting ferromagnetic particles. In the simulations of Fig. 2, this ferromagnetic-like regime holds for muc ≥ 150μB and B < 5 T.
External fields increase the canting angle of all particles whose Néel vector p is not parallel to the field direction; however, at the same time, the uncompensated moment tends to align the Néel vector with the field, so that spin canting becomes less effective. As a result, the spin canting angle continues to be controlled only by thermal fluctuations until the alignment of the canting moment becomes energetically more favorable than that of muc: at this point, a so-called spin-flop transition takes place through rotation of the Néel vector by 90°. In bulk antiferromagnets, this is a sudden event that occurs at the spin-flop field Bsf ≈ (2BEBa)1/2 predicted by mean-field theory.58 This result does not hold for the equilibrium magnetization of AF nanoparticles, because thermally activated spin canting occurs in all fields. As shown by our simulations, the spin-flop field is defined, in this case, by the intersection of the Langevin law with the high-field regime M = χ⊥B of perfect antiferromagnets (Fig. 2b). For sufficiently large values of α (e.g., α ≈ 0.025 for the 50 K simulations of Fig. 2), the spin-flop field for the equilibrium magnetization is then given by Bsfe = αBE. Contrary to bulk antiferromagnetism,39 magnetic anisotropy does not affect Bsfe; instead, it increases the slope of M(B) in the Langevin saturation regime, until it becomes indistinguishable from the spin-flop regime (Fig. 3). This occurs because the additional Néel vector misalignment produced by randomly oriented anisotropy axes enhances the induced spin canting and its contribution to the equilibrium magnetization already in fields <Bsfe. Vice versa, the same anisotropy effect reduces the alignment of the canting moment above Bsfe.
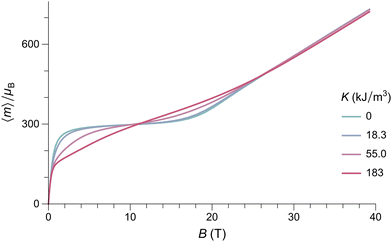 | ||
| Fig. 3 Numerical simulations of the T = 50 K equilibrium magnetization of randomly oriented AF particles with muc = 300μB and selected values of the anisotropy constant. Other model parameters are the same as in Fig. 2. | ||
The defect moment model illustrated above is our starting point for assessing the validity of the modified Langevin fit we used to estimate the distribution of muc from M(B) measurements, and for testing the origin of the uncompensated moment in ferritin cores. For this purpose, we used eqn (4) to calculate M(B) at 50 K for an ensemble of randomly oriented particles with the same lognormal distribution of muc obtained from the modified Langevin fit, together with model parameters representative for ferritin, that is, K = 18.3 kJ m−3 (Section 5.2), BE = 320 T, and M0V = 6000μB (Fig. 4b). According to this simulation, the spin-flop transition is expected to occur at ∼10 T, instead of (2BEBa)1/2 ≈ 36 T. This is beyond the maximum field used in our M(B) measurements, but well below the ∼50 T maximum field used in experiments that failed to detect such a transition.38,39 The lack of a spin-flop transition below 50 T has been attributed to larger-than-expected values of BE and/or Ba.38,39 As shown by our simulations, Bsfe is not affected by single particle anisotropy, while the >5 times larger exchange field required to push Bsfe beyond the maximum field range of available measurements does not comply with BE values obtained from high-field estimates of the AF susceptibility.39 Therefore, the only plausible explanation for the discrepancy between the simulation of Fig. 4 and actual high-field measurements of M(B) is that the defect model of Néel61 does not provide a correct description of the in-field magnetic moment of ferritin cores.
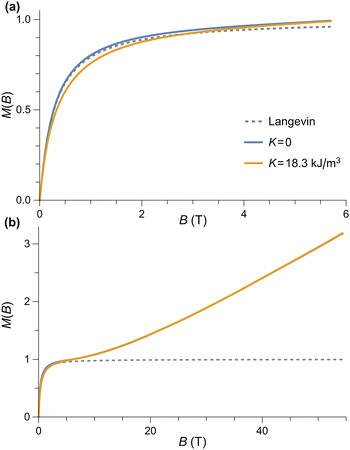 | ||
| Fig. 4 Numerical simulations of the T = 50 K equilibrium magnetization of randomly oriented AF particles with the lognormal distribution of magnetic moments deduced from the modified Langevin fit of M(B) measurements (logarithmic mean: 215μB, logarithmic standard deviation: 0.963), calculated using the Langevin model (dashed line), and the AF model of Fig. 2 (solid lines). (a) and (b) Represent the same simulations over different field ranges. | ||
As far as the effect of anisotropy on the shape of M(B) is concerned, a relatively small but non-negligible reduction of the equilibrium magnetization occurs over the 0.5–3 T field range, before the onset of saturation (Fig. 4a). This alters the magnetic moment distribution obtained by the modified Langevin fit, lowering the apparent mean moment by ∼40% and increasing the apparent moment distribution width by ∼30%. A-posteriori corrections of the Langevin fit according to these results, however, would not be meaningful, since the absence of a spin-flop transition in fields ≤50 T requires a different model for the superparamagnetic behavior of ferritin. Therefore, we look for spin configurations that produce a net spontaneous moment that is not parallel to the Néel vector. A possible source for such spin configurations is surface anisotropy, because it affects the orientation of surface spins with respect to the bulk.
Surface spins are often assumed to be in a disordered, spin-glass-like state created by a distribution of exchange field vectors pointing to different directions.62,63 The exchange interaction between surface and internal spins manifests itself through exchange bias, that is, the horizontal shift of FC hysteresis. The existence of this exchange bias in horse-spleen ferritin10 and in our sample (see Section 4), along with data from dynamic Mössbauer spectroscopy,34 testifies for the existence of a surface spin layer in ferritin cores. Due to the sensitivity of exchange interactions to the position of ions, surface spins can take multiple configurations that are not necessarily associated to a complete disorder, as seen for instance with the spike, throttled, and two-pole configurations obtained from simulations of ferrimagnetic nanoparticles.64 These configurations decrease the net moment of particles with ferrimagnetic order, but represent a possible source of spontaneous moments in AF nanoparticles. Furthermore, the exchange coupling between surface and internal spins can alter the AF ordering of the whole particle.65 Recent simulations of small AF nanoparticles demonstrate this effect, with spike, throttled, and disordered internal spin configurations, as well as spin canting (Fig. 11 and 12 in Laura-Ccahuana and De Biasi66). Most importantly, these simulations show that surface anisotropy increases the spin-flop field and/or limits spin flopping to subregions of the particles or suppresses it completely, so that the bulk magnetization does no longer show the effects of a spin-flop transition.66 Similar effects might also occur at interfaces between different phases in a polyphase model of ferritin cores, especially if secondary phases consist of few surface atomic layers.28 Specific sources of spin canting moment include topological chiral magnetism induced by the Dzyaloshinskii–Moriya exchange interaction on surfaces and interfaces.67
In principle, the equilibrium magnetization of AF particles with surface anisotropy can be calculated by evaluating eqn (2) with the Hamiltonian64,66
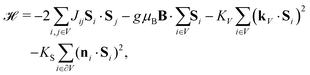 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) εs is produced by a zero-field canting angle εs (ESI:† Spontaneous spin canting).
εs is produced by a zero-field canting angle εs (ESI:† Spontaneous spin canting).
As expected, the equilibrium magnetization of AF particles with a spontaneous canting moment is equivalent to the sum of a Langevin term that describes the superparamagnetism of mc, and a linear term M = χ⊥B that accounts for the induced spin canting (Fig. 5a). Because mc is already perpendicular to the Néel vector, there is no spin-flop transition. The M(B) curve resulting from the same distribution of moments used to simulate uncompensated moment now contains a linear term M = χB comparable with the non-paramagnetic component ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (mB/kBT) + χB of the model used to fit M(B) data (Fig. 5b). The normalized slope χ/Ms of the linear term is ∼40% smaller than the fitted value at 50 K. A good agreement, on the other hand, is obtained at 250 K. The temperature-dependent mismatch is due to the fact that this model does not account for the effects of single-particle anisotropy, and in particular surface anisotropy, on χ.
(mB/kBT) + χB of the model used to fit M(B) data (Fig. 5b). The normalized slope χ/Ms of the linear term is ∼40% smaller than the fitted value at 50 K. A good agreement, on the other hand, is obtained at 250 K. The temperature-dependent mismatch is due to the fact that this model does not account for the effects of single-particle anisotropy, and in particular surface anisotropy, on χ.
3.3 The role of distributed parameters
Magnetic properties of ferritin are usually expressed in terms of averaged quantities or treated as single-valued parameters (e.g., K, Ba, the blocking temperature Tb). This approach is correct only when it is applied to intrinsic properties of the material, such as the sublattice magnetizations and exchange constants, and the bulk magnetocrystalline anisotropy. Parameters that do not represent intrinsic properties of an AF crystal, such as the magnetic moment and the anisotropy field, must be treated as statistical distributions to avoid incorrect interpretations, as shown by the following example. The mean ferritin magnetic moment of ∼350μB obtained from simple10,68 or distributed (this work) Langevin fits is usually attributed to an uncompensated moment matching one of the three models proposed by Néel.61 The first Néel model associates muc with defects randomly distributed among the AF sublattices: in this case, muc ≈ μFe(cN)1/2, where N ≈ 2500 is the total number of Fe ions in ferritin, μFe ∼ 5μB their magnetic moment, and c ≪ 1 the concentration of defects. The good match between 〈m〉 estimates obtained with c = 1 and with the Langevin fit has often been used as a validation of this model,10,30,31 even though a rigorous probabilistic analysis shows the largest mean moment 〈muc〉max ≈ 0.56μFeN1/2 is obtained with c = 0.5.Magnetic moment estimates obtained from ferritin nanoparticles with different iron loadings support a power law of the form m ∝ Np with p comprised between 1/2 and 2/3, the latter being the exponent expected from the uncompensated moments arising from surface spins belonging to one sublattice only.32 The same empirical power law applies to a large compilation of available data on ferritin and ferrihydrite, which yields p ≈ 0.59 ± 0.06, with no systematic differences related to particle composition (Fig. 6). The maximum possible defect moment 〈muc〉max associated with p = 1/2 is compatible only with two measurements out of a total of 28, so that the Néel defect model must be discarded. The empirical trend 〈m〉 ≈ 0.4μFeN2/3 fits the data almost optimally. Its compatibility with a surface-spin-canting origin of the magnetic moment is discussed below.
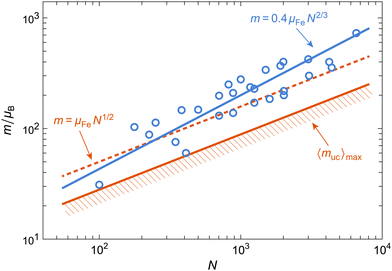 | ||
| Fig. 6 Mean magnetic moment vs. number of Fe atoms in ferritin and ferrihydrite particles (circles), obtained from a compilation of literature data.10,30–32,69–79 Lines show best fits with different power laws described in the text. | ||
A better insight into the origin of the peculiar magnetic properties of ferritin is provided by the joint analysis of the magnetic moment and anisotropy distributions, through the relation between m, Ba, K, and Tb imposed by the Néel–Arrhenius model
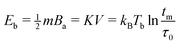 | (6) |
We also tried the alternative model of fitting measured equilibrium magnetization curves with two distinct magnetic moments, as proposed by Brem et al.27 Replication of this approach with our data yields superparamagnetic and linear contributions that are almost identical to our original model, with a slightly smaller misfit (Fig. S20, ESI†). The magnetic moments m1 = 97μB and m2 = 540μB and the relative superparamagnetic contributions (57% and 43%, respectively) are similar to those obtained by Brem et al. for horse-spleen ferritin, where m2 was attributed to magnetite. Using a magnetic moment of 4.1μB per formula unit of Fe3O4, magnetite must contain ∼20% of the ∼2000 Fe atoms in our ferritin cores in order to explain the magnetic moment of 540μB attributed to this phase. The model of Brem et al. requires the two moments to be fully uncoupled in order to be modeled by the linear combination of two independent Langevin functions, in which case their contributions to the remanent magnetization would add linearly in the same proportions as the superparamagnetic contributions. However, the magnetite-like component deduced from our IRM measurements contributes to ∼0.6% of the total blocked magnetization, much less than deduced from the two-moment Langevin model.27 This discrepancy is too large to be explained by uncertainties in the Langevin fit or in fits of the IRM acquisition curves. Therefore, we must conclude that ferritin cores are made either by a single phase or by different phases with rigidly coupled spins, justifying the representation of the core magnetization by a fixed magnetic moment.
3.4 Surface-spin model for ferritin
As discussed above, surface spin canting in ferritin cores appears to be the only source of a spontaneous magnetic moment that is compatible with all magnetic characterizations reported so far. This model represents the basis of our approach to fit our equilibrium magnetization curves and obtain the magnetic moment distribution (see Section 4.4). Along with the anisotropy field distribution obtained from the analysis of IRM acquisition curves, these results allow to verify the consistency of all magnetometry measurements, as explained in the following.If the magnetic moment of ferritin cores is controlled by surface effects, we can expect m = NsμFeηs to be proportional to the number Ns of surface spins, their magnetic moment μFe ≈ 5μB, and the degree ηs = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) εs of canting, regardless of the detailed spin configuration. Internal spins might also experience some canting through coupling with the surface.66 In all cases, the source of spin canting is related to the surface, and therefore, we assume Ns = κsV2/3 with κs = (36π)1/3(ρfNA/uf)2/3, where ρf ≈ 3.9 g cm−3 is the density of ferritin cores,80NA the Avogadro constant, and uf ≈ 96 g mol−1 the molar mass per Fe atom obtained with the chemical formula 5Fe2O3·9H2O of six-line ferrihydrite. The resulting expression m = κsμFeηsV2/3 explains the data compilation in Fig. 6, yielding ηs ≈ 0.4 if only surface spins are canted. Much lower canting angles are required if spin canting extends to internal spins.66 Alternate compositions have been proposed for the ferritin mineral core:17 if this composition is indeed significantly different from that of ferrihydrite, it does not affect the magnetic moment, as seen in Fig. 6.
εs of canting, regardless of the detailed spin configuration. Internal spins might also experience some canting through coupling with the surface.66 In all cases, the source of spin canting is related to the surface, and therefore, we assume Ns = κsV2/3 with κs = (36π)1/3(ρfNA/uf)2/3, where ρf ≈ 3.9 g cm−3 is the density of ferritin cores,80NA the Avogadro constant, and uf ≈ 96 g mol−1 the molar mass per Fe atom obtained with the chemical formula 5Fe2O3·9H2O of six-line ferrihydrite. The resulting expression m = κsμFeηsV2/3 explains the data compilation in Fig. 6, yielding ηs ≈ 0.4 if only surface spins are canted. Much lower canting angles are required if spin canting extends to internal spins.66 Alternate compositions have been proposed for the ferritin mineral core:17 if this composition is indeed significantly different from that of ferrihydrite, it does not affect the magnetic moment, as seen in Fig. 6.
According to the above model for the magnetic moment, the distribution of lnm, which is usually assumed to be Gaussian when fitting M(B) curves, is given by gm = gκμη * gV2/3, where gκμη and gV2/3 are the distributions of ln(κsμFeηs) and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V2/3, respectively, and “*” is the convolution operator. Deconvolution of gm obtained from fitting M(B) curves with gV2/3 obtained from TEM observations thus yields an estimate of gκμη, from which the distribution of ηs easily derived. The maximum range of this distribution should not exceed ηs = 1 for a physically reasonable spin canting model.
V2/3, respectively, and “*” is the convolution operator. Deconvolution of gm obtained from fitting M(B) curves with gV2/3 obtained from TEM observations thus yields an estimate of gκμη, from which the distribution of ηs easily derived. The maximum range of this distribution should not exceed ηs = 1 for a physically reasonable spin canting model.
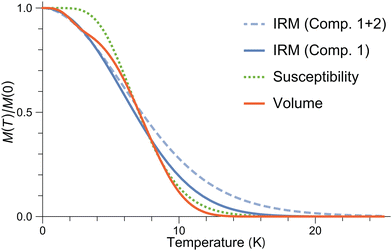
The surface spin model must also satisfy the Néel–Arrhenius expression for the energy barrier (eqn (6)) when the distributions of m, Ba and Tb are considered. The normalized temperature dependence Mr(T)/Mr(0) of the saturation remanent magnetization Mr yields, by definition, the integral of the blocking temperature distribution, fb(T). The function fb(T) can also be reconstructed from Eb = mBa/2 using the distributions of m and Ba obtained from M(B) and from IRM acquisition curves, respectively. These distributions, however, are extremely broad, so that the product mB depends critically on the type of relation existing between m and B, and not just on the respective mean values. In the case of ferrimagnetic SD particles with spontaneous magnetization Ms, m = MsV and Ba = 2K/Ms are independent variables, because Ms is a fixed material property. Accordingly, the distribution of ln(mBa) is given by the convolution of the distributions of lnm and lnBa, respectively. This approach, however, does not hold for AF particles, where Ms = m/V is itself distributed. Accordingly, in the case of ferritin, convolution of the distributions of lnm and lnBa yields an extremely broad distribution of energy barriers, which does not match fb(T) (Fig. S21, ESI†).
The correct expression for the anisotropy field of AF particles obtained from eqn (6) is Ba = 2K/m: in this case, Ba is inversely proportional to the magnetic moment, and the two factors in Eb = mBa/2 are no longer independent variables. The inverse relation between m and Ba can be understood by considering that the work required to reverse all spins of the AF lattice must be provided by the Zeeman energy of the magnetic moment in the switching field Bsw, so that a smaller magnetic moment must be compensated by a larger Bsw ∝ Ba. The above model for m yields Ba = 2KV1/3/κsμFeηs. If V is a narrow distribution, as in the case of ferritin cores, any size dependence of K and ηs is negligible, and Ba is the product of almost completely independent statistical variables. The resulting anisotropy field distribution is then given by ga ≈ g2K/κμ * gV1/3 * gη−1, where g2K/κμ, gV1/3, and gη−1 are the distributions of ln(2K/κsμFe), ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V1/3, and ln
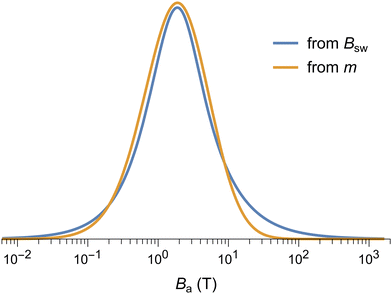
V1/3, and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η−1, respectively so that ga can be reconstructed from estimates of K, V, and m obtained from magnetometry measurements. On the other hand, ga can also be obtained directly from IRM acquisition curves, using the well-known relation Ba = 2.083Bsw for randomly oriented, uniaxial SD particles.81 The two reconstructions of the anisotropy field distribution must coincide if the surface spin model described above correctly describes the spin configuration of ferritin cores.
η−1, respectively so that ga can be reconstructed from estimates of K, V, and m obtained from magnetometry measurements. On the other hand, ga can also be obtained directly from IRM acquisition curves, using the well-known relation Ba = 2.083Bsw for randomly oriented, uniaxial SD particles.81 The two reconstructions of the anisotropy field distribution must coincide if the surface spin model described above correctly describes the spin configuration of ferritin cores.
4 Results
4.1 Electron paramagnetic resonance
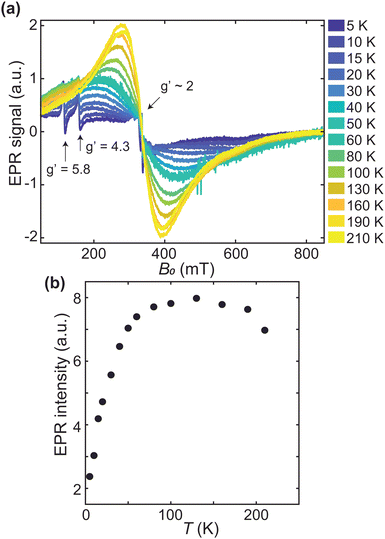
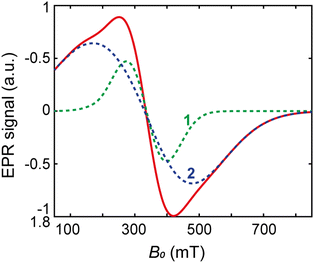
Fig. 7a shows the continuous wave 9 GHz EPR spectra between 5 and 210 K. The most prominent feature is a broad signal with a linewidth of ∼100 mT at 190 K, which is centered at g′ = 2.0. This broad signal is due to the mineral core in the protein shell of ferritin, in agreement with what has been reported in literature.13,14,21,22,25 Three narrow signals overlap with the broad spectrum at g′ = 2.0, 4.3, and 5.8, respectively (arrows). The g′ = 4.3 and g′ = 5.8 signals are usually attributed to mononuclear rhombic Fe(III) sites13,21,22,52,82 and high-spin Fe(III) in methemoglobin,83 respectively. Multiple lines at g′ = 2.052,83 might be ascribed to radical impurities, Cu(II), and possibly a small indication of Mn(II),22 but the origin is not further investigated. The amplitude of the g′ = 4.3 signal is inversely proportional to the logarithm of temperature, as expected from a paramagnetic contribution (data not shown). The other two narrow signals at g′ = 2.0 and 5.8 follow qualitatively the same trend.The lineshape of the broad signal, which is due to the magnetic moment of ferritin cores (Fig. 7a), is nearly Lorentzian at higher temperatures. Below 100 K, the shape becomes more asymmetric and is better fitted to a Gaussian shape. At 5–10 K, the amplitude of the broad signal has decreased to the point of being barely identifiable. The double integral of the broad EPR component, which reflects the total number of ferritin-core spins in the sample, increases with temperature, reaching a plateau at 100 K, followed by a slight decrease above 180 K (Fig. 7b). The increase in EPR signal amplitude with temperature is typical for superparamagnetic particles with an antiferromagnetic ground state,14,21,23,43 and can be explained by the fact that only unblocked particles, whose fraction increases with temperature, contribute to the signal. Once all particles are unblocked, a paramagnetic behavior, characterized by a decrease of the EPR spectral amplitude with increasing temperature is observed. Therefore, the maximum value of the signal intensities (Fig. 7b), at T ∼ 100 K, marks the transition from a regime of progressive unblocking of the magnetic moments to a regime where all moments are unblocked, thus representing the maximum blocking temperature of ferritin cores.
EPR simulations provide further insights into the nature of the broad signals. For this purpose, the ferritin core is considered as a single large spin S resulting from the coupling of individual iron ions in the core.50,51 The corresponding spin Hamiltonian, used to describe the spectra, is given by
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = μBS·g·B + S·D·S, = μBS·g·B + S·D·S, | (7) |
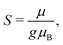 | (8) |
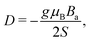 | (9) |
Simulations based on a single component produce a poor fit to the data (Fig. S5, ESI†), suggesting that at least two components are needed in order to capture the relevant spectral features. Automated two-component fitting approaches, however, yield unphysical results even in the case of limited parameter sets (see ESI:† “EPR alternative fitting approach”). This is because the line shape of high-spin systems such as ferritin does not depend in a simple manner on D and S. Furthermore, very different component combinations can fit broad line shapes equally well, so that meaningful fitting results depend critically on the initial parameter guess.
Physically meaningful initial parameter guesses have been obtained at selected temperatures by visually matching the measured spectra with a set of components covering a wide range of values for D, S and the Gaussian broadening parameter Hstrain (see ESI:† “EPR simulations of individual components”). Because of the excessive computation time required for simulating realistic values of S in excess of ∼100, the scaling procedure of Fittipaldi et al.50,51
| Sreal = S·n, Dreal = D/n, Treal = T·n | (10) |
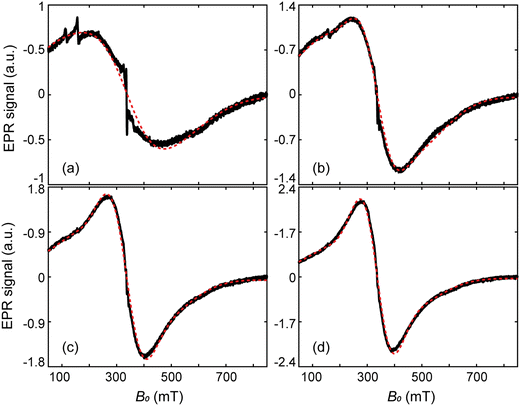 | ||
| Fig. 8 Selected EPR spectra (black lines) and their simulations (red dashed lines), at 30 K (a), 80 K (b), 130 K (c), and 190 K (d). | ||
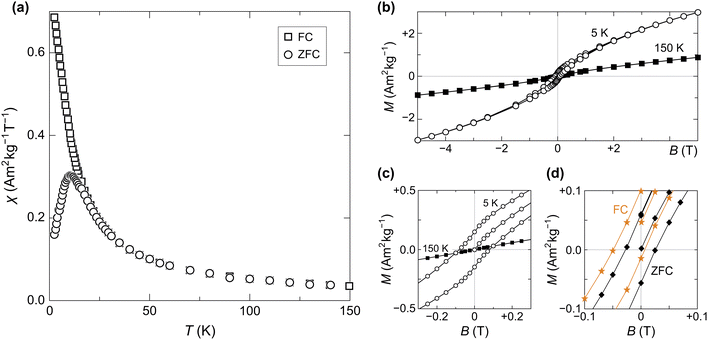
4.2 DC susceptibility and hysteresis
The superparamagnetic behaviour of human-liver ferritin is well captured by FC-ZFC measurements (Fig. 10a). The curves bifurcate at Tb,max ≈ 24 K, which corresponds to the largest unblocking temperature of the particles. The ZFC data display a peak at![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) b = 10.5 ± 0.5 K, in agreement with an earlier characterization of ferritin.10 The relation
b = 10.5 ± 0.5 K, in agreement with an earlier characterization of ferritin.10 The relation ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) b < Tb,max is indicative of a distribution of blocking temperatures. The opening of the hysteresis loop below
b < Tb,max is indicative of a distribution of blocking temperatures. The opening of the hysteresis loop below ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) b confirms the blocking process and the occurrence of magnetic irreversibility (Fig. 10b). The slight horizontal offset of the FC hysteresis loops highlights the presence of an exchange coupling field Bex ≈ 25 mT, persistent at 5 and 25 K (Fig. 10d). This exchange field is similar to Bex ≈ 32 mT reported for horse-spleen ferritin.10
b confirms the blocking process and the occurrence of magnetic irreversibility (Fig. 10b). The slight horizontal offset of the FC hysteresis loops highlights the presence of an exchange coupling field Bex ≈ 25 mT, persistent at 5 and 25 K (Fig. 10d). This exchange field is similar to Bex ≈ 32 mT reported for horse-spleen ferritin.10
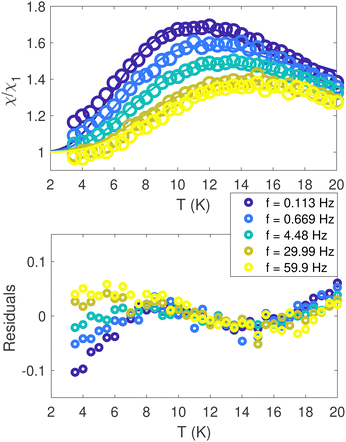 | ||
| Fig. 11 AC-magnetic moment and susceptibility of human-liver ferritin, probed in the sub-kHz frequency range. Top panel: Normalized in-phase susceptibility data (circles) and fit (solid line) to eqn (11). Bottom panel: Residuals of the fit. | ||
 | ||
| Fig. 12 (a) Measured isothermal magnetization curves (dots) and corresponding best fits with eqn (12) (lines), at temperatures indicated by numbers. Residuals, defined as the difference between measurements and model, normalized by the measured magnetization at 7 T, are plotted below. (b) Same as (a), after subtracting the modeled linear term from each curve. The 15 and 20 K magnetizations have been multiplied by 1.13 and 1.05, respectively, for better visualization. (c) Logarithmic mean of the magnetic moment distribution at measurement (dots, with 2σ error bars). The dashed line is the best-fitting antiferromagnetic magnon law obtained from >50 K moment estimates, with μm(0) = 215.4μB and α = 0.0043. (d) Non-paramagnetic susceptibility χ from the χB term in eqn (12) (black dots with 2σ error bars, left axis), and 1/χ (red dots with 2σ error bars, right axis). The dashed line represents the best-fitting Curie–Weiss law above 150 K, with Θ = −194 K. | ||
4.3 AC susceptibility
The in-phase AC susceptibility χ′(T) (Fig. 11) shows a broad peak that shifts towards higher temperatures upon increasing the frequency of the AC field.84 In-phase measurements have been fitted to a model derived from Gittleman et al.,85 while the imaginary part was ignored, due to its low SNR (see Fig. S18, ESI†). Full χ′(T) curves were calculated by integrating the analytical expression85 for χ′ over a distribution Γ(Eb) of anisotropy energy barriers Eb, thereby relaxing any assumption about the analytical dependence of Eb on the particles volume distribution: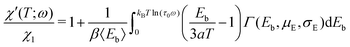 | (11) |
Eqn (11) was used to fit the AC susceptibility measurements using the Gamma function Γ(Eb,μE,σE) with mean μE and width parameter σE as energy barrier distribution.54 The attempt time was fixed to 9 ps, based on reported AC susceptibility ferritin data.30
The mean and standard deviation of the energy-barrier distribution used to fit the data (eqn (11)) are 144.74 K and 57.02 K, respectively. Note that the scaling parameter, β, decreased by 30%, upon decreasing the frequency.
4.4 Equilibrium magnetization
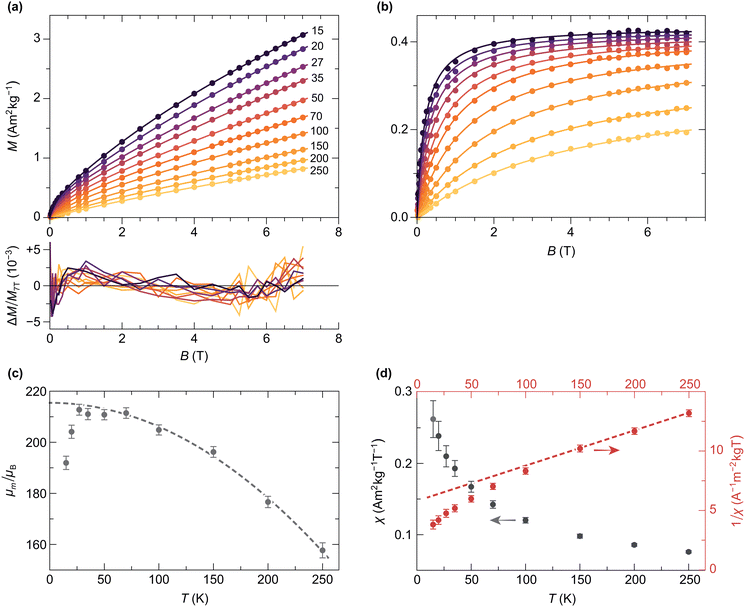
Isothermal magnetization curves acquired in fields up to 7 T at temperatures ≥15 K (Fig. 12a) are close to equilibrium: the residual hysteresis opening at 15 K is ∼3% of Ms, and drops to ∼0.5% at 27 K. A modified Langevin model of the form M(B) =![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (B,f) + χB was used to fit the equilibrium magnetization, where
(B,f) + χB was used to fit the equilibrium magnetization, where ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is a superparamagnetic term resulting from the partial alignment of unblocked magnetic moments with distribution f in the applied field, and χB is a linear term that includes superantiferromagnetic and paramagnetic contributions. In case of isotropic particles with identical magnetic moments m that are sufficiently large to ignore quantization effects, the superparamagnetic term is proportional to the Langevin function
is a superparamagnetic term resulting from the partial alignment of unblocked magnetic moments with distribution f in the applied field, and χB is a linear term that includes superantiferromagnetic and paramagnetic contributions. In case of isotropic particles with identical magnetic moments m that are sufficiently large to ignore quantization effects, the superparamagnetic term is proportional to the Langevin function ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (ξ) = cothξ − ξ−1 with ξ = mB/kBT, where kB is the Boltzmann constant, and T the absolute temperature.30,32 This model reproduces the equilibrium magnetization calculations for canted spins discussed in Section 3.2 (Fig. 5).
(ξ) = cothξ − ξ−1 with ξ = mB/kBT, where kB is the Boltzmann constant, and T the absolute temperature.30,32 This model reproduces the equilibrium magnetization calculations for canted spins discussed in Section 3.2 (Fig. 5).
Single-particle magnetic anisotropy decreases the magnetic moment alignment of mechanically blocked, randomly oriented particles as soon as the linear regime of ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) is left.59,86,87 In the limit case of infinite uniaxial anisotropy, particles possess only two magnetic states with m parallel or antiparallel to the easy axis, in which case
is left.59,86,87 In the limit case of infinite uniaxial anisotropy, particles possess only two magnetic states with m parallel or antiparallel to the easy axis, in which case ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) is replaced by
is replaced by ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (ξ) = 〈cos
(ξ) = 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h(ξ
h(ξ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ)〉, where 〈·〉 denotes the average of individual particle contributions over all angles ϕ between easy axes and field. This function was originally proposed by Néel,61 and used by Gilles41 as a model for ferritin superparamagnetism.
ϕ)〉, where 〈·〉 denotes the average of individual particle contributions over all angles ϕ between easy axes and field. This function was originally proposed by Néel,61 and used by Gilles41 as a model for ferritin superparamagnetism. ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) and
and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) have the same slope at B = 0, but their B → ∞ limits are 1 and 1/2, respectively. Particles of volume V and finite anisotropy constant K are characterized by intermediate equilibrium magnetization functions comprised between
have the same slope at B = 0, but their B → ∞ limits are 1 and 1/2, respectively. Particles of volume V and finite anisotropy constant K are characterized by intermediate equilibrium magnetization functions comprised between ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) and
and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) , whose shape is controlled by the anisotropy parameter κ = KV/kBT. Unfortunately, these functions cannot be expressed analytically, so that
, whose shape is controlled by the anisotropy parameter κ = KV/kBT. Unfortunately, these functions cannot be expressed analytically, so that ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) or
or ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) are used instead, regardless of the effective particle anisotropy.10,30,56,68,87 The Langevin function is a good approximation of the superparamagnetic behavior for κ < 2 (maximum error: 2%), and still considerably better than
are used instead, regardless of the effective particle anisotropy.10,30,56,68,87 The Langevin function is a good approximation of the superparamagnetic behavior for κ < 2 (maximum error: 2%), and still considerably better than ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) for κ < 10 (maximum error: 20%). Using K = 18.3 kJ m−3 for our ferritin sample (see Section 5.3) and the volume of spherical cores with a diameter of 7 nm (Fig. 1), the κ < 2 and κ < 10 conditions are fulfilled for T > 100 K and T > 24 K, respectively, which means that
for κ < 10 (maximum error: 20%). Using K = 18.3 kJ m−3 for our ferritin sample (see Section 5.3) and the volume of spherical cores with a diameter of 7 nm (Fig. 1), the κ < 2 and κ < 10 conditions are fulfilled for T > 100 K and T > 24 K, respectively, which means that ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) is a valid model for all measurements shown in Fig. 12a, except the 15 K one.
is a valid model for all measurements shown in Fig. 12a, except the 15 K one.
Implementation of the superparamagnetic term for a single-valued magnetic moment yields large model residuals with systematic trends (Fig. S17, ESI†), indicating that the real moment distribution is a broad function. Therefore, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) needs to be integrated over the moment distribution f(m), usually assumed to be a lognormal function with unknown logarithmic mean μm and logarithmic standard deviation σm.41,68 Furthermore, the presence of paramagnetic spins, suggested by EPR measurements, requires to split the linear term of the fitting function into a term associated with the ferritin cores, and another term for the paramagnetic contributions. The resulting model is given by
needs to be integrated over the moment distribution f(m), usually assumed to be a lognormal function with unknown logarithmic mean μm and logarithmic standard deviation σm.41,68 Furthermore, the presence of paramagnetic spins, suggested by EPR measurements, requires to split the linear term of the fitting function into a term associated with the ferritin cores, and another term for the paramagnetic contributions. The resulting model is given by
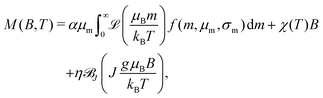 | (12) |
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) J is the Brillouin function describing the magnetization of paramagnetic spins with total spin quantum number J and magnetic moment gμB. The scaling factors α and η account for the unknown concentration of ferritin cores and paramagnetic spins, respectively. The use of Ms = αμ ensures that the saturation magnetization has the same temperature dependence as the magnetic moment, as expected for a superparamagnetic system where saturation is reached by magnetic moment rotation only. The paramagnetic term is justified by the identification of a corresponding EPR component with g′ = 4.3, originating from mononuclear Fe3 + ions with J = S = 5/2. This EPR component covers a large field range and is therefore dominant over other paramagnetic contributions with g′ = 2 and 5.8. In order to avoid model instabilities caused by the similar shapes of the Langevin and Brillouin functions, the shape of the latter has been fixed using J = 5/2 while maintaining g unconstrained.
J is the Brillouin function describing the magnetization of paramagnetic spins with total spin quantum number J and magnetic moment gμB. The scaling factors α and η account for the unknown concentration of ferritin cores and paramagnetic spins, respectively. The use of Ms = αμ ensures that the saturation magnetization has the same temperature dependence as the magnetic moment, as expected for a superparamagnetic system where saturation is reached by magnetic moment rotation only. The paramagnetic term is justified by the identification of a corresponding EPR component with g′ = 4.3, originating from mononuclear Fe3 + ions with J = S = 5/2. This EPR component covers a large field range and is therefore dominant over other paramagnetic contributions with g′ = 2 and 5.8. In order to avoid model instabilities caused by the similar shapes of the Langevin and Brillouin functions, the shape of the latter has been fixed using J = 5/2 while maintaining g unconstrained.
All M(B) curves in the 15–250 K range have been fitted globally, that is, with common temperature-independent parameters α, η, σm, g, and one set of temperature-dependent parameters μm and χ for each curve. The assumption that σm does not depend on temperature is justified by the fact that the width of a broad moment distribution is relatively insensitive to possible differences between the temperature dependencies of small and large magnetic moments. Parameter confidence intervals have been calculated using a Monte Carlo error estimation, which consisted in adding random errors to the data, based on the standard deviation of the random component of model residuals. Residuals are comprised between ±0.5% of the maximum magnetization at 7 T (Fig. 12a), with a common field-dependent trend limited to ±0.2% and a random component associated with measurement errors. The small systematic misfit might be caused by a non-lognormal distribution of magnetic moments, by deviations from the Langevin model due to single particle anisotropy, or by a small field dependence of χ. An almost complete saturation of the superparamagnetic contribution in the 7 T maximum field is attained at the lowest temperatures (Fig. 12b), meaning that the moment distribution can be recovered from the data, up to a small fraction of smallest moments, whose magnetization saturates in larger fields.
The temperature dependencies of μm and χ (Fig. 12c and d) are qualitatively similar to those obtained by Makhlouf et al.10 and Gilles et al.56 The maximum mean moment 〈m〉 = exp(μm + σm2/2) ≈ 333μB is slightly smaller than the single-valued estimate of ∼350μB obtained from horse-spleen ferritin using a simple Langevin fit with linear term.10 The temperature dependence of μm is characterized by two opposed trends: a ∼10% increase over the 15–27 K range, followed by a quadratic decrease compatible with the bulk antiferromagnetic magnon law, μm(T) = μm(0)(1 − aT2) (Fig. 12c).68 The initial increase μm(T) is likely an artifact of the Langevin model. As previously mentioned, the equilibrium magnetization of particles with finite anisotropy becomes proportional to ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (ξ) at T → 0. In a Langevin fit, this function is approximated by ∼0.5
(ξ) at T → 0. In a Langevin fit, this function is approximated by ∼0.5![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (2ξ). Because ξ ∝ m, the apparent moment obtained from the Langevin fit decreases as the appropriated model function changes from
(2ξ). Because ξ ∝ m, the apparent moment obtained from the Langevin fit decreases as the appropriated model function changes from ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (ξ) to
(ξ) to ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) (ξ). The non-paramagnetic susceptibility χ decreases monotonically with temperature, approaching a Curie–Weiss law with ΘCW ≈ −194 K above ∼100 K (Fig. 12d). Deviations from this trend are expected in the case of AF nanoparticles, because of superantiferromagnetic contributions arising for instance from uncompensated spin planes.39 Spin frustration might also contribute to χ, as seen by similar temperature dependencies encountered in systems dominated by this effect.88
(ξ). The non-paramagnetic susceptibility χ decreases monotonically with temperature, approaching a Curie–Weiss law with ΘCW ≈ −194 K above ∼100 K (Fig. 12d). Deviations from this trend are expected in the case of AF nanoparticles, because of superantiferromagnetic contributions arising for instance from uncompensated spin planes.39 Spin frustration might also contribute to χ, as seen by similar temperature dependencies encountered in systems dominated by this effect.88
4.5 Coercivity distributions
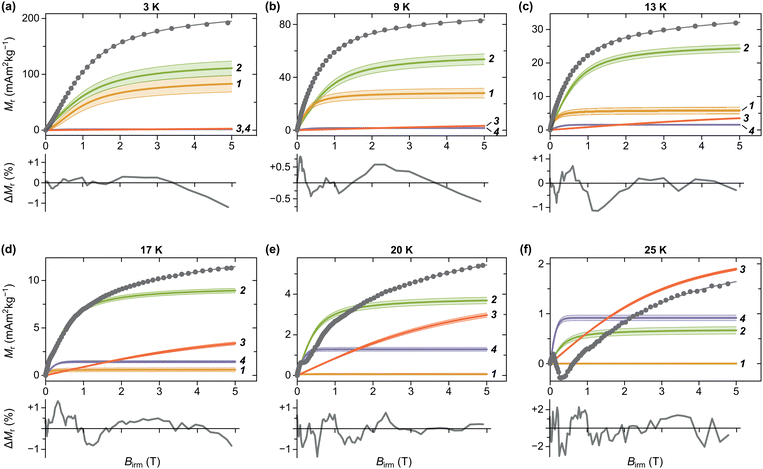
IRM acquisition curves Mr(B) describe the acquisition of a remanent magnetization from an initially demagnetized state after the application of increasingly large fields, until the so-called saturation remanent magnetization Mrs is reached. Only particles that are blocked over the time needed to zero the magnetic field and measure the magnetic moment (about a minute in case of MPMS measurements) contribute to the IRM. Accordingly, the amplitude decrease of Mr(B) with increasing temperature is caused by the progressive unblocking of magnetic moments (Fig. 13), and Mrs(T) is the integral of a blocking temperature distribution probed by remanent magnetization measurements.IRM curves become non-monotonic around 20 K, with an inflection around 0.15 T. The negative slope section denotes a low-coercivity phase that acquires a negative remanent magnetization. Because of the nature of the IRM acquisition protocol, which is formally equivalent to a partial hysteresis between B = 0 and Birm, negative Mr(B) slopes must be associated with inverted hysteresis,89 a phenomenon that arises from the exchange coupling between phases with different coercivities. These phases can be detected by fitting Mr(B) with a linear combination of model curves representing their individual contributions:
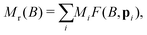 | (13) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (log
(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B,log
B,log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μB,σB) with logarithmic mean μB and standard deviation σB,90,92 or, more often, by slightly left-skewed generalizations of the normal distribution.91,93 Depending on the distribution skewness, μB is more or less close to the median acquisition field B1/2, which is the field required to acquire half of the saturation remanent magnetization.
μB,σB) with logarithmic mean μB and standard deviation σB,90,92 or, more often, by slightly left-skewed generalizations of the normal distribution.91,93 Depending on the distribution skewness, μB is more or less close to the median acquisition field B1/2, which is the field required to acquire half of the saturation remanent magnetization.
Coercivity distributions do not have necessarily an intrinsic physical meaning, being just defined as the first derivative of magnetization curves. A notable exception is represented by uniaxial single-domain particles described by the Stoner–Wohlfarth model.81 In this case, f(B) represents the relative contribution of particles with switching field Bsw = B to Mrs. Ferritin behaves as an assemblage of non-interacting Stoner–Wohlfarth particles, as seen from the identity between the shape of IRM acquisition curves and curves obtained by applying the same protocol to samples with a previously imparted negative saturation remanent magnetization.94,95 Well below the blocking temperature, the switching field is related to the anisotropy field Ba = 2KV/m by Bsw = ζBa with ζ ≈ 0.524, if particles are randomly oriented.96
A linear combination of four coercivity components of the form
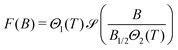 | (14) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (x) is a sigmoidal function with
(x) is a sigmoidal function with ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (0) = 0 and
(0) = 0 and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (∞) = 1, based either on the Langevin or the tanh function, Θ1(T) is a function describing the cumulative blocking temperature distribution of the corresponding component, with Θ1(0) = 1, B1/2 is the median acquisition field at 0 K, and Θ2(T) is a monotonically decreasing function describing the decline of B1/2 with temperature, caused by thermally activated moment switching.96 The effects of exchange coupling between a higher- and a lower-coercivity component are modelled by multiplying F(B) of the lower-coercivity component with a smoothed sign function, centered at the mean value of the exchange field, which roughly coincides with the inflection point of the IRM curve (ESI:† “Equilibrium magnetization models”).
(∞) = 1, based either on the Langevin or the tanh function, Θ1(T) is a function describing the cumulative blocking temperature distribution of the corresponding component, with Θ1(0) = 1, B1/2 is the median acquisition field at 0 K, and Θ2(T) is a monotonically decreasing function describing the decline of B1/2 with temperature, caused by thermally activated moment switching.96 The effects of exchange coupling between a higher- and a lower-coercivity component are modelled by multiplying F(B) of the lower-coercivity component with a smoothed sign function, centered at the mean value of the exchange field, which roughly coincides with the inflection point of the IRM curve (ESI:† “Equilibrium magnetization models”).
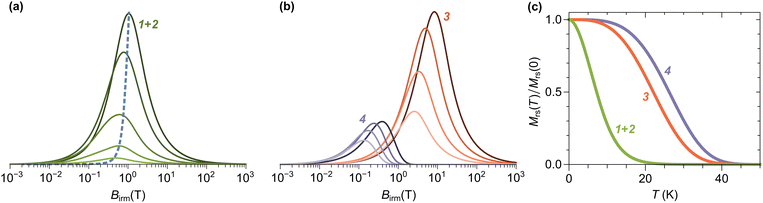
Below ∼15 K, the IRM is dominated by two coercivity components, C1 and C2, which contribute to 96% of the total Mrs. The blocking temperatures of the other two components, C3 and C4, are much larger than those of the bulk sample, contributing mainly to the IRM curves acquired at 20 and 25 K. In the case of C4, the maximum Tb is close to that of magnetoferritin.97 C1 and C2 are characterized by slightly different temperature and field dependencies, with B1/2 ≈ 1 T at 3 K. C3 and C4 are characterized by strongly contrasting median acquisition fields, with B1/2 ≈ 3.2 T and ∼0.12 T, respectively, at 20 K. C3 is heavily unsaturated at 5 T. Extrapolation of the model function used to fit this component to higher fields suggests that saturation occurs above 50 T (Fig. 14b), similarly to what has been reported for goethite.98 The field dependence of C4 is within the range that can be expected from ferrimagnetic minerals: equidimensional magnetite and maghemite nanoparticles with sizes above 4 nm are characterized by coercivities of 40–50 mT at 5 K.99,100 The larger median field of C4 might be explained by additional contributions from shape and surface anisotropy, in the case of smaller, irregular crystals partially replacing the Fh core.
C3 and C4 are coupled by an exchange field Bex ≈ 82 mT. At fields ≪Bex, C4 acquires a significant fraction of its saturation remanent magnetization, while C3 is still close to its initial demagnetized state, owing to its much larger coercivity. As C3 becomes progressively magnetized in the positive direction, negative exchange coupling causes C4 to be switched to the opposite direction, leading to a decrease of the total IRM. When C4 is negatively saturated, around 200 mT, the total IRM starts to increase again, due to the continuing IRM acquisition of C3. The non-monotonic IRM acquisition characteristics of these two negatively coupled components becomes clearly visible above 20 K, when C1 and C2 are almost completely superparamagnetic, no longer contributing to the remanent magnetization.
While the identification of C3 and C4 with independent entities is justified by the exchange coupling signature, the existence of C1 and C2 as independent components, instead of a single component, might just reflect the need to use two model functions to describe the complex shape of a single coercivity distribution.91 Because of their similar field and temperature dependencies, C1 and C2 are merged into a single component, labelled as C1+2. C1+2 is characterized by a very broad coercivity distribution, which extends over ∼4 orders of magnitude (Fig. 14a), and a maximum blocking temperature of ∼20 K (Fig. 14c), which is close to the merging point of FC-ZFC low-field magnetization curves (Fig. 10a). The temperature dependence of B1/2, which can be identified with the coercivity distribution peaks in Fig. 14a, is well described by the thermal activation model of Egli and Lowrie101 for the switching field of randomly oriented single-domain particles with uniaxial anisotropy energy mBa/2, when Ba = 2B1/2(T = 0) is taken from the extrapolation of the IRM fitting model to 0 K, and m = 325μB is assumed (dashed line in Fig. 14a). The required magnetic moment is close to the mean value of ∼333μB derived from the Langevin model of isothermal magnetization curves. Consideration of the random particle orientation is very important, as simpler thermal activation models based on aligned anisotropy axes102 require unrealistically large moments of the order of ∼1000μB to fit the distribution maxima in Fig. 14a.
5 Discussion
In this work, we present a comprehensive investigation of human-liver ferritin by in-depth electron paramagnetic resonance and an extensive set of magnetometry techniques. The goal is to determine the spin-structure of ferritin in order to elucidate the composition of the ferritin core in terms of magnetic phases. Fig. 15 shows the combination of techniques used to determine the properties of ferritin cores and produce a model for their spin configuration. Magnetometry measurements yield the magnetic moment, blocking temperature, and energy barrier distributions, while EPR provides an important constraint on the paramagnetic contribution to M(B) curves, as well as independent estimates of the anisotropy field and the blocking temperature over a much shorter time range of the order of 0.1 ns. Comparison with magnetometric blocking temperatures permits to verify the Néel–Arrhenius law and estimate the attempt time of thermal activations. The volume distribution of ferritin cores is obtained from TEM observations and yields, in combination with the anisotropy field distribution, an estimate of the magnetocrystalline anisotropy constant (see Section 5.2 for details). The volume and magnetic moment distributions provide also important constraints on the spin configuration of ferritin cores.The combination of this unusually broad set of experimental data shows that several of the previous approaches to interpret ferritin data give inconsistent results, requiring a new theoretical model to fit the data and derive the magnetic properties of this iron-oxide nanoparticle. One of the crucial findings is that the distribution of magnetic parameters that do not reflect intrinsic properties of the core material, such as μ(m) and Ba, need to be taken into account explicitly.
The following discussion starts with the properties of ferritin derived from the EPR analysis, and continues with key parts of the analysis of magnetometry results. The latter leans heavily on Section 3, which describes the framework on which the interpretation is based. The discussion is concluded by the joint interpretation of EPR and magnetometric models, leading to the description of the spin structure of the core of human-liver ferritin.
5.1 EPR simulations
In this section we describe the EPR spectra of ferritin, which are characterized by broad signal attributed to the core material (Fig. 7). Compared to standard EPR signals, ferritin spectra are extremely broad and the changes with temperature are small, thus lacking clearly resolved features. The several hundred mT width and the overall Gaussian shape at temperatures smaller than 100 K suggest an ensemble of ferritin cores with slightly different properties resulting in a distribution of EPR parameters. To analyze the EPR spectra, we use a quantum-mechanical description of the magnetic properties of ferritin cores, and in particular, we focus on the lineshape and its temperature dependence. This approach allows us to directly obtain the spin structure of ferritin from the simulated EPR spectra. For other approaches see “Other possible approaches…” in ESI.†There are several challenges associated with analysing the EPR spectra. For high-spin systems such as ferritin, variations in the lineshape due to the spin state S and the zero-field splitting D are not systematic (see Fig. S13, ESI†), making it challenging to predict which parameters should be used in the simulations of the EPR spectra. Therefore, equivalent simulated spectra can be obtained by many different sets of EPR parameters, such as S and D, defying standard optimization methods. As an illustration of this problem, an attempt to perform an automatic fit by varying just a few parameters did not lead to a global minimization of the model misfits (see ESI:† “EPR alternative fitting approach”). Therefore, a different approach based on the use of carefully chosen model spectra (see Section 4.1) was used, as discussed in the following.
A minimum of two components are required to simulate the experimental spectra in a satisfactory manner (Fig. S5, ESI†vs.Fig. 8b). Simulations with more than two components were not attempted, to avoid an excessive number of free parameters. No assumptions were made about the temperature behaviour, such as, for example, that the relative weight of the components or the D values have to be constant for all temperatures, even if these assumptions might be justified by certain models.50 The model parameters for the two components E1 and E2 were selected from simulated spectral lineshapes obtained for a range of D and S values (see: “EPR Model simulations”, and Fig. S13, ESI†). A summary of the parameters used in the final simulations is given in Table S1 and Fig. S8 (ESI†). The temperature dependence of the parameters does not exclude a systematic variation of D with temperature, but the trend is not sufficiently well defined to support further interpretations.
How different are the two components E1 and E2 chosen for fitting EPR measurements? For all temperatures, D1 is 2.5 times smaller than D2, on average. However, D and S are not independent, but inversely related (eqn 9), so that a change in D can be compensated by the inverse change in S without changing the overall shape (see ESI:† “EPR S–D inverse compensation”). For instance, in the case of equal D values for both components, S1 must be ∼2.5 times smaller than S2 to obtain the same total EPR spectrum. The two components do not necessarily represent two distinct families of ferritin, rather they should be considered as a mathematical construct to represent an overall broad distribution. The hypothesis of an underlying broad distribution is supported by the fact that the Gaussian broadening used in the simulations exceeds the D parameters by at least an order of magnitude, which can only be explained by a distribution of ferritin-core spin configurations within the ferritin population. The overall Gaussian lineshape of the EPR signal below 100 K reveals an inhomogeneous broadening typical of a resonance that consists of centers with a distribution of anisotropic magnetic parameters. The resonance narrows at higher temperatures, yielding an overall Lorentzian lineshape above 100 K, revealing that a dynamic process averages the differences in the anisotropy of the different centers. Such a line narrowing at higher temperatures was attributed to anisotropy averaging46 or, alternatively, anisotropic melting.47,48
EPR results can be compared with ferritin properties reported in the literature by deriving μ and Ba from Sreal and Dreal through eqn (8) and (9), respectively. Our range of estimates for μ is within the range published by Brem et al.27 (128–556μB) and by Koralewski et al.103 (133–239)μB. On the other hand, our estimated interval of 0.1–0.3 T for Ba is independent of scaling, and agrees well with the 0.08 ≤ Ba ≤ 0.27 T range reported in the literature13,104 for 5.4–7.0 nm ferritin cores. Previous EPR studies on horse-spleen and human-spleen ferritin focused on describing qualitative aspects of the EPR lineshape (EPR intensity and width variations vs. temperature and different ferritin samples), all agreeing on the broad signal located at g′ = 2.0 and its observed temperature dependence.13,14,21,23,24,105 However, a few EPR spectra present a more asymmetric lineshape, especially at lower fields,23,24 the shape of which does not agree well with our spectra.
5.2 Ferritin properties derived from magnetometry
Combined analysis of M(B) curves, AC susceptibility and IRM curves highlights the inconsistency of models used in the literature to interpret the magnetic properties of ferritin (see Section 3). IRM acquisition curves (Fig. 13) support the existence of multiple magnetic phases. The main phase, which we attribute to Fh cores, has a median blocking temperature of ∼8 K and contributes to ∼96% of the remanent magnetization at 3 K. The remaining magnetization is carried by a magnetite-like low-coercivity phase (∼0.6%), exchange-coupled with a high-coercivity phase, which become dominant above ∼17 K. The very large saturation field of the high-coercivity phase is compatible with goethite nanoparticles,98 and possibly also wüstite.106 The contribution of these two secondary phases in our sample is negligibly small, compared to estimates obtained with diffractometric techniques (e.g., 30% magnetite in horse-spleen and human-liver ferritin).6 While these secondary phases must coexist within the same protein shells due to their exchange coupling, it is not clear whether they represent fully altered ferritin cores, or if they coexist with Fh as intermediate alteration products. In any case, non-Fh phases detected with the analysis of IRM curves are negligible. The main IRM component exhibits a magnetic behavior explainable with a fixed total magnetic moment, whose distribution is given by the Langevin model described in Section 4.4. This does not exclude that this component consists of two or more phases with a sufficiently strong magnetic coupling, such that the vector sum of their magnetic moments does not change during isothermal magnetization measurements.Another proof for the above conclusion is provided through the analysis of the relations existing between blocking temperature, magnetic moment, and anisotropy field distributions. In case of single-domain particles with a fixed spin configuration, these relations are established by the Néel–Arrhenius model (eqn (6)). We start with the normalized temperature dependence of the saturation remanent magnetization Mrs corresponding to the sum of the IRM components C1 and C2, which we attributed to Fh (Fig. 16). The normalized saturation remanent magnetization Mrs(T)/Mrs(0) of C1+2, coincides, by definition, with the integral of the blocking temperature distribution fb(T) of the Fh cores. Assuming the anisotropy constant K to be the same for all ferritin cores, one can expect from eqn (6) that V is proportional to Tb, so that a rescaled version cfV(cV) of the volume distribution fV(V) obtained from TEM statistics (Fig. 1) will match fb(T) for a certain value of the proportionality constant c = V/Tb. Indeed, a good match with the IRM component C1 is obtained using c ≈ 20 nm3 K−1 (Fig. 16). The match is less good if one considers C1+2, because of the wider composite blocking temperature distribution. It is therefore possible that C1 and C2 represent two distinct groups of ferritin cores with a narrower and a wider anisotropy distribution, respectively, so that the narrow anisotropy distribution of C1 is well approximated by a mean K value. In this case, K = c−1kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t/τ0 ≈ 19 kJ m−3 is obtained for C1 using τ0 = 10−11 s84 and t = 5 s for the IRM measurement time. Comparable values have been reported in the literature, e.g., K ∼ 25 kJ m−3 for horse spleen ferritin,38 and K ∼ 17 kJ m−3 for bacterial ferrihydrite.69 A slightly worse match is obtained when a similar rescaling procedure is applied to the distribution of Eb derived from susceptibility measurements (Fig. 16). In this case, the lack of contributions at temperatures smaller than 4 K reflects the shape of the gamma distribution used to fit the measurements. The relatively well-constrained value of the bulk anisotropy K suggests that most Fe ions are embedded in a crystalline structure.
t/τ0 ≈ 19 kJ m−3 is obtained for C1 using τ0 = 10−11 s84 and t = 5 s for the IRM measurement time. Comparable values have been reported in the literature, e.g., K ∼ 25 kJ m−3 for horse spleen ferritin,38 and K ∼ 17 kJ m−3 for bacterial ferrihydrite.69 A slightly worse match is obtained when a similar rescaling procedure is applied to the distribution of Eb derived from susceptibility measurements (Fig. 16). In this case, the lack of contributions at temperatures smaller than 4 K reflects the shape of the gamma distribution used to fit the measurements. The relatively well-constrained value of the bulk anisotropy K suggests that most Fe ions are embedded in a crystalline structure.
Our surface-spin model of ferritin (Section 3.4) predicts that the distribution of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m, which we assumed to be Gaussian when fitting M(B) curves, is given by gm = gκμη * gV2/3, where gκμη and gV2/3 are the distributions of ln(κsμFeηs) and ln
m, which we assumed to be Gaussian when fitting M(B) curves, is given by gm = gκμη * gV2/3, where gκμη and gV2/3 are the distributions of ln(κsμFeηs) and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V2/3, respectively, and “*” is the convolution operator. Because κs and μFe are fixed quantities, and the standard deviation σ ≈ 0.08 of ln
V2/3, respectively, and “*” is the convolution operator. Because κs and μFe are fixed quantities, and the standard deviation σ ≈ 0.08 of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V2/3 is much smaller than σ ≈ 0.96 for ln
V2/3 is much smaller than σ ≈ 0.96 for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m, the moment distribution is controlled mainly by the degree of spin canting ηs = sin
m, the moment distribution is controlled mainly by the degree of spin canting ηs = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) εs, and thus, by the surface anisotropy. The distribution gη of ηs obtained from the deconvolution of the empirical moment and volume distributions (Fig. S22, ESI†) is almost perfectly Gaussian, owing to the fact that gm used in the Langevin model was a normal distribution. About 96% of the distribution is comprised between ηs ≈ 1% and ∼50%, which is a reasonable upper limit for the alignment of surface spins.
εs, and thus, by the surface anisotropy. The distribution gη of ηs obtained from the deconvolution of the empirical moment and volume distributions (Fig. S22, ESI†) is almost perfectly Gaussian, owing to the fact that gm used in the Langevin model was a normal distribution. About 96% of the distribution is comprised between ηs ≈ 1% and ∼50%, which is a reasonable upper limit for the alignment of surface spins.
Finally, we compare the anisotropy-field distributions obtained from IRM acquisition curves and from the magnetic moment and volume distributions, respectively. In the first case, we identify the distribution of Ba with the IRM coercivity component C1+2, using the relation Bsw = ζBa between Ba and the switching field of single-domain particles well below the blocking temperatures. In the case of randomly oriented particles with uniaxial anisotropy,96ζ ≈ 0.524. In the second case, the distribution of lnBa is given by ga = g2K/κμ * gV1/3 * gη−1 (Section 3.4). A good match between the two estimates is obtained using Ba = 1.8Bsw (Fig. 17). The corresponding ζ ≈ 0.56 is slightly larger than the value expected for randomly oriented uniaxial single-domain particles and might be explained by a single-particle anisotropy with a small degree of non-uniaxiality.
In summary, the modified Langevin model used to fit M(B) curves (Section 4.4), the lack of a spin-flop transition (Section 3.2), the magnetic moment distribution (Sections 3.3 and 3.4), the coercivity distribution (Section 4.5) and the compatibility of volume, magnetic moment, blocking temperature, and anisotropy field distributions with the Néel–Arrhenius model (Section 3.4, Fig. 17) point, altogether, to a model for the spin structure of ferritin cores where the magnetic moment arises from surface-spin canting, rather than randomly distributed defects in the AF sublattices. The ferritin cores behave as single-domain particles with uniaxial magnetocrystalline anisotropy. The wide distribution of m is explained by the variability of spin configurations deviating from the two-sublattice AF model, rather than the volume distribution. Despite the strong heterogeneity of magnetic configurations, all ferritin cores appear to share a well-defined magnetic anisotropy constant K. This is consistent with a model where spins are rigidly coupled and switching occurs by uniform rotation, so that most of the work necessary to overcome the energy barrier originates from the intrinsic anisotropy of the AF sublattices. Finally, the wide distribution of switching fields, from ∼0.03 to >30 T, is also a direct consequence of this model, which predicts Bsw ∝ m−1 for AF particles with a spontaneous moment m. In particular, m → 0 yield extremely large switching fields, which are limited only by the sublattice exchange field BE.
The above model explains magnetometry measurements almost completely. As discussed in Section 4.5 only ∼4% of the total remanent magnetization is carried by phases that cannot be associated with a Fh core composition. M(B) curves contain a paramagnetic contribution that is carried by a small fraction (∼6.5%, Table 2) of mononuclear Fe3+ atoms. This fraction of ∼6.5% is obtained from the ratio αμm/η between the saturation magnetization of these atoms and the Fh cores in eqn (12). The last magnetic parameter that describes the ferritin cores is the non-paramagnetic susceptibility χ that contributes with a linear term χB to the M(B) curves. This term originates from the field-induced spin canting of surface spins and of the inner spins with AF order. The estimate of χ at 50 K obtained from M(B) curves fits with eqn (12) is ∼1.4 times larger than the value expected from the simple model of spin-canted AF nanoparticles discussed in Section 5.3.2 (Table 2). Measurements of horse-spleen ferritin up to 50 T show that the slope of M(B) curves measured at 4.2 K continues to decrease up to ∼35 T, before merging with the superantiferromagnetic trend.39 It is therefore possible that the excess susceptibility in our fits of M(B) curves limited to a maximum field of 7 T is caused by the linear approximation of a small residual curvature due to superparamagnetic contributions that saturate in much larger fields. These contributions might require a magnetic moment distribution with a heavier left tail associated with much smaller Fh cores or isolated core fragments, as suggested by the measured volume distribution (Fig. 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ; Ba—anisotropy field; σB—standard deviation of the distribution of ln
μ; Ba—anisotropy field; σB—standard deviation of the distribution of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba; Bc—coercive field of hysteresis; Eb—energy barrier; σE—standard deviation of the distribution of ln
Ba; Bc—coercive field of hysteresis; Eb—energy barrier; σE—standard deviation of the distribution of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eb; K uniaxial anisotropy constant; σK—standard deviation of the distribution of ln
Eb; K uniaxial anisotropy constant; σK—standard deviation of the distribution of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K; Mp/MFh—paramagnetic saturation magnetization, normalized by the saturation magnetization of the superparamagnetic contribution; Np/NFh—number of paramagnetic Fe atoms, normalized by number of superparamagnetic atoms of ferritin core; χ/χc—non-paramagnetic susceptibility in M(B) fits with eqn (12), normalized by the value expected from superparamagnetic particles with spin canting moments (Section 3.2)
K; Mp/MFh—paramagnetic saturation magnetization, normalized by the saturation magnetization of the superparamagnetic contribution; Np/NFh—number of paramagnetic Fe atoms, normalized by number of superparamagnetic atoms of ferritin core; χ/χc—non-paramagnetic susceptibility in M(B) fits with eqn (12), normalized by the value expected from superparamagnetic particles with spin canting moments (Section 3.2)
| Property | From magnetometry | From EPR |
|---|---|---|
| a Mean, Fig. 12c, 0 K. b Langevin fit. c Median of C1 + 2, 3 K. d C1 + 2, 3 K. e Hysteresis. f T b of C1 + 2. g T b of C1 + 2. h Eqn (6). i Eqn (6). j η/αμm in eqn (12). k η〈m〉/αμmNμFe in eqn (12). l 50 K, Fig. 5b. m For n = 10, 30, i.e., S = 100 and S = 300, respectively. n E1 & E2, 20 K. o For S = 300; for S = 100 Np/NFh = 4 × 10−4 From ESI, section “Ferritin core and mononuclear Fe(III) EPR intensities”. | ||
| μ/μB | 337a | 200, ∼1000m |
| σ μ | 0.947b | — |
| B a (T) | 1.9c | 0.1–0.3n |
| σ B | 1.44d | — |
| B c (T) | 0.08e | — |
| E b/kB | 227f | — |
| σ E | 0.679g | — |
| K (kJ m−3) | 19h | — |
| σ K | 0.417i | — |
| M p/MFh | 2.39j | |
| N p/NFh | 0.0645k | 0.0036o |
| χ/χc | ∼1.4l | — |
5.3 Comparison between EPR and magnetometry
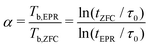 | (15) |
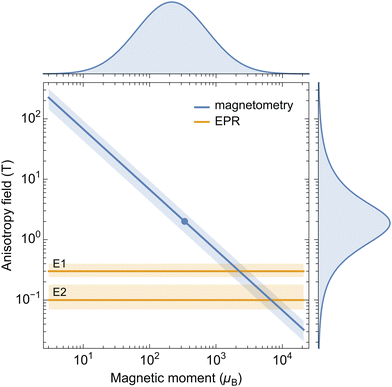 | ||
| Fig. 18 Anisotropy field (Ba) vs. magnetic moment (μ) from EPR (components E1 and E2 at 20 K) and from magnetometry. Shading around the magnetometry and EPR trends correspond to the quartiles of TB distribution (Fig. 16) and to the range of EPR parameters yielding similar simulated spectra, respectively. The dot represents the averages of Ba and μ obtained from magnetometry. The distributions of μ and Ba obtained from magnetometry are plotted on the corresponding axes. | ||
The intersection between the constraints plotted in Fig. 18 gives a rough estimate of the anisotropy fields and magnetic moments probed by EPR, which are centered around Ba ≈ 0.2 T and μ ≈ 4000μB, respectively. This combination of parameters is off by a factor ∼10 with respect to mean values obtained from magnetometry (Ba ≈ 2 T and μ ≈ 337μB). This discrepancy originates from the ∼10 times smaller anisotropy fields of E1 and E2. A possible explanation for this difference is discussed in the next section.
Surface anisotropy complicates the description of the particle magnetization by introducing intermediate magnetic states along the path that produces a field-induced reversal of the bulk magnetic moment.111 In practice, the switching process begins by reversing discrete groups of surface spins in increasingly large fields, until reversal of the internal core spins completes the process. As a result, single-particle hysteresis contains several discrete magnetization jumps corresponding to partial reversals,111 instead of the single jump at Bsw of two-state particles. The way multistep magnetic moment reversals are recorded depends on the measurement protocol. In the case of IRM acquisition curves, partial reversals of surface spins will not be recorded, because the strong exchange coupling with the internal core spins recovers the initial spontaneous moment as soon as the field is removed. Accordingly, switching occurs only in a field that is sufficiently strong to reverse the internal core spins. As shown in Section 5.2, this field is given by Ba = 2KV/m, where K is the anisotropy constant of the AF-coupled core spins. On the other hand, the entire sequence of partial reversals is recorded by the hysteresis loop (Fig. 10). As a result, the coercive field of hysteresis, Bc ≈ 0.1 T, is ∼10 times smaller than the median switching field B1/2 ≈ 1 T obtained from IRM curves. For comparison, randomly oriented Stoner–Wohlfarth particles112 are characterized by B1/2/Bc ≈ 1.2. Like hysteresis, EPR spectra are expected to record all transitions between magnetic states, and therefore also partial reversals occurring at lower fields. The apparent anisotropy field of EPR spectra is therefore more similar to the coercive field of hysteresis than the field required for a complete reversal. This explains why a direct comparison of EPR and magnetometry data, as in Fig. 18, does not work.
The existence of multiple magnetic states for the ferritin cores questions the applicability of the Langevin model for fitting M(B) curves, since particles in the superparamagnetic state can undergo thermally activated transitions between any pair of states. Intermediate states with partially reversed surface spins have higher energies than the ground states, and the whole sequence of reversal steps is represented by a path in a multidimensional energy landscape, which connects a series of local minima distributed along a “valley” running from a ground state to its opposite.113 The presence of local minima along this valley raises the probability of finding particles with these discrete intermediate states, compared to the continuous transition between ground states of particles with no intermediate states. Close to the blocking temperature, the probability of magnetic configurations different from ground states is negligibly small, and intermediate states do not play any role. At higher temperatures, the existence of multiple states with different energy levels has a similar effect as multiaxial anisotropy, and deviations from the Langevin law can be expected to be smaller than those produced by uniaxial anisotropy (Section 3.2), owing to the smaller switching fields associated with transitions between intermediate states. Because the effect of uniaxial anisotropy is small in the temperature range of our M(B) measurements (Fig. 4), the Langevin model is expected to be a good representation of the equilibrium magnetization even in the case of particles whose magnetic moment is not reversed in a single step. Consequently, the Langevin model, as applied in the present context is a good approximation for the magnetic properties of ferritin.
6 Conclusions
In this work, we have probed the magnetic response of a sample of human liver ferritin with a broad set of available experimental techniques and at different excitation frequencies, sparsely covering the DC-to-9 GHz interval. While magnetic analyses of ferritin are not new, our synergetic comparison of magnetometry and electron paramagnetic resonance offers, for the first time, an in-depth description of ferritins spin behavior. Our methods reconcile recurring discrepancies on the origin of the magnetic moment in ferritin on the one hand, while offering a quantitative approach to the challenging determination of spin Hamiltonian components emerging from EPR data fitting on the other hand, over a temperature range extending close to the DC-blocking temperature.With regard to EPR data, the broad and seemingly featureless nature of the spectra can be well captured by at least two components, with S and D parameters returning an anisotropy field in the 0.1–0.6 T range, and an S parameter above 50. These two components most likely represent a broad distribution of magnetic properties. While the magnetic moment can only indirectly be derived from the EPR data, the technique identifies also paramagnetic contributions, providing information complementary to magnetometry.
Moreover, a more complete understanding of the magnetometry data of ferritin, which has been the subject of extensive debate, can be achieved with IRM acquisition data. IRM acquisition curves reveal (i) the mineral composition of the protein core, which complements the information from other methods, such as energy-resolved electron microscopy; (ii) the blocking temperature distribution, in reasonable agreement with the particle volume distribution and the assumption of a single anisotropy constant; and (iii) the existence of a negative exchange field between the dominant antiferromagnetic phase and a minor ferrimagnetic phase within the same core. This exchange interaction prevents the magnetic moments of the two phases to display independent superparamagnetic behaviours.
From a new theoretical description of the induced magnetization data we conclude that the magnetic moment of ferritin is controlled mainly by spin canting caused by surface anisotropy. The wide distribution of magnetic moments can be explained by the strong heterogeneity of surface-spin configurations, to which the EPR spectrum seems to be particularly sensitive. Because of the inverse proportionality relation between magnetic moment and anisotropy field imposed by the Néel–Arrhenius law, the coercivity of ferritin is also represented by a broad distribution.
Author contributions
LB devised the experiments, analyzed the data, and reviewed the manuscript. JLM devised EPR measurements, did the experiments and analysis, wrote parts of the manuscript, HvdZ read and reviewed the manuscript, VC did experiments and analysis and corrected the manuscript, AL did magnetometry measurements, RE implemented theoretical models for magnetometry analysis, analyzed the data, wrote parts of the manuscript and revised it. MH supervised the project, did part of the EPR analysis, and writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Dutch Research Council (NWO) through an Idea Generator grant (NWA.1228.191.414) to L. B. and M. H., titled “Is air pollution behind dementia? Unravelling the origin of magnetite nanoparticles in the brain”. J. A. L.-M. acknowledges the financial support provided by NWO, through Nanofront project number NF17SYN05. A. L. acknowledges NWO for financial support, through the Industrial Partnership Programmes IPP 680-91-013. L. B. is grateful to Andrew Webb, Louise van der Weerd and Ernst Suidgeest for useful discussions. We thank Lionel Ndamba for checking the purity of ferritin and Maria Fittipaldi for helpful discussions.References
- N. Chasteen and P. M. Harrison, J. Struct. Biol., 1999, 126, 182–194 CrossRef CAS PubMed.
- D. Finazzi and P. Arosio, Arch. Toxicol., 2014, 88, 1787–1802 CrossRef CAS PubMed.
- P. Arosio, L. Elia and M. Poli, IUBMB Life, 2017, 69, 414–422 CrossRef CAS PubMed.
- G. Bartzokis, T. A. Tishler, P. H. Lu, P. Villablanca, L. L. Altshuler, M. Carter, D. Huang, N. Edwards and J. Mintz, Neurobiol. Aging, 2007, 28, 414–423 CrossRef CAS PubMed.
- C. Quintana, S. Bellefqih, J. Laval, J.-L. Guerquin-Kern, T.-D. Wu, J. Avila, I. Ferrer, R. Arranz and C. Patiño, J. Struct. Biol., 2006, 153, 42–54 CrossRef CAS PubMed.
- C. Quintana and L. Gutiérrez, Biochim. Biophys. Acta, Gen. Subj., 2010, 1800, 770–782 CrossRef CAS PubMed.
- O. Strbak, L. Balejcikova, M. Kmetova, J. Gombos, J. Kovac, D. Dobrota and P. Kopcansky, Int. J. Mol. Sci., 2021, 22, 8487 CrossRef CAS PubMed.
- Y. Gossuin, R. N. Muller and P. Gillis, NMR Biomed., 2004, 17, 427–432 CrossRef CAS PubMed.
- L. Bossoni, I. Hegeman-Kleinn, S. G. van Duinen, M. Bulk, L. H. P. Vroegindeweij, J. G. Langendonk, L. Hirschler, A. Webb and L. van der Weerd, Magn. Reson. Med., 2022, 87, 1276–1288 CrossRef CAS PubMed.
- S. A. Makhlouf, F. T. Parker and A. E. Berkowitz, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, R14717–R14720 CrossRef CAS.
- I. Alenkina, M. Oshtrakh, Z. Klencsár, E. Kuzmann, A. Chukin and V. Semionkin, Spectrochim. Acta, Part A, 2014, 130, 24–36 CrossRef CAS PubMed.
- D. E. Madsen, M. F. Hansen, J. Bendix and S. Mørup, Nanotechnology, 2008, 19, 315712 CrossRef CAS PubMed.
- E. Wajnberg, L. J. El-Jaick, M. P. Linhares and D. M. Esquivel, J. Magn. Reson., 2001, 153, 69–74 CrossRef CAS PubMed.
- M. P. Weir, T. J. Peters and J. F. Gibson, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1985, 828, 298–305 CrossRef CAS PubMed.
- Z. Jang, B. Suh, A. Lascialfari, R. Sessoli and F. Borsa, Appl. Magn. Reson., 2012, 19, 557–562 CrossRef.
- Y. Gossuin, D. Hautot, R. Muller, Q. Pankhurst, J. Dobson, C. Morris, P. Gillis and J. Collingwood, NMR Biomed., 2005, 18, 469–472 CrossRef CAS PubMed.
- M. Koralewski, L. Balejčíková, Z. Mitróová, M. Pochylski, M. Baranowski and P. Kopčanský, ACS Appl. Mater. Interfaces, 2018, 10, 7777–7787 CrossRef CAS PubMed.
- E. Schäfer-Nolte, L. Schlipf, M. Ternes, F. Reinhard, K. Kern and J. Wrachtrup, Phys. Rev. Lett., 2014, 113, 217204 CrossRef PubMed.
- E. Lee, D. H. Kim, J. Hwang, K. Lee, S. Yoon, B. J. Suh, K. Hyun Kim, J.-Y. Kim, Z. H. Jang, B. Kim, B. I. Min and J.-S. Kang, Appl. Phys. Lett., 2013, 102, 133703 CrossRef.
- E. S. Grant, L. T. Hall, L. C. L. Hollenberg, G. McColl and D. A. Simpson, ACS Nano, 2023, 17, 372–381 CrossRef CAS PubMed.
- S. Aime, B. Bergamasco, D. Biglino, G. Digilio, M. Fasano, E. Giamello and L. Lopiano, Biochim. Biophys. Acta, Mol. Basis Dis., 1997, 1361, 49–58 CrossRef CAS PubMed.
- V. Nandwana, S.-R. Ryoo, S. Kanthala, A. Kumar, A. Sharma, F. Castro, Y. Li, B. Hoffman, S. Lim and V. Dravid, RSC Adv., 2017, 7, 34892–34900 RSC.
- J. Boas and G. J. Troup, Biochim. Biophys. Acta, 1971, 229, 68–74 CrossRef CAS PubMed.
- N. Deighton, A. Abu-Raqabah, I. J. Rowland, M. C. R. Symons, T. J. Peters and R. J. Ward, J. Chem. Soc., Faraday Trans., 1991, 87, 3193–3197 RSC.
- F. S. Otsuka, M. C. G. Otaduy, O. R. Nascimento and C. E. G. Salmon, Braz. J. Phys., 2022, 52, 94 CrossRef CAS.
- Y.-H. Pan, K. Sader, J. J. Powell, A. Bleloch, M. Gass, J. Trinick, A. Warley, A. Li, R. Brydson and A. Brown, J. Struct. Biol., 2009, 166, 22–31 CrossRef CAS PubMed.
- F. Brem, G. Stamm and A. M. Hirt, J. Appl. Phys., 2006, 99, 123906 CrossRef.
- N. Gálvez, B. Fernández, P. Sánchez, R. Cuesta, M. Ceolín, M. Clemente-León, S. Trasobares, M. López-Haro, J. J. Calvino, O. Stéphan and J. M. Domínguez-Vera, J. Am. Chem. Soc., 2008, 130, 8062–8068 CrossRef PubMed.
- G. Jutz, P. van Rijn, B. Santos Miranda and A. Böker, Chem. Rev., 2015, 115, 1653–1701 CrossRef CAS PubMed.
- S. H. Kilcoyne and R. Cywinski, J. Magn. Magn. Mater., 1995, 140–144, 1466–1467 CrossRef CAS.
- M. S. Seehra, V. S. Babu and A. Manivannan, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3513–3518 CrossRef CAS.
- J. C. E. Harris, J. E. Grimaldi, D. D. Awschalom, A. Chiolero and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 3453–3456 CrossRef CAS.
- R. Brooks, J. Vymazal, R. Goldfarb, J. Bulte and P. Aisen, Magn. Reson. Med., 1998, 40, 227–235 CrossRef CAS PubMed.
- G. C. Papaefthymiou, Biochim. Biophys. Acta, Gen. Subj., 2010, 1800, 886–897 CrossRef CAS PubMed.
- F. M. Michel, V. Barrón, J. Torrent, M. P. Morales, C. J. Serna, J.-F. Boily, Q. Liu, A. Ambrosini, A. Cristina Cismasu and G. E. Brown, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2787–2792 CrossRef CAS PubMed.
- T. G. St Pierre, N. T. Gorham, P. D. Allen, J. L. Costa-Krämer and K. V. Rao, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 024436 CrossRef.
- N. J. O. Silva, V. S. Amaral, A. Uritzberea, R. Bustamante, A. Millán, F. Palacio, E. Kampert, U. Zeitler, S. de Brion, O. Iglesias and A. Labarta, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104427 CrossRef.
- R. P. Guertin, N. Harrison, Z. X. Zhou, S. McCall and F. Drymiotis, J. Magn. Magn. Mater., 2007, 308, 97–100 CrossRef CAS.
- N. J. O. Silva, A. Millán, F. Palacio, E. Kampert, U. Zeitler, H. Rakoto and V. S. Amaral, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104405 CrossRef.
- N. J. O. Silva, V. S. Amaral, L. D. Carlos, B. Rodríguez-González, L. M. Liz-Marzán, T. S. Berquó, S. K. Banerjee, V. de Zea Bermudez, A. Millán and F. Palacio, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 134426 CrossRef.
- C. Gilles, P. Bonville, K. K. W. Wong and S. Mann, Eur. Phys. J. B, 2000, 17, 417–427 CrossRef CAS.
- N. Noginova, F. Chen, T. Weaver, E. P. Giannelis, A. B. Bourlinos and V. A. Atsarkin, J. Phys.: Condens. Matter, 2007, 19, 246208 CrossRef CAS PubMed.
- R. J. Usselman, S. E. Russek, M. T. Klem, M. A. Allen, T. Douglas, M. Young, Y. U. Idzerda and D. J. Singel, J. Appl. Phys., 2012, 112, 084701 CrossRef PubMed.
- R. Berger, J. Kliava, J.-C. Bissey and V. Baïetto, J. Appl. Phys., 2000, 87, 7389–7396 CrossRef CAS.
- R. Berger, J.-C. Bissey, J. Kliava, R. Berger and J.-C. Bissey, J. Phys.: Condens. Matter, 2000, 12, 9347–9360 CrossRef CAS.
- R. Berger, J.-C. Bissey, J. Kliava, H. Daubric and C. Estournès, J. Magn. Magn. Mater., 2001, 234, 535–544 CrossRef CAS.
- R. J. Usselman, M. T. Klem, M. Allen, E. D. Walter, K. Gilmore, T. Douglas, M. Young, Y. Idzerda and D. J. Singel, J. Appl. Phys., 2005, 97, 10M523 CrossRef.
- Y. L. Raikher and V. I. Stepanov, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6250–6259 CrossRef CAS PubMed.
- M. M. Yulikov and P. A. Purtov, Appl. Magn. Reson., 2005, 29, 1613–7507 CrossRef.
- M. Fittipaldi, R. Mercatelli, S. Sottini, P. Ceci, E. Falvo and D. Gatteschi, Phys. Chem. Chem. Phys., 2016, 18, 3591–3597 RSC.
- M. Fittipaldi, L. Sorace, A.-L. Barra, C. Sangregorio, R. Sessoli and D. Gatteschi, Phys. Chem. Chem. Phys., 2009, 11, 6555–6568 RSC.
- P. Kumar, M. Bulk, A. Webb, L. van der Weerd, T. Oosterkamp, M. Huber and L. Bossoni, Sci. Rep., 2016, 6, 38916 CrossRef CAS PubMed.
- V. Barrón and J. Torrent, Geochim. Cosmochim. Acta, 2002, 66, 2801–2806 CrossRef.
- F. Luis, E. del Barco, J. M. Hernández, E. Remiro, J. Bartolomé and J. Tejada, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 11837–11846 CrossRef CAS.
- S. Mørup, Surf. Sci., 1985, 156, 888–892 CrossRef.
- C. Gilles, P. Bonville, H. Rakoto, J. M. Broto, K. K. W. Wong and S. Mann, J. Magn. Magn. Mater., 2002, 241, 430–440 CrossRef CAS.
- S. V. Komogortsev, D. A. Balaev, A. A. Krasikov, S. V. Stolyar, R. N. Yaroslavtsev, V. P. Ladygina and R. S. Iskhakov, AIP Adv., 2021, 11, 015329 CrossRef CAS.
- A. N. Bogdanov, A. V. Zhuravlev and U. K. Rössler, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 094425 CrossRef.
- P. J. Cregg and L. Bessais, J. Magn. Magn. Mater., 1999, 202, 554–564 CrossRef CAS.
- M. Hanson, C. Johansson and S. Mørup, J. Phys.: Condens. Matter, 1993, 5, 725–732 CrossRef CAS.
- L. Néel, C. R. Hebd. Seances Acad. Sci., 1961, 252, 4075–4080 Search PubMed.
- R. H. Kodama, A. E. Berkowitz, E. J. McNiff and S. Foner, J. Appl. Phys., 1997, 81, 5552 CrossRef CAS.
- R. H. Kodama, J. Magn. Magn. Mater., 1999, 200, 359–372 CrossRef CAS.
- J. Mazo-Zuluaga, J. Restrepo and J. Mejía-López, J. Appl. Phys., 2008, 103, 113906 CrossRef.
- R. H. Kodama and A. E. Berkowitz, in Surface Effects in Magnetic Nanoparticles, ed. D. Fiorani, Springer, New York, 1st edn, 2005, ch. 6, pp. 189–216 Search PubMed.
- D. Laura-Ccahuana and E. De Biasi, J. Magn. Magn. Mater., 2022, 549, 169018 CrossRef CAS.
- H. Yang, J. Liang and Q. Cui, Nat. Rev. Phys., 2023, 5, 43–61 CrossRef.
- N. J. Silva, V. S. Amaral and L. D. Carlos, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 1–6 Search PubMed.
- D. Balaev, A. A. Krasikov, A. A. Dubrovskiy, S. I. Popkov, S. V. Stolyar, O. A. Bayukov, R. S. Iskhakov, V. P. Ladygina and R. N. Yaroslavtsev, J. Magn. Magn. Mater., 2016, 410, 171–180 CrossRef CAS.
- C. Rani and S. D. Tiwari, J. Magn. Magn. Mater., 2015, 385, 272–276 CrossRef CAS.
- D. Balaev, S. V. Stolyar, Y. V. Knyazev, R. N. Yaroslavtsev, A. I. Pankrats, M. Vorotynov, A. A. Krasikov, D. A. Veikanov, O. A. Bayukov, V. P. Ladygina and R. S. Iskhakov, Results Phys., 2022, 35, 105340 CrossRef.
- M.-E. Y. Mohie-Eldin, R. B. Frankel and L. Gunther, J. Magn. Magn. Mater., 1994, 135, 65–81 CrossRef CAS.
- Z. Yuan, P. Atanassov, A. M. Alsmadi, S. G. E. te Velthuis, U. Welp, C. I. Hammetter, R. Hjelm and H. Nakotte, J. Appl. Phys., 2006, 99, 08Q509 CrossRef.
- M. B. Madsen and S. Mørup, Hyperfine Interact., 1986, 27, 329–332 CrossRef CAS.
- Y. Guyodo, R. Banerjee, S. K. an Lee Penn, D. Burleson, T. S. Berquó, T. Seda and P. Solheid, Phys. Earth Planet. Inter., 2006, 154, 222–233 CrossRef CAS.
- D. Balaev, S. I. Popkov, A. A. Krasikov, A. D. Balaev, A. A. Dubrovskiy, S. V. Stolyar, R. N. Yaroslavtsev, V. P. Ladygina and R. S. Iskhakov, Phys. Solid State, 2017, 59, 1940–1946 CrossRef CAS.
- A. Punnoose, T. Phanthavady, M. S. Seehra, N. Shah and G. P. Huffman, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 054425 CrossRef.
- C.-W. Hsieh, B. Zheng and S. Hsieh, Chem. Commun., 2010, 46, 1655–1657 RSC.
- S.-B. Cho, B. J. Kim, B. J. Suh and Z. Jang, J. Korean Phys. Soc., 2004, 45, 485–489 CAS.
- T. Hiemstra and W. H. Van Riemsdijk, Geochim. Cosmochim. Acta, 2009, 73, 4423–4436 CrossRef CAS.
- E. C. Stoner and E. P. Wohlfarth, Philos. Trans. R. Soc., A, 1948, 240, 599–642 CrossRef.
- E. Vroegindeweij, L. Bossoni, A. Boon, J. Wilson, M. Bulk, J. Labra-Muñoz, M. Huber, A. Webb, L. van der Weerd and J. Langendonk, NeuroImage: Clin., 2021, 30, 102657 CrossRef PubMed.
- R. S. Silva, P. C. Morais, F. Qu, A. M. Alcalde, N. O. Dantas and H. S. L. Sullasi, Appl. Phys. Lett., 2007, 90, 253114 CrossRef.
- P. D. Allen, T. G. St Pierre, W. Chua-anusorn, V. Ström and K. V. Rao, Biochem. Biophys. Acta, 2000, 1500, 186–196 CAS.
- J. I. Gittleman, B. Abeles and S. Bozowski, Phys. Rev. B: Solid State, 1974, 9, 3891–3897 CrossRef CAS.
- M. Respaud, J. Appl. Phys., 1999, 86, 556–561 CrossRef CAS.
- D. E. Madsen, S. Mørup and M. F. Hansen, J. Magn. Magn. Mater., 2006, 305, 95–99 CrossRef CAS.
- J. Khatua, M. Gomilšek, J. C. Orain, A. M. Strydom, Z. Jagličić, C. V. Colin, S. Petit, A. Ozarowski, L. Magnin-Thro, M. S. Ramachandra Rao, A. Zorko and P. Khuntia, Commun. Phys., 2022, 5, 99 CrossRef CAS.
- M. J. O'Shea and A. L. Al-Sharif, J. Appl. Phys., 1994, 75, 6673 CrossRef.
- D. J. Robertson and D. E. France, Phys. Earth Planet. Inter., 1994, 82, 223–234 CrossRef CAS.
- R. Egli, J. Geophys. Res., 2003, 108, 2081 CrossRef.
- P. P. Kruiver, M. J. Dekkers and D. Heslop, Earth Planet. Sci. Lett., 2001, 189, 269–276 CrossRef CAS.
- X. Zhao, M. Fujii, Y. Suganuma, X. Zhao and Z. Jiang, J. Geophys. Res.: Solid Earth, 2018, 123, 8298–8311 CrossRef.
- L. X. Tian, C. Q. Cao, Q. S. Liu and Y. P. Pan, Chin. Sci. Bull., 2010, 55, 3174–3180 CrossRef CAS.
- R. Egli, in Magnetic Measurement Techniques for Materials Characterization, ed. V. Franco and B. Dodrill, Springer Nature Publishing Group, New York, 2021, pp. 455–604 Search PubMed.
- H. Pfeiffer, Phys. Status Solidi A, 1990, 118, 295–306 CrossRef.
- B. M. Moskowitz, R. B. Frankel, S. A. Walton, D. P. E. Dickson, K. K. W. Wong, T. Douglas and S. Mann, J. Geophys. Res., 1997, 102, 22671–22680 CrossRef CAS.
- P. Rochette, P.-E. Mathé, L. Esteban, H. Rakoto, J.-L. Bouchez, Q. Liu and J. Torrent, Geophys. Res. Lett., 2005, 32, L22309 CrossRef.
- D. Carunto, G. Carunto and C. O'Connor, J. Phys. D: Appl. Phys., 2007, 40, 5801–5809 CrossRef.
- T. N. Shendruk, R. D. Desautels, B. W. Southern and J. van Lierop, Nanotechnology, 2007, 18, 455704 CrossRef.
- R. Egli and W. Lowrie, J. Geophys. Res., 2002, 107, 2209 CrossRef.
- L. Breth, D. Suess, C. Vogler, B. Bergmair, M. Fuger, R. Heer and H. Brueckl, J. Appl. Phys., 2012, 112, 023903 CrossRef.
- M. Koralewski, M. Pochylski and J. Gierszewski, J. Nanopart. Res., 2013, 15, 1902 CrossRef PubMed.
- S. H. Bell, M. P. Weir, D. P. Dickson, J. F. Gibson, G. A. Sharp and T. J. Peters, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1984, 787, 227–236 CrossRef CAS PubMed.
- R. Krzyminiewski, Z. Kruczyński, B. Dobosz, A. Zajac, A. Mackiewicz, E. Leporowska and S. Folwaczna, Appl. Magn. Reson., 2011, 40, 321–330 CrossRef CAS PubMed.
- M. Gheisari, M. Mozaffari, M. Acet and J. Amighian, J. Magn. Magn. Mater., 2008, 320, 2618–2621 CrossRef CAS.
- S. Ueno and M. Sekino, Biomagnetics: Principles and Applications of Biomagnetic Stimulation and Imaging, CRC Press, 2018, p. 234 Search PubMed.
- S. Mørup, D. E. Madsen, C. Frandsen, C. R. H. Bahl and M. F. Hansen, J. Phys.: Condens. Matter, 2007, 19, 213202 CrossRef.
- I. S. Jacobs and C. P. Bean, Phys. Rev., 1955, 100, 1060–1067 CrossRef.
- A. Aharoni, J. Appl. Phys., 1999, 86, 1041–1046 CrossRef CAS.
- R. Skomski, J. P. Liu, C. B. Rong and D. J. Sellmyer, J. Appl. Phys., 2008, 103, 07E139 CrossRef.
- D. J. Dunlop, J. Geophys. Res.: Solid Earth, 2002, 107, EPM 4-1–EPM 4-22 Search PubMed.
- M. Winklhofer, K. Fabian and F. Heider, J. Geophys. Res., 1997, 102, 22695–22709 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01358h |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2023 |