The inert pair effect on heavy noble gases: insights from radon tetroxide

Abstract

A quantum chemical survey of radon and xenon tetroxides (NgO₄, Ng = Xe, Rn) is reported herein. The intermediate species, which are formed in their explosive decomposition back to their elemental states (Ng and O₂), were also studied and their energetics were compared. While T_d symmetric RnO₄ has a minimum energy structure, its standard enthalpy of formation is 88.6 kJ mol⁻¹ higher than for XeO₄. The reason for this higher instability lies in what is known as the inert pair effect. This work establishes that the high-valent chemical trends of the sixth period of groups 13–15 are indeed extended to group 18.

---

Introduction

The chemistry of xenon was a milestone in 20th century chemistry, challenging previous assumptions on the chemical inertness of noble gases. This was spurned with the discovery by Bartlett¹ of xenon hexafluoroplatinate. It was found that xenon^2,3 in particular presents a rich and varied chemistry and the least ‘noble’ of the periodic group.

It has been assumed⁴ that due to its lower ionization energy, the chemistry of radon should be richer than that of xenon but this proposition has so far not been extensively tested in experimental conditions. The most stable isotope of radon is ²²²Rn having a half-life of 3.8 days. This, along with its radioactivity, poses a significant operational challenge in isolating and identifying new compounds. The most widely known compound of radon is its difluoride⁵ (RnF₂) identified in 1962, around the same time as the first xenon complex. A few cations such as RnO⁺, RnH⁺, RnOH⁺, and RnOH₂⁺ have also been identified in a plasma ion source.⁶ However, the vast majority of recent works on radon compounds has been in silico.^7–12

The highest formal oxidation state in the noble gas group is VIII, as exemplified by xenon tetroxide, an explosive gas identified by Selig et al¹³ and structurally characterized by electron diffraction few years later by Gundersen et al.¹⁴ Its explosive character accounts for its high endothermicity¹⁵ (Δ_fH^⊖_{298 K} = +642 kJ mol⁻¹). Slepkov et al¹⁶ performed a detailed DFT study of the potential energy surface of XeO₄ and predicted the existence of a short lived isomer Xe(η²-O₂)₂ that would act as an intermediate in the decomposition reaction. Though the redox state of the dihaptic dioxo ligand was not clearly stated from their account, the determined (OPBE) HOMO–LUMO gap in Xe(η²-O₂)₂ was just 0.38 eV, hinting at a possible multiconfigurational character in the wavefunction. Vent-Schmidt and coworkers¹⁷ identified for the first time the new Xe^VIII species XeO₃(η²-O₂) synthesized by the UV photo-irradiation of XeO₄. This was the most recent incursion into Xe^VIII chemistry.

Herein, we address the nature of the chemical bond in three molecules RnO₄, RnO₂(η²-O₂), and Rn(η²-O₂)₂, none of which have ever been identified. We investigate their stability toward decomposition and establish the points of commonality and differences in the chemistry of xenon and radon, given that the oxides of the former are better studied. High level coupled-cluster techniques namely CCSD(T) and Mk-CCSD(T) were used in the process as quantitative tools to obtain the formation enthalpies.

Results and discussion

The experimental Xe–O bond length in XeO₄ determined by electron diffraction is 1.736 Å, and the O–O distance is 2.832 Å.¹⁴ The geometries of NgO₄ (Ng = Xe, Rn) were optimized at the CCSD(T)/DKH-TZVPP level, and the bond distances are displayed on Fig. 1. The calculated values are in good agreement with the experimental ones for XeO₄ (1.756 Å and 2.867 Å, respectively), differing at the most by 0.035Å.

Fig. 1 Structural features of the CCSD(T)/DKH-TZVPP optimized structures of xenon and radon tetroxides.

RnO₄ exhibits T_d point group symmetry as expected and is a confirmed to be minimum on the potential energy surface, i.e., possessing all real vibrational modes. The calculated bond lengths of this compound are, as expected, slightly larger than those of the xenon congener.

The bond strengths in RnO₄ are, however, palpably inferior to those of XeO₄, as is apparent from the comparison of the calculated vibrational frequencies (Table 1 and Fig. S1, ESI†). The Ng–O stretches with t₂ symmetry in particular are both IR active and appear at a lower frequency for RnO₄ than for XeO₄.

Table 1 Calculated vibrational modes of NgO₄ at the CCSD(T)/DKH-TZVPP level compared to the experimental spectra of XeO₄ measured by Selig et al.¹³

Mode	RnO4 (cm^−1)	XeO4 (cm^−1)	XeO4 Exp.^13 (cm^−1)
e	205	264
t 2	225	306	306
a 1	706	777
t 2	799	873	877

---

To understand why the Ng–O bonds in RnO₄ are weaker than in XeO₄, a more detailed electronic structure analysis of the CCSD orbitals was carried via Natural Bond Orbital analysis. The Natural Population Analysis (NPA) in particular affords some insight into the distribution of the electrons within the levels of the formal Ng^VIII tetroxides (Table 2).

Table 2 NBO analysis of the CCSD/DKH-TZVPP natural orbitals: electron occupation and composition of orbitals

Natural population	XeO4	RnO4
NAO Ng 5s/6s	1.416	1.534
NAO Ng 5p/6p	2.889	2.691
	NLMO composition
σ(Ng–O)	47.1% Xe + 52.9% O	47.0% Rn + 53.0% O
π1(Ng–O)	6.2% Xe + 93.8% O	5.4% Rn + 94.6% O
π2(Ng–O)	6.5% Xe + 93.5% O	5.8% Rn + 94.2% O

---

It is found that in the XeO₄ case, the electrons assigned to Xe are 2.889 e⁻ in the 5p orbital set, while the 5s orbital holds 1.416 e⁻. By comparison, the Rn atom in RnO₄ holds more electrons in the 6s orbitals (1.534 e⁻) and fewer electrons in the 6p orbitals (2.691 e⁻).

The Natural Localized Molecular Orbitals (NLMO) indicate a strong covalent Ng–O σ bond in both tetroxides and a very faint O → Ng π donor–acceptor interaction.

Thus far, the difference in the formation of Ng–O bonds appears to be down to the different radial structure of the valence orbitals in Rn with respect to Xe.

To probe into the origin of the weaker Rn–O bonds, a computational experiment was performed: the formation enthalpies were calculated with and without the DKH2 relativistic Hamiltonian. The experimental¹⁵ standard enthalpy of formation of XeO₄ is +642.2 kJ mol⁻¹, which is extremely well matched by the CCSD(T)/CBS//CCSD(T)/DKH-TZVPP approach that yields +642.6 kJ mol⁻¹ (Fig. 2). Radon tetroxide is less stable by 88.6 kJ mol⁻¹ (21.2 kcal mol⁻¹).

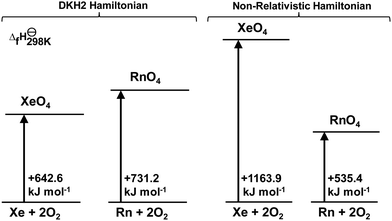Fig. 2 Sketch of the enthalpies of formation at room temperature of XeO₄ and RnO₄ calculated at the CCSD(T)/CBS//CCSD(T)/DKH-TZVPP level of theory.

Since there is no reason to assume that the kinetics of the decomposition process of RnO₄ is substantially different to XeO₄, the former can safely be predicted to exist on account of these results with a degree of confidence.

The non-relativistically optimized structures have very different thermodynamic features from the relativistic models. Without relativity, XeO₄ would be more explosive by almost two-fold (521.3 kJ mol⁻¹), and RnO₄ would be less endothermic by nearly 200 kJ mol⁻¹. This provides evidence that relativistic effects have a drastic influence on the valence orbitals in both Xe and Rn compounds and consequently play a major role in their high-valent chemistry.

However, this effect can best be exemplified by the mean radial expectation values 〈r〉 that provide a measure of the changes that relativity imposes on the valence shells at the Hartree–Fock level (Table S1, ESI†).

The 5s orbital in Xe already suffers a considerable radial contraction (0.111 a.u.) with respect to its non-relativistic counterpart, but Rn by far exhibits the largest changes with a considerable contraction of both the 6s and 6p orbitals, −0.368 and −0.191 a.u., respectively. This major contraction of the 6s orbital in Rn accounts for the augmented NPA of RnO₄ with relation to the XeO₄ NPA.

The relativistic radial contraction¹⁸ of the s and p shells on heavy elements has been known for some time. In particular, the inert pair effect initially formulated by Sidgwick¹⁹ in the 1930s and later found²⁰ to be a consequence of relativity has been a mainstay in the chemical behavior of the heavy elements of groups 13–15. Generally, the electron pair in the 6s² shell of the heavy elements becomes progressively less chemically accessible to engage in chemical bonds, which would result in Tl^III, Pb^IV, and Bi^V compounds. Such compounds exhibit a more unfavorable standard enthalpy of formation than each of the lighter congeners In^III, Sn^IV, and Sb^V. This feature is best exemplified when comparing the values of the standard reduction potentials E°(Sn^II/Sn^IV) = −0.088 V vs. E°(Pb^II/Pb^IV) = +1.69 V for heavy elements of group 14.

The inert pair effect is generally not considered for elements in groups 16–18 since the chemistry of polonium, astatine, and radon is so poorly known. These results clearly show that the chemistry of Rn^VIII is also affected by the inert pair effect.

The paper by Slepkov et al¹⁶ provided a detailed account into the possible decomposition pathway of XeO₄, predicting the existence of a di-haptic isomer Xe(η²-O₂)₂ as the intermediate. It is, therefore, natural to address the next leading question, which is how the energetics of this process compares in the case of RnO₄.

While the authors discuss the frontier orbitals of Xe(η²-O₂)₂, they do not provide an in-depth discussion into the oxidation state of the di-haptic oxides. Furthermore, the calculated HOMO–LUMO gap is notoriously small (0.38 eV), making it a species with high chemical potential (reactive) and possible multiconfigurational character. Our examination of the CCSD or even MP2 natural orbitals does indeed confirm that there are two competing configurations in the Xe(η²-O₂)₂ molecule. For a more orthodox and accurate treatment of the electronic structure in this molecule, a CASPT2(22,15) geometry optimization was conducted for the ground states of both Xe(η²-O₂)₂ and Rn(η²-O₂)₂. Both the quintet and triplet states were explored but lead to the dissociation of either both or one of the O₂˙ ligands, respectively; thus, only the singlet state potential energy surface presents a bound minimum.

The outcome of the calculation is that the structure can be described as a superoxide with spin coupling mediated by the Ng fragment (cf. Section 3 of the ESI†). This indicates that there is significant O₂⁻⋯O₂⁻ through bond interaction despite the fragments being over 4 Å apart. Formally, this amounts to oxidation state II, Rn^II(η²-O₂)₂ and Xe^II(η²-O₂)₂, in both species.

One possibility not covered in the Slepkov paper¹⁶ is the existence of a stepwise decomposition intermediate NgO₂(η²-O₂). Thus, the structure of these dioxides was optimized and their electronic structure analyzed herein. Both structures are minima and their ground singlet states exhibit a single configurational description. Triplet states were explored with this geometry but this leads to a local minimum with a dissociated oxygen atom.

Either species is quite unique in their geometry as they show a distorted tetrahedral shape with no symmetry consistent with an AX₃E type VSEPR stereochemistry;²¹ in addition, one bond of the dihaptic O₂ fragment is weaker than the other (cf.Fig. 3 and Section 4 of the ESI†). The dihaptic η²-O₂ ligand may best be described as a peroxide ligand (O₂²⁻). As such, the formal oxidation state of the Ng atom in NgO₂(η²-O₂) may appropriately be considered to be +VI. Comparison of the NPA occupations of the ns shells between the NgO₂(η²-O₂) (Table S6, ESI†) species and the corresponding tetroxides (Table 2) establish that indeed there is a much stronger participation of the latter than in the former.

Fig. 3 Dioxo-radon peroxide (a) and radon di-superoxide (b).

The decomposition processes of the tetroxides will therefore involve a successive descent of oxidation number in the order VIII → VI → II → 0.

In a general overview of the xenon and radon species studied so far (Fig. 4), it may be seen that the energetics of the Ng(η²-O₂)₂ and NgO₂(η²-O₂) species is surprisingly similar between the two elements. The biggest contrast still remains the disparate enthalpies of formation of the two noble gas tetroxides. The joining together of two oxygen atoms to form XeO₂(η²-O₂) is endergonic (+69.3 kJ mol⁻¹), which may be a hint as to why XeO₄ is still isolable given a low temperature or solvent.

Fig. 4 Thermodynamics of the formation of xenon and radon oxides, peroxides and superoxides at the CCSD(T)/CBS//CCSD(T)/DKH-TZVPP levels (black) and Mk-CCSD(T)/CBS//CASPT2(22,15)/x2c-TZVPP (blue). Highlighted in red is the value obtained by Slepkov et al¹⁶ at the ZORA:PBE/TZ2P level. The numbers placed at the top are the enthalpies relative to the parent tetroxide.

The value reached by Slepkov et al for the enthalpy of formation of Xe(η²-O₂)₂ was +633 kJ mol⁻¹; this value is fairly close to the one reached in this work by a proper multireference method, +600.3 kJ mol⁻¹. This is indicative that approximate density functionals of the GGA type exhibit some degree of tolerance for multireference character if the single determinant represents of about 60% of the wavefunction.

In finalizing, it is important to stress that when performing an in silico prediction of the existence of any species, the term ‘stability’ is not very helpful,²² particularly if the systems in question are endothermic with respect to decomposition. But it may be concluded that RnO₄ is a more difficult system to synthesise and isolate. XeO₄ is typically obtained from the acid dehydration of a metal perxenonate (XeO₆⁴⁻).¹⁷ Presumably, a perradonate RnO₆⁴⁻ with high enough lattice energy might be isolated and likewise transformed using very low temperature matrices. The e symmetry vibrational modes, corresponding to a scissor-like motion of the oxygen atoms in RnO₄, display a lower energy (205 cm⁻¹) than in XeO₄ (265 cm⁻¹), which is indication that thermal decomposition may occur more easily for RnO₄.

The detection of NgO₂(η²-O₂) and Ng(η²-O₂)₂ species, having nearly the same energy with respect to their constituent elements, either through vibrational spectroscopy or mass spectrometry of an ionized derivative will rely on their kinetic stability toward decomposition.

Conclusion

The noble gas tetroxides NgO₄ (Ng = Xe,Rn) were examined computationally, and a systematic comparison of the bonding features, vibrational properties, and energetics was carried out.

The most interesting finding is that the inert pair effect is present in group 18 species. This is reflected in the higher standard enthalpy of formation of RnO₄ relative to XeO₄. The cause of this effect was demonstrated to be relativity, in line with what is known for the heavy elements of groups 13–15. Chemical bonding evaluated through NBO analysis is shown to be residually more ionic in the case of RnO₄, largely by less π(O → Ng) donation. Considering the respective Mulliken electronegativities²³ of the two elements, Xe: 5.85 eV, Rn: 5.1 eV, which is to be expected.

The fleeting intermediate species in the decomposition process of the tetroxides were also analyzed, namely, Ng(η²-O₂)₂ and NgO₂(η²-O₂). While the former can be formally classified as a superoxide, it displays unique spin coupling between both the superoxide ligands mediated by the noble gas atom. This multiconfigurational singlet state sets the stage for dioxygen dissociation. NgO₂(η²-O₂) is a unique peroxide structure, whereby the dihaptic group is asymmetrically coordinated to the noble gas atom.

The chemistry of radon may be rich and varied, and there are promising indications^7–12 that this is the case. Fitzsimmons and Klobukowski¹¹ examined a family of organic xenon and radon fluorides and showed that Rn species were thermodynamically more stable than the Xe congeners. Recently, a study has been published by Um and coworkers¹² where their best estimation of the formation enthalpy for RnF₆ was −584 kJ mol⁻¹, whereas for XeF₆, the value was −264 kJ mol⁻¹. In contrast to the oxides, it appears that the fluorides of radon and xenon are generally exergonic. This peculiarity is likely a consequence of the much higher effective nuclear charge in fluorine that stabilizes the polarization of the bonds. Although a highest valent species such as RnF₈ might be envisioned, the results of the present study indicate that the also highest valent RnO₄ is less likely to be within reach.

Methods

The ORCA 5.0.3 package²⁴ was used in all the single reference systems. The Douglas–Kroll–Hess^25,26 relativistic Hamiltonian to second order (DKH2) was employed in all the calculations. Coupled Cluster^27,28 Singles Doubles and iterated Triples [CCSD(T)] optimizations and frequencies were obtained using the relativistically recontracted DKH-def2-TZVPP basis sets²⁹ for oxygen and the SARC-DKH-TZVPP basis sets^30,31 for Xe and Rn. The Resolution of Identity^32,33 was employed in all the ORCA runs with an automatically³⁴ generated density fitting basis set (AutoAux). A finite nucleus model was taken into account via the Gaussian nucleus model.³⁵ No symmetry constraints were imposed in the optimizations.

A two point extrapolation³⁶ to the complete basis set (CBS) was used employing the Martin³⁷ formula.

where A is a system-dependent constant and n is the cardinal number of the basis set in use. To solve this system of equations, two single point runs with the x2c-TZVPP (n = 3) and x2c-QZVPP (n = 4) relativistic basis sets were performed, and the resulting energies used in the extrapolation.^36,38 The notation “method/basis set 1//method 2/basis set 2” is adopted throughout and signifies that geometry optimization and numerical frequencies were carried out with method 2/basis set 2, while the final energy of the stationary point is obtained with method/basis set 1.

Geometry optimizations of the multireference systems Ng(η²-O₂)₂ were all performed using OpenMolcas³⁹ version 19.11 employing the DKH2 relativistic Hamiltonian, the x2c-TZVPP basis set on all the elements with resolution of identity⁴⁰ charge decomposition (RICD) of multicentre two electron integrals via the atomic compact (aCCD) auxiliary basis set.⁴¹ The explicit correlation space was made up of 22 electrons in 15 orbitals [CASSCF(22,15)] corresponding to all the valence p orbitals in Ng and O. The resulting multiconfigurational self-consistent field wavefunction was correlated to second order under the CASPT2 formalism. The geometries were optimized using the latest analytic gradient implementations⁴² in OpenMolcas whereby state specific (1 root) CASPT2(22,15) nuclear gradients were minimized. A diagonal Fock approximation was used in the CASPT2 optimizations (non-iterative CASPT2). An imaginary level shift of 0.2i au was used in the perturbative step to avoid intruder states and consequent discontinuities in the energy landscape.

The CASPT2(22,15) optimized structures of the Ng(η²-O₂)₂ systems obtained with OpenMolcas underwent a single point energy evaluation in ORCA with Mukherjee's⁴³ multireference coupled cluster variant Mk-CCSD(T) with the x2c-TZVPP and x2c-QZVPP basis sets in a similar manner as above to obtain the CBS extrapolated energies.

Standard enthalpies of formation of NgO₄ and NgO₂(η²-O₂) were computed as the sum of the electronic energies obtained from the CBS extrapolation and the thermal corrections (H_corr) for the enthalpy at standard temperature and pressure at the level of theory of the optimization [CCSD(T)/DKH-TZVPP].

The enthalpies of the multireference systems Ng(η²-O₂)₂ were calculated using the following formula.where the thermal corrections H_corr were calculated with the optimization method in OpenMolcas.

Natural Bond Orbital⁴⁴ (NBO) analyses were performed using the CCSD natural orbitals obtained from the optimization procedure.

Radial distribution functions were plotted using MultiWfn 3.8.⁴⁵

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding from Fundação para a Ciência e a Tecnologia is acknowledged for this work through the RadonChem grant ref. PTDC/QUI-QFI/31896/2017. Institutional grants UIDB/04046/2020 and UIDP/04046/2020 (BioISI), UIDB/00100/2020 (CQE), and LA/P/0056/2020 (IMS) are also acknowledged. The authors thank Prof. Maria José Calhorda for helpful discussions and critical analysis of the manuscript. Prof. Frank Neese is thanked for providing access to computing facilities.

References

1. N. Bartlett, Proc. Chem. Soc., 1962, 218.
2. F. Grandinetti, Noble Gas Chemistry: Structure, Bonding, and Gas-Phase Chemistry, Wiley, 2018.
3. G. J. Schrobilgen, in The Periodic Table I: Historical Development and Essential Features, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2019, pp. 157–196.
4. L. Stein, Radiochim. Acta, 1983, 32, 163–172.
5. P. R. Fields, L. Stein and M. H. Zirin, J. Am. Chem. Soc., 1962, 84, 4164–4165.
6. N. A. Golovkov, I. I. Gromova, M. Janicki, Y. V. Norseyev, V. G. Sandukovsky and L. Vasaros, Radiochem. Radioanal. Lett., 1980, 44, 67–78.
7. M.-S. Liao and Q.-E. Zhang, J. Phys. Chem. A, 1998, 102, 10647–10654.
8. M. Filatov and D. Cremer, Phys. Chem. Chem. Phys., 2003, 5, 1103–1105.
9. E. Tsivion and R. B. Gerber, Phys. Chem. Chem. Phys., 2010, 12, 11791–11794.
10. R. Juarez, C. Zavala-Oseguera, J. O. C. Jimenez-Halla, F. M. Bickelhaupt and G. Merino, Phys. Chem. Chem. Phys., 2011, 13, 2222–2227.
11. A. Fitzsimmons and M. Klobukowski, Theor. Chem. Acc., 2013, 132, 1314.
12. J. Kang, I. Park, J. H. Shim, D. Y. Kim and W. Um, Sci. Rep., 2023, 13, 2898.
13. H. Selig, H. H. Claassen, C. L. Chernick, J. G. Malm and J. L. Huston, Science, 1964, 143, 1322–1323.
14. G. Gundersen, K. Hedberg and J. L. Huston, J. Chem. Phys., 1970, 52, 812–815.
15. S. R. Gunn, J. Am. Chem. Soc., 1965, 87, 2290–2291.
16. V. Slepkov, S. Kozlova and S. Gabuda, J. Phys. Chem. A, 2011, 115, 7811–7814.
17. T. Vent-Schmidt, J. T. Goettel, G. J. Schrobilgen and S. Riedel, Chem. – Eur. J., 2015, 21, 11244–11252.
18. P. Pyykko, Chem. Rev., 1988, 88, 563–594.
19. N. V. Sidgwick, Annu. Rep. Prog. Chem., 1933, 30, 120–128.
20. B. J. Austin and V. Heine, J. Chem. Phys., 1966, 45, 928–933.
21. R. J. Gillespie, Chem. Soc. Rev., 1992, 21, 59–69.
22. R. Hoffmann, P. V. Schleyer and H. F. Schaefer, Angew. Chem., Int. Ed., 2008, 47, 7164–7167.
23. J. Emsley, The Elements, Oxford University Press, 1991.
24. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
25. N. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
26. B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748.
27. R. J. Bartlett and G. D. Purvis, Int. J. Quantum Chem., 1978, 14, 561–581.
28. R. J. Bartlett, Annu. Rev. Phys. Chem., 1981, 32, 359–401.
29. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
30. J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842–1849.
31. D. A. Pantazis and F. Neese, Theor. Chem. Acc., 2012, 131, 1292.
32. E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41–51.
33. N. Frank, J. Comput. Chem., 2003, 24, 1740–1747.
34. G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562.
35. L. Visscher and K. G. Dyall, At. Data Nucl. Data Tables, 1997, 67, 207–224.
36. V. Vasilyev, Comput. Theor. Chem., 2017, 1115, 1–3.
37. J. M. L. Martin, Chem. Phys. Lett., 1996, 259, 669–678.
38. P. Pollak and F. Weigend, J. Chem. Theory Comput., 2017, 13, 3696–3705.
39. I. Fernández Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. Gonzalez, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesolowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15(11), 5925–5964.
40. O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518.
41. F. Aquilante, R. Lindh and T. B. Pedersen, J. Chem. Phys., 2007, 127, 114107.
42. Y. Nishimoto, J. Chem. Phys., 2021, 154, 194103.
43. U. Sinha Mahapatra, B. Datta and D. Mukherjee, J. Phys. Chem. A, 1999, 103, 1822–1830.
44. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0 edn., 2023.
45. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01347b

---