 Open Access Article
Open Access ArticleQuantifying methyl tunneling induced (de)coherence of nitroxides in glassy ortho-terphenyl at low temperatures†
Andrea
Eggeling
 ,
Janne
Soetbeer
,
Janne
Soetbeer
 ,
Luis
Fábregas-Ibáñez
,
Daniel
Klose
,
Luis
Fábregas-Ibáñez
,
Daniel
Klose
 and
Gunnar
Jeschke
and
Gunnar
Jeschke
 *
*
Laboratory of Physical Chemistry, ETH Zurich, Vladimir-Prelog-Weg 2, Zurich, Switzerland. E-mail: gjeschke@ethz.ch
First published on 3rd April 2023
Abstract
The low-temperature Hahn echo decay signal of the pyrroline-based nitroxide H-mNOHex in ortho-terphenyl (OTP) shows two contributions on distinct time scales. Tunneling of the nitroxide's methyl groups cause electron spin echo envelope modulation (ESEEM) on a faster time scale compared to the slower matrix-induced decoherence contribution arising from nuclear pair ESEEM. Here we introduce the methyl quantum rotor (MQR) model that describes tunneling ESEEM originating from multiple methyl rotors coupled to the same electron spin. By formulating the MQR model based on a rotation barrier distribution P(V3), we account for the different local environments in a glassy matrix. Using this framework, we determine the methyl groups' rotation barrier distribution from experimental Hahn echo decay/two-pulse ESEEM data by a non-linear fitting approach. The inferred distributions are in good agreement with density functional theory (DFT) calculations of the methyl groups' rotation barriers in the low-temperature regime where tunneling constitutes the dominant methyl proton exchange process. In addition to comparing our results with previous decoherence studies performed on the same spin system, we experimentally confirm the characteristic properties of methyl tunneling by demonstrating that P(V3) is magnetic field independent and predominantly temperature independent between 10 and 50 K. This confirms the assignment of the fast Hahn echo decay contribution to methyl tunneling, showcasing how pulsed EPR sequences can coherently probe this quantum phenomenon for commonly employed nitroxide spin-labels.
1 Introduction
Decoherence of electron spins in nitroxides in various solvents has been extensively studied over the last decades with electron paramagnetic resonance (EPR). The influence of deuteration of the nitroxide and matrix,1–4 methyl groups,5–7 matrix proton concentration8,9 and temperature4,10 have been the focus of previous in-depth studies. The low-temperature Hahn echo decay signal of nitroxides with geminal methyl groups consists of two contributions on distinct time scales.4,11 The slower matrix-related contribution originates from nuclear pair ESEEM12 and in recent efforts has been modelled with correlated cluster expansion (CCE)13 to quantitatively predict the phase memory time of unpaired electrons in biologically relevant matrices.12,14 The faster contribution has only recently been attributed to methyl tunneling of the nitroxide's methyl groups by regularized noise spectroscopy.11 A theoretical study predicted this effect for the two-pulse electron spin echo envelope modulation (ESEEM), i.e. Hahn echo, experiment several decades ago.15 Excitation and detection of tunneling coherence has originally been demonstrated by applying the three-pulse ESEEM experiment on a methyl group containing Mn(II)-doped metal–organic framework.16 It is of great importance to understand this methyl group related (de)coherence contribution to the Hahn echo decay signal of nitroxides at low temperatures, since the majority of nitroxide spin-labels used for structure elucidation of biological macromolecules with EPR spectroscopy feature geminal methyl groups.17,18 Electron spin decoherence induced by protonated methyl groups has recently been suggested as a means for filtering contributions in EPR-based distance distribution measurements.19 This technique was applied to elucidating kinetics of substrate binding to calmodulin.20 Moreover, analysis of electron spin decoherence in a methyl group-rich environment proposed that methyl groups with a high rotation barrier enhance electron spin decoherence while those with a low barrier suppress it.8,21 Thus, understanding the fast Hahn echo decay contribution is also a prerequisite for quantitatively predicting the matrix methyl groups' contribution to electron spin decoherence.Here, we aim to characterize the fast contribution in the Hahn echo decay of nitroxides with geminal methyl groups in a glassy matrix by considering methyl tunneling ESEEM at low temperatures. Rotation of the methyl group gives rise to a threefold potential with a characteristic rotation barrier V3, which depends on local hindrance and therefore is sensitive to its chemical environment.23 A classical description for methyl group rotation suffices at ambient temperatures, where the main process for methyl group proton position exchange is stochastic hopping over the rotation barrier.23,24 Even at temperatures of 80 K, slow methyl group rotations are detectable in the electron spin echo.25 In the present low-temperature study, we describe the methyl group as a quantum rotor, where tunneling through the potential wells by wavefunction overlap becomes the dominant proton position exchange process. The wavefunction overlap leads to a splitting of degenerate energy levels (with quantum number r) by the tunneling frequency ν(r)t as illustrated in Fig. 1a.22 In the low-temperature regime, we approximate that only the energy levels with quantum number r = 0 are significantly populated and consider these three tunneling states (A, Ea, Eb) in the spin systems' Hamiltonian.11,16 There is a non-trivial dependence of the ground state tunneling frequency νt on the rotation barrier V3, since for higher rotation barriers the wavefunction overlap gets smaller leading to smaller energy level splittings and consequently smaller tunneling frequencies (see Fig. 1b). Since in low-temperature EPR measurements, the investigated nitroxide is distributed in a glassy matrix, we consider a distribution of rotation barriers P(V3) to account for different local environments of the nitroxides' geminal methyl groups.8,26 This approach has already been established to explain experimental findings in neutron scattering measurements of glassy polymers containing methyl groups by considering a Gaussian rotation barrier distribution,27,28 or a sum thereof.29,30 Due to the non-linear dependence between V3 and νt, a Gaussian distribution of rotation barriers P(V3), shown in Fig. 1c, corresponds to a skewed distribution of tunneling frequencies P(νt),31 as shown in Fig. 1d.
 | ||
| Fig. 1 Rotation barrier, tunneling frequency and energy levels of the methyl rotor. (a) Illustration of the threefold potential of the methyl group rotation with a rotation barrier V3 = 1600 K. The energy levels within the potential wells, characterized by the ro-librational quantum number r = 0, 1,…, are split by the tunneling frequency ν(r)t due to overlap of the wavefunctions. (b) The tunneling frequency νt of the ground state (r = 0) and the rotation barrier V3 are related by the hindered rotor model and have a non-trivial dependence.22 Due to this relation, (c) a Gaussian distribution of rotation barriers P(V3) corresponds to a (d) skewed distribution of tunneling frequencies P(νt). | ||
In this work, we investigate the fast (de)coherence contribution of methyl group containing nitroxides depending on the magnetic field, matrix and methyl group deuteration, and temperature by analyzing and comparing inferred rotation barrier distributions from Hahn echo decay/two-pulse ESEEM measurements. The matrix-driven decoherence contribution is treated as a background function which dampens the methyl tunneling ESEEM contribution. In Section 2, we present the theoretical framework of methyl tunneling ESEEM in the Hahn echo experiment and how we apply this to a glassy system. Section 3 explains the experimental set-up, computational procedures and extraction of the rotation barrier distribution from experimental data. Then, we summarize the magnetic-field independence of the methyl tunneling process, the influence of matrix deuteration on the rotation barrier and the temperature dependence of the tunneling ESEEM and rotation barrier distribution in Section 4. At the end, we conclude with our findings on methyl tunneling ESEEM in nitroxides with geminal methyl groups and give an overview of possible applications of this quantum mechanical phenomenon.
2 Theory
2.1 Tunneling ESEEM Hamiltonian
The total Hamiltonian for M methyl groups coupled to an electron spin can be split into a spin Hamiltonian and a tunneling Hamiltonian. Considering a single methyl group (M = 1), the spin Hamiltonian depends on the methyl group rotation angle ϕ which characterizes the localized states of the rotor (0°, 120°, 240°). In this case, the spin Hamiltonian reads| Ĥ(ϕ) = ĤZ + AI(ϕ)ŜzÎ1,z + AII(ϕ)ŜzÎ2,z + AIII(ϕ)ŜzÎ3,z | (1) |
 | (2) |
 | (3) |
| Îk·Îl = Îk,xÎl,x + Îk,yÎl,y + Îk,zÎl,z. | (4) |
In case of two methyl groups (M = 2) coupled to the same electron spin, the spin Hamiltonian in full state space takes the form
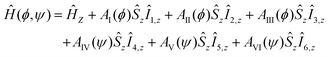 | (5) |
 | (6) |
| Individual rotors | ||
|---|---|---|
| m | V 3,m – relaxed (K) | V 3,m – constrained (K) |
| 1 | 1553 | 1610 |
| 2 | 1506 | 1671 |
| 3 | 1516 | 1675 |
| 4 | 1476 | 1667 |
| Coupled rotors – relaxed | |||
|---|---|---|---|
| m | V 3,1 (K) | V 3,m (K) | W 3 (K) |
| 2 | 1660 | 1643 | 24 |
| 3 | 1464 | 1462 | 0 |
| 4 | 1495 | 1539 | 16 |
| Coupled rotors – constrained | |||
|---|---|---|---|
| m | V 3,1 (K) | V 3,m (K) | W 3 (K) |
| 2 | 1795 | 1848 | −10 |
| 3 | 1637 | 1677 | 2 |
| 4 | 1625 | 1669 | 5 |
2.2 Tunneling ESEEM in a glassy matrix
The introduced approaches for preparing the full state Hamiltonian for M = 1, 2 are used to numerically simulate single-orientation tunneling ESEEM signals for a specific set of rotation barriers V3,1 and V3,2 with the density operator formalism either as single rotors or in a coupled basis. Thereby, we aim to understand the spin dynamics of M methyl rotors contributing to the experimental tunneling ESEEM signal. For M > 2, this numerical approach is computationally not easily feasible anymore, since the spin Hamiltonian dimension becomes 21+3M and in a coupled rotor basis the tunneling Hamiltonian has dimension 3M, leading to dim(Ĥtot) = 21+3M·3M.Fig. 2 presents the simulated single-orientation signals for two combinations of rotation barriers. Similar to nuclear ESEEM arising from several nuclei simultaneously coupling to the same electron spin,35,36 the methyl rotor simulations indicate that for a single-orientation the time-dependent ESEEM amplitude E obtained from M methyl groups is the product of all individual methyl rotor ESEEM amplitudes Em. This massively simplifies the expression for the M methyl rotor time-dependent ESEEM amplitude
 | (7) |
The tunneling process becomes dominant at low temperatures. At such temperatures, we measure the investigated nitroxide in a glassy environment, which usually consists of the preferred solvent and an added glass former. In such a disordered sample, the local environment of individual nitroxides and, in particular their methyl groups, differs. The local structural differences influence the methyl rotation barrier due to its sensitivity to local hindrance. We account for this by considering a distribution of rotation barriers for all M methyl groups in the sample and by averaging over the different local environments according to
 | (8) |
 | (9) |
 | (10) |
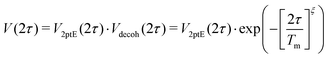 | (11) |
3 Materials and methods
3.1 Spin systems and EPR measurements
The paramagnetic molecules under investigation were pyrroline-based nitroxide radicals with protonated (H-mNOHex) and deuterated geminal methyl groups (D-mNOHex) illustrated in Fig. 3a and b. The synthesis of both nitroxides was reported previously by Soetbeer et al.4 The matrix was protonated or deuterated ortho-terphenyl (OTP/dOTP, Fig. 3c and d), which importantly does not contain methyl groups. We measured the nitroxides at a concentration of 20 μM in either matrix. The sample was melted at 70 °C with a heat gun prior to flash-freezing in liquid nitrogen resulting in a glassy frozen sample. EPR measurements at Q-band frequencies of ∼34.4 GHz were performed on a commercial spectrometer (Bruker ElexsysII E580) equipped with a 200 W travelling wave tube amplifier and a homebuilt resonator for 3 mm outer diameter capillaries.37 Experiments at W-band frequencies (∼94.1 GHz) were carried out on a Bruker Elexsys E680 X-/W-band spectrometer in an EN 680-1021H resonator. The same sample mixture was filled into a 3 mm o.d. quartz capillary for Q-band and in a 0.5 mm i.d./0.9 mm o.d. quartz capillary for W-band measurements, respectively. We measured the electron spin decoherence with the Hahn echo, i.e. two-pulse ESEEM, pulse sequence (Fig. 3e) at the magnetic field value corresponding to the maximum of the nitroxide spectrum. We used a pulse length of 12 ns/16 ns for the π/2-pulse and 24 ns/32 ns for the π-pulse, at Q-band and W-band, respectively. A two-step phase cycle [(+x) − (−x)] was applied on the π/2-pulse for receiver offset correction while the phase of the π-pulse [(+x)] was kept constant. The integration window (12 ns) for echo acquisition was always placed symmetrically around the echo maximum and kept constant for all measurements. The signal was recorded at temperatures between 10 K and 80 K and the shot repetition time was adjusted for changes in T1 such that the magnetization fully recovered in between shots. W-band measurements were only carried out at a temperature of 40 K.3.2 DFT-based rotation barrier calculations
We performed energy calculations within the open-shell Kohn–Sham density functional theory (DFT) in ORCA version 5.0.238 in vacuum to get information on properties of the geminal methyl groups of H-mNOHex. Initially, the geometry of the nitroxide structure (Fig. 3a) truncated between the two successive triple bonds and saturated with a hydrogen atom was optimized, using the B3LYP functional with the def2-TZVP basis set in combination with D3BJ dispersion correction. We intentionally performed all calculations in vacuum without adding an implicit solvent since the determined rotation barriers should serve as a reference when analyzing rotation barrier distributions of the nitroxide in a glassy matrix. We determined the rotation barriers of all four methyl groups in two different approaches: first with a relaxed surface scan allowing all other atoms to change position and adapt to the current dihedral angle of the observed methyl group. This provides insight into the lowest possible rotation barrier in vacuum, since all other interactions of the system are minimized. Second, using a constrained energy scan, where we fix the position of all atoms and allow only the dihedral angle of the observed methyl group to change. This should provide a reference for a higher yet possible rotation barrier in vacuum since unfavorable interactions within the system cannot be avoided. The obtained energy profile was corrected for the minimal energy and evaluated according to | (12) |
 | (13) |
3.3 Determining the rotation barrier distribution
To investigate the tunneling ESEEM contribution and infer a rotation barrier distribution from experimental data, we simulated tunneling ESEEM signals and kernels numerically using the density operator formalism. To this end, we adapted MATLAB39 implementations of the Hahn echo/two-pulse ESEEM sequence11 and of the three-pulse ESEEM sequence16 to single orientations of the nitroxide and improved computational efficiency of the simulation script. For the kernel simulations, we adapted all simulation parameters to the experimental conditions and only considered on-resonance excitation of the electron spin. We evaluated the orientation averaging in eqn (9) over a weighted grid of 841 different orientations using the sphgrid-function from EasySpin version 5.2.29.40Inference of the rotation barrier distribution from experimental data is not feasible by directly solving the inverse problem of eqn (10), because the kernel in eqn (9) is ill-conditioned (condition number ∼1016), which would lead to an unstable and unreliable solution. Therefore, we either used a parametric or a non-parametric model to characterize the rotation barrier distribution. For a non-parametric model, a non-parametric vector represents the rotation barrier distribution. In this case, a non-negativity constraint together with regularization methods stabilize the solution. We applied Tikhonov regularization with the normalized cumulative periodogram (NCP)41,42 selection criterion of the regularization parameter within a range of α = [1 × 104, 5 × 106]. This selection criterion aims to find an α-value such that the power spectrum of the fit residuals matches that of white noise, which is favorable to account for all different frequency contributions present in the signal.43 We put boundaries on the regularization parameter value, since the non-parametric fitting algorithm for our model can be very prone to both under- and oversmoothing of the rotation barrier distribution. The rotation barrier distribution was inferred via regularized least-squares
 | (14) |
 | (15) |
 | (16) |
4 Results and discussion
4.1 Magnetic-field independence of tunneling ESEEM
The main characteristic of methyl tunneling is that the process is independent of the external magnetic field.16 Therefore, we investigated the decoherence behavior of H-mNOHex in OTP at Q-band (∼1.2 T) and W-band frequency (∼3.3 T), respectively, and compare the matrix relaxation process and the inferred rotation barrier distributions in Fig. 4a.Already from the experimental Hahn echo decay two distinct contributions to the decoherence behavior can be identified at both magnetic fields. Unexpectedly, we find a slightly slower relaxation contribution by the matrix at Q-band frequencies. The fitted phase memory time Tm is slightly longer than at W-band frequencies independent of the model (parametric or non-parametric) employed for the rotation barrier distribution. Since we still used hard but longer pulses at W-band and the spectrum becomes broader at higher magnetic fields, the excited spins are not completely identical for Q- and W-band. In other words, there is more orientation selection at W-band than at Q-band, which might have a small impact on the phase memory time. Moreover, this certainly influences the methyl tunneling ESEEM, which relies on the orientation-dependent hyperfine interaction. However, since still a large fraction of spins around the spectrum maximum is excited at both magnetic fields, we expect only minor differences in the apparent rotation barrier distributions. This is confirmed when comparing the Gaussian rotation barrier distributions which are almost identical for Q-band and W-band (Fig. 4a). From the non-parametric rotation barrier distribution it becomes clear that rotation barriers between 1500 K and 2000 K are the main contribution to the methyl tunneling ESEEM signal. This range coincides very well with the mean of the Gaussian rotation barrier distribution, making V3,av a good parameter to describe the tunneling behavior of the nitroxide's methyl groups. Additionally, the distribution mean is in agreement with the DFT-calculated rotation barriers for the truncated molecule in vacuum with the average rotation barrier V3,av being shifted ∼100 K higher than the results from the constrained one-dimensional energy surface scan (see Table 1). In general, this is consistent with the expectation that overall the methyl groups' rotation is more hindered in a matrix than in vacuum, suggesting that intermolecular interactions between the nitroxides' methyl groups and the matrix molecules influence the rotation barrier. However, in a glassy matrix, also more favourable local environments appear to be possible since the rotation barrier distribution has small contributions below the rotation barrier value of the relaxed surface scan, where the molecule can avoid energetically unfavourable interactions. This effect might be imposed by our choice of a Gaussian distribution of rotation barriers. On the other hand, strain in the glass can lead to an energetically unfavourable geometry of the nitroxide's heterocycle, which in turn might indeed lower the rotation barrier of the geminal methyl groups. The distribution mass at low rotation barriers (1000–1500 K) is not related to the methyl tunneling process, which is also visually recognizable by the large confidence intervals in this region. We will discuss this artefact in the inferred rotation barriers in Section 4.2. In the 1500–2000 K range, the distribution width of the parametric model overlays well with the peak(s) of the non-parametric distributions, where the confidence interval is smaller compared to the regions <1500 K and >2000 K. We can thus conclude that the rotation barriers of the methyl groups in glassy OTP are distributed between 1500 K and 2000 K. At both magnetic fields the methyl groups present in this glassy matrix experience very similar rotation barrier distributions as expected for the field-independent tunneling process.
4.2 Tunneling ESEEM upon matrix deuteration
The local environment around the methyl group influences the hindrance of rotation24 and thereby determines the rotation barrier. In a disordered system, such as the glassy matrix, non-bonding interactions46 between the investigated methyl group and the molecular environment mainly control the rotation barrier. These interactions can be either of intra- or intermolecular nature.23,47 Matrix deuteration might alter the methyl group's local environment and therefore the interactions governing the rotation barrier. Usually this so-called “external isotope effect” has only a weak impact on the rotation barrier.24 To assess whether tunneling ESEEM is sufficiently sensitive for revealing such a weak effect, we extracted rotation barrier distributions of H-mNOHex from Hahn echo decay/two-pulse ESEEM data recorded at Q-band in either OTP or dOTP and show the results in Fig. 4b.As expected, matrix deuteration prolongs the overall phase memory time of the nitroxide at 10 K by a factor of three.4 Therefore, the tunneling ESEEM contribution is even more prominently visible in the Hahn echo decay for deuterated matrices. Moreover, the modulation depth appears very similar for H-mNOHex in OTP and dOTP upon visual comparison of the Hahn echo decay traces, which is a first indication of a similar tunneling behavior in both matrices. Both Gaussian distributions include rotation barriers between 1500 K and 2000 K, which are also certain contributions to the non-parametric rotation barrier distributions. This is also in good agreement with the previously discussed rotation barrier distributions extracted at different magnetic fields and slightly higher temperature (see Fig. 4a).
Nevertheless, the extracted Gaussian rotation barrier distributions differ in means as well as widths for H-mNOHex in protonated and deuterated matrix. The rotation barrier distribution for OTP is centered at a higher V3,av of 1798 K compared to 1699 K for the investigated nitroxide in dOTP, whereas this distribution is much broader (Δσ ≈ 100 K). For H-mNOHex in OTP the distribution mass at high rotation barriers present in the non-parametric distribution is consistent with the right shift of its Gaussian distribution. Other reasons explaining the discrepancy become clear when taking into account the different contributions in the non-parametric distributions individually and analyzing their corresponding tunneling ESEEM signal. The results are illustrated in Fig. S2 (see ESI†) for the magnetic field and matrix deuteration analysis. From this analysis we can certainly conclude that the low rotation barrier contributions, which correspond to high tunneling frequencies, aim to fit the nuclear ESEEM modulations stemming from molecule protons and matrix deuterons, which still show a significant modulation depth and are visible in two-pulse ESEEM traces recorded at Q-band frequencies. According to the fit residuals in Fig. 4, the deuterium ESEEM for H-mNOHex in dOTP is detected for longer interpulse delays τ than the proton ESEEM in the OTP case. Since the deuterium ESEEM is such a prominent feature in the Hahn echo decay signals, most likely optimal solutions for the Gaussian rotation barrier distribution contain high tunneling frequencies masking the deuterium nuclear ESEEM leading to a broad distribution. The Gaussian distribution width reduces when applying a moving mean filter on the experimental trace before the fitting procedure. This filter smooths out the nuclear ESEEM without impacting the modulation depth of the tunneling ESEEM contribution, which is important for an accurate inference of the rotation barrier distribution. Thereby, the Gaussian rotation barrier distribution width is narrowed by around 70 K (see Fig. S3 in ESI†).
The difference in V3,av of the rotation barrier distribution for H-mNOHex in OTP and dOTP remains unaffected by the moving mean filter. Another aspect, which must be considered and might impact the mean of the rotation barrier distribution, is the glass structure of the two glass formers. The glass transition temperatures of OTP (243 K)48 and dOTP (248 K)49 are almost identical. This suggests a very similar glass structure, especially given the cis-arrangement of the phenyl rings, which is crucial for the glass formation of terphenyls and which is not altered by perdeuteration.50,51 Therefore, we assume that also the local environment of and the available free volume around the methyl groups is almost identical for OTP and dOTP. For this reason, we propose that the rotation barrier distribution is unaffected or only slightly affected by matrix deuteration.
As mentioned earlier, matrix deuteration prolongs the overall phase memory time, which allows the methyl tunneling ESEEM evolution to be more prominent in the recorded data owed to its reduced dampening by the matrix relaxation contribution.11 We thus expect that deuterated matrices enable a higher information content on the tunneling process and thereby benefit a more accurate inference of the rotation barrier distribution. Moreover, when fitting the Gaussian rotation barrier distribution for the measurements in OTP and dOTP globally, the agreement of the model fit with the OTP trace remains unaffected, although, the global solution is very close to the rotation barrier distribution for dOTP (see Fig. S4–S8 in ESI†). Therefore, we conclude that the inferred rotation barrier distribution from nitroxides in deuterated matrix is expected to be closer to the ground truth than for its protonated equivalent. We suggest to perform such measurements with protonated methyl groups in a deuterated environment to increase the phase memory time of the matrix decoherence contribution and thus gain the most information to obtain more robust rotation barrier distribution results.
For simulations of this kind it is important to ensure that the numerical evaluation of the kernel in eqn (9) is accurate, particularly for grid-based integration due to its rather slow convergence with number of orientations in the grid. This is especially crucial for fitting the two-pulse ESEEM data of a deuterated matrix as the phase memory time is long and the tunneling ESEEM very prominent. Fig. S9 (ESI†) illustrates the effect of a limited grid of orientations for H-mNOHex in dOTP data recorded at 10 K, where insufficient orientation averaging leads to a fitted tunneling ESEEM contribution that is non-smooth.
4.3 Temperature dependence of tunneling ESEEM
Tunneling through potential barriers becomes the dominant proton position exchange process at low temperatures, where all molecular motion is frozen out. The temperature dependence of methyl group tunneling has previously been studied for γ-irradiated methyl malonic acid with continuous wave (CW) EPR and shows an almost temperature-independent behavior in the low-temperature regime.52 Therefore, we investigated the temperature dependence of the tunneling ESEEM contribution to the two-pulse ESEEM signal between 10 K and 80 K, and illustrate the results in Fig. 5. The individual time-domain fits as well as inferred Gaussian rotation barrier distributions are shown in the Fig. S4–S7 (ESI†). | ||
| Fig. 5 Temperature dependence of matrix decoherence parameters and the inferred rotation barrier distributions of H-mNOHex in OTP and dOTP. The rotation barrier distribution parameters were fitted (a) individually and (b) globally for the Hahn echo decay signals acquired in protonated and deuterated matrix. The Gaussian rotation barrier distribution is described by the average rotation barrier V3,av and the distribution's standard deviation σ. The distribution parameters evaluated from fitting the OTP (orange) and dOTP (blue) signals individually are shown in the color according to their matrix. The globally inferred distribution parameters are shown in green. The phase memory time Tm and stretch parameter ξ characterize the matrix dependent relaxation process and are always fitted individually for OTP (orange) and dOTP (blue). The shaded areas represent the bootstrapped 95%-confidence interval. The dashed line indicates the arithmetic mean of the DFT-calculated constrained energy scan rotation barriers for all four methyl groups as a reference (see Table 1). | ||
The matrix decoherence contribution characterized by the phase memory time Tm and the stretched exponent ξ (see Fig. 5) indicates the already well-studied low-temperature behavior4 of H-mNOHex in OTP and dOTP. We compare the phase memory time results of a stretched exponential (SE) model and sum of two stretched exponentials (SSE) model, which was introduced previously,4 to the Vdecoh results of the MQR model to validate this model's accuracy in describing the matrix-related contribution to the Hahn echo decay/two-pulse ESEEM signal. When fitting the SE model, we omitted the first several microseconds of data to better isolate the data with pure matrix decoherence contribution. The results can be found in Fig. S10 (ESI†). The phase memory times evaluated with the MQR model are very similar to the results obtained for the slow-decaying component of the SSE model (Tm,2) by Soetbeer et al.4 in the low-temperature range up to 50 K for dOTP and 60 K for OTP. Above these temperatures, the matrix relaxation is in better agreement with the SE model, indicating that the description of the Hahn echo decay with two distinct contributions is limited to the previously defined low-temperature regime (10–60 K)4 and is certainly no longer valid above 60 K. This is compatible with the early empirical finding of convergence of Tm to a low-temperature maximum only below 60 K.53 Another, most likely thermally-activated, process becomes dominant leading to phase memory loss at higher temperatures. The sudden temperature-dependent change in phase memory time and stretched exponent is more pronounced for a deuterated matrix.
It has been reported that classical rotation of tempone methyl groups gets slow on the ENDOR timescale below 80 K,54 however, librations in general remain relevant below that temperature.4 Moreover, the fast decaying contribution, which we attribute to methyl tunneling,11 is not easily identifiable above 60 K, since the matrix-induced decoherence becomes very fast and a single stretched exponential suffices to fit the decay trace. This trend is also clearly visible in the extracted Gaussian rotation barrier distributions parameterized by V3,av and σ shown in Fig. 5. At first glance, it appears as if the results for H-mNOHex in the different matrices, OTP and dOTP, may not be consistent. In the previous section, we discussed for an illustrative example where these differences in distribution mean and width might originate from and that fit quality is not impacted when globally extracting the rotation barrier distribution for H-mNOHex in OTP and dOTP. Therefore, we interpret the global distribution parameters to reflect the temperature dependence of the methyl tunneling effect.
In the temperature range of 10 K to 60 K the average rotation barrier lies between 1700 K and 1800 K, which is about 100–200 K higher than the DFT-calculated rotation barrier for the truncated molecule in vacuum. These V3,av-values are also around 150 K higher than the rotation barriers evaluated by Soetbeer et al. for H-mNOHex in OTP (νt = 225 kHz, V3 = 1636 K) and dOTP (νt = 175 kHz, V3 = 1682 K).11 The distribution width is rather broad, meaning σ varies between 100 K and 280 K, while the spread of rotation barriers decreases with increasing temperature as shown in Fig. 6a. This temperature-dependent feature is observed for the individual OTP and dOTP fits as well as in the global distribution fit. Such an observation may provide information on changes in the methyl groups' local environment. In our case, the measurements are performed in a glassy (i.e. amorphous) matrix, and we thus interpret the narrowing of the rotation barrier distribution as an increase in free volume available to the solute.55,56 As a result, the rotation barriers of all methyl groups in the amorphous ensemble become alike due to their similar local environments. Relative to V3,av, this leads to fewer methyl groups in very favourable or strongly hindering environments. From our analysis we cannot conclude whether this narrowing of the rotation barrier distribution is characteristic for a given glassy matrix, since we lack experimental reference data to determine the sensitivity of methyl tunneling ESEEM to quantify the temperature-related increase in free volume of a glass. Moreover, free volume void size at the glass transition temperature varies quite strongly between different glass formers57 and the ratio between glass transition temperature and measurement temperature might also play a role. To gain more insight into this phenomenon a larger sample set consisting of the same methyl group containing nitroxide in various glassy matrices would need to be studied in the low-temperature regime.
The average of the global distribution increases slightly from 1720 K at 10 K to its maximal value of 1790 K at 60 K, until there is a sudden decrease of V3,av for temperatures above 60 K (see Fig. 5). This leads to a distribution of smaller rotation barriers, i.e. of higher tunneling frequencies (as shown in Fig. 6b). Our findings differ from the temperature behavior found for γ-irradiated methyl malonic acid52 and the methyl group containing Mn(II)-doped metal–organic framework,16 where the observed tunneling frequency decreases for increasing temperature. Their temperature behaviour can be fitted with the model explained by Prager and Heidemann,24 which is based on linear coupling of the rotor to individual phonons or a spectrum thereof. This model takes the phonon-coupling into account by two terms, the breathing and the shaking term, which shift the tunnelling frequency in opposite directions.24 However, these measurements were performed on single crystals and microcrystalline powder samples, respectively, where we do not expect a distribution of rotation barriers due to different local environments and where a description in terms of phonon-coupling is appropriate. In glasses, low-temperature dynamics of the matrix must be described in terms of local modes rather than phonons.58 Therefore, it is not reasonable to directly compare the temperature dependence of the tunneling ESEEM investigated here with the aforementioned spin systems. If the general features of the phonon-coupling model24 apply analogously to local modes in glasses, our results suggest dominance of the shaking term below 60 K. This term modulates the orientation of the rotational potential and reduces tunnel splitting, corresponding to an apparently higher barrier. Interpreting the results above 60 K in terms of the phonon-coupling model would mean that the so-called breathing term dominates. This term modulates the strength of the rotation potential and causes an increase in tunnel frequency, corresponding to an apparently lower barrier. Below we shall discuss a different possible explanation for the behavior above 60 K. For the individual temperature-dependent distributions of H-mNOHex in OTP the sudden decrease in the average rotation barrier already appears at temperatures higher than 50 K (Fig. 5a). For H-mNOHex in OTP and dOTP, this drop is observed at different temperatures. This difference might originate from the longer Tm in case of the deuterated matrix, which enables a clearer separation of the tunneling ESEEM and matrix-induced decoherence contribution in time, as discussed above. The negative slope of V3,av(T) above the drop-off temperature is almost identical for all fitting approaches, which indicates that the same change in relaxation behavior occurs independent of the matrix. Therefore, this relaxation process is nitroxide-related and is probably linked to the methyl groups slowly starting to rotate with increasing temperature (moving towards the borderline regime defined by Soetbeer et al.4). Between 60 K and 80 K, we suggest an intermediate regime to describe the decoherence behavior as we observe a competition between quantum-mechanical and classical methyl group rotation, given that the characteristic frequencies of both processes match the anisotropic electron-methyl proton hyperfine coupling differences.8,59 Additionally, the scaling of the methyl tunneling ESEEM contribution becomes unreasonable for temperatures above 60 K (see Fig. S4–S7 in ESI†), which underlines that at these temperatures the separation of the methyl tunneling contribution from the matrix relaxation contribution is no longer feasible. Hence, for higher temperatures another model is needed to describe the decoherence characterization of nitroxides with methyl groups since the tunneling parameters of our model become unreliable.
To further evaluate the temperature behavior of the methyl tunneling ESEEM exhibited at low temperatures, we compare experimental data of the nitroxide with protonated (H-mNOHex) and deuterated (D-mNOHex, Fig. 3b) methyl groups in OTP. Deuteration of the methyl groups leads to an increase of the moment of inertia I of the rotor (because the rotor becomes heavier) which reduces the energy splitting of the ro-librational states r of the rotor (see Fig. 1)22 and introduces nuclear quadrupole coupling to the spin Hamiltonian.60 Assuming that the rotation barrier remains the same upon deuteration of the methyl groups, the DFT-calculated constrained rotation barrier for methyl group m = 1, given in Table 1, results in a tunneling frequency of 260 kHz and 71 Hz for protonated and deuterated CH3-groups, respectively. Therefore, the methyl tunneling ESEEM becomes negligible for deuterated geminal methyl groups in nitroxides since frequencies in the Hz-range are not resolved on the time scale of the pulsed EPR-experiment due to dominance of decoherence induced by matrix nuclei. Comparing the data from these two nitroxides allows us to validate our findings of the different temperature regimes. Therefore, we fitted the two-pulse ESEEM data of H-mNOHex and D-mNOHex with a SE model, as if the relaxation only depends on the matrix process at low temperature. Subsequently, we applied a Hamming window to the fit residual and performed a spectral analysis of the residual oscillation by Fourier transformation. We illustrate the results in Fig. S11 (ESI†). For D-mNOHex, the SE model is suitable in the temperature range between 10 K and 50 K, showing that the dominating relaxation process is matrix-driven. As expected, the spectrum of the fit residual contains both proton and deuterium ESEEM frequencies. In addition, we find a small low-frequency contribution around 1 MHz which becomes larger for temperatures between 50 K and 70 K, but almost disappears at 80 K. For H-mNOHex, the SE model describes the Hahn decay traces between 10 K and 60 K insufficiently, resulting in a strongly oscillating fit residual. Its spectrum reveals a contribution at the nuclear ESEEM frequency of protons. Moreover, in the temperature range between 10 K and 50 K, a low-frequency contribution is not fitted by the SE model, which has a constant large intensity over the mentioned temperature range. We attribute this contribution to tunneling ESEEM of the protonated methyl groups of H-mNOHex, since its peak lies in the frequency range consistent with the extracted rotation barrier distributions. Above 50 K, this low-frequency peak becomes very similar for H-mNOHex and D-mNOHex, implying that its origin is no longer methyl tunneling. This semi-quantitative analysis validates the discussed temperature range in which methyl tunneling ESEEM can be observed and analyzed in a protonated matrix. We expect the same observations for H-mNOHex and D-mNOHex in a deuterated matrix.
5 Conclusion
We have introduced the MQR model to describe the low-temperature Hahn echo/two-pulse ESEEM data of pyrroline-nitroxides featuring two pairs of geminal methyl groups in glassy matrices. Besides the slow, matrix-driven decoherence, the MQR framework models the faster signal contribution in terms of methyl tunneling ESEEM of M methyl groups coupled to an electron spin. Moreover, the model takes into account different local environments present in a glassy system by a distribution of rotation barriers representing the methyl group ensemble in the sample. Thereby, we successfully inferred rotation barrier distributions related to the methyl tunneling ESEEM contribution in the two-pulse ESEEM data of H-mNOHex under different experimental conditions.Firstly, we have demonstrated the independence of the tunneling ESEEM signal from the magnetic field and matrix deuteration at low temperatures, both of which are characteristic for the tunneling process. We have shown that the inferred distribution of rotation barriers must be interpreted with care, since methyl tunneling is not the only process that induces ESEEM-related features in the Hahn echo decay. For a robust inference of the rotation barrier distributions, we recommend matrix deuteration as this measure prolongs the phase memory time, thereby prohibiting a damping of the methyl tunneling ESEEM associated with the faster matrix-induced decoherence observed in case of a protonated glass former.
Secondly, we have investigated the temperature dependence of methyl tunneling between 10 K and 80 K by comparing extracted rotation barrier distributions from two-pulse ESEEM data. Comparison of the phase memory times obtained from fits with the SE, SSE and the MQR model for the Hahn echo decay signal showed that Tm extracted with the MQR model coincided with Tm,2 of the SSE model up to ∼50 K and started agreeing with the SE model at temperatures above 50 K. Upon increasing the temperature from 10 K to 60 K, a narrowing of the Gaussian rotation barrier distribution was observed, which we attributed to an increase in free volume in the glassy matrix. Future investigations will need to assess the sensitivity of the tunneling ESEEM, i.e. of the rotation barrier distribution, to its local environment, in particular regarding the influence of different glass formers. Moreover, for temperatures above 50 K and 60 K for protonated and deuterated matrix, respectively, a sudden decrease of the rotation barriers occurs, which we rationalized as a crossover regime from quantum mechanical to classical rotation of the methyl groups. This temperature behavior differs from the one observed in previous studies on crystalline samples,16,52 indicating different coupling of methyl tunneling to matrix vibrations in glassy samples. In the temperature range between 10 K and 50 K, where the methyl tunneling ESEEM is an important contribution to the Hahn echo/two-pulse ESEEM signal, we validated the MQR-based assessment by an independent, semi-quantitative approach. To this end, we performed a spectral analysis of the fit residual when describing the Hahn echo decay by an SE model.
We believe methyl tunneling ESEEM to be an interesting phenomenon for applications beyond relaxation studies. The title of this work already implies that methyl tunneling contributes to the observed electron spin decoherence of nitroxides but methyl tunneling ESEEM itself is a coherent phenomenon which contains valuable information of the methyl groups' local environment. At sufficiently low temperatures the tunneling frequency of quantum rotors is theoretically tractable and detectable by coherent manipulation of the electron spin with pulsed ESEEM experiments. Therefore, we do not believe the fast decaying contribution in the two-pulse Hahn echo signal to be attributable to a decoherence process of the spin system. In the future, a mathematical framework should be established to interpret methyl tunneling ESEEM in other experimental techniques that coherently excite and detect this quantum-mechanical effect. Since the methyl groups' rotation barriers are sensitive to local environment changes, future studies based on tunneling ESEEM would offer access to new exciting types of short range structural information on nitroxide spin-labelled macromolecules such as proteins.
Author contributions
Conceptualization: AE, JS, GJ. Methodology: AE. Experiments: AE, JS. Data analysis: AE. Visualization: AE. Software: AE, LFI. Supervision: DK, GJ. Writing – original draft: AE. Writing – review and editing: AE, JS, LFI, DK, GJ.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Swiss National Science Foundation (SNSF200020_188467) and by the Research Commission of ETH Zurich (ETH-35 18-2). JS thanks the Günthard Foundation for a PhD scholarship.Notes and references
- I. Brown, Time Domain Electron Spin Resonance, Wiley, 1979, vol. 6, pp. 195–229 Search PubMed.
- R. Ward, A. Bowman, E. Sozudogru, H. El-Mkami, T. Owen-Hughes and D. G. Norman, J. Magn. Reson., 2010, 207, 164–167 CrossRef CAS PubMed.
- H. El Mkami, R. Ward, A. Bowman, T. Owen-Hughes and D. G. Norman, J. Magn. Reson., 2014, 248, 36–41 CrossRef CAS PubMed.
- J. Soetbeer, M. Hülsmann, A. Godt, Y. Polyhach and G. Jeschke, Phys. Chem. Chem. Phys., 2018, 20, 1615–1628 RSC.
- K. Nakagawa, M. B. Candelaria, W. W. C. Chik, S. S. Eaton and G. R. Eaton, J. Magn. Reson. (1969), 1992, 98, 81–91 CrossRef CAS.
- V. Kathirvelu, C. Smith, C. Parks, M. A. Mannan, Y. Miura, K. Takeshita, S. S. Eaton and G. R. Eaton, Chem. Commun., 2009, 454–456 RSC.
- A. Rajca, V. Kathirvelu, S. K. Roy, M. Pink, S. Rajca, S. Sarkar, S. S. Eaton and G. R. Eaton, Chem. – Eur. J., 2010, 16, 5778–5782 CrossRef CAS PubMed.
- A. Zecevic, G. R. Eaton, S. S. Eaton and M. Lindgren, Mol. Phys., 1998, 95, 1255–1263 CrossRef CAS.
- S. M. Jahn, E. R. Canarie and S. Stoll, J. Phys. Chem. Lett., 2022, 13, 5474–5479 CrossRef CAS PubMed.
- S. Huang, J. T. Paletta, H. Elajaili, K. Huber, M. Pink, S. Rajca, G. R. Eaton, S. S. Eaton and A. Rajca, J. Org. Chem., 2017, 82, 1538–1544 CrossRef CAS PubMed.
- J. Soetbeer, L. F. Ibáñez, Z. Berkson, Y. Polyhach and G. Jeschke, Phys. Chem. Chem. Phys., 2021, 23, 21664–21676 RSC.
- G. Jeschke, J. Magn. Reson. Open, 2023, 14–15, 100094 CrossRef.
- W. Yang and R.-B. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085315 CrossRef.
- E. R. Canarie, S. M. Jahn and S. Stoll, J. Phys. Chem. Lett., 2020, 11, 3396–3400 CrossRef CAS PubMed.
- A. R. Sørnes and N. P. Benetis, Chem. Phys. Lett., 1998, 287, 590–596 CrossRef.
- M. Šimėnas, D. Klose, M. Ptak, K. Aidas, M. Maczka, J. Banys, A. Pöppl and G. Jeschke, Sci. Adv., 2020, 6, eaba1517 CrossRef PubMed.
- F. Torricella, A. Pierro, E. Mileo, V. Belle and A. Bonucci, Biochim. Biophys. Acta, Proteins Proteomics, 2021, 1869, 140653 CrossRef CAS PubMed.
- C. S. Klug, M. T. Lerch and J. B. Feix, Nitroxides, The Royal Society of Chemistry, 2021, pp. 392–419 Search PubMed.
- T. Schmidt and G. M. Clore, Chem. Commun., 2020, 56, 10890–10893 RSC.
- T. Schmidt, J. Jeon, W.-M. Yau, C. D. Schwieters, R. Tycko and G. M. Clore, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2122308119 CrossRef CAS PubMed.
- M. Kveder, B. Rakvin and J. You, J. Chem. Phys., 2019, 151, 164124 CrossRef PubMed.
- R. M. Dimeo, Am. J. Phys., 2003, 71, 885–893 CrossRef CAS.
- A. J. Horsewill, Prog. Nucl. Magn. Reson. Spectrosc., 1999, 35, 359–389 CrossRef CAS.
- M. Prager and A. Heidemann, Chem. Rev., 1997, 97, 2933–2966 CrossRef CAS PubMed.
- S. A. Dzuba, K. M. Salikhov and Y. D. Tsvetkov, Chem. Phys. Lett., 1981, 79, 568–572 CrossRef CAS.
- A. J. Moreno, A. Alegría, J. Colmenero and B. Frick, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 5983–5986 CrossRef CAS.
- A. J. Moreno, A. Alegría and J. Colmenero, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 060201 CrossRef.
- A. J. Moreno, A. Alegria, J. Colmenero, R. Mukhopadhyay and B. Frick, J. Non-Cryst. Solids, 2001, 287, 242–245 CrossRef CAS.
- R. M. Dimeo and D. A. Neumann, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 014301 CrossRef.
- R. M. Dimeo, D. A. Neumann, Y. Glanville and D. B. Minor, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 104201 CrossRef.
- J. Colmenero, R. Mukhopadhyay, A. Alegría and B. Frick, Phys. Rev. Lett., 1998, 80, 2350–2353 CrossRef CAS.
- S. Khazaei and D. Sebastiani, J. Chem. Phys., 2017, 147, 194303 CrossRef PubMed.
- G. Jeschke, Appl. Magn. Reson., 2021, 635–651 Search PubMed.
- F. Apaydin and S. Clough, J. Phys. C: Solid State Phys., 1968, 1, 932 CrossRef.
- L. G. Rowan, E. L. Hahn and W. B. Mims, Phys. Rev., 1965, 137, A61–A71 CrossRef.
- W. B. Mims, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 5, 2409–2419 CrossRef.
- Y. Polyhach, E. Bordignon, R. Tschaggelar, S. Gandra, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2012, 14, 10762–10773 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- MATLAB, (R2019b), The MathWorks Inc., Natick, Massachusetts, 2018 Search PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- P. C. Hansen, M. E. Kilmer and R. H. Kjeldsen, BIT Numer. Math., 2006, 46, 41–59 CrossRef.
- T. H. Edwards and S. Stoll, J. Magn. Reson., 2018, 288, 58–68 CrossRef CAS PubMed.
- B. W. Rust and D. P. O'Leary, Inverse Probl., 2008, 24, 034005 CrossRef.
- L. Fábregas-Ibáñez, G. Jeschke and S. Stoll, J. Magn. Reson., 2022, 339, 107218 CrossRef PubMed.
- L. Fábregas Ibáñez, G. Jeschke and S. Stoll, Magn. Reson., 2020, 1, 209–224 CrossRef PubMed.
- A. J. Moreno, A. Alegría, J. Colmenero and B. Frick, Phys. B: Condens. Matter, 2000, 276–278, 361–362 CrossRef CAS.
- A. J. Horsewill, R. M. Green and A. M. Alsanoosi, Quantum Aspects of Molecular Motions in Solids, Berlin, Heidelberg, 1987, pp. 28–32 Search PubMed.
- W. Schnauss, F. Fujara and H. Sillescu, J. Chem. Phys., 1992, 97, 1378–1389 CrossRef CAS.
- S. A. Lusceac, C. Koplin, P. Medick, M. Vogel, N. Brodie-Linder, C. LeQuellec, C. Alba-Simionesco and E. A. Rössler, J. Phys. Chem. B, 2004, 108, 16601–16605 CrossRef CAS.
- J. N. Andrews and A. R. J. P. Ubbelohde, Proc. R. Soc. London, Ser. A, 1955, 228, 435–447 CAS.
- W. Ping, D. Paraska, R. Baker, P. Harrowell and C. A. Angell, J. Phys. Chem. B, 2011, 115, 4696–4702 CrossRef CAS PubMed.
- S. Clough and J. R. Hill, J. Phys. C-Solid State Phys., 1974, 7, L20–L21 CrossRef CAS.
- G. Jeschke and Y. Polyhach, Phys. Chem. Chem. Phys., 2007, 9, 1895–1910 RSC.
- A. Barbon, M. Brustolon, A. L. Maniero, M. Romanelli and L.-C. Brunel, Phys. Chem. Chem. Phys., 1999, 1, 4015–4023 RSC.
- D. Turnbull and M. H. Cohen, J. Chem. Phys., 1961, 34, 120–125 CrossRef CAS.
- R. P. White and J. E. G. Lipson, Macromolecules, 2016, 49, 3987–4007 CrossRef CAS.
- Q. Ma, Y. Wang, Y. Gu, N. Zhao, S. Luo, L. Wang, Y. Hu and J. Fang, AIP Adv., 2022, 12, 015207 CrossRef.
- H. R. Schober, J. Non-Cryst. Solids, 2011, 357, 501–505 CrossRef CAS.
- Y. D. Tsvetkov and S. A. Dzuba, Appl. Magn. Reson., 1990, 1, 179 CrossRef CAS.
- S. Stoll and D. Goldfarb, eMagRes, American Cancer Society, 2017, pp. 495–510 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01299a |
| This journal is © the Owner Societies 2023 |




