Efficient automatic construction of atom-economical QM regions with point-charge variation analysis

Abstract

The setup of QM/MM calculations is not trivial since many decisions have to be made by the simulation scientist to achieve reasonable and consistent results. The main challenge to be tackled is the construction of the QM region to make sure to take into account all important parts of the adjacent environment and exclude less important ones. In our previous work [F. Brandt and Ch. R. Jacob, Systematic QM Region Construction in QM/MM Calculations Based on Uncertainty Quantification, J. Chem. Theory Comput., 2022, 18, 2584–2596.], we introduced the point charge variation analysis (PCVA) as a simple and reliable tool to systematically construct QM regions based on the sensitivity of the reaction energy with respect to variations of the MM point charges. Here, we assess several simplified variants of this PCVA approach for the example of catechol O-methyltransferase and apply PCVA for another system, the triosephosphate isomerase. Furthermore, we extend its scope by applying it to a DNA system. Our results indicate that PCVA offers an efficient and versatile approach of the automatic construction of atom-economical QM regions, but also identify possible pitfalls and limitations.

---

1 Introduction

When studying enzymes and their catalytic mechanisms, experimental approaches often reach their limit and the underlying question needs to be tackled computationally. Since enzymes are very large molecular structures with thousands of atoms and the system size additionally increases by adding substrates, co-factors, and solvent molecules, efficient approaches are needed which provide a sufficient accuracy at low computational effort. Multilevel approaches such as quantum mechanics/molecular mechanics (QM/MM) calculations¹ meet the aforementioned requirements. They divide the target system into at least two subsystems, a small one usually including the active site or other interesting parts of the enzyme, which is calculated on a quantum-mechanical (QM) level, and a large one containing the remaining parts of the enzyme and the solvent, treated using molecular mechanics (MM).^2–4

Unfortunately, QM/MM is far away from being an easy-to-use black box approach. Setting up a reasonable QM/MM calculation requires numerous considerations by the scientist, which can result in significantly different outcomes. Therefore, systematic schemes for automating such decisions are desperately needed (for a recent review, see ref. 5). Most important is the choice of a suitable QM region. It should be defined such that it covers all desired effects in the calculation and is at the same time as small as possible. The choice of the QM region determines both the accuracy of a QM/MM calculation and the associated computational effort. Thus, it has been subject to numerous studies regarding the convergence of energies, charges, and other properties with changes in the QM region composition.^6–10

Constructing a suitable QM region requires more than including residues by their distance from the active site, as such a purely distance-based approach does not guarantee to take into account all important residues on the one hand and to exclude residues which only have a small effect on the quantity of interest on the other hand. For this reason, several different schemes have been proposed which aim at obtaining a medium-sized, atom-economical QM region that provides reliable QM/MM reaction energies. These methods include free energy perturbation analysis,¹¹ charge deletion analysis (CDA),^12,13 charge shift analysis (CSA),⁹ Fukui shift analysis (FSA),¹⁴ self-parametrizing system-focused atomistic models (SFAM)¹⁵ as well as a method based on protein sequence/structure evolution.¹⁶

Previously, we developed an approach for systematic QM region construction, the point charge variation analysis (PCVA). Compared to the well-investigated CSA and FSA it is computationally cheaper but equally reliable.¹⁷ PCVA is based on the variation of MM point charges for the amino acids and the subsequent evaluation of (reaction) energies to identify the residues with the highest electrostatic effect on the QM region. For this, only a single geometry optimization for the system including a minimal QM region (ideally substrates only) is required, followed by one single point calculation for each amino acid in the enzyme. Afterwards, the resulting sensitivities for each residue are correlated to the respective active site-residue distance, which results in an indicator ranking. Based on this ranking, an atom-economical QM region (defined at 16 residues by Kulik et al.⁹) can be constructed.

PCVA worked well for the catechol O-methyltransferase (COMT) compared to the CSA and FSA results of Kulik and co-workers^9,14 with much lower computational effort for the construction of the QM region. In this work, we want to address whether additional simplifications or variations can be introduced to further decrease computational cost without loss of accuracy. In addition, we will investigate the ability of PCVA to reasonably work for other systems than COMT. For this, we apply the approach to the triosephosphate isomerase (TIM) which has been a subject to CDA in earlier work,¹² and we extend PCVA to the use for a non-protein system, namely a DNA system which has been extensively investigated concerning QM/MM energy convergence by Roßbach and Ochsenfeld.¹⁸

2 Point charge variation analysis for automatic QM region construction

Previously, we developed PCVA for the automatic construction of QM regions.¹⁷ In the following, we will briefly recall the main features of PCVA. It is based on uncertainty quantification^19,20 and considers the reaction energy as the main quantity of interest (QoI) in the investigation of enzymatic reactions,

ΔE^reaction_QM/MM = E_QM/MM(product) − E_QM/MM(reactants). (1)

Here, the QM/MM energy of the reactants or product, respectively, can be expressed as

E_QM/MM = E^emb_QM(A,V_B) + E_MM(B) + E_int,ne(A,B), (2)

in which E^emb_QM(A,V_B) represents the embedded QM energy of subsystem A including the electrostatic interaction between the two subsystems, E_MM(B) is the MM energy of subsystem B, and E_int,ne(A,B) refers to the non-electrostatic interaction between A and B.

The QM/MM reaction energy is subjected to a local sensitivity analysis^19–21 with respect to collective variations Δq_MM of the MM point charges. The collective variations themselves depend on the size of variation Δq and are chosen such that the sum of the MM point charges is preserved .

We previously introduced two types of collective point-charge variations.¹⁷ In the first, which we referred to as global PCVA (gPCVA), the MM charges of all protein atoms are varied simultaneously by an equal magnitude Δq, while all solvent MM charges are changed equally to preserve the total system charge. This can be expressed as

where N^protein_B and N^solvent_B are the numbers of protein and solvent atoms in subsystem B, respectively. This approach allows us to estimate the overall sensitivity of the QM/MM reaction energy to point-charge variations.

The second type, called single amino acid PCVA (saaPCVA), aims at assessing the effect of individual amino acid residues on the QM/MM energy. In this case, variations of the MM charges of the ith amino acid are considered individually,

Here, N_aa,i represents the number of atoms in the ith amino acid and N_B is the number of all MM atoms in the system. While the charge preservation limits gPCVA to be applied in solvated systems only, saaPCVA can also be used for calculations in vacuum as it is sufficient to distribute the counter charge only over the remaining MM point charges of all other amino acids.

To assess the effect of these collective point-charge variations on the QoI, we consider the derivative of the QM/MM reaction energy with respect to these collective point-charge variations, i.e.,

For the automatic construction of QM regions based on saaPCVA, we introduced the QM region indicator,

Θ_i = δ_iE_QM/MM/COM_i, (6)

where δ_iE_QM/MM is the saaPCVA sensitivity found for the i-th amino acid and COM_i is the center-of-mass distance between the i-th amino acid and the active center (i.e., a minimal QM region). This indication gives a higher weight to amino acids that are close to the active center. QM regions are then constructed by including a chosen number of amino acids with the highest Θ_i. A flowchart of how this method is realized computationally can be found in the ESI† (Fig. S1).

The construction of QM regions with saaPVCA only requires QM calculations with a minimal QM region. To further minimize its computational effort, we previously established additional simplifications.¹⁷ First, we showed that it is sufficient to consider only the QM energies and to neglect the MM energies, since only the QM energy significantly changes between reactants and products, while the MM energies remains mainly constant. Second, the evaluation of different simplification strategies for saaPCVA revealed that the evaluation of the QM energy sensitivity only for the reactant structure (or the product structure) is sufficient in enzymatic reactions and makes it obsolete to assess the reaction energy, i.e.,

The derivatives necessary to calculate this sensitivity are evaluated numerically and it was shown that using a forward two-point finite difference formula delivers reasonable results. To ensure comparability to previous results, the analysis is performed consistently for a variation of −0.5 per amino acid. For a system containing 214 amino acids (as for COMT considered below) treated according to the saaPCVA scheme (Fig. S1, ESI†) with a one-sided variation of −0.5 for the reactant only, 214 single point calculations with a minimal QM region are needed. These can be completed on a short time scale compared to QM/MM geometry calculations with larger QM regions. Further information on timings can be found in Table S5 (ESI) of ref. 17.

3 Assessment of further PCVA schemes for COMT

3.1 System

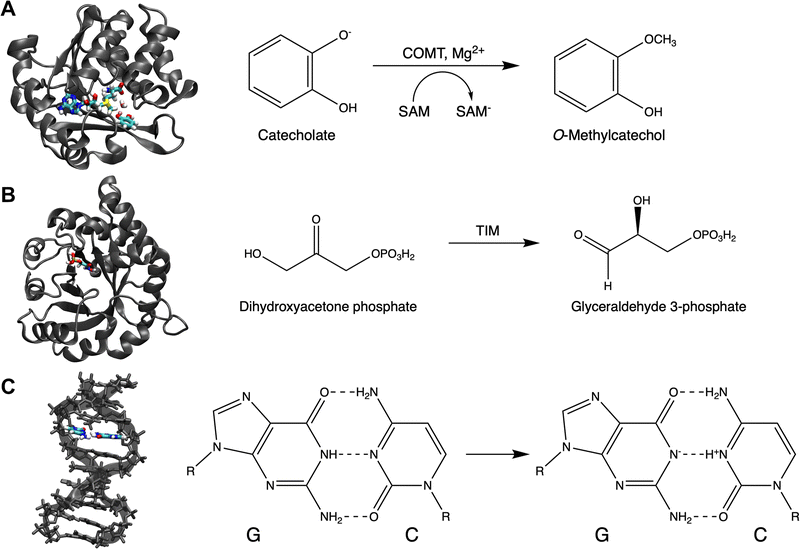
In the past, saaPCVA has been applied exclusively for a minimal QM region containing substrates only without covalent bonds crossing the QM–MM border. In this work, we additionally apply it to a QM region containing the ligands and additional catalytic active side residues, as well as to a QM region without ligands only consisting of catalytic amino acids. Furthermore, we will inspect whether one gets reasonable results performing saaPCVA for an enzyme structure without solvation shell, and even directly starting from the available crystal structures without pre-processing to save computational effort and time. These simplifications and variants will be further discussed below.

The system used to test further PCVA schemes is the catechol O-methyltransferase (COMT),²² which was also targeted in the work of Kulik and co-workers regarding systematic QM region determination⁹ and in our previous work on PCVA.¹⁷ The structural monomer model, which is based on the crystal structure (PDB: 3BWM) and processed as described in the Computational Details, contains the neutral S-adenosyl methionine (SAM), the catecholate anion (CAT), and the catalytically active Mg²⁺ (see Fig. 1A). These three ligands also represent the minimal QM region used in saaPCVA originally, while in the assessment of larger QM regions a water molecule close to Mg²⁺ is additionally considered (see Fig. 1A).

Fig. 1 Representation of the three different test systems with the minimal QM regions (substrates or reacting bases, respectively) highlighted and corresponding reaction schemes. (A) COMT monomer with SAM, CAT, Mg²⁺ and a water molecule. (B) TIM with DHAP. (C) DNA double helix.

3.2 Results

In addition to the standard saaPCVA approach established in our previous work¹⁷ and referred to as standard in the following, we tested six further variants (see Table 1). For standard, the saaPCVA calculations are performed based on the equilibrated starting structure of COMT solvated in water. The solvent water is held fixed during subsequent optimizations with a minimal QM region containing SAM, CAT and Mg²⁺ (see Fig. 1A).

Table 1 Overview on the seven different saaPCVA variants regarding preparation prior to saaPCVA runs, composition of QM region, solvent environment and constrained regions in the QM/MM optimization. eq. – equilibration, opt. – optimization, lig. – ligands, act. res. – active site residues, cryst. str. – crystal structure

Variant	Preparation	QM region	Environment	Constraints
Standard	MM eq. + QM/MM opt.	Ligands	TIP3P water	Solvent
Active	MM eq. + QM/MM opt.	lig. + 5 act. res.	TIP3P water	Solvent
No lig	MM eq. + QM/MM opt.	5 act. res.	TIP3P water	Solvent
Vac	MM eq. + QM/MM opt.	Ligands	Vacuum	None
Vac fix	MM eq. + QM/MM opt.	Ligands	Vacuum	MM atoms
Cryst	QM/MM opt. of cryst. str.	Ligands	Vacuum	None
Cryst fix	QM/MM opt. of cryst. str.	Ligands	Vacuum	MM atoms

---

Based on standard, we added five additional active site residues to the minimal QM region (ASP140, LYS143, ASP168, ASN169 and GLU198²³) to assess the effect of a larger QM region including ligands and catalytically important residues on the saaPCVA results (referred to as active). Similarly, we tested the no lig approach, in which the aforementioned active site residues form the QM region, but the ligands are completely removed from the system to investigate whether ligands are crucial for PCVA or whether there is no need to include them, which can save efforts for parametrizing the ligands.

The further four saaPCVA schemes have in common that they are performed in vacuum, which means the solvation shell is completely removed from the system to decrease the computational cost. As for the standard variant, the QM region contains the three ligands only. In the first scheme (vac), we simply removed all water molecules from the equilibrated COMT starting structure and performed saaPCVA based on the resulting vacuum system. Since in this case the whole system is geometry-optimized in vacuum without a fixed water environment we additionally tested an approach with a completely fixed MM protein environment (vac fix), i.e., only the QM region is optimized. The two remaining schemes (cryst and cryst fix) are similar to the aforementioned ones, except for the fact that the optimization is directly performed based on the crystal structure (PDB: 3BWM) without the previous equilibration steps to assess the need for pre-processing.

All these seven different saaPCVA calculations were performed according to the established protocol (see Fig. S1, ESI†) and evaluated in the same way assessing sensitivities and indicators for each amino acid (see Fig. S2–S8, ESI†). Here, it is important to mention that residues already included in the minimal QM region (for no lig and active) are not considered in the sensitivity and indicator calculation. Additionally, these residues are always included in the construction of atom-economical 16-residue QM regions. The compositions of the seven different corresponding QM regions are given in Table S2 (ESI†).

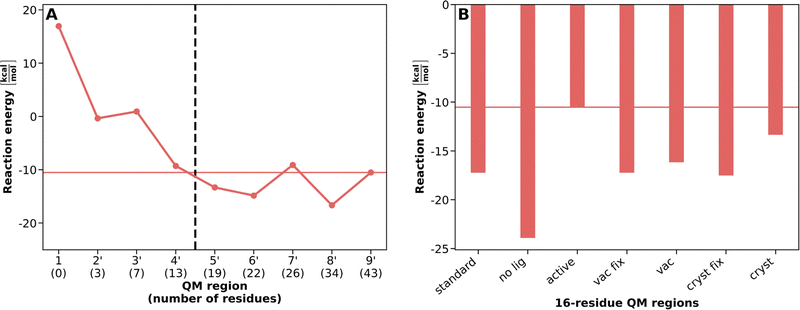
Fig. 2A presents the VDD ligand charges and Fig. 3A the reaction energies for PCVA-constructed QM regions of increasing size as already shown in ref. 17. An overview of the residues present in each of these QM regions is given in Table S1 (ESI†). For the assessment of atom-economical QM regions based on the different PCVA schemes, we consider the results of the largest QM region (9′, containing 43 amino acid residues) constructed by standard saaPCVA (ligands as minimal QM region, equilibrated structure in water) as our best estimate for the comparison with the constructed atom-economical, 16-residue QM regions.

Fig. 2 QM ligand Voronoi charge convergence for QM regions constructed based on PCVA. Best estimate results (corresponding to QM region 9′) are indicated by a solid horizontal line. (A) Convergence of Mg²⁺ (blue), SAM (magenta) and CAT (yellow) VDD charges with increasing QM region size (adapted from ref. 17). (B) Corresponding ligand charges of atom-economical 16-residue QM regions (indicated by dashed vertical line in A) constructed using different simplified PCVA variants.

Fig. 3 QM/MM reaction energy convergence for QM regions constructed based on PCVA. Best estimate results (corresponding to QM region 9′) are indicated by a solid horizontal line. (A) Convergence of the QM/MM reaction energy ΔE^reaction_QM/MM for the methyl transfer reaction in COMT with increasing QM region size (adapted from ref. 17). (B) Corresponding reaction energies of atom-economical 16-residue QM regions (indicated by dashed vertical line in A) constructed using different simplified PCVA variants.

To evaluate the suitability of the different PCVA schemes, we compare the VDD charges for SAM, CAT, and Mg²⁺ as well as the QM/MM reaction energy. It is important to note that independently of the underlying PCVA scheme, after the construction of a QM region, geometry optimizations were performed for reactant and product starting from an equilibrated structure in water. We compare the 16-residue QM regions constructed using the newly introduced variants to the QM regions of increasing size constructed by the standard saaPCVA approach as applied in ref. 17 (see Fig. 2B and 3B) to evaluate their performance.

Regarding the VDD charges (Fig. 2), there are only very small differences between the different PCVA variants for the Mg²⁺ and CAT charges, which means the convergence behavior is reflected in the 16-residue QM region results. However, for SAM there are significant differences between the variants. The standard as well as all vac and cryst 16-residue results represent the charge convergence for medium-sized QM regions up to 22 residues, but are about 0.2 lower than the best estimate. In contrast, especially the active but also the no lig charges are much closer to the best estimate because important SAM-coordinating residues are already included from the beginning and do not have to be detected by PCVA. Consequently, including active site residues into the minimal QM region prior to PCVA may improve charges in constructed atom-economical QM regions for large ligands with a strong ability of charge redistribution.

Regarding the reaction energy (Fig. 3), vac, vac fix, and cryst fix deliver results similar to standard PCVA at about −17 kcal mol⁻¹, which is about 6 kcal mol⁻¹ below the best estimate (−10.5 kcal mol⁻¹) but agrees reasonably with the large QM region regime (e.g. 8′: −17 kcal mol⁻¹). Surprisingly, the cryst PCVA energy delivers a better energy with about −13 kcal mol⁻¹ compared to the best estimate. This can be a result of a specific combination of amino acids in the QM region. Including active site residues in the PCVA approach (active) leads to the best result in full agreement with the best estimate energy, which again implies improvements of this approach compared to standard. The QM region constructed by no lig PCVA delivers the worst reaction energy (about −24 kcal mol⁻¹), which indicates ligands being crucial to be included in the minimal QM region, as they affect the importance of specific residues for a consistent QM region.

Table S3 (ESI†) compares the residues included in atom-economical QM regions for the different simplified PCVA schemes. Here, detailed information is given about the indicator rank of each amino acid present in one of the constructed 16-residue QM regions for each scheme. For example, the no lig PCVA misses several crucial amino acids such as GLY65, ALA66, GLU89 or HIS141 and detects other amino acids like LEU166 or SER195, which explains the differences especially in the reaction energy compared to the other approaches. The active as well as all the vac and cryst schemes perform similar to each other, which could also be seen for the energies and charges. Most of the time, if one approach misses a certain important amino acid its rank is still is close to 16.

In general, we showed that performing saaPCVA in a system without water molecules and furthermore with starting by directly optimizing a crystal structure without previous processing delivers reasonable results. This makes the already simple standard saaPCVA approach for constructing QM regions more easily applicable. Our results indicate that it is crucial to include the substrates in the minimal QM region that is used as basis of saaPCVA. In addition to that, extra active site residues may be included to improve the results especially concerning consistent ligand charges. Nevertheless, the application of saaPCVA with a minimal, substrates-only QM region delivers results with sufficient accuracy if the extension of the QM region is not applicable due to computational restrictions or if there is no reliable reference for the active site residues to be included.

4 Application of PCVA to triosephosphate isomerase

4.1 System

The triosephosphate isomerase (TIM) is crucial for all organisms performing glycolysis. It catalyzes the reaction from dihydroxyacetone phosphate (DHAP) to glyceraldehyde 3-phosphate (GAP) and is known for its distinctive α/β barrel structure called TIM barrel²⁴ (see Fig. 1B). The starting monomer structure is based on the protein crystal structure 7TIM²⁵ from the PDB with a co-crystallized phopsphoglycolohydroxamic acid (PGH), which is a well-known TIM inhibitor. To get reactant and product starting structures PGH was replaced with DHAP and GAP, respectively, and the structures were processed as described in Section 6. For cryst saaPCVA, the initial structure with PGH was used. The minimal QM region contains only the corresponding ligand, either PGH, DHAP or GAP.

TIM was used as target for the first attempts of systematic QM region construction in 1991 by Bash et al.,¹² who used a technique later referred to as charge deletion analysis (CDA).¹³ Here, we will compare the CDA results with our PCVA approach and discuss advantages and disadvantages of both methods.

4.2 Results

First, the QM region size was radially increased around the substrate in 0.5 Å steps to later compare this distance-based approach with the systematic PCVA approach. The composition of each QM region can be found in Table S4 (ESI†). The convergence of the DHAP VDD charge and of the reaction energy with increasing QM region size is shown in Fig. 4A and C, respectively. The DHAP charge drops significantly from about 0 to −0.28 with region 4 and then again slightly increases for regions 6 and 7, but in the end again converges to about −0.28. The reaction energy converges starting with region 3 to around 9 kcal mol⁻¹, which is in very good agreement with the results of Bash et al. of about 8 kcal mol⁻¹.¹² Only for region 7, the reaction energy represents an outlier with about 25 kcal mol⁻¹, which can be the result of a specific combination of amino acids.

Fig. 4 QM/MM convergence for QM regions in TIM constructed with the exclusively distance-based approach and corresponding global point charge variation analysis. Best estimate results (corresponding to QM region 9) are indicated by solid horizontal lines. (A) Convergence of DHAP VDD charges with increasing QM region size. Grayscale lines indicate the ligand charges for varied MM point charges. (B) Sensitivity of the VDD charges to global point charge variations Δq^tot_MM,I. (C) Reaction energies ΔE^reaction_QM/MM for the interconversion reaction from DHAP to PGH in TIM with increasing QM region size. Grayscale lines indicate the change in reaction energy with varied MM point charges. (D) Sensitivity δΔE^reaction_QM/MM of the reaction energy to global point charge variations Δq^tot_MM,I.

In addition, we applied the global PCVA approach (gPCVA) to the system, in which all MM protein atom charges are varied simultaneously by a small value and the system charge is held constant by adding counter charges to all MM water molecule atoms. Previously, we found that this can give an indication of the accuracy of the resulting charges and reaction energies.¹⁷ The sensitivity of the DHAP VDD charge strongly increases until region 4. This behavior has also be seen for COMT and is a result of the increase in charge distribution opportunities inside the QM region. Afterwards, a slightly decreasing trend in the sensitivity can be observed, which corresponds to the expected behavior. For the reaction energy sensitivity we observe an increase with the first two residues added (region 2) and a subsequent constant decrease. Although region 7 leads to a higher reaction energy compared to similar-sized-regions, its sensitivity fits into the decreasing behavior with larger QM regions, i.e., this outlier is not detected by the gPCVA.

The standard and cryst saaPCVA calculation were performed analogously to those of COMT and the subsequent evaluation again delivered sensitivities and QM region indicators for each amino acids (see Fig. S9 and S10, ESI†). Based on the indicator ranking of the standard approach, new QM regions were constructed which are equal in size to the distance-based ones. The composition of these regions can be found in Table S5 (ESI†). Subsequently, the convergence of the VDD charges and reaction energies was investigated and gPCVA was applied to these systematically constructed QM regions (Fig. 5).

Fig. 5 QM/MM convergence for QM regions in TIM constructed based on PCVA and corresponding global point charge variation analysis. Best estimate results (corresponding to QM region 9′) are indicated by solid horizontal lines. (A and D) Convergence of DHAP VDD charges (A) and reaction energies ΔE^reaction_QM/MM for the interconversion reaction from DHAP to PGH in TIM (D) with increasing QM region size. Grayscale lines indicate the values for varied MM point charges. (B and E) Sensitivity of the VDD charges (B) and of the reaction energy (E) to global point charge variations Δq^tot_MM,I. (C and F) Corresponding DHAP charges (C) and reaction energies (F) of atom-economical 16-residue QM regions (indicated by dashed vertical line in A) constructed using different PCVA schemes as well as CDA results (from ref. 12, based on a 12-residue QM region).

Already with region 3′, the DHAP VDD charge starts to converge to about −0.25, with only the region 5′ value being off (see Fig. 5A). This indicates a better convergence behavior than in the distance-based case. Similarly, the sensitivity starts to slightly decrease with region 3′ (see Fig. 5B). For the reaction energy, we can see a similar convergence behavior as in the distance-based case. Starting from region 2′, the energy oscillates around the best estimate of about 9 kcal mol⁻¹, with an outlier for region 5′ (see Fig. 5D). Simultaneously, the sensitivity strongly decreases after the usual peak for region 2′ and converges at a low level from region 5′ onwards (see Fig. 5E). Overall, the construction of QM regions using the systematic saaPCVA approach leads to a slightly better convergence and lower gPCVA sensitivity behavior compared to the distance-based inclusion of amino acids. This confirms the suitability of saaPCVA for the systematic construction of QM regions.

To assess the accuracy of atom-economical QM regions, we constructed regions with the 16 highest-ranked amino acids based on the indicators of standard and cryst PCVA and compared the corresponding charges and reaction energies to the best estimates (see Fig. 5C and F). Regarding VDD charges, standard delivers a charge 0.15 higher than for the best estimate (−0.25). The cryst saaPCVA performs much better with a charge of −0.23. The CDA-constructed QM region results in a charge lying between the two PCVA variants at about −0.15. Concerning the reaction energy, we observed the reversed behavior for the two PCVA schemes. Here, standard performs better with a reaction energy about 10 kcal mol⁻¹ below the best estimate (9 kcal mol⁻¹) while for cryst, the reaction energy is nearly 20 kcal mol⁻¹ higher. The CDA result is again between the two with about 22 kcal mol⁻¹.

Table S6 (ESI†) compares the residue ranks of the two different PCVA variants and CDA with each other. What stands out is that the residues detected by CDA are mainly charged residues, which are often not detected by saaPCVA, such as ARG98, ARG99, GLU104 or LYS112. On the other hand, CDA misses several neutral residues very close to the ligand, which are detected by PCVA, e.g., GLY171, SER211 or LEU230. As these residues may also have an important catalytic role, CDA is considered to not perform reasonably in this case. In the comparison between standard and cryst PCVA there are only minor differences. The first approach ranks ASN213 and VAL231 unter the highest ranked 16 residues, while the latter one detects CYS126 and ALA163, exclusively. All other 14 residues are part of both constructed atom-economical QM regions.

As the results for 16-residue QM regions do not follow a clear trend, we added the 17th-ranked residue to the QM region, which is the catalytic HIS95 residue in both cases (labelled standard+95 and cryst+95). This residue is also detected by CDA and is thus potentially relevant. Unfortunately, the inclusion of HIS95 increases the DHAP charges for standard and cryst significantly. Interestingly, the reaction energy for standard PCVA is not affected, while for cryst the energy is improved to about 7 kcal mol⁻¹, close to the best estimate. Overall, these results underline the ability of single amino acids to strongly change QM charges and reaction energies. This indicates the need to further develop new approaches based on PCVA which do not only account for electrostatic effects and are able to better detect catalytic residues. Additionally, with respect to the 14-residue QM region 5′ being an outlier in DHAP charge and reaction energy (see Fig. 4), an atom-economical QM region size of around 16 amino acids seems not to be adequate for the TIM system to get reliable and consistent results. Thus, the use of a predefined, fixed size for an atom-economical QM region has to be revisited in future work.

5 Extension of PCVA for DNA systems

5.1 System

So far, we have applied PCVA for QM region construction to protein systems. In the following, we will assess whether this approach can also be used for a DNA system to quantify and evaluate the effect of single bases on properties of the QM region. Instead of amino acids here the sensitivities of single (nucleo)bases are target of the analysis, which is why we will refer to single base PCVA (sbPCVA) in this specific case.

We chose a B-DNA system (PDB: 1ZEW,²⁶ see Fig. 1C) with 10 basepairs (bp) as test system, which was also used in the work on QM/MM energy convergence by Roßbach and Ochsenfeld.¹⁸ In line with ref. 18, we do not perform geometry optimizations for this system, but directly start with single point calculations on the given structure differing from the procedure in the protein case. Due to the lack of substrates in this system the minimal QM region is represented by the two bases G7 and C14 performing a proton-transfer reaction (highlighted in Fig. 1C).

5.2 Results

In a first step, we reproduced the reaction energy convergence for the distance-based case similar to ref. 18. Here, we defined the base pair G7-C14 as the minimal QM region 1 and consequently added the adjacent pair A6-T15 for region 2, then pair A8-T13, and so on. An overview of the different regions is given in Table S7 (ESI†). In Fig. 6C, the dark blue graph represents the reaction energy with increasing QM region size for the distance-based inclusion of base pairs. The energy drastically decreases with 2 and 3 bp in the QM region, respectively, and converges at about 27.4 kcal mol⁻¹ starting from 5 bp, which overall corresponds to the results in ref. 18.

Fig. 6 Sensitivities and reaction energy convergence for DNA. (A) QM reactant energy sensitivities for bases in the DNA system. Bases 7 and 14 are not considered since they are part of the minimal QM region. Both strands of the double helix are represented in blue and red, respectively. (B) Same as A but here the total reaction energies are considered. (C) Convergence of the reaction energy for the proton transfer reaction between base 7 and 14 with increasing QM region size. Distance-based approach and different PCVA approaches are indicated in different colors.

Based on the minimal QM region containing the base pair G7-C14, we performed sbPCVA analogous to the saaPCVA scheme. A single point calculation is performed for each of the remaining 18 bases in which the charges of the corresponding base are varied. Afterwards, sensitivities are calculated for each base. In contrast to protein systems, here we will waive the calculation of indicators because they do not add value to the results since we deal with a linear distance behavior due to the structural properties of a DNA helix, and will thus use the sensitivity ranking directly for the construction of QM regions.

The sbPCVA was performed in two different ways. In the first scheme, we only use the QM energy of the reactant structure and calculate the sensitivity as the difference between the QM energy of the undistorted and the distorted structure (see Fig. 6A, results shown for a variation of −0.5 per base). Bases A6 and A8 show a very high sensitivity, which was expected since they are adjacent to C7 in the minimal QM region. The sensitivities of the remaining bases in this strand (5′-3′) behave nearly distance-dependent. The same behavior could have been expected in the other strand (3′-5′) for bases T13 and T15, but those two sensitivities are clearly lower than for example the sensitivities of the more distant bases C11, C12 and A16. These results indicate that the effect of single bases on the QM region is not exclusively distance-dependent.

The second scheme uses the total reaction energy instead of the QM reactant energy (see Fig. 6B). In contrast to the first scheme, in this case T13 and T15 show the highest sensitivities compared to the other bases on the 3′-5′ strand. This is a result of additionally accounting for the product structure when evaluating reaction energies, since the structure of the two target bases change significantly after the proton transfer. Nevertheless, the bases on the 5′-3′ strand again show a higher overall sensitivity, especially base A6.

Based on these sensitivity results we constructed different-sized QM regions according to 4 different schemes. Firstly, we distinguish between the two aforementioned schemes (reactant and reaction) and second we distinguish between single and pairwise inclusion (single and pairs). In the single inclusion scheme, we simply add bases according to their respective sensitivity without considering the corresponding counter base. With that also non-complete base pairs can be included in a QM region. In the pairwise inclusion scheme, complete base pairs are ranked and included into the QM region based on the sum of their sensitivities. The resulting QM regions can be found in Table S7 (ESI†).

The reaction energy with increasing QM region size was then calculated and evaluated for the different schemes and compared to the distance-based case (see Fig. 6C). It can be clearly seen that the single inclusion scheme (reactant single and reaction single) does not work properly, since we observe a worse convergence behavior than for the distance-based inclusion (distance). This underlines the expectation that always including complete base pairs to the QM region is necessary to gain reasonable results in DNA systems. Both pairwise inclusion schemes (reactant pairs and reaction pairs) lead to a similar convergence as for distance-based inclusion. Starting from 5 bp, both reaction energies converge at about 27.4 kcal mol⁻¹.

At first glance, sbPCVA seems to be not necessary for QM region construction since it resembles the distance-based results. But it can be helpful to estimate the distance-dependent decrease in the strength of the effect on the target base pair with no need to perform QM/MM calculations for medium- to large-sized QM regions. The sensitivities can be helpful to consider which distant base pairs still have a high impact on the target base pair and which ones can be neglected in a productive QM/MM run. Especially for larger and more complex DNA structures than the helix used in this work, for instance DNA origami structures, sbPCVA could be a useful tool to quantify base-dependent effects.

6 Conclusions

In this work, we presented further developments and test cases for our previously reported PCVA approach¹⁷ which was shown to be a simple and reliable approach for systematic QM region construction based on uncertainty quantification.

Since standard saaPCVA worked well for COMT compared to computationally more expensive methods such as CSA and FSA, we tested several variations and further simplifications for this system. It turned out that starting saaPCVA directly from a protein crystal structure in vacuum without pre-processing delivers equally reasonable results compared to the standard PCVA variant. Moreover, we showed that it can be beneficial to include several important active site residues to the minimal QM region prior to saaPCVA. In general, if the additional computational cost is considered to be reasonable and if there is clarity about the important active site residues we recommend to include these amino acids in the QM region which is then used for saaPCVA.

To prove the applicability of PCVA for other systems we assessed it for the enzyme TIM. The convergence of VDD ligand charges and reaction energies is slightly improved for different-sized saaPCVA-constructed QM regions compared to distance-based construction of the QM region. Also sensitivity convergence calculated with the global PCVA approach is slightly better for PCVA-constructed regions. The assessment of atom-economical QM regions constructed from standard and cryst PCVA and the comparison to a 12-residue QM region constructed based on the CDA approach from Bash et al. revealed minor difficulties for both methods. The results indicate that the inclusion of specific single amino acids can highly affect the QM region properties especially in the case of catalytically active residues. Therefore, before applying any QM region construction method to a new system, it has to be studied carefully with respect to its active site and possible other important amino acids.

Connected to the aforementioned impact of single amino acids our results indicate fixed-size, 16-residue QM regions to not always be sufficient for every system to produce reliable results. Therefore, in future investigations a more systematic approach to identify an optimal, system-dependent QM region size must be developed. To this end, it could be interesting to investigate the correlation of system and QM region size as well as the introduction of specific QM region size cutoffs.

To test its versatility, we extended the application of PCVA to a DNA system and introduced the single base PCVA (sbPCVA) analogous to saaPCVA. For the quite small and simple test system with 20 base pairs the construction of QM regions based on PCVA-calculated sensitivities did not significantly improve the reaction energy convergence compared to distance-based inclusion. Nevertheless, regarding the sensitivities, deviations from a clear distance-dependent trend have been observed. With that sbPCVA can be a helpful tool to at least estimate a reasonable QM region size to get consistent results especially when it comes to more complex DNA systems.

Altogether, we were able to add new useful functionalities to the PCVA approach and we verified its success in systematic QM region construction. We set the starting point for new application cases especially for non-protein systems and further developments by assessing important difficulties and problems in QM region construction not only occurring for PCVA. In particular, an approach must be developed which helps to systematically calculate the ideal QM region size for any system. Furthermore, still all approaches considered here exclusively focus on the electrostatic effect of amino acids and by that might miss important non-electrostatic interactions. This problem should be addressed in the future to further improve the setup process of QM/MM calculations.

Computational details

Preparation of the starting structures and molecular dynamics calculations were performed using GROMACS 2019.3^27,28 with the AMBER99SB-ILDN²⁹ force field. The different substrates were parametrized using Antechamber^30,31 and acpype.^32,33

For COMT, the equilibrated initial structure provided by Kulik et al.⁹ was solvated in TIP3P³⁴ water molecules in a cubic simulation box with 1 nm distance from the enzyme to the borders. After neutralizing the system by adding six sodium cations, the solvent molecules and ions were minimized with the enzyme structure held fixed. Finally, a spherical droplet with a radius of 33 Å from the COMT center of mass was extracted. It contained COMT with substrates, sodium ions and the corresponding water molecules and was used as starting structure for the QM/MM calculations. For QM/MM calculations starting from the vacuum structure, the water molecules and ions were deleted from the spherical droplet structure. For QM/MM calculations starting from the crystal structure the corresponding PDB structure (3BWM³⁵) was modified by converting the co-crystallized 3,5-dinitrocatechol to catecholate and then directly used for calculation.

The TIM product structure with co-crystallized inhibitor phosphoglycolohydroxamic acid (PGH) was prepared starting from the monomer A of the crystal structure (PDB: 7TIM²⁵) by solvating and neutralizing (3 sodium ions) following the same protocol as mentioned before. Afterwards, the structure was minimized and equilibrated in an NVT and NPT ensemble, respectively. The equilibrated structure was then used for the QM/MM calculations. The reactant and product structures were prepared analogously with preceding modification of the co-crystallized PGH to dihydroxyacetone phosphate (DHAP) and glyceraldehyde phosphate (GAP), respectively. For calculations starting from the crystal structure the PGH-bound structure was used without solvation and ions.

The DNA structure which is based on the PDB structure 1ZEW²⁶ was directly taken from the ESI of ref. 18 and used for QM/MM calculations without further modifications. Only single point calculations were performed for the DNA system as suggested by Roßbach and Ochsenfeld.

All QM/MM calculations were performed using the Amsterdam Modeling Suite (AMS Version 2020.203).³⁶ The Amsterdam Density Functional (ADF) engine³⁷ was used for the QM part applying density functional theory (DFT) with the PBE exchange–correlation functional,³⁸ for which we previously showed a reasonable behavior of the HOMO–LUMO gap of COMT,¹⁷ employing a DZ and a TZP Slater-type orbital basis set³⁹ for all geometry optimizations and single point calculations, respectively. In case of occurring convergence problems during the geometry optimizations (especially for TIM) the optimization was started using the B3LYP^40,41 XC functional and afterwards continued with PBE. For the MM region, the ForceField engine of AMS was used with the AMBER95 force field,⁴² which was extended by parameters for the substrates. The FIRE⁴³ minimization algorithm was used for all QM/MM geometry optimizations with all MM solvent molecules and ions fixed to their initial coordinates. All charges evaluated for charge convergence tests are calculated from the Voronoi deformation density (VDD)⁴⁴ of the reactant structures only.

The QM/MM input files were generated using the PDB2ADF tool provided by AMS for protein systems and using a Python script (included in the data set at ref. 45) inspired by the functionality of PDB2ADF for the DNA system. Electrostatic embedding as implemented in AMS⁴⁶ was applied for the interaction between the QM and MM regions. Link atoms in the protein systems were placed on the C_α–C and C_α–N bonds only including the α-carbon atom in the QM region for single QM amino acids, while also including the remaining backbone atoms between two subsequent QM amino acids to reduce the number of link atoms. In the DNA system link atoms were placed on the N-glycosidic bond only including the bases to the QM region and let the negatively charged backbone remaining in the MM region. Over-polarization at the boundary region is handled in AMS by setting the point charge of the MM boundary atom to zero and redistributing it over the remaining MM atoms conserving the total charge.⁴⁶ Residues included in the different-sized QM regions for each system are listed in the ESI,† in S1 and S2 (COMT), S4 and S5 (TIM), and S7 (DNA), which also list the corresponding QM region charges and the numbers of atoms and link atoms.

The analysis of results and the modification of input files regarding point charge variation were achieved with Python. Plots were generated with Matplotlib^47,48 and structures were visualized using Visual Molecular Dynamics (VMD).⁴⁹

Data availability

Data for this paper, including all necessary PDB files of the starting structures, the modified AMBER95 force field for the use with AMS, substrate and ion AMS fragment files, as well as the AMS input files for all geometry optimizations and single point calculations, are available at Zenodo at https://doi.org/10.5281/zenodo.7752677.

Author contributions

Felix Brandt: conceptualization (equal), investigation (lead), software (lead), visualization (lead), writing – original draft (lead), writing – review and editing (equal). Christoph R. Jacob: conceptualization (equal), writing – review and editing (equal).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. A. Warshel and M. Levitt, Theoretical studies of enzymic reactions: dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme, J. Mol. Biol., 1976, 103, 227–249.
2. M. J. Field, P. A. Bash and M. Karplus, A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations, J. Comput. Chem., 1990, 11, 700–733.
3. J. Gao, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, VCH, New York, 1995, vol. 7, pp. 119–185.
4. G. Groenhof, in Biomolecular Simulations: Methods and Protocols, ed. L. Monticelli and E. Salonen, Methods in Molecular Biology, Humana Press, Totowa, NJ, 2013, pp. 43–66.
5. K.-S. Csizi and M. Reiher, Universal QM/MM approaches for general nanoscale applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2023, e1656,  DOI:10.1002/wcms.1656 , in press.
6. C. V. Sumowski and C. Ochsenfeld, A Convergence Study of QM/MM Isomerization Energies with the Selected Size of the QM Region for Peptidic Systems, J. Phys. Chem. A, 2009, 113, 11734–11741.
7. D. Flaig, M. Beer and C. Ochsenfeld, Convergence of Electronic Structure with the Size of the QM Region: Example of QM/MM NMR Shieldings, J. Chem. Theory Comput., 2012, 8, 2260–2271.
8. G. Jindal and A. Warshel, Exploring the Dependence of QM/MM Calculations of Enzyme Catalysis on the Size of the QM Region, J. Phys. Chem. B, 2016, 120, 9913–9921.
9. H. J. Kulik, J. Zhang, J. P. Klinman and T. J. Martínez, How Large Should the QM Region Be in QM/MM Calculations? The Case of Catechol O-Methyltransferase, J. Phys. Chem. B, 2016, 120, 11381–11394.
10. R. Mehmood and H. J. Kulik, Both Configuration and QM Region Size Matter: Zinc Stability in QM/MM Models of DNA Methyltransferase, J. Chem. Theory Comput., 2020, 16, 3121–3134.
11. S. Sumner, P. Söderhjelm and U. Ryde, Effect of Geometry Optimizations on QM-Cluster and QM/MM Studies of Reaction Energies in Proteins, J. Chem. Theory Comput., 2013, 9, 4205–4214.
12. P. A. Bash, M. J. Field, R. C. Davenport, G. A. Petsko, D. Ringe and M. Karplus, Computer simulation and analysis of the reaction pathway of triosephosphate isomerase, Biochemistry, 1991, 30, 5826–5832.
13. R.-Z. Liao and W. Thiel, Convergence in the QM-only and QM/MM modeling of enzymatic reactions: a case study for acetylene hydratase, J. Comput. Chem., 2013, 34, 2389–2397.
14. M. Karelina and H. J. Kulik, Systematic Quantum Mechanical Region Determination in QM/MM Simulation, J. Chem. Theory Comput., 2017, 13, 563–576.
15. C. Brunken and M. Reiher, Automated Construction of Quantum–Classical Hybrid Models, J. Chem. Theory Comput., 2021, 17, 3797–3813.
16. M. A. Hix, E. M. Leddin and G. A. Cisneros, Combining Evolutionary Conservation and Quantum Topological Analyses To Determine Quantum Mechanics Subsystems for Biomolecular Quantum Mechanics/Molecular Mechanics Simulations, J. Chem. Theory Comput., 2021, 17, 4524–4537.
17. F. Brandt and C. R. Jacob, Systematic QM Region Construction in QM/MM Calculations Based on Uncertainty Quantification, J. Chem. Theory Comput., 2022, 18, 2584–2596.
18. S. Roßbach and C. Ochsenfeld, Influence of Coupling and Embedding Schemes on QM Size Convergence in QM/MM Approaches for the Example of a Proton Transfer in DNA, J. Chem. Theory Comput., 2017, 13, 1102–1107.
19. R. Smith, Uncertainty Quantification: Theory, Implementation, and Applications, Society for Industrial and Applied Mathematics, Philadelphia, 2014.
20. T. J. Sullivan, Introduction to Uncertainty Quantification, Springer, New York, NY, 1st edn, 2015.
21. D. G. Cacuci, Sensitivity & Uncertainty Analysis, Theory, Chapman and Hall/CRC, Boca Raton, 1st edn, 2003, vol. 1.
22. J. Axelrod and R. Tomchick, Enzymatic O-Methylation of Epinephrine and Other Catechols, J. Biol. Chem., 1958, 233, 702–705.
23. N. Patra, E. I. Ioannidis and H. J. Kulik, Computational Investigation of the Interplay of Substrate Positioning and Reactivity in Catechol O-Methyltransferase, PLoS One, 2016, 11, e0161868.
24. R. K. Wierenga, The TIM-barrel fold: a versatile framework for efficient enzymes, FEBS Lett., 2001, 492, 193–198.
25. R. C. Davenport, P. A. Bash, B. A. Seaton, M. Karplus, G. A. Petsko and D. Ringe, Structure of the triosephosphate isomerase-phosphoglycolohydroxamate complex: an analog of the intermediate on the reaction pathway, Biochemistry, 1991, 30, 5821–5826.
26. F. A. Hays, A. Teegarden, Z. J. R. Jones, M. Harms, D. Raup, J. Watson, E. Cavaliere and P. S. Ho, How sequence defines structure: a crystallographic map of DNA structure and conformation, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 7157–7162.
27. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718.
28. Gromacs Version 2019.6, 2020 DOI:10.5281/zenodo.3685922, URL: http://www.gromacs.org/.
29. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Improved side-chain torsion potentials for the Amber ff99SB protein force field, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958.
30. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174.
31. J. Wang, W. Wang, P. A. Kollman and D. A. Case, Automatic atom type and bond type perception in molecular mechanical calculations, J. Mol. Graphics Model., 2006, 25, 247–260.
32. A. W. Sousa da Silva and W. F. Vranken, ACPYPE – AnteChamber PYthon Parser interfacE, BMC Res. Notes, 2012, 5, 367.
33. Acpype, 2021, URL: https://github.com/alanwilter/acpype.
34. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
35. K. Rutherford, I. Le Trong, R. E. Stenkamp and W. W. Parson, Crystal Structures of Human 108V and 108M Catechol O-Methyltransferase, J. Mol. Biol., 2008, 380, 120–130.
36. Software for Chemistry and Materials, Amsterdam, Ams, Amsterdam Modelling Suite, 2020, URL: http://www.scm.com.
37. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.
39. E. Van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1-118, J. Comput. Chem., 2003, 24, 1142–1156.
40. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
41. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627.
42. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197.
43. E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural Relaxation Made Simple, Phys. Rev. Lett., 2006, 97, 170201.
44. C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, Voronoi deformation density (VDD) charges: assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis, J. Comput. Chem., 2004, 25, 189–210.
45. F. Brandt and Ch. R. Jacob, Data Set: Efficient automatic construction of atom-economical QM regions with point-charge variation analysis, Zenodo, 2023 DOI:10.5281/zenodo.7752677.
46. Software for Chemistry and Materials, Hybrid Engine Manual—Hybrid 2020 documentation, 2020, URL: https://www.scm.com/doc.2020/Hybrid/index.html.
47. J. D. Hunter, Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 2007, 9, 90–95.
48. Matplotlib Version 3.4.2, 2021 DOI:10.5281/zenodo.4743323, URL: https://matplotlib.org.
49. W. Humphrey, A. Dalke and K. Schulten, VMD – Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38.

---

Footnote

† Electronic supplementary information (ESI) available: Additional tables and figures showing PCVA sensitivity and indicator rankings as well as the compositions of the different considered QM regions. See DOI: https://doi.org/10.1039/d3cp01263h

---