Dynamics of transition dipole moment orientation in representative fluorescent proteins

Abstract

Molecules of fluorescent proteins (FPs) exhibit distinct optical directionality. This optical directionality is characterized by transition dipole moments (TDMs), and their orientation with respect to the molecular structures. Although our recent observations of FP crystals allowed us to determine the mean TDM directions with respect to the framework of representative FP molecules, the dynamics of TDM orientations within FP molecules remain to be ascertained. Here we describe the results of our investigations of the dynamics of TDM directions in the fluorescent proteins eGFP, mTurquoise2 and mCherry, through time-resolved fluorescence polarization measurements and microsecond time scale all-atom molecular dynamics (MD) simulations. The investigated FPs exhibit initial fluorescence anisotropies (r₀) consistent with significant differences in the orientation of the excitation and emission TDMs. However, based on MD data, we largely attribute this observation to rapid (sub-nanosecond) fluorophore motions within the FP molecular framework. Our results allow improved determinations of orientational distributions of FP molecules by polarization microscopy, as well as more accurate interpretations of fluorescence resonance energy transfer (FRET) observations.

---

Introduction

Since their discovery,¹ fluorescent proteins (FPs) have found an ever-increasing range of applications in biological sciences. FPs now form a basis of many genetically encoded probes of molecular processes that take place in living cells and organisms.² FP-based probes take advantage of various biophysical properties of FPs. One of the FP optical properties utilized in genetically encoded probes is directionality.

Fluorescent proteins behave like antennas (Fig. 1), exhibiting distinct directionality of light absorption and emission. As in other fluorescent molecules and linear optical phenomena, this directionality is characterized by a vector, the transition dipole moment (TDM). The probability of light absorption by an FP molecule is proportional to the cos² of the angle between the electric field vector of the excitation light and the direction of the TDM that characterizes the excitation process (xTDM). The direction of the emitted fluorescence and its polarization is determined by the TDM that characterizes the process of fluorescence emission (mTDM). Since knowing the xTDM and mTDM directions allows making insights into molecular orientation from observations of fluorescence resonance energy transfer (FRET) or from various polarization microscopy measurements, precise knowledge of TDM directions in fluorescent proteins is important.

Fig. 1 Directionality of light absorption and emission by FPs. (a) Excitation light (blue) polarized parallel to the direction of the xTDM is absorbed by the FP molecule, leading to emission of fluorescence (green). Fluorescence is emitted preferentially in directions perpendicular to the mTDM. (b) Excitation light polarized perpendicular to the direction of the xTDM is not absorbed by the FP molecule, leading to no fluorescence.

Over the past years, several attempts have been made to determine the TDM directions within FP molecules. Although observations of crystals of the green fluorescent protein yielded a TDM orientation,³ the results were marred by errors.⁴ The angle between the xTDM characterizing the 405 nm excitation and the stretching vibration of the C=O bond within the GFP fluorophore was established by vibrational dichroism measurements.⁵ Quantum mechanical calculations yielded TDM directions in a number of FP fluorophores,^6,7 although the calculated TDM direction in the GFP fluorophore differs significantly from that determined experimentally. Our own observations of FP crystals recently yielded the directions⁸ of xTDMs and mTDMs with respect to the molecular framework of several representative fluorescent proteins: mTurquoise2, eGFP, mCherry and mEos4b (Fig. 2).

Fig. 2 Directions of excitation transition dipole moments in fluorescent proteins with respect to the atomic structure of the fluorophore. (a) mTurquoise2; (b) eGFP; (c) mCherry. (adapted from ref. 8).

Although the published TDM directions represent a major step in understanding the directionality of FP properties, they are only the mean TDM directions within the studied FP molecules, and do not provide information on the dynamics of the TDM direction within the FP molecules. Since FP fluorophores undergo both thermal and excitation-induced conformational changes, understanding the dynamics of the TDM directions in FPs represents an important part of understanding FP optical directionality. The present study aims to ascertain the temporal and spatial range of TDM orientations in representative FPs, in order to improve our understanding of directionality of their optical properties. Here we present and discuss the results of our observations of time-resolved measurements of fluorescence anisotropy of solutions of representative FPs, along with results of molecular dynamics simulation studies that allow detailed interpretation of our optical measurements.

Results and discussion

Time-resolved fluorescence anisotropy measurements

In order to investigate the dynamics of TDM orientations, we performed time-resolved measurements of fluorescence anisotropy of representative FPs, namely, the cyan FP mTurquoise2, the green FP eGFP, and the red FP mCherry. The results of our measurements are summarized in Fig. 3 and Table 1 and Fig. S1 and S2 (ESI†). Briefly, the examined FPs exhibited fluorescence lifetimes between 1.0 (mCherry) and 4.8 (mTurquoise2) nanoseconds. Interestingly, only mCherry exhibited clear double-exponential decay kinetics. The initial anisotropy values (r₀) in all three FPs corresponded to initial values of the xTDM-mTDM angle (β₀) around 10°. In case of mCherry (investigated using a microscope and a focused laser beam) we ascertained the influence of illumination intensity on fluorescence anisotropy measurements, and found only insignificant effects (Fig. S3, ESI†).

Fig. 3 Results of time resolved fluorescence measurements of mTurquoise2, eGFP, and mCherry. (a) Fluorescence intensity as a function of time. Colored line and bars: mean values ± standard deviation; black line: exponential fit. (b) Fluorescence anisotropy (r, in gray) and the corresponding angle β (in color) as a function of time. Mean values ± standard deviations are shown. Black line: exponential fit of r; dotted black line: exponential fit of β.

Table 1 Results of time-resolved fluorescence measurements (mean values ± 95% confidence intervals)

	mTurquoise2	eGFP	mCherry
Fluorescence lifetime (τ)	4.80 ± 0.02 ns	2.73 ± 0.01 ns	1.63 ± 0.04 ns 1.02 ± 0.05 ns (62%, 38%)
Initial fluorescence anisotropy (r0)	0.368 ± 0.000	0.370 ± 0.001	0.386 ± 0.001
Initial angle xTDM–mTDM (β0)	13.4 ± 0.1°	12.9 ± 0.2°	8.9 ± 0.2°
Rotational correlation time (τrot)	15.0 ± 0.1 ns	16.9 ± 0.1 ns	14.0 ± 0.1 ns

---

MD simulations

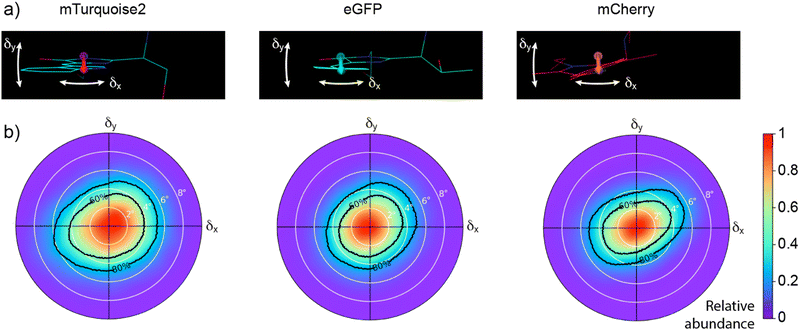
In order to verify, extend, and interpret our experimental observations, we performed molecular dynamics (MD) simulations. The MD simulations allowed us to characterize the TDM motions relative to the FP scaffold (Fig. 4 and 5 and Fig. S4, ESI† and Table 2). Briefly, the distributions of TDM orientations are well approximated by Gaussian distributions, characterized by a standard deviation close to 4° (Fig. 4). The directions of TDM angular deviations from a mean TDM orientation are distributed fairly evenly (Fig. 5), perhaps with the exception of mCherry, in which the TDM does show a preference to deviate from its mean orientation along a direction about 25° from the fluorophore plane.

Fig. 4 MD simulations of distributions of TDM orientations due to thermal motions of the fluorophore within the FP β-barrel. (a) Sizes and frequencies of angular deviations δ (integrated over all directions), for all three fluorescent proteins, along with Gaussian distribution fits.

Fig. 5 MD simulations of distributions of TDM orientations due to thermal motions of the fluorophore within the FP β-barrel. (a) Directions of angular deviations within the fluorophore plane (δ_x) and perpendicular to the fluorophore plane (δ_y) for the investigated FPs. (b) Radial plots showing distributions (magnitudes and directions) of angular deviations δ from a mean TDM orientation for the investigated FPs. Cumulative probabilities for each TDM direction are indicated by black isolines.

Table 2 Results of MD simulations: dynamics of TDM directions within the FP molecule

	mTurquoise2	eGFP	mCherry
Standard deviation of δ	4.3°	3.9°	3.7°
Direction of δmax	23°	42°	24°
Direction of δmin	117°	119°	108°
Standard deviation of δmax	4.9°	4.3°	4.4°
Standard deviation of δmin	3.7°	3.7°	2.9°

---

Our MD simulations also allowed us to model results of our time-resolved fluorescence polarization measurements. The results of such modeling are summarized in Fig. 6 and Table 3. Briefly, our MD data show rapid (femtosecond time scale) motions of the fluorophore within the β-barrel. These motions should account for a 5° apparent angle between the xTDM and mTDM in all three studied FPs.

Fig. 6 MD-simulated time-resolved fluorescence polarization. In color: values of the angle β between xTDM and mTDM at instants separated by the indicated time intervals. In black/gray: values of fluorescence anisotropy (r) as a function of time. Mean values and standard deviations of β and r are indicated. Dotted lines: fits of values of β and r obtained from time-resolved fluorescence polarization measurements (same as shown in Fig. 3b)

Table 3 Results of MD simulations: predictions of time-resolved fluorescence observations (mean ± 95% confidence intervals)

	mTurquoise2	eGFP	mCherry
Initial fluorescence anisotropy (r0)	0.396 ± 0.001	0.396 ± 0.001	0.396 ± 0.001
Initial angle xTDM–mTDM (β0)	4.6 ± 0.0°	4.9 ± 0.0°	5.0 ± 0.0°
Rotational correlation time (τrot)	14.2 ± 0.0 ns	14.0 ± 0.0 ns	14.6 ± 0.0 ns

---

Discussion

We have now investigated the dynamics of TDM orientations in three commonly used FPs, namely mTurquoise2, eGFP and mCherry, whose fluorophores are present, respectively, in most blue, green/yellow and red FPs. Our work combines an experimental approach (measurements of fluorescence anisotropy) with a computational approach (MD simulations) that supplements the experimental observations and allows their detailed interpretation. A key result of our time-resolved fluorescence polarization observations is the value of initial anisotropy, r₀. For eGFP, our value of r₀ (0.372) lies close to the middle of previously published values,^9–18 which range from 0.34¹⁰ to 0.4,⁹ with most being between 0.36 and 0.38. Although many of the published values of r₀ appeared only as a side note in articles focused on other aspects of FP dynamics, it is nonetheless comforting that our results conform to those obtained previously. We have not been able to find previously published values of r₀ for mTurquoise2 or mCherry. Since our measurements of mTurquoise2 were carried out under conditions similar to those used for measurements of eGFP, we are confident that the two FPs exhibit very similar initial fluorescence anisotropies. Our measurements at different illumination intensities (mCherry, Fig. S3, ESI†) did not reveal any artifacts (i.e., bleaching, heating). Since the local illumination intensities in our mTurquoise2 and eGFP measurements were 6 orders of magnitude lower than in our mCherry measurements, such artifacts are likely to be negligible.

The experimentally determined values of r₀ can be used to calculate the angle (β₀) between the xTDM and mTDM. The values of β₀ lie slightly above (in case of mTurquoise2 and eGFP) or below (mCherry) 10°. Because of the time scales of our observations, the experimentally derived values of r₀ and β₀ characterize fluorescence emitted after numerous vibrations of the fluorophore (as those occur on femto- and picosecond time scales), but before appreciable rotational diffusion of the FP β-barrel.

Apart from values of r₀ and β₀, our measurements also yield values of fluorescence lifetimes and rotational correlation times, which are in line with previously published values. Monoexponential fluorescence decay kinetics were observed in mTurquoise2 and eGFP, likely due to the relatively high pH (7.5) used,¹⁹ limiting the fraction of protonated fluorophore moieties. In contrast, since fitting by a single exponential did not produce a satisfactory fit in mCherry, the data were fitted by two exponentials, yielding two fluorescence lifetimes (1.6 ns and 1.0 ns), exhibited by close to 60 and 40% of the molecules, respectively. We attribute the double-exponential kinetics to distinct protonation states of the fluorophore.

In order to extend and complement our experimental findings, we used MD simulations. Since FP TDM directions obtained previously by quantum-mechanical (QM) calculations⁶ deviate considerably from those established by various experimental methods,^5,8 we chose not to combine our molecular simulations with QM calculations. Instead, we used the published experimentally determined TDM directions with respect to the atomic framework of the fluorophore,⁸ and we approximated the mechanical and coulombic properties of the excited state of the fluorophore by those of the ground state.

Our MD simulations allow us to model and interpret time-resolved fluorescence polarization observations similar to those we performed. By sampling our MD simulations at intervals (20 ps) similar to those used in our time-resolved fluorescence measurements (50 ps for mTurquoise2 and eGFP; 100 ps for mCherry), and fitting the data using the same procedures, we obtained values (shown in Fig. 6 and Fig. S4, ESI†) of the xTDM-mTDM angle β (including the initial angle β₀) and the expected fluorescence polarization r (including the value of r₀) that can be compared to the experimentally derived counterparts (shown in Fig. 3b and Fig. S2, ESI†).

Importantly, because the MD simulations (unlike our optical measurements) are observations of a single molecule, the standard deviations of MD-derived values of β and r (shown in Fig. 6) are relatively large. However, because a high number of samples can be extracted from our MD traces (up to 50 000), the standard errors of the mean, and therefore the widths of the confidence intervals (Table 3 and Fig. 4, ESI†) are small. To allow good understanding of our data, we show both the standard deviations and confidence intervals.

The MD-derived values of r₀ (and the corresponding angle β₀) result purely from rapid thermal fluorophore motions within the β-barrel of the FP molecule, as no electronic effects were included in our MD simulations. The MD-derived values of β₀ are almost identical among the three FPs. Interestingly, the values of β₀ obtained from MD simulations (around 5°) are somewhat smaller than those obtained from time resolved fluorescence polarization measurements (around 10°). We see several factors that might contribute to this difference. A likely important factor is the fact that the event of light absorption by the fluorophore leads to vibrational excitation,²⁰ which is not accounted for in our MD simulations. Furthermore, as mentioned above, our MD simulations did not include a quantum-mechanical component explicitly simulating the electronically excited state of the fluorophore. This choice was made because published QM predictions of TDM directions⁶ do not agree particularly well with experimental observations.^5,8 It is also possible that the force field used in our MD simulations generally underestimates the extent of fluorophore motions. The accuracy of our assumption of identical xTDM and mTDM directions within the atomic framework of the fluorophore may also be limited, although the published mean xTDM and mTDM directions differ only little (∼1°) in mTurquoise2 and eGFP. Finally, some inconsistencies between the angles β observed in the present study in FP solutions and a previous study on FP crystals⁸ may arise due to differences between the two molecular environments. Taking these factors into considerations, we interpret our results by concluding that a large part (around 7°) of the β₀ determined through optical measurements is likely due to fast thermal motions of the fluorophore in an electronically and vibrationally excited state, while the remainder is due to differences in xTDM and mTDM orientations within the atomic framework of the fluorophore.

Apart from simulating motions of the fluorophore, we have also interrogated our MD simulations for rates of rotational diffusion of FP molecules (Fig. 6 and Fig. S4, ESI†). The results are in good agreement with recently published results of MD simulations of rotational diffusion of eGFP.²¹ The differences between our results obtained by MD and by time-resolved optical measurements are small. However, it is worth noting that the rotational correlation times were derived from fitting of the first 5 ns of our simulations, before onset of non-monoexponential kinetics (Fig. S4, ESI†). Because of this, and because the force field used for our MD simulations (using a low viscosity TIP3P water model) is not optimal for studying molecular diffusion, we consider the experimentally measured rotational diffusion parameters more accurate than the MD results.

Experimental

Time-resolved fluorescence anisotropy measurements

Measurements were carried out using proteins expressed heterologously in E. coli and purified as described before.⁸ The plasmids were obtained as kind gifts from the laboratories of R. Campbell (eGFP), D. Gadella (mTurquoise2), and R. Tsien (mCherry). Prior to measurements, the purified proteins were diluted in buffer (10 mM Tris–HCl, pH 7.5) to an optical density of 0.1 at their respective absorption maxima.

Time resolved fluorescence intensity and anisotropy measurements of mTurquoise2 and eGFP were performed using a setup similar to a published one,⁹ consisting of a 150 fs pulsed Ti:Sapphire laser (Mira-HP, Coherent) tuned to 900 nm, equipped with a frequency doubling unit (Harmonics, Coherent). The beam was restricted by a diaphragm to a diameter of 2 mm and power of 2 μW. Pulse repetition rate was reduced to 3.75 MHz by a pulse picker (pulseSelect, APE). Polarization of excitation light was rotated using a flip-in zero order achromatic (350–500 nm) half-wave plate (WPAC4-22-N2, Karl Lambrecht Corp.) and purified by a rotating Glan-laser polarizer (MGTYA20, Karl Lambrecht Corp.). Fluorescence was detected in a direction perpendicular to excitation. Polarization of the detected fluorescence was selected using a Glan-laser polarizer (MGTYA20, Karl Lambrecht Corp.). Emitted light (500 nm for mTurquoise2; 510 nm for eGFP) was selected by a spectrograph (9030-DS, Sciencetech Inc.; slit width 0.05 mm), and detected overnight by a time-correlated single-photon counting detector (C10373-02, Hamamatsu Photonics; temporal resolution of 3.05 ps, binned to 20 ps bins). The instrument response function, measured using a scattering solution of Ludox, is shown in Fig. S5 (ESI†). The G-factors (0.250) were calculated from intensities of horizontally and vertically polarized fluorescence excited with light polarized horizontally.

Measurements of mCherry solutions were performed using a SP8 Falcon FLIM microscope (Leica, temporal resolution of 97 ps) and a Leica 10X HC PL Fluotar objective lens (NA 0.3). Fluorescence was excited by a pulsed (200 ps, 40 MHz) laser (SuperK EXTREME EXW-12, NTK Photonics) tuned to 516 nm, using 5 μW illumination intensity. Polarization of emitted light (603–669 nm) was selected using a polarizer located behind a confocal pinhole. The instrument response function, estimated using LASX software, is shown in Fig. S5 (ESI†). The G factor (1.058 ± 0.002) was measured using a concentrated (2 mM) solution of Rhodamine G (Sigma–Aldrich). Values of fluorescence anisotropy were adjusted for depolarization by the objective lens.²²

All measurements were performed in triplicates. The logarithmic values of the observed fluorescence intensity traces were fitted by a linear fit, yielding a fluorescence lifetime constant (τ). The logarithmic values of mCherry fluorescence were also fitted by a double-exponential function (ln (F(t)) = exp (x₁ ln(−t/τ₁) + x₂ ln(−t/τ₂)). The time-resolved fluorescence anisotropy (r) data were analyzed by performing a linear fit of ln(r), yielding values of the time constant (τ_rot) from the slope and the initial fluorescence anisotropy (r₀) from the y-axis intersect (Fig. S2, ESI†). Values of fluorescence anisotropy were used to calculate the angle (β) between the xTDM and mTDM (, including the initial value of this angle (β₀).

Molecular dynamics simulations

MD simulations were performed using AMBER 16 or AMBER 18²³ packages, using the Amber14 force field, and the provided FP structures as a starting point. For the fluorophores of eGFP and mCherry, available parameters (mixing Amber14 and GAFF force fields) were used. For the fluorophore of mTurquoise2, partial charges were calculated using the R. E. D. Server Development,²⁴ using homology with available chromophores, and Amber14 and GAFF amino acid parameters. Protein molecules were solvated using a 10 nm cubic water box, and potassium ions were added to reach system neutrality. The solvated system was minimized and equilibrated using the NVT ensemble (200 ps), and further equilibrated using the target NTP ensemble (4 ns; 1 atm, 2 ps relaxation time, isotropic scaling). During these equilibrations, weak restraints to the protein were applied (10 kcal mol⁻¹ Å⁻²). After this, the system was further equilibrated for 10 ns without restraints, followed by a 1 μs production run. All production simulations were run using pmemd, using periodic boundary conditions. PME and a cutoff of 12 Å were used for the electrostatic and van der Waals interactions, respectively. Shake algorithm was enabled to allow 2 fs simulation step. Langevin dynamics with collision frequency set to 1 ps⁻¹ was used to control temperature. Coordinates were stored every 20 ps. Fluorophore orientations were analyzed and visualized using Python and the NumPy,²⁵ SciPy,²⁶ and matplotlib²⁷ libraries. Rotational diffusion of the whole protein was calculated using the rotdif function of the AMBER package by generating 500 random vectors across the C_α atoms of the protein and calculating the rotational matrix required to overlap the investigated frames.²⁸

The TDM motions were evaluated by assuming the TDM to lie within a plane fitted through the heavy atoms of the fluorophore participating in the conjugated bond system, at the published angle⁸ with respect to the line connecting the centers of the fluorophore aromatic rings (Fig. 2). To characterize the TDM motions within the β-barrel, we aligned the C_α atoms of the simulated FP structures with the published FP structures as reference, and calculated the mean TDM direction. Finally, for each time point, we calculated the angular deviation (δ) between the instant and mean TDM directions, as well as its components in the directions within the fluorophore plane (δ_x) and perpendicular to it (δ_y).

Time-resolved fluorescence anisotropy was modeled as follows. For each investigated time interval, the angle (β) between the TDM orientations in pairs of MD frames separated by that time interval was calculated. The expected fluorescence anisotropy (r) was calculated in a similar manner. Values of initial fluorescence anisotropy (r₀) were obtained by fitting values of ln (r) for times shorter than 5 nanoseconds by a line (Fig. S4, ESI†), and extrapolating to time equal to zero. Values of β₀ were calculated from values of r₀ (.

Conclusions

Our combined experimental and computational results provide a detailed quantitative description of the dynamics of TDM directions in representative fluorescent proteins, with applications in FRET and polarization microscopy experiments. Our results largely explain a seeming contradiction between the published virtually identical mean xTDM and mTDM orientations in the studied FPs,⁸ and observations of time-resolved fluorescence anisotropies that suggest differences between xTDM and mTDM orientations within the FP molecular framework. The results will allow better understanding of widths of orientational distributions observed in model membrane-tethered FP-bearing constructs,²⁹ as well as in other FP-labeled proteins, such as G proteins,^30,31 in which the molecular orientation of the FP moiety reports on the functional state of the studied protein. By allowing more accurate insights into the structure of FP-bearing membrane proteins, our results will aid in rational development of genetically encoded probes of G protein signaling³² and other cellular processes, as well as in elucidating molecular mechanisms of cell signaling. Our results will also improve our understanding FRET³³ between FP molecules, used in numerous genetically encoded probes.³⁴

Author contributions

P. K. carried out MD simulations, fluorescence anisotropy measurements, and analysed the data; H. M.-S. supervised and assisted in the MD simulations; J. M. expressed and purified the studied FPs, and co-supervised the project; J. L. supervised the project and wrote the manuscript, with contributions from P. K., H. M.-S. and J. M.

Conflicts of interest

J. L. has an ownership stake in Innovative Bioimaging, L. L. C., which, however, did not contribute to the presented work. Other authors have no conflicts to declare.

Acknowledgements

The research was supported by ERDF/ESF project ChemBioDrug CZ.02.1.01/0.0/0.0/16_019/0000729 (J. L.) and the Czech Science Foundation project 23-05983S (J. M.). The MD simulations were carried out using computational resources of the IOCB computational facility. The optical measurements were performed using resources of the IOCB optical microscopy facility.

References

1. M. Chalfie, Y. Tu, G. Euskirchen, W. W. Ward and D. C. Prasher, Science, 1994, 263, 802–805.
2. E. C. Greenwald, S. Mehta and J. Zhang, Chem. Rev., 2018, 118, 11707–11794.
3. F. I. Rosell and S. G. Boxer, Biochemistry, 2003, 42, 177–183.
4. X. Shi, J. Basran, H. E. Seward, W. Childs, C. R. Bagshaw and S. G. Boxer, Biochemistry, 2007, 46, 14403–14417.
5. D. Stoner-Ma, E. H. Melief, J. Nappa, K. L. Ronayne, P. J. Tonge and S. R. Meech, J. Phys. Chem. B, 2006, 110, 22009–22018.
6. T. Ansbacher, H. K. Srivastava, T. Stein, R. Baer, M. Merkx and A. Shurki, Phys. Chem. Chem. Phys., 2012, 14, 4109–4117.
7. M. Khrenova, I. Topol, J. Collins and A. Nemukhin, Biophys. J., 2015, 108, 126–132.
8. J. Myšková, O. Rybakova, J. Brynda, P. Khoroshyy, A. Bondar and J. Lazar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 32395–32401.
9. K. Suhling, D. M. Davis and D. Phillips, J. Fluoresc., 2002, 12, 91–95.
10. A. Volkmer, V. Subramaniam, D. J. Birch and T. M. Jovin, Biophys. J., 2000, 78, 1589–1598.
11. G. Striker, V. Subramaniam, C. A. Seidel and A. Volkmer, J. Phys. Chem. B, 1999, 103, 8612–8617.
12. A. J. Visser, A. H. Westphal, V. V. Skakun and J. W. Borst, Methods Appl. Fluoresc., 2016, 4, 035002.
13. M. A. Hink, R. A. Griep, J. W. Borst, A. Van Hoek, M. H. Eppink, A. Schots and A. J. Visser, J. Biol. Chem., 2000, 275, 17556–17560.
14. T. Masters, R. Marsh, T. Blacker, D. Armoogum, B. Larijani and A. Bain, J. Chem. Phys., 2018, 148, 134311.
15. J. M. Mullaney, R. B. Thompson, Z. Gryczynski and L. W. Black, J. Virol. Methods, 2000, 88, 35–40.
16. J. Hunt, A. H. Keeble, R. E. Dale, M. K. Corbett, R. L. Beavil, J. Levitt, M. J. Swann, K. Suhling, S. Ameer-Beg and B. J. Sutton, J. Biol. Chem., 2012, 287, 17459–17470.
17. M. A. Uskova, J.-W. Borst, M. A. Hink, A. van Hoek, A. Schots, N. L. Klyachko and A. J. Visser, Biophys. Chem., 2000, 87, 73–84.
18. S. T. Hess, E. D. Sheets, A. Wagenknecht-Wiesner and A. A. Heikal, Biophys. J., 2003, 85, 2566–2580.
19. F.-J. Schmitt, B. Thaa, C. Junghans, M. Vitali, M. Veit and T. Friedrich, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1581–1593.
20. C. Fang, R. R. Frontiera, R. Tran and R. A. Mathies, Nature, 2009, 462, 200–204.
21. Y. Teijeiro-Gonzalez, A. Crnjar, A. J. Beavil, R. L. Beavil, J. Nedbal, A. Le Marois, C. Molteni and K. Suhling, Biophys. J., 2021, 120, 254–269.
22. D. Axelrod, Biophys. J., 1979, 26, 557–573.
23. D. A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson and H. Gohlke, AMBER 2018, University of California, San Francisco, 2018.
24. E. Vanquelef, S. Simon, G. Marquant, E. Garcia, G. Klimerak, J. C. Delepine, P. Cieplak and F.-Y. Dupradeau, Nucleic Acids Res., 2011, 39, W511–W517.
25. S. V. D. Walt, S. C. Colbert and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 22–30.
26. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser and J. Bright, Nat. Methods, 2020, 17, 261–272.
27. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
28. V. Wong and D. A. Case, J. Phys. Chem. B, 2008, 112, 6013–6024.
29. A. Bondar, O. Rybakova, J. Melcr, J. Dohnálek, P. Khoroshyy, O. Ticháček, Š. Timr, P. Miclea, A. Sakhi and V. Marková, Commun. Biol., 2021, 4, 1–12.
30. A. Bondar and J. Lazar, J. Biol. Chem., 2017, 292, 9690–9698.
31. A. Bondar and J. Lazar, J. Biol. Chem., 2014, 289, 1271–1281.
32. A. Bondar and J. Lazar, FEBS J., 2021, 288, 2570–2584.
33. N. Nunthaboot, F. Tanaka, J. W. Borst and A. J. Visser, J. Photochem. Photobiol., A, 2022, 423, 113584.
34. L. Lindenburg and M. Merkx, Sensors, 2014, 14, 11691–11713.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01242e

---