Influence of intramolecular dynamics on the relaxation spectra of simple liquids

Abstract

The shape of the structural relaxation peak in the susceptibility spectra of liquids is of great interest, as it promises to provide information about the distribution of molecular mobilities and dynamic heterogeneity. However, recent studies suggest a generic shape of this peak near the glass transition temperature irrespective of the liquid under investigation, which somehow reduces the information contained in the peak shape. By contrast, at higher temperatures, say, around the melting point, the situation is different and the peak shape varies strongly between different liquids. In this study, we investigate molecules with a ring-tail structure and address the question how intramolecular dynamics influences the peak shape at these temperatures. Using depolarized light scattering and dielectric spectroscopy, we observe a bimodal relaxation, which we attribute to the fact that the reorientation of the ring group to some extent decouples from the rest of the molecule. This shows that the relaxation spectra are sensitive to details of the molecular motions at high temperatures, whereas in the supercooled state this microscopic information seems to give way to a generic shape, probably due to the onset of cooperativity which extends across different intramolecular moieties.

---

1. Introduction

The traditional view regarding the spectral shape of the structural relaxation in dynamic measurements is that at high temperatures all molecules perform rotational diffusion with more or less a single relaxation time, which leads to an approximately mono-exponential rotational correlation function or a symmetric Debye-peak in frequency domain measurements. As the temperature is lowered below the melting point, the dynamics is supposed to become heterogeneous, meaning that there exist different regions in the liquid with differing characteristic times of molecular motion. This emerging distribution of relaxation times leads to a broadening of the relaxation peak on lowering the temperature towards the glass transition.

However, in recent years it became obvious that this simple picture in many cases is not supported by observations. On the one hand, a broadening relative to the Debye shape often is still present at temperatures even far above the melting point,^1–5 and on the other hand it was shown recently that in the absence of cross-correlations the rotational correlation function in the supercooled regime close to the glass transition temperature shows a generic shape for different classes of liquids, including van der Waals, hydrogen bonding and even ionic systems.⁶ This was demonstrated by analyzing depolarized light scattering spectra, which are sensitive mainly to the self-part of the correlation function of the off-diagonal elements of the polarizability tensor of the molecule, and is also supported by NMR measurements.^7,8 Of course these results raise the question how exactly the peak shape is connected to dynamic heterogeneity, as this implies a generic distribution of relaxation times irrespective of the molecular details.

However, very recently a study on a homologous series of polyalcohols including glycerol, threitol, xylitol and sorbitol showed that the relaxation peak of these systems broadens with increasing chain length.⁹ By comparing light scattering spectra of sorbitol at temperatures above the melting point with correlation times of different CH-bonds obtained by ¹³ C-NMR,¹⁰ it became clear that the observed broadening is due to increasing intramolecular dynamic heterogeneity caused by dynamic decoupling of different CH-bonds. These heterogeneities seem to persist near the glass transition temperature and their occurrence might be related to the fact that polyalcohols form a strong H-bonding network leading to hindered reorientation of the carbon backbone. Motion requires breaking of several H-bonds, and even then only subgroups of the molecule are free to rotate.

Site specific NMR measurements of different molecules have shown that the intramolecular heterogeneity decreases with decreasing temperature,⁷ suggesting that the shape of the structural relaxation reflecting the intermolecular distribution of relaxation times might only be observed at low temperatures, while at high temperatures intramolecular degrees of freedom might alter the shape. In order for this to be visible in light scattering or dielectric spectra, these degrees of freedom need to be separated in timescale and must involve the rotation of an optically anisotropic or a dipolar part of the molecule, respectively.¹¹

First indications of bimodal light scattering spectra of non-hydrogen bonding molecules with a ring-tail structure were reported in ref. 12 and along these lines the main aim of this paper is to determine the molecular origin of such a bimodal behavior at temperatures above the melting point of the liquid, as a first step to understand the influence of different molecular properties affecting the spectral shape of the structural relaxation. We therefore employ several ring-tail structured molecules, differing in chain length, dipole moment and/or optical anisotropy. By a detailed comparison of dielectric and light scattering measurements we will show that the faster relaxation process is due to the ring group rotating independently of the rest of the molecule. Thus, also in non-hydrogen bonding liquids, intramolecular degrees of freedom can lead to complex relaxation spectra, at least at high temperatures.

2. Experimental details

Table 1 shows the investigated substances with their abbreviations, suppliers, melting points and chemical purities. The chemical structure of some of the molecules is shown in Fig. 1. Depolarized dynamic light scattering (DDLS) spectra were measured using a scanning multipass tandem Fabry Perot interferometer (TFPI) by JRS Scientific Instruments in backscattering geometry. As light source, a Coherent Verdi V2 laser with a wavelength of 532 nm was used. In order to suppress higher order transmissions of the TFPI,^13–15 the scattered light was passed through a narrow-band dielectric filter before detection.

Table 1 Table of investigated substances

Substance	Abbreviation	Supplier	T m (K)	Chemical purity (%)
a Specified by the supplier. b Determined by DSC measurements.
Toluene		Acros Organics	178^a	99.8
n-Tridecane	C13	Alfa Aesar	268^a	98
1-Phenyloctane	P8	Alfa Aesar	225^a	98
1-Phenyltridecane	P13	TCI America	283^a	99
1-Phenylnonadecane	P19	TCI America	309–314^a	98
1-Octylimidazole	Im8	Iolitec	—	98
1-Dodecylimidazole	Im12	Iolitec	289^b	98
8-Phenyl-1-octanol	P8ol	Sigma Aldrich	285^b	98
1-Bromo-3-n-octylbenzene	BrP8	TCI America	249^b	97

---

Fig. 1 Structure formula of the investigated molecules consisting of a linear chain and an aromatic ring.

The experiment probes the spectral density I(ω) of the scattered light. The generalized susceptibility χ(ω) was then calculated using the fluctuation dissipation theorem:

where n(ω,T) = (exp(ħω/k_BT) − 1)⁻¹ is the Bose factor and χ′′(ω) is the imaginary part of the generalized susceptibility. To obtain susceptibility spectra in a frequency range of approximately 200 MHz to 3 THz, we carried out up to five measurements with different mirror spacings and therefore different free spectral ranges, which were combined, by adjusting their amplitude, to obtain a smooth susceptibility χ′′(ω), a standard procedure, which is detailed, e.g., in ref. 16–20.

For the TFPI measurements all samples were filled into rectangular suprasil cuvettes with an inner diameter of 10 mm, sealed by a PTFE plug, except the P8ol and P19 samples, which were flame sealed to prevent reaction of the substances with oxygen at elevated temperatures. All substances that are liquid at room temperature were filtered using a 200 nm syringe filter to remove dust, except P8ol, which was not filtered due to its high viscosity, and P19, which has a wax-like consistency at ambient conditions and was measured without further purification. All samples were mounted in a home-built sample oven to reach the desired temperatures.

Dielectric loss spectra in the frequency range of approximately 10 Mhz to 2 GHz were obtained using a RF impedance analyzer (model E4991A by Agilent). The sample was contained in a cylindrical coaxial capacitor mounted in a home-built cryostat. More details about the experimental setup can be found in ref. 21. Since the obtained dielectric loss and TFPI spectra overlap in the frequency range of 200 MHz to 2 GHz, comparison of both can be used to investigate differences in the spectral shape between the two methods.

Fit procedure

Since all of the measurements in this work were carried out at temperatures above the melting point, the main relaxation of molecular reorientation takes place in the MHz to GHz range and usually is partly superimposed with high frequency features of the spectra. In order to disentangle these contributions, it is necessary to use a curve fitting approach which is able to describe the whole spectrum.

In ref. 22 a procedure was introduced to describe optical Kerr effect (OKE) spectra of n-alkanes at temperatures above the melting point in the GHz to THZ range. In this approach four different contributions to the spectra were identified, namely α- and β-relaxation, fast β-dynamics and libration, and a fit function was assigned to every one of these contributions, so that the superposition describes the whole spectrum. The α- and β-process were described by a Debye and a Cole-Cole function, respectively, and the fast β-dynamics and librations by Brownian oscillator functions. As finally all contributions were superimposed, the Debye and Cole–Cole functions need to be suppressed in the oscillatory regime by subtracting a “dropoff” term. For the example of the Debye function this results in:

with the relaxation time τ, an amplitude factor A and the dropoff frequency Ω, which was set to the characteristic frequency of the libration.

Besides the above mentioned work, there exists a large body of dielectric as well as light scattering studies that analyze high frequency spectra in detail,^23–29 where most of the studies use a similar analysis approach combining several relaxation and damped oscillator models, often using more than 4 model functions. In particular when the liquids are cooled to the point where the main relaxation peak shifts out of the frequency window of the used methods,^{13,14,19,20,30–32} the full complexity of the high frequency dynamics is revealed and a minimum between the main relaxation peak and the microscopic peak is observed. At higher temperatures, however, where the main relaxation peak is visible in the frequency window, these features are in general not visible and the spectra are made up of the main relaxation peak and a more or less pronounced microscopic peak, separated by some form of plateau. This case is shown in Fig. 2a for n-tridecane (C13). The dashed line represents a fit via a superposition of a Cole–Davidson (CD) function for the main relaxation peak, a Brownian oscillator function (BO) for the microscopic peak and a Debye function to account for the plateau region separating the main relaxation from the microscopic peak. Both, Cole–Davidson and Debye functions are supressed in the regime of the microscopic peak in analogy to the procedure of reference.²² We note that we use a Cole–Davidson function to describe the main relaxation peak instead of a number of Debye peaks because frequency temperature superposition (FTS) has been observed to hold for the unimodal main relaxation peaks in DDLS spectra of several substances from the glass transition up to temperatures close to the boiling point.^4,32–34 Thus, the usage of several model functions to describe the main relaxation peak is not required unless pronounced bimodal peak structures are observed.

Fig. 2 TFPI spectra of C13 (a) and P13 (b) at 360 K normalized to their maximum amplitude. The dashed curve represents a fit of the data viaeqn (2) and the colored curves denote the different components of the fit function (see text).

Fig. 2b shows the TFPI spectrum of P13 at 360 K normalized to its maximum amplitude. Comparing both spectra, it becomes obvious that the main relaxation peak of P13 shows a pronounced bimodal structure, consisting of two contributions, which will be called “slow” and “fast” process in the following. Accordingly, two Cole–Davidson functions are used, both suppressed in the regime of the microscopic peak at the frequency of the Brownian oscillator.

In total, the resulting fit function for a spectrum with a bimodal main relaxation peak therefore reads:

where the indices “slow” and “fast” refer to the parameters of the respective Cole–Davidson functions, “D” to the ones of the Debye function and “BO” to the Brownian oscillator model used to describe the microscopic dynamics. This procedure is suitable to describe all TFPI spectra of different substances presented in this work.

At this point it should be noted that the main relaxation peak in the spectrum of C13, regardless of the absence of the bimodal structure, clearly differs from the generic shape of the structural relaxation observed for many liquids close to the glass transition temperature. With a stretching parameter of β_CD = 0.86 it has a steeper high frequency slope than the generic shape, which is not uncommon at temperatures far above the glass transition temperature.³³ Interestingly, the stretching parameter of the slow process in the spectrum of P13 is with β_slow = 0.77 similar to that of the unimodal main relaxation peak of C13, which, considering the chemical structures of the molecules, could already suggest that both have a similar microscopic origin. Stretching parameters of the slow and fast contributions for all liquids, that show a bimodal main relaxation, can be found in Table 2. It should be noted that treating both processes that are so close in timescale as independent can only be an approximation. Since the two contributions are in general highly superimposed, no conclusions will be drawn based on the absolute values of stretching parameters obtained in this work.

Table 2 Stretching parameters of the slow and fast process obtained viaeqn (2) for the substances with a bimodal main relaxation peak

Substance	Temperature (K)	β slow	β fast
P8	360	0.71	0.79
P13	380	0.71	0.49
P19	440	0.78	0.27
P8ol	350	0.67	0.39
Im12	360	0.64	0.42
BrP8	300	0.44	0.89

---

3. Results and discussion

1-Phenylalkanes

Fig. 3 shows TFPI spectra of the 1-phenylalkanes P8, P13 and P19 at several temperatures normalized to their maximum amplitude and the peak time constant τ_slow of their respective slow process. The latter were determined using eqn (2) and the temperature ranges were chosen, so that both peaks are visible within the experimental frequency window. In order to better compare the spectra the data of P19 were additionally shifted in amplitude. All presented spectra share the bimodality of the main relaxation peak highlighted in Fig. 2b, in a less pronounced way for P8 and more pronounced in the spectra of P19. Just by visual inspection of the spectra it is obvious that the relative amplitude of the fast process seems to increase with increasing temperature and the separation between slow and fast process seems to increase with increasing chain length.

Fig. 3 TFPI spectra of P8 (a), P13 (b) and P19 (c) at several temperatures normalized to their maximum amplitude and the peak time constant of the slow process. The insets show sections of the spectra to highlight changes in the spectral shape of the main relaxation peak. The dashed curves are fits via eqn (2) with fixed parameters β_slow and β_fast (see text).

To visualize the effect of chain length on the spectra, we compare spectra of the three substances at similar τ_slow. Fig. 4 shows TFPI spectra of P8 at 300 K (τ_slow ⋍ 93 ps), P13 at 360 K (τ_slow ⋍ 107 ps) and P19 at 420 K (τ_slow ⋍ ps) normalized in the same way as in Fig. 3.

Fig. 4 TFPI spectra of P8, P13 and P19 at similar τ_slow (see text) normalized as in Fig. 3. The inset shows τ_slow/τ_fast for the three substances and respective temperature ranges.

As a measure of separation the ratio τ_slow/τ_fast is calculated for all substances and temperatures. For the fits represented as dashed curves in Fig. 3, which were used to obtain τ_slow and τ_fast, the parameters β_slow and β_fast were fixed for each substance to the values obtained at the most suitable temperature (see Table 2).

The inset of Fig. 4 shows the separation of the peak time constants of fast and slow process for the three substances. The data points obtained for the three particular data sets shown in the main figure are represented as diamonds. It becomes obvious that the separation increases with the length of the alkyl chain and therefore the curve fitting confirms the observations already made by visual inspection of the spectra. In addition to this chain length dependence the separation shows a decrease with increasing temperature, which is due to the fact that the processes merge with the microscopic dynamics in the investigated temperature range.

Because of the increasing separation of the processes with increasing alkyl chain length, it was the initial hypothesis that the observed bimodality emerges due to dynamic decoupling of the phenyl ring and the alkyl chain. To test this, TFPI spectra of mixtures of P13 and C13 as well as P13 and toluene were investigated, as C13 resembles the chain group of P13 while toluene is similar to the ring group. The idea was to determine to which region of the spectra the dynamics of C13 and toluene contribute in mixtures with P13, expecting toluene to contribute to the faster phenyl ring process of P13 while C13 should reorient approximately on the timescale of the P13 alkyl chains, and thus contribute to the slow process. Fig. 5 shows the TFPI spectra of P13, C13 and mixtures of P13 and C13 as well as P13 and toluene at 360 K. The data were normalized with respect to the slow process as before and the spectra of mixtures of P13 and toluene were aditionally shifted in amplitude to be comparable. For the fits of the mixtures the parameters β_slow and β_fast were fixed to the values obtained for the spectrum of P13. For the spectra of C13 and toluene the unimodal approach of Fig. 2a was used. The spectra of the mixtures of P13 and toluene show an increase in amplitude in the region of the fast process with increasing volume fraction of toluene, indicating that toluene molecules seem to reorient on the timescale of the fast process. The spectra of the mixtures of P13 and C13 on the other hand show a relative decrease of amplitude in the region of the fast process with increasing volume fraction of C13 indicating motion of C13 molecules on the timescale of the slow process. These results confirm that the fast process arises due to reorientation of the phenyl ring being decoupled from the motion of the alkyl chain.

Fig. 5 TFPI spectra of P13, C13, mixtures of P13 and C13 as well as mixtures of P13 and toluene at 360 K. Concentrations are given as volume fractions of C13 or toluene respectively. The spectra were shifted in amplitude in order to collapse the low frequency flanks.

Comparison of different ring groups

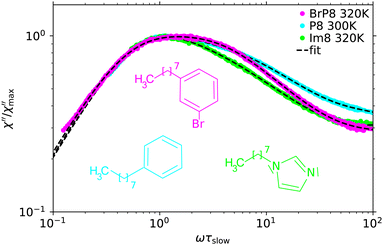
To investigate if the observed effect is an exclusive property of systems containing a phenyl ring or a common feature of systems consisting of a linear chain attached to a ring group, we compare TFPI spectra of P8, Im8 and BrP8. These molecules all consist of an alkyl chain of length n = 8 with different ring groups attached to the end (see Fig. 1). Fig. 6 shows a section of the TFPI spectra of Im8 at 320 K, P8 at 300 K and BrP8 at 320 K normalized with respect to the slow process. The presented section is chosen to highlight differences in the spectral shape of the main relaxation peak between the substances and the presented temperatures were again chosen, so that τ_slow ≈ 100 ps is similar for all spectra.

Fig. 6 TFPI spectra of BrP8 at 320 K, P8 at 300 K and Im8 at 320 K to highlight differences in the spectral shape of the main relaxation peak between the substances. The spectra have been normalized with respect to the slow relaxation.

Comparing the spectra one notices significant differences in the spectral shape of the main relaxation peak. Similar to the spectrum of P8, the spectrum of BrP8 shows a bimodal main relaxation while the peak of Im8 is more narrow and can be described by a single Cole–Davidson function with β_CD = 0.45 to good approximation. To determine if the alkylimidazoles simply do not share the bimodal structure of the main relaxation peak observed for the other substances, we also investigated Im12 in an attempt to further separate the two processes, provided they exist. Fig. 7 shows the TFPI spectra of Im8 at 320 K and Im12 at 360 K applying the same normalization as before. The fit of the Im8 spectrum was obtained using eqn (2) with β_slow and β_fast fixed to the values obtained for Im12 (see Table 2). Using this curve fitting approach, the amplitude of the fast process needed to describe the spectrum has a much smaller amplitude for Im8 than for Im12. This comparison shows that the spectra of the alkylimidazoles exhibit a bimodal structure of the main relaxation peak similar to that of the other investigated substances. Only the relative amplitude of the fast process is smaller and therefore a larger separation of the processes, i.e., a longer alkyl chain is required to observe the separation in the spectra.

Fig. 7 TFPI spectra of Im12 at 360 K and Im8 at 320 K normalized with respect to the slow process. Black curves are fits to the data and colored curves denote the Cole–Davidson components describing the slow and the fast process (see text).

Inspecting Fig. 6 one might argue that the relative amplitude of the fast process depends on the molecular structure of the ring group of the molecule under study. A link between scattering amplitude in depolarized (VH) geometry and molecular properties is given by the relation for the scattering intensity:

I_VH ∝ N·β², (3)

where N is the number density of molecules in the scattering volume and β the optical anisotropy parameter.^35,36 Since we assigned the fast process to reorientation of the ring group, we suggest that the relative amplitude of the fast process should be correlated with the part of the optical anisotropy of the molecule that is related to the ring group.

To qualitatively test this idea, we performed density functional (DFT) calculations to obtain the anisotropy parameter β for the different ring groups. For these calculations the program Orca (version 4.2.1) was used with the functionals B3LYP and def2-TZVPP as the basis set and the starting positions of the atoms were determined by the molecule visualizer Avogadro (version 1.20). Since the ring groups on their own would be ions, the chargeless rings imidazole (Im), benzene (P) and bromobenzene (BrP) were used for these calculations. The resulting anisotropy parameters are β_Im = 3.46 Å, β_P = 5.79 Å and β_BrP = 9.15 Å. This result qualitatively matches the observation made in Fig. 6, where the relative amplitude of the fast process increases with increasing β² of the ring group. Beyond such a qualitative comparison, however, the influence of the optical anisotropy on the relative amplitude of the fast process is hard to judge, since slow and fast process are strongly superimposed but differ in their τ_slow/τ_fast ratio so that quantitative measures of the strength cannot be reliably extracted. Moreover, the strength will also depend on other parameters such as the degree of coupling of the intramolecular degrees of freedom. Thus, we will refrain from a quantitative discussion of the strength of processes.

Comparison of dielectric spectroscopy and depolarized dynamic light scattering

In order to further check our interpretation of the microscopic origin of the bimodality of the light scattering spectra, we performed dielectric spectroscopy (DS) on molecules where the dipole moment is located either on the chain or on the ring group. For the first case P8ol was chosen because of its similarity to the 1-phenylalkanes in terms of molecular structure and the fact that it contains a hydroxyl group at the end of the chain group opposite to the phenyl ring. The hydroxyl group dominates the overall molecular dipole moment, considering its dipolar strength of μ_OH ≈ 1.68 D compared to the dipole moment μ_π ≈ 0.36 D located at the phenyl ring.³⁷ Therefore, DS is mainly sensitive to the reorientation of the alkyl chain end. Thus, if the assignment of the fast process to reorientation of the phenyl ring is correct, just an unimodal peak shape should be observed in the dielectric loss.

Fig. 8a shows dielectric loss spectra of P8ol at several temperatures. The dielectric loss was curve fitted using the Cole–Davidson model. Analyzing the stretching parameters one notices that β_CD is approximately constant for temperatures where a sufficient part of the high frequency flank of the α-peak is visible in the frequency window. In fact all spectra can in good approximation be described by a Cole–Davidson function with fixed β_CD = 0.59 as shown in the inset of Fig. 8a.

Fig. 8 Dielectric loss of P8ol (a), Im12 (b) and BrP8 (c) at several temperatures. The P8ol spectra were curve fitted by the Cole–Davidson model and the inset shows the superposition of the spectra obtained by fitting with fixed β_CD and presentation in terms of the reduced frequency ωτ_α. The spectra of Im12 and BrP8 were curve fitted with a superposition of two Cole–Davidson functions (see text).

Fig. 9a shows the TFPI spectrum of P8ol at 350 K and the dielectric loss spectra at 349.3 K and 291.7 K combined to form a master curve by shifting the spectrum at 291.7 K with a factor τ_α(291.7K)/τ_α(349.3K).

Fig. 9 Comparison of TFPI spectra and dielectric loss spectra of P8ol (a), Im12 (b) and BrP8 (c) normalized to their maximum amplitude. The dielectric loss spectra have additionally been shifted in amplitude for better comparison. Dielectric loss spectra are combined with a shifted spectrum at a lower temperature as an estimate for their possible high frequency spectral shape (see text). Colored curves denote the two Cole–Davidson functions which were superimposed to describe the dielectric loss of Im12 and BrP8.

Both dielectric spectra were shifted in amplitude for better comparison and it turns out that the dielectric loss peak shows a unimodal shape and is significantly more narrow than the main relaxation peak in the TFPI spectra, which has a bimodal structure similar to that of the 1-phenylalkanes and was again described by eqn (2). Stretching parameters can be found in Table 2.

To demonstrate that both DS and DDLS can be sensitive to intramolecular dynamic heterogeneity depending on its influence on the optical anisotropy of molecular subunits in the case of DDLS and on the total molecular dipole moment in case of DS, we additionally investigated the substances BrP8 and Im12. In contrast to P8ol the dipole vector of these molecules has a substantial component perpendicular to the chain located at the ring group. Thus, the reorientation of the ring group has a non-negligible influence on the molecular dipole vector and should therefore be visible in the dielectric loss. Fig. 8b and c shows dielectric spectra of Im12 and BrP8 at several temperatures. The spectra of both substances show a bimodal main relaxation peak and therefore are described by a superposition of two Cole–Davidson functions.

Fig. 9b and c show a comparison of TFPI and dielectric loss spectra of Im12 and BrP8. The spectra were normalized to their maximum amplitude and the dielectric loss spectra were additionally shifted in amplitude for better comparison. In the same way as for part (a) of the figure the frequency axis of the dielectric spectra at lower temperatures was rescaled by the ratio τ(T_high)/τ(T_low), in this case using the time constants of the slow process. The total fit function and the colored curves denoting the two Cole–Davidson contributions shown in Fig. 9b and c are the ones decomposing the dielectric spectrum at the higher temperature. Thus, it becomes obvious that the spectra do not perfectly superimpose, probably due to temperature dependencies of the relative amplitudes and the separation between the two processes, like it was demonstrated in the case of the 1-phenylalkanes in Fig. 3. It should also be mentioned that the shifted dielectric loss spectra from lower temperatures can only be seen as a rough estimate of the high frequency spectral shape at higher temperatures.

While the spectra exhibit a bimodal shape in both methods, there are also clear differences: For example, the relative amplitude of the fast process seems to differ between the two methods. This result can be explained by comparing the respective directions of the dipole vectors of the molecules, which are illustrated in Fig. 9, and the optical anisotropy of their respective ring groups. Since the direction of the dipole vector is similar for both molecules, reorientation of the ring group has comparable impact on the total molecular dipole moment, resulting in similar dielectric loss spectra. By contrast, the part of the optical anisotropy related to the ring group differs strongly between the two molecules, resulting in differences in the spectral shape between light scattering and dielectric spectroscopy.

4. Conclusions

Against the background of a generic spectral shape of the structural relaxation, which was recently reported for different classes of supercooled liquids close to the glass transition, the present paper raises the question in how far the spectral shape diversity observed at high temperatures reflects individual molecular properties. As model systems, in the present study several molecules consisting of a linear alkyl chain attached to an aromatic ring were investigated and it was shown that the depolarized light scattering spectra show a bimodal main relaxation peak at temperatures above the melting point. By analyzing the spectra of 1-phenylalkanes it was demonstrated that the two contributions separate with increasing chain length. In mixtures of 1-phenyltridecane with n-tridecane or toluene, the toluene molecules contribute to the spectral region of the fast process and the n-tridecane molecules to the spectral region of the slow process, indicating that the fast process arises due to reorientation of the phenyl ring decoupled from the alkyl chain motion. Furthermore, by analyzing the spectra of similar systems with different ring groups, i.e., alkylimidazoles and 1-bromo-3-n-octylbenzene, it was demonstrated that this phenomenon is not exclusive to 1-phenylalkanes but rather a feature shared by many systems with similar molecular structure. DFT calculations of the anisotropy parameter of the different ring groups indicate that the relative amplitude of the fast process correlates with the optical anisotropy of the ring group, as one would intuitively expect considering the suggested origins of fast and slow process.

We also compared DS and DDLS measurements of 8-phenyl-1-octanol, 1-dodecylimidazole and 1-bromo-3-n-octylbenzene. Our experiments show, that there are significant differences in sensitivity of both methods regarding this form of intramolecular dynamic heterogeneity. In contrast to DDLS the dielectric loss spectra of 8-phenyl-1-octanol show no sign of a bimodal main relaxation, since DS is mainly sensitive to reorientation of the chain end to which the hydroxyl group is attached. In the case of 1-dodecylimidazole and 1-bromo-3-n-octylbenzene, where the reorientation of the ring group has a substantial influence on the molecular dipole moment vector, both methods show a bimodal main relaxation. How reorientation of different dynamically decoupled molecular units appears in DDLS and DS therefore depends on their optical anisotropy and how they contribute to the molecular dipole moment.

All in all, our results show that the diverse spectral shapes observed in light scattering as well as dielectric spectroscopy above the melting point clearly are sensitive to intramolecular heterogeneities to an extent that in the presented cases individual spectral features can be clearly assigned to molecular subunits. This is in stark contrast to the generic shape of the structural relaxation, which is observed on approaching the glass transition temperature. Although most of the molecules considered in the present study cannot be supercooled far enough due to their tendency towards crystallization, one may expect that the growing importance of inter- and intramolecular cooperativity will diminish the differences observed around the melting point on approaching the glass transition. However, to explore the crossover between these two regimes in more detail has to be left open for further studies.

Author contributions

Th. B., F. P., T. B. and R. Z. conceptualized experiments, R. Z. and F. P. performed experiments and analyzed data, R. Z. wrote the original draft, Th. B., F. P., and T. B. edited and reviewed the draft. Th. B. provided resources, acquired funding and supervised the experiments and data analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support by the Deutsche Forschungsgemeinschaft under grant no. BL 1192/3 is gratefully acknowledged.

Notes and references

1. P. Lunkenheimer, L. Pardo, M. Köhler and A. Loidl, Phys. Rev. E, 2008, 77, 031506.
2. P. Lunkenheimer, U. Schneider, R. Brand and A. Loid, Contemp. Phys., 2000, 41, 15–36.
3. U. Schneider, R. Brand, P. Lunkenheimer and A. Loidl, Eur. Phys. J. E, 2000, 2, 67–73.
4. B. Schmidtke, N. Petzold, B. Potzschner, H. Weingartner and E. Rössler, J. Phys. Chem. B, 2014, 118, 7108–7118.
5. H. Cummins, G. Li, W. Du, J. Hernandez and N. Tao, J. Condens. Matter Phys., 1994, 6, A51.
6. F. Pabst, J. P. Gabriel, T. Böhmer, P. Weigl, A. Helbling, T. Richter, P. Zourchang, T. Walther and T. Blochowicz, J. Phys. Chem. Lett., 2021, 12, 3685–3690.
7. M. Becher, T. Körber, A. Doöβ, G. Hinze, C. Gainaru, R. Böhmer, M. Vogel and E. Rössler, J. Phys. Chem. B, 2021, 125, 13519–13532.
8. T. Körber, R. Stäglich, C. Gainaru, R. Böhmer and E. A. Rössler, J. Chem. Phys., 2020, 153, 124510.
9. T. Böhmer, J. P. Gabriel, R. Zeißler, T. Richter and T. Blochowicz, Phys. Chem. Chem. Phys., 2022, 24, 18272–18280.
10. B. Sixou, L. David, M. Margulies, J.-Y. Cavaillé and G. Vigier, Mol. Simul., 2001, 27, 243–265.
11. M. Rams-Baron, B. Yao, S. Cheng, M. Dulski and M. Paluch, J. Phys. Chem. Lett., 2021, 12, 11303–11307.
12. F. Pabst, PhD thesis, 2022.
13. N. Surovtsev, J. Wiedersich, V. Novikov, E. Rössler and A. Sokolov, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 14888.
14. J. Gapiński, W. Steffen, A. Patkowski, A. Sokolov, A. Kisliuk, U. Buchenau, M. Russina, F. Mezei and H. Schober, J. Chem. Phys., 1999, 110, 2312–2315.
15. H. Barshilia, G. Li, G. Shen and H. Cummins, Phys. Rev. E, 1999, 59, 5625.
16. G. Li, W. Du, X. Chen, H. Cummins and N. Tao, Phys. Rev. A, 1992, 45, 3867.
17. G. Li, W. Du, A. Sakai and H. Cummins, Phys. Rev. A, 1992, 46, 3343.
18. W. Du, G. Li, H. Z. Cummins, M. Fuchs, J. Toulouse and L. Knauss, Phys. Rev. E, 1994, 49, 2192.
19. A. Brodin and E. A. Rössler, Eur. Phys. J. B, 2005, 44, 3–14.
20. J. Wiedersich, N. Surovtsev, V. Novikov, E. Rössler and A. Sokolov, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 064207.
21. M. Appel, T. L. Spehr, R. Wipf, C. Moers, H. Frey and B. Stühn, J. Chem. Phys., 2013, 139, 184903.
22. A. J. Farrell, M. Gonzalez-Jimenez, G. Ramakrishnan and K. Wynne, J. Phys. Chem. B, 2020, 124, 7611–7624.
23. T. Fukasawa, T. Sato, J. Watanabe, Y. Hama, W. Kunz and R. Buchner, Phys. Rev. Lett., 2005, 95, 197802.
24. T. Sonnleitner, D. A. Turton, G. Hefter, A. Ortner, S. Waselikowski, M. Walther, K. Wynne and R. Buchner, J. Phys. Chem. B, 2015, 119, 8826–8841.
25. D. A. Turton, J. Hunger, A. Stoppa, G. Hefter, A. Thoman, M. Walther, R. Buchner and K. Wynne, Terahertz Technology and Applications III, 2010, pp. 130–139.
26. D. A. Turton, J. Hunger, A. Stoppa, A. Thoman, M. Candelaresi, G. Hefter, M. Walther, R. Buchner and K. Wynne, J. Mol. Liq., 2011, 159, 2–8.
27. A. Stoppa, A. Nazet, R. Buchner, A. Thoman and M. Walther, J. Mol. Liq., 2015, 212, 963–968.
28. I. Płowaś-Korus and R. Buchner, Phys. Chem. Chem. Phys., 2019, 21, 24061–24069.
29. I. Płowaś-Korus and R. Buchner, J. Mol. Liq., 2021, 340, 116838.
30. J. Wiedersich, N. Surovtsev and E. Rössler, J. Chem. Phys., 2000, 113, 1143–1153.
31. J. Wuttke, J. Hernandez, G. Li, G. Coddens, H. Cummins, F. Fujara, W. Petry and H. Sillescu, Phys. Rev. Lett., 1994, 72, 3052.
32. N. Petzold and E. Rössler, J. Chem. Phys., 2010, 133, 124512.
33. B. Schmidtke, N. Petzold, R. Kahlau and E. Rössler, J. Chem. Phys., 2013, 139, 084504.
34. N. Petzold, B. Schmidtke, R. Kahlau, D. Bock, R. Meier, B. Micko, D. Kruk and E. Rössler, J. Chem. Phys., 2013, 138, 12A510.
35. B. J. Berne and R. Pecora, Dynamic light scattering: with applications to chemistry, biology, and physics, Courier Corporation, 2000.
36. F. Pabst and T. Blochowicz, J. Chem. Phys., 2022, 157, 244501.
37. C. L. Yaws, Thermophysical properties of chemicals and hydrocarbons, William Andrew, 2008.

---