A total scattering study of prenucleation structures in saturated aqueous magnesium sulfate – observation of extended clusters

Abstract

Through a combination of X-ray and neutron total scattering and Empirical Potential Structure Refinement (EPSR) we explore the prenucleation structures of saturated aqueous magnesium sulfate. The atomistic model we present reveals a system characterised by isolated octahedral aquo magnesium species Mg(H₂O)₆, magnesium sulfate pairs (Mg(H₂O)₅SO₄) and extended clusters built from corner-sharing MgO₆ and SO₄ polyhedra. Many of these features are directly observed in the crystal structures of the known solid form hydrates, including isolated polyhedra, corner sharing chains and rings, and it is only for the extended 3D polyhedral networks of the lower hydrates (mono- & di-) that no proto structures are observed in 2M solution. Looking at the average first solvation shell of the sulfate anion we see a complex and flexible environment that commonly includes water molecules brought into proximity by a coordinated hydrated magnesium. What emerges is a high probability that 10 water molecules will be observed in a combined tetrahedral/octahedral arrangement with a further 7 taking up more dispersed positions giving an average coordination of 17. The tendency for ions to aggregate into clusters allows areas of bulk water to exist that exhibit subtle differences in structure to that of pure water.

---

Introduction

Magnesium sulfate is a compound of great interest; it has been located on Mars and is thought to be an important indicator in the search for past life and crucial to the understanding of the hydrological history of the planet.¹ It is also believed to be present in the mysterious bright spots seen on the dwarf planet Ceres that circles in the asteroid belt.² Medicinally the heptahydrate (the most thermodynamically stable form) is used externally as Epsom (bath) salts and internally to treat magnesium deficiency, indeed a recent study has suggested the possibility of using a magnesium supplement in this form as a supportive treatment for COVID-19 patients.³ In agriculture it is used to increase the magnesium and sulfur content of soils, promoting the growth of certain magnesium-hungry crops (without significantly altering the pH)⁴ and it is used as a brewing salt in beer making.⁵ In its anhydrous form it is used in the laboratory as a desiccant and in the construction industry in the preparation of specific cements.⁶ There has also been sporadic interest in using magnesium sulfate hydrates as thermochemical heat storage materials.⁷

Magnesium sulfate in the solid-state

In its anhydrous form magnesium sulfate is hygroscopic and it is thus usually encountered in one of its many hydrated forms, MgSO₄·xH₂O (x = 0–2, 4–7, 9 & 11 have known crystal structures).^8–17 The relative stability and crystallisation pathways of these hydrates is complex, for example at atmospheric pressure the undecahydrate is unstable above 275 K and breaks down into a mixture of crystalline heptahydrate and saturated solution,¹⁸ whereas at a pressure of 0.9 GPa and temperature of 240 K it decomposes to a mixture of ice VI and the enneahydrate.¹⁶

Magnesium sulfate in aqueous solution

As referenced above there are extensive reports in the literature describing the crystal structures of the various magnesium sulfate hydrates, but far fewer studies attempt to probe the nature of its structure in solution. Early work by Robson looked at the stability of the various magnesium sulfate hydrates as crystallised from solution at various temperatures and suggested “a relation between the degree of crystallographic perfection exhibited by a salt and the rate at which it comes to equilibrium with its aqueous solution.”¹⁹ Balasubramanian and co-workers²⁰ describe a molecular dynamics study showing the water coordination around sulfate decreasing as the concentration increases due to ion pair formation; whereas much earlier Raman studies by Daly and co-workers²¹ provide no evidence for this Mg/SO₄ ion pairing suggesting instead that these are solvent separated. Vchirawongkwin and co-workers²² describe a combined large angle X-ray scattering and ab initio quantum mechanical charge field (QMCF) molecular dynamics (MD) study of aqueous Li₂SO₄ concluding that sulfate exhibits an average coordination number of slightly less than 12. Chipera and Vaniman²³ undertook a detailed study of the stability of magnesium hydrates and their crystallisation from solution at various temperatures and vapour pressures, ultimately concluding that the system is highly complex.

A small number of total X-ray scattering studies have been conducted looking at water coordination around various cations, including Mg²⁺, such as that by Skipper and co-workers²⁴ and whilst these show the expected octahedral coordination around magnesium, they do not look at anion solvation or use an atomistic modelling approach. A combined total scattering and computational modelling study was recently reported by Wang and co-workers and this did use an atomistic model to look at the structure of magnesium nitrate and we will compare some of our results to theirs.²⁵ A similar study was also conducted by Jensen and co-workers looking at amorphous magnesium/calcium carbonates.²⁶

In the wider context of clustering in solution Svärd and co-workers²⁷ have reported impressive studies of molecular systems (fenoxycarb) using a whole barrage of techniques from dynamic light scattering and small angle X-ray scattering to molecular dynamics simulations looking at the molecular clustering in isopropanol solutions. These show evidence of cluster size growth with increasing concentration; however, these studies tend to focus on the larger scale structures (up to a micrometre) and provide less direct evidence of the intermolecular structures at the heart of the clusters. Intriguingly they also present evidence of smaller clusters in solutions preheated to higher temperatures which is a possible explanation of the “history of solution” phenomena.

Our work, described herein, can be best considered as a direct experimental extension to the molecular dynamic studies of Balasubramanian and co-workers²⁰ and a parallel study to that of Wang and co-workers; it is the first in a number of studies in which we will expand on the use of total X-ray scattering and Empirical Potential Structure Refinement to probe the structure of magnesium sulfate solutions at different concentrations and temperatures. What makes this approach so powerful is its ability to visualise directly molecular interactions such as hydrogen bonds, and thus allow conjecture around nucleation phenomena.

Experimental methods

Neutron and X-ray total scattering measurements

To investigate the structure of a metal salt in aqueous solution it is useful to combine two types of experimental probes. Neutrons are scattered strongly by hydrogen atoms and provide information predominantly from the water structure. An additional advantage is the ability to significantly alter the contribution to the scattering profile through isotopic substitution. X-rays are only weakly scattered by hydrogen atoms but provide a much stronger signal from the atoms of the solute. Thus, combining these two probes provides holistic information on all components of the system.

Neutron data were collected using the Small Angle Neutron Diffractometer for Amorphous and Liquid Samples (SANDALS) at the ISIS spallation neutron source at the Rutherford Appleton Laboratory, UK. To take advantage of the beamline's optimisation for hydrogen/deuterium substitution three isotopically unique solutions of 2M MgSO₄ were measured: (i) fully deuterated, (ii) hydrogenated and (iii) an equimolar mixture of the two. The samples were presented to the neutron beam in a 1 mm path length flat-plate null coherent scattering titanium/zirconium cell and kept at ambient temperature and pressure. Scattering data were accumulated for approximately 8 hours per sample and correction and calibration data were recorded from the empty instrument, the empty sample cell and a VNb null scattering slab. X-ray data were measured in-house on a modified Rigaku Spider curved image plate system which has been previously described.²⁸ The sample was secured in a 2 mm borosilicate capillary and exposed for 3 hours with corresponding empty capillary and empty instrument measurements also being made. All data were corrected for absorption, multiple scattering, non-sample scattering and were scaled to optimally follow the total scattering cross section of the sample (normalisation). All data corrections were performed using GUDRUN or GUDRUNX as appropriate to the incident radiation.²⁹ Whilst a detailed description of the methods can be found in the publications associated with these programs, a brief summary is provided below for completeness; this closely follows the description reported by Headen.

A neutron scattering experiment measures the differential scattering cross section³⁰ and after appropriate corrections returns the total structure factor, F(Q). As neutrons are scattered from nuclei we can take advantage of the different scattering lengths, b_i, possessed by different isotopes. In this case it is the substitution of hydrogen (b_H = −3.74 fm) for deuterium (b_D = 6.67 fm) that provides 3 complimentary data sets for samples with the same chemical, but different isotopic, composition and this places strong constraints on the structure refinement. Here, the measured quantity, F_i(Q), is the weighted sum of the different partial structure factors arising from pairs of atoms, α, β.

where c_α is the atomic fraction of species α, b_α is its neutron scattering length, Q is the magnitude of the momentum transfer of the scattered neutrons given by Q = 4π(sinθ)/λ, S_αβ(Q) is the partial structure factor solely for species α and β and a δ_αβ = 1 for the case of α = β and 0 in all other cases to avoid double counting. Analogous scattering equations are available for X-ray data allowing this data to further constrain any fitted structure, with an added complication that these must explicitly include the atomic form factors as detailed by Soper.³¹

S _αβ (Q) encodes information pertaining to correlations between species α and β, and is defined in Q-space as given by:

Here, ρ₀ is the atomic number density for the sample and g_αβ(r) describes the partial distribution function for the relative density of atoms of species β as a function of their distance, r, from species α. The total radial distribution function, f(r) is thus given by the weighted sum of the partial radial distribution functions describing the sample,and is directly related to the measured data F(Q) through its Fourier transform:

Empirical potential structure refinement

X-ray and neutron data were fitted using the empirical potential structure refinement approach (EPSR) which produces an atomistic ensemble consistent with the combined scattering data. This method is described in detail elsewhere,³² but starts with an equilibrated Monte Carlo simulation based on selected seed potentials. The observed scattering data is then introduced by iteratively modifying an empirical potential that is formulated from the difference between the observed and calculated structure factors. Prior chemical knowledge is included in the form of restraints, describing, for example, the shape of a molecular species or limiting the closest approach of atom pairs.

In this work a model of box edge 30.60 Å was found sufficient to satisfactorily fit the data and consisted of 250 magnesium cations (Mg²⁺), 250 sulfate anions (SO₄²⁻), 6938 water molecules (H₂O) and a number density of 0.1074 atoms per ų giving the desired sample density. The seed potentials are detailed in Table 1 and are based on a Leonard-Jones potential plus a coulomb term and are adapted from Balasubramanian and co-workers²⁰ and Sambasivarao and Somisetti.³³

Table 1 Seed potential parameters used for EPSR model where q is the partial charge and σ and ε are the ‘particle size’ and potential well depth of the Lennard-Jones potential respectively. The site label denotes the atom reference in the EPSR model and distinguishes between the sulfate oxygen O1, and the water oxygen Ow. Total of 250 Mg²⁺, 250 SO₄²⁻ and 6938 H₂O

Site label	# of atoms	σ/Å	ε/kJ mol^−1	q/e
Mg1	250	0.80	1.90	2.00
S1	250	0.73	3.55	2.40
O1	1000	0.84	3.20	−1.10
Ow	6938	0.65	2.10	−0.85
Hw	13 876	0.00	0.00	0.42

---

Initial refinements produced some features in the F(r) at low r values that we did not observe in the experimental data and it was necessary to include several minimum distance restraints to prevent atom pairs becoming unrealistically close, full details are provided in Table S1 of the ESI.† Once the refinement had converged a further 6000 iterations were performed to allow accumulations of alternative (but equally likely) ensembles for later statistical analysis. A small part of the refined model is depicted in Fig. 1a.

Fig. 1 Atomistic model with selected features isolated. (a) Section of the complete model box, (b) fully hydrated magnesium, (c) bridging sulfate, (d) region of bulk water, and (e) example hydration shell of sulfate (out to 5 Å).

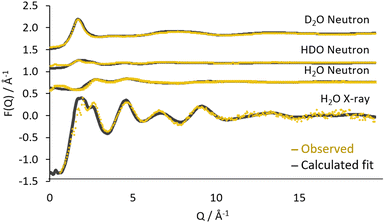
The fit of the calculated data to the combined observed data, plotted as F(Q) is shown in Fig. 2 and as the f(r) in Fig. 3. Generally, a good agreement is found between the refined model and the experimental data for both radiation sources as well as the deuterated systems.

Fig. 2 EPSR refinement for 2.00 M MgSO₄ where yellow crosses denote experimental data and solid lines represent the model fit. The x-axis is shown from Q = 0.42 Å⁻¹ which corresponds to 2π/(half box length) below which the simulated data become unreliable. Data sets are offset on the y-axis.

Fig. 3 Observed f(r) (yellow dots) and EPSR fit (grey lines) for the neutron and X-ray data. Data sets are offset on the y-axis. Around the 1 Å region the f(r) is dominated by hydrogen interactions and these are poorly represented in the X-ray scattering data (small scattering factor of hydrogen). This region is often omitted form the fit entirely.

A small discrepancy can be seen at low Q in the H₂O neutron data, this originates from the uncertainty in the inelasticity corrections implemented during the correction of the data.³⁴

Interpretation of the refined model

To successfully interpret the refined model, it is necessary to derive further quantities from the EPSR generated ensemble and the most easily visualised of these is the spatial density function (SDF). When plotted, this depicts volumes of space enclosing the highest density regions that contain a specified percentage of atom A around a central atom B. If A represents water and B sulfate, and an appropriate radial cut off is applied, the resultant figure will show the first solvation shell, as described in more detail in Fig. 8 later in the discussion. Adjusting the radial cut off enables visualisation of more distant shells and adjusting the percentage level plotted aids interpretation of the more persistent features. More quantitative insight can be gained by considering these SDF plots in combination with other derived data such as coordination numbers (nearest neighbours within a given radial distance) and calculated pair-wise radial distribution function (RDF) plots (one-dimensional spherically averaged nearest neighbour distributions).

Results and discussion

Prominent model features

The most striking feature to emerge in the model following the introduction of the empirical potential is the electrostatic association of sulfate and magnesium ions to form discrete clusters of various sizes. These are dispersed in what can be considered as bulk water regions and examples can be observed directly in the atomistic ensembles of the model (Fig. 1). The development of these features is consistent with the experimental data.

Magnesium environment

As would be expected the magnesium adopts an octahedral geometry for its first solvation shell, and this can be most clearly seen in the coordination number statistics derived from the atomistic ensembles, seen in Fig. 4a. The numbers observed here are in good general agreement with those reported by Wang and co-workers when comparing to their water-salt ratio of (WSR) 30 – our 2M MgSO₄ solution has a WSR of 24.²⁵

Fig. 4 (a) Coordination numbers of magnesium (Mg1) to sulfate (O1) and water (Ow), for r = 1.0–2.5 Å, showing a predominantly 6-coordinate environment & (b) distribution of angles around the magnesium, plotted for Ow⋯Mg⋯Ow (blue), Ow⋯Mg⋯O1 (grey) and O1⋯Mg⋯O1 (yellow). The deviations from the ideal octahedral values of 90 and 180° can be interpreted with the aid of the most common fragments depicted in Fig. 5 below.

Using the values taken from Fig. 4a, which gives the probability of finding different numbers of water molecules (Ow) coordinated to magnesium (Mg1), we see the most probable number is 5 herein formalised as Mg1⋯Ow = 5, and this, paired with the most probable number of coordinated sulfate anions given by Mg1⋯O1 = 1, gives the 6-coordinate environment depicted in Fig. 5a. A similar approach to interpreting the coordination statistics suggests a number of additional, but less common, environments as depicted in Fig. 5b–d. Fig. 4b shows the distribution of bond angles and is consistent with the proposed coordination environments – for example the fully hydrated magnesium (blue in Fig. 4b) shows angles most tightly distributed around 90° and 180° as would be expected for this more regular geometry, whereas the sterically hindered cis-sulfate environment (yellow in Fig. 4b) results in a wider spread of angles.

Fig. 5 The most common first shell magnesium environments, taken directly from the refined ensemble, with distributions obtained from the coordination statistics. Formulae and dashed lines indicate that some of these may form the basis for larger clusters. The missing 5% are fragments based on higher numbers of coordinated sulfates.

The distribution of distances within these 6-coordinate fragments can be visualised in the site–site radial distribution functions (RDF) depicted for the case of magnesium⋯sulfate in Fig. 6a and magnesium⋯water in Fig. 6b. The RDFs of both species show two distinct features, the first narrow distribution representing the 6-coordinate first shell with distances in the range 1.95–2.07 Å (Wang and co-workers report a slightly longer distance of 2.1 Å),²⁵ and the second broader feature describing either far-side sulfate oxygens (O1) or a second solvation shell in the case of water (Ow) with distances in the range 4.20–4.35 Å. In both cases the shorter distances have a narrower distribution possibly providing evidence of contact ion pairing (CIP), as described by Zhang and co-workers.³⁵ The more distant feature in Fig. 6a is due to the three cross-sulfate oxygens, these are likely to adopt a much wider range of distances due to dynamic rotational motion and flexibility in the Mg⋯S⋯O1 angle. The Mg⋯H₂O RDF has a much weaker second feature representing the second solvation shell around the magnesium ion; this is necessarily less well-defined due to a much larger number of potential configurations.

Fig. 6 Correlation distances observed within the site-site RDF for the octahedral clusters from a central magnesium to (a) sulfate oxygen (red) and sulfur (yellow) and (b) water oxygen – plots are the calculated RDFs based on the fitted model.

The distances observed in these aqueous phase clusters follow a similar trend to those observed in their crystalline counterparts, with the Mg⋯O1 distances being shorter than the Mg⋯O_w distances; this can be attributed to the larger charge density and overall affinity between the magnesium⋯sulfate ions compared to magnesium⋯water. More specifically, the Mg⋯Ow distances observed in our model are found to fall within the same range as those observed in crystalline MgSO₄·xH₂O (2.0–2.2 Å), however those of the Mg⋯O1 are significantly (0.5 Å) shorter even than those found in anhydrous MgSO₄. We hypothesise that this is due to a different hierarchy of competing forces in solution compared to the solid-state – hydrogen bonding, for instance, may be more dominant in solution leading to areas of higher density and shorter interatomic distances.

Comparing the RDF of our magnesium clusters to those from a purely computational study by Balasubramanian and co-workers we see a general similarity but with slight differences in the absolute correlation values.²⁰ Intriguingly, the authors describe larger distances for Mg⋯O1 compared to Mg⋯Ow in contrast to our observations and those seen in the solid-state.

From direct examination of the refined model, it can be seen that magnesium coordinated to 5 water molecules often acts as a cap terminating an extended chain, this is corroborated in Fig. 5a showing a 50% occurrence of [Mg(H₂O)₅SO₄}⁻; this is in very good agreement with a value of 48% reported by Wang and co-workers for the case of WSR = 30 Mg(NO₃)₂. The 20% occurrence of forms depicted in Fig. 5c & 5d are most likely to occur in the middle of more extended and branched chains – indeed these can be directly observed in the and these are discussed in more detail in the extended clusters section.

Sulfate environment

The average first coordination shell around the sulfate is somewhat complex and dominated both by isolated water molecules hydrogen bonding to the sulfate oxygen and those brought into proximity through the coordinated magnesium hydrate clusters.

Firstly, we will consider the direct association of sulfate with a hydrated magnesium ion. The S1⋯Mg1 coordination numbers (r = < 6 Å, Fig. S2, ESI†) reveal approximately 7% of the sulfates are fully hydrated (isolated) and 35% form pairs with a single magnesium. The formation of ion pairs is not surprising as it enables charge balancing at a local level. The higher coordination numbers (38% to 2, 17% to 3, & 3% to 4) represent more complex clusters building into straight and branched chain motifs alongside a smaller number of cyclic 8-membered rings. These clusters are further stabilised by hydrogen bonding though bridging water molecules between the sulfate oxygens and magnesium ‘coordinated’ waters - acting as an interface between the cluster and the bulk water regions.

Considering now the sulfate coordination in terms of proximal water molecules we can see from Fig. 7a that within the range r = 5.0 Å we get an average number of 17. The distances observed in the RDF (Fig. 7b) largely agree with those of previous studies with the first feature centred at r = 3.91 Å comparing to that of (3.82 Å) from a computational study of aqueous sulfate.²² The average first coordination shell contains a broad range of distances encompassing directly hydrogen bonded water molecules at shorter distances as well as a significant number of more loosely associated and distant water molecules – these will be described below.

Fig. 7 (a) Average coordination numbers determined through S1 (sulfate) to Ow (water) distances within the range r = 1.0–5.0 Å. This range was chosen to include all contributions to what is a rather diffuse first solvation shell – and matches that used to generate the SDF in Fig. 8 (b) calculated partial RDF for sulfur (S1) to water oxygen (Ow), key interaction distances are denoted.

Examining the SDF plot shown in Fig. 8a the density lobes are seen to occupy a superimposed tetrahedral and octahedral arrangement (Fig. S1, ESI† shows that the octahedral arrangement is the most dominant feature). This density distribution arises from several different local situations; in the case of an isolated fully hydrated sulfate, these represent two modes of hydrogen bonded water, namely end-on and bridging (Fig. 8b). Using this interpretation, rather than the solvation shell extending to 5Å gives a value of 10 (6 octahedral + 4 tetrahedral) that is in better agreement to those of previous studies based on pure sulfate ion systems suggesting a coordination number between 9.4–12.32.^22,36 However, by far the most common situation is where the waters of the coordinated magnesium are bought into proximity to the populate the octahedral sites (Fig. 8c) – the tetrahedral sites are then occupied by end-on hydrogen bonded free water molecules. An example of this situation is illustrated in Fig. 1e.

Fig. 8 Spatial density function plot of an isolated SO₄²⁻@H₂O for the 10% most likely positions in the first solvation shell. The plotted volumes enclose the highest density regions that contain 10% of water molecules within a radius limit of 5.0 Å. (a) Illustrates the distribution of density nodes between the tetrahedral and octahedral cases, (b) depicts superimposed representations of the associated hydrogen bonding modes and (c) represents the magnesium predisposing a water molecule into an octahedral site.

Regions predominately occupied by water

The dissolution of MgSO₄ into solution causes a subtle, but significant disruption to the previously described structure of pure water³¹ – this can be seen graphically in SDF plots of Fig. 9. The perturbation seen in the average hydrogen bonding network is most evident in the structure of the 2nd solvation shell (Fig. 9c and d). Although less extreme than some examples in the literature, such as MgClO₄, the changes are clear and indicate a forced change in the water arrangement as it accommodates the ionic species.³⁷

Fig. 9 SDF for H₂O@H₂O interactions for radius 1.0–5.0 Å and isosurface = 10% & 30% for 2M MgSO₄ and a pure water EPSR refinements.

The 1st solvation shell of the MgSO₄ water (Fig. 9a) extends out to approximately 3.5 Å and shows a similar distribution in space to that of pure water (Fig. 9b), although with an increased density along the direction of the dotted line in Fig. 9a. It should be remembered that these SDF plots show the direct water environment averaged over the entire system, means the differences observed are almost certainly due to cases where the central water molecule interacts directly with a magnesium or is hydrogen bonded to a sulfate oxygen.

The 2nd solvation shell shows more significant differences, especially evident in the formation of a break in the lobe indicated by the dotted line in Fig. 9c. This disruption to the pure water structure is a behaviour previously seen in the literature, for example the dissolution of magnesium perchlorate causing a full collapse of the second shell into the first.³⁷

This disruption can be further evidenced by examining the Ow–Ow RDF shown in Fig. 10. Although probably of limited significance, a small increase can be observed in the magnitude of the peak representing the first solvation shell and this is consistent with the previous observation of an increased density indicated in Fig. 9a. Looking towards the second and third solvation shells, it is clear that the presence of the solute disrupts these features completely. Being cautious of discussing features approaching half the simulation box size - it can be observed directly from the model that the regions dominated by water rarely extend beyond 15 Å which does not leave much ‘space’ for these features to develop.

Fig. 10 Comparison of the partial RDF for Ow–Ow for 2 M MgSO₄ (yellow) and pure water (grey). The solvation shell ranges are highlighted, with a noticeable difference in the 2nd solvation shell for 2 M MgSO₄.

Overall, it appears that the high degree of dispersal of the solute minimises any extended regions of pure water although the structures we observe are similar in the first shell but becoming more disrupted further out as the proximity to solute ions increases.

Extended clusters

With a description of the component ion environments in place, it is now possible to consider the longer-range order and clustering of the magnesium sulfate. Visual inspection of the model reveals extended clusters and chains that grow through corner-sharing SO₄ and MgO₆ polyhedra (Fig. 11). This monodentate configuration is the lowest energy form identified in computational studies by Zhang and co-workers.³⁵

Fig. 11 Example extended chains/clusters from the refined model. (a) Ring formation, (b) straight chain (c) branched chains and (d) ion pairs. Water molecules completing the octahedral coordination of magnesium are not shown for clarity.

Using a combination of coordination number and cluster size statistics we can build a picture of how these clusters extend. 25% of the magnesium ions form isolated [Mg(H₂O)₆] entities (Fig. 4a coordination number = 0) but only 7% of the sulfates exist in a similar isolated [SO₄(H₂O)_x] environment (Fig. S2, ESI† coordination number = 0). 34% of the magnesium and sulfate ions come together to form isolated ion-pairs [Mg(H₂O)₅SO₄] with the remaining ions involved in extended clusters –{Mg(H₂O)_x(SO₄)_6−x}– whose numbers tail off rapidly above a cluster size of 5 (Fig. 12).

Fig. 12 Cluster size analysis. The cluster size of 0 is with reference to the magnesium and included to normalise the remaining values. A cluster size of 1 corresponds to a magnesium/sulfate pair and a cluster size of 2 may comprise either (Mg–SO₄–Mg) or (SO₄–Mg–SO₄).

Interestingly, and inferred directly from observation of there being fewer isolated sulfate anions than magnesium cations, we see a corresponding numerical imbalance of these in the extended clusters with a greater number of sulfates – this is an observation of the negative charge ion structures theorised by Zhang and co-workers.³⁵ Another significant observation is the lack of 3-dimensional structures which is probably a result of their increased steric instability in solution. A more detailed representation of the cluster distribution is presented in the ESI† (Fig. S3).

We can now briefly consider the potential for longer range interactions between isolated magnesium and sulfate ions. A theoretical study by Mamatkulov and co-workers present evidence of water separated ion pairs, however, this is not something we observe either by examination of the refined model or in comparison of the SO₄⋯Mg (Fig. 6a) and SO₄⋯H₂O (Fig. 7b) RDF plots.³⁸ Specifically, we do not see a shift to longer distance of the first peak that would indicate insertion of water between the sulfate and magnesium – in fact we observe a shortening of this distance indicating a greater attractive association into ion-pairs.

Finally, it is pertinent to compare the features of the refined model to the crystal structures of the various solid form hydrates. The crystal structures of the higher hydrates, specifically the hexa-, hepta-, nona- and undecahydrate, all comprise isolated octahedral aquo magnesium species Mg(H₂O)₆ and sulfate molecules SO₄ and these we also observe as dominant features in the EPSR model. The pentahydrate crystal structure comprises chains of alternating corner sharing polyhedra in a trans configuration, which again we observe in the refined model (Fig. 11c). The tetrahydrate crystal structure comprises cis linked corner sharing polyhedra that form discrete rings containing 2Mg(H₂O)₄ and 2SO₄ units and a number of these are observed in the model (Fig. 11a). The lower hydrate solid forms, the mono- and dihydrate form 3D connected networks of polyhedra, and these we do not observe in the current model. One can postulate that fragments of these might be observed in supersaturated solutions, and a study of such systems is currently ongoing. The discrete anion/cation pairs that we observe in solution do not feature in the known solid form structures and these probably act as stepping stones to the formation of extended clusters.

Conclusions

Total scattering and large-box modelling using the Empirical Potential Structure Refinement (EPSR) approach have, for the first time, given a holistic picture of the structural motifs present in saturated aqueous magnesium sulfate. Analysis of the refined model has revealed a structure dominated by octahedral magnesium ions often with 4 or 5 coordinated water molecules with the remaining sites enabling the growth of clusters into extended and branched chains. Indeed, these beginnings of extended order and longer-range structures form a basis from which the onset of crystallisation could be imagined and corresponding chains and rings formed from corner sharing polyhedra are present in the various known crystalline hydrates. The nature of the sulfate environment has been shown to be more complex than seen in previous studies due to the influence of hydrated magnesium coordinating directly to the sulfate and enlarging the first shell hydration sphere.^22,36 However, a clear, average picture of a combined tetrahedral and octahedral arrangement of water molecules arises from the spherical density function plots. The atomistic model we present reveals (with magnesium as reference) a system comprising 25% isolated octahedral aquo magnesium species (Mg(H₂O)₆), 34% magnesium sulfate pairs (Mg(H₂O)₅SO₄) with the remining 41% being involved in extended clusters built from corner-sharing MgO₆ and SO₄ polyhedra with a maximum observed cluster size of 10. Using the sulfate as reference, we see a slightly different balance with only 7% being isolated, a matching number of 34% forming ion pairs and a larger percentage (59%) being involved in extended clusters – thus the extended clusters contain more sulfate than magnesium.

Author contributions

Daniel J. M. Irving: formal analysis, methodology, visualization, investigation, writing – original draft; Mark E. Light: supervision, writing – review & editing, visualization; Matilda P. Rhodes: investigation; Terence Threlfall: conceptualization; Thomas F. Headen: methodology, validation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Science and Technology Facilities Council for the award of beamtime on SANDALS through beamtime request RB2000142,³⁹ the use of the IRIDIS High Performance Computing Facility and associated support services at the University of Southampton and DJMI acknowledges the EPSRC for DTP funding (EP/R513325/1).

Notes and references

1. A. Wang, J. J. Freeman, B. L. Jolliff and I.-M. Chou, Geochim. Cosmochim. Acta, 2006, 70, 6118–6135.
2. A. Nathues, M. Hoffmann, M. Schaefer, L. Le Corre, V. Reddy, T. Platz, E. A. Cloutis, U. Christensen, T. Kneissl, J.-Y. Li, K. Mengel, N. Schmedemann, T. Schaefer, C. T. Russell, D. M. Applin, D. L. Buczkowski, M. R. M. Izawa, H. U. Keller, D. P. O’Brien, C. M. Pieters, C. A. Raymond, J. Ripken, P. M. Schenk, B. E. Schmidt, H. Sierks, M. V. Sykes, G. S. Thangjam and J.-B. Vincent, Nature, 2015, 528, 237–240.
3. C.-F. Tang, H. Ding, R.-Q. Jiao, X.-X. Wu and L.-D. Kong, Eur. J. Pharmacol., 2020, 886, 173546.
4. C. Neuhaus, C.-M. Geilfus and K.-H. Mühling, J. Plant Nutr. Soil Sci., 2014, 177, 741–747.
5. E. M. R. Rees and G. G. Stewart, J. Inst. Brew., 1997, 103, 287–291.
6. W. Gong, H. Yu, H. Ma, N. Wang and L. He, Emerging Mater. Res., 2020, 9, 618–627.
7. K. Posern and Ch Kaps, Thermochim. Acta, 2010, 502, 73–76.
8. P. J. Rentzeperis and C. T. Soldatos, Acta Crystallogr., 1958, 11, 686–688.
9. M. Weil, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2007, 63, i172.
10. F. C. Hawthorne, L. A. Groat, M. Raudsepp and T. S. Ercit, Neues Jahrb. Mineral., Abh., 1987, 157, 121–132.
11. H. Ma, D. L. Bish, H.-W. Wang and S. J. Chipera, Am. Mineral., 2009, 94, 622–625.
12. W. H. Baur, Acta Crystallogr., 1962, 15, 815–826.
13. W. H. Baur and J. L. Rolin, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 1448–1455.
14. A. Zalkin, H. Ruben and D. H. Templeton, Acta Crystallogr., 1964, 17, 235–240.
15. W. H. Baur, Acta Crystallogr., 1964, 17, 1361–1369.
16. A. D. Fortes, K. S. Knight and I. G. Wood, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 2017, 73, 47–64.
17. F. E. Genceli, M. Lutz, A. L. Spek and G.-J. Witkamp, Cryst. Growth Des., 2007, 7, 2460–2466.
18. A. D. Fortes, F. Browning and I. G. Wood, Phys. Chem. Miner., 2012, 39, 419–441.
19. H. L. Robson, J. Am. Chem. Soc., 1927, 49, 2772–2783.
20. G. Balasubramanian, S. Murad, R. Kappiyoor and I. K. Puri, Chem. Phys. Lett., 2011, 508, 38–42.
21. F. P. Daly, C. W. Brown and D. R. Kester, J. Phys. Chem., 1972, 76, 3664–3668.
22. V. Vchirawongkwin, B. M. Rode and I. Persson, J. Phys. Chem. B, 2007, 111, 4150–4155.
23. S. J. Chipera and D. T. Vaniman, Geochim. Cosmochim. Acta, 2007, 71, 241–250.
24. N. T. Skipper, G. W. Neilson and S. C. Cummings, J. Phys.: Condens. Matter, 1989, 1, 3489–3506.
25. Y. Wang, G. Wang, D. T. Bowron, F. Zhu, A. C. Hannon, Y. Zhou, X. Liu and G. Shi, Phys. Chem. Chem. Phys., 2022, 24, 22939–22949.
26. A. C. S. Jensen, S. Imberti, W. J. E. M. Habraken and L. Bertinetti, J. Phys. Chem. C, 2020, 124, 6141–6144.
27. M. Svärd, K. R. Devi, D. Khamar, D. Mealey, D. Cheuk, J. Zeglinski and Å. C. Rasmuson, Phys. Chem. Chem. Phys., 2018, 20, 15550–15559.
28. D. J. M. Irving, D. A. Keen and M. E. Light, Rev. Sci. Instrum., 2021, 92, 043107.
29. A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2011, 44, 714–726.
30. H. E. Fischer, A. C. Barnes and P. S. Salmon, Rep. Prog. Phys., 2005, 69, 233.
31. A. K. Soper, J. Phys.: Condens. Matter, 2007, 19, 335206.
32. A. K. Soper, Mol. Simul., 2012, 38, 1171–1185.
33. S. V. Sambasivarao and O. Acevedo, J. Chem. Theory Comput., 2009, 5, 1038–1050.
34. A. K. Soper, Int. Scholarly Res. Not., 2013, 2013, 1–67.
35. X. Zhang, Y. Zhang and Q. Li, THEOCHEM, 2002, 594, 19–30.
36. L. C. Smeeton, J. D. Farrell, M. T. Oakley, D. J. Wales and R. L. Johnston, J. Chem. Theory Comput., 2015, 11, 2377–2384.
37. S. Lenton, N. H. Rhys, J. J. Towey, A. K. Soper and L. Dougan, Nat. Commun., 2017, 8, 919.
38. S. I. Mamatkulov, K. F. Rinne, R. Buchner, R. R. Netz and D. J. Bonthuis, J. Chem. Phys., 2018, 148, 222812.
39. D. J. M. Irving, M. E. Light, M. P. Rhodes, T. Threlfall and T. F. Headen, STFC ISIS Neutron Muon Source DOI:10.5286/ISIS.E.RB2000142-1.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01157g

‡ Current address: School of Chemistry, University of Edinburgh, Edinburgh, EH9 3FJ, UK.

---