Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A quest for ideal electric field-driven MX@C70 endohedral fullerene memristors: which MX fits the best?†
Lucie
Tučková
 ab,
Adam
Jaroš
ab,
Adam
Jaroš
 ac,
Cina
Foroutan-Nejad
ac,
Cina
Foroutan-Nejad
 *ad and
Michal
Straka
*ad and
Michal
Straka
 *a
*a
aInstitute of Organic Chemistry and Biochemistry of the Czech Academy of Sciences, Flemingovo nám. 2, CZ-16610, Prague, Czech Republic. E-mail: straka@uochb.cas.cz
bFaculty of Chemical Engineering, University of Chemistry and Technology Prague, Technická 3, CZ-16628, Prague, Czech Republic
cFaculty of Science, Charles University, Albertov 2038/6, CZ-12843, Prague, Czech Republic
dInstitute of Organic Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224, Warsaw, Poland. E-mail: cforoutan-nejad@icho.edu.pl
First published on 28th April 2023
Abstract
Endohedral fullerenes with a dipolar molecule enclosed in the fullerene cage have great potential in molecular electronics, such as diodes, switches, or molecular memristors. Here, we study a series of model systems based on MX@D5h(1)-C70 (M = a metal or hydrogen, X = a halogen or a chalcogen) endohedral fullerenes to identify potential molecular memristors and to derive a general formula for rapid identification of potential memristors among analogous MX@Cn systems. To obtain sufficiently accurate results for switching barriers and encapsulation energies, we perform a benchmark of ten DFT functionals against ab initio SCS-MP2 and DLPNO-CCSD(T) methods at the complete basis set limit. The whole series is then investigated using the PBE0 functional which was found to be the most efficient vs. the ab initio methods. Nine of the 34 MX@C70 molecules studied are predicted to have suitable switching barriers to be considered as potential candidates for molecular switches and memristors. We have identified several structure–property relationships for the switching barrier and response of the systems to the electric field, in particular the dependence of the switching barrier on the available space for M–X switching and faster response of the system to the electric field with a larger dipole moment of MX and MX@C70.
1. Introduction
Owing to the continually increasing demand for computational power, society seeks new ways and technologies to make computing faster and more powerful. The growth of computational power is currently most successfully being pushed forward through an increasingly efficient parallelization1,2 and ongoing miniaturization, with the ultimate vision of devices made of single-molecule components. A possible way of continuing the current performance scaling trend is switching from the traditional von Neumann architecture (the data are stored in the memory unit and processed in the processor) to a new type of logic circuits3–5 and employment of the in-memory computing6–8 using memristors, devices whose conductivity at present is defined the current that has passed through them in the past.9,10 In recent years, the design of memristor-based logic circuits has attracted the attention of many research groups.4,8,11–17 Memristors can be considered as a single circuit element or as a combination of a resistor and a switch/rheostat.18 They are promising devices, yet only a few examples of a memristor are known in the realm of molecular electronics.19–25 Classical computers suffer from energy dissipation and latency due to the data transfer between the processing and storage units, i.e., the von Neumann bottleneck. Because a memristor can serve at the same time as a memory unit and as a processing unit, the energy dissipation is decreased, and the latency implied by the data transfer between the memory and processing units is reduced to a minimum.In our pilot studies, we predicted that endohedral fullerenes with general formula MX@Cn (where M is a metal or hydrogen, X a nonmetal, and Cn an elliptical fullerene, for example, D5h(1)-C70) behave like molecular memristors.25,26 According to our predictions, a sufficiently large applied external field may enable switching between the local minima (states) of MX in C70 (‘writing regime’), which in turn leads to differential conductivity of the molecule that can be recognized (‘reading regime’) by a small voltage applied on the electrodes, vide infra. We have labelled this system as a switching diode; however, the conductance hysteresis of such a system reminds that of a memristor.25,26 The predicted principle as such was recently experimentally proven on two analogous systems: Gd@C82, coined as a molecular electret,20 and Sc2C2@Cs(hept)-C88, coined as a logic-in-memory device.24 In Gd@C82, the Gd3+ ion inside the cage moves to utilize a voltage applied at the gate electrode (VG) which leads to distinct conductivity modes of the molecule with respect to the voltage applied on the source and drain electrodes (VSD). This system operates at a temperature of 1.6 K. In Sc2C2@Cs(hept)-C88, switching between conductivity states is realized via voltage-induced changes in the geometry of the encapsulated Sc2C2 moiety that is also related to a change of the dipole moment in the system. Here, the switching is operated only using one pair of electrodes, in a similar way to our pilot proposal of MX@C70 devices.26 The Sc2C2@Cs(hept)-C88 device was shown to successfully perform Boolean logic operations at room temperature, suggesting that endohedral fullerenes are indeed feasible candidates for the design of new molecular devices.25,26
In this work, encouraged by the experimental confirmation of the predicted principles, we perform a computational pre-screening for new memristor-like molecules based on 34 MX@D5h(1)-C70 endohedral fullerene systems, where M is a metal or hydrogen, and X is a halogen or a chalcogen. Notably, analogous MX@Cn systems – though with larger fullerene cages – have been spotted in mass-spectroscopic studies; namely one or both of the LuCl@C2(99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917)-C90 and LuCl@C2(99
917)-C90 and LuCl@C2(99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914)-C90 isomers27 and also the series of sodium halide fullerenes NaCl@C2n (2n
914)-C90 isomers27 and also the series of sodium halide fullerenes NaCl@C2n (2n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120–244), NaBr@C2n (2n
120–244), NaBr@C2n (2n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110–240), and NaI@C2n (2n
110–240), and NaI@C2n (2n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116–198).28 One of the referees of this work suggested that the existence of endohedral NaCl@C2n species is unlikely because of the lack of charge transfer between the metal atom and the cage which should contribute to the stabilization of such endohedral species. In the ESI,† we present an in silico proof that the endohedral (NaCl@C70) system is by ca. 40–60 kcal mol−1 more stable than the endo–exohedral (Na@C70-Cl) species in various binding modes, see Table S1 and Fig. S1 (ESI†). Furthermore, various endohedral fullerenes with the general formula of M2X@Cn have also been prepared to date.29–32
116–198).28 One of the referees of this work suggested that the existence of endohedral NaCl@C2n species is unlikely because of the lack of charge transfer between the metal atom and the cage which should contribute to the stabilization of such endohedral species. In the ESI,† we present an in silico proof that the endohedral (NaCl@C70) system is by ca. 40–60 kcal mol−1 more stable than the endo–exohedral (Na@C70-Cl) species in various binding modes, see Table S1 and Fig. S1 (ESI†). Furthermore, various endohedral fullerenes with the general formula of M2X@Cn have also been prepared to date.29–32
Although the large-scale synthesis of the MX@C70 systems studied here seems to be inaccessible at the moment, molecular surgery methods come across as a step in the right direction.33–36 Very recently, Gao et al.37 successfully performed insertion of LiF and [BeF]+ into an open-cage C60 fullerene. This was enabled thanks to the interaction of the ‘bait’ hydroxy groups at the rim of the orifice with the metal atom.37 Because the subsequent closing of the open-cage fullerene is sometimes possible,33,38 the suggested MX@C70 species may be very probably eventually synthesized and employed in molecular circuits.
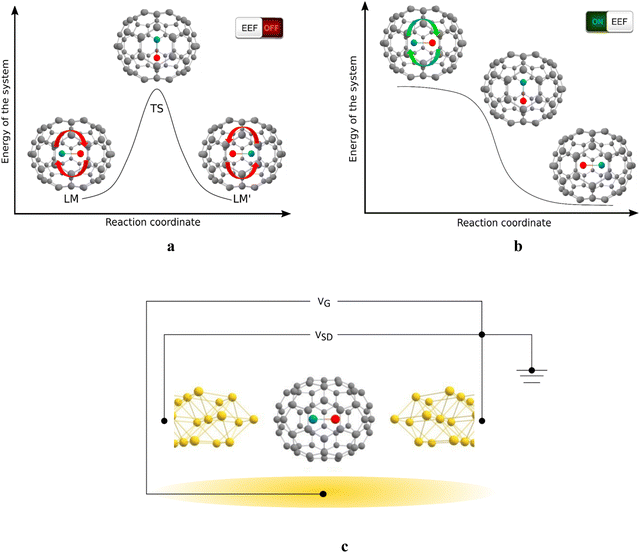
The studied MX@C70 systems and their function are illustrated in Fig. 1. In an MX@C70 fullerene memristor, the dipolar MX molecule polarizes the electrons of the fullerene shell (an example is shown in Fig. S2, ESI†) and makes the whole system behave like a p–n junction, i.e., a diode, when a low VSD (to prevent switching) is applied between the source and the drain electrodes.25,26 Geometrically, the MX lies on or close to the longest axis of symmetry of the elliptical C70 cage, see Fig. 1. This creates a bistable system with two local minima, LM and LM′, connected via a (presumably one) transition state, TS, see Fig. 1a. Note that this principle can be applied also to other elliptical cages, such as C78 or C90.39 In the D5h(1)-C70 cage studied here, the LM and LM′ are equivalent in a free molecule but once the MX@C70 is inserted in an electric circuit, LM and LM′ become two different states with respect to the polarity of the voltage applied to the device.
Under certain conditions, the MX can be flipped between the LM and LM′, for example, when the applied VSD surpasses a threshold that changes the nature of one of the minima to a transition state, Fig. 1b. Both the size of the switching barrier, i.e., the barrier against the MX flip and the response to the applied electric field (EF) depend on the type of the cage and the enclosed MX. The switching can be facilitated by an additional voltage applied through the gate electrode (VG in Fig. 1c) the role of which is to stabilize the TS via EF–dipole interaction.20,25 We have previously predicted that VG of 0.8 V Å−1 acting upon an arbitrary VSD leads to a further minimization of the switching barrier by ca. 1.5–4.0 kcal mol−1 (depending on the particular system). Because this effect is rather marginal, we use a two-electrode setup that mimics the Sc2C2@Cs(hept)-C88 experiment discussed above.24 Switching the MX between LM and LM′ changes the polarity of the MX@C70 molecule, and consequently its transmission properties.25
Because the synthesis of endohedral fullerenes is typically a tedious procedure40–43 involving a stochastic cage formation and subsequent time-consuming purification, or a multistep fullerene surgery synthesis,33–36 one can use the advantages of computational chemistry and pre-select proper systems by a computational screening. A functional fullerene memristor should feature two key properties:
(i) The system should have a suitable intrinsic switching barrier (ISB) that is high enough to keep the state of the memristor intact in the absence of the external voltage or when low ‘measuring’ voltage is applied. The switching barrier should drop fast enough with an applied voltage to make the flipping of MX (‘writing of the state’) possible. If the barrier is too high, the system may undergo ionization instead of switching at high fields; if it is too low, the endohedral molecule tumbles inside the cage due to thermal effects, thus causing the loss of the recorded information. Switching is a critical step that can be achieved only for specific systems.
(ii) The system should have a sufficient rectification ratio (RR) to make the ‘reading of the state’ of the system possible. RR can be simply defined as the ratio of current passing through the device at a certain bias voltage and current passing at the same but reverse bias voltage. For the proper function of reading, the desired RR should be greater than 1, that is, the LM and LM′ states must differ in conductivity when the system is connected to the electrodes.
To achieve our goal, we studied 34 systems with MX encapsulated in the D5h(1)-C70 fullerene cage to identify potential candidates for MX@D5h(1)-C70 memristors. The studied systems were selected because of their well-defined electronic and spin states. Method calibration on five preselected systems was performed first to find a reliable DFT level for production calculations. With a reasonable computational level chosen, we evaluated intrinsic switching barriers and their response to the oriented external EF. The studied systems feature a wide range of intrinsic switching barriers ranging from a few up to ∼95 kcal mol−1. We further examine which molecular properties (e.g., M–X bond length and M–X dipole moment) control the switching barrier and its response to the EF. Based on our analyses, we propose a general method to identify the right MX molecules for an ellipsoid fullerene with an arbitrary cavity size.
In the following, we discuss the computational methods in Section 2, and the computational benchmark in Section 3.1. In Section 3.2 we study the calculated intrinsic (zero-field) switching barriers as well as their response to the applied EF in the two-electrode setup, and the key factor(s) defining the systems’ properties and behaviour. Conclusions are drawn and candidates for molecular MX@C70 memristors are proposed in Section 4.
2. Methods
For the method calibration, the local minima and transition states (LM, LM′, and TS in Fig. 1) of a pre-selected test set of five MX@C70 molecules (MX = KF, CsF, LiCl, CuCl, and ZnS) were taken. The test set was selected to include both the main group and transition metals and also to sample the energy spectrum of B97D344,45/def2-SVP46,47 pre-calculated intrinsic switching barriers (1–80 kcal mol−1). Throughout the calibration, the geometries were optimized at various DFT and ab initio levels. The following density functional theory (DFT) functionals were used: BLYP48–50 and PBE51,52 generalized gradient approximation (GGA) functionals; the TPSS53 meta-GGA functional; the TPSSh53,54 and M0655 meta-hybrid functionals; the B97D3,44,45 B3LYP,49,56–58 PBE0,51,52,59 and BHLYP48,49,60 hybrid functionals; and the ωB97X61 range-separated functional. The D3 empirical dispersion correction62 was employed throughout the DFT optimizations. The def2-SVP,46,47 def2-TZVP,46 and def2-QZVP63 basis sets were employed for carbon and the lighter metal/anion atoms. The relativistic MWB effective core potentials were used for the following atoms: Rb,64 Cs,64 Sr,65 Ba,65 Ag,66 Au,66 Cd,66 and Hg.66The LM and TS of the test set systems were further optimized at the ab initio SCS-MP2 (spin-component-scaled) level67,68 using the largest affordable def2-TZVP46 basis set. The SCS-MP2 has been previously shown to perform well for the energetics of noble-gas endohedral fullerene systems.69–71 The stationary points on the potential energy surface of the optimized molecules were verified as minima and transition states by analysis of the harmonic vibrational frequencies. Imaginary frequencies smaller than 10 cm−1 were considered as originating from numerical inaccuracies.
The DFT optimizations were performed using the Gaussian 16, revision C software,72 the SCS-MP2 optimizations were done using the Turbomole 7.5.1 software.73,74 The ORCA, version 4.2.0 program package75 was used for the SCS-MP2/def2-SVP, SCS-MP2/def2-TZVP, DLPNO-CCSD76/def2-TZVP, and DLPNO-CCSD(T)77/def2-TZVP single-point calculations. For calculations of the switching characteristics under the influence of the electric field (EF), a uniform oriented EF was applied along the main D5 axis of symmetry using the Field keyword in Gaussian 16.72
Single-point computations were performed to assess the basis set superposition error (BSSE) using converged geometries of the MX@C70 systems. The BSSE-corrected encapsulation energies (EEBSSE) were calculated using the Boys and Bernardi78 counterpoise correction method according to the following equation:
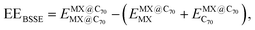 | (1) |
The SCS-MP2 encapsulation energies at the complete basis set (CBS) limit were computed employing Helgaker's extrapolation formula,79
 | (2) |
3. Results and discussion
3.1. DFT vs. ab initio benchmark. Structures and energetics
The considered systems are too large for doing productive work using accurate ab initio methods, in particular the geometry optimizations under electric field. Density functional theory (DFT) is a reasonably accurate and affordable option here but should be properly calibrated for the purpose. Because experimental data are hardly available, we employed single-point SCS-MP2 and DLPNO-CCSD(T) ab initio calculations to calibrate the DFT approaches, in particular for the LM and TS geometries (only SCS-MP2), switching barriers, and encapsulation energies (eqn (3) below) of MX in C70. Both SCS-MP2 and DLPNO-CCSD(T) should be reasonably accurate for calculations of energetics in fullerenes and weakly-bonded systems.70,71,80–82 DLPNO-CCSD(T) can be considered as a benchmark for the closed-shell systems like those studied here. To maximize the efficiency, we first sought for an accurate yet affordable ab initio level with respect to the basis set and level of correlation, which was in turn used as a reference point for the evaluation of DFT methods. The benchmark was done on a set of five preselected systems (MX@C70; MX = KF, CsF, LiCl, CuCl, and ZnS) using ten different DFT functionals and the D3 dispersion correction. The basis set convergence was investigated for both the DFT and the ab initio approaches.| EE = E(MX@C70) − (E(MX) + E(C70)), | (3) |
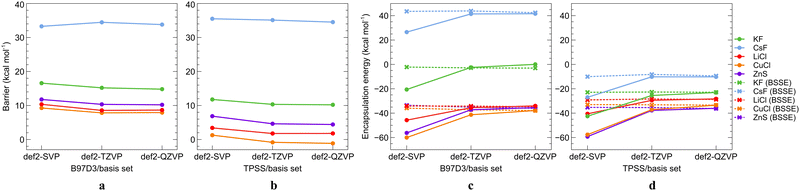
The structures of the minima and transition states used for the ab initio single-point calculations were initially obtained at the B97D3/def2-SVP level.71 The basis set convergence of the SCS-MP2 method for ISBs and EEs was tested using the def2-SVP, def2-TZVP, and def2-QZVP basis sets. Detailed discussion on the basis set convergence in the ab initio mode is given in the ESI.† Based on results in Tables S2 and S3 (ESI†), we consider the def2-TZVP basis set as sufficiently converged for calculations of ISBs. For EEs, we note that the BSSE correction is compulsory in the ab initio mode. For highly accurate EEs, we recommend using the CBS extrapolation formula, as even the def2-QZVP results are not fully converged (Table S3).
To investigate the convergence of the ISB and EE with the level of correlation, the single-point SCS-MP2, DLPNO-CCSD, and DLPNO-CCSD(T) energies using the largest affordable def2-TZVP basis set were calculated (Table 1). We can see a smooth convergence along the series, SCS-MP2 already covers most of the electron correlation, the SCS-MP2 data underestimate the DLPNO-CCSD(T) results by ∼2 kcal mol−1 (Table 1), except for LiCl@C70 where the SCS-MP2 result slightly overestimates the DLPNO-CCSD(T) value.
| MX → | KF | CsF | LiCl | CuCl | ZnS |
|---|---|---|---|---|---|
| SCS-MP2 | 10.9 | 42.2 | −1.2 | 1.5 | 2.8 |
| DLPNO-CCSD | 11.6 | 45.7 | −2.1 | 6.1 | 4.2 |
| DLPNO-CCSD(T) | 12.1 | 43.6 | −1.8 | 3.9 | 4.0 |
The BSSE-corrected ab initio encapsulation energies are reported in Table 2. The SCS-MP2 results under-/over-estimate the DLPNO-CCSD(T) data, up to ∼5 kcal mol−1. Evidently, the differences are not systematic here, however, the accuracy of SCS-MP2 is acceptable.
| MX → | KF | CsF | LiCl | CuCl | ZnS |
|---|---|---|---|---|---|
| SCS-MP2 | −23.5 | −26.8 | −28.0 | −30.3 | −39.3 |
| DLPNO-CCSD | −26.1 | −26.2 | −25.8 | −26.6 | −29.1 |
| DLPNO-CCSD(T) | −27.6 | −29.4 | −28.8 | −29.3 | −34.5 |
In summary, the ab initio calculated ISBs converge fast regarding the basis set requirements, while one should use extrapolation methods and counterpoise correction to get accurate numbers for EEs. Regarding the electronic correlation effects, the ISBs are already well converged using SCS-MP2 versus the DLPNO-CCSD(T) reference, while for accurate EEs, one may need to go for DLPNO-CCSD(T) where possible. For the computational screening work below, we can infer from Table S3 (ESI†) that BSSE-corrected EEs obtained using the def2-TZVP basis set are converged within up to 7 kcal mol−1 from the CBS extrapolated results, which is sufficient for our purposes. For further calibration of DFT functionals, we chose the SCS-MP2/def2-TZVP level as the reference method as it is the best affordable level that allows for efficient geometry optimizations while providing reasonably accurate results.
Note that the geometries used for the ab initio benchmark above were obtained with the B97D3 functional. Below we show that B97D3 does not provide the best geometries. To prove that this does not affect the results of the ab initio benchmark above, we re-evaluated the ab initio ISBs with geometries optimized with the best performing PBE0 functional. The results obtained with PBE0 structures in Table S4 (ESI†) show trends consistent with results obtained with B97D3 structures in Table 1.
Because structure optimizations are easier to perform using DFT, in Table S8 (ESI†) we eventually compared EEs calculated at the DFT-D3/def2-TZVP (using TPSS and B97D3) levels using the geometries optimized employing both the def2-SVP and def2-TZVP basis sets. The results do not differ significantly. The root-mean-square deviations of atomic coordinates (RMSDs) between structures optimized using the def2-SVP and def2-TZVP basis sets are on average 0.024 Å (Table S9, ESI†). Thus, even the small def2-SVP basis set should be sufficient for the DFT geometry optimizations. One may safely employ the usual scheme of obtaining geometries with a smaller basis set and computing the energetics with a larger basis set.
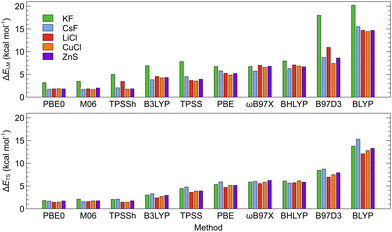
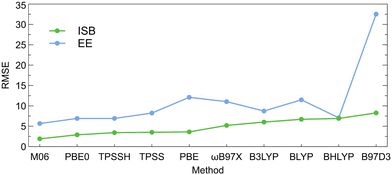
The ISBs and EEs calculated using the DFT-D3 energies and single-point SCS-MP2 energies for the DFT-D3-optimized structures are compared in Tables S20 and S21 (ESI†). The root-mean-square errors between the DFT-D3 and SCS-MP2 values (RMSE; calculated as described in the ESI†) are illustrated on Fig. 4. Here, also, M06 and PBE0 functionals provide values that are the closest to the SCS-MP2/def2-TZVP results. The PBE0 functional provided generally the best price/performance ratio, while the M06 functional appears slightly more expensive (∼20% longer CPU time).
Overall results of the calibration indicate that the choice of the DFT functional is the most important factor that affects the calculated ISBs as well as EEs while both properties converge smoothly with the basis set size when DFT is used. By comparing various parameters of the studied systems calculated at the DFT level and the reference ab initio SCS-MP2/def2-TZVP level, we were able to identify the DFT level(s) that provide the most precise results with respect to the reference. PBE0-D3 and M06-D3 consistently turn out as the most reliable DFT functionals. The basis set convergence is smooth for the ISBs, and the def2-SVP basis set thus provides sufficient accuracy at a low computational cost, needed for computational screening. For EEs, at least the def2-TZVP basis set should be used. Counterpoise correction is marginal for DFT-calculated intrinsic switching barriers but important for encapsulation energies, and more so at ab initio levels, where CBS methods should be applied.
3.2. Screening of the full set of MX@C70 systems
The results for ISBs of the studied series are given in Table 3. It provides a shortlist of systems and illustrates how the barrier increases with M/X down the periodic table, i.e., with the increasing size of the corresponding M/X. Apparently, the size of the barrier reflects the size of the M(X), vide infra.
For some systems, no ISB could be found. For these, we performed detailed scans of the MX rotation that revealed a very shallow potential energy hypersurface (PES) for the movement of the encapsulated molecule inside C70 and no intrinsic barrier against the rotation of MX. This is true for small MX molecules, such as HF, HCl, or LiF. Because a reasonable ISB is one of the conditions for a working memristor, we refrained from further characterization of these systems. For the rest, we predict ISB starting from ∼3 kcal mol−1 for LiCl up to ∼95 kcal mol−1 for CsCl at the PBE0-D3/def2-SVP level.
Interestingly, the MO@C70 (M = Ca, Sr, Ba, Zn, Hg) oxide systems exhibit a more complex PES with a third local minimum (LM′′) that corresponds to the geometry shown in Fig. S4 (ESI†). For CaO, SrO, and HgO, the LM′′ state lies 6.4, 1.6, and 9.4 kcal mol−1 above the LM, respectively. However, for BaO and ZnO, the LM′′ is located 0.5 and 3.1 kcal mol−1 below the LM, respectively. The BaO and ZnO systems were disqualified from further studies as the additional minimum complicates the EF calculations. Population analysis of LM′′ in these systems reveals a strong charge shift between the cage and MX. This phenomenon will be investigated elsewhere.
Three main factors make up the switching barrier: the steric repulsion between MX and C70 in the TS geometry, and the distortion of the MX and C70 counterparts upon transition from LM to TS. As shown in Fig. S5 (ESI†), the major contribution to ISB is in almost all systems the repulsion interaction. The strain of the C70 and MX grows in importance for large systems (e.g., CsF, KCl, RbCl, CsCl, SrS, and BaS); however, it is almost negligible for smaller MXs. Furthermore, the MX strain seems to be more prominent in chlorides, whereas the strain of C70 protrudes more in sulphides.
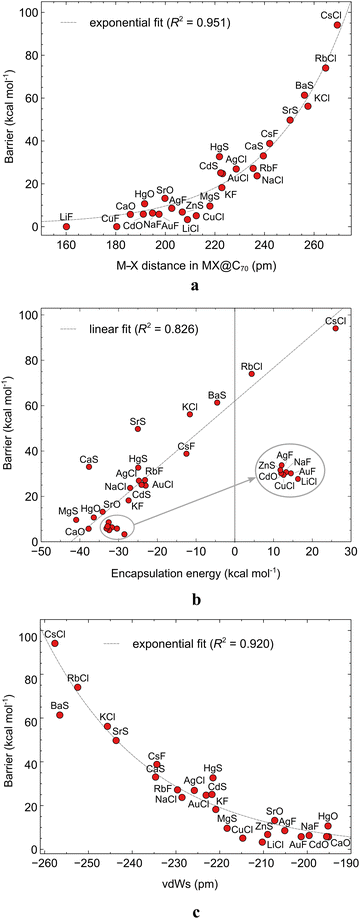
It is interesting to know, for a possible future rational design of molecular memristors with similar systems, whether and how the size of ISB correlates with the molecular properties of the enclosed MX or MX@C70 itself. The various calculated properties of MX and MX@C70 are reported in Table S22 (ESI†). We found two clear correlations: the exponential dependence of the ISB on the M–X bond length (Fig. 5a) and the linear dependence of the ISB on the EE (Fig. 5b). There is a clear trend in these plots: the longer the M–X bond or the higher the EE, the higher the ISB. This could be expected based on a simple geometrical reasoning: the larger the encapsulated MX molecule, the more difficult it is to rotate it through the flattened central part of the elliptical C70. Some exceptions can be found for this structure–property relationship; the most distinct ones are KF@C70 and HgS@C70 systems which feature almost identical M–X bond length but the ISB of the former compound is by 14.5 kcal mol−1 lower than that of the latter. Apparently, other properties of MX may fine-tune the observed trend, but we did not find any further meaningful correlations in this particular case. The relationship between the bond lengths and the ISBs can be rationalized by the fact that it is not expected that MX systems, in particular, if X is a halogen, interact with the interior of the fullerene cages.
One can also rationalize the ISBs in terms of the noncovalent interaction of MX with the equatorial region of C70: the larger the clash between the MX and the interior of the cage, the higher the ISB. To examine this hypothesis, we plotted the difference between the van der Waals cavity size of the fullerene and the van der Waals radii of MX species. In all cases where the MX is in the TS geometry, there is a clash between the two species. Interestingly, this simple parameter, which we coin the van der Waals strain, vdWs in Fig. 5c, correlates perfectly with the ISB values (R2 = 0.92). This finding is critical because it helps to estimate the switching barrier of MX systems encapsulated within any ellipsoid fullerene of an arbitrary size. The same trend can be observed also for the difference of the cage width and the M–X bond length (Fig. S6, ESI†).
Notably, for two molecules, RbCl@C70 and CsCl@C70, we have obtained positive encapsulation energies, 4.4 and 26.0 kcal mol−1 respectively. In the case of these two systems, the length of the M–X bond is significantly shortened upon encapsulation (see Table S22, ESI†), specifically by 17.2 and 24.7 pm respectively. As mentioned above, EE is an indicator of the stability of an endohedral fullerene. The forced distortion of the MX geometry contributes to the destabilization of the whole system. Furthermore, the correlations in Fig. 5 indicate that the M–X bond length is connected to the size of the EE. This can be rationalized again by the geometrical nature of the MX@C70: the larger the encapsulated molecule the larger the EE.
For studying the response of ISB to oriented EF, we selected systems with negative encapsulation energies and with ISBs from ca. 3 to 50 kcal mol−1. The EF was applied along the C5 axis of the C70 cage to simulate the effect of VSD (Fig. 1). Fields between 0.21 and 1.03 V Å−1 were employed to study the behaviour of the systems; these non-round values originate from calculations that used atomic units (0.21 V Å−1 ∼ 0.004 a.u.).
The results are collected in Fig. 6. The switching voltage, i.e., the voltage at which the rotation of the dipole from LM to LM′ is barrierless, is different for each of the systems. Nine of the studied MX@C70 systems (MX = LiCl, CuCl, CaO, AuF, CdO, NaF, ZnS, AgF, and MgS) approach the switching voltage <1.03 V Å−1, which should be experimentally achievable in a two-electrode setup. The ISBs of these molecular switches are, however, lower than 10 kcal mol−1 (Table 3). These systems are thus suitable for in-memory processing or short-time memory data storage, vide infra. Especially, systems with barriers of ∼5 kcal mol−1 or smaller are suitable only for operating at low temperatures. It is worth noting that even the systems with a small non-zero switching barrier are practically applicable for in-memory processing. However, the advantage of having a system with zero switching barrier (at a certain voltage) is that the frequency of the process will reach the realm of 1012 to 1015 per second which is the rate of a single molecular vibration, i.e., terahertz and more.83 Furthermore, at room temperature, the switching barrier seems to go down by ca. 1 kcal mol−1 for all considered EFs via thermal effects (Table S23, ESI†).
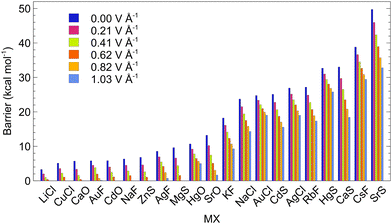 | ||
| Fig. 6 The dependence of the switching barrier on the electric field applied in the direction of VSD for the MX@C70 molecules; calculated at the PBE0-D3/def2-SVP level. | ||
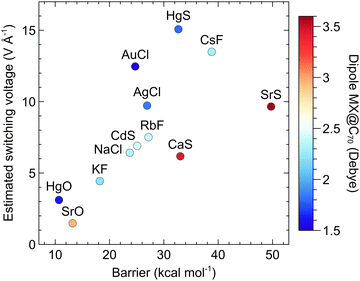
For the systems, which did not reach a sufficiently low switching barrier (i.e., at least ∼1 kcal mol−1) upon the application of the largest field, we extrapolated the exponential barrier-field dependence (Fig. S7, ESI†) to estimate the switching voltage. Table 4 reveals that for most of these systems, the estimated switching voltage (ESV) is much higher than what is experimentally achievable. Previously, the switching function was studied also in a four-electrode setup.20,25 In this arrangement, the secondary field (gate voltage, VG) applied perpendicularly to VSD (Fig. 1c) helps to stabilize the TS relatively to LM via EF–dipole interaction,20,25 but the barrier is only marginally lowered by VG (∼1–4 kcal mol−1). For this reason, we refrained from demanding calculations using a four-electrode setup. We just note in passing, that some of the systems in Table 4 may reach a realistic ESV if a sufficient secondary field is applied.
| MX → | HgO | SrO | KF | NaCl | AuCl | CdS | AgCl | RbF | HgS | CaS | CsF | SrS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ISB (kcal mol−1) | 10.7 | 13.2 | 18.2 | 23.7 | 24.7 | 25.1 | 26.9 | 27.2 | 32.7 | 33.0 | 38.8 | 49.7 |
| ESV (V Å−1) | 3.11 | 1.48 | 4.43 | 6.42 | 12.46 | 6.90 | 9.72 | 7.51 | 15.07 | 6.17 | 13.49 | 9.65 |
Are there any correlations between the ESV and properties of MX or MX@C70? One may expect that an M–X with a larger dipole moment responds better to the applied EF. We analyzed possible relationships among the ISB, ESV, and molecular properties of the studied systems. We found out that the main factor affecting the switching function is, indeed, the magnitude of the dipole moment of the whole molecule MX@C70. Fig. 7 shows that for similar barriers (e.g., in the case of CaS and HgS) the systems with higher ESV (thus a weaker response of the MX@C70 to the EF) have also smaller dipole moments (e.g., the dipole moment of HgS@C70 is smaller than that of CaS@C70 by ∼1.7 Debye). The same, but somehow weaker trend can be seen in Fig. S8 (ESI†), where colour map denotes the dipole moment of the free MX molecule. This fact can be used as another rule of thumb: the higher the dipole moment of an MX or MX@Cn, the steeper the decrease of the switching barrier with applied EF.
4. Conclusions
In this work, we performed an in silico search for potential molecular memristors based on endohedral fullerenes of the general formula MX@D5h(1)-C70, where M is a metal or hydrogen, and X is a halogen or a chalcogen, via the characterization of MX encapsulation energies (EE), intrinsic switching barriers (ISB) for the flip of MX in the C70 cage, and the response of the switching barriers to an oriented external electric field (EF).To find an appropriate DFT protocol for production calculations with reasonable accuracy vs. cost ratio, we first performed extensive DFT against ab initio benchmark using SCS-MP2 and DLPNO-CCSD(T) as the reference methods, including convergence to the complete basis set limit. The benchmark revealed a critical dependence of both ISBs and EEs on the DFT functional, and also a significant dependence of EEs on the basis set in the ab initio mode, while the basis set requirements were found to be less demanding in the DFT mode. The PBE0-D3/def2-SVP level provides a good compromise between accuracy and cost for structure optimizations and calculations of the switching barriers. For encapsulation energies at the DFT level, at least the def2-TZVP basis set should be used on top of the PBE0-D3/def2-SVP geometries.
Employing the calibrated PBE0-D3/def2-SVP level, in total nine MX@C70 out of the 34 studied systems have been identified as potential candidates for molecular memristors or switches, the MX being LiCl, CuCl, CaO, AuF, CdO, NaF, ZnS, AgF, and MgS. We have further shown that ISBs of the MX@C70 systems correlate with the M–X bond length because the switching is controlled by the difference between the size of the enclosed species and the width of the fullerene (here called the van der Waals strain, vdWs).
Based on these observations, a general guideline can be formulated for the screening of analogous candidates for molecular memristors. Tuning of the ISB can be realized by tuning the bond length of the enclosed diatomic molecule: the shorter the bond length the lower the barrier. This could be further generalized to other than diatomic molecules as there is a clear connection between the barrier and how sterically demanding the enclosed species are. This is also connected to the working temperature of the systems as the kinetic of the switching depends both on the height of the barrier and on the temperature. One could thus utilize less sterically demanding endohedral species while working in lower temperatures and vice versa. The van der Waals strain between the MX and the interior of the cage defined in this work can be used as a parameter for identifying the ideal MX for a particular cage. The vdWs value ranged between −220 and −195 pm is the ideal strain to ensure a large enough and yet operable switching barrier.
The response to the external EF, i.e., the rate at which the switching barrier drops with an increasing EF, strongly correlates with the dipole moment of both the MX@C70 and the diatomic molecule alone: the larger the dipole moment the stronger the response to the EF. This enables tuning in a broader sense; if one strives to achieve a greater separation between the electric currents that allow switching and those that move through the system without switching, systems with lower dipole moments are suitable. Systems with larger dipole moments can be expected to exhibit larger sensitivity to the applied EF.
The studied systems may ultimately serve as molecular memristors and, once manufactured, find applications in short-term memory data storage, memristor-aided or memristor-based logic circuits, and for in-memory computing purposes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Czech Science Foundation (21-17806S). Computational resources were partially supplied by the project e-INFRA CZ project (ID: 90140), supported by the Ministry of Education, Youth and Sports of the Czech Republic. C. F. N. thanks the National Science Centre, Poland, 2020/39/B/ST4/02022 for funding this work.References
- P. Gepner and M. F. Kowalik, Multi-Core Processors: New Way to Achieve High System Performance, in International Symposium on Parallel Computing in Electrical Engineering (PARELEC’06), 2006, pp. 9–13.
- B. Venu, Multi-core processors-an overview, arXiv, 2011, preprint, arXiv:11103535 DOI:10.48550/arXiv.1110.3535.
- J. J. Yang, D. B. Strukov and D. R. Stewart, Memristive devices for computing, Nat. Nanotechnol., 2013, 8(1), 13–24 CrossRef CAS PubMed.
- I. Vourkas and G. C. Sirakoulis, Emerging Memristor-Based Logic Circuit Design Approaches: A Review, IEEE Circuits Syst. Mag., 2016, 16(3), 15–30 Search PubMed.
- P. Holzinger and M. Reichenbach, The HERA Methodology: Reconfigurable Logic in General-Purpose Computing, IEEE Access, 2021, 9, 147212 Search PubMed.
- D. Ielmini and H. S. P. Wong, In-memory computing with resistive switching devices, Nat. Electron., 2018, 1(6), 333–343 CrossRef.
- A. Sebastian, M. Le Gallo, R. Khaddam-Aljameh and E. Eleftheriou, Memory devices and applications for in-memory computing, Nat. Nanotechnol., 2020, 15(7), 529–544 CrossRef CAS PubMed.
- M. D. Marco, M. Forti, F. Corinto and L. Chua, Unfolding Nonlinear Dynamics in Analogue Systems With Mem-Elements, IEEE Trans. Circuits Syst. I: Regul. Pap., 2021, 68(1), 14–24 Search PubMed.
- L. O. Chua and S. M. Kang, Memristive devices and systems, Proc. IEEE, 1976, 64(2), 209–223 Search PubMed.
- D. B. Strukov, G. S. Snider, D. R. Stewart and R. S. Williams, The missing memristor found, Nature, 2008, 453(7191), 80–83 CrossRef CAS PubMed.
- M. A. Zidan, J. P. Strachan and W. D. Lu, The future of electronics based on memristive systems, Nat. Electron., 2018, 1(1), 22–29 CrossRef.
- N. Uysal, B. Zhang, S. K. Jha and R. Ewetz, XMAP: Programming Memristor Crossbars for Analog Matrix–Vector Multiplication: Toward High Precision Using Representable Matrices, IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst., 2022, 41(6), 1827–1841 Search PubMed.
- V. Ntinas, A. Ascoli, I. Messaris, Y. Wang, V. Rana and S. Menzel, et al., Toward Simplified Physics-Based Memristor Modeling of Valence Change Mechanism Devices, IEEE Trans. Circuits Syst. II: Express Briefs, 2022, 69(5), 2473–2477 Search PubMed.
- M. di Marco, M. Forti, R. Moretti, L. Pancioni, G. Innocenti and A. Tesi, Feedforward control of multistability in memristor circuits, in 2021 28th IEEE International Conference on Electronics, Circuits, and Systems (ICECS), 2021, pp. 1–6.
- M. Di Marco, M. Forti, L. Pancioni, G. Innocenti and A. Tesi, Memristor Neural Networks for Linear and Quadratic Programming Problems, IEEE Trans. Cybern., 2022, 52(3), 1822–1835 Search PubMed.
- J. Fu, Z. Liao and J. Wang, Level Scaling and Pulse Regulating to Mitigate the Impact of the Cycle-to-Cycle Variation in Memristor-Based Edge AI System, IEEE Trans. Electron Devices, 2022, 69(4), 1752–1762 CAS.
- L. Gao, F. Alibart and D. B. Strukov, Programmable CMOS/Memristor Threshold Logic, IEEE Trans. Nanotechnol., 2013, 12(2), 115–119 CAS.
- I. Abraham, The case for rejecting the memristor as a fundamental circuit element, Sci. Rep., 2018, 8(1), 10972 CrossRef PubMed.
- T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari and L. Joly, et al., Robust spin crossover and memristance across a single molecule, Nat. Commun., 2012, 3, 938 CrossRef PubMed.
- K. Zhang, C. Wang, M. Zhang, Z. Bai, F. F. Xie and Y. Z. Tan, et al., A Gd@C82 single-molecule electret, Nat. Nanotechnol., 2020, 1–6 Search PubMed.
- H. B. Li, B. E. Tebikachew, C. Wiberg, K. Moth-Poulsen and J. Hihath, A Memristive Element Based on an Electrically Controlled Single-Molecule Reaction, Angew. Chem., Int. Ed., 2020, 59(28), 11641–11646 CrossRef CAS PubMed.
- N. D. Paul, U. Rana, S. Goswami, T. K. Mondal and S. Goswami, Azo Anion Radical Complex of Rhodium as a Molecular Memory Switching Device: Isolation, Characterization, and Evaluation of Current–Voltage Characteristics, J. Am. Chem. Soc., 2012, 134(15), 6520–6523 CrossRef CAS PubMed.
- S. Goswami, A. J. Matula, S. P. Rath, S. Hedström, S. Saha and M. Annamalai, et al., Robust resistive memory devices using solution-processable metal-coordinated azo aromatics, Nat. Mater., 2017, 16(12), 1216–1224 CrossRef CAS PubMed.
- J. Li, S. Hou, Y. R. Yao, C. Zhang, Q. Wu and H. C. Wang, et al., Room-temperature logic-in-memory operations in single-metallofullerene devices, Nat. Mater., 2022, 21(8), 917–923 CrossRef CAS PubMed.
- A. Jaroš, E. F. Bonab, M. Straka and C. Foroutan-Nejad, Fullerene-Based Switching Molecular Diodes Controlled by Oriented External Electric Fields, J. Am. Chem. Soc., 2019, 141(50), 19644–19654 CrossRef PubMed.
- C. Foroutan-Nejad, V. Andrushchenko and M. Straka, Dipolar molecules inside C70: an electric field-driven room-temperature single-molecule switch, Phys. Chem. Chem. Phys., 2016, 18(48), 32673–32677 RSC.
- Y. Wang, Y. Shi, X. Fan, J. Ren and X. Kong, Encapsulation of an Ionic Bond in Fullerenes: What is the Difference?, Inorg. Chem., 2019, 58(6), 3601–3605 CrossRef CAS PubMed.
- X. Fan, Y. Wang and X. Kong, Generation of sodium halide endohedral metallofullerenes in the gas phase, Rapid Commun. Mass Spectrom., 2020, 34(15), e8826 CrossRef CAS PubMed.
- F. F. Li, N. Chen, M. Mulet-Gas, V. Triana, J. Murillo and A. Rodríguez-Fortea, et al., Ti2S@D3h(24109)-C78: a sulfide cluster metallofullerene containing only transition metals inside the cage, Chem. Sci., 2013, 4(9), 3404–3410 RSC.
- N. A. Samoylova, S. M. Avdoshenko, D. S. Krylov, H. R. Thompson, A. C. Kirkhorn and M. Rosenkranz, et al., Confining the spin between two metal atoms within the carbon cage: redox-active metal–metal bonds in dimetallofullerenes and their stable cation radicals, Nanoscale, 2017, 9(23), 7977–7990 RSC.
- A. Liu, M. Nie, Y. Hao, Y. Yang, T. Wang and Z. Slanina, et al., Ho2O@C74: Ho2O Cluster Expands within a Small Non-IPR Fullerene Cage of C2(13333)-C74, Inorg. Chem., 2019, 58(8), 4774–4781 CrossRef CAS PubMed.
- W. Yang, G. Velkos, S. Sudarkova, B. Büchner, S. M. Avdoshenko and F. Liu, et al., Carbon cage isomers and magnetic Dy⋯Dy interactions in Dy2O@C88 and Dy2C2@C88 metallofullerenes, Inorg. Chem. Front., 2022, 9(22), 5805–5819 RSC.
- K. Komatsu, M. Murata and Y. Murata, Encapsulation of Molecular Hydrogen in Fullerene C60 by Organic Synthesis, Science, 2005, 307(5707), 238–240 CrossRef CAS PubMed.
- M. Murata, Y. Murata and K. Komatsu, Surgery of fullerenes, Chem. Commun., 2008, 6083–6094 RSC.
- S. Bloodworth, G. Sitinova, S. Alom, S. Vidal, G. R. Bacanu and S. J. Elliott, et al., First Synthesis and Characterization of CH4@C60, Angew. Chem., Int. Ed., 2019, 58(15), 5038–5043 CrossRef CAS PubMed.
- L. Gan, Molecular Containers Derived from [60]Fullerene through Peroxide Chemistry, Acc. Chem. Res., 2019, 52(7), 1793–1801 CrossRef CAS PubMed.
- R. Gao, Z. Liu, Z. Liu, T. Liang, J. Su and L. Gan, Open-Cage Fullerene as a Selective Molecular Trap for LiF/[BeF]+, Angew. Chem., Int. Ed., 2023, 62(12), e202300151 CrossRef CAS PubMed.
- R. Zhang, M. Murata, A. Wakamiya, T. Shimoaka, T. Hasegawa and Y. Murata, Isolation of the simplest hydrated acid, Sci. Adv., 2017, 3(4), e1602833 CrossRef PubMed.
- D. E. Manolopoulos and P. W. Fowler, An Atlas of Fullerenes, 1995 Search PubMed.
- D. H. Parker, K. Chatterjee, P. Wurz, K. R. Lykke, M. J. Pellin and L. M. Stock, et al., Fullerenes and giant fullerenes: Synthesis, separation, and mass spectrometric characterization, Carbon, 1992, 30(8), 1167–1182 CrossRef CAS.
- J. B. Howard, A. L. Lafleur, Y. Makarovsky, S. Mitra, C. J. Pope and T. K. Yadav, Fullerenes synthesis in combustion, Carbon, 1992, 30(8), 1183–1201 CrossRef CAS.
- A. A. Popov, S. Yang and L. Dunsch, Endohedral Fullerenes, Chem. Rev., 2013, 113(8), 5989–6113 CrossRef CAS PubMed.
- G. Churilov, A. Popov, N. Vnukova, A. Dudnik, N. Samoylova and G. Glushenko, Controlled synthesis of fullerenes and endohedral metallofullerenes in high frequency arc discharge, Fullerenes, Nanotubes, Carbon Nanostruct., 2016, 24(11), 675–678 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789 CrossRef CAS PubMed.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157(3), 200–206 CrossRef CAS.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta--Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401 CrossRef PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119(23), 12129–12137 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120(1), 215–241 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58(8), 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98(45), 11623–11627 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110(13), 6158–6170 CrossRef CAS.
- A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98(2), 1372–1377 CrossRef CAS.
- J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- F. Weigend, F. Furche and R. Ahlrichs, Gaussian basis sets of quadruple zeta valence quality for atoms H–Kr, J. Chem. Phys., 2003, 119(24), 12753–12762 CrossRef CAS.
- T. Leininger, A. Nicklass, W. Küchle, H. Stoll, M. Dolg and A. Bergner, The accuracy of the pseudopotential approximation: non-frozen-core effects for spectroscopic constants of alkali fluorides XF (X = K, Rb, Cs), Chem. Phys. Lett., 1996, 255(4), 274–280 CrossRef CAS.
- M. Kaupp, P. v R. Schleyer, H. Stoll and H. Preuss, Pseudopotential approaches to Ca, Sr, and Ba hydrides. Why are some alkaline earth MX2 compounds bent?, J. Chem. Phys., 1991, 94(2), 1360–1366 CrossRef CAS.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Energy-adjusted ab initio pseudopotentials for the second and third row transition elements, Theor. Chim. Acta, 1990, 77(2), 123–141 CrossRef CAS.
- C. Hättig and F. Weigend, CC2 excitation energy calculations on large molecules using the resolution of the identity approximation, J. Chem. Phys., 2000, 113(13), 5154–5161 CrossRef.
- S. Grimme, Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel-and antiparallel-spin pair correlation energies, J. Chem. Phys., 2003, 118(20), 9095–9102 CrossRef CAS.
- P. Pyykkö, C. Wang, M. Straka and J. Vaara, A London-type formula for the dispersion interactions of endohedral A@B systems, Phys. Chem. Chem. Phys., 2007, 9(23), 2954–2958 RSC.
- C. Wang, M. Straka and P. Pyykkö, Formulations of the closed-shell interactions in endohedral systems, Phys. Chem. Chem. Phys., 2010, 12(23), 6187–6203 RSC.
- A. Jaroš, Z. Badri, P. L. Bora, E. F. Bonab, R. Marek and M. Straka, et al., How Does a Container Affect Acidity of its Content: Charge-Depletion Bonding Inside Fullerenes, Chem. – Eur. J., 2018, 24(17), 4245–4249 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb and J. R. Cheeseman, et al., Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- TURBOMOLE V7.5.1 2021, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from https://www.turbomole.org.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank and Y. J. Franzke, et al., TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations, J. Chem. Phys., 2020, 152(18), 184107 CrossRef CAS PubMed.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327 Search PubMed.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138(3), 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139(13), 134101 CrossRef PubMed.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19(4), 553–566 CrossRef CAS.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106(23), 9639–9646 CrossRef CAS.
- A. Hesselmann and T. Korona, On the accuracy of DFT-SAPT, MP2, SCS-MP2, MP2C, and DFT + Disp methods for the interaction energies of endohedral complexes of the C60 fullerene with a rare gas atom, Phys. Chem. Chem. Phys., 2011, 13(2), 732–743 RSC.
- C. Foroutan-Nejad, M. Straka, I. Fernández and G. Frenking, Buckyball Difluoride F2–@C60+—A Single-Molecule Crystal, Angew. Chem., Int. Ed., 2018, 57(42), 13931–13934 CrossRef CAS PubMed.
- A. Jaworski and N. Hedin, Local energy decomposition analysis and molecular properties of encapsulated methane in fullerene (CH4@C60), Phys. Chem. Chem. Phys., 2021, 23(38), 21554–21567 RSC.
- N. Darwish, C. Foroutan-Nejad, L. Domulevicz, J. Hihath and I. Díez-Pérez, Principles of Molecular Devices Operated by Electric Fields, Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, The Royal Society of Chemistry, 2021, ch. 5, pp. 147–94 10.1039/9781839163043-00147.
Footnote |
| † Electronic supplementary information (ESI) available: Relative energies of endohedral NaCl@C70 and endo–exohedral Na@C70-Cl isomers (Table S1) and their geometries (Fig. S1). Natural charges of C70 and KF@C70 (Fig. S2). Basis set convergence at the ab initio level (Tables S2, S3 and Fig. S3). Switching barriers and encapsulation energies calculated using various ab initio and DFT methods (Tables S4–S8, S20 and S21). Structural parameters (selected bond lengths and root-mean-square differences of atomic positions) of molecular structures optimized with different methods (Tables S9 and S11–S19). SCS-MP2 single-point energies of DFT optimized structures (Table S10). A scheme of the potential energy hypersurface of MO@C70 systems with additional local minima (Fig. S4). Contributions to intrinsic switching barriers (Fig. S5). Electronic structure properties of the studied systems calculated at the PBE0-D3 level (Table S22). The correlation between the intrinsic switching barrier and the difference of the C70 width and MX bond length (Fig. S6). Switching barriers calculated employing energies and enthalpies at 298.15 K (Table S23). Extrapolations of the barrier–voltage dependences for systems with a barrier between 10 and 50 kcal mol−1 (Fig. S7). The correlation among switching barriers, estimated switching voltages, and dipole moments of the free MX (Fig. S8). See DOI: https://doi.org/10.1039/d3cp01149f |
| This journal is © the Owner Societies 2023 |