Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles study of electronic and optical properties in 1-dimensional oligomeric derivatives of telomestatin†
Joëlle
Mérgola-Greef
 a and
Bruce F.
Milne
a and
Bruce F.
Milne
 *ab
*ab
aMarine Biodiscovery Centre, Department of Chemistry, University of Aberdeen, Meston Building, Meston Walk, AB24 3UE, Old Aberdeen, UK. E-mail: bruce.milne@abdn.ac.uk
bCFisUC, Department of Physics, University of Coimbra, Rua Larga, 3004-516 Coimbra, Portugal
First published on 24th April 2023
Abstract
Real-space self-interaction corrected (time-dependent) density functional theory has been used to investigate the ground-state electronic structure and optical absorption profiles of a series of linear oligomers inspired by the natural product telomestatin. Length-dependent development of plasmonic excitations in the UV region is seen in the neutral species which is augmented by polaron-type absorption with tunable wavelengths in the IR when the chains are doped with an additional electron/hole. Combined with a lack of absorption in the visible region this suggests these oligomers as good candidates for applications such as transparent antennae in dye-sensitised solar energy collection materials. Due to strong longitudinal polarisation in their absorption spectra, these compounds are also indicated for use in nano-structured devices displaying orientation-sensitive optical responses.
1. Introduction
Organic materials (OM) have seen huge increases in optical and electronic applications in recent years.1–3 The list includes flexible/wearable electronic devices, organic light-emitting diodes (OLED), organic field-effect transistors (OFET), (bio)sensors and the harvesting, storage and transmission of energy.4–7 In addition, there is great interest in OM for electron spin-manipulation in quantum data processing and storage.8,9In particular, 1-dimensional (1D) components approaching the quantum confinement limit of atomic chains have received considerable attention due to their unique properties.10,11 Atomic chains themselves are the ideal model for this but in practice are too limited for real-world use. Pseudo-1D systems such as carbon nanotubes show considerable promise but again are limited in applicability due to difficulties in controlling their geometrical and electronic structure in order to realise predicted properties.12–14
Organic polymer/oligomer systems based on π-conjugated heterocycles with applications in (opto)electronics are well known (e.g. polypyrroles, polythiophenes, polyacenes).8,15,16 These closely approach the 1D limit and great effort has gone into tailoring their properties for usable device applications. Unfortunately, the modifications inevitably lead to considerable alterations in the size of the basic monomer units which in turn change the charge/spin carrier density profile and also alter the machinability of the materials.14,17
Natural products (NP) have long been a source of inspiration for chemists, particularly in the drug-discovery field. In materials science, NP tend to have their greatest influence in areas such as biomaterials based on soft matter and macromolecular biomimetics.18–20
The NP R-telomestatin (Fig. 1) is a macrocyclic compound produced by the organism Streptomyces anulatus 3533-SV4 which has shown to display specific binding to the telomeric G-quadruplex DNA structure and has strong telomerase inhibitory activity.21,22 Telomestatin is composed of seven conjugated oxazole rings with macrocycle closure by a single thiazoline heterocycle. This structure is a ribosomally-synthesised, post-translationally modified peptide (RiPP) with the original precursor sequence being CTTSSSSS. In the biosynthetic pathway, this sequence has been found to be incorporated into a longer precursor peptide, TisC, which is then processed by various enzymes to yield the final product.23
The similarity between the basic structural features of telomestatin and known organic optoelectronic materials such as polypyrrole and polythiophene is striking. Furthermore, recent developments in the enzymatic modification of synthetic peptides to produce azole rings such as oxazole, thiazole and selenothiazole in the laboratory suggest that polymeric structures based on these motifs can be produced in a high-yield, environmentally friendly way.24–26
The current work starts with a summary of the theoretical methods employed followed by an investigation of the ground- and excited-state electronic properties of a series of linear oligomeric oxazole chains inspired by the telomestatin structure. We begin with an analysis of the static electric polarisability of the oligomers where, using highly-converged MP2 calculations, we benchmark our self-interaction corrected TDDFT (SIC-TDDFT) method. We then further investigate the ground-state properties of the polyoxazoles through the evolution of their electronic density of states (DOS) to gain a insight into changes in the electronic structure with chain length. Finally, the optical absorption properties of the chains are studied using time-propagation SIC-TDDFT to probe the excited-state electronic behaviour of the oligomers in their neutral and electron-/hole-doped states.
2. Theory
2.1 Real-space DFT
Density functional theory (DFT),27,28 using (semi-)local functionals of the electronic charge density is well suited to discretization on real-space grids.29 In the current work the Octopus code is used which employs regular spatial grids within a user-defined volume of space for this purpose and does not make use of a basis-set expansion of the Kohn–Sham wavefunctions with atom-centered or plane-wave basis functions.30–33Convergence of calculated properties thus depend only on the grid spacing and the size of simulation box chosen. This has the added convenience that real-space calculations of this type are inherently scalable on (massively) parallel computing platforms and therefore able to provide the same level of accuracy for extremely large systems as might be expected for small molecules using quantum chemical DFT implementations.34
In the following, electron spin is neglected in order to simplify notation but these equations can easily be generalized to include this additional degree of freedom.
We solve the ground-state (time-independent) Kohn–Sham system of N coupled one-particle Schrödinger equations
| hKSφm(r) = εmφm(r) (m = 1,…,N) | (1) |
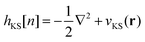 | (2) |
 | (3) |
 | (4) |
| vKS = vext(r) + vH[n(r)] + vxc[n(r)] | (5) |
The classical electrostatic mean-field interaction between the electrons is described by the Hartree potential vH[n(r)] which is conventionally written as
 | (6) |
| ∇2vH[n(r)] = −4πn(r) | (7) |
 | (8) |
2.2 Real-time TDDFT
Once the ground state orbitals φm(r) have been obtained using the real-space DFT scheme outlined above we can insert them into the time-dependent Kohn–Sham equation | (9) |
 | (10) |
If we are working with small perturbations such as those that would be found in ordinary UV-Vis absorption processes, we can assume that the processes are linear with respect to the size of the perturbing force and apply a small impulse (or ‘kick’) to add a finite momentum ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) to the electrons
to the electrons
φm(r,δt) = ei![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) zφm(r,0) zφm(r,0) | (11) |
In the case where we are interested in optical absorption, we can use the dipole approximation and save the induced dipole μ(t) at various points throughout the propagation. This dipole trajectory can then be Fourier transformed to obtain the frequency-dependent dynamic polarisability, α(ω), of the system
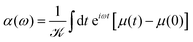 | (12) |
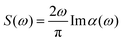 | (13) |
2.3 Sternheimer linear response
Solution of the TDDFT equations in the time domain provides an efficient route to the full dipole response spectrum, as shown above. However, whilst the accuracy of the polarisabilities obtained is good enough for prediction of optical absorption spectra it is dependent on the length of the propagations used. More accurate polarisability values for a given frequency can be obtained from perturbation theory with less computational effort but the cost rises rapidly with the number of frequencies required, limiting its practical use to small numbers of discrete frequencies.Within the framework of TDDFT, the Sternheimer equation serves this purpose and permits the calculation of frequency-(in)dependent (hyper)polarisabilites using only the occupied Kohn–Sham orbitals, φm and without the need for infinite sums over unoccupied states.37,38 For a monochromatic perturbing field F = λδv(r)cos(ωt) we get (to first-order) the variation of the density as
 | (14) |
| {ĥKS − εm ± ω + iη}δφm(r, ±ω) = −PcδĥKS(±ω)φm(r) | (15) |
Once δn(r,ω) has been obtained from self-consistent solution of eqn (15), the polarisability tensor αij can be calculated as
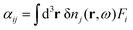 | (16) |
3. Methods
3.1 Geometry optimization
Geometries were optimized at the DFT level using the Orca software package (version 5.0.3).40 The re-regularized SCAN meta-GGA functional (r2SCAN) was chosen as it has been shown to provide equal or better geometries for diverse molecular systems when compared with more computationally expensive hybrid functionals and is competitive with correlated wavefunction methods.41,42 Although r2SCAN does include short- to intermediate-range VdW effects, as with all other (semi-)local functionals it is not capable of describing long range dispersion interactions. For this reason the accurate and computationally efficient density-dependent D4 dispersion correction‡ was added to r2SCAN during all geometry calculations.43–46The r2SCAN-D4 method was combined with the Def2-TZVP basis set.47,48 Although the original tests46 of the accuracy of r2SCAN-D4 with respect to geometrical parameters were performed with the more complete Def2-QZVP basis, in this work it was found that the Def2-TZVP basis lead to mean absolute deviations relative to the Def2-QZVP basis of approximately 0.001 Å in bond lengths (maximum 0.002 Å) and 0.002 degrees in bond angles (maximum 0.060 degrees) for a test system of the methyl-capped oxazole dimer. It was therefore concluded that the r2SCAN-D4/Def2-TZVP method would be sufficiently accurate for this study.
3.2 Time-propagation TDDFT
As stated in the Theory section we employed real-space grids for the discretization of the (TD)DFT equations with the Octopus code version 12.0. The exchange and correlation terms were approximated using the modified Perdew–Zunger local-density approximation (LDA).49–51 This was provided by the LibXC library version 5.2.3.52,53The LDA calculations were augmented by including the average-density self-interaction correction (ADSIC) which corrects the Kohn–Sham potential vKS to remove the spurious interactions of each electron with itself which arise from the Hartree term (see eqn (6)). The correction to the potential for a system containing N electrons is obtained as
 | (17) |
The addition of the self-interaction correction is particularly important for the current work as we were interested in the effect of doping of the compounds under study with added electrons and the uncorrected LDA fails to yield bound anionic systems. ADSIC corrects this failure and in all cases studied here the additional electron was bound indicating that the anions were stable.
Scalar relativistic pseudopotentials for the ADSIC-LDA calculations were taken from the standard norm-conserving LDA set available from the Pseudo Dojo website and distributed with Octopus.55–58 Spin–orbit contributions were not considered as these were expected to be insignificant in the context of the current study.
Convergence testing of the grid spacing and the radius of the atom-centred spheres used to construct the simulation box was performed for the linear six-membered oxazole oligomer. It was found that with a spacing of 0.2 Å and radius of 6 Å, the Fermi energy (EFermi) of the neutral species was converged to better than 0.01 eV. Upon varying the electron number, for monocationic species the same combination of spacing and radius was used but in order to obtain the same convergence of EFermi it was necessary to double the radius to 12 Å.
All time-propagation TDDFT calculations of absorption spectra used a time step of 0.003 ħ eV−1 (0.00197 fs) which was found to yield stable propagations and maintain energy conservation. The propagations were carried out for 8000 steps to give a total time of 24 ħ eV−1 (15.8 fs).
3.3 Static polarisability calculations
Calculation of static polarisabilities, α0, for the various oligomer chains was performed at the TDDFT level (LDA and ADSIC-LDA) by solving the Sternheimer equation for ω = 0.39 As the chains studied were neutral, the grid spacing of 0.2 Å and radius of 6 Å were used. In order to ensure accurate results in the perturbation calculations, the electronic states were converged more tightly by setting the eigensolver tolerance to 10−10 Hartree.For comparison, benchmark values for the polarisabilities were obtained using second-order Møller–Plesset (MP2) perturbation theory with the Orca software. In order to be consistent with the TDDFT polarisability calculations, scalar relativistic effects were included in the MP2 calculations using the zero-order regular approximation (ZORA).59,60 Convergence of the polarisabilities was tested with the sequence of polarised basis sets ZORA-Def2-SVP, ZORA-Def2-TZVP and ZORA-Def2-QZVPP. As the diffuse-augmented ZORA basis sets were not available internally in the Orca software, the uncontracted diffuse functions from the corresponding Def2-SVPD, Def2-TZVPD and Def2-QZVPPD basis sets were obtained from the Basis Set Exchange (https://www.basissetexchange.org/) and added to the recontracted ZORA basis sets.61 The SARC auxiliary basis sets were used along with the resolution of the identity (RI) approximation for the Hartree–Fock calculations.62 Similarly, the subsequent MP2 correlation treatment also used the RI approximation and employed the internal Def2/C auxiliary basis sets.63
For guidance, and clarification of discussions, below, an example of the coordinate system used in these calculations is shown in Fig. S1 (ESI†).
4. Results and discussion
4.1 Static polarisabilities
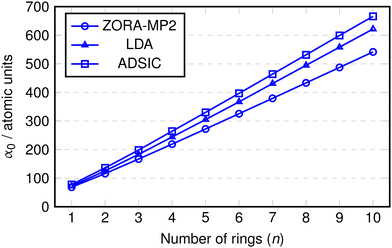
TDDFT using conventional (semi)local density functional approximations such as LDA or GGA is known to overestimate the polarisabilities of conjugated molecular chains which could adversely impact the calculation of their optical properties (see eqn (12)).64–67 For this reason we performed calculations of the static polarisability, α0, with the ADSIC method and compared them against benchmark MP2 values. As a further test, uncorrected LDA calculations were included in order to evaluate the difference made by the self interaction correction. All polarisability values were converged to ∼1 a.u. (the MP2 values to < 0.5 a.u.).Fig. 2 shows the values of α0 obtained for the polyoxazole chains (n = 1–10). In all cases, the polarisability appears to increase in a linear fashion up to the chain with n = 10. The only deviation from this linearity appeared as a small change in slope at around n = 2 or 3, so the data was replotted as α0 divided by the number of rings in the chain (Fig. 3).
 | ||
| Fig. 2 Static isotropic polarizability (α0) of oxazole chains. Lines added between points to emphasize trends. | ||
 | ||
| Fig. 3 Static isotropic polarizability (α0) of oxazole chains divided by number of rings (n). Lines added between points to emphasize trends. | ||
In this replotted form, it is clear that there is a large decrease in α0/n on formation of the initial inter-ring conjugation at n = 2, with smaller decreases seen as a consequence of adding subsequent rings to the core of the chain. The benchmark MP2 results indicate a clear convergence towards a fixed value of α0/n at approximately n = 5 and as expected, the uncorrected LDA data shows a gradual increase in α0/n as the chain length becomes larger. Conversely, the ADSIC data indicates that the self-interaction correction removes this spurious effect and leads to converged α0/n values (the final two points are identical) and suggests that the correct physical picture is obtained with this method.
It is interesting to note that rather than improving on the absolute value of the LDA polarisability, ADSIC actually leads to slightly larger α0/n values. This is in contrast to the effect seen for SIC-LDA in simple hydrogen chains, however, these do not display the extended π-conjugation found in the polyoxazole oligomers.68 The overestimation relative to LDA seen here was small and judged to be of little consequence in relation to the present study, particularly because whereas LDA yielded unbound anionic species (i.e. the energy of added electrons was positive), ADSIC correctly gave bound anions for all chain lengths studied in the optical absorption calculations (see below) permitting study of both hole- and electron-doped species in addition to the neutral chains.
The benchmark MP2 calculations and the fact that the SIC-TDDFT results agree with them provides reliable evidence that the polyoxazole oligomers should display polarisabilities that may be modulated in a linear fashion simply by tuning the length parameter, n. This is expected to have important consequences for their electrical and optical properties and suggests that these are interesting candidates for organic materials applications.69
In addition, the fact that the ADSIC calculations appear to give the correct physics with respect to this property (albeit with a small positive shift in α0/n relative to the MP2 benchmark data) was seen as evidence that the calculated optical absorption properties of the polyoxazole chains obtained at the ADSIC level would be similarly reliable.
4.2 Density of states
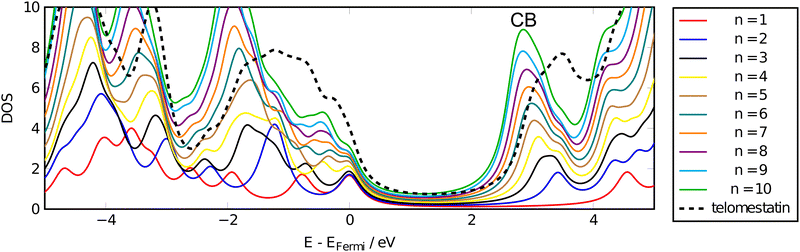
The density of states calculated at the ADSIC level for the neutral oxazole oligomers are shown in Fig. 4. For clarity, the energy axis has been zeroed by subtracting the Fermi energy, EFermi, from the state energies.A large decrease in the gap energy can be seen ongoing from n = 1 to n = 2, corresponding to the formation of the inter-ring conjugation in the dimer. Thereafter, a gradual red-shift in the peak energy accompanies the elongation of the oligomer chain along with a linear growth of the DOS corresponding to the development of a discrete conduction band (CB) centred at ∼3 eV above EFermi. These data are consistent with the picture obtained from the changes in polarisability per ring (α0/n) seen in the previous section.
Similarly, on going from n = 2 to n = 3, a split is seen in the CB peak. This is once again presumably due to the introduction of the third, central, oxazole ring and the continued existence of the n = 2 peak as a shoulder at ∼3.5 eV in the longer chains indicates that the terminal oxazoles contribute differently to the CB and that the main peak at ∼3 eV can be ascribed to the core heterocycles within the chain. This core/termini structure can be seen in the linear n = 7 telomestatin analogue in Fig. 1 The discrete nature of the CB peak in the longer oligomers indicates an increased density of CB states suggesting that these oligomers should display good electrical conductivity either when electrons are excited to the CB by optical absorption or by doping of the oligomers with excess electrons which will populate the lowest CB states.
The DOS obtained for telomestatin shows a different distribution of both the occupied valence region and the CB. These differences can be explained qualitatively by the all-cis conformation of telomestatin versus the all-trans conformation of the linear oligomers due to differences in strain on the conjugated π-system.
4.3 Optical absorption spectra
 | ||
| Fig. 5 Isotropic TD-ADSIC absorption spectra of neutral oligomeric oxazole chains. Vertical dashed lines indicate visible region. Spectra shifted by +0.25 eV.70 | ||
For comparison, the absorption spectrum of telomestatin was calculated at the same level of theory. When compared to the experimental UV-Vis spectrum of telomestatin (ESI in Doi et al., 200670), the calculated spectrum was found to agree well in terms of the relative peak positions but showed a systematic underestimation of the peak energies (ESI,† Fig. S3). The solvent used in obtaining the experimental UV-Vis spectrum of telomestatin was not reported (given the other experimental details, however, it is likely that the final solvent in the synthesis, CH2Cl2 was used). It is reasonable to expect that the well-known underestimation of excitation energies by TD-LDA (even with the ADSIC correction) is likely to be significantly larger than minor alterations due to switching between nonpolar solvents capable of dissolving telomestatin, therefore justifying the use of the +0.25 eV shift in the context of the present work.
Adding a rigid shift of +0.25 eV to the calculated spectrum to match the energy of the dominant experimental peak gave an excellent fit to the experimental spectral features and resulted in errors of ∼0.1 eV in the remaining peak positions. Because of the good fit of the shifted TD-ADSIC data to the experimental spectrum of the natural product and the chemical similarity of the linear oligomers, the same rigid shift was subsequently applied to all other calculated spectra.
Looking at the spectra for the linear chains Fig. 5, it can be seen that the simplest system (n = 1) displays a single peak at 5.8 eV. Consistent with formation of the inter-ring π-conjugation for n = 2, the main peak shifts to 4.6 eV with formation of a shoulder approximately 0.3 eV above this. At n = 3, these two features reverse relative intensity with the higher energy peak becoming largest. As was seen for the polarisability and DOS, above, on going to chains with n > 3, the main peak is seen to gradually undergo a red-shift as the chain length increases. This shift can be seen to be converging towards a value of ∼4.1 eV suggesting that further growth of the conjugated core should not significantly impact the energy of this peak.
Unlike the peak energy, the peak intensity continues to grow in a linear fashion up to the maximum chain length studied here (n = 10). This is indicative of a plasmonic collective excitation which begins in the chains with n > 2 (i.e. those with the core-termini structure) and suggests that both the energy and intensity of this plasmonic mode of the polyoxazole chains can be modulated by controlled synthesis of oligomers of a specific length. Further rationale for the length-dependence can be seen in ESI,† Fig. S4 which shows that the response corresponding to this peak is dominated by the longitudinal component polarised along the polyoxazole chain (see Fig. S1, ESI†). A small contribution comes from the in-plane transverse component and almost no contribution is seen with through-plane transverse polarisation.
Interestingly, the intensities of the first two absorption peaks for telomestatin are almost identical to those of the linear chain with the same number of oxazole rings (n = 7). A clear difference between the two compounds can be seen in the peak energies which are blue-shifted by approximately 0.5 eV. This is in line with increased strain on the conjugated π-system in the all-cis macrocyclic telomestatin and suggests that the absorption spectra of the acyclic compounds should be sensitive indicators of conformational change. Combined with the intense absorption associated with plasmonic excitations, this may have applications in sensing of metal ions where binding to e.g. the polyoxazole nitrogens can be expected to induce alterations in the cis/trans balance within the chain.
 | ||
| Fig. 6 Isotropic TD-ADSIC absorption spectra of hole-doped (mono-cationic) oligomeric oxazole chains. Vertical dashed lines indicate visible region. Spectra shifted by +0.25 eV.70 | ||
 | ||
| Fig. 7 Isotropic TD-ADSIC absorption spectra of electron-doped (mono-anionic) oligomeric oxazole chains. Vertical dashed lines indicate visible region. Spectra shifted by +0.25 eV.70 | ||
The largest changes in the absorption spectra for the doped species are seen in the IR region with electron-doping and from the visible into the IR for the hole-doped chains. These doping-induced peaks correspond to the formation of spin polaron (SP) gap states which have been well characterised in conjugated organic polymers.71,72 In polyanilines, (electro)chemical oxidation or reduction of the conducting polymer leads to creation of electronic transitions involving such gap states which vary in energy from the near IR to near UV.73 A characteristic doped-polyaniline absorption associated with these states occurs at ∼0.7 eV in good agreement with the predictions for the polyoxazole chains.74,75
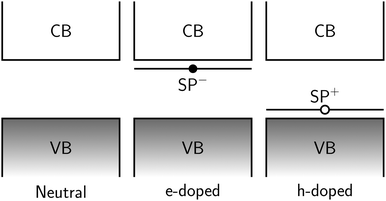
Fig. 8 gives a schematic indication of the distribution of these states in the doped species relative to the band gap. In hole-doped species, excitation occurs from the top of the valence band (VB) to the unoccupied SP+ state at bottom of gap. Similarly, in the electron-doped species, excitation occurs from the occupied SP− the bottom of the conduction band (CB).
In both cases, the excitation energy involved is substantially smaller than the band gap, hence the appearance of the peaks at much lower energies than seen in the spectra of the corresponding neutral species. VB → SP+ and SP− → CB gaps are chain-length dependent and converge to less than 0.05 eV for n = 10 providing a rationale for the observed modulation of the associated absorption energies.
In the hole-doped species the additional IR absorption is seen to be longitudinally-polarised in the same way as the UV plasmonic excitations (Fig. S5, ESI†) with no contribution from the transverse components of the response. Contrary to this, in the electron-doped species (Fig. S6, ESI†), the IR absorption is seen to be comprised of almost equal contributions from the longitudinal- and transverse-polarised response components. This suggests that the VB → SP+ excitation is best described by a 1-dimensional (quasi)particle in a box model whereas the SP− → CB excitation corresponds more to a conventional molecular one-electron absorption with no spatial discrimination.
Experimental measurement of polaronic optical excitation would necessarily involve nuclear relaxation through the electron/hole coupling to system phonons, which cannot be explicitly modelled by the current calculations due to the clamped nuclei (i.e. Born–Oppenheimer) approximation. However, it is felt that the current results reliably indicate the nature of the polaron states in electron/hole-doped oligomers such as the polyoxazoles.
5. Conclusions
In the present work, a series of linear oligomers based on the polyoxazole structure of the natural product telomestatin were studied. Self-interaction corrected time-dependent density functional theory within the real-space/time-propagation formalism was used to investigate both the ground- and excited-state electronic structure of oligomers with lengths varying from one to ten oxazole rings.It was found that the polyoxazoles display semiconductor character with a band gap converging to ∼2.5 eV as chain length increases with length-dependent formation of a discrete and compact conduction band (CB). On photo-excitation (or electron-doping) and population of the CB it is expected that they should display significant conductivity due to the large density of states in the low CB region. In addition, the oligomers display linear growth of the static polarisability which again marks them as potentially interesting as electrically conducting materials since this property can be systematically tuned by controlling oligomer length during synthesis.69 We have also shown that the neutral chains have polarisation-dependent maxima in their absorption spectra at ∼4.1 eV with length-dependent intensity, suggestive of collective plasmonic excitations.76 This is consistent with the anisotropy of the static polarisability values which are also dominated by the longitudinal tensor component (Fig. S2, ESI†). On electron/hole doping they develop additional absorption peaks in the IR region which for the hole-doped species also display polarisation dependence.
The tunability of the oligomer's intrinsic electronic properties and combination of UV/IR absorption in the doped species suggests that the polyoxazoles could have important applications as optically transparent electronic materials in areas such as window-based photovoltaics.77,78 The hole-doped species are of particular interest because of the longitudinal polarisation of their optical response in both the IR and UV regions.
Substitutions of the oxygen atom in the individual heterocycles could also be envisioned as a route to fine-tuning the chains' properties. Heavier Group 16 elements such as Sulfur could be used in analogy with polythiophene to alter the band gap of the polyazole oligomers studied here. Beyond this, Selenium or even Tellurium can be expected to radically alter both the gap and the conduction band DOS as they are known to exert a significant effect on the structure of the lowest unoccupied molecule orbital (LUMO) in organic chromophores.79,80 In addition, the greatly enhanced spin–orbit effects in the later Group 16 elements can be expected to produce large alterations in inter-system crossing probabilities allowing control of the optical emission properties of the oligomers.79,81
Further studies of cis/trans conformational effects on the DOS of the oligomeric chains along with alteration of the terminating groups or macrocyclisation would help to clarify the contributions coming from these sources. Similarly, modulation of the DOS and even suppression of the band gap to induce (semi-)metallic nature by π-stacking and supramolecular organisation in materials made from these oligomers can be expected and therefore investigation of these effects is warranted.82
The convergence of the polaron gaps towards very low energies also suggests that the doped polyoxazoles should display significant electrical conductivity. As with the absorption spectra, it should be possible to tune the conductivity through modulating the chain length. Controlling the density of polaron-type charge carriers in organic materials has been demonstrated to have applications in fields as diverse as molecular sensing and photovoltaic materials.73,83 The stability/lifetime of the polaron states is expected to be reinforced by supramolecular effects such as π-stacking or hydrogen-bonding in bulk materials or thin films.84 Further work is under way to investigate the structure and properties of such supramolecular assemblies involving the polyoxazoles and their group 16 analogues.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Industrial Biotechnology Innovation Centre (IBioIC, doctoral training grant BB/W059899/1). This work was also supported by national funds from the Portuguese FCT – Fundação para a Ciência e a Tecnologia, I. P., within the projects UIDB/04564/2020 and UIDP/04564/2020. The authors thank the Laboratory for Advanced Computing (LCA) of the University of Coimbra, Portugal for technical support. The authors would also like to acknowledge the support of the Maxwell Compute Cluster funded by the University of Aberdeen. All 2D chemical structures in this work were created using Marvin version 23.1, ChemAxon (https://www.chemaxon.com).References
- J. Hu, T. W. Odom and C. M. Lieber, Acc. Chem. Res., 1999, 32, 435–445 CrossRef CAS.
- Y. L. Shi and X. D. Wang, Adv. Funct. Mater., 2021, 31, 2008149 CrossRef CAS.
- Y. S. Zhao and J. Yao, One-Dimensional Nanostructures: Principles and Applications, American Chemical Society, 2013, ch. Organic One-Dimensional Nanostructures: Construction and Optoelectronic Properties, pp. 381–395 Search PubMed.
- H. Sun, Y. Zhang, J. Zhang, X. Sun and H. Peng, Nat. Rev. Mater., 2017, 2, 1–12 CAS.
- A. Machín, K. Fontánez, J. C. Arango, D. Ortiz, J. D. León, S. Pinilla, V. Nicolosi, F. I. Petrescu, C. Morant and F. Márquez, Materials, 2021, 14, 2609 CrossRef PubMed.
- A. Saad, S. Biswas, E. Gkaniatsou, C. Sicard, E. Dumas, N. Menguy and N. Steunou, Chem. Mater., 2021, 33, 5825–5849 CrossRef CAS.
- N. A. Minder, S. Ono, Z. Chen, A. Facchetti and A. F. Morpurgo, Adv. Mater., 2012, 24, 503–508 CrossRef CAS PubMed.
- S. Majumdar, R. Laiho, P. Laukkanen, I. J. Väyrynen, H. S. Majumdar and R. Österbacka, Appl. Phys. Lett., 2006, 89, 122114 CrossRef.
- O. Bubnova, Z. U. Khan, H. Wang, S. Braun, D. R. Evans, M. Fabretto, P. Hojati-Talemi, D. Dagnelund, J. B. Arlin, Y. H. Geerts, S. Desbief, D. W. Breiby, J. W. Andreasen, R. Lazzaroni, W. M. Chen, I. Zozoulenko, M. Fahlman, P. J. Murphy, M. Berggren and X. Crispin, Nat. Mater., 2014, 13, 190–194 CrossRef CAS PubMed.
- G. W. Bryant, J. Optic., 2016, 18, 074001 Search PubMed.
- J. Yan, Z. Yuan and S. Gao, Phys. Rev. Lett., 2007, 98, 216602 CrossRef PubMed.
- J. Silva, B. F. Milne and F. Nogueira, EPJ Web. Confer., 2020, 233, 05009 CrossRef CAS.
- J. Silva, B. F. Milne and F. Nogueira, J. Phys. Chem. A, 2018, 122, 5666–5670 CrossRef CAS PubMed.
- X. Bao, Q. Ou, Z. Q. Xu, Y. Zhang, Q. Bao and H. Zhang, Adv. Mater. Technol., 2018, 3, 1800072 CrossRef.
- S. S. Fernandes, M. Belsley, A. I. Pereira, D. Ivanou, A. Mendes, L. L. Justino, H. D. Burrows and M. M. M. Raposo, ACS Omega, 2018, 3, 12893–12904 CrossRef PubMed.
- A. Lauchner, A. E. Schlather, A. Manjavacas, Y. Cui, M. J. McClain, G. J. Stec, F. J. G. D. Abajo, P. Nordlander and N. J. Halas, Nano Lett., 2015, 15, 6208–6214 CrossRef CAS PubMed.
- J. Kimpel, W. He, Y. Cheng and T. Michinobu, J. Org. Chem., 2022, 87, 9384–9390 CrossRef CAS PubMed.
- F. H. Kohnke, J. P. Mathias and J. F. Stoddart, Angew. Chem., Int. Ed. Engl., 1989, 28, 1103–1110 CrossRef.
- C. Sanchez, H. Arribart and M. M. G. Guille, Nat. Mater., 2005, 4, 277–288 CrossRef CAS PubMed.
- O. O. Ige, L. E. Umoru and S. Aribo, ISRN Mater. Sci., 2012, 2012, 1–20 CrossRef.
- K. Shin-ya, K. Wierzba, K. Matsuo, T. Ohtani, Y. Yamada, K. Furihata, Y. Hayakawa and H. Seto, J. Amer. Chem. Soc., 2001, 123, 1262–1263 CrossRef CAS PubMed.
- M. Y. Kim, H. Vankayalapati, K. Shin-Ya, K. Wierzba and L. H. Hurley, J. Amer. Chem. Soc., 2002, 124, 2098–2099 CrossRef CAS PubMed.
- K. Amagai, H. Ikeda, J. Hashimoto, I. Kozone, M. Izumikawa, F. Kudo, T. Eguchi, T. Nakamura, H. Osada, S. Takahashi and K. Shin-Ya, Sci. Rep., 2017, 7, 1–8 CrossRef CAS PubMed.
- J. Koehnke, A. F. Bent, D. Zollman, K. Smith, W. E. Houssen, X. Zhu, G. Mann, T. Lebl, R. Scharff, S. Shirran, C. H. Botting, M. Jaspars, U. Schwarz-Linek and J. H. Naismith, Angew. Chem., Int. Ed., 2013, 52, 13991–13996 CrossRef CAS PubMed.
- J. Koehnke, F. Morawitz, A. F. Bent, W. E. Houssen, S. L. Shirran, M. A. Fuszard, I. A. Smellie, C. H. Botting, M. C. Smith, M. Jaspars and J. H. Naismith, ChemBioChem, 2013, 14, 564–567 CrossRef CAS PubMed.
- W. E. Houssen, A. F. Bent, A. R. McEwan, N. Pieiller, J. Tabudravu, J. Koehnke, G. Mann, R. I. Adaba, L. Thomas, U. W. Hawas, H. Liu, U. Schwarz-Linek, M. C. Smith, J. H. Naismith and M. Jaspars, Angew. Chem., Int. Ed., 2014, 53, 14171–14174 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- F. Nogueira, A. Castro and M. A. L. Marques, in A Tutorial on Density Functional Theory, ed. C. Fiolhais, F. Nogueira and M. A. L. Marques, Springer Berlin Heidelberg, Berlin, Heidelberg, 2003, pp. 218–256 Search PubMed.
- N. Tancogne-Dejean, M. J. T. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni, A. A. Correa, U. De Giovannini, A. Delgado, F. G. Eich, J. Flick, G. Gil, A. Gomez, N. Helbig, H. Hübener, R. Jestädt, J. Jornet-Somoza, A. H. Larsen, I. V. Lebedeva, M. Lüders, M. A. L. Marques, S. T. Ohlmann, S. Pipolo, M. Rampp, C. A. Rozzi, D. A. Strubbe, S. A. Sato, C. Schäfer, I. Theophilou, A. Welden and A. Rubio, J. Chem. Phys., 2020, 152, 124119 CrossRef CAS PubMed.
- X. Andrade, D. Strubbe, U. De Giovannini, A. H. Larsen, M. J. T. Oliveira, J. Alberdi-Rodriguez, A. Varas, I. Theophilou, N. Helbig, M. J. Verstraete, L. Stella, F. Nogueira, A. Aspuru-Guzik, A. Castro, M. A. L. Marques and A. Rubio, Phys. Chem. Chem. Phys., 2015, 17, 31371–31396 RSC.
- J. Alberdi-Rodriguez, M. J. T. Oliveira, P. García-Risueño, F. Nogueira, J. Muguerza, A. Arruabarrena and A. Rubio, Computational Science and Its Applications – ICCSA 2014, Cham, 2014, pp. 607–622 Search PubMed.
- X. Andrade, J. Alberdi-Rodriguez, D. A. Strubbe, M. J. T. Oliveira, F. Nogueira, A. Castro, J. Muguerza, A. Arruabarrena, S. G. Louie, A. Aspuru-Guzik, A. Rubio and M. A. L. Marques, J. Phys. Cond. Matt., 2012, 24, 233202 CrossRef PubMed.
- J. Jornet-Somoza, J. Alberdi-Rodriguez, B. F. Milne, X. Andrade, M. A. Marques, F. Nogueira, M. J. Oliveira, J. J. Stewart and A. Rubio, Phys. Chem. Chem. Phys., 2015, 17, 26599–26606 RSC.
- B. J. Austin, V. Heine and L. J. Sham, Phys. Rev., 1962, 127, 276 CrossRef.
- P. Schwerdtfeger, Chem. Phys. Chem., 2011, 12, 3143–3155 CrossRef CAS PubMed.
- R. M. Sternheimer, Phys. Rev., 1954, 96, 951 CrossRef CAS.
- G. D. Mahan, Phys. Rev. A, 1980, 22, 1780 CrossRef CAS.
- X. Andrade, S. Botti, M. A. Marques and A. Rubio, J. Chem. Phys., 2007, 126, 184106 CrossRef PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- E. Caldeweyher, J. M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC.
- S. Ehlert, U. Huniar, J. Ning, J. W. Furness, J. Sun, A. D. Kaplan, J. P. Perdew and J. G. Brandenburg, J. Chem. Phys., 2021, 154, 061101 CrossRef CAS PubMed.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- P. A. M. Dirac, Math. Proc. Cambridge Philos. Soc., 1930, 26, 376–385 CrossRef CAS.
- F. Bloch, Zeit. Phys., 1929, 57, 545–555 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- M. A. Marques, M. J. Oliveira and T. Burnus, Comput. Phys. Commun., 2012, 183, 2272–2281 CrossRef CAS.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- C. Legrand, E. Suraud and P. G. Reinhard, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 1115 CrossRef CAS.
- M. van Setten, M. Giantomassi, E. Bousquet, M. Verstraete, D. Hamann, X. Gonze and G.-M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54 CrossRef CAS.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- D. R. Hamann, Phys. Rev. B, 2017, 95, 239906 CrossRef.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Phys. Commun., 2014, 81, 446 CAS.
- S. Faas, J. G. Snijders, J. H. van Lenthe, E. van Lenthe and E. J. Baerends, Chem. Phys. Lett., 1995, 246, 632–640 CrossRef CAS.
- E. V. Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1998, 105, 6505 CrossRef.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Info. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- M. A. L. Marques and E. K. U. Gross, Lect. Notes Phys., 2003, 144–184 Search PubMed.
- P. L. de Boeij, Lect. Notes Phys., 2006, 706, 317–322 Search PubMed.
- B. Champagne, E. A. Perpète, S. J. V. Gisbergen, E. J. Baerends, J. G. Snijders, C. Soubra-Ghaoui, K. A. Robins and B. Kirtman, J. Chem. Phys., 1998, 109, 10489 CrossRef CAS.
- S. J. van Gisbergen, P. R. Schipper, O. V. Gritsenko, E. J. Baerends, J. G. Snijders, B. Champagne and B. Kirtman, Phys. Rev. Lett., 1999, 83, 694 CrossRef CAS.
- C. D. Pemmaraju, S. Sanvito and K. Burke, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 121204 CrossRef.
- A. Gillet, S. Cher, M. Tassé, T. Blon, S. Alves, G. Izzet, B. Chaudret, A. Proust, P. Demont, F. Volatron and S. Tricard, Nanoscale Horiz., 2021, 6, 271–276 RSC.
- T. Doi, M. Yoshida, K. Shin-Ya and T. Takahashi, Org. Lett., 2006, 8, 4165–4167 CrossRef CAS PubMed.
- J. L. Bredas, J. C. Scott, K. Yakushi and G. B. Street, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 1023 CrossRef CAS.
- J. L. Bredas and G. B. Street, Acc. Chem. Res., 1985, 18, 309–315 CrossRef CAS.
- C. K. Tan and D. J. Blackwood, Sens. Actuators, B, 2000, 71, 184–191 CrossRef CAS.
- S. Stafström, J. L. Brédas, A. J. Epstein, H. S. Woo, D. B. Tanner, W. S. Huang and A. G. MacDiarmid, Phys. Rev. Lett., 1987, 59, 1464 CrossRef PubMed.
- W. Zheng, Y. Min, A. G. MacDiarmid, M. Angelopoulos, Y. H. Liao and A. J. Epstein, Synth. Metals, 1997, 84, 63–64 CrossRef CAS.
- R. L. Gieseking, Mater. Horiz., 2022, 9, 25–42 RSC.
- A. S. M. Sayem, A. Lalbakhsh, K. P. Esselle, J. L. Buckley, B. O'Flynn and R. B. Simorangkir, IEEE Open J. Antennas Propag., 2022, 3, 1109–1133 Search PubMed.
- T. Baron, W. Naim, I. Nikolinakos, B. Andrin, Y. Pellegrin, D. Jacquemin, S. Haacke, F. Sauvage, F. Odobel, T. Baron, B. Andrin, Y. Pellegrin, D. Jacquemin, F. Odobel, W. Naim, F. Sauvage, I. Nikolinakos and S. Haacke, Angew. Chem., 2022, 134, e202207459 CrossRef.
- E. I. Carrera and D. S. Seferos, Macromolecules, 2015, 48, 297–308 CrossRef CAS.
- T. P. Kaloni, G. Schreckenbach and M. S. Freund, Sci. Rep., 2016, 6, 1–18 CrossRef PubMed.
- R. Acharya, S. Cekli, C. J. Zeman, R. M. Altamimi and K. S. Schanze, J. Phys. Chem. Lett., 2016, 7, 693–697 CrossRef CAS PubMed.
- T. P. Kaloni, P. K. Giesbrecht, G. Schreckenbach and M. S. Freund, Chem. Mater., 2017, 29, 10248–10283 CrossRef CAS.
- S. Tang, W. Qiu, X. Xu, S. Xiao, Y. Tong, X. Wang and S. Yang, Adv. Func. Mater., 2022, 32, 2110284 CrossRef CAS.
- O. Dumele, J. Chen, J. V. Passarelli, S. I. Stupp, O. Dumele, S. I. Stupp, J. Chen and J. V. Passarelli, Adv. Mater., 2020, 32, 1907247 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01140b |
| ‡ A bug was later discovered in the D4 code in Orca 5.0.3 which might have adversely impacted the calculated geometries. However, after checking with the standalone DFTD4 code43–45 it was found that for r2SCAN-D4 the Orca dispersion energies were within 0.5% of the reference values and were therefore considered reliable. |
| This journal is © the Owner Societies 2023 |