 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Current-density pathways in figure-eight-shaped octaphyrins†
Qian
Wang
 ,
Jaakko
Pyykkö
,
Maria
Dimitrova
,
Jaakko
Pyykkö
,
Maria
Dimitrova
 ,
Stefan
Taubert
,
Stefan
Taubert
 and
Dage
Sundholm
and
Dage
Sundholm
 *
*
Department of Chemistry, Faculty of Science, P.O. Box 55 (A.I. Virtanens plats 1), FIN-00014 University of Helsinki, Finland. E-mail: Dage.Sundholm@helsinki.fi
First published on 18th April 2023
Abstract
We have calculated the current density induced by an external magnetic field in a set of figure-eight-shaped expanded porphyrinoids. The studied octaphyrins can be divided into three classes (N2, N4, and N6) based on the number of the inner hydrogen atoms of the pyrrole rings. Using the Runge–Kutta method, the current density is split into diatropic and paratropic contributions that are analyzed separately. The calculations show that one common ring current consists of two rather independent pathways. Each of them follows the outer side of the molecular frame of one half of the molecule and passes to the inner side of the frame on the other half. The ring-current pathways are similar to the ones for [12]infinitene. However, the current density of the octaphyrins is more complex having many branching points and pathways. Vertical through-space current-density pathways pass in the middle of the molecules through a plane that is parallel to the figure-eight-shaped view of the molecules when the magnetic field is perpendicular to the plane. The isolectronic N2 and the N4 dication sustain a weak paratropic ring current inside the molecule, which is also observed in the 1H NMR magnetic shielding constant of the inner hydrogen atoms. The diatropic current-density contribution dominates in the studied molecules. For the N4 and N6 molecules, the global current-density pathways are only diatropic and N6 sustains the strongest global diatropic current-density flux of 13.2 nA T−1.
1 Introduction
Porphyrinoids consisting of a number of interconnected π-conjugated pyrrole rings play important roles in biological systems and are also widely used in technological and medical applications.1–9 Expanded porphyrinoids have more than four pyrrole rings in the macrocycle leading to a large flexibility.10–12 The structural flexibility is limited by the strain in the porphyrinoid macroring rendering unusual molecular structures and peculiar molecular properties possible.13 The molecular structures can interconvert from Möbius to Hückel topology by protonation/deprotonation or even without external stimuli at room temperature.11,14The first octaphyrin with a twisted figure-eight conformation belonging to the C2 point group was synthesized in 2001.15 It has intramolecular hydrogen bonds between the nitrogen moieties of the pyrrole rings that are broken under acidic conditions and form an intermolecular hydrogen-bond network to the counter anions leading to changes in the topology of the molecular structure.11,16,17 The molecular topology can be adjusted by changing the number of electrons in the conjugated orbitals. [36]octaphyrin with formally 36 electrons in the aromatic pathway adopts a Möbius aromatic conformation, whereas the corresponding [38]octaphyrin has a Hückel aromatic structure.16 Turcasarin or decaphyrin(1.0.1.0.0.1.0.1.0.0), which is the first figure-eight-shaped porphyrinoid that has been synthesized, has a highly twisted structure and two helical conformations that slowly interconvert at room temperature.14
The number of electrons in the conjugated orbitals or more generally the number of occupied conjugated orbitals determines whether porphyrinoids or other ring-shaped molecules are aromatic or antiaromatic. The 1H NMR chemical shifts of the β hydrogen atoms and of the inner hydrogen atoms of the pyrrole rings are used for estimating the aromatic nature of porphyrinoids. The nonaromatic range of the 1H NMR chemical shifts are δ = [6.0–6.5] ppm. The corresponding magnetic shielding range obtained in calculations is σ = [25.5–26.0] ppm since the magnetic shielding of the tetramethylsilan (TMS) reference is about 32 ppm.18 In aromatic porphyrinoids, the 1H NMR signal of the β hydrogen atoms are shifted towards larger δ (smaller σ) values and the 1H NMR signal of the inner ones to smaller δ (larger σ) values. For antiaromatic porphyrinoids the 1H NMR signals are shifted in the opposite direction.10
The number of electrons in the conjugated orbitals or equivalently the number of occupied conjugated orbitals can be adjusted by changing the number of inner hydrogen atoms or by charging the molecule. The aromatic character also depends on the topology of the molecular structure.10,13,19–25
The octaphyrins studied in this work adopt figure-eight-shaped conformations because of structural strain and intramolecular hydrogen-bonding interactions.11,15 The nonplanar and twisted molecular structures of the studied octaphyrins render quantitative determination of their aromatic character challenging.26 The ring-current model originally developed for understanding the 1H NMR shifts of planar aromatic molecular rings27,28 might not be applicable to figure-eight-shaped porphyrinoids because the ring current pathway is not obvious and more than one current-density pathway is possible.
In this study, we investigate a series of octaphyrins and their dications which are structurally related to the synthesized [36]octaphyrin (denoted N4 in this work).15 Their aromatic character is studied in detail by calculating the magnetically induced current density, which we also separate into diatropic and paratropic contributions. The current density pathways are visualized and their strengths are determined by numerical integration. The 1H NMR magnetic shielding density of the inner hydrogen atoms are visualized yielding a deeper understanding of reported 1H NMR chemical shifts of figure-eight-shaped porphyrinoids.
2 Computational methods
2.1 Employed methods and software
The molecular structures that were assumed to belong to the C2 symmetry point group were fully optimized with Turbomole.29–32 The structure optimizations were performed at the density functional theory (DFT) level using the B3LYP functional and the def2-TZVP basis sets.33–36 Dispersion interactions were considered at the semiempirical D3(BJ) level.37,38 Calculations of the vibrational frequencies showed that the optimized C2 structures are minima on the potential energy surface.39The aromatic character of the octaphyrins has been assessed by calculating the magnetically induced current density using the gauge-including magnetically induced current (GIMIC) method.40–42 The C2 axis shown with the black line in Fig. 1 is parallel to the stacked pyrroles and the C–C bond in the center of the molecule. The current-density pathways were obtained by applying an external magnetic field perpendicular to the C2 axis shown in the upper picture of Fig. 1. The direction of the magnetic field is shown with a green dashed arrow in the lower picture of Fig. 1. The tropicity of the current density is determined by following the streamlines of the magnetically induced current density. In ring-shaped molecules, the direction of the current density across the integration plane can be used for determining the tropicity of the ring current, whereas in this case a more advanced approach must be used. We consider the flux direction positive (diatropic) when it flows in the clockwise direction, while it is paratropic when it flows in the opposite direction when looking towards the negative z axis for B = (0,0,z).42,43 We placed integration planes along the A and B directions as shown in Fig. 1. The planes denoted A1, A2, B1 and B2 are perpendicular to the paper plane and parallel to the external magnetic field. The strength of the current density passing through the plane can be obtained by numerically integrating the current density passing through it. Molecular rings are aromatic when the integrated current strength is positive, whereas the figure-eight-shaped octaphyrins can be considered aromatic when they are dominated by global diatropic contributions to the current density.
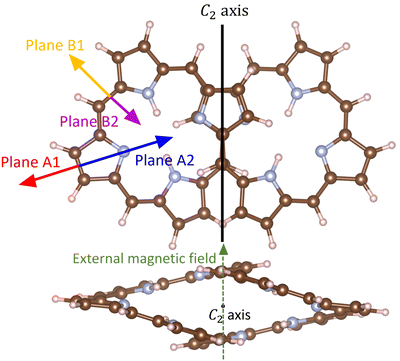 | ||
| Fig. 1 The placement of the integration planes for determining the strength of the current-density pathways is shown with the colored arrows. The planes are perpendicular to the reader. The external magnetic field is oriented perpendicular to the figure-eight view of the molecule. In the lower picture the C2 axis that is shown as a dot points towards the reader. The pictures have been made with VESTA and PowerPoint.55 | ||
A small ring-current strength generally suggests that molecular rings are non-aromatic and they are antiaromatic when the ring current is dominated by paratropic contributions to the ring current. Figure-eight-shaped octaphyrins can analogously be considered antiaromatic when they are dominated by global paratropic contributions to the current density and globally non-aromatic when they sustain weak global current-density pathways.
2.2 Nuclear magnetic shielding densities
Calculations of nuclear magnetic resonance (NMR) shielding tensors using response theory yield the density matrix and the magnetically perturbed density matrices,44,45 which are used as input data in GIMIC calculations of magnetically induced current-density susceptibilities.Spatial contributions to the elements of NMR shielding tensors, which we call the nuclear magnetic shielding density, can be expressed using the Biot–Savart law as the scalar product of the magnetically induced current-density susceptibility  multiplied with the first derivative of the vector potential of the nuclear magnetic moment with respect to the strength of the magnetic moment in the limit of vanishing magnetic moment
multiplied with the first derivative of the vector potential of the nuclear magnetic moment with respect to the strength of the magnetic moment in the limit of vanishing magnetic moment 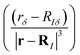 .46–53 The Biot–Savart expression for calculating the shielding tensor elements then reads
.46–53 The Biot–Savart expression for calculating the shielding tensor elements then reads
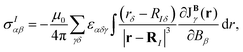 | (1) |
The spatial contributions to NMR shielding constants can be calculated with the GIMIC program.52,53 Visualization of the integrand in eqn (1) shows the spatial contributions to the elements of the magnetic shielding tensor of nucleus I. When the external magnetic field is aligned along the z axis, the current-density contribution to the nuclear magnetic shielding of planar or nearly planar aromatic (antiaromatic) molecules mainly originates from σzz, which is explicitly given by
 | (2) |
2.3 Separating diatropic and paratropic contributions
We have calculated the magnetically induced current density susceptibility of the six figure-eight-shaped octaphyrins to assess their aromatic character. The aim is to investigate how the aromatic character depends on the number of inner hydrogen atoms or the total charge of the molecule.The tropicity of the current density can be determined locally for single rings because the ring current passing through a plane cutting the ring continues around the ring. When the current-density flux is in the classical direction, the current density is diatropic, whereas the paratropic current density flows in the opposite direction. For fused aromatic and antiaromatic rings, it is more difficult to determine the tropicity in a single point,56,57 because tropicity is a global property. The tropicity of the current density of figure-eight-shaped molecules is therefore difficult to determine from the direction of the flux passing a plane that cuts the stream.58 In the figure-eight-shaped [12]infinitene, the ring current is diatropic on the outside of molecule. The diatropic ring current continues to the inside of the other half of the molecule where the diatropic current-density flux seems to be paratropic. However, even though it is seemingly paratropic, the vortex cannot suddenly change its tropicity. It is still diatropic because the main part of the current-density pathway is in the diatropic direction. Thus, the only way to determine the tropicity is to follow the vector field around the vortex and calculate the tropicity in discrete points along the trajectory.
The diatropic or paratropic contributions to the current density of a given point in space is here determined by following the vector field around the whole vortex to the starting point. The trajectory around the vortex is calculated using the Runge–Kutta algorithm.59,60
The next point ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) n+1 along the trajectory of the current density can be estimated from the current-density vector
n+1 along the trajectory of the current density can be estimated from the current-density vector ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) in the present position
in the present position ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) n by using the Runge–Kutta method
n by using the Runge–Kutta method
 | (3) |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 = h
1 = h![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (
(![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) n),
n),  ,
,  , and
, and  . h is the step length.
. h is the step length.
The cross product ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (
(![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) n) ×
n) × ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (
(![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) n+1) is calculated for each step along the trajectory. The tropicity (τ) of the current density in the chosen grid point is obtained by calculating the scalar product with the vector of the external magnetic field and adding the contributions from each trajectory step around the whole vortex.
n+1) is calculated for each step along the trajectory. The tropicity (τ) of the current density in the chosen grid point is obtained by calculating the scalar product with the vector of the external magnetic field and adding the contributions from each trajectory step around the whole vortex.
 | (4) |
The sign of τ yields the tropicity of the current density in the studied grid point. The diatropic and paratropic current densities can be identified and separated by repeating the procedure for all grid points of a discretized representation of the current density. The diatropic and paratropic contributions can then be analyzed separately.
3 Results and discussion
3.1 Molecular structures
The studied octaphyrins consist of eight pyrrole rings interconnected at the α carbon atoms via methine bridges. The figure-eight-shaped molecules have in the middle of the molecule a sandwich-like structure consisting of two pyrrole rings with the nitrogen atoms pointing in different directions.The studied octaphyrins can be grouped into three classes based on the number of occupied conjugated orbitals. The molecular structures are shown in Fig. 2. We use the N2, N4 and N6 notation, where the number of inner hydrogen atoms are indicated. In o-N2, the inner hydrogen atoms are connected to adjacent nitrogen atoms, whereas in p-N2 they are in opposite positions. The o-N2 structure is energetically 26 kJ mol−1 below p-N2. At room temperature the inner hydrogen atoms might migrate yielding an equilibrium between the tautomer structures, which has been observed for free-base porphyrin derivatives and for expanded porphyrinoids.61,62
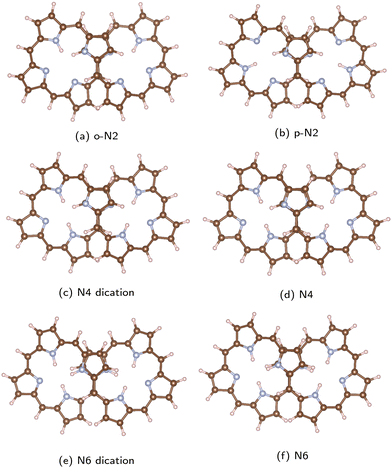 | ||
| Fig. 2 The optimized molecular structures of the studied octaphyrins are shown. Carbon atoms are brown, the nitrogen atoms are blue and the hydrogen atoms are white. The pictures have been made with VESTA.55 | ||
The molecular structure optimizations show that the distance between the stacked pyrrole rings depends on the number of occupied conjugated orbitals. The distances between the pyrrole rings reported in Table 1 show that molecules with same number of electrons in the conjugated orbitals have practically the same distance between the stacked pyrrole rings, whereas the interaction between the two strands at the crossing point is stronger for the molecules with more electrons in the conjugated orbitals leading to a shorter distance between the pyrrole rings. The distance is 3.40–3.44 Å in o-N2, p-N2 and N4 dication. The shortest distance of 3.27 Å was obtained for N6. N4 and the N6 dication have an intermediate distance of 3.31–3.35 Å between the stacked pyrrole rings.
| Molecule | Distance | HOMO–LUMO gap |
|---|---|---|
| o-N2 | 3.41 | 1.55 |
| p-N2 | 3.40 | 1.38 |
| N4 dication | 3.44 | 1.51 |
| N4 | 3.31 | 1.17 |
| N6 dication | 3.35 | 1.06 |
| N6 | 3.27 | 1.72 |
The octaphyrins are not ordinary planar molecules but doubly Möbius-twisted figure-eight-shaped molecules with a linking number (Lk) of two.22,63 The linking number can be arbitrarily divided into twist (Tw) and writhe (Wr).64–67 Since the topology of molecular structures is figure-eight shaped, Tw is close to zero and the Lk number of two consists mainly of Wr.
The aromatic character of Möbius-twisted molecules follows largely the generalized aromaticity rule stating that molecules are Hückel aromatic according to the ordinary 4n + 2 rule when they have an even Lk including zero, whereas the ones with an odd Lk obey the 4n aromaticity rule of singly twisted Möbius twisted molecules.20,22,63,68 In this case, the studied molecules have an Lk of about two implying that they follow the same aromaticity rules as for example benzene and cyclobutadiene. The third option, namely nonaromaticity occurs for example when the global conjugation is too weak for sustaining global current-density pathways.
3.2 Counting electrons and orbitals
The number of π electrons is usually used as a first estimate of the aromatic nature of planar molecular rings. The electron-counting rules have later been extended to non-planar molecules. A generalization of the aromaticity rules to figure-eight-shaped molecules is complicated.58The N2 molecules and the N4 dication have formally 34 electrons in the aromatic pathway. N4 and the N6 dication have 36 electrons, whereas N6 has formally 38 electrons in the aromatic pathway. This is probably not a proper way to count the number of electrons in the aromatic pathway because the electrons in all conjugated bonds can be part of the aromatic pathway(s). Therefore, we consider that N2 and the isoelectronic N4 dication have 50 electrons in the conjugated bonds. The pyrrole rings contribute with 5, each meso carbon with 1 and each inner hydrogen with 1 electron. N4 and the isoelectronic N6 dication have 52 electrons and N6 has 54 electrons in the conjugated bonds. Assuming a singlet ground state with all orbitals doubly occupied, the number of occupied conjugated orbitals are 25, 25, 26, 26 and 27 for N2, the N4 dication, N4, the N6 dication and N6, respectively. Since molecules with odd number of occupied conjugated orbitals are generally aromatic,69 N2, the N4 dication and N6 are expected to be aromatic. Planar molecules with even number of occupied conjugated orbitals are expected to be antiaromatic suggesting that N4 and the isoelectronic N6 dication are antiaromatic.
3.3 Magnetically induced current-density susceptibilities
The aromatic character and the degree of aromaticity of porphyrinoids can be estimated from molecular magnetic properties like magnetically induced ring currents and 1H NMR chemical shifts as well as from the thermodynamic stability, bond-length alternations and optical spectra.13 External magnetic fields induce current densities in atoms and molecules, the strength of which can be used for determining the aromatic nature of ring-shaped molecules. We focus here on the global flux of the magnetically induced current-density susceptibilities, their branching points and through-space pathways. We mainly omit discussion of detailed vortex structures in the current density. Since the studied molecules belong to the C2 point group, we discuss the current density in half the molecule because it is for symmetry reasons the same in the other half.A significant contribution to the current-density pathways of the studied octaphyrins flows along the outer edge of the molecule in one half of it and continues to the inner side of the other half and vice versa as illustrated with the green and blue circles in Fig. 3. These contributions to the global current-density flux consist of two independent non-intersecting pathways as in [12]infinitene.58 However, we find that the current density of the octaphyrins has branching points near the stacked pyrrole rings in the middle of the molecule as shown in the left picture of Fig. 3. These pathways are in common for the studied figure-eight-shaped octaphyrins that have largely the same junctions and current-density pathways, whereas the strengths of the current-density pathways differ. Detailed current-density pathways are shown in Fig. 4 and discussed in Section 3.5.
 | ||
| Fig. 3 The current density and its branching points in N4. Two independent global ring currents are illustrated with the red and blue circle, respectively. Examples of current-density junctions are showed in the left picture, where the current-density direction is indicated with bright green arrows. The current-density pictures have been made with Paraview and PowerPoint.70 | ||
 | ||
| Fig. 4 Strong current-density pathways (left) and the vertical throughspace current-density pathways at two different positions (right) of the studied molecules. In (a), p-N2 is shown as an example for molecules with 25 occupied conjugated orbitals. In (b), N4 represents the molecules with 26 occupied conjugated orbitals and N6 in (c) has 27 occupied conjugated orbitals. The independent current-density pathways in the two halves of the molecules are shown in purple and red, respectively. The right pictures show the vertical through-space current-density pathways. The direction of the through-space ring current is from dark green in one half to light green in the other half of the molecule. The pictures have been made with Paraview.70 | ||
3.4 Diatropic and paratropic current-density contributions
The figure-eight-shaped molecular structure renders determination of diatropic and paratropic current densities difficult. To avoid mixing of diatropic and returning paratropic contributions to the current densities (or vice versa), we separate them by using the Runge–Kutta method. The diatropic current density of the N4 dication is shown in the left picture of Fig. 5 and the paratropic one to the right. The paratropic contribution to the current density of the N4 dication shows that it is confined to the inner part of half of the molecule. In the middle of the molecule it passes through the space to the other strand. There are two independent paratropic ring currents of this kind. Local paratropic contributions to the current density are found inside the pyrrole rings. The diatropic contribution to the current density dominates. The separation of the current densities of the other molecules reveals that the molecules can be divided into two classes. The molecules with 25 occupied conjugated orbitals behave like the N4 dication, whereas N4, the N6 dication and N6 do not sustain any significant global paratropic ring current inside the octaphyrin ring. Their global current-density pathways are mainly diatropic. | ||
| Fig. 5 The separated diatropic (upper left) and paratropic (upper right) contributions to the current density of the N4 dication (lower). N2 and the N4 dication have similar paratropic contributions to the current density. The N6 dication, N4 and N6 have no significant global paratropic current-density pathways. The color scheme corresponds to the strength of the current density with yellow being the strongest and black represents the weakest one. The pictures have been made with Paraview.70 More pictures are shown in the ESI.† | ||
3.5 Current-density pathways
The studied octaphyrins have similar current densities when they have the same number of electrons, whereas the strength of the current-density pathways differs for N2, N4 and N6 with different number of occupied conjugated orbitals. Visualization of the current density with Paraview shows that N2 and the N4 dication sustain two independent paratropic ring currents inside the two halves of the molecules. The current density is shown in Fig. 5. More pictures are found in the ESI.† The paratropic ring currents pass between the two molecular strands in the middle of the molecule. The current density of the molecules with 25 occupied conjugated orbitals has two strong figure-eight-shaped diatropic current-density pathways that passes from the outer edge of one side of the molecule to the inner side of the other half. The current density generally follows the molecule frame, whereas in the studied molecules there are through-space current-density pathways. The through-space diatropic ring current arriving from the edge continues on the inside of the octaphyrin.For the molecules with 26 occupied conjugated orbitals, there are two strong independent diatropic outer current-density loops in the upper and lower halves of the molecule. The current density flows through the space from the outer part of one half to the outer part of the other one at the Cβ atoms of the stacked pyrroles. A pathway on the outside of one half of the molecule turns to the inner side of the other half and returns to the outside. There are also two relatively isolated current-density loops as shown in the purple and red in the left picture of Fig. 4(b). A global current-density pathway on the outside of the whole molecule passes through the space from one half of the molecule (dark green) to the other half (light green) as shown in the upper right picture of Fig. 4(b).
N6 with 27 conjugated orbitals has two strong diatropic porphyrin-like ring current with through-space pathways between the strands. The diatropic current-density pathway around the frame to some extent follows the skeleton to generate figure-eight-shaped pathways. In the middle of the molecule, the diatropic ring current makes a shortcut to the other strand forming a porphyrin-like ring current. There is a vertical through-space current-density pathway from the outer edge of one half to the outer edge of the other one. The current-density pathways make shortcuts from the inside to the outside between the pyrrole rings.
The distance between the strands decreases with increasing number of occupied conjugated orbitals. When the stacking distance shrinks, the interaction between the strands increases leading to stronger through-space current-density pathways. Separation of the current density into diatropic and paratropic ones show that the molecules with 26 and 27 occupied conjugated orbitals do not sustain any significant global paratropic current-density pathways. More pictures are shown in the ESI.†
3.6 Current-density strengths
The strengths of the current-density pathways are determined by numerically integrating the current density passing through selected planes cutting the molecular frame. Integration through the bond between a methine group and a pyrrole ring (plane B) is accurate because strong atomic vortices are avoided. The current-density flux at plane B consists of an inner and an outer pathway. However, the inner one may consist of a paratropic contribution and the returning diatropic ring current along the outer edge. The strength of the paratropic contribution can be determined by integrating the separated paratropic current-density flux. The diatropic current-density contribution consists of several global pathways whose strengths are difficult to determine separately.The integration of the current-density flux passing through plane A that cuts the pyrrole ring provides more information about the different pathways. N4, the N6 dication and N6 do not sustain any global paratropic ring current implying that the current strengths on the outside and inside are due to diatropic and returning diatropic current-density pathways. Different current-density strengths at plane A and B suggest that there are local current-density pathways at the pyrrole ring and that there is a diatropic current-density pathway turning from the inside to the outside between the two planes. Since the pathways consist of local vortices and global current-density pathways of different lengths, it is hard to determine the strengths of the individual pathways.
Integration of the current-density pathways shows that the studied octaphyrins are dominated by diatropic current-density contributions. The strength of the diatropic current-density pathways passing through plane B is 13.2 nA T−1 for N6. For N4 and the N6 dication the corresponding current-density strengths are 9.9 nA T−1 and 10.8 nA T−1, respectively. Thus, the strengths of the current-density pathways are about as strong as for benzene.40 The strengths of the diatropic current-density pathway of the N2 molecules and the N4 dication passing through plane B are in the range of 5.1 nA T−1 to 7.0 nA T−1. Thus, they are about a factor of two weaker than for the three other octaphyrins. Furthermore, N2 and the N4 dication sustain a weak paratropic current-density pathway whose strengths are −0.4 nA T−1, −1.3 nA T−1 and −1.1 nA T−1 for o-N2, p-N2 and the N4 dication, respectively (Table 2).
| Molecule | Diatropic | Paratropic |
|---|---|---|
| o-N2 | 7.0 | −0.4 |
| p-N2 | 5.5 | −1.3 |
| N4 dication | 5.1 | −1.1 |
| N4 | 9.9 | 0.0 |
| N6 dication | 10.8 | 0.0 |
| N6 | 13.2 | 0.0 |
The current density passing through plane A consists of a positive flux on the outside of the β carbon atoms and a negative contribution on the inside of them. There is a positive contribution between the α carbon atoms and a negative contribution passing on the inside of the nitrogen atom. The positive current-density contributions are either a diatropic or returning paratropic current-density pathway. Analogously, the negative contributions originate from paratropic or returning diatropic current-density pathways.
The contributions can be identified to originate from global diatropic current-density pathways on the outside; a local diatropic current-density pathway around the β positions; a local paratropic ring current inside the pyrrole ring; a local diatropic ring current around the nitrogen moiety and a local ring current around the nitrogen atom. The global diatropic current-density pathways return on the inside of the pyrrole ring and are mixed with the paratropic ring current in the N2 molecules and in the N4 dication. The exact strengths of the diatropic current-density pathways are difficult to determine. The diatropic current-density pathway is stronger at plane B than at plane A because some of the current-density flux turns from the inside to the outside between the planes. The current density profiles at plane A and B are given in the ESI.†
3.7 Shielding densities of the octaphyrins
The Biot–Savart expression in eqn (2) shows that the contributions from e.g., the negative and positive of the relative x directions with respect to nucleus I have the opposite sign, when the current density has largely the same direction on both sides of the nucleus. The sign change leads to the alternating shielding and deshielding contributions as shown in Fig. 6.52,53 | ||
| Fig. 6 The spatial contributions to the 1H NMR shielding constants of the inner hydrogen atoms. Shielding and deshielding contributions are shown in red and blue, respectively. The pictures have been made with Paraview.70 | ||
Since the inner protons of the pyrrole rings are sensitive to the magnetic shielding or deshielding due to the ring-current, these signals are useful for estimating the aromatic character of porphyrinoids. The averaged 1H NMR shielding constants of the inner hydrogen atoms shift are 18.3 ppm for o-N2, 16.9 ppm for p-N2 and 16.7 ppm for the N4 dication with 25 occupied conjugated orbitals.
For N4 and the N6 dication with 26 occupied conjugated orbitals the averaged 1H NMR shielding constants are 21.3 ppm and 22.5 ppm, respectively. The average of the calculated 1H NMR magnetic shielding for the inner hydrogen atoms of N4 are in the middle of the range of [18.75, 23.41] ppm for the experimental ones.15 The nuclear magnetic shielding of the TMS reference is assumed to be 32 ppm.
The averaged 1H NMR shielding constants of the inner hydrogen atoms of N6 with 27 occupied conjugated orbitals is 28.1 ppm. The smaller shielding values for N2 and the N4 dication is most likely due to the paratropic ring current passing on the inside of the inner hydrogen atoms and also due to the weak diatropic current density.
The spatial contributions to the shielding constants of the inner hydrogen atoms in Fig. 6 does not reveal any large differences. The N2 dication and o-N2 have similar red and blue patterns, whereas the colors in the shielding density of p-N2 are paler. However, the integrated shielding constants are very similar for the three molecules. The stronger diatropic current-density flux of N6 is also reflected in the shielding density. However, the contributions from the red and blue areas to some extent cancel leading to a shielding constant for the inner hydrogen atom that is 5–7 ppm larger than for N4 and the N6 dication.
The averaged 1H NMR shielding constants of the hydrogen atoms in the β positions are 26.4 ppm, 25.8 ppm and 25.6 ppm for o-N2, p-N2 and the N4 dication, respectively, which are slightly larger than the corresponding values of 24.6 ppm, 23.8 ppm and 24.2 ppm for N4, the N6 dication and N6, respectively. The average 1H NMR magnetic shielding of the hydrogen atoms in the β position of 24.6 ppm agrees well with the experimental values that are in the range of [24.33–25.89] ppm.15
The larger 1H NMR shielding constants of the β hydrogen atoms for N4, the N6 dication and N6 are due to the stronger diatropic current-density flux near them. When using the same shielding scale as used for planar porphyrinoids, the average 1H NMR shielding constants in Table 3 would suggest that the studied molecules are largely nonaromatic or weakly antiaromatic. However, the current-density calculations show that they are dominated by diatropic current-density pathways. The aromaticity rules for porphyrinoid rings cannot be applied to the figure-eight-shaped octaphyrins.
4 Conclusion
In the studied figure-eight-shaped octaphyrins, the distance between the stacked pyrrole rings in the middle of the molecules shrinks with increasing number of electrons in the conjugated orbitals leading to a stronger through-space current-density flux from one strand to the other. The molecules have two figure-eight-shaped current-density pathways that take the outer route on one half of the molecule and the inner one on the other half, which is similar to the two ring-current pathways of [12]infinitene. The current density consists of many pathways. The current density has many branching points and through-space pathways from one strand to the other. For the figure-eight-shaped octaphyrins, the aromaticity does therefore not follow the expected alternating aromatic character based on Hückel's rule.The magnetic shielding constant of the inner hydrogen atoms provides information about the strength and direction of the current-density pathway passing the inner hydrogen atom. However, interpretations based on the experimental 1H NMR spectrum are more or less impossible without calculating the current density that yields the nuclear magnetic shielding density.
The integrated current-density strengths as well as the calculated 1H NMR shielding constants suggests that o-N2, p-N2 and the N4 dication with 25 occupied conjugated orbitals sustain two independent paratropic ring currents inside the two halves of the molecule. However, the diatropic current density dominates. They have several diatropic pathway that are difficult to separate and whose strengths are difficult to determine. N4 and the N6 dication with 26 occupied conjugated orbitals do not sustain any global paratropic ring currents and the diatropic current-density pathways are stronger than for N2 and the N4 dication. N6 does not sustain any global paratropic ring current. Its diatropic current-density flux of 13.2 nA T−1 is the strongest one among the studied molecules. Thus, the strength of its global current-density pathway is about half the one of free-base porphyrin.71 The strengths of the diatropic current-density flux of N4 and the N6 diaction are 9.9 nA T−1 and 10.8 nA T−1, respectively, which are about as strong as for benzene,72 whereas N2 and the N4 dication sustain a diatropic current-density flux whose strength is half the one for benzene.
Since N2 and the N4 dication sustain weak global diatropic current-density pathways and an even weaker global paratropic current-density pathway, they are weakly aromatic. N4 and the N6 dication do not sustain any global paratropic current-density pathway. Since their global diatropic current-density pathways are as strong as for benzene, they can be considered aromatic. Since N6 sustain the strongest global diatropic current-density pathway of the studied octaphyrins and no global paratropic current-density pathway, it is the strongest aromatic molecule among the studied ones. However, the strength of the global current-density pathway suggests that it is half as aromatic as free-base porphyrin.
Author contributions
QW performed calculations and visualized the current densities. JP developed the computational method for separating diatropic and paratropic contributions to the current density. MD and ST supervised the GIMIC usage. QW and DS wrote the first version of the manuscript. All authors contributed to the final text.Conflicts of interest
There are no conflict of interests.Acknowledgements
This work was supported by the China Scholarship Council (pre-doctoral fellowship to Q. W.). The research has been supported by The Academy of Finland through projects 314821 and 340583. CSC – the Finnish IT Center for Science is acknowledged for computer time.References
- A. R. Battersby, C. J. Fookes, G. W. Matcham and E. McDonald, Nature, 1980, 285, 17–21 CrossRef CAS PubMed.
- Z. Zhou and Z. Shen, Isr. J. Chem., 2016, 56, 119–129 CrossRef CAS.
- M. Biesaga, K. Pyrzyńska and M. Trojanowicz, Talanta, 2000, 51, 209–224 CrossRef CAS PubMed.
- Y. Zhang and J. F. Lovell, Theranostics, 2012, 2, 905–915 CrossRef CAS PubMed.
- H. Huang, W. Song, J. Rieffel and J. F. Lovell, Front. Phys., 2015, 3, 23 Search PubMed.
- M. Wikström, Cytochrome c Oxidase, John Wiley & Sons, Ltd, 2010 Search PubMed.
- D. M. Lopes, J. C. Araujo-Chaves, L. R. Menezes and I. L. Nantes-Cardoso, in Metastable, Spintronics Materials and Mechanics of Deformable Bodies, ed. S. Sivasankaran, P. K. Nayak and E. Günay, IntechOpen, Rijeka, 2019, ch. 10 Search PubMed.
- J. Min Park, J. H. Lee and W.-D. Jang, Coord. Chem. Rev., 2020, 407, 213157 CrossRef.
- R. E. Blankenship, Molecular mechanisms of photosynthesis, John Wiley & Sons, Ltd, 3rd edn, 2021 Search PubMed.
- S. Saito and A. Osuka, Angew. Chem., Int. Ed., 2011, 50, 4342–4373 CrossRef CAS PubMed.
- W.-Y. Cha, T. Soya, T. Tanaka, H. Mori, Y. Hong, S. Lee, K. H. Park, A. Osuka and D. Kim, Chem. Commun., 2016, 52, 6076–6078 RSC.
- N. Shivran, S. C. Gadekar and V. G. Anand, Chem. – Asian J., 2017, 12, 6–20 CrossRef CAS PubMed.
- J. Kim, J. Oh, A. Osuka and D. Kim, Chem. Soc. Rev., 2022, 51, 268–292 RSC.
- J. L. Sessler, S. J. Weghorn, V. Lynch and M. R. Johnson, Angew. Chem., Int. Ed. Engl., 1994, 33, 1509–1512 CrossRef.
- J.-Y. Shin, H. Furuta, K. Yoza, S. Igarashi and A. Osuka, J. Am. Chem. Soc., 2001, 123, 7190–7191 CrossRef CAS PubMed.
- J. M. Lim, J.-Y. Shin, Y. Tanaka, S. Saito, A. Osuka and D. Kim, J. Am. Chem. Soc., 2010, 132, 3105–3114 CrossRef CAS PubMed.
- S.-i Ishida, T. Higashino, S. Mori, H. Mori, N. Aratani, T. Tanaka, J. M. Lim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2014, 126, 3495–3499 CrossRef.
- S. Taubert, H. Konschin and D. Sundholm, Phys. Chem. Chem. Phys., 2005, 7, 2561–2569 RSC.
- R. Herges, Nature, 2007, 450, 36–37 CrossRef CAS PubMed.
- L. N. Wirz, M. Dimitrova, H. Fliegl and D. Sundholm, J. Phys. Chem. Lett., 2018, 9, 1627–1632 CrossRef CAS PubMed.
- N. Jux, Angew. Chem., Int. Ed., 2008, 47, 2543–2546 CrossRef CAS PubMed.
- P. W. Fowler and H. S. Rzepa, Phys. Chem. Chem. Phys., 2006, 8, 1775–1777 RSC.
- M. Stepień, L. Latos-Grażyński, N. Sprutta, P. Chwalisz and L. Szterenberg, Angew. Chem., Int. Ed., 2007, 46, 7869–7873 CrossRef PubMed.
- M. Stepień, N. Sprutta and L. Latos-Grażyński, Angew. Chem., Int. Ed., 2011, 50, 4288–4340 CrossRef PubMed.
- M. Mori, T. Okawa, N. Iizuna, K. Nakayama, J. M. Lintuluoto and J.-I. Setsune, J. Org. Chem., 2009, 74, 3579–3582 CrossRef CAS PubMed.
- I. Casademont-Reig, T. Woller, M. Torrent-Sucarrat, E. Matito and M. Alonso, Chem. – Eur. J., 2022, 29, e202202264 Search PubMed.
- J. A. Pople, Mol. Phys., 1958, 1, 175–180 CrossRef CAS.
- R. McWeeny, Mol. Phys., 1958, 1, 311–321 CrossRef CAS.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding and C. Hättig, et al. , J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- TURBOMOLE V7.5 2020, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.org.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. Deglmann, K. May, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2004, 384, 103–107 CrossRef CAS.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CAS.
- D. Sundholm, M. Dimitrova and R. J. F. Berger, Chem. Commun., 2021, 57, 12362–12378 RSC.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- T. Helgaker, M. Jaszuński and K. Ruud, Chem. Rev., 1999, 99, 293–352 CrossRef CAS PubMed.
- R. M. Stevens, R. M. Pitzer and W. N. Lipscomb, J. Chem. Phys., 1963, 38, 550–560 CrossRef CAS.
- C. J. Jameson and A. D. Buckingham, J. Phys. Chem., 1979, 83, 3366–3371 CrossRef CAS.
- C. J. Jameson and A. D. Buckingham, J. Chem. Phys., 1980, 73, 5684–5692 CrossRef CAS.
- M. Ferraro, P. Lazzeretti, R. Viglione and R. Zanasi, Chem. Phys. Lett., 2004, 390, 268–271 CrossRef CAS.
- A. Soncini, P. Fowler, P. Lazzeretti and R. Zanasi, Chem. Phys. Lett., 2005, 401, 164–169 CrossRef CAS.
- G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, J. Comput. Chem., 2018, 39, 511–519 CrossRef CAS PubMed.
- R. K. Jinger, H. Fliegl, R. Bast, M. Dimitrova, S. Lehtola and D. Sundholm, J. Phys. Chem. A, 2021, 125, 1778–1786 CrossRef CAS PubMed.
- H. Fliegl, M. Dimitrova, R. J. F. Berger and D. Sundholm, Chemistry, 2021, 3, 1005–1021 CrossRef CAS.
- P. J. Mohr, D. B. Newell and B. N. Taylor, J. Phys. Chem. Ref. Data, 2016, 45, 043102 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- D. Sundholm, R. J. F. Berger and H. Fliegl, Phys. Chem. Chem. Phys., 2016, 18, 15934–15942 RSC.
- J. E. Barquera-Lozada, J. Comput. Chem., 2019, 40, 2602–2610 CrossRef CAS PubMed.
- M. Orozco-Ic, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 6404–6409 RSC.
- C. D. T. Runge, Math. Ann., 1895, 46, 167–178 CrossRef.
- W. Kutta, Z. Math. Phys., 1901, 46, 435–453 Search PubMed.
- D. Sundholm, H. Konschin and M. Häser, Chem. – Eur. J., 1999, 5, 267–273 CrossRef CAS.
- B. Szyszko, N. Sprutta, P. Chwalisz, M. Stępień and L. Latos-Grażyński, Chem. – Eur. J., 2014, 20, 1985–1997 CrossRef CAS PubMed.
- S. M. Rappaport and H. S. Rzepa, J. Am. Chem. Soc., 2008, 130, 7613–7619 CrossRef CAS PubMed.
- G. Călugăreanu, Czech. Math. J., 1961, 11, 588–625 Search PubMed.
- W. F. Pohl, Indiana Univ. Math. J., 1968, 17, 975–985 CrossRef.
- J. H. White, Am. J. Math., 1969, 91, 693–728 CrossRef.
- F. B. Fuller, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 815–819 CrossRef CAS PubMed.
- E. Heilbronner, Tetrahedron Lett., 1964, 5, 1923–1928 CrossRef.
- R. R. Valiev, T. Kurten, L. I. Valiulina, S. Y. Ketkov, V. N. Cherepanov, M. Dimitrova and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 1666–1674 RSC.
- J. Ahrens, B. Geveci and C. Law, in Visualization Handbook, ed. C. D. Hansen and C. R. Johnson, 2005, pp. 717–731 Search PubMed.
- H. Fliegl and D. Sundholm, J. Org. Chem., 2012, 77, 3408–3414 CrossRef CAS PubMed.
- H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Pictures of separated diatropic and paratropic current densities, pictures of current-density pathways, picture showing a branching point of a current-density pathway, integrated current-density strengths, current-density profiles, Cartesian coordinates of the molecular structures, and 1H NMR magnetic shielding constants. See DOI: https://doi.org/10.1039/d3cp01062g |
| This journal is © the Owner Societies 2023 |
