Isotopic dependence of intramolecular and intermolecular vibrational couplings in cooperative hydrogen bond networks: singly hydrated phenyl-α-D-mannopyranoside as a case study

Abstract

Hydrogen bonding (HB) is associated with frequency shifts, spectral broadening and intensity variation of the vibrational bands of the donor stretching modes. This is true in all systems, from the most basic molecular models, to more complex ones, and biological molecules. In the gas phase, the latter can be either fully isolated, with only intramolecular HB, or micro-solvated. The conformations of such systems are stabilized by networks of intramolecular and intermolecular HB where the donor groups can be coupled. This has been well-identified in the case of singly hydrated monosaccharides and in particular for phenyl-α-D-mannopyranoside, where the addition of a single water molecule reduces the number of observed conformations to a unique one, stabilized by such a cooperative network of intramolecular and intermolecular HB. In the present study we have re-examined this prototypical system to scrutinize subtle effects of isotopic substitution in the solvent molecule. Besides the obvious isotopic shift, coupling between intramolecular modes of sugar and water is observed, promoted by the intermolecular HB. The systematic substitution of water with heavy water, or methanol, also allowed the decomposition of the relation between HB strength and frequency shift.

---

Introduction

Ever since the discovery of hydrogen bonding (HB) interactions around the 1920s–1930s, both intermolecular HB interactions, that is between different molecular entities, and intramolecular HB interactions, between different functional groups within a single molecule, have been the centre of interest for scientists seeking to understand countless processes of molecular origin. Vibrational spectroscopy has always been considered as a very powerful probe for probing these forces.¹ It has been quickly recognized that the spectral signatures of the stretching modes of donor groups encode information regarding non-covalent interactions in which they are engaged. When a polar group is engaged in HB, the frequency, intensity and width of its donating stretching band are modified with respect to the “free” vibration. Although this has been observed and modelled over decades, there are still debates on the relation between these experimental spectral signatures of covalent bond vibrations and the nature and strength of the non-covalent HB perturbation. For instance, the Badger–Bauer rule, which has held true since the late 30s,² states that the stronger the interaction, the larger must be the stretching frequency red-shift of the donor group. However, there have been counter-examples, and spectroscopists continue to design model systems to challenge this rule.³ This illustrates that the spectroscopic manifestations of HB interactions are actually very complex to understand. Nevertheless, the governing HB networks of more complicated molecular assemblies have been characterized by gas phase vibrational spectroscopy. As complexity increases, so does the vibrational picture. In particular, vibrational couplings and resonances come into play. For instance, vibrational resonances between modes from two interacting molecules can be “universally” promoted by HB interactions, as demonstrated by systematic chemical or isotopic substitution.⁴

In the case of flexible biomolecules, HB plays an equally important role as chemical bonding. It rigidifies specific conformations within the molecules and dictates the influence of the solvent. This has been studied by vibrational spectroscopy in the gas phase for peptides.^5–8 Systematic approaches on several model systems allowed identification of the spectral signatures of biological motifs such as β-strands, γ- and β-turns. In the case of hydrates, perturbation theory-based models established relations between the intramolecular coupling of the O–H stretching modes of water and the strength of intermolecular bonding.⁹ Vibrational spectroscopy was also used to explore the role of HB interactions in DNA nucleobases and analogues. Their biological activity and aggregation properties rely on strong intermolecular hydrogen bonding with neighbouring molecules.^10,11

Sugars represent another important group of biomolecules, with numerous OH groups that can orient themselves to create complex cooperative networks of hydrogen bonds.¹² Pioneered by the group of John Simons in Oxford,¹³ their conformational preferences have been investigated by gas phase spectroscopy, starting from monosaccharides,^14,15 their hydrates^12,16 and growing rapidly to larger oligomers,^17–19 to complexes with peptides,^20,21 or to glycoconjugated systems, beyond the biological context.²² Their high conformational flexibility makes their study by vibrational spectroscopy a difficult task. The large number of O–H stretching bands all gather in a relatively small spectral window and are often coupled. In the case of hydrated complexes, where the water stretching bands overlap the sugar contributions, isotopic substitution with heavy water has been used to decipher the contributions from the sugar to the ones from the solvent molecules,^23,24 by shifting down the water bands by about 1000 cm⁻¹, in the O–D stretching region, which enabled determination of the conformational choices of the scrutinized systems, from multi-hydrated monosaccharides, to mono-hydrates of disaccharides.²⁵

In the present work, we have re-examined the system that was first studied as a monosaccharide–heavy water complex in the gas phase: phenyl-α-D-mannopyranoside (apMan). The unique populated structure and conformation of the singly hydrated complex apMan-water (apMan-W), as determined by the early work of Simons et al.,¹² are shown in Fig. 1, which also illustrates the normal mode motions and nomenclature which will be used thereafter. We further explored the principle of isotopic substitution by studying the most abundant isotope of apMan (apManH4) complexed with H₂O, HOD, D₂O, CH₃OH and CH₃OD, as well as the substituted apManD4, where all the hydroxyl groups are deuterated, isolated and interact with D₂O. We focused our attention on subtle spectroscopic manifestations of isotopic substitution, aiming at probing the intermolecular forces in a more intimate way via the spectroscopy of intramolecular donor groups.

Fig. 1 The most stable, uniquely observed, clockwise conformation “c_ins4” of apMan-W and the notation of the OH groups. This c conformation corresponds to the most stable and most abundant conformation of the isolated molecule.¹² The apMan–methanol complex adopts the same c_ins4 conformation with the methyl group replacing the free hydroxyl of water (fw). The notation and normal mode analysis of the vibrational modes discussed thereafter are also given.

Methods

Experimental

We employed a well-established experimental approach that has been extensively used to obtain conformer selective and mass-resolved vibrational spectra of non-volatile compounds and clusters in the gas phase, including biomolecules²⁶ and in particular sugars.²⁷

The solid compounds were vaporized by laser desorption coupled to a supersonic jet of rare gas at 5 bars of backing pressure and expanded through a 500 μm cylindrical pulsed valve (Jordan PSV) into the source vacuum chamber (P = 10⁻⁴ mbar during valve operation). Experiments were conducted with either neon or argon as a carrier gas without any effect on the observed spectra presented thereafter. The desorption laser beam (Minilite Continuum, 10 Hz, 500 μJ per pulse, 1064 nm) was focused down to a size similar to the nozzle diameter onto the surface of the desorption sample.

For complex formation, the supersonic jet carrier gas was seeded with the room temperature vapour pressure of pure H₂O, pure D₂O, a blend of H₂O : HOD : D₂O obtained by mixing H₂O and D₂O in a 1 : 1 ratio. Such mixtures which led to intensity ratios close to the expected 1 : 2 : 1 H₂O : HOD : D₂O ratio (as shown in Fig. 2c) allowed considering that H₂O and D₂O densities were identical and stable for both isotopic species. It also allowed simultaneous recording of the data for the different isotopic forms under the exact same experimental conditions. Then, we can considered that cluster size distributions were similar for both H₂O and D₂O hydrates. The same precautions were taken for methanol spectra which were recorded with a 1 : 1 mixture of CH₃OH : CH₃OD. In both cases, we observed a slight excess of the natural isotopomers (Fig. 2c and f).

Fig. 2 TOF mass spectra of the various isotopic species studied here, recorded at the most intense peak of their respective 2c-REMPI spectrum. (a) apMan-H₂O with pure H₂O seeding the carrier gas, (b) apMan-D₂O, with the carrier gas seeded by pure D₂O, (c) apMan-H₂O, apMan-HOD and apMan-D₂O, with a 1 : 1 H₂O : D₂O mixture (ω_exc = 36 713 cm⁻¹); (d) apMan-D_n=1,4 (ω_exc = 36 728 cm⁻¹); (e) apMan-D_n=1,4-D₂O (ω_exc = 36 713 cm⁻¹); (f) apMan-CH₃OH/CH₃OD (ω_exc = 36 709 cm⁻¹). In all cases, ω_ion = 32 258 cm⁻¹.

The numerous collisions occurring at the early stage of the expansion cooled down the desorbed molecules and stabilized the complexes. They were then transported with the molecular beam towards the differentially pumped ionization region of a linear time-of-flight (TOF) mass spectrometer, where they interacted with the spectroscopy lasers, separated from the source chamber by a 2 mm skimmer.

The molecules and complexes are detected by measuring their two-color resonantly enhanced multiphoton ionization (2c-REMPI) spectra. The excitation photons were obtained from a frequency doubled dye laser (Lambda Physics PDL3002, 10 Hz, Coumarin 540a, 500 μJ per pulse) scanned over the UV range of the π–π* electronic transition of the phenyl ring of apMan (36 000–37 000 cm⁻¹). The ionization photons were obtained from a Nd:YAG pumped UV OPO system (Horizon Continuum, 10 Hz, 32 258 cm⁻¹, 2 mJ per pulse). Both UV beams propagated in the same direction in the vacuum chamber and overlapped spatially and in time at the centre of the TOF ionization zone. The excitation laser was collimated to form a 2 mm parallel beam, while the ionization beam was focused in the overlap zone using a 1 m lens. The produced ions were then mass-separated using a Wiley-MacLaren LTOF system with a resolution that allowed for clear identification of the different isotopic substances observed in this study (see Fig. 2). For all systems under study, resonant 2-photons ionization (R2PI) spectroscopy (the one color version of REMPI) could provide very satisfactory results both in terms of ionization yields and spectroscopy. The lower energy of the ionization photons of the 2C-REMPI scheme allowed minimizing the amount of excess energy in the complex ions and then prevented misleading signals issued from fragmenting larger clusters.

To record conformer specific, mass-resolved vibrational spectra of the systems under study, we used a double resonance infrared ion depletion (IRID) spectroscopy scheme.²⁶ The tunable infrared source was a Nd:YAG pumped OPO/OPA system (LaserVision) covering the range of the O–D and O–H stretching modes between 2300 and 3800 cm⁻¹. The intensity of the spectra was corrected for a gradual increase in laser power from 2400 cm⁻¹ to 3800 cm⁻¹. Finally, the spectral calibration of the OPO/OPA system was achieved by measuring atmospheric water absorption lines by means of a photoacoustic detector located inside the laser casing, close to its output.

Desorption sample preparation

The preparation of our desorption samples used to consist of rubbing a solid graphite substrate bar against a mixture of the analyte powder and graphite. In the present work, we used a new method, inspired from the process of matrix assisted laser desorption ionization (MALDI) imaging sample preparation robots,²⁸ and from the method experimented by Küpper et al.,²⁹ but at a much lower cost and level of sophistication, which comes with the advantage of simplicity and versatility. We used a simple action aerograph (Iwata Aerograph Revolution Mini Line-M2 HP) to spray a 5 mg mL⁻¹ solution of apMan in ethanol on the surface of the graphite bar, using 1.5 bar nitrogen at room temperature as a spray carrier. The spray opening and distance to the graphite bar (typically 2 cm) were set so that its plume covers the 2 mm width of the bar. The ethanol solvent evaporates readily when it reaches the surface of the bar, leaving a thin, uniform layer of the analyte on the surface. The details of this sample preparation method are beyond the scope of the present paper but we can briefly review its advantages. First, it is much more reproducible and scalable. Second, it can be applied to any sample texture (dry, moist or flaky powders, oily liquids, and greasy solids) provided that they can be dissolved and stick to the graphite surface during solvent evaporation. It leads to a much improved stability of the source, which is the key for pump–probe experiments such as our double resonance spectroscopy scheme. Most importantly, it is much more conservative in analyte consumption as it reduces the used amounts by about one order of magnitude. In the present work, this “spraying” method required no more than few milligrams of apMan for the complete experimental work, while it would have needed several tens of mg (up to 100 mg) with the “rubbing” method.

Deuteration

All compounds were commercially available and used without any further purification (apMan from Carbosynth Ltd, water and methanol isotopes from Sigma-Aldrich).

For the deuteration of apMan, we repeated two to three cycles of H/D exchange with an excess of deuterated methanol and freeze-drying. This led to the distribution of deuterium on the hydroxyl groups of apMan (Fig. 2d).

Computational

The conformational landscape of apMan-W was thoroughly investigated by Simons et al.^12,24 and does not need further exploration. In the present study, we focused on the uniquely observed, most stable conformer of apMan-W identified from the initial study.¹² This complex adopts a fully cooperative conformation where the water molecules are inserted between OH4 and OH6, in an all clockwise conformations, noted “c_ins4”, to follow the nomenclature followed in the initial paper,¹² shown in Fig. 1.

All calculations were performed at the B3LYP(D3)/cc-pVTZ level of theory. We have recalculated the energies and vibrational spectra for all isotopic forms of the complexes at this level. For the sake of verification, we have also recalculated the relative energies of about 20 conformations of apMan-W, which confirmed that the new level of theory does not invalidate the results from the initial study.

When binding energies were calculated, they were corrected for the basis set superposition error (BSSE), using the routine counterpoise method.

All quantum chemistry calculations were performed using Gaussian 16, Rev. B 0.1.³⁰

Results

Experimental vs. computational spectral comparison

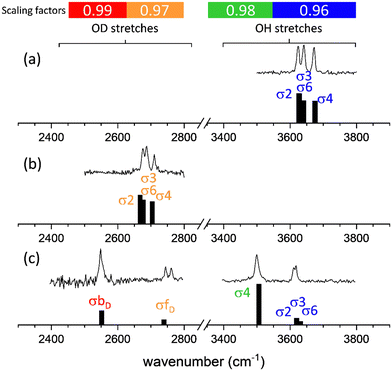
The agreement between the calculated and experimental spectra of non-hydrated apMan and apManD4, and of the heavy water singly hydrated complex, apMan–D₂O is illustrated in Fig. 3.

Fig. 3 Comparison between the IRID and B3LYP(D3)/cc-pVTZ computational spectra of (top) apMan, (middle) apManD4 and (bottom) apMan-D₂O. The assignment of the bands σ_n refers to the stretching mode of the OHn group of the mannoside, and σfw and σbw refer to the stretching of the free and bound hydroxy groups of water, respectively. The free or intramolecularly bound O–H frequencies (blue zone) are scaled by 0.96, the intermolecular donor O–H frequencies (green zone) are scaled by 0.98, the free or intramolecularly bound O–D frequencies (orange zone) are scaled by 0.97 and the intermolecular donor O–D frequencies (red zone) are scaled by 0.99.

For comparison with the observed IRID spectra, we produced synthetic spectra by applying interaction and isotope specific scaling factors to the calculated harmonic frequencies. Uniform scaling factors of 0.96 applied to all calculated O–H/O–D stretching frequencies lead to a satisfactory qualitative agreement with the experimental data and lead to the same conclusions of the present work. However, we have decided to apply different scaling factors depending on the isotopomer and on the nature of the interactions in which the hydroxyl groups are engaged, which provide a much improved quantitative correspondence between the experimental and calculated spectra.

The O–H stretching frequencies of groups either free or involved in intramolecular non-covalent interactions were multiplied with a factor of 0.96. The stretching frequencies of the O–H groups involved as donors in intermolecular HB were scaled by 0.98. These scaling factors were determined using the same calibration procedure, based on frequency calculations for benchmark systems (monosaccarides and disaccharides, either isolated or singly hydrated), already applied in the past.²² For deuterated species, using the scaling factors determined for the O–H stretching modes led to systematic underestimation of the vibrational frequencies of the O–D groups. Much-improved agreement was achieved for scaling factors of 0.97 for the free or intra-molecularly bound O–D stretching frequencies, and 0.99 for the frequencies of the O–D groups involved as donors in inter-molecular bonding. These four scaling factors have been applied to all calculated frequencies reported hereafter.

The interaction and isotope specific scaling factors used here illustrate that these scaling factors not only take anharmonicity into account, as too often considered, but they also correct for the overall approximations and errors of the method and level of theory.

Higher scaling factors for O–D stretches than for O–H stretches can be considered as an anharmonicity effect. Indeed, the D isotope being heavier, the associated vibrational reduced mass is higher and their vibrational states lie lower than the H isotope states at the same vibrational potential. This also implies that the vibrational motion of O–D explores a smaller range of interatomic distances than the O–H motion. Since the harmonic approximation is more valid at the bottom of the potential and for small vibrational motions, we can assume that the O–D motions are closer to the harmonic approximation than the O–H motions and the O–D's scaling factors are closer to 1 (0.97 vs. 0.96 and 0.99 vs. 0.98).

The difference between the scaling factors of the intramolecular and the intermolecular donor groups cannot be interpreted similarly. Although hydrogen bonding increases the anharmonicity and the span of the donor stretching vibrational motions, the scaling factors we determine are higher (closer to 1) for strongly hydrogen bonded donor groups (0.98 vs. 0.96 and 0.99 vs. 0.97). We can then only conclude that the level of theory used here overestimates the effect of intermolecular interactions on the donor band frequencies but it certainly does not show that the motions are less anharmonic.

2c-REMPI spectra

2c-REMPI spectra of apMan-H₂O, apMan-HOD, and apMan-D₂O are essentially identical, as shown in Fig. 4. The 2c-REMPI spectroscopy reflects the populations of the structures adopted under our experimental conditions. In the present case, there is no doubt that isotopic substitution has no influence on the conformational distribution of apMan-W and we observe only the most stable conformation of the complex, shown in Fig. 4.

Fig. 4 2c-REMPI of the three isotopic species of apMan-W, recorded simultaneously for the three isotopes, and for apMan-CH₃OH/D.

Fig. 4 also features the 2c-REMPI spectrum of the methanol complex apMan-CH₃OH. It is strikingly similar to the apMan-W spectra. We can then conclude that under our experimental conditions, the methanol complex adopts the same unique c_ins4 conformation as the hydrated complex, with the methyl group replacing the free hydroxyl group of water. As for the hydrate isotopes, the 2c-REMPI spectrum of the methanol complex is insensitive to the deuteration state of the methanol moiety and the apMan-CH₃OD spectrum is identical.

IRID spectra

Fig. 5 displays the IRID spectra of apMan, its complexes apMan-H₂O, apMan-HOD and apMan-D₂O, and the corresponding calculated scaled harmonic spectra. In the case of apMan-HOD, two isomers coexist: (i) apMan-H*OD (light blue in Fig. 5b) where the water molecule is bound to apMan via its O–H group and (ii) apMan-HOD* (dark blue in Fig. 5b), bound via the O–D group of water. Fig. 1 illustrates the normal mode analysis, which enables identification of the vibrational motions associated with the observed bands.

Fig. 5 Experimental and calculated vibrational spectra of (a) apMan-H₂O, (b) apMan-HOD and (c) apMan-D₂O. For the apMan-HOD isotopomer, the scaled calculated spectra for both possible isomers apMan-H*OD in light blue, and for apMan-HOD* in dark blue, are shown. The weak free O–D observed and calculated intensities have been multiplied by 3 to be more easily visible.

In spite of the weak intensity of its mass peak, we could observe the IRID spectrum of apManD4-D₂O, shown in Fig. 6, together with the IRID spectra of apMan-CH₃OH, apMan-CH₃OD, and compared to the IRID spectra of the three isotopomers of apMan-W.

Fig. 6 IRID spectra of apMan-H₂O/HDO/D₂O, apManD4-D₂O, apMan-CH₃OH and apMan-CH₃OD.

For all the complexes studied here, Table 1 summarizes the calculated and experimental frequencies, frequency shifts and the splitting between the coupled vibrations.

Table 1 Experimental and calculated frequencies (in cm⁻¹), splitting and HB induced frequency shifts of isolated apMan, and the complexes with water, heavy water, methanol and heavy methanol. The HB-induced frequency shifts are given only for systems where it can be measured without intermolecular coupling. For each system, the experimental frequencies are given above the calculated ones that are in italics. The calculated frequencies are scaled by the isotope and interaction-dependant scaling factors defined in the text

	σfwH	σfwD	σ4–σbwH/D	σ4	σbwD
		Central (splitting)	Sym./asym. (splitting)	(HB shift)	(HB shift)
a The overlap with the σ4 apMan-HOD* prevents a precise determination of the frequency of the σ4–σbwH/D symmetric mode.
apMan	—	—	—	3672	—
	—	—	—	3675	—
apMan-H2O	3727	—	3507/3465 (42)	—	—
	3718	—	3523/3468 (55)	—	—
apMan-H*OD	—	2735 (4)	>3500^a/3474 (>34)^a	—	—
		2724	3524/3473 (51)	—	—
apMan-HOD*	3717	—	—	3500 (−172)	2559 (−168)
	3712	—	—	3506 (−169)	2563
apMan-D2O	—	2753 (15)	—	3499 (−173)	2547
	—	2739	—	3506 (−169)	2552
apMan(D4)-D2O	—	2756 (18)	2595/2557 (38)	—	—
	—	2739	2589/2542 (47)	—	—
apMan-CH3OH	—	—	3485/3430 (55)	—	—
	—	—	3512/3455 (67)	—	—
apMan-CH3OD	—	—	—	3434 (−238)	2574 (−144)
	—	—	—	3467 (−208)	2576

---

Intramolecularly bound hydroxyl stretching modes

The partly unresolved bands located between 3600 and 3650 cm⁻¹ are assigned to the σ2, σ3 and σ6 stretching motions of the OH2, OH3 and OH6 groups of apMan, respectively. These groups are involved in relatively weak intramolecular interactions, constrained by the rigid ⁴C₁ pyranose ring of apMan. OH2 and OH3 do not interact with the water molecule. OH6 does, but only on the O6 oxygen side, as an acceptor. It is then normal that the stretching frequencies of these three groups are unaffected by the water isotopic substitution.

Free water band σfw

The band located at 3727 cm⁻¹ in the spectrum of apMan-H₂O (Fig. 5a) and 3717 cm⁻¹ for apMan-HOD (Fig. 5b) is assigned to the σfw_H stretching mode of the free OH group of water in the apMan-HOD* isomer. This slight difference between these observed frequencies (3727 cm⁻¹vs. 3718 cm⁻¹) is properly reproduced by the scaled harmonic calculated frequencies (3718 cm⁻¹vs. 3712 cm⁻¹). It reflects the intramolecular coupling between σfw_H and σbw_H in apMan-H₂O, inherited from the coupling between the symmetric and asymmetric stretching modes of both O–H vibrators of H₂O. In apMan-HOD*, the increased energy gap between σbw_D and σfw_H breaks down the intramolecular coupling. Since one effect of this coupling is to increase the energy gap between the coupled modes, it increases the σfw_H frequency in apMan-H₂O. In apMan-HOD*, the coupling is off and the σfw_H frequency is lowered.

For apMan-H*OD (Fig. 5b) and apMan-D₂O (Fig. 5c), σfw_D is observed at 2735 cm⁻¹ and 2753 cm⁻¹, respectively. We can note a striking difference with σfw_H of apMan-H₂O and apMan-HOD* (Fig. 5a and b, respectively): a doublet structure is observed in the O–Ds region, while a single line is found for the free O–H stretches.

When unexpected differences between H and D-containing molecular assemblies are observed, one often invokes H/D exchange as a possible cause. However, in the present case, it is very unlikely that this can explain the appearance of the doublet associated with σfw_D. Indeed, the sugar molecules are evaporated downstream of the supersonic expansion and the water molecules seed the carrier gas upstream. Although the molecules meet in the collision rich region of the jet, it is unlikely that there are enough many-body encounters between evaporated sugars and water molecules to generate significant amounts of H/D exchange products. Moreover, we performed double resonance spectroscopy, targeting a specific conformation of the system. The correspondence between the 2c-REMPI spectra of the various isotopomers of apMan-W complexes (Fig. 4) indicates that there is no other conformation formed upon deuteration of the water molecules. Since the conformational relaxation and cooling occur simultaneously in the collision rich zone of the supersonic jet, it is unlikely that H/D exchange between heavy water and mannoside can be relaxed into the exact same unique cooperative conformation of the complex (Fig. 1).

The broadening or splitting of σfw_D could also be due to contamination from larger hydrated clusters fragmenting in the singly hydrated mass channel. However, several experimental precautions have been taken to prevent such large distributions of hydrated clusters: the same σfw_D doublets have been observed independent of the carrier gas, the backing pressure and whether the experiments were conducted with the carrier gas being seeded with pure D₂O or with the H₂O : HOD : D₂O mix. In the latter case, the densities of H₂O and D₂O were similar and there is no reason for significantly different size distributions. Finally, the R2PI spectra of multiple-hydrated apMan (up to three water molecules)²⁴ are well resolved and do not overlap the apMan-W REMPI band probed for measuring the IRID spectra reported here.

We propose that the doublet structure near the σfw_D band of apMan-D₂O and apMan-H*OD is due to a resonance between the fundamental σfw_D and an overtone or a combination band of lower energy vibrational bands. For such coupling to be so efficient, it is likely that it involves vibrational motion kinetically linked or involving the free O–D group. In the calculated spectra of apMan-D₂O and apMan-H*OD, there are a large number of normal modes involving the bending or rocking motions of OH4, and the bending of the water molecule, in the range between 1200 and 1500 cm⁻¹. It is difficult to identify which modes contribute to this coupling. We believe that the water bending mode, which directly involves the motion of the free D atom and which may be highly kinetically coupled to the free O–D motion, is central to this coupling.

The IRID spectrum of apManD4-D₂O (Fig. 6) also features a doublet structure in the region of σfw_D. The similarity with the doublet of apMan-D₂O confirms the proposed important role of the water bending modes in the coupling at the origin of the doublet. Indeed, the other possible modes involving the bending and rocking of the sugar hydroxyl groups in the vicinity of the water molecules will be shifted upon deuteration of the sugar moiety, which should affect the coupling.

Intermolecularly bound hydroxyl stretching modes

Between 3400 and 3550 cm⁻¹, a strong doublet dominates the spectra of apMan-H₂O (Fig. 5a) and apMan-H*OD (Fig. 5b). It corresponds to the symmetric (noted s) and asymmetric (noted as) coupled stretching motions of σ4, the sugar OH4 donor group, and σbw_H, the water donor group bw_H. Although the complexes are not symmetric, the “s” and “as” notation is used to reflect the motions of the vibrators in these modes, in analogy to the symmetric and asymmetric stretching modes in symmetric molecules such as water or carbon dioxide. In the s mode, the sugar H4 and the water-bound H both move in phase, while they are out-of-phase in the as mode, as pictured in Fig. 1. The splitting between the corresponding calculated frequencies is smaller for apMan-H*OD than for apMan-H₂O (51 cm⁻¹vs. 55 cm⁻¹). It is difficult to evaluate experimentally this splitting as the symmetric mode of apMan-H*OD and the σ4 mode of apMan-HOD* overlaps. It seems, however, confirmed by the well resolved as band observed at 3465 cm⁻¹ for apMan-H₂O, and at 3474 cm⁻¹ for apMan-H*OD. As a qualitative interpretation, this difference of splitting is likely to be due to the absence of σfw_H in apMan-H*OD and, consequently, the absence of the intramolecular coupling between σfw_H and σbw_H.

For the deuterium bound complexes apMan-HOD* and apMan-D₂O, σbw_D is found to be around 2550 cm⁻¹. We can note a manifestation of the intramolecular coupling between the water O–D symmetric and asymmetric vibrators in the difference between the frequencies of σb_D measured for apMan-HOD* (2559 cm⁻¹) and for apMan-D₂O (2547 cm⁻¹). In the latter, the intramolecular coupling between both s and as water O–D stretching modes increases the splitting between the corresponding vibrational bands, while there is no such coupling in HOD. As mentioned above, this effect is well-reproduced by the scaled anharmonic frequency calculations.

Another point can be noted by the examination of the donor bound bands of the isotopomers of apMan-W and of apMan-CH₃O_H/D complexes (Fig. 6). The symmetric band of the σbw_H/σ4 mode in the spectrum of apMan-H₂O is accompanied by a shoulder on its blue side, while the corresponding band in the apManD4-D₂O spectra is not. Similarly, there are several bands next to the H donor-bound bands of apMan-CH₃OH and they are not observed for the corresponding bound OD of apMan-CH₃OD. This indicates that these bands are also due to resonances with overtones or combination bands of lower energy vibrational modes. They do not originate from contamination either from spectra of larger fragmenting clusters, or from other 1 : 1 complexes with virtually the same conformation, differing only by a slight variation in the relative orientation of both subunits of the complexes. For apMan-H₂O and apMan-CH₃OH, such quasi-degenerate conformations exist and their calculated energy differences are on the order of 0.2 kJ mol⁻¹, well below the precision of the level of theory. They differ only by the orientation of the free hydroxyl group of water or of the methyl group of methanol, as shown in Fig. 7. The very small differences between the calculated spectra of these variations are below the bandwidth of the IR laser and do not allow deciphering whether only one or both conformers are observed. Moreover, if they were responsible for the bands forming shoulders on the side of the main observed bands, they should be as easily observed in the spectra of apMan-D₂O and apMan-CH₃OD.

Fig. 7 Variations of the most stable conformers of (top) apMan-H₂O and (bottom) apMan-CH₃OH. The calculated spectra of each conformer are compared to the experimental spectra of the right. The colors of the bars refer to the box color of each conformer.

Complexation-induced frequency shifts and binding energies

When the H donors’ stretching frequencies of complexes reflect the effects of hydrogen bonding and the competing effects of intra- and inter-molecular vibrational coupling, as in apMan-H₂O and apMan-H*OD spectra, it is difficult to extract the pure H bonding frequency shift, which can provide information on the relative intermolecular strength, according to the Badger Bauer rule.² In apMan-HOD* and in apMan-D₂O, a single strong band associated to the sugar-bound σ4 mode is observed at 3499 cm⁻¹ and 3500 cm⁻¹. In these cases, the intermolecular coupling is absent and the uncoupled band frequency falls in between the bands of the coupled modes observed for apMan-H₂O/H*OD, in agreement with calculation. This methos allows us to determine a frequency shift of ca. 170 cm⁻¹ (3672 cm⁻¹ for σ4 in the spectrum of the isolated molecule – Fig. 3a – vs. 3499 cm⁻¹ in the HOD* complex or 3500 cm⁻¹ in the D₂O complex – Fig. 5b and c), purely induced by the intermolecular HB with water, without the vibrational intermolecular coupling perturbation. It can be compared to the 238 cm⁻¹ redshift of σ4 in apMan-CH₃OD, also perturbed only by the intermolecular H bonding.

Comparing the spectrum of apMan-H₂O and of apMan-CH₃OH (Fig. 6), one can appreciate that the σbw_H/σ4 doublet is found at a significantly lower energy for the methanol complex. The central frequency of the doublet of apMan-CH₃OH is 3457 cm⁻¹, 29 cm⁻¹ below the central frequency of the apMan-H₂O doublet (3486 cm⁻¹). Likewise, the σ4 band of apMan-CH₃OD is found at 3434 cm⁻¹ (Fig. 6, bottom), 65 cm⁻¹ below the σ4 band of apMan-D₂O (3499 cm⁻¹ – Fig. 5c). The σbw_D band in apMan-CH₃OD at 2574 cm⁻¹ indicates a red shift of 144 cm⁻¹ in comparison to the isolated CH₃OD frequency (2718 cm⁻¹).³¹ apMan-HOD* is the most readily comparable complex with apMan-CH₃OD. We measured its σbw_D frequency at 2559 cm⁻¹, leading to a 168 cm⁻¹ shift with respect to the free OD stretching frequency of HOD in the gas phase (2727 cm⁻¹).³² The calculated binding energy of apMan-CH₃OH is 60 kJ mol⁻¹, compared to 57 kJ mol⁻¹ for apMan-H₂O. The difference between these computed values is close to the accuracy of the computational method. Moreover, they reflect the global binding energy, while the frequency shifts we measure are witnesses of the local, mode specific interactions in which the groups are engaged as donors. The larger σ4 shift in apMan-CH₃OD indicates that the interaction of OH4 as a donor with the hydroxyl group of methanol is stronger than that with water. In contrast, the larger σbw_D shift in apMan-HOD* than in apMan-CH₃OD indicates that the interaction of water as a donor to O6 is stronger than that of methanol. Once again, this is well reproduced in the calculated intermolecular distances provided by the calculations. The H4–O_methanol distance (1.83 Å) is shorter than the H4–O_water distance (1.85 Å), and the O_methanol–O6 distance (1.85 Å) is longer than the O_water–O6 distance (1.83 Å).

Conclusions

In this study, subtle spectroscopic manifestations of isotopic substitution have been scrutinized, beyond the mere isotopic shifts, and analysed in synergy with quantum chemistry calculation, in a prototypical cooperative hydrated complex formed by an important monosaccharide, apMan, and water. This system has already been thoroughly studied by Simons et al. to identify its conformational preferences.^12,24 Expectedly, isotopic substitution does not affect the conformational landscape of this system.

For all spectral signatures considered here, the B3LYP-D3/cc-pVTZ computational results are in excellent qualitative and quantitative agreement with the experimental observation. We have identified vibrational scaling factors for hydroxyl stretching modes that depend on the strength of the non-covalent interaction the modes are involved in, and of the isotopic substitution. These refined scaling factors improve the quantitative agreement between experimental and computed spectra.

The exploitation of spectroscopic signatures of the isotopic substitution allows interrogation of the influence of intermolecular HB on vibrational couplings, either intramolecular bonding between the symmetric and asymmetric stretching modes of water, or intermolecular bonding between the stretching modes of the donor OH of apMan and water. Since it exists only because of the intermolecular HB between both molecules, this latter coupling must encode information on the interaction, still to be unveiled.

Water deuteration (or methylation, with apMan-CH₃OH) can be considered as a switch to “turn on or off” the intermolecular coupling between the symmetric and asymmetric stretching modes involving the motion of the donor hydroxyl groups of the mannoside and of the water, in competition with the similar, but intramolecular, coupling between the symmetric and asymmetric stretching modes of water. By “turning off” the intermolecular coupling, we have evidenced the relative strength of the intermolecular interaction of apMan with water and methanol and proved that if the overall interaction is stronger with methanol, the donor interaction OH⋯O6 is stronger for water than for methanol, while the OH4⋯O one is stronger for methanol. Moreover, by measuring the frequency of the uncoupled σ4 vibration of the donor hydroxyl of apMan in apMan-D₂O, apMan-HOD* and apMan-CH₃OD, we can determine the complexation-induced frequency shift free of the perturbation from the coupling with the donor stretching of the other moiety of the complex. In these cases, and in these cases only, we can relate the frequency shifts to the Badger–Bauer rule,² which is verified here. The calculated binding energies of the water and methanol complexes are the same but these values relate to the overall strength of both HB involved. The σ4 frequency redshifts are larger in the methanol complexes and the local OH4–O_methanol interaction appears stronger than the OH4–O_water interaction, as indicated by calculated intermolecular distances. In contrast, the OH_water–O6 interaction is stronger than the OH_methanol–O6 one, which is why the calculated bonding energies are similar for both systems. Such consideration may help calibrating more sophisticated computational approaches than the one used here, aiming at describing in detail vibrational couplings, anharmonic effects, and more generally non-covalent interactions.

We have also observed signatures of resonances with the donor O–H stretching that are absent for donor O–D bands. Similarly, we have also shown resonances with the free O–D stretches that are not observed for free O–H stretching modes. The complex spectroscopy shows if these systems in the mid-IR, the so called “fingerprint region”, prevented identifying unambiguously the modes involved in these resonances.

The simulation of coupled hydroxyl stretching modes is considered as a difficult challenge for the spectroscopy of large and flexible molecular assemblies, in particular those of biological interest containing sugar components. The system under study has been chosen for its relative simplicity. The fact that only one conformation is populated under the molecular beam conditions, along with its simple and well resolved spectroscopy makes this investigation a case study for understanding how substitutions, either isotopic or methylated, can reveal properties of non-covalent interactions from the spectroscopy of hydroxyl stretches and the results of this study provide useful benchmarks for studying more challenging systems with similar properties.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

AC post-doctoral fellowship was funded by LabEx PALM (ANR-10-LABX-0039-PALM). This work was performed using HPC resources from the “Mésocentre” computing center of Centrale Supélec and École Normale Supérieure Paris-Saclay supported by CNRS and Région Île-de-France (https://mesocentre.centralesupelec.fr/). The authors want to acknowledge the help of Nicolas Elie and Dr David Touboul for first trying the spraying methods for sample preparation.

References

1. R. M. Badger and S. H. Bauer, Spectroscopic Studies of the Hydrogen Bond I. A Photometric Investigation of the Association Equilibrium in the Vapor of Acetic Acid, J. Chem. Phys., 1937, 5, 605–608.
2. R. M. Badger, The Relation Between the Energy of a Hydrogen Bond and the Frequencies of the O–H Bands, J. Chem. Phys., 1940, 8, 288–289.
3. S. Bhattacharyya, S. Ghosh and S. Wategaonkar, O–H stretching frequency red shifts do not correlate with the dissociation energies in the dimethylether and dimethylsulfide complexes of phenol derivatives, Phys. Chem. Chem. Phys., 2021, 23, 5718–5739.
4. T. L. Fischer, T. Wagner, H. C. Gottschalk, A. Nejad and M. A. Suhm, A Rather Universal Vibrational Resonance in 1:1 Hydrates of Carbonyl Compounds, J. Phys. Chem. Lett., 2021, 12, 138–144.
5. E. Gloaguen, M. Mons, K. Schwing and M. Gerhards, Neutral Peptides in the Gas Phase: Conformation and Aggregation Issues, Chem. Rev., 2020, 120, 12490–12562.
6. N. Mazo, C. D. Navo, F. Peccati, J. Andreo, C. Airoldi, G. Goldsztejn, P. Çarçabal, I. Usabiaga, M. Sodupe, S. Wuttke, J. H. Busto, J. M. Peregrina, E. J. Cocinero and G. Jiménez-Osés, Conformationally Restricted β-Sheet Breaker Peptides Incorporating Cyclic α-Methylisoserine Sulfamidates, Chem. – Eur. J., 2022, e202202913.
7. G. Goldsztejn, V. R. Mundlapati, V. Brenner, E. Gloaguen and M. Mons, Molecules, 2022, 27.
8. J. L. Fischer, K. N. Blodgett, C. P. Harrilal, P. S. Walsh, Z. S. Davis, S. Choi, S. H. Choi and T. S. Zwier, Conformer-Specific Spectroscopy and IR-Induced Isomerization of a Model γ-Peptide: Ac-γ4-Phe-NHMe, J. Phys. Chem. A, 2022, 126, 1837–1847.
9. W. Chin, F. Piuzzi, I. Dimicoli and M. Mons, Probing the competition between secondary structures and local preferences in gas phase isolated peptide backbones, Phys. Chem. Chem. Phys., 2006, 8, 1033–1048.
10. A. Camiruaga, I. Usabiaga, P. Pinillos, F. J. Basterretxea, J. A. Fernández and R. Martínez, Aggregation of nucleobases and metabolites: Adenine-theobromine trimers, J. Chem. Phys., 2023, 158, 64304.
11. E. Nir, K. Kleinermanns and M. S. de Vries, Pairing of isolated nucleic-acid bases in the absence of the DNA backbone, Nature, 2000, 408, 949–951.
12. P. Çarçabal, R. A. Jockusch, I. Hunig, L. C. Snoek, R. T. Kroemer, B. G. Davis, D. P. Gamblin, I. Compagnon, J. Oomens and J. P. Simons, Hydrogen bonding and cooperativity in isolated and hydrated sugars: mannose, galactose, glucose, and lactose, J. Am. Chem. Soc., 2005, 127, 11414–11425.
13. J. P. Simons, R. A. Jockusch, P. Çarçabal, I. Hung, R. T. Kroemer, N. A. Macleod and L. C. Snoek, Sugars in the gas phase. Spectroscopy, conformation, hydration, co-operativity and selectivity, Int. Rev. Phys. Chem., 2005, 24, 489–531.
14. F. O. Talbot and J. P. Simons, Sugars in the gas phase: the spectroscopy and structure of jet-cooled phenyl beta-D-glucopyranoside, Phys. Chem. Chem. Phys., 2002, 4, 3562–3565.
15. R. A. Jockusch, F. O. Talbot and J. P. Simons, Sugars in the gas phase - Part 2: the spectroscopy and structure of jet-cooled phenyl beta-D-galactopyranoside, Phys. Chem. Chem. Phys., 2003, 5, 1502–1507.
16. I. Hunig, A. J. Painter, R. A. Jockusch, P. Çarçabal, E. M. Marzluff, L. C. Snoek, D. P. Gamblin, B. G. Davis and J. P. Simons, Adding water to sugar: A spectroscopic and computational study of alpha- and beta-phenylxyloside in the gas phase, Phys. Chem. Chem. Phys., 2005, 7, 2474–2480.
17. R. A. Jockusch, R. T. Kroemer, F. O. Talbot, L. C. Snoek, P. Çarçabal, J. P. Simons, M. Havenith, J. M. Bakker, I. Compagnon, G. Meijer and G. von Helden, Probing the glycosidic linkage: UV and IR ion-dip spectroscopy of a Lactoside, J. Am. Chem. Soc., 2004, 126, 5709–5714.
18. P. Çarçabal, I. Hunig, D. P. Gamblin, B. Liu, R. A. Jockusch, R. T. Kroemer, L. C. Snoek, A. J. Fairbanks, B. G. Davis and J. P. Simons, Building up key segments of N-glycans in the gas phase: Intrinsic structural preferences of the alpha(1,3) and alpha(1,6) dimannosides, J. Am. Chem. Soc., 2006, 128, 1976–1981.
19. C. S. Barry, E. J. Cocinero, P. Çarçabal, D. P. Gamblin, E. C. Stanca-Kaposta, S. M. Remmert, M. C. Fernández-Alonso, S. Rudić, J. P. Simons and B. G. Davis, ‘Naked’ and hydrated conformers of the conserved core pentasaccharide of N-linked glycoproteins and its building blocks, J. Am. Chem. Soc., 2013, 135, 16895–16903.
20. E. J. Cocinero, P. Çarçabal, J. P. Simons and B. G. Davies, Sensing the anomeric effect in a solvent-free environment, Nature, 2011, 469, 76–79.
21. E. J. Cocinero, P. Carcabal, T. D. Vaden, B. G. Davis and J. P. Simons, Exploring Carbohydrate-Peptide Interactions in the Gas Phase: Structure and Selectivity in Complexes of Pyranosides with N-Acetylphenylalanine Methylamide, J. Am. Chem. Soc., 2011, 133, 4548–4557.
22. R. Lozada-Garcia, D. Mu, M. Plazanet and P. Çarçabal, Molecular gels in the gas phase? Gelator–gelator and gelator–solvent interactions probed by vibrational spectroscopy, Phys. Chem. Chem. Phys., 2016, 18, 22100–22107.
23. N. Mayorkas, S. Rudić, E. J. Cocinero, B. G. Davis and J. P. Simons, Carbohydrate hydration: heavy water complexes of α and β anomers of glucose, galactose, fucose and xylose, Phys. Chem. Chem. Phys., 2011, 13, 18671–18678.
24. N. Mayorkas, S. Rudić, B. G. Davis and J. P. Simons, Heavy water hydration of mannose: the anomeric effect in solvation, laid bare, Chem. Sci., 2011, 2, 1128–1134.
25. M. Pincu, E. J. Cocinero, N. Mayorkas, B. Brauer, B. G. Davis, R. B. Gerber and J. P. Simons, Isotopic Hydration of Cellobiose: Vibrational Spectroscopy and Dynamical Simulations, J. Phys. Chem. A, 2011, 115, 9498–9509.
26. A. M. Rijs and J. Oomens, in Gas-Phase IR Spectroscopy and Structure of Biological Molecules, ed. A. M. Rijs and J. Oomens, Springer, Cham, 2014.
27. E. J. Cocinero and P. Çarçabal, Carbohydrates, Top. Curr. Chem., 2015, 364, 299–333.
28. C. R. Anderton, R. K. Chu, N. Tolić, A. Creissen and L. Paša-Tolić, Utilizing a Robotic Sprayer for High Lateral and Mass Resolution MALDI FT-ICR MSI of Microbial Cultures, J. Am. Soc. Mass Spectrom., 2016, 27, 556–559.
29. Z. Huang, T. Ossenbrüggen, I. Rubinsky, M. Schust, D. A. Horke and J. Küpper, Development and Characterization of a Laser-Induced Acoustic Desorption Source, Anal. Chem., 2018, 90, 3920–3927.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallin, 2016.
31. R. W. Larsen, P. Zielke and M. A. Suhm, Hydrogen-bonded OH stretching modes of methanol clusters: A combined IR and Raman isotopomer study, J. Chem. Phys., 2007, 126, 194307.
32. T. Shimanouchi, Tables of molecular vibrational frequencies. Consolidated volume II, J. Phys. Chem. Ref. Data, 1977, 6, 993–1102.

---