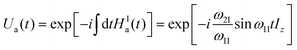Double nutation cross-polarization between heteronuclear spins in solids†
Received
17th February 2023
, Accepted 14th April 2023
First published on 17th April 2023
Abstract
We study transfer of magnetization from one nuclear spin species to another in solid-state nuclear magnetic resonance by cross-polarization (CP) employing radiofrequency irradiation that causes simultaneous nutations around a pair of orthogonal axes. Under such DOuble NUTation (DONUT), polarization transfer proceeds in an unexplored arena of what we refer to as the nutation frame, which represents the interaction frame with respect to the Hamiltonian that drives nutation. The effect of DONUT is to develop either the zero-quantum or double-quantum secular component of the heteronuclear dipolar interaction, causing flip-flop or flop-flop exchange of the spin states. We demonstrate DONUT CP in polycrystalline adamantane, glycine, and histidine, also examining folding of the CP spectrum under magic-angle spinning as well as the buildup behavior of the magnetization in comparison with the conventional CP scheme. In addition, we put forth a concept of spin relaxation in the nutation frame, which is a straightforward extension of the well-known concept of spin relaxation in the rotating frame.
1. Introduction
Cross-polarization (CP) is a technique of solid-state nuclear magnetic resonance (NMR) spectroscopy to enhance the sensitivity1–3 by transferring the magnetization from one nuclear spin species, I, to another, S, through simultaneous applications of radio-frequency (rf) irradiation in such a way that the Hartmann–Hahn condition is fulfilled.4 Usually, CP takes place in a doubly rotating frame, where the coordinate systems for I and S are rotated separately around the static magnetic field at their respective Larmor frequencies. A few exceptions include cases in which the source spins are paramagnetic electrons, where the large difference in the gyromagnetic ratios makes it rather straightforward to implement CP in the rotating frame for the source electron spins and the laboratory frame for the target nuclear spins.5–8
In this work, we report on CP proceeding in a different arena realized through simultaneous nutations of the source spins I around two separate magnetic fields B1 and B2 at frequencies ω1I = −γIB1 and ω2I = −γIB2, where γI is the gyromagnetic ratio of spin I. Such DOuble NUTation (DONUT) is driven by a propagator UI(t) of the form UI(t) = exp(−iω1ItB1·I)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iω2ItB2·I). The idea of multiple nutation was first put forth by Khaneja and Nielsen, who studied homonuclear dipolar recoupling with the Triple Oscillating Field techniqUe (TOFU12), and then extended by Straasø et al. to the Four-Oscillating FielD (FOLD) technique.13 Later on, DONUT was applied to heteronuclear decoupling by Takeda et al.14
exp(−iω2ItB2·I). The idea of multiple nutation was first put forth by Khaneja and Nielsen, who studied homonuclear dipolar recoupling with the Triple Oscillating Field techniqUe (TOFU12), and then extended by Straasø et al. to the Four-Oscillating FielD (FOLD) technique.13 Later on, DONUT was applied to heteronuclear decoupling by Takeda et al.14
Here, we restrict ourselves to DONUT with B1 = (−ω1I/γI,0,0) and B2 = (0,0,−ω2I/γI), so that the propagator UI(t) is represented in the form
| | UI(t) = exp(−iω1ItIx)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iω2ItIz). exp(−iω2ItIz). | (1) |
The rf Hamiltonian
HIrf(
t) that results in the propagator
UI(
t) in
eqn (1) is straightforwardly obtained with
HIrf(
t) =
i![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) IUI−1
IUI−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14,15
14,15:
| | | H2(t) = ω2Ie−iω1ItIxIzeiω1ItIx. | (4) |
DONUT, as well as nutation around triple- and quadruple-oscillating fields,
12,13 requires smooth modulations of the rf pulses, which can be implemented with modern NMR spectrometers.
In DONUT CP, it is in the interaction frame with respect to H1 = ω1IIx (eqn (3)) that the source spins I contact with the target spins S. To represent this interaction frame, we coin a term, the nutation frame. Then, the essence of DONUT CP can be stated conveniently as polarization transfer that takes place between the source spin I in the nutation frame and the target spin S in the rotating frame. Transformation from the rotating frame to the nutation frame is analogous to a well-known transformation from the laboratory frame to the rotating frame, in which a static magnetic field vanishes, whereas a resonant rf field in the former becomes stationary in the latter, as described in Fig. 1(a). In DONUT, another time-dependent field B2 is applied, such that, in the rotating frame, B2 follows a circular trajectory around the stationary field B1 at the nutation frequency ω1I. By performing a transformation from the rotating frame into the nutation frame, B1 vanishes and B2 becomes stationary (Fig. 1(b)).
 |
| | Fig. 1 (a) (left) A schematic drawing of a static magnetic field B0 and a magnetic field B1 rotating about B0 at the Larmor frequency ω0 = −γB0, where γ is the gyromagnetic ratio of the spins of interest. In a reference frame rotating around B0 at ω0, B0 vanishes and B1 is stationary (right). (b) In addition to the rotating field B1, a time-dependent component, B2, is applied (left) such that, in the rotating frame, it draws a circular trajectory rotating at an angular frequency ω1 = |γ|B1 (middle). Another transformation through rotation around B1 at ω1 leads to a frame, which we call the nutation frame, in which B1 vanishes while B2 now becomes stationary (right). This work follows the convention in which the Larmor precession is clockwise for positive γ, and nutation is counterclockwise for both positive and negative γ.9–11 | |
So far, a number of variants of CP have been proposed.16–29 They improve robustness against the mismatch of the Hartmann–Hahn condition and/or the efficiency of spin-locking. Conversely, one noteworthy feature of DONUT CP is the way that the spin interactions are manipulated in the nutation frame; they acquire time dependence with mixed frequencies ω1I ± ω2I. This is analogous to a frequency mixer, an electrical device used to literally mix a pair of alternating current signals with different frequencies, say, ωp and ωq, into another pair of signals with frequencies ωp ± ωq. The mixing leads to a different condition for polarization transfer from the conventional Hartmann–Hahn condition.
In the following, we describe the principle of DONUT CP, deriving the modified Hartmann–Hahn condition both in static and magic-angle spinning (MAS) cases. Then, we discuss the practical aspects of implementing DONUT using rf irradiation with modulation, with a note on the sign of the phase of the rf signals set in the transmitter of the NMR spectrometer and that of the rf field that develops inside the coil and is felt by the nuclear spins. We demonstrate 1H–13C DONUT CP in adamantane and glycine, and 1H–15N DONUT CP in histidine.
2. Theory
We consider a dipolar-coupled heteronuclear spin system, I and S, under DONUT CP, taking account of the dipolar interaction HIS, the interaction HSrf corresponding to monotonic rf irradiation applied to the target spin S with an intensity ω1S along, say, the x axis, and the interaction HIrf = H1 + H2(t) of the source spin I with the rf field that drives DONUT. The net Hamiltonian Hrot(t) in the rotating frame is represented as| | | Hrot(t) = H1 + H2(t) + HSrf + HIS(t). | (5) |
Here, H1 and H2(t) are given in eqn (3) and (4), and HSrf and HIS are| | 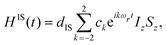 | (7) |
where dIS is the dipolar coupling constant, given, with the gyromagnetic ratios γI and γS and the internuclear distance rIS, by| |  | (8) |
and ωr is the sample spinning frequency. Under MAS, the spinning axis is tilted by  from the static field B0, so that the coefficient ck in eqn (7) is represented as
from the static field B0, so that the coefficient ck in eqn (7) is represented as| |  | (10) |
| |  | (11) |
where β and γ are the Euler angles of the internuclear vector with respect to the reference frame fixed in the spinning sample container.
The time evolution of the system is governed by a propagator U(t), which is written as
| | 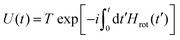 | (12) |
with
| | | U1(t) = exp(−iω1ItIx), | (14) |
| |  | (15) |
| | | Hnut(t) = U1−1(t)(Hrot(t) − H1)U1(t). | (16) |
Hnut(
t) is the Hamiltonian in the nutation frame,
i.e., in the interaction frame with respect to
H1, given by
| | | Hnut(t) = ω2IIz + ω1SSx + HISnut(t), | (17) |
with
| | 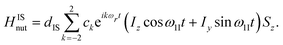 | (18) |
By tilting the rotating frame for spin
S such that the effective field points in the
z direction, we rewrite
Hnut(
t) as
| | | Hnut(t) = ω2IIz + ω1SSz + HISnut(t), | (19) |
| |  | (20) |
Another transformation of the dipolar interaction
HISnut(
t) to the interaction frame with respect to
ω2IIz +
ω1SSz leads to
| |  | (21) |
| | 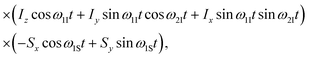 | (22) |
which can be rewritten as
| |  | (23) |
where
Δ and
Σ are defined to be the difference and the sum of the nutation frequencies
ω1I and
ω2I:
Now, the Hartmann–Hahn conditions can be obtained by invoking the time independence of the dipolar Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) IS (eqn (23)). In contrast to the conventional CP and a number of its variants, it is the mixed frequencies Δ and Σ that determine the Hartmann–Hahn conditions.
IS (eqn (23)). In contrast to the conventional CP and a number of its variants, it is the mixed frequencies Δ and Σ that determine the Hartmann–Hahn conditions.
2.1 Static case
Let us first consider the case of static samples, setting ωr = 0. Since ω1I and ω2I are positive, so is Σ. It follows that ω1S = Σ > 0 leads to a time-independent, zero-quantum component| |  | (26) |
which is quite similar to the secular contribution found in the conventional CP schemes, except that the coefficient of the flip-flop term, dIS/8, is halved in the case of DONUT CP compared to that in the conventional CP, dIS/4.
To obtain the Hartmann–Hahn conditions that involve Δ, we separately deal with the following three cases.
Case (i): ω1I > ω2I
Since Δ > 0, we find that ω1S = Δ gives a time-independent term
| | 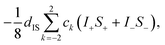 | (27) |
which carries the double-quantum flop-flop term. Thus, the polarization of the target spin
S is expected to be enhanced negatively. The double-quantum exchange in stationary samples is one interesting feature of DONUT CP, in contrast to the conventional CP where it is possible only in rotating samples.
30
Case (ii): ω1I = ω2I
Δ = 0, and no ω1S > 0 interfering with the e±iΔt term is found.
Case (iii): ω1I < ω2I
Δ < 0, and ω1S = −Δ > 0 leads to the zero-quantum secular term, so that positive enhancement of the magnetization of the target spins S is expected.
The matching conditions and the corresponding secular terms responsible for polarization transfer are summarized in Table 1.
Table 1 The Hartmann–Hahn (H–H) conditions for stationary samples and the secular terms of the dipolar interaction under DONUT CP
|
|
H–H condition |
Secular terms |
|
ω
1I > ω2I |
ω
1S = Δ |
∝I+S+ + I−S− |
|
ω
1S = Σ |
∝I+S− + I−S+ |
|
ω
1I = ω2I |
ω
1S = Σ |
∝I+S− + I−S+ |
|
ω
1I<ω2I |
ω
1S = −Δ |
∝I+S− + I−S+ |
|
ω
1S = Σ |
∝I+S− + I−S+ |
2.2 MAS case
In the case of MAS, the time dependence induced by the sample spinning can compensate for the energy mismatch. Thus, the Hartmann–Hahn conditions are found, irrespective of the mutual size relation between ω1I and ω2I. The zero-quantum secular term follows fromand the double-quantum term fromwhere n = ±1, ±2.
Now, the nutation frequency ω1S for the target spins that fulfils the Hartmann–Hahn condition can be negative, as is also the case for the conventional CP.30 The effect of negative ω1S will be discussed below.
2.3 A note on the initial π/2 pulse
Let us recall the two conditions for CP to take place:3 (a) the Hartmann–Hahn condition is fulfilled, (b) the magnetization of the source spins is locked along the effective field in the relevant frame of reference. So far, we have considered (a) alone. In the conventional CP, to fulfill (b), a π/2 pulse is applied to flip the magnetization of the source spin into the xy-plane before the pulse for the Hartmann–Hahn contact is applied, and the phase of the former has to be shifted by π/2 with respect to that of the latter. Interestingly, in DONUT CP, the initial π/2 pulse is unnecessary, provided that the z axis is chosen to be the axis of the second nutation, since, in the nutation frame, the only existing field points in the z direction, which is parallel to the initial magnetization of the source spin. It should be noted that, if the second nutation axis is not parallel to the z axis, the initial π/2 pulse is required.
3. Experimental
To let spins I evolve under HIrf(t) given in eqn (2), the rf irradiation is applied with an amplitude ωa(t) given by| |  | (32) |
with a phase ϕ(t)| |  | (33) |
and a frequency offset Δω(t)| | Δω(t) = ω2I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω1It. ω1It. | (34) |
To obtain the profile of such additional phase modulation that incorporates the frequency modulation (eqn (34)), we rewrite HIrf(t) as| | | HIrf(t) = HIa(t) + HIb(t), | (35) |
| | HIb(t) = ωa(t)[Ix![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(t) + Iy ϕ(t) + Iy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(t)]. ϕ(t)]. | (37) |
We also rewrite UI(t), originally given in eqn (1), aswhere| | 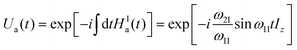 | (39) |
| |  | (40) |
with| |  | (41) |
| |  | (42) |
In the interaction frame with respect to HIa(t), the profile of the phase modulation is given bywhile that of the amplitude modulation is unchanged and is given simply by ωa(t). Examples of the waveforms of the amplitude ωa(t) and the phase ϕ(t) − ψ(t) are given in the ESI.†
The relationship between the sign of the phase of the rf signal programmed by the user of an NMR spectrometer and the sign of the phase of the rf field that is actually produced has been discussed extensively. According to the instructive papers by Levitt,10,11 when a pulse sequence involves phase modulation, it is necessary to set the sign of the phase depending on both the sign of the gyromagnetic ratio and the way that the carrier wave at the Larmor frequency ω0 is generated in the transmitter of the spectrometer, through mixing of a pair of synthesized rf signals at an intermediate frequency ωIF and a local frequency ωLO. For spins with a positive gyromagnetic ratio, the sign of the phase needs to be reversed when the carrier signal is generated through up-conversion, namely ω0 = ωIF + ωLO, whereas the sign has to be kept unaltered in the case of down-conversion, i.e., ω0 = |ωIF + ωLO|. It is recommended that the user of the spectrometer is aware of whether up-conversion or down-conversion is employed in the transmitter being used, so as to make the right choice of the sign of the phase.
In the present work, we implemented DONUT of the 1H spins (positive gyromagnetic ratio) on home-built NMR spectrometers31–33 in nominal 9.4 T and 7 T magnets, setting the intermediate frequency ωIF at 180 MHz and the local frequency ωLO at 220 MHz (120 MHz) + δ, mixing them in the transmitter to yield signals at ωIF ± ωLO, and passing them through a 400 MHz (300 MHz) bandpass filter, thereby choosing ωIF + ωLO = 400 MHz (300 MHz) + δ. Here, δ, determined by the actual field strength, was on the order of several tens of kHz in this work. Thus, the signal was up-converted. Taking advantage of employing the open-architecture home-built spectrometer, we unambiguously chose to reverse the sign of the phase given in the pulse program.
To check if the sequence worked as intended, we carried out 1H double-nutation experiments in liquid water. In Fig. 2, the first points of the quadrature-demodulated 1H NMR signal, obtained after applying DONUT for incremented time intervals of up to 50 μs, are plotted. The data reflect the trajectory of the 1H magnetization, initially in thermal equilibrium, onto the xy plane. The case of (ω1I/2π, ω2I/2π) = (20 kHz, 0 kHz), shown in Fig. 2(a), is simply the conventional nutation around the x axis, and the resultant trajectory is expected to draw a circular pattern on the yz plane, and its projection onto the xy plane showed a linear profile. For a finite ω2I/2π of 10 kHz, the xy projection of the trajectory drew an arc (Fig. 2(b)). With increasing frequency ω2I/2π of the second nutation, the deviation from the linear profile became more prominent (Fig. 2(c)–(f)).
 |
| | Fig. 2 Trajectories of the 1H magnetization of liquid water under double nutation applied with frequencies (ω1/2π, ω2/2π) of (a) (20 kHz, 0 kHz), (b) (20 kHz, 10 kHz), (c) (20 kHz, 20 kHz), (d) (20 kHz, 30 kHz), (e) (20 kHz, 40 kHz), and (f) (20 kHz, 50 kHz) for incremented time intervals up to 50 μs. The position of each circle represents the in-phase and the quadrature parts of the first sampling point of the measured FID. The magnitude of the complex data point was normalized to that obtained with the conventional π/2 pulse. Solid lines represent the trajectories of the magnetization (inset) and their projection onto the (x,y) plane obtained by numerically solving the Bloch equation with the initial magnetization being along the z axis and under application of the double-nutation by rf irradiation with amplitude ωa(t) and phase ϕ(t) − ψ(t) given in eqn (32) and (43). | |
To examine the trajectory of the 1H magnetization in the Bloch sphere, we numerically solved the Bloch equations,34 under the rf irradiation corresponding to the Hamiltonian given in eqn (41), with a normalized initial magnetization to be (0,0,1). In Fig. 2(b)–(f), also shown are the calculated three-dimensional trajectories of the magnetization and its projection onto the xy plane, which were found to explain the observed dependence of the transverse magnetization on the duration of the DONUT pulse, and therefore convinced us that the pulse sequence of DONUT was indeed working as we intended.
4. Results and discussion
4.1 CP spectra
Fig. 3(a) shows 13C magnetizations enhanced by DONUT CP obtained for a stationary powder sample of adamantane as a function of the amplitude ω1S of the rf field applied to the target 13C spins. Following Meier,30 we henceforth refer to the ω1S dependence of the S magnetization as the CP spectrum. The CP spectrum depicted with blue circles in the figure was obtained with DONUT applied to the source 1H spins with nutation frequencies (ω1I/2π, ω2I/2π) of (20 kHz, 50 kHz), whereas the CP spectrum with the swapped combination, i.e., (ω1I/2π, ω2I/2π) = (50 kHz, 20 kHz), is shown with red circles. For both of these cases, time dependence with the mixed frequencies |ω1I ± ω2I|, namely, ca. 2π·30 kHz and 2π·70 kHz, is expected to develop. Indeed, when the 13C nutation frequency ω1S was closer to these values, the 13C magnetization was enhanced, as demonstrated in Fig. 3(a). For (ω1I/2π, ω2I/2π) = (50 kHz, 20 kHz), the 13C magnetization was negatively enhanced for ω1S ∼ Δ of around 2π·30 kHz. This is consistent with the theory discussed above, which derived the double-quantum nature of the secular component of the heteronuclear dipolar interaction in the nutation frame for the source spins and in the rotating frame for the target spins for the case of ω1I > ω2I.
 |
| | Fig. 3
1H–13C Hartmann–Hahn matching profiles of DONUT CP measured for adamantane in a magnetic field of 7 T under (a) the static condition and (b) MAS at 9 kHz. Red and blue circles represent the ω1S dependence obtained with (ω1I/2π, ω2I/2π) of (50 kHz, 20 kHz) and (20 kHz, 50 kHz), respectively. The contact time was 7 ms. | |
In Fig. 3(b), the Hartmann–Hahn matching profiles, obtained with DONUT CP under MAS at 9 kHz, are shown. Now, the observed DONUT-CP spectrum was such that the individual peak in the static case (Fig. 3(a)) split into sidebands with a separation corresponding to the spinning speed, just like in the case of the conventional CP under MAS. The feature of negative enhancement for the case of ω1I > ω2I and ω1S = Δ is retained.
Fig. 4 shows a 13C DONUT-CP spectrum of the methylene carbon obtained in polycrystalline glycine under MAS at 23 kHz with DONUT applied at the 1H spins with (ω1I/2π, ω2I/2π) of (90 kHz, 60 kHz). With ω1I > ω2I, Δ/2π = 30 kHz, and ωr/2π = 23 kHz, the expected double-quantum exchange with negative enhancement of the 13C magnetization was observed at around ω1S/2π of 76 kHz (n = 2), 53 kHz (n = 1), and 7 kHz (n = − 1). The positive peak of the DONUT-CP spectrum in Fig. 4 is assigned as the n = −2 sideband of the DONUT-CP spectrum, which ought to be at around −2π·16 kHz, but folded back to the positive position at |Δ − 2ωr| of ca. +2π·16 kHz. In addition, the zero-quantum exchange, instead of the double-quantum exchange, was observed for the folded-back peak. It is interesting to make a comparison with the well-known peak folding in the conventional CP under MAS, where the double-quantum exchange alone takes place for the folded-back peak.30
 |
| | Fig. 4
13C nutation frequency dependence of methylene 13C magnetization in 9.5%-2-13C-labeled glycine under DONUT CP with (ω1I/2π, ω2I/2π) of (90 kHz, 60 kHz) in a magnetic field of 9.4 T under MAS at 23 kHz. The contact time was 0.15 ms. | |
4.2 Magnetization buildup
Fig. 5(a) shows a 15N spectrum of a polycrystalline sample of 15N-labeled histidine in the form of a τ tautomer (Fig. 5(b)).35 The three peaks are assigned as the α, ε2, and δ1 sites, respectively, as indicated in the figure. Fig. 6 compares the buildup behaviors of the 15N magnetizations in histidine under the conventional CP and the DONUT CP schemes under MAS at 20 kHz. In the former, the source 1H spins were irradiated with continuous-wave (cw) rf with an intensity ω1I/2π of 35 kHz, while in the latter, DONUT with ω1I/2π = 80 kHz and ω2I/2π = 45 kHz was applied. To the target 15N spins, cw rf irradiation was applied with intensities of 17 kHz and 16 kHz, which were experimentally found to be optimal in the respective measurements.
 |
| | Fig. 5 (a) 15N spectrum of polycrystalline 15N-labeled histidine, obtained with DONUT CP in 9.4 T under MAS at 20 kHz with a contact time of 3 ms. (b) The structure of a neutral τ tautomer of histidine. | |
 |
| | Fig. 6 Contact-time dependence of the 15N magnetization of (a) the α, (b) the ε2 and (c) the δ1 sites of 15N-labeled polycrystalline histidine, measured in a magnetic field of 9.4 T under MAS at 20 kHz by DONUT CP (red circles) and conventional CP (black squares). | |
For all three nitrogen sites in histidine, the initial buildup was slower in DONUT CP than in the conventional CP. Indeed, the slopes of the buildup curve at the beginning of the contact time were less steep by factors of 2.5, 2.1, and 2.0 for the α, ε2, and δ1 sites for DONUT CP compared to the conventional CP. For the ε2 nitrogen, which has a covalent bond to the hydrogen atom and is therefore close to the latter, transient oscillation was observed. The period of oscillation in DONUT CP was found to be longer than that in the conventional CP by a factor of ca. 1.6. The slower buildup and the longer period of the transient oscillation are ascribed to the down-scaling of the heteronuclear dipolar interaction in the nutation frame by the factor of 2.
Interestingly, for the α and ε2 sites, as the contact time was increased up to several hundreds of microseconds, the buildup curves for the conventional CP began to decay, while those for DONUT CP continued to grow. Eventually, for all three sites, DONUT CP led to larger 15N magnetization when increasing the contact time further, up to several milliseconds. Since the way that the rf irradiation was applied to the 15N spins was the same for both CP schemes, it was the relaxation of the 1H spins that led to the difference.
When a spin species with a relatively low gyromagnetic ratio, like 15N, is the target, it is often not feasible or desirable to apply too much rf power, such that one has to bear a relatively low nutation frequency ω1S. Then, in the conventional CP, one has to reduce the intensity of the rf field applied to the source spins as well to fulfill the Hartmann–Hahn condition. Even though this is not the case if one employs ultrafast MAS, access to such a state-of-art facility is still limited. In addition, ultrafast MAS is not compatible with samples with a relatively large volume, which is often desirable to gain sensitivity. Even though the concept of time-averaged precession frequency (TAPF) can be a solution in CP to the low-gyromagnetic-ratio spin species, the 1H relaxation can be so fast that it is difficult to optimize the performance of magnetization transfer.36,37 Conversely, in DONUT CP, various combinations of ω1I and ω2I can be chosen such that the effect of relaxation is not so serious.
The overall profile of the CP buildup curve is determined by the balance between the two competing processes, namely transfer of polarization and relaxation. As discussed above, the polarization transfer was indeed slower in DONUT CP than in the conventional CP, because of the smaller magnitude of the secular heteronuclear dipolar interaction in the nutation frame. In DONUT CP, the arena in which spins I undergo relaxation is the nutation frame, in contrast to the rotating frame in the conventional CP schemes. Here, we introduce a symbol T1ν to represent the time constant of spin–lattice relaxation of spins I in the nutation frame, in analogy with T1ρ that represents spin–lattice relaxation in the rotating frame. The subscript ν (nu) appropriately reminds one of the nutation frame, just like the subscript ρ (rho) does of the rotating frame.
The dynamics of spin–lattice relaxation in the nutation frame require development of the method to experimentally determine T1ν, collection of data in a number of systems under various experimental conditions, and an extension of the relaxation theory that is well-established in the case of the rotating frame3 by incorporating the relevant spin interactions. The expression for the effective homonuclear dipolar interaction under DONUT, already given in ref. 12 in the case of simultaneous nutations around the x and the y axes with a common rate ω1I = ω2I = C, includes quite a few terms, some of which can interfere with the time dependence caused by sample spinning. As a result, T1ν as a function of ω1I, ω2I, and ωr would show a somewhat complex profile. Although systematic studies on these subjects are outside the scope of the current work, what the results of DONUT CP demonstrated in this work imply is that, in some cases, spin–lattice relaxation in the nutation frame can be slower than that in the rotating frame. When this is indeed the case, the slower buildup rate due to the reduced heteronuclear dipolar interaction can be more than compensated for by the benefit of the longer T1ν.
5. Summary
The nutation frame is the interaction frame with respect to the Hamiltonian responsible for driving nutation. DONUT CP causes transfer of nuclear spin polarization in solids between the source spins in the nutation frame and the target spins in the rotating frame. The Hartmann–Hahn condition Δ = ω1S for ω1I > ω2I leads to double-quantum exchange, and the other Hartmann–Hahn conditions to zero-quantum exchange. Under MAS, the peak of the DONUT-CP spectrum at the negative frequency folds back to the positive region, accompanying sign inversion in the intensity of the magnetization. In DONUT CP, the magnitude of the secular part of the dipolar interaction is half that in the conventional CP, resulting in a slower buildup rate. Nevertheless, there exist cases in which the maximum attainable enhancement exceeds that in the conventional CP, when spin relaxation in the nutation frame is slow enough.
Author contributions
Yu Wang: investigation, visualization, writing – original draft. Kazuyuki Takeda: conceptualization, supervision, investigation, visualization, writing – review & editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work has been supported by JST CREST (grant number JPMJCR1873) and the MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) (grant number JPMXS0120330644).
Notes and references
- A. Pines, M. Gibby and J. S. Waugh, J. Chem. Phys., 1973, 59, 569–590 CrossRef CAS.
- J. Schaefer and E. O. Stejskal, J. Am. Chem. Soc., 1976, 98, 1031–1032 CrossRef CAS.
-
M. Mehring, Principles of High Resolution NMR in Solids, Springer-Verlag, Berlin, Heidelberg, New York, 2nd, edn, 1983 Search PubMed.
- S. Hartmann and E. Hahn, Phys. Rev., 1962, 128, 2042–2053 CrossRef CAS.
- A. Henstra, P. Ducksen, J. Schmidt and W. Wenckebach, J. Magn. Reson., 1988, 77, 389–393 Search PubMed.
- A. Henstra, P. Dirksen and W. Wenckebach, Phys. Lett. A, 1988, 134, 134–136 CrossRef CAS.
- A. Henstra and W. Wenckebach, Mol. Phys., 2008, 106, 859–871 CrossRef CAS.
- A. Henstra and W. Wenckebach, Mol. Phys., 2014, 112, 1761–1772 CrossRef CAS.
-
R. R. Ernst, G. Bodenhausen and A. Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Oxford University Press, 1987 Search PubMed.
- M. H. Levitt, J. Magn. Reson., 1997, 126, 164–182 CrossRef CAS.
- M. H. Levitt and O. G. Johannessen, J. Magn. Reson., 2000, 142, 190–194 CrossRef CAS PubMed.
- N. Khaneja and N. C. Nielsen, J. Chem. Phys., 2008, 128, 015103 CrossRef PubMed.
- L. A. Straasø, M. Bjerring, N. Khaneja and N. C. Nielsen, J. Chem. Phys., 2009, 130, 225103 CrossRef PubMed.
- K. Takeda, A. Wakisaka and K. Takegoshi, J. Chem. Phys., 2014, 141, 224202 CrossRef PubMed.
- Y. Ishii and T. Terao, J. Chem. Phys., 1998, 109, 1366 CrossRef CAS.
- A. C. Kolbert and A. Bielecki, J. Magn. Reson., Ser. A, 1995, 116, 29–35 CrossRef CAS.
- R. Fu, P. Pelupessy and G. Bodenhausen, Chem. Phys. Lett., 1997, 264, 63–69 CrossRef CAS.
- S. Zhang, B. H. Meier, S. Appelt, M. Mehring and R. R. Ernst, J. Magn. Reson., Ser. A, 1993, 101, 60–66 CrossRef CAS.
- S. Hediger, P. Signer, M. Tomaselli, R. R. Ernst and B. H. Meier, J. Magn. Reson., 1997, 125, 291–301 CrossRef CAS.
- S. Hediger, B. H. Meier and R. R. Ernst, Chem. Phys. Lett., 1993, 213, 627–635 CrossRef CAS.
- M. Baldus, D. Geurts, S. Hediger and B. Meier, J. Magn. Reson., Ser. A, 1996, 118, 140–144 CrossRef CAS.
- S. Hediger, B. Meier and R. Ernst, Chem. Phys. Lett., 1995, 240, 449–456 CrossRef CAS.
- W. K. Peng and K. Takeda, J. Magn. Reson., 2007, 188, 267–274 CrossRef CAS PubMed.
- T. Matsunaga, I. Matsuda, T. Yamazaki and Y. Ishii, J. Magn. Reson., 2021, 322, 106857 CrossRef CAS PubMed.
- W. Peng, K. Takeda and M. Kitagawa, Chem. Phys. Lett., 2006, 417, 58–62 CrossRef CAS.
- K. Takeda, Y. Noda, K. Takegoshi, O. Lafon, J. Trébosc and J.-P. Amoureux, J. Magn. Reson., 2012, 214, 340–345 CrossRef CAS PubMed.
- S. Hediger, B. Meier, N. D. Kurur, G. Bodenhausen and R. Ernst, Chem. Phys. Lett., 1994, 223, 283–288 CrossRef CAS.
- G. Metz, X. Wu and S. O. Smith, J. Magn. Reson., Ser. A, 1994, 110, 219–227 CrossRef CAS.
- S. Zhang, B. H. Meier and R. R. Ernst, J. Magn. Reson., Ser. A, 1994, 108, 30–37 CrossRef CAS.
- B. Meier, Chem. Phys. Lett., 1992, 188, 201–207 CrossRef CAS.
- K. Takeda, Rev. Sci. Instrum., 2007, 78, 033103 CrossRef PubMed.
- K. Takeda, J. Magn. Reson., 2008, 192, 218–229 CrossRef CAS PubMed.
- K. Takeda, Annu. Rep. NMR Spectrosc., 2011, 74, 355–393 CrossRef CAS.
-
A. Abragam, Principle of Nuclear Magnetism, Oxford University Press, 1961 Search PubMed.
- S. Li and M. Hong, J. Am. Chem. Soc., 2011, 133, 1534–1544 CrossRef CAS PubMed.
- K. Takegoshi and C. McDowell, J. Magn. Reson., 1986, 67, 356–361 CAS.
- Z. D. Žujović and G. A. Bowmaker, J. Magn. Reson., 2006, 181, 336–341 CrossRef PubMed.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iω2ItB2·I). The idea of multiple nutation was first put forth by Khaneja and Nielsen, who studied homonuclear dipolar recoupling with the Triple Oscillating Field techniqUe (TOFU12), and then extended by Straasø et al. to the Four-Oscillating FielD (FOLD) technique.13 Later on, DONUT was applied to heteronuclear decoupling by Takeda et al.14
exp(−iω2ItB2·I). The idea of multiple nutation was first put forth by Khaneja and Nielsen, who studied homonuclear dipolar recoupling with the Triple Oscillating Field techniqUe (TOFU12), and then extended by Straasø et al. to the Four-Oscillating FielD (FOLD) technique.13 Later on, DONUT was applied to heteronuclear decoupling by Takeda et al.14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−iω2ItIz).
exp(−iω2ItIz).![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) IUI−1
IUI−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14,15:
14,15:
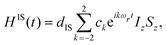

 from the static field B0, so that the coefficient ck in eqn (7) is represented as
from the static field B0, so that the coefficient ck in eqn (7) is represented as

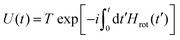

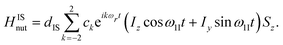


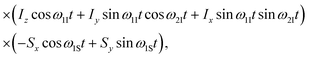

![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) IS (eqn (23)). In contrast to the conventional CP and a number of its variants, it is the mixed frequencies Δ and Σ that determine the Hartmann–Hahn conditions.
IS (eqn (23)). In contrast to the conventional CP and a number of its variants, it is the mixed frequencies Δ and Σ that determine the Hartmann–Hahn conditions.
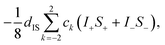


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω1It.
ω1It.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(t) + Iy
ϕ(t) + Iy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ(t)].
ϕ(t)].