Electrocatalytic reduction of CO₂ on size-selected nanoclusters of first-row transition metal nanoclusters: a comprehensive mechanistic investigation

Abstract

Recycling CO₂ back to fuels offers an ideal solution to control anthropogenic global CO₂ emissions as well as providing a sustainable green solution to alternative energy resources from a cheap and earth-abundant carbon source. Size-selected nanoclusters open a novel area in catalysis as these atomically precise nanoclusters possess unique electronic and catalytic properties different from larger nanoparticles and traditional bulk catalysts. In this work, we have investigated the ability of first-row transition metal nanoclusters (Sc–Cu) of varying sizes (3 to 10 atoms) for CO₂ electroreduction (CO₂RR). Employing computational hydrogen model (CHE), we have performed detailed analyzes on various CO₂RR electrocatalytic reaction pathways on all nanocluster surfaces. We have identified a general trend of decreasing adsorption energies while moving across the periodic table from Sc to Cu. Moreover, we have found a general preference for CHO* mediated pathways over COH* mediated pathways for methane formation. The CHO* mediated pathways prefer the reaction route via CHO* → CH₂O* → CH₂OH* → CH₂* → CH₃* → CH₄ + * on most of the nanocluster surfaces. In addition, we have established that methanol formation is greatly disfavored on all nanocluster surfaces, and the release of CO and HCOOH is greatly suppressed on all nanoclusters. We have identified several nanoclusters as potential nanocluster-based electrocatalysts for CO₂RR for methane formation with relatively lower limiting potential values below 0.50 V. CO₂ electroreduction versus hydrogen evolution reaction (HER) competition was also evaluated on various nanoclusters, and we identified a number of nanoclusters (Ti₆, V₅, V₆, Mn₄, Mn₇, Mn₁₀, Fe₄, Fe₈, Fe₁₀, Ni₄, and Cu₅) that can suppress the formation of HER over CO₂RR. We have also established a linear scaling relationship between the adsorption free energies of various CO₂RR adsorbates to the adsorption free energies of CO₂*, O*, and C* adsorbates. We have found that scaling free energy relationships that exit on heterogeneous catalysts such as the correlation between the adsorption energies of AH_x with the adsorption energies of atom A (A = C, N, O, S, etc.) often breaks on nanocluster surfaces, especially for adsorbates with more than one binding motifs.

---

Introduction

One of the defining environmental, energy, and societal challenges of the 21st century is how to efficiently control global warming and the associated climate change by reducing anthropogenic CO₂ emissions. Recycling CO₂ into useful chemicals, in particular to fuels such as carbon monoxide (CO), formic acid (HCOOH), methanol (CH₃OH), and methane (CH₄) is an excellent strategy to reduce CO₂ emissions.^1–4 Moreover, it offers a simultaneous sustainable energy solution to the rapid depletion of fossil fuel resources. Even though CO₂ is an inexpensive, abundant, and renewable C1 source for synthesizing many chemicals, the activation and subsequent chemical transformation of CO₂ is a formidable challenge due to its chemical inertness.

Although there have been many heterogeneous catalysts with different supports and promoters reported for the direct hydrogenation of CO₂ with H₂, these catalysts exhibit some serious drawbacks such as high operating temperatures and pressures (>200 °C and 50–100 atm pressures), lack of catalyst tuning and formation of undesirable by-products.^5,6 Electrochemical reduction of CO₂ (CO₂RR) is an alternative way of achieving CO₂ reduction and has the distinct advantage that it operates at room temperature and atmospheric pressure. Moreover, the electrocatalytic activity and selectivity can be easily controlled by varying the electrode potentials.^7–11 Among many metals tested, Cu is the only metal that has been experimentally shown to produce higher-order reduction products such as methane or ethylene, albeit with higher overpotentials for CO₂RR.^12,13 Although many metals have been proposed for electrocatalytic reduction of CO₂, industrial-level large-scale conversion is still a formidable challenge. Moreover, hydrogen evolution reaction (HER), a competing side reaction, often prohibits the efficacy of the CO₂RR catalysts. The development of highly efficient robust catalyst made of cheap and earth-abundant metals are an inevitable necessity to convert the enormous amount of CO₂ that is released into the atmosphere to control global emissions.

Nanocatalysis, more specifically catalysis by nanoparticles (NPs) has gained significant momentum recently due to their high activity and selectivity as well as low metal cost replacing the traditional metal-based bulk catalysts.^14–19 Nanoclusters (NCs), a subclass of nanoparticles with a fewer number of metal atoms (typically <150 atoms) and subnanometre clusters (size-selected nanoclusters of very few atoms typically <30), a further subclass of NCs, often exhibit unique electronic and catalytic properties different from their superclass NPs or bulk materials primarily due to size-induced quantum effects.^19,20 These properties depend on the cluster size, cluster composition, shape, increased density of exposed low-coordinated unsaturated sites, and high surface-to-volume ratio. Subnanometre clusters show particular promise in the field of nanocatalysis as the addition or removal of an atom can impart dramatic effects on their catalytic activity and selectivity.

CO₂RR studies for several metal NPs (Cu, Ni, Au, Ag, Bi, Pd, Sn, etc.) were reported previously.^21–41 These studies in general show different CO₂RR activities and selectivities for NPs of different sizes, which often exhibit enhanced CO₂RR activities compared to metal surfaces. For instance, CO₂ to CO reduction shows significant improvement on Au₂₅ nanoclusters compared to larger Au NPs or Au surfaces.³³ Salehi-Khojin et al. and Kim et al. have shown the enhanced catalytic activity and selectivity for silver NPs.^35,41 Studies on Pd NPs for CO₂RR show significant enhancement in the faradaic efficiency from 5.8% to 91.2% and an 18.4-fold increase in current density when the size of the Pd NPs reduced from 10.3 nm to 3.7 nm.³⁹ Different redox behavior for Cu₅ and Cu₂₀ NPs were reported by Vajda and co-workers.³⁶ Manthiram et al. have demonstrated that Cu NPs supported on glassy carbon exhibit 4 times higher methanation current densities compared to high purity Cu foil electrodes.⁴² Similarly, Peter Strasser and co-workers have shown that Cu NPs in the 2–15 nm size range were analyzed for CO₂ electroreduction and found a dramatic increase in the activity and selectivity for CO with decreasing Cu particle size, particularly below 5 nm.⁴³ Overpotentials as low as 340 mV were reported for nanostructured Sn catalysts.⁴⁴ Bismuth nanoparticles anchored on reduced graphene oxide (Bi/rGO) show very high faradaic efficiency up to 98% for CO₂ reduction to formic acid.³² The ultimate downsizing of subnanoclusters to one single atom leads to a novel area in nanocatalysis termed “single atom catalysis (SAC).^45,46 Ni and Cu SACs were reported for CO₂RR with excellent faradaic efficiency and current density.^23,47 Besides electrocatalytic CO₂ reduction, the NP size effects on thermal catalysis (direct hydrogenation of CO₂ with H₂) were also reported. Most importantly, Stefan Vajda and co-workers reported that Cu₄ is the most active low-pressure catalyst reported to date for the direct CO₂ hydrogenation to CH₃OH and the removal of one atom from Cu₄ to Cu₃ reduces the activity of CH₃OH production drastically, by more than 50%.^48,49 They also reported that catalytic activity for methanol formation depends on cluster size and varies in the order Cu₄ > Cu₂₀ > Cu₃.

Several theoretical studies have reported for electrocatalytic reduction of CO₂ on nanoclusters. Using the computational hydrogen electrode (CHE) model, Nørskov and co-workers provided the first theoretical insights into copper's unique ability to reduce CO₂ to methane and other hydrocarbons.⁵⁰ They proposed a CHO* intermediate pathway and found the potential-determining step (PDS) is the formation of CHO* species from CO* (* indicates an adsorbed species). Asthagiri et al. based on their theoretical work proposed an alternative reaction route that involves the formation of COH* (hydroxymethylidyne) intermediate.^51,52 DFT studies have been reported for the electroreduction of CO₂ on larger NPs such as Au₃₈ and Au₅₅, Pd₃₈ and Pd₅₅, Au₂₅(SCH₃)₁₈, Cu₈₅, and Cu₇₉ as well as on tetra-atomic subnanometer metal clusters (Co₄, Fe₄, Cu₄, Ni₄, and Pt₄) for CO₂RR.^{33,37–39,53–56} In a recent work, we have investigated systematically the size effect of Cu subnanometre clusters (Cu_nn = 3–6) and found that nanoclusters with odd numbers of electrons, Cu₃ and Cu₅, and clusters with even numbers of electrons, Cu₄ and Cu₆, exhibit similar activity and selectivity.⁵⁷ In general, the electrochemical steps which are endergonic on Cu₃ and Cu₅ are exergonic on Cu₄ and Cu₆, and vice versa. These results show that even a single Cu atom can alter the entire reaction pathway at the subnanometre level.

Most of the previous computational work was centered on a few metal clusters such as Cu, Ni, Pd, etc. as support information to complement experimental work. In this work, we are systematically evaluating the ability of the atomically precise subnanometre nanoclusters of first-row transition metals (TMs) (Sc–Cu) with 3 to 10 metal atoms for CO₂ electrocatalytic reduction. Our major goal is to identify the potential first-row TM nanoclusters that can be used as CO₂ electroreduction catalysts for the reduction of CO₂ to higher-order reduction products such as methane or methanol with high-efficacy as a sustainable green energy solution to recycling CO₂ back to fuel. Moreover, we aimed at elucidating any general trend in the CO₂RR activity and selectivity on these metal clusters as well as identifying the most preferred reaction pathways on various nanoclusters. Moreover, if exits, we tried to establish linear scaling relationships between the free energies of adsorbates on these metal nanoclusters. We have not discussed the synthesizability of the various nanoclusters as it is beyond the scope of our detailed work on the DFT investigation on the first-row TM nanoclusters for CO₂ electroreduction and the elucidation of the general trend on activity and selectivity for CO₂RR on these nanoclusters.

Computational methods

Global minimum configurations of the various nanoclusters at the DFT level were determined using birmingham parallel genetic algorithm (BPGA).⁵⁸ We used GIGA, a recent advanced version of the BPGA which was coupled to Vienna ab initio simulation package (VASP)^59–62 for local DFT relaxations.⁶³ BPGA uses a pool-based methodology to relax and evaluate the geometries in parallel and has been successfully applied previously to locate the global minimum of pure and alloyed nanoclusters of varied sizes.^64–69

Gamma-point spin-polarized DFT method was used for local DFT relaxations employing a plane-wave basis set and Perdew–Burke–Erzenhof (PBE)⁷⁰ exchange–correlation GGA functional. The ion–electron interaction is treated with projected augmented wave (PAW) pseudopotentials.⁷¹ A plane wave cutoff energy of 400 eV was applied and Methfessel–Paxton⁷² smearing with a Sigma value of 0.01 eV was used to improve convergence. The final geometries in the pool including the global minimum were reoptimized with tighter convergence criteria (10⁻⁶ eV in energy and 0.01 eV Å⁻¹ in force and a higher plane wave cut-off energy of 600 eV) to get more accurate geometries and energy values. We have also included van der Waals correction through Grimme's DFT-D3^73,74 method during re-optimization. We have found that all nanoclusters retained similar geometrical arrangements with minor shifts in some of the atom positions.

Global minimum and other lower energy configurations were used for locating the most stable adsorbate configurations on each of the nanoclusters. Optimization of the cluster-adsorbate complexes was carried out using local DFT relaxations employing VASP. We use the same optimization strategy (PBE functional, DFT-D3 corrections, tighter convergence, and plane wave cut-off energy of 600 eV) for the relaxation of cluster-adsorbate bound complexes for locating the most preferred binding sites on different nanoclusters. The Bader method was used for charge analysis.⁷⁵ Free energy of the adsorbates were computed by performing vibrational analysis on adsorbates assuming the nanoclusters were immobilized on some supports. Thermal corrections (zero-point energy corrections, enthalpy and entropy corrections) were computed using harmonic vibrational frequencies of the adsorbates at 298.15 K employing VASPKIT,⁷⁶ and these corrections were then added to the DFT electronic energies to get the free energies of the adsorbates. It should be noted that all the reported Gibbs free energy values are standard values, ΔG⁰ and is calculated at 298.15 K.

Computational hydrogen electrode model (CHE)^50,77 was used to calculate the reaction free energy changes (ΔG) for various electrochemical steps. According to the CHE model, the free energy change for an electrochemical step can be calculated as:

ΔG[A* + (H⁺ + e⁻) → AH*] = μ(AH*) − μ(A*) − [μ(H⁺) + μ(e⁻)] (1)

In the CHE model, the chemical potential of the (H⁺/e⁻) pair is equal to half the chemical potential of the gas-phase H₂ molecule. The total chemical potential of the proton–electron pair as a function of applied potential U, at all temperatures, can be calculated as:

μ(H⁺) + μ(e⁻) = 0.5μ(H₂(g)) − |e|U (2)

At the applied potential U, the free energy of the proton–electron pair is shifted by −|e|U which implies that the CO₂RR step in which proton–electron pairs are transferred becomes less endergonic at negative applied potential bias. At U = U_L where U_L is the limiting potential, ΔG becomes zero and ΔG becomes negative at any U < U_L. At standard conditions, ΔG = ΔG⁰ + |e|U and for a reaction to be spontaneous, ΔG should be less than or equal to zero. The limiting potential is the minimum bias to be applied (least-negative potential) which makes all the electrochemical steps in the reaction pathway become downhill (exergonic) in free energy. This potential corresponds to the highest endergonic free energy step in the reaction pathway. The limiting potential is always negative and is measured in volts (V) whereas the corresponding free energy of the potential-determining step (PDS) is positive and is measured in eV. For instance, if CO* → CHO* is the potential-determining step (PDS) with a free energy change of the PDS of 1.0 eV for the CO₂RR on a particular material, a negative potential of −1.0 V should be applied to make all the electrochemical steps be exergonic. The CHE model is a thermodynamic model and ignores the kinetic barriers for (H⁺/e⁻) pair transfers to adsorbate species. It assumes that the barriers for proton transfer to adsorbed species are small enough to be surmountable at room temperatures. Previous studies on the proton transfer barriers for the reduction of O₂ to OOH and OH to H₂O on Pt supports this assumption as these proton transfer barriers lie in the range of 0.15 to 0.25 eV for zero applied potential and decrease with increasing applied voltage.^78,79 The thermodynamic free energy changes for various electrochemical steps predicted by the CHE model can be used as a catalytic descriptor for the favorability of the CO₂ electroreduction on various nanocluster surfaces. Further details regarding DFT energy correction of gas-phase molecules, solvent corrections, and liquid-phase corrections were provided in the ESI.†

Results and discussions

Global minimum configurations of first-row TM nanoclusters Sc_n–Cu_n (n = 3–10)

Structural characterization and locating the global minima of nanoclusters is one of the primary steps in the modeling of nanocatalysts as the catalytic activity and selectivity are often dependent on the size and shape of the nanoclusters. Moreover, the multitude of possible geometrical arrangements for a given nanocluster composition makes the potential energy surface (PES) highly complex as a variety of configurations can have very similar energies. Atomically precise smaller-sized nanoclusters require an accurate description of the PES at the DFT level as the quantum size effects tend to dominate as the system decreases. We have performed an extensive search for locating the global minimum configurations for all the first-row TM nanoclusters employing the GIGA version of the birmingham parallel genetic algorithm (BPGA) at the DFT level.

The first step in the GA run is to generate a number of random geometries (10 in this study) followed by relaxing these geometries into local minima to form the initial pool population. Based on the crossover and mutation rate, GA crossover and mutation operations are applied to the members of the pool to generate new structures. For crossover operation, a pair of clusters are selected from the pool using a weighted roulette-wheel selection method⁸⁰ and they undergo mating using a variant of the Deaven and Ho phenotypic cut-and-splice method⁸¹ to generate a single offspring. Different mutation operations such as “move”, “rotate”, “twist”, “partial inversion”, “rattle” etc. are performed on a randomly selected cluster through roulette-wheel selection. Skin mutation will keep 80% of the cluster atoms remain intact and the remaining 20% atoms will be placed in random positions around the cluster; rattle mutation operation will choose a random atom and move 40% of the cluster atoms nearest to that atom; change core mutation will change the core of the cluster; rotation and twist mutations will rotate and twist a percentage of cluster atoms; partial inversion operation will invert a subclass of cluster atoms with respect to their geometrical center; tunnel operation will move one of the atoms farthest from the center to the other side of the cluster. The overall objective of these operations is to update the pool with diverse geometries to avoid stagnation after a few generations.

For each cluster, we have run the genetic algorithm for a minimum of 400 generations and often more than 1500 generations. Each generation involves the relaxation of the newly generated geometry via crossover or mutation operations. Another parallel run was also performed to make sure that both the BPGA runs arrive at the same global minimum configurations for all the clusters. The global minimum configurations for first-row TM nanoclusters (Sc_n–Cu_n, n = 3–10) were shown in Fig. 1. The geometry, spin-state, and point group of the global minimum of the Sc–Cu clusters are given in Table 1.

Fig. 1 Top panel: Global minimum geometries for first-row TM nanoclusters (Sc_n–Cu_n, n = 3–10). Bottom panel: Some representative examples of the cluster-adsorbates.

Table 1 Geometry description, point group symmetry and spin state for the global minimum configurations of the first-row TM nanoclusters Sc_n–Cu_n (n = 3–10) determined through birmingham parallel genetic algorithm (BPGA) using PBE functional

	Geometry	Symmetry	Spin state
Sc3	Isosceles triangle	C 2V	2
Sc4	Tetrahedron	D 2d	3
Sc5	Trigonal bipyramid	D 3H	6
Sc6	Octahedron	D 4h	5
Sc7	Pentagonal bipyramid	C 5h	6
Sc8	Dodecahedron	C 2V	5
Sc9	Tri-capped trigonal prism	C s	8
Sc10	Tri-capped Pentagonal bipyramid	C s	7
Ti3	Isosceles triangle	C 2V	3
Ti4	Tetrahedron	D 2d	5
Ti5	Trigonal bipyramid	C 2	3
Ti6	Octahedron	D 4h	5
Ti7	Pentagonal bipyramid	D 5h	1
Ti8	Dodecahedron	C s	3
Ti9	Bicapped Pentagonal bipyramid	C 2V	3
Ti10	Bicapped quadrilateral antiprism	D 2	3
V3	Isosceles triangle	C 2V	2
V4	Parallelogram	C 2h	3
V5	Buckled tetragonal pyramid	C s	2
V6	Tetragonal bipyramid	C 2	3
V7	Distorted PBP	C s	2
V8	Hexagonal bipyramid	D 3d	1
V9	Bicapped buckled pentagonal bipyramid	C 1	2
V10	Bicapped square antiprism	D 4	1
Cr3	V-Shaped	C s	7
Cr4	Butterfly-shaped	D 2	3
Cr5	Distorted tetragonal bipyramid	C 2	7
Cr6	Bicapped butterfly	C 1	3
Cr7	Distorted pentagonal bipyramid	C 1	7
Cr8	Dodecahedron	C 2	1
Cr9	Bicapped distorted pentagonal bipyramid	C 1	5
Cr10	Tricapped distorted pentagonal bipyramid	C 1	1
Mn3	Equilateral triangle	D 3H	16
Mn4	Tetrahedron	C 3	11
Mn5	Trigonal bipyramid	C s	14
Mn6	Octahedron	C 2V	3
Mn7	Distorted pentagonal bipyramid	C s	6
Mn8	Dodecahedron	C s	19
Mn9	Bicapped pentagonal bipyramid	C s	16
Mn10	Bicapped tetragonal antiprism	D 2d	13
Fe3	Isosceles triangle	C s	11
Fe4	Tetrahedron	D 2d	13
Fe5	Trigonal bipyramid	D 3h	19
Fe6	Octahedron	C s	21
Fe7	Distorted pentagonal bipyramid	C 2	23
Fe8	Capped pentagonal bipyramid	C s	25
Fe9	Tricapped trigonal prism	C 1	27
Fe10	Tricapped pentagonal bipyramid	C 3V	29
Co3	Isosceles triangle	C s	8
Co4	Butterfly-shaped	D 2d	11
Co5	Trigonal bipyramid	D 3h	14
Co6	Octahedron	O h	15
Co7	Capped Octahedron	C 3v	16
Co8	Dodecahedron	C 2	17
Co9	Tricapped Trigonal prism	D 3h	18
Co10	Bi-Octahedron	C 2h	21
Ni3	Equilateral triangle	D 3h	3
Ni4	Tetrahedron	D 2d	5
Ni5	Trigonal bipyramid	D 3h	5
Ni6	Octahedron	D 3d	9
Ni7	Capped octahedron	C 3V	9
Ni8	Dodecahedron	C 2v	9
Ni9	Tri-capped trigonal prism	D 3h	9
Ni10	Tetra-capped Octahedron	T d	9
Cu3	Isosceles triangle	C 2v	2
Cu4	Parallelogram	D 2h	1
Cu5	W-Shaped	C 2v	2
Cu6	Equilateral triangle	D 3h	1
Cu7	Pentagonal bipyramid	D 5h	2
Cu8	Dodecahedron	D 2d	1
Cu9	Bicapped buckled pentagonal bipyramid	C s	2
Cu10	Bicapped tetragonal antiprism	D 2d	1

---

For nanoclusters with three metal atoms, an isosceles triangular arrangement is the global minimum configuration for all first-row TM nanoclusters except for Cr, Mn, and Ni. Cr₃ shows a V-shaped arrangement whilst Mn₃ and Ni₃ show an equilateral triangle arrangement. Tetrahedral, distorted tetragonal (butterfly-shape), and parallelogram are the global minimum configurations for clusters with four atoms. The global minimum for first-row metal nanoclusters with five, six, and seven atoms prefer in general, a trigonal bipyramid (TBP) octahedron (O_h), and pentagonal bipyramid (PBP) arrangement. These arrangements often exhibit reduced symmetries owing to the elongation or contraction of some of the metal–metal bonds. There are exceptions such as tetragonal bipyramid for V₆, W-shaped planar arrangement for Cu₅, and capped octahedron for Co₇ and Ni₇. Dodecahedron with varied symmetries is the global minimum configuration for all first-row nanoclusters with eight atoms except for V₈ and Fe₈ which prefer hexagonal bipyramid and capped pentagonal bipyramid geometries as the global minima. Tricapped tetragonal prism is the global minimum configuration for Sc₉, Fe₉, Co₉, and Ni₉. Bicapped pentagonal bipyramid with varying degrees of distortion is the preferred geometrical arrangement for global minimum configuration for Ti₉, V₉, Cr₉, and Mn₉ whilst Cu₉ prefers a tricapped octahedral arrangement. Sc₁₀, Cr₁₀, and Fe₁₀ adopt a tricapped pentagonal bipyramid configuration for the global minimum. Other clusters adopt different configurations such as bi-capped tetragonal antiprism for Ti₁₀, Cu₁₀, and Mn₁₀, bi-capped square antiprism for V₁₀, bi-octahedra for Co₁₀, and tetra-capped O_h for Ni₁₀. The geometrical arrangement for Mn₁₀ and Cu₁₀ exhibits a D_2d symmetry in its bicapped tetragonal antiprism arrangement and can be considered as a spiro-pentagonal bipyramid configuration similar to spiropentane. We have also noticed alternative shorter (1.7–1.8 Å) and longer bond lengths for Cr clusters in the range of (2.5–2.7 Å). The existence of the shorter bonds between Cr atoms may be attributed to the higher-order quintuple bonds as experimentally characterized in a number of dichromium complexes.^82,83

We then performed an extensive search for the energetically most preferred binding sites on the reoptimized global minimum configurations. We have considered all the possible unsymmetrical edges and metal atom sites for binding the adsorbates as well as different binding modes and orientations of the adsorbates. In addition to the global minimum configurations, we have also considered other lower energy configurations for locating the adsorbate binding sites as the energy difference between the global minimum and these low-lying configurations is often very small. We have sampled all the nanoclusters configurations obtained in the genetic algorithm search that falls within 0.5 eV of the global minimum energy. This leads to a significantly higher number of initial configurations for adsorbates on nanoclusters for geometry relaxation. We performed such an extensive search on cluster-adsorbate complexes to reaffirm that we found the most stable adsorbate binding site on the nanocluster. Nørskov et al. and Asthagiri et al. proposed the lowest energy reaction pathways for CO₂ electroreduction via CHO* and COH* adsorbates on metallic Cu surfaces, respectively.^50,51 We have chosen the adsorbate species involved in these pathways for our CO₂RR studies on first-row TM nanoclusters.

Activation of CO₂

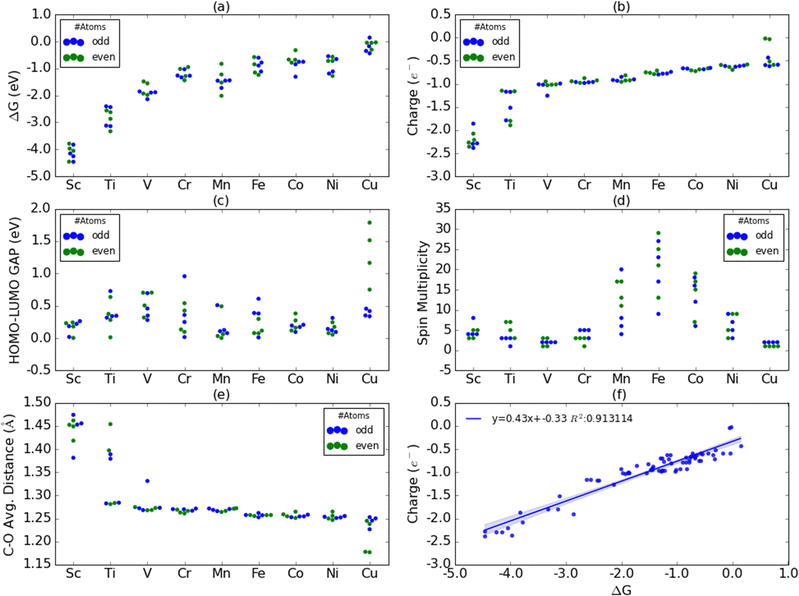
CO₂ activation is one of the primary challenges in the CO₂ recycling process due to the high thermodynamic stability of the CO₂. We have evaluated the adsorption free energies (or chemisorption energies) of CO₂ on various first-row TM nanoclusters and are shown in Fig. 2(a). The adsorption free energies are highest on Sc nanoclusters followed by on Ti nanoclusters as evident from Fig. 2(a). Sc and Ti nanoclusters exhibit the CO₂ adsorption energies in the range of −3.8 eV to −4.5 eV and −2.4 eV to −3.1 eV, respectively. All other TM nanoclusters show relatively lower adsorption energies compared to Sc and Ti. The adsorption energies for V (−1.5 eV to −2.1 eV), Cr (−1.0 to −1.4 eV), Mn (−0.8 eV to −2.0 eV), Fe (−0.6 eV to −1.15 eV) Co (−0.32 eV to −1.31 eV) Ni (−0.55 eV to −1.28 eV) and Cu (+0.14 eV to −0.44 eV) nanoclusters are smaller than CO₂ adsorption energies on Sc and Ti nanoclusters. Among all the nanoclusters studied Cu nanoclusters exhibit the lowest CO₂ adsorption free energies.

Fig. 2 (a) CO₂* adsorption free energies (ΔG, eV) (b) residual charges (e⁻) on CO₂ moiety, (c) HOMO–LUMO gaps of CO₂* (d) spin multiplicity of CO₂*, (e) average C–O bond distances in CO₂* adsorbates, and (f) correlation between CO₂* adsorption free energies and residual charges on CO₂* for various Sc, Ti, V, Cr, Mn, Fe, Co, Ni and Cu nanoclusters of 3 to 10 atom sizes. Residual charge indicates the total Bader charge density resides on CO₂ moiety on binding on cluster moiety. The labels ‘odd’ and ‘even’ indicate whether the total cluster atoms are odd or even number composition.

Fig. 2(b) shows the residual charges on CO₂ moiety on the nanoclusters. Bader charge analysis has shown that there is always a net negative charge accumulation of approximately 2e⁻ on the two O atoms of the CO₂ moiety on binding on all the nanoclusters. Depending on the charge accumulation or depletion on the C atom of the CO₂, the overall residual charges on nanoclusters vary. We have found a trend of increasing positive charge on the C atom of CO₂ moving from Sc to Cu. Except on Sc₃ and Sc₄ clusters, all other Sc clusters show a small increase in electron density on the C atom of the CO₂. All other first-row TM nanoclusters show a depletion of electron density on the C atom and carry a positive charge. From the linear regression plot in Fig. 2(f), we have identified a strong correlation between the residual charges on CO₂ moiety and the adsorption free energies. Fig. 2(c) and (d) show the HOMO–LUMO gaps and spin multiplicities on CO₂-bound nanoclusters. We could not find a direct correlation between the adsorption energies with HOMO–LUMO gaps or spin multiplicities. Mn, Fe, and Co nanoclusters exhibit significantly higher spin state multiplicities whilst Cu shows only two spin states: singlet or doublets. We have also analyzed the changes in the C–O bond distances of CO₂* on various nanoclusters and the average bond distances of the two C–O bond distances were plotted in Fig. 2(e). The significantly larger activation of CO₂ on Sc and Ti nanoclusters was also reflected in the CO₂ bond elongation.

Electrochemical adsorption of CO₂

The first step in the electrochemical reduction of CO₂ (CO₂RR) is the transfer of a proton–electron (H⁺ + e⁻) pair to CO₂ to form electrochemical adsorption species COOH*. However, there is a competition between chemisorption of CO₂ (CO₂*) versus electrochemical adsorption of CO₂ (COOH*). The COOH* adsorption free energies are shown in Fig. 3(a). As in the case of CO₂* adsorption free energies, the free energy values show a regular decrease across the first-row TM nanoclusters from Sc to Cu. In Fig. 3(c), we have plotted the difference between chemisorption free energies of CO₂* and adsorption free energies of COOH*. It can be seen that Sc clusters show a greater preference for chemisorbed CO₂* species. In general, we have seen a trend that moving from early TMs (Sc–V) to mid TMs (Cr–Fe) to late TMs (Co–Cu), the difference between CO₂* adsorption energies and COOH* electrochemical adsorption energies decreases. Except for Fe, Co, Ni, and Cu, all other metal clusters show a general preference for chemisorbed CO₂* species. Similar to CO₂*, we have seen a decrease in the residual negative charges on COOH* moiety in moving from early to late first-row TM nanoclusters (Fig. 3(b)). We have also identified a similar correlation between adsorption free energies and residual charges on COOH* species (Fig. 3(d)). Bader charge analysis shows that each O atom of the COOH* carries a negative charge of ∼1e⁻ and the H atom carries a positive charge of ∼0.5e⁻. Moving from Sc to Cu, we have seen a trend of reduction in the electron density on the C atom of the COOH* and the overall positive charge on the C atom depends on the extent to which electron density depletion occurs around the C atom of the COOH* species.

Fig. 3 (a) COOH* adsorption free energies (ΔG, eV), (b) residual charges (e⁻) on COOH*, (c) difference in CO₂* and COOH*adsorption free energies (eV), and (d) correlation between COOH* adsorption free energies and residual charges on COOH* for various Sc–Cu nanoclusters. Residual charge indicates the total Bader charge density resides on COOH moiety on binding on cluster moiety.

Adsorption of CO and other CO₂RR intermediates

The adsorption energy of CO* is one of the important factors that determine whether the electrochemical reduction reaction proceeds beyond the two-electron reduction process. CO is weakly coordinated on most of the metal surface and easily escapes from the surface forming the free CO as the major CO₂RR product prohibiting the formation of the higher-order six or eight electron reduction products such as CH₃OH or CH₄. In Fig. 4(a) we have shown the adsorption energies of CO on various nanoclusters. Similar to CO₂*, the adsorption free energies of CO* are significantly larger on Sc and Ti nanoclusters. Moreover, we have seen a significant stretching of C–O bonds on Sc and Ti nanoclusters (1.35 Å to 1.52 Å) and a decrease in the C–O stretching effect in moving from early TM nanoclusters to late TM nanoclusters. We have seen that for all cluster-CO adsorbates, there is always an increase of ∼ 1e⁻ charge density on the O atom of the CO moiety. We have seen increased electron density on the C atom results in the higher overall negative charge on CO moiety on Sc and Ti clusters. In general, we have seen a trend of reduced electronic density on C of the CO moving from early- to mid-to late first-row TM nanoclusters and the overall residual charge resides on CO moiety varies depending on the extent to which depletion of electron density happens on C atoms. We have also established a correlation between CO* adsorption energy and residual charges on CO moiety which is shown in Fig. 4(d).

Fig. 4 (a) CO* adsorption free energies (ΔG, eV), (b) residual charge (e⁻) on CO*, (c) C–O bond distances (Å) in CO*, and (d) correlation between CO* adsorption free energies and residual charges on CO* for various Sc–Cu nanoclusters. Residual charge indicates the total Bader charge density resides on CO moiety on binding on cluster moiety.

We have shown the adsorption free energies, residual charges, HOMO–LUMO gaps, spin multiplicities, and correlation between adsorption free energies with residual charges and HOMO–LUMO gaps for all adsorbates in Fig. S1–S6 (ESI†). We have identified that in general, all adsorbates show stronger adsorption free energies on early first-row TM nanoclusters and the adsorption free energies show a general trend of reduced binding affinity as we move across the periodic table from early to late first-row TMs (Fig. S1, ESI†). Some exceptions in the general trend are expected which can be attributed to the stability differences that arise from the rearrangement of cluster atoms on binding with the adsorbates and the associated spin state changes. A similar trend of decreasing residual charge density on adsorbate species on Sc to Cu nanoclusters was also identified (Fig. S2, ESI†). However, a similar high correlation between adsorption free energies and residual charges on CO₂*, COOH*, and CO* species were not observed for other adsorbates except for CHO* and CH₂O* (Fig. S3, ESI†). All other adsorbates show a coefficient of determination (R²) value below 0.70. The adsorbates exhibit a range of spin multiplicities on all TM nanoclusters except for Cu which shows only singlet and doublet states. We have noted that there exists no correlation between the adsorption free energies with spin multiplicities or HOMO–LUMO gaps of different adsorbates.

Electrochemical reduction of CO₂

We now turn to the CO₂RR reaction pathways to various reduction products such as methanol, methanol, carbon monoxide, and formic acid using the CHE model. Each reduction step involves the transfer of a proton–electron (H⁺ + e⁻) pair to the adsorbates. A schematic representation of the mechanism is shown in Scheme 1. In the first proton–electron transfer step, the hydrogenation on CO₂ can either form formate (OCHO*) species or carboxyl (COOH)* species. The (H⁺ + e⁻) transfer can hydrogenate either the C or the O atom of the adsorbates and leads to different reaction intermediates. The formate (OCHO*) species is an end product and releases formic acid in the second proton–electron transfer step albeit with a huge endergonic energy requirement. As we are interested in the reduction of CO₂ to higher-order reduction products such as methane and methanol, we will focus on the COOH* pathway. The carboxyl species (COOH*) can release formic acid (HCOOH) by hydrogenating the C atom or form a CO* adsorbate by eliminating a water molecule by hydrogenating the O atom. The CO* can be released from the nanocluster surface as a free CO molecule if it is weakly coordinated or can lead to the formation of CHO* or COH* intermediates depending on the hydrogenation site on CO* in the third (H⁺ + e⁻) transfer step. Most metal surfaces weakly adsorb CO which can be easily desorbed from the surface leading to CO as the major product prohibiting further CO₂RR reduction steps. Further electrochemical (H⁺ + e⁻) transfers to CHO* and COH* species and the subsequent intermediates lead to various CO₂RR reduction pathways (Scheme 1) depending on the hydrogenation sites. To differentiate between these steps, we have listed them below:

Scheme 1 Various CO₂RR electrochemical steps via CHO* and COH* pathways.

CHO* mediated pathways to methane

Path I: * + CO₂ → COOH* → CO* → CHO* → CH₂O* → CH₃O* → O* + CH₄ → OH* → * (3)

Path II: * + CO₂ → COOH* → CO* → CHO* → CH₂O* → CH₂OH* → CH₂* → CH₃* → CH₄ + * (4)

Path III: * + CO₂ → COOH* → CO* → CHO* → CHOH* → CH₂OH* → CH₂* → CH₃* → CH₄ + * (5)

Path IV * + CO₂ → COOH* → CO* → CHO* → CHOH* → CH* → CH₂* → CH₃* → CH₄ + * (6)

COH* mediated pathways to methane

Path V: * + CO₂ → COOH* → CO* → COH* → C* → CH* → CH₂* → CH₃* → CH₄ + * (7)

Path VI: * + CO₂ → COOH* → CO* → COH* → CHOH* → CH* → CH₂* → CH₃* → CH₄ + * (8)

Path VII: * + CO₂ → COOH* → CO* → COH* → CHOH* → CH₂OH* → CH₂* → CH₃* → CH₄ + * (9)

CHO* mediated pathways to methanol

Path VIII: * + CO₂ → COOH* → CO* → CHO* → CH₂O* → CH₃O* → CH₃OH + * (10)

Path IX: * + CO₂ → COOH* → CO* → CHO* → CH₂O* → CH₂OH* → CH₃OH + * (11)

Path X: * + CO₂ → COOH* → CO* → CHO* → CHOH* → CH₂OH* → CH₃OH + * (12)

COH* mediated pathways to methanol:

Path XI: * + CO₂ → COOH* → CO* → COH* → CHOH* → CH₂OH* → CH₃OH + * (13)

In Table S5 (ESI†), we have shown the adsorption free energies of various adsorbates, and in Fig. 5, we have shown the thermodynamic free energy changes for CHO* and COH* mediated electrochemical steps for CO₂RR on early TMs (Sc–V) nanoclusters. Similar endergonic/exergonic free energy changes for various electrochemical steps on other first-row TM clusters were shown in the ESI† (Fig. S7 and S8). The endergonicity or exergonicity associated with each electrochemical step will decide the thermodynamically favorable reaction pathways and the extent to which a step is preferred over a competing side reaction step which in turn depends on the relative stabilities of the adsorbates. The formation of COOH* is highly exergonic on Sc–V clusters while the formation of CO* from COOH* is mildly exergonic or mildly endergonic on Sc–V clusters. The COH* formation in the third (H⁺ + e⁻) transfer step is a highly disfavored endergonic process whilst the formation of CHO* species is a favorable mildly exergonic process. In a similar way, we can identify the thermodynamical preferences for the formation of other adsorbates such as the preference for the formation of CH₂O* over CHOH from CHO* adsorbates. However, a general trend for the formation of different adsorbates cannot be easily elucidated from these endergonic/exergonic free energy change plots.

Fig. 5 Free energy changes (eV) for various electrochemical steps in the CO₂RR process on Sc, Ti, and V clusters. Step numbers 1–8 show the total number of (H⁺ + e⁻) pairs transferred relative to CO₂.

To facilitate further in-depth insights into CO₂RR on various first-row TM nanoclusters, we have made detailed analyzes of the various reaction pathways (Path I to Path XI) including both CHO* and COH* mediated pathways to methane and methanol formation by examining the thermodynamic free energy changes associated with each electrochemical step. From these thermodynamic free energy changes, we have determined the PDS as well as the free energy changes of the PDS for all these different CHO* and COH* reaction pathways on all nanoclusters which are summarized in Table S6 (ESI†). From all these various CHO* and COH* mediated pathways, we have identified for all nanoclusters, the most preferred CO₂RR reaction route that requires the lowest free energy change of the PDS and are given in Table 2. The preferred CHO* and COH* mediated pathways for CO₂RR on Sc to Cu TM nanoclusters and the free energy change of the PDS are presented in Fig. 6.

Table 2 Lowest energy CO₂RR reaction pathways and the potential-determining step (PDS) on each nanocluster

Lowest energy pathways^a	Clusters	PDS
a CHO* Path I: * + CO2 → COOH* → CO* → CHO* → CH2O* → CH3O* → O* + CH4 → OH* → * CHO* Path II: * + CO2 → COOH* → CO* → CHO* → CH2O* → CH2OH* → CH2* → CH3* → CH4^+; CHO Path III: * + CO2 → COOH* → CO* → CHO* → CHOH* → CH2OH* → CH2* → CH3* →CH4 + *; CHO Path IV: * + CO2 → COOH* → CO* → CHO* → CHOH* → CH* → CH2* → CH3* → CH4 + *; COH* Path V: * + CO2 → COOH* → CO* → COH* → C* → CH* → CH2* → CH3* → CH4 + *; COH* Path VI * + CO2 → COOH* → CO* → COH* → CHOH* → CH* → CH2* → CH3* → CH4 + *; COH* Path VII: * + CO2 → COOH* → CO* → COH* → CHOH* → CH2OH* → CH2* → CH3* → CH4 + *.
CHO* Path I	Co6	CO* → CHO*
	Cu4, Cu6, Cu8 Cu10	CO* → CHO*
CHO* Path II	Sc4–Sc10; Ti3–Ti5, Ti8; V4, V8, V9, Cr5, Cr6, Cr9	CH2O* → CH2OH*
	Cr3, Cr7, Cr10	COOH* → CO*
	Cr4, Cr8	CH2OH* → CH2*
	Mn5, Mn7, Mn10	CH3* → CH4 + *
	Mn8, Fe3, Fe7–Fe10, Co3–Co5, Co7–Co10, Ni3–Ni5, Ni7–Ni9, Cu3, Cu5 Cu7	CO* → CHO*
CHO* Path III	V10, Mn4, Mn9	CHO* → CHOH*
CHO* Path IV	Mn3, Mn6, Cu9	CHO* → CHOH*
COH* Path V	Sc3, Ti6, Ti9, Ti10, V5, V7, Fe5, Ni6, Ni10	CO* → COH*
	V6	CH* → CH2*
COH* Path VI	Ti7, V3, Fe4	CO* → COH*
COH* Path VII	Fe6	CO* → COH*

---

Fig. 6 The lowest energy pathways for CO₂RR on first-row TM nanoclusters (Sc–Cu). The free energy change of the PDS for CO₂RR were shown in each bar. The blue and red bars represent the CHO* and COH* mediated pathways, respectively. The limiting potential values corresponds to the negative of the free energy change of the PDS in Volts (V). See Table 2 for the PDS for various nanoclusters.

From thermodynamic free energy changes associated with CO* → CHO* and CO* → COH* steps, we have found in general that the formation of COH* adsorbate from CO* in the third (H⁺ + e⁻) pair transfer step is greatly disfavored on first-row TM clusters compared to the formation of the CHO* adsorbates. Similarly, we have identified general preferences that CHO* on the fourth electrochemical step prefers CH₂O* adsorbate (CHO* → CH₂O* vs. CHOH); CH₂O* on the fifth electrochemical step prefers CH₃O* adsorbate (CH₂O* → CH₃O* vs CH₂OH), and CH₃O* on the six electrochemical steps prefers the formation of CH₄ (CH₃O* → O* + CH₄ vs CH₃OH). This gives the impression that the CO₂RR prefers to proceed through CHO* Path I (CHO* → CH₂O* → CH₃O* → CH₄ + O* → OH* → *) as in the case of CHO* Path I reported for CO₂RR on Cu surface by Nørskov and co-workers.⁵⁰ However, we have noticed that the removal of the OH* species (OH* → * + H₂O) in the eight (H⁺ + e⁻) electrochemical step (Fig. 7) is an uphill process that requires significantly larger endergonic free energy changes and is the PDS for the formation of CH₄via CHO* Path I on all first-row TM nanoclusters except on Co₆ and Cu clusters with even-numbered cluster configurations (Cu₄, Cu₆, Cu₈, and Cu₁₀) for which CO* → CHO* is the PDS for CHO* Path I. Due to the larger endergonicity associated with the OH* removal step, CHO* Path I is not a preferred reaction route except on these five nanoclusters (Co₆, Cu₄, Cu₆, Cu₈, and Cu₁₀).

Fig. 7 Free energy change (ΔG, eV) for the OH* removal step (OH* → * + H₂O) in the CHO* mediated Path I.

Further detailed investigations on various reaction pathways reveal that alternative pathways via CHO* Paths II to IV and COH* Paths V to VII can lead to CH₄ without passing through the highly endergonic OH* removal step. We have found that CHO* Path II is the lowest energy pathway for CO₂RR on a majority of the clusters (Table 2). Clusters Co₆, Cu₄, Cu₆, Cu₈, and Cu₁₀ prefer CHO* Path I; V₁₀, Mn₄, and Mn₉ prefer CHO* Path III; Mn₃, Mn₆, and Cu₉ prefer CHO* Path IV; Sc₃, Ti₆, Ti₉, T₁₀, V₅, V₆, V₇, Fe₅, Ni₆, and Ni₁₀ prefers COH* Path V; Ti₇, V₃ and Fe₄ COH* Path VI; and Fe₆ prefers COH* Path VII (Table 2). With a few exceptions, we have found in general that the electrochemical step CO* → CHO* is the PDS on first-row TM nanoclusters from Fe to Cu for the CHO* Path II. For early TM nanoclusters Sc, Ti, and V, we have found that the electrochemical step for the formation of CH₂OH* adsorbate from the CH₂O* (CH₂O* → CH₂OH*) is the PDS for CHO* Path II. For the clusters that exhibit CHO* Path I as the preferred reaction route, CO* → CHO* is the PDS as in the case of the reported work of Nørskov, and co-workers⁵⁰ on Cu metal surface. For clusters that prefer CHO* Paths III and IV, the electrochemical step CHO* → CHOH* is the PDS. With a single exception on V₆, CO* → COH* is the PDS on all the clusters that prefer COH* mediated pathways. The limiting potential for a reaction pathway is determined by the electrochemical step with the largest endergonic free energy change in that pathway which is directly related to the relative stabilities of the adsorbates for the PDS step. It should be noted that some nanoclusters undergo geometrical rearrangement on binding with adsorbates and the energetic cost associated with these structural arrangements is a major factor that decides the thermodynamic stabilities of the adsorbates. Most importantly, we have found that all the preferred lowest energy pathway for all first-row TM nanoclusters leads exclusively to the formation of CH₄ and none of them prefers the exclusive formation of methanol. The methanol vs. methane selectivity depends on two electrochemical steps: the preference for the formation of CH₃OH or CH₂* from CH₂OH* adsorbate and the preference for the formation of CH₃OH or CH₄ + O* from CH₃O* adsorbate. We have found a greater preference for CH₂OH* → CH₂* and CH₃O* → CH₄ +O* paths on all nanoclusters which eventually leads to the formation of CH₄. Moreover, it is evident from Table S6 (ESI†) that although COH* mediated pathways are preferred on some of the nanocluster surfaces, there is strong competition from the CHO* mediated pathways as free energy changes of the PDS for CHO* pathways do not show any significant differences from the free energy changes of the PDS for COH* mediated pathways on these nanoclusters. A further detailed discussion of the CO₂RR on all the first-row TMs is given below:

(i) CO₂RR on early first-row TM nanoclusters (Sc, Ti, and V). Sc nanoclusters exhibit a much greater stabilization of adsorbates than other transition metals in the first row. Both Sc and Ti clusters show a preference for the CHO* mediated Path II of CO₂RR, with the PDS being the formation of CH₂OH* from CH₂O*. The COH* mediated Path V is slightly preferred over Path II on Sc₃, with the PDS being the conversion of CO* to COH*. The limiting potentials on Sc clusters falls between −1.34 V to −1.53 V and −0.61 V to −0.95 V on Ti clusters, with Ti₆ having the lowest potential. The limiting potential values on vanadium clusters significantly reduced to −0.35 V to −0.64 V compared to the limiting potentials on Sc and Ti clusters. V₄ exhibits the lowest limiting potential on vanadium clusters with a limiting potential of −0.35 V. CHO* mediated pathways were favored on V₄ and V₈–V₁₀ clusters and COH* mediated pathways were favored on V₃ and V₅–V₇ clusters. The PDS of all the different pathways are listed in Table 2.

Although CO₂RR on some of the Ti and V clusters as well on Sc₃ prefer to proceed through COH* intermediate, the limiting potentials for the CHO* and COH* pathways differ by only 0.10 eV on most of these clusters, and hence, both these pathways are possible for CO₂RR. The relative preference for the various reaction routes depends on the stability of the adsorbate-bound complexes which in turn depends on the geometry rearrangement of the cluster moieties from their global minimum configurations on binding with adsorbate species. For example, the cluster moiety V₈ in the COH*–V₈ shows significant changes from its global minimum configuration and the energetic cost associated with the reorganization of the cluster moiety on adsorbate binding leads to the lower thermodynamic stability of the COH* adsorbates which in turn results in a highly disfavored endergonic uphill process for the formation of COH* species from CO*.

(ii) CO₂RR on mid first-row TM nanoclusters (Cr, Mn, and Fe). The CO₂RR on all Cr clusters prefers to proceed through the CHO* Path II with relatively smaller limiting potentials in the range of −0.18 V to −0.56 V with Cr₇ having the lowest limiting potential followed by Cr₁₀ (−0.29 V). Similar to Cr clusters, Mn clusters prefer CHO* mediated reaction pathways for CO₂ electroreduction with Mn₅ having the lowest limiting potential value of −0.21 V. The competing COH* mediated pathways were greatly disfavored on Cr and Mn clusters owing to the larger endergonicity associated with the PDS CO* → COH*. There is no specific preference for a particular CHO* path and the PDS varies depending on the stability of the different intermediates on different Cr and Mn clusters and are listed in Table 2. Iron clusters exhibit a general preference for CHO* Path II with the electrochemical step CO* → CHO* as the PDS. Fe₄, Fe₅, and Fe₆ clusters prefer both CHO* and COH* mediated pathways due to similar endergonic free energy changes associated with the PDS CO* → CHO* and CO* → COH*. The limiting potentials fall in the range of −0.37 V to −0.55 V on all Fe clusters except on Fe₆ which shows a limiting potential value of −0.75 V.

(iii) CO₂RR on late first-row TM nanoclusters (Co, Ni, and Cu). The CHO* Path II is the preferred CO₂RR on cobalt clusters except on Co₆ with limiting potential in the range of −0.44 V to −0.80 V with CO* → CHO* as the PDS step. Co₆ prefers CHO* Path I due to the lower endergonicity associated with the removal of OH* adsorbate from the cluster surface. The CO₂RR on cobalt clusters greatly disfavored the COH* mediated pathway owing to the larger endergonicity associated with the electrochemical step CO* → COH* which is in the range of ∼1 eV. Nickel clusters in general exhibit a greater preference for CHO* Path II with CO* → CHO* as the PDS. The limiting potential values ranges from −0.60 V to −0.86 V. However, on most of the Ni clusters, the stabilities of the CHO* and COH* adsorbates do not show any significant difference, and hence, both these reaction routes are possible on Ni clusters.

Copper clusters with even-number composition (Cu₄, Cu₆, Cu₈, and Cu₁₀) prefer the CO₂RR via CHO* Path I with significantly larger limiting potential (−0.75 V to −1.10 V); the lowest limiting potential is exhibited by Cu₁₀. On the other hand, clusters with odd-number compositions Cu₃, Cu₅, and Cu₇ prefer the reaction path CHO* Path II, and Cu₉ prefers the reaction CHO* Path IV with relatively smaller limiting potentials (−0.36 V to −0.50 V). COH* pathways are greatly disfavored on all Cu clusters due to the larger endergonic free energy change (>1.1 eV) associated with the PDS CO* → COH*. The CHO* Path I is not favored on clusters with odd-number compositions due to the larger endergonicity (>1 eV) associated with the OH* removal step. It should be noted that CHO* Path I is the lower energy route proposed by Nørskov and co-workers for the formation of CH₄ on the Cu surface with a limiting potential of −0.74 V for the key step CO* → CHO*.⁵⁰ In a previous work, we have reported detailed studies on the alternating nature of endergonicity and exergonicity associated with various electrochemical steps on Cu clusters with odd- and even-number compositions (Cu₃–Cu₆) as well as the relationship between the free energy changes with the spin state and HOMO–LUMO gap of the Cu adsorbates using ωB97XD density functional and a localized atomic orbital basis set.⁵⁷ Although the present work shows some discrepancies in the free energy values which is acceptable due to the usage of different DFT functional and basis set, in general, the overall trend and conclusions remain intact. The Cu₁₀ shows a limiting potential of −0.75 V, a value that is very close to the limiting potential on the Cu surface by Nørskov and co-workers.⁵⁰ This implies that clusters with a greater number of atoms with even number composition resemble more close to the Cu surface.

In short, we have seen stronger binding affinity for all the adsorbates on early TM nanoclusters and a general trend of reduced binding affinity across the first-row TM nanoclusters from Sc to Cu with the highest adsorption free energies on Sc and lowest on Cu. Among the differently sized nanoclusters of the same clusters, the adsorption free energies do not exhibit significant deviation as most of the adsorption free energies fall within a range of 0.3–0.5 eV of the average adsorption energies for that particular metal nanocluster. Still, we have noticed that clusters with smaller numbers of atoms, especially three or four atoms exhibit somewhat larger deviations in adsorption free energies compared to cluster compositions with larger numbers of metal atoms. It should be noted that we should also need to consider the energetic cost associated with the rearrangement of cluster atoms from their global minimum configurations on binding with adsorbates while discussing the endergonicity/exergonicity associated with each electrochemical step. All metal nanoclusters except Cu show a range of spin states for different adsorbates. However, we could not find a direct relationship between the adsorption free energies and hence, endergonicity/exergonicity associated with each electrochemical step with the spin-states of the various adsorbates. On the contrary, adsorbates on Cu nanoclusters exhibit alternating exergonicity and endergonicity based on the spin-state of the adsorbates. Similarly, we could not find a direct link between the endergonicity/exergonicity associated with each electrochemical step and the HOMO–LUMO gap for adsorbates on all nanoclusters except on Cu. On Cu clusters, the proton–electron pair transfers to singlet adsorbates to form doublet adsorbates are considerably higher endergonic step due to the larger HOMO–LUMO gap on singlet adsorbates and vice versa. We have also established that although CO₂RR can proceed through various CHO* and COH* mediated pathways, all these pathways lead to the formation of methane on all first-row TM nanoclusters.

Competition between CO, HCOOH, and H₂ formations

Based on the free energy change of the PDS values for CO₂RR, we have identified several nanoclusters that can reduce CO₂ to CH₄ with relatively lower limiting potential values (i.e., the negative potential that should be applied to make all the electrochemical steps exergonic which corresponds to the free energy change of the PDS). Cr₇ exhibits the lowest free energy change of the PDS with a value of 0.18 eV (i.e., the limiting potential value is −0.18 V) followed closely by the Mn₇ cluster with a limiting potential value of −0.21 V. Nanoclusters Cr₁₀, Cr₅, Cr₉, V₄, Cu₅, Fe₄, Fe₃, and Fe₁₀ shows relatively lower limiting potentials in the range of −0.29 V to −0.39 V, and clusters Cr₆, Cu₉, Co₃, V₅, Cr₈, Cu₃, Fe₈, Fe₇, Mn₈, Cu₇, and Mn₄ exhibits limiting potentials in the range of −0.40 V to −0.50 V. We have found in general that nanoclusters of mid-transition metals i.e., Cr, Mn, and Fe exhibit relatively lower limiting potential values for CO₂RR to methane.

One of the major hindrances in CO₂ electroreduction to higher-order reduction products such as methane or methanol is the formation of two-electron reduction products such as CO, HCOOH, and H₂. The COOH* species can either release free formic acid (HCOOH) by hydrogenating the C atom of the COOH* species or CO* by eliminating a water molecule by hydrogenating the O atom of the COOH* species in the second (H⁺ + e⁻) transfer step. One of the major drawbacks of CO₂RR on metal surfaces is the weak adsorption of CO and its subsequent escape from the surface through an easier desorption process. Due to the availability of the unsaturated coordinate sites, CO is chemisorbed on nanoclusters and hence the desorption requires the breaking of much stronger metal–CO bonds resulting in significantly larger desorption energies as evident from Fig. 8(a). Among all the metal clusters, Cr₃ (0.32 eV) shows the smallest CO desorption energy. Cu clusters Cu₇–Cu₁₀ also show relatively smaller CO desorption energies around 0.5–0.6 eV. Since CO desorption is a thermodynamically disfavored process on all the metal clusters, the CO* adsorbates are readily available for further reduction steps and may lead to the formation of higher-order reduction products such as methane.

Fig. 8 (a) Free energy changes (ΔG, eV) for CO desorption and HCOOH formation in the second (H⁺ + e⁻) transfer step; (b) free energy changes (ΔG, eV) of the PDS for CO₂RR and HER and (c) relative free energy changes of PDS for CO₂RR and HER (ΔG(CO₂RR-HER), eV) on various first-row TM nanoclusters.

Except on Cu clusters with even-number atom composition (Cu₄, Cu₆, Cu₈, and Cu₁₀), the release of formic acid in the second (H⁺ + e⁻) transfer step on all other nanoclusters requires significantly higher endergonic free energy changes (>0.8 eV) (Fig. 8(a)). This implies that COOH* species cannot be easily desorbed from the nanocluster surface as free formic acid and hence, COOH* is available on the nanocluster surface for further reduction steps. Of the Cu clusters with even-number atom compositions, Cu₈ shows the lowest endergonic free energy change (0.17 eV) for formic acid release while Cu₄, Cu₆, and Cu₁₀ show a relatively larger endergonic free change in the range of 0.44 eV to 0.55 eV. In short, we can see that the release of formic acid from the nanocluster surfaces is not an easy step except on Cu₈ and the COOH* species is available for further reduction steps.

The competing hydrogen evolution reaction (HER) is another major challenge that hinders the efficacy of the CO₂ electroreduction catalysts. An efficient catalyst should be able to suppress the competing HER side reaction. The free energy change of the PDS for HER reaction on various nanoclusters were shown in Fig. 8(b) along with the free energy change of the PDS for CO₂RR. To get a clear idea of the relative preference for CO₂RR versus HER, we have plotted the difference in the free energy changes of the PDS for CO₂RR and HER in Fig. 8(c). An endergonic (positive) free energy difference means HER happens before CO₂RR and an exergonic (negative) free energy difference means CO₂RR happens before HER. It can be seen that there are only a few nanoclusters that favor CO₂RR over HER. From the PDS difference plot, it can be seen that HER is greatly favored on Sc clusters as the limiting potential for CO₂RR is significantly larger compared to HER and at the applied limiting potential for CO₂RR, the HER triggers first. On most of the nanocluster surfaces, the hydrogen absorption (* + (H⁺ + e⁻) → H*) is weak and the adsorbed hydrogen can be easily released leading to higher HER evolution at much lower limiting potentials. Still, we have identified a number of nanoclusters such as Ti₆, V₅, V₆, Mn₄, Mn₇, Mn₁₀, Fe₄, Fe₈, Fe₁₀, Ni₄, and Cu₅ as possible electrocatalysts which show a preference for CO₂RR over HER by 0.2 eV or more.

Linear scaling relationships for CO₂RR on first-row TM nanoclusters

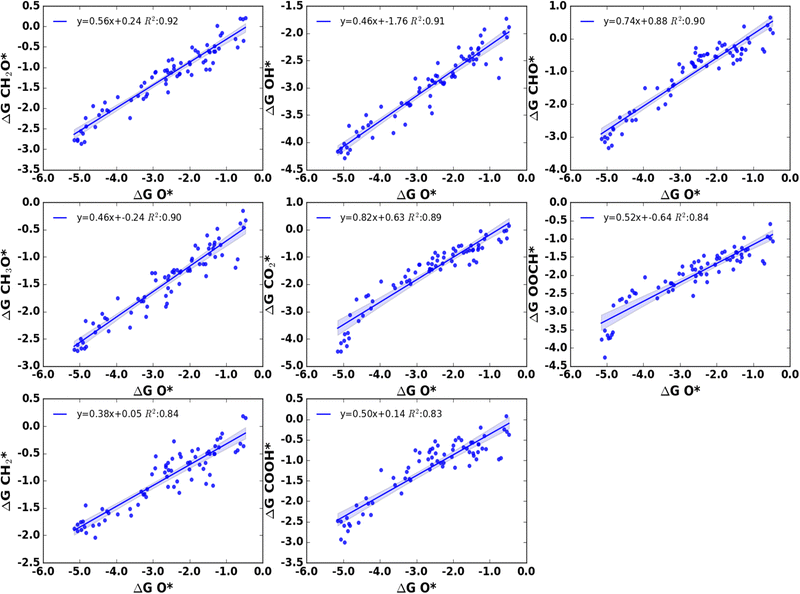
Linear scaling relationships which relate the binding energies of chemically related adsorbates across different catalytic surfaces have been successfully applied to understand the reactivity trends across a vast material space. We have investigated whether there exists a linear scaling relationship using our data on adsorption free energies on Sc to Cu first-row TM nanoclusters. In Fig. 9, we have shown the linear free energy relation between CO₂* adsorption free energies and adsorption free energies of other adsorbates with coefficient determination (R²) values higher than 0.80. We have found a strong correlation between the adsorption free energies of CO₂* with the adsorption free energies of COOH*, OOCH*, CHO*, CH₂O*, O*, CO*, OH*, and CH₃O* with coefficient determination (R²) values larger than 0.85. In all these cluster-adsorbate complexes except on O*, OH*, and CH₃O*, both the C and O can take part in the bonding process with the metal cluster moiety. In general, we have noticed that the binding free energies for adsorbates that can bind through both C and O atoms show an excellent correlation with the binding free energies of CO₂*. A single O atom is the sole binding motif for three adsorbates O*, OH*, and CH₃O* and a high correlation for the adsorption free energies of these three adsorbates with CO₂* adsorption energies implies that binding through O determines the extent of correlation with CO₂* adsorption energies. Adsorption free energies of other adsorbates CHOH*, CH₂*, and C* also exhibit relatively higher correlations with the adsorption free energies of CO₂* adsorbate with R² values in the range of 0.80–0.82 eV. Moreover, we have found that COH*and CH₂OH* adsorption free energies do not exhibit a significant correlation with CO₂* adsorption free energies. In these adsorbates along with CHOH*, the O atom is not readily available for binding and the primary binding motif is the C atom. This implies a higher correlation above 0.85 with CO₂* adsorption free energies are possible only for adsorbates that can bind through the O atom.

Fig. 9 Liner scaling relationship between adsorption free energies of CO₂* and various adsorbates with the coefficient of determination (R²) value ≥0.80.

Fig. 10 and 11 show the linear scaling relationships between O* and C* adsorbates. We have seen that the adsorption energies of O* correlate very well with the adsorption energies of CH₂O*, OH*, CHO*, CH₃O*, and CO₂* with R² values in the range of 0.89 to 0.92. In addition, adsorption free energies of CH₂*, OOCH*, and COOH* also exhibit relatively better correlations (R² = 0.83–0.84) with O* adsorption free energies. All these adsorbates except CH₂* species can bind on the nanoclusters through the O atom. It should be noted that CH₂O* and CHO* which are often considered as C-bound adsorbates on metal surfaces for linear scaling relation studies, show a significantly larger correlation with O* adsorption energies on nanoclusters. Surprisingly, we have found the adsorption free energies of CH₂* adsorbate correlates relatively well with the adsorption free energies of O* with an R² value of 0.84. All other adsorbates including CO*, COH*, CHOH*, and CH₂OH* do not correlate well with O* in their linear free energy relationship (Table S4, ESI†). It should be noted that a free O is unavailable to participate in bonding with the metal clusters for COH*, CHOH*, and CH₂OH*. CO* adsorbates although use its two binding motifs C and O atoms for binding on some of the nanoclusters especially for early first-row TMs, it mostly uses the C atom for bonding on cluster moieties, and a lower correlation in the linear free energy relationship can be attributed to this observation. This argument is further supported by the fact that a higher correlation (R² = 0.80) exists between the adsorption free energies of CO* and C*.

Fig. 10 Liner scaling relationship between adsorption free energies of O* and various adsorbates with the coefficient of determination (R²) value ≥0.80.

Fig. 11 Liner scaling relationship between adsorption free energies of C* and various adsorbates with the coefficient of determination (R²) value ≥0.80.

The adsorption free energies of C* show a better linear scaling relationship with the adsorption free energies of CH* with an R² value of 0.85. In addition, C* shows a relatively better correlation with CO*, COH*, CH₂O*, CHOH*, CO₂* and CHO* within a range of R² value of 0.80–0.82 in their free energy relationship. Of these adsorbates, COH* and CHOH* do not have a free O atom that can take part in binding on nanoclusters and their predominant binding motif is the C atom, and the CO* adsorbate as discussed above binding through the C atom on most of the nanoclusters. Other adsorbates CH₂O*, CO₂*, and CHO* are bidentate which can use C and/or O atoms for binding on nanoclusters.

Although there are exceptions, in general, we have found that the adsorption energies of adsorbates that contain O atom which can participate in bonding interactions with cluster moiety show a higher correlation with adsorption free energies of CO₂* or O* compared to that of C* adsorbates. C* adsorption energies exhibit a relatively better correlation with species that use the C atom as the main binding motif such as COH*, CHOH*, and CO*. We have found that the linear scaling relationship that exists in heterogeneous catalysts such as the correlation between the adsorption energies of AH_x with the adsorption energies of atom A (A = C, N, O, S, etc.) breaks on nanocluster surfaces if the adsorbate has more than one atom that can act as a binding motif on nanoclusters. Some discrepancies in the linear scaling relationship were expected due to the scattering of the adsorption energies around the linear relationships. The scattering of the adsorption energies primarily arises from the differences in the adsorption sites on nanoclusters and the relative stabilities of the different adsorbates.

Conclusions

We have investigated the CO₂RR activity and selectivity on first-row TM nanoclusters (Sc–Cu) containing 3 to 10 atoms. The global minimum configurations of all the nanoclusters were determined using the GIGA version of the birmingham parallel genetic algorithm (BPGA). We have also determined the best adsorbate binding positions for various CO₂RR adsorbates on nanoclusters. The adsorption free energies for all the adsorbates, in general, show a trend of decreasing while moving across the first-row TMs from Sc to Cu. For some of the adsorbates, we have found a strong correlation between the adsorption free energies and residual charges on the adsorbates. We have found that CHO* mediated pathways are preferred, in general, over COH* mediated pathways for CH₄ production. Due to the larger endergonicity associated with the OH* removal step for the CHO* Path I: * + CO₂ → COOH* → CO* → CHO* → CH₂O* → CH₃O* → O* + CH₄ → OH* → *, CO₂RR via this reaction pathway is greatly disfavored on all nanoclusters except on Cu clusters containing even number of atom compositions. We have identified an alternative lowest reaction route via CHO* Path II: * + CO₂ → COOH* → CO* → CHO* → CH₂O* → CH₂OH* → CH₂* → CH₃* → CH₄ + * which can proceed to CH₄ without passing through the highly endergonic OH* removal step on most of the clusters. With a limited number of exceptions, for the reaction route via CHO* Path II, the potential-determining step is the formation of CH₂OH* from CH₂O* (CH₂O* → CH₂OH*) on most of the Sc to Mn nanoclusters whilst the potential-determining step for the CHO* Path II is the formation of CHO* intermediate from CO* (CO* → CHO*) on Fe to Cu nanoclusters. Moreover, Cu clusters with even numbers of cluster atom compositions prefer the reaction route via CHO* Path I with CO* → CHO* as the potential-determining step, similar to the reported work of Nørskov and co-workers on Cu metal surfaces.⁵⁰ On many metal nanoclusters, we have found that COH* mediated pathways can compete with CHO* Path II. Unlike CHO* mediated pathways, we have not found a preference for any particular COH* pathway and the potential-determining step varies depending on the relative stabilities of different adsorbates and the free energy changes associated with various electrochemical steps for their formation. Our studies on CH₄ vs CH₃OH selectivity establish that methanol formation is greatly disfavored on all nanoclusters irrespective of which is the preferred CO₂RR reaction pathway (CHO* or COH* mediated pathway) on all nanoclusters. Most importantly, the formation of side reaction products CO and HCOOH is greatly suppressed on all nanoclusters due to the high endergonicity associated with the release of CO and HCOOH from the nanocluster surface. Moreover, unlike on metal surfaces where CO is weakly bound to the catalyst surface, the availability of the uncoordinated binding sites on nanoclusters allows the chemisorption of CO on the cluster surface. Desorption of CO from the nanocluster surfaces is often a high endergonic step as it requires the breaking of strong metal–CO bonds and hence, these CO* species are readily available for further reduction steps leading to the formation of higher-order reduction product, methane. We have found that several nanoclusters Cr₁₀, Cr₅, Cr₉, V₄, Cu₅, Fe₄, Fe₃, Fe₁₀, C_r6, Cu₉, Co₃, V₅, Cr₈, Cu₃, Fe₈, Fe₇, Mn₈, Cu₇, and Mn₄ exhibit relatively lower limiting potential values and can be considered as a potential nanocluster-based electrocatalysts for CO₂RR for methane formation. We have also compared the limiting potentials for CO₂RR and HER and found that HER triggers at much lower potentials on most of the nanocluster surface. Still, we have identified a number of nanoclusters (Ti₆, V₅, V₆, Mn₄, Mn₇, Mn₁₀, Fe₄, Fe₈, Fe₁₀, Ni₄, and Cu₅) as possible electrocatalysts which show a preference for CO₂RR over HER by 0.2 eV or more.

We have also tried to establish a linear scaling relationship on nanoclusters based on adsorption free energies of CO₂*, C*, and O*. With few exceptions, we have found in general that the adsorption free energies of adsorbates that can bind through O atom on the nanoclusters show a higher correlation with the adsorption free energies of CO₂* or O* compared to that of C* adsorbates. On the other hand, the adsorption energies of C* adsorbates show a higher level of correlation with the adsorption energies of COH*, CH₂OH*, CHOH*, and CO* adsorbates whose O atoms are not readily available for binding on nanocluster surfaces. A breaking of scaling relationships that exits on heterogeneous catalysts such as the correlation between the adsorption energies of AH_x with the adsorption energies of atom A (A = C, N, O, S, etc.) was observed for adsorbates that can bind on nanocluster through more than one atom such as CH₂O*.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

RKR would like to thank the IT Research Computing group at the Texas A&M University at Qatar and the University of Birmingham's BlueBEAR HPC facility (http://www.bear.bham.ac.uk/bluebear) for providing computational resources and support. RKR acknowledges the UK's national HPC Facility, ARCHER, via membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431). RKR acknowledges Prof. Richard Catlow, Cardiff University for his valuable suggestions and comments on the work. ENB acknowledges that this publication was made possible by National Priorities Research Program (NPRP) Grant NPRP11S-0116-180320 from the Qatar National Research Fund (a member of Qatar Foundation) and the use of computational resources at Texas A&M University at Qatar (TAMUQ).

References

1. D. D. Zhu, J. L. Liu and S. Z. Qiao, Recent Advances in Inorganic Heterogeneous Electrocatalysts for Reduction of Carbon Dioxide, Adv. Mater., 2016, 28(18), 3423–3452,  DOI:10.1002/adma.201504766.
2. J. Eppinger and K. W. Huang, Formic Acid as a Hydrogen Energy Carrier, ACS Energy Lett., 2017, 2(1), 188–195,  DOI:10.1021/acsenergylett.6b00574.
3. G. A. Olah, Beyond Oil and Gas: The Methanol Economy, Angew. Chem., Int. Ed., 2005, 44, 2636,  DOI:10.1002/anie.200462121.
4. S. Sun, H. Sun, P. T. Williams and C. Wu, Recent Advances in Integrated CO₂ capture and Utilization: A Review, Sustainable Energy Fuels, 2021, 5(18), 4546–4559,  10.1039/d1se00797a.
5. S. Saeidi, N. A. S. Amin and M. R. Rahimpour, Hydrogenation of CO₂ to Value-Added Products—A Review and Potential Future Developments, J. CO2 Util., 2014, 5, 66–81,  DOI:10.1016/j.jcou.2013.12.005.
6. S. G. Jadhav, P. D. Vaidya, B. M. Bhanage and J. B. Joshi, Catalytic Carbon Dioxide Hydrogenation to Methanol: A Review of Recent Studies, Chem. Eng. Res. Des., 2014, 92, 2557–2567,  DOI:10.1016/j.cherd.2014.03.005.
7. I. Sullivan, A. Goryachev, I. A. Digdaya, X. Li, H. A. Atwater, D. A. Vermaas and C. Xiang, Coupling Electrochemical CO₂ Conversion with CO₂ Capture, Nat. Catal., 2021, 4(11), 952–958,  DOI:10.1038/s41929-021-00699-7.
8. L. Rotundo, R. Gobetto and C. Nervi, Electrochemical CO₂ Reduction with Earth-Abundant Metal Catalysts, Curr. Opin. Green Sustain. Chem., 2021, 31,  DOI:10.1016/j.cogsc.2021.100509.
9. Y. Xue, Y. Guo, H. Cui and Z. Zhou, Catalyst Design for Electrochemical Reduction of CO₂ to Multicarbon Products, Small Methods, 2021, 5(10), 2100736,  DOI:10.1002/smtd.202100736.
10. F. Liang, K. Zhang, L. Zhang, Y. Zhang, Y. Lei and X. Sun, Recent Development of Electrocatalytic CO₂ Reduction Application to Energy Conversion, Small, 2021, 17(44), 2100323,  DOI:10.1002/smll.202100323.
11. D. T. Whipple and P. J. A. Kenis, Prospects of CO₂ Utilization via Direct Heterogeneous Electrochemical Reduction, J. Phys. Chem. Lett., 2010, 1(24), 3451–3458,  DOI:10.1021/jz1012627.
12. M. Gattrell, N. Gupta and A. Co, A Review of the Aqueous Electrochemical Reduction of CO₂ to Hydrocarbons at Copper, J. Electroanal. Chem., 2006, 1–19,  DOI:10.1016/j.jelechem.2006.05.013.
13. Y. Hori, A. Murata and R. Takahashi, Formation of Hydrocarbons in the Electrochemical Reduction of Carbon Dioxide at a Copper Electrode in Aqueous Solution, J. Chem. Soc., Faraday Trans. 1, 1989, 85(8), 2309–2326.
14. D. Astruc, Introduction: Nanoparticles in Catalysis, Chem. Rev., 2020, 120(2), 461–463,  DOI:10.1021/acs.chemrev.8b00696.
15. E. C. Tyo and S. Vajda, Catalysis by Clusters with Precise Numbers of Atoms, Nat. Nanotechnol., 2015, 10(7), 577–588,  DOI:10.1038/NNANO.2015.140.
16. I. Chakraborty and T. Pradeep, Atomically Precise Clusters of Noble Metals: Emerging Link between Atoms and Nanoparticles, Chem. Rev., 2017, 117(12), 8208–8271,  DOI:10.1021/acs.chemrev.6b00769.
17. F. Li, D. R. MacFarlane and J. Zhang, Recent Advances in the Nanoengineering of Electrocatalysts for CO₂ Reduction, Nanoscale, 2018, 10(14), 6235–6260,  10.1039/c7nr09620h.
18. Y. Dai, Y. Wang, B. Liu and Y. Yang, Metallic Nanocatalysis: An Accelerating Seamless Integration with Nanotechnology, Small, 2015, 11(3), 268–289,  DOI:10.1002/smll.201400847.
19. L. Liu and A. Corma, Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles, Chem. Rev., 2018, 118(10), 4981–5079,  DOI:10.1021/acs.chemrev.7b00776.
20. A. Munir, K. S. Joya, T. Ul haq, N. U. A. Babar, S. Z. Hussain, A. Qurashi, N. Ullah and I. Hussain, Metal Nanoclusters: New Paradigm in Catalysis for Water Splitting, Solar and Chemical Energy Conversion, ChemSusChem, 2019, 12(8), 1517–1548,  DOI:10.1002/cssc.201802069.
21. M. Jia, C. Choi, T.-S. Wu, C. Ma, P. Kang, H. Tao, Q. Fan, S. Hong, S. Liu, Y.-L. Soo, J. Qiu and Z. Sun, Carbon-Supported Ni Nanoparticles for Efficient CO₂ Electroreduction, Chem. Sci., 2018, 9(47), 8775–8780,  10.1039/c8sc03732a.
22. J. Wei, H.-L. Ya, S.-N. Qin, H. Zhang, Z.-Q. Tian and J.-F. Li, Efficient CO₂ Electroreduction on Pd-Based Core–Shell Nanostructure with Tensile Strain, J. Electroanal. Chem., 2021, 896,  DOI:10.1016/j.jelechem.2021.115205.
23. G. Hwa Jeong, Y. Chuan Tan, J. Tae Song, G.-Y. Lee, H. Jin Lee, J. Lim, H. Young Jeong, S. Won, J. Oh and S. Ouk Kim, Synthetic Multiscale Design of Nanostructured Ni Single Atom Catalyst for Superior CO₂ Electroreduction, Chem. Eng. J., 2021, 426, 131063,  DOI:10.1016/j.cej.2021.131063.
24. L.-B. Zhang, T. Tang, J. Fu, S. Niu, C. He, J.-S. Hu and L.-J. Wan, Molecular Linking Stabilizes Bi Nanoparticles for Efficient Electrochemical Carbon Dioxide Reduction, J. Phys. Chem. C, 2021, 125(23), 12699–12706,  DOI:10.1021/acs.jpcc.1c03790.
25. Y.-B. Chang, C. Zhang, X.-L. Lu, W. Zhang and T.-B. Lu, Graphdiyene Enables Ultrafine Cu Nanoparticles to Selectively Reduce CO₂ to C²⁺ Products, Nano Res., 2022, 15(1), 195–201,  DOI:10.1007/s12274-021-3456-2.
26. Z. Zhu, Z. Li, X. Wei, J. Wang, S. Xiao, R. Li, R. Wu and J. S. Chen, Achieving Efficient Electroreduction of CO₂ to CO in a Wide Potential Window by Encapsulating Ni Nanoparticles in N-Doped Carbon Nanotubes, Carbon N. Y, 2021, 185, 9–16,  DOI:10.1016/j.carbon.2021.08.072.
27. Y. Li, C. Chen, R. Cao, Z. Pan, H. He and K. Zhou, Dual-Atom Ag₂/Graphene Catalyst for Efficient Electroreduction of CO₂ to CO, Appl. Catal., B, 2020, 268,  DOI:10.1016/j.apcatb.2020.118747.
28. X. Ma, J. Tian, M. Wang, M. Shen and L. Zhang, Polymeric Carbon Nitride Supported Bi Nanoparticles as Highly Efficient CO₂ Reduction Electrocatalyst in a Wide Potential Range, J. Colloid Interface Sci., 2022, 608, 1676–1684,  DOI:10.1016/j.jcis.2021.10.049.
29. Q. He, J. H. Lee, D. Liu, Y. Liu, Z. Lin, Z. Xie, S. Hwang, S. Kattel, L. Song and J. G. Chen, Accelerating CO₂ Electroreduction to CO Over Pd Single-Atom Catalyst, Adv. Funct. Mater., 2020, 30(17), 2000407,  DOI:10.1002/adfm.202000407.
30. B. Ávila-Bolívar, V. Montiel and J. Solla-Gullón, On the Activity and Stability of Sb₂O₃/Sb Nanoparticles for the Electroreduction of CO₂ toward Formate, J. Electroanal. Chem., 2021, 895,  DOI:10.1016/j.jelechem.2021.115440.
31. W. Zheng, C. Guo, J. Yang, F. He, B. Yang, Z. Li, L. Lei, J. Xiao, G. Wu and Y. Hou, Highly Active Metallic Nickel Sites Confined in N-Doped Carbon Nanotubes toward Significantly Enhanced Activity of CO₂ Electroreduction, Carbon N. Y, 2019, 150, 52–59,  DOI:10.1016/j.carbon.2019.04.112.
32. Y.-X. Duan, K.-H. Liu, Q. Zhang, J.-M. Yan and Q. Jiang, Efficient CO₂ Reduction to HCOOH with High Selectivity and Energy Efficiency over Bi/RGO Catalyst, Small Methods, 2020, 4(5), 1900846,  DOI:10.1002/smtd.201900846.
33. D. R. Kauffman, D. Alfonso, C. Matranga, P. Ohodnicki, X. Deng, R. C. Siva, C. Zeng and R. Jin, Probing Active Site Chemistry with Differently Charged Au₂₅^q Nanoclusters (q = −1, 0, +1), Chem. Sci., 2014, 5(8), 3151,  10.1039/c4sc00997e.
34. C. Zhao, X. Dai, T. Yao, W. Chen, X. Wang, J. Wang, J. Yang, S. Wei, Y. Wu and Y. Li, Ionic Exchange of Metal–Organic Frameworks to Access Single Nickel Sites for Efficient Electroreduction of CO₂, J. Am. Chem. Soc., 2017, 139(24), 8078–8081,  DOI:10.1021/jacs.7b02736.
35. C. Kim, H. S. Jeon, T. Eom, M. S. Jee, H. Kim, C. M. Friend, B. K. Min and Y. J. Hwang, Achieving Selective and Efficient Electrocatalytic Activity for CO₂ Reduction Using Immobilized Silver Nanoparticles, J. Am. Chem. Soc., 2015, 137(43), 13844–13850,  DOI:10.1021/jacs.5b06568.
36. R. Passalacqua, S. Parathoner, G. Centi, A. Halder, E. C. Tyo, B. Yang, S. Seifert and S. Vajda, Electrochemical Behaviour of Naked Sub-Nanometre Sized Copper Clusters and Effect of CO₂, Catal. Sci. Technol., 2016, 6(18), 6977–6985,  10.1039/c6cy00942e.
37. H. Mistry, R. Reske, Z. Zeng, Z.-J. Zhao, J. Greeley, P. Strasser and B. R. Cuenya, Exceptional Size-Dependent Activity Enhancement in the Electroreduction of CO₂ over Au Nanoparticles, J. Am. Chem. Soc., 2014, 136(47), 16473–16476,  DOI:10.1021/ja508879j.
38. D. R. Kauffman, D. Alfonso, C. Matranga, H. Qian and R. Jin, Experimental and Computational Investigation of Au₂₅ Clusters and CO₂: A Unique Interaction and Enhanced Electrocatalytic Activity, J. Am. Chem. Soc., 2012, 134(24), 10237–10243,  DOI:10.1021/ja303259q.
39. D. Gao, H. Zhou, J. Wang, S. Miao, F. Yang, G. Wang, J. Wang and X. Bao, Size-Dependent Electrocatalytic Reduction of CO₂ over Pd Nanoparticles, J. Am. Chem. Soc., 2015, 137(13), 4288–4291,  DOI:10.1021/jacs.5b00046.
40. Z. Zhang, M. Chi, G. M. Veith, P. Zhang, D. A. Lutterman, J. Rosenthal, S. H. Overbury, S. Dai and H. Zhu, Rational Design of Bi Nanoparticles for Efficient Electrochemical CO₂ Reduction: The Elucidation of Size and Surface Condition Effects, ACS Catal., 2016, 6(9), 6255–6264,  DOI:10.1021/acscatal.6b01297.
41. A. Salehi-Khojin, H. R. M. Jhong, B. A. Rosen, W. Zhu, S. Ma, P. J. A. Kenis and R. I. Masel, Nanoparticle Silver Catalysts That Show Enhanced Activity for Carbon Dioxide Electrolysis, J. Phys. Chem. C, 2013, 117(4), 1627–1632,  DOI:10.1021/jp310509z.
42. K. Manthiram, B. J. Beberwyck and A. P. Alivisatos, Enhanced Electrochemical Methanation of Carbon Dioxide with a Dispersible Nanoscale Copper Catalyst, J. Am. Chem. Soc., 2014, 136(38), 13319–13325,  DOI:10.1021/ja5065284.
43. R. Reske, H. Mistry, F. Behafarid, B. Roldan Cuenya and P. Strasser, Particle Size Effects in the Catalytic Electroreduction of CO₂ on Cu Nanoparticles, J. Am. Chem. Soc., 2014, 136(19), 6978–6986,  DOI:10.1021/ja500328k.
44. S. Zhang, P. Kang and T. J. Meyer, Nanostructured Tin Catalysts for Selective Electrochemical Reduction of Carbon Dioxide to Formate, J. Am. Chem. Soc., 2014, 136(5), 1734–1737,  DOI:10.1021/ja4113885.
45. X. F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Single-Atom Catalysts: A New Frontier in Heterogeneous Catalysis, Acc. Chem. Res., 2013, 46(8), 1740–1748,  DOI:10.1021/ar300361m.
46. H. Zhang, G. Liu, L. Shi and J. Ye, Single-Atom Catalysts: Emerging Multifunctional Materials in Heterogeneous Catalysis, Adv. Energy Mater., 2018, 8(1), 1701343,  DOI:10.1002/aenm.201701343.
47. Y. Wang, Z. Chen, P. Han, Y. Du, Z. Gu, X. Xu and G. Zheng, Single-Atomic Cu with Multiple Oxygen Vacancies on Ceria for Electrocatalytic CO₂ Reduction to CH₄, ACS Catal., 2018, 8(8), 7113–7119,  DOI:10.1021/acscatal.8b01014.
48. C. Liu, B. Yang, E. Tyo, S. Seifert, J. DeBartolo, B. von Issendorff, P. Zapol, S. Vajda and L. A. Curtiss, Carbon Dioxide Conversion to Methanol over Size-Selected Cu₄ Clusters at Low Pressures, J. Am. Chem. Soc., 2015, 137(27), 8676–8679,  DOI:10.1021/jacs.5b03668.
49. B. Yang, C. Liu, A. Halder, E. C. Tyo, A. B. F. Martinson, S. Seifert, P. Zapol, L. A. Curtiss and S. Vajda, Copper Cluster Size Effect in Methanol Synthesis from CO₂, J. Phys. Chem. C, 2017, 121(19), 10406–10412,  DOI:10.1021/acs.jpcc.7b01835.
50. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, How Copper Catalyzes the Electroreduction of Carbon Dioxide into Hydrocarbon Fuels, Energy Environ. Sci., 2010, 3(9), 1311–1315,  10.1039/c0ee00071j.
51. X. Nie, M. R. Esopi, M. J. Janik and A. Asthagiri, Selectivity of CO₂ Reduction on Copper Electrodes: The Role of the Kinetics of Elementary Steps, Angew. Chem., Int. Ed., 2013, 52(9), 2459–2462,  DOI:10.1002/anie.201208320.
52. X. Nie, W. Luo, M. J. Janik and A. Asthagiri, Reaction Mechanisms of CO₂ Electrochemical Reduction on Cu(111) Determined with Density Functional Theory, J. Catal., 2014, 312, 108–122,  DOI:10.1016/j.jcat.2014.01.013.
53. K. S. Rawat, A. Mahata and B. Pathak, Thermochemical and Electrochemical CO₂ Reduction on Octahedral Cu Nanocluster: Role of Solvent towards Product Selectivity, J. Catal., 2017, 349, 118–127,  DOI:10.1016/j.jcat.2017.03.011.
54. H. Dong, Y. Li and D. Jiang, First-Principles Insight into Electrocatalytic Reduction of CO₂ to CH₄ on a Copper Nanoparticle, J. Phys. Chem. C, 2018, 122(21), 11392–11398,  DOI:10.1021/acs.jpcc.8b01928.
55. C. Liu, H. He, P. Zapol and L. A. Curtiss, Computational Studies of Electrochemical CO₂ Reduction on Subnanometer Transition Metal Clusters, Phys. Chem. Chem. Phys., 2014, 16(48), 26584–26599,  10.1039/c4cp02690j.
56. R. Shanmugam, A. Thamaraichelvan, T. K. Ganesan and B. Viswanathan, Computational Evaluation of Sub-Nanometer Cluster Activity of Singly Exposed Copper Atom with Various Coordinative Environment in Catalytic CO₂ transformation, Appl. Surf. Sci., 2017, 396, 444–454,  DOI:10.1016/j.apsusc.2016.10.174.
57. R. K. Raju, P. Rodriguez and R. L. Johnston, Can a Single Valence Electron Alter the Electrocatalytic Activity and Selectivity for CO₂ Reduction on the Subnanometer Scale?, J. Phys. Chem. C, 2019, 123(23), 14591–14609,  DOI:10.1021/acs.jpcc.9b04745.
58. J. B. A. Davis, A. Shayeghi, S. L. Horswell and R. L. Johnston, The Birmingham Parallel Genetic Algorithm and Its Application to the Direct DFT Global Optimisation of IrN (N = 10–20) Clusters, Nanoscale, 2015, 7(33), 14032–14038,  10.1039/c5nr03774c.
59. G. Kresse and J. Furthmüller, Efficiency of Ab Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50,  DOI:10.1016/0927-0256(96)00008-0.
60. G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid–Metalamorphous–Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269,  DOI:10.1103/PhysRevB.49.14251.
61. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
62. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561,  DOI:10.1103/PhysRevB.47.558.
63. M. Jäger, R. Schäfer and R. L. Johnston, GIGA: A Versatile Genetic Algorithm for Free and Supported Clusters and Nanoparticles in the Presence of Ligands, Nanoscale, 2019, 11(18), 9042–9052,  10.1039/c9nr02031d.
64. A. Granja-Delrío, H. A. Abdulhussein and R. L. Johnston, DFT-Based Global Optimization of Sub-Nanometer Ni-Pd Clusters, J. Phys. Chem. C, 2019, 123(43), 26583–26596,  DOI:10.1021/acs.jpcc.9b05970.
65. F. Buendía, J. A. Vargas, R. L. Johnston and M. R. Beltrán, Study of the Stability of Small AuRh Clusters Found by a Genetic Algorithm Methodology, Comput. Theor. Chem., 2017, 1119, 51–58,  DOI:10.1016/j.comptc.2017.09.008.
66. H. A. Hussein and R. L. Johnston, The DFT-Genetic Algorithm Approach for Global Optimization of Subnanometer Bimetallic Clusters, Elsevier Ltd., 1st edn, 2018, Vol. 12.  DOI:10.1016/B978-0-08-102232-0.00004-X.
67. P. Ferrari, H. A. Hussein, C. J. Heard, J. Vanbuel, R. L. Johnston, P. Lievens and E. Janssens, Effect of Palladium Doping on the Stability and Fragmentation Patterns of Cationic Gold Clusters, Phys. Rev. A, 2018, 97(5), 1–10,  DOI:10.1103/PhysRevA.97.052508.
68. M. Jäger, R. Schäfer and R. L. Johnston, First Principles Global Optimization of Metal Clusters and Nanoalloys, Adv. Phys. X, 2018, 3(1), 1077–1108,  DOI:10.1080/23746149.2018.1516514.
69. H. A. Hussein, I. Demiroglu and R. L. Johnston, Application of a Parallel Genetic Algorithm to the Global Optimization of Medium-Sized Au–Pd Sub-Nanometre Clusters, Eur. Phys. J. B, 2018, 91(2), 34,  DOI:10.1140/epjb/e2017-80314-2.
70. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
71. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
72. M. Methfessel and A. T. Paxton, High-Precision Sampling for Brillouin-Zone Integration in Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3616–3621,  DOI:10.1103/PhysRevB.40.3616.
73. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465,  DOI:10.1002/JCC.21759.
74. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
75. W. Tang, E. Sanville and G. Henkelman, A Grid-Based Bader Analysis Algorithm without Lattice Bias, J. Phys.: Condens. Matter, 2009, 21(8), 84204,  DOI:10.1088/0953-8984/21/8/084204.
76. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code, Comput. Phys. Commun., 2021, 267, 108033,  DOI:10.1016/J.CPC.2021.108033.
77. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886,  DOI:10.1021/jp047349j.
78. M. J. Janik, C. D. Taylor and M. Neurock, First-Principles Analysis of the Initial Electroreduction Steps of Oxygen over Pt(111), J. Electrochem. Soc., 2009, 156(1), B126–B135,  DOI:10.1149/1.3008005.
79. V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, The Oxygen Reduction Reaction Mechanism on Pt(111) from Density Functional Theory Calculations, Electrochim. Acta, 2010, 55, 7975–7981,  DOI:10.1016/j.electacta.2010.02.056.
80. R. L. Johnston, Evolving Better Nanoparticles: Genetic Algorithms for Optimising Cluster Geometries, J. Chem. Soc., Dalton Trans., 2003, 3(22), 4193–4207,  10.1039/b305686d.
81. D. M. Deaven and K. M. Ho, Molecular Geometry Optimization with a Genetic Algorithm, Phys. Rev. Lett., 1995, 75(2), 288–291,  DOI:10.1103/PhysRevLett.75.288.
82. R. H. Duncan Lyngdoh, H. F. Schaefer, R. B. King and M. M. Metal-Metal, Bond Distances and Bond Orders in Binuclear Metal Complexes of the First Row Transition Metals Titanium through Zinc, Chem. Rev., 2018, 118(24), 11626–11706,  DOI:10.1021/acs.chemrev.8b00297.
83. L.-C. Wu, C.-W. Hsu, Y.-C. Chuang, G.-H. Lee, Y.-C. Tsai and Y. Wang, Bond Characterization on a Cr–Cr Quintuple Bond: A Combined Experimental and Theoretical Study, J. Phys. Chem. A, 2011, 115(45), 12602–12615,  DOI:10.1021/jp203080j.

---

Footnote

† Electronic supplementary information (ESI) available: Energy corrections (gas-phase, liquid, and solvent corrections); coefficient of determination (R²) values for linear free energy relationship between the adsorption free energies of CO₂*, C*, and O* with other adsorbates; adsorption free energies (ΔG, eV), residual charges (e⁻), HOMO–LUMO gaps (eV), and spin multiplicities of various adsorbates on first-row transition metal nanoclusters; correlations between residual charges and HOMO–LUMO gaps with adsorption free energies for various adsorbates; free energy changes (eV) for various electrochemical steps in the CO₂RR process on mid to late TM nanoclusters (Cr–Cu); potential-determining step (PDS) for various CHO* and COH* mediated pathways and the free energy changes of the PDSs. See DOI: https://doi.org/10.1039/d3cp00739a

---