Open Access Article
Open Access ArticleCO and CO2 adsorption mechanism in Fe(pz)[Pt(CN)4] probed by neutron scattering and density-functional theory calculations†
Ángel
Fernández-Blanco
ab,
Lucía
Piñeiro-López
c,
Mónica
Jiménez-Ruiz
a,
Stephane
Rols
a,
José
Antonio Real
 d,
Jose
Sanchez Costa
d,
Jose
Sanchez Costa
 c,
Roberta
Poloni
c,
Roberta
Poloni
 *e and
J. Alberto
Rodríguez-Velamazán
*e and
J. Alberto
Rodríguez-Velamazán
 *a
*a
aInstitut Laue Langevin, 71 Avenue des Martyrs, Grenoble, CS 20156-38042, France. E-mail: velamazan@ill.eu
bUniversity of Grenoble-Alpes, SIMaP, Grenoble, F-38042, France
cIMDEA Nanociencia, Ciudad Universitaria de Cantoblanco, Faraday 9, Madrid, 28049, Spain
dDepartamento de Química Inorgánica, Insituto de Ciencia Molecular (ICMol), Universidad de Valencia, Paterna, 46980, Spain
eUniversity of Grenoble-Alpes, SIMaP, Grenoble-INP, CNRS, F-38042 Grenoble, France. E-mail: roberta.poloni@grenoble-inp.fr
First published on 27th March 2023
Abstract
We study the binding mechanism of CO and CO2 in the porous spin-crossover compound Fe(pz)[Pt(CN)4] by combining neutron diffraction (ND), inelastic neutron scattering (INS) and density–functional theory (DFT) calculations. Two adsorption sites are identified, above the open-metal site and between the pyrazine rings. For CO adsorption, the guest molecules are parallel to the neighboring gas molecules and perpendicular to the pyrazine planes. For CO2, the molecules adsorbed on-top of the open-metal site are perpendicular to the pyrazine rings and those between the pyrazines are almost parallel to them. These configurations are consistent with the INS data, which are in good agreement with the computed generalized phonon density of states. The most relevant signatures of the binding occur in the spectral region around 100 cm−1 and 400 cm−1. The first peak blue-shifts for both CO and CO2 adsorption, while the second red-shifts for CO and remains nearly unchanged for CO2. These spectral changes depend both from steric effects and the nature of the interaction. The interpretation of the INS data as supported by the computed binding energy and the molecular orbital analysis are consistent with a physisorption mechanism for both gases. This work shows the strength of the combination of neutron techniques and DFT calculations to characterize in detail the gas adsorption mechanism in this type of materials.
1 Introduction
Metal organic frameworks (MOFs) are hybrid and crystalline materials composed of metal centers connected by organic ligands. The resulting 3D frameworks exhibit ultrahigh porosity and large surface areas that can be modulated for specific applications due to the wide availability of metal-ligand combinations. For this reason, MOFs have been extensively studied for applications in many different fields of science such as catalysis,1–4 drug delivery5 or gas adsorption,6,7 separation,8,9 sensing4,10–12 and storage,8,13 among others. One of the applications that has attracted the most attention in recent years is the capture of polluting gases emitted from anthropogenic sources. Special attention has been paid to carbon dioxide due to its strong impact on the greenhouse effect.14–16 Other gases, like carbon monoxide, can also play an important role in climate change and the development of capture strategies is interesting not just for environmental concerns but also for the possibility of reusing them in other industrial chemical processes.17Hofmann-like clathrates with general formula Fe(pz)[M(CN)4] (pz = pyrazine, M = Ni, Pd, Pt)18 are a versatile class of MOFs with octahedrally coordinated Fe(II) centers connected by cyanide ligands, CN−, to a square-planar open-metal site, M(II). The resulting Fe[MII (CN)4]∞ layers are pillared by bidentated aromatic ligands resulting in three-dimensional networks. These materials are interesting for gas capture applications due to the combination of open-metal M(II) sites and bistable Fe(II) spin-crossover centers. These can undergo a spin-state switch under the influence of external stimuli such as temperature, pressure, light or incorporation of guest molecules. The presence of unsaturated metal centers can, potentially, enhance the adsorption capacity,19 whereas their bistability can be used for sensing applications. Several studies of gas adsorption have been published20–26 since their discovery in 2001,18 including the interplay between spin-crossover and guest molecules. Recently, the member of the series Fe(pz)[M(CN)4] with M = Pt(II) has shown significantly higher CO2 and CO uptake capacities compared to other MOFs with larger surface areas.27 In this work, we focus our interest in these Hofmann-like clathrates upon CO2 and CO loading. We report a detailed study of gas adsorption mechanism of CO and CO2 in Fe(pz)[Pt(CN)4] in the low-spin state by means of neutron scattering techniques and density–functional theory calculations. We identified the two adsorption sites, on top of the open-metal site and between the pyrazine rings, and the most stable orientational configuration of the guest molecules and the pyrazine ligands of the framework was determined. The inelastic neutron scattering results assisted by DFT calculations show signatures of a hindrance of the pyrazine libration and the out-of-plane movement of cyanide ligands when the gas is adsorbed. Together with the computed binding energy and a molecular orbital analysis, these results agree with a physisorption mechanism for both gases.
2 Methods
Sample preparation
Dehydrated powder samples of Fe(pz)[Pt(CN)4] and its deuterated homologue Fe(d4-pz)[Pt(CN)4] were prepared as described elsewhere.18,21,28,29 The samples were activated by heating them overnight at 100 °C in air to obtain the anhydrous form of the compound.28,29 For the neutron scattering experiments, the samples were loaded in the sample holder inside a glove box under inert gas.Neutron diffraction
Neutron diffraction experiments were performed in the high-intensity two-axis diffractometer D20 installed on the high-flux reactor at the Institut-Laue Langevin (ILL) in Grenoble, France. A wavelength of 1.54 Å was used. The empty and gas-loaded samples were measured at 100 K. Rietveld refinements and calculations of the structures were performed using the FullProf suite of programs.30,31 The schematic illustrations of the crystal structures and magnetic arrangements were obtained with the VESTA program.32Inelastic neutron scattering
Inelastic neutron scattering experiments were performed in the indirect geometry-type spectrometer IN1-LAGRANGE installed on the hot neutron source of the high-flux reactor at ILL.33,34 Monochromators of Si(111), Si(311) and Cu(220) were selected to collect the data for energy transfers of [8–129], [92–215] and [173–427] cm−1, respectively. The measurements were done at 30 K for both the empty and loaded materials. A post-processing treatment of normalization to monitor counts and subtraction of the empty sample holder was done using LAMP.35A complementary measurement before and upon CO adsorption was performed in the instrument PANTHER for the low energy region. PANTHER is a themal-neutron direct-geometry time-of-flight spectrometer optimized for energy transfers in the range [2–60] meV which is installed on the H12 thermal beam tube at the ILL. All data were collected at 10 K using an initial energy of 50 meV.
Gas adsorption
The powder samples were placed inside a cylindrical aluminium sample holder connected to a sample stick adapted for gas adsorption. A manifold gas pumping system was attached to the stick through a capillary and the temperature control was achieved using either a closed-cycle cryostat (IN1-LAGRANGE) or an Orange cryostat (D20 and PANTHER). The samples were first evacuated and then loaded to saturation by initially injecting the gas doses at room temperature and then lowering the temperature of the sample holder (to 100 K for CO and 200 K for CO2), creating a cold point to force the gas to move towards the sample and facilitate the adsorption. For CO2, the saturation loading is about 1.5 mol of CO2 per Fe mol, as determined experimentally from adsorption isotherms.21,24 In the absence, to the best of our knowledge, of published absorption isotherms for CO, we estimate the saturation loading at about 2 CO mol per Fe mol from the kinetic uptake experiments reported by Ibarra et al.27 Our ND, DFT and INS results are consistent with these saturation loading values (vide infra).Computational details
The DFT calculations were performed with the Quantum Espresso package36–38 (v 6.4) within the generalized gradient approximation (GGA) of Perdew, Burke and Ernzerhof (PBE)39 and long-range interactions described with the semiempirical approach proposed by Grimme (PBE+D2).40,41 We use the Rappe–Rabe–Kaxiras–Joannopoulos ultrasoft (rrkjus) pseudopotentials42 without semicore states in valence. The convergence threshold on forces is 0.0001 Ry Bohr−1 and the wavefunctions and charge density cutoffs are set to 100 and 1000 Ry, respectively. All the calculations are performed using the low-spin (S = 0) electronic configuration for the Fe(II) atoms. The Brillouin zone is sampled using a 3 × 3 × 3 Monkhorst–Pack k-point grid. The Becke–Johnson (BJ) damping scheme43,44 together with the D3 Grimme approach (PBE+D3+BJ) was also used to perform a Bader charge analysis in the loaded MOFs. The same pseudopotentials, force thresholds, Monkhorst–Pack k-point grid, wavefunctions and charge density cutoffs than for PBE+D2 were used for this functional.The inelastic scattering data collected on IN1-LAGRANGE are compared with the computed scattering function S(Q,ω) given by45–47
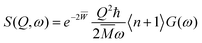 | (1) |
 n is the thermal-equilibrium occupation number of the vibrational state and
n is the thermal-equilibrium occupation number of the vibrational state and 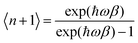 with
with 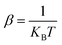 . The exponential term is the Debye–Waller factor for neutron attenuation by thermal motion and ω the phonon frequencies obtained by employing the ph.x package in Quantum Espresso.36Q corresponds to the kinematical range of IN1-LAGRANGE. A convolution with a Gaussian function is also applied to account for the resolution of the monochromators with a standard deviation of 3.0 cm−1 for the range [0–478] cm−1 and around 0.01ω for [478–4033] cm−1, close to the experimental resolution of IN1-LAGRANGE which is 0.02–0.03ω.33
. The exponential term is the Debye–Waller factor for neutron attenuation by thermal motion and ω the phonon frequencies obtained by employing the ph.x package in Quantum Espresso.36Q corresponds to the kinematical range of IN1-LAGRANGE. A convolution with a Gaussian function is also applied to account for the resolution of the monochromators with a standard deviation of 3.0 cm−1 for the range [0–478] cm−1 and around 0.01ω for [478–4033] cm−1, close to the experimental resolution of IN1-LAGRANGE which is 0.02–0.03ω.33
Orientation of the pyrazines
The orientational configuration of the pyrazine rings depends on the nature and amount of the guest molecules incorporated in the material. Recently, the present authors reported an ordered structure for the empty Hofmann clathrate Fe(pz)[Pt(CN)4] with the pyrazine ligands oriented in a perpendicular configuration.49 The ordered structure is found below the spin-transition temperature (ca. 285 K), whereas at higher temperature the Fe(II) atoms switch to HS and the pyrazines display a dynamic disorder.50 In presence of adsorbed molecules, the orientation of the pyrazines can remain perpendicular48 or change to a parallel configuration as reported for water,20 depending on the type and amount of adsorbed gas. To study this, we have collected diffraction data on the deuterated homologue, taking advantage of the sensitivity of this technique to the deuterium position and consequently to the pyrazine orientation. The different configurations where explored also by DFT calculations by studying an increasing number of adsorbed CO and CO2 molecules: 1, 1.5, and 2 molecules per formula unit (f.u.) both in the parallel and the perpendicular configuration of the pyrazines. To accomodate the perpendicular configuration, a supercell with lattice parameters and
and 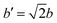 is used, where a and b are the lattice parameters of the primitive cell. The PBE+D2 lattice parameters of the bare MOF are a = 10.096 Å, b = 10.097 Å, and c = 6.711 Å.48
is used, where a and b are the lattice parameters of the primitive cell. The PBE+D2 lattice parameters of the bare MOF are a = 10.096 Å, b = 10.097 Å, and c = 6.711 Å.48
3 Results and discussion
Neutron diffraction
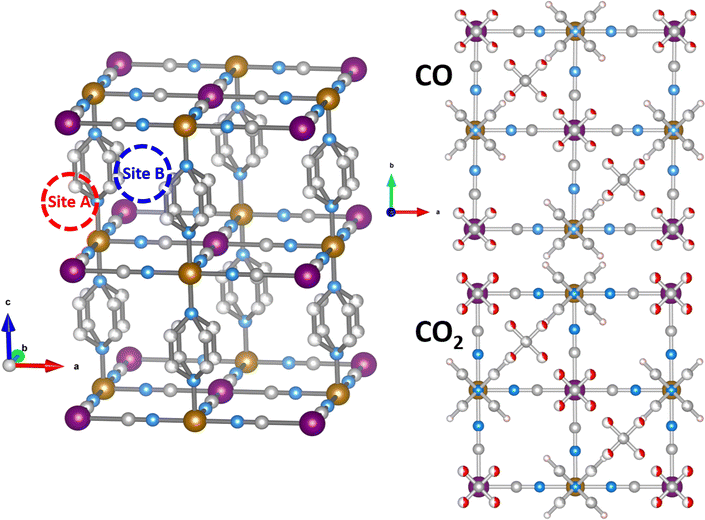
We used neutron diffraction data collected on gas-loaded Fe(d4-pz)[Pt(CN)4] to get insight into the configuration of the pyrazine moieties. The absence of the peaks characteristic of a perpendicular configuration (Fig. S1, ESI†) is a strong indication to discard this possibility. Additionally, some peaks related to the parallel configuration show an increase of intensity (although this could be also in part correlated with the presence of gas molecules in the structure). Therefore we used the parallel configuration to build a starting model, which is consistent with DFT calculations (see below). In subsequent refinements, some disorder was allowed between the possible positions of the pyrazine.The initial model of the bare Fe(pyrazine)[Pt(CN)4] with parallel pyrazines is used as starting point for a Rietveld fit to the experimental neutron diffraction pattern of the gas-loaded compounds (see Fig. S2 for the case of CO, ESI†). Initially, no guest molecules were included in the model and all the structural parameters were kept fixed. The residual scattering density obtained in this way allows us to distinguish two bonding sites for the guest molecules: (i) on top of the open-metal site (site A) and (ii) between the pyrazine rings (site B). The higher density is found in site A, which is an indication of a preference for this site. The residual density observed, located mainly in the z = 0 plane, is indicative of a position of the gas molecules in parallel to the Pt[CN]4 plane. The guest molecules were then incorporated to the model. Initially, these molecules were placed disordered in two perpendicular positions (see Fig. 1), and 2 and 1.5 molecules per f.u. were considered for CO and CO2, respectively (with site A always fully occupied, since it shows a significantly higher residual density). With this model, the disorder of the pyrazine rings between their two possible positions was estimated by a fit to the gas-loaded Fe(d4-pz)[Pt(CN)4] patterns, with refined values of 35(2) and 30(3) % for CO and CO2, respectively. This disorder was then fixed in the ensuing refinements. Finally, constrained fits (due to the quality of the data and the number of parameters) of the gas-loaded Fe(pyrazine)[Pt(CN)4] patterns (see details in the ESI†) yielded the structural models presented in Fig. 1. The structures present a slight monoclinic distorsion (of ca. 0.5° in γ for both CO and CO2), in agreement with DFT results (vide infra). The ordering of the pyrazine rings in a preferentially parallel configuration implies the existence of two non-equivalent B sites, one with more space available than the other. Attempts to introduce gas molecules in the site with less available space produced worse fits. A total occupancy of 2 CO molecules per f.u. gave the best agreement for the CO-loaded material, with both A and B sites fully occupied.
For CO2, the best fits are obtained with a total occupancy of 1.69(6) CO2 molecules per f.u. (the A site was considered fully occupied while the occupancy of guest molecules in the B site was allowed to vary). The refinement of the disorder among the possible orientations of the guest molecules allowed by the proposed model did not give significant improvement of the fits, thus the disordered configurations were retained.
Predicted configuration
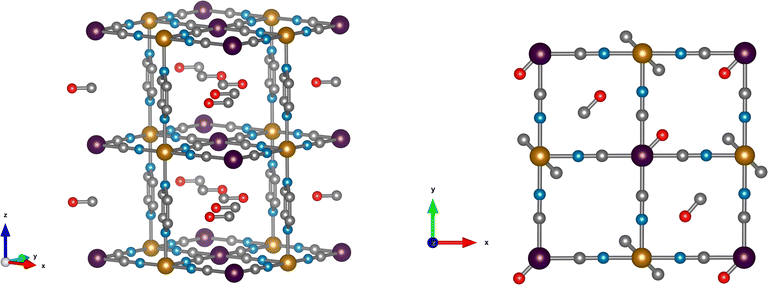
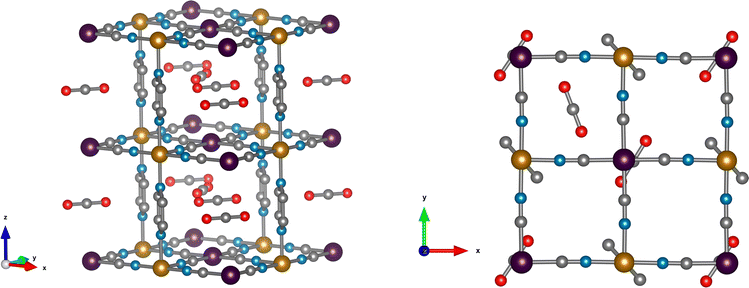
DFT calculations are used to resolve the most stable configuration in the ground state. For CO, we find a perpendicular orientation of the pyrazines upon adsorption of 1 molecule per f.u. while for 1.5 and 2 CO per f.u. a parallel orientation is predicted. The energy differences between the two configurations are −0.029 eV, 0.007 eV, and 0.119 eV, respectively, per formula unit. Therefore, for the predicted saturation loading of 2 CO per f.u., the parallel orientation of the pyrazine ring is the most stable. This is consistent with the neutron diffraction patterns of CO-loaded Fe(d4-pz)[Pt(CN)4]. For 1.5 and 2 CO per f.u., the two binding sites obtained in our calculations agree with neutron diffraction: on-top of the open-metal site (site A), and between the pyrazine rings (site B). The occupancy of site B is 0.5 for 1.5 CO per f.u. and 1.0 for 2 CO per f.u. The A site is always fully occupied. The CO molecules are oriented perpendicular to the pyrazine planes and parallel to the Pt[CN]4 plane (see Fig. 2), regardless of the amount of gas. The unit cell presents a monoclinic distortion (γ = 89.55°), in agreement with the neutron diffraction results.In the case of CO2, the orientation of the pyrazines is parallel for 1 and 1.5 CO2 per f.u. with a corresponding energy difference between parallel and perpendicular of 0.016 and 0.036 eV per f.u., respectively. Only the parallel configuration could be converged for 2 molecules, suggesting that large interatomic forces could prevent a perpendicular configuration in this case. For a loading of 1 CO2 per f.u. the molecules are located only on site A and are perpendicular to the pyrazine planes. When 1.5 and 2 molecules per f.u. are considered, CO2 locates in both sites A and B. The molecules in site A are again perpendicular to the pyrazine planes, while the molecules in site B are almost parallel to the pyrazine planes and perpendicular to the neighbouring CO2 (Fig. 3). While molecules in site B are parallel to the Pt(CN)4 plane for a loading of 1.5 CO2, for a 2 molecule-loading, the CO2 molecules are tilted off-plane. In the first case, the molecules on-top of the platinum in site A move slightly off the metal position (see Fig. 3). Also in this case, the structure is monoclinically distorted (γ = 89.51°), consistent with the neutron diffraction results.
Amount of gas adsorbed
Neutron diffraction on the deuterated compound suggests that most of the pyrazines are in parallel orientation for both the CO- and CO2-loaded materials. DFT confirms that this configuration only occurs when 1.5 or 2 molecules of CO are adsorbed per open-metal-site. Therefore, we can deduce that more than one molecule has been adsorbed. Since adsorption isotherms are not available for CO, we estimate the saturation loading at about 2 CO mol per Fe mol from kinetic uptake experiments,27 which are in agreement with our neutron diffraction results. The combination of INS and DFT calculations is consistent with this loading value. In the case of CO2, a parallel configuration is predicted by DFT for all the loading values considered. We have retained the value of 1.5 molecules per f.u. in our calculations, which is consistent with the saturation loading for CO2 determined experimentally from adsorption isotherms (about 1.5 mol of CO2 per Fe mol21,24), and with the refined value of ca. 1.7 obtained by neutron diffraction. The changes in the INS data are consistent with these loading values (vide infra).Inelastic neutron scattering
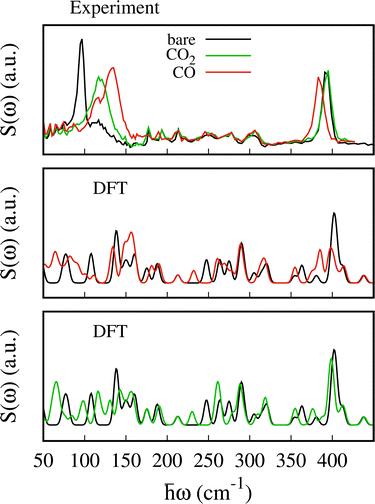
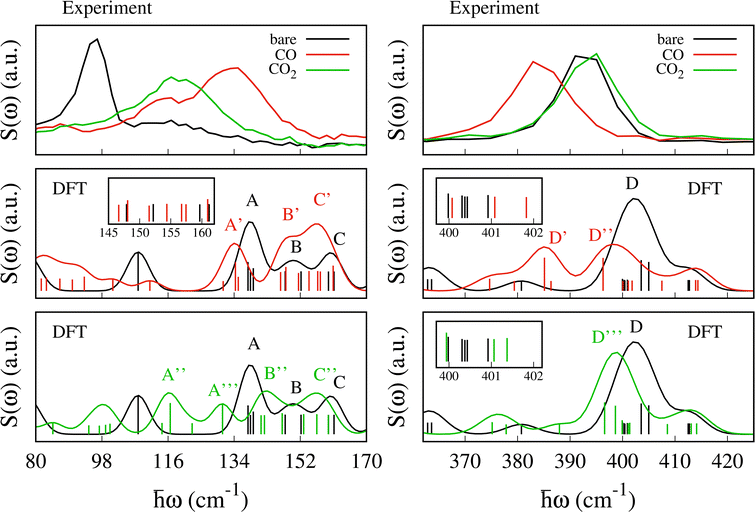
The experimental spectra for the empty MOF and upon CO and CO2 adsorption are shown in Fig. 4 (upper panel) together with the scattering function computed using eqn (1) (lower panel). For the bare material the pyrazines are considered perpendicular in agreement with previous calculations and experimental findings.48,49 The scattering function upon CO adsorption in Fig. 4 is computed by adopting the configuration described in the previous section with 2 molecules per f.u. and pyrazines in a parallel orientation. For CO2, we consider 1.5 molecules per f.u. and a parallel orientation of the pyrazines.The experimental errors are reported in Fig. S4 and S5 (ESI†) upon CO and CO2 adsorption, respectively. Data were collected up to 427 cm−1. We note that at low energy the assignation of the vibrational modes from the calculations is more challenging compared to higher energy. While at around 400 cm−1 a good agreement between experiment and DFT is found,48,51 low energy modes present larger relative errors possibly due to the underlying approximations (basis set and functional choice may affect this part of the spectra). Besides, the density of states is computed only at the Γ point and therefore some dispersive low energy modes may not be well described in our calculations. This is possibly the case for the spectral region between 100 and 400 cm−1 where the simulations give a few well defined peaks that are substantially less intense in the experiment. For example, because the intense peak at 288 cm−1 is an in-plane rotation of the pyrazine around the axis perpendicular to the plane of aromatic ring, we suspect it should exhibit a non negligible dispersion along the z axis. Thus, a proper calculation of the density of states, i.e. integrated over the Brillouin zone, would possibly lead to a broader peak as in the experiment.
At higher energies (not reported here), the vibrational modes of the pyrazine [700–1500] cm−1 and cyanide stretching modes [2100–2200] cm−1 which appear with intense and well-defined peaks, were found to undergo negligible changes upon SO2 adsorption.48 The experimental data show two well defined peaks for the bare MOF centered at ca. 96 and 396 cm−1 and less resolved peaks between them. The first peak at 96 cm−1 blueshifts and becomes broader and less intense upon CO and CO2 adsorption. It blueshifts to 133 cm−1 for CO and to ca. 116 cm−1 for CO2. The second peak at 396 cm−1 redshifts upon CO adsorption while it is negligibly affected by the CO2 uptake.
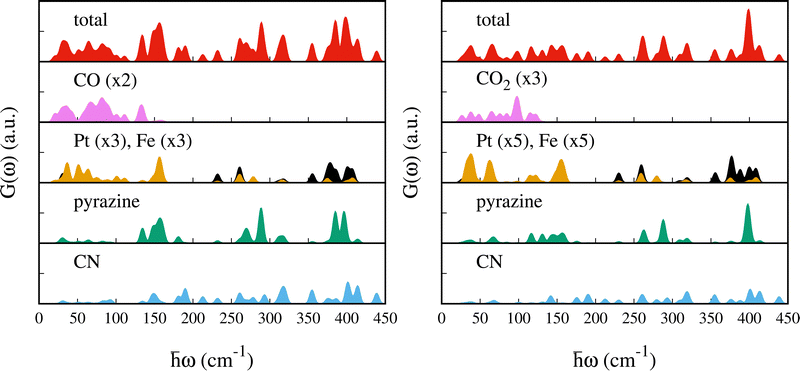
To assist the analysis of the inelastic scattering data, we compute the partial G(ω) for each atom or group of atoms in the case of CO and CO2 adsorption (see Fig. 5). The distribution of the specific contributions to the total G(ω) is similar in the two cases, and to the case of SO2.48 Below 100 cm−1 the spectra are dominated by vibrations of the heavy atoms, Fe and Pt, with the Pt being the dominant one. A minor contribution from the pyrazines and cyanides can be observed as well, together with the vibrational modes of CO or CO2 (mainly rotational or translational modes). For the intense peak which is found in the experiment at ca. 96 cm−1 and predicted around 150 cm−1, the main contributions arise from the pyrazine, cyanides and the Pt atoms. In the region [100–400] cm−1 we find vibrations from all the atoms. In this region, Felix et al.52 identified the characteristic Fe–Npz and Fe–NCN stretching modes using Raman and nuclear inelastic scattering for Fe(pz)[Ni(CN)4] at 306 and 381 cm−1, respectively. We identified these modes upon CO adsorption at 311.3 and 318.0 cm−1 for Fe–Npz stretching and at 374.7 and 386.4 cm−1 for Fe–NCN. For CO2, Fe–Npz stretchings appear at 309.25 and 320.11 cm−1 and Fe–NCN stretchings at 387.97 and 375.16 cm−1. Finally, the peaks at 400 cm−1 have a strong contribution from the pyrazines and a smaller contribution from CN and Pt.
Signature at 100 cm−1
Upon CO and CO2 adsorption, the peak at 96 cm−1 blue-shifts giving rise to a broader and less intense peak. We note that this signature is confirmed for the CO adsorption by the INS spectra collected on PANTHER which are shown in Fig. S6 (ESI†). The intense peak at 96.7 cm−1 measured on PANTHER for the bare material should correspond to the intense band measured at the same energy on IN1.As shown in Fig. 4 and 6 the gas adsorption results in a larger shift for CO (37 cm−1) than CO2 (20 cm−1). The previously studied SO2 molecule resulted in a shift of 29 cm−1 (see ref. 48). This is well reproduced by the computed S(ω) reported in Fig. 6. In this region, the calculations predict two peaks centered at ca. 107 cm−1 and 138 cm−1 for the bare MOF. The first one corresponds to a libration of the pyrazine ligand around the z-axis, while the second, named A in Fig. 6, contains three vibrational modes: (i) a collective mode involving in-plane and out-of-plane movements of the CN groups and a libration of the pyrazine around the z-axis at 137.8 cm−1, (ii) a rigid out-of-plane twisting of the Fe(CN)4N2 octahedra at 138.5 cm−1 and (iii) an out-of-plane vibration of the cyanide together with a small libration of the pyrazine at 139.2 cm−1.48
The first peak at 107.9 cm−1 blue-shifts to 134.3 cm−1 (under peak A′) upon CO adsorption and to 116.6 cm−1 (under peak A′′) upon CO2 adsorption. In the new mode, the initial pyrazine libration is coupled with a libration of the CO and with a small translation of the CO2, respectively. The shift is substantially larger for CO. We attribute the blue-shift to the hindered rotation of the pyrazines. As shown in more detail in the next section, this mode is the most sensitive to both the amount of adsorbed gas and the type of molecule. The band A′ that arises upon CO adsorption includes two additional modes at 131.0 and 135.1 cm−1. The first one results from a pure libration of the CO. The second one is the result of the red-shift of the mode located at 137.8 cm−1 in peak A, i.e. mode (i) described above. A similar situation is found for CO2: the mode at 137.8 cm−1 under peak A red-shifts to 130.9 cm−1, under peak A′′′. Because the shift of the mode at 107 cm−1 is significantly smaller for CO2 (9.6 cm−1) than for CO (27.4 cm−1), two separate peaks (A′′ and A′′′) are observed for CO2 and one for CO (peak A′). The peak A′′ includes as well two additional translational modes of CO2 at 122.5 and 114.4 cm−1.
The other two vibrational modes under peak A, i.e. (ii) 138.5 and (iii) 139.2 cm−1, undergo a blueshift to 146.6 (142.3) and 151.5 cm−1 (141.3), upon CO adsorption (CO2), respectively, resulting in peak B′ (B′′). For these modes, a larger blueshift is found for CO (8 and 12.3 cm−1) than CO2 (3.8 and 2.1 cm−1). This blue-shift can be attributed to the increase in the cyanide out-of-plane bending force constant due to steric hindrance.
For the bare MOF, the two vibrational modes under peak B, at 147.9 and 152.2 cm−1, correspond to an in-plane movement of the Pt atoms together with a rigid back-and-forth movement of the pyrazines and Fe atom. Upon CO adsorption, we observe a small blue-shift to 148.1 and 154.4 cm−1, respectively, (peaks B′ and C′). In the case of CO2, the first red-shifts by 0.8 cm−1 (peak B′′) and the second blue-shifts by 0.7 cm−1 (beginning of peak C′′). Finally, under peak C, two vibrational modes are found at 159.7 and 161.2 cm−1 for the bare MOF. These are similar to the modes of peak B but in this case the rigid displacement of the pyrazine together with the Fe atoms occurs in-plane. A shift to lower energies is found upon CO (CO2) adsorption from 159.7 to 156.7 (156.5) cm−1 and from 161.2 to 157.5 (159.6) cm−1 under peak C′ (C′′). In the case of CO adsorption, a new vibrational mode located at 160.9 is found under peak C′. This corresponds to a collective mode consisting of a libration of the pyrazines and the CO and an in-plane movement of the Pt.
Signature at 400 cm−1
The intense peak centered at 396 cm−1 in the experiment undergoes a red-shift to 383 cm−1 and a small decrease in intensity upon CO adsorption, while no significant change is found upon CO2 adsorption. In this region, the computed S(ω) for the bare MOF predicts an intense peak at ca. 400 cm−1, named D, and a smaller peak at ca. 411 cm−1. Upon CO adsorption, peak D shifts to lower energy and splits into peak D′ at 385 cm−1 and D′′ at 396 cm−1 (see Fig. 6). For CO2, the computed S(ω) exhibits a single peak, named D′′′, located almost at the same position as D (ca. 399 cm−1). For both molecules, we see a small peak centered at around 413 cm−1 which moves negligibly with respect to the bare material.For the bare MOF, peak D is a combination of seven vibrational modes (400.0, 400.3, 400.4, 400.4, 400.9, 403.6 and 405.0 cm−1). Two of these, at 403.6 and 405.0 cm−1, dominate the intensity of the S(ω) and are associated with a torsion of the pyrazines. With CO, they undergo a red-shift by 18.4 and 8.7 cm−1, giving rise to peak D′ at 385.1 cm−1 and peak D′′ at 396.3 cm−1, respectively. For CO2 the associated red-shift is smaller (7.0 and 6.4 cm−1) and gives rise to peak D′′′ (two modes at 396.6 and 398.6 cm−1). This result differs from the case of SO2 adsorption where the two modes are almost unchanged.48 The intensity of the other five modes under peak D is a factor of two lower and only two of them (400.0 and 400.3 cm−1) undergo a noticeable shift upon gas adsorption. These involve large displacements of the two Fe atoms and result in tilting and distortion of the octahedra together with an in-plane movement of the Pt atoms. Upon CO (CO2) adsorption, the first blue-shifts by 7.5 (8.6) cm−1 from 400.0 to 407.5 (408.5) cm−1 and falls under peak D′′ (D′′′). The second one red-shifts by 13.6 (12.3) cm−1 from 400.3 to 386.4 (388.0) under peak D′ (D′′′). The two remaining modes at 400.4 cm−1 under peak D are out-of-plane movements of CN groups which are anti-symmetric with respect to the Fe atom and result in a rigid movement of the Fe(N)4 planar complex. They undergo a small blue-shift to 401.1 and 401.8 cm−1 for CO and 401.1 and 401.4 cm−1 for CO2, respectively. Finally, the vibrational mode at 400.9 cm−1 consists of distortions of the two octahedra resulting primarily from the movement of the Fe atoms which are almost unchanged after adsorption (400.1 cm−1 for CO and 399.9 cm−1 for CO2).
Effect of amount of adsorbed gas on the spectral features
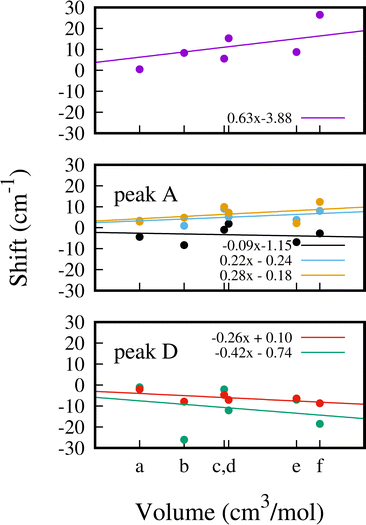
In Fig. 7 we show a comparison of the computed G(ω) for 1, 1.5 and 2 CO adsorbed molecules with the experimental INS data (see Fig. 6). In the presence of a single molecule, it can be observed that neither of the two characteristic signatures of adsorption occurs. The peaks at around 108, 138 and 400 cm−1 do not undergo any displacement, whereas in the other two cases, both peaks are shifted upon adsorption. We performed a similar comparison for 1 and 1.5 CO2 molecules adsorbed per f.u. (see Fig. S7, ESI†). In an attempt to differentiate the steric effect from the nature of the binding, we report the shift of the 6 most characteristic and intense modes as a function of the volume occupied by the adsorbed molecules. The computed van der Waals volume is considered in each case. Specifically, we report the shift upon adsorption for the mode at 107.9 cm−1 (upper panel), for the three modes under peak A (middle panel) and for the two modes dominating the intensity of peak D (lower panel) in Fig. 8.The energy of mode at 107.9 cm−1 exhibits the strongest dependence on the occupied volume upon adsorption, reaching a maximum displacement of 27 cm−1 when 2 CO per f.u. are adsorbed. Interestingly, when 1 SO2 (point c, 23.8 cm3 mol−1) and 1.5 CO per f.u. (point d, 24.2 cm3 mol−1) are considered, the displacement of this mode differs considerably by 9.7 cm−1 even though the occupied volume is similar in the two cases. This indicates a dependence not only on the volume but also on the nature of the gas and the associated interactions established within the cavity. For the three modes under peak A (137.8, 138.5 and 139.2 cm−1) we find overall a smaller shift upon adsorption and the correlation between energy shift and occupied volume is weaker, in particular for the mode at 137.8−1 (black data) which exhibits the weakest correlation with the gas volume.
The two modes under peak D (403.6 and 405.0 cm−1) overall red-shift upon adsorption. The mode at 403.6 cm−1 shows a strong dependence on volume and on the molecule choice, whereas the mode at 405.0 has a weak correlation between energy shift and occupied volume.
Binding mechanism
Carbon monoxide is a strong σ-donor and a good π-acceptor.53 It can donate electron charge from the σ-HOMO (highest occupied molecular orbital) orbital, mostly localized in the carbon atom, to an empty d-orbital of the metal and receive back electron charge from an occupied d orbital of the metal into the empty π*-LUMO (lowest unoccupied molecular orbital) orbitals (i.e. via backdonation). When it binds on top of an open-metal site with a square-planar coordination, a strong electron-donor σ-bonding can occur when the σ-HOMO orbital of the molecule can donate to the the dz2 orbital. In this case, the Pt(II) metal cation exhibits a doubly occupied dz2 and therefore cannot act as an electron acceptor. In order to decrease the repulsion, the CO tilts down in a configuration almost parallel to the Pt(CN)4 plane with the Pt–C–O bond angle being θ = 94.7° (PBE+D2). In the case of CO2 on top of the metal site, we find no mixing of the metal-molecule orbitals, as expected from an electrostatic/dispersion interaction (see PDOS in Fig. S8, ESI†).The strength of the π-acceptor interaction was computed by performing a Bader charge analysis using PAW pseudopotentials and the PBE+D3+BJ functional. For the CO on site A, the analysis revealed a small charge transfer from the MOF to the molecule of 0.05 electrons, confirming a weak backbonding interaction. A negligible charge transfer is predicted for CO2.
For CO, the metal–ligand charge transfer causes a decrease of the C–O bond order due to the antibonding character of the π*-LUMO orbitals. This is confirmed by the C–O bond distances being always larger for the CO adsorbed on site A (1.142 Å) than in site B (1.139 Å). The longer C–O bond distances can cause a red-shift of the stretching CO frequency with respect to the free CO. The stronger the backbonding, the weaker the C–O bond and the lower the stretching frequency. The computed C–O stretching frequency for gas phase CO appears at approx. 2123 cm−1 while upon adsorption on site A it is around 2092 cm−1. The typical red-shift for a strong backbonding interaction is normally more than 100 cm−1, e.g. the experimental shift for Cr(CO)6 is of ca. 143 cm−1.53 As expected, the stretching frequencies of the CO located between the pyrazines remain unchanged upon adsorption consistent with the absence of backbonding.
In the case of CO2, a backbonding interaction would increase the O–C–O bond distances due to the antibonding character of the π*-LUMO orbitals, resulting in lower stretching frequencies. Here, the O–C–O distances remain almost unchanged with respect to the free CO2 (1.172 Å versus 1.174 Å) and the symmetric and antisymmetric stretching frequencies shift by less than 10 cm−1.
The computed bond distances in site A using PBE+D2 are Pt–C = 3.37 Å for CO and Pt–C = 3.39 Å for CO2 while the total binding energies (including site A and site B) are 0.278 and 0.435 eV, respectively (see Fig. 2). These decrease to 0.029 (CO) and 0.002 (CO2) eV when the PBE functional is used without the Grimme correction, indicating that van der Waals interactions are dominating the binding in both cases. In order to further assess the role of the open metal site in the binding mechanism, we computed the binding energy of CO and CO2 adsorbed between two [Pt(CN)4] planes (representing site A) and between two pyrazines (representing site B) and removing the rest of the framework. This is done by fixing the atomic coordinates to the relaxed geometry in the MOF and by removing the pyrazine ligands and the planes respectively. We imposed cell parameters of a = b = c = 20 Å in both cases to avoid interactions between periodic images. We employed PBE+D2 for this comparison. For CO, the computed binding energies are 0.190 and 0.088 eV for the molecule adsorbed respectively on pseudo-site A and B. For CO2 these are 0.256 and 0.142 eV, respectively. This comparison indicates a stronger contribution of the [Pt(CN)4] plane to the binding energy. For SO2, a larger relative decrease in binding energy (up to 64.4%; it may be lower if a second binding site was possible for SO2) was predicted when comparing the full MOF and the [Pt(CN)4] fragments (see Table 1) in contrast with CO (31.4%) and CO2 (41.1%).
| SO248 | CO | CO2 | ||||
|---|---|---|---|---|---|---|
| E bind | d(S–Pt) | E bind | d(CA–Pt) | E bind | d(CA–Pt) | |
| PBE | 0.239 | 2.90 | 0.029 | 3.39 | 0.002 | 3.44 |
| PBE+D2 | 0.769 | 2.93 | 0.278 | 3.37 | 0.435 | 3.39 |
| PBE+D2+U | 0.617 | 2.93 | 0.283 | 3.37 | 0.453 | 3.39 |
| PBE+D2[U] | 0.730 | 2.93 | 0.284 | 3.37 | 0.445 | 3.39 |
We also compute the binding energies employing a DFT+U approach to improve the description of the localized d electrons54 and to study how the change in hybridization of the d states of Pt, upon Hubbard U correction, affects the binding mechanism. The U parameters are computed self-consistently using linear-response55 by employing ortho-atomic projectors, and are 5.2 eV for Pt and Fe 7.5 eV for Fe.48 The DFT+U binding energy computed by setting the atomic coordinates to the optimized PBE+D2 are 0.283 eV for CO and 0.453 eV for CO2 (see Table 1). These values, together with the bond distances CA–Pt (CA refers to the C atom of the molecule on site A), change negligibly when a full optimization of the geometry is performed. All the values of binding energies and bond distances are reported in Table S2 (ESI†). Because the use of DFT+U may lead to a bias in the calculation of total energy differences,56 we also report the binding energy computed using a DFT+U density-corrected approach. This consists in using the PBE+D2 total energy evaluated on the PBE+D2+U electronic density, an approach named PBE+D2[U].54 The computed binding energies using this approach by employing the DFT+D2 geometry (and the fully relaxed DFT+D2+U structure) are 0.284 eV (0.445 eV) and 0.291 eV (0.454 eV), respectively, for CO (CO2).
In the case of CO and CO2, the almost similar values of binding energies and bond distances obtained for DFT, DFT+U and DFT[U] is in agreement with a weak interaction between the gas and the open-metal site which is negligibly affected when the U is applied to the Pt atom. Conversely, for SO2, the interaction with the open-metal site is stronger and the use of Hubbard U approach further modifies the binding energy (see Table 1). Based on these results together with the above analysis of the binding mechanism, we conclude that both CO and CO2 adsorption occur via a physisorption mechanism.
4 Conclusion
By combining neutron scattering data and DFT calculations we determine the gas adsorption sites and fully characterize the adsorption mechanism of CO and CO2 in the Fe(pz)[Pt(CN)4] Hofmann-type clathrate. When the MOF adsorbs 2 CO molecules per f.u. these orient parallel to each other but perpendicular with respect to the pyrazine rings. In contrast, when the uptake is 1.5 CO2 per f.u., the molecules adsorbed on top of the open-metal cation (site A) orient perpendicular to the pyrazines, while the molecules in the center of the pore (site B) are pseudo-parallel resulting in ‘T’-shape configuration of neighbouring CO2. In both cases the guest molecules are parallel to the Fe[Pt(CN)4]∞ planes. The main signatures of the INS spectra upon adsorption of 2 CO and 1.5 CO2 per f.u. occur in the peaks located at ca. 100 cm−1 and 400 cm−1. The first blue-shifts significantly upon CO and CO2 adsorption, with a larger shift for CO, while the second slightly red-shifts only in the presence of CO. DFT calculations confirm these signatures and allow us to characterize the blue-shift as due to a hindered libration of the pyrazine and the out-of-plane movement of cyanide ligands when the gas is adsorbed. The red-shift of the peak at 400 cm−1 results mostly from a lowering in energy of a mode that involves a torsion of the pyrazine. The DFT-predicted energy of the modes yielding the most intense INS features is studied with respect to the pore volume occupied upon adsorption by different amounts and types of gas. The predicted shift of these modes shows that those at ca. 107.9 and 403.6 cm−1 are the most sensitive upon volume and the nature of the gas. For both CO and CO2, the adsorption mechanism is dominated by electrostatic and van der Waals forces (physisorption) with the latter dominating the binding. A weak backbonding metal-to-ligand charge transfer is predicted for the CO located on site A while no charge transfer was predicted for CO2.In conclusion, this work reports the gas adsorption mechanism of CO and CO2 in the Hofmann-like clathrate Fe(pz)[Pt(CN)4] for which large adsorption capacities were previously reported when compared to other MOFs with larger surface areas.27 We have made use of the information obtained from neutron diffraction, inelastic neutron scattering and density-functional theory calculations in a complementary way. The results suggest that only a few modes depend on the nature of the adsorbed gas and, although the use of these modes as a reference to selectively detect one gas over the other seems complicated, the experimental signatures are clearly different when the saturation points are reached.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work benefited from the support of ILL via the PhD contract of A. F. B. and the beamtime allocation under experiment numbers 5-22-795 (https://doi.ill.fr/10.5291/ILL-DATA.5-22-795), 7-05-506 (https://doi.ill.fr/10.5291/ILL-DATA.7-05-506) and 7-05-510 (https://doi.ill.fr/10.5291/ILL-DATA.7-05-510). Calculations were performed using resources granted by GENCI under the TGCC grant number A0130907211. Additionally, the Dahu platform of the CIMENT infrastructure, which is supported by the Rhone-Alpes region (GRANT CPER07 13 CIRA) and the Equip@Meso project, was employed for the calculations.References
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Metal–organic framework materials as catalysts, Chem. Soc. Rev., 2009, 38, 1450 RSC.
- Y.-B. Huang, J. Liang, X.-S. Wang and R. Cao, Multifunctional metal–organic framework catalysts: synergistic catalysis and tandem reactions, Chem. Soc. Rev., 2017, 46, 126–157 RSC.
- A. Herbst and C. Janiak, MOF catalysts in biomass upgrading towards value-added fine chemicals, CrystEngComm, 2017, 19, 4092–4117 RSC.
- M. Bagheri, M. Y. Masoomi and A. Morsali, A MoO3–Metal–Organic Framework Composite as a Simultaneous Photocatalyst and Catalyst in the PODS Process of Light Oil, ACS Catal., 2017, 7, 6949–6956 CrossRef CAS.
- P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Férey, R. E. Morris and C. Serre, Metal-Organic Frameworks in Biomedicine, Chem. Rev., 2012, 112, 1232–1268 CrossRef CAS PubMed.
- M. Ding, R. W. Flaig, H.-L. Jiang and O. M. Yaghi, Carbon capture and conversion using metal-organic frameworks and MOF-based materials, Chem. Soc. Rev., 2019, 48, 2783–2828 RSC.
- C.-T. Yang, A. R. Kshirsagar, A. C. Eddin, L.-C. Lin and R. Poloni, Tuning Gas Adsorption by Metal Node Blocking in Photoresponsive Metal-Organic Frameworks, Chem. – Eur. J., 2018, 24, 15167–15172 CrossRef CAS PubMed.
- H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Recent advances in gas storage and separation using metal–organic frameworks, Mater., 2018, 21, 108–121 CAS.
- J.-R. Li, R. J. Kuppler and H.-C. Zhou, Selective gas adsorption and separation in metal–organic frameworks, Chem. Soc. Rev., 2009, 38, 1477 RSC.
- L. He, Y. Liu, J. Liu, Y. Xiong, J. Zheng, Y. Liu and Z. Tang, Core-Shell Noble-Metal@Metal-Organic-Framework Nanoparticles with Highly Selective Sensing Property, Angew. Chem., Int. Ed., 2013, 52, 3741–3745 CrossRef CAS PubMed.
- H.-Y. Li, S.-N. Zhao, S.-Q. Zang and J. Li, Functional metal-organic frameworks as effective sensors of gases and volatile compounds, Chem. Soc. Rev., 2020, 49, 6364–6401 RSC.
- A. Gamonal, C. Sun, A. L. Mariano, E. Fernandez-Bartolome, E. Guerrero-SanVicente, B. Vlaisavljevich, J. Castells-Gil, C. Marti-Gastaldo, R. Poloni, R. Wannemacher, J. Cabanillas-Gonzalez and J. S. Costa, Divergent Adsorption-Dependent Luminescence of Amino-Functionalized Lanthanide Metal Organic Frameworks for Highly Sensitive NO2 Sensors, J. Phys. Chem. Lett., 2020, 11, 3362–3368 CrossRef CAS PubMed.
- B. Li, H.-M. Wen, W. Zhou, J. Xu and B. Chen, Porous Metal-Organic Frameworks: Promising Materials for Methane Storage, Chem, 2016, 1, 557–580 CAS.
- A. S. Bhown and B. C. Freeman, Analysis and Status of Post-Combustion Carbon Dioxide Capture Technologies, Environ. Sci. Technol., 2011, 45, 8624–8632 CrossRef CAS PubMed.
- G. T. Rochelle, Amine Scrubbing for CO2 Capture, Science, 2009, 325, 1652–1654 CrossRef CAS PubMed.
- Z. Hu, Y. Wang, B. B. Shah and D. Zhao, CO2 Capture in Metal-Organic Framework Adsorbents: An Engineering Perspective, Adv. Sustain. Syst., 2019, 3, 1800080 CrossRef.
- F. Feyzbar-Khalkhali-Nejad, E. Hassani, A. Rashti and T.-S. Oh, Adsorption-based CO removal: Principles and materials. J. Environ, Chem. Eng., 2021, 9, 105317 CAS.
- V. Niel, J. M. Martínez-Agudo, M. C. Muñoz, A. B. Gaspar and J. A. Real, Cooperative Spin Crossover Behavior in Cyanide-Bridged Fe(II)-M(II) Bimetallic 3D Hofmann-like Networks (M = Ni, Pd, and Pt), Inorg. Chem., 2001, 40, 3838–3839 CrossRef CAS PubMed , PMID: 11466039.
- Ü. Kökçam-Demir, A. Goldman, L. Esrafili, M. Gharib, A. Morsali, O. Weingart and C. Janiak, Coordinatively unsaturated metal sites (open metal sites) in metal-organic frameworks: design and applications, Chem. Soc. Rev., 2020, 49, 2751–2798 RSC.
- P. D. Southon, L. Liu, E. A. Fellows, D. J. Price, G. J. Halder, K. W. Chapman, B. Moubaraki, K. S. Murray, J.-F. Létard and C. J. Kepert, Dynamic Interplay between Spin-Crossover and Host-Guest Function in a Nanoporous Metal-Organic Framework Material, J. Am. Chem. Soc., 2009, 131, 10998–11009 CrossRef CAS PubMed.
- M. Ohba, K. Yoneda, G. Agustí, M. Muñoz, A. Gaspar, J. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Bidirectional Chemo-Switching of Spin State in a Microporous Framework, Angew. Chem., Int. Ed., 2009, 48, 4767–4771 CrossRef CAS PubMed.
- Z. Arcís-Castillo, F. Muñoz-Lara, M. Muñoz, D. Aravena, A. Gaspar, J. Sánchez-Royo, E. Ruiz, M. Ohba, R. Matsuda, S. Kitagawa and J. Real, Reversible Chemisorption of Sulfur Dioxide in a Spin Crossover Porous Coordination Polymer, Inorg. Chem., 2013, 12777–12783 CrossRef PubMed.
- C. H. Pham and F. Paesani, Guest-Dependent Stabilization of the Low-Spin State in Spin-Crossover Metal–Organic Frameworks, Inorg. Chem., 2018, 57, 9839–9843 CrossRef CAS PubMed.
- J. T. Culp, D.-L. Chen, J. Liu, D. Chirdon, K. Kauffman, A. Goodman and J. K. Johnson, Effect of Spin-Crossover-Induced Pore Contraction on CO2–Host Interactions in the Porous Coordination Polymers [Fe(pyrazine)M(CN)4] (M = Ni, Pt), EurJIC, 2013, 4, 511–519 Search PubMed.
- M. M. Deshmukh, M. Ohba, S. Kitagawa and S. Sakaki, Absorption of CO2 and CS2 into the Hofmann-Type Porous Coordination Polymer: Electrostatic versus Dispersion Interactions, J. Am. Chem. Soc., 2013, 135, 4840–4849 CrossRef CAS PubMed.
- T. Kosone, A. Hori, E. Nishibori, Y. Kubota, A. Mishima, M. Ohba, H. Tanaka, K. Kato, J. Kim, J. A. Real, S. Kitagawa and M. Takata, Coordination nano-space as stage of hydrogen ortho-para conversion, R. Soc. Open Sci., 2015, 150006 CrossRef PubMed.
- D. Alvarado-Alvarado, J. H. González-Estefan, J. G. Flores, J. R. Álvarez, J. Aguilar-Pliego, A. Islas-Jácome, G. Chastanet, E. González-Zamora, H. A. Lara-García, B. Alcántar-Vázquez, M. Gonidec and I. A. Ibarra, Water Adsorption Properties of Fe(pz)[Pt(CN)4] and the Capture of CO2 and CO, Organometallics, 2020, 39, 949–955 CrossRef CAS.
- G. Agustí, R. Ohtani, K. Yoneda, A. Gaspar, M. Ohba, J. Sánchez-Royo, M. C. Muñoz, S. Kitagawa and J. Real, Oxidative Addition of Halogens on Open Metal Sites in a Microporous Spin-Crossover Coordination Polymer, Angew. Chem., Int. Ed., 2009, 48, 8944–8947 CrossRef PubMed.
- R. Ohtani, K. Yoneda, S. Furukawa, N. Horike, S. Kitagawa, A. B. Gaspar, M. C. Muñoz, J. A. Real and M. Ohba, Precise Control and Consecutive Modulation of Spin Transition Temperature Using Chemical Migration in Porous Coordination Polymers, J. Am. Chem. Soc., 2011, 133, 8600–8605 CrossRef CAS PubMed.
- J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B: Condens. Matter, 1993, 192, 55–69 CrossRef.
- https://www.ill.eu/sites/fullprof/ .
- K. Momma and F. Izumi, VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. Ivanov, M. Jiménez-Ruiz and J. Kulda, IN1-LAGRANGE – the new ILL instrument to explore vibration dynamics of complex materials, J. Phys.: Conf. Ser., 2014, 554, 012001 CrossRef.
- ILL DATA. https://doi.ill.fr/10.5291/ILL-DATA.7-05-506, Proposal number 7-05-506.
- G. Kearley, J. Tomkinson, A. Navarro, J. López González and M. Fernández Gómez, Symmetrised quantum-mechanical force-fields and INS spectra: s-triazine, trichloro-s-triazine and pyrazine, Chem. Phys., 1997, 216, 323–335 CrossRef CAS.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfá, D. Brunato, R. Car, I. Carnimeo, C. Carvazzoni, S. de Gironcoli, P. Delugas, F. F. Ruffino, A. Ferreti, N. Mazari, I. Timrov, A. Urru and S. Baroni, QUANTUM ESPRESSO toward the exascale, J. Chem. Phys., 2020, 152, 154105-1–154105-11 CrossRef PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Dispersion-Corrected Mean-Field Electronic Structure Methods, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Optimized pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover books on physics; Dover Publications, 1996 Search PubMed.
- D. Price and J. Carpenter, Scattering function of vitreous silica, J. Non-Cryst. Solids, 1987, 92, 153–174 CrossRef CAS.
- S. N. Taraskin and S. R. Elliott, Connection between the true vibrational density of states and that derived from inelastic neutron scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 117–123 CrossRef CAS.
- A. Fernández-Blanco, L. Piñeiro-López, M. Jiménez-Ruiz, S. Rols, J. A. Real, J. A. Rodríguez-Velamazán and R. Poloni, Probing the SO2 Adsorption Mechanism in Hofmann Clathrates via Inelastic Neutron Scattering and Density Functional Theory Calculations, J. Phys. Chem. C, 2022, 126, 8090–8099 CrossRef.
- A. Fernández-Blanco, L. A. Mariano, L. Piñeiro-López, J. A. Real, J. S. Costa, R. Poloni and J. A. Rodríguez-Velamazán, Hidden ordered structure in the archetypical Fe(pyrazine)[Pt(CN)4] spin-crossover porous coordination compound, CrystEngComm, 2022, 24, 6349–6356 RSC.
- J. A. Rodríguez-Velamazán, M. A. González, J. A. Real, M. Castro, M. C. Muñoz, A. B. Gaspar, R. Ohtani, M. Ohba, K. Yoneda, Y. Hijikata, N. Yanai, M. Mizuno, H. Ando and S. Kitagawa, A Switchable Molecular Rotator: Neutron Spectroscopy Study on a Polymeric Spin-Crossover Compound, J. Am. Chem. Soc., 2012, 134, 5083–5089 CrossRef PubMed.
- R. Poloni, D. Machon, M. V. Fernandez-Serra, S. Le Floch, S. Pascarelli, G. Montagnac, H. Cardon and A. San-Miguel, High-pressure stability of Cs6C60, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125413 CrossRef.
- G. Félix, M. Mikolasek, H. Peng, W. Nicolazzi, G. Molnár, A. I. Chumakov, L. Salmon and A. Bousseksou, Lattice dynamics in spin-crossover nanoparticles through nuclear inelastic scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 024422 CrossRef.
- G. Miessler; P. Fischer and D. Tarr, Inorganic Chemistry, Pearson Education, 5th edn, 2013 Search PubMed.
- L. A. Mariano, B. Vlaisavljevich and R. Poloni, Improved Spin-State Energy Differences of Fe(II) Molecular and Crystalline Complexes via the Hubbard U-Corrected Density, J. Chem. Theory Comput., 2021, 17, 2807–2816 CrossRef CAS PubMed , PMID: 33831303.
- I. Timrov, N. Marzari and M. Cococcioni, Hubbard parameters from density-functional perturbation theory, Phys. Rev. B, 2018, 98, 085127 CrossRef.
- L. A. Mariano, B. Vlaisavljevich and R. Poloni, Biased Spin-State Energetics of Fe(II) Molecular Complexes within Density-Functional Theory and the Linear-Response Hubbard U Correction, J. Chem. Theory Comput., 2020, 16, 6755–6762 CrossRef CAS PubMed , PMID: 33108722.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00670k |
| This journal is © the Owner Societies 2023 |