Protonation of serine: conformers, proton affinities and gas-phase basicities at the “gold standard” and beyond

Abstract

The potential energy surfaces (PESs) of serine and its protonated counterparts are investigated to determine the structures of the minima. A total of 95 neutral serine, 15 N-(amino-) and 46 O-(carbonyl-)protonated serine conformers are found. Their relative energies, geometries and harmonic vibrational frequencies are determined at the MP2/aug-cc-pVDZ level of theory. To obtain highly accurate thermodynamic values, further computations are performed: the ten conformers with the lowest relative energies from each molecule type (neutral, N- and O-protonated) are further optimized using the explicitly correlated CCSD(T)-F12a/cc-pVDZ-F12 method (for neutral serine, harmonic vibrational frequencies were also computed). In addition, auxiliary corrections were determined: basis-set effects up to CCSD(T)-F12b/cc-pVQZ-F12, electron correlation effects up to CCSDT(Q), core correlation and second-order Douglas–Kroll relativistic effects along with zero-point energy contributions. Two important thermodynamic parameters (at 298.15 K), proton affinity (PA)/gas-phase basicity (GB) are calculated considering the two different protonation sites: 218.05 ± 0.2/209.86 ± 0.6 kcal mol⁻¹ and 205.87 ± 0.2/196.36 ± 0.3 kcal mol⁻¹ for the amino and carbonyl sites, respectively. The uncertainty of the determined values was approximated based on various sources including auxiliary corrections, basis-set effects, harmonic vibrational frequencies.

---

I. Introduction

Amino acids are some of the most important and fundamental molecules of life. For this reason, they have been investigated intensively both theoretically and experimentally. Their conformational study leads to accurate vibrational and rotational data that can be used in experiments to identify them, especially in interstellar media (where traces of amino acids, including serine have been detected), and to study formational processes, we need more and more accurate results.^1–8 Amino acids are bulky, yet quite flexible molecules, which makes their study complicated. The two thermodynamic parameters, absolute proton affinity (PA) and gas-phase basicity (GB) are important values in biochemistry, in protonation processes.⁹ They can also be used to explain fragmentation reactions in mass spectrometry as they are related to the proton affinities of individual amino acids^10,11 and to determine whether the N- or C-terminal remains uncharged.¹² On the experimental side, the results for serine will be discussed in more detail in the corresponding sections, here we would only like to highlight the main points. The conformations of the neutral amino acid have been studied using matrix-isolation FT-IR spectroscopy^13–15 or FT-MW spectroscopy.¹⁶ In total, they prove the existence of 13 different conformers. The field of protonated serine is not so well explored: two of the protonated serines have been detected by Wu¹⁷ by IRMPD spectroscopy and there are indications that the protonated serine also forms dimers/octamers.^18,19 For the PA and GB values, there are Fourier transform ion cyclotron resonance mass spectrometry^20,21 and electrospray ionization-ion mass spectrometry measurements,²² and there are four reviews on the topic.^9,17,23,24

From the theoretical side, many authors have been involved in the search for serine and protonated serine conformers.^14,25–34 For neutral serine, we found the one published by He and Allen²⁵ to be the highest in terms of the level of theory and in the number of conformers found. They systematically mapped the conformational space with rotating the most flexible parts of the molecule, and performed geometry optimizations at the RHF/6-31G* level. In total they found 89 conformers and after higher level, MP2/cc-pVTZ optimizations, this number was reduced to 85. The 12 lowest-energy conformers were subjected to MP2/aug-cc-pVTZ reoptimizations together with vibrational frequency and correction computations while the important spectroscopic parameters of these structures were also determined. For protonated serine, Miao et al.³⁰ and Riffet et al.³² carried out convenient search using density functional theory. In Miao et al.'s work, 108 initial geometries for protonated serine were optimized, from which they obtained 14 different amino protonated conformers at the B3LYP/6-31G* level and they further optimized them at B3LYP/6-311+G** level. They mentioned that along with the preferred amino site, carbonyl protonation can also occur, however they did not discuss this further in their paper. As they examined serine conformers too (they found 74 of them, but also investigated deprotonation), PA and GB values were calculated. Riffet and co-workers explored the conformational space of the neutral, protonated (and deprotonated) serine in two ways: the first one was based on a chemical approach, they constructed different conformers with rotation along C–C, C–N or C–O bonds leading to several hundreds of trial structures while the second strategy involved using the polarizable AMOEBA force field. They optimized geometries at B3LYP, B97-D and M06-2X levels using the 6-31+G(d,p) basis set. A total of 74 neutral and 13 amino-protonated conformers were found, while the lowest-energy ones were further analyzed with composite methods up to G4. The PA and GB values have also been determined with quantum chemical tools by many authors.^{11,17,26,31,32,35–38} In general, we cannot find coupled-cluster results on this topic, as the size of these molecules can be treated more conveniently with DFT. When we have ab initio methods, the highest level of geometries is MP2, while searches are performed with HF method or MP2 with small basis sets. As it has been discussed which density functional to use to obtain accurate thermodynamic properties with DFT,³⁹ whereas He et al.⁴⁰ examined the accuracy of ab initio methods using different corrections for a large number of test molecules. It was shown that MP2 values contain large errors compared to coupled-cluster results.

Similar to our previous studies on amino acids,^41–44 we would like to add novelties to this theoretical field by the means of possibly revealing new conformers for both the neutral and protonated serine, using a higher level of theory for the conformational mapping. For the protonated serine we are also investigating the protonation at other site(s), in particular the yet neglected carbonyl site. In terms of the applied level of theory, we aim to reach the “gold standard”, as we report the first coupled-cluster geometries of the amino acid serine and its protonated analogue, with harmonic vibrational frequencies computed at CCSD(T)-F12a/cc-pVDZ-F12 level for the neutral amino acid, and at MP2/aug-cc-pVDZ level for the protonated serine. To go beyond the “gold standard” level, we take many corrections into account: basis-set effects up to quadruple zetas, electron correlation effects up to perturbative quadruples, core correlation corrections, and second-order scalar relativistic corrections. The PA and GB values are also determined considering large number of conformers at this high level of theory, with appropriate approximations of the uncertainty.

II. Computational details

A. Conformers of serine and protonated serine

To begin our study, we need to find as many conformers of serine (both the neutral and protonated forms) as possible, to be able to achieve the desired accuracy. We take the global minimum conformer of He and Allen²⁵ as the starting point of the search for the serine geometries. In the case of the protonated conformers we need to investigate the possible protonation sites. Similarly to cysteine,⁴³ we attach a proton to the amino, carbonyl and the two hydroxyl groups, getting HOOC-CH-(NH₃⁺)-CH₂-OH, ⁺(HO)₂C-CH-(NH₂)-CH₂-OH, ⁺(H₂O)OC-CH-(NH₂)-CH₂-OH, and HOOC-CH-(NH₂)-CH₂-OH₂⁺, respectively. For each protonation site, we generate two initial geometries: the protonated amino group is rotated by 60°, the protonated carbonyl group is in either cis or trans orientation, while for the protonated hydroxyl groups the H–O–H planes are perpendicular to each other. We optimize these structures at the MP2/aug-cc-pVDZ level of theory and also perform harmonic vibrational frequency computations. Note that the protonation of the carboxyl group's hydroxyl part does not lead to stable structures, analogous to glycine and cysteine, even after testing with attaching protons to different conformers. Upon investigating the protonation of the side chain's functional group analogously, we obtain the same results, it does not lead to stable geometries, whereas the protonation of the thiol group was a possibility for cysteine. We can therefore speak of N-(amino-) and O-(carbonyl-) protonated serine conformers.

To systematically map the conformational space of the species, we have to consider which torsional angles describe the internal rotations. The sketches in Fig. 1 show the axes corresponding to these rotations. In the case of the neutral (Fig. 1A) and N-protonated serine (Fig. 1B), we have to rotate five parts of the molecule: the (protonated) amino, the carboxyl, the two hydroxyl groups and the side chain. For the O-protonated molecule (Fig. 1C) we have an additional important axis (six in total), the protonated carbonyl group. To reduce the number of the initial geometries, we need to think about symmetry. Both the neutral and protonated forms have C₁ point-group symmetry if we consider the whole molecule, but the protonated amino group has a three-fold rotational symmetry, thereupon reducing our N-protonated dataset to one third. The protonated carboxyl group also has planar symmetry halving the number of the O-protonated initial geometries.

Fig. 1 Sketches describing the internal rotations of the neutral (A), N-protonated (B) and the O-protonated (C) serine molecules.

The computational time of the whole mapping process depends on two things: the number of the initial structures and the time needed for the optimization of these geometries. The first is determined by the resolution of the rotations and the second by the level of theory. We choose 60° for the step size (6 steps for each axis) and the MP2⁴⁵ method with cc-pVDZ⁴⁶ and 6-31++G**⁴⁷ basis sets based on our results for cysteine.⁴³ Thus, for each basis set, the number of the initial geometries to be optimized is 6⁵ = 7776 for the neutral serine (Fig. 1A), 6⁵/3 = 2592 for the N-protonated form (Fig. 1B, considering the three-fold symmetry of the protonated amino group) and 6⁶/2 = 23 328 for the O-protonated serine (Fig. 1C, considering the two-fold symmetry of the protonated carboxyl group). In the next step, the different optimized geometries of the neutral and protonated counterparts are selected separately for both basis sets. The selection is based on an energy and a geometry constraint: the relative energy of the structures must differ by at least 0.01 kcal mol⁻¹ and/or the A rotational constant must differ by at least 3 × 10⁻⁴ cm⁻¹. At the selected stationary points we perform MP2/aug-cc-pVDZ⁴⁶ geometry optimizations and we also compute the harmonic vibrational frequencies to determine whether we have a saddle point or a minimum. For the data analysis, we use our own program, written in Python, while the ab initio electronic structure computations are performed using the MOLPRO⁴⁸ and MRCC^49,50 program packages.

B. Benchmark structures and energies

We take the ten lowest-energy conformers (based on the MP2/aug-cc-pVDZ relative energies) of the neutral, N-protonated and O-protonated serine and perform further benchmarking using the explicitly-correlated coupled-cluster singles, doubles and perturbative triples method (CCSD(T)-F12a)^51,52 with three different basis sets. With the cc-pVDZ-F12⁵³ basis set, we reoptimize the MP2 geometries and even perform harmonic vibrational frequency computations (the latter only for the neutral forms), while with the cc-pVTZ-F12 and cc-pVQZ-F12 basis sets we determine single-point energies. For the QZ basis sets, the CCSD(T)-F12b method is recommended, as it is expected to be more accurate,^48,54,55 so we also apply this method and finally use these relative energies for the benchmark results. These composite relative energies consist of the following (each computation is performed at the CCSD(T)-F12a/cc-pVDZ-F12 geometries):

– CCSD(T)-F12b/cc-pVQZ-F12 single-point relative energies.

– Coupled-cluster triples (δT)⁵⁶ and perturbative quadruples (δ(Q))⁵⁷ corrections. These are computed with the 6-31G basis set as defined below. In the case of the glycine⁴¹ it was shown that the 6-31G basis set grants sufficient accuracy in comparison to smaller (3-21G) and larger (cc-pVDZ) basis sets.

δT = CCSDT/6-31G − CCSD(T)/6-31G, (1)

δ(Q) = CCSDT(Q)/6-31G − CCSDT/6-31G. (2)

– Core correlation corrections (Δ_core), defined as the following:

Δ_core = AE-CCSD(T)-F12a/cc-pCVTZ-F12 − FC-CCSD(T)-F12a/cc-pCVTZ-F12. (3)

The all-electron (AE) and frozen-core (FC) energies are computed at the CCSD(T)-F12a/cc-pCVTZ-F12 level of theory.⁵⁸ In the former case we correlate not only the electrons on the valence shells, but the 1s² electrons for the C, N and O atoms as well.

– Second-order Douglas–Kroll (DK)⁵⁹ relativistic corrections (Δ_rel.) are obtained using the AE-CCSD(T) method with the aug-cc-pwCVTZ-DK⁶⁰ basis set:

Δ_rel. = DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK − AE-CCSD(T)/aug-cc-pwCVTZ. (4)

– Zero-point vibrational energy corrections (Δ_ZPE) characterized by the MP2/aug-cc-pVDZ harmonic vibrational frequencies.

Finally, we get the benchmark electronic (equilibrium, E_e) and adiabatic (ZPE corrected, H₀) energies by summarizing the preceding values:

E_e = CCSD(T)-F12b/cc-pVQZ-F12 + δT + δ(Q) + Δ_core + Δ_rel; (5)

H₀ = CCSD(T)-F12b/cc-pVQZ-F12 + δT + δ(Q) + Δ_core + Δ_rel + Δ_ZPE. (6)

C. Proton affinity and gas-phase basicity computations

Consider the following gaseous reaction:

BH⁺_(g) → B_(g) + H⁺_(g), (R1)

where BH⁺ is the protonated conjugate acid, B is the analogue gaseous base and H⁺ is a free proton. The PA and the GB equal to the enthalpy (ΔH) and the Gibbs free energy (ΔG) changes of the above reaction, respectively. To determine these values theoretically, the ab initio computations alone are not sufficient, therefore we need the help of the canonical ensembles. We treat the rotations and the vibrations with the rigid rotor and harmonic oscillator models. Using standard statistical mechanics expressions, we obtain the thermal corrections for the translational, vibrational and rotational enthalpies and entropies. The different conformers are weighted by their populations according to the Boltzmann-distribution:where x_i is the relative population of the ith conformer and is the molar standard Gibbs free energy of the ith conformer relative to the most stable conformer.

III. Results and discussion

1. Conformer search

For the neutral serine, out of the 7776 initial geometries, the cc-pVDZ basis set yields 184, while the 6-31++G** basis set suggests 168 potential minimum candidates with the MP2 method, based on our energy/geometry constraints. Further optimization (and vibrational analysis) of these structures with the aug-cc-pVDZ basis set yields 95 minimum geometries in total. The difference between the number of candidates and the final minimum geometries can be explained by the fact, that many separate conformers converge to the same minimum at higher level of theory (of course, there are transition states and non-convergent computations, as well). The energy distribution of the 95 minimum structure can be seen in Fig. 2. We have points practically continuously from 0.00 kcal mol⁻¹ to 11.21 kcal mol⁻¹, and here we have a roughly 2 kcal mol⁻¹ jump as the last two minima has the relative energies of 13.65 and 13.68 kcal mol⁻¹, respectively. The most comprehensive systematic ab initio search for the serine conformers was published by He and Allen in 2016,²⁵ where they found 85 different geometries, which is the highest number in the current literature, however it is still 10 less, than present in this study. For the cysteine,⁴³ we showed that the two initial basis sets can be utilized together for amino acid conformer search, as they both found unique geometries (a geometry that was found by only one of the two basis sets). In the present case, the smaller cc-pVDZ basis set reveals ten (one with 1.52 kcal mol⁻¹ relative energy) unique conformers, while the larger, diffuse function containing 6-31++G** basis set gives only one unique conformer, with 3.95 kcal mol⁻¹ relative energy.

Fig. 2 MP2/aug-cc-pVDZ relative energy distributions of the 95 neutral (green), 15 N-protonated (blue) and the 46 O-protonated (red) serine conformers.

The systematic mapping for the protonated serine was performed separately for the two possible sites (amino and carbonyl). From the 2592 initially N-protonated geometries we obtain 34 and 27 different structures with the cc-pVDZ and 6-31++G** basis sets, respectively. The initially O-protonated data set, yields 136 and 129 arrangements to be optimized with the aug-cc-pVDZ basis set. Filtering the MP2/aug-cc-pVDZ results, we obtain 15 amino-protonated conformers, and there is only one unique conformer (found with the cc-pVDZ basis set), N12, in the higher energy region. The energy distribution of the N-protonated conformers is shown in Fig. 2. There are four conformers in the low energy region (≤4.14 kcal mol⁻¹), with the remainder in the 8.89–13.97 kcal mol⁻¹ range. In total, we have 46 carbonyl-protonated minima, in this case, unique conformers have been revealed by both basis sets, 8 by the smaller one and 4 by the larger. These have diverse relative energies, as they are distributed in the whole energy range (0.00–29.17 kcal mol⁻¹, Fig. 2). The curve can be divided into three parts: one consists of the global minimum, the second part is in the 5.87–11.56 kcal mol⁻¹ range with 13 conformers while the rest is in the last region, between 16.02 and 29.17 kcal mol⁻¹. The energy difference between the highest N-protonated and the lowest O-protonated conformer is 0.92 kcal mol⁻¹, which means that this low-energy conformer can be easily formed experimentally also. Upon analyzing the initially O-protonated data set, we have found some interesting “Cyclized” by-products similarly like in the case of the analogous cysteine amino acid.⁴³ These structures have a three-membered N–C–C ring, one of which is shown in Fig. 3. In addition to this, five other by-product minima are found, they differ in the orientation of the three OH groups (for geometries, see ESI†). They have energies of 37.10–41.44 kcal mol⁻¹ relative to the N-protonated lowest-energy minimum, which is in the range of the carbonyl-protonated conformers, so once again, the analysis has to be supplemented with bond matrices. Previous PES investigation focused only on the amino-protonated conformers and they found 14 (ref. 30) and 13 (ref. 32) amino-protonated structures, whereas we have uncovered 15 N-protonated and 46 O-protonated conformers.

Fig. 3 One of the six Cyclized (N–C–C ring) by-product minimum structures found upon the search for O-protonated serine conformers.

2. Benchmark geometries, energies and corrections

At temperatures of 0 K and 298.15 K only the conformers with the lowest relative energies are populated according to the Boltzmann-distribution, so in order to obtain PA and GB values with high accuracy, we took the first ten neutral, amino- and carbonyl-protonated serine conformers, optimized their structures with CCSD(T)-F12a/cc-pVDZ-F12 and computed different energy corrections. The selection was based on the MP2/aug-cc-pVDZ relative energies (it is important to note, since there are changes in the energy order if we consider the CCSD(T)-F12b/cc-pVQZ-F12 or the benchmark energies).

The final nine neutral serine conformers can be seen in Fig. 4. The Roman numerals increase with increasing benchmark energies. Conformer number 5 (MP2/aug-cc-pVDZ relative energy: 1.52 kcal mol⁻¹) also converges (at the coupled-cluster level) to the global minimum structure, I. To determine, which MP2 geometry belongs to the global minimum, we compared the rotational constants of conformer 1 and 5 to I, and we found that conformer 1 corresponds to I. We will use MP2 harmonic frequencies later, so this determining step is crucial. All nine serine conformers, except V and IX are stabilized by the strong O–H⋯N interaction between the amino group and the hydroxyl group of the carboxyl group or the sidechain. Weaker O–H⋯O and N–H⋯O intramolecular interactions can also be observed in all structures. The computed relative energies are summarized in Table 1. Previous results showed, that for the analogous cysteine, the MP2 geometries might have larger errors than the usual, so we have included a column with the relative energies computed by the coupled-cluster method at the MP2 geometries. The average difference between the CC computations with the MP2 geometries and with the CC geometries is 0.01 kcal mol⁻¹, so for this amino acid, the lower-level optimization seems to be correct. There is a change in the order of the minima as we increase the level of theory, as conformer number 4 becomes III and number 3 corresponds to IV. The explicitly correlated CCSD(T)-F12a single-point computations with the cc-pVTZ-F12 and cc-pVQZ-F12 basis sets show excellent basis-set convergence as the discrepancy is smaller than 0.01 kcal mol⁻¹ in most of the cases, but never reaches 0.02 kcal mol⁻¹. Our previous computations showed that there is not much difference between the relative energies given by the CCSD(T)-F12a and CCSD(T)-F12b methods for cysteine, but we have tested this also for serine, and obtained similar results, an effect less than 0.01 kcal mol⁻¹ for each conformer. The computed auxiliary corrections for the neutral amino acid are shown in Fig. 5 (left). The correlation of the 1s² electrons of the molecule changes the relative energies by an average of 0.02 kcal mol⁻¹. This contribution is the highest for V, VIII and IX: 0.04, 0.03 and 0.03 kcal mol⁻¹, respectively. Second-order Douglas–Kroll relativistic effects are negligible, as they barely reach 0.01 kcal mol⁻¹ with rounding. Full-T and (Q) corrections vary in signs and magnitudes as they range from −0.02 to 0.04 kcal mol⁻¹, the sum of them is important, as the highest values are 0.05 kcal mol⁻¹ for IV and 0.07 kcal mol⁻¹ for IX. The sum of the auxiliary corrections is 0.04 kcal mol⁻¹ on average with the maximum of 0.09 kcal mol⁻¹ for IX. Adding these to the CCSD(T)-F12b/cc-pVQZ-F12 single-point energies gives the benchmark relative equilibrium energies. There is no change in the order of the conformers, and the uncertainty can be estimated with the basis-set effect and the average of the summarized auxiliary corrections . From the vibrational frequency computations, we can calculate the zero-point energy corrections. For the neutral serine, we compute ZPEs with MP2 and CC methods too, considering the computing cost and the increase in the accuracy, we consistently use the MP2 vibrational frequencies. On average, the difference between the ZPE correction of the two levels of theory is 0.06 kcal mol⁻¹, in agreement with the results for cysteine.⁴³ As indicated in Table 1, these values are negative, except for III, and about ten times larger than the previous corrections. Finally, we obtain the 0 K relative enthalpy values. There are two changes in the order of the conformers, III–IV and VIII–XI. The uncertainty here can be approximated from four sources: the basis-set effects (0.01 kcal mol⁻¹), the auxiliary corrections (0.04 kcal mol⁻¹), the difference between the MP2 and CC ZPE corrections (0.06 kcal mol⁻¹) and the neglected anharmonicity (which can have an effect of 0.01–0.1 kcal mol⁻¹ for amino acids,^40,61,62 we consider it to be 0.05 kcal mol⁻¹ uniformly), in conclusion, we suggest . The thermal corrections (from −0.06 to 0.36 kcal mol⁻¹) give us the 298.15 K enthalpies, the order is restored to the original but upon considering the entropic contributions (from −0.78 to 0.16 kcal mol⁻¹), there are many exchanges, and even the global minimum will be different (II). The thermal corrections are very sensitive to low-frequency vibrations, so the accuracy of these last two values is difficult to estimate, definitely worse, than in the case of the 0 K values.

Fig. 4 Structures of the first nine neutral serine conformers at the CCSD(T)-F12a/cc-pVDZ-F12 level of theory. The selection was based on the MP2/aug-cc-pVDZ relative energies and the numbering reflects the benchmark energy order.

Table 1 Benchmark relative energies, corrections, relative enthalpies (at 0 K and 298.15 K) and relative Gibbs free energies (298.15 K) of the nine lowest-lying serine conformers. All data are in kcal mol⁻¹

Name^a	MP2	CC//MP2	CCSD(T)-F12a			CCSD(T)-F12b	Σ corr.	ΔEe^i	Δ ZPE	ΔH0^k	ΔH298.15^l	ΔG298.15^m
	aVDZ^b	DZ^c	DZ^d	TZ^e	QZ^f	QZ^g
a Conformer name based on the benchmark/MP2 relative energies. b MP2/aug-cc-pVDZ relative energies at MP2/aug-cc-pVDZ geometries. c CCSD(T)-F12a/cc-pVDZ-F12 relative energies at MP2/aug-cc-pVDZ geometries. d CCSD(T)-F12a/cc-pVDZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. e CCSD(T)-F12a/cc-pVTZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. f CCSD(T)-F12a/cc-pVQZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. g CCSD(T)-F12b/cc-pVQZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. h Sum of the auxiliary corrections: Δcore + Δrel + δT + δ(Q). i Benchmark relative equilibrium energies obtained by CCSD(T)-F12b/cc-pVQZ-F12 + Σcorr. j Zero-point corrections obtained by MP2/aug-cc-pVDZ harmonic vibrational frequencies. k Benchmark adiabatic relative energies obtained as ΔEe + ΔZPE. l Relative enthalpy at 298.15 K. m Relative Gibbs free energy at 298.15 K.
I/1	0.00	0.00	0.00	0.00	0.00	0.00	+0.00	0.00	+0.00	0.00	0.00	0.00
II/2	0.42	0.52	0.50	0.50	0.49	0.48	+0.04	0.52	−0.27	0.25	0.44	−0.09
III/4	0.92	0.62	0.63	0.63	0.64	0.64	+0.01	0.64	+0.10	0.74	0.68	0.84
IV/3	0.88	0.88	0.87	0.86	0.85	0.85	+0.05	0.90	−0.34	0.56	0.69	0.44
V/6	1.52	1.48	1.47	1.47	1.47	1.47	+0.03	1.50	−0.16	1.35	1.48	1.17
VI/7	1.55	1.82	1.82	1.82	1.82	1.82	−0.01	1.81	−0.16	1.65	1.78	1.58
VII/8	1.65	1.88	1.87	1.87	1.87	1.87	−0.02	1.85	−0.09	1.76	1.84	1.74
VIII/9	1.94	2.20	2.20	2.20	2.19	2.19	+0.04	2.22	−0.27	1.95	2.15	1.48
IX/10	2.24	2.47	2.45	2.46	2.45	2.45	+0.09	2.53	−0.61	1.92	2.28	1.50

---

Fig. 5 The auxiliary energy corrections of the deepest serine (left), N-protonated serine (middle) and O-protonated serine (right) minima. For further details, see eqn (1)–(4).

Experimentally, the gas-phase neutral serine conformers are well studied. We have summarized these findings in Table 2, in comparison with our structures. In 2004, Lambie and co-workers¹³ reoptimized the serine structures from a previous study at DFT/B3LYP/6-31++G** level of theory and performed frequency computations. Based on the calculated spectra, they were able to validate the presence of their four lowest-energy conformers with matrix-isolation FT-IR spectroscopy, in Ar at 15 K. One year later, Jarmelo et al.¹⁴ analyzed the potential energy surface of serine and optimized the found geometries with DFT/B3LYP/6-31++G**, and computed their frequencies. They also used matrix-isolation infrared spectroscopy technique to identify nine conformers in Ar matrix. In 2007 the group of Alonso¹⁶ also explored the conformers of serine theoretically and then did experiments. They vaporized solid serine by laser ablation, expanded it in supersonic jet and recorded the spectrum using the Fourier transform microwave method. They recorded the existence of seven conformers using the predicted rotational and quadrupole coupling constants. More recently, in 2015, an international collaboration¹⁵ also revisited the previously reported conformers theoretically, took the fourteen lowest-energy structures, reoptimized them and calculated their vibrational spectra and IR intensities. They evaporated serine into a vacuum chamber, mixed it with argon or nitrogen and performed matrix-isolation IR spectroscopy measurements and also using NIR laser irradiation to change the conformer ratios. At the end, they measured nine of the predicted structures, two of which are indistinguishable with this experimental setup (7 and 10 in their nomenclature), but their coexistence is suggested. A conformer with very short life-time was also detected, but its geometry could not be clearly identified. In Table 2 we have also included our results with three different nomenclatures, where it is possible. The naming is based on MP2/aug-cc-pVDZ, our benchmark relative energies and the calculated relative Gibbs free energies. The order of the conformers in our and other authors’ work largely overlap and the absence of our conformer 5 is in agreement with the fact, that upon higher-level geometry optimization, it converges to the global minimum. However, the most important conclusion is that summarily ten serine conformers were detected in different experimental setups, some of them by multiple groups, we have also found these geometries on the potential energy surface and we have also revealed other possible minima.

Table 2 Comparison of the experimentally detected conformers with our computed structures found during the mapping of the serine PES

This work^a	Blanco^b	Jarmelo^c	Lambie^d	Najbauer^e^f
a Conformer names based on: arabic numerals: MP2/aug-cc-pVDZ relative energies, Roman numerals: benchmark relative energies present in this study, (arabic numerals): 298.15 K relative Gibbs free energies. b Conformer names based on hydrogen bond motifs (ref. 16). c Conformer names based on DFT/B3LYP/6-311++G(d,p) relative energies after ZPE correction (ref. 14). d Conformer names based on DFT/B3LYP/6-31++G** relative energies after ZPE correction (ref. 13). e Conformer names based on 0 K relative Gibbs free energies acquired by DFT/B3LYP/6-31++G** and using harmonic frequencies (ref. 15). f Authors have found an additional, short-lived conformer, but they could not determine its structure doubtlessly. g Conformer 5 converged to conformer I during geometry optimization at higher level of theory. h Authors could not distinguish between these two conformers unambiguously in the experiment, but they concluded that both of them were present in the matrix.
1/I/(2)	IIb	2	SER2	2
2/II/(1)	Ia	1	SER1	1
3/IV/(4)	IIb	4	SER4	4
4/III/(3)	IIc	3	SER3	3
5/I/(2)^g
6/V/(5)	IIIβb	7		7^h
7/VI/(8)	IIa	5		6
8/VII/(9)		9
9/VIII/(6)		6		5
10/IX/(7)
11		8
12	IIIβc			10^h

---

The coupled-cluster geometries of the ten N-protonated conformers are shown in Fig. 6. The Roman numerals increase with increasing benchmark relative energies and the lower index indicates the protonation site. Obviously, the O–H⋯N hydrogen bonds are prohibited by the protonation, but we can identify N–H⋯O and the weaker O–H⋯O–H interactions. Experimentally, two amino protonated conformers have been detected by IRMPD spectroscopy,⁶³ I_N/N1 (as SH01) and VIII_N/N8 (as SH02), and recent studies also involve protonated serine dimers/octamers, not monomers.^18,19 The computed relative energies are given in Table 3. The coupled-cluster computations based on the MP2 geometries and the CC optimized structures agree within a few hundredths of a kcal mol⁻¹, so there is no significant geometry effect. With applying the more sophisticated CC method, the conformers N6 and N7 get changed in the order of the structures. The triple and quadruple zeta basis sets show nice convergence, the largest deviation is in the case of X_N, where the difference is ∼0.03 kcal mol⁻¹ between the TZ and QZ results. The amino-protonated conformers do not show significant differences whether we use the F12a or F12b methods with the cc-pVQZ-F12 basis set. In Fig. 5 (middle), it can be seen that the core correction is negligible for the first three conformers, but becomes more severe for the last ones, as for VII_N, VIII_N and IX_NΔ_core is 0.06, 0.07 and 0.07 kcal mol⁻¹, respectively. On average the core correction is 0.04 kcal mol⁻¹. The Δ_rel corrections are negative in all cases, the largest absolute value is 0.02 kcal mol⁻¹ (for VII_N, VIII_N and IX_N), while the average is 0.01 kcal mol⁻¹. The triple and perturbative quadruple excitation corrections also have negative signs and both components are important, the average being 0.03 kcal mol⁻¹ while the maximum is 0.07 kcal mol⁻¹ (for V_N). Summarizing these with the QZ relative energies leads to the equilibrium energies, with the estimated uncertainty of 0.03 kcal mol⁻¹, and the energy order remains the same. The ZPE corrections have negative contributions to the ΔH₀ values, and the uncertainty of the enthalpy values can be estimated to be 0.1 kcal mol⁻¹. The thermal contributions (from −0.10 to 0.28 kcal mol⁻¹) give the 298.15 K enthalpy values while subtracting the TS term, where T is the temperature and S is the entropy, (from −1.11 to 0.29 kcal mol⁻¹), we obtain the relative Gibbs free energies.

Fig. 6 Structures of the first ten N-protonated serine conformers at the CCSD(T)-F12a/cc-pVDZ-F12 level of theory. The selection was based on the MP2/aug-cc-pVDZ relative energies and the numbering reflects the benchmark energy order, while the lower index denotes the protonation site.

Table 3 Benchmark relative energies, corrections, relative enthalpies (at 0 K and 298.15 K) and relative Gibbs free energies (298.15 K) of the ten lowest-lying N-protonated serine conformers. All data are in kcal mol⁻¹

Name^a	MP2	CC//MP2	CCSD(T)-F12a			CCSD(T)-F12b	Σ corr.	ΔEe^i	Δ ZPE	ΔH0^k	ΔH298.15^l	ΔG298.15^m
	aVDZ^b	DZ^c	DZ^d	TZ^e	QZ^f	QZ^g
a Conformer name based on the benchmark/MP2 relative energies. b MP2/aug-cc-pVDZ relative energies at MP2/aug-cc-pVDZ geometries. c CCSD(T)-F12a/cc-pVDZ-F12 relative energies at MP2/aug-cc-pVDZ geometries. d CCSD(T)-F12a/cc-pVDZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. e CCSD(T)-F12a/cc-pVTZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. f CCSD(T)-F12a/cc-pVQZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. g CCSD(T)-F12b/cc-pVQZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. h Sum of the auxiliary corrections: Δcore + Δrel + δT + δ(Q). i Benchmark relative equilibrium energies obtained by CCSD(T)-F12b/cc-pVQZ-F12 + Σcorr. j Zero-point corrections obtained by MP2/aug-cc-pVDZ harmonic vibrational frequencies. k Benchmark adiabatic relative energies obtained as ΔEe + ΔZPE. l Relative enthalpy at 298.15 K. m Relative Gibbs free energy at 298.15 K.
IN/N1	0.00	0.00	0.00	0.00	0.00	0.00	+0.00	0.00	+0.00	0.00	0.00	0.00
IIN/N2	0.59	0.67	0.67	0.65	0.65	0.65	−0.02	0.63	−0.01	0.62	0.72	0.44
IIIN/N3	3.35	3.69	3.67	3.69	3.68	3.69	−0.02	3.67	−0.11	3.55	3.65	3.30
IVN/N4	4.14	4.50	4.49	4.50	4.49	4.50	−0.04	4.46	−0.15	4.31	4.50	3.57
VN/N5	8.89	8.88	8.89	8.88	8.90	8.90	−0.04	8.85	−0.24	8.61	8.71	8.53
VIN/N7	9.25	9.07	9.08	9.09	9.11	9.11	−0.02	9.09	−0.40	8.68	8.76	8.58
VIIN/N6	9.02	9.10	9.08	9.11	9.11	9.11	+0.04	9.15	−0.22	8.93	9.10	8.60
VIIIN/N8	9.47	9.10	9.11	9.13	9.13	9.12	+0.02	9.15	−0.27	8.88	9.08	8.41
IXN/N9	9.84	9.50	9.51	9.53	9.53	9.53	+0.04	9.57	−0.42	9.15	9.43	8.32
XN/N10	9.88	9.54	9.55	9.56	9.59	9.59	−0.03	9.56	−0.08	9.48	9.38	9.67

---

From the ten O-protonated structures, we obtain nine at the CCSD(T)-F12a/cc-pVDZ-F12 level of theory, these are shown in Fig. 7. The Roman numerals increase with increasing benchmark relative energies and the lower index indicates the protonation site. The conformers O2 and O9 converge to the same, II_O structure. Only the global minimum has the very strong intramolecular O–H⋯N hydrogen bond, which explains the ∼6.00 kcal mol⁻¹ higher energy for conformer II_O. Due to the rather low energy (less than 14 kcal mol⁻¹) relative to the N-protonated minima the O-protonation can easily occur experimentally. Another stabilizing interaction present in these geometries is the O–H⋯O–H. The further computed results are shown in Table 4. The MP2 and CC geometries have an excellent agreement as the CC optimization changes the relative energies by only a few hundredths of kcal mol⁻¹. The O5, O6 and O7 conformers vary in order with increasing level of theory and finally, the TZ and QZ relative energy order is the same. In terms of basis-set convergence, we can say that the carbonyl protonation has the largest deviation between the TZ and QZ results, but still under 0.02 kcal mol⁻¹. The difference between the F12a and F12b energies is once again negligible. The auxiliary corrections (Fig. 5 (right)) are the most significant for these O-protonated structures. Δ_core happens to be quite large, 0.05 kcal mol⁻¹ on average, with the maximum of 0.08 kcal mol⁻¹ for VII_O. The second-order relativistic correction is smaller than 0.00 kcal mol⁻¹, except for III_O and IV_O (0.01 kcal mol⁻¹) and also for VII_O (−0.02 kcal mol⁻¹). The post-(T) corrections are also the largest, compared to neutral and N-protonated serine, and in every case, except for VII_O, the perturbative quadruple contribution is much more important. In summary, this post-(T) correction always has a positive sign, its average is 0.04 kcal mol⁻¹, and the maximum is 0.06 kcal mol⁻¹. On average the value of the summarized corrections for the carbonyl-protonated amino acids is 0.09 kcal mol⁻¹ which is quite high compared to the neutral (0.04 kcal mol⁻¹) and N-protonated (0.03 kcal mol⁻¹) correction values. The final equilibrium energy order does not change, the conformers rather get higher relative energies, the uncertainty is about 0.1 kcal mol⁻¹. As it can be seen in Table 4, the Δ_ZPE corrections are always negative, and they also have the largest values in this study (for VII_O, it is −0.98 kcal mol⁻¹). The 0 K enthalpy values rearrange the order, as IV_O becomes the second and VII_O the fourth conformer, while our educated guess for the uncertainty is 0.12 kcal mol⁻¹. Contributions to convert the 0 K relative enthalpies to 298.15 K range from 0.04 to 0.19 kcal mol⁻¹, and to obtain the Gibbs free energies, an entropic term between −0.11 and −0.37 kcal mol⁻¹ is required.

Fig. 7 Structures of the first nine O-protonated serine conformers at the CCSD(T)-F12a/cc-pVDZ-F12 level of theory. The selection was based on the MP2/aug-cc-pVDZ relative energies and the numbering reflects the benchmark energy order, while the lower index denotes the protonation site.

Table 4 Benchmark relative energies, corrections, relative enthalpies (at 0 K and 298.15 K) and relative Gibbs free energies (298.15 K) of the nine lowest-lying O-protonated serine conformers. All data are in kcal mol⁻¹

Name^a	MP2	CC//MP2	CCSD(T)-F12a			CCSD(T)-F12b	Σ corr.	ΔEe^i	Δ ZPE	ΔH0^k	ΔH298.15^l	ΔG298.15^m
	aVDZ^b	DZ^c	DZ^d	TZ^e	QZ^f	QZ^g
a Conformer name based on the benchmark/MP2 relative energies. b MP2/aug-cc-pVDZ relative energies at MP2/aug-cc-pVDZ geometries. c CCSD(T)-F12a/cc-pVDZ-F12 relative energies at MP2/aug-cc-pVDZ geometries. d CCSD(T)-F12a/cc-pVDZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. e CCSD(T)-F12a/cc-pVTZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. f CCSD(T)-F12a/cc-pVQZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. g CCSD(T)-F12b/cc-pVQZ-F12 relative energies at CCSD(T)-F12a/cc-pVDZ-F12 geometries. h Sum of the auxiliary corrections: Δcore + Δrel + δT + δ(Q). i Benchmark relative equilibrium energies obtained by CCSD(T)-F12b/cc-pVQZ-F12 + Σcorr. j Zero-point corrections obtained by MP2/aug-cc-pVDZ harmonic vibrational frequencies. k Benchmark adiabatic relative energies obtained as ΔEe + ΔZPE. l Relative enthalpy at 298.15 K. m Relative Gibbs free energy at 298.15 K.
IO/O1	0.00	0.00	0.00	0.00	0.00	0.00	+0.00	0.00	+0.00	0.00	0.00	0.00
IIO/O2	5.87	6.12	6.14	6.12	6.11	6.11	+0.06	6.17	−0.38	5.80	5.87	5.76
IIIO/O3	6.27	6.20	6.23	6.22	6.20	6.20	+0.09	6.29	−0.37	5.93	6.12	5.77
IVO/O4	6.35	6.32	6.34	6.30	6.29	6.29	+0.09	6.38	−0.67	5.71	5.83	5.54
VO/O6	6.87	6.87	6.89	6.86	6.86	6.85	+0.11	6.96	−0.59	6.37	6.49	6.20
VIO/O7	7.10	6.94	6.96	6.93	6.91	6.91	+0.09	7.00	−0.57	6.43	6.59	6.23
VIIO/O5	6.41	7.00	6.94	6.98	6.99	6.98	+0.08	7.07	−0.98	6.09	6.13	5.98
VIIIO/O8	7.31	7.24	7.21	7.18	7.17	7.17	+0.08	7.25	−0.78	6.47	6.63	6.26
IXO/O10	7.98	7.94	7.93	7.90	7.89	7.89	+0.10	7.99	−0.72	7.27	7.43	7.07

---

3. Proton affinity and gas-phase basicity

Our work is relevant and adds to previous, well-conducted theoretical studies on the PA and GB of serine. We have gone beyond the “gold standard” coupled-cluster theory to determine these properties, considering different corrections to achieve high accuracy, took different protonation sites and large number of conformers into account. Table 5 shows the calculated thermodynamic values for the amino acid serine. We have included the corrections and the equilibrium proton affinities as well as the 0 K and 298.15 K PAs and the 298.15 K GBs. We speak of several PAs and GBs since we can break down the values into multiple groups: the most favored site is the amino one and it dominates the protonation process, however, we also aim to investigate the carbonyl protonation as well. These results have also been subdivided, whether we consider only the global minima of the neutral serine and its protonated counterparts or conformer mixtures. It is important to note, that when considering Gibbs free energies, conformer II becomes the global minimum, thus these values were calculated considering this II structure for the GBs, not the I, as in the case of PAs. The population of each conformer was calculated via the Boltzmann-distribution in the case of mixtures. The full-T corrections have one of the smallest contributions to the equilibrium PAs. For the amino protonation it is −0.04/−0.03 kcal mol⁻¹ whether we consider only the global minima/conformer mixtures, and it has an even smaller effect on the O-protonation (0.01/0.02 kcal mol⁻¹). (Q) values are almost the same for the N-protonation (−0.04 kcal mol⁻¹ in both cases), while it becomes more significant for the carbonyl protonation (−0.08/−0.07 kcal mol⁻¹). The Δ_core correction has the largest value among the auxiliary corrections as it is above 0.1 kcal mol⁻¹ for both sites (except if we consider the O-protonation with only the global minimum, then it is 0.09 kcal mol⁻¹). To obtain the 0 K proton affinities (enthalpy change) we have to add the ZPE component to the equilibrium PAs. This reduces ΔE_e by approximately 8–9 kcal mol⁻¹ depending on which site are we investigating. For these 0 K PAs considering conformer mixtures causes a change of −0.22 kcal mol⁻¹ for the amino protonation and exactly the double, −0.44 kcal mol⁻¹ for the carbonyl protonation. The final 0 K PA values are 216.72 kcal mol⁻¹ for the N-protonation and 204.20 kcal mol⁻¹ for the O-protonation. To convert our values to 298.15 K we need to calculate the vibrational and rotational thermal effects and the translational enthalpy of the proton (1.48 kcal mol⁻¹ at 298.15 K). This increases the PA values by 1.26/1.33 and 1.56/1.67 kcal mol⁻¹ for the minima/mixture protonation for the two sites. The difference in the proton affinities caused by taking conformer mixtures into account is −0.30 and −0.54 kcal mol⁻¹ for the amino and carbonyl site, respectively. Our 298.15 K PA values are 218.05 and 205.87 kcal mol⁻¹ for the amino and carbonyl sites, respectively. Finally, we obtain the GB values if we calculate the entropic term (−8.03/−8.20 and −8.88/9.51 kcal mol⁻¹) and add it to the PA values. This results in GB of 209.86 kcal mol⁻¹ for the amino protonation and 193.36 kcal mol⁻¹ for the carbonyl protonation.

Table 5 Proton affinity (at 0 K and 298.15 K), auxiliary correction and gas-phase basicity (298.15 K) values for the different sites of serine (in kcal mol⁻¹)

	ΔEQZ^a	δT^b	δ(Q)^c	Δ core	Δ rel.	ΔEe^f	Δ ZPE	ΔH0^h	ΔH298^i	ΔG298^j
a CCSD(T)-F12b/cc-pVQZ-F12 equilibrium proton affinities at CCSD(T)-F12a/cc-pVDZ-F12 geometries. b Full-T correction obtained by CCSDT – CCSD(T) with 6-31G basis set at CCSD(T)-F12a/cc-pVDZ-F12 geometries. c Perturbative quadruples correction obtained by CCSDT(Q) – CCSDT with 6-31G basis set at CCSD(T)-F12a/cc-pVDZ-F12 geometries. d Core-correlation correction obtained as the difference between AE-CCSD(T)-F12a/cc-pCVTZ-F12 and FC-CCSD(T)-F12a/cc-pCVTZ-F12 proton affinities at CCSD(T)-F12a/cc-pVDZ-F12 geometries. e Douglas–Kroll relativistic correction obtained as the difference between Douglas–Kroll AE-CCSD(T)/aug-cc-pwCVTZ-DK and AE-CCSD(T)/aug-cc-pwCVTZ proton affinities at CCSD(T)-F12a/cc-pVDZ-F12 geometries. f Benchmark equilibrium proton affinities obtained by CCSD(T)-F12b/cc-pVQZ-F12 + Δcore + Δrel + δT + δ(Q). g Zero-point corrections obtained by MP2/aug-cc-pVDZ harmonic vibrational frequencies. h Benchmark 0 K proton affinities obtained as ΔEe + ΔZPE. i Benchmark proton affinities (298.15 K). j Benchmark gas-phase basicities (298.15 K). k Due to the change in the global minimum in the case of the relative Gibbs free energies, for the GB, the II conformer was considered. l In the average mixtures, the population of the conformers were calculated by Boltzmann-distribution.
I–IN^k	225.05	−0.04	−0.04	+0.12	−0.02	225.07	−8.57	216.50	217.76	209.72
I–IO^k	211.63	+0.01	−0.08	+0.09	−0.05	211.60	−7.83	203.77	205.33	196.46
Average N^l	225.43	−0.03	−0.04	+0.13	−0.03	225.46	−8.74	216.72	218.05	209.86
Average O^l	212.22	+0.02	−0.07	+0.10	−0.05	212.21	−8.00	204.20	205.87	196.36

---

Of course, a few words need to be said about the uncertainty of the PA and GB values. For the equilibrium PAs we can make some predictions with the help of the corrections: on average, it is 0.02 kcal mol⁻¹, so we can use it as an “error bar”. Things get more complicated when we move on to 0 K proton affinities as adding the ZPE corrections introduces new sources of error. The neglected anharmonicity has been studied by He et al. for the GBs of various molecules,⁴⁰ and it was found to be about 0.15 kcal mol⁻¹, we consider the same amount for the proton affinities. The level of theory difference (MP2 vs. CC) on the frequencies should be the same (0.06 kcal mol⁻¹) as in the case of the neutral serine ZPE. Finally, we obtain an uncertainty estimate of 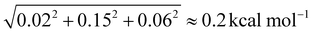. For 298.15 K PA, we previously found, that the effect of the choice of MP2 vs. CC theory on the ZPE and thermal corrections is under 0.1 kcal mol⁻¹,⁴¹ we take this value instead of 0.06 kcal mol⁻¹, leading to the uncertainty of 0.2 kcal mol⁻¹. The final values to be considered are the gas-phase basicities. In the case of glycine, we found that the deviation should be separated for the protonation sites. The MP2 vs. CC frequency effect for the N-protonation is between 0.50 and 0.55 kcal mol⁻¹ while for the O-protonation, it is 0.20–0.25 kcal mol⁻¹ (we consider the larger values in both cases), leading to the uncertainty of ∼0.6 kcal mol⁻¹ for the N-protonation, and ∼0.3 kcal mol⁻¹ for the O-protonation GBs.

From an experimental point of view, the gas-phase basicity can be more readily determined, whereas the proton affinity requires more evaluation. There are well-done measurements e.g. using Fourier transform ion cyclotron resonance mass spectrometry^20,21 or electrospray ionization-ion mass spectrometry²² with different evaluation methods (equilibrium measurements, reaction bracketing, kinetic or thermokinetic method). However, we would like to highlight four articles based on critically evaluating the published results and correcting them where it is needed, for summary, see Table 6. In 1997, Harrison⁹ reviewed the experimental data available in the literature on amino acids and peptides and found that the GB values were well-established and are in a good agreement, while the PA values derived from them needed to be disentangled, as the uncertainties can be up to 2–3 kcal mol⁻¹. Finally, Harrison suggested 207.6 kcal mol⁻¹ for serine GB and 215.2 kcal mol⁻¹ for serine PA with the uncertainty of 1–2 kcal mol⁻¹ and 2–3 kcal mol⁻¹, respectively. A year later, another review was carried out by Hunter and Lias.²³ They revised and compiled the available data on gas-phase basicities and proton affinities for nearly 1700 molecular, radical and atomic neutral species (including theoretical work). For serine they predicted the PA to be 218.4 kcal mol⁻¹ and the GB to be 210.4 kcal mol⁻¹, both of them with an uncertainty less than 1.9 kcal mol⁻¹. Bouchoux's contributions to this subject should also be noted. In 2003, six amino acids and thirty of their di- and tri-peptides were discussed,¹⁷ as previous experimental data were evaluated using a more accurate, thermokinetic method. The new method gave the results 216.04 ± 1.03 kcal mol⁻¹ and 207.94 ± 1.03 kcal mol⁻¹ for the PA and GB, respectively. Eight years later,²⁴ Bouchoux published another, widespread review on the gas-phase protonation thermochemistry of amino acids. After analyzing theoretical and experimental work, a PA of 217.8 kcal mol⁻¹ and a GB of 207.8 kcal mol⁻¹ were proposed. Our results show general agreement with the previously suggested results, however if one considers the applied level of theory and the predicted accuracy, future work might adjust the recommended values based on our ab initio predictions.

Table 6 Comparison of the 298.15 K proton affinity and the 298.15 K gas-phase basicity values of serine in the literature with our results

	PA (kcal mol^−1)		GB (kcal mol^−1)
	Value	Uncertainty	Value	Uncertainty
Harrison^9	215.2	2–3	207.6	1–2
Hunter and Lias^23	218.4	<1.9	210.4	<1.9
Bouchoux and Salpin^17	216.04	1.03	207.94	1.03
Bouchoux^24	217.8	—	207.8	—
Present work	218.05	0.2	209.86	0.6

---

IV. Summary and conclusions

We have explored the conformational landscape of the neutral and the N- and O-protonated serine (protonation at the carbonyl group, as the protonation of the side chain or the carboxyl OH group does not seem to be stable) by rotating along the axes describing the internal torsional motions with a resolution of 60°. We choose the MP2 method using the 6-31++G** and cc-pVDZ basis sets for locating stationary points, and both of them proved to be useful, as both basis sets found unique conformers. In total, we have 95 neutral, 15 amino- and 46 carbonyl-protonated minimum structures at the MP2/aug-cc-pVDZ level of theory in the 0.00–13.68, 0.00–13.97 and 0.00–29.17 kcal mol⁻¹ relative energy ranges, respectively. In addition, six by-product conformers, in which we can find a three-membered ring (N–C–C), were located on the PES. The number of conformers found is higher in any case, than in currently available papers,^25,30,32 while another important aspect is that all of the experimentally detected conformers^13–16 were found by this mapping process.

Another novelty in this manuscript is that the ten lowest-energy conformers (of each molecular group) were subjected to further benchmarking: we performed CCSD(T)-F12a/cc-pVDZ-F12 geometry optimizations (harmonic vibrational frequency calculations for the neutral serine). Furthermore, we carried out a comprehensive analysis of the various corrections to achieve sub-chemical accuracy, namely: basis-set effects up to CCSD(T)-F12b/cc-pVQZ-F12, electron correlation effects up to CCSDT(Q), core correlation and Douglas–Kroll relativistic effects, zero-point vibrational energy corrections, some of which proved to be necessary for accurate results. With the help of statistical thermodynamics, relatively simple harmonic oscillator and rigid rotor models, we determined 0 K PA/298.15 K PA/298.15 K GB for serine to be 216.72 ± 0.2/218.05 ± 0.2/209.86 ± 0.6 kcal mol⁻¹ for the amino site and 204.20 ± 0.2/205.87 ± 0.2/196.36 ± 0.3 kcal mol⁻¹ for the carbonyl site, showing nice agreement with as well as further improving the suggested results.^9,17,23,24 We report the first PA and GB values that went beyond the CCSD(T) method for serine on both sites, as we have employed the explicitly correlated version and computed the same contributions as in the case of the individual neutral and protonated serine (basis-set effects, electron correlation corrections, second-order scalar relativistic effects, core correlation corrections). These values can be used as benchmark references for future PA/GB value recommendations for serine.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the National Research, Development and Innovation Office–NKFIH, K-125317; Project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for financial support.

References

1. J. L. Bada, D. P. Glavin, G. D. McDonald and L. Becker, Science, 1998, 279, 362–365.
2. E. Herbst, Chem. Soc. Rev., 2001, 30, 168–176.
3. Y. Kuan, S. B. Charnley, H. Huang, W. Tseng and Z. Kisiel, Astrophys. J., 2003, 593, 848–867.
4. V. Blagojevic, S. Petrie and D. K. Bohme, Mon. Not. R. Astron. Soc., 2003, 339, L7–L11.
5. J. L. Snow, G. Orlova, V. Blagojevic and D. K. Bohme, J. Am. Chem. Soc., 2007, 129, 9910–9917.
6. J. E. Elsila, J. P. Dworkin, M. P. Bernstein, M. P. Martin and S. A. Sandford, Astrophys. J., 2007, 660, 911–918.
7. S. Ioppolo, G. Fedoseev, K.-J. Chuang, H. M. Cuppen, A. R. Clements, M. Jin, R. T. Garrod, D. Qasim, V. Kofman, E. F. van Dishoeck and H. Linnartz, Nat. Astron., 2021, 5, 197–205.
8. V. Barone and C. Puzzarini, EPJ Web Conf., 2020, 246, 00021.
9. A. G. Harrison, Mass Spectrom. Rev., 1997, 16, 201–217.
10. A. R. Dongré, J. L. Jones, Á. Somogyi and V. H. Wysocki, J. Am. Chem. Soc., 1996, 118, 8365–8374.
11. C. Bleiholder, S. Suhai and B. Paizs, J. Am. Soc. Mass Spectrom., 2006, 17, 1275–1281.
12. B. Paizs and S. Suhai, Mass Spectrom. Rev., 2005, 24, 508–548.
13. B. Lambie, R. Ramaekers and G. Maes, J. Phys. Chem. A, 2004, 108, 10426–10433.
14. S. Jarmelo, L. Lapinski, M. J. Nowak, P. R. Carey and R. Fausto, J. Phys. Chem. A, 2005, 109, 5689–5707.
15. E. E. Najbauer, G. Bazsó, R. Apóstolo, R. Fausto, M. Biczysko, V. Barone and G. Tarczay, J. Phys. Chem. B, 2015, 119, 10496–10510.
16. S. Blanco, M. E. Sanz, J. C. López and J. L. Alonso, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20183–20188.
17. G. Bouchoux and J.-Y. Salpin, Eur. J. Mass Spectrom., 2003, 9, 391–402.
18. F. X. Sunahori, G. Yang, E. N. Kitova, J. S. Klassen and Y. Xu, Phys. Chem. Chem. Phys., 2013, 15, 1873–1886.
19. V. Scutelnic, M. A. S. Perez, M. Marianski, S. Warnke, A. Gregor, U. Rothlisberger, M. T. Bowers, C. Baldauf, G. von Helden, T. R. Rizzo and J. Seo, J. Am. Chem. Soc., 2018, 140, 7554–7560.
20. G. S. Gorman, J. P. Speir, C. A. Turner and I. J. Amster, J. Am. Chem. Soc., 1992, 114, 3986–3988.
21. J. W. McKieman, C. E. A. Beltrame and C. J. Cassady, J. Am. Soc. Mass Spectrom., 1994, 5, 718–723.
22. C. Afonso, F. Modeste, P. Breton, F. Fournier and J.-C. Tabet, Eur. J. Mass Spectrom., 2000, 6, 443–449.
23. E. P. L. Hunter and S. G. Lias, J. Phys. Chem. Ref. Data, 1998, 27, 413–656.
24. G. Bouchoux, Mass Spectrom. Rev., 2012, 31, 391–435.
25. K. He and W. D. Allen, J. Chem. Theory Comput., 2016, 12, 3571–3582.
26. T. C. Dinadayalane, G. N. Sastry and J. Leszczynski, Int. J. Quantum Chem., 2006, 106, 2920–2933.
27. G. Mancini, M. Fusè, F. Lazzari, B. Chandramouli and V. Barone, J. Chem. Phys., 2020, 153, 124110.
28. M. Pecul, Chem. Phys. Lett., 2006, 418, 1–10.
29. S. Gronert and R. A. J. O’Hair, J. Am. Chem. Soc., 1995, 117, 2071–2081.
30. R. Miao, C. Jin, G. Yang, J. Hong, C. Zhao and L. Zhu, J. Phys. Chem. A, 2005, 109, 2340–2349.
31. M. Noguera, L. Rodríguez-Santiago, M. Sodupe and J. Bertran, THEOCHEM, 2001, 537, 307–318.
32. V. Riffet, G. Frison and G. Bouchoux, Phys. Chem. Chem. Phys., 2011, 13, 18561.
33. K. M. Uddin, P. L. Warburton and R. A. Poirier, J. Phys. Chem. B, 2012, 116, 3220–3234.
34. V. Barone, M. Fusè, F. Lazzari and G. Mancini, J. Chem. Theory Comput., 2023, 19, 1243–1260.
35. S. Gronert, D. C. Simpson and K. M. Conner, J. Am. Soc. Mass Spectrom., 2009, 20, 2116–2123.
36. Z. B. Maksić and B. Kovačević, Chem. Phys. Lett., 1999, 307, 497–504.
37. Z. B. Maksić, B. Kovačević and R. Vianello, Chem. Rev., 2012, 112, 5240–5270.
38. G. Bouchoux, S. Huang and B. S. Inda, Phys. Chem. Chem. Phys., 2011, 13, 651–668.
39. N. F. Brás, M. A. S. Perez, P. A. Fernandes, P. J. Silva and M. J. Ramos, J. Chem. Theory Comput., 2011, 7, 3898–3908.
40. X. He, L. Fusti-Molnar and K. M. Merz, J. Phys. Chem. A, 2009, 113, 10096–10103.
41. A. B. Nacsa and G. Czakó, Phys. Chem. Chem. Phys., 2021, 23, 9663–9671.
42. A. Á. Dékány and G. Czakó, J. Comput. Chem., 2022, 43, 19–28.
43. A. B. Nacsa and G. Czakó, J. Phys. Chem. A, 2022, 126, 9667–9679.
44. E. M. Orján, A. B. Nacsa and G. Czakó, J. Comput. Chem., 2020, 41, 2001–2014.
45. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
46. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
47. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
48. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see https://www.molpro.net.
49. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and Á. Ganyecz, J. Chem. Phys., 2020, 152, 074107.
50. M. Kállay, P. R. Nagy, D. Mester, L. Gyevi-Nagy, J. Csóka, P. B. Szabó, Z. Rolik, G. Samu, J. Csontos, B. Hégely, Á. Ganyecz, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and R. A. Horváth, MRCC, a quantum chemical program suite, http://www.mrcc.hu.
51. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
52. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
53. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102.
54. D. Manna, M. K. Kesharwani, N. Sylvetsky and J. M. L. Martin, J. Chem. Theory Comput., 2017, 13, 3136–3152.
55. M. K. Kesharwani, N. Sylvetsky, A. Köhn, D. P. Tew and J. M. L. Martin, J. Chem. Phys., 2018, 149, 154109.
56. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041–7050.
57. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
58. J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108.
59. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
60. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48.
61. T. Szidarovszky, G. Czakó and A. G. Császár, Mol. Phys., 2009, 107, 761–775.
62. V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 10094–10111.
63. R. Wu and T. B. McMahon, ChemPhysChem, 2008, 9, 2826–2835.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates (Å) of the 95 neutral, 15 N-protonated, 46 O-protonated and 6 “Cyclized” by-product conformers at the MP2/aug-cc-pVDZ level of theory. Also Cartesian coordinates (Å) of the lowest-energy 9 neutral, 10 N-protonated and 9 O-protonated conformers at the CCSD(T)-F12a/cc-pVDZ-F12 level of theory. See DOI: https://doi.org/10.1039/d3cp00612c

---