Photofragmentation specificity of photoionized cyclic amino acids (diketopiperazines) as precursors of peptide building blocks

Abstract

The photoionisation and photofragmentation of the two cyclic dipetides cyclo(alanyl-glycine) cGA and cyclo(glycyl-glycine) cGG, have been studied combining experiments and simulations. State selected fragments from the ionized molecules are detected using photo-electron photo-ion coincidence (PEPICO) measurements and specific fragmentation paths are identified and characterized via the use of ion-neutral coincidence maps. The simulations, performed using Quantum Chemistry methods, allow us to infer the fragmentation mechanisms of the ionized and excited molecules. We show that ring opening is followed by emission of the neutral fragments CO and HNCO. In the case of cGG the emission of neutral CO leads to a metastable structure that breaks producing small cationic fragments. The studied cyclic dipeptides evolve under ionizing radiation generating different small aziridin moieties and oxazolidinones. These two species are key reactants to elongate producing peptide chains. The corresponding mechanisms have been computed and show that the reaction requires very low energy and may occur in the presence of ionizing radiation.

---

1. Introduction

The response and evolution of molecules of biological interest interacting with ionising radiation is fundamental not only for biology, where the damage by ionizing radiation strongly depends on the structural and chemical properties of the biomolecular constituents of life matter and can be related to processes initiated at the atomic and molecular level, but also in biotechnological applications, such as biosensors and molecular electronics. Moreover in astrochemistry and astrobiology, key information on the origin of life is provided by the understanding of the chemistry of relatively simple molecules in environments resembling primordial conditions, either on Earth or extraterrestrial objects where external agents may have triggered amino acid condensation, for example, in aqueous¹ or fluctuating² environments.

In the particular case of amino acids interacting with highly-charged and energetic ions in the gas phase^3–5 the ionized and excited molecules present competitive decay channels: in addition to the so-called Coulomb explosion, leading to direct bond cleavages(s) and emission of two or several charged fragments, ultrafast isomerization has also been observed, with hydrogen migration being the most common alternative pathway. Interestingly, the interaction of clusters of amino acids with α particles in the gas phase leads to the formation of peptide bonds, thus being a possible source of prebiotic molecules.⁶ Gas phase peptide bond formation has also been observed in CID-MS/MS experiments of electrosprayed clusters of serine–serine dipeptides⁷ and the following photoexcitation of proton bound peptide complexes.⁸

A dipeptide can exist in two different structures, a linear or a cyclic one, depending on the formation of one or two peptide bonds between the carboxylic and amino groups of the two amino acids and the elimination of one or two water molecules. The common feature of any cyclo dipeptide built on α amino acids is the 2,5-diketopiperazine (DKP) six member ring, which results in a peculiar behavior in the photoionization and photofragmentation of the cyclo dipeptide.^9,10 At variance with the fragmentation of amino acids, DKP derivatives have attracted less attention. Zhang et al.¹¹ reported the VUV photoinduced fragmentation of cyclo(alanyl-alanine), cyclo(glycyl-glycine) and cyclo(glycil-valine) up to 11 eV, while the fragmentation of a series of both protonated and deprotonated cyclo-dipeptides has been studied by Guo et al.^12,13 We have recently shown⁹ that the VUV irradiation of cyclo(alanyl-alanine) (cAA), besides being an excellent source of CO and HNCO prebiotic species can also produce oxazolidinone intermediates. In the same study, we proposed a model where the interaction among the oxazolidinone intermediate and other neutral and charged fragments released in the molecular decomposition of cAA⁺ may lead either to the reconstruction of the cyclic cationic dipeptide or to the formation of longer linear peptide chains via almost barrierless processes, thus proposing a new mechanism for the formation of more complex biomolecules as oligo-peptides.

In this context, a question arises whether the different amino acids in cyclo dipeptides, i.e. different side chains attached to the DKP skeleton, may affect the behaviour of the irradiated molecules and their potential as prebiotic building blocks. To advance the understanding of this key open question, in this work we have studied the photoionisation and photofragmentation of the two cyclic dipetides cyclo(alanyl-glycine) cGA and cyclo(glycyl-glycine) cGG, combining experiments and simulations and compared the results with those previously obtained for cyclo(alanyl-alanine) cAA.^9,10 From the experimental side photoelectron spectroscopy and mass spectrometry combined with the photoelectron–photoion coincidence (PEPICO) and ion-neutral experiments have been used to investigate the state-selective fragmentation of the dipeptides as a function of the molecular internal energy. Since their introduction in 1967¹⁴ PEPICO experiments have been proved to be the most suited approach to study dissociation dynamics providing branching ratios towards the different channels, absolute decay rates and energy partitioning among the products.^15,16 Ion-neutral coincidence experiments,¹⁰ on the other hand, allow us to identify the correlated pair of charged and neutral fragments released in the two-body fragmentation of a cation and from the map of the ion-neutral coincidence events sequential fragmentation paths can be proposed. Then ab initio molecular dynamics simulations and potential energy surface exploration on the one hand allow us to interpret the PEPICO and ion-neutral coincidence results inferring the fragmentation mechanisms in the ionized and excited molecules and on the other predict the reactivity of the newly formed species. This methodology, recently detailed in ref. 10 for the case of cAA, has allowed us to investigate the potential capability of DKP species to somehow ‘survive’ VUV irradiation, either reconstituting the cationic dipeptide structure or even giving rise to the formation of more complex species.

The experimental methods and details of the simulations are presented in Section 2, while the results are presented and discussed in Section 3. Finally Section 4 is devoted to some conclusions.

2. Methods

2.1 Experimental

The photoemission and electron–ion coincidence measurements were performed at the CIPO beamline¹⁷ of the Elettra synchrotron radiation facility, using a monochromatic photon beam of 60 eV. The end-station is equipped with a 150 mm radius hemispherical electron energy analyser (VG 220i) and a time-of-flight (TOF) ion mass spectrometer mounted opposite to each other at the magic angle, i.e. approximately 55° with respect to the linearly polarized photon beam, in order to cancel out angular effects in the photoionisation cross section of the different molecular orbitals. All details of the experimental apparatus and procedures have been presented and discussed in ref. 10 and references therein, and therefore will be only briefly summarised here. The hemispherical analyser and TOF spectrometers have been operated independently for photoelectron (PE) spectroscopy or photoion mass spectrometry (MS) measurements, or ‘in conjunction’ for photoelectron–photoion coincidence (PEPICO) experiments. The 2D position sensitive detector (PSD) in the electron analyzer^18,19 provides an acquisition window and an energy resolution of about 10% and 2% of the pass energy, respectively. The PE spectra reported in Fig. 1 have been measured with a pass energy of 10 eV, an overall energy resolution of about 200 meV and an acquisition time of about 10 s per point.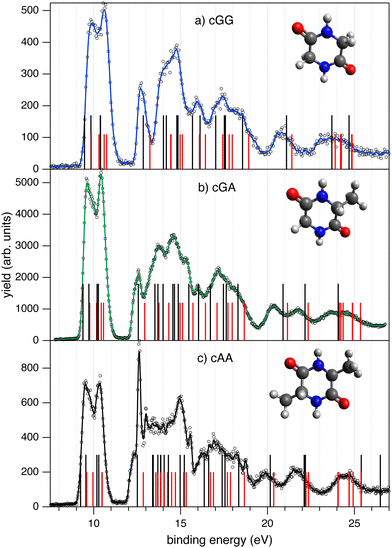

Fig. 1 The photoelectron spectra of cGG (panel a) and cGA (panel b) measured at 60 eV photon energy. The experimental results (open circles) and the three-point smoothing of the data (continuous blue and green lines, respectively) are compared to the results of the theoretical calculations. OVGF/6-311G(d,p) calculations are reported as black vertical bars while IP-EOM-CCSD results are reported as red vertical bars. The vertical double ionisation potential is calculated to be at 25.48 and 25.09 eV for cGG and cGA, respectively. The PE spectrum of cAA in panel (c) from ref. 10 is shown for comparison (reproduced with the author's permission). Some contamination caused by water degassing from the samples is present in the spectra, see for instance the narrow feature at 12.62 eV in cAA due to the H₂O⁺ ground state. The presence of this contamination can also be seen in the more selective PEPICO results in Fig. 2. The structure of each molecule is shown as an inset in their respective panels.

For MS measurements, the repeller and extractor electrodes of the TOF spectrometer are polarized with antisymmetric voltages up to 370 V cm⁻¹ and operated in pulsed mode, triggered by a 1 kHz pulse generator. In the PEPICO mode the extraction is triggered by either the signal due to the detection of a photoelectron or by the one from a pulse generator running at 100 Hz, a frequency comparable with the photoelectron counting rate during PEPICO acquisitions. The latter is used for measurement of the so-called ‘random mass spectrum’ generated by uncorrelated particles. The random mass spectrum has to be evaluated and subtracted from the measured electron–ion coincidence spectrum after appropriate normalization to their respective number of triggers. From these background subtracted PEPICO spectra, the next step in the data analysis consists of integrating the yield of each fragment over the region of mass-to-charge ratio m/z ± 0.5. Finally, these yields are reported versus the binding energy, BE = hv-KE, see Fig. 2, where hv is the photon energy and KE is the electron kinetic energy. The PEPICO measurements have been performed at a fixed photon energy of 60 eV, with an analyser pass energy of 30 eV and by scanning the KE over the range of interest in steps of 2.7 eV to provide sufficient overlap between two adjacent KE settings in the electron analyser. The entire KE scan is then repeated several times to improve the statistics. The stability of the apparatus is checked by PE measurements performed before and after each PEPICO acquisition.

Fig. 2 The yields of the most intense fragments in the PEPICO spectra of the cGA (left panel) and cGG (right panel) dipeptides are reported versus molecular binding energy. The sum of all PEPICO fragments is also reported vs. binding energy in the bottom panel. The presence of water outgassed from the sample is clearly visible, and it has been used to calibrate the kinetic energy scale. In the top panel of each sample, the mass spectrum obtained as a sum of all PEPICO mass spectra measured in the binding energy range 8–25 eV is reported. The m/z of the main fragments is indicated in this panel, while the suggested assignments are reported in Table 1.

The ion-neutral coincidence experiments have been performed at the CNR-ISM in Rome, using a Wiley-McLaren TOF mass spectrometer operated with constant extracting voltages and equipped with a rare gas discharge lamp (see ref. 10, 20, 21 and the ESI,† of ref 10 and 22). Following the same procedure and data analysis already described for the cAA case,^10,22 this set-up has been used to investigate the delayed emission of neutral fragments²³ in cGA and cGG, see Fig. 3. Briefly, when a non-stationary singly charged ion, the ‘parent ion’ P_ion, undergoes two-body fragmentation in the extraction/acceleration regions of the TOF spectrometer, then the lighter daughter ion, D_ion, is suddenly accelerated and will reach the TOF detector at a shorter time than the P_ion nominal flight time. The correlated neutral fragment, N_frag, will continue its free flight at a constant speed and may or may not be detected at a flight time longer than the P_ion nominal flight time.

Fig. 3 The ion-neutral coincidence map of cGA and cGG showing the arrival times TOF₁ and TOF₂ of the ion-neutral pairs. The experimental data, in black, are the sum of the acquisitions performed at photon energies 21.22, 16.85 and 11.62 eV, added up to improve the visibility of the traces in the plot. The individual maps are reported in Fig. S1 of the ESI.† The mass spectrum measured at 21.22 eV is shown in the bottom panel, indicating the main fragments. While horizontal and vertical lines represent random coincidences, the correlated events appear as an enhanced density of points along ‘traces’, which have been simulated using a custom Igor Pro²⁴ procedure based on the calculation of the electric field in the apparatus obtained by the SIMION 8.0 program²⁵ to provide unambiguous assignment of the P_ion → D_ion + N_frag reaction paths, see ref. 10 for the details. The simulated ‘traces’ are reported in red, superimposed to the experimental data and labeled by capital letters assigned in the legend.

The distribution of the arrival times of these (D_ion, N_frag) pairs produces the ‘traces’ in Fig. 3 and allows us to determine the corresponding P_ion → D_ion + N_frag reaction paths. In our set-up, considering the geometry of the TOF and the applied voltages, the residence time in the extraction/acceleration regions is in the range of 790–850 ns for cGG⁺ and 840–900 ns for cGA⁺. So, for fragmentation events happening within these time limits it has been possible to correlate the fragmentation of a parent ion to its ion-neutral products. Each trace originates at the TOF₁ of P_ion, corresponding to ‘late’ fragmentation events, and asymptotically converges to the TOF₁ of D_ion, corresponding to ‘early’ fragmentation events. ‘Early’ and ‘late’ times here are in relation to the time spent in the extraction/acceleration regions of the spectrometer, and refer respectively to prompt fragmentation, i.e. ‘early’, and fragmentation happening just before entering the free fly tube, i.e. ‘late’. Considering that ‘early’ fragmentation events have a lower detection efficiency for N_frag, due to the still low KE and directionality of motion acquired by P_ion at the time of fragmentation, each trace naturally fades out towards its convergence limit at TOF₁ of D_ion. Therefore, only an ion optics simulation of the process allows one to reliably extract the reaction path, P_ion → D_ion + N_frag. A fit of the intensity distribution of the coincidence events along the traces might in principle provide relevant information on the kinetics of the fragmentation. However, the unknown detection efficiency for neutral species in the set-up¹⁰ and the unknown ion's internal energy, due to the detection of electrons with unselected kinetic energy prevent the use of these data to extract thermochemical and kinetics information on the photofragmentation. It is also important to clarify that the different traces obtained in ion-neutral coincidence spectra correspond to individual events, and thus do not assure sequentiality. In this work, simulations have been performed using a custom Igor Pro²⁴ procedure based on calculation of the electric field in the apparatus obtained by the SIMION 8.0 program.²⁵

The background pressure in the vacuum chamber was about 2 × 10⁻⁸ mbar. Each one of the two samples, cGG (C₄H₆N₂O₂, mass m = 114 amu, CAS 106-57-0) and cGA (C₅H₈N₂O₂, mass m = 128 amu, CAS 4526-77-6) is in the form of powder at standard ambient temperature and pressure. The samples have been introduced in the vacuum chamber in a crucible and sublimated at a temperature of 80 °C and 90 °C for cGG and cGA, respectively.

2.2 Computational details

Quantum chemistry calculations were performed for the simulation of the photoelectron spectra and the fragmentation of all the diketopiperazines. Photoelectron spectra were estimated calculating ionisation potentials from valence shells using two different methods: (i) the equation of motion coupled cluster method^26–29 including single and double excitation^30,31 (EOM-CCSD) in combination with the Karlsruhe basis-set def2-QZVPP³² and (ii) the electron propagation theory (EPT) of correlated electron quasiparticle method within the Outer Valence Greens Function propagator, OVGF^33–36 and the 6-311G** basis set, considering an NVE microcanonical-ensemble. For the study of the fragmentation of the ionized DKPs we have used a combination of molecular dynamics simulation and exploration of the potential energy surfaces. This strategy has been previously employed with success for ionized molecules and molecular clusters.^{4–6,10,37–45}Ab initio molecular dynamics allow following the fragmentation pathways for the first hundreds of femtoseconds after ionisation. We have used the atom-centred density matrix propagation (ADMP) formalism^46–48 at the DFT level of theory, in particular using the B3LYP functional^49–52 with the 6-31++G(d,p) basis set.^53,54 All simulations were performed with a time step of Δt = 0.1 fs, a fictitious mass of μ = 0.1 a.u., to ensure adiabaticity during the propagation, and a maximum propagation time of t_max = 500 fs. To mimic experimental conditions, a typical excess/excitation internal energy of E_exc = 10 and 15 eV, was used to consider states prepared upon ionisation, where the excess of excitation energy is randomly redistributed on the nuclear degrees of freedom. We considered a total of 100 trajectories for each value of excitation energy, and performed statistics over them (see the ESI†). For the calculation of the energy barriers in the pathways leading to the observed exit channels, further exploration of the potential energy surface was carried out at the DFT B3LYP/6-311++G(d,p) level of theory. Relative energies in the PES were corrected with the zero point energy (ZPE). The combination of ab initio molecular dynamics simulations and the exploration of the PES (see also the ESI†) allowed us to obtain the fragmentation mechanisms that explain the moieties observed in the PEPICO experiments. All calculations were carried out using the Gaussian16 code.⁵⁵

3. Results and discussion

Photoelectron spectroscopy is a powerful tool to probe the relationship between the electronic structures of the neutral molecule and its cationic states reached in the photoionization event. This relationship depends on the measurable ionization energy and the change in the molecular geometry following ionization. Quantum chemistry methods calculate the minimum energy geometries of both initial neutral and final singly charged states and their results provide the assignment of the photoelectron spectrum. The experimental photoemission spectra of cGG and cGA measured in this work together with cAA from ref. 10 are shown in Fig. 1. The structure of the three molecules (see the insets in Fig. 1) is made by the central DKP ring and side chains made by the combination of one or two H atoms and methyl groups, depending on the constituent amino acids. Thus the three spectra share some common features, like the two bands at BE < 11 eV, a gap up to about 12 eV and then several broad features up to and above BE 20 eV. Both cGG and cGA spectra display a single feature just above 12 eV, which merges in a broader band (partially masked by the water contamination at 12.62 eV in the case of cAA). The cGG spectrum is consistent with the one previously reported in the literature.⁵⁶ The energy of the first feature in the photoelectron spectra increases from 9.53 ± 0.05 eV in cAA,¹⁰ to 9.61 ± 0.05 eV in cGA and finally 9.88 ± 0.05 eV in cGG, mirroring the variation in the ionisation potential, IP, of the constituent amino acids, the IP being about 150 meV larger in glycine than in alanine.⁵⁷ Furthermore, the ionization energies of the two amino acids⁵⁷ are higher than the ones for the corresponding cyclodipeptides. This is at variance with the findings in cyclodipeptides with aromatic chains,⁵⁸ where the orbitals of the DKP ring provide molecular stabilization with respect to the aromatic rings of the side chains, which are the frontier orbitals of the molecule.

Consistent with the experimental observations, the theoretical analysis of the PE spectra of the three diketopiperazine derivatives shows that the four lowest direct ionisation values (from HOMO to HOMO−3) require less than 11 eV of excitation energy, with a gap between this first group and the HOMO−4 above 12 eV. As the main structural differences among the three cyclic amino acids are the addition of one or two methyl group(s), it is reasonable to attribute this gap to their common features. Indeed, analyzing the orbital participation in the HOMO−4, we observe that in all three cases it corresponds to a combination of π orbitals in the carbonyl groups C=O of the DKPs, while the first four orbitals (HOMO to HOMO−3) are formed via the participation of the lone-pairs of the heteroatoms with some contribution from the bonding orbitals located in the ring.

Both theoretical methods employed to simulate the photoelectron spectra (OVGF and EOM-CCSD) provide similar results, and agree with the experimental results reproducing fairly well the measured bands (and gaps). In the energy region near the second ionization threshold the theory slightly overestimates the binding energies corresponding to ionization from inner valence electrons.

The photofragmentation of the cyclic dipeptides has been studied by analyzing the PEPICO spectra. This type of experiments provide state-selected mass spectra, where a fragmentation pattern can be correlated to specific molecular orbitals, within the experimental energy resolution. Furthermore, the first onset of the PEPICO yields provide a rough indication of the appearance energy of the fragment itself. As commonly observed in other polyatomic molecules, higher excitation energies, E_exc = BE − IP, are needed in order to release a larger number of smaller fragments due to increased bond breakage. On the other hand, the signal of the intact molecular ions for the three cyclodipeptides, m/z 142, 128 and 114 for cAA, cGA and cGG respectively, are observed only in the lower excitation energy region. In all cases, while only a couple of fragmentation channels exists in the region BE < 11 eV, in the energy range above 12 eV the molecules rapidly become unstable showing a large amount of fragmentation products. Here, we find a relevant common feature in the three DKPs: the direct release at relatively low energies of neutral CO and HNCO, i.e. neutral molecules that have been regarded as heavily involved in the abiotic synthesis of prebiotic species (see e.g. ref. 59 and 60 and references therein). This behaviour was previously observed for cAA.^10,42 As has already been discussed in relation with the photoelectron spectra (Fig. 1), at lower energies electronic density is localized in the bonds forming the DKP ring. Therefore their charge depletion may lead to the prompt opening of the ring. A wavefunction analysis performed using the Quantum Theory Atoms in Molecules⁶¹ of the most stable configuration for the three singly charged diketopiperazines, shows how the CO–CHCH₃ bond, for cAA and cGA, or CO–CH₂ bond, for cGG, are the most labile and consequently they will be the most likely ones to break upon ionization. The opening of the ring allows the direct release of neutral CO and HNCO moieties, which would lead to the m/z 114 (cAA), 100 (cGA) and 86 (cGG) fragments in the case of CO release, and to m/z 99 (cAA), 85 (cGA) and 71 (cGG) for the HNCO release. In the ab initio molecular dynamics simulation results, we see how the most statistically reactive channel for the three DKPs, i.e. the channel most frequently observed in the molecular dynamic simulations, is the direct formation from HNCO (in this case, we define as reactive channels those that lead to the breaking of more than one bond, thus producing at least two fragments). Furthermore, the release of these fragments, HNCO and CO, is implicated in almost all of the reactive simulations (see Tables S1–S3 of the ESI†). The photofragmentation of the cyclic dipeptides has been studied by analyzing the PEPICO spectra. This type of experiment provides state-selected mass spectra, where a fragmentation pattern can be correlated to specific molecular orbitals, within the experimental energy resolution. Furthermore, the first onset of the PEPICO yields provide a rough indication of the appearance energy of the fragment itself. As commonly observed in other polyatomic molecules, higher excitation energies, E_exc = BE − IP, are needed in order to release a larger amount of smaller fragments due to increased bond breakage. On the other hand, the signal of the intact molecular ions for the three cyclodipeptides, m/z 142, 128 and 114 for cAA, cGA and cGG respectively, are observed only in the lower excitation energy region. In all cases, while only a couple of fragmentation channels exists in the region BE < 11 eV, in the energy range above 12 eV the molecules rapidly become unstable showing a large amount of fragmentation products. Here, we find a relevant common feature in the three DKPs: the direct release at relatively low energies of neutral CO and HNCO, i.e. neutral molecules that have been regarded as heavily involved in the abiotic synthesis of prebiotic species (see e.g. ref. 59 and 60 and reference therein). This behaviour was previously observed for cAA.^10,42 As has been already discussed in relation with the photoelectron spectra (Fig. 1), at lower energies electronic density is localized in the bonds forming the DKP ring. Therefore their charge depletion may lead to the prompt opening of the ring. A wavefunction analysis performed using the Quantum Theory Atoms in Molecules⁶¹ of the most stable configuration for the three singly charged diketopiperazines, shows how the CO–CHCH₃ bond, for cAA and cGA, or CO–CH₂ bond, for cGG, are the most labile and consequently they will be the most likely ones to break upon ionization. The opening of the ring allows the direct release of neutral CO and HNCO moieties, which would lead to the m/z 114 (cAA), 100 (cGA) and 86 (cGG) fragments in the case of CO release, and to m/z 99 (cAA), 85 (cGA) and 71 (cGG) for the HNCO release. Note that it was observed how in the mass spectrum of cAA (Fig. 1 and 2 of ref. 9) the intensity of the charged fragment after CO release is much smaller than that for the HNCO-loss. A similar situation arises in cGA, where the equivalent fragment [cGA-CO]⁺ at m/z 100 is not observed within the sensitivity of the present experiment. As it will be shown below, this is the consequence of the higher stability of the charged product generated after the direct release of HNCO; on the other hand, less stable species are reached after the CO release and, therefore, less energy is needed for their further fragmentation.

Despite these common fragmentation aspects in the loss of CO and HNCO, we observe certain counter-intuitive trends that make the evolution of DKPs after ionization something far from trivial or general. In order to obtain insight into these differences, a combined experimental-theoretical methodology has been employed. Some of these results are reported in Table 1, together with the assignment of all relevant peaks in the PEPICO spectra. Experimentally, ion-neutral coincidence experiments have been performed to investigate the delayed emission of neutral fragments. Within the sensitivity of this technique as implemented in our apparatus, it is possible to track the fragmentation process P_ion → D_ion + N_frag provided the fragmentation occurs during the residence time of the parent ion in the extraction/acceleration region of the spectrometer.¹⁰ Then, following the same approach as for cAA,⁴³ Quantum Chemistry calculations have been performed to explore the potential energy surface of the two cyclic dipeptides cGA and cGG, and to determine all relevant fragmentation mechanisms. This provides the energy of the optimised structures of each fragment as well as the energy barriers connecting them along fragmentation patterns. Fig. 3 shows the ion-neutral coincidence spectra of cGA and cGG (see ref. 10 for cAA). In these maps, the direct loss of CO and HNCO by the molecular ion (paths labeled A and B, respectively) are clearly visible as delayed fragmentation processes for both cGA and cGG. This supports the theoretical hypothesis of the relevance of the direct formation of HNCO and CO in the photodegradation of DKPs as proposed by the analysis of the AIMD. The corresponding theoretical results for energetics of these direct loss pathways are shown in the potential energy surface in Fig. 4, together with cAA reported in ref. 10 for comparison (for further PES exploration of the three DKPs see Fig. S3–S5 in the ESI†). Following the initial vertical ionization (VIP), adiabatic relaxation occurs, culminating in the singly charged form of the DKPs. We can identify this point as the adiabatic ionization potential (AIP), and compare it with the estimated appearance energy's experimental value obtained in the PEPICO spectra. In all cases the mechanism starts with the ring opening after cleavage of the CO–CHCH₃ or CO–CH₂ bonds, followed by the release of a (D_ion, N_frag) pair in a further step. Lower energy barriers are needed to produce HNCO, while the release of CO implies overcoming transition states ∼0.5 eV higher in energy.

Table 1 The main fragments observed in the PEPICO measurement of cGA and cGG, Fig. 2, are reported with their proposed assignment, first onset in PEPICO experiments (estimated uncertainties 0.2–0.4 eV) and theoretically predicted appearence energy, AE_th values

Assignment	cGA			cGG
	m/z	PEPICO (eV)	AEth (eV)	m/z	PEPICO (eV)	AEth (eV)
a Adiabatic value. b Vertical value.
M^+	128^+	9.1^a	9.30^b	114^+	9.2^a	9.40^b
(M-CO)^+	100^+	—	10.21/10.65	86^+	10.1	10.71
(M-HNCO)^+	85^+	9.5	9.79	71^+	10.2	10.41
(H3C2NO)^+	57^+	11.9	—	57^+	∼13.3	11.73
(H6C2N)^+	44^+	12.1	—	—	—	—
(HNCO)^+	—	—	—	43^+	12.1	—
(H2NCH2)^+	30^+	11.9	—	30^+	12.0	11.73
(CO)^+	28^+	13.9	—	28^+	15.4	—

---

Fig. 4 Fragmentation paths leading to the emission of neutral CO (in red) and HNCO (in blue) molecules for (a) cAA⁺, (b) cGA⁺ and (c) cGG⁺. In the lower panel (c), the fragmentation pathway from 86⁺ to 30⁺ is also shown. Relative energies are presented in eV referred to the neutral molecules and were obtained at the B3LYP/6-311++G(d,p) level of theory. Adiabatic ionization potentials (AIPs) for cAA, cGA and cGG are 8.84, 9.04 and 9.16 eV respectively, and they are consistent with the experimental determination of the first onset of the PEPICO signal for their respective molecules reported in Table 1.

A careful exploration of the ion-neutral coincidence maps for cGG, shows a fragmentation pathway that directly connects fragment 86⁺ with 30⁺. Considering the large difference in m/z connecting these two fragments, we studied this channel in more detail by constructing the potential energy surface of cGG and focusing on the possible fragmentation routes from 86⁺ (Fig. 4c). This fragment originates after the breaking of the CO–CH₂ bond of the ring and the direct loss of the terminal CO. From here, the redistribution of the charge leads to the breaking of one of the CO-NH peptide bonds, giving rise to fragment 57⁺ (relative energy 11.26 eV in the figure). This minimum corresponds to a meta-stable state in which the two fragments are linked through an intermolecular hydrogen bond, and it is protected from prompt decay by a very small energy barrier (0.2 eV) that gives rise to the transfer of H producing fragment 30⁺. The shape of the potential energy surface for this pathway provides the connection 86⁺ → 30⁺ (path D in Fig. 3) and explains why fragment 57⁺, which should be an intermediate product between 86⁺ and 30⁺, has a very low intensity in the PEPICO spectra of cGG in Fig. 2.

In Fig. 3 we see that for cGA, CO loss is followed by NH loss, but this sequential process does not occur for cGG, being the first step, CO loss leading to 86⁺, the only one observed. Most probably the low energy barriers needed to produce a very stable fragment CH₂NH₂⁺ (30⁺) (see Fig. 4) is the reason behind this experimental observation of the dominant 86⁺ → 30⁺ channel.

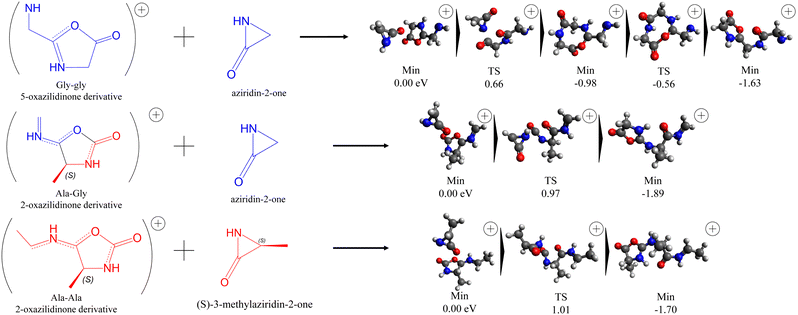
After the assignment of the main fragmentation paths resulting from the ionization of cGA and cGG, we now discuss the possible role of these molecules as prebiotic species. In a previous work,⁴² we have shown theoretically how small neutral fragments obtained after the fragmentation of singly-charged cAA dipeptide, combined with a reactive charged moiety (5-oxazolidinones) that can also be obtained from isomerisation cAA⁺, may act as a neutral ‘seed’ and reactive agent, to support a mechanism of peptide chain elongation. Fig. 5 reports a schematic representation of the aziridine derivatives that may act as a highly reactive key intermediates of the mechanism for elongating peptide chains. In the first column, the three DKPs are displayed, with alanine units in red and those corresponding to glycine in blue. The second column features a representative peptide chain, highlighting these same units. The third column illustrates how cyclisation of each unit results in the formation of aziridine derivatives. Then, if one considers cAA to be composed of two alanine unit cells (see the first structure in Fig. 5a) that have lost OH and H at the carboxylic and amino ends, respectively, a fragment of mass 71 amu is the ‘residue’, i.e. the unit cell that will be replicated in a peptide chain (see the second structure in Fig. 5a). That is, if we split symmetrically cAA in two identical fragments, each half would be a fragment with mass 71 amu. In a similar way, cGA and cGG, could be divided into their ‘unit cells’, where the one of glycine has a mass of 57 amu (see Fig. 5b and c). After ionization, photodegradation may lead to the formation of both ‘seeds’ in their cationic or neutral forms. The latter implies the formation of a three-member ring and therefore the formation of aziridine derivatives⁴² (see the third structure of each series in Fig. 5). The fragmentation leading to the formation of these residues, which in the case of cAA provided the necessary ‘seed’ for further reactivity, looks trivial since only two bonds must be broken splitting the target molecules in half. Nevertheless, the capricious nature of these apparently very similar diketopiperazines shows up again. While fragment 57⁺ (attributable to the glycine ‘unit cell’) is one of the most prominent signals for cGA, it is not observed in the PEPICO spectra of cGG. Moreover, fragment 71⁺ (attributable to the alanine ‘unit cell’), while observed in cAA, it has not been detected in cGA measurements. The absence of fragment 57⁺ in cGG has already been previously discussed when analyzing the ion-neutral coincidence spectrum. Even though the fragment is formed in an intermolecular bonded structure, low-in-energy barriers lead to a fast evolution towards smaller fragments, making the 57⁺ moiety a metastable fragment not observed in the experiments. The reason why fragment 71⁺ is not formed in the fragmentation after ionization of cGA is not trivial. After analyzing the potential energy surface of this diketopiperazine, all possible reaction pathways that could potentially lead to this fragment lead instead to different ones. Therefore, consistent with the experimental evidence that fragment 71⁺ was not observed neither in PEPICO nor in ion-neutral coincidence measurements, also theoretically we could not identify any path leading to 71⁺ in our calculations (see Fig. S3–S5 of the ESI†). At the heart of this significantly different and quite unpredictable behaviour among the three cyclic dipeptides, the electronic charge distribution controlling bonding properties and fast molecular rearrangement following photoionisation are likely playing a role.

Fig. 5 Graphical view of the decomposition of the three 2,5-diketopiperazines producing aziridin intermediates that could act as prebiotic ‘seeds’. (a) cAA, (b) cGA and (c) cGG. In red are represented the 'unit cells' corresponding to the alanine (A) part while in blue are drawn those of glycine (G).

As alternative ‘reactive moieties’ for peptide elongation we have also identified the 2- and 5-oxazolidinone species. The former can be obtained through the recombination of charged and neutral aziridin ‘seeds’ via a barrierless reaction as previously discussed for 71 in ref. 9. These mechanisms were obtained theoretically through relaxed scans, where the distance between the atoms forming the new bond is shortened while the rest of the structure is allowed to relax into the configuration of minimum energy (see Fig. 6a). 2-Oxazolidinone derivatives, on the other hand, can be formed for every singly-charged diketopiperazine after the first bond-break (see Fig. 6a); isomerization of the original ionized cyclic structure leads to the corresponding 2-oxazolidinone in a single step with relatively low energy barriers, accessible for the excitation in these experiments (see Fig. S3–S5 of the ESI†).

Fig. 6 (a) Formation of 5-oxazolidinone derivatives from arizidin ‘seeds’. In red are represented the 'unit cells' corresponding to the alanine part while in blue are drawn those of glycine. (b) The formation of 2-oxazolidinone derivatives from each 2,5-diketopiperazine. Energy barriers are presented in eV referred to the neutral most stable conformers and were obtained at a B3LYP/6-311++G(d,p) level of theory.

With these two ingredients, ‘seeds’ and ‘reactive moieties’, we have theoretically studied the mechanisms of elongation producing peptide chains, considering all possible combinations of both reactants. Fig. 7 shows some of the relevant mechanisms obtained through the relaxed scans. From the scan, we have located the highest points and optimized the geometry of the first order transition states that connect reactants and products. We can see in Fig. 7 that, for the example of the cationic 5-oxazolidinone derivative obtained from cGG and the arizidin-2-one moiety (neutral fragment of mass 57 amu), the reaction takes place with a low energetic barrier (0.66 eV). This behaviour is observed in all the reactions considered. In particular, the process proceeds as follows: first, a new peptide bond is formed as the seed's amino group bonds with the carboxylic carbon of the oxazolidinone derivative; this triggers the opening of the oxazolidinone ring, creating the new peptide chain. Then, a new oxazolidinone ring is created with the atoms of the newly formed peptide bond. Thus, the final fragment has two differentiated parts: a non-reactive peptide chain and a reactive oxazolidinone ring that could be involved in further capturing of new ‘seeds’, resulting again in the elongation of the peptide chain and reconstitution of the reactive oxazolidinone site (see the lowest in energy reactive channel in Fig. S3–S5 in the ESI†).

Fig. 7 Elongation of the peptide chain with the interaction of aziridin neutral seeds and different reactive 2-oxazolidinones and 5-oxazolidinones. Below each snapshot of the mechanism of elongation we present the relative energies in eV with respect to the initial structures. All structures were obtained at the B3LYP/6-311++G(d,p) level of theory. To check if dispersion effects could be relevant, all stationary points were also calculated with the M06-2X functional.

This theoretically proposed mechanism suggests a new possible route for peptide elongation in the gas phase. However, it doesn't solve the question of homochirality in life. Oxazolidinones have been recognized as non-desired intermediates for peptide elongation as their tautomerization can lead to the loss of optical purity. Within the proposed mechanism one could argue that, even though tautomerization is possible, the energetic barriers for peptide elongation are much lower compared to those for tautomerization (see Fig. S6 in the ESI†). Additionally, the proposed mechanism retains the original chirality of its components. As in our experiments and calculations we have only considered ‘S’ enantiomers, all longer peptides show the same chirality. However, if the fragments had ‘R’ chirality, the same energetic barriers would take place for peptide elongation, and therefore, although conserving the optical purity, would not show the preference or an imbalance between R and S enantiomers.

4. Conclusions

In summary, we have studied the ionization and subsequent fragmentation of two cyclic dipetides, cyclo(alanyl-glycine) cGA and cyclo(glycyl-glycine) cGG, induced by VUV radiation. In particular, we report results from three different techniques: (i) photoelectron spectroscopy, which allows us to characterize the electronic structure and ionization energies of different states; (ii) photoelectron–photoion coincidence measurement (PEPICO) spectroscopy, which allows identifying state-selected fragmentation channels; and (iii) ion-neutral coincidence maps, which allow providing unambiguous assignment of some reaction paths. In addition to these experiments, we have performed a thorough computational study using quantum chemistry simulations, where (i) ionization has been simulated using the equation of motion coupled cluster method (EOM-CCSD) and the electron propagation theory (EPT); (ii) fragmentation was studied by means of molecular dynamics with the atom-centred density matrix propagation (ADMP) formalism; and (iii) the potential energy surface was explored using density functional theory (DFT), locating the transition states and the intermediates in the paths of the most relevant fragments observed experimentally, thus proposing the corresponding fragmentation mechanisms. These calculations provide insight into the different processes taking place in the photo-ionization induced fragmentation of these two molecules. We have compared our results to those previously obtained for the cyclo(alanyl-alanine) cAA.^9,10

Starting from the study of the molecular rearrangement and fragmentation following VUV ionisation, and investigating the reactivity among some of the products, we also explored theoretically the potential of DKP species to survive radiation or even act as intermediates for the construction of oligopeptides, as already proposed in cAA.⁹ We have shown that in the three cationic diketopiperazines (DKPs), cGG, cGA and cAA, a similar evolution occurs at the beginning, just after photo-ionization, i.e. ring opening at the C–C_α bond that has been weakened to a greater extent in the cationic form with respect to the neutral canonical molecule. This ring opening can be followed either by the loss of neutral moieties, or by molecular rearrangement. In the first situation, neutral CO and HNCO are emitted with high probability, i.e. low energy barriers. In the second one, cationic oxazolidinone structures are formed.

Finally, we have explored the possibility of peptide bond formation using the fragmentation products as ‘reagents’, thus leading to the formation and elongation of a peptide chain. To this end, we have shown that two ‘reactive moieties’ are needed: cationic oxazolidinones and neutral aziridin molecules, and both are products that can be obtained in the VUV irradiation of DKPs molecules. However, specific oxazolidinone and aziridin structures are obtained for each cyclic dipeptide. Thus, depending on which DKP is irradiated, different peptide chains might be formed via different mechanisms, making this process neither trivial nor general for cyclic dipeptides.

The joint experimental-theoretical approach here adopted is crucial to obtain a complete picture of the great variety of processes that occur in the photo-ionization of peptides, in the identification of the species produced, as well as in their reactivity. Although the three discussed molecules a priori look like very similar, specificity is observed in their chemical behaviour and in their response to photoionization.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This article is based upon work from COST action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). The authors acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). This work was partially supported by MICINN (Spanish Ministry of Science and Innovation) project PID2019-110091GB-I00 funded by MCIN/AEI/10.13039/501100011033, the “María de Maeztu” (CEX2018-000805-M) Program for Centers of Excellence in RD, MAECI Italy-Sweden project “Novel molecular tools for the exploration of the nanoworld”, and PRIN 20173B72NB project “Predicting and controlling the fate of bio-molecules driven by extreme-ultraviolet radiation”. D. B.-L. acknowledges the FPI grant associated with MICINN project CTQ2016-76061-P. H. Z. acknowledges the Swedish Research Council for the individual project grant with contract no. 2020-03437. M. H. S. acknowledges the Swedish Research council (Grant no. 2016-03675) and the Carl Trygger Foundation (Grant no. 17:436).

Notes and references

1. R. B. Martin, Biopolymers: Original Research on Biomolecules, 1998, 45, 351–353.
2. N. Lahav, D. White and S. Chang, Science, 1978, 201, 67–69.
3. S. Maclot, M. Capron, R. Maisonny, A. Lawicki, A. Mery, J. Rangama, J. Chesnel, S. Bari, R. Hoekstra, T. Schlatholter, B. Manil, L. Adoui, P. Rousseau and B. Huber, Chem. Phys. Chem., 2011, 12, 930–936.
4. S. Maclot, D. G. Piekarski, A. Domaracka, A. Mery, V. Vizcaino, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau and S. Díaz-Tendero, J. Phys. Chem. Lett., 2013, 4, 3903–3909.
5. D. G. Piekarski, R. Delaunay, S. Maclot, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau, A. Domaracka and S. Díaz-Tendero, Phys. Chem. Chem. Phys., 2015, 17, 16767–16778.
6. P. Rousseau, D. G. Piekarski, M. Capron, A. Domaracka, L. Adoui, F. Martn, M. Alcam, S. Díaz-Tendero and B. A. Huber, Nat. Commun., 2020, 11, 3818.
7. M. Nihamkin, A. Isaak, A. Albeck, Y. Mastai and Y. Toker, J. Phys. Chem. Lett., 2020, 11, 10100–10105.
8. S. Lee, S. J. Valentine, J. P. Reilly and D. E. Clemmer, J. Am. Chem. Soc., 2011, 133, 15834–15837.
9. D. Barreiro-Lage, P. Bolognesi, J. Chiarinelli, R. Richter, H. Zettergren, M. H. Stockett, L. Carlini, S. Diaz-Tendero and L. Avaldi, J. Phys. Chem. Lett., 2021, 12, 7379–7386.
10. J. Chiarinelli, D. Barreiro-Lage, P. Bolognesi, R. Richter, H. Zettergren, M. H. Stockett, S. Daz-Tendero and L. Avaldi, Phys. Chem. Chem. Phys., 2022, 24, 5855–5867.
11. L. Liyun Zhang, L. Jia, L. Zhang, H. Guo, Z. Zhou, J. Weng and F. Qi, Amino Acids, 2012, 43, 279–287.
12. Y. Guo, S. Cao, D. Wei, X. Zong, X. Yuan, M. Tang and Y. Zhao, J. Mass Spectrom., 2009, 44, 1188–1194.
13. Y.-C. Guo, S.-X. Cao, X.-K. Zong, X.-C. Liao and Y.-F. Zhao, Spectrosc., 2009, 23, 131–139.
14. B. Brehm and E. V. Puttkamer, Z. Naturforsch., 1967, 22A, 8–11.
15. T. Baer, J. Booze and K. Weitzel, Vacuum Ultraviolet Photoionization and Photodissociation of Molecules and Clusters, World Scientific, Singapore, 1991, pp. 259–96.
16. T. Baer, A. Bodi and B. Sztaray, Encyclopedia of Spectroscopy and Spectrometry, Academic Press Ltd-Elsevier Science Ltd, 2017, vol. 3, pp. 635–649.
17. A. Derossi, F. Lama, M. Piacentini, T. Prosperi and N. Zema, Rev. Sci. Instrum., 1995, 66, 1718–1720.
18. G. Cautero, R. Sergo, L. Stebel, P. Lacovig, P. Pittana, M. Predonzani and S. Carrato, Nucl. Instrum. Meth. A, 2008, 595, 447–459.
19. R. H. Menk, M. Antonelli, G. Brajnik, J. Bufon, C. Dri, D. Giuressi, A. Gubertini, C. Nichetti, G. Pinaroli and P. Pittana, et al. , AIP Conf. Proc., 2019, 060071.
20. A. Cartoni, P. Bolognesi, E. Fainelli and L. Avaldi, J. Chem. Phys., 2014, 140, 184307.
21. V. Adebomi, R. D. Cohen, R. Wills, H. A. H. Chavers, G. E. Martin and M. Raj, Angew. Chem., Int. Ed., 2019, 58, 19073–19080.
22. P. Bolognesi, A. Casavola, A. Cartoni, R. Richter, P. Markus, S. Borocci, J. Chiarinelli, S. Tošić, H. Saadeh and M. Masič, et al. , J. Chem. Phys., 2016, 145, 191102.
23. S. Martin, R. Brédy, A.-R. Allouche, J. Bernard, A. Salmoun, B. Li and L. Chen, Phys. Rev. A, 2008, 77, 062513.
24. Wavemetrics Inc., Igor Pro, https://www.wavemetrics.com.
25. Scientific Instrument Services, Inc., SIMION, https://www.simion.com.
26. H. Koch and P. Jo/rgensen, J. Chem. Phys., 1990, 93, 3333–3344.
27. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
28. H. Koch, R. Kobayashi, A. Sanchez de Meras and P. Jorgensen, J. Chem. Phys., 1994, 100, 4393–4400.
29. M. Kállay and J. Gauss, J. Chem. Phys., 2004, 121, 9257–9269.
30. R. J. Bartlett and G. D. Purvis, Int. J. Quantum Chem., 1978, 14, 561–581.
31. G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
32. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762.
33. L. S. Cederbaum, J. Phys. B: At. Mol. Phys., 1975, 8, 290–303.
34. L. S. Cederbaum and W. Domcke, Theoretical Aspects of Ionization Potentials and Photoelectron Spectroscopy: A Green's Function Approach, John Wiley & Sons, Ltd, 1977, pp. 205–344.
35. J. Linderberg and Y. Öhrn, Propagators in Quantum Chemistry, John Wiley & Sons, Ltd, 2004.
36. H. H. Corzo and J. V. Ortiz, in Löwdin Volume, ed. J. R. Sabin and E. J. Brändas, Academic Press, 2017, vol. 74, pp. 267–298.
37. M. Capron, S. Díaz-Tendero, S. MacLot, A. Domaracka, E. Lattouf, A. Lawicki, R. Maisonny, J. Y. Chesnel, A. Mery, J. C. Poully, J. Rangama, L. Adoui, F. Martín, M. Alcamí, P. Rousseau and B. A. Huber, Chem. – Eur. J., 2012, 18, 9321–9332.
38. S. Maclot, R. Delaunay, D. G. Piekarski, A. Domaracka, B. A. Huber, L. Adoui, F. Martín, M. Alcamí, L. Avaldi, P. Bolognesi, S. Díaz-Tendero and P. Rousseau, Phys. Rev. Lett., 2016, 117, 073201.
39. N. G. Kling, S. Díaz-Tendero, R. Obaid, M. R. Disla, H. Xiong, M. Sundberg, S. D. Khosravi, M. Davino, P. Drach, A. M. Carroll, T. Osipov, F. Martín and N. Berrah, Nat. Commun., 2019, 10, 2813.
40. M. McDonnell, A. C. LaForge, J. Reino-González, M. Disla, N. G. Kling, D. Mishra, R. Obaid, M. Sundberg, V. Svoboda, S. Daz-Tendero, F. Martn and N. Berrah, J. Phys. Chem. Lett., 2020, 11, 6724–6729.
41. P. Rousseau, J. Gonzaález-Vázquez, D. G. Piekarski, J. Kopyra, A. Domaracka, M. Alcamí, L. Adoui, B. A. Huber, S. Díaz-Tendero and F. Martín, Sci. Adv., 2021, 7, eabg9080.
42. D. Barreiro-Lage, P. Bolognesi, J. Chiarinelli, R. Richter, H. Zettergren, M. H. Stockett, L. Carlini, S. Díaz-Tendero and L. Avaldi, J. Phys. Chem. Lett., 2021, 12, 7379–7386.
43. D. Barreiro-Lage, C. Nicolafrancesco, J. Kočišek, A. Luna, J. Kopyra, M. Alcam, B. A. Huber, F. Martn, A. Domaracka, P. Rousseau and S. Daz-Tendero, Phys. Chem. Chem. Phys., 2022, 24, 941–954.
44. D. Mishra, J. Reino-González, R. Obaid, A. C. LaForge, S. Daz-Tendero, F. Martn and N. Berrah, Phys. Chem. Chem. Phys., 2022, 24, 433–443.
45. S. Ganguly, D. Barreiro-Lage, N. Walsh, B. Oostenrijk, S. L. Sorensen, S. Díaz-Tendero and M. Gisselbrecht, Commun. Chem., 2022, 5, 16.
46. H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763.
47. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302.
48. H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704.
49. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
50. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
51. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
52. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Chem. Phys., 1994, 98, 11623–11627.
53. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
54. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
55. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
56. A. P. W. Arachchilage, F. Wang, V. Feyer, O. Plekan and K. C. Prince, J. Chem. Phys., 2010, 133, 174319.
57. P. Cannington and N. S. Ham, J. Electron Spectr. Relat. Phenom., 1983, 32, 139–151.
58. E. Molteni, G. Mattioli, P. Alippi, L. Avaldi, P. Bolognesi, L. Carlini, F. Vismarra, Y. Wu, R. Borrego Varillas, M. Nisoli, M. Singh, M. Valadan, C. Altucci, R. Richter and D. Sangalli, Phys. Chem. Chem. Phys., 2021, 23, 26793–26805.
59. M. Ferus, V. Laitl, A. Knizek, P. Kubelk, J. Sponer, J. Kára, J. Sponer, B. Lefloch, G. Cassone and S. Civiš, Astron. Astrophys., 2018, 616, A150.
60. A. Lazcano and J. L. Bada, Origins Life Evol. B, 2003, 33, 235–242.
61. R. F. Bader, Chem. Rev., 1991, 91, 893–928.

---

Footnote

† Electronic supplementary information (ESI) available: cGG and cGG ion-neutral coincidence experiments performed at three different photon energies; stationary points of the potential energy surface corresponding to the fragmentation channels of cAA⁺, cGA⁺ and cGG⁺; single-step mechanisms leading to tautomerization of the three oxazolidinone derivatives discussed in the main text; and statistics of the ADMP molecular dynamics simulations for cAA⁺, cGA⁺ and cGG⁺. See DOI: https://doi.org/10.1039/d3cp00608e

---