Open Access Article
Open Access ArticleFirst-principles study on unidirectional proton transfer on anatase TiO2 (101) surface induced by external electric fields†
Takahiro
Chiba
a,
Kenji
Iida
 *a,
Shinya
Furukawa
*a,
Shinya
Furukawa
 a and
Jun-ya
Hasegawa
a and
Jun-ya
Hasegawa
 ab
ab
aInstitute for Catalysis, Hokkaido University, N21 W10 Kita-ku, Sapporo, 001-0021 Hokkaido, Japan. E-mail: k-iida@cat.hokudai.ac.jp
bInterdisciplinary Research Center for Catalytic Chemistry, National Institute of Advanced Industrial Science and Technology, Central 5, 1-1-1 Higashi, Tsukuba, Ibaraki 305-8565, Japan
First published on 12th March 2023
Abstract
The electric field (EF) effect on hydrogen or proton transfer (PT) via hydroxyl groups on an anatase TiO2 (101) surface is examined using first-principles density functional theory and the modern theory of polarization. This study focuses on unidirectional surface PT caused by external EFs at various orientations toward the surface. The preferred PT pathway can change depending on the magnitude and direction of the EF. Detailed analysis reveals that the variation in the energy profile with the EF is significantly different from that determined by the classical electric work of an EF carrying a point charge. The EF effect on the energy profile of the PT is governed by the rearrangement of the chemical bond network at the interface between the water molecules and the surface.
Introduction
The electric field (EF) effect in solid–molecule interfaces has been extensively studied owing to the interest in manipulating surface chemical processes and understanding electrochemical reactions.1–5 Planar solid surfaces in conventional electrocatalysts have been widely used to investigate the EF effect, and the direction of the applied EF is assumed to be perpendicular to the solid surfaces.1,2 However, recent experimental studies have focused on controlling the EF effect in complex systems with laterally non-uniform interfaces.3,6,7 An oriented EF generated by a scanning tunneling microscope tip was used to accelerate non-redox chemical reactions, such as the Diels–Alder reaction,3 extending the applicability of the EF effect to control chemical processes other than electrochemical reactions. Furthermore, the EF effect on heterogeneous materials with complex interfaces has attracted increasing attention.6,7 Catalytic activity in the dehydrogenation of hydrocarbons was improved by applying a bias voltage to a powdered catalyst, and proton transfer (PT) on the oxide surface has been considered to be enhanced by the external EF.6,8,9 However, the EF effect on heterogeneous materials is complex because the magnitude and direction of the EFs vary in space due to EFs generated by electric polarization in the interface region; that is, the gross EFs point in various directions on the material surface. Therefore, a theoretical study is required to understand the EF effect.Numerous theoretical and computational studies have been performed to understand solid surfaces under external EFs.1,10–12 First-principles density functional theory (DFT) calculations with a sawtooth-type electrostatic potential have been used to calculate the effect of a surface-perpendicular external EF. However, the sawtooth potential cannot be applied when the EF is parallel to the material surface, and electronic polarization cannot be uniquely defined for periodic systems.13,14 Therefore, an alternative to the sawtooth potential is required to investigate the EF effect on heterogeneous materials.
The Berry phase theory is used to evaluate the macroscopic polarization of periodic systems13,14 and is applicable to the investigation of the EF effect, irrespective of the orientation of the EF toward the material surface. EF-induced electronic polarization of various dielectric materials has been investigated in condensed matter and device physics research.15 However, the Berry phase theory has not been applied to complex chemical processes with multiple elementary steps, despite the expectation that the energy profile will change significantly with the EF.
In this study, we performed DFT calculations to investigate the EF effect on hydrogen or proton transfer via hydroxyl groups on an anatase TiO2 (101) surface. Hereafter, both hydrogen and proton transfers are denoted as PT because hydrogen and protons cannot be clearly distinguished in the PT process. The interface between TiO2 and water under an external EF has been widely studied to understand catalytic and spectroscopic properties.9,16–18 Herein, the Berry phase theory formula is combined with an approximated formula for evaluating the energy profile under an external EF. This formula is applied to the PT process that includes numerous chemical bond formations and dissociations under external EFs. We reveal the atomic-scale mechanism of PT on the surface depending on the direction and intensity of the external EFs.
Theoretical methods
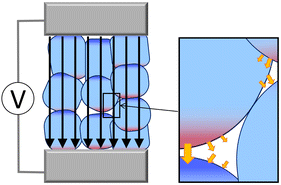
The central purpose of this study is to elucidate the EF effect on a heterogeneous material, as shown in Fig. 1.6–9 The steam reforming reaction of hydrocarbons was experimentally studied using the system illustrated in Fig. 1, where water vapor (i.e., not aqueous solution) was supplied.6,8,9 This system is regarded as a complex one because a small electric current can induce a wide variation in the resulting direction and intensity of the gross EF owing to EFs generated by electronic polarization of the constituents. Therefore, the Berry phase theory13,14 was used to investigate the effect of external EFs with various orientations toward the material surface. We calculated the difference in the macroscopic polarization ΔP caused by changes in the geometrical structure during the PT process, where the macroscopic polarization P is the dipole moment per unit volume. Subsequently, we evaluated the energy change ΔE depending on an external EF using the formula:| ΔE(ε) = ΔE(ε = 0) − ΩΔP·ε | (1) |
Our approach assumes that electronic polarization directly induced by the EF can be neglected. This assumption is valid within the context of this study owing to the low-magnitude EF that is used (less than 2 × 109 V m−1). A detailed discussion is provided in Section S1 in the ESI.†
Computational details
DFT calculations were performed using the Quantum Espresso program19 with the dispersion-corrected PBE functional (PBE-D2)20–23 and the projector augmented wave (PAW) pseudopotential.24 The cell volume was 3.78 × 10.43 × 30.00 Å3 along the x ([0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]), y ([10
0]), y ([10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]), and z ([101]) directions, respectively. The cutoff energies for the wave function and electron density were 62 and 600 Ry, respectively. The number of k-points was 3 × 1 × 1 for the geometry optimization and the Nudged Elastic Band (NEB)25 calculation, and 9 × 6 × 3 for the Berry phase calculation to confirm the convergence of the Berry phase with respect to the number of k-points. Geometry optimizations in the NEB calculation were performed until the forces were less than 0.05 eV Å−1. The VESTA program was used to visualize the electron density.26
]), and z ([101]) directions, respectively. The cutoff energies for the wave function and electron density were 62 and 600 Ry, respectively. The number of k-points was 3 × 1 × 1 for the geometry optimization and the Nudged Elastic Band (NEB)25 calculation, and 9 × 6 × 3 for the Berry phase calculation to confirm the convergence of the Berry phase with respect to the number of k-points. Geometry optimizations in the NEB calculation were performed until the forces were less than 0.05 eV Å−1. The VESTA program was used to visualize the electron density.26
Fig. 2 shows the H2O/TiO2 system in which water molecules are adsorbed on the stoichiometric anatase (101) surface. The H2O/anatase (101) interface has been widely studied experimentally and theoretically.27–34 In Fig. 2(b), the black line indicates a unit cell containing two water molecules. The surface water coverage of the present system corresponds to the water monolayer on the surface investigated in previous studies.30–33 The geometric structure of the bottom two O–Ti–O trilayers is fixed to that of the bulk anatase. The oxygen atoms of the water molecules (Ow) are bound to the undercoordinated 5-fold Ti atoms (Ti5c) on the surface, and the Ow–H bonds point toward the surface undercoordinated 2-fold oxygen atoms (O2c) due to the H⋯O2c hydrogen bonds. The orientation of the monolayer H2O molecules was governed by the hydrogen bond, as previously reported.32
TiO2 surfaces other than the anatase (101) are not examined in this study because our primary focus is on the EF effect depending on the direction and magnitude of the applied EF. An H2O monolayer was chosen to focus on the PT governed by the interaction between H2O and the surface; water was assumed to be present as a low-pressure vapor. Previous experimental studies have examined analogous systems consisting of the surface and water vapor that generates a water monolayer or submonolayer on the surface.31,33,34 Multilayer adsorption on the surface, i.e., the interface between an aqueous solution and the surface, is beyond the scope of this study.
Fig. 3 illustrates the PT mechanism investigated in this study. The H atoms hop between the water molecules and the surface and transfer to the next unit cell (i), followed by the rotation of OH and H2O moieties (ii). The PT process was traced using the NEB method, and unidirectional PT on the surface was expressed. PT in the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [1
0] and [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] directions was examined, as shown in Fig. 2(b). Comparing these pathways yields insights into the EF effect governed by the quantum mechanical interactions between water and the surface.
] directions was examined, as shown in Fig. 2(b). Comparing these pathways yields insights into the EF effect governed by the quantum mechanical interactions between water and the surface.
 | ||
| Fig. 3 Scheme of the PT investigated in this study. The cyan H atoms are identical under the periodic boundary condition. | ||
Results and discussion
Fig. 4 shows an energy diagram of the PT on the surface. The PT process primarily comprises proton hoppings and O–H group rotations. These steps are denoted as Hop and Rot, respectively, in Fig. 4, with the PT direction indicated by cyan arrows. The horizontal and vertical directions are [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [10
0] and [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], respectively, as defined in Fig. 2(b). The geometrical structures of the intermediates are shown in Fig. S2 in the ESI.†
], respectively, as defined in Fig. 2(b). The geometrical structures of the intermediates are shown in Fig. S2 in the ESI.†
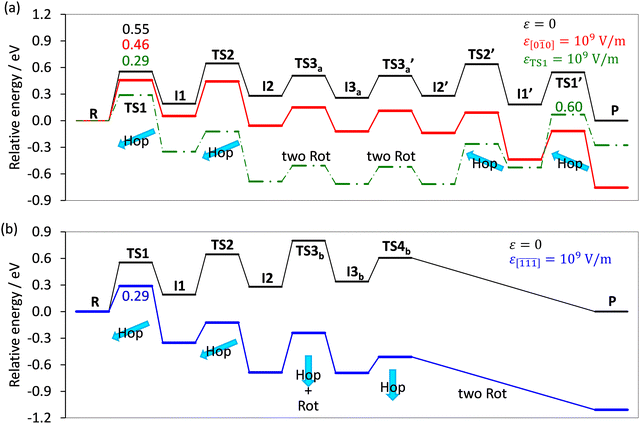
The energy diagram of PT along the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction without an applied EF is shown by the solid black line in Fig. 4(a). Both the R → I1 and I1 → I2 steps are attributed to the proton hopping from Ow to O2c owing to the two water molecules in the unit cell. The Ow–H and O2c–H groups simultaneously rotate in the I2 → I3a step. The energy diagram is symmetric around I3a because the geometry change from I3a to P is almost identical to that from I3a to R; thus, the states after I3a are denoted by adding a prime (′) to the corresponding states before I3a. The first hopping process (R → I1) has the highest activation energy (0.55 eV) among the elementary steps. The apparent activation energy is determined by the energy difference between R and TS2 (0.65 eV), whereas TS1 determines the apparent activation energy under the EF. The geometric structure of P is equivalent to that of R, except that the sum of transferred distance of the two H atoms in each H2O molecule is one unit cell length. Therefore, the energies of R and P are identical, provided an external EF is not applied. However, the symmetry in the energy profiles is broken with the applied EF; thus, R and P are no longer energetically equivalent.
0] direction without an applied EF is shown by the solid black line in Fig. 4(a). Both the R → I1 and I1 → I2 steps are attributed to the proton hopping from Ow to O2c owing to the two water molecules in the unit cell. The Ow–H and O2c–H groups simultaneously rotate in the I2 → I3a step. The energy diagram is symmetric around I3a because the geometry change from I3a to P is almost identical to that from I3a to R; thus, the states after I3a are denoted by adding a prime (′) to the corresponding states before I3a. The first hopping process (R → I1) has the highest activation energy (0.55 eV) among the elementary steps. The apparent activation energy is determined by the energy difference between R and TS2 (0.65 eV), whereas TS1 determines the apparent activation energy under the EF. The geometric structure of P is equivalent to that of R, except that the sum of transferred distance of the two H atoms in each H2O molecule is one unit cell length. Therefore, the energies of R and P are identical, provided an external EF is not applied. However, the symmetry in the energy profiles is broken with the applied EF; thus, R and P are no longer energetically equivalent.
Fig. 4(b) shows the energy diagram for PT along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction. The steps from R to I2 are identical to those shown in Fig. 4(a). PT along the [10
] direction. The steps from R to I2 are identical to those shown in Fig. 4(a). PT along the [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction occurs through the I2 → I3b and I3b → P steps, with the two H2Ow moieties rotating in the I3b → P step. TS1 exhibits the largest activation energy for an elementary step (0.55 eV), although TS3b has a comparable energy of 0.52 eV. The apparent activation energy is determined by TS3b and is 0.80 eV.
] direction occurs through the I2 → I3b and I3b → P steps, with the two H2Ow moieties rotating in the I3b → P step. TS1 exhibits the largest activation energy for an elementary step (0.55 eV), although TS3b has a comparable energy of 0.52 eV. The apparent activation energy is determined by TS3b and is 0.80 eV.
Fig. 5 illustrates the geometrical structures of the major transition states, TS1 and TS3b. The black arrows indicate the transferred H atoms. In both the transition states, the transferred H atom bridges Ow and O2c, and the Ow atom is bound to a Ti5c atom. The Ow–Ti5c bond distance changes from 2.33 Å (R) to 1.85 Å (I1) via TS1 and from 1.87 Å (I2) to 2.35 Å (I3b) via TS3b, indicating the formation and dissociation of the Ow–Ti5c chemical bond during this process. The Ow–Ti5c bond is strongly distorted in the transition states due to the Ow⋯H⋯O2c bonds; that is, the transition states include proton hopping and geometric distortion of the TiO2 surface. The calculation shows that the atomic-scale details of the bond rearrangement at the interface between water molecules and the surface govern the transition states of the PT. Atomic-scale insights are essential for understanding the EF effect on the energy profile.
Fig. 4 shows the energy diagram for a 109 V m−1 applied EF, which corresponds to the typical EF intensity generated in electric double layers.2 The present study mainly focuses on the interface between the surface and water vapor (i.e., not aqueous solution), generating a water monolayer or submonolayer on the surface. The 109 V m−1 EF is approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times stronger than the external EF used by Sekine et al., where water vapor was used for the steam reforming reaction of hydrocarbons.6,35 However, if heterogeneous interfaces generate strong EFs owing to the enhancement of electronic polarization by the small electric current (Fig. 1), the theoretical system corresponds to the experimental system. A direct comparison between the present theoretical result and experiment is difficult because the local EF intensity in the experimental system cannot be adequately measured because of its complexity. However, at least, PT on various metal-oxide species under EFs was investigated in the experimental studies.6,8,9,35
000 times stronger than the external EF used by Sekine et al., where water vapor was used for the steam reforming reaction of hydrocarbons.6,35 However, if heterogeneous interfaces generate strong EFs owing to the enhancement of electronic polarization by the small electric current (Fig. 1), the theoretical system corresponds to the experimental system. A direct comparison between the present theoretical result and experiment is difficult because the local EF intensity in the experimental system cannot be adequately measured because of its complexity. However, at least, PT on various metal-oxide species under EFs was investigated in the experimental studies.6,8,9,35
The solid red line in Fig. 4(a) shows the energy diagram under an EF applied in the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction. The energies decrease, particularly in the R → I1 and I1 → I2 steps, and the activation energy of the PT in TS1 decreases by 0.09 eV. The rate-determining step given by the apparent activation energy changes from TS2 to TS1 because TS2 is largely stabilized. The green dashed line in Fig. 4(a) shows the energy diagram for a 109 V m−1 EF applied parallel to the ΔP direction during the R → TS1 step. The barrier to TS1 decreases substantially because the parallel alignment of ε and ΔP yields a large energy change, defined by ΔP·ε (eqn (1)). In contrast, the TS1′ barrier increases, indicating that the EF direction should coincide with the net direction of PT rather than the ΔP direction during the R → TS1 step to efficiently induce unidirectional PT along the [0
0] direction. The energies decrease, particularly in the R → I1 and I1 → I2 steps, and the activation energy of the PT in TS1 decreases by 0.09 eV. The rate-determining step given by the apparent activation energy changes from TS2 to TS1 because TS2 is largely stabilized. The green dashed line in Fig. 4(a) shows the energy diagram for a 109 V m−1 EF applied parallel to the ΔP direction during the R → TS1 step. The barrier to TS1 decreases substantially because the parallel alignment of ε and ΔP yields a large energy change, defined by ΔP·ε (eqn (1)). In contrast, the TS1′ barrier increases, indicating that the EF direction should coincide with the net direction of PT rather than the ΔP direction during the R → TS1 step to efficiently induce unidirectional PT along the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] pathway. We have also investigated the application of an EF along the [010] direction (Fig. S3 in the ESI†), showing that the PT along the [0
0] pathway. We have also investigated the application of an EF along the [010] direction (Fig. S3 in the ESI†), showing that the PT along the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction becomes endothermic by the applied EF. The dependence of the activation energy on the EF direction indicates that the EF effect cannot be explained by considering only one elementary step because the change in energy under the EF differs among the various steps.
0] direction becomes endothermic by the applied EF. The dependence of the activation energy on the EF direction indicates that the EF effect cannot be explained by considering only one elementary step because the change in energy under the EF differs among the various steps.
The external EF also promotes PT along the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] pathway when the EF is applied in the [1
] pathway when the EF is applied in the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction. The corresponding energy diagram is indicated by the blue line in Fig. 4(b). Compared with the energy profile without the EF (black line), the activation energy at TS1 markedly decreases from 0.55 to 0.29 eV, whereas that at TS3b remains almost unchanged. Therefore, TS3b is the rate-determining step, regardless of external EF application.
] direction. The corresponding energy diagram is indicated by the blue line in Fig. 4(b). Compared with the energy profile without the EF (black line), the activation energy at TS1 markedly decreases from 0.55 to 0.29 eV, whereas that at TS3b remains almost unchanged. Therefore, TS3b is the rate-determining step, regardless of external EF application.
This study mainly focuses on the effect of the parallel EFs. The energy change when the EF is perpendicular to the surface was also examined and was significantly smaller (10–30 times) than any of those with the parallel EFs.
Fig. 6 shows the dependence of activation energy in the elementary steps TS1, TS3a, and TS3b on the magnitude of the EF |ε|. TS1 is common to the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [1
0] and [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] pathways. However, the EF direction differs between them. The results shown in Fig. 6 were interpolated; however, the calculations for different field strengths yield identical results when using the present formula (eqn (1)) that neglects the polarization induced by the applied EF. As shown in Fig. 6, the TS1 plots share the same y-intercept, but their gradients with respect to |ε| are different. The direction of ΔP in TS1 is closer to [1
] pathways. However, the EF direction differs between them. The results shown in Fig. 6 were interpolated; however, the calculations for different field strengths yield identical results when using the present formula (eqn (1)) that neglects the polarization induced by the applied EF. As shown in Fig. 6, the TS1 plots share the same y-intercept, but their gradients with respect to |ε| are different. The direction of ΔP in TS1 is closer to [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] than [0
] than [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]; therefore, the gradient for the [1
0]; therefore, the gradient for the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] process is steeper than that for the [0
] process is steeper than that for the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] process. The order of the magnitude of the activation energies depends on the EF. When |ε| is less than 1.4 × 109 V m−1, TS1 in the [0
0] process. The order of the magnitude of the activation energies depends on the EF. When |ε| is less than 1.4 × 109 V m−1, TS1 in the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] pathway exhibits the highest activation energy. When |ε| is between 1.4 × 109 V m−1 and 2.0 × 109 V m−1, the activation energy of TS3b in the [1
0] pathway exhibits the highest activation energy. When |ε| is between 1.4 × 109 V m−1 and 2.0 × 109 V m−1, the activation energy of TS3b in the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] pathway is the highest. This variation suggests that the preferred PT pathway depends on the EF magnitude. The energy diagram profiles vary qualitatively owing to differences in the EF dependence among the elementary steps.
] pathway is the highest. This variation suggests that the preferred PT pathway depends on the EF magnitude. The energy diagram profiles vary qualitatively owing to differences in the EF dependence among the elementary steps.
 | ||
| Fig. 6 Dependence of the activation energy of elementary steps on the EF. The energy shown in Fig. 4 is indicated by the circle marker. | ||
As per eqn (1), the energy change versus EF is determined by ΔP·ε. Thus, the displacement of the H atom, ΔrH, can provide a large contribution to ΔP. Fig. 7 summarizes the direction and magnitude of ΔP and ΔrH for the major transition states (TS1, TS3a, and TS3b). The black arrows reflect the exact magnitudes and directions of ΔP and ΔrH. The horizontal and vertical directions are [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [10
0] and [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], respectively, as defined in Fig. 2(b). No clear correlation between ΔP and ΔrH is evident, indicating that ΔP cannot be evaluated solely using ΔrH. Therefore, the variation in the activation energy with EF (Fig. 4 and 6) is significantly different from that determined by the classical electric work of an EF carrying a point charge. A previous theoretical study on oxygen-charged defects in MgO and SiO2 indicated that the effective polarization-work charge under an EF is not equal to the transported charge of the migrating atom.36
], respectively, as defined in Fig. 2(b). No clear correlation between ΔP and ΔrH is evident, indicating that ΔP cannot be evaluated solely using ΔrH. Therefore, the variation in the activation energy with EF (Fig. 4 and 6) is significantly different from that determined by the classical electric work of an EF carrying a point charge. A previous theoretical study on oxygen-charged defects in MgO and SiO2 indicated that the effective polarization-work charge under an EF is not equal to the transported charge of the migrating atom.36
The change in the atomic charge of the migrating H atoms (ΔqH) can influence ΔP. Bader charge analysis indicated that the charges on the H atoms remained almost unchanged during the PT process: 0.57–0.66e and 0.61–0.65e for the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] and [1
0] and [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] pathways, respectively, indicating that the contribution of ΔqH is negligible.
] pathways, respectively, indicating that the contribution of ΔqH is negligible.
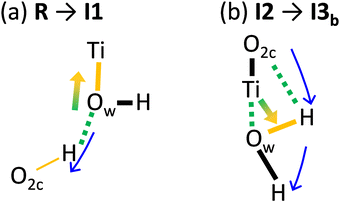
To elucidate the dependence of the energy profile on the EF, we analyzed the PT mechanism at the atomic scale. Fig. 8(a)–(c) show the variation in the electron density during the elementary steps passing through the transition states shown in Fig. 7. The variation was defined as the difference in electron density between the two intermediate states. The variation in electron density is superimposed on the geometrical structure of the intermediate state immediately after the corresponding transition state. Fig. 8(a) shows the R → I1 step passing through TS1, where the H–Ow bond is dissociated, and the O2c–H bond is formed. A large variation in the electron density is observed around the Ti–Ow–H moiety (black dotted circle) due to the PT (blue arrow). The mechanism of the electron density variation is illustrated in Fig. 9(a). The H–Ow bond dissociates (green dashed line) owing to the PT (blue arrow). Subsequently, the electron density in the Ti–Ow moiety (orange bar) increases, owing to the change from physisorption to chemisorption in the Ti–Ow interaction as the bond distance decreases from 2.33 Å to 1.85 Å. Overall, the chemical bond rearrangement in the Ti–Ow–H–O2c moiety causes electron transfer from the H–Ow moiety to the Ow–Ti moiety (green-orange arrow in Fig. 9(a)). The electron and proton transfers occur in opposing directions; thus, the total polarization increases, as shown in Fig. 7.
 | ||
| Fig. 8 Variation in the electron density. The increase and decrease in the electron density are illustrated with yellow and cyan, respectively. The threshold of the density is set to the same value for comparison. The colors of atoms are the same as those of Fig. 2. For example, in (a), the electron density difference between R and I1 is superimposed on the geometrical structure of I1. | ||
Fig. 8(b) illustrates the I2 → I3a step (passing through TS3a) in which the simultaneous rotations of the Ow–H and O2c–H groups occur. Compared with Fig. 8(a), the variation in the electron density is small because chemical bond rearrangement does not occur. The Ti atom bound to the Ow–H group moves 0.11 Å in the direction (black arrows) opposite to that of the PT (blue arrows). Geometric distortion due to the Ti–Ow bond and hydrogen bonding between the H and the Ow in the next unit cell causes stress, which results in the movement of the Ti atom. The polarizations caused by the Ti displacement and PT cancel each other, resulting in a small total variation in ΔP in the I2 → I3a step despite ΔrH in the I2 → I3a step being larger than that in the R → I1 step (Fig. 7). These results reveal the significance of geometry changes in the H2O moiety and the surface in the EF effect on the PT.
Fig. 8(c) illustrates the I2 → I3b step (passing through TS3b), and Fig. 9(b) illustrates the corresponding polarization mechanism. In this step, the H–O2c bond is dissociated and the Ow–H bond is formed, followed by rotations of the regenerated H2Ow moiety. The Ti–Ow bond is broken during the PT as the bond length increases from 1.87 Å to 2.35 Å. Therefore, electron density in the Ti–Ow region decreases. Overall, the electronic charge is transferred from the Ti–Ow to the Ow–H region, as depicted by the green-orange arrow in Fig. 9(b). In this step, the amount of polarization is governed by the bond dissociation at the O2c–H and Ti–Ow moieties and the Ow–H bond formation. The resultant polarizations cancel each other, and the net polarization is small, as shown in Fig. 7. The mechanisms illustrated in Fig. 9 do not fit the classical charge transfer model. The amount of polarization is determined by the rearrangement of the chemical bond network at the interface between the water molecules and the surface, and quantum mechanical interactions at the interface region govern the EF effect on the energy profile of the PT.
Conclusion
We studied the EF effect on PT on a metal oxide surface using the first-principles computational method. The Berry phase theory was used to calculate the polarization, and we elucidated the dependence of the PT energy profile on the direction and magnitude of the EF. The variation in the polarization was notable during the Ow–H bond dissociation, which was significantly enhanced by the EF. No clear correlation exists between the polarization and displacement of H atoms, indicating that the polarization cannot be explained as the classical electric work of an EF carrying a point charge. The variation in the electron density reveals that the charge transfer in the PT is caused by the chemical bond rearrangement at the interface between the water molecules and the surface; that is, the quantum mechanical interaction at the interface region governs the EF effect on the PT energy profile. Furthermore, the non-negligible contribution of the geometric distortion of the surface to the EF effect infers the importance of the metal oxide species on which PTs take place. Because of the low computational cost for evaluating the EF effect, the present method is a potential candidate for investigations of more complex systems, such as the interface between an aqueous solution and the surface at which the route of PT may be diverse. In this regard, this study presents the theoretical approach to investigate the EF effect on various chemical processes in which the distribution of the EF is non-uniform in space with respect to material surfaces.Author contributions
K. I. and S. F. planned the research. T. C., K. I., and J. H. wrote the manuscript. T. C. performed the calculations. All authors have checked the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was financially supported by JSPS KAKENHI (grant no. 19K15513 and JP20H02685) and the Collaborative Research Program of the Institute for Chemical Research, Kyoto University (grant no. 2022-61). This work was also supported by the MEXT project “Integrated Research Consortium on Chemical Sciences” and the Photo-excitonix Project of Hokkaido University. Most of the theoretical computations were performed using the computational resources of the Grand Chariot supercomputer provided by Hokkaido University through the HPCI System Research Project (Project ID: hp220135). Some of the computations were performed at the RCCS (Okazaki, Japan, Project: 22-IMS-C002), Super Computer System, Institute for Chemical Research (Kyoto University), and ACCMS (Kyoto University).References
- G. Karlberg, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 5158 RSC.
- C. F. Gorin, E. S. Beh and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 186–189 CrossRef CAS PubMed.
- C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef PubMed.
- S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091–1098 CrossRef CAS PubMed.
- T. Stuyver, D. Danovich, J. Joy and S. Shaik, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1438 CAS.
- Y. Sekine, M. Haraguchi, M. Matsukata and E. Kikuchi, Catal. Today, 2011, 171, 116–125 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Mater. Chem. A, 2018, 6, 8265–8270 RSC.
- R. Manabe, S. Okada, R. Inagaki, K. Oshima, S. Ogo and Y. Sekine, Sci. Rep., 2016, 6, 1–7 CrossRef PubMed.
- K. Takise, A. Sato, S. Ogo, J. G. Seo, K.-I. Imagawa, S. Kado and Y. Sekine, RSC Adv., 2019, 9, 27743–27748 RSC.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067 CrossRef CAS PubMed.
- M. P. Hyman and J. W. Medlin, J. Phys. Chem. B, 2005, 109, 6304 CrossRef CAS PubMed.
- P. Deshlahra, E. E. Wolf and W. F. Schneider, J. Phys. Chem. A, 2009, 113, 4125 CrossRef CAS PubMed.
- R. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651 CrossRef CAS PubMed.
- R. Resta, Rev. Mod. Phys., 1994, 66, 899 CrossRef CAS.
- R. Resta and D. Vanderbilt, Physics of Ferroelectrics: A Modern Perspective, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 31–68 Search PubMed.
- Z. Futera and N. J. English, J. Phys. Chem. C, 2016, 120, 19603–19612 CrossRef CAS.
- C. Dette, M. A. Perez-Osorio, S. Mangel, F. Giustino, S. J. Jung and K. Kern, J. Phys. Chem. C, 2017, 121, 1182–1187 CrossRef CAS.
- M. Zhou and H. Wang, JACS Au, 2021, 2, 188–196 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- V. Barone, M. Casarin, D. Forrer, M. Pavone, M. Sambi and A. Vittadini, J. Comput. Chem., 2009, 30, 934 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- A. Vittadini, A. Selloni, F. P. Rotzinger and M. Grätzel, Phys. Rev. Lett., 1998, 81, 2954–2957 CrossRef CAS.
- Y. He, A. Tilocca, O. Dulub, A. Selloni and U. Diebold, Nat. Mater., 2009, 8, 585–589 CrossRef CAS PubMed.
- C. Sun, L.-M. Liu, A. Selloni, G. Q. M. Lu and S. C. Smith, J. Mater. Chem., 2010, 20, 10319–10334 RSC.
- H. Sun, D. J. Mowbray, A. Migani, J. Zhao, H. Petek and A. Rubio, ACS Catal., 2015, 5, 4242–4254 CrossRef CAS.
- L. E. Walle, A. Borg, E. M. J. Johansson, S. Plogmaker, H. Rensmo, P. Uvdal and A. Sandell, J. Phys. Chem. C, 2011, 115, 9545–9550 CrossRef CAS.
- A. Tilocca and A. Selloni, Langmuir, 2004, 20, 8379–8384 CrossRef CAS PubMed.
- G. S. Herman, Z. Dohnálek, N. Ruzycki and U. Diebold, J. Phys. Chem. B, 2003, 107, 2788–2795 CrossRef CAS.
- K. Shirai, T. Sugimoto, K. Watanabe, M. Haruta, H. Kurata and Y. Matsumoto, Nano Lett., 2016, 16, 1323–1327 CrossRef CAS PubMed.
- T. Yabe and Y. Sekine, Fuel Process. Technol., 2018, 181, 187–198 CrossRef CAS.
- N. Salles, L. Martin-Samos, S. De Gironcoli, L. Giacomazzi, M. Valant, A. Hémeryck, P. Blaise, B. Sklenard and N. Richard, Nat. Commun., 2020, 11, 1–7 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Electronic polarization directly induced by external electric field; geometrical structures; Cartesian coordinates of optimized structures. See DOI: https://doi.org/10.1039/d3cp00577a |
| This journal is © the Owner Societies 2023 |