Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Neutron scattering study of polyamorphic THF·17(H2O) – toward a generalized picture of amorphous states and structures derived from clathrate hydrates†
Paulo H. B.
Brant Carvalho
 *a,
Mikhail
Ivanov
*a,
Mikhail
Ivanov
 a,
Ove
Andersson
a,
Ove
Andersson
 b,
Thomas
Loerting
b,
Thomas
Loerting
 c,
Marion
Bauer
c,
Chris A.
Tulk
d,
Bianca
Haberl
c,
Marion
Bauer
c,
Chris A.
Tulk
d,
Bianca
Haberl
 d,
Luke L.
Daemen
d,
Jamie J.
Molaison
d,
Luke L.
Daemen
d,
Jamie J.
Molaison
 d,
Katrin
Amann-Winkel‡
d,
Katrin
Amann-Winkel‡
 c,
Alexander P.
Lyubartsev
c,
Alexander P.
Lyubartsev
 a,
Craig L.
Bull
a,
Craig L.
Bull
 ef,
Nicholas P.
Funnell
ef,
Nicholas P.
Funnell
 e and
Ulrich
Häussermann
e and
Ulrich
Häussermann
 a
a
aDepartment of Materials and Environmental Chemistry, Stockholm University, SE-10691 Stockholm, Sweden. E-mail: paulo.barros@mmk.su.se; Fax: +46 (8) 152187; Tel: +46 (8) 51770000
bDepartment of Physics, Umeå University, SE-90187 Umeå, Sweden
cInstitute of Physical Chemistry, University of Innsbruck, A-6020 Innsbruck, Austria
dNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
eISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Didcot, Oxon OX11 7XN, UK
fSchool of Chemistry, University of Edinburgh, David Brewster Road, Edinburgh EH9 3FJ, Scotland, UK
First published on 15th May 2023
Abstract
From crystalline tetrahydrofuran clathrate hydrate, THF–CH (THF·17H2O, cubic structure II), three distinct polyamorphs can be derived. First, THF–CH undergoes pressure-induced amorphization when pressurized to 1.3 GPa in the temperature range 77–140 K to a form which, in analogy to pure ice, may be called high-density amorphous (HDA). Second, HDA can be converted to a densified form, VHDA, upon heat-cycling at 1.8 GPa to 180 K. Decompression of VHDA to atmospheric pressure below 130 K produces the third form, recovered amorphous (RA). Results from neutron scattering experiments and molecular dynamics simulations provide a generalized picture of the structure of amorphous THF hydrates with respect to crystalline THF–CH and liquid THF·17H2O solution (∼2.5 M). Although fully amorphous, HDA is heterogeneous with two length scales for water–water correlations (less dense local water structure) and guest–water correlations (denser THF hydration structure). The hydration structure of THF is influenced by guest–host hydrogen bonding. THF molecules maintain a quasiregular array, reminiscent of the crystalline state, and their hydration structure (out to 5 Å) constitutes ∼23H2O. The local water structure in HDA is reminiscent of pure HDA-ice featuring 5-coordinated H2O. In VHDA, the hydration structure of HDA is maintained but the local water structure is densified and resembles pure VHDA-ice with 6-coordinated H2O. The hydration structure of THF in RA constitutes ∼18 H2O molecules and the water structure corresponds to a strictly 4-coordinated network, as in the liquid. Both VHDA and RA can be considered as homogeneous.
1 Introduction
Clathrate hydrates (CHs) are inclusion compounds of water and guest species, which are trapped within polyhedral cages provided by the hydrogen-bond network of water molecules. There are numerous CH forming guest species, ranging from single atom noble gases to sizable organic molecules, such as tetrahydrofuran (THF). CHs have been intensely investigated for their natural occurrence in cold/slightly pressurized environments (e.g., CH4 hydrate) and for potential applications in gas storage (e.g., CO2, H2 hydrates).1–3 Near ambient pressure, CHs occur in two major structures: cubic structure I (CS-I) with space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n, and cubic structure II (CS-II) with space group Fd
n, and cubic structure II (CS-II) with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Their composition can be described as (2D+6T)·46H2O and (16D+8H)·136H2O, respectively, where D, T, and H denote dodecahedral (512), tetrakaidecahedral (51262), and hexakaidecahedral (51264) polyhedral cages. Accounting for the van der Waals radius of water,4 the internal free diameter of D, T, and H cages is 5.0, 5.9, and 6.7 Å, respectively. There is a natural relation between the size of the guest species and the crystal structure. Larger molecules, such as THF and SF6, fit only in H cages and thus adopt the CS-II structure and attain a strict 8H·136H2O (1
m. Their composition can be described as (2D+6T)·46H2O and (16D+8H)·136H2O, respectively, where D, T, and H denote dodecahedral (512), tetrakaidecahedral (51262), and hexakaidecahedral (51264) polyhedral cages. Accounting for the van der Waals radius of water,4 the internal free diameter of D, T, and H cages is 5.0, 5.9, and 6.7 Å, respectively. There is a natural relation between the size of the guest species and the crystal structure. Larger molecules, such as THF and SF6, fit only in H cages and thus adopt the CS-II structure and attain a strict 8H·136H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17) water-rich composition.5 When both cages are occupied in binary clathrate hydrate systems (i.e., containing only one kind of guest) their occupancy is often at the 80 to 90% level, resulting in compositions 1
17) water-rich composition.5 When both cages are occupied in binary clathrate hydrate systems (i.e., containing only one kind of guest) their occupancy is often at the 80 to 90% level, resulting in compositions 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6–1
6–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.5.6
6.5.6
Similar to water–ice, CHs display the phenomenon of pressure-induced amorphization (PIA) at low temperatures. This was first recognized with THF- and SF6-CHs7 and later especially studied with other CS-II systems containing larger organic molecules (e.g., acetone, cyclobutanone) and a water-rich 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 composition.8–13 Pure hexagonal ice, ice Ih, undergoes PIA around 1 GPa at temperatures below 140 K to high-density-amorphous (HDA)14 ice which can be converted to a densified form, very-high-density-amorphous (VHDA), when annealed above 1 GPa at about 160 K.15 Both HDA and VHDA ices can be recovered to ambient pressure at low temperature, where they have densities 1.17 and 1.26 g cm−3,16 which is substantially higher than that for crystalline ice Ih (∼0.93 g cm−3 at 80 K)17 and reflects the increased coordination of water molecules in the amorphous forms to 5-fold (HDA) and 6-fold (VHDA).18 The PIA behavior of CS-II 1
17 composition.8–13 Pure hexagonal ice, ice Ih, undergoes PIA around 1 GPa at temperatures below 140 K to high-density-amorphous (HDA)14 ice which can be converted to a densified form, very-high-density-amorphous (VHDA), when annealed above 1 GPa at about 160 K.15 Both HDA and VHDA ices can be recovered to ambient pressure at low temperature, where they have densities 1.17 and 1.26 g cm−3,16 which is substantially higher than that for crystalline ice Ih (∼0.93 g cm−3 at 80 K)17 and reflects the increased coordination of water molecules in the amorphous forms to 5-fold (HDA) and 6-fold (VHDA).18 The PIA behavior of CS-II 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 CHs is strikingly similar to ice Ih, occurring around 1.3 GPa below 130 K.7,19,20 However, there is a decisive difference in that the obtained “HDA” form is not recoverable, but reverts to crystalline CS-II CH upon pressure release.7 Yet, an amorphous state can be stabilized and made recoverable when heating the HDA form at pressures greater than 1 GPa to 160–180 K.21 This annealing leads to densification, which again appears similar to the creation of VHDA ice from the HDA form.16 PIA may be a general phenomenon of CHs, at least for CS-II-type ones, since it has been also observed for CS-II CHs with both types of cages occupied (and thus containing guest species in substantial higher concentrations). In the latter case, PIA is at somewhat higher pressures, around 1.5 GPa.
17 CHs is strikingly similar to ice Ih, occurring around 1.3 GPa below 130 K.7,19,20 However, there is a decisive difference in that the obtained “HDA” form is not recoverable, but reverts to crystalline CS-II CH upon pressure release.7 Yet, an amorphous state can be stabilized and made recoverable when heating the HDA form at pressures greater than 1 GPa to 160–180 K.21 This annealing leads to densification, which again appears similar to the creation of VHDA ice from the HDA form.16 PIA may be a general phenomenon of CHs, at least for CS-II-type ones, since it has been also observed for CS-II CHs with both types of cages occupied (and thus containing guest species in substantial higher concentrations). In the latter case, PIA is at somewhat higher pressures, around 1.5 GPa.
Amorphous hydrates derived from PIA of CHs raise a number of fundamental questions, including the arrangement of the guest species in the amorphous water matrix, their hydration structure, and importantly, the structure of the amorphous water matrix itself. In a recent contribution we analyzed the amorphous forms originating from Ar–CH, Ar·6.5H2O.22 Ar–CH also adopts CS-II, but the hydrophobic (single atom) guest occupies both types of cages, D and H. It was found that Ar·6.5H2O realizes three structurally distinct amorphous forms (polyamorphs): (i) heterogeneous Ar–CH–HDA in which the originally two crystallographically different Ar guests remain distinct as differently dense Ar–water hydration structures. (ii) Ar–CH–VHDA and (iii) recovered amorphous (RA) Ar–CH with homogeneous hydration environments around (undistinguishable) Ar atoms, which correspond to frozen solutions of immiscible Ar and water where, on average, 15 and 11 water molecules coordinate the Ar atoms, in the respective VHDA and RA structures. The local water structures of Ar–CH–HDA and –VHDA show some analogy to those of the corresponding amorphous ices, featuring H2O molecules in 5- and 6-fold coordination with neighboring molecules. However, they are considerably less dense. Ar–CH–RA possesses a strictly 4-coordinated H2O network.
In this work we revisit THF–CH, a CS-II representative with the water-rich 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 composition and a large-sized guest, that in contrast with hydrophobic Ar is capable of hydrogen-bond formation with the hosting water molecules. The PIA of THF–CH was studied earlier by in situ neutron diffraction experiments but the structures of THF–CH–HDA and –VHDA were only superficially evaluated. Recovered THF–CH–RA was reported20,21 but seems to have never been the subject of structural elucidation by neutron diffraction. It has been speculated that because of the more water-rich composition THF–CH–RA may feature a denser local water structure in comparison to amorphous Ar–CH–RA, perhaps more relating to that of HDA ice.22 We will discuss results for THF–CH in comparison with Ar–CH. Since THF is soluble in water, amorphous forms of THF–CH can be also compared with THF–water solution.
17 composition and a large-sized guest, that in contrast with hydrophobic Ar is capable of hydrogen-bond formation with the hosting water molecules. The PIA of THF–CH was studied earlier by in situ neutron diffraction experiments but the structures of THF–CH–HDA and –VHDA were only superficially evaluated. Recovered THF–CH–RA was reported20,21 but seems to have never been the subject of structural elucidation by neutron diffraction. It has been speculated that because of the more water-rich composition THF–CH–RA may feature a denser local water structure in comparison to amorphous Ar–CH–RA, perhaps more relating to that of HDA ice.22 We will discuss results for THF–CH in comparison with Ar–CH. Since THF is soluble in water, amorphous forms of THF–CH can be also compared with THF–water solution.
2 Experimental and computational details
2.1 Neutron scattering
A fully deuterated THF (Aldrich, ≥99.5 atom % 2H) in H2O (Aldrich, 99.9 atom % 2H) sample was prepared by mixing the liquids prior to experiments at the ideal composition THF·17H2O (THF-d8·172H2O). Neutron diffraction experiments on the liquid sample were run at 285 K on the GLAD diffractometer in the Intense Pulse Neutron Source (IPNS), Argonne National Laboratory, USA. The sample (ca. 2 g) was placed in a null scattering TiZr sample can and attached to the tail of a Displex closed cycle cryo-pump. Total scattering data were collected (for 18 hours) and corrected for background, empty cell scattering, multiple scattering, inelastic scattering and normalized against vanadium.Experiments targeting solid THF–CH employed a slight excess of THF (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16.5) to ensure complete consumption of water when crystallizing THF–CH by cooling below 277 K. Solid THF (with a melting point of 165 K) was not detectable in subsequent diffraction experiments at 80–130 K. In situ neutron powder diffraction experiments studying THF–CH–HDA and –VHDA at 130 K were performed at the PEARL diffractometer at ISIS, Rutherford Appleton Laboratory, UK.23–25 Data are reproduced from our previous work where also the experimental details, data reduction and correction are described.13
16.5) to ensure complete consumption of water when crystallizing THF–CH by cooling below 277 K. Solid THF (with a melting point of 165 K) was not detectable in subsequent diffraction experiments at 80–130 K. In situ neutron powder diffraction experiments studying THF–CH–HDA and –VHDA at 130 K were performed at the PEARL diffractometer at ISIS, Rutherford Appleton Laboratory, UK.23–25 Data are reproduced from our previous work where also the experimental details, data reduction and correction are described.13
THF–CH–RA was prepared by compressing CS-II THF–CH in a piston cylinder to 1.8 GPa at 77 K followed by heat-cycling to 180 K and decompressing, according to the protocol by Bauer et al.21Ex situ neutron powder diffraction experiments on THF–CH–RA were performed at the SANDALS diffractometer at the ISIS facility.26 Samples (ca. 1 g) were loaded in a flat plate cell machined from null scattering TiZr alloy for data collection (for 12 hours) and data were corrected for empty instrument, background, multiple scattering, inelastic scattering and normalized against vanadium.
2.2 Molecular dynamics
The input structure, a 2 × 2 × 2 supercell of CS-II THF–CH, was generated with the GenIce code.27 The simulation box was created with 1088 orientationally-disordered water molecules following the Bernal–Fowler ice rules28 and 136 THF molecules filling all H cages, with ca. 34 Å initial cell dimensions. The supercell size was deemed sufficient to capture the main features of the system, as shown in our earlier work.6,13 Molecular dynamics (MD) simulations were carried out using GROMACS 2020.4.29 Interactions were described with the OPLS-AA force field30 for THF and TIP4P/Ice for water.31 Corrections to Lennard-Jones parameters between the heavier atoms in THF and the oxygen atom in water, as introduced by Wu et al.,32 were applied to improve the agreement with experimental data of mutual solubility of THF and water. Geometric combination rules were applied for all other non-bonded cross terms. Three-dimensional periodic boundary conditions were used in all systems. Both van der Waals and electrostatic cut-off radii were set to 14 Å and the neighbor lists were constructed using the Verlet scheme.33 Long-range electrostatic interactions were accounted for with the particle–mesh Ewald (PME) method34,35 with grid spacing of 1.2 Å and cubic interpolation. Long-range dispersion corrections were applied to both energy and pressure. The lengths of all carbon–hydrogen bonds in THF were constrained using the LINCS algorithm.36 During the simulations, the temperature was kept constant using the stochastic velocity rescaling thermostat developed by Bussi et al.37 with a time constant of 1 ps. Pressure was stabilized with the isotropic Berendsen barostat38 during equilibration runs and Parrinello–Rahman barostat39 during production runs. A time constant of 2 ps was used for both barostats. The simulation time step of 1 fs was used for all simulations. The data obtained during production runs were used to calculate the average properties of the systems. While the duration of the equilibration runs varied for different conditions, all the production runs lasted for 1 ns if not stated otherwise.The simulations were performed in three main stages: isothermal compression, isobaric heating, and recovery. The simulation at a given step started with an equilibration run from the last frame of the previous step and continued with a production run. First, after the energy of the crystalline THF–CH was minimized, the system was subjected to isothermal compression at 130 K from atmospheric pressure up to 2.5 GPa in steps of 0.1 GPa. Each equilibration step was carried out for 1 ns. Longer equilibration runs were necessary at pressures close to amorphization to reach convergence (verified by energy and volume change). The duration of the runs was increased to 100 ns at 1.7 GPa and 20 ns for all other pressures between 1.5 and 2.0 GPa. At the second stage, pressure-amorphized systems at 2.0 GPa were isobarically heated from 130 to 200 K in 10 K steps and then up to 230 K in 15 K steps, with subsequent cooling following the same temperature steps as with heating. All equilibration runs during the heating stage lasted for 50 ns, and after each temperature drop, the system was equilibrated for 10 ns. At the last stage, 130 K, the system was decompressed to atmospheric pressure. Finally, the recovered system was heated up to 280 K (above the potential models melting point) at atmospheric pressure in 20 K steps (except for 190 to 200 K temperature change). The duration of the equilibration runs was 50 ns. VMD40 was used to analyze resulting trajectories and VMD and Diamond41 were used to create visualizations. Gromacs was used to calculate radial distribution functions and MDANSE42 to simulate total neutron scattering functions for direct comparison with experimental data. The XaNSoNS code43 was also used for the simulation of neutron scattering functions of single-frame atomic coordinates (snapshots). We accounted for deuteration in all calculations of neutron structure factors. It is important to note that if MD is implemented in NVT or NPT ensemble, different masses do not affect canonically averaged structural properties, including PDFs.
3 Results and discussion
3.1 Distinct amorphous forms of THF hydrate
The PIA of fully deuterated THF–CH was previously analyzed in an in situ neutron diffraction study at 130 K13 and the data are reevaluated here. In this experiment, PIA (to THF–CH–HDA) was observed at 1.2 GPa and subsequent annealing at 170 K produced THF–CH–VHDA. It was then not possible to decompress and measure RA comparably in situ in the pressure cell at ambient conditions. Instead, for this work, RA was produced according to Bauer et al.21 and neutron diffraction/total scattering data were measured ex situ. THF–CH–RA is only (meta)stable at atmospheric pressure. Similar to hyperquenched glassy THF–CH44 it has a tendency toward phase separation into THF and stacking-disordered ice, ice Isd, before complete crystallization as CS-II above 140 K, so measurements were made at lower temperature, 80 K, whereas data of the other amorphous states refer to 130 K.The formation of the three amorphous states at 130 K was also simulated by MD. Compression was carried out to 2.5 GPa and PIA was observed at 1.6 GPa. The ESI,† provides a density vs. pressure curve (Fig. S1, ESI†) as compared to previous work. In our previous results,13 we observed the onset of amorphization at 1.3 GPa but PIA covered a broader interval (from 1.3 to 1.7 GPa), which was attributed to the limited simulation times used. In this work we increased simulation times, which extended the stability of the crystalline CS-II to 1.5 GPa. PIA was then seen as an abrupt process starting at 1.6 GPa and ending at 1.7 GPa. Although the pressure is shifted compared to experiment, this result reflects better the experiment, as PIA is a first-order-like transition.13,20 From the completely amorphized structure at 2.0 GPa, we simulated densification of THF–CH–HDA by heat-cycling to 230 K. This temperature is higher than in experiments (170–180 K), which according to the protocol shown in another publication,22 compensates for the microsecond scales in MD compared to the hour-long annealing experiments. The measured densification is comparable to experiment. Recovery was simulated in a 200 ns long equilibration simulation setting pressure to 1 atm alongside a subsequent 1 ns production run.
The neutron structure factor functions S(Q) of the three amorphous states are shown in Fig. 1, together with that of the liquid with composition 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 at 285 K. According to the Faber–Ziman formalism,45 the S(Q) of a multi-component system can be expressed as a sum of total interference functions of neutron-weighted partials, i.e.,
17 at 285 K. According to the Faber–Ziman formalism,45 the S(Q) of a multi-component system can be expressed as a sum of total interference functions of neutron-weighted partials, i.e.,
| S(Q) = F(Q)/σcoherent, |
Q is the scattering vector, σ is the total coherent scattering cross section, α and β are components in a (atomic) pair correlation, c and b are respective concentration and scattering length of each component. Thus, the dominant contributors to the S(Q) functions of THF–CH polyamorphs and liquid are 2H–2H and 2H–O correlations which encompass both types of intermolecular correlations: those between guest (THF) and water, and those between water molecules. The S(Q) functions in Fig. 1 are dominated by the first diffraction peak (FDP), which correlates with intermediate range (3–6 Å) structural organization. Accordingly, the FDP should account for nearest neighbor THF–water correlations, as well as nearest and second nearest neighbor water–water correlations. The FDP may display variable widths and/or a “fine structure” (i.e., split feature, shoulder/asymmetric broadening, cf.Fig. 1(b)) which contains information on the kind and radial extent of local ordering, as subsequently discussed. Also, the position of the FDP is an indicator of the density of the sample, i.e., a larger Q value means a higher density. Generally, there is reasonably good agreement between measured and MD simulated S(Q), considering pressure and temperature differences and the general discrepancy between MD simulated structures to achieve completely relaxed VHDA and RA within the simulation time scale.
The location of the FDP is similar for HDA and VHDA (both above 2.0 Å−1) and similar for RA and the liquid (both below 2.0 Å−1), reflecting the similar densities within each pair. H2O densities (disregarding the THF mass) from MD simulations are summarized in Table 1. According to the MD results, the total density of crystalline THF–CH at 130 K just before PIA (1.5 GPa) is 1.080 g cm−3, and that of HDA just after PIA (1.7 GPa) is 1.254 g cm−3. This 16% density increase corresponds to a volume decrease of 14%, which is in fair agreement with the estimate for the experimental volume decrease by Suzuki (about 20%).20 Further density increase, when transforming HDA (1.287 g cm−3 at 2.0 GPa, 130 K) to VHDA (1.328 g cm−3 at 2.0 GPa, 130 K in MD), is 3.1%, which again correlates well with the change in piston displacement in the experiment reported by Bauer et al.21 following Suzuki's protocol20 (5.7% by heating to 150 K at 1.5 GPa) and their own protocol (7.6% by heating to 180 K at 1.8 GPa). Modeled RA at 1 atm and 130 K has a density of 1.081 g cm−3 and, thus, is substantially expanded (by 23%) compared to VHDA. The density of metastable RA is about 9% higher than that of stable crystalline THF–CH (at 130 K).
| H2O Density (g cm−3) [130 K] | Crystalline | HDA | VHDA | RA | Liquid |
|---|---|---|---|---|---|
| a Experimental data refer to fully deuterated sample. Actual 2H2O density 0.916 g cm−3 at 1 atm and 1.013 g cm−3 at 1 GPa. | |||||
| 1 atm | 0.809 (0.848a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13) 13) |
— | — | 0.883 | 0.823 [280 K] (0.815 [278 K]5) |
| 1.5 GPa | 0.882 (0.923 [1 GPa]a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13) 13) |
— | — | — | — |
| 1.7 GPa | — | 1.024 | — | — | — |
| 2.0 GPa | — | 1.051 | 1.085 (1.14 [1 GPa]12) | — | — |
In the experimental neutron S(Q), the FDP is clearly split for HDA, with contributions at 2.12 and 2.30 Å−1, whereas that for VHDA was assumed to be a single peak at 2.34 Å−1 in the earlier work.13 There is, however, considerable broadening and MD simulations (which were not performed for VHDA in the earlier work) suggest a split feature/shoulder also for THF–CH–VHDA. The experimental FDP of RA includes a shoulder at lower Q. The relatively sharp nature of this feature (marked in Fig. 1(a)) indicates ice Isd formation.44 The S(Q) of the liquid is very similar to the amorphous portion of the RA structure factor and and also indicates an asymmetric broadening. When compared to the Ar–CH system,22 only the S(Q) of the HDA polyamorph unambiguously displayed a split feature of the FDP. Although fully amorphous, Ar–CH–HDA was identified as heterogeneous because of (local) structural features that are remnant to the CS-II crystal structure. As we will show later, also THF–CH–HDA is structurally heterogeneous (but for a different reason) whereas the “fine structure” of the FDP of the S(Q) of VHDA, RA, and the liquid will be attributed to THF–H2O hydrogen bonding. In contrast with THF–CH–RA, Ar–CH–RA does not show a tendency for phase segregation (i.e. formation of ice Isd) and appears homogeneous up to around 120 K where crystallization to CS-II occurs.22
3.2 THF hydration structures
The structural features of disordered materials are conveniently analyzed by pair distribution functions (PDFs) in real space (r). PDFs are defined asa Fourier transform of the structure factor where ρ is the number density (number of atoms per volume). Partial S(Q)s and, accordingly, g(r)s, may be obtained from neutron scattering experiments using isotope substituted samples22,46 or, more conveniently, extracted from MD simulations.
Fig. 2 shows MD simulated PDFs gTHF–water(r) – referring to the radial distribution function of THF–water pairs with respect to the center of mass of each water and THF molecule – for amorphous, liquid, and crystalline THF–CH together with the cumulative coordination numbers nTHF–water(r) (Fig. 2(b)).
Crystalline THF–CH shows typical (zero) values of g(r) between sharp coordination shells defined by the translational symmetry in the crystal structure. In crystalline THF–CH, a THF molecule in the H cage is separated from water molecules by 4.7 Å on average (first peak). In the MD model, THF molecules appear freely rotating (unhindered rotational motion). Yet, the shoulder indicated in Fig. 2(a) shows anisotropy from hydrogen bonding between ether–O and H2O. THF–H2O hydrogen bonding has been investigated several times. Alavi et al.47 showed from MD simulations that host–guest hydrogen bond formation is non-negligible in CS-II THF–CH with a reaction energy of roughly 8.3 kJ mol−1. THF–H2O hydrogen bonds are short-lived and thermally activated, since the phenomenon disrupts the hydrogen ordering in the water framework causing Bjerrum-L-type orientational defects (no H atoms between two water–O atoms) in the structure. Sengupta et al.48 found using solid-state NMR that the reorientation barrier for THF within CS-II is 19.7 kJ mol−1 at 200 K, thus demonstrating that hydrogen bonds between THF and water are significant. The importance of Bjerrum defects in a CH structure was further demonstrated by Nguyen et al.,49 revealing with liquid-state NMR that after temporary guest–host hydrogen bonds, water reorientation in crystalline CHs induced by Bjerrum defects significantly destabilizes crystalline CH phases.
PDFs of the amorphous forms and the liquid are characteristic with considerably broader peaks. Again, HDA and VHDA are very similar and so are RA and liquid, with maxima at 4.60 and 4.75 Å, respectively. The weak shoulder of the first peak in the crystalline g(r) is developed into a pronounced, almost separated, feature with a maximum at the same interatomic distance, around 4.0 Å. This is attributed to a static ether–O⋯H–OH hydrogen bond which brings the centers of gravity of the two molecules to the same distance for all of them. Through visual analysis of the MD trajectories, we found that THF is arrested in the polyamorphs (static hydrogen bond) but rotating in the liquid (280 K, dynamic hydrogen bond). Fig. 3 shows explicitly gO–THF–H–water(r), i.e., correlations between the atoms involved in the hydrogen bond. The peak maximum appears at 1.9 Å, which corresponds well to normal hydrogen bonding. RA displays the sharpest peak because hydrogen bond is “well”-defined in the relaxed amorphous structure and THF is immobile. In the liquid the situation is similar, but the hydrogen bond is “averaged out” because the structure and dynamics of hydration water around an organic molecule are non-uniform.
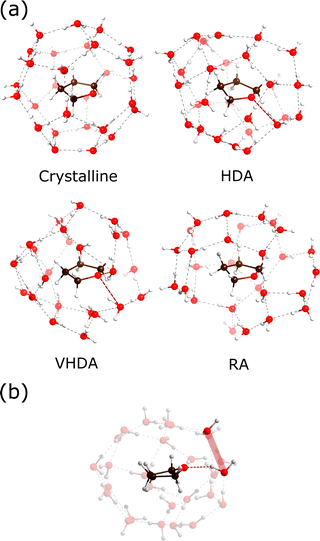
Fig. 4 shows the hydration structures with MD snapshots. These follow from the cumulative coordination number plots. THF molecules in crystalline THF–CH attain a sharp hydration value of 28 at 5.10 Å (cf.Fig. 2(b)), which corresponds to the H-cage environment. If we define arbitrarily a coordination shell at 5 Å for the polyamorphs and the liquid, we observe a similar coordination number for HDA and VHDA, 23–24 molecules, and 18 and 16 for RA and the liquid, respectively.
The THF coordination appears anisotropic in the polyamorphs, which can be seen in Fig. 4(a), due to the planar nature of the guest molecule. As for crystalline THF–CH, ether–O forming hydrogen bonds produce Bjerrum-type defects that modify the surrounding water network (highlighted in Fig. 4(b)). As shown by Titantah and Karttunen50 from ab initio calculations, water molecules in the hydration shell of organic molecules involved in hydrogen-bond exchange exhibit different time scales due to very different dynamical behaviors. To what extent host–guest hydrogen bonding and Bjerrum defects affect the structure and stability of amorphous CHs is still unclear, although their destabilizing effect in crystalline CHs could be expected to play a role in amorphous CH states.
Lastly, we address the arrangement of the THF molecules in the various forms. Fig. 5(a and b) shows the MD simulated PDFs gTHF–THF(r) and the corresponding nTHF–THF(r) for amorphous, liquid and crystalline THF–CH. As for gTHF–water(r) (Fig. 2), partials refer to the center of mass of THF molecules. Crystalline THF–CH shows a sharp peak at 7.5 Å, which corresponds to the distance between H-cage centers. It is important to recognize the similarity of HDA to crystalline CS-II (i.e. representing a “remnant” crystalline structure). The value of gTHF–THF(r) falls to zero above 8 Å, suggesting translational periodicity of THF molecules in THF–CH–HDA. From Fig. 5(b) it is also clear that both crystalline and THF–CH–HDA attain 4 neighbors above 7.5 Å, with zero gTHF–THF(r) between 8.2 and 9.8 Å. However, the nearest neighbor PDF peak is broadened in HDA, which means that THF molecules move significantly from their crystalline equilibrium positions. In contrast, VHDA shows a broad distribution of nearest neighbor THF–THF distances. The distance across the free THF molecule is about 4.1 Å. At short distances below 5 Å, the non-zero gTHF–THF(r) indicates clustering of THF molecules via hydrogen bonds (water-mediated THF interactions, including a hydrogen-bond donor interaction between the OH of water and the ether–O of THF and an acceptor interaction between the O atom of water and a hydrogen atom of the α-methylene carbon of THF) as described by Shultz and Vu51 from vibrational spectroscopic investigations of THF–water complexes.
Functions gTHF–THF(r) of RA and liquid are quite similar. Both are characterized by very broad distributions and similar clustering of THF (via H2O). In the liquid state, the broad distribution attains a maximum at 8.5 Å with a tail extending down to 4 Å. The maximum in the broad THF–THF distance distribution for RA is below 8 Å. The RA state can be considered a frozen solution of THF–water, which will be explicitly shown by the subsequent analysis of local water structures.
3.3 Local water structures
How are the water molecules arranged in amorphous hydrates and how does the local structure compare to those in amorphous ices? In amorphous CHs, the hydrogen-bond network of the host water molecules has to accommodate simultaneously the guests hydration structure. Thus, the local water structure in amorphous hydrates is expected to vary with the concentration and size of the guest species. For water-rich 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 THF–CH–HDA and –VHDA there may be similarities to the corresponding amorphous water ices.
17 THF–CH–HDA and –VHDA there may be similarities to the corresponding amorphous water ices.
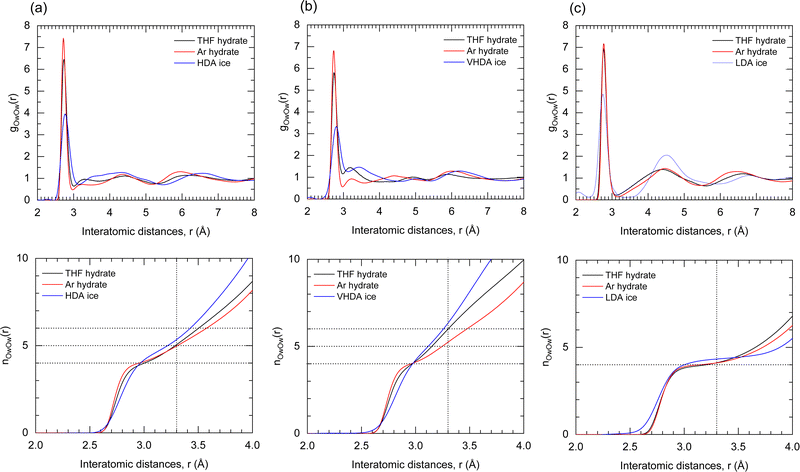
Fig. 6 shows the water O–O PDF, gOw–Ow(r), for amorphous, liquid, and crystalline THF–CH together with the cumulative coordination numbers, nOw–Ow(r) (Fig. 6(b)). For amorphous ices the first coordination shell is usually defined out to r = 3.3 Å.52 For crystalline THF–CH values of gOw–Ow(r) are zero between the sharp shells defined by the translational periodicity. Maxima corresponding to the first and second shell are at 2.76 Å and 4.47 Å, respectively. The gOw–Ow(r) for THF–CH–VHDA and –HDA are very similar and the additional maximum at 3.2 Å indicates that molecules are coordinated by more than four molecules in the nearest neighbor environment. The integrated water coordination number, nOw–Ow(r), indeed produces average coordination numbers of 6 and 5, respectively (referring to MD simulations at 2 GPa), which are also the coordination numbers of the corresponding amorphous water ices (albeit at atmospheric pressure).53 We thus propose that, since the hydration structure of THF is virtually the same in THF–CH–HDA and –VHDA, the densification to VHDA is then essentially corresponding to a densification of the local water structure, from 5- to 6-coordinated.
Returning to the FDP feature in the experimental neutron S(Q)s (Fig. 1), our revised analysis of the heterogeneity of the HDA phase reveals that the distinct densities observed can be attributed to the different characteristic distances (length-scales) over which water–water and THF–water correlations occur in the system. Specifically, we now assign the denser local structure to guest–water correlations. Note that this interpretation is reversed from earlier work,13 which lacked VHDA simulations to fully interpret the local water structure and transformations upon annealing.
The water structure of THF–CH–RA is then clearly distinguished from those of -HDA and -VHDA. The almost zero value of gOw–Ow(r) around r = 3.2 Å and the rather pronounced oscillations at higher r indicate a high degree of tetrahedrality of the hydrogen-bond network. The nOw–Ow(r) for RA shows a plateau around four molecules. Both gOw–Ow(r) and nOw–Ow(r) for RA bear great resemblance to the liquid which also represents a tetrahedral network, albeit with lower density (cf.Table 1). When compared to the corresponding state of amorphous ice, LDA, one important difference is that LDA is clearly less dense than liquid water, whereas THF–CH–RA has a similar density as the liquid phase. LDA constitutes a true polyamorph form of ice alongside HDA and VHDA, with clear transitions taken place in a sharp, first-order-like manner. There has been no evidence of such sharp transitions between THF–CH–VHDA and –RA, which raises the possibility of a continuum of states on the downstroke transition upon recovery. Further investigation of the in situ decompression of THF–CH–VHDA below 130 K is required to clarify this possible distinction.
Inelastic neutron scattering is a uniquely powerful technique to study vibrational dynamics of materials and has been used to show the nature of hydrogen bonding in amorphous ices ex situ and distinguish different polyamorphs.54 INS studies in situ would allow further insight into the similarity/dissimilarity of the water structure in amorphous CHs allowing, for instance, unambiguous assignment of the role of hydrogen bonding.
3.4 Toward a general picture – and subjects to be further investigated
The comparison of amorphous forms of THF–CH (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17) and earlier investigated Ar–CH, Ar·6.5H2O (along with amorphous ices) is instructive and should allow some generalizations. In the Ar–CH system, both types of cages (small, D, and large, H cages) are occupied. Ar–Ar distances are much shorter (5.5–6.5 Å) than THF–THF distances. In addition, Ar is a small-sized guest species with a lower hydration number. With both types of cages filled, water is confined to a “thin-walled” porous space where the hydrogen-bond network accommodates simultaneously the guests hydration structure. In contrast, the empty D cages in THF–CH give rise to “thick-walled” porous space with a more “independent” water structure – where a fraction of water molecules is not involved in guest coordination.
17) and earlier investigated Ar–CH, Ar·6.5H2O (along with amorphous ices) is instructive and should allow some generalizations. In the Ar–CH system, both types of cages (small, D, and large, H cages) are occupied. Ar–Ar distances are much shorter (5.5–6.5 Å) than THF–THF distances. In addition, Ar is a small-sized guest species with a lower hydration number. With both types of cages filled, water is confined to a “thin-walled” porous space where the hydrogen-bond network accommodates simultaneously the guests hydration structure. In contrast, the empty D cages in THF–CH give rise to “thick-walled” porous space with a more “independent” water structure – where a fraction of water molecules is not involved in guest coordination.
It is inferred that structure-II CHs generally yield the polyamorphs HDA, VHDA and RA. HDA follows from PIA and is typically heterogeneous (remnant crystalline CH). As shown in this work THF–CH–HDA has two length scales for water–water correlations (less dense local water structure) and for THF–water correlations (denser hydration structure). In addition, THF molecules maintain a quasi-periodic arrangement. As earlier shown, in Ar–CH–HDA the hydration structures of Ar atoms originating from two different cage environments have different densities, less dense for Ar atoms associated with large H cages and denser for Ar atoms associated with the smaller D cages.22 Because of their heterogeneous nature CH–HDA materials will revert to the crystalline CS-II structure upon decompression. This behavior is unlike amorphous ice in its HDA state, which can be retained on decompression. Upon annealing at high pressures, CH–HDA transforms into the VHDA form in which either the water structure (in the case of water-rich, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 CHs) or the hydration structure of guest atoms originating from H cages (as in Ar–CH) densify. Upon decompression CH-VHDA relaxes and turns into the RA polyamorph. The recovered form is (meta)stable at low temperatures, but hydrogen bonding may destabilize the amorphous CH structure towards ice crystallization even below 140 K.21 Unlike amorphous VHDA-ice that can be retained, the presence of a solute impedes the recovery of denser amorphous CHs. CH–VHDA and CH–RA can be considered as homogeneous, frozen solutions at high and ambient pressure, respectively. Upon relaxation in the decompression procedure the coordination number changes from 6 in CH–VHDA to 4 in CH–RA. It remains unclear whether the coordination number, shown in Fig. 6(b), changes in a jump-like manner, similar to the way known for pure water, or continuously.
17 CHs) or the hydration structure of guest atoms originating from H cages (as in Ar–CH) densify. Upon decompression CH-VHDA relaxes and turns into the RA polyamorph. The recovered form is (meta)stable at low temperatures, but hydrogen bonding may destabilize the amorphous CH structure towards ice crystallization even below 140 K.21 Unlike amorphous VHDA-ice that can be retained, the presence of a solute impedes the recovery of denser amorphous CHs. CH–VHDA and CH–RA can be considered as homogeneous, frozen solutions at high and ambient pressure, respectively. Upon relaxation in the decompression procedure the coordination number changes from 6 in CH–VHDA to 4 in CH–RA. It remains unclear whether the coordination number, shown in Fig. 6(b), changes in a jump-like manner, similar to the way known for pure water, or continuously.
The local water structures for CH–HDA and –VHDA will depend on the composition (cage occupancy), with water-rich 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 most resembling that of the corresponding amorphous water ices. Fig. 7 shows the PDFs and cumulative coordination numbers for oxygen–oxygen interactions of the amorphous forms of THF– and Ar–CH compared to the corresponding amorphous pure water–ices. HDA–CH and VHDA–CH with water-rich composition attain 5- and 6-coordinated water structures, correspondingly, analogous to HDA and VHDA ice. Guest-rich (1
17 most resembling that of the corresponding amorphous water ices. Fig. 7 shows the PDFs and cumulative coordination numbers for oxygen–oxygen interactions of the amorphous forms of THF– and Ar–CH compared to the corresponding amorphous pure water–ices. HDA–CH and VHDA–CH with water-rich composition attain 5- and 6-coordinated water structures, correspondingly, analogous to HDA and VHDA ice. Guest-rich (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∼6) compositions hinder the densification of the local water structure. The water coordination of Ar–CH–HDA and –VHDA is increased to only 4.7 and 5,22 respectively.
∼6) compositions hinder the densification of the local water structure. The water coordination of Ar–CH–HDA and –VHDA is increased to only 4.7 and 5,22 respectively.
In contrast, the water structure of the CH–RA appears independent on the composition and represents always a 4-coordinated network, which resembles LDA-ice and the structure of liquid solutions.
To corroborate the influence of hydrogen bonding on guest hydration structures, isotropic and weakly interacting guests with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 composition, e.g., SF6–CH, should be further investigated. Further, it will be important to also obtain more insight on amorphous CHs originating from crystalline CS-I. PIA of CS-I CHs occurs at higher pressures compared to CS-II CHs,6 above 2 GPa. However, there has been only two experimental studies. CH4–CH was pressurized to 3.2 GPa at 100 K, resulting in an amorphous HDA-type sample with a split FDP, which could then be annealed into CH4–CH–VHDA at temperatures below 220 K.55 Although at considerably higher pressures, this behavior is analogous to CS-II produced HDA and VHDA polyamorhps. However, recovery experiments were not performed in this study and it is not yet clear whether there is also a RA form. Xe–CH was shown to amorphize above 4 GPa at 95 K in a sluggish fashion, producing a quasi-crystalline state in which Xe atoms retained a high degree of long-range ordering.6 This state is not recoverable to ambient pressure. Also, annealing experiments performed at 150–170 K around 5 GPa did not produce a recoverable amorphous form. It may be that the large size of Xe makes Xe–CH exceptional and Kr–CH should represent a better target for studying polyamorphism originating from CS-I CHs.
17 composition, e.g., SF6–CH, should be further investigated. Further, it will be important to also obtain more insight on amorphous CHs originating from crystalline CS-I. PIA of CS-I CHs occurs at higher pressures compared to CS-II CHs,6 above 2 GPa. However, there has been only two experimental studies. CH4–CH was pressurized to 3.2 GPa at 100 K, resulting in an amorphous HDA-type sample with a split FDP, which could then be annealed into CH4–CH–VHDA at temperatures below 220 K.55 Although at considerably higher pressures, this behavior is analogous to CS-II produced HDA and VHDA polyamorhps. However, recovery experiments were not performed in this study and it is not yet clear whether there is also a RA form. Xe–CH was shown to amorphize above 4 GPa at 95 K in a sluggish fashion, producing a quasi-crystalline state in which Xe atoms retained a high degree of long-range ordering.6 This state is not recoverable to ambient pressure. Also, annealing experiments performed at 150–170 K around 5 GPa did not produce a recoverable amorphous form. It may be that the large size of Xe makes Xe–CH exceptional and Kr–CH should represent a better target for studying polyamorphism originating from CS-I CHs.
4 Conclusions
The amorphous materials derived from THF–CH were investigated with neutron scattering experiments and MD simulations. THF–CH is a CS-II representative with the water-rich THF·17H2O composition and a large-sized guest. From crystalline THF–CH, we derived three distinct amorphous forms: HDA obtained from PIA of THF–CH; VHDA, obtained by heat-cycling HDA at high pressure; and RA, produced by decompressing VHDA to atmospheric pressure. Our results provide a comprehensive understanding of the local structure of amorphous THF hydrates compared to crystalline THF–CH and liquid THF–water solution with the same composition.We followed the changes between amorphous states and elucidated the structure of these polyamorphs from neutron structure factor functions S(Q) of fully deuterated samples. The calculated density increase from crystalline THF–CH (at 1.5 GPa) to HDA (at 1.7 GPa) is 16%. The densities of HDA and VHDA (only observable in situ) at 2 GPa and 130 K are 1.287 and 1.328 g cm−3, respectively, whereas that of RA (at 1 atm) is 1.081 g cm−3. We found that HDA is heterogeneous with a less dense local water structure and a denser THF hydration structure. The hydration structure of THF in HDA is influenced by guest–host hydrogen bonding, with THF molecules maintaining a quasiregular array similar to the crystalline state. Water molecules in THF–CH–HDA are coordinated by more than four molecules in the nearest neighbor environment. Upon decompression, HDA reverts to the crystalline CS-II structure, unlike amorphous ice which can be retained. Annealing HDA at 180 K and 2 GPa causes further density increase by 3.1% essentially corresponding to a densification of the local water structure, from 5- in HDA to 6-coordinated in VHDA. VHDA maintains the THF hydration structure of HDA but shows a densified local water structure resembling pure VHDA-ice with 6-coordinated water molecules. On the other hand, the THF hydration structure in RA is considerably less dense and the water network is strictly 4-coordinated, similar to the liquid state. Both VHDA and RA can be considered as homogeneous amorphous forms.
Author contributions
Brant Carvalho, P. H. B.: conceptualization, investigation, data curation, formal analysis, methodology, validation, visualization, writing – original draft. Mikhail Ivanov: investigation, data curation, methodology, validation. Ove Andersson: conceptualization, investigation, data curation, methodology, resources, validation, supervision. Thomas Loerting: conceptualization, investigation, data curation, methodology, resources, validation, supervision. Marion Bauer: investigation, data curation, resources. Chris A. Tulk: investigation, data curation, methodology. Bianca Haberl: investigation, data curation, formal analysis, methodology. Luke L. Daemen: investigation, data curation, formal analysis, methodology. Jamie J. Molaison: investigation, data curation, methodology. Katrin Amann-Winkel: formal analysis, methodology. Alexander P. Lyubartsev: methodology, validation, supervision. Craig L. Bull: investigation, data curation, methodology, validation. Nicholas P. Funnell: investigation, data curation, methodology, validation. Ulrich Häussermann: conceptualization, investigation, data curation, formal analysis, methodology, visualization, project administration, funding acquisition, writing – original draft. All authors contributed to revising the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been funded by the Swedish Foundation for Strategic Research (SSF) within the Swedish National Graduate School in neutron scattering (SwedNess). This research used resources of the Intense Pulse Neutron Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. Experiments at the ISIS Neutron and Muon Source were supported by beamtime allocations RB900029, RB1710205, and RB1820254 from the Science and Technology Facilities Council.Notes and references
- E. D. S. Jr. and C. A. Koh, Clathrate Hydrates of Natural Gases, CRC Press, 2007 Search PubMed.
- W. L. Mao, H. Kwang Mao, A. F. Goncharov, V. V. Struzhkin, Q. Guo, J. Hu, J. Shu, R. J. Hemley, M. Somayazulu and Y. Zhao, Science, 2002, 297, 2247–2249 CrossRef CAS PubMed.
- A. Gupta, G. V. Baron, P. Perreault, S. Lenaerts, R.-G. Ciocarlan, P. Cool, P. G. Mileo, S. Rogge, V. V. Speybroeck, G. Watson, P. V. D. Voort, M. Houlleberghs, E. Breynaert, J. Martens and J. F. Denayer, Energy Storage Mater., 2021, 41, 69–107 CrossRef.
- J. A. Ripmeester, S. Alavi and C. I. Ratcliffe, An Introduction to Clathrate Hydrate Science, John Wiley & Sons, Ltd, 2022, ch. 1, pp. 1–26 Search PubMed.
- S. R. Gough and D. W. Davidson, Can. J. Chem., 1971, 49, 2691–2699 CrossRef CAS.
- P. H. B. B. Carvalho, A. Mace, O. Andersson, C. A. Tulk, J. Molaison, A. P. Lyubartsev, I. M. Nangoi, A. A. Leitão and U. Häussermann, Phys. Rev. B, 2021, 103, 064205 CrossRef.
- Y. P. Handa, J. S. Tse, D. D. Klug and E. Whalley, J. Chem. Phys., 1991, 94, 623–627 CrossRef CAS.
- O. Andersson and Y. Nakazawa, J. Phys. Chem. B, 2015, 119, 3846–3853 CrossRef CAS PubMed.
- O. Andersson and U. Häussermann, J. Phys. Chem. B, 2018, 122, 4376–4384 CrossRef CAS PubMed.
- O. Andersson and G. P. Johari, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174201 CrossRef.
- O. Andersson and G. P. Johari, J. Chem. Phys., 2008, 129, 234505 CrossRef PubMed.
- O. Andersson, P. H. Carvalho, Y. J. Hsu and U. Häussermann, J. Chem. Phys., 2019, 151, 014502 CrossRef PubMed.
- P. H. B. Carvalho, A. Mace, C. L. Bull, N. P. Funnell, C. A. Tulk, O. Andersson and U. Häussermann, J. Chem. Phys., 2019, 150, 204506 CrossRef PubMed.
- O. Mishima, L. D. Calvert and E. Whalley, Nature, 1984, 310, 393–395 CrossRef CAS.
- R. J. Nelmes, J. S. Loveday, T. Strässle, C. L. Bull, M. Guthrie, G. Hamel and S. Klotz, Nat. Phys., 2006, 2, 414–418 Search PubMed.
- T. Loerting, C. Salzmann, I. Kohl, E. Mayer and A. Hallbrucker, Phys. Chem. Chem. Phys., 2001, 3, 5355–5357 RSC.
- W. F. Kuhs and M. S. Lehmann, in The Structure of Ice-Ih, ed. F. Franks, Cambridge University Press, 1986, vol. 2, pp. 1–66 Search PubMed.
- J. L. Finney, D. T. Bowron, A. K. Soper, T. Loerting, E. Mayer and A. Hallbrucker, Phys. Rev. Lett., 2002, 89, 205503 CrossRef CAS PubMed.
- R. G. Ross and P. Andersson, Can. J. Chem., 1982, 60, 881–892 CrossRef CAS.
- Y. Suzuki, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–4 Search PubMed.
- M. Bauer, D. M. Többens, E. Mayer and T. Loerting, Phys. Chem. Chem. Phys., 2011, 13, 2167–2171 RSC.
- P. H. B. B. Carvalho, P. I. R. Moraes, A. A. Leitão, O. Andersson, C. A. Tulk, J. Molaison, A. P. Lyubartsev and U. Häussermann, RSC Adv., 2021, 11, 30744–30754 RSC.
- O. Andersson, P. H. B. Carvalho, C. L. Bull, N. P. Funnell, M. Guthrie and U. Häussermann, Exploration of the pressure-induced amorphization and glassy states of THF-clathrate II, STFC ISIS Neutron and Muon Source, 2017 Search PubMed.
- O. Andersson, P. H. B. Carvalho, C. L. Bull, N. P. Funnell and U. Häussermann, Structural changes in pressure-amorphized THF-clathrates, STFC ISIS Neutron and Muon Source, 2018 Search PubMed.
- C. L. Bull, N. P. Funnell, M. G. Tucker, S. Hull, D. J. Francis and W. G. Marshall, High Press. Res., 2016, 36, 493–511 CrossRef.
- T. Loerting, J. L. Finney, D. T. Bowron, K. Amann-Winkel and M. Bauer, Crystallization of clathrate hydrates from amorphous THF–water solutions, STFC ISIS Neutron and Muon Source, 2010 Search PubMed.
- M. Matsumoto, T. Yagasaki and H. Tanaka, J. Comput. Chem., 2018, 39, 61–64 CrossRef CAS PubMed.
- J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. L. Abascal, E. Sanz, R. G. Fernández and C. Vega, J. Chem. Phys., 2005, 122, 234511 CrossRef CAS PubMed.
- J. Y. Wu, L. J. Chen, Y. P. Chen and S. T. Lin, J. Phys. Chem. C, 2015, 119, 1400–1409 CrossRef CAS.
- S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- K. Brandenburg and H. Putz, Crystal Impact: Bonn, Germany, 2008 Search PubMed.
- G. Goret, B. Aoun and E. Pellegrini, J. Chem. Inf. Model., 2017, 57, 1–5 CrossRef CAS PubMed.
- V. S. Neverov, SoftwareX, 2017, 6, 63–68 CrossRef.
- C. A. Tulk, Y. Ba, D. D. Klug, G. McLaurin and J. A. Ripmeester, J. Chem. Phys., 1999, 110, 6475–6483 CrossRef CAS.
- T. E. Faber and J. M. Ziman, Philos. Mag., 1965, 11, 153–173 CrossRef CAS.
- P. H. B. Carvalho, A. Mace, O. Andersson, C. A. Tulk, J. Molaison and U. Häussermann, J. Solid State Chem., 2020, 285, 121220 CrossRef.
- S. Alavi, R. Susilo and J. A. Ripmeester, J. Chem. Phys., 2009, 130, 174501 CrossRef PubMed.
- S. Sengupta, J. Guo, K. C. Janda and R. W. Martin, J. Phys. Chem. B, 2015, 119, 15485–15492 CrossRef CAS PubMed.
- N. N. Nguyen, R. Berger, M. Wagner, J. Thiel, H.-J. Butt and R. Graf, J. Phys. Chem. C, 2021, 125, 15751–15757 CrossRef CAS.
- J. T. Titantah and M. Karttunen, J. Am. Chem. Soc., 2012, 134, 9362–9368 CrossRef CAS PubMed.
- M. J. Shultz, P. Bisson and T. H. Vu, J. Chem. Phys., 2014, 141, 18C521 CrossRef PubMed.
- G. Malenkov, J. Phys.: Condens. Matter, 2009, 21, 35 CrossRef PubMed.
- T. Loerting, K. Winkel, M. Seidl, M. Bauer, C. Mitterdorfer, P. H. Handle, C. G. Salzmann, E. Mayer, J. L. Finney and D. T. Bowron, Phys. Chem. Chem. Phys., 2011, 13, 8783 RSC.
- A. I. Kolesnikov, J. Li, S. F. Parker, R. S. Eccleston and C.-K. Loong, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3569–3578 CrossRef CAS.
- C. A. Tulk, D. D. Klug, J. J. Molaison, A. M. dos Santos and N. Pradhan, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 054110 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Density versus pressure plot from simulations and experiments comparing the present work to previous results. See DOI: https://doi.org/10.1039/d3cp00539a |
| ‡ Current address: Max Planck Institute for Polymer Research and Johannes Gutenberg University Mainz, 55128 Mainz, Germany. |
| This journal is © the Owner Societies 2023 |