Exciton diffusion in poly(3-hexylthiophene) by first-principles molecular dynamics

Abstract

Poly(3-hexylthiophene) (P3HT) is a polymer used in organic solar cells as a light absorber and an electron donor. Photogenerated excitons diffuse and dissociate into free charge carriers provided they reach the absorber boundaries. The device efficiency is therefore dependent on the exciton diffusion. Although measurements can be performed for example by time-resolved photoluminescence, a quantitative modeling is highly desirable to get an insight into the relationship between the atomic structure at finite temperature and the diffusion coefficient of the exciton. This is the objective of the present work, achieved by resorting to first-principles molecular dynamics in combination with the restricted open-shell approach to model the singlet excited state. The maximally localized Wannier functions and their centers are used to monitor and localize the electron and the hole along the dynamics. The resulting diffusion coefficient is in close agreement with available measurements.

---

1. Introduction

The use of organic materials such as polymers or small molecules in solar cells enables the reduction of the fabrication cost and realization of flexible modules. By changing the constituent molecules, a higher tunability than the one provided by inorganic materials is possible, and recently efficiencies close to 20% have been obtained with polymer donors and non-fullerene acceptors, with record values for ternary bulk-heterojunction (BHJ)¹ and solid additive-treated BHJ² devices. The active layers of BHJ solar cells are blends of two families of organic materials, electron donors and electron acceptors. When light is absorbed, an exciton is generated and diffuses. At the donor/acceptor interface, the exciton dissociates into a free electron and a hole, which are subsequently collected to generate an electrical current. However if the diffusion length of the exciton is too short to reach the interface, the exciton undergoes recombination before being able to generate any current, thus not contributing to any energy harvesting. Our goal is to provide a guideline from atomic scale modeling for the rational design of organic materials with the highest possible exciton diffusion length.

The exciton diffusion length is expressed as , where D is the diffusion coefficient and τ is the exciton lifetime. In the present work, an important step toward our ultimate goal (quantify L) is made by focusing on the diffusion coefficient D. The exciton diffusion coefficient can be measured experimentally, for instance by time resolved photoluminescence.³ From a theoretical standpoint, the Frenkel–Holstein Hamiltonian scheme has been applied to various organic polymers⁴ and more recently to 2D systems.⁵ First-principles molecular dynamics (FPMD) can provide alternatively a valuable atomic-scale picture of the dynamical process at finite temperature and link the atomic and electronic structures to the efficiency of a diffusion process. Vibronic effects are included a priori and do not need to be added, while inclusion of ad hoc contributions from intermolecular charge transfer⁶ is not necessary. Moreover, our dynamical approach being based on density-functional theory (DFT) as in any FPMD scheme, possible couplings between atomic and electronic motions are intrinsically accounted for, thus including the cases of trapping and polarons implying coupling with atomic vibrations. The assessment of the degree of the predictive power of a computational scheme is a stringent comparison with the available experimental data. To this aim, we focus on poly(3-hexylthiophene) (P3HT), a polymer widely used in BHJ solar cells. The structure of P3HT has been extensively characterized,^7,8 and the exciton diffusion coefficient has been measured in the crystalline domains (see Table 2).⁹

The structure of P3HT (at T = 0 K) is presented in Fig. 1 (at the top). In this figure, the structures are relaxed within the framework of DFT for the calculation of the electronic structure as described below. The P3HT polymer is usually modeled by a segment containing a finite number of thiophenes and methyl groups instead of the hexyl chains, to reduce the computational workload. Penta(3-methylthiophene) (penta3MT) (Fig. 1, bottom) is an example of such molecules and was chosen by Schwermann et al.¹⁰ to study the exciton diffusion. At room temperature, however, penta3MT molecules fold and the heterocycles at the extremities are free to rotate (see Fig. 2). This conformational change complicates the observation of an exciton transfer between molecules. To overcome this difficulty, Schwermann et al.¹⁰ used a restraining potential to obtain the free energy of the exciton transfer as a function of the distance between two molecules.

Fig. 1 Atomic models of the polymers P3HT and P3MT and of the molecule of penta3MT. Carbon atoms are represented in brown, sulfur in yellow, and hydrogen in white. The simulation cell boundaries are indicated by dashed red lines.

Fig. 2 Representative snapshot of the structure at 300 K of the penta3MT molecule shown in Fig. 1. The molecule underwent a rotation along the x axis, a bending, and one thiophene group at the extremity of the molecule rotated (black arrow). These conformational changes break the alternation in the thiophene orientation.

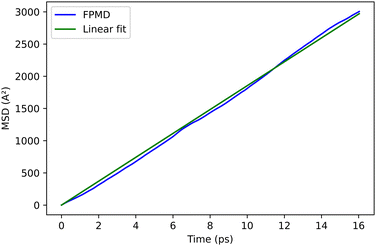
In the present work, we propose an alternative modeling strategy relying on the use of periodic boundary conditions to model a virtually infinite polymer instead of a small molecule. At finite temperature, we show that the polymer keeps a crystalline arrangement, with a structure that depends on the length of the lateral chains, hexyl in P3HT or methyl in poly(3-methylthiophene) (see Fig. 1, middle). The type of structure (conformers) and the lattice parameters obtained by our simulation results are in good agreement with known experimental structures, specifically Form I of P3HT; this specific structure is the thermodynamically stable one generally obtained during the fabrication of organic solar cells, and the planar configuration is the one resulting upon doping (see Fig. 3). Concerning the diffusion coefficient D, we track the exciton by calculating the maximally localized Wannier functions and related Wannier centers¹¹ of the bound electrons and holes. The exciton diffusion coefficient is estimated by computing the mean square displacement using the generated trajectory. In this way, our procedure is free from any hypothesis regarding the mechanism of the exciton transfer, for example, Förster¹² or Dexter.¹³ The resulting diffusion coefficient is in quantitative agreement with the measurements.

Fig. 3 Schematic representation of the crystalline structures of P3HT: Form I in pristine P3HT⁷ (left side) and planar geometry of doped P3HT¹⁴ (right side).

The paper is organized as follows. In Section 2, we provide a description of the first-principles molecular dynamics method applied to describe the first excited singlet state. Section 3 presents the approach used to localise the exciton via the Wannier centers, with an illustration in the case of the penta3MT molecule. Section 4 and Section 5 are focused on the exciton diffusion in P3MT and P3HT, respectively. Conclusions are drawn in the final Section 6.

2. Computational method

Molecular dynamics (MD) simulations are performed using the Car–Parrinello (CP) method¹⁵ as implemented in the developers version 4.3 of the CPMD code.¹⁶ We select for the exchange–correlation part of the Kohn–Sham total energy, the formulation proposed by Perdew, Burke and Ernzerhof (PBE).¹⁷ The valence-core interactions are described by norm-conserving Troullier–Martins¹⁸ pseudopotentials. Valence electrons are represented on a plane-wave basis set with a cutoff of 70 Ry, and the Brillouin zone sampling is limited to the Γ point. A fictitious electron mass of 400 a.u. and a time step Δt = 0.1 fs (4 a.u.) are chosen to ensure optimal conservation of the constants of motion. The ionic temperature is controlled with a Nosé–Hoover^19–21 thermostat chain,²² whereas for the fictitious electronic kinetic energy we use a Blöchl–Parrinello thermostat.²³ Masses of the thermostats (in units of corresponding frequencies) are taken equal to 2500 cm⁻¹ for the ions and 5000 cm⁻¹ for the fictitious electronic degrees of freedom.

Excited-state processes in organic molecules most often proceed in the lowest excited singlet (S₁) or triplet (T₁) states. Higher excited states have short lifetimes^24–26 and undergo radiationless relaxation to S₁, as per Kasha's rule.²⁷ Therefore, in our study we only considered the S₁ state, which can be described by the restricted open-shell Kohn–Sham (ROKS) method. The ROKS^28–30 formalism has been successfully applied for the modeling of photoreactions³¹ and carefully benchmarked on experimental data.³² Within the ROKS, the exciton remains in the S₁ state without the possibility to relax into S₀, unless resorting to a specific approach of non-adiabatic dynamics (surface hopping).³³ For regioregular P3HT films, the exciton lifetimes reported in the literature range from 400 to 850 ps,^34–36 and hence are considerably longer than the time span of our trajectories. The ROKS approach is therefore perfectly suited to monitor the diffusion of the exciton in the S₁ state representative of the exciton prior its recombination to S₀. We recall that the ROKS approach used here has been consistently formulated within the DFT framework^28–30 and, as such, its transferability is the one granted by this underlying theory provided that electronic states do not involve transitions above the first excited state.

Since the exciton transfer between polymer chains is specifically targeted, the inclusion of appropriate dispersion forces becomes crucial. We have chosen to disentangle these van der Waals (vdW) dispersion interactions from the main body of the Kohn–Sham Hamiltonian following the semiempirical vdW “D3” approach by Grimme et al.,^37,38 as opposed to a first-principles treatment of the van der Waals (vdW) interactions with a Wannier scheme.^39,40 The intra- and inter-molecular forces resulting from the combination of DFT and the Grimme-D3 model implicitly contain all the ingredients that led to the development of the HJ-aggregate models for the P3HT.^41,42

The simulation protocol used is the following. The electronic structure of the initial configuration formed by one or several molecules is first converged to the ground state S₀ in the standard Kohn–Sham formalism with a convergence criterion of the accuracy of 10⁻⁶ a.u. on the total energy. The ionic structure is subsequently relaxed to a local minimum, which serves as the initial configuration for the second part of the calculation within the ROKS approach. Hence, the electronic structure is converged in the S₁ excited state at the same accuracy (10⁻⁶ a.u) and the ionic structure is relaxed. A short dynamical run in the microcanonical NVE ensemble is done to check the stability of the configuration before controlling the temperature. A rescaling of the velocities is applied during the initial 10 000 steps (∼1 ps) to bring the system to 10 K before moving to canonical NVT simulations. The temperature is then gradually increased with a Nose–Hoover thermostat during 6 ps, first to T = 100 K and finally to T = 300 K during 40 ps. During the step at T = 300 K, the maximally localized Wannier functions (MLWFs) minimizing the spread¹¹ are computed upon Kohn–Sham unitary transformations of the non-localized Kohn–Sham orbitals. To minimize the Vanderbilt spread functional, the iterative steepest descent algorithm is used and the iterations are done until the convergence criterion (residual error lower than 8 × 10⁻⁵) is reached. The centers of mass of the obtained localized orbitals, the Wannier function centers (WFCs), are then used to provide a clear picture of the electronic degrees of freedom. WFC trajectories are obtained by sampling the dynamical trajectory every ten simulation steps (Fig. 4). The CPMD input file for the calculation of the WFC trajectory is provided in the ESI.†

Fig. 4 Atomic coordinates (r) and electronic orbitals (ψ) are propagated according to the Car–Parrinello equations of motion. The spread minimization for the calculation of the Wannier functions and centers is done on selected configurations along the dynamical trajectory.

3. Exciton localisation in penta3MT

We first focus on penta3MT, a small molecule containing five thiophene units (52 atoms, i.e. 5 S, 25 C, and 22 H) of the P3HT polymer as shown in the bottom panel of Fig. 1. The WFCs are sketched in Fig. 5 for the ground state S₀ and for the first excited singlet state S₁ and superimposed on the atomic structure. In the case of a double bond, i.e. two Wannier centers in the middle of a C=C bond, the WFCs are highlighted in green, while they are plotted in grey otherwise. A perfect alternation of double and single bonds characterizes the S₀ state. An example of MLWFs is shown to illustrate the character of these localized orbitals. In the S₁ state, the Wannier center of the hole is shown in red, while the blue color is chosen for the electron. The two WFCs are separated by a distance of 6 Å. The MLWFs of both the electron and the hole, although localized according to the procedure indicated, have still a rather large spread, as shown by the isosurface representation in the bottom panel of Fig. 5, contrary to other MLWFs corresponding to bonding states. Because of the topology of the molecule, the MLWFs spread along the backbone of the system. The MLWF dispersions of both the hole and the electron amount to 6.5 Å. This value being larger than the separation between the two WFCs (6 Å), we can infer that the electron and the hole form a bound pair. Another feature worthy of note is the fact that in this S₁ state, the alternation of single and double bonds is disrupted in the vicinity of the electron and the hole.

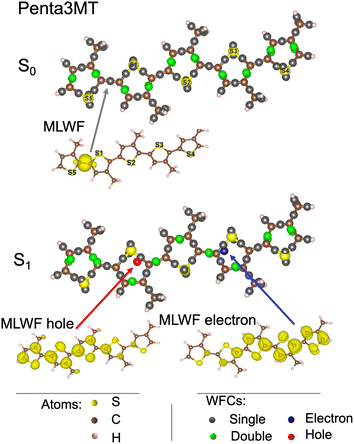Fig. 5 Wannier function centers (WFCs) of the S₀ and S₁ states of penta3MT at 0 K, and examples of maximally localized Wannier functions (MLWFs).

As mentioned above, at room temperature, the structure of a penta3MT molecule departs from its initial planarity and the thiophene groups at the boundary undergo barrierless rotations. The penta3MT molecule is therefore not suited to the modeling of the exciton transfer in a system expected to maintain a better degree of structural organization. For this reason, we consider virtually infinite polymers subject to periodic boundary conditions (PBCs) in the following sections.

4. Exciton diffusion in P3MT

4.1 Exciton in a single P3MT polymer

Our first target is P3MT, a polymer characterized by shorter lateral chains than P3HT, as shown in Fig. 1. Since the number of atoms is smaller, the computational workload is reduced while preserving the main structural features related to our study. The simulation cell is adapted to host six thiophenes in the x direction, which corresponds to L_x = 23.26 Å, whereas the dimensions L_y and L_z in the other directions are large enough to prevent any interactions between the molecules. The number of atoms in this polymer is equal to 60 (6 sulfur, 30 C and 24 H). A major difference with respect to the penta3MT is that the electron and hole MLWFs extend over all the thiophenes (Fig. 6), instead of half the molecule as in the case of penta3MT. This result is in line with the existence of delocalised electronic modes (polarons) in P3HT.⁴³ In Fig. 6, the WFCs of the electron and the hole are separated by 9.5 Å and their spreads are equal to 7.6 Å.

Fig. 6 Wannier function centers (WFCs) and maximally localized Wannier functions (MLWFs) of the electron and hole in the S₁ state in a single polymer of P3MT at 0 K. The boundaries of the simulation cell are indicated by dashed red lines.

4.2 Exciton diffusion in a system of two P3MT polymers

Minimal energy structure. To inspect the exciton transfer between P3MT polymers, we constructed a simulation cell containing two P3MT polymers, amounting to 120 atoms, as shown in Fig. 7. The size of the simulation cell along the x direction is identical to the one used for the single polymer (L_x = 23.26 Å). The dimensions along the other two directions y and z (L_y = 7.26 Å and L_z = 7.14 Å) are selected by minimising the total energy and/or stress tensor. The resulting structure is a square lattice of P3MT polymers spaced by 3.57 Å in the z direction. The natural configuration of the lattices of P3HT is not planar but assumes Form I (Fig. 3). Yet, a P3HT planar configuration can be realized upon intercalation of dopants.¹⁴ The distance between the polymer chains, which corresponds in this planar configuration to the π–π distance, has been determined experimentally and turns out to be 3.55 ± 0.05 Å. On these grounds, we have verified that our computational set-up is able to quantitatively reproduce the experimental structure.

Fig. 7 Simulation cell hosting two P3MT polymers of infinite length, ensured by the periodic boundary conditions. The distance between the two polymers is d_π–π = 3.57 Å in the z direction. The cell boundaries are indicated by dashed red lines.

Structure in the S₁ state at room temperature. The initial configuration shown in Fig. 7 is thermalized at 300 K in the S₁ state within the ROKS formalism, following the procedure indicated in the methodological section. The resulting structure is shown in Fig. 8. The square pattern of the lattice is preserved also at finite temperature, together with the π–π distance along the z direction. Along the x axis, a sliding of one polymer with respect to the second one has occurred and results in a shift of the thiophenes initially aligned in the x–y plane, as shown in the right panel (side view) of the figure. This shift is expected from the balance of the interactions between the two polymers: the attractive van der Waals interaction on one hand and the steric repulsion among the CH₃ groups and electrostatic repulsion between thiophenes belonging to different polymers^44,45 on the other hand. Clearly, the PBCs allow for a readjustment of the two polymers without any bond breaking or unphysical conformational changes. This equilibrated structure is well suited for the observation of the exciton transfer from a polymer to the neighbour one along the z direction.

Fig. 8 Snapshots of the two P3MT polymers equilibrated at 300 K in the S₁ state along the y–x, x–y and x–z planes.

Exciton transfer. The snapshot of Fig. 9, taken at room temperature in the S₁ state, shows the WFCs of the electron and the hole with respectively red and blue spheres. For the sake of completeness, we also added the WFCs of the chemical bonds on the two polymers in Fig. 9. The alternation of single and double bonds is kept in the polymer not hosting the exciton. We have shown in the case of penta3MT (Fig. 5) that this alternation is a fingerprint of the ground state, whereas the presence of the exciton in the S₁ state induces a perturbation of this regular arrangement. This observation supports the hypothesis of a mechanism of excitation energy transfer (EET)²⁴ from a polymer in the S₁ excited state to a neighbour one in the S₀ ground state. Hereafter, based on these results, the exciton is assumed to be located at the center of mass between the electron and hole WFCs.

Fig. 9 Left: Wannier centers (WFCs) in the P3MT polymer hosting the exciton (bottom molecule) and in the second polymer (top molecule). Right: Schematic of the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) occupation associated with the exciton transfer (schematized by a pink arrow).

Diffusion coefficient. To compute the exciton diffusion coefficient, we use the trajectory of the Wannier centers of the hole and the electron obtained by the quoted spread functional minimization every ten simulation steps for a total simulation time of at least 40 ps at T = 300 K. The WFCs of the electron and the hole have a y coordinate that remains approximately located at L_y/2, a signature of the absence of any transfer between molecules along the y direction. The mean square displacement (MSD) of the WFC exciton in the direction along the stacking is obtained from its coordinate z_e aswhere N is the total number of intervals Δt along the 40 ps trajectory, and mΔt ranges from 0 to 16 ps (see Fig. 10). The MSD expressed as in eqn (1) shows a linear trend as a function of time. The polymeric character of the system targeted limits the degrees of freedom of a general three-dimensional process, thus allowing converging the calculation of the diffusion coefficient in an affordable time (less than 20 ps here) to 9.3 × 10⁻³ cm² s⁻¹ as determined from the slope of the MSD, with a standard deviation smaller than 10⁻⁵ cm² s⁻¹. Such a value is in good agreement, apart from a slight overestimation, with the reported measurement of 7.9 × 10⁻³ cm² s⁻¹ in highly crystalline and regio-regular P3HT (Table 2).⁹ This can then be regarded providing a convincing benchmark of our simulation protocol on periodically repeated molecules containing six thiophenes. Our approach has been shown to be able to catch all essential features of the exciton processes occurring in this type of material.

Fig. 10 Mean square displacement of the exciton WFC in the dimer of P3MT.

5. Exciton diffusion in P3HT

In the former paragraph, we have shown that following the trajectory of the WFCs of both the electron and the hole is a practical tool to determine the exciton diffusion coefficient in appreciable agreement with the data reported in the literature. We remark, however, that the experimental measurements were done on P3HT, a polymer carrying hexyl groups instead of methyl ones as lateral chains. One could argue that the impact of shorter chains should be negligible since the transfer does not proceed in the (y) direction of the chains. However, we show in the present section that considering hexyl chains results in a significant modification of the lattice structure, in close agreement with Form I observed experimentally⁸ in the absence of doping. This, in turn, might have an influence on the electronic properties and, ultimately, on the dynamical behavior of an exciton.

The starting system in our simulations is a simulation cell containing two P3HT polymers in a planar configuration. For this specific system, the total number of atoms is 300, namely 12 S, 120 C, and 168 H atoms. The planar configuration is kept during a simple geometry relaxation, but when dynamics are allowed and the temperature rises to T = 10 K (by an NVT thermostat control), a conformational change toward Form I occurs spontaneously. This conformation persists at T = 300 K (Fig. 11 and 12).

Fig. 11 Evolution of the structure of the periodic system of two P3HT polymers from a planar configuration at T = 0 K to Form I at room temperature (representative snapshot, the alkyl chains fluctuating dynamically).

Fig. 12 Evolution of the structure of the periodic system of two P3HT polymers from planar at T = 0 K to Form I at room temperature (representative snapshot, the alkyl chains fluctuating dynamically). View of the system of Fig. 11 on the x–y plane.

The π–π distance, defined as the shortest distance between the two polymer chains, is d_π–π = 3.5 ± 0.1 Å. The stacking distance is different in this lattice structure and equal to d_stack = 3.7 ± 0.1 Å. The two polymers are tilted of θ = 23 ± 3°. These values are in quantitative agreement with the measurements by electron and X-ray diffraction^7,8 as reported in Table 1.

Table 1 Main structural parameters of the P3HT stacking

	Present work	Experiments^7,8
d π–π (Å)	3.5 ± 0.1	3.4
d stack (Å)	3.7 ± 0.1	3.8
θ (°)	23 ± 3	26 ± 5

---

The trajectories of the electron and hole WFCs are monitored at T = 300 K. We remark that the average distance between the electron and hole (7.6 Å) during this trajectory is typical of a Frenkel exciton.²⁶ The values of the diffusion coefficient, obtained from the mean square displacement of the exciton WFCs, as explained above, are reported in Table 2 along with the experimental value, in fairly good agreement with the present calculations. The reduction of the diffusion coefficient in the P3HT compared to the P3MT can be rationalized by the reduction of the effective cross-section of the π–π interaction in Form I compared to the planar configuration, due to a geometric effect. The simulation cell size, containing two molecules of six thiophenes periodically repeated, is sufficiently large to capture all the features of the excitonic diffusion process.

Table 2 Exciton diffusion coefficients as obtained from our calculation and corresponding experimental value

	D (10^−3 cm^2 s^−1)
P3MT	9.3
P3HT	8.0
P3HT, exp.^9	7.9

---

The results obtained provide convincing support to our computational first principles approach for the polymer carrying hexyl chains, spontaneously reverting to its natural Form I at room temperature. Structural parameters are in excellent quantitative agreement with available measurements. At finite temperature, our model is also able to reproduce with appreciable accuracy the diffusion coefficient characterizing the motion of the exciton in the S₁ state. The result is in quantitative agreement with data from time-resolved spectroscopy, thus serving as a benchmark not only for structural but also for the excitonic properties of the system.

6. Conclusions

The present work proposes a methodology for the calculation of the diffusion coefficient of an exciton in the S₁ state. The reliability and predictivity of the method are demonstrated in the case of P3HT, a conjugated polymer used worldwide for applications in organic photovoltaic materials. We rely on dynamical simulations able to produce relatively long-lasting atomic trajectories at room temperature, within the FPMD framework. The ROKS formalism is then applied to describe the S₁ excited state. The motion of the exciton is obtained in terms of the WFCs of the electron and hole thus providing a practical tool to visualize such an evolving electronic structure bypassing the calculation and storage workload that accumulation of extended wavefunctions would imply.

In the case of the P3HT system targeted in this work, we show that two important characteristics of the material have to be considered. The first one is its virtually infinite length, accounted for by appropriate use of the periodic boundary conditions. This avoids uncontrolled conformational changes of the polymer structure and preserves an ordered structure, along with the π–π interactions, also at finite temperature, compatible with a realistic system in which an exciton transfer is expected to occur. The second important feature is represented by the chains, in the sense that their full length allows observing the Form I lattice. If methyl groups replace the original hexyl ones, the resulting structure is nonetheless still realistic, but models a planar arrangement observed experimentally in doped P3HT.

The Wannier functions and centers (along with their associated spread) show that the exciton is delocalised along the polymer chain and transfers from one polymer monomer to the next one with a diffusion coefficient in good agreement with reported experiments. Our approach paves the route to thorough and reliable computational characterization of the exciton transfer that will serve as a guideline for the comprehension of advantages and limitations of other molecular systems, thus offering a guideline for a rational design of organic materials with exciton diffusion lengths sufficient to grant a good efficiency of next-generation photovoltaic devices.

Author contributions

C. O. Diarra: investigation, software, validation, and visualization. M. Boero: methodology, writing – review and editing. E. Steveler: supervision, writing – review and editing. T. Heiser: conceptualization, writing – review and editing. E. Martin: supervision, methodology, and writing – original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the High Performance Computing Center of the University of Strasbourg for supporting this work by providing scientific support and access to computing resources. Part of the computing resources were funded by the Equipex Equip@Meso project (Programme Investissements d'Avenir) and the CPER Alsacalcul/Big Data. Calculations on the larger systems (oligomers) were performed by using resources from GENCI (Grand Equipement National de Calcul Intensif) (grant no. 0910296 and 0905071). This work of the Interdisciplinary Institute HiFunMat, as part of the ITI 2021-2028 program of the University of Strasbourg, CNRS and Inserm, was supported by IdExUnistra (ANR-10-IDEX-0002) and SFRI (STRAT’US project, ANR-20-SFRI-0012) under the framework of the French Investments for the Future Program.

Notes and references

1. H. Chen, S. Y. Jeong, J. Tian, Y. Zhang, D. R. Naphade, M. Alsufyani, W. Zhang, S. Griggs, H. Hu, S. Barlow, H. Y. Woo, S. R. Marder, T. D. Anthopoulos, I. McCulloch and Y. Lin, Energy Environ. Sci., 2023, 16, 1062–1070.
2. C. Li, X. Gu, Z. Chen, X. Han, N. Yu, Y. Wei, J. Gao, H. Chen, M. Zhang, A. Wang, J. Zhang, Z. Wei, Q. Peng, Z. Tang, X. Hao, X. Zhang and H. Huang, J. Am. Chem. Soc., 2022, 144, 14731–14739.
3. J. D. A. Lin, O. V. Mikhnenko, J. Chen, Z. Masri, A. Ruseckas, A. Mikhailovsky, R. P. Raab, J. Liu, P. W. M. Blom, M. A. Loi, C. J. García-Cervera, I. D. W. Samuel and T.-Q. Nguyen, Mater. Horiz., 2014, 1, 280–285.
4. W. Barford, E. R. Bittner and A. Ward, J. Phys. Chem. A, 2012, 116, 10319–10327.
5. S. M. Janke, M. B. Qarai, V. Blum and F. C. Spano, J. Chem. Phys., 2020, 152, 144702.
6. N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163.
7. N. Kayunkid, S. Uttiya and M. Brinkmann, Macromolecules, 2010, 43, 4961–4967.
8. M. Brinkmann, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 1218–1233.
9. H. Ohkita, Y. Tamai, H. Benten and S. Ito, IEEE J. Sel. Top. Quantum Electron., 2016, 22, 100–111.
10. C. Schwermann and N. L. Doltsinis, Phys. Chem. Chem. Phys., 2020, 22, 10526–10535.
11. N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419–1475.
12. T. Förster, Ann. Phys., 1948, 437, 55–75.
13. D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850.
14. V. Untilova, H. Zeng, P. Durand, L. Herrmann, N. Leclerc and M. Brinkmann, Macromolecules, 2021, 54, 6073–6084.
15. R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474.
16. Jointly by IBM Corporation and by Max Planck Institute, Stuttgart, CPMD code, 2022, https://github.com/CPMD-code.
17. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
18. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
19. S. Nosé, Mol. Phys., 1984, 52, 255–268.
20. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
21. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
22. G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643.
23. P. E. Blöchl and M. Parrinello, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 9413–9416.
24. N. Turro, Modern Molecular Photochemistry, University Science Books, 1991.
25. A. H. Zewail, Femtochemistry: Ultrafast Dynamics of the Chemical Bond (World Scientific Series in 20th Century Chemistry), World Scientific, 1994.
26. A. Köhler and H. Bässler, Electronic Processes in Organic Semiconductors: An Introduction, Wiley, 1st edn, 2015.
27. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19.
28. I. Frank, J. Hutter, D. Marx and M. Parrinello, J. Chem. Phys., 1998, 108, 4060–4069.
29. S. Grimm, C. Nonnenberg and I. Frank, J. Chem. Phys., 2003, 119, 11574–11584.
30. C. Nonnenberg, S. Grimm and I. Frank, J. Chem. Phys., 2003, 119, 11585–11590.
31. I. Frank, Chem. Phys. Lett., 2018, 702, 76–81.
32. I. Frank, J. Hutter, D. Marx and M. Parrinello, J. Chem. Phys., 1998, 108, 4060–4069.
33. N. L. Doltsinis and D. Marx, Phys. Rev. Lett., 2002, 88, 166402.
34. S. Cook, H. Liyuan, A. Furube and R. Katoh, J. Phys. Chem. C, 2010, 114, 10962–10968.
35. W. Beek, M. Wienk and R. Janssen, Adv. Funct. Mater., 2006, 16, 1112–1116.
36. S. Cook, A. Furube and R. Katoh, Energy Environ. Sci., 2008, 1, 294–299.
37. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
38. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
39. P. L. Silvestrelli, Phys. Rev. Lett., 2008, 100, 053002.
40. T. Ikeda and M. Boero, J. Chem. Phys., 2015, 143, 194510.
41. F. Paquin, H. Yamagata, N. J. Hestand, M. Sakowicz, N. Bérubé, M. Côté, L. X. Reynolds, S. A. Haque, N. Stingelin, F. C. Spano and C. Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155202.
42. F. C. Spano and C. Silva, Annu. Rev. Phys. Chem., 2014, 65, 477–500.
43. O. P. Dimitriev, D. A. Blank, C. Ganser and C. Teichert, J. Phys. Chem. C, 2018, 122, 17096–17109.
44. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534.
45. C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00533j

---