Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Location of Artinite (Mg2CO3(OH)2·3H2O) within the MgO–CO2–H2O system using ab initio thermodynamics†
Joshua S.
Tse
 a,
James
Grant
b,
Jonathan M.
Skelton
a,
James
Grant
b,
Jonathan M.
Skelton
 c,
Lisa J.
Gillie
*a,
Runliang
Zhu
c,
Lisa J.
Gillie
*a,
Runliang
Zhu
 d,
Giovanni L.
Pesce
e,
Richard J.
Ball
d,
Giovanni L.
Pesce
e,
Richard J.
Ball
 f,
Stephen C.
Parker
f,
Stephen C.
Parker
 *b and
Marco
Molinari
*b and
Marco
Molinari
 *a
*a
aDepartment of Chemistry, University of Huddersfield, Queensgate, Huddersfield HD1 3DH, UK. E-mail: M.Molinari@hud.ac.uk; L.J.Gillie@hud.ac.uk
bDepartment of Chemistry, University of Bath, Claverton Down, Bath, BA2 7AY, UK. E-mail: S.C.Parker@bath.ac.uk
cDepartment of Chemistry, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
dCAS Key Laboratory of Mineralogy and Metallogeny, and Guangdong Provincial Key Laboratory of Mineral Physics and Materials, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou 510640, P. R. China
eDepartment of Mechanical and Construction Engineering, Northumbria University, Newcastle upon Tyne, NE1 8ST, UK
fDepartment of Architecture and Civil Engineering, University of Bath, Bath, BA2 7AY, UK
First published on 15th June 2023
Abstract
The MgO–CO2–H2O system have a variety of important industrial applications including in catalysis, immobilisation of radionuclides and heavy metals, construction, and mineralisation and permanent storage of anthropogenic CO2. Here, we develop a computational approach to generate phase stability plots for the MgO–CO2–H2O system that do not rely on traditional experimental corrections for the solid phases. We compare the predictions made by several dispersion-corrected density-functional theory schemes, and we include the temperature-dependent Gibbs free energy through the quasi-harmonic approximation. We locate the Artinite phase (Mg2CO3(OH)2·3H2O) within the MgO–CO2–H2O phase stability plot, and we demonstrate that this widely-overlooked hydrated and carbonated phase is metastable and can be stabilised by inhibiting the formation of fully-carbonated stable phases. Similar considerations may apply more broadly to other lesser known phases. These findings provide new insight to explain conflicting results from experimental studies, and demonstrate how this phase can potentially be stabilised by optimising the synthesis conditions.
1. Introduction
Magnesium hydrates and carbonates within the MgO–CO2–H2O system have a wide variety of applications including in catalysis,1–4 the treatment of industrial carcinogenic heavy-metal waste,5 the immobilisation of nuclear waste,6 as fire retardants,7 in construction,8 in high-magnesian biogenic calcites,9 and in carbon-mineralization reactions for permanent storage of anthropogenic carbon dioxide.10–13 Magnesium is also one of the most abundant elements in the Earth's mantle,14 and Mg-rich minerals are thought to exist in significant quantities on dwarf planets15 and other extra-terrestrial bodies.16Measuring phase stability is essential to predicting which material phase will form under a given set of conditions, and hence for understanding and controlling the structure and resultant properties. This problem has drawn intensive research17 from both experiment and theory and across many fields of organic18 and inorganic chemistry.19–25 The stability of different phases is conceptually described by phase diagrams, which capture the relationships between equilibrium and metastable phases, the activities of component species, and external conditions including pressure, volume and temperature, in an elegant way that can be used to predict the nature and composition of a material.26,27
Whereas the major species in the MgO–CO2–H2O phase diagram, such as Magnesia and Magnesite, are relatively well studied, minor phases have received comparatively less attention. One such example is the Artinite phase, which was first observed by Brugnatelli in 190228 and is a naturally-occurring metastable phase formed at low temperature. The crystal structure of Artinite has been analysed using X-ray diffraction29 and the thermodynamic properties have been determined using calorimetry.30 A few studies have also examined the thermodynamic stability of Artinite at low temperature,31–33 but comparatively little is known on the stability of Artinite with respect to other phases in the MgO–CO2–H2O system. Given that the materials in this system are found under a wide range of conditions, both natural and anthropogenic, a better understanding of where this phase sits within the MgO–CO2–H2O phase diagram is potentially important to a range of disciplines.
For prediction and generation of phase diagrams, the “brute force” option is to use so-called global exploration methods to sample the potential-energy landscape, but this approach quickly becomes intractable as the number of variables (i.e. phases) increases.34–37 When data on experimentally-identified materials and their structures is available, there are alternative, cheaper methodologies using computer simulation that can be employed whose capabilities are often overlooked.21,38–42 The most accurate and reliable way of calculating phase diagrams, i.e. the current “gold standard” is to employ a consistent and accurate ab initio methodology to all the phases, so that the resulting predictions are independent of experimental thermodynamic data. It is however critical that the choice of methodology is appropriate to the system being studied (i.e. transferable across different material phases, which may display significant differences in chemical bonding), but also feasible given the available computational power. Transferability can be a particular challenge for systems such as MgO–CO2–H2O that display multiple types of bonding across the phase space. For example, the bonding between Mg and different ligands (e.g. hydroxyl groups, water molecules and carbonate anions) is strongly ionic, whereas the intramolecular bonding within the ligands is predominantly covalent, and some of the layered magnesium hydroxides may also display interlayer van der Waals dispersion interactions.
In this work, we compare a series of different approaches, all without the inclusion of experimentally derived corrections, to construct first-principles phase stability plots for the MgO–CO2–H2O system in order to study the thermodynamics of the under-explored Artinite phase. To account for the hierarchy of chemical bonding, we compare predictions made using density–functional theory with the popular PBE generalised-gradient approximation functional and three van der Waals corrected functionals used successfully in the literature for simulations of these materials.43–46 We also assess the impact of using the quasi-harmonic approximation to derive the temperature dependence of the Gibbs free energy. This comprehensive study allows us to compare the predictions made from ab initio thermodynamic models with different approximations, and to assess the accuracy and reliability of the different flavours of DFT for studying the hydrated and carbonated phases of magnesian and other mineral systems.
2. Methodology
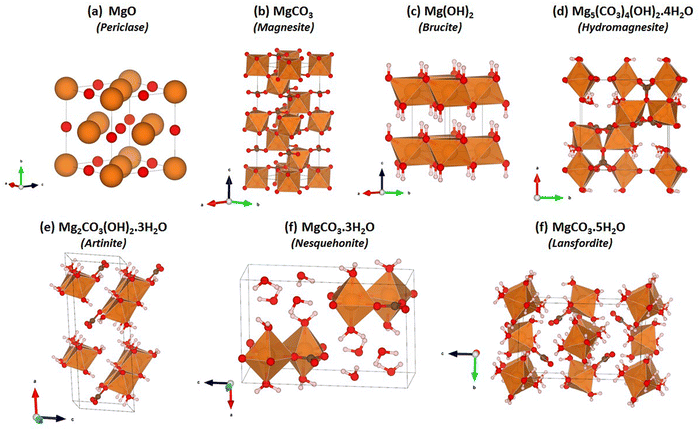
The VASP code47–49 was used to carry out DFT calculations on the seven structures shown in Fig. 1. These structures are known, experimentally reported phases within the MgO–CO2–H2O system, and are discussed in detail in the ESI.† The valence wavefunctions were described by a plane-wave basis and the core electrons were described using projected augmented-wave pseudopotentials.50 As our baseline, we used the Perdew–Burke–Ernzerhof51 generalised-gradient approximation (PBE GGA) to model electron exchange and correlation. We also considered three different functionals including van der Waals forces, viz. PBE with the DFT-D3 correction (PBE-D3),52 optB86b-vdW53,54 and optB88-vdW.53 These approaches are improvements over the well-established PBE-D2,55 where a dispersion correction is computed from the atomic polarizabilities and added to the PBE total energy. In PBE-D3, the polarizability is modulated by the local environments of the atoms, and for optB86b-vdW and optB88-vdW the correction is implemented as a modification to the exchange correlation functional itself.56 The plane-wave cut-off energy was set to 500 eV. A 4 × 4 × 4 Monkhorst-Pack k-point mesh was used to integrate the electronic Brillouin zone for all the phases apart from Brucite, for which a 6 × 6 × 4 k-point mesh was used. These settings were chosen based on explicit convergence tests on the total energies. During the electronic wavefunction optimisations the total energies were converged to 10−6 eV. For geometry optimisations the relaxation of the atomic structures was deemed to have converged when the forces acting on the atoms were below 10−2 eV Å−1.The vibrational frequencies and elastic-constant matrices were calculated using the finite-displacement routines implemented in VASP, the latter of which were used to calculate the bulk moduli by averaging the first nine elastic constants (c11:c33).57–59
For quasi-harmonic approximation (QHA) calculations, harmonic phonon calculations were performed using the Phonopy code60 on a set of 10 expansions and contractions around the equilibrium volume (approx. ±5%). The forces were determined in a 2 × 2 × 2 supercell for all phases apart from Brucite, for which we used a 3 × 3 × 2 expansion, with VASP as the force calculator. For calculating the thermal properties, the Brillouin zone was integrated by sampling with the following regular Γ-centred q-point meshes, which were converged individually for each structure: 30 × 30 × 30 for Artinite, Brucite, Hydromagnesite, Lansfordite and Nesquehonite, 36 × 36 × 36 for Periclase and 48 × 48 × 48 mesh for Magnesite. Details of the QHA free energy calculations are provided in the ESI.†
The phase stability plots where generated using SurfinPy 2.61,62 We note here several limitations in the procedure used here, viz.: (1) we do not account for the possibility of the coexistence of several phases, miscibility gaps, and the possible existence of different polymorphs (unless explicitly stated); (2) we similarly do not account for the possibility of unknown phases that may arise at high pressure; and (3) we do not account for the anharmonic effects that may play an important role at elevated temperature.
3. Results and discussion
3.1 Structure of Mg2CO3(OH)2·3H2O (Artinite)
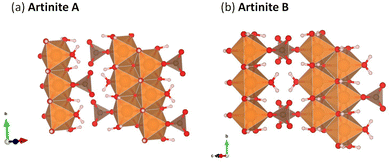
Mg2CO3(OH)2·3H2O (Artinite)63 crystallises in a monoclinic C2/m structure containing both hydroxyl and carbonate groups with Mg2+ in an octahedral coordination environment. The structure features Brucite (Mg(OH)2)-like 1D rods with equatorial Mg–OH bonds and apical Mg–OH2 and Mg–CO3 bonds. In naturally-occurring Artinite the apical H2O and CO32− ligands are randomly distributed. However, it is not feasible to replicate this using the small unit cell used in our DFT calculations, and we have therefore constructed two models with different, fixed distributions (Fig. 2). We suggest that the most facile means to properly account for the random distribution of these groups would be classical Monte Carlo and energy-minimization techniques based on force fields, but this is beyond the scope of the present study. Both models have rows of alternating CO32− and H2O along the 〈010〉 (b) direction. Structure A has alternating CO32− and H2O along the 〈101〉 direction (i.e. on opposite octahedral faces), while structure B has either H2O–H2O or CO32−–CO32− along the 〈101〉 direction (i.e. on the same octahedral faces).Physical properties of the two models including the predicted lattice parameters and elastic constants are presented in Table 1. The predictions for both Artinite structures made using all four DFT techniques give generally excellent agreement with available experimental measurements, with the notable exception of a 6% underestimation of the enthalpy of formation using PBE. This highlights the importance of accurately describing vdW interactions. For both Artinite structures the DFT methods including dispersion corrections predict a decrease in the cell volume compared to experiments. We also performed similar calculations on the other phases shown in Fig. 1, and structural data and predictions of the physical properties are given in the ESI† (Tables S1–S4).
| Expt. | optB86b-vdW | optB88-vdW | PBE-D3 | PBE | |||||
|---|---|---|---|---|---|---|---|---|---|
| Artinite A Mg2CO3(OH)2·3H2O | |||||||||
| a | 6.30663 | 6.28 | −0.41% | 6.284 | −0.34% | 6.303 | −0.05% | 6.371 | 1.04% |
| B | 6.23163 | 6.113 | −1.90% | 6.116 | −1.85% | 6.109 | −1.97% | 6.186 | −0.73% |
| C | 16.56063 | 16.558 | −0.01% | 16.567 | 0.04% | 16.598 | 0.23% | 16.768 | 1.25% |
| α = γ | 90.0063 | 90 | 0.00% | 90 | 0.00% | 90 | 0.00% | 90 | 0.00% |
| B | 99.1063 | 97.77 | −1.39% | 97.75 | −1.41% | 97.87 | −1.29% | 98.69 | −0.46% |
| Volume | 642.563 | 629.82 | −1.97% | 630.88 | −1.81% | 633.01 | −1.48% | 653.27 | 1.68% |
| ΔHf | −2920.6064 | −2896.12 | −0.01% | −2943.26 | 0.01% | −2844.29 | −0.03% | −2738.62 | −0.06% |
| B | 64.1 | 65.1 | 62.8 | 56.4 | |||||
| c11 | 103 | 104 | 103 | 95 | |||||
| c12 | 28 | 29 | 27 | 24 | |||||
| c13 | 65 | 66 | 63 | 54 | |||||
| c15 | 0 | 0 | 0 | 0 | |||||
| c22 | 122 | 124 | 120 | 113 | |||||
| c23 | 32 | 33 | 31 | 28 | |||||
| c25 | 0 | 0 | 0 | 0 | |||||
| c33 | 101 | 103 | 99 | 88 | |||||
| c35 | 0 | 0 | 0 | 0 | |||||
| c44 | 16 | 16 | 17 | 17 | |||||
| c46 | 0 | 0 | 0 | 0 | |||||
| c55 | 23 | 24 | 24 | 24 | |||||
| c66 | 40 | 41 | 39 | 35 | |||||
| Artinite B (Mg2CO3(OH)2·3H2O) | |||||||||
| a | 6.30663 | 6.314 | −0.20% | 6.293 | −0.13% | 6.298 | 0.12% | 6.38 | 1.17% |
| b | 6.23163 | 6.14 | −1.34% | 6.147 | −1.28% | 6.151 | −1.46% | 6.223 | −0.14% |
| c | 16.56063 | 16.547 | −0.37% | 16.499 | −0.33% | 16.505 | −0.08% | 16.709 | 0.90% |
| α = γ | 90.0063 | 90 | 0.00% | 90 | 0.00% | 90 | 0.00% | 90 | 0.00% |
| B | 99.1063 | 98.06 | −1.22% | 97.94 | −1.23% | 97.93 | −1.10% | 98.84 | −0.31% |
| Volume | 642.563 | 635.1 | −1.61% | 632.2 | −1.44% | 633.25 | −1.15% | 655.45 | 2.02% |
| ΔHf | −2920.6064 | −2843.25 | −0.01% | −2895.72 | 0.01% | −2942.75 | −0.03% | −2738.57 | −0.06% |
| B | 64.3 | 65.3 | 62.6 | 56.4 | |||||
| c11 | 100 | 102 | 100 | 92 | |||||
| c12 | 29 | 30 | 29 | 25 | |||||
| c13 | 65 | 65 | 62 | 53 | |||||
| c15 | 0 | 0 | 0 | 0 | |||||
| c22 | 122 | 124 | 120 | 114 | |||||
| c23 | 32 | 32 | 30 | 27 | |||||
| c25 | 0 | 0 | 0 | 0 | |||||
| c33 | 105 | 106 | 102 | 90 | |||||
| c35 | 0 | 0 | 0 | 0 | |||||
| c44 | 14 | 14 | 15 | 16 | |||||
| c46 | 0 | 0 | 0 | 0 | |||||
| c55 | 20 | 21 | 21 | 23 | |||||
| c66 | 41 | 42 | 41 | 35 | |||||
3.2 Phase stability plots of Mg-rich phases I: theoretical framework
To derive our phase stability plots, we assume that the Mg-rich phases in Fig. 1 can be formed through the reaction scheme in eqn (1):| xMgO + yH2O + zCO2 → A | (1) |
| δGT,p = μA − xμMgO − yμH2O − zμCO2 = 0 | (2) |
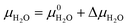 | (3) |
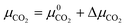 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(px/pθ) where pθ is the standard pressure of 1 bar. As both MgO and the products in eqn (1) are solid phases, we assume that:
ln(px/pθ) where pθ is the standard pressure of 1 bar. As both MgO and the products in eqn (1) are solid phases, we assume that:| μMgO = μ0MgO | (5) |
| μA = μ0A | (6) |
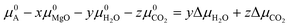 | (7) |
| δGT,p = ΔG0f − yΔμH2O − zΔμCO2 | (8) |
| ΔG0f = yΔμH2O + zΔμCO2 | (9) |
ΔG0f = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln((pH2O)y·(pCO2)z) ln((pH2O)y·(pCO2)z) | (10) |
We can therefore find the values of ΔμH2O and ΔμCO2 (or (pH2O)y and (pCO2)z) for which the Mg-rich phases are more or less stable than MgO. This procedure can be applied to all the solid phases to identify which is the most stable, provided that the free energy ΔG0f is known for each Mg-rich phase. These free energies can be calculated using eqn (11):
 | (11) |
In the harmonic model, the free energies are calculated from:
| G(T) = U0 + Aphonon(T) = U0 + UZPE + Avib(T) | (12) |
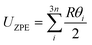 | (13) |
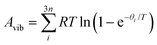 | (14) |
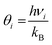 | (15) |
In the QHA model, the harmonic approximation is modified to include the effect of volume changes due to thermal expansion at finite temperature. This is practically achieved by applying the harmonic approximation to a series of contracted and expanded unit cells about the equilibrium volume V0. Using this method, the Gibbs free energy is obtained at a specific temperature T and pressure p as:65
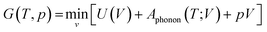 | (16) |
For gaseous species, the standard free energy varies significantly with temperature, and as plane-wave DFT simulations are designed for condensed-phase systems we use experimental data to determine the temperature-dependent free energy term for the gaseous species:
| G = U0 + UZPE + (H − H0(T) − TSexpt(T)) | (17) |
3.3 Phase stability plots of Mg-rich phases II: free energy at T = 0 K
We first verify our methodology against an experimental phase stability plot composed of the well-characterised Mg-rich phases. Fig. 3(a) shows the phase stability plots of Brucite (Mg(OH)2), Magnesite (MgCO3) and Periclase (MgO) obtained from experiments, while Fig. 3(b) shows the phase stability plot containing all the Mg-rich phases predicted using optB86b-vdW. These diagrams are predicted at T = 0 K, i.e. the Avib terms in eqn (12) are set to zero, which also simplifies eqn (17) to:| G = U0 + UZPE | (18) |
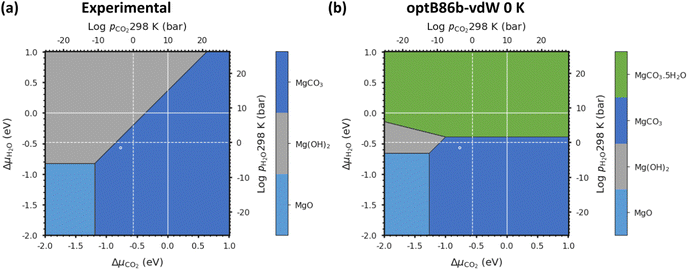 | ||
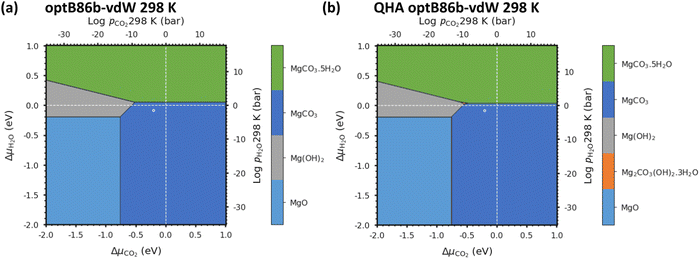
| Fig. 3 (a) Phase stability plot of Mg(OH)2 (Brucite), MgCO3 (Magnesite) and MgO (Periclase) constructed using experimental data. (b) Predicted phase stability plot including all Mg-rich phases calculated using optB86b-vdW and eqn (18) with both solid and gaseous phases at 0 K: MgO, MgCO3, Mg(OH)2 and MgCO3·5H2O. The solid and dashed white lines correspond to 1 bar pressure at 0 K and 298 K, respectively, and the white circles indicate atmospheric conditions of 400 ppm CO2 and 32 mbar of H2O at 298 K. | ||
For the experimental phase stability plot in Fig. 3(a), ΔG0f is calculated using the corrected enthalpies of formation defined in eqn (19), where ΔHexpt(298 K → 0 K) is the change in enthalpy from 298 K to 0 K. Thermodynamic data was taken from the NIST database,68 but experimental values are only available for these well studied phases.
| δHexpt(0 K) = ΔHexpt(298 K) − ΔHexpt(298 → 0 K) | (19) |
This first test for a thermodynamic modelling strategy is to evaluate the relative stability of Mg(OH)2, MgO and MgCO3 following the procedure outlined in eqn (18). The triple point (where all three phases co-exist; Table 2) was calculated from the experimental data to be at ΔμCO2 = −1.18 eV and ΔμH2O = −0.83 eV, whereas using optB86b we predict the point to occur at ΔμCO2 = −1.27 eV and ΔμH2O = −0.66 eV. This is excellent agreement, with differences of only 0.08 eV for ΔμCO2 and 0.17 eV for ΔμH2O.
| Temperature (K) | ΔμCO2 (eV) | ΔμH2O (eV) | p CO2 (bar) (298 K) | p H2O (bar) (298 K) | |
|---|---|---|---|---|---|
| Brucite Mg(OH)2, Magnesite MgCO3 and Periclase MgO triple point | |||||
| Experimental | 0 | −1.18 | −0.83 | 10−10.9 | 10−6.1 |
| optb86B | 0 | −1.27 | −0.66 | 10−12.4 | 10−3.1 |
| Brucite Mg(OH)2, Magnesite MgCO3 and Lansfordite MgCO3·5H2O triple point | |||||
| optb86B | 0 | −1.00 | −0.40 | 10−9.2 | 103.0 |
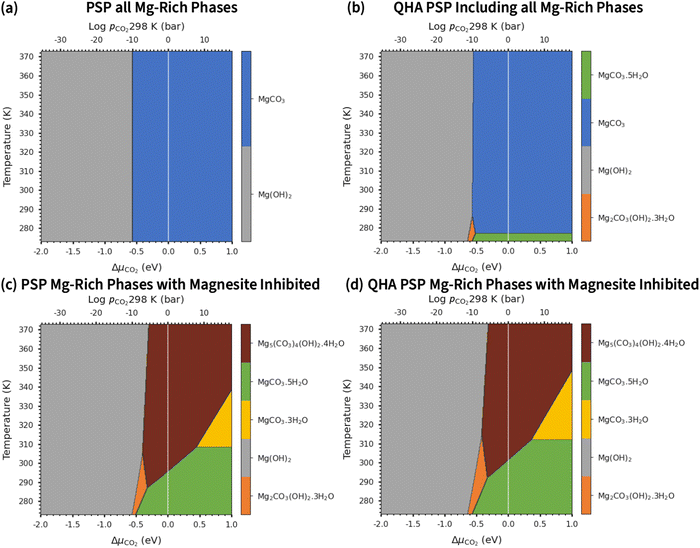
Due to the limited literature data on Lansfordite (MgCO3·5H2O) and Artinite (Mg2CO3(OH)2·3H2O), we are not able to include these phases on the experimental phase stability plot. However, at pCO2 = pH2O = 1 bar at 298 K (where the dashed white lines cross in Fig. 3(b)), the most thermodynamically stable phase is predicted to be Magnesite (MgCO3), whereas at pCO2 = pH2O = 1 bar at 0 K (where the solid white lines cross in Fig. 3(b)) the predicted stable phase is Lansfordite. This agrees well with both computational43 and experimental71 data.
As noted above, one of our aims is to evaluate the thermodynamic stability without requiring experimental data for the condensed phases, not least as comparison with experiment is then a rigorous check on the reliability. Nevertheless, inclusion of experimentally-derived corrections does represent a valuable tool for demonstrating the viability of DFT for modelling a given system as shown in Chaka et al.43 Comparing the performance of the different DFT methods, we find that optB86b-vdW gives the most accurate representation of the thermodynamics, as the triple point between the Brucite (Mg(OH)2), Magnesite (MgCO3) and Periclase (MgO) phases is closest to the experimental one.
3.4 Phase stability plots of Mg-rich phases III: harmonic and quasi-harmonic free energies
Accounting for the temperature dependence of the free energy in the phase stability plot, in particularly the entropy term, is important, as the most thermodynamically stable phase is likely to vary with temperature.We choose a temperature range between 273 K and 373 K, i.e. where liquid water is present, which are appropriate conditions for industrial6 and nuclear waste reprocessing5 applications, for construction materials,8,72 and for catalysis.2–4 The vibrational entropy of the Mg-rich phases is included in the calculation of ΔG0f for Δμ = −2 to +1 eV, with entropies for the solid phases calculated using eqn (13)–(15) and entropies for gaseous species taken from the NIST database.68
We showed in the previous two sections that optB86b-vdW provides a good description of the experimental phase stability plot of the well-characterised Mg-rich phases, and that the predicted phase stability plots obtained using the different DFT methods are all shifted relative to each other. We therefore consider here only the results obtained with optB86b-vdW, but as before the phase stability plots predicted using the other DFT techniques are available in Fig. S3–S5 (ESI†) for comparison.
We organise the results in this section into three parts, showing first the free energies of Mg-rich phases at different pCO2 as a function of temperature at constant pH2O = 1 bar, followed by the phase stability plots as a function of pCO2 and pH2O at a fixed T = 298 K, and finally the phase stability as a function of pCO2 and temperature at constant pH2O.
3.5 Phase stability at constant pH2O = 1 bar
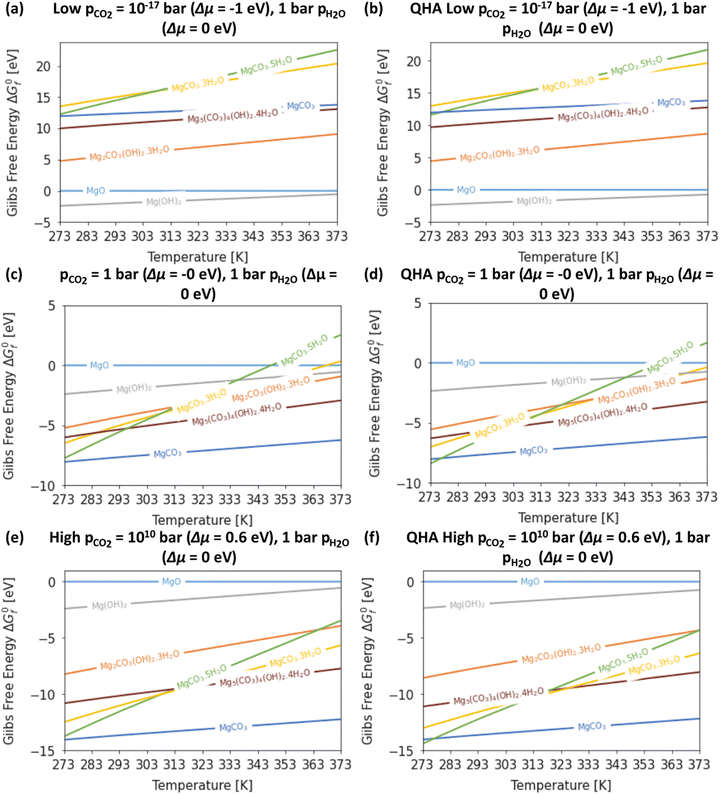
Fig. 4 compares the formation free energies of the different phases as a function of temperature, computed using optB86b-vdW with the harmonic and quasi-harmonic free energies, over the 273–373 K temperature range and a variety of pCO2 with a fixed pH2O = 1 bar. These phase stability plots consider the effect of varying pCO2 and thus provide insight into how this variable impacts the synthesis of the Mg-rich phases, that is, we can identify all the phases appearing at different values of pCO2, which enables us to resolve very small energy differences between phases.At ΔμCO2 = −1 eV (low CO2 pressure, pCO2 = 10−17 bar) and ΔμH2O = 0 eV (pH2O = 1 bar) the most thermodynamically stable phase is predicted to be Brucite (Mg(OH)2) (Fig. 4a and b). Using optB86b and the QHA free energies, Artinite shows no phase transitions at low CO2 pressure, identified by intersections of its free-energy curve with other compounds, over the temperature range modelled. Increasing the temperature stabilises phases that contain less water per Mg2+ ion, due to the evaporative loss of H2O.
The harmonic free energies predict that at ΔμCO2 = ΔμH2O = 0 eV, corresponding to standard conditions with pCO2 = pH2O = 1 bar, MgCO3 is the most thermodynamically stable phase at all temperatures (Fig. 4c),43,71 whereas the QHA predicts that Lansfordite becomes the most stable phase at 277 K (Fig. 4d). If the formation of MgCO3 is kinetically inhibited, which has been demonstrated experimentally,73 then the metastable Hydromagnesite (Mg5(CO3)4(OH)2·4H2O) phase becomes the most stable above 295 K. Under these conditions Artinite has two phase boundaries at 321 K (Artinite Mg2CO3(OH)2·3H2O/Nesquehonite MgCO3·3H2O) and 314 K (Artinite Mg2CO3(OH)2·3H2O/Lansfordite MgCO3·5H2O) (Fig. 4c). The 332 and 320 K predicted using the QHA free energies are shifted to slightly higher values (Fig. 4d).
We also compared the phase stability plots under atmospheric conditions for the different DFT techniques (Fig. S3–S5, ESI†), which all show very similar features to the phase stability plots computed under standard conditions. The predicted phase transition temperatures are tabulated in Tables S5–S7 (ESI†).
At ΔμCO2 = 0.6 eV (high CO2 pressure, pCO2 = 1010 bar) and ΔμH2O = 0 eV (pH2O = 1 bar) the most thermodynamically stable phase at all temperatures is predicted to be MgCO3 (Fig. 4e), as with pCO2 = pH2O = 1 bar (Fig. 4e and f). When the formation of MgCO3 is inhibited, at T < 290 K Lansfordite (MgCO3·5H2O) is predicted to be the second most stable phase, with Nesquehonite (MgCO3·3 H2O) favoured between 308–316 K, and Mg5(CO3)4(OH)2·4H2O favoured only at T > 316 K. At high pCO2 Artinite has one phase boundary at 364 K (Artinite Mg2CO3(OH)2·3H2O/Lansfordite MgCO3·5H2O). Increasing the temperature results in phase transitions associated with the loss of one H2O per MgO unit. Again, we see a similar trend using the QHA where the phase transition temperatures are shifted ∼5–10 K higher compared to those computed using the harmonic free energies.
3.6 Phase stability of Mg-rich phases as a function of pCO2 and pH2 at 298 K
Fig. 5a shows that with pCO2 = pH2O = 1 bar the most thermodynamically stable phase is MgCO3. In general, all the DFT techniques show excellent agreement, with small shifts in the predicted phase-transition pressures (see Fig. S6, ESI†). As ΔμCO2 is increased, phases with a higher carbon content are thermodynamically stabilised, whereas increasing ΔμH2O stabilises the hydrated phases. As the temperature is raised from 0 to 298 K (Fig. 3), the QHA predicts that Artinite appears at the triple point between Brucite Mg(OH)2, Magnesite MgCO3 and Lansfordite MgCO3·5H2O. We can also compare the predicted pressures of the triple point using the harmonic and QHA free energies. Values for the Artinite triple points obtained from the QHA are given in Table 3.| Temperature (K) | ΔμCO2 (eV) | ΔμH2O (eV) | p CO2 (bar) (298 K) | p CO2 (bar) (298 K) | |
|---|---|---|---|---|---|
| Brucite Mg(OH)2, Magnesite MgCO3, Periclase MgO triple point | |||||
| HA | 298 | −0.76 | −0.20 | 10−13.4 | 10−3.4 |
| QHA | 298 | −0.76 | −0.20 | 10−13.4 | 10−3.5 |
| Brucite Mg(OH)2, Magnesite MgCO3, Lansfordite MgCO3·5H2O triple point | |||||
| HA | 298 | −0.52 | 0.05 | 10−9.1 | 100.9 |
| QHA | — | — | — | — | — |
| Brucite Mg(OH)2, Magnesite MgCO3, Artinite Mg2CO3(OH)2·3H2O triple point | |||||
| HA | — | — | — | — | — |
| QHA | 298 | −0.33 | 0.23 | 10−5.8 | 104.1 |
| Brucite Mg(OH)2, Artinite Mg2CO3(OH)2·3H2O, Lansfordite MgCO3·5H2O triple point | |||||
| HA | — | — | — | — | — |
| QHA | 298 | −0.40 | 0.26 | 10−7.0 | 104.6 |
| Brucite Mg(OH)2, Artinite Mg2CO3(OH)2·3H2O, Magnesite MgCO3 triple point | |||||
| HA | — | — | — | — | — |
| QHA | 298 | −0.29 | 0.24 | 10−5.1 | 104.2 |
Testing the validity of these phase stability plots using experimental techniques is challenging, as changing the pressure of one reference state independently can be difficult to achieve in practice. One method is to put MgCO3 under vacuum and decrease the pressure of both CO2 and H2O simultaneously, which would probe a diagonal line on the phase stability plot. The pressure at which MgCO3 transforms to MgO could then be determined and compared to the modelling results. Alternatively, the phase stability plots could be changed to show the effect of temperature and pCO2, which we consider in the following section.
3.7 Phase stability of Mg-rich phases as a function of pCO2O and temperature with a fixed pH2O = 1 bar
Experimental phase stability plots as a function of temperature and pCO2 at 1 bar pH2O have been derived by Hill et al.71 and Schott et al.,74 both based on the earlier work of Langmuir et al.31 Hill et al. results71 predict that only Brucite (Mg(OH)2) and Magnesite (MgCO3) are thermodynamically stable, whereas, Schott et al.74 predict that MgCO3 is unstable and only forms at high temperature and high pCO2. There is only one study, by Schott et al., that predicts a small region of stability for Artinite (Mg2CO3(OH)2·3H2O). This contradicts Hill et al.,71 although Parry et al.75 have demonstrated that Artinite may be stable under conditions relevant to nuclear waste storage. It is important to note that the experimental phase stability plots predict different conditions under which phase transitions between the Mg-rich phases are expected to occur. Experimentally, MgCO3 has been shown to form at 185 °C and pCO2 = 140 bar, but the formation of MgCO3 at ambient temperature is virtually impossible.76,77 As Magnesite will be the predominant phase at most CO2 pressures in the T vs. pCO2 phase stability plot, inhibiting its growth produces a variety of new phases. The appearance of these phases has repercussions for the sequestration of CO2 and shows that metastable carbonate-containing phases are more important than the anhydrous magnesium carbonate (Magnesite). More generally, this has implications for applications where the evolution over time of phases in the MgO–H2O–CO2 system is an important factor, for example during the storage of industrial6 or nuclear5 waste materials, in construction,8,72 where Mg binders have to remain stable over a long period of time, or during catalytic cycles where the formation of metastable phases may lead to poisoning.2–4 Multiple phase transitions may occur during the process that ultimately leads to MgCO3 formation. Indeed, Ostwald's rule78 states that nucleation from solution occurs in steps, where the most thermodynamically unstable phases form first, followed by a step towards the most thermodynamically-stable phase. While this rule does not always hold true,79 a larger number of phases increases the likelihood that Ostwald's rule applies.79Fig. 6 compares our calculated phase stability plots as a function of temperature and ΔμCO2 at a fixed ΔμH2O = 0 eV (pH2O = 1 bar), computed using the harmonic and quasi-harmonic free energies, and either including all the Mg-rich phases or with the formation of MgCO3 inhibited. Comparable phase stability plots obtained using the other functionals can be found in Fig. S7 and S8 (ESI†).
Under standard pH2O and CO2-rich conditions, using the optB86b functional and the harmonic free energies, Lansfordite (MgCO3·5H2O) is metastable below ∼310 K, above which Nesquehonite (MgCO3·3H2O) becomes the more thermodynamically-stable phase. This prediction compares well with the work of Hill et al.71 and Schott et al.,74 who predict the transition to occur at 283 K. Further evidence for the existence of this transition is provided by Ming et al.80 who observed that MgCO3·5H2O crystals dehydrate to MgCO3·3H2O at 285 K under atmospheric pH2O and pCO2. However, our modelling predicts these transitions to occur at higher pCO2 and at temperatures of 308/312 K based on the harmonic and QHA energies. This phase transition was also investigated in a computational study by Chaka et al.,43 who obtained a transition temperature of ∼340 K but countered this by applying an experimental correction to the free energy of MgCO3·5H2O. This is possibly an indication of the shortcomings of the description of van der Waals forces in DFT in general, and of the treatment in the DFT+D2 method used in that study specifically.
There is debate in the literature about the thermodynamic stability of Artinite Mg2CO3(OH)2·3H2O. Our ab initio phase stability plots predict a small stability region for Artinite at low temperature (Fig. 6c), which is only found in some of the experimental studies.74,75 Using the QHA free energies increases the stability of this phase over a broader range of temperatures (Fig. 6d). We note however that the complexity of the Artinite structure that arises from the random distribution of the CO32− and H2O ligands is only partially considered in this study, as we use a single model structure. A random distribution would give some additional configurational entropy that would further stabilise Artinite. This is consistent with the work of Schott et al.,74 which suggests that Mg2CO3(OH)2·3H2O is stable at low temperatures and low pCO2. We also note that there are multiple entropy values for Mg2CO3(OH)2·3H2O in the literature.31,71,74 This makes it difficult to compare unambiguously our predictions to experiments, but, as our ab initio phase stability plots do not require any experimental corrections for the solid phases, and are therefore not biased towards particular sets of measurements, we can consider them truly predictive. With this in mind our results confirm that Mg2CO3(OH)2·3H2O is likely to remain a rare phase and one deserving of future investigation, but the favourable comparison between our predicted phase stability plots and literature data suggests that our predictions may be accurate enough to identify the synthesis conditions required to form specific Mg-rich phases.
However, we highlight a key assumption of our methodology, namely that the vibrational properties of the different phases are purely harmonic. This assumption may lead to deviation from experiment under some conditions, particularly at elevated temperature. On the other hand, using the quasi-harmonic approximation to account for thermal expansion, as we have done in the present study, did not significantly change the results despite a ten-fold increase in the computational cost.81 Despite these potential shortcomings, a key advantage of this thermodynamic framework is that it can be used unambiguously to compare the DFT functionals and the different techniques to account for entropy. It could also be used with a global-exploration structure search to identify potential unknown phases and place them on the phase stability plots. Similarly, although this work examines the MgO–CO2–H2O system, the methodology is completely general and could be applied to a wide variety of other systems, subject to choosing an appropriate theoretical description for treating the compounds in the system under study.
4. Conclusions
In this work, we have developed an ab initio thermodynamics framework to situate the mineral Artinite (Mg2CO3(OH)2·3H2O) within the phase space of other Mg hydroxides and carbonates. We find that the widely-overlooked Artinite phase is metastable and can be stabilised by inhibiting the formation of Magnesite (MgCO3), thus providing an explanation for the experimental controversy over the conditions under which this rare phase can be observed.31,71,74Our methodology has several advantages over alternatives, viz.: (1) it can identify overlooked materials that may be stable under specific conditions of temperature and partial pressures of water and carbon dioxide; (2) it can be used to identity competing and metastable phases, such as Artinite; and (3) it does not rely on the availability and accuracy of solid-phase experimental thermodynamic data. The latter in particular means that the present results can inform the future development of synthetic strategies to target and selectively stabilise specific phases of interest.
Our theoretical results also show that the inclusion of van der Waals dispersion corrections to density–functional theory is necessary to accurately predict the thermodynamic properties of the MgO–CO2–H2O system. Such corrections are particularly important for phases that display large numbers of hydrogen bonds, such as Artinite. On the other hand, applying the quasi-harmonic approximation does not lead to a significant improvement in the accuracy of our predictions over the harmonic approximation. Finally, we note that a potential limitation of our study is that we do not fully treat the disorder in Artinite, because of the limitations of our ab initio calculations, which may provide additional (entropic) stabilisation. Future work on this system should therefore consider applying classical molecular dynamics or Monte Carlo simulations to better take disorder into account.
Data availability
Raw data are available from https://doi.org/10.17632/s96szk84zb.1.Author contributions
Conceptualization: JST, JMS, MM, SCP; Data curation: JST; Formal Analysis: JST, JMS; Funding acquisition: MM, LJG, SCP, RZ; Investigation: All authors; Methodology: JST, MM, SCP; Project administration: MM, SCP; Supervision: MM, LJG, SCP; Resources: MM, SCP; Validation: JST, MM, SCP; Visualization: JST, MM; Writing – original draft: JST, MM; Writing – review & editing: All authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the UK Engineering and Physical Sciences Research Council (EPSRC; EP/K025597/1 and EP/R010366/1), the Royal Society (Newton Advanced Fellowship NA150190), UK Research and Innovation (UKRI; MR/T043121/1), and the Collaborative Computational Project 5 (CCP5), which is funded by the EPSRC (EP/J010480/1), for financial support. The computational work made use of the UK national HPC service, ARCHER/ARCHER2, via the Materials Chemistry Consortium (MCC), which is funded by the EPSRC (EP/L000202/1, EP/R029431/1 and EP/X035859/1). We also made use of the Balena HPC (University of Bath), and the Orion computing facility and the Violeta HPC (University of Huddersfield).References
- D. Thomele, G. R. Bourret, J. Bernardi, M. Bockstedte and O. Diwald, Angew. Chem., Int. Ed., 2017, 56, 1407–1410 CrossRef CAS PubMed.
- U. C. Rajesh, V. S. Pavan and D. S. Rawat, ACS Sustainable Chem. Eng., 2015, 3, 1536–1543 CrossRef CAS.
- G. Fan, F. Li, D. G. Evans and X. Duan, Chem. Soc. Rev., 2014, 43, 7040–7066 RSC.
- D. Jiang, S. H. Overbury and S. Dai, J. Phys. Chem. Lett., 2011, 2, 1211–1215 CrossRef CAS PubMed.
- W. Liu, F. Huang, Y. Liao, J. Zhang, G. Ren, Z. Zhuang, J. Zhen, Z. Lin and C. Wang, Angew. Chem., Int. Ed., 2008, 47, 5619–5622 CrossRef CAS PubMed.
- S. A. Walling, H. Kinoshita, S. A. Bernal, N. C. Collier and J. L. Provis, Dalton Trans., 2015, 44, 8126–8137 RSC.
- L. A. Hollingbery and T. R. Hull, Polym. Degrad. Stab., 2010, 95, 2213–2225 CrossRef CAS.
- P. De Silva, L. Bucea and V. Sirivivatnanon, Cem. Concr. Res., 2009, 39, 460–465 CrossRef CAS.
- J. J. M. Lenders, A. Dey, P. H. H. Bomans, J. Spielmann, M. M. R. M. Hendrix, G. de With, F. C. Meldrum, S. Harder and N. A. J. M. Sommerdijk, J. Am. Chem. Soc., 2012, 134, 1367–1373 CrossRef CAS PubMed.
- K. S. Lackner, Science, 2003, 300, 1677–1678 CrossRef CAS PubMed.
- A. L. Harrison, G. M. Dipple, I. M. Power and K. U. Mayer, Geochim. Cosmochim. Acta, 2015, 148, 477–495 CrossRef CAS.
- J. Matter and P. Kelemen, Nat. Geosci., 2009, 2, 837–841 CrossRef CAS.
- M. T. Dunstan, A. Jain, W. Liu, S. P. Ong, T. Liu, J. Lee, K. A. Persson, S. A. Scott, J. S. Dennis and C. P. Grey, Energy Environ. Sci., 2016, 9, 1346–1360 RSC.
- A. Hermann and M. Mookherjee, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13971–13976 CrossRef CAS PubMed.
- M. C. De Sanctis, E. Ammannito, A. Raponi, S. Marchi, T. B. McCord, H. Y. McSween, F. Capaccioni, M. T. Capria, F. G. Carrozzo, M. Ciarniello, A. Longobardo, F. Tosi, S. Fonte, M. Formisano, A. Frigeri, M. Giardino, G. Magni, E. Palomba, D. Turrini, F. Zambon, J. P. Combe, W. Feldman, R. Jaumann, L. A. McFadden, C. M. Pieters, T. Prettyman, M. Toplis, C. A. Raymond and C. T. Russell, Nature, 2015, 528, 241–244 CrossRef CAS PubMed.
- W. M. Calvin, T. V. V. King and R. N. Clark, J. Geophys. Res.: Planets, 1994, 99, 14659–14675 CrossRef CAS.
- A. Walsh, Nat. Chem., 2015, 7, 274 CrossRef CAS PubMed.
- A. Halperin, M. Kröger and F. M. Winnik, Angew. Chem., Int. Ed., 2015, 54, 15342–15367 CrossRef CAS PubMed.
- R. Gautier, X. Zhang, L. Hu, L. Yu, Y. Lin, T. O. L. Sunde, D. Chon, K. R. Poeppelmeier and A. Zunger, Nat. Chem., 2015, 7, 308–316 CrossRef CAS PubMed.
- M. Bajdich, M. García-Mota, A. Vojvodic, J. K. Nørskov and A. T. Bell, J. Am. Chem. Soc., 2013, 135, 13521–13530 CrossRef CAS PubMed.
- G. Gao, N. W. Ashcroft and R. Hoffmann, J. Am. Chem. Soc., 2013, 135, 11651–11656 CrossRef CAS PubMed.
- I. Pallikara and J. M. Skelton, Phys. Chem. Chem. Phys., 2021, 23, 19219–19236 RSC.
- J. Zhang, H. Dong, X. Li, Z. Wang and D. Xiao, Phys. Chem. Chem. Phys., 2022, 24, 20848–20855 RSC.
- A. J. Samin, J. Alloys Compd., 2021, 879, 160455 CrossRef CAS.
- M. Wolloch, M. E. Gruner, W. Keune, P. Mohn, J. Redinger, F. Hofer, D. Suess, R. Podloucky, J. Landers, S. Salamon, F. Scheibel, D. Spoddig, R. Witte, B. Roldan Cuenya, O. Gutfleisch, M. Y. Hu, J. Zhao, T. Toellner, E. E. Alp, M. Siewert, P. Entel, R. Pentcheva and H. Wende, Phys. Rev. B, 2016, 94, 174435 CrossRef.
- G. Coquerel, Chem. Soc. Rev., 2014, 43, 2286–2300 RSC.
- P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. Xu and L. G. M. Pettersson, Chem. Rev., 2016, 116, 7463–7500 CrossRef CAS PubMed.
- S. C. L. Brugnatelli, Rend., R. Ist. Lomb. Sci. Lett., 1902, 35, 869–874 Search PubMed.
- H. Jagodzinski, Tschermaks Mineral. Petrogr. Mitt., 1965, 10, 297–330 CrossRef CAS.
- R. A. Hemingway and B. S. Robie, U.S. Geol. Surv. J. Res., 1973, 1, 535–546 Search PubMed.
- D. Langmuir, J. Geol., 1965, 73, 730–754 CrossRef CAS.
- G. Baron and J. Wyart, Acad. Sci. Comptes rendus, 1958, 247, 485–487 CAS.
- A. V. Kazakov, M. M. Tikhomirova and V. I. Plotnikova, Int. Geol. Rev., 1959, 1, 1–39 CrossRef.
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef CAS PubMed.
- M. Jansen, I. V. Pentin and J. C. Schön, Angew. Chem., Int. Ed., 2012, 51, 132–135 CrossRef CAS PubMed.
- S. M. Woodley and A. A. Sokol, Angew. Chem., Int. Ed., 2012, 51, 3752–3754 CrossRef CAS PubMed.
- R. Martoák, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 75503 CrossRef PubMed.
- J. Rogal, S. V. Divinski, M. W. Finnis, A. Glensk, J. Neugebauer, J. H. Perepezko, S. Schuwalow, M. H. F. Sluiter and B. Sundman, Phys. Status Solidi B, 2014, 251, 97–129 CrossRef CAS.
- Y. Du, B. Wooler, M. Nines, P. Kortunov, C. S. Paur, J. Zengel, S. C. Weston and P. I. Ravikovitch, J. Am. Chem. Soc., 2015, 137, 13603–13611 CrossRef CAS PubMed.
- X. Dong, H. Zhou, H. Yang, J. Yuan, K. Jin, F. Zhou, D. Yuan, L. Wei, J. Li, X. Wang, G. Zhang and Z. Zhao, J. Am. Chem. Soc., 2015, 137, 66–69 CrossRef CAS PubMed.
- L. Malavasi, G. A. Artioli, C. Ritter, M. C. Mozzati, B. Maroni, B. Pahari and A. Caneschi, J. Am. Chem. Soc., 2010, 132, 2417–2420 CrossRef CAS PubMed.
- S. Ping Ong, L. Wang, B. Kang and G. Ceder, Chem. Mater., 2008, 20, 1798–1807 CrossRef.
- A. M. Chaka and A. R. Felmy, J. Phys. Chem. A, 2014, 118, 7469–7488 CrossRef CAS PubMed.
- J. Grant, G. L. Pesce, R. J. Ball, M. Molinari and S. C. Parker, RSC Adv., 2016, 6, 16066–16072 RSC.
- D. M. S. Martins, M. Molinari, M. A. Gonçalves, J. P. Mirão and S. C. Parker, J. Phys. Chem. C, 2014, 118, 27308–27317 CrossRef CAS.
- T. V. Shapley, M. Molinari, R. Zhu and S. C. Parker, J. Phys. Chem. C, 2013, 117, 24975–24984 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 22201 CrossRef PubMed.
- G. Stefan, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef PubMed.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- N. A. Brincat, S. C. Parker, M. Molinari, G. C. Allen and M. T. Storr, Inorg. Chem., 2014, 53, 12253–12264 CrossRef CAS PubMed.
- N. A. Brincat, S. C. Parker, M. Molinari, G. C. Allen and M. T. Storr, Dalton Trans., 2015, 44, 2613–2622 RSC.
- M. Molinari, N. A. Brincat, G. C. Allen and S. C. Parker, Inorg. Chem., 2017, 56, 4468–4473 CrossRef PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. Symington, J. Tse, M. Molinari, A. Marmier and S. Parker, J. Open Source Software, 2019, 4, 1210 CrossRef.
- J. S. Tse, M. Molinari, S. C. Parker and A. R. Symington, J. Open Source Software, 2022, 7, 4014 CrossRef.
- M. Akao and S. Iwai, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 3951–3953 CrossRef.
- R. C. Weast, CRC Handbook of Chemistry & Physics, CRC Press Inc., 61st edn, 1980 Search PubMed.
- A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174301 CrossRef.
- L. N. Kantorovich, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 3520–3534 CrossRef CAS PubMed.
- L. N. Kantorovich, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 3535–3548 CrossRef CAS PubMed.
- M. W. N. I. of S. T. (U. S. Chase), NIST-JANAF Thermochemical Tables, Standard Reference Data Program National Institute of Standards and Technology, Washington, D.C. Woodbury, N.Y., 4th edn., 1998.
- A. M. Chaka, A. R. Felmy and O. Qafoku, Chem. Geol., 2016, 434, 1–11 CrossRef CAS.
- J. P. Allen, A. Marmier and S. C. Parker, J. Phys. Chem. C, 2012, 116, 13240–13251 CrossRef CAS.
- R. J. Hill, J. H. Canterford and F. J. Moyle, Miner. Mag., 1982, 46, 453–457 CrossRef CAS.
- W. S. Chiang, G. Ferraro, E. Fratini, F. Ridi, Y.-Q. Yeh, U.-S. Jeng, S.-H. Chen and P. Baglioni, J. Mater. Chem. A, 2014, 2, 12991–12998 RSC.
- M. Haenchen, V. Prigiobbe, R. Baciocchi and M. Mazzotti, Chem. Eng. Sci., 2008, 63, 1012–1028 CrossRef CAS.
- J. Schott and J. L. Dandurand, C. R. Acad. Sci., Ser. IIc: Chim., 1975, 280, 1247 CAS.
- S. A. Parry, L. O’Brien, A. S. Fellerman, C. J. Eaves, N. B. Milestone, N. D. Bryan and F. R. Livens, Energy Environ. Sci., 2011, 4, 1457–1464 RSC.
- F. Farhang, T. K. Oliver, M. Rayson, G. Brent, M. Stockenhuber and E. Kennedy, Chem. Eng. J., 2016, 303, 439–449 CrossRef CAS.
- K. Sandengen, L. O. Josang and B. Kaasa, Ind. Eng. Chem. Res., 2008, 47, 1002–1004 CrossRef CAS.
- W. Ostwald, J. Phys. Chem., 1897, 22, 289–330 CAS.
- S.-Y. Chung, Y.-M. Kim, J.-G. Kim and Y.-J. Kim, Nat. Phys., 2009, 5, 68–73 Search PubMed.
- D. W. Ming and W. T. Franklin, Soil Sci. Soc. Am. J., 1985, 49, 1303–1308 CrossRef CAS.
- A. Erba, M. Shahrokhi, R. Moradian and R. Dovesi, J. Chem. Phys., 2015, 142, 44114 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00518f |
| This journal is © the Owner Societies 2023 |