Fragment imaging in the infrared photodissociation of the Ar-tagged protonated water clusters H₃O⁺–Ar and H⁺(H₂O)₂–Ar

Abstract

Infrared photodissociation of protonated water clusters with an Ar atom, namely H₃O⁺–Ar and H⁺(H₂O)₂–Ar, was investigated by an imaging technique for mass-selected ions, to reveal the intra- and intermolecular vibrational dynamics. The presented system has the advantage of achieving fragment ion images with the cluster size- and mode-selective photoexcitation of each OH stretching vibration. Translational energy distributions of photofragments were obtained from the images upon the excitation of the bound (ν_b) and free (ν_f) OH stretching vibrations. The energy fractions in the translational motion were compared between ν_b^I and ν_f^I in H₃O⁺–Ar or between ν_b^II and ν_f^II in H⁺(H₂O)₂–Ar, where the labels “I” and “II” represent H₃O⁺–Ar and H⁺(H₂O)₂–Ar, respectively. In H₃O⁺–Ar, the ν_f^I excitation exhibited a smaller translational energy than ν_b^I. This result can be explained by the higher vibrational energy of ν_f^I, which enabled it to produce bending (ν₄) excited H₃O⁺ fragments that should be favored according to the energy-gap model. In contrast to H₃O⁺–Ar, the ν_b^II excitation of an Ar-tagged H₂O subunit and the ν_f^II excitation of an untagged H₂O subunit resulted in very similar translational energy distributions in H⁺(H₂O)₂–Ar. The similar energy fractions independent of the excited H₂O subunits suggested that the ν_b^II and ν_f^II excited states relaxed into a common intermediate state, in which the vibrational energy was delocalized within the H₂O–H⁺–H₂O moiety. However, the translational energy distributions for H⁺(H₂O)₂–Ar did not agree with a statistical dissociation model, which implied another aspect of the process, that is, Ar dissociation via incomplete energy randomization in the whole H⁺(H₂O)₂–Ar cluster.

---

Introduction

Infrared spectroscopy of molecular clusters (or complexes) has been a growing field in gas-phase experiments for a few decades.^1–11 The vibrational signatures of clusters appearing in the infrared spectra provide detailed information on their geometrical structures, bonding natures, and interaction potentials. Besides the studies of those static properties, studies on relaxation dynamics from vibrationally excited states populated by infrared absorption have also attracted attention^{1,2,5,12–17} though there have been relatively fewer experimental studies.

Ion imaging¹⁸ is one of the powerful tools to explore chemical dynamics involving fragmentation (or scattering) processes.^19–23 Reisler and co-workers applied photofragment imaging technique to study the vibrational predissociation of a neutral molecular cluster system with infrared laser excitation.²⁴ They also exploited resonance-enhanced multiphoton ionization (REMPI) to achieve the detection of neutral fragments in selected rovibrational states. Since their pioneering work, state-specific predissociation dynamics has extensively been investigated for hydrogen-bonded clusters.^25–29 However, there is a general difficulty in the gas-phase experiments on neutral systems regarding the size selection of target clusters. Though there are a few techniques for the size selection of neutrals, for example the rare-gas scattering method,⁴ a versatile technique that can be easily employed in experiments to investigate the dynamics has not been established thus far. In infrared photofragment imaging, size-selective photoexcitation is accomplished by tuning the excitation energy to a single vibrational band, whose resonant energy is specific to a certain size of interest. In some cases, infrared absorption energies are not strongly dependent on the cluster size (e.g., the free OH stretching modes seen in an (H₂O)_n system^30–33), and therefore the experiments on those targets suffer from size contamination. Size mixtures of neutral clusters complicate spectral peak assignments even in a simple system.³⁴ Without a clear characterization of the spectral features and corresponding vibrational modes, it is challenging to take a series of measurements to explore the mode dependence in the predissociation process of neutral clusters.

Recently, photofragment ion imaging for mass-selected ionic species has been established by several groups, including our group.^35–38 In contrast to the experiments for neutral clusters, one of the most significant advantages in those for charged clusters is the ease of size selection prior to photoexcitation. This new imaging scheme has been applied to visible/ultraviolet photodissociation reactions to study electronically excited state dynamics.^39–52 Vibrationally excited state dynamics can also be studied by infrared excitation. The first application to infrared photodissociation was for the H₂O⁺–Ar complex ion.⁵³ The mode-selective excitation of several vibrational modes of H₂O⁺–Ar was successfully performed, and the processes involved in the energy redistribution from the vibrationally excited states into the rotational and translational degrees of the fragments were discussed based on the image analyses.

In the present paper, we report the infrared photodissociation imaging of H₃O⁺–Ar and H⁺(H₂O)₂–Ar, representing the smallest sizes of protonated water clusters with an Ar atom. The protonated water cluster H⁺(H₂O)_n is one of the most-studied systems in gas-phase infrared spectroscopy.^54–80 The size-dependent structures of this cluster have attracted considerable attention for obtaining a microscopic understanding of the hydration form of protons in water. For the purpose of recording the photodissociation action spectra of the cluster ions, an inert gas atom or molecule, such as Ar, is often employed as a “messenger” tag, as proposed in the early work by Lee and co-workers.^55,57 The structures of H₃O⁺–Ar and H⁺(H₂O)₂–Ar were fully characterized, and the spectral features clearly assigned in the mid-infrared region, including OH stretching modes and higher-order combination bands.^{68,69,71,72,79,80} On the other hand, their relaxation dynamics from vibrationally excited states followed by Ar dissociation are much less understood. In this study, photofragment ions [H₃O⁺ or H⁺(H₂O)₂] produced upon photoexcitation with a linearly polarized infrared laser were detected as images to obtain the translational energy and angular distributions of the dissociation products. Two contrasting modes of OH stretching vibrations of each cluster ion, hereafter represented as ν_b and ν_f, were chosen for photoexcitation. For H₃O⁺–Ar, the stretching mode of the Ar-bound OH group of the H₃O⁺ moiety is denoted as ν_b^I, and the asymmetric stretching mode of the other two free OH groups is denoted as ν_f^I. For H⁺(H₂O)₂–Ar, ν_b^II is defined as the symmetric OH stretching mode in an H₂O moiety attached to an Ar atom, whereas ν_f^II is the asymmetric OH stretching of the other, untagged H₂O moiety. The imaging apparatus designed for the mass-selected ions was exploited to examine the mode dependence in the photofragment recoil distributions from H₃O⁺–Ar and H⁺(H₂O)₂–Ar. In addition, the processes involved in the vibrational energy redistribution are discussed in terms of the cluster size (the number of internal degrees of freedom).

Experimental and computational methods

The home-made imaging apparatus used in the present study was almost identical to that reported previously³⁶ as shown in Fig. S1 (ESI†). The details of the infrared photodissociation procedures were also described recently.⁵³ A supersonic jet of an H₂O/Ar gas mixture expanded at ∼5 × 10⁵ Pa was ionized at ∼3 mm downstream from the exit of the pulsed valve by an electron beam which crossed transversely at an energy of ∼70 eV. The generated cluster ions were accelerated into a custom-made, linear-type double reflectron mass spectrometer operated in the pulsed mode. After reflection by the first reflectron, the mass-separated cluster ion, H₃O⁺–Ar or H⁺(H₂O)₂–Ar, was irradiated with a pulsed mid-infrared light (∼1 mJ pulse⁻¹, via a Nd:YAG-pumped OPO/OPA laser, LaserVision) at the middle of the double reflectron. In the imaging experiment, the excitation energy was tuned at one of the OH stretching modes of the cluster of interest. The infrared frequency of the present laser system was calibrated with an ambient H₂O vapor spectrum,⁸¹ and the resolution was estimated to be ∼4 cm⁻¹. It was confirmed that photofragment ions losing the Ar atom, H₃O⁺ and H⁺(H₂O)₂, were produced by a one-photon process from the laser power dependence of the fragment yields. These fragment ions were then reflected in the second reflectron, and the 2D projections of the recoiling photofragment ion distributions were collected by microchannel plates coupled to a phosphor screen (Photonis, 3040FM, 60 : 1, ϕ40). The detected ion positions were read out by a CMOS camera (Toshiba Teli, BU238M) monitoring the phosphor screen. Image accumulation was conducted typically for ∼100 000 laser shots. The entire experiment was operated at a 10 Hz repetition rate. Slice imaging techniques were not employed in ion detection in the present study. The translational energy and angular distributions of the photofragment ions were derived from the sliced images reconstructed by the pBASEX method.⁸²

In this study, the shape of the electrodes of the second reflectron was partially modified compared to in our original setup.³⁶ Details of the modification of the second reflectron are described in the ESI† with the results of the evaluation experiments. The improved electrodes were designed based on the ideas in previous papers.^83,84 The performance of the new imaging electrodes was evaluated with ultraviolet photolysis of Ca⁺Ar complex, and the photofragment Ca⁺ image exhibited a better resolution than the previous one. The residual velocity spread for Ca⁺ was found to be Δv = 130 m s⁻¹. The narrowest velocity distribution in the present infrared experiments was Δv ∼ 260 m s⁻¹ for the ν_b^II excitation of H⁺(H₂O)₂–Ar, and thus the apparatus was confirmed to have sufficient image resolution.

The infrared spectra of H₃O⁺–Ar and H⁺(H₂O)₂–Ar measured in this study are shown in Fig. 1a and b, respectively. These spectra well reproduced the previously reported results.^{68,69,71,72,79,80} For H₃O⁺–Ar, the Ar-bound OH stretching mode (ν_b^I) and the asymmetric stretching mode of the free OH groups (ν_f^I) were chosen in the imaging experiment. The excitation energies were set on the R-branch peak at 3142 cm⁻¹ for ν_b^I and on the Q-branch peak of the K = 0 ← 1 sub-band at 3550 cm⁻¹ for ν_f^I, as indicated by the arrows in Fig. 1a. For the imaging experiment of H⁺(H₂O)₂–Ar, the excitation energies were set as 3524 cm⁻¹ for the symmetric OH stretch of an Ar-tagged H₂O moiety (ν_b^II) and as 3697 cm⁻¹ for the asymmetric OH stretch of an untagged H₂O moiety (ν_f^II). These energies correspond to a peak top of each vibrational band, as depicted in Fig. 1b. The rotational temperature, T_rot, in the present ion source was roughly estimated to be 40–60 K by simulating the ν_f^I sub-band structure over the range 3520–3640 cm⁻¹ using the PGOPHER program.⁸⁵ The results of the spectral simulation are shown in Fig. S4 (ESI†).

Fig. 1 Mid-infrared photodissociation spectra for (a) H₃O⁺–Ar and (b) H⁺(H₂O)₂–Ar recorded by monitoring the fragment ion yields of the Ar dissociation channel. Orange and blue arrows indicate the excitation energies in the imaging experiments for the ν_b and ν_f vibrational modes, respectively. See the text for the definitions of the ν_b and ν_f modes. Gray arrows for H₃O⁺–Ar indicate the other vibrational bands: the bending overtones (*1/*2), the combination band of ν_b^I and the low-frequency intermolecular stretch (*3), and the symmetric free OH stretch (*4). Gray arrows for H⁺(H₂O)₂–Ar are the symmetric OH stretch of the untagged H₂O (**1) and the asymmetric OH stretch of tagged H₂O (**2).

Ab initio calculations were performed to obtain the harmonic vibrational frequencies of H₃O⁺–Ar, H⁺(H₂O)₂–Ar, and H⁺(H₂O)₂ at the MP2/aug-cc-pVTZ level utilizing the Gaussian16 package.⁸⁶ The calculated frequencies were scaled by a factor of 0.950 and used for the statistical model calculations described below. Though there are a few experimental frequencies available in the literature, low-frequency modes are much less known experimentally than the OH stretching vibrations, especially for bare H⁺(H₂O)₂. Therefore, all the values were taken from the calculated results. Nevertheless, the difference between the experimental and theoretical frequencies was small in the present study. For example, the theoretical frequencies for the OH stretching vibrations of H₃O⁺–Ar and H⁺(H₂O)₂–Ar differed only by <2% from the experimental values. For H⁺(H₂O)₂–Ar, the binding energy of Ar, D₀, was also calculated at the same level. In the calculation, the basis-set superposition error was corrected using the counterpoise method. Furthermore, in order to estimate the statistical translational energy distributions of the fragments, numerical calculations of phase space theory (PST) combined with orbiting transition state theory^87,88 were performed. In the PST calculation, the internal temperatures of H₃O⁺–Ar and H⁺(H₂O)₂–Ar were assumed to be 50 K as estimated in the photodissociation spectrum. The calculated results at other temperatures (20 and 80 K) were found to cause only marginal (<2%) differences in the translational energy distribution.

Results and discussion

Photofragment images and translational energy distributions

The four vibrational modes chosen for the imaging experiments are schematically depicted in Fig. 2. The illustrations are based on the normal mode analyses by the harmonic vibrational calculations at the MP2/aug-cc-pVTZ level. More quantitative descriptions for the displacement of the H atoms in each vibrational mode are summarized in Tables S1 and S2 (ESI†). For the ν_b^II vibration of H⁺(H₂O)₂–Ar, the bound OH group had more than a three times larger amplitude than the other free OH groups of the Ar-tagged H₂O moiety, whereas the two free OH groups of the untagged H₂O moiety almost equally vibrated in the ν_f^II mode.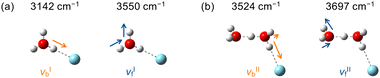

Fig. 2 Schematic illustrations for the ν_b and ν_f modes of (a) H₃O⁺–Ar and (b) H⁺(H₂O)₂–Ar. Arrows represent the normal mode displacement vectors of the H atoms. Quantitative descriptions for the displacement vectors are given in Tables S1 and S2 (ESI†). Excitation energies chosen for the imaging experiments are also indicated.

Images of the photofragment ions produced upon the ν_b and ν_f excitations of H₃O⁺–Ar and H⁺(H₂O)₂–Ar are shown in Fig. 3a and b, respectively. The background signals were removed by subtracting the images taken with the infrared laser off. All of the images exhibited an almost isotropic distribution with respect to the laser polarization direction (E).

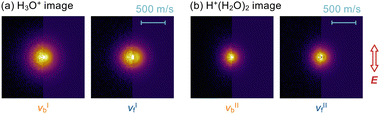Fig. 3 Ion images upon the ν_b and ν_f excitations of (a) H₃O⁺–Ar and (b) H⁺(H₂O)₂–Ar recorded by detecting the photofragment H₃O⁺ and H⁺(H₂O)₂ ions, respectively. The left half of each image is the raw collected image, and the right half is the central slice of the pBASEX⁸² reconstructed distribution. The polarization direction of the dissociation laser, E, is shown in the inset. The velocity scale is common to all the images.

The photofragment angular distribution is expressed as I(θ) = (1/4π)[1 + βP₂(cos θ)],⁸⁹ where β is the anisotropy parameter, which varies from −1 to +2; P₂(cos θ) is the second-order Legendre polynomial; and θ is the angle between the laser polarization and the fragment recoil direction. The experimental β value was determined at the most probable velocity of each distribution. For the ν_b^I and ν_f^I modes of H₃O⁺–Ar, the β values were obtained as +0.06 ± 0.02 and −0.13 ± 0.01, respectively. The theory of calculating β for rotationally resolved photoexcitation has been previously described in detail elsewhere.^90,91 H₃O⁺–Ar is a near-prolate symmetric top, and the β value for the J′, K′ ← J′′, K′′ transition of a symmetric top molecule depends on the J′′, K′′ values and the type of rotational branch (P, Q, or R). In the special case of J′′ ≫ K′′, which is true in the present experiment because the most probable values were J′′ = 11 and K′′ = 1 at T_rot = 50 K (see Fig. S5, ESI† for the simulated profiles of the rotational lines), the theoretical β values could be calculated as +0.5 for the P and R branches and −1 for the Q branch. The observed β values were positive at the R-branch peak (ν_b^I) and negative at the Q-branch peak (ν_f^I) in the experiment, and thus consistent with the theoretical prediction for the β signs. Quantitatively, both of the experimental β values exhibited lower anisotropy than those from theory due to the longer dissociation lifetime than the rotational period of H₃O⁺–Ar (∼11 ps at 50 K). For H⁺(H₂O)₂–Ar, the lack of clear rotational structure in the spectrum and the low symmetry of the H⁺(H₂O)₂–Ar rotor preclude the analysis of theoretical β. The experimental values were determined as β = +0.08 ± 0.04 for ν_b^II and +0.04 ± 0.03 for ν_f^II. The isotropic β values are likely to reflect the long dissociation lifetime of H⁺(H₂O)₂–Ar, as in the case of H₃O⁺–Ar.

Translational energy release (E_t), which is defined as the sum of the translational energies of the photofragments, reflects the energy redistribution processes from the photoexcited states. Fig. 4a and b show the experimental E_t distributions upon the ν_b^I and ν_f^I excitations of H₃O⁺–Ar, respectively. The binding energy of Ar for H₃O⁺–Ar was previously reported in the theoretical studies as D₀ = 1634 cm⁻¹ at the CCSD(T) level with extrapolation to the complete basis set limit (note that the harmonic frequencies used for the zero-point correction were calculated using the aug-cc-pVTZ-PP basis set).⁹² The available energies of the photodissociation, E_avl = hν − D₀, were thus calculated to be 1508 cm⁻¹ for ν_b^I and 1916 cm⁻¹ for ν_f^I. Both of the E_t distributions peaked near the energy origin, showing that the large internal excitation of the fragment H₃O⁺ ions was preferred in the photodissociation process. This was also the case in the E_t distributions for H⁺(H₂O)₂–Ar as displayed in Fig. 4c and d. The binding energy of H⁺(H₂O)₂–Ar, D₀ = 655 cm⁻¹, calculated at the MP2/aug-cc-pVTZ (zero-point corrected) level gave E_avl values of 2869 cm⁻¹ for ν_b^II and 3042 cm⁻¹ for ν_f^II. The Maxwell–Boltzmann-like shapes of the E_t distributions were obtained irrespective of the excited modes and the cluster sizes.

Fig. 4 E _t distributions obtained from the ion images. Panels (a) and (b) show the E_t distributions for the ν_b^I and ν_f^I excitations of H₃O⁺–Ar, respectively, while panels (c) and (d) show the corresponding distributions for H⁺(H₂O)₂–Ar. The experimental distributions (solid curves) are compared with the PST calculations (broken curves). See the text for more information on the PST model. In panels (e) and (f), the E_t distributions are plotted against the E_t/E_avl ratio, and the distributions for the ν_b and ν_f excitations in each panel are normalized to the area. In all the panels, the shaded regions in all the experimental plots represent the statistical errors of the measurement.

Assuming that intracluster vibrational energy redistribution (IVR) has completed prior to dissociation, the E_t distribution can be predicted by a statistical model calculation. The PST model^87,88 has been widely used in various systems, including the unimolecular dissociation of gas-phase ions.⁹³ In the PST calculation, the fragment rovibrational states that satisfy the conservation of the total energy and angular momentum are equally populated. The calculated results for H₃O⁺–Ar are compared with the experimental values in Fig. 4a and b (broken curves). Apparently, the PST prediction gave a much larger E_t than the experimental distribution both for ν_b^I and ν_f^I, suggesting that there was a propensity for internal excitation of the H₃O⁺ fragment unlike complete energy randomization. A similar trend was found for H⁺(H₂O)₂–Ar, as depicted in Fig. 4c and d.

The E_t distributions for the ν_b and ν_f excitations are compared in Fig. 4e for H₃O⁺–Ar and 4f for H⁺(H₂O)₂–Ar. The distributions were plotted against the translational energy fraction of the available energy, E_t/E_avl, in order to remove the differences in the magnitude of E_avl between the ν_b and ν_f excitations. The E_t fraction was apparently mode dependent for H₃O⁺–Ar, and the ν_f^I excitation tended to provide photofragment ions with a larger fraction of internal energy than the ν_b^I excitation. In marked contrast to H₃O⁺–Ar, the plots for H⁺(H₂O)₂–Ar were nearly identical within their experimental errors, indicating that the dissociation processes were independent of the excited modes (or of the excited H₂O subunits in the cluster). The possible origins of the mode dependence are discussed in the following sections.

Dissociation mechanism of H₃O⁺–Ar

Fig. 5a shows the energy diagram for the infrared photodissociation of H₃O⁺–Ar including the vibrational levels of the photofragment H₃O⁺ ion, which were reported previously.^94–97 In the energy range of the present experiment, vibrationally excited H₃O⁺ fragments in the umbrella (ν₂) and the bending (ν₄) states can be produced. The ± labels represent the splitting states of an inversion doublet, as is well-known in NH₃.⁹⁸

Fig. 5 (a) Energy diagram for the photodissociation of H₃O⁺–Ar. The vibrational energy levels of the fragment H₃O⁺ ion are taken from ref. 94–97. (b) Energy diagram for the photodissociation of H⁺(H₂O)₂–Ar. The fragment vibrational levels are estimated by the Beyer–Swinehart algorithm.

For the H₃O⁺–Ar system, several vibrational states related to the ν₂ and ν₄ modes of H₃O⁺ are energetically accessible. The situation is distinct from that in H₂O⁺–Ar where only the vibrationally ground state of H₂O⁺ can be produced as reported in a recent study,⁵³ though the geometrical features of these two systems are very similar. Experimentally, the entire E_t distributions for H₃O⁺–Ar are mostly within E_t/E_avl < 0.4 with the peaks at E_t/E_avl ∼ 0.02, while the plots for H₂O⁺–Ar exhibited broader distributions toward E_t/E_avl = 1 and peaked around E_t/E_avl ∼ 0.2. Considering that the vibrationally excited channels are available only for H₃O⁺–Ar, the smaller E_t fraction and deviation from the PST model for H₃O⁺–Ar could likely be explained by preferential deposition of E_avl into the H₃O⁺ vibrational energy.

The dissociation process that primarily produces vibrationally excited fragments is consistent with the energy-gap-law model.^99,100 The model proposes that, in the relaxation of excited vibrational states, the process involving a smaller change in the effective quantum numbers is more favorable. Therefore, according to this model, the vibrational energies in the excited OH stretching states can be more efficiently transferred into the intramolecular vibrational states (the ν₂ and/or ν₄ modes) than the highly excited rotational and translational states of H₃O⁺ corresponding to the intermolecular bending and stretching modes in H₃O⁺–Ar, respectively. Similar results conforming to the energy-gap law have been reported in infrared photodissociation studies for a variety of small neutral clusters.^{25–28,101,102}

It would be a straightforward assumption to attribute the difference in the E_t fractions between ν_b^I and ν_f^I seen in Fig. 4e to the geometrical nature of each vibrational mode. The ν_b^I excitation in the bound OH group seems to provide the energy into the dissociation coordinate more directly, resulting in a larger E_t. The ν_f^I excitation is conversely predicted to require an extensive energy redistribution into the intramolecular modes including ν₂ and ν₄ before the energy reaches the dissociation coordinate. Unlike the present H₃O⁺–Ar system, however, the E_t fractions for the bound and free OH excitations were reported to be quite similar in H₂O⁺–Ar.⁵³ Considering that no vibrationally excited state is available as the dissociative state in the case of H₂O⁺, the energetics of the accessible vibrational states of the fragment H₃O⁺ ion should also be important for interpreting the mode-dependent E_t fraction in H₃O⁺–Ar. In Fig. 5a, a qualitative difference can be found for the ν_b^I and ν_f^I excitations; that is, the ν₄^± exit channels are open only for the latter. Thus, the smaller E_t fraction for ν_f^I can reasonably be attributed to the production of the ν₄ excited H₃O⁺ fragments. In that case, ∼85% of E_avl would be deposited into the ν₄ vibration, giving rise to a slow component with E_t/E_avl < 0.15 for ν_f^I.

On the basis of the spectroscopic observations, ν₄ could be expected to be an efficient acceptance mode for the OH stretching vibrations in the present system. It has been recognized that Ar-tagged H₃O⁺ complexes exhibit strong Fermi resonance between the bound OH stretching fundamentals and the bending overtones.^79,103–105 A large Fermi coupling constant was reported also for the ν_f^I mode of H₃O⁺–Ar in a recent theoretical calculation.⁷⁹ The Fermi resonance is one of the anharmonic effects that plays an important role in the vibrational-energy-transfer processes¹⁰⁶ and may help with efficient relaxation from the ν_f^I state to the bending overtone states of H₃O⁺–Ar. After relaxation into the “doorway” overtone states of the bending mode, further energy redistribution should proceed for dissociation. Among those processes, if one quantum of the bending vibration of H₃O⁺–Ar is released into other degrees of freedom, including the intermolecular stretching mode, the consequent dissociation would be correlated with the ν₄^± exit channels shown in Fig. 5a. This is not the case in the ν_b^I excitation, since the ν₄ vibration should be completely relaxed to cause Ar dissociation by the excitation energy of ν_b^I. In conclusion, the ν_f^I excitation of H₃O⁺–Ar preferentially gives the ν₄ excited fragments resulting from the vibrational energy redistribution into the bending coordinate, which may be facilitated by the Fermi coupling, and this is a plausible origin of the smaller E_t fraction for the ν_f^I excitation.

It should be noted that the rest of the available energies for the ν₄⁺ and ν₄⁻ dissociation channels (358 and 290 cm⁻¹, respectively) are too small to explain the whole E_t distribution for the ν_f^I excitation. Therefore, the production of the ν₄^± excited fragments was not the exclusive dissociation pathway. From the structureless E_t distribution, the fractions into other dissociation channels associated with the fragment ν₂ vibration could not be identified experimentally. A more complete characterization of the dissociation processes must therefore await future studies, especially a theoretical investigation of the vibrational dynamics.

Dissociation mechanism of H⁺(H₂O)₂–Ar

The energy diagram for the H⁺(H₂O)₂–Ar dissociation is shown in Fig. 5b. The vibrational levels of the H⁺(H₂O)₂ fragment were calculated by the Beyer–Swinehart algorithm¹⁰⁷ using the theoretical harmonic vibrational frequencies at the MP2/aug-cc-pVTZ level. The diagram clearly displays a drastic increase in the vibrational density of states of the photofragment ion compared to H₃O⁺, which is mainly caused by the low-frequency intermolecular vibrations between the two H₂O subunits. The number of vibrational states reachable with the photon energy of the experiment was more than 100 times greater than that of H₃O⁺. The available fragment channels included the fundamentals from six H₂O–H⁺–H₂O intermolecular vibrations coupled with the umbrella motion (<600 cm⁻¹), one shared proton stretch (∼900 cm⁻¹), and four bending vibrations (1400–1700 cm⁻¹).

From the mode-independent E_t distributions (Fig. 4f) and the large number of vibrational states in the H⁺(H₂O)₂ moiety (Fig. 5b), one might expect a statistical-like behavior (i.e., complete IVR) in the H⁺(H₂O)₂–Ar dissociation process. However, the PST calculations did not reproduce the experimental E_t distributions, as shown in Fig. 4c and d. The observed energy release into the translational degree of freedom was smaller than in the statistical model, indicating a propensity for energy redistribution into the internal degrees of H⁺(H₂O)₂. Therefore, even in H⁺(H₂O)₂–Ar, the Ar dissociation upon the OH stretching excitation proceeded via a nonstatistical manner, probably associated with the energy-gap model.

The ν_b^II and ν_f^II modes of H⁺(H₂O)₂–Ar corresponded to the OH stretching vibrations of the Ar-tagged and untagged H₂O subunits, respectively. The absence of mode dependence in the E_t distribution thus suggested that the vibrational energy given by the infrared photon was likely delocalized over H₂O–H⁺–H₂O intermolecular bonds prior to the Ar dissociation. Consequently, the entire process can be summarized as the dissociation scheme in Fig. 6. The OH stretching excited states, ν_b^II and ν_f^II, were predicted to relax into a common intermediate state, where the vibrational energy was spread to the two H₂O subunits. Though the intermediate state could not be identified in the present experiment, a possible candidate for the acceptance mode is the bending vibration, in analogy with H₃O⁺–Ar discussed above. The H₂O–H⁺–H₂O intermolecular modes may be concomitantly excited in the intermediate state, promoting energy delocalization between the two H₂O molecules. In contrast, since the experimental E_t distribution did not coincide with the PST model, the energy randomization was not completed into all vibrational degrees including the H⁺(H₂O)₂–Ar intermolecular stretching coordinate. That is, the dissociation directly proceeded from the intermediate state (the top right of Fig. 6), while the statistical dissociation via complete IVR (the bottom right of Fig. 6) was unfavorable. The faster energy delocalization over the H₂O–H⁺–H₂O unit than the Ar intermolecular bond presumably originated from the ionic intermolecular bond involving the shared proton. The intermolecular interaction in H₂O–H⁺–H₂O was much greater than the charge-induced interaction with the Ar atom and thus provided the higher-frequency intermolecular modes that should be coupled more efficiently with the OH vibrations. The hierarchical manner in the vibrational energy redistribution has also been pointed out in previous gas-phase studies on neutral clusters.^15,108

Fig. 6 Dissociation scheme for H⁺(H₂O)₂–Ar upon the OH stretching excitation proposed in the present study. The ν_b^II and ν_f^II excited states relax into a common intermediate state (middle). The Ar dissociation proceeds prior to the complete IVR (complete energy randomization in the whole cluster), providing internally hot H⁺(H₂O)₂ fragments (top right). Statistical dissociation following the complete IVR is an unfavorable process (bottom right, broken arrows).

The stepwise relaxation processes of the OH vibrations of the protonated water clusters were observed in the solution phase. Previous pump–probe spectroscopic measurements on protonated water clusters including H⁺(H₂O)₂ in acetonitrile revealed that the OH vibrational energy is redistributed over the water clusters within a few hundred femtoseconds, and a further energy relaxation from the clusters into the solvent molecules is a slower process (>1 ps).^109,110 Thus, the gas-phase relaxation scheme in Fig. 6, which proposes an internally hot H⁺(H₂O)₂ intermediate and secondary energy transfer into the Ar dissociation coordinate, shares a common feature with the condensed phase, although the environments are very different.

It is also worth comparing the present system with the neutral water clusters investigated by Reisler and co-workers.^111,112 From the photofragment images upon the hydrogen-bonded OH stretching excitation, it was concluded that the dissociation of (H₂O)₂ was a nonstatistical process in accordance with the energy-gap law,¹¹¹ while that of (H₂O)₃ could be well characterized as a statistical dissociation.¹¹² As for the present ionic clusters, a statistical behavior did not appear even in H⁺(H₂O)₂–Ar, though the number of available fragment vibrational states was greater than that of (H₂O)₃. Thus, a transition to the statistical behavior in the H⁺(H₂O)_n–Ar system may occur at a larger size region. However, there is a difference in the structural motif between small clusters of (H₂O)_n and H⁺(H₂O)_n. The cyclic trimer structure of neutral (H₂O)₃,¹¹³ in which all the monomer subunits are bound with each other, could potentially facilitate efficient vibrational energy redistribution into the whole cluster through the intermolecular bonds. Such a concerted behavior of the monomer constituents in the cyclic structure may lead to the statistical dissociation unlike the chain-like H⁺(H₂O)₂–Ar. From this perspective, future imaging studies on ionic clusters of a different type of structural motif should provide deeper insights into the vibrational relaxation dynamics in intermolecular networks.

Conclusions

The dissociation processes of H₃O⁺–Ar and H⁺(H₂O)₂–Ar via mode-selective excitations of the OH stretching vibrations (ν_b and ν_f) were investigated using imaging apparatus for mass-selected ions. The obtained photofragment images provided information on the fragment translational energy distributions in the dissociation following vibrational relaxation. Irrespective of the excited vibrational modes, the translational energy releases were smaller than in the statistical PST predictions for both H₃O⁺–Ar and H⁺(H₂O)₂–Ar, which suggested that the production of vibrationally excited fragment ions was favorable in accordance with the energy-gap model. In H₃O⁺–Ar, the free OH stretching (ν_f^I) excitation resulted in a smaller translational energy fraction than in the bound OH stretch (ν_b^I). This mode-specific behavior could probably be attributed to the preferential energy flow from ν_f^I to the bending coordinates within the H₃O⁺ moiety, giving rise to bending excited H₃O⁺ that was not energetically accessible for the ν_b^I excitation. For H⁺(H₂O)₂–Ar, in contrast, the bound OH stretching mode (ν_b^II) of the Ar-tagged H₂O subunit and the free OH stretching mode (ν_f^II) of the untagged H₂O subunit exhibited identical translational energy releases. The Ar dissociation thus proceeded after energy delocalization between two H₂O subunits through the ionic intermolecular interaction of H⁺(H₂O)₂. On the other hand, a discrepancy between the experiment and the PST calculation indicated that energy randomization into all the vibrational modes including the intermolecular modes associated with Ar was not completed prior to dissociation.

The photodissociation imaging scheme for the ionic clusters does not need to employ any detection probe methods (e.g., REMPI) as for neutral clusters. Though the present scheme cannot achieve the state-selective detection of fragments, the imaging procedure with mass selection of targets still offers a complementary and universal way to investigate the size- and mode-specific dissociation dynamics of vibrationally excited cluster ions. Future imaging experiments using different tag atoms (different D₀ values) and deuterium isotopomers for tuning the vibrational levels would provide further information into the vibrational dynamics of H⁺(H₂O)_n.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Grant-in-Aid for Japan Society for the Promotion of Science (JSPS) Challenging Exploratory Research (No. 25620007). Y. I. and Y. N. acknowledge the Division for Interdisciplinary Advanced Research and Education (DIARE) of Tohoku University. All calculations were performed using Research Center for Computational Science, Okazaki, Japan (Project: 21-IMS-C054).

References

1. R. E. Miller, Science, 1988, 240, 447.
2. D. J. Nesbitt, Chem. Rev., 1988, 88, 843.
3. T. S. Zwier, Annu. Rev. Phys. Chem., 1996, 47, 205.
4. U. Buck and F. Huisken, Chem. Rev., 2000, 100, 3863.
5. E. J. Bieske and O. Dopfer, Chem. Rev., 2000, 100, 3963.
6. W. H. Robertson and M. A. Johnson, Annu. Rev. Phys. Chem., 2003, 54, 173.
7. N. R. Walker, R. S. Walters and M. A. Duncan, New J. Chem., 2005, 29, 1495.
8. J. M. Lisy, J. Chem. Phys., 2006, 125, 132302.
9. L. MacAleese and P. Maître, Mass Spectrom. Rev., 2007, 26, 583.
10. N. C. Polfer and J. Oomens, Mass Spectrom. Rev., 2009, 28, 468.
11. K. R. Asmis and D. M. Neumark, Acc. Chem. Res., 2012, 45, 43.
12. M. F. Vernon, J. M. Lisy, H. S. Kwok, D. J. Krajnovich, A. Tramer, Y. R. Shen and Y. T. Lee, J. Phys. Chem., 1981, 85, 3327.
13. M. F. Jarrold, A. J. Illies, N. J. Kirchner, W. Wagner-Redeker, M. T. Bowers, M. L. Mandich and J. L. Beauchamp, J. Phys. Chem., 1983, 87, 2213.
14. L. Oudejans and R. E. Miller, Annu. Rev. Phys. Chem., 2001, 52, 607.
15. Y. Yamada, Y. Katsumoto and T. Ebata, Phys. Chem. Chem. Phys., 2007, 9, 1170.
16. M. I. Lester and S. J. Klippenstein, Acc. Chem. Res., 2018, 51, 978.
17. K. Grygoryeva, J. Rakovský, O. Votava and M. Fárník, J. Chem. Phys., 2018, 149, 094303.
18. D. W. Chandler and P. L. Houston, J. Chem. Phys., 1987, 87, 1445.
19. A. J. R. Heck and D. W. Chandler, Annu. Rev. Phys. Chem., 1995, 46, 335.
20. P. L. Houston, Acc. Chem. Res., 1995, 28, 453.
21. M. N. R. Ashfold, N. H. Nahler, A. J. Orr-Ewing, O. P. J. Vieuxmaire, R. L. Toomes, T. N. Kitsopoulos, I. A. Garcia, D. A. Chestakov, S.-M. Wu and D. H. Parker, Phys. Chem. Chem. Phys., 2006, 8, 26.
22. M. N. R. Ashfold and D. H. Parker, Phys. Chem. Chem. Phys., 2014, 16, 381.
23. A. G. Suits, Rev. Sci. Instrum., 2018, 89, 111101.
24. G. Li, J. Parr, I. Fedorov and H. Reisler, Phys. Chem. Chem. Phys., 2006, 8, 2915.
25. A. K. Samanta, L. C. Ch’ng and H. Reisler, Chem. Phys. Lett., 2013, 575, 1.
26. A. K. Samanta, G. Czakó, Y. Wang, J. S. Mancini, J. M. Bowman and H. Reisler, Acc. Chem. Res., 2014, 47, 2700.
27. A. K. Samanta, Y. Wang, J. S. Mancini, J. M. Bowman and H. Reisler, Chem. Rev., 2016, 116, 4913.
28. A. S. Case, C. G. Heid, S. H. Kable and F. F. Crim, J. Chem. Phys., 2011, 135, 084312.
29. K. M. Kapnas and C. Murray, J. Chem. Phys., 2020, 152, 194301.
30. B. Zhang, Y. Yu, Z. Zhang, Y. Y. Zhang, S. Jiang, Q. Li, S. Yang, H. S. Hu, W. Zhang, D. Dai, G. Wu, J. Li, D. H. Zhang, X. Yang and L. Jiang, J. Phys. Chem. Lett., 2020, 11, 851.
31. B. Zhang, Y. Yu, Y. Y. Zhang, S. Jiang, Q. Li, H. S. Hu, G. Li, Z. Zhao, C. Wang, H. Xie, W. Zhang, D. Dai, G. Wu, D. H. Zhang, L. Jiang, J. Li and X. Yang, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 15423.
32. G. Li, Y. Y. Zhang, Q. Li, C. Wang, Y. Yu, B. Zhang, H. S. Hu, W. Zhang, D. Dai, G. Wu, D. H. Zhang, J. Li, X. Yang and L. Jiang, Nat. Commun., 2020, 11, 5449.
33. Y. Y. Zhang, C. Wang, G. Li, X. Zang, Y. Yu, H. S. Hu, J. Yang, W. Zhang, D. Dai, G. Wu, L. Jiang, X. Yang and J. Li, Cell Rep. Phys. Sci., 2022, 3, 100748.
34. I. León, R. Montero, A. Longarte and J. A. Fernández, J. Phys. Chem. Lett., 2021, 12, 1316.
35. J. A. Maner, D. T. Mauney and M. A. Duncan, J. Phys. Chem. Lett., 2015, 6, 4493.
36. K. Okutsu, Y. Nakashima, K. Yamazaki, K. Fujimoto, M. Nakano, K. Ohshimo and F. Misaizu, Rev. Sci. Instrum., 2017, 88, 053105.
37. M. D. Johnston, W. L. Pearson, G. Wang and R. B. Metz, Rev. Sci. Instrum., 2018, 89, 014102.
38. Z. Hua, S. Feng, Z. Zhou, H. Liang, Y. Chen and D. Zhao, Rev. Sci. Instrum., 2019, 90, 013101.
39. B. M. Rittgers, D. Leicht and M. A. Duncan, J. Phys. Chem. A, 2020, 124, 9166.
40. N. J. Dynak, B. M. Rittgers, J. E. Colley, D. J. Kellar and M. A. Duncan, J. Phys. Chem. Lett., 2022, 13, 4786.
41. B. M. Rittgers, J. H. Marks, D. J. Kellar and M. A. Duncan, J. Chem. Phys., 2022, 157, 114302.
42. Y. Nakashima, K. Okutsu, K. Fujimoto, Y. Ito, M. Kanno, M. Nakano, K. Ohshimo, H. Kono and F. Misaizu, Phys. Chem. Chem. Phys., 2019, 21, 3083.
43. Y. Ito, Y. Nakashima, K. Okutsu, M. Nakano, K. Ohshimo and F. Misaizu, Chem. Phys. Lett., 2020, 739, 37022.
44. Y. Nakashima, Y. Ito, K. Okutsu, M. Nakano and F. Misaizu, Phys. Chem. Chem. Phys., 2020, 22, 16926.
45. Y. Ito, Y. Nakashima, K. Okutsu, M. Nakano and F. Misaizu, J. Chem. Phys., 2022, 157, 124304.
46. M. D. Johnston, S. P. Lockwood and R. B. Metz, J. Chem. Phys., 2018, 148, 214308.
47. M. D. Johnston, M. R. Gentry and R. B. Metz, J. Phys. Chem. A, 2018, 122, 8047.
48. S. P. Lockwood, T. Chunga and R. B. Metz, J. Phys. Chem. A, 2021, 125, 7425.
49. H. Liang, Z. Zhou, Z. Hua, Y. Zhao, S. Feng, Y. Chen and D. Zhao, J. Phys. Chem. A, 2019, 123, 4609.
50. Z. Zhou, H. Liang, Z. Hua, S. Feng, D. Zhao and Y. Chen, J. Chem. Phys., 2019, 150, 226101.
51. Z. Zhou, S. Feng, Z. Hua, Z. Li, Y. Chen and D. Zhao, J. Chem. Phys., 2020, 152, 134304.
52. Z. Hua, Y. Zhao, G. Hu, S. Feng, Q. Zhang, Y. Chen and D. Zhao, J. Phys. Chem. Lett., 2021, 12, 4012.
53. Y. Nakashima, Y. Ito, M. Kominato, K. Ohshimo and F. Misaizu, J. Chem. Phys., 2021, 154, 174301.
54. H. A. Schwarz, J. Chem. Phys., 1977, 67, 5525.
55. M. Okumura, L. I. Yeh, J. D. Myers and Y. T. Lee, J. Chem. Phys., 1986, 85, 2328.
56. L. Yeh, M. Okumura, J. D. Myers, J. M. Price and Y. T. Lee, J. Chem. Phys., 1989, 91, 7319.
57. M. Okumura, L. I. Yeh, J. D. Myers and Y. T. Lee, J. Phys. Chem., 1990, 94, 3416.
58. L. I. Yeh, Y. T. Lee and J. T. Hougen, J. Mol. Spectrosc., 1994, 164, 473.
59. J. C. Jiang, Y. S. Wang, H. C. Chang, S. H. Lin, Y. T. Lee, G. Niedner-Schatteburg and H. C. Chang, J. Am. Chem. Soc., 2000, 122, 1398.
60. K. R. Asmis, N. L. Pivonka, G. Santambrogio, M. Brummer, M. Kaposta, D. M. Neumark and L. Wöste, Science, 2003, 299, 1375.
61. Y. S. Wang, C. H. Tsai, Y. T. Lee, H. C. Chang, J. C. Jiang, O. Asvany, S. Schlemmer and D. Gerlich, J. Phys. Chem., 2003, 107, 4217.
62. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Science, 2004, 304, 1134.
63. J.-W. Shin, N. I. Hammer, E. G. Diken, M. A. Johnson, R. S. Walters, T. D. Jaeger, M. A. Duncan, R. A. Christie and K. D. Jordan, Science, 2004, 304, 1137.
64. T. D. Fridgen, T. B. McMahon, L. MacAleese, J. Lemaire and P. Maitre, J. Phys. Chem. A, 2004, 108, 9008.
65. J. M. Headrick, J. C. Bopp and M. A. Johnson, J. Chem. Phys., 2004, 121, 11523.
66. C. Lin, C. Wu, Y. Wang, Y. T. Lee, H. Chang, J. Kuo and M. L. Klein, Phys. Chem. Chem. Phys., 2005, 7, 938.
67. C. Wu, C. Lin, H. Chang, J. Jiang, J. Kuo and M. L. Klein, J. Chem. Phys., 2005, 122, 074315.
68. J. M. Headrick, E. G. Diken, R. S. Walters, N. I. Hammer, R. A. Christie, J. Cui, E. M. Myshakin, M. A. Duncan, M. A. Johnson and K. D. Jordan, Science, 2005, 308, 1765.
69. N. I. Hammer, E. G. Diken, J. R. Roscioli, M. A. Johnson, E. M. Myshakin, K. D. Jordan, A. B. McCoy, X. Huang, J. M. Bowman and S. Carter, J. Chem. Phys., 2005, 122, 244301.
70. K. Mizuse, A. Fujii and N. Mikami, J. Chem. Phys., 2007, 126, 231101.
71. L. R. McCunn, J. R. Roscioli, M. A. Johnson and A. B. McCoy, J. Phys. Chem. B, 2008, 112, 321.
72. G. E. Douberly, R. S. Walters, J. Cui, K. D. Jordan and M. A. Duncan, J. Phys. Chem. A, 2010, 114, 4570.
73. K. Mizuse, N. Mikami and A. Fujii, Angew. Chem., Int. Ed., 2010, 49, 10119.
74. K. Mizuse and A. Fujii, Phys. Chem. Chem. Phys., 2011, 13, 7129.
75. K. Mizuse and A. Fujii, J. Phys. Chem. Lett., 2011, 2, 2130.
76. K. Mizuse and A. Fujii, J. Phys. Chem. A, 2012, 116, 4868.
77. K. Mizuse and A. Fujii, Chem. Phys., 2013, 419, 2.
78. J. A. Fournier, C. J. Johnson, C. T. Wolke, G. H. Weddle, A. B. Wolk and M. A. Johnson, Science, 2014, 344, 1009.
79. Q. R. Huang, T. Nishigori, M. Katada, A. Fujii and J. L. Kuo, Phys. Chem. Chem. Phys., 2018, 20, 13836.
80. D. C. McDonald II, J. P. Wagner, A. B. McCoy and M. A. Duncan, J. Phys. Chem. Lett., 2018, 9, 5664.
81. NIST Mass Spectrometry Data Center, William E. Wallace, director, “Infrared Spectra” in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 2022, p. 20899.
82. G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989.
83. V. Papadakis and T. N. Kitsopoulos, Rev. Sci. Instrum., 2006, 77, 083101.
84. S. Trippel, M. Stei, R. Otto, P. Hlavenka, J. Mikosch, C. Eichhorn, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, J. Phys.: Conf. Ser., 2009, 194, 012046.
85. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221.
86. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
87. C. E. Klots, J. Phys. Chem., 1971, 75, 1526.
88. W. J. Chesnavich and M. T. Bowers, J. Am. Chem. Soc., 1976, 98, 8301.
89. R. N. Zare, Mol. Photochem., 1972, 4, 1.
90. R. N. Zare, Ber. Bunsenges. Phys. Chem., 1982, 86, 422.
91. M. J. Weida and C. S. Parmenter, J. Chem. Phys., 1997, 107, 7138.
92. S. Borocci, P. Cecchi, M. Giordani and F. Grandinetti, Eur. J. Mass Spectrom., 2015, 21, 171.
93. W. J. Chesnavich and M. T. Bowers, J. Am. Chem. Soc., 1977, 99, 1705.
94. D. Liu, N. N. Haese and T. J. Oka, Chem. Phys., 1985, 82, 5368.
95. D. Liu and T. Oka, Phys. Rev. Lett., 1985, 54, 1787.
96. M. Gruebele, M. Polak and R. J. Saykally, J. Chem. Phys., 1987, 87, 3347.
97. X. Huang, S. Carter and J. M. Bowman, J. Phys. Chem. B, 2002, 106, 8182.
98. G. Herzberg, Molecular Spectra and Molecular Structure, Vol. II. Infrared and Raman Spectra of Polyatomic Molecules, Krieger, Malabar, 1991.
99. J. A. Beswick and J. Jortner, J. Chem. Phys., 1980, 74, 6725.
100. G. E. Ewing, J. Phys. Chem., 1987, 91, 4662.
101. R. E. Miller, Acc. Chem. Res., 1990, 23, 10.
102. H. Reisler, Annu. Rev. Phys. Chem., 2009, 60, 39.
103. A. B. McCoy, T. L. Guasco, C. M. Leavitt, S. G. Olesen and M. A. Johnson, Phys. Chem. Chem. Phys., 2012, 14, 7205.
104. J. W. Li, M. Morita, K. Takahashi and J. L. Kuo, J. Phys. Chem. A, 2015, 119, 10887.
105. J. A. Tan, J. W. Li, C. Chiu, H. Y. Liao, H. T. Huynh and J. L. Kuo, Phys. Chem. Chem. Phys., 2016, 18, 30721.
106. G. E. Ewing, J. Phys. Chem., 1986, 90, 1790.
107. T. Beyer and D. Swinehart, Commun. ACM, 1973, 16, 379.
108. D. Kwasniewski, M. Butler and H. Reisler, Phys. Chem. Chem. Phys., 2019, 21, 13968.
109. N. Ottosson, L. Liu and H. J. Bakker, J. Phys. Chem. B, 2016, 120, 7154.
110. F. Dahms, R. Costard, E. Pines, B. P. Fingerhut, E. T. J. Nibbering and T. Elsaesser, Angew. Chem., Int. Ed., 2016, 155, 10600.
111. L. C. Ch’ng, A. K. Samanta, G. Czakó, J. M. Bowman and H. Reisler, J. Am. Chem. Soc., 2012, 134, 15430.
112. L. C. Ch’ng, A. K. Samanta, Y. Wang, J. M. Bowman and H. Reisler, J. Phys. Chem. A, 2013, 117, 32.
113. F. N. Keutsch, J. D. Cruzan and R. J. Saykally, Chem. Rev., 2003, 103, 2533.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the improvement in the imaging apparatus; Results of the spectral simulations for the ν_f^I band of H₃O⁺-Ar; normal mode descriptions of the ν_b^I and ν_f^I modes in H₃O⁺-Ar and H⁺(H₂O)₂-Ar. See DOI: https://doi.org/10.1039/d3cp00469d

---