 Open Access Article
Open Access ArticleRocking motion in solid proteins studied by the 15N proton-decoupled R1ρ relaxometry†
Alexey
Krushelnitsky
 *,
Günter
Hempel
,
Hannes
Jurack
and
Tiago Mendes
Ferreira
*,
Günter
Hempel
,
Hannes
Jurack
and
Tiago Mendes
Ferreira

Institut für Physik, Martin-Luther-Universität Halle-Wittenberg, Betty-Heimann-Str. 7, 06120, Halle (Saale), Germany. E-mail: krushelnitsky@physik.uni-halle.de
First published on 1st June 2023
Abstract
Recently it has been revealed that proteins in solid samples undergo slow overall rocking. The parameters of this motion depend on intermolecular interactions. Therefore, the characterization of the rocking motion enables one to investigate protein–protein interactions. NMR R1ρ relaxometry is the most suitable tool to study slow molecular motions. However, the time scale of the rocking motion is on the edge of the dynamics window of the standard R1ρ experiment, precluding the R1ρ data analysis from being precise and reliable. In this work, we apply a modified R1ρ relaxation method to characterize the slow motion in solids with much higher precision and reliability. The modification is the simultaneous use of a strong 1H-CW pulse and a weak/moderate 15N spin-lock pulse. We demonstrate theoretically and experimentally that under this condition, R1ρ decays have a significantly better signal-to-noise ratio and a much shorter “dead time” caused by the initial oscillations compared to the conventional R1ρ experiment. Moreover, the proton-decoupled R1ρ's can be measured at a much smaller difference between the spin-lock and MAS frequencies; thus, much slower molecular motions can be sampled. The proton decoupling during the 15N spin-lock pulse also suppresses the interfering coherent spin–spin relaxation pathway at low spin-lock fields, which overlaps the Bloch–McConnell (chemical exchange) range of R1ρ dispersions. The proton-decoupled and standard R1ρ experiments were used to study the rocking motion of 15N,2H-enriched protein GB1 in two solid forms, microcrystals and lyophilized amorphous powder. The most striking finding is that the correlation function of this motion consists of two components with very different correlation times, 2–20 μs and a few hundred μs. The rocking motion parameters in microcrystals and powder are quite different, revealing the distinct nature of inter-protein interactions in these two samples.
Introduction
R 1ρ-relaxometry is a powerful NMR technique that enables a detailed study of molecular dynamics in the microsecond time scale.1–7 Unlike measurements of the motionally averaged dipolar, quadrupolar or chemical shift anisotropy (CSA) interactions, the relaxation methods allow obtaining both amplitudes and correlation times of molecular motions. This is why the relaxation experiments are more informative, although more time-consuming than many other experimental approaches. The relaxation rate is proportional to the spectral density function J(ω), where ω/2π is the resonance (for the case of R1) or spin-lock (for the case of R1ρ) frequency. To get more exact information on the correlation function of motion, one has to measure the relaxation rates in a wide range of ω. There are, however, some natural limitations in varying ω that are difficult to circumvent. Large ω values in R1ρ-experiments are limited by the hardware (amplifiers and probes) and the sample heating effect. On the other hand, the spin-lock field in static experiments cannot be set to values lower or comparable to the local field since the relaxation, in this case, is dependent on both spin-lock and local fields, and the data analysis would be more difficult and ambiguous. Under magic angle spinning (MAS), the R1ρ relaxation rate corresponding to the heteronuclear dipolar and CSA relaxation mechanisms is proportional to the combination of the spectral density functions J(ωSL ± ωMAS) and J(ωSL ± 2ωMAS),2,8,9 where ωSL/2π and ωMAS/2π are the spin-lock and MAS frequencies. Setting ωSL = ωMAS or ωSL = 2ωMAS (rotary resonance conditions, at which the anisotropic interactions are recoupled) unfortunately does not allow measuring J(0), that is the low-frequency limit of the spectral density function. In this case, the amplitude of the relaxation decay becomes zero, and the amplitude of the initial transient oscillations of the decay (see detailed discussion below) becomes so large that the reliable determination of the relaxation rate in the vicinity of the rotary resonance condition is simply impossible.10In this work, we apply a modification of the R1ρ experiment to suppress these interfering effects and to observe slower motions that are not possible to observe using only a standard conventional R1ρ pulse sequence. This modification is a high-power proton decoupling during the X-channel spin-lock pulse (Fig. 1). This approach was first suggested about 20 years ago.11 Effectively, the proton decoupling can “switch off” the dipolar relaxation mechanism of slow molecular motions and thus, the R1ρ relaxation is caused dominantly by the CSA mechanism. The proton decoupling also suppresses the interfering coherent spin–spin relaxation mechanism,12 and thus, the relaxation rates can be measured and rigorously analysed at small spin-lock fields, which is impossible using a standard R1ρ experiment. This method was applied in some previous studies of biomolecular dynamics,13,14 however, this was done only in a phenomenological fashion.
Here we present an analytical and numerical description of this experiment and demonstrate its advantages by applying it to studying a specific type of molecular mobility – rocking motions of proteins in solid samples. Proteins in solid state (e.g. in microcrystals) are not rigidly fixed by inter-molecular contacts; they undergo restricted motion as a whole. This kind of protein dynamics was reported for the first time by Paul Schanda and co-workers,15 and then this observation was confirmed in a few subsequent studies.10,16,17 Using standard 15N R1ρ experiments, the angular amplitude and the time scale of the rocking motion were estimated to be only few degrees and few tens microseconds, respectively.10 These numbers are however not precise since this motional time scale is on the edge of the dynamic window of the standard R1ρ experiment. As shown below, the proton-decoupled 15N R1ρ experiment enables to extend this window towards slower motions. This approach is demonstrated in the comparative experimental study of the same protein (GB1) in two different solid forms – microcrystals and lyophilized amorphous powder. The parameters of the rocking motion are obviously determined by the strength and nature of the inter-protein interactions. Protein globules in these two samples have rather different intermolecular contacts. Microcrystals contain a large amount of solvent, protein globules are separated by a hydration layer, and they all have native (or very close to native) tertiary structure. In dehydrated amorphous powder, protein structures are distorted by unnatural both intra- and inter-molecular electrostatic interactions and hydrogen bonds network since solvent molecules do not saturate hydrophilic and H-bond sites.18,19 One may therefore expect that the rocking motion parameters in these two samples are different, and we aimed to investigate this quantitatively.
Experimental details
Samples
Uniformly 15N,2H-enriched GB1 microcrystalline protein was purchased from Giotto Biotech, Italy. The sample packed in a 3.2 mm rotor was the same sample used in our previous work.10 It contains ∼20% of back-exchanged protons at labile sites. Partial back-exchange of labile protons is a compromise between suppressing proton-driven spin diffusion and keeping the NMR signal at a reasonable level. The lyophilized protein sample was prepared by dissolving 15N,2H-enriched protein (also purchased from Giotto Biotech) in a mixture of 20% H2O–80% D2O at a concentration of 5% by weight and subsequent lyophilization. The dissolution – lyophilization cycle was repeated twice. After that, the powder was packed in a 3.2 mm rotor and kept at room temperature under vacuum for three days to ensure the sample had minimum amount of water molecules. Then the rotor was sealed with a drive cap. The microcrystalline and amorphous samples were stored in a fridge at +5 C and −20 C, respectively.NMR experiments
The experiments were conducted on a Bruker Avance 600 spectrometer using a 3.2 mm E-free MAS probe. Unlike our previous publication,10 in this work, we observe the 15N signal directly, without indirect proton detection. Proton detection has, of course, better signal-to-noise ratio, however, for the 15N R1ρ experiment, it has the following disadvantage. The proton spectrum of the microcrystalline sample has two quite intensive peaks corresponding to residual solvent protons. These peaks are supposed to be suppressed by proper phase cycling. However, this suppression is not perfect; there are always certain distortions of the baseline around the solvent peaks. These distortions do not pose any problem if one aims at observing a spectrum. However, they hamper precise measurements of the signal intensity of the spectrum lines that are not far away from the solvent peaks. For different 15N spin-lock pulse lengths, these distortions are not uniform; thus, they induce additional error scatter of 15N R1ρ relaxation decays. This scatter nullifies the advantage of indirect proton detection. As for the lyophilized sample, there is no intensive solvent peak in the proton spectrum, but the proton line is wider than the nitrogen one; again, we saw no significant advantage of indirect proton detection. On top of that, direct 15N detection enables filtering out the Lys side chain peaks, which is impossible using 1D proton detection. In a few cases, we have compared the R1ρ decays measured using 15N and 1H detection, the decays look very similar, but 15N detection provides a somewhat better signal-to-noise ratio. Thus, all the relaxation experiments presented below were conducted using the pulse sequence shown in Fig. 1. Prior to the repetition delay, we applied the compensating spin lock/decoupling pulse, the duration of which is a difference between the maximum spin-lock used in the experiments and the current spin-lock field (not shown in Fig. 1). This was done to keep the duty cycle the same for all durations of the spin-lock pulses.The proton decoupling during the 15N spin-lock pulse may cause additional sample heating, especially in samples with high ionic strength. Although this heating effect is not much different from that caused by proton decoupling during FID acquisition, it is advisable to control the sample temperature and/or to take measures against it. In our experiments, heating was practically negligible because of the usage of the E-free probe. The details of measuring the heating effect are presented in ESI.†
Fig. 2 shows 1D 15N spectra for two samples. The powder spectrum reveals no narrow lines because proteins in the amorphous state have a distribution of conformations caused by inter-protein interactions, which leads to a heterogeneous distribution of chemical shifts. Since we look at the overall motion of protein globules, detection of 2D 15N–1H correlation site-resolved spectra is not helpful; for the lyophilized sample it is not possible anyway. Thus, all the experiments were conducted in 1D mode, and for plotting the relaxation decays, the integral intensity (area) of the spectrum in the range 95–140 ppm was used. All the R1ρ experiments were performed at a MAS rate of 18 kHz. The temperature calibration of the MAS probe was performed using a MAS rotor with methanol. Typical values of the experimental parameters: CP contact time 1.5 ms, 1H π/2 pulse 2.8 μs, acquisition time 12 ms and 25 ms for the lyophilized and microcrystalline samples, respectively. 15N spin-lock power was calibrated using the nutation experiment with proton decoupling during the 15N pulse. Proton decoupling is necessary to avoid the influence of the 15N–1H dipolar coupling on the nutation curve. The spin-lock frequency must be calibrated as precise as possible since R1ρ dispersion curves may have a steep dependence, see below. While measuring standard R1ρ (i.e. without the proton irradiation during the 15N spin-lock pulse), a 1H π-pulse was applied in the middle of the 15N spin-lock pulse. This was done to avoid the dipolar-CSA cross-correlation effect.20
 | ||
| Fig. 2 15N CP MAS spectra of two GB1 samples. The processing was performed using Topspin software with Lorenzian line broadening of 20 Hz. | ||
The motionally averaged 15N–1H dipolar couplings were measured using the R-PDLF sequence21 under magic angle spinning of 10 kHz. The 1H to 15N magnetization transfer step was done using a cross-polarization transfer with a contact time of 50 μs. Such short CP time ensures that the interaction of only covalently bound 15N–1H pairs is observed. R1871 recoupling blocks were used with π-pulses having a length of 5.55 microseconds. The indirect time increments used were equal to 22.22 microseconds; 64 points were measured in the indirect dimension. For the determination of the dipolar coupling, the dipolar modulation measured was Fourier transformed. The 15N–1H dipolar coupling was calculated by dividing the dipolar splitting obtained by the scaling factor 0.315. The projections of the 2D Fourier-transformed spectra for two samples and different temperatures are presented in the ESI.†
Numerical simulations
The numerical simulations of the 15N R1ρ decays were performed using the Spinach software library for MATLAB.22 It enables computationally efficient Liouville space simulations by using MATLAB's efficient handling of sparse matrices. Spinach's primary strength is to generate low-dimensional matrix representations for Liouville space operators and state vectors. This reduction of the problem dimension does not require extensive polynomial scaling of a computational cost with an increasing number of spins, which is a major advantage over e.g., SIMPSON.Our R1ρ simulation contains several loops over different parameters. From the inside out, they are iterated in the following order: first, the time domain is rasterized via the Spinach evolution() method. Second, the individual 15N/13C spin-lock and simultaneous 1H decoupling pulses are simulated for every rotor period. Finally, the duration of the 1H decoupling pulses and the power levels of the 15N/13C spin-lock and the 1H decoupling pulses can be varied. The results are stored in the form of a multidimensional density matrix trajectory. For every set of parameters, the observable magnetization in the dependence of the spin-lock pulse duration was saved to an output file. The powder average is calculated via singlerot() in the lab frame, so the Fokker–Planck algorithm is utilized. A double-rotating frame transformation is performed for both spin types. Our code enables not only CW 1H decoupling but also rotor synchronised pulsing with variable number and duration of the pulses per one rotor period. In this work however, only the CW mode was used. The Spinach simulation is split into two separate files: one input and one simulation file. This has been done in accordance to Spinach simulation examples. The code is presented in the ESI.†
Data analysis
Relaxation decays
A remarkable feature of R1ρ relaxation decays is initial transient oscillations,10,12 which appear if the spin-lock and local fields have comparable values. The nature of these oscillations can be explained qualitatively as follows. The local field components perpendicular to the spin-lock field cause precession of the magnetization vector around the spin-lock axis. Such precession manifests itself as oscillations on the relaxation decay. Under MAS, the amplitude of these oscillations increases upon approaching the rotary resonance condition (spin-lock and MAS frequencies are the same). This is illustrated by Fig. 3, which presents simulated relaxation decays at several spin-lock frequencies.In the standard experiment (i.e. without 1H decoupling), the amplitude of the oscillations increases as the difference between the MAS and spin-lock frequencies decreases. These oscillations comprise a “dead time” of the R1ρ decay. The mean relaxation rate of a multiexponential decay is the initial slope.10,23 If the initial slope is hidden by the oscillations, it cannot be determined from an experimental decay. As demonstrated by the right panel of Fig. 3, proton decoupling almost completely suppresses these oscillations. Fig. 4 presents examples of the R1ρ decays measured with and without proton pulse during the 15N spin-lock. Because of the B1-field inhomogeneity, the initial oscillations of the experimental decays vanish much faster than those of the simulated ones.10 Proton decoupling, as demonstrated by Fig. 4, also decreases the amplitude of the initial oscillations and hence, makes the “dead time” shorter. Still, it cannot suppress those entirely since it does not affect CSA.
Another significant effect of the proton decoupling is the increased normalized amplitude of the relaxation decay denoted in Fig. 4 as Ad. Fig. 5 shows the decay amplitude Ad as a function of the spin-lock field for the standard and proton-decoupled R1ρ experiments. It is seen that proton decoupling significantly increases the signal-to-noise ratio of the relaxation measurements, especially at small differences between the spin-lock and MAS frequencies. The initial oscillations and low decay amplitude prevent reliable R1ρ measurements at small difference |ωMAS − ωSL| for the standard experiment. For this reason, we measured standard R1ρ up to the spin-lock 15 kHz that is, the minimum difference between MAS and spin-lock frequencies was 3 kHz. For the proton-decoupled experiment, we measured R1ρ up to the spin-lock 17 kHz. In this case, the difference |ωMAS − ωSL| was three times less, which enables sampling significantly slower motions. Decreasing this frequency difference has decisive importance, as will be demonstrated below.
 | ||
| Fig. 5 Amplitude decay Ad (see Fig. 4) as a function of the spin-lock field for the standard (solid circles) and proton-decoupled (open circles) relaxation experiments. The experiments were performed on the lyophilized powder sample. The experimental error corresponds to the size of the circles. | ||
The mean relaxation rates R1ρ (i.e. the initial slope) were determined by fitting the decays using multi-exponential formula, the details are presented in ESI.†
Analytical formula for the hetero-nuclear dipolar relaxation mechanism of the proton-decoupled R1ρ
The formulae for the dipolar and CSA relaxation mechanisms of the standard R1ρ rate were derived previously:2,9,24 | (1) |
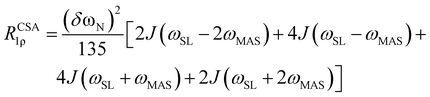 | (2) |
The proton decoupling during spin-lock does not affect RCSA1ρ, only Rdip1ρ, eqn (1), should contain one more parameter, the proton decoupling frequency ωH. This formula was derived by us analytically; see details in ESI.† It looks as
 | (3) |
It is seen that if ωH = 0, then eqn (3) converts to eqn (1). Eqn (3) corresponds to the first part of eqn (S54) (ESI†) that is the spin-lattice relaxation of 15N nuclei. In general, one has to consider the cross-relaxation rate between 15N and 1H (the second part of eqn (S54), ESI†). If the proton pulse is however much stronger than the 15N spin-lock pulse and MAS rate (ωH ≫ ωSL, ωMAS), then the cross-relaxation rate is negligible, which directly follows from eqn (S53) (ESI†). Such inequality also prevents the cross-polarisation between 15N and 1H since the parameters ωH, ωSL and ωMAS are far away from the Hartmann–Hahn match condition. In our experiments, we always kept ωH/2π equal to 100 kHz.
To check the validity of eqn (3), we performed Spinach simulations of the proton-decoupled R1ρ experiment. Fig. 6 compares analytical (eqn (3)) and numerical simulations of the relaxation rate Rdip1ρ as a function of the motional correlation time. The spectral density function in the analytical calculations (eqn (3)) was used in the form
 | (4) |
 | ||
| Fig. 6 Comparison of the analytical (eqn (3), dashed curves) and Spinach-simulated (symbols) dipolar relaxation rates at different strengths of the proton decoupling pulse (indicated in the figure) and correlation times. Numerical simulations were performed for the two-site jumps of the 15N–1H vector. The angle between two directions (sites) of the 15N–1H vector 16°, this corresponds to the order parameter S2 = 0.943. MAS 18 kHz, 15N spin-lock 8 kHz, 15N–1H distance 1.02 Å. | ||
 | ||
| Fig. 7 The ratio of the proton-decoupled R1ρ to the standard R1ρ as a function of the correlation time. The Spinach-simulated relaxation rate values are taken from Fig. 6. | ||
HORROR and B1 field inhomogeneity
It is already known that while measuring 15N R1ρ in proteins under MAS, one has to avoid the so-called HORROR condition25 that occurs when spin-lock frequency equals half of the MAS frequency.3,10 At this condition, the homonuclear 15N–15N dipolar interaction is recoupled. This interaction is too weak compared to the 15N–1H coupling and does not contribute to the relaxation rate. However, it induces similar oscillations in the initial part of the relaxation decay as the ones considered above. Since the amplitude and the frequency of these oscillations are small, they extend to longer times increasing the “dead time” of the decay. To quantify this effect, we conducted Spinach R1ρ relaxation simulations in the vicinity of the HORROR condition for the 15N–1H spin pair and for a system of four nuclei, one 1H and three 15Ns. The results of these simulations are shown in Fig. 8. | ||
| Fig. 8 15N dipolar R1ρ (without proton decoupling) simulations as function of the spin-lock frequency in the vicinity of the HORROR condition. Dashed line – analytical simulation using eqn (1) and spectral density in the form of eqn (4), symbols – Spinach simulations, that were performed for three different nuclei systems indicated in the figure. N–H distance in all cases was 1.02 Å. Parameters of the simulations: MAS 18 kHz, 2 site jumps with the angular amplitude 6° (S2 = 0.9918) and correlation time 10.8 μs. 4-Nuclei systems are assumed to be rigid, during the jumps, they rotate as a whole around the axis perpendicular to the plane of the structures. In the 4-nuclei systems, the signal of only central 15N nucleus was observed. Thin lines indicate the phenomenological description of the HORROR peak as described in the text. | ||
As it is seen, at typical 15N–15N distances in a polypeptide chain, the 15N–15N dipolar coupling causes the appearance of a spurious narrow peak in the R1ρ dispersion at the HORROR condition. An analytical description of this peak is hardly possible since the determination of the initial slope (i.e. mean relaxation rate) from fitting a slowly oscillating decaying function is uncertain. Thus, the relaxation rates within the HORROR point vicinity may have only approximate values and cannot be attributed to the relaxation itself. These values are distorted, and they should not be analysed in terms of dynamic parameters. We described the HORROR peak (shown by thin solid lines in Fig. 8) by a phenomenological function
 | (5) |
The experimental data (Fig. 9) also reveal the HORROR peak, but it is much wider than in the case of the numerical simulations. The source of this discrepancy is readily understood if one considers the RF field inhomogeneity. In practice, a single R1ρ experiment will never relate to a single spin-lock frequency but to a distribution that depends on the coil and the occupied volume by the sample in the rotor. To describe the R1ρ dispersion in this case, one needs to use the distribution function:
 | (6) |
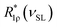 is the mean relaxation rate averaged over a distribution of the spin-lock frequencies, R1ρ(ν) is the sum of the rates determined by eqn (2), (3) and (5), Pinhom(νSL,ν) is the function describing the distribution of the spin-lock frequencies at a certain mean spin-lock frequency νSL. From Fig. 9 it is seen that the distribution function Pinhom(νSL,ν) is highly asymmetric. To describe the data in Fig. 9, we used the truncated Gaussian distribution function, i.e. we assumed the integration limits “min” and “max” in eqn (6) to be unequally spaced with respect to νSL. Then the distribution function can be expressed as
is the mean relaxation rate averaged over a distribution of the spin-lock frequencies, R1ρ(ν) is the sum of the rates determined by eqn (2), (3) and (5), Pinhom(νSL,ν) is the function describing the distribution of the spin-lock frequencies at a certain mean spin-lock frequency νSL. From Fig. 9 it is seen that the distribution function Pinhom(νSL,ν) is highly asymmetric. To describe the data in Fig. 9, we used the truncated Gaussian distribution function, i.e. we assumed the integration limits “min” and “max” in eqn (6) to be unequally spaced with respect to νSL. Then the distribution function can be expressed as | (7) |
 | ||
| Fig. 9 Experimental R1ρ dispersions measured in two GB1 samples within the vicinity of the HORROR condition. Solid and open symbols – standard and proton-decoupled (proton decoupling 100 kHz) R1ρ rates, respectively. Red lines – simulated dispersions assuming no B1 inhomogeneity. These curves were calculated using eqn (1) and (5). Spectral density function in eqn (1) was used in the form of eqn (4), order parameter and the correlation time were adjusted so that the simulated lines coincide with the experimental data on the edges of the HORROR peaks. Blue lines – dispersions simulated using eqn (6). The height of the HORROR peak (parameter H in eqn (5)) was adjusted to achieve the best coincidence between the experimental and the simulated data. | ||
| Min | Max | k | |
|---|---|---|---|
| GB1 powder | ν SL(1 − 3k) | ν SL(1 + 0.3k) | 0.1 |
| GB1 microcrystals | ν SL(1 − 3k) | ν SL(1 + 0.4k) | 0.07 |
It is seen that the spin-lock frequency distribution for the two samples is somewhat different. This looks reasonable since the B1 inhomogeneity depends not only on the geometry of a coil in a probe, but also on the volume and location of a sample inside the rotor. In our case, the samples were slightly different: the powder sample occupied the whole inner volume of the MAS rotor, while the microcrystalline sample was packed in the rotor with spacers that limited its volume. Thus, slightly different distribution functions for these samples can be explained.
One may ask, why do we need to describe the HORROR peaks whereas these data should be excluded from the analysis anyway? The answer is: we need to use the inhomogeneity distribution function while fitting the whole R1ρ dispersion. This necessity is demonstrated by Fig. 10, which compares simulated R1ρ dispersions using eqn (1) and (6) for different motional correlation times. If the correlation time is relatively short, then the R1ρ dispersions are flat and including B1 inhomogeneity in the analysis is not necessary. However, when the motional correlation time has a value around few hundred microseconds, the dispersion becomes very nonlinear and steep. Neglecting the B1 inhomogeneity may result in an error up to 40%, especially at small differences between the spin-lock and MAS frequencies. Thus, HORROR is an interfering effect; however, it helps determining the B1 inhomogeneity distribution function, which is necessary for the correct quantitative analysis of the relaxation data in the whole range of spin-lock frequencies. Measuring the HORROR R1ρ peak should hardly be a routing procedure for determining the B1 field distribution function, this can be done in a less time-consuming way, see e.g. ref. 28. We measured the HORROR peak in detail first of all for visual demonstration of the HORROR effect on the R1ρ rates and typical range of the spin-lock frequencies that should be avoided while measuring R1ρ dispersions.
 | ||
| Fig. 10 Simulated R1ρ dispersions for different motional correlation times assuming no B1 inhomogeneity (black lines) and B1 inhomogeneity distribution function for the powder sample (red lines), see details in the text. These curves were calculated using eqn (1) and (6), respectively, the spectral density function was assumed to be in the form of eqn (4). The order parameter can be chosen arbitrarily since it only shifts the whole plot in a vertical direction. | ||
Results and discussion
Fig. 11 shows the R1ρ dispersions measured for two samples at three temperatures. For both samples, the HORROR peak was measured only at T = 19 °C; at two other temperatures, the relaxation rates within the range from 8 to 12 kHz were not measured.Spin-spin and Bloch–McConnell contributions to the relaxation rates
Before presenting the fitting results, we would like to discuss the observed R1ρ decrease with increasing spin-lock frequency at small values of the latter (Fig. 11). Such a decrease cannot be reproduced using eqn (1)–(3). Only two mechanisms can be responsible for this behaviour: Bloch–McConnell dispersion29 and spin–spin (coherent) contribution to the relaxation rate R1ρ mentioned in the Introduction. The Bloch–McConnell contribution to the relaxation rate is the relaxation mechanism due to the modulation of the isotropic chemical shift by conformational transitions of molecules. This is one of the standard approaches to observe slow molecular dynamics in liquids30,31 and in solids.7,32–34 Spin–spin contribution is a relaxation of 15N nuclei over proton dipole–dipole reservoir to the lattice; it becomes significant only at low spin-lock fields. The limiting step in this relaxation pathway is the cross-relaxation rate between nitrogens and protons. Coherent contribution is an interfering effect since it provides no information about molecular dynamics and hides the incoherent contribution to the relaxation rate. There were some attempts to take it into account35 or to suppress it using homonuclear proton decoupling,36 proton isotopic dilution,37 and conducting the experiments at high MAS rates.38 None of these approaches, however, appeared to be robust and applicable at all values of the spin-lock field. The proton-decoupled R1ρ experiment solves this problem in the best way. Since proton decoupling disrupts the connection between protons and nitrogens, the cross-relaxation rate becomes negligibly small, and thus, the interfering spin–spin contribution can be suppressed completely.Fig. 11 demonstrates that the R1ρ dispersions at small spin-lock frequencies for the standard and proton-decoupled experiments are quite different. For the standard experiment, the R1ρvs. νSL dependence is appreciably steeper than that for the proton-decoupled one. As discussed above, the standard R1ρ is sensitive to both Bloch–McConnell and spin–spin contributions, whereas the proton-decoupled R1ρ can only be affected by the Bloch–McConnell mechanism. From this, we may draw two conclusions.
First, if high MAS rates are not used, the interfering spin–spin relaxation mechanism can affect standard R1ρ rates at small spin-lock fields even in proton-diluted protein samples. The ratio between the spin–spin and spin–lattice contributions to R1ρ at small spin-lock fields is determined by proton density in a sample, MAS rate and motional parameters. The estimation of this ratio a priori is not possible in all cases; this is however easy to do using the comparison of the standard and proton-decoupled R1ρ dispersions. Note that the proton-decoupled R1ρ experiment makes possible measuring Bloch–McConnell dispersions even in fully protonated samples.
One may see that the spin–spin contribution in the powder sample is more significant than in the microcrystalline sample. This most reasonably can be explained by a different proton density in the samples. We tried to keep the back-exchange fraction of protons in both samples the same; this, however, seems to be not the case. We could not completely avoid contact of the powder sample with atmospheric vapour during the sample preparation, and/or probably, the deuteration of the two samples was somewhat different, or there were some other unknown to us reasons affecting the amount of protons in the samples. In any case, for the proton-decoupled experiment, all this plays no role.
Second, the powder and microcrystalline samples reveal different proton-decoupled R1ρ dispersions at small spin-lock frequencies: in the powder sample, one may observe the R1ρ decrease upon increasing spin-lock frequency whereas in the microcrystalline sample, the dispersions are nearly flat. In the proton-decoupled experiment, such dispersion can be attributed to the Bloch–McConnell mechanism only, which unambiguously signifies slow conformational dynamics of a protein structure. The Bloch–McConnell dispersions in the microcrystalline GB1 sample measured previously using site-selective 2D-mode of the R1ρ experiment5 have shown that two segments of the protein structure undergo slow conformational transitions. This does not contradict to our data since we measure the integral signal from the whole protein. Only 18 out of 56 residues in GB1 reveal appreciable Bloch–McConnell dispersions5 and thus, the dispersion step in the 1D-experiment can be barely visible. The powder sample, however, shows noticeable Bloch–McConnell dispersion (Fig. 11, left panel), which directly points to more significant conformational dynamics. This can hardly be an inherent internal dynamics since in the dehydrated state, all the conformational protein motions can be only suppressed, but not enhanced.
We suggest the following explanation of the difference between the Bloch–McConnell dispersions in the powder and microcrystalline samples. The dispersion in the frequency range of a few kHz corresponds to a motional correlation time of the order of few hundred microseconds. This value corresponds to the correlation time of one of the components of the rocking motion correlation functions (see below). This coincidence may indicate that the rocking motion is accompanied by conformational changes of a protein structure. We suppose this is bending/twisting a protein globule upon rocking motion. Proteins in dry powder are tied to each other by a variety of inter-globular contacts (hydrogen bonds and sterical hindrances). Thus, it is difficult to imagine that they can undergo a motion as a whole as stiff, rigid bodies without any structural deformations. In the crystalline state, inter-protein contacts are weaker, proteins are separated by a solvent layer and there are no unnatural inter-globular hydrogen bonds. Hence, proteins in a crystal may move more independently from each other. Thus, their rocking motion is accompanied by much smaller structural deformations, if at all, than protein molecules in the dry powder sample. To prove or disprove this hypothesis, obviously more experimental data are needed.
Rocking motion parameters
Now let us consider the results of fitting the relaxation rates. The fitting parameters were obtained using eqn (6) and the distribution function parameters presented in Table 1. Since the HORROR peak data were excluded from fitting, we did not include the HORROR contribution (eqn (5) and eqn (6); the relaxation rate R1ρ(ν) under the integral in eqn (6) was a sum of RCSA1ρ (eqn (2)) and Rdip1ρ (eqn (3)) only. Using these equations, we may fit only the R1ρ's measured at the spin-lock frequencies above 12–12.5 kHz (see Fig. 11). It is unclear if the rates measured at the frequencies between 6.5–7 and 8–8.2 kHz can be included in the fitting. This range of the spin-lock frequencies corresponds to the minimum between the Bloch–McConnell dispersion and the HORROR peak (Fig. 11). We are not sure whether the Bloch–McConnell contribution to the relaxation rate is negligible at this point or not. For this reason, we performed the fitting, including and excluding the rates measured between 6.5 and 8.2 kHz.Before fitting, one has to assume a correlation function model. The simplest single exponential correlation function (the spectral density has a form of eqn (4)) cannot describe the data adequately since the discrepancy between the experimental data and fitting curves was too large. Distribution of the correlation times (Gaussian or log-normal) could not significantly improve the fitting quality. We could fit the data reasonably well only if we assume two different components of the correlation function with very different correlation times. In this case, the spectral density function has the form:
 | (8) |
 and
and  for the powder and microcrystalline samples, respectively. So, in the fitting procedure, we used these values of the coupling constants. The values of the fitting parameters are presented in Table 2. Fitting was performed using the Monte–Carlo algorithm, as done in our previous work.10
for the powder and microcrystalline samples, respectively. So, in the fitting procedure, we used these values of the coupling constants. The values of the fitting parameters are presented in Table 2. Fitting was performed using the Monte–Carlo algorithm, as done in our previous work.10
| T/°C | S 2 | A | τ F/μs | τ S/ms |
|---|---|---|---|---|
| Powder sample | ||||
| R 1ρ measured at νSL > 12 kHz | ||||
| 9 | 0.9929 ± 0.0018 | 0.727 ± 0.13 | 23.88 ± 1.2 | 1.2 ± 1.0 |
| 19 | 0.9936 ± 0.0007 | 0.811 ± 0.07 | 18.65 ± 1 | 0.43 ± 0.3 |
| 29 | 0.992 ± 0.0022 | 0.698 ± 0.13 | 20.2 ± 1 | 1.35 ± 1.15 |
| Powder sample | ||||
| R 1ρ measured at 6.5 kHz < νSL< 8.2 kHz and νSL > 12 kHz | ||||
| 9 | 0.9918 ± 0.0025 | 0.697 ± 0.13 | 15.55 ± 0.5 | 0.85 ± 0.82 |
| 19 | 0.9931 ± 0.0007 | 0.819 ± 0.05 | 12.8 ± 0.5 | 0.28 ± 0.22 |
| 29 | 0.9917 ± 0.002 | 0.727 ± 0.11 | 14.7 ± 0.35 | 0.89 ± 0.73 |
| Microcrystalline sample | ||||
| R 1ρ measured at νSL > 12 kHz | ||||
| 9 | 0.971 ± 0.012 | 0.32 ± 0.1 | 2.68 ± 0.07 | 1.58 ± 0.73 |
| 19 | 0.983 ± 0.004 | 0.442 ± 0.07 | 2.2 ± 0.08 | 0.7 ± 0.27 |
| 29 | 0.989 ± 0.009 | 0.525 ± 0.04 | 2.24 ± 0.08 | 0.44 ± 0.085 |
| Microcrystalline sample | ||||
| R 1ρ measured at 6.5 kHz < νSL< 8.2 kHz and νSL > 12 kHz | ||||
| 9 | 0.975 ± 0.01 | 0.363 ± 0.1 | 2.52 ± 0.06 | 1.38 ± 0.85 |
| 19 | 0.982 ± 0.005 | 0.446 ± 0.08 | 2.02 ± 0.07 | 0.77 ± 0.34 |
| 29 | 0.989 ± 0.007 | 0.556 ± 0.03 | 2.03 ± 0.06 | 0.39 ± 0.07 |
Several features of the obtained results have to be mentioned. First, the inclusion or exclusion of the relaxation rates measured at frequencies below the HORROR peak affects the results for only the powder sample. Even for the powder sample, the difference is not dramatic. We believe that fitting the rates measured for this sample only at νSL > 12 kHz is more relevant since (a) it provides better fitting quality and (b) the Bloch–McConnell contribution seems to be relatively large, unlike the microcrystalline sample, and one may expect that it is still significant at spin-lock frequencies around 7–8 kHz.
Second, the accuracy of various fitting parameters is different. The most accurately determined parameter is τF. Its value is determined primarily by the ratio of the standard and proton-decoupled R1ρ's, see Fig. 7. This demonstrates the advantage of the simultaneous analysis of these two types of the relaxation rates; proton-decoupled R1ρ dispersions alone would not be as informative. The least precise value is τS. The information about the slow correlation function component is contained only in the proton-decoupled R1ρ's measured at small frequency difference (νMAS − νSL), namely in the strong R1ρ raising up upon approaching the spin-lock frequency to the MAS point (Fig. 11). This frequency range is inaccessible for the standard R1ρ's, and it is clear that without the proton-decoupled data, the slow component of the rocking motion would not be detected at all. At the same time, these data are difficult to measure precisely because of the initial oscillations. In addition, even a small miscalibration of the spin-lock frequency at small (νMAS − νSL) may lead to a significant error in the analysis. We also would like to add that the fitting parameters τS and A have very strong inter-correlation. Fixing one of these parameters during fitting significantly reduces the fitting uncertainty of the other one.
Third, as mentioned above, while fitting the data we assumed no correlation times distributions, which is an obvious simplification of molecular dynamics in such complex system. Our data do not allow unambiguous determination of the correlation times distribution function. Still, there are some indications that the distributions do exist. First, one may see that both samples reveal very weak, if at all, temperature dependence of the motional correlation times, except τS in the microcrystalline sample. This seems to be strange, but this can be explained by distributions of the correlation times. The distributions conceal visible temperature dependence, which cannot be experimentally observed within a narrow temperature range. Second, there is an unexpected temperature dependence of the order parameter of the fast motion in the microcrystalline sample: the order parameter increases from 0.975 (T = 9 °C) to 0.989 (T = 29 °C), see Table 2, which means that the amplitude of the rocking motion decreases roughly twice with increasing temperature. Such unnatural apparent behaviour can also be explained by introducing the distribution function for the correlation time τF. The details of this analysis is presented in ESI.† The slow component probably also has correlation time distribution; on the other hand, this distribution should not be very wide since GB1 and SH3 proteins in crystal form undergo no rocking motion in the millisecond time scale.39
Fourth, the most important conclusion is that the rocking motion parameters for microcrystalline and powder samples differ. The motional amplitude is appreciably higher for microcrystals than for amorphous powder. This is reasonable since proteins in powder have tighter and stronger inter-molecular contacts. This is in line with the previous studies of another protein, ubiquitin, which has different rocking motion amplitudes in two different crystal packings.10,15 As for the bimodal form of the rocking motion correlation function, the available data are not sufficient for its unambiguous physical interpretation. It is natural to suppose that the fast component corresponds to the wobbling of individual proteins, which is independent from neighbours, and the slow mode of the correlation function reflects collective motions of large protein assemblies. This is, however, only speculations. More abundant data obtained for different proteins and at different conditions are necessary to ascribe the correlation function components to specific physical processes, which is our plan for future studies.
Conclusions
High-power proton decoupling during the 15N spin-lock pulse in the R1ρ experiment provides several significant methodological advantages that make the experiment more reliable, precise and informative. The most important advantage is that the proton decoupling enables measuring R1ρ rates at a much smaller difference between the spin-lock and MAS frequencies, thus making possible to observe much slower molecular motions. The experimental HORROR peak in the R1ρ dispersions, which corresponds to the condition of recoupling the homonuclear 15N–15N dipolar interaction, is wider than in the case of numerical simulations because of the B1 field inhomogeneity. This is an interfering effect; on the other hand, it may help to determine the B1 field inhomogeneity distribution function.Studying protein rocking motion in two solid samples by R1ρ relaxometry has demonstrated that the simultaneous analysis of both standard and proton-decoupled relaxation rates provides the most exact results. Still, we do not overestimate the accuracy of the obtained values of the dynamic parameters since the data treatment is associated with some assumptions and uncertainties. Despite that, the R1ρ data analysis enables drawing several important qualitative conclusions on the nature of the protein rocking motion. The rocking motion properties depend on the strength and nature of the inter-protein contacts. In lyophilized powder, the inter-protein interactions are more tight and abundant than in microcrystals; thus, the rocking motion amplitude in the powder sample must be smaller, which is demonstrated by our data. There is an indication of a possible bending/twisting of protein globules, which accompanies rocking motion in the powder sample. This follows from the analysis of the Bloch–McConnell parts of the R1ρ dispersions; however, this supposition still needs to be confirmed. The most surprising result is that the rocking motion correlation function consists of two components with correlation times of around a few microseconds and hundreds of microseconds. However, the physical nature of such a form of the correlation function is not yet clear.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Prof. Kay Saalwächter is thanked for his constant and comprehensive support of this project. This research was supported by the Deutsche Forschungsgemeinschaft, grant number KR 3033/1-1.References
- E. G. Keeler and A. McDermott, Chem. Rev., 2022, 122, 14940–14953 CrossRef CAS PubMed.
- P. Rovo, Sol. State Nucl. Magn. Reson., 2020, 108, 101665 CrossRef CAS PubMed.
- L. Vugmeister, D. Ostrovsky, A. Greenwood and R. Fu, J. Magn. Reson., 2022, 337, 107171 CrossRef PubMed.
- P. Rovo, C. A. Smith, D. Gauto, B. L. de Groot, P. Schanda and R. Linser, J. Am. Chem. Soc., 2019, 141, 858–869 CrossRef CAS PubMed.
- C. Öster, S. Kosol and J. R. Lewandowski, Sci. Rep., 2019, 9, 11082 CrossRef PubMed.
- A. A. Smith, M. Ernst, S. Riniker and B. H. Meier, Angew. Chem., Int. Ed., 2019, 131, 9483–9488 CrossRef.
- P. Schanda and M. Ernst, Prog. Nucl. Magn. Reson. Spectrosc., 2016, 96, 1–46 CrossRef CAS PubMed.
- U. Haeberlen and J. S. Waugh, Phys. Rev., 1969, 185, 421–429 CrossRef.
- R. Kurbanov, T. Zinkevich and A. Krushelnitsky, J. Chem. Phys., 2011, 135, 184104 CrossRef PubMed.
- A. Krushelnitsky, D. Gauto, D. C. R. Camargo, P. Schanda and K. Saalwächter, J. Biomol. NMR, 2018, 71, 53–67 CrossRef CAS PubMed.
- A. Krushelnitsky, R. Kurbanov, D. Reichert, G. Hempel, H. Schneider and V. Fedotov, Sol. State Nucl. Magn. Reson., 2002, 22, 423–438 CrossRef CAS PubMed.
- D. L. VanderHart and A. N. Garroway, J. Chem. Phys., 1979, 71, 2773–2787 CrossRef CAS.
- A. Krushelnitsky, D. Faizullin and D. Reichert, Biopolymers, 2004, 73, 1–15 CrossRef CAS PubMed.
- A. Krushelnitsky and D. Reichert, Appl. Magn. Reson., 2004, 27, 501–518 CrossRef CAS.
- P. Ma, Y. Xue, N. Coquelle, J. D. Haller, Z. Yuwen, I. Ayala, O. Mikhailovskii, D. Willbold, J.-P. Colletier, N. Skrynnikov and P. Schanda, Nat. Commun., 2015, 6, 8361 CrossRef CAS PubMed.
- J. M. Lamley, C. Oster, R. A. Stevens and J. R. Lewandowski, Angew. Chem., Int. Ed., 2015, 51, 15374–15378 CrossRef PubMed.
- V. Kurauskas, S. A. Izmailov, O. N. Rogacheva, A. Hessel, I. Ayala, J. Woodhouse, A. Shilova, Y. Xue, T. Yuwen, N. Coquelle, J.-P. Colletier, N. R. Skrynnikov and P. Schanda, Nat. Commun., 2017, 8, 145 CrossRef PubMed.
- J. A. Rupley and G. Careri, Adv. Protein Chem., 1991, 41, 37–172 CrossRef CAS PubMed.
- K. Griebenow and A. M. Klibanov, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 10969–10976 CrossRef CAS PubMed.
- V. Kurauskas, E. Weber, A. Hessel, I. Ayala, D. Marion and P. Schanda, J. Phys. Chem. B, 2016, 120, 8905–8913 CrossRef CAS PubMed.
- S. V. Dvinskikh, H. Zimmermann, A. Maliniak and D. Sandström, J. Magn. Reson., 2004, 168, 194–201 CrossRef CAS PubMed.
- H. J. Hogben, M. Krzystyniak, G. T. P. Charnock, P. J. Hore and I. Kuprov, J. Magn. Reson., 2011, 208, 179–194 CrossRef CAS PubMed.
- D. A. Torchia and A. Szabo, J. Magn. Reson., 1982, 49, 107–121 CAS.
- A. Krushelnitsky, T. Zinkevich, B. Reif and K. Saalwächter, J. Magn. Reson., 2014, 248, 8–12 CrossRef CAS PubMed.
- N. C. Nielsen, H. Bildsoe, H. J. Jakobsen and M. H. Levitt, J. Chem. Phys., 1994, 101, 1805–1812 CrossRef CAS.
- Z. Tosner, A. Purea, J. O. Struppe, S. Wegner, F. Engelke, S. J. Glaser and B. Reif, J. Magn. Reson., 2017, 284, 20–32 CrossRef CAS PubMed.
- H. Nagashima, J. Trebosc, O. Lafon, F. Pourpoint, P. Paluch, M. J. Potrzebowski and J.-P. Amoureux, Sol. State Nucl. Magn. Reson., 2017, 87, 137–142 CrossRef CAS PubMed.
- A. Wurl, K. Saalwächter and T. M. Ferreira, Magn. Reson., 2023, 4, 115–127 CrossRef.
- H. M. McConnell, J. Chem. Phys., 1958, 28, 430–431 CrossRef CAS.
- A. G. Palmer, C. D. Kroenke and J. P. Loria, Methods Enzymol., 2001, 339, 204–238 CAS.
- A. J. Baldwin and L. E. Kay, J. Biomol. NMR, 2013, 55, 211–218 CrossRef CAS PubMed.
- P. Ma, J. D. Haller, J. Zajakala, P. Macek, A. C. Sivertsen, D. Willbold, J. Boisbouvier and P. Schanda, Angew. Chem., Int. Ed., 2014, 53, 4312–4317 CrossRef CAS PubMed.
- D. Marion, D. F. Gauto, I. Ayala, K. Giandoreggio-Barranco and P. Schanda, ChemPhysChem, 2019, 20, 276–284 CrossRef CAS PubMed.
- M. D. Shannon, T. Theint, D. Mukhopadhyay, K. Surewicz, W. K. Surewicz, D. Marion, P. Schanda and C. P. Jaroniec, ChemPhysChem, 2019, 20, 311–317 CrossRef CAS PubMed.
- K. Akasaka, S. Ganapathy, C. A. McDowell and A. Naito, J. Chem. Phys., 1983, 78, 3567–3572 CrossRef CAS.
- P. Tekely, D. Canet, J.-J. Delpuech and J. Virlet, Magn. Res. Chem., 1990, 28, S10–S14 CrossRef CAS.
- A. Krushelnitsky, T. Zinkevich, D. Reichert, V. Chevelkov and B. Reif, J. Am. Chem. Soc., 2010, 132, 11850–11853 CrossRef CAS PubMed.
- J. R. Lewandowski, H. J. Sass, S. Grzesiek, M. Blackledge and L. Emsley, J. Am. Chem. Soc., 2011, 133, 16762–16765 CrossRef CAS PubMed.
- A. Krushelnitsky and K. Saalwächter, Magn. Reson., 2020, 1, 247–259 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the relaxation decays analysis; results of the data fitting assuming distribution of the correlation times; details of measurements 1H-15N dipolar couplings; details of quantifying the rf-pulses heating effect; analytical derivation of eqn (3); Spinach code for the R1ρ numerical simulations. See DOI: https://doi.org/10.1039/d3cp00444a |
| This journal is © the Owner Societies 2023 |




