Open Access Article
Open Access ArticleEfficient radiative cooling of tetracene cations C18H12+: absolute recurrent fluorescence rates as a function of internal energy
Jérôme
Bernard
 *a,
MingChao
Ji
*a,
MingChao
Ji
 b,
Suvasthika
Indrajith
b,
Mark H.
Stockett
b,
Suvasthika
Indrajith
b,
Mark H.
Stockett
 b,
José E.
Navarro Navarrete
b,
Naoko
Kono
b,
Henrik
Cederquist
b,
Serge
Martin
a,
Henning T.
Schmidt
b,
José E.
Navarro Navarrete
b,
Naoko
Kono
b,
Henrik
Cederquist
b,
Serge
Martin
a,
Henning T.
Schmidt
 b and
Henning
Zettergren
b and
Henning
Zettergren
 b
b
aInstitut Lumière Matière (iLM), UMR5306 Université Lyon 1-CNRS, Université de Lyon, 69622 Villeurbanne, France. E-mail: jerome.bernard@univ-lyon1.fr
bDepartment of Physics, Stockholm University, Roslagstullsbacken 21, SE-106 91, Stockholm, Sweden
First published on 21st March 2023
Abstract
We have measured recurrent fluorescence (RF) cooling rates of internally hot tetracene cations, C18H12+, as functions of their storage times and internal energies in two different electrostatic ion-beam storage rings – the cryogenic ring DESIREE with a circumference of 8.6 meters in Stockholm and the much smaller room temperature ring Mini-Ring in Lyon, which has a circumference of 0.71 meters. The RF rates were measured to be as high as 150 to 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s−1 for internal energies in the 7 to 9.4
s−1 for internal energies in the 7 to 9.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV energy range, where we have probed the time evolution of the internal energy distribution with nanosecond laser pulses with a 1 kHz repetition rate. These RF rates are found to be significantly higher than those of previously investigated smaller PAHs such as e.g. anthracene and naphthalene, for which the lowest non-forbidden electronic excited state, the D2 state, is populated with a smaller probability by inverse internal conversion. Furthermore, the D2–D0 transition rate is smaller for these smaller molecules than for tetracene. The complementary features of the two storage rings allow for RF rate measurements in a broader internal energy range than has been possible before. The smaller sampling period of about 6 μs in Mini-Ring is ideal to study the cooling dynamics of the hotter ions that decay fast, whereas DESIREE with a sampling period of about 60 μs is better suited to study the colder ions that decay on longer timescales ranging up to hundreds of milliseconds. The excellent agreement between the two series of measurements in the region where they overlap demonstrates the complementarity of the two electrostatic ion-beam storage rings.
eV energy range, where we have probed the time evolution of the internal energy distribution with nanosecond laser pulses with a 1 kHz repetition rate. These RF rates are found to be significantly higher than those of previously investigated smaller PAHs such as e.g. anthracene and naphthalene, for which the lowest non-forbidden electronic excited state, the D2 state, is populated with a smaller probability by inverse internal conversion. Furthermore, the D2–D0 transition rate is smaller for these smaller molecules than for tetracene. The complementary features of the two storage rings allow for RF rate measurements in a broader internal energy range than has been possible before. The smaller sampling period of about 6 μs in Mini-Ring is ideal to study the cooling dynamics of the hotter ions that decay fast, whereas DESIREE with a sampling period of about 60 μs is better suited to study the colder ions that decay on longer timescales ranging up to hundreds of milliseconds. The excellent agreement between the two series of measurements in the region where they overlap demonstrates the complementarity of the two electrostatic ion-beam storage rings.
1 Introduction
The presence of Polycyclic Aromatic Hydrocarbons (PAHs) in a substantial number of interstellar objects is supported by the detection of specific infrared (IR) vibrational bands occurring after excitation via, for example, absorption of UV light from a nearby star.1–4 Knowledge of cross sections for UV and visible light absorption and of dissociation and radiative cooling rates of PAHs are crucial in order to be able to characterize the photo-stability of PAHs in the interstellar medium (ISM).The survival of PAHs depends on the UV photon absorption rate, which is related to the photon flux and the absorption cross-section, and the competition between two main relaxation pathways: unimolecular dissociation and radiative cooling (by fluorescence, IR vibrational emission, etc.).5–7 This topic has motivated substantial theoretical8–11 and experimental efforts12–18 in order to characterize the physics and the chemistry of this family of molecules (see Tielens19 for a review). Using a compact room-temperature electrostatic ion-beam storage ring, the Mini-Ring, Martin et al.15,20,21 have demonstrated experimentally that the recurrent fluorescence (RF) process, which was initially proposed by Léger et al.22 under the name of Poincaré fluorescence, plays a major role for the survival of small PAH cations (naphthalene, anthracene, pyrene…) with internal energies exceeding the dissociation energy threshold. RF is a two-step process including the Inverse Internal Conversion (IIC) process, where internal excitation energy can be viewed as being transferred from the highly vibrationally excited electronic ground state to electronically excited states with much less vibrational energy leading to the emission of a fluorescence photon through an electronic transition. Calculations of RF rates are based on the estimates of the densities of vibrational states of the different electronic levels at a given total internal energy (i.e., electronic plus vibrational energy) and the transition probabilities of the possible electronic and vibrational transitions. The ratio between the densities of states of the electronically excited state and the ground state should, in general, lead to small probabilities for the IIC process. However, this is compensated by rather high electronic transition probabilities that lead to non-negligible RF rates at least in some internal energy ranges and in relation to typical dissociation and IR vibrational emission rates.23 Indeed, it has been shown that the competition between dissociation and RF is strongly dependent on the internal energy and occurs mainly in the 5–9 eV range for small PAHs with less than twenty carbon atoms such as, e.g., naphthalene (C10H8) and anthracene (C14H10) where the corresponding lifetimes are in the 0.1–10 ms range.15,20,21 Moreover, vibronic (Herzberg–Teller) coupling has recently been shown to enhance RF cooling compared to theoretical predictions where this coupling has been left out.24 The RF process should lead to significantly higher survival probabilities, which, for instance, may help explain the unexpectedly high abundances of cyanonaphtelene isomers observed in the Taurus molecular cloud -1 (TMC-1).25
In order to form a more solid basis for astrophysical modeling work, it would be very useful to explore if there are general trends in the PAHs radiative-cooling rates. For instance, the energy of the D2 state (often the lowest non-forbidden electronic state in PAHs) tends to decrease with increasing PAH size. This trend favors higher densities of vibrational states in the D2 state and, therefore, favors the IIC process, which should lead to higher RF rates and faster radiative cooling. However, the oscillator strength of the D2–D0 could be PAH-specific since it depends critically on the molecular structure. There is, therefore, a need for systematic investigations of the radiative cooling of the different classes of PAHs or PANHs, such as for examples peri- or catacondensed PAHs or substituted PAHs with methyl-, ethyl-, cyano- or other groups.
Electrostatic ion storage devices such as electrostatic ion-beam traps26–30 or electrostatic ion-beam storage rings31–36 are well suited for studies of the dynamics of molecular processes in the ms to second time-range37 such as spontaneous or thermionic electron emission,38–41 unimolecular statistical dissociation,27,42 slow isomerization43 or radiative cooling,44–48 processes where rates may vary over several orders of magnitude depending on the internal energy.
In this paper, we report on measurements of the radiative cooling rates of tetracene cations performed at the Double ElectroStatic Ion Storage Ring ExpEriment, DESIREE in Stockholm (Sweden), and at Mini-Ring in Lyon (France). The time evolution of the internal energy distribution (IED) up to 100 ms is deduced from laser-induced dissociation decays recorded at various storage times. RF rates are then deduced from a detailed analysis of the IED time evolution. The separation of single and two-photon absorption contributions is also discussed. Finally, a global simulation of the time evolution of the IED of tetracene, including dissociation-, RF-, and IR-rates is presented.
2 Experimental set-ups
The experimental set-ups, at DESIREE (Fig. 1) and at Mini-Ring (Fig. 2) have been described in details elsewhere.20,34,35,49 Here, we focus mainly on features used for the present measurements.2.1 DESIREE
DESIREE is operated at 13 K in a vacuum chamber where the residual gas pressure is so low that it can only be estimated via the storage lifetime measurements of beams of stable ions. The beam-storage lifetime which may be up to hours50 is limited by collisions between the stored ions and the very few rest gas molecules (mainly H2). The rest gas pressure in DESIREE is estimated to be about 10−14 mbar.35At DESIREE, tetracene cations were produced in an electron cyclotron resonance (ECR) plasma ion source and from a vapor of heated commercial tetracene powder (Sigma-Aldrich, purity 98%, used without further purification). The tetracene cations were accelerated to 20 keV forming a continuous ion beam. The typical average currents measured at the end of the storage cycles were about 0.4 nA. The beam was chopped in bunches of 66.8 μs, corresponding approximately to the time for one revolution of 20 keV tetracene cations stored in DESIREE's symmetric ring, which is shown in Fig. 1. The flight time of the ions from the source to the storage ring is known and, in the following, the time t refers to the time at which the ions were extracted from the ion source. The symmetric ring was almost filled with a close-to-homogeneous density of ions, except for a very small time (about 1.6 μs) needed to switch on the voltage on the injection electrodes. After several revolutions, the stored ion bunches spread longitudinally such that the ring is filled entirely with an almost homogeneous ion density.
During storage, neutral fragments resulting from unimolecular dissociation of initially hot cations or cations heated by laser absorption were detected either by the imaging detector (ID), which is an assembly of microchannel plates (MCPs), a phosphor screen and a fast camera51 or by a system composed of a glass plate electron converter and MCPs (see Fig. 1). A tunable OPO laser (EKSPLA NT 200 series, 1 kHz repetition rate, 5 ns pulses, 210 μJ pulse−1 at 430 nm) was used to excite the stored cations and induce prompt and delayed dissociation. The laser beam was injected in a merged-beam configuration, i.e., collinearly to the tetracene cation beam in the injection section of DESIREE. The time overlap between the laser and the ion beam is estimated to be 8 μs corresponding to about 12% of the revolution time.
The prompt signal, i.e., the neutral fragment counts recorded on the glass-plate detector right after the laser pulse was used to optimize the overlap between the laser beam and the stored cations. However, the data recorded with this detector, which is due to prompt dissociation will not be discussed hereafter. We will rather focus on the data recorded with the ID, which was used to detect neutral fragments resulting from delayed photo-dissociation at each n + 1/2 turn after laser shots as a function of time t′, where t′ is the storage time with respect to the laser pulse time tL as a reference (t′ = t − tL). As the laser shots were not synchronized with the revolution time of the stored cations, the chance for the same cation to absorb two photons from two different laser pulses might not be completely negligible. However, the analysis of decays recorded with different laser pulse energies and repetition rates showed that the re-heating from such several-photon absorption was in fact negligible. Fig. 3 shows a typical raw spectrum recorded with DESIREE for tetracene cations using a laser wavelength of 430 nm and a repetition rate of 500 Hz (first laser pulse fired at tL = 0.7 ms). As can be seen in the inset of Fig. 3, the laser-induced decays were found to last more than one millisecond. It was therefore necessary to adapt the laser repetition rate to prevent any overlap between two successive decays.
The two main dissociation channels of tetracene cations are the losses of C2H2 and H.18 Given the kinetic energy of the tetracene cations considered here (Ek(C18H12) = 20 keV), the detection efficiency of the neutral fragment H is expected to be extremely low due to its low kinetic energy ((Ek(H) = Ek(C18H12)/228) = 88 eV). Due to its 26 times higher kinetic energy, the detection efficiency of the C2H2 neutral fragment is expected to be much higher than that of the H fragment. In addition, the collection efficiency, which is related to the kinetic energy release (KER), is also much lower for H than C2H2 fragments. Therefore, the count rate is dominated by C2H2 hits on the detectors. In ref. 18, the branching ratios for these channels were found to be very weakly dependent on the internal energy in the 10.5 to 12 eV internal energy range, which is the energy range of interest for the present study. Therefore, the assumption of constant branching ratios was used in the present data analysis and modeling.
Note that the total decay rate of the stored ions can be measured via any of the decay processes, e.g., by detecting any of the possible fragments (H or C2H2) or by detecting the RF or IR photons. After laser absorption, the product of the branching ratio times the detection efficiency is in large favor of the C2H2 detection and this is the method we use here.
2.2 Mini-ring
The general principle of the Mini-Ring experiment (Fig. 2) is very similar to the one performed at DESIREE, although the designs of the electrodes of the two storage rings are very different. The two main differences are the much smaller size of Mini-Ring, which offers the possibility to record decay curves with a higher sampling rate, and the higher background gas pressure (about 1.5 × 10−9 mbar) that restricts the storage lifetime to about 300 ms for Mini-Ring.The 10 GHz Nanogan ECR ion source used for Mini-Ring is slightly different from the 2.4 GHz Monogan ECR used at DESIREE. Yet, the fragmentation mass spectra recorded via a Faraday cup placed in the ion beam line in between the selection magnet and the rings were found to be in close agreement suggesting that the initial IEDs of the stored tetracene cations were similar in the two experiments.
The ion beam kinetic energy was set to 12 keV for Mini-Ring. Therefore, the tetracene cation revolution time was 7.42 μs. The bunch duration was set to 6.8 μs to fill the Mini-Ring almost completely with a homogeneous ion density, except for about 600 ns corresponding to the rise time of the voltage of the injection deflector. Neutral fragments resulting from unimolecular dissociation events due to delayed dissociation of hot or laser-excited tetracene cations were detected at every turn by micro-channel plates as indicated in Fig. 2. Collisions with the rest gas were also contributing to the neutral counts and had to be subtracted in the data analysis process. Similarly to DESIREE, the time reference in the present analysis is the time at which the ions were produced in the source. The time of flight between the ion source and the buncher is 16 μs for 12 keV tetracene cations.
The same model of OPO laser as in the DESIREE experiments (EKSPLA NT 200 series) was used to excite the stored tetracene cations in a time range of tL = 0.5–100 ms in a merged parallel beam configuration for the ion- and laser beams. The laser decays presented in this paper were recorded with a wavelength of 430 nm. The choice of this wavelength is not very critical as long as it corresponds to a sufficiently high absorption cross-section and leads to dissociation lifetimes that correspond to several turns in the rings. Other tests at 410, 450, and 470 nm have been performed and have led to results that are consistent with those for 430 nm. In addition, different laser pulse energies were used to study the contributions from one and two-photon absorption as a function of the storage time.
3 Experimental results
3.1 Spontaneous decays analysis
The ECR ion sources provided tetracene cation beams with fairly broad internal energy distributions extending quite far above the dissociation energy of tetracene cations C18H12+, in both experiments. Here, spontaneous decay refers to delayed dissociation events of the hottest tetracene cations injected in the storage rings. With DESIREE, the spontaneous decay could be followed over more than five decades (counts in ordinates of Fig. 4a) due to the high detection efficiency and low background (the very small background is due either to collisions with the tiny residual gas or to the intrinsic background counts of the detector), while Mini-Ring was limited to about 3 decades due to collisions with the rest gas. Therefore, from 1 to 100 ms only DESIREE could be used to investigate the spontaneous decay, whereas the Mini-Ring counts were dominated by background counts in this time range. At the Mini-Ring residual gas pressure of 2 × 10−9 mbar the 1/e tetracene cation beam lifetime was limited to about 0.2 s at 12 keV (see Fig. 4). However, due to the smaller period of revolution, 7.4 μs in Mini-Ring compared to 66.4 μs in DESIREE, and a shorter transport beam line the decay could be measured at shorter times and with a better resolution from 30 μs to 1 ms in Mini-Ring. The first data point could be taken at 63 μs in Mini-Ring whereas it was at 167 μs in DESIREE, with respect to the same time reference, i.e., the time at which the ions were extracted from the ion source. In the following, we will also show that this difference in sampling rate is of interest for the investigations of laser-induced decays. This clearly shows the complementarity of the measurements with DESIREE and Mini-Ring. | ||
| Fig. 4 (a) Spontaneous decay recorded with Mini-Ring (blue dots). The gray line is an exponential fit of the data at t > 10 ms corresponding to the neutral counts resulting from collisions with the background gas. From this fit, the 1/e beam lifetime is found to be about 200 ms. The red dots show the background subtracted spontaneous decay. The black dotted line is a t−1 law fit on the 10 first points of the spontaneous decay. The dashed and the solid black lines are the results of the fits using the empirical model (eqn (1)) using a constant and time-varying quenching time, respectively. (b) Spontaneous decay recorded with DESIREE (red dots). The black dotted line is a t−1 law based on the first points of the spontaneous decay. The black line is the result of the fit using the empirical model (eqn (1)) with a time-varying quenching time. | ||
It is well-established that for broad IEDs, spontaneous decays are expected to follow a t−1 power law when dissociation is the main energy relaxation process.52 In Fig. 4, the typical spontaneous decays recorded with Mini-Ring and DESIREE over a time range of 100 ms show, in both cases, a strong deviation from a pure t−1 power law. This is a clear evidence of the presence of a non-dissociative process that quenches the spontaneous decay. This quenching is interpreted as the result of cooling through RF processes, which shift the IED to lower energies by emission of RF (visible or near IR-red) photons in the ms or sub-ms time range.
A semi-empirical model, which quantifies the effect of vibrational infrared-emission cooling has been presented in ref. 52 and is summarized through eqn (1) below. In eqn (1), N(t) represents the number of neutral fragments detected at time t, N0 is a normalization constant proportional to, but not equal to the number of ions that were initially stored, τ is the effective quenching time and δ is related to the deviation from the t−1 power law, which is expected in the short time range for an infinitely broad IED, i.e., an IED that would be constant in the relevant internal-energy range. The same mathematical expression has also been used in ref. 53 to model the RF cooling in the spontaneous decay of anthracene cations.
 | (1) |
The DESIREE spontaneous decay curve shown in the lower panel of Fig. 4 is clearly less steep compared to the one recorded with Mini-Ring. In DESIREE, it is expected from ion trajectory simulations that when tetracene cations decay by the loss of one hydrogen atom, the remaining C18H11+ fragments can still be stored although they have a slightly lower kinetic energy. Therefore, in case the remaining internal energy of the fragment remains high enough, it can dissociate and contribute to the spontaneous decay curve.44 Hence, the long-time range counts are mostly contributed by this sequential dissociation process in DESIREE. It has been verified experimentally that this is not the case in Mini-Ring due to smaller kinetic energy acceptance. Nevertheless, we attempted to use the same quenching law as for the Mini-Ring spontaneous decay curve (eqn (1)) with a time-varying quenching time. A good agreement has been obtained for τ0 = 0.35 ms, δ = 0.15 and γ = 0.25 ms−1. The parameters are found radically different from those obtained from the Mini-Ring decay curve. It can be explained by differences in the radiative cooling properties of tetracene cations and C18H11+ fragments, and by different internal energies since the fragments have been cooled by the dissociation process. A more sophisticated model, such as the one implemented for perylene cations in ref. 44 is required to account for sequential dissociation. Such a model is not presented here since the main aim of the present paper is to provide more detailed information on the radiative cooling of tetracene cations by following the time evolution of the IED using laser absorption.
During the Mini-Ring experiment, we observed that the spontaneous decay curve depends significantly on the initial conditions of the ion source, especially at shorter times. Under cold source conditions, for instance, when using low power (about 0.5 W) of the 10 GHz microwave and rather high pressure in the ion source by injection of Ar support gas (pressure was not measured directly in the plasma chamber, but an increase in pressure was measured in the next vacuum chamber), the recorded mass spectrum (not shown here) shows a reduced fragment peak (H-loss) compared to the hot conditions (high microwave power and low pressure). Compared to hot conditions, cold source conditions result in a reduction of the total count rate in the spontaneous decay and in a less steep decay curve. Since the IED of the ions injected into the ring can be significantly shifted towards lower energies the two main decay processes (dissociation and RF cooling) have, on average, much smaller rates for such an ion ensemble.
3.2 Laser induced decays analysis
A normalization factor has been used to obtain a good overlap between the two decay curves around 50 μs. Nevertheless, the slope of the Mini-Ring decay is found to be slightly steeper than that of the DESIREE decay. At such short storage times, this difference may be attributed to two reasons: (i) the slight difference of about 80 μs in the flight time from the ions source to laser absorption, which means that the tetracene cations had a bit more time to cool down before reaching DESIREE than before reaching Mini-Ring. (ii) The initial IEDs of the tetracene cations from the two ion sources were slightly different.
Following ref. 16 as a simple first approach, we fit the laser-induced decay curves recorded with Mini-Ring using A × t−α power laws. The resulting values of the power α reflect the steepness of the decay curves. The results of such fits are displayed in Fig. 6 for laser firing times of tL = 0.5, 1.5, and 2.5 ms (fits for 1.0 and 2.0 ms are not shown for clarity of the figure). The values of α were found to be 0.92, 0.77, 0.68, 0.64, and 0.59 for tL = 0.5, 1.0, 1.5, 2.0, 2.5 ms, respectively. In the tL range of 0.5 to 2.5 ms, the decay induced by two-photon absorption is expected to be so fast that its contribution to the second measured point after a 1.5 turn in Mini-Ring can be neglected. However, for tL ≥ 3 ms (not shown), the determination of the value of α is more difficult as the two-photon absorption decay gets slower (but still much faster the single absorption decay), its contribution to the second, third, etc., points of the measured decay is not negligible anymore. For this reason, we focus in this section on the above-mentioned time range of 0.5 to 2.5 ms.
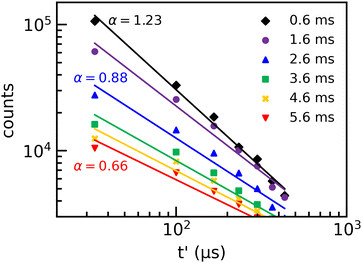
In Fig. 7, we present laser-induced decays recorded at DESIREE for laser firing times in the tL = 0.6 to 5.6 ms range with 1 ms steps. The decays recorded at DESIREE in this short storage time range are less sensitive to contributions from two-photon absorption than those recorded with Mini-Ring. Two-photon absorption leads to fast decays that are shorter than half the ion revolution time. Therefore, decays recorded up to tL = 5.6 ms are strongly dominated by single-photon absorption events. Nevertheless, because of the large contribution of the spontaneous decay at tL = 0.6 ms, the laser-induced decay curve could be determined with reliable precision only for the 6 first turns after the laser shot in that case.
Fits using the A × t−α power law have been performed for each decay curve and are shown in Fig. 7. The agreement between the power-law fits and the experimental data is not as good as for the Mini-Ring results. Moreover, α is found to be more sensitive to the selected time range, i.e. the number of data points used in the fitting procedure. This indicates that the recorded decays at DESIREE deviate more from the power law model than those of Mini-Ring. The fitting procedure leads to values of α that decrease from 1.2 to 0.5 for tL = 0.6 to 5.6 ms, respectively. These values are significantly larger than those obtained from Mini-Ring's data as shown in the inset of Fig. 8. However, the values of α obtained from the data of both storage rings are found to decrease rapidly with tL and to follow a similar trend. Therefore, this power law fit method resulting in the determination of the parameter α should be considered as a rough, first approach interpretation as the absolute value depends on the number of data points included, i.e., on the time range of the fit. It can be used only to determine the general trend versus the storage time.
The contribution from two-photon absorption appears at shorter storage times for Mini-Ring than for DESIREE. For a first basic demonstration of the importance of the contribution of two-photon absorption, the laser-induced decays are fitted using the same power law as in Section 3.2.1. To highlight the magnitude of the two-photon contribution, we have included only the first five points where the contribution from two-photon absorption is expected to be maximum.
In Fig. 8, we show the values of α resulting from the fitting procedure as a function of tL up to 100 ms for the decays recorded at DESIREE (blue data points) and Mini-Ring (red data points). In the range from 0.5 to 5 ms, the single-photon contribution is dominant. The decrease of α as a function of tL within this range reflects the shift of the high energy edge (HEE) of the IED towards lower energies. From tL = 5 to 20 ms, α increases from 0.5 to 0.9. This effect is explained by the summed contributions of single-photon and two-photon absorption with an increasing proportion of the two-photon contribution, whereas the single-photon contribution decreases. From 20 ms to 100 ms, the values of α decrease monotonically, but at a much slower rate than in the range of 0.5 to 5 ms. This shows that the IED is still shifting toward the low energies after 20 ms even though the global effect of the cooling is much slower than before 5 ms. This suggests that IR-emission is the most important cooling mechanism on the longest timescales probed in the present experiments, as it is slower and less efficient than RF cooling.23
In contrast, the contribution from three-photon absorption to the observed decay curves can be neglected. The expected internal energy after 3 photons absorption is given by E3ph = 3hν + Ei(t), where hν = 2.88 eV (430 nm) and Ei(t) is the internal energy of a tetracene cation at time t. The model presented below in Section 4 predicts the internal energy to be about 3.3 eV at 100 ms storage time. Therefore, the total internal energy after absorption of 3 photons is about 12 eV, which corresponds to a dissociation lifetime of about 20 μs,18 which is too short to be observed as a delayed dissociation event in DESIREE.
Since α takes approximately the same value of 0.5 at 5 and 50 ms, it can be inferred that the internal energy of the tetracene cations has decreased by approximately the energy of one photon, i.e., 2.88 eV, in this time range. Therefore, the average energy shift rate, ΔE/Δt, is estimated to be approximately 60 eV s−1.
4 Modeling of laser-induced decays
The model used in the present work has already been described in much detail in previous papers.15,20,45 In contrast to the simple power law analysis used in the previous section, this model provides detailed information about the time evolution of the IED and the cooling rate as a function of the internal energy.In brief, the laser-induced decays are modeled independently of each other by calculating the number of neutral fragments emitted at each n + 1/2 (starting at n = 0) turns after the laser shot using a parameterized Gaussian IED and using the internal-energy-dependent dissociation rates of Fig. 9. Therefore, a model decay curve S(t) is a weighted sum of individual exponential decays at a given internal energy S(E,t) given by eqn (2).
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) is the hyperbolic sine function, Δt is the neutral-fragment collection time that corresponds to the time spent by the ions in the straight line of the ring that is in front of the detector (Δt ≈ 7.68 μs and Δt ≈ 0.7 μs for DESIREE and Mini-Ring, respectively); kdiss(E) and ktot(E) are the dissociation and total rates (respectively) evaluated at internal energy E.
) is the hyperbolic sine function, Δt is the neutral-fragment collection time that corresponds to the time spent by the ions in the straight line of the ring that is in front of the detector (Δt ≈ 7.68 μs and Δt ≈ 0.7 μs for DESIREE and Mini-Ring, respectively); kdiss(E) and ktot(E) are the dissociation and total rates (respectively) evaluated at internal energy E.
 | ||
| Fig. 9 Dissociation rates from ref. 18 (kdiss, black solid curve), theoretical RF rates (kRF,th, black dashed curve), theoretical IR emission rates (kRF,th, black dotted curve), and measured rates with Mini-Ring (kRF,meas Mini-Ring, red diamonds) and DESIREE (kRF,meas DESIREE, black squares). | ||
The dissociation rates reported in Fig. 9 were estimated via measurements of Diedhou et al.18 using the Arrhenius law. The total decay curve at a given tL is obtained by the weighted sum of all the contributions to the total decay of each internal E, according to eqn (3).
 | (3) |
In this model, we have added the contribution of the two-photons absorption to improve the overall model-experiment agreement and to get a better understanding of the evolution of the decay curves for large storage times. Accounting for two-photon absorption was important to model the decay curves for tL > 3 ms for Mini-Ring and tL > 6 ms for DESIREE. Compared to simulations performed in the cases of naphthalene and anthracene in previous studies at Mini-Ring,20,21 the extension of the simulations above tL = 6 ms allow us to follow the evolution of IEDs for lower internal energies. In these previous simulations, the knowledge of the dissociation rates was sufficient since, after laser absorption, the IED was shifted into an energy range where dissociation dominates over radiative cooling. In the case of tetracene, because of the high RF rates, photon absorption brings the IED quite close to the crossing point between dissociation and RF rates at internal energies of about 10.5 eV. This is the reason why, in eqn (2), it was needed to consider the total rate ktot = kdiss + kRF + kIR and to multiply by the dissociation branching ratio defined as:
 | (4) |
| E (eV) | k diss (s−1) | k thIR (s−1) | k thRF (s−1) |
|---|---|---|---|
| 7 | 0.01 | 220 | 214 |
| 7.2 | 0.03 | 226 | 270 |
| 7.4 | 0.08 | 233 | 335 |
| 7.6 | 0.19 | 239 | 412 |
| 7.8 | 0.46 | 245 | 501 |
| 8 | 1 | 252 | 604 |
| 8.2 | 2 | 258 | 720 |
| 8.4 | 5 | 264 | 853 |
| 8.6 | 10 | 271 | 1001 |
| 8.8 | 21 | 277 | 1167 |
| 9 | 40 | 283 | 1351 |
| 9.2 | 75 | 290 | 1554 |
| 9.4 | 137 | 296 | 1777 |
| E (eV) | Γ diss | E (eV) | Γ diss |
|---|---|---|---|
| Before absorption | Before absorption | After absorption | After absorption |
| 7 | 4.7 × 10−5 | 9.9 | 0.18 |
| 7.2 | 1.1 × 10−4 | 10.1 | 0.25 |
| 7.4 | 2.2 × 10−4 | 10.3 | 0.33 |
| 7.6 | 4.6 × 10−4 | 10.5 | 0.42 |
| 7.8 | 9.1 × 10−4 | 10.7 | 0.51 |
| 8.0 | 1.7 × 10−3 | 10.9 | 0.59 |
| 8.2 | 3.2 × 10−3 | 11.1 | 0.67 |
| 8.4 | 5.8 × 10−3 | 11.3 | 0.74 |
| 8.6 | 1.0 × 10−2 | 11.5 | 0.80 |
| 8.8 | 1.7 × 10−2 | 11.7 | 0.84 |
| 9.0 | 2.8 × 10−2 | 11.9 | 0.88 |
| 9.2 | 4.6 × 10−2 | 12.1 | 0.90 |
| 9.4 | 7.1 × 10−2 | 12.3 | 0.93 |
The evolution of the dissociation branching ratio as a function of internal energy can be analyzed from the values given in Table 2. From 10.5 to 12 eV, which is the expected internal energy range after laser excitation, the branching ratios are estimated to increase from 0.53 to 0.93. For instance, around 10.5 eV, tetracene cations have approximately a 50% chance of decaying by emission of a neutral fragment and a 50% chance to emit an RF photon. For internal energies below 10.5 eV, the dissociation branching ratio drops very fast as can be seen in Table 2. Therefore, for storage times greater than 10 ms, the number of neutral fragments resulting from single-photon absorption drops dramatically, giving room for the observation of the two-photon absorption process.
4.1 IED in the case of single-photon absorption
A selection of typical Mini-Ring and DESIREE laser-induced decays are displayed in Fig. 10 and 11, respectively, for comparison with the present model. Fig. 11a shows the transition between pure single photon absorption decays (for tL in the 0.6 to 10.6 ms range) and decays with increasingly important two-photon absorption contributions for tL in the 10.6–20.6 ms range. With the present model, it has been possible to disentangle the single and two-photon contributions (dotted and dashed curves, respectively). Qualitatively, as the ions cool down with time, the proportion of ions that can dissociate due to the absorption of a single photon decreases with time as can be seen in Fig. 11a. Accordingly, a rather fast decrease of the single-photon contribution is observed in Fig. 11. The single-photon contribution is found to be close to negligible for tL > 40.6 ms as shown in Fig. 11a, where laser-induced decays could be nicely fitted by using the two-photon absorption contribution only.The present model has been used to simulate the decay curves recorded with Mini-Ring in the 0.5 to 2.5 ms storage time range (solid lines in Fig. 10). A very good agreement between the simulated and experimental decay curves was obtained by adjusting independently the Gaussian IED parameters (center, width, and amplitude) for each decay. As expected, the resulting IEDs, displayed in Fig. 12, shift regularly towards lower energies with increasing storage time. The energy shift rate can be estimated from the time of evolution of the HEE, defined here as the energy at half of the amplitude of the IED. It is found to be about ΔE/Δt = −550 eV s−1 around an internal energy of 9 eV (Te ≈ 1150 K), which is significantly higher than for anthracene20 and naphthalene.54 For instance, tetracene cools about six times faster than anthracene.
 | ||
| Fig. 12 Time evolution of the IED after single photon absorption for tL in the 0.5 to 2.5 ms range resulting from the fitting procedure of the corresponding laser-induced decays in Mini-Ring. The vertical red dashed lines indicate the energies at which further data analysis was performed to determine the measured rates displayed in Fig. 13. | ||
It is possible to extract population decay rates as a function of storage time at different excitation energies from the simulated IEDs of Fig. 12. In Fig. 13, we have plotted the population decay curves N(E0,t) at fixed values of the internal energy E0 in the 8.2–9.4 eV range in steps of 0.2 eV (following the dashed vertical lines of Fig. 13). These N(E0,t) curves are nicely fitted by exponential decay laws whose rates are referred to as ‘measured’ total decay rate, kmeas(E0), that include RF, dissociation, and IR processes. The obtained values (see Table 3) were found to be in the range from 600 to 1100 s−1 for internal energies in the 8.2–9.4 eV range. The RF rates can be estimated from these values after correction of the IR decay rate.
| E (eV) | k meastot | k meastot | k measRF | k iterRF | η coolRF |
|---|---|---|---|---|---|
| DESIREE | Mini-Ring | Iterative | |||
| 7 | 169 | 147 | 139 | 39 | |
| 7.2 | 257 | 234 | 175 | 58 | |
| 7.4 | 344 | 321 | 217 | 75 | |
| 7.6 | 432 | 408 | 267 | 92 | |
| 7.8 | 519 | 494 | 324 | 108 | |
| 8 | 607 | 581 | 391 | 123 | |
| 8.2 | 694 | 569 | 666 | 466 | 137 |
| 8.4 | 660 | 629 | 552 | 127 | |
| 8.6 | 752 | 714 | 648 | 142 | |
| 8.8 | 843 | 794 | 755 | 155 | |
| 9 | 934 | 865 | 874 | 168 | |
| 9.2 | 1025 | 921 | 1006 | 180 | |
| 9.4 | 1116 | 949 | 1150 | 192 |
The time evolution of the number of tetracene cations of internal energy E0 is governed by the following master rate equation (eqn (5)):
 | (5) |
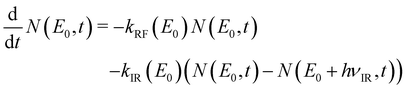 | (6) |
 | (7) |
| kmeas(E0) = kRF(E0) + γkIR(E0) | (8) |
| kRF(E0) = kmeas(E0) − γkIR(E0) | (9) |
 | ||
| Fig. 14 Time evolution of the IED in the range 0.6 to 5.6 ms resulting from the fitting procedure of the corresponding laser-induced decays in DESIREE. | ||
Boissel et al.23 have defined a global cooling rate ηcool in order to compare the cooling efficiencies of the RF and IR emission processes. Following the same method, we have estimated the ηIRcool of tetracene and we obtained a value of about 6 s−1 in the present internal energy range. Likewise, the ηRFcool listed in Table 3 were defined as:
 | (10) |
The same model has been employed to simulate the decay curves that were recorded with DESIREE in the 0.6–5.6 ms storage time range. Likewise, the centers and amplitudes of the corresponding IEDs were free adjustable parameters and the widths were set to a fixed value of 1 eV (standard deviation). Some of the simulated decay curves have been plotted in Fig. 11 together with the experimental ones. A very good agreement between simulated and experimental decay curves could be obtained. The corresponding IEDs are displayed in Fig. 14. Accordingly to IEDs obtained from the Mini-Ring experiment, a similar shift of the IED towards low energies is observed for increasing storage times. Yet, the energy shift rate is found to be ΔE/Δt = −450 eV s−1 from 0.6 to 2.6 ms, which is slightly smaller than the value obtained from the Mini-Ring experiment but still in the same order of magnitude. This slight difference may be attributed to the slight difference in internal energy at which the estimation of the energy shift rate is done, i.e. 8.5 eV for DESIREE and 9 eV for Mini-Ring. At longer storage times, from 2.6 to 5.6 ms, the energy shift rate was found to be significantly smaller: ΔE/Δt = −150 eV s−1. In this storage time range, the HEEs of the IED decreased from 8.1 down to 7.6 eV. This shows, as expected from the theoretical RF rates displayed in Fig. 9, that the cooling due to RF is highly dependent on internal energy.
The measured rates kmeastot have been estimated from the IEDs of Fig. 14 for a series of internal energies (7 to 8.2 eV in steps of 0.2 eV) using the same procedure as already discussed above in the Mini-Ring case. The kmeastot rates were found to be in the 160–700 s−1 range for internal energies ranging from 7 to 8.2 eV, respectively. At the commonly investigated internal energy of 8.2 eV, the agreement between DESIREE and Mini-Ring measurements is remarkable (cf.Table 3). In Table 3 and Fig. 9, we remark that, in the presently considered energy range (7 to 9.4 eV), the dissociation rate is close to being negligible.
For internal energies in the present range of DESIREE experiments, the kmeasRF = kmeastot− 0.1 × kthIR − kthdiss values were not found to agree well with the theoretical ones (kthRF) of Table 1. Since these approximate kthRF rates were used initially in the simulations of the decay curves used to determine the IEDs, it can be expected that more accurate IEDs should be obtained by re-iterating the fitting procedure including the kmeasRF instead of kthRF. After this second iteration an overall agreement between the iterative RF rates kiterRF and those used in the simulations, i.e., the kmeasRF was obtained. This procedure led to slight modifications of the IEDs between the first and second iterations.
In previous studies of anthracene and naphthalene with Mini-Ring,15,20,54 it was not necessary to account for the radiative rates (neither RF nor IR) because their effect on the laser-induced decay was negligible. However, in the present case, since the RF process is much more efficient and since the decay was observed on a much longer time scale with DESIREE, including the RF rate in the simulations improved significantly the agreement between the simulated and experimental laser-induced decay curves. The effect on the IEDs is mainly on the low-energy side since the RF process modifies the shape of the decays at long times. In the end, this iterative procedure brings a small but significant correction to the measured RF rate values (see Table 3).
4.2 IED in the case of one and two photons absorption
Although the probability of two-photon absorption is expected to be much smaller than single-photon, its contribution becomes dominant after tL = 6 ms and 10 ms in the laser-induced decays recorded with Mini-Ring and DESIREE, respectively. In the following, we will restrict the discussion to the two-photon contribution to the decay curves recorded with DESIREE. We have extended the above model in order to simulate the decay curves using the weighted sum of single-photon and two-photon decay curves. The ratio between the double and single photon absorption weighting factors was treated as an additional free parameter. The best agreement between the simulated and experimental laser-induced decays was obtained for a ratio of 0.002 between the decays caused by two- and one-photon absorption. Fig. 11a shows a very good agreement between the experimental and simulated decay curves for tL from 10.6 to 20.6 ms for which the two-photon contribution has been taken into account. The two-photon contribution is displayed in Fig. 11 for tL = 14.6 and 20.6 ms (dashed curves). It corresponds to a fast decay that dominates the global decay curves at short times (t′ < 150 μs). For tL = 10.6 ms, only the first data point of the decay is dominated by the two-photon contribution. As tetracene cations cool down with time, the two-photon decay becomes slower with increasing storage time. In addition, the single-photon decay becomes much slower than the two-photon decay, such that its contribution can be neglected in the decays recorded at tL > 50.6 ms.Unlike the simulations discussed in Section 4.1, when including the two-photon contribution the widths of the different IEDs, were treated as free independent parameters. Fig. 11b shows the simulated and experimental decay curves and the corresponding IEDs for tL = 30.6 to 90.6 ms. In Fig. 15, we display the evolution of the IED as a function of tL in the whole range of the present DESIREE experiment (0.6 to 90.6 ms). The IED shifts rather fast in the 0.6–10.6 ms range (red curves in Fig. 15) and rather slowly afterwards (blue curves in Fig. 15) down to 3.5 eV for tL = 90.6 ms. The average energy shift rate is estimated to ΔE/Δt = −42 eV s−1 between 10 ms and 60 ms, which is consistent with the above value of −60 eV s−1 resulting from the power-law modeling (see Section 3 and Fig. 8).
However, it is much more difficult to estimate the total rates (kmeastot for tL > 20.6 ms) than in the case where the one photon absorption is dominant. The IEDs resulting from the model present important fluctuations, probably due to too low statistics in the decay curves especially for tL ≥ 40 ms. In Fig. 16, the centers of the IEDs have been plotted as a function of the storage time. This plot illustrates again that, at short times (≤10 ms), there is a fast cooling process that can be attributed to RF cooling as it follows the same trend as the model. The efficiency of the RF cooling decreases with time as the tetracene cations get colder because the RF rate is highly dependent on internal energy. Further radiative cooling after 90.6 ms is expected to be dominated by vibrational IR emission.
 | ||
| Fig. 16 IED center as a function of storage time deduced from DESIREE experiments (blue triangles) and from the global simulation of the IED time evolution (red squares, see text). | ||
4.3 IED global simulation
A simulation of the overall time evolution of the IED during storage from 0 to 200 ms has been performed using the same model as used in ref. 20 for the IEDs of anthracene cations. Eqn (5), which governs the time evolution of tetracene cations of a given internal energy E0 has been solved numerically under the assumptions described in 4.1 leading to eqn (6). Variable time steps have been used to account for the fact that the rates governing the evolution of the IED vary by several orders of magnitude from t = 0 to 1 s.The initial IED at t = 0 was assumed to be a Gaussian function whose center and width were set to 7.5 eV and 1.4 eV, respectively. These values were chosen to obtain a good agreement with the centers of IEDs found from 0.6 to 5.6 ms (cf. 16). The dissociation and IR rates were taken from Table 1 (kthdiss and kthIR, respectively) and the RF rates were taken from Table 3 (kRF,iter).
In Fig. 17, we show the computed IEDs from 0 to 1 s. It is noteworthy that the shape of the IED varies significantly with time, especially at the beginning of the cooling process. This is mainly due to the RF process that is very efficient at internal energies of around 7.5 eV to feed the population around 6.1 eV because of the emission of a photon via the D2–D0 transition of 1.4 eV. After 100 ms, the center of the IED is found at about 3 eV, in relatively good agreement with the 3.5 eV for 90.6 ms IED of Fig. 16. After 100 ms, the cooling process is very slow because the IR vibrational cooling only remains efficient. According to the present model, by extending the calculation to longer times, we found that about 2 s are needed to reach an internal vibrational energy of about 0.15 eV. Fig. 16 compares the centers of the IEDs calculated with this global simulation and the ones resulting from the simulated decays from Fig. 14 and 15. The relatively good agreement shows that the RF and IR cooling processes were rather well described by the global simulation.
 | ||
| Fig. 17 Evolution of the IED as a function of time. The initial IED corresponds to the curve at 0 ms. | ||
5 Summary and conclusions
In this paper, we have investigated the cooling processes of tetracene cations on an extended internal energy range by using two different electrostatic storage rings Mini-Ring and DESIREE. The main results are the determination of the cooling rates for specific internal energies, E0, in combination with the understanding of how important highly efficient RF processes are for tetracene. Using both rings, detailed information on the cooling was provided by analyzing the spontaneous decay and the time evolution of laser-induced decays as a function of the storage time. Mostly due to their differences in size and in background gas pressure, the two electrostatic ion storage rings allow for the investigation of different time ranges corresponding to different internal energy ranges. We have shown that a first insight into the effect of the radiative cooling processes could be obtained by fitting the laser-induced decays with power law functions. This simple first approach revealed a very fast RF cooling process of hot tetracene cations during the five first milliseconds of storage. It also revealed that after about 20 ms of storage, two-photon absorption is responsible for the main part of the laser-induced decays. The two-photon absorption was used to determine an average internal-energy shift rate of the IED of ΔE/Δt = −60 eV s−1 in the time range of around 20 ms corresponding to an internal energy of about 5 eV. A more sophisticated approach was used to simulate laser-induced decay curves and fit them to the experimental ones by solving master rate equations and adjusting the parameters of Gaussian IEDs. The total rates and subsequently the RF rates were then determined from the resulting IEDs in the internal energy range of 7 to 9.4 eV using the decay curves recorded at the shorter laser delay times tL ≤ 5.6 ms with Mini-Ring, considering single photon absorption only. These measured RF rates agree rather well with theoretical ones, although some parameters of the model, such as the probability of transition and the energy of the involved D2–D0 electronic transition, may suffer from some uncertainties. To further investigate the radiative cooling after 10 ms, a more accurate analysis had to be developed due to the increasing contribution of two-photon absorption to the decay curves. Therefore for each laser-induced decay recorded with DESIREE for laser firing times tL up to 90.6 ms, we have determined the corresponding IEDs considering the two contributions, i.e., single and double photon absorption. The single-photon contribution was found to be negligible for tL ≥ 50 ms. Finally, a complete simulation of the time evolution of the IED has been performed. It includes, as inputs, the presently measured RF rates, and theoretical dissociation and IR rates. The resulting time evolution of the IED agrees rather well with the one resulting from Mini-Ring and DESIREE experiments. Compared to previously investigated smaller PAH, we found that tetracene is cooling about 6 times faster than anthracene.15,20 This highlights the importance of taking the RF process into account for accurate predictions of the survival probabilities of PAHs in astrophysical environments.24 Additional experiments supported by theoretical investigations are needed to determine if a general tendency exists for the efficiency of the RF cooling process as a function of the size and/or shape (cata- or peri-condensed) of PAH cations in order to determine their resilience against dissociation and hence abundances in e.g. the ISM.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work is based upon work from COST Action (CA18212) – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). Part of this work was performed at the Swedish National Infrastructure, DESIREE (Swedish Research Council Contracts No. 2017-00621 and 2021-00155), and the authors thank the staff of DESIREE for their crucial contributions. Part of this work was performed at the Mini-Ring ion storage ring, and the authors wish to thank the local technical staff (G. Montagne) for the maintenance of this set-up during the experimental runs. HC, HTS and HZ acknowledge funding from the Swedish Research Council (contract no. 2019-04379, 2018-04092 and 2020-03437). MHS, HC, HTS, HZ, and acknowledge support from the project grant “Probing charge- and mass-transfer reactions on the atomic level” (2018.0028) from the Knut and Alice Wallenberg Foundation. JB and SM acknowledge funding from the Agence Nationale pour la Recherche, ANR grant no. ANR-21-CE30-0010, SynPAHcool.Notes and references
- A. Leger and J. L. Puget, Astron. Astrophys., 1984, 137(1), L5–L8 CAS.
- L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., Lett., 1985, 290, L25–L28 CrossRef CAS.
- A. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- J. J. Jensen, S. F. Hönig, S. Rakshit, A. Alonso-Herrero, D. Asmus, P. Gandhi, M. Kishimoto, A. Smette and K. R. W. Tristram, Mon. Not. R. Astron. Soc., 2017, 470, 3071–3094 CrossRef CAS.
- J. Montillaud, C. Joblin and D. Toublanc, Astron. Astrophys., 2013, 552, A15 CrossRef.
- D. J. Stock, W. D.-Y. Choi, L. G. V. Moya, J. N. Otaguro, S. Sorkhou, L. J. Allamandola, A. G. G. M. Tielens and E. Peeters, Astrophys. J., 2016, 819, 65 CrossRef.
- D. J. Stock and E. Peeters, Astrophys. J., 2017, 837, 129 CrossRef.
- G. Malloci, C. Joblin and G. Mulas, Chem. Phys., 2007, 332, 353–359 CrossRef CAS.
- J. Montillaud, C. Joblin and D. Toublanc, EAS Publ. Ser., 2011, 46, 447–452 CrossRef CAS.
- A. I. S. Holm, H. A. B. Johansson, H. Cederquist and H. Zettergren, J. Chem. Phys., 2011, 134, 044301 CrossRef CAS PubMed.
- O. Lacinbala, F. Calvo, C. Dubosq, C. Falvo, P. Parneix, M. Rapacioli, A. Simon and T. Pino, J. Chem. Phys., 2022, 156, 144305 CrossRef CAS PubMed.
- C. Joblin, P. Boissel, A. Leger, L. D’Hendecourt and D. Defourneau, Astron. Astrophys., 1995, 299, 835 CAS.
- B. West, C. Joblin, V. Blanchet, A. Bodi, B. Sztáray and P. M. Mayer, J. Phys. Chem. A, 2012, 116, 10999–11007 CrossRef CAS PubMed.
- B. West, F. Useli-Bacchitta, H. Sabbah, V. Blanchet, A. Bodi, P. M. Mayer and C. Joblin, J. Phys. Chem. A, 2014, 118, 7824–7831 CrossRef CAS PubMed.
- S. Martin, J. Bernard, R. Brédy, B. Concina, C. Joblin, M. Ji, C. Ortega and L. Chen, Phys. Rev. Lett., 2013, 110, 063003 CrossRef CAS PubMed.
- M. Ji, J. Bernard, L. Chen, R. Brédy, C. Ortéga, C. Joblin, A. Cassimi and S. Martin, J. Chem. Phys., 2017, 146, 044301 CrossRef CAS PubMed.
- B. West, S. Rodriguez Castillo, A. Sit, S. Mohamad, B. Lowe, C. Joblin, A. Bodi and P. M. Mayer, Phys. Chem. Chem. Phys., 2018, 20, 7195–7205 RSC.
- M. Diedhiou, J. Burner, B. J. West and P. M. Mayer, Chem. Phys. Lett., 2019, 726, 93–98 CrossRef CAS.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081 CrossRef CAS.
- S. Martin, M. Ji, J. Bernard, R. Brédy, B. Concina, A. R. Allouche, C. Joblin, C. Ortega, G. Montagne, A. Cassimi, Y. Ngono-Ravache and L. Chen, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 053425 CrossRef.
- C. Ortega, N. Kono, M. Ji, R. Brédy, J. Bernard, C. Joblin, A. Cassimi, Y. Ngono-ravache, L. Chen and S. Martin, J. Phys.: Conf. Ser., 2015, 635, 032051 CrossRef.
- A. Léger, P. Boissel and L. d'Hendecourt, Phys. Rev. Lett., 1988, 60, 921–924 CrossRef PubMed.
- P. Boissel, P. de Parseval, P. Marty and G. Lefèvre, J. Chem. Phys., 1997, 106, 4973–4984 CrossRef CAS.
- M. H. Stockett, J. N. Bull, H. Cederquist, S. Indrajith, M. Ji, J. E. N. Navarrete, H. T. Schmidt, H. Zettergren and B. Zhu, Resilience of small PAHs in interstellar clouds: Efficient stabilization of cyanonaphthalene by fast radiative cooling, arXiv, 2022, preprint, arXiv:2209.05229 [astro-ph.GA], DOI:10.48550/arXiv.2209.05229.
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef CAS PubMed.
- D. Zajfman, O. Heber, L. Vejby-Christensen, I. Ben-Itzhak, M. Rappaport, R. Fishman and M. Dahan, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, R1577–R1580 CrossRef CAS.
- O. Aviv, Y. Toker, M. Errit, K. G. Bhushan, H. B. Pedersen, M. L. Rappaport, O. Heber, D. Schwalm and D. Zajfman, Rev. Sci. Instrum., 2008, 79, 083110 CrossRef CAS PubMed.
- T. Doussineau, P. Paletto, P. Dugourd and R. Antoine, J. Am. Soc. Mass Spectrom., 2015, 26, 7–13 CrossRef CAS PubMed.
- P. Reinhed, A. Orbán, S. Rosén, R. Thomas, I. Kashperka, H. Johansson, D. Misra, A. Fardi, L. Brännholm, M. Björkhage, H. Cederquist and H. Schmidt, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 621, 83–90 CrossRef CAS.
- J. Bernard, B. Wei, A. Bourgey, R. Brédy, L. Chen, M. Kerleroux, S. Martin, G. Montagne, A. Salmoun and B. Terpend-Ordacière, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 262, 105–116 CrossRef CAS.
- S. P. Møller, Nucl. Instrum. Methods Phys. Res., Sect. A, 1997, 394, 281–286 CrossRef.
- T. Tanabe and K. Noda, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 496, 233–237 CrossRef CAS.
- S. Jinno, T. Takao, Y. Omata, A. Satou, H. Tanuma, T. Azuma, H. Shiromaru, K. Okuno, N. Kobayashi and I. Watanabe, Nucl. Instrum. Methods Phys. Res., Sect. A, 2004, 532, 477–482 CrossRef CAS.
- J. Bernard, G. Montagne, R. Brédy, B. Terpend-Ordacière, A. Bourgey, M. Kerleroux, L. Chen, H. T. Schmidt, H. Cederquist and S. Martin, Rev. Sci. Instrum., 2008, 79, 075109 CrossRef CAS PubMed.
- H. T. Schmidt, R. D. Thomas, M. Gatchell, S. Rosén, P. Reinhed, P. Löfgren, L. Brännholm, M. Blom, M. Björkhage, E. Bäckström, J. D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, L. Liljeby, A. Källberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W. D. Geppert, K. G. Rensfelt, H. Danared, A. Paál, M. Masuda, P. Halldén, G. Andler, M. H. Stockett, T. Chen, G. Källersjö, J. Weimer, K. Hansen, H. Hartman and H. Cederquist, Rev. Sci. Instrum., 2013, 84, 055115 CrossRef CAS PubMed.
- R. von Hahn, A. Becker, F. Berg, K. Blaum, C. Breitenfeldt, H. Fadil, F. Fellenberger, M. Froese, S. George, J. Göck, M. Grieser, F. Grussie, E. A. Guerin, O. Heber, P. Herwig, J. Karthein, C. Krantz, H. Kreckel, M. Lange, F. Laux, S. Lohmann, S. Menk, C. Meyer, P. M. Mishra, O. Novotný, A. P. OConnor, D. A. Orlov, M. L. Rappaport, R. Repnow, S. Saurabh, S. Schippers, C. D. Schröter, D. Schwalm, L. Schweikhard, T. Sieber, A. Shornikov, K. Spruck, S. Sunil Kumar, J. Ullrich, X. Urbain, S. Vogel, P. Wilhelm, A. Wolf and D. Zajfman, Rev. Sci. Instrum., 2016, 87, 063115 CrossRef CAS PubMed.
- M. Gatchell and H. Zettergren, Commun. Chem., 2022, 5, 28 CrossRef PubMed.
- E. K. Anderson, A. F. Schmidt-May, P. K. Najeeb, G. Eklund, K. C. Chartkunchand, S. Rosén, A. Larson, K. Hansen, H. Cederquist, H. Zettergren and H. T. Schmidt, Phys. Rev. Lett., 2020, 124, 173001 CrossRef CAS PubMed.
- J. Rajput, L. Lammich and L. H. Andersen, Phys. Rev. Lett., 2008, 100, 153001 CrossRef PubMed.
- S. Tomita, J. U. Andersen, H. Cederquist, B. Concina, O. Echt, J. S. Forster, K. Hansen, B. A. Huber, P. Hvelplund, J. Jensen, B. Liu, B. Manil, L. Maunoury, S. B. Nielsen, J. Rangama, H. T. Schmidt and H. Zettergren, J. Chem. Phys., 2006, 124(2), 024310 CrossRef CAS PubMed.
- S. Iida, S. Kuma, M. Kuriyama, T. Furukawa, M. Kusunoki, H. Tanuma, K. Hansen, H. Shiromaru and T. Azuma, Phys. Rev. A, 2021, 104, 043114 CrossRef CAS.
- M. Goto, J. Matsumoto, H. Shiromaru, Y. Achiba, T. Majima, H. Tanuma and T. Azuma, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 033406 CrossRef.
- K. Saha, V. Chandrasekaran, O. Heber, M. A. Iron, M. L. Rappaport and D. Zajfman, Nat. Commun., 2018, 9, 912 CrossRef CAS PubMed.
- M. H. Stockett, J. N. Bull, J. T. Buntine, E. Carrascosa, M. Ji, N. Kono, H. T. Schmidt and H. Zettergren, J. Chem. Phys., 2020, 153, 154303 CrossRef CAS PubMed.
- F.-Q. Chen, N. Kono, R. Suzuki, T. Furukawa, H. Tanuma, P. Ferrari, T. Azuma, J. Matsumoto, H. Shiromaru, V. Zhaunerchyk and K. Hansen, Phys. Chem. Chem. Phys., 2019, 21, 1587–1596 RSC.
- G. Ito, T. Furukawa, H. Tanuma, J. Matsumoto, H. Shiromaru, T. Majima, M. Goto, T. Azuma and K. Hansen, Phys. Rev. Lett., 2014, 112, 183001 CrossRef CAS PubMed.
- V. Chandrasekaran, B. Kafle, A. Prabhakaran, O. Heber, M. Rappaport, H. Rubinstein, D. Schwalm, Y. Toker and D. Zajfman, J. Phys. Chem. Lett., 2014, 5, 4078–4082 CrossRef CAS PubMed.
- A. E. K. Sundén, M. Goto, J. Matsumoto, H. Shiromaru, H. Tanuma, T. Azuma, J. U. Andersen, S. E. Canton and K. Hansen, Phys. Rev. Lett., 2009, 103, 143001 CrossRef PubMed.
- R. D. Thomas, H. T. Schmidt, G. Andler, M. Björkhage, M. Blom, L. Brännholm, E. Bäckström, H. Danared, S. Das, N. Haag, P. Halldén, F. Hellberg, A. I. S. Holm, H. A. B. Johansson, A. Källberg, G. Källersjö, M. Larsson, S. Leontein, L. Liljeby, P. Löfgren, B. Malm, S. Mannervik, M. Masuda, D. Misra, A. Orbán, A. Paál, P. Reinhed, K.-G. Rensfelt, S. Rosén, K. Schmidt, F. Seitz, A. Simonsson, J. Weimer, H. Zettergren and H. Cederquist, Rev. Sci. Instrum., 2011, 82, 065112 CrossRef CAS PubMed.
- E. Bäckström, D. Hanstorp, O. M. Hole, M. Kaminska, R. F. Nascimento, M. Blom, M. Björkhage, A. Källberg, P. Löfgren, P. Reinhed, S. Rosén, A. Simonsson, R. D. Thomas, S. Mannervik, H. T. Schmidt and H. Cederquist, Phys. Rev. Lett., 2015, 114, 143003 CrossRef PubMed.
- S. Rosén, H. T. Schmidt, P. Reinhed, D. Fischer, R. D. Thomas, H. Cederquist, L. Liljeby, L. Bagge, S. Leontein and M. Blom, Rev. Sci. Instrum., 2007, 78, 113301 CrossRef PubMed.
- J. U. Andersen, H. Cederquist, J. S. Forster, B. A. Huber, P. Hvelplund, J. Jensen, B. Liu, B. Manil, L. Maunoury, S. Brøndsted Nielsen, U. V. Pedersen, H. T. Schmidt, S. Tomita and H. Zettergren, Eur. Phys. J. D, 2003, 25, 139–148 CrossRef CAS.
- J. Bernard, L. Chen, R. Brédy, M. Ji, C. Ortéga, J. Matsumoto and S. Martin, Nucl. Instrum. Methods Phys. Res., Sect. B, 2017, 408, 21–26 CrossRef CAS.
- S. Martin, J. Matsumoto, N. Kono, M.-C. Ji, R. Brédy, J. Bernard, A. Cassimi and L. Chen, Nucl. Instrum. Methods Phys. Res., Sect. B, 2017, 408, 209–212 CrossRef CAS.
- J. Szczepanski, J. Drawdy, C. Wehlburg and M. Vala, Chem. Phys. Lett., 1995, 245, 539–548 CrossRef CAS.
| This journal is © the Owner Societies 2023 |