Halogen bonds with carbenes acting as Lewis base units: complexes of imidazol-2-ylidene: theoretical analysis and experimental evidence

Abstract

ωB97XD/aug-cc-pVDZ and ωB97XD/aug-cc-pVTZ calculations were performed on complexes of imidazol-2-ylidene that are linked by halogen bonds. This singlet carbene acts as the Lewis base through a lone electron pair located at the carbon centre. The XCCH, XCN and X₂ units were chosen here as those that interact through the X Lewis acid halogen centre (X = Cl, Br and I); if X = F the complexes are linked by interactions which are not classified as halogen bonds. The properties of interactions that occur in complexes are analyzed using the results of DFT calculations which are supported by parameters derived from the Quantum Theory of Atoms in Molecules, QTAIM, and the Natural Bond Orbital, NBO, approaches. The energy decomposition analysis, EDA, applied here provided additional characteristics of interactions linking complexes analyzed. The majority of complexes are linked by the medium in strength and strong halogen bonds which often possess characteristics typical for covalent bonds. Searches through the Cambridge Structural Database were also performed and structures analogues to complexes analyzed theoretically were found, and these structures are also discussed in this study.

---

Introduction

Carbenes are understood most often as neutral compounds that contain divalent carbon atoms.¹ Since the latter centre possesses six valence electrons, two of them are nonbonding electrons. These two electrons may be located in two different orbitals and their spins are parallel for the σ¹p_π¹ triplet state or characterized by opposite spins for the singlet carbenes, and they may occupy the same σ or p_π orbital.²

The divalent character of the carbon atom has been discussed and contested in various studies since substituents often influence electron charge shifts which may lead in stable singlet carbenes to the carbon-heteroatom link that possesses the double bond character.² This is why other definitions of carbene compounds were proposed, such as the one proposed by Bertrand and co-workers² that these are “compounds with a neutral dicoordinate carbon atom featuring either two singly occupied nonbonding orbitals (triplet state) or alternatively both a lone pair and an accessible vacant orbital (singlet state).” Carbenes play a crucial role in numerous chemical reactions and processes, for example, they act as transient intermediates.²

Metallylenes, which are heavier analogues of carbenes, such as silylenes (R₂Si), germylenes (R₂Ge), stannylenes (R₂Sn), and plumbylenes (R₂Pb) (R substituents attached to the tetrel centre need not be the same) are often the subject of various studies.³ It is often considered that the valency of the tetrel centre of these analogues of carbenes is two. In contrast to carbenes, these analogues have a lower ability to form hybrid orbitals.³ Hence the heavier tetrel centres are characterized by the (ns)²(np)² valence bond configuration, at least approximately. It is expected that for the singlet state, the lone pair electrons of these heavier analogues are inert due to the very high s-character of the corresponding orbital. In a recent study,⁴ for example, MP2/aug-cc-pVTZ calculations were performed on dihalometallylenes to analyze their Lewis acid and Lewis base properties. For germylenes, Ge⋯Cl, Ge⋯Br, and Ge⋯O interactions were found. The germanium centre acts here as the electrophilic one. The Ge⋯O interactions in the above mentioned germylene complexes may be classified as the π-hole tetrel bonds.⁴

In general various earlier studies have shown that the heavier analogues of carbenes, metallylenes, possess a Lewis acid character because of the vacant p orbital but they do not have the Lewis base properties in spite of the existence of a lone electron pair.⁴ This is in contrast to the carbon centres of carbenes that possess the Lewis base properties since they may donate electrons in various interactions and reactions,^5–8 and the hydrogen bonds were a subject of numerous studies.^9–11 Special attention is paid in various studies to the role of carbenes not only in different types of interactions but also in different processes and in catalysis.^1,2 For example, nucleophilic activation of sulfur hexafluoride by N-heterocyclic carbenes and N-heterocyclic olefins was analyzed,¹² and it was discussed that N-heterocyclic carbenes (NHCs) possess strong nucleophilic properties interacting with different Lewis acid sites.¹² The role of NHCs in numerous processes of organic chemistry was discussed in earlier¹³ and more recent studies.¹⁴

However attention is paid in this study to the carbene species that are linked with Lewis acid centres through halogen bonds. Several studies related to the latter topic may be mentioned here; the study on the stable carbene iodine adduct since the halogen bond in the 1,3-diethyl-2-iodo-4,4-dimethylimidazolium iodide crystal structure was analyzed,¹⁵ the theoretical calculations were performed on simple complexes linked through halogen bonds,^16–18 the hydrogen bond and halogen bond interactions for singlet and triplet diphenylcarbenes were discussed on the basis of high level DLPO-CCSD(T) calculations,¹⁹ and the halogen bond interaction in complexes of anionic N-heterocyclic carbenes was analyzed in a recent study.²⁰

The studies on carbene complexes mentioned above concern halogen bond interactions that are very important and are often treated as counterparts of hydrogen bonds.^21–24 These interactions often play a crucial role in arrangements of molecules and ions in crystals. The halogen bond is often compared with other Lewis acid–Lewis base interactions.^25–28 Similar to the case of other interactions there are different factors that influence the strength of halogen bonds.^29,30 These factors have been analyzed in detail recently.³⁰ Hence one can see that there are only a few studies on halogen bonds in complexes of carbenes, and often they do not concern the halogen bond directly. That is why the aim of this study is to analyse the halogen bonds that link the imidazol-2-ylidene moiety with XCCH, XCN and X₂ Lewis acid units (X = F, Cl, Br and I). The choice of the latter species is dictated by the Lewis acid properties of X-centres and it guarantees a wide range of halogen bond strengths. That is why it is also possible to follow the process of the transfer of halonium ions; for very strong halogen bonds the halogen centre detaches from the Lewis acid unit and attaches to the Lewis base centre of carbene. This halonium ion transfer for other Lewis base units (not carbenes) was analyzed in earlier studies.^31–34 The singlet state of the imidazol-2-ylidene species was chosen since it is lower in energy than its triplet analogue (Scheme 1 shows this state to be compared with the more general singlet and triplet CR₁R₂ carbene species).

Scheme 1 The singlet and triplet states of carbenes and the singlet state of NHC species.

Cambridge Structural Database^35,36 searches were also performed in this study to find complexes where NHC species are linked with Lewis acid units through halogen bonds. The DFT calculations that were performed in this study for the simple complexes of imidazol-2-ylidene mentioned above were supported by results of the Quantum Theory of Atoms in Molecules (QTAIM) approach^37,38 and the Natural Bond Orbital (NBO) method.^39,40

Computational methods

DFT calculations for the complexes analyzed in this study have been carried out with the use of the Gaussian16 set of codes.⁴¹ The ωB97XD functional⁴² as well as aug-cc-pVDZ and aug-cc-pVTZ basis sets (aug-cc-pVDZ-PP and aug-cc-pVTZ-PP for iodine)^43–48 were applied. It has been justified that for analyses of interactions, the ωB97XD functional, in connection with the Dunning-style aug-cc-pVDZ and aug-cc-pVTZ basis set provides more reliable results than other functionals and basis sets.⁴⁹ Frequency calculations have been carried out at both ωB97XD/aug-cc-pVDZ and ωB97XD/aug-cc-pVTZ levels for optimized structures and imaginary frequencies were not found; thus these systems correspond to energetic minima. The complexes of the imidazol-2-ylidene moiety that act as the Lewis base unit through the lone pair of the carbon centre with XCCH, XCN and X₂ Lewis acid units (X = F, Cl, Br and I) were calculated. The latter species act as the electrophiles through the σ-holes of the X halogen centres. Hence for the majority of the complexes investigated here links by halogen bonds are observed. Fig. 1 shows molecular graphs of selected halogen bonded complexes. The interactions of the imidazol-2-ylidene moiety with the FCCH, FCN and F₂ species that were chosen initially as possible Lewis acid units are not classified as halogen bonds. These interactions are discussed in the next sections.

Fig. 1 The molecular graphs of complexes of imidazol-2-ylidene with (a) BrCCH, (b) ClCN, and (c) Cl₂; big circles correspond to attractors, small circles to critical points, green ones to bond critical points and red ones to ring critical points.

DFT was applied in previous studies to analyze carbene and organic biradical species;⁵⁰ it was found that DFT is not appropriate for calculations on multireference systems.⁵⁰ In another related study⁵¹ it was found that several functionals well reproduce geometries and energies of carbenes. For example, the ωB97X-D3 seems to be one of the best functionals to reproduce the energy difference between the singlet and triplet states of carbenes. Hence it seems to be justified to apply ωB97XD/aug-cc-pVDZ and ωB97XD/aug-cc-pVTZ levels in this study. It is worth mentioning that the T1 diagnostics⁵² performed here for complexes analyzed does not show their multireference character.

The BP86-D3/TZ2P level was applied to perform the energy decomposition analysis, EDA, calculations for the above-mentioned complexes that were optimized at the ωB97XD/aug-cc-pVTZ level. Thus the BP86 functional^53,54 with the Grimme dispersion corrections⁵⁵ was applied, and with the uncontracted Slater-type orbitals (STOs) as basis functions with triple-ζ quality for all elements.⁵⁶ Relativistic scalar ZORA corrections⁵⁷ were applied for systems containing heavier halogen atoms (Br and I). The EDA calculations^58,59 were performed with the use of the ADF2019 program.^57,60 The total interaction energy, E_int, in this EDA decomposition scheme contains terms shown in eqn (1).

E_int = E_elstat + E_Pauli + E_orb + E_disp (1)

The term E_elstat corresponds usually to the attractive interactions (formally negative) and it also corresponds, from the physical point of view, to the quasi-classical electrostatic interaction between the unperturbed charge distributions of atoms. The Pauli repulsion, E_Pauli, is the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments to the wave function that obeys the Pauli principle through antisymmetrisation and renormalization of the product wave function. The orbital interaction, E_orb, corresponds to effects of the charge transfer and polarization, i.e. to electron charge shifts resulting from complexation. The dispersion interaction energy, E_disp, is also included in this scheme.

The ADF2019 program^57,60 was also used to calculate the Wiberg index^61,62 and the delocalization index, DI.^63,64 The ‘Quantum Theory of Atoms in Molecules’, QTAIM,^37,38 was applied to analyse characteristics of the bond critical points corresponding to interactions occurring in the structures discussed in this study; these are the halogen bonds and interactions which occur in complexes containing the FCCH, FCN and F₂ Lewis acid units. The QTAIM charges were also calculated.

The AIMAll program⁶⁵ was used to perform molecular graphs and electrostatic potential maps for systems optimized at the ωB97XD/aug-cc-pVTZ level. The NBO 6.0 program⁶⁶ implemented in the ADF2019 set of codes^57,60 was applied to perform NBO calculations. The latter method was applied to calculate the orbital–orbital energies as well as the NBO charges. Hence for the systems optimized at the ωB97XD/aug-cc-pVTZ level, the BP86-D3/TZ2P NBO calculations were performed with the use of ADF 2019.302 program codes.

Searches through the Cambridge Structural Database, CSD^35,36 were performed to find crystal structures containing the NHC motifs linked through halogen bonds with the Lewis acid units, i.e. to find systems similar to those resulting from theoretical calculations.

Results and discussion

Crystal structures

Searches through the Cambridge Structural Database, CSD,^35,36 were performed to find crystal structures which contain the imidazol-2-ylidene skeleton, i.e. the CNCCN ring. The following criteria of accuracy for these searches were applied: 3D coordinates determined, no disordered structures, no errors, no polymeric structures, no powder structures, R-factor less or equal to 7.5%, and only single crystal structures.

These searches are restricted to a part of systems analyzed theoretically in this study. The first search concerns the structures containing the above-mentioned ring that is connected with the X₂ molecule through the X–X⋯C link (X halogen atoms in X–X species are not necessarily the same elements) that may be classified as the halogen bond. The carbon centre is the electron donor here through the lone electron pair. There are no structures in the CSD that meet the above conditions. However it is probable that for the X–X⋯C interaction the halonium ion transfer occurs and leads to the X⁻⋯⁺X–C arrangement.⁶⁷ Hence the second search was performed to find structures containing the CNCCN ring and the X⋯X–C connection; as before, X halogen atoms are not necessarily the same elements; the same search criteria as before were chosen. For X⋯X(C) distances a condition was fixed that they are shorter than the sum of corresponding van der Waals radii. The radii that were proposed by Bondi⁶⁸ and that are included in the CSD were applied here.

The 5.43 version of the CSD in the above searches was used, with all updates up to November 2022. 97 crystal structures which contain 150 X⋯X–C connections fulfilling the above criteria were found. However only in 62 connections does the halogen anion act as the Lewis base; in the remaining structures the halogen Lewis base centre is part of a larger ion or molecule. In the case of systems with halogen anions as the Lewis base units, the following halogen bonds were found; C–I⋯I⁻ (13 cases), C–Br⋯Br⁻ (18), C–Cl⋯Cl⁻ (9), C–I⋯Br⁻ (14), C–I⋯Cl⁻ (1), C–Br⋯I⁻ (5), C–Br⋯Cl⁻ (1) and C–Cl⋯Br⁻ (1). These arrangements correspond to rather strong halogen bonds that are close to linearity.

Fig. 2 shows the histogram of the C–X⋯X⁻ angles. One can see that systems characterized by angles lower than 160° do not occur. This means that the substituents in the NHC motifs do not strongly disturb the linearity of the C–X⋯X⁻ interactions. In crystal structures found in the search mentioned above there are various substituents connected with the nitrogen centres of the CNCCN ring that could disturb the above-mentioned linearity. Only in two cases, in crystal structures of bis(2-bromo-2-imidazolinium) tetrabromo-copper(II)⁶⁹ and 2-chloroimidazolium aqua-trichloro-copper(II)⁷⁰ are hydrogen atoms attached to the nitrogen centers where C–Br⋯Br and C–Cl⋯Cl angles are equal to 176.1° and 169.6°, respectively. However in these structures the C–X bonds are connected with more complex anions, CuBr₄²⁻ and [CuCl₃(H₂O)]⁻, respectively; these links do not belong to the sample of Fig. 2.

Fig. 2 The histogram of C–X⋯X⁻ angles of the sample containing 62 systems.

The searches discussed above indicate that the halogen bond interactions of singlet carbenes with dihalogens are strong enough that the cleavage of X₂ molecule occurs as well as the transfer of a halonium cation to the carbon centre possessing a lone electron pair. Fig. 3 shows examples of crystal structures that were found in the second search. Fig. 3a shows the fragment of the 1,3-diethyl-2-iodo-4,5-dimethylimidazolium iodide crystal structure where the C–I⋯I⁻ halogen bonds occur.⁷¹ Similar charge assisted halogen bonds occur in the crystal structure of 2-bromo-2,3-dihydro-1,3-diisopropyl-4,5-dimethylimidazol-2-ium bromide.⁷²Fig. 3b shows the fragment of this structure where the C–Br⋯Br⁻ arrangements are observed.

Fig. 3 Fragments of crystal structures of (a) 1,3-diethyl-2-iodo-4,5-dimethylimidazolium iodide, (b) 2-bromo-2,3-dihydro-1,3-diisopropyl-4,5-dimethylimidazol-2-ium bromide, and (c) 2,4,5-tribromo-1-methyl-1H-imidazole.

It was mentioned above that more than 50% of the second search contained the C–X⋯X arrangements, i.e. halogen bonds where the Lewis base units are more complex than simple halide anions. Fig. 3c shows an example, the fragment of the 2,4,5-tribromo-1-methyl-1H-imidazole crystal structure where the C–Br⋯Br halogen bonds are observed.⁷³

Complexes of imidazol-2-ylidene – geometries

Table 1 presents selected geometrical parameters of the complexes analyzed theoretically here. Fig. 1 and 4 show molecular graphs of selected complexes with geometries resulting from DFT optimizations. For each complex, ωB97XD/aug-cc-pVDZ and ωB97XD/aug-cc-pVTZ calculations were performed (results are collected in the upper and bottom rows of Table 1, respectively). The R–X (R = C, X) bond lengths of the Lewis acid units, the X⋯C intermolecular distances as well as the R–X⋯C angles are given in this table. Additionally the R–X₀ bond lengths of the separated Lewis acid species not involved in interactions with imidazol-2-ylidene and any other moiety are presented.

Table 1 Geometrical (in Å, degrees) parameters of the analyzed complexes. R–X₀ and R–X (R = C, X) bond lengths in isolated Lewis acid units and in complexes are presented, as well as X⋯C distances and R–X⋯C angles; ωB97XD/aug-cc-pVDZ and ωB97XD/aug-cc-pVTZ results are in the upper and bottom rows, respectively

Lewis acid	R–X0	R–X	X⋯C	R–X⋯C
a Energy of this complex is lower by 2.4 kcal mol^−1 than the energy of the corresponding linear system (for ωB97XD/aug-cc-pVDZ results).
FCCH^a	1.279	1.271	3.380	80.6
	1.271	1.263	3.427	81.6
FCCH	1.279	1.276	3.811	180.0
	1.271	—	—	—
ClCCH	1.650	1.656	3.129	180.0
	1.639	1.644	3.151	179.4
BrCCH	1.796	1.817	2.971	180.0
	1.790	1.809	2.998	179.2
ICCH	2.003	2.058	2.837	180.0
	1.993	2.044	2.855	180.0
FCN	1.255	1.263	3.346	180.0
	1.239	1.254	3.093	66.7
ClCN	1.643	1.654	2.978	180.0
	1.632	1.642	2.991	179.4
BrCN	1.793	1.830	2.809	180.0
	1.787	1.822	2.827	180.0
ICN	2.006	2.108	2.648	180.0
	1.996	2.094	2.658	179.9
Cl2	2.018	2.605	1.732	179.9
	1.998	2.584	1.721	180.0
Br2	2.299	2.695	1.979	180.0
	2.282	2.674	1.974	180.0
I2	2.697	2.927	2.315	180.0
	2.669	2.896	2.325	180.0

---

Fig. 4 The molecular graphs of complexes of imidazol-2-ylidene with (a) F₂, (b) FCCH, and (c) FCN; big circles correspond to attractors, small circles to critical points, green ones to bond critical points and red ones to ring critical points.

Let us look at complexes containing a fluorine centre, i.e. complexes of the imidazol-2-ylidene species with F₂, FCCH and FCN units. In the case of the C₃N₂H₄⋯F₂ complex, the fluorine molecule has been attached to the imidazol-2-ylidene moiety (Fig. 4a). This is a situation different to that described in an early study⁷¹ and occurring for the interaction of 1,3-diethyl-4,5-dimethylimidazol-2-ylidene with iodine where the dihalogen species is attached to carbene. It may be treated as the nucleophilic attack of the carbene on the iodine molecule that leads to the 1,3-diethyl-2-iodo-4,5-dimethylimidazolium iodide observed in the crystal structure.⁷¹ It was pointed out that the latter moiety is the transition state of the above-mentioned nucleophilic attack since the C–I–I arrangement is close to linearity (this angle is equal to 176.0°).⁷¹ However the complex with the fluorine molecule (Fig. 4a) and other complexes of Cl₂, Br₂ and I₂ containing the X–X⋯C linear arrangements (see Table 1) and analyzed theoretically here correspond to energetic minima (Fig. 1 shows an example of the complex with Cl₂ species). This may suggest that the 1,3-diethyl-2-iodo-4,5-dimethylimidazolium iodide observed in the crystal structure⁷¹ is not a transition state but it also corresponds to the energetic minimum.

Fig. 4b presents the complex of the imidazol-2-ylidene species with the FCCH molecule. One can see two intermolecular links here. The C–F⋯C link that could be classified as the halogen bond is far from the linearity. The fluorine centre is negatively charged here as the QTAIM and NBO approaches indicate; however the electrostatic potential at fluorine is slightly positive but very close to zero (see the following sections for a discussion of the charges and electrostatic potentials). The latter may confirm the occurrence of a very weak halogen bond here. Another link that is probably classified as the N–H⋯C hydrogen bond also seems to be a weak interaction. Thus one may expect a significant contribution of the dispersion forces that stabilize this complex. It is worth mentioning that this “non-linear” structure (the C–F⋯C angle amounts to 81.6° at the ωB97XD/aug-cc-pVTZ level) optimized within the DFT approach occurs for both the DZ and TZ Dunning style basis sets applied here. However, the linear system corresponding to the local energetic minimum where the C–F⋯C angle is equal to 180° was optimized at the ωB97XD/aug-cc-pVDZ level only (see Table 1), and the trials to optimize the linear structure at the ωB97XD/aug-cc-pVTZ level that corresponds to the energetic minimum were not successful.

Fig. 4c presents the molecular graph of the complex of imidazol-2-ylidene with an FCN molecule. The N–H⋯N hydrogen bond and the weak C⋯C interaction are observed here. Thus the non-linear structure was also optimized at the ωB97XD/aug-cc-pVTZ level; however the ωB97XD/aug-cc-pVDZ calculations show the linear C–F⋯C arrangement.

Let us discuss links between the carbon centre of imidazol-2-ylidene and the heavier halogen centers (Cl, Br and I). These optimized structures correspond to energetic minima and they are linear, or nearly so since the C–X⋯C or X–X⋯C angle is not less than 179°. It has been pointed out in various studies that the intermolecular distance roughly expresses the strength of interaction,⁷⁴ especially for the hydrogen bonded systems.⁷⁵ This means that for shorter distances stronger interactions are observed, up to very short distances where such interactions are extremely strong and they often correspond to typical covalent bonds. The results in Table 1 show that the X⋯C intermolecular distance decreases with the increase of the atomic number of halogen centre for complexes of XCCH and XCN species. In contrast, in the case of complexes with the X₂ dihalogen molecule this distance increases with the increase of the halogen atomic number. These relationships roughly express the trends of the increase and decrease of the strength of halogen bond interactions. The relationships concerning complexes with dihalogen molecules may be slightly surprising since the trend observed here is opposite to other trends presented in other studies. One may relate the increase of the X⋯C intermolecular distance with the increase of the van der Waals radius for heavier halogen atoms. However that is not a case for complexes of XCCH and XCN. This is discussed here in later sections.

One can see (Table 1) that the complexation results in the lengthening of the C–X or X–X bond length (so-called red-shift of the corresponding bond stretching frequency). Only in the case of FCCH complexes is the slight shortening of the C–F bond resulting from complexation observed. However one can see that these complexes are linked by specific interactions that were roughly discussed above. It seems that for the majority of complexes analyzed in this study the greater elongation occurs for stronger interactions. For example, taking into account the ωB97XD/aug-cc-pVTZ results of calculations, the elongation of the C–X bond of 0.005, 0.019 and 0.051 Å occurs for the complexes of ClCCH, BrCCH and ICCH species, respectively. For the complexes of XCN the following elongations occur, 0.010, 0.035 and 0.098 Å, for ClCN, BrCN and ICN Lewis acid units, respectively. The large elongations of 0.586, 0.392 and 0.227 Å occur for Cl₂, Br₂ and I₂ complexes, respectively. The latter should correspond to very strong, covalent in nature, interactions. However in the case of complexes of dihalogens this elongation decreases with the increase of the halogen atomic number.

Fig. 5 presents the correlation between the R–X percentage bond elongation, Δr (expressed by eqn (2)) and the X⋯C intermolecular distance. This relationship is expressed by the quadratic function. It is an excellent correlation (R² = 0.99) which shows that both parameters, the intermolecular X⋯C distance as well the elongation of the R–X bond, may be treated as a rough estimation of the strength of interaction.

Δr = [(r_R–X – r_R–X⁰)/r_R–X⁰] × 100% (2)

There are the following designations here; r_R–X is the C–X or the X–X bond length of the Lewis acid unit in the complex while r_R–X⁰ is the bond length in the unit not involved in the interaction with the imidazol-2-ylidene moiety or in an interaction with any other species. This parameter roughly corresponds to the strength of the interactions, particularly it may express the strength of the hydrogen bond.⁷⁶ A more complex parameter based on this bond length and on the topological QTAIM characteristics was also introduced.⁷⁶ However it was checked for the hydrogen bond interactions that both parameters described above do not work correctly for so-called blue-shifting hydrogen bonds.^76,77 The Δr parameter is used here for the first time to evaluate halogen bond strength.

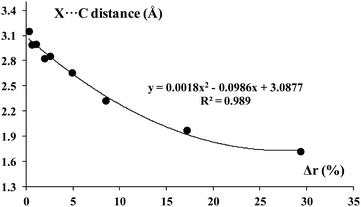Fig. 5 The relationship between the R–X bond elongation (percentage), Δr (eqn (2)) and the X⋯C distance (Å).

QTAIM and NBO parameters

Table 2 presents the QTAIM parameters of the R–X⋯C links (R = C or X) that are classified as halogen bonds. The characteristics of the X⋯C bond critical point, BCP, as well as the QTAIM charges of the centres of the above link are included. The delocalization index, DI,^63,64 which is roughly related to the bond order and to the covalency of interaction is also presented in this table. This index concerns X⋯C contacts.

Table 2 The characteristics of the X⋯C bond critical points (in a.u.) for systems analysed in this study. The electron density at BCP, ρ_BCP, the total electron energy density at BCP, H_BCP and the Laplacian of the electron density, ∇²ρ_BCP, are presented. The QTAIM charges (in a.u.) are also given, X-ch – the charge of halogen in contact with the imidazol-2-ylidene unit, R-ch – the charge of the atom connected with X (carbon or halogen), C-ch – the charge of carbon of the Lewis base unit that is in contact with halogen. The delocalization index concerning X⋯C intermolecular contact, DI (a.u.) is also given. These are the ωB97XD/aug-cc-pVTZ results

Lewis acid	ρ BCP	H BCP	∇^2ρBCP	X-ch	C-ch	R-ch	DI
FCCH	0.004	0.001	0.015	−0.684	0.799	0.188	0.033
ClCCH	0.011	0.002	0.037	−0.029	0.812	−0.450	0.126
BrCCH	0.018	0.001	0.050	0.191	0.818	−0.641	0.198
ICCH	0.029	−0.002	0.063	0.372	0.817	−0.099	0.327
FCN	—	—	—	−0.680	0.800	1.816	0.064
ClCN	0.016	0.002	0.049	0.044	0.812	1.062	0.161
BrCN	0.026	0.000	0.063	0.254	0.822	0.841	0.260
ICN	0.043	−0.007	0.071	0.412	0.826	0.679	0.445
Cl2	0.216	−0.156	−0.238	0.095	1.146	−0.779	1.172
Br2	0.140	−0.076	−0.005	0.183	0.991	−0.649	0.996
I2	0.082	−0.031	0.071	0.213	0.873	−0.491	0.748

---

Let us discuss BCPs at the X⋯C bond paths that correspond to the halogen bonds. One can see that for the complex of FCCH the non-linear C–F⋯C arrangement is observed with the long F⋯C distance equal to 3.427 Å (Table 1). This is why the electron density at the BCP, ρ_BCP, for this link amount is only 0.004 au. In the case of the FCN complex the bond path corresponding to the C–F⋯C contact is not even observed (see Fig. 4 and Table 2).

It has been highlighted in various studies that ρ_BCP is related to the strength of interactions, especially for the hydrogen bond systems in which correlations between the ρ_BCP value and other measures of the strength of interaction were found.^78,79 One can see that for complexes considered here the ρ_BCP value increases with the increase of the atomic number of the halogen centre for complexes of XCCH as well as for complexes of XCN. The reverse situation is observed for X₂ complexes where ρ_BCP decreases in the following order Cl₂ > Br₂ > I₂. Thus the ρ_BCP parameter is in agreement with other parameters expressing the strength of interactions which were discussed so far; the elongation of the R–X bond and the X⋯C distance.

It was pointed out that interactions may be classified on the basis of two QTAIM parameters, H_BCP and ∇²ρ_BCP, i.e. the total electron energy density at BCP and the Laplacian of the electron density at BCP, respectively. In particular this classification was performed for the hydrogen bond.^75,80 The negative ∇²ρ_BCP value indicates the covalent character of the interaction that occurs for covalent bonds usually (consequently in such a case H_BCP has to be negative). However for the positive ∇²ρ_BCP value, H_BCP may be negative which indicates the partly covalent character of the interaction. Thus the following classification was proposed, for hydrogen bonds⁸⁰ that may be extended for other types of interactions, ∇²ρ_BCP < 0 for very strong interactions, ∇²ρ_BCP > 0 and H_BCP < 0 for strong interactions, H_BCP > 0 (and consequently ∇²ρ_BCP > 0) for medium in strength and for weak interactions. The results of Table 2 show that H_BCP < 0 for complexes of ICCH and ICN as well as for Cl₂, Br₂ and I₂ complexes. Even more, for Cl₂ and Br₂ complexes ∇²ρ_BCP < 0. Hence it may be assumed that the C–Cl and C–Br covalent bonds are formed for the latter structures and that in these cases the 2-chloro-imidazol-2-ylidene and 2-bromo-imidazol-2-ylidene species interact with chloride and bromide anions, respectively. The formation of a 2-iodo-imidazol-2-ylidene iodide structure that is observed in the crystal structures of similar carbene iodine adducts⁷¹ may also be discussed since H_BCP is negative here. One may also consider that the properties of complexes described in this study model the process of the transfer of halonium ion that was discussed in previous studies.^31–34

The DI index may be treated as the next measure of the strength of interaction, and the DI values are inserted in Table 2. The DI value is greater for the greater value of ρ_BCP, for the shorter X⋯C distance and for the greater elongation of the R–X bond resulting from complexation.

Let us discuss the charges of centres corresponding to the halogen bond links. These are integrated QTAIM charges. One can see that for all complexes of imidazol-2-ylidene the positive charge of the carbon playing the role of the Lewis base centre is observed. Although it is an electron donor through the lone electron pair. The halogen centre possesses negative charge for complexes of FCCH, ClCCH and FCN. In all remaining complexes the halogen centres are positively charged.

Table 2 presents also the charges of R-centres (R is a carbon or halogen connected with the X halogen centre being in contact with imidazol-2-ylidene). It is worth noting that R is negative for X₂ Lewis acid units and that for these X₂ molecules the difference between charges decreases with the increase of the atomic number of halogen. This means that in the X₂ complexes considered here the great polarization of the Cl–Cl bond is observed that decreases for the Br–Br bond and next for I–I.

The latter results are confirmed by the NBO parameters presented in Table 3. The NBO charges show the same tendencies as those that are described here for QTAIM charges. The R centre is also negative for the X₂ species and the difference between charges of the centers of these molecules (between halogens) decreases with the increase of the atomic number of halogen. The charge of the halogen in contact with the carbene moiety increases in sub-series of XCCH and XCN complexes with the increase of the atomic number of X while for the sub-series of X₂ complexes the decrease is observed. The charge of fluorine in the FCCH and FCN units is negative and the charge of the carbon centre in the imidazol-2-ylidene molecule is positive. Hence there is an excellent agreement with the QTAIM charges here in spite of their different definitions; the NBO atomic charges are calculated as the sums of orbital occupancies (and the charge of a nucleus)^39,40,77 while in the QTAIM approach there is the division of a space of chemical species (ions or molecules) into regions attributed to atoms. The QTAIM atomic charge is the result of integration of the electron density of the atomic region (the charge of a nucleus is also taken into account here).^37,38,77

Table 3 NBO charges (in a.u.) of R–X⋯C links (marked by “ch” subscript) and NBO orbital–orbital energies, E_NBO's (kcal mol⁻¹) of complexes analyzed here. Wiberg indices of X⋯C contacts, WI's (a.u.), are given. These are the BP86-D3/TZ2P//ωB97XD/aug-cc-pVTZ results. The electrostatic potentials, EP's (a.u.), at σ-holes of X-centres of Lewis acid units optimized separately are included here, they correspond to the ωB97XD/aug-cc-pVTZ level^a

Lewis acid	EP	E NBO	X ch	C ch	R ch	WI
a EP at the fluorine centre for the F2 molecule is equal to +0.023 a.u., EP at the carbon divalent centre of the imidazol-2-ylidene unit is equal to −0.078 a.u. b n(Cl/Br) → σ*CCl/CBr overlaps occur here while for the remaining complexes these are n(C) → σ*RX overlaps.
FCCH	0.003	0.23	−0.211	0.019	0.429	0.004
ClCCH	0.035	3.14	0.125	0.031	−0.105	0.040
BrCCH	0.046	7.63	0.162	0.045	−0.180	0.087
ICCH	0.058	17.93	0.216	0.074	−0.296	0.193
FCN	0.028	1.03	−0.209	0.007	0.648	0.011
ClCN	0.060	5.19	0.129	0.030	0.141	0.061
BrCN	0.070	13.26	0.147	0.057	0.077	0.130
ICN	0.082	33.42	0.177	0.097	−0.019	0.285
Cl2	0.041	2.49^b	0.118	0.282	−0.686	1.029
Br2	0.047	4.03^b	0.076	0.237	−0.558	0.819
I2	0.050	120.73	0.047	0.173	−0.411	0.587

---

However it is worth mentioning that the concept of charges such as those that rule the electrostatic interactions was criticized in several studies.^78–80 It was pointed out that the electrostatic potentials indicate sites of possible nucleophilic or electrophilic attacks or simply sites of interactions with electron donors and acceptors; in other words, they indicate the Lewis acid and Lewis base sites.

Fig. 6 shows molecular graphs with the molecular surfaces of selected species that act as the Lewis acid units in complexes discussed in this study. These surfaces are characterized by the electron density of 0.001 a.u. and they concern the units optimized separately at the ωB97XD/aug-cc-pVTZ level. For such surfaces the electrostatic potential (EPs) maps are calculated and presented in this figure. The change in EP is shown by colour; from positive EP values indicated by blue to negative values marked by red colour. It is worth mentioning that the scale of EP changes is determined for each molecule separately. The above-mentioned electron density value of 0.001 a.u. for surfaces of species discussed was proposed by Bader and coworkers⁸⁴ since it approximately corresponds to the van der Waals spheres.

Fig. 6 The molecular graphs of (a) FCCH, (b) BrCCH, (c) ClCN, and (d) I₂. The surfaces of the electron density of 0.001 a.u. are presented with the maps of the electrostatic potential (EP), the blue color corresponds to the positive EP value while the red color corresponds to the negative EP value.

The EP maps presented in Fig. 6 are in line with the σ-hole concept^81–83 which explains that there is the depletion of an electron charge at some centres. In the case of the systems analyzed in this study such depletion occurs at halogen centres in the elongation of C–X and X–X bonds. The latter decrease of the electron charge leads to the increase of EP at the halogen centre, up to positive values and that leads to the Lewis acid properties of this centre. One can see that EP at X-centre is positive for all Lewis acid units considered in this study (Table 3). The EP value increases with the increase of the halogen centre atomic number for each series of units, XCCH, XCN and X₂. Fig. 7 shows the EP surface of the imidazol-2-ylidene molecule. The negative EP at the carbon that acts as the Lewis acid centre is observed; thus one can see the EP values better explain the properties of molecules and ions than charges; the QTAIM and NBO charges of this centre are positive.

Fig. 7 The molecular graph of imidazol-2-ylidene. The surface of the electron density of 0.001 a.u. is presented with the map of the electrostatic potential (EP), in which the blue color corresponds to the positive EP value while the red color corresponds to the negative EP value.

Table 3 also presents the Wiberg index values for C⋯X contacts in the complexes analyzed here. The Wiberg index, similarly as the DI index, is related to the bond order and to the strength of the interaction. Fig. 8 presents an excellent correlation between these indices for complexes discussed in this study. Table 3 shows also the NBO energies corresponding to the n(C) → σ*_RX orbital–orbital overlaps that may be treated as a signatures of the formation of halogen bonds.⁷⁷ These energies increase in the following order F < Cl < Br < I for HCCX and XCN series of complexes. In a case of complexes of X₂ this overlap is observed only for the complex of I₂, the large energy of 120.7 kcal mol⁻¹ is observed here. However the NBO approach indicates for this complex the formation of a C–I–I hyperbond with the corresponding orbital occupancy amounting to 3.884 and the percentage contributions of C–I and I–I bonds equal to 55.6 and 44.4, respectively. In a case of complexes of Cl₂ and Br₂ the C–Cl and C–Br bonds are observed, respectively, within the NBO approach (bond orbitals occur here). Thus other overlaps of the n(Cl/Br) → σ*_CCl/CBr type are observed here, with rather low corresponding energies (Table 3).

Fig. 8 The dependence between the DI index and the Wiberg index for the X⋯C distance, for complexes analyzed here.

The energy decomposition analysis and the halonium cation transfer process

Table 4 shows the interaction energies and results of their decomposition for the complexes analyzed here. Let us discuss complexes with Cl, Br and I halogen centres of the Lewis acid units acting as electron acceptors. The complexes of FCCH and FCN are linked by interactions that are not classified as halogen bonds rather while the interaction of the imidazol-2-ylidene molecule with F₂ leads to the attachment of fluorine atoms to the carbon centre of the Lewis base unit. One can see that the strength of interaction increases in the following order for complexes of XCCH and XCN; Cl < Br < I. This means that the interaction energy becomes “more negative” for this order. The reverse order is observed for the complexes of X₂; very strong interactions are observed here, with the ∣ΔE_int∣value up to 61.6 kcal mol⁻¹ for the complex of the Cl₂ Lewis acid unit. However interactions for the series of X₂ complexes are not related to intermolecular ones rather to the C–X covalent bonds. At least the NBO and QTAIM approaches show the formation of covalent bonds for complexes of Cl₂ and Br₂ species. In the case of the complex with I₂ the total electron energy density at I⋯C BCP, H_BCP is negative while the ∇²ρ_BCP value is positive, which indicates at least a partially covalent interaction. Besides, the large energy related to the n(C) → σ*_II overlap amounting to 120.7 kcal mol⁻¹ is observed here. In the case of the very similar 1,3-diethyl-2-iodo-4,5-dimethylimidazolium iodide moiety that occurs in the crystal structure this interaction was classified as the covalent bond.⁷¹ Thus one can see that the E_int values collected in Table 4 concern the dissociation energies of C–X bonds rather for complexes of X₂ and that it is a reason of the reverse order of the increase of the strength of interaction here in comparison with complexes of XCCH and XCN species. In a case of weaker interactions of X₂ species that are not classified as covalent bonds the same order as for the XCCH and XCN units is observed. For example the H₂O⋯X₂ complexes were analyzed and the interaction energies were calculated for the following complexes; H₂O⋯F₂, H₂O⋯Cl₂, H₂O⋯Br₂ and H₂O⋯I₂; they are equal to −0.67, −2.01, −2.97, and −4.57 kcal mol⁻¹, respectively (MP2/6-311++G(d,p) level; the 6-311+G(d) basis set for iodine was applied).^85–87

Table 4 The total interaction energy, E_int, and their terms; the Pauli repulsion, E_Pauli, the electrostatic energy, E_elstat, the orbital–orbital interaction energy, E_orb, the dispersion energy, E_disp for complexes analyzed here (all in kcal mol⁻¹). The percentage contributions of the E_elstat, and E_orb, attractive interaction energy terms in the sum of all attractive terms are presented (%E_disp = 100% − %E_elstat − %E_orb). These are the BP86-D3/TZ2P//ωB97XD/aug-cc-pVTZ results

Lewis acid	E int	E Pauli	E elstat	E orb	E disp	%Eelstat	%Eorb
FCCH	−3.29	4.56	−3.41	−2.37	−2.06	43.5	30.2
ClCCH	−3.94	6.41	−6.20	−3.20	−0.94	60.0	30.9
BrCCH	−7.91	13.13	−12.76	−7.06	−1.21	60.7	33.6
ICCH	−13.67	31.43	−27.61	−15.77	−1.71	61.2	35.0
FCN	−9.42	13.09	−13.70	−6.24	−2.56	60.9	27.7
ClCN	−7.12	10.24	−10.96	−5.44	−0.95	63.2	31.4
BrCN	−12.86	21.72	−21.06	−12.26	−1.27	60.9	35.4
ICN	−21.57	55.13	−46.50	−28.16	−2.05	60.6	36.7
Cl2	−61.58	404.85	−224.66	−240.14	−1.63	48.2	51.5
Br2	−45.61	260.50	−165.56	−138.46	−2.09	54.1	45.2
I2	−32.85	146.30	−103.47	−73.10	−2.59	57.8	40.8

---

Fig. 9 shows a correlation (linear and polynomial regressions are presented) between the electron density at the X⋯C BCP, ρ_BCP, and the interaction energy, E_int, for complexes discussed here, the species containing fluorine centre are excluded from this correlation. Thus it is in line with numerous earlier studies where it was found that the former value is related to the strength of interaction.^{74,75,78–80}

Fig. 9 The dependence between the electron density at the X⋯C BCP (a.u.) and the interaction energy (kcal mol⁻¹), E_int, for complexes analyzed here.

Table 4 shows the contributions to the total interaction energies; one can see that for the majority of systems analyzed here the electrostatic interaction energy, E_elstat, is the main attractive energy term. In a case of complexes of X₂, the electrostatic and orbital energies, E_elstat and E_orb, respectively, are comparable. Even in a case of the complex of Cl₂ the orbital energy is a more important attractive term than the electrostatic one. This is not surprising since in the covalent in nature interactions, such as those occurring in the complexes of X₂, the interaction energies related to the electron charge shifts are important, and E_orb is an energy related to such shifts. The dispersion energy, E_disp, does not exceed 1.5% of the sum of attractive terms for complexes of X₂, for other complexes this value does not exceed 9.5%. The E_disp term is more important for complexes with a fluorine centre; its percentage contribution in the sum of attractive terms amounts to 26.3% and 11.4% in the FCCH and FCN complexes, respectively.

The total electron energy density, H_BCP, expresses at least the covalent character of the interaction if it is negative.^77–80 The same concerns the sum of Pauli repulsion term and the electrostatic term (E_Pauli + E_elstat that is named as the steric energy in the decomposition scheme applied in this study). If the steric energy is positive, it means that the electrostatic interaction is not sufficient to counteract the repulsion and that the processes related to electron charge transfers, expressed by the orbital energy rule the stability of the system. Hence the greater positive steric energy indicates the interaction in the complex considered is more related to the covalency since the greater electron charge shifts occur for such systems to reduce the repulsion interaction.⁷⁴Fig. 10 presents the linear correlation between the total electron energy density at BCP and the steric energy; both these parameters express the covalent character of the interaction. A similar correlation for different σ-hole bonds was found in a previous study; however another decomposition interaction energy scheme was applied there.⁸⁸

Fig. 10 The dependence between the total electron energy density at the X⋯C BCP, H_C⋯_X, (a.u.) and the steric energy (kcal mol⁻¹) for complexes analyzed here.

The latter findings are in agreement with other studies where it was indicated that so-called non-covalent interactions may be expressed in coulombic terms; electrostatic and polarization.^89,90 The polarization term is understood in the latter studies as one related to the electron charge shifts resulting from the complexation.

One can see that for systems analyzed here a broader spectrum of halogen bond interactions is observed; from weaker ones to those where the transfer of the halonium cation occurs and this cation is attached to the carbon centre of the imidazol-2-ylidene molecule. This occurs in the case of X₂ complexes. In general, one may say that for the whole sample of complexes considered here the process of the halonium ion transfer is modelled; R–X⋯C ↔ R⁻⋯⁺X–C. Fig. 11 shows this process for the sample of complexes analyzed in this study. The change of DI and Wiberg indices is presented; these indices are considered for the X⋯C contact and for the R–X bond. This is a very similar process to the proton transfer that occurs in numerous hydrogen bonded systems and that was described in a similar way.⁷⁵ For weak interactions there are greater X⋯C distances accompanied by low values of DI and Wiberg indices; R–X bond lengths are short here and are accompanied by high values of indices. For the stronger interactions the shortening of X⋯C distances occurs and the elongation of the R–X bonds. That is accompanied by the increase and decrease of the corresponding values of indices, respectively. In extreme cases the halonium cation is attached to the carbon centre of imidazol-2-ylidene; as it is observed for the complex of Cl₂.

Fig. 11 The relationship between the index of X⋯C distance and the index of the R–X bond, full circles correspond to the DI index and empty ones to the Wiberg index.

Conclusions

Calculations on complexes of the imidazol-2-ylidene moiety with HCCX, XCN, and X₂ Lewis acid units were performed. The divalent carbon acts here as the Lewis base centre through a lone electron pair while the X-halogen acts as the Lewis acid centre through a σ-hole. It was found that these complexes are linked by halogen bonds, except for species with the fluorine centre, since for the FCCH and FCN units more complicated links are formed while the F₂ molecule is attached to the carbon centre of the imidazol-2-ylidene molecule forming C–F bonds. Very strong interactions with Cl₂, Br₂ and I₂ species are observed that possess numerous characteristics of covalency. Even in the case of two first Lewis acid units the C–Cl and C–Br bonds are formed that are accompanied by the occurrence of Cl⁻ and Br⁻ anions, respectively, according to the NBO and QTAIM approaches. Weaker interactions with XCCH and XCN species are observed compared with those with X₂ units. Hence for complexes analyzed in this study the process of halonium cation transfer may be modelled.

The energy decomposition analysis, EDA, shows that for complexes with XCCH and XCN units the electrostatic interaction energy is the most important attractive term of the total interaction energy, next there is the orbital energy term and the contribution of dispersion interaction energy is much less important. The complexes with FCCH and FCN species are exceptions since here the dispersion is also important, however not as much as other attractive terms. In the case of complexes with X₂ moieties (X = Cl, Br, I), the electrostatic and orbital terms are important and comparable while the dispersion contribution is meaningless.

The search through the Cambridge Structural Database, CSD, for complexes of imidazol-2-ylidene derivatives with X₂ molecules show that for all of these structures the C–X covalent bonds are formed, which is in agreement with theoretical calculations which show the covalent character of interactions with dihalogen molecules.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author wishes to thank Eusko Jaurlaritza, grant number IT-1584-22, for the funding support.

References

1. Advances in Carbene Chemistry, ed. U. H. Brinker, Jai Press, Greenwich and Stamford, 1994 and 1998, vol. 1 and 2.
2. D. Bourissou, O. Guerret, F. P. Gabbaï and G. Bertrand, Chem. Rev., 2000, 100, 39–91.
3. Y. Mizuhata, T. Sasamori and N. Tokitoh, Chem. Rev., 2009, 109, 3479–3511.
4. S. J. Grabowski, Crystals, 2022, 12, 112.
5. P. S. Skell and A. Y. Garner, J. Am. Chem. Soc., 1956, 78, 3409–3411.
6. P. S. Skell and A. Y. Garner, J. Am. Chem. Soc., 1956, 78, 5430–5433.
7. P. S. Skell and R. C. Woodworth, J. Am. Chem. Soc., 1956, 78, 4496–4497.
8. P. S. Skell, Tetrahedron, 1985, 41, 1427–1428.
9. A. J. Arduengo III, S. F. Gamper, M. Tamm, J. C. Calabrese, F. Davidson and H. A. Craig, J. Am. Chem. Soc., 1995, 117, 572–573.
10. I. Alkorta and J. Elguero, J. Phys. Chem., 1996, 100, 19367–19370.
11. M. Palusiak and M. Jabłoński, Phys. Chem. Chem. Phys., 2009, 11, 5711–5719.
12. S. Huang, Y. Wang, C. Hu and X. Yan, Chem. – Asian J., 2021, 16, 2687–2693.
13. W. A. Herrmann and C. Köcher, Angew. Chem., Int. Ed. Engl., 1997, 36, 2162–2187.
14. M. Vasiliu, K. C. Edwards, D. Tapu, C. E. Castillo, T. H. Stein, R. Craciun, A. J. Arduengo III and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 2658–2669.
15. N. Kuhn, T. Kratz and G. Henkel, J. Chem. Soc., Chem. Commun., 1993, 1778–1779.
16. Q. Li, Y. Wang, Z. Liu, W. Li, J. Cheng, B. Gong and J. Sun, Chem. Phys. Lett., 2009, 469, 48–51.
17. J. E. Del Bene, I. Alkorta and J. Elguero, Chem. Phys. Lett., 2017, 685, 338–343.
18. M. D. Esrafili and N. Mohammadirad, J. Mol. Model., 2013, 19, 2559–2566.
19. R. G. Shirazi, F. Neese, D. A. Pantazis and G. Bistoni, J. Phys. Chem. A, 2019, 123, 5081–5090.
20. J. Frosch, M. Koneczny, T. Bannenberg and M. Tamm, Chem. – Eur. J., 2021, 27, 4349–4363.
21. P. Metrangolo and G. Resnati, Chem. Eur. J., 2001, 7, 2511–2519.
22. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
23. P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395.
24. E. Parisini, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Chem. Soc. Rev., 2011, 40, 2267–2278.
25. S. Scheiner, Int. J. Quantum Chem., 2013, 113, 1609–1620.
26. S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288.
27. S. J. Grabowski, Phys. Chem. Chem. Phys., 2013, 15, 7249–7259.
28. S. Scheiner, CrystEngComm, 2013, 15, 3119–3124.
29. R. Parra and S. J. Grabowski, Int. J. Mol. Sci., 2022, 23, 11289.
30. M. Michalczyk, B. Kizior, W. Zierkiewicz and S. Scheiner, Phys. Chem. Chem. Phys., 2023, 25, 2907–2915.
31. L. Turunen and M. Erdélyi, Chem. Soc. Rev., 2020, 49, 2688–2700.
32. S. B. Hakkert and M. Erdélyi, J. Phys. Org. Chem., 2015, 28, 226–233.
33. A. C. Reiersølmoen, S. Battaglia, S. Øien-Ødegaard, A. K. Gupta, A. Fiksdahl, R. Lindh and M. Erdélyi, Chem. Sci., 2020, 11, 7979–7990.
34. N. Bedin, A. Karim, M. Reitti, A. C. C. Carlsson, F. Topić, M. Cetina, F. Pan, V. Havel, F. Al-Ameri, V. Sindelar, K. Rissanen, J. Gräfenstein and M. Erdélyi, Chem. Sci., 2015, 6, 3746–3756.
35. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, B72, 171–179.
36. R. Wong, F. H. Allen and P. Willett, J. Appl. Crystallogr., 2010, 43, 811–824.
37. R. F. W. Bader, Atoms in Molecules, a Quantum Theory, Oxford University Press, Oxford, UK, 1990.
38. Quantum Theory of Atoms in Molecules: Recent Progress in Theory and Application, ed. C. Matta, R. J. Boyd, Wiley-VCH, Weinheim, Germany, 2007.
39. F. Weinhold and C. Landis, Valency and Bonding, a Natural Bond Orbital Donor—Acceptor Perspective, Cambridge University Press, Cambridge, UK, 2005.
40. R. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
42. Y. Minenkov, A. Singstad, G. Occhipinti and V. R. Jensen, Dalton Trans., 2012, 41, 5526–5541.
43. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023.
44. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
45. D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358–1371.
46. D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1995, 103, 4572–4585.
47. A. G. Yurieva, O. K. Poleshchuk and V. D. Filimonov, J. Struct. Chem., 2008, 49, 548–552.
48. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
49. L. A. Burns, A. Vázquez-Mayagoitia, B. G. Sumpter and C. D. Sherrill, J. Chem. Phys., 2011, 134, 084107.
50. J. Gräfenstein and D. Cremer, Phys. Chem. Chem. Phys., 2000, 2, 2091–2103.
51. R. G. Shirazi, D. A. Pantazis and F. Neese, Mol. Phys., 2020, 118, e1764644.
52. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Symp., 1989, S23, 199–207.
53. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
54. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
55. S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104.
56. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
57. G. T. E. Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
58. H. Umeyama and K. Morokuma, J. Am. Chem. Soc., 1977, 99, 1316–1332.
59. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759.
60. E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, O. Baseggio, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo and P. M. Boerrigter, et al., ADF2019, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2019, Available online: http://www.scm.com.
61. K. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
62. I. Mayer, J. Comput. Chem., 2007, 28, 204–221.
63. X. Fradera, M. A. Austen and R. F. M. Bader, J. Phys. Chem. A, 1999, 103, 304–314.
64. X. Fradera, J. Poater, S. Simon, M. Duran and M. Solà, Theor. Chem. Acc., 2002, 107, 362–371.
65. A. Todd and T. K. Keith, AIMAll (Version 11.08.23), Gristmill Software, Overland Park KS, USA, 2011, (http://aim.tkgristmill.com).
66. E. D. Glendening, C.-R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
67. M. Haukka, P. Hirva and K. Rissanen, Dihalogens as Halogen Bond Donors, chapter in the book, in Non-Covalent Interactions in the Synthesis and Design of New Compounds, ed. A. M. Maharramov, K. T. Mahmudov, M. N. Kopylovich, A. J. L. Pombeiro, John Wiley & Sons, Inc., 1st edn, 2016, pp. 187–197.
68. J. Bondi, J. Phys. Chem., 1964, 68, 441–451.
69. I. Diaz, V. Fernandez, J. L. Martinez, L. Beyer, A. Pilz and U. Muller, Z. Naturforsch., B: J. Chem. Sci., 1998, 53, 933–938.
70. G. Valle and R. Ettorre, Acta Crystallogr., 1992, C48, 919–921.
71. N. Kuhn, T. Kratz and G. Henkel, Chem. Commun., 1993, 1778–1779.
72. N. Kuhn, A. Abu-Rayyan, K. Eichele, S. Schwarz and M. Steimann, Inorg. Chim. Acta, 2004, 357, 1799–1804.
73. T. Peppel and M. Kockerling, Z. Kristallogr. - New Cryst. Struct., 2009, 224, 597–598.
74. S. J. Grabowski, Phys. Chem. Chem. Phys., 2017, 19, 29742–29759.
75. S. J. Grabowski, Chem. Rev., 2011, 11, 2597–2625.
76. S. J. Grabowski, Chem. Phys. Lett., 2001, 338, 361–366.
77. S. J. Grabowski, Understanding Hydrogen Bonds, Theoretical and Experimental Views, The Royal Society of Chemistry, United Kingdom, Cambridge, 2021.
78. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
79. E. Espinosa and E. Molins, J. Chem. Phys., 2000, 113, 5686–5694.
80. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161.
81. P. Politzer, K. E. Riley, F. A. Bulat and J. S. Murray, Comput. Theor. Chem., 2012, 998, 2–8.
82. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
83. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
84. R. F. W. Bader, M. T. Carrol, J. R. Cheeseman and C. Chang, J. Am. Chem. Soc., 1987, 109, 7968–7979.
85. M. I. Bernal-Uruchurtux, G. Kerenskaya and K. C. Janda, Int. Rev. Phys. Chem., 2009, 28, 223–265.
86. I. Alkorta, I. Rozas and J. Elguero, J. Phys. Chem. A, 1998, 102, 9278–9285.
87. A. K. Pathak, T. Mukherjee and D. K. Maity, J. Phys. Chem. A, 2008, 112, 744–751.
88. S. J. Grabowski and W. A. Sokalski, ChemPhysChem, 2017, 18, 1569–1577.
89. T. Clark, J. S. Murray and P. Politzer, Phys. Chem. Chem. Phys., 2018, 20, 30076–30082.
90. J. S. Murray and P. Politzer, Crystals, 2020, 10, 76.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00348e

---