Open Access Article
Open Access ArticleElectron-atom Compton profiles due to the intramolecular motions of the H and D atoms in HD
Yuichi
Tachibana
a,
Yuuki
Onitsuka
 a,
Satoru
Kanaya
a,
Hirohiko
Kono
a,
Satoru
Kanaya
a,
Hirohiko
Kono
 b and
Masahiko
Takahashi
b and
Masahiko
Takahashi
 *a
*a
aInstitute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai 980–8577, Japan. E-mail: masahiko@tohoku.ac.jp
bDepartment of Chemistry, Graduate School of Science, Tohoku University, Sendai 980-8578, Japan
First published on 15th February 2023
Abstract
We report an atomic momentum spectroscopy (AMS) experiment on HD, performed at a scattering angle of 135° and at an incident electron energy of 2.0 keV. The electron-atom Compton profiles due to the intramolecular motions of the H and D atoms in HD were obtained. The two Compton profiles are shown to be identical with each other in both shape and intensity, proving that the experimental responses of the intramolecular atomic motions are disentangled from the effect of molecular translational motion. It is also shown that the Compton profiles are in agreement with associated quantum chemistry-based calculations, indicating that the large momentum transfer limit is achieved under the experimental conditions. These observations demonstrate the ability of AMS not only to map the intramolecular motion of each atom with different masses but also to perform elemental composition analysis of a molecular system.
1. Introduction
Atomic momentum spectroscopy (AMS)1 is an experimental method that employs the electron-atom Compton scattering at a large scattering angle (θ > 90°) and at incident electron energies (E0's) of the order of keV or higher. Here the instantaneous motion of an atom causes Doppler broadening of the energy of the quasi-elastically backscattered electrons in the electron energy loss (EEL) spectrum, with the band peak position being related to the mass of the scattering atom. For a gaseous molecular target, one or more bands thus appear in the EEL spectrum. The shape of a band is usually determined by the intrinsic instrumental response (IR) function employed as well as the motion of the corresponding scattering atom which is due to the center-of-mass molecular translational motion, molecular vibration and molecular rotation. Clearly, AMS possesses a potential ability to map the intramolecular motion of each atom with different masses. If the ability becomes directly and widely available, AMS would work as a new molecular spectroscopy technique with the marked feature. AMS is in sharp contrast to the existing techniques such as vibrational spectroscopy2 that measures frequencies of normal modes, often represented by collective motion of many (or all) of the constituent atoms.Recently, a series of attempts towards the end mentioned above has been made for the simplest molecule, H2. The attempts are classified into the following three issues. Firstly, based on the systematic study on the effect of translational motion of noble gases,3 the general protocol for data analysis4 has been developed, which enables one to disentangle the experimental response of the intramolecular atomic motion from the effect of molecular translational motion as well as the intrinsic IR function. Note that the word “intramolecular” used here includes both molecular vibration and rotation, as the former is essentially inseparable from the latter without imposing the Eckart frame on the Schrödinger equation.2,5 Secondly, the validity of the range of the plane-wave impulse approximation (PWIA),6,7 which is the key to directly relate the experimental response to the intramolecular atomic motion, has been elucidated by carefully analyzing the E0 dependence or the asymptotic behavior of the Compton profile shape.8 Lastly, instead of the classical kinetic energy model previously used,9 the quantum chemistry-based AMS theory4 has been developed to predict, within the PWIA, the Compton profile due to the intramolecular atomic motion for diatomic molecules. The theory has proven its accuracy by reproducing the experimental results of H2 satisfactorily.4,8 In this way, AMS can now quantitatively identify and discuss the experimental response of not only H2 but also many other diatomic molecules.
In the present work, we performed an AMS experiment on the simplest heteronuclear diatomic molecule, HD. To our knowledge, two AMS experiments were reported previously for this molecule.10,11 Cooper and others10 measured an EEL spectrum for HD in a gas cell at θ = 100° and at E0 = 2.25 keV. They reported a relative intensity of the H- and D-atom bands as IH/ID = 0.96 ± 0.05, the value being close to unity that the PWIA predicts. Later, Vos and Went11 measured EEL spectra for HD in an effusive gas beam at θ = 135° and at three different E0's. They reported the IH/ID value of 1.14, 1.07 and 1.01 at E0 = 2.0, 4.0 and 6.0 keV, respectively. It was then concluded that the larger IH/ID values than unity at lower E0's were probably due to the partial overlap of the H- and D-atom bands in combination with the failure of the impulse approximation. Clearly, these previous studies are controversial. This controversy may arise partly by the noticeable difference in the effect of molecular translational motion on the EEL spectrum between the gas cell and effusive gas beam.3 Here, in contrast to the previous studies,10,11 we present the Compton profiles due only to the intramolecular motions of the H and D atoms in HD, obtained by disentangling those from the effect of molecular translational motion as well as the intrinsic IR function. Furthermore, the experimental Compton profiles are compared in both shape and intensity with each other and with associated quantum chemistry-based calculations. These results are discussed to unambiguously demonstrate the ability of AMS not only to map the intramolecular motion of each atom with different masses but also to perform elemental composition analysis of a molecular system.
2. Experiment
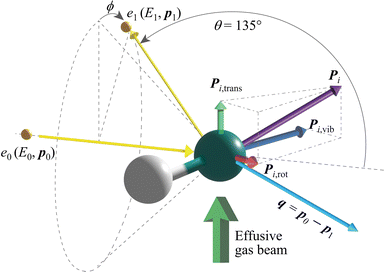
Fig. 1 shows AMS scattering by a gaseous HD molecule schematically. It can be described as| e0(E0, p0) + HD → e1(E1, p1) + HD, | (1) |
| Eloss = E0 − E1, | (2) |
| q = p0 − p1. | (3) |
Within the PWIA,6,7Eloss is related to the mass Mi and initial momentum Pi of the scattering atom i (i = H, D) through the following equation:
 | (4) |
 that corresponds to the recoil with the scattering atom being stationary (i.e.Pi = 0). The second term is the Doppler broadening caused by Pi, which is the sum of the momenta of the scattering atom due to the molecular translational motion (Pi,trans), molecular vibration (Pi,vib) and molecular rotation (Pi,rot). Energy analysis of the scattered electrons can thus provide direct information about Mi, as well as Pi in the form of Pi·q.
that corresponds to the recoil with the scattering atom being stationary (i.e.Pi = 0). The second term is the Doppler broadening caused by Pi, which is the sum of the momenta of the scattering atom due to the molecular translational motion (Pi,trans), molecular vibration (Pi,vib) and molecular rotation (Pi,rot). Energy analysis of the scattered electrons can thus provide direct information about Mi, as well as Pi in the form of Pi·q.
The experiment on HD was carried out at θ = 135° 0.4° and at E0 = 2.0 keV, thus achieving a q value of 22.4 a.u. For the experiment, a multi-channel AMS apparatus was used. Since details of the apparatus are described elsewhere,12 only a brief account of it is given here. An incident electron beam of 1 mm diameter was generated by a thermal electron gun that consisted of a tungsten filament. The beam current was collected in a Faraday cup and was kept at around 500 nA during the measurements. Quasi-elastic electron backscattering occurred where the electron beam collided with a HD molecule in an effusive gas beam. Here the gas beam direction was perpendicular to the electron beam direction. HD gas of a chemical purity of 98% was obtained from Cambridge Isotope Laboratories, Inc. and used at room temperature. The scattered electrons were angle-limited by apertures so that a spherical electron energy analyzer accepted those at θ = 135° over azimuthal angle (ϕ) ranges from 0° to 72.5°, from 107.5° to 252.5° and from 287.5° to 360°. A pair of decelerating electrostatic lenses were employed for the electrons before their entrance to the analyzer with a typical deceleration ratio of around 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, in order to achieve a higher energy resolution. The electrons having passed through the analyzer were detected with a position-sensitive detector. Both energies (E1's) and azimuthal angles (ϕ's) of the scattered electrons were determined from their arrival positions at the detector. Note that the multi-channel technique used in this apparatus substantially increases not only the collection efficiency of the scattered electrons but also the accuracy of the experimental data compared with the traditional single channel measurements, as drifts in the electron beam current and fluctuations in target gas density affect all channels in the same way. In addition, since gaseous HD molecules used in the present study were randomly oriented in space, what the AMS experiment measured corresponds to the Compton profiles of the H and D atoms in a spherically-averaged HD molecule.
1, in order to achieve a higher energy resolution. The electrons having passed through the analyzer were detected with a position-sensitive detector. Both energies (E1's) and azimuthal angles (ϕ's) of the scattered electrons were determined from their arrival positions at the detector. Note that the multi-channel technique used in this apparatus substantially increases not only the collection efficiency of the scattered electrons but also the accuracy of the experimental data compared with the traditional single channel measurements, as drifts in the electron beam current and fluctuations in target gas density affect all channels in the same way. In addition, since gaseous HD molecules used in the present study were randomly oriented in space, what the AMS experiment measured corresponds to the Compton profiles of the H and D atoms in a spherically-averaged HD molecule.
The experimental raw data of HD were obtained by subtracting ϕ-angle dependent EEL spectra measured at an ambient pressure of 2.5 × 10−5 Pa in the vacuum chamber from those at 2.0 × 10−4 Pa, in order to remove unexpected background signals. The instrumental energy resolution was about 0.6 eV at full width at half maximum (FWHM). The same experiment was also conducted for Kr gas (>99.999%) to have a highly accurate approximation of the intrinsic IR function. This is because Kr is a heavy atom and it does not have intramolecular motion, while its mean recoil energy 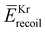 can be regarded as zero under the experimental conditions employed.3 No impurities were observed in the EEL spectra of Kr.
can be regarded as zero under the experimental conditions employed.3 No impurities were observed in the EEL spectra of Kr.
3. Theoretical calculations
Basically, the q value of 22.4 a.u. employed in the present experiment is so large that q ≫ 2π/R with R being the internuclear distance of HD. The AMS scattering event can thus be regarded incoherent, as in neutron Compton scattering.6,7 The double differential cross section (DDCS) for the AMS scattering by a HD molecule is then given by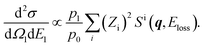 | (5) |
 | (6) |
The DDCS can thus be described, within the PWIA, as
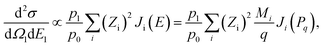 | (7) |
 | (8) |
 | (9) |
In the present study, the Compton profiles due to the intramolecular motions of the H and D atoms in HD were calculated in the following manner. For a spherically-averaged HD molecule in the rotational state with a rotational quantum number ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , the momentum distribution ρ
, the momentum distribution ρ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,i(Pi) of the scattering atom is given by4
,i(Pi) of the scattering atom is given by4
 | (10) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (PiR) is the spherical Bessel function of order
(PiR) is the spherical Bessel function of order ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . f(R − Re) is the vibrational wave function and at room temperature it can be approximated as a ground state wave function, (μω/πħ)1/4exp[−μω(R − Re)2/2ħ] with μ, ω and ħ being the reduced mass, angular frequency and reduced Planck's constant, respectively. The Compton profiles are given, within the PWIA, by
. f(R − Re) is the vibrational wave function and at room temperature it can be approximated as a ground state wave function, (μω/πħ)1/4exp[−μω(R − Re)2/2ħ] with μ, ω and ħ being the reduced mass, angular frequency and reduced Planck's constant, respectively. The Compton profiles are given, within the PWIA, by | (11) |
 | (12) |
4. Results and discussion
Fig. 2 shows examples of EEL spectra of HD, which were measured at ϕ = 0° and 180°. It can be seen from the figure that two bands appear at around 3.7 and 1.9 eV, respectively. The former band is attributed to the H atom and the latter one is to the D atom, as their band peak positions are consistent with the theoretical values of and
and  . Also can be seen is that the peak position of the H (D) atom band at ϕ = 0° is slightly shifted to the lower energy loss compared to the theoretical
. Also can be seen is that the peak position of the H (D) atom band at ϕ = 0° is slightly shifted to the lower energy loss compared to the theoretical  (
( ) value, while that at ϕ = 180° is to the higher energy loss. This forward-backward asymmetry in the band peak position is exactly due to the effect of molecular translational motion, which largely depends on the ϕ-angle.3,4 Besides, an additional band appears centered at around 0.3 eV, with an intensity comparable to those of the H- and D-atom bands. The additional band can rationally be attributed to the impurity amount (2%) of the used HD gas. For example, suppose an impurity species containing one C atom. In this case,
) value, while that at ϕ = 180° is to the higher energy loss. This forward-backward asymmetry in the band peak position is exactly due to the effect of molecular translational motion, which largely depends on the ϕ-angle.3,4 Besides, an additional band appears centered at around 0.3 eV, with an intensity comparable to those of the H- and D-atom bands. The additional band can rationally be attributed to the impurity amount (2%) of the used HD gas. For example, suppose an impurity species containing one C atom. In this case,  of a C atom is calculated to be 0.31 eV and the value corresponds reasonably well with the observed one (c.a. 0.3 eV). The intensity of the impurity band can also be understood if considering the abundance ratio of the impurity to HD, as the DDCS is proportional to the square of Zi (see eqn (7)).
of a C atom is calculated to be 0.31 eV and the value corresponds reasonably well with the observed one (c.a. 0.3 eV). The intensity of the impurity band can also be understood if considering the abundance ratio of the impurity to HD, as the DDCS is proportional to the square of Zi (see eqn (7)).
The experimental EEL spectra of HD at each ϕ-angle were analyzed based on the general protocol.4 The present data analysis involves the following three steps. Firstly, it was checked whether or not our gas beam model3 was applicable to the experimental results of the present work. It is evident from Fig. 3 that the ϕ-angle dependence of the H- and D-atom band peak positions are well reproduced by using the most probable velocity of HD in the effusive gas beam,3,14vmp = (3kBT/MHD)1/2 with MHD being the mass of the HD molecule. This observation means also that since the H and D atoms are the atoms constituting the HD molecule, they have the same translational velocity: the molecular translational motion affects the H- and D-atom bands in the same way.
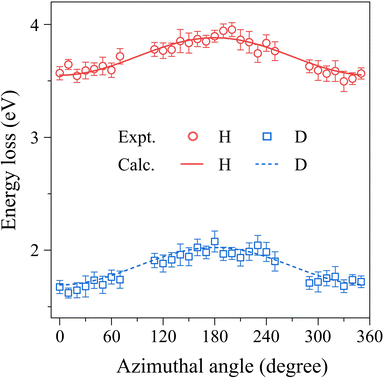 | ||
| Fig. 3 Comparison between experiment and theory for the ϕ-angle dependence of the H- and D-atom band peak positions. | ||
The second step of the data analysis was to align the individual EEL spectra measured at each ϕ-angle. Namely, they were shifted so that the peak positions of the H atom band at each ϕ were all aligned to the  value of the H atom. A ϕ-angle integrated EEL spectrum of HD was then generated and is shown in Fig. 4(a), which was obtained by summing up the aligned EEL spectra. A curve fitting to the impurity band was subsequently attempted in order to remove it from the aligned EEL spectrum. Here, since the impurity species were unknown, the convolution of the intrinsic IR function and a combination of three Gaussian functions was used as a fitting function. It can be seen from Fig. 4(a) that the obtained fitting curve reproduces well the impurity band shape. The result of removing the impurity band is shown in Fig. 4(b). Also included in the figure is a Doppler broadening spectrum of the molecular translational motion, which was calculated by using our gas beam model.3 The convolution of the spectrum of molecular translational motion and the intrinsic IR function was regarded as the practical IR function in this case. The last step of the data analysis was to disentangle the Compton profiles due to the intramolecular motions of the H and D atoms from the practical IR function, by using the convolution theorem.15 This theorem tells one that since Fourier transform (FT) of the convolution of two functions is the product of FTs of each function, the Compton profiles due to the intramolecular H-and D-atom motions can be obtained by dividing the FT of the experiment by that of the practical IR function and then taking the inverse FT of the result of the division. The result is shown in Fig. 4(c). It looks like that the H- and D-atom bands have similar intensities, as reported in the previous studies.10,11 Here, since the H- and D-atom bands are slightly overlapped in energy, a deconvolution of the two bands was attempted by a curve fitting to each of those respectively with a combination of three Gaussian functions, in order to have the Compton profiles of the H and D atoms, JH(E) and JD(E), separately. Results of the least-squares fit are shown by dashed lines and their sum is represented by the solid line. Furthermore, when converting Ji(E) to Ji(Pq), the following normalization constraint was placed on Ji(Pq):
value of the H atom. A ϕ-angle integrated EEL spectrum of HD was then generated and is shown in Fig. 4(a), which was obtained by summing up the aligned EEL spectra. A curve fitting to the impurity band was subsequently attempted in order to remove it from the aligned EEL spectrum. Here, since the impurity species were unknown, the convolution of the intrinsic IR function and a combination of three Gaussian functions was used as a fitting function. It can be seen from Fig. 4(a) that the obtained fitting curve reproduces well the impurity band shape. The result of removing the impurity band is shown in Fig. 4(b). Also included in the figure is a Doppler broadening spectrum of the molecular translational motion, which was calculated by using our gas beam model.3 The convolution of the spectrum of molecular translational motion and the intrinsic IR function was regarded as the practical IR function in this case. The last step of the data analysis was to disentangle the Compton profiles due to the intramolecular motions of the H and D atoms from the practical IR function, by using the convolution theorem.15 This theorem tells one that since Fourier transform (FT) of the convolution of two functions is the product of FTs of each function, the Compton profiles due to the intramolecular H-and D-atom motions can be obtained by dividing the FT of the experiment by that of the practical IR function and then taking the inverse FT of the result of the division. The result is shown in Fig. 4(c). It looks like that the H- and D-atom bands have similar intensities, as reported in the previous studies.10,11 Here, since the H- and D-atom bands are slightly overlapped in energy, a deconvolution of the two bands was attempted by a curve fitting to each of those respectively with a combination of three Gaussian functions, in order to have the Compton profiles of the H and D atoms, JH(E) and JD(E), separately. Results of the least-squares fit are shown by dashed lines and their sum is represented by the solid line. Furthermore, when converting Ji(E) to Ji(Pq), the following normalization constraint was placed on Ji(Pq):
 | (13) |
Since the nuclear charges of the H and D atoms are the same (ZH = ZD = 1), the relative intensity of the H- and D-atom bands in the EEL spectrum is therefore maintained in that of the resulting JH(Pq) and JD(Pq):
 | (14) |
The Compton profiles thus obtained as JH(Pq) and JD(Pq) are presented in Fig. 5. This figure enables one to directly compare the experimental responses of the intramolecular H- and D-atom motions in HD. A first look at Fig. 5 may reveal that the Compton profiles of the H and D atoms are indistinguishable, within the experimental uncertainties, from each other both in shape and in intensity. On one hand, this observation is entirely as expected. Namely, for the HD molecule, the momentum of the H atom in the intramolecular motion has to be opposite in direction but equal in magnitude to that of the D atom (|PH,vib + PH,rot| = |PD,vib + PD,rot|). However, since the H and D atoms have the same translational velocity, PH,trans = (MH/MD) × PD,trans. Thus the net momenta of the H and D atoms in the laboratory frame motion are different from each other (|PH,trans + PH,vib + PH,rot| ≠ |PD,trans + PD,vib + PD,rot|). The observation made in Fig. 5 therefore guarantees that the experimental responses of the intramolecular motions of the two atoms have certainly been disentangled from the effects of molecular translational motion. On the other hand, the observation is supported by the associated quantum chemistry-based calculations that also predict the same Compton profile for the H and D atoms. The agreement between experiment and theory reveals that both the Compton profiles of the H and D atoms in HD, as well as that of the H atom in H2,4,8 reach the high q limit at q = 22.4 a.u. (θ =135° and E0 = 2.0 keV), where the experimental conditions fulfill the requirements of the PWIA.
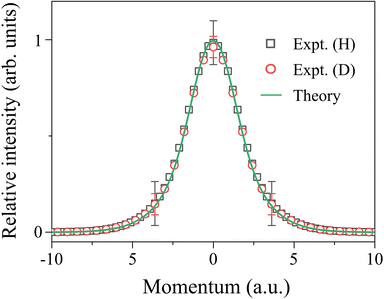 | ||
| Fig. 5 Comparison between Compton profiles due to the intramolecular motions of the H and D atoms in HD. The solid line represents associated quantum chemistry-based calculations. | ||
Nevertheless, the genuine value of the comparison made in Fig. 5 may lie in that AMS has proven its two abilities. One is the ability to map the intramolecular motion of each atom with different masses. It is illustrated by the agreement in shape between the experimental Compton profiles of the H and D atoms. Another is the ability to perform elemental composition analysis, which is illustrated by the agreement in intensity between the two experimental Compton profiles. The relative intensity of the two has been found to be unity within the experimental uncertainties (IH/ID = 1.01 ± 0.05). Since the nuclear charges of the H and D atoms are the same, IH/ID is determined only by the ratio of the numbers of the H and D atoms contained in a HD molecule (see eqn (7)). The observed IH/ID value of unity thus tells one that the composition ratio of H and D is 1 to 1 in HD. In this way, the comparison made in Fig. 5 demonstrates that AMS can be used as a molecular spectroscopy technique, which combines the ability to map the intramolecular motion of each atom with different masses and the ability to perform elemental composition analysis of a molecular system. The accuracy and reliability of the two abilities are verified through the agreement in both shape and intensity between experiment and theory.
It should be noted, however, that the above-discussed two abilities have already been tested by neutron Compton scattering (NCS).16 This is a matter of course, because AMS is the electron analogue of NCS. Nevertheless, there would be a difference in practical application between the two methods, which originates from the difference in nature of the projectile–target interaction. Since the neutron–nucleus scattering is described by a delta function,16 the main targets of NCS have been condensed matter (liquids and solids). On the other hand, application of AMS may be best suited to low density targets such as gaseous molecules, molecules adsorbed on surfaces and very thin films, in order to avoid multiple electron scattering. Furthermore, although NCS has reported a strong anomalous ratio of the H- and D-atom cross sections for HD (liquid at 20 K),17 the present study has clearly revealed that there is no anomaly in AMS measurements on gaseous HD molecules. In addition, the ability of AMS to perform elemental composition analysis is also analogous to that of Rutherford backscattering spectroscopy (RBS) using ion particles such as He2+.18 In this regard, in contrast to the lower accuracy of RBS for lighter atoms,19 the present study has demonstrated that AMS provides high accuracy for the lightest and second lightest atoms despite their small cross sections compared to those for heavier atoms with larger Zi. AMS would therefore be very useful, in particular for low density targets containing light atoms.
Conclusions
In summary, we reported the AMS study on HD. The AMS experiments were performed at θ = 135° and at E0 = 2.0 keV, thus achieving the q value of 22.4 a.u. The experimental data of HD were analyzed by using the general protocol and the gas beam model, in order to disentangle the experimental responses of the intramolecular H- and D-atom motions from the effect of molecular translational motion as well as the intrinsic IR function. The resulting Compton profiles have been found to be identical with each other and with the associated quantum chemistry-based calculations in both shape and intensity. These observations have revealed that the Compton profiles reach the high q limit under the experimental conditions employed. The observations have also revealed that AMS can be used as a molecular spectroscopy technique, which combines the ability to map the intramolecular motion of each atom with different masses and the ability to perform elemental composition analysis of a molecular system.Finally, it may be worthwhile to discuss some future prospects of AMS. The next crucial step in establishing AMS as a new molecular spectroscopy technique is that the reach of AMS should be extended to polyatomic molecules. In this regard, there has been no theory that provides reliable Compton profiles for polyatomic molecules, while the experiment is already ready. We have thus developed a quantum chemistry-based AMS theory for polyatomic molecules and will report it shortly. We believe one of the most important applications of AMS would be in the real-time measurement of the intramolecular force acting on a specific atom in a transient species,20 based on Ehrenfest's theorem that relates the time derivative of the expectation value of the momentum operator P to the expectation value of the force.
Author contributions
MT designed and supervised the present AMS study. YT and SK performed the experiments and data analysis under the supervision of YO. YT and YO made the quantum chemistry-based calculations under the supervision of HK. YT, HK and MT wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the JSPS KAKENHI Grant Numbers 20J12788, 21H04672 and 21K18926. This work was also supported by The Murata Science Foundation.References
- M. Vos, Phys. Rev. A., 2001, 65, 012703 CrossRef.
- E. B. Wilson, Jr., J. C. Decius and P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications, New York, 1980 Search PubMed.
- M. Yamazaki, Y. Tachibana and M. Takahashi, J. Phys. B: At., Mol. Opt. Phys., 2019, 52, 065205 CrossRef CAS.
- Y. Tachibana, Y. Onitsuka, H. Kono and M. Takahashi, Phys. Rev. A, 2022, 105, 052813 CrossRef CAS.
- C. Eckart, Phys. Rev., 1935, 47, 552–558 CrossRef CAS.
- V. F. Sears, Phys. Rev. B, 1984, 30, 44–51 CrossRef CAS.
- G. I. Watson, J. Phys.: Condens. Matter, 1996, 8, 5955–5975 CrossRef CAS.
- Y. Onitsuka, Y. Tachibana and M. Takahashi, Phys. Chem. Chem. Phys., 2022, 24, 19716–19721 RSC.
- R. Moreh and D. Nemirovsky, J. Chem. Phys., 2010, 133, 084506 CrossRef CAS PubMed.
- G. Cooper, A. P. Hitchcock and C. A. Chatzidimitriou-Dreismann, Phys. Rev. Lett., 2008, 100, 043204 CrossRef CAS PubMed.
- M. Vos and M. R. Went, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 065204 CrossRef.
- M. Yamazaki, M. Hosono, Y. Tang and M. Takahashi, Rev. Sci. Instrum., 2017, 88, 063103 CrossRef PubMed.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, Van Nostrand Reinhold, New York, 1979, vol. 4 Search PubMed.
- N. F. Ramsey, in Atomic, Molecular, and Optical Physics: Atoms and Molecules, ed. F. B. Dunning and R. G. Hulet, Academic Press, New York, 1996, vol. 29B Search PubMed.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, New York, 2nd edn, 1992 Search PubMed.
- S. Lovesey, Theory of Neutron Scattering from Condensed Matter, Clarendon Press, Oxford, 1984, vol. 1 Search PubMed.
- C. A. Chatzidimitriou-Dreismann, T. Abdul-Redah and M. Krzystyniak, Phys. Rev. B, 2005, 72, 054123 CrossRef.
- W. K. Chu, J. W. Mayer and M. A. Nicolet, Backscattering Spectrometry, Academic Press, New York, 1978 Search PubMed.
- C. R. Gosett, Nucl. Instrum. Methods Phys. Res., Sect. B, 1989, 40–41, 813–816 CrossRef.
- Y. Tachibana, Y. Onitsuka, M. Yamazaki and M. Takahashi, Atoms, 2021, 9, 19 CrossRef.
| This journal is © the Owner Societies 2023 |