Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insights into the deviation from piecewise linearity in transition metal complexes from supervised machine learning models†
Yael
Cytter
a,
Aditya
Nandy
 ab,
Chenru
Duan
ab,
Chenru
Duan
 ab and
Heather J.
Kulik
ab and
Heather J.
Kulik
 *ab
*ab
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
bDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 22nd February 2023
Abstract
Virtual high-throughput screening (VHTS) and machine learning (ML) with density functional theory (DFT) suffer from inaccuracies from the underlying density functional approximation (DFA). Many of these inaccuracies can be traced to the lack of derivative discontinuity that leads to a curvature in the energy with electron addition or removal. Over a dataset of nearly one thousand transition metal complexes typical of VHTS applications, we computed and analyzed the average curvature (i.e., deviation from piecewise linearity) for 23 density functional approximations spanning multiple rungs of “Jacob's ladder”. While we observe the expected dependence of the curvatures on Hartree-Fock exchange, we note limited correlation of curvature values between different rungs of “Jacob's ladder”. We train ML models (i.e., artificial neural networks or ANNs) to predict the curvature and the associated frontier orbital energies for each of these 23 functionals and then interpret differences in curvature among the different DFAs through analysis of the ML models. Notably, we observe spin to play a much more important role in determining the curvature of range-separated and double hybrids in comparison to semi-local functionals, explaining why curvature values are weakly correlated between these and other families of functionals. Over a space of 187.2k hypothetical compounds, we use our ANNs to pinpoint DFAs for which representative transition metal complexes have near-zero curvature with low uncertainty, demonstrating an approach to accelerate screening of complexes with targeted optical gaps.
1. Introduction
Virtual high-throughput screening (VHTS)1–8 with first-principles density functional theory (DFT) accelerated by machine learning (ML)9–15 has advanced the discovery of new molecules and materials. Nevertheless, such workflows inherit the limitations of the density functional approximations (DFAs) used in practice. The failures of DFT are prominent for the cases where chemical discovery efforts are most needed (e.g., open-shell radicals, transition–metal-containing systems, and strained bonds).16–20 Although DFT is widely used in theoretical studies of transition metal complexes,21,22 common approximations to the exchange–correlation (xc) functional, however, introduce self-interaction errors (SIEs).22–26 These SIEs result in fundamental errors in the description of dissociation energies,24,27–30 barrier heights,31 band gaps,32,33 electron affinities,34–36 and thermodynamic properties.37 Because the exact energy functional should be piecewise linear with respect to fractional removal or addition of charge,38 the global curvature, that is the second derivative of the energy E with respect to charge q, is considered a good measure for many-electron self-interaction error also known as delocalization error (DE). A number of efforts in tailoring functionals to eliminate this DE,39–43 for example, by tuning, have been successful for improving DFT predictions of optical properties (e.g., the gap between the highest-occupied molecular orbital, HOMO, and lowest unoccupied molecular orbital, LUMO).44A potential solution to overcome these limits is to climb up a “Jacob's ladder”45 of DFAs, where functionals on higher rungs include greater complexity such as higher-order derivatives of the density, Hartree–Fock (HF) exchange, and long-range correlation from perturbation theory (i.e., MP2) to recover dispersive interactions from first principles. Doing so has been shown to increase accuracy for organic molecules, but simply climbing to higher rungs does not always guarantee improvements in challenging systems such as transition metal complexes.46,47 While transition metal complexes are key targets for chemical discovery due to their widespread applications in catalysis4,48–54 and energy utilization (e.g., in redox flow batteries,55 solar cells,56 and molecular switches57), their electronic structure is uniquely challenging to describe.18 The variable nature of metal, oxidation state, and spin of transition metal complexes introduces combinatorial explosion in design spaces11,58 that cannot be exhaustively explored by either first-principles methods or experiments, motivating ML acceleration.59–65 Open-shell transition metal complexes are particularly difficult to study due to their near-degenerate d orbitals that may introduce significant multireference (MR) character.66–70 Furthermore, their properties are highly sensitive to the choice of DFA and the resulting biases will be passed down to and encoded in ML models trained on this data. For example, ML-accelerated discovery based on semi-local DFT will identify lead TMCs targeted for specific spin state properties (e.g., spin-crossover or SCO) with weaker-field ligands than those found by hybrid-DFT-derived ML models.63
In general, choosing the “right” rung a priori in ML model training or discovery efforts may be impractical if reference benchmarks are not established, and, instead, a single low-cost, heavily tested DFA (e.g., PBE or B3LYP) is usually employed. Nevertheless, when careful studies of smaller data sets have been carried out, they have revealed DFA dependence (e.g., on the fraction of HF exchange) of property evaluations for both organic molecules71–73 and transition metal complexes.74–78 An alternative paradigm that has recently emerged is to train ML models that can predict appropriate parameters or methods for first-principles simulation, including the selection of active spaces,79,80 detection of multi-reference character,81–83 or identification of the best DFT functional to reproduce higher-level reference calculations.84,85 ML models have been developed as improved xc functionals,86–90 for example, by training on the correct fractional charge energetics needed to recover piecewise linearity. In a complementary approach, Corminboeuf and coworkers trained ML models to predict the degree of curvature or DE of small organic molecules to suggest parameters for optimal tuning of functional parameters.91 Marom and coworkers recently developed ML models to predict the appropriate Hubbard U for use in DFT+U.92
We recently curated93 a set of around 1000 transition metal complexes to train artificial neural networks (ANNs) on 23 DFAs to predict properties across multiple rungs of “Jacob's ladder”.45 We showed that requiring consensus among the DFAs improved predictions when compared to experiment.93 Extending upon this work, we now leverage the same dataset to reveal trends in curvature with DFA. In this work, we compute the curvatures of the complexes in the dataset for each of the 23 DFAs. We identify different trends in curvature values (i.e., as judged through correlations in the data) for functionals from distinct rungs. We train machine learning models (e.g., ANNs) on this data set and analyze the most important features of each model to better understand what aspects of chemical composition most strongly influence the curvature of a transition metal complex for a given DFA. We then use these ANN models to screen a space of 187k hypothetical complexes to pinpoint DFAs that would yield piecewise linearity in representative complexes. We validate these leads, demonstrating ANNs as an efficient approach to rapidly identify DFAs and compounds for which approximate DFT will recover exact conditions.
2. Methods
2a. Data set and details of DFT calculations
We employed a data set curated in prior work,93 which consists of the equilibrium geometries of 948 isolated mononuclear transition metal complexes obtained with density functional theory (DFT). As in prior studies,59–61,93–95 we studied M(II)/M(III) complexes (M = Cr, Mn Fe, or Co) with high-spin (HS) and low-spin (LS) multiplicities defined as follows: quintet–singlet for d4 Mn(III)/Cr(II) and d6 Co(III)/Fe(II), sextet-doublet for d5 Fe(III)/Mn(II), and quartet-doublet d3 Cr(III) and d7 Co(II) (Table S1, ESI†). These metal centers were studied in octahedral complexes with ligands containing a variety of metal-coordinating atoms and a range of charge states (Table S2, ESI†).While the structures were obtained from prior work,93 we briefly describe the protocol to generate them here. All geometry optimizations were carried out using TeraChem96 v1.9, as automated by molSimplify.94,97 These calculations used the unrestricted B3LYP98,99 hybrid functional for non-singlet states and restricted B3LYP for singlet states, with the LACVP* basis set, which corresponds to the LANL2DZ100 effective core potential for the transition metals and heavier elements (I or Br) and the 6-31G* basis for all other elements. In all calculations, level shifting of 1.0 Ha on virtual majority-spin orbitals and 0.1 Ha on virtual minority-spin orbitals was employed. Geometry optimizations used the L-BFGS algorithm in translation rotation internal coordinates (TRIC)101 to the default tolerances of 4.5 × 10−4 Hartree bohr−1 for the maximum gradient and 1 × 10−6 Hartree for the change in self-consistent field (SCF) energy between steps.
Average curvature calculations were calculated according to ref. 102:
| 〈Curvature〉 = εNHOMO − εN−1LUMO, | (1) |
The ML model training set for each functional only includes complexes where the HOMO and LUMO errors have the same sign. The HOMO error is defined as ΔE − εNHOMO, and the LUMO error is defined as εN−1LUMO − ΔE, where ΔE = EN − EN−1, and EN is defined as the total energy of a system with N electrons.104 This screening ensures that the average curvature defined in eqn (1) is well defined for all the complexes included in the ML model training process. All structures and data sets used to train machine learning models in this work are available on Zenodo at the DOI: https://doi.org/10.5281/zenodo.7497666.
2b. ML model training
In this work, we followed the same protocol described in previous work93 for training ML models. We use revised auto-correlations61 (RACs) as descriptors for all our machine learning models. RACs are sums of products and differences of five atom-wise heuristic properties (i.e., topology, identity, electronegativity, covalent radius, and nuclear charge) on the 2D molecular graph. As motivated previously,61 we applied a maximum bond depth of three and eliminated RACs that were invariant over the mononuclear octahedral transition metal complexes, leaving 151 RACs in total. With the inclusion of oxidation state, spin multiplicity, and total ligand charge, we obtained a feature set of 154 descriptors in total. For both kernel ridge regression (KRR) and artificial neural network (ANN) models, the hyperparameters were selected using Hyperopt105 with 200 evaluations on a range of hyperparameters, using a random 80%/20% train/test split and 20% of the training data as the validation set. As in prior work,83,93,94 recursive feature addition (RFA) was carried out on random-forest-ranked features (i.e., RF-RFA) to select the feature set that gives the best-performing KRR model on the basis of mean absolute error. All KRR models were implemented in scikit-learn106 with a radial basis function kernel. All ANN models were trained with the Adam optimizer107 up to 2000 epochs, and dropout,108 batch normalization,109 and early stopping110 were applied to avoid over-fitting.We use the latent space distance as an uncertainty metric to control design space prediction errors, as in prior work111,112 (Fig. S1, ESI†). The distance is calculated within Keras113 as the Euclidean distance in latent space between the test point and each training point. The latent distances between each test complex and the 10 nearest training complexes were averaged to determine the uncertainty score for that test complex. For the design space predictions, we chose a conservative latent distance cutoff of 0.2 for all functionals based on the distribution of the mean latent distances of the different ANNs, where each ANN corresponds to a different functional (Fig. S2, ESI†). All machine learning models and data sets used to train machine learning models in this work are available on Zenodo at the DOI: https://doi.org/10.5281/zenodo.7497666.
For feature analysis of the ANN models, we used the SHAP (SHapley Additive exPlanations)114 Python code. We used 20% of the training set as the background data to initialize the KernelExplainer method. We then obtained SHAP values over the test set. For each model, we averaged over the absolute SHAP values of the test set for the different features to determine a SHAP value for each feature. Each feature was then averaged over the different functionals in a functional group, and we selected the 15 features with the highest mean values as important.
3. Results and discussion
3a. Data set analysis
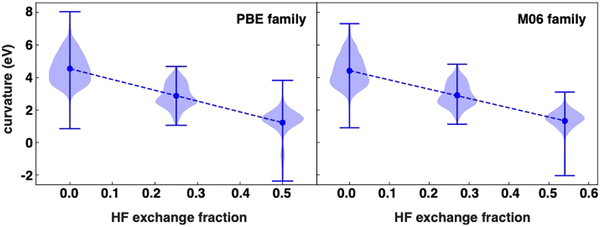
We first analyze the calculated curvature values in our dataset. While the curvature values are symmetric around a mean for some functionals, the distributions are less apparently normal than in prior work on organic molecules.91 Nevertheless, expected trends hold, with the highest values corresponding to curvatures ranging from 1 to 8 eV for GGA functionals (i.e., PBE, BP86 and BLYP). Increasing the HF exchange fraction results in a decrease of the mean of the distribution (Table S4, ESI†). This can be observed when comparing functionals that differ mostly by the fraction of HF exchange included in the functional (Fig. 1). There is a clear linear decrease in the mean curvature in the PBE family of functionals, that is, PBE, PBE0 and PBE-DH, as the HF fraction increases from 0.0 to 0.5, although the standard deviation and range of the distribution does not shift monotonically with HF fraction (Fig. 1). While the average of our PBE0 data is comparable to what has been reported for a set of small organic molecules,91 the range and spread of the data is larger here owing to the more diverse behavior of transition metals and their capacity to support multiple spin states.The same behavior with HF exchange fraction can be seen for the M06-based family, M06-L, M06 and M06-2X, which exhibit similar changes in curvature values to those seen in the PBE family as a function of HF exchange fraction (Fig. 1). The rates of decrease, measured as the curvature as a function of the HF exchange fraction (HFX), are comparable between the two families, with slopes of −6.6 eV per HFX and −5.7 eV per HFX for PBE and M06 families respectively (Fig. 1). Extrapolating these values suggests mean curvatures would be close to zero at around 66% HF exchange, but, as evident from the distributions, selecting this HF exchange fraction would also lead to a long tail of overcorrected (i.e., negative curvature) compounds (Fig. 1). This slope is not universal for all functional families; the mean curvature of dispersion-corrected functionals, DSD-BLYP-D3BJ, DSD-PBEB95-D3BJ and DSD-PBEP86-D3BJ, decreases linearly from −0.5 to −1.5 eV as the HF fraction in the xc functional increases, with a slope five times higher (Fig. S3, ESI†). The reason for this stronger variation with modest changes in HF exchange is likely due to the fact that the double hybrids vary much more significantly in other components of the functional, i.e., the form of the pure DFT exchange and correlation functional components.
For the two double hybrids that both employ PBE GGA exchange (i.e., DSD-PBEB95-D3BJ with 69% exchange and DSD-PBEP86-D3BJ with 71% exchange), we can isolate the effects to both HF exchange variation and the change in the correlation from B95 to P86. While we would expect the average curvature to decrease from DSD-PBEB95-D3BJ to DSD-PBEP86-D3BJ by only around 0.1–0.15 eV based on the trends in HF exchange tuning for the PBE and M06 families, the difference in the means is larger (−1.20 eV versus −1.55 eV, Table S4, ESI†). Nevertheless, it is also evident that shifts in the tails of the distribution have a large influence over the computed mean (i.e., with more positive curvatures computed with DSD-PBEB95-D3BJ), likely also exaggerating the shift in the means. As for the difference of DSD-BLYP-D3BJ compared to the other two functionals, the significant differences from the pure DFT exchange correlation functional lead to a mean curvature value of −0.55 eV that is nevertheless around what we would expect from analysis of the PBE and M06 families (i.e., near-zero curvature at around 66% exchange). Thus, the double hybrids are not entirely inconsistent with trends observed for simpler functionals.
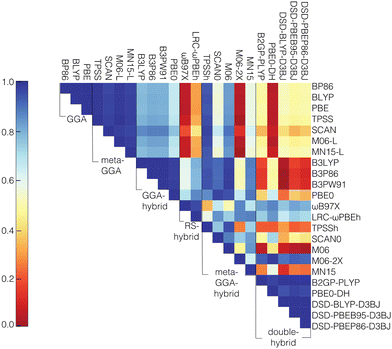
We next computed the correlation (i.e., Pearson's r) between the curvature values of the different functionals. The functionals from different rungs of “Jacob's ladder”45 have low correlation, especially in comparison to the correlations of the individual HOMO and LUMO energies among the different functionals (Fig. 2 and Fig. S4, S5, ESI†). The lowest Pearson's r values in the HOMO and LUMO cases are 0.95, whereas the lowest values among the curvature correlations are close to zero. This lower correlation in curvature values is likely because large ranges of HOMO and LUMO values cancel to form smaller overall ranges of curvature values over which correlations will be weaker, while individual HOMO or LUMO values have significant dependence on total charge or size of a transition metal complex,93,94 leading to higher Pearson's r values. Interestingly, of the double hybrids, PBE0-DH shows the highest correlations of the HOMO and LUMO with GGA and meta-GGA families, while it shows the lowest correlations of the curvature. In contrast, M06-2X, which has the lowest correlations for the HOMO and LUMO with GGA and meta-GGA family members of any meta-GGA hybrid, also has the lowest correlations for the curvature values (Fig. S4 and S5, ESI†).
For the correlation of curvatures between different functionals within the same “rung” of Jacob's ladder, the results agree with previous work93 where it was shown that the GGA and meta-GGA groups were highly correlated among themselves when considering the adiabatic high-spin to low-spin splitting, a property that was also sensitive to the choice of DFT functional. In the present work, the lowest correlation values observed within the GGA and meta-GGA families for curvature are 0.99 and 0.97, respectively. Despite the strong correlation among pure meta-GGAs, we observe that the meta-GGA hybrids are the least correlated family, likely due to the introduction of a range of HF exchange fractions. The lowest correlation in curvature is observed between M06-2X (54% exchange) and TPSSh (10% exchange). The low correlation of M06-2X with other functionals in the same family is also consistent with our previous observations on frontier orbital energies and spin splittings.93 While curvature might be expected91,115 to depend linearly on the degree of HF exchange, our own results indicate that over a wider range of HF exchange fractions, non-linear effects on curvature arise due to a change in the character of the frontier orbitals. In general, the correlation between the highly parameterized M06-2X and the other meta-GGA hybrid functionals is always the lowest, with the highest correlation of 0.74 observed with SCAN0 (25% exchange), signifying a large variability between M06-2X and the rest of the meta-GGA family. Thus, machine learning models trained on each of these individual data sets can be expected to learn distinct curvature–structure mappings.
3b. Training ML models to predict curvature
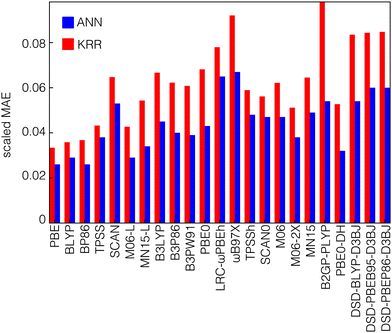
We trained both kernel ridge regression (KRR) and artificial neural network (ANN) ML models to predict electronic structure properties of transition metal complexes (see Methods). We employ feature selection with RF-RFA when training the KRR models, whereas we apply no feature engineering to the ANN models (see Methods). We trained ML models on the transition metal complex dataset to predict the average curvature as well as the HOMO energy of the N-electron system and the LUMO energy of the N−1-electron system (i.e., the two quantities that determine the average curvature). We evaluate accuracy from the value of the scaled mean absolute error (MAE) of these models, which is defined as the absolute difference between the predictions and the exact results divided by the range spanned by the training set values. The HOMO and LUMO energies are predicted equally well by KRR and ANN models, with scaled MAEs of 0.013 and 0.010 for KRR and ANN models respectively for HOMO energy predictions and scaled MAEs of 0.013 and 0.012 for LUMO energy predictions averaged over all functionals (Fig. S6, ESI†). These errors are consistent with results obtained previously on similar datasets of transition metal complexes.83 In contrast to the HOMO or LUMO models, we observe that the average curvature is consistently better predicted by the ANN models than the KRR models for all functionals (Fig. 3). However, the scaled errors are consistently higher than those for the orbital energies, with a mean scaled MAE of 0.044 for ANN predictions and 0.062 for KRR models across all functionals. This increase in scaled MAE is expected because the range of curvature values is much smaller than the range of individual HOMO or LUMO values. Considering differences in data set size and diversity, errors previously observed for ML models trained to predict QM7 curvature values are largely comparable as well.91The most significant difference of the ANN models relative to the KRR models is seen for double-hybrid functionals, where the ANN performs around 30–45% better (i.e., lower scaled MAE) than the KRR model (44% in B2GP-PLYP). While this discrepancy is large, this observation is consistent with previous observations for the closely related task of HOMO–LUMO gap prediction, where an ANN outperformed the KRR model by 16–24% depending on the dataset.83 In addition, ANN models were shown to perform better when predicting the adiabatic spin-splitting energy, where the KRR MAE was shown to be higher than that of ANN for most functionals.93 Both spin splitting and HOMO–LUMO gap are similar to the curvature in that they are defined as energy differences, leading to smaller ranges of values than the individual frontier HOMO or LUMO energies.
It is worthwhile to note that the training set of each functional is unique and the size of each data set could affect the results. After pruning the original dataset to eliminate ambiguous curvature values (see Methods), the remaining datasets are not the same size for all functionals (Fig. S7, ESI†). The fewest ambiguous curvature values are present for pure (i.e., GGA or meta-GGA) functionals because they tend to have strongly positive HOMO and LUMO errors (i.e., positive curvatures) so these data sets are larger than the sets for functionals that incorporate HF exchange. In practice, this means that hybrid GGA and hybrid meta-GGA functionals each have data sets with approximately 550 items on average, and double-hybrid functionals are, in most cases, trained on the smallest datasets, with approximately 280 points on average in each dataset. While some points in the work from which we curate the present dataset did not converge,93 our datasets are primarily reduced due to the presence of opposing HOMO and LUMO sign errors that make estimating the average curvature from eqn (1) not suitable. Somewhat surprisingly, we observe that ANNs outperform KRR models most for the double hybrids with the smallest data sets, and we observe relatively comparable performance of KRR and ANN models for the larger GGA dataset sizes where both perform well. Nevertheless, holding the model fixed and comparing functionals, we do observe that models trained on the larger GGA datasets have consistently lower MAEs than those trained on double hybrids.
To attempt to assess the effect of the size of the training set on the results, we trained models for each functional using both KRR and ANN on a dataset that contains compounds with valid curvature values for all functionals. This dataset is necessarily very small, with only 64 complexes, in comparison to the individual DFA datasets because different functionals lead to distinct HOMO and LUMO errors (Fig. S7, ESI†). The 64-complex dataset is particularly small because it is the subset of complexes for which a meaningfully valued curvature is obtained for all 23 functionals. The MAEs are much higher than those of the original DFA-specific datasets as a result (Fig. S8, ESI†). For the models trained on substantially less data, the ANN models predicting the curvature for double-hybrid functionals are no longer clearly superior to the KRR models. Additionally, the BP86 ANN model has a scaled MAE more than twice as large as that of KRR when trained on the small dataset whereas it had a 40% lower error over the original dataset (Fig. 3). Taken together with our earlier observations on more moderate dataset size ranges of around 300–600 points, it is worth noting that once the dataset size is not much larger than the number of metals, oxidation, and spin states present in the set, the learning task is much more difficult. However, as long as there are multiple examples of each metal with a range of ligands, ANNs are likely to remain preferable to KRR models, even when the dataset size is modest (ca. 300 points). We thus conclude that while the variability (in terms of size and composition) of the different sets may be significant when comparing the different models, working with the largest available datasets is likely the optimal way to achieve good model accuracy So, in the rest of this work we will refer to models trained on the original larger datasets.
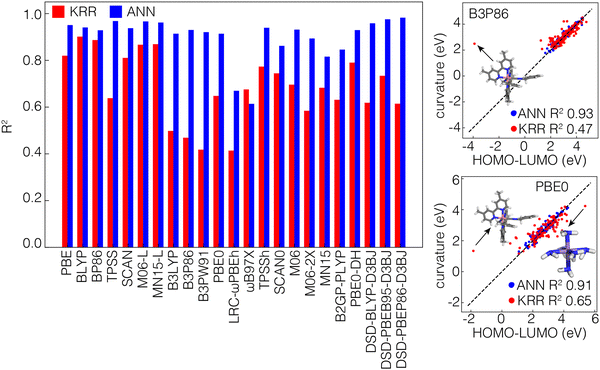
To evaluate the internal consistency of the KRR and ANN models, we subtract the individual ML model predictions of the HOMO energy of the N-electron systems and LUMO energy of the N−1-electron systems and compare this value to the direct curvature predictions from ML models. Despite the fact that individual frontier orbital energy predictions from the KRR and ANN models were of comparable accuracy, indirect calculations of the curvature from predicted HOMO and LUMO values by the ANN are much more consistent with the direct predictions (i.e., R2 close to 1) compared to the KRR (Fig. 4). The differences between the direct and indirect approaches are lowest in GGA functionals and are most apparent in hybrid-GGA functionals. A closer look at the distributions of these predictions shows that a specific complex of Co with two 4,4′-dimethyl-2,2′-bipyridine ligands and two benzyl iscocyanide ligands is consistently an outlier in the KRR predictions and is not well predicted by these models (Fig. 4). For multiple ML models trained on different functionals, the predicted HOMO–LUMO difference of this compound is significantly lower than the curvature. Even if we disregard these outliers, our observations still encourage the use of the ANN over the KRR model for performance. So for the rest of this work, we will therefore focus on the ANN models only.
3c. Feature importance analysis
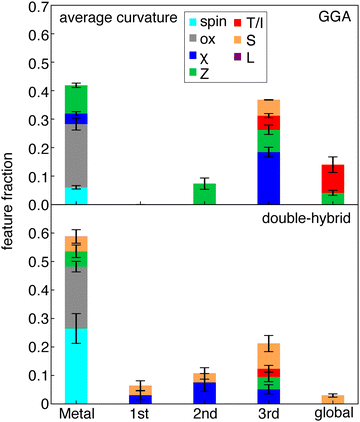
By analyzing the most important features in ML model predictions, we can achieve interpretability of otherwise black-box structure–property mappings. We employ SHAP analysis (see Methods) to interpret our ANN models. SHAP uses game theory to calculate the impact of a feature on the resulting target value.114 The average value of the impact of a feature can be used as a measure of its importance. SHAP is model-agnostic (i.e., and thus can be used with the ANNs trained here) and performs a perturbation around the points of the training data to calculate the impact on the model. We selected SHAP because we can directly interpret the ANN models, which perform better than the KRR models on our learning task, as opposed to recursive feature addition into KRR models that we had carried out in prior work,93 while still providing insights into which RAC features are the most important for model prediction. From SHAP analysis, we observe that the metal center is most important for predicting curvature, followed by more distant features (i.e., three bond paths away) (Fig. 5 and Fig. S9, ESI†).It is worth noting that we attribute the oxidation state of the complex to the metal center because our ligands are redox innocent. This oxidation state is a universally large and expected contributor to the prediction of the curvature because it can be expected to alter the global ionization potential and electron affinity as well as the extent to which a particular DFT functional deviates from ideality. If this feature were instead attributed as a global feature, then the contributions three-bond paths away would dominate for most functionals. Nevertheless, the nature of the most important metal-centered features in curvature models varies considerably between different families of functionals (Fig. 5 and Fig. S9, ESI†). For functionals with higher HF exchange fractions (e.g., double hybrids), spin and oxidation state become dominant metal-centered features, whereas for semi-local functionals oxidation state has an overriding effect in comparison to spin (Fig. 5).
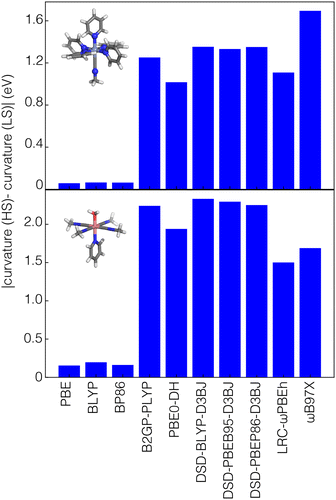
To understand the origin of this difference, we obtained the difference in curvature between high- and low-spin states for four representative complexes, each with a different metal center: Cr(III)(pyridine)5(methylisocyanide), Mn(II)(furan)4(H2O)(CO), Fe(III)(furan)5(methylisocyanide), and Co(II)(methylisocyanide)4(H2O)(pyridine). These selected complexes have a mix of strong-field (i.e., CO or methylisocyanide) and weak-field (i.e., H2O, furan) ligands. We focus on differences in results among GGA, range-separated-hybrid and double-hybrid families because they have the greatest differences in the relative importance of spin state for curvature prediction according to SHAP analysis (Fig. 6 and Fig. S10, ESI†). In these examples, the difference in curvature between spin states with GGA functionals are close to zero and no larger than around 0.3 eV for any of the GGAs considered (i.e., PBE, BLYP, or BP86, Fig. 6 and Fig. S10, ESI†). In comparison, both double hybrids and range-separated hybrids have curvatures that differ in magnitude by around 1 eV or more between spin states (Fig. 6 and Fig. S10, ESI†).
This dependence on spin present in the RS- and double-hybrid ML models could be attributed to differences in how the HF term in the exchange–correlation functional reduces the Coulomb term specifically in the cases of opposite spin projection. However, it is surprising then that global hybrids lack this behavior. After the metal features, atoms three bonds away are the most significant for curvature predictions (Fig. 5). This suggests significant size-dependence in the curvature. This trend holds for all functionals and is strongest for GGAs. This agrees with our expectation that charge addition in larger complexes delocalizes over more of the complex, resulting in lower apparent curvature.
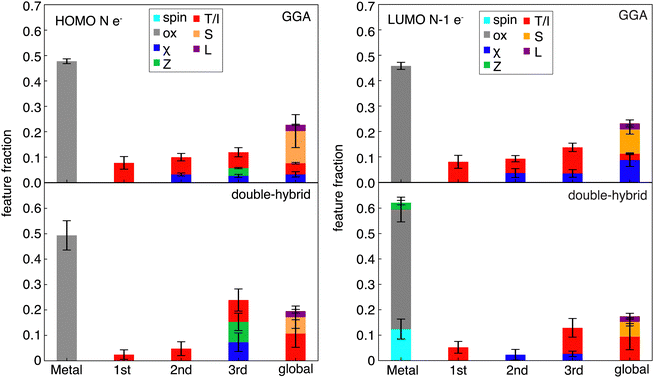
Despite some differences in feature importance in models trained on curvatures from differing functionals, the most important features in the individual HOMO and LUMO are more consistent, in agreement with RF-RFA KRR feature importance observations from prior work93 (Fig. 7 and Fig. S11, S12, ESI†). Nevertheless, limited differences are apparent. For both HOMO and LUMO SHAP analysis, the GGAs show more overall dependence on the chemical structure, whereas double hybrids tend to more strongly emphasize distant (i.e., three bond paths or more) features. Both HOMO and LUMO models depend significantly on more distant (i.e., three bonds or more) atoms, indicating the size dependence of the HOMO and LUMO energies. This observation is in agreement with previous results83 that showed strong global dependence and a lower metal-local dependence of the HOMO energy in RF-RFA KRR feature selection. Both the HOMO and LUMO features, however, show overriding dependence on the oxidation state in terms of metal-centered features. The SHAP analysis does not contradict observations from RF-RFA KRR, but since SHAP analysis not only selects the important features but also assigns them a weight with a SHAP value, it emphasizes that while oxidation state is the only metal-related feature selected, it has high importance.
Unlike the case of curvature, in the HOMO of the N-electron system models, spin is not one of the important features in any of the functional families (Fig. 7). The dependence of curvature on the spin state instead appears to stem from the LUMO of the N−1-electron system, which shows spin dependence only in the RS-hybrid and double-hybrid functionals. Both the HOMO and LUMO model predictions also depend on ligand charge, which was not one of the significant features according to SHAP analysis of the curvature models, emphasizing stronger dependence on oxidation state of the individual HOMO and LUMO values than for their difference (i.e., in curvature). Overall, despite curvature being derived from HOMO and LUMO properties inherently, it shows distinct and functional–sensitive property importance, as judged by SHAP analysis. This suggests that errors can be attributed to different sources for different functional families (e.g., metal spin in RS- and double-hybrids).
3d. Large-scale exploration of curvature in transition metal chemical space
To obtain a broader understanding of the relationship between the DFT curvature and chemical properties, we apply the trained HOMO, LUMO and curvature models to a space of 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 hypothetical transition metal complexes. As described in previous work83 the space of theoretical complexes contains HS and LS M(II/III) (M = Cr, Mn, Fe, or Co) centers in complex with 36 unique ligands derived from the original data set.83 Thus, this set is interpolative in nature but contains many complexes not used in the training data of the model. These new complexes have properties (e.g., size and charge) distinct from those of the data set we used to train our ANN models, specifically because different ligand combinations in this larger set were absent from the training data. To ensure suitability of ANN model predictions on this data set, we apply the latent distance criteria111 as an uncertainty quantification (UQ) metric (see Methods) and retain only complexes that are below the latent distance threshold for all functionals. This UQ cutoff leaves us with 155
200 hypothetical transition metal complexes. As described in previous work83 the space of theoretical complexes contains HS and LS M(II/III) (M = Cr, Mn, Fe, or Co) centers in complex with 36 unique ligands derived from the original data set.83 Thus, this set is interpolative in nature but contains many complexes not used in the training data of the model. These new complexes have properties (e.g., size and charge) distinct from those of the data set we used to train our ANN models, specifically because different ligand combinations in this larger set were absent from the training data. To ensure suitability of ANN model predictions on this data set, we apply the latent distance criteria111 as an uncertainty quantification (UQ) metric (see Methods) and retain only complexes that are below the latent distance threshold for all functionals. This UQ cutoff leaves us with 155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 295 complexes, but we lack ground-truth performance to confirm that this UQ step improves predictions over the large set. Instead, we compared the ANN prediction of the curvature from the indirect method (i.e., the difference between the HOMO of the N-electron system and the LUMO of the N−1-electron system) to the directly predicted curvature and assess agreement (i.e., the R2) between the two predictions. Although the R2 value is already good before filtering, it improves for most functionals after removing high-uncertainty data (Fig. S13, ESI†). This observation provides support for the applicability of our models to the UQ-curated design space.
295 complexes, but we lack ground-truth performance to confirm that this UQ step improves predictions over the large set. Instead, we compared the ANN prediction of the curvature from the indirect method (i.e., the difference between the HOMO of the N-electron system and the LUMO of the N−1-electron system) to the directly predicted curvature and assess agreement (i.e., the R2) between the two predictions. Although the R2 value is already good before filtering, it improves for most functionals after removing high-uncertainty data (Fig. S13, ESI†). This observation provides support for the applicability of our models to the UQ-curated design space.
Next, we analyze the molecules that have the lowest absolute curvature predictions for the ANNs trained on different functionals. We focus on complexes that are in the lowest 20% (31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 complexes) of the distribution of absolute curvatures. We make observations grouped over the GGA, meta-GGA, RS-hybrid and double-hybrid families. The lowest 20% of the GGA and meta-GGA curvatures ranges between 1–3 eV, and the most common ligands in this subset are 4-tert-butylphenyl isocyanide, thiopyridine, and cyanopyridine, which are relatively large ligands (Fig. S14, ESI†). For the RS-hybrid and double-hybrid families on the other hand, the lowest absolute curvatures range between −0.3 and 0.3 eV. The most dominant ligands in this low-curvature region in the double-hybrid family are again 4-tert-butylphenyl isocyanide and thiopyridine as in the GGA families but in addition, some smaller ligands (such as NCO− and SH2) also appear frequently (Fig. S14, ESI†). For the RS-hybrids, the most common ligands in low-curvature complexes are smaller weak-field ligands such as SH2, OH− and F− (Fig. S14, ESI†). Thus, large ligands do not necessarily lead to zero curvature in RS-hybrids, and weak-field ligands lead to zero curvatures only for some families of functionals. For the RS-hybrids, large ligands generally lead to overcorrection and negative curvatures. From a metal-center perspective, no unifying picture of curvature is present across all families of functionals. While Co is the primary metal observed in low-curvature complexes for GGAs and meta-GGAs and Mn is the least represented, the reverse is true for RS-hybrids (Fig. S15, ESI†). Hybrid and non-hybrid functionals also differ in the spin state that dominates the low-curvature regime, where hybrid functionals show a distinct preference for low curvatures for complexes in HS states, whereas non-hybrids favor HS and LS states equally (Fig. S16, ESI†). This observation is consistent with our earlier model feature analysis. In terms of oxidation state, only RS-hybrids have equal numbers of +2 and +3 oxidation state compounds with low curvature, whereas other families prefer +3 oxidation states (Fig. S17, ESI†). This observation is somewhat surprising because the ionization potential increases with increasing oxidation state and curvature values could be expected to increase as a result.
059 complexes) of the distribution of absolute curvatures. We make observations grouped over the GGA, meta-GGA, RS-hybrid and double-hybrid families. The lowest 20% of the GGA and meta-GGA curvatures ranges between 1–3 eV, and the most common ligands in this subset are 4-tert-butylphenyl isocyanide, thiopyridine, and cyanopyridine, which are relatively large ligands (Fig. S14, ESI†). For the RS-hybrid and double-hybrid families on the other hand, the lowest absolute curvatures range between −0.3 and 0.3 eV. The most dominant ligands in this low-curvature region in the double-hybrid family are again 4-tert-butylphenyl isocyanide and thiopyridine as in the GGA families but in addition, some smaller ligands (such as NCO− and SH2) also appear frequently (Fig. S14, ESI†). For the RS-hybrids, the most common ligands in low-curvature complexes are smaller weak-field ligands such as SH2, OH− and F− (Fig. S14, ESI†). Thus, large ligands do not necessarily lead to zero curvature in RS-hybrids, and weak-field ligands lead to zero curvatures only for some families of functionals. For the RS-hybrids, large ligands generally lead to overcorrection and negative curvatures. From a metal-center perspective, no unifying picture of curvature is present across all families of functionals. While Co is the primary metal observed in low-curvature complexes for GGAs and meta-GGAs and Mn is the least represented, the reverse is true for RS-hybrids (Fig. S15, ESI†). Hybrid and non-hybrid functionals also differ in the spin state that dominates the low-curvature regime, where hybrid functionals show a distinct preference for low curvatures for complexes in HS states, whereas non-hybrids favor HS and LS states equally (Fig. S16, ESI†). This observation is consistent with our earlier model feature analysis. In terms of oxidation state, only RS-hybrids have equal numbers of +2 and +3 oxidation state compounds with low curvature, whereas other families prefer +3 oxidation states (Fig. S17, ESI†). This observation is somewhat surprising because the ionization potential increases with increasing oxidation state and curvature values could be expected to increase as a result.
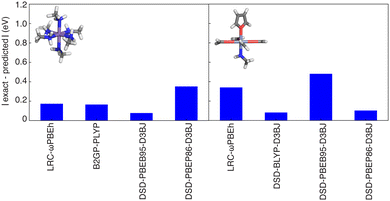
One of the primary use cases for ANNs trained to predict curvature is to enable identification of one or more appropriate functionals to use for property prediction while recovering piecewise linearity. We thus verify design space predictions on representative complexes with each of the four metals studied in this work (i.e., HS Fe, Mn, and Co as well as an LS Cr complex). None of the selected complexes were present in the original training data but due to the way the design space was constructed (i.e., from new combinations of the ligands and metals that are present in the training data), they are relatively similar to training data and thus model performance should be comparable to test set performance. For each of these complexes, the ANN models predict a value close to zero curvature for at least four functionals for each of these complexes. Typically, the functionals selected with curvatures close to zero (i.e., within the mean test set error of 0.4 eV) are double hybrids or range-separated hybrids. We then carried out DFT geometry optimizations and single-point energy calculations (see Methods) to verify these ANN predictions. The differences between the calculated and predicted curvature are typically less than 0.5 eV (Fig. 8). For example, the ANN-predicted curvatures for HS Mn(III)(methylamine)6 and Cr(II)(formaldehyde)4(methylamine)(furan) are within 0.2 eV of the calculated values for the LRC-ωPBEh range-separated hybrid and the double hybrids (i.e., B2GP-PLYP and DSD-PBEB95-D3BJ for the Mn complex, DSD-BLYP-D3BJ and DSD-PBEP86-D3BJ for the Cr complex). Neither of these complexes were present in the global (i.e., all DFA) training or test data, with the closest examples to HS Mn(III)(methylamine)6 being HS Mn(III)(porphyrin)(methylamine)2 and the closest example to LS Cr(II)(formaldehyde)4(methylamine)(furan) being HS Cr(II)(formaldehyde)4(ammonia)2.116 An exception to this good performance is Fe(III)(furan)4(ammonia)2 where the ANN trained on LRC-ωPBEh predicted a curvature ∼1 eV smaller than the calculated value, although the performance of other functionals (e.g., B2GP-PLYP) is closer to the test error (Fig. S18, ESI†). The closest complexes to HS Fe(III)(furan)4(ammonia)2 in the train or test data were other complexes of furan in combination with stronger-field carbonyl or weaker-field water, and the only complexes in the LRC-ωPBEh training or test data were a homoleptic furan complex and a heteroleptic furan-containing complex with a single methylisocyanide ligand.116 Even in cases where errors exceeded the test set MAE, we were still able to identify one or more functionals with curvature close to zero, suggesting the possible application of this approach in the chemical discovery of transition metal complexes.
4. Conclusions
Using a dataset of nearly one thousand transition metal complexes, we computed and analyzed the average curvature (i.e., deviation from piecewise linearity) for 23 density functional approximations spanning multiple rungs of “Jacob's ladder”. Over this set, we observed a wide range of curvature values that nevertheless followed expected qualitative trends, such as the high positive curvatures in semi-local GGA and meta-GGA functionals in the range of 1–8 eV that was lowered by around 5–6 eV per unit of HF exchange within a family of functionals. While we observed correlations for most functionals within the same “rung”, we also observed reduced correlation among meta-GGA hybrids, especially for M06-2X and TPSSh, likely as a consequence of both the correlation and exchange terms differing substantially. We then trained artificial neural networks and kernel ridge regression machine learning models to predict both curvature and the associated HOMO and LUMO energies for each of these 23 functionals. We observed superior performance of the ANNs, especially when it came to predicting properties for specific outlier compounds. Using SHAP analysis, we interpreted the ANN model prediction and discovered a specific spin state dependence for range-separated hybrid and double-hybrid functionals that was absent from other functionals, potentially explaining why curvature values are weakly correlated between these and other families of functionals.Beyond the strong influence of metal oxidation state on curvature, metal-distant features three bonds or more from the metal played the second-most important role. We rationalized the differences in feature importance observed with different functionals here from prior work93 that used RF-RFA KRR to determine that selected functionals were feature-invariant for the HOMO. We showed that the HOMO level is indeed consistent across functionals, with strong contributions from atoms three bond paths away from the metal or more along with the metal oxidation state. We instead observed that the strong spin-state dependence of curvature for double hybrids arises from differences in the LUMO, where metal spin contributes for double hybrids but not for semi-local functionals. Nevertheless, the majority of features are more consistent across functional families than across properties, still supporting conclusions from prior work93 that feature analysis is relatively insensitive to functional-dependent errors.
We explored a space of over one hundred thousand hypothetical complexes to uncover chemical trends in the composition of complexes predicted to have zero curvature. We observed that the ligands commonly present in low-curvature complexes depended on the family of the DFA, with large ligands having the lowest curvature values for semi-local GGA functionals but not necessarily for range-separated hybrids. Finally, we demonstrated the potential benefit these curvature-predicting ANNs by identifying and validating compounds that were predicted to have near-zero curvature for at least four DFAs. Thus, this approach provides a low-cost means of screening compound spaces and selecting a DFA that will have low curvature for the relevant transition metal complex. We envision this approach being particularly useful in screening compounds for targeted optical gaps where recovering piecewise linearity will be especially beneficial in reducing the computational cost.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge early support by the Department of Energy under grant number DE-SC0018096 (for Y. C.). This work was also supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing, Office of Basic Energy Sciences, via the Scientific Discovery through Advanced Computing (SciDAC) program. Generation of the datasets in this work were supported by the Office of Naval Research under grant numbers N00014-18-1-2434 and N00014-20-1-2150 (to A. N. and C. D.). A. N. was partially supported by a National Science Foundation Graduate Research Fellowship under Grant #1122374. C. D. was partially supported by a seed fellowship from the Molecular Sciences Software Institute under NSF grant OAC-1547580. H. J. K. holds an Alfred P. Sloan award in Chemistry, which supported this work. The authors thank Yeongsu Cho, Adam H. Steeves, and Gianmarco Terrones for providing a critical reading of the manuscript.References
- Y. N. Shu and B. G. Levine, Simulated Evolution of Fluorophores for Light Emitting Diodes, J. Chem. Phys., 2015, 142, 104104 CrossRef PubMed.
- R. Gomez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D. G. Ha, T. Wu, G. Markopoulos, S. Jeon, H. Kang, H. Miyazaki, M. Numata, S. Kim, W. L. Huang, S. I. Hong, M. Baldo, R. P. Adams and A. Aspuru-Guzik, Design of Efficient Molecular Organic Light-Emitting Diodes by a High-Throughput Virtual Screening and Experimental Approach, Nat. Mater., 2016, 15, 1120–1127 CrossRef CAS PubMed.
- I. Y. Kanal, S. G. Owens, J. S. Bechtel and G. R. Hutchison, Efficient Computational Screening of Organic Polymer Photovoltaics, J. Phys. Chem. Lett., 2013, 4, 1613–1623 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities, Chem. Rev., 2018, 119, 2453–2523 CrossRef PubMed.
- M. Foscato and V. R. Jensen, Automated in Silico Design of Homogeneous Catalysts, ACS Catal., 2020, 10, 2354–2377 CrossRef CAS.
- S. Curtarolo, G. L. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The High-Throughput Highway to Computational Materials Design, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- J. K. Nørskov and T. Bligaard, The Catalyst Genome, Angew. Chem., Int. Ed., 2013, 52, 776–777 CrossRef PubMed.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Combinatorial Screening for New Materials in Unconstrained Composition Space with Machine Learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094104 CrossRef.
- P. O. Dral, Quantum Chemistry in the Age of Machine Learning, J. Phys. Chem. Lett., 2020, 11, 2336–2347 CrossRef CAS PubMed.
- J. P. Janet, C. Duan, A. Nandy, F. Liu and H. J. Kulik, Navigating Transition-Metal Chemical Space: Artificial Intelligence for First-Principles Design, Acc. Chem. Res., 2021, 54, 532–545 CrossRef CAS PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine Learning for Molecular and Materials Science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- A. Chen, X. Zhang and Z. Zhou, Machine Learning: Accelerating Materials Development for Energy Storage and Conversion, InfoMat, 2020, 2, 553–576 CrossRef CAS.
- M. Gastegger, J. Behler and P. Marquetand, Machine Learning Molecular Dynamics for the Simulation of Infrared Spectra, Chem. Sci., 2017, 8, 6924–6935 RSC.
- J. Westermayr and P. Marquetand, Machine Learning for Electronically Excited States of Molecules, Chem. Rev., 2020, 121, 9873–9926 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for Density Functional Theory, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- A. D. Becke, Perspective: Fifty Years of Density-Functional Theory in Chemical Physics, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- C. J. Cramer and D. G. Truhlar, Density Functional Theory for Transition Metals and Transition Metal Chemistry, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- C. Duan, F. Liu, A. Nandy and H. J. Kulik, Putting Density Functional Theory to the Test in Machine-Learning-Accelerated Materials Discovery, J. Phys. Chem. Lett., 2021, 12, 4628–4637 CrossRef CAS PubMed.
- H. Y. S. Yu, S. H. L. Li and D. G. Truhlar, Perspective: Kohn-Sham Density Functional Theory Descending a Staircase, J. Chem. Phys., 2016, 145, 130901 CrossRef PubMed.
- S. Niu and M. B. Hall, Theoretical Studies on Reactions of Transition-Metal Complexes, Chem. Rev., 2000, 100, 353–406 CrossRef CAS PubMed.
- R. Haunschild, T. M. Henderson, C. A. Jiménez-Hoyos and G. E. Scuseria, Many-Electron Self-Interaction and Spin Polarization Errors in Local Hybrid Density Functionals, J. Chem. Phys., 2010, 133, 134116 CrossRef PubMed.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, Many-Electron Self-Interaction Error in Approximate Density Functionals, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, Density Functionals That Are One- and Two- Are Not Always Many-Electron Self-Interaction-Free, as Shown for H2+, He2+, Lih+, and Ne2+, J. Chem. Phys., 2007, 126, 104102 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Insights into Current Limitations of Density Functional Theory, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- T. Schmidt, Kümmel, S. One- and Many-Electron Self-Interaction Error in Local and Global Hybrid Functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 165120 CrossRef.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, Spurious Fractional Charge on Dissociated Atoms: Pervasive and Resilient Self-Interaction Error of Common Density Functionals, J. Chem. Phys., 2006, 125, 194112 CrossRef PubMed.
- A. D. Dutoi and M. Head-Gordon, Self-Interaction Error of Local Density Functionals for Alkali–Halide Dissociation, Chem. Phys. Lett., 2006, 422, 230–233 CrossRef CAS.
- T. Bally and G. N. Sastry, Incorrect Dissociation Behavior of Radical Ions in Density Functional Calculations, J. Phys. Chem. A, 1997, 101, 7923–7925 CrossRef CAS.
- Y. Zhang and W. Yang, A Challenge for Density Functionals: Self-Interaction Error Increases for Systems with a Noninteger Number of Electrons, J. Chem. Phys., 1998, 109, 2604–2608 CrossRef CAS.
- B. G. Johnson, C. A. Gonzales, P. M. W. Gill and J. A. Pople, A Density Functional Study of the Simplest Hydrogen Abstraction Reaction. Effect of Self-Interaction Correction, Chem. Phys. Lett., 1994, 221, 100–108 CrossRef CAS.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, Localization and Delocalization Errors in Density Functional Theory and Implications for Band-Gap Prediction, Phys. Rev. Lett., 2008, 100, 146401 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Fractional Charge Perspective on the Band Gap in Density–Functional Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115123 CrossRef.
- D. J. Tozer and F. De Proft, Computation of the Hardness and the Problem of Negative Electron Affinities in Density Functional Theory, J. Phys. Chem. A, 2005, 109, 8923–8929 CrossRef CAS PubMed.
- A. M. Teale, F. De Proft and D. J. Tozer, Orbital Energies and Negative Electron Affinities from Density Functional Theory: Insight from the Integer Discontinuity, J. Chem. Phys., 2008, 129, 044110 CrossRef PubMed.
- M. J. G. Peach, A. M. Teale, T. Helgaker and D. J. Tozer, Fractional Electron Loss in Approximate Dft and Hartree–Fock Theory, J. Chem. Theory Comput., 2015, 11, 5262–5268 CrossRef CAS PubMed.
- X. Zheng, M. Liu, E. R. Johnson, J. Contreras-García and W. Yang, Delocalization Error of Density-Functional Approximations: A Distinct Manifestation in Hydrogen Molecular Chains, J. Chem. Phys., 2012, 137, 214106 CrossRef PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- R. Baer, E. Livshits and U. Salzner, Tuned Range-Separated Hybrids in Density Functional Theory, Annu. Rev. Phys. Chem., 2010, 61, 85–109 CrossRef CAS PubMed.
- S. Refaely-Abramson, R. Baer and L. Kronik, Fundamental and Excitation Gaps in Molecules of Relevance for Organic Photovoltaics from an Optimally Tuned Range-Separated Hybrid Functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075144 CrossRef.
- M. Srebro and J. Autschbach, Does a Molecule-Specific Density Functional Give an Accurate Electron Density? The Challenging Case of the Cucl Electric Field Gradient, J. Phys. Chem. Lett., 2012, 3, 576–581 CrossRef CAS PubMed.
- I. Dabo, A. Ferretti, N. Poilvert, Y. Li, N. Marzari and M. Cococcioni, Koopmans’ Condition for Density-Functional Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115121 CrossRef.
- N. L. Nguyen, N. Colonna, A. Ferretti and N. Marzari, Koopmans-Compliant Spectral Functionals for Extended Systems, Phys. Rev. X, 2018, 8, 021051 Search PubMed.
- L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, Excitation Gaps of Finite-Sized Systems from Optimally Tuned Range-Separated Hybrid Functionals, J. Chem. Theory Comput., 2012, 8, 1515–1531 CrossRef CAS PubMed.
- J. P. Perdew and K. Schmidt, Jacob's Ladder of Density Functional Approximations for the Exchange–Correlation Energy, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- F. Tran, J. Stelzl and P. Blaha, Rungs 1 to 4 of Dft Jacob's Ladder: Extensive Test on the Lattice Constant, Bulk Modulus, and Cohesive Energy of Solids, J. Chem. Phys., 2016, 144, 204120 CrossRef PubMed.
- B. G. Janesko, Replacing Hybrid Density Functional Theory: Motivation and Recent Advances, Chem. Soc. Rev., 2021, 50, 8470–8495 RSC.
- P. Huo, C. Uyeda, J. D. Goodpaster, J. C. Peters and T. F. Miller III, Breaking the Correlation between Energy Costs and Kinetic Barriers in Hydrogen Evolution Via a Cobalt Pyridine-Diimine-Dioxime Catalyst, ACS Catal., 2016, 6, 6114–6123 CrossRef CAS.
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Towards Operando Computational Modeling in Heterogeneous Catalysis, Chem. Soc. Rev., 2018, 47, 8307–8348 RSC.
- P. B. Arockiam, C. Bruneau and P. H. Dixneuf, Ruthenium(II)-Catalyzed C–H Bond Activation and Functionalization, Chem. Rev., 2012, 112, 5879–5918 CrossRef CAS PubMed.
- D. M. Schultz and T. P. Yoon, Solar Synthesis: Prospects in Visible Light Photocatalysis, Science, 2014, 343, 1239176 CrossRef PubMed.
- D. W. Shaffer, I. Bhowmick, A. L. Rheingold, C. Tsay, B. N. Livesay, M. P. Shores and J. Y. Yang, Spin-State Diversity in a Series of Co(II) Pnp Pincer Biomide Complexes, Dalton Trans., 2016, 45, 17910–17917 RSC.
- C. Tsay and J. Y. Yang, Electrocatalytic Hydrogen Evolution under Acidic Aqueous Conditions and Mechanistic Studies of a Highly Stable Molecular Catalyst, J. Am. Chem. Soc., 2016, 138, 14174–14177 CrossRef CAS PubMed.
- M. Schilling, G. R. Patzke, J. Hutter and S. Luber, Computational Investigation and Design of Cobalt Aqua Complexes for Homogeneous Water Oxidation, J. Phys. Chem. C, 2016, 120, 7966–7975 CrossRef CAS.
- B. Dunn, H. Kamath and J. M. Tarascon, Electrical Energy Storage for the Grid: A Battery of Choices, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- A. Yella, H. W. Lee, H. N. Tsao, C. Y. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Gratzel, Porphyrin-Sensitized Solar Cells with Cobalt (II/III)-Based Redox Electrolyte Exceed 12 Percent Efficiency, Science, 2011, 334, 629–634 CrossRef CAS PubMed.
- S. Goswami, K. Aich, S. Das, A. K. Das, D. Sarkar, S. Panja, T. K. Mondal and S. Mukhopadhyay, A Red Fluorescence ‘Off-on’ Molecular Switch for Selective Detection of Al3+, Fe3+ and Cr3+: Experimental and Theoretical Studies Along with Living Cell Imaging, Chem. Commun., 2013, 49, 10739–10741 RSC.
- A. M. Virshup, J. Contreras-García, P. Wipf, W. Yang and D. N. Beratan, Stochastic Voyages into Uncharted Chemical Space Produce a Representative Library of All Possible Drug-Like Compounds, J. Am. Chem. Soc., 2013, 135, 7296–7303 CrossRef CAS PubMed.
- C. Duan, J. P. Janet, F. Liu, A. Nandy and H. J. Kulik, Learning from Failure: Predicting Electronic Structure Calculation Outcomes with Machine Learning Models, J. Chem. Theory Comput., 2019, 15, 2331–2345 CrossRef CAS PubMed.
- J. P. Janet, L. Chan and H. J. Kulik, Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network, J. Phys. Chem. Lett., 2018, 9, 1064–1071 CrossRef CAS PubMed.
- J. P. Janet and H. J. Kulik, Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure-Property Relationships, J. Phys. Chem. A, 2017, 121, 8939–8954 CrossRef CAS PubMed.
- J. P. Janet and H. J. Kulik, Predicting Electronic Structure Properties of Transition Metal Complexes with Neural Networks, Chem. Sci., 2017, 8, 5137–5152 RSC.
- J. P. Janet, F. Liu, A. Nandy, C. Duan, T. H. Yang, S. Lin and H. J. Kulik, Designing in the Face of Uncertainty: Exploiting Electronic Structure and Machine Learning Models for Discovery in Inorganic Chemistry, Inorg. Chem., 2019, 58, 10592–10606 CrossRef CAS PubMed.
- J. P. Janet, S. Ramesh, C. Duan and H. J. Kulik, Accurate Multiobjective Design in a Space of Millions of Transition Metal Complexes with Neural-Network-Driven Efficient Global Optimization, ACS Cent. Sci., 2020, 6, 513–524 CrossRef CAS PubMed.
- A. Nandy, J. Z. Zhu, J. P. Janet, C. Duan, R. B. Getman and H. J. Kulik, Machine Learning Accelerates the Discovery of Design Rules and Exceptions in Stable Metal-Oxo Intermediate Formation, ACS Catal., 2019, 9, 8243–8255 CrossRef CAS.
- N. J. DeYonker, K. A. Peterson, G. Steyl, A. K. Wilson and T. R. Cundari, Quantitative Computational Thermochemistry of Transition Metal Species, J. Phys. Chem. A, 2007, 111, 11269–11277 CrossRef CAS PubMed.
- W. Jiang, N. J. DeYonker and A. K. Wilson, Multireference Character for 3d Transition-Metal-Containing Molecules, J. Chem. Theory Comput., 2012, 8, 460–468 CrossRef CAS PubMed.
- J. Wang, S. Manivasagam and A. K. Wilson, Multireference Character for 4d Transition-Metal-Containing Molecules, J. Chem. Theory Comput., 2015, 11, 5865–5872 CrossRef CAS PubMed.
- C. A. Gaggioli, S. J. Stoneburner, C. J. Cramer and L. Gagliardi, Beyond Density Functional Theory: The Multiconfigurational Approach to Model Heterogeneous Catalysis, ACS Catal., 2019, 9, 8481–8502 CrossRef CAS.
- K. Boguslawski, P. Tecmer, O. Legeza and M. Reiher, Entanglement Measures for Single-and Multireference Correlation Effects, J. Phys. Chem. Lett., 2012, 3, 3129–3135 CrossRef CAS PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A Look at the Density Functional Theory Zoo with the Advanced Gmtkn55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- S. P. Veccham and M. Head-Gordon, Density Functionals for Hydrogen Storage: Defining the H2bind275 Test Set with Ab Initio Benchmarks and Assessment of 55 Functionals, J. Chem. Theory Comput., 2020, 16, 4963–4982 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, How Accurate Are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Composed of Main-Group Elements?, J. Chem. Theory Comput., 2016, 12, 4303–4325 CrossRef CAS PubMed.
- S. R. Mortensen and K. P. Kepp, Spin Propensities of Octahedral Complexes from Density Functional Theory, J. Phys. Chem. A, 2015, 119, 4041–4050 CrossRef CAS PubMed.
- O. S. Siig and K. P. Kepp, Iron(II) and Iron(III) Spin Crossover: Toward an Optimal Density Functional, J. Phys. Chem. A, 2018, 122, 4208–4217 CrossRef CAS PubMed.
- M. Bursch, A. Hansen, P. Pracht, J. T. Kohn and S. Grimme, Theoretical Study on Conformational Energies of Transition Metal Complexes, Phys. Chem. Chem. Phys., 2021, 23, 287–299 RSC.
- M. Radon, Benchmarking Quantum Chemistry Methods for Spin-State Energetics of Iron Complexes against Quantitative Experimental Data, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870 RSC.
- D. Coskun, S. V. Jerome and R. A. Friesner, Evaluation of the Performance of the B3lyp, Pbe0, and M06 Dft Functionals, and Dbloc-Corrected Versions, in the Calculation of Redox Potentials and Spin Splittings for Transition Metal Containing Systems, J. Chem. Theory Comput., 2016, 12, 1121–1128 CrossRef CAS PubMed.
- P. Golub, A. Antalik, L. Veis and J. Brabec, Machine Learning-Assisted Selection of Active Spaces for Strongly Correlated Transition Metal Systems, J. Chem. Theory Comput., 2021, 17, 6053–6072 CrossRef CAS PubMed.
- W. Jeong, S. J. Stoneburner, D. King, R. Li, A. Walker, R. Lindh and L. Gagliardi, Automation of Active Space Selection for Multireference Methods Via Machine Learning on Chemical Bond Dissociation, J. Chem. Theory Comput., 2020, 16, 2389–2399 CrossRef CAS PubMed.
- C. Duan, F. Liu, A. Nandy and H. J. Kulik, Data-Driven Approaches Can Overcome the Cost-Accuracy Trade-Off in Multireference Diagnostics, J. Chem. Theory Comput., 2020, 16, 4373–4387 CrossRef CAS PubMed.
- C. Duan, F. Liu, A. Nandy and H. J. Kulik, Semi-Supervised Machine Learning Enables the Robust Detection of Multireference Character at Low Cost, J. Phys. Chem. Lett., 2020, 11, 6640–6648 CrossRef CAS PubMed.
- F. Liu, C. Duan and H. J. Kulik, Rapid Detection of Strong Correlation with Machine Learning for Transition-Metal Complex High-Throughput Screening, J. Phys. Chem. Lett., 2020, 11, 8067–8076 CrossRef CAS PubMed.
- C. Duan, A. Nandy, R. Meyer, N. Arunachalam and H. J. Kulik, A Transferable Recommender Approach for Selecting the Best Density Functional Approximations in Chemical Discovery, Nat. Comput. Sci., 2023, 3, 38–47 CrossRef.
- S. McAnanama-Brereton and M. P. Waller, Rational Density Functional Selection Using Game Theory, J. Chem. Inf. Model., 2018, 58, 61–67 CrossRef CAS PubMed.
- S. Dick and M. Fernandez-Serra, Machine Learning Accurate Exchange and Correlation Functionals of the Electronic Density, Nat. Commun., 2020, 11, 3509 CrossRef CAS PubMed.
- J. Kirkpatrick, B. McMorrow, D. H. P. Turban, A. L. Gaunt, J. S. Spencer, A. Matthews, A. Obika, L. Thiry, M. Fortunato, D. Pfau, L. R. Castellanos, S. Petersen, A. W. R. Nelson, P. Kohli, P. Mori-Sanchez, D. Hassabis and A. J. Cohen, Pushing the Frontiers of Density Functionals by Solving the Fractional Electron Problem, Science, 2021, 374, 1385–1389 CrossRef CAS PubMed.
- L. Li, S. Hoyer, R. Pederson, R. Sun, E. D. Cubuk, P. Riley and K. Burke, Kohn-Sham Equations as Regularizer: Building Prior Knowledge into Machine-Learned Physics, Phys. Rev. Lett., 2021, 126, 036401 CrossRef CAS PubMed.
- H. Ma, A. Narayanaswamy, P. Riley and L. Li, Evolving Symbolic Density Functionals, Sci. Adv., 2022, 8, eabq0279 CrossRef PubMed.
- J. Hermann, Z. Schätzle and F. Noé, Deep-Neural-Network Solution of the Electronic Schrödinger Equation, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed.
- A. Fabrizio, B. Meyer and C. Corminboeuf, Machine Learning Models of the Energy Curvature Vs Particle Number for Optimal Tuning of Long-Range Corrected Functionals, J. Chem. Phys., 2020, 152, 154103 CrossRef CAS PubMed.
- M. Yu, S. Yang, C. Wu and N. Marom, Machine Learning the Hubbard U Parameter in DFT+U Using Bayesian Optimization, npj Comput. Mater., 2020, 6, 1–6 CrossRef.
- C. Duan, S. Chen, M. G. Taylor, F. Liu and H. J. Kulik, Machine Learning to Tame Divergent Density Functional Approximations: A New Path to Consensus Materials Design Principles, Chem. Sci., 2021, 12, 13021–13036 RSC.
- A. Nandy, C. Duan, J. P. Janet, S. Gugler and H. J. Kulik, Strategies and Software for Machine Learning Accelerated Discovery in Transition Metal Chemistry, Ind. Eng. Chem. Res., 2018, 57, 13973–13986 CrossRef CAS.
- S. Gugler, J. P. Janet and H. J. Kulik, Enumeration of De Novo Inorganic Complexes for Chemical Discovery and Machine Learning, Mol. Syst. Des. Eng., 2020, 5, 139–152 RSC.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. L. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr, J. W. Snyder Jr, C. Song, A. V. Titov, I. S. Ufimtsev, L.-P. Wang and T. J. Martínez, Terachem: A Graphical Processing Unit-Accelerated Electronic Structure Package for Large-Scale Ab Initio Molecular Dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1494 CAS.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, Molsimplify: A Toolkit for Automating Discovery in Inorganic Chemistry, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed.
- A. D. Becke, Density-Functional Thermochemistry. Iii. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- P. J. Hay and W. R. Wadt, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- L.-P. Wang and C. Song, Geometry Optimization Made Simple with Translation and Rotation Coordinates, J. Chem. Phys., 2016, 144, 214108 CrossRef PubMed.
- T. Stein, J. Autschbach, N. Govind, L. Kronik and R. Baer, Curvature and Frontier Orbital Energies in Density Functional Theory, J. Phys. Chem. Lett., 2012, 3, 3740–3744 CrossRef CAS PubMed.
- D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O’Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer, A. Y. Sokolov, K. Patkowski, A. E. DePrince, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, Psi4 1.4: Open-Source Software for High-Throughput Quantum Chemistry, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- Q. Zhao, E. I. Ioannidis and H. J. Kulik, Global and Local Curvature in Density Functional Theory, J. Chem. Phys., 2016, 145, 054109 CrossRef PubMed.
- J. C. Bergstra, D. D. Yamins and D. Hyperopt, A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms, Proceedings of the 12th Python in science conference, 2013, pp. 13–20.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, Scikit-Learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- D. P. Kingma and J. Ba, 2015.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, Dropout: A Simple Way to Prevent Neural Networks from Overfitting, J. Mach. Learn. Res., 2014, 15, 1929–1958 Search PubMed.
- S. Ioffe and C. Szegedy, International conference on machine learning, 2015, pp. 448–456 Search PubMed.
- L. Prechelt, Automatic Early Stopping Using Cross Validation: Quantifying the Criteria, Neural Networks, 1998, 11, 761–767 CrossRef PubMed.
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A Quantitative Uncertainty Metric Controls Error in Neural Network-Driven Chemical Discovery, Chem. Sci., 2019, 10, 7913–7922 RSC.
- A. Nandy, C. Duan and H. J. Kulik, Using Machine Learning and Data Mining to Leverage Community Knowledge for the Engineering of Stable Metal–Organic Frameworks, J. Am. Chem. Soc., 2021, 143, 17535–17547 CrossRef CAS PubMed.
- E. D. Michael Ganger and H. Wei, Double Sarsa and Double Expected Sarsa with Shallow and Deep Learning, J. Data Anal. Inf. Process., 2016, 4, 159–176 Search PubMed.
- S. M. Lundberg, S.-I. Lee, A Unified Approach to Interpreting Model Predictions, Advances in Neural Information Processing Systems 30 (NIPS 2017), 2017.
- T. Z. H. Gani and H. J. Kulik, Unifying Exchange Sensitivity in Transition Metal Spin-State Ordering and Catalysis through Bond Valence Metrics, J. Chem. Theory Comput., 2017, 13, 5443–5457 CrossRef CAS PubMed.
- Y. Cytter, A. Nandy, C. Duan and H. J. Kulik, Data for Insights into the Deviation from Piecewise Linearity in Transition Metal Complexes from Supervised Machine Learning Models, 2023 DOI:10.5281/zenodo.7497666 . (Accessed February 10, 2023).
Footnote |
| † Electronic supplementary information (ESI) available: Metal centers, oxidation and spin states in dataset; ligands in training set; DFT functionals used in this work; MAE and fraction of data as a function of latent distance; mean latent distance as a function of functional; mean and standard deviation of curvature distributions; dispersion corrected mean distribution vs. HF exchange fraction; Pearson correlation for the HOMO energies of 23 DFT functionals; Pearson correlation for the LUMO energies of 23 DFT functionals; MAE of KRR and ANN HOMO and LUMO predictions; dataset size of 23 functionals; MAE of KRR and ANN curvature predictions using a joint uniform dataset; SHAP feature selection for curvature models; HS and LS curvature difference examples; SHAP feature selection for the HOMO energy; SHAP feature selection for the LUMO energy; design space R2 of the curvature vs. HOMO–LUMO; low curvature ligand distribution; low curvature metal distribution; low curvature spin multiplicity distribution; low curvature oxidation state distribution; design space verification (PDF). See DOI: https://doi.org/10.1039/d3cp00258f |
| This journal is © the Owner Societies 2023 |