Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dyes for guest–host liquid crystal applications: a general approach to the rapid computational assessment of useful molecular designs†
Mark T.
Sims‡
 ,
Laurence C.
Abbott
,
Laurence C.
Abbott
 ,
Richard J.
Mandle§
,
Richard J.
Mandle§
 ,
John W.
Goodby
and
John N.
Moore
,
John W.
Goodby
and
John N.
Moore
 *
*
Department of Chemistry, University of York, York YO10 5DD, UK. E-mail: john.moore@york.ac.uk
First published on 3rd April 2023
Abstract
A set of experimental dichroic order parameters ranging from ca. +0.66 to −0.22 was obtained by recording polarized UV-visible absorption spectra from aligned samples of fifteen different guest anthraquinone and azo dyes in the nematic host 4-cyano-4′-pentylbiphenyl (5CB). DFT-optimised structures were calculated for between 1 and 16 conformers/tautomers of each dye, and their relative energies, UV-visible absorption wavelengths, oscillator strengths, transition dipole moments, molecular surface tensors and quadrupole tensors were obtained and used in subsequent calculations. A simple approach provided calculated UV-visible absorption spectra of the dyes that gave a qualitative match with the experimental spectra, and the calculated peak positions showed a linear correlation with the experimental values across the full visible range of ca. 350–700 nm. A short-range, shape-based, mean-field orienting potential based on the calculated surface tensors was combined with the calculated transition dipole moment vectors to give calculated dichroic ratios of the dyes that showed a linear correlation across the full range of experimental values. A modification of this mean-field orienting potential to include a long-range, electrostatic component based on the calculated quadrupole tensors gave a slightly improved linear correlation but a slightly worse overall match to the experimental values. The results show that short-range, shape-based interactions dominate the orienting potential for the systems studied here, with the inclusion of long-range quadrupole interactions providing a slightly better model for only some of the dyes. Overall, the use of a mean-field approach allied with molecular properties that can be calculated with relative ease and low computational expense has provided calculated peak positions and dichroic ratios that show good matches and correlations with experimental data from a variety of dye structures without the need to input any experimental data from the dyes. Hence, this method may provide a general and rapid approach to predicting the optical properties of dyes in liquid crystal hosts, enabling candidate dye structures to be screened prior to synthesis.
Introduction
The alignment of guest dye molecules dissolved in an aligned liquid crystal host is a well-established effect that can result also in the bulk alignment of the transition dipole moments (TDMs) of the dyes. This TDM alignment results in the absorption properties of the bulk material generally depending on, and varying with, its orientation relative to polarized incident light, which has led to a diverse range of applications for dye-doped liquid crystal materials.1–12 For example, an electric field that switches the bulk orientation of an aligned liquid crystal host also switches the orientation of the guest dye molecules and their TDMs, and hence it can be used to switch between transparent and coloured states. This switching effect can be utilised for guest–host applications in display devices,1–4 including those that may be able to operate without polarizers or colour filters, and in smart windows5 designed to give energy-efficient lighting and temperature control in the built environment. In another example, aligned guest–host systems can be polymerised to produce thin-film polarizers for use in display-screen coating and other applications,6–8 and where the optical performance of the film is determined by the dye alignment, which becomes fixed on polymerisation. The utility of suitable guest–host systems is well established but their practical applications have been restricted to some extent by the limited availability of materials that can meet the stringent performance criteria, with one of the most significant barriers being a lack of dyes that can exhibit a sufficient degree of alignment. A large number of synthetic studies have been reported, comprising a significant body of work, in which a wide range of dyes including those from the azo,1,2,13,14 anthraquinone,15–17 tetrazine,18,19 perylene,20 and naphthalimide21–24 dye classes have been synthesised and assessed experimentally. However, the vast majority of these dyes do not exhibit a sufficiently high degree of alignment for practical use.The bulk TDM alignment of a guest dye is typically quantified by the dichroic order parameter, S, which is determined experimentally from polarized UV-visible absorption measurement as Sexp, according to eqn (1), where A‖ and A⊥ are the absorbance values measured with the electric vector of incident polarized light oriented parallel and perpendicular, respectively, to the average orientation of the host molecules, termed the director, and the experimental dichroic ratio Rexp = A‖/A⊥. S may take values between 1 and −0.5, and is 0 for isotropic systems. Systems exhibiting positive values of S are termed positive dichroics, and values in the region of ≥0.75, but ideally higher, are typically required for practical use.15 Negative dichroics have received less attention to date but, similarly, practical applications may require highly negative values of S in the region of ≤−0.38.
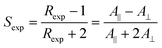 | (1) |
In recent work, we have been developing an understanding of dye alignment in liquid crystal hosts through experimental studies allied with computational studies using a combination of time-dependent density functional theory (TD-DFT) calculations and molecular dynamics (MD) simulations that are computationally expensive (with such simulations taking several days/weeks).25–29 In the computational work, our initial approach to obtaining a calculated dichroic order parameter, Scalc, used eqn (2).25–28 The term in brackets is the order parameter of the TDM within the dye molecule, where βTDM is a fixed angle between the TDM vector and the principal molecular (z) axis of the dye, as obtained from TD-DFT calculations. Szz is the molecular order parameter of a uniaxial dye within a uniaxial host, obtained from MD simulations as an ensemble average given by eqn (3), where θ is the angle between the principal (z) axis of each dye molecule and the host director.
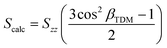 | (2) |
 | (3) |
 | (4) |
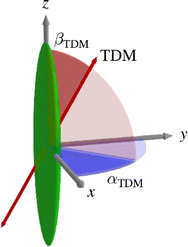 | ||
| Fig. 1 Schematic diagram of the molecular frame defined by x, y and z axes, the TDM axis, and the angles αTDM and βTDM relating them. | ||
We have also considered the more complex effect of molecular flexibility resulting in dynamic variations in the TDM angle within the molecular frame of the dye.28
Overall, this approach enabled us to rationalise non-intuitive trends in experimental dichroic order parameters of dyes in terms of their molecular shapes, TDM orientations, and molecular flexibilities, and for dyes with single and multiple visible transitions, and positive and negative dichroic order parameters. Our studies suggested that the approach might be extended from rationalising observed trends to predicting trends of hypothetical dye structures. However, a major drawback of this combination of MD and TD-DFT methods as a predictive approach is the long time scale (ca. days or weeks) required for MD simulations of large enough systems to enable meaningful analysis, which is exacerbated by the relatively low concentrations of dyes (≤2 wt%) needed to model the experimental systems. Additional limitations to the generality and quantitative accuracy of the method arise from the choice and suitability of the force-field used in the MD simulations.
The calculation of molecular alignment by considering a relatively large number of molecules explicitly in fully atomistic MD simulations is inherently computationally demanding. An alternative approach that is widespread in the field of liquid crystals is mean-field theory, in which the many-body problem is reduced to a one-body problem by considering the molecular alignment in a liquid crystalline phase to arise from an average orienting potential in which the structure of a molecule experiencing this potential can be specified and varied at the atomistic level. The mean-field approximation is significant, but the success of such theories in describing orientational order within liquid crystal systems, perhaps most notably via Maier–Saupe theory,30 has shown their validity and value in aiding the understanding of alignment processes.
In mean-field theory in general, the orientational energy, U, of a molecule within a liquid-crystalline phase is expressed as a function of the Euler angles α, β and γ, which describe the rotation from a set of laboratory fixed axes (termed the laboratory frame) to a set of molecular axes (termed the molecular frame), as shown in Fig. 2.
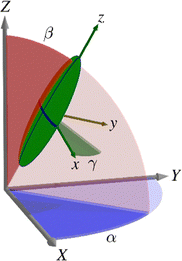 | ||
| Fig. 2 Schematic diagram showing the relative orientation of the laboratory frame axes (X, Y, Z), the molecular frame axes (x, y, z), and the Euler angles (α, β, γ) relating them. | ||
In a uniaxial host, in which the laboratory frame is typically defined by the director, the orientational energy is independent of the angle α due to the symmetry of the phase. The orientational distribution function, f(β,γ), may be determined from any definition of this orientational energy according to eqn (5), assuming a Boltzmann distribution of energies in the system and where kB is the Boltzmann constant and T is the temperature of the system.31
 | (5) |
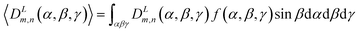 | (6) |
Quantitatively, the surface tensor model defines the orientational energy of a molecule according to eqn (7), where ε is an adjustable parameter describing the strength of the orienting potential of the host, and ψ is the angle between the normal to any point on the molecular surface, S, and the director. If the molecular surface is considered to comprise a set of small discrete planar surface elements, eqn (7) may be considered in terms of these surface elements tending to align parallel to the director (and the surface normals perpendicular to the director).38
 | (7) |
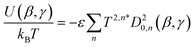 | (8) |
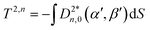 | (9) |
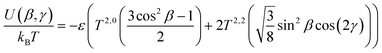 | (10) |
In neutral (uncharged) guest–host systems the first term of this expansion may be neglected, but the second two terms have been the subject of significant research. Early work suggested that molecular dipoles are of little importance to molecular alignment,48 but later work has been divided, with some studies agreeing,49–51 and others suggesting this may not be the case.52–54 The interaction between molecular quadrupoles and an electric field gradient arising from the host has been extensively studied, and there is a significant body of work showing a close match between experimental and calculated orientational order parameters using a quadrupole term in the expression for the orientational energy,37,44,49,50,55–57 Although alternative mean-field treatments of electrostatic interactions have been proposed,58,59 the quadrupole interaction remains one of the most widespread.
Quantitatively, the quadrupole interaction may be expressed by eqn (11), where FZZ is the electric field gradient of the host in the lab frame, Qxx, Qyy and Qzz are Cartesian elements of the traceless, diagonal molecular quadrupole tensor in the molecular frame,60,61 and the expression takes a comparable form to that of the short-range interactions given by eqn (10). Values of FZZ can be fitted in order to optimise a match between calculated and experimental orientational order parameters obtained from NMR experiments. Alternatively, a method has been proposed to derive the electric field gradient from experimental dielectric permittivity values.62
 | (11) |
In this work, we present experimental polarized UV-visible absorption spectra of 15 different dyes dissolved in the widely studied nematic host, 5CB (4-cyano-4′-pentylbiphenyl), from which we determine experimental dichroic order parameters of each of the absorption bands. We then present the results of DFT optimisations and TD-DFT calculations on each of the dyes, combined with mean-field calculations as described above, to provide a general computational approach that enables the absorption wavelengths and dichroic order parameters of the dyes to be predicted without the input of any experimental data from the dyes themselves.
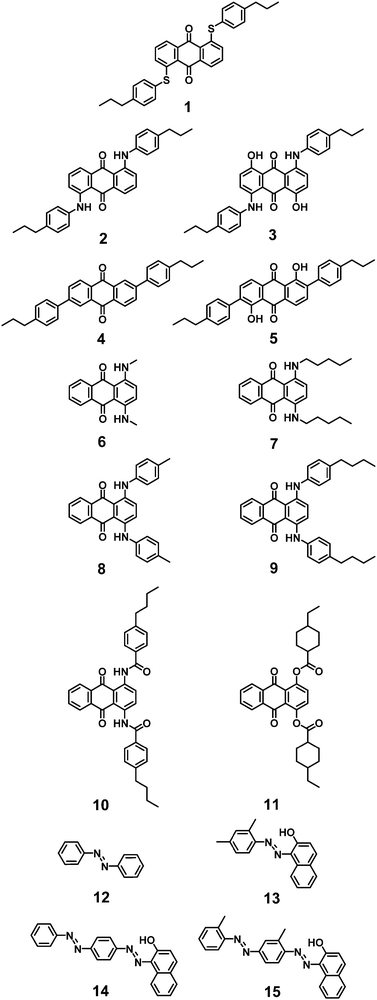
Initially, we calculate the dichroic order parameters using the surface tensor model alone, based on only the shapes of the dye molecules and on the calculated orientations of the transition dipole moment vectors giving rise to the transitions. We then extend the method to a combined model that also includes the interaction of the molecular quadrupoles with the electric field gradient of the host, enabling an assessment of the significance of the two contributions. The dyes used in this work are from the anthraquinone and azo dye classes, which are the most studied in the context of guest–host devices,15 and they were selected to provide a wide range of absorption maxima and dichroic order parameters. The structures of the dyes are shown in Fig. 3.
Methods
Experimental
The syntheses of the 1,5- and 2,6-disubstituted anthraquinone dyes 1–5,63 and the 1,4-disubstituted anthraquinone dyes 9 and 1029 have been described previously. The synthesis of dye 11 is described in the ESI.† The purities of dyes 6–8 and 12–15 (Sigma-Aldrich; ≥96%) were verified by 1H NMR spectroscopy, and they were used as received. 5CB (Merck) was also used as received. The nematic-isotropic transition temperature, TNI, of 5CB was taken as 308.15 K.31Dye-5CB mixtures were made up at concentrations of ca. 0.5 mol%, heated above the clearing point, then slowly cooled to room temperature while sonicating to ensure full dissolution of the dyes. Planar-aligned cells (20 μm pathlength; Instec) were filled with the guest–host mixtures by capillary action while heated above the clearing point. After cooling to room temperature, the alignment was verified by visual inspection under a microscope with crossed polarizers. No evidence of dye precipitation was observed. Polarized UV-visible absorption spectra of the aligned samples were recorded using an Agilent Cary 8454 spectrophotometer, with a rotatable Glan-laser polarizer (Newport 10GL08) between the source and the sample. The samples were held at 298.0 ± 0.1 K in a temperature-controlled holder custom built at the University of York. Equivalent polarized spectra of a cell containing 5CB alone were recorded using the same method, and were subtracted from those of the dye-5CB mixtures to obtain the spectra presented.
Computational methods
DFT optimisations and TD-DFT calculations were performed using the Gaussian 09 software package64 at the PBE0/6-311G(d,p) level,65,66 shown previously to be effective at predicting visible transitions in a range of organic chromophores.67 The calculations were carried out on isolated molecules without a solvent field, and the absence of any negative calculated frequencies confirmed that the structures were at energy minima. The 20 lowest-energy electronic transitions to excited singlet states were calculated.Molecular surfaces for surface tensor calculations were calculated using the MSMS algorithm,68 using a probe radius of 3 Å as used previously,28 and a density of 10 Å−2 was used for the surface triangulation. Diagonalised Cartesian forms of the second-rank surface tensors, t and T, were calculated using the methods described previously,28 enabling the Cartesian components of T to be converted into the spherical components according to T2,0 = 3Tzz/√6 and T2,2 = (Txx − Tyy)/2, and as used in eqn (8)–(10). Molecular quadrupoles were defined from the centre of mass of each molecule, providing a consistent definition for all molecules. The translational variation of the quadrupoles for dyes exhibiting permanent dipoles was tested, as discussed briefly in the ESI.†
Results and discussion
Experimental data
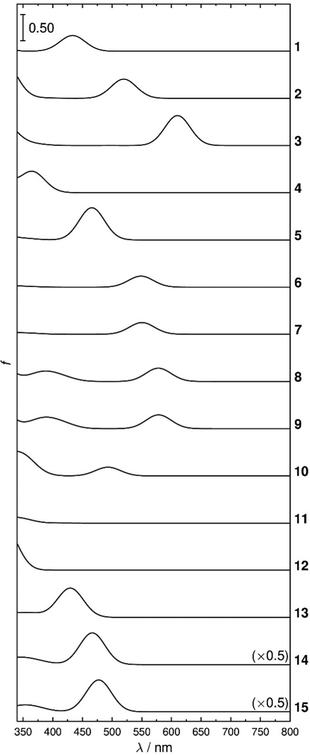
The dye-5CB guest–host samples exhibited a wide range of colours, as demonstrated by photographs of the aligned samples and by the range of band positions in their polarized UV-visible absorption spectra shown in Fig. 4. The absorption profiles of anthraquinone dyes 1–5 and 9–10 in 5CB are very similar to those we obtained in the nematic host E7,27,29 which is a mixture of 5CB (51 wt%) and three other cyanobiphenyl-containing compounds. The absorption profiles of the alkyl-substituted 1,4-diamino anthraquinones 6 and 7 exhibit very similar profiles to each other, and their aromatic analogues, 8 and 9, show visible absorption bands at similar positions, with additional bands at shorter wavelength. The 1,4-disubstituted anthraquinones 10 and 11 both exhibit short-wavelength bands at ca. 350 nm, with 10 exhibiting an additional longer wavelength band at ca. 500 nm. Azo dyes 13–15 all have a common 1-arylazo-2-naphthol structure and all exhibit absorption bands at ca. 500 nm, with the dis-azo dyes 14 and 15 having additional bands at ca. 350 nm, whereas the parent compound 12 (azobenzene) has a strong absorption band only at <350 nm. The absorption maxima from these spectra are given in Table 1.| Dye | λ exp/nma | S exp |
|---|---|---|
| a Taken from the spectrum with the highest absorbance at the peak. b Short-wavelength cut-off. | ||
| 1 | 465 | 0.64 |
| 2 | 553 | 0.54 |
| 3 | 695 | 0.49 |
| 4 | 367 | 0.62 |
| 5 | 483 | 0.66 |
| 6 | 654 | 0.32 |
| 7 | 655 | 0.12 |
| 8 | 653 | 0.33 |
| 419 | −0.04 | |
| 9 | 655 | 0.35 |
| 423 | −0.06 | |
| 10 | 507 | −0.22 |
| 345 | 0.47 | |
| 11 | 345 | −0.21 |
| 12 | 340b | 0.35 |
| 13 | 496 | 0.32 |
| 14 | 516 | 0.46 |
| 357 | 0.37 | |
| 15 | 530 | 0.40 |
| 360 | 0.32 | |
The experimental dichroic order parameter values, Sexp, are given in Table 1, and they were determined as the mean dichroic ratio calculated using eqn (1) across the width of each visible band. The width of each band was defined generally by the wavelengths of the full-width at half-maximum, but in some cases also by the short-wavelength cut-off of 340 nm arising from absorption by the host, or by the wavelength of minimum absorbance between absorption bands; these limits are shown in Fig. S1 in the ESI† along with plots of dichroic ratio against wavelength. The dichroic order parameters showed a small average variation of ≤0.025 when they were recalculated with the maximum and minimum dichroic ratios in the ranges over which the respective mean ratios were determined (Table S1, ESI†), giving a high degree of confidence in these experimental values.
The dichroic order parameters of anthraquinones 1–5 and 9–10 in 5CB show variations between dyes that match the trends we reported previously for the same dyes in E7,27 but the absolute values are uniformly lower, which is consistent with the orientational order parameter of ca. 0.55 for host 5CB69 being lower than that of ca. 0.64 for host E7 at 25 °C.25,29 The 1,4-disubstituted anthraquinones 6–11 all exhibit lower dichroic order parameters than dyes 1–5, consistent with their less rod-like shapes. Dyes 8–10 all exhibit dichroic order parameters with opposing signs for the short- and long-wavelength bands, which is indicative of the respective TDMs having quite different orientations within the molecular frames, as we have reported previously for dyes 9 and 10.29 The bands of the azo dyes 12–15 all have dichroic order parameters in the range 0.32–0.46, with the highest order parameters being exhibited by the long-wavelength bands of the most rod-like bis-azo dyes 14 and 15.
Overall, the range of the 20 dichroic order parameters listed in Table 1, with a spread between −0.22 for the long-wavelength band of dye 10 and 0.66 for dye 5, and the range of 20 absorption maxima, with a spread from ca. 340 nm for dye 12 to 695 nm for dye 3, provides a suitably wide experimental data set with which to assess the scope of the computational methods.
DFT optimisations and TD-DFT calculations
The mean-field approaches described in the introduction enable the orientational order parameter to be calculated from either a single surface tensor, a single quadrupole tensor, or a combination of the two, and the expressions given above are limited to determining the orientational order parameter arising from a single structure. The approximation of using a single (static) structure may be appropriate for small molecules, such as those to which mean-field methods are often applied, and possibly for some of the dyes studied here, such as 6 and 12. However, for many dyes, including the other dyes in this study, this approximation may be considered invalid. For example, our previous studies have demonstrated that dyes 1–5 exhibit multiple conformers and various degrees of flexibility resulting from bond rotations within the linking groups between the anthraquinone cores and the substituent groups,28 in addition to conformational flexibility in the alkyl chains; and similar effects may be expected for related anthraquinone dyes such as 7–11. For azo dyes, any asymmetric groups attached to the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– linkage will give rise to multiple possible conformers,70 and hydroxyl groups such as those in dyes 13–15 mean that azo-hydrazone tautomerisation may also be significant.71–73
N– linkage will give rise to multiple possible conformers,70 and hydroxyl groups such as those in dyes 13–15 mean that azo-hydrazone tautomerisation may also be significant.71–73
Desirable criteria for a screening method include both speed and generality, and hence essentially preclude MD methods requiring classical force-fields that may require parameterisation for less common groups, such as we have described previously,27 or ab initio MD methods, which are typically very computationally demanding. As a compromise between sampling representative conformers and achieving an acceptable computation time, we adopted the general approach of optimising a selected set of conformers for each dye. Inevitably, such a choice of conformers is somewhat arbitrary, but they were chosen here as those arising from rotation about formal single bonds, and those arising from azo-hydrazone tautomerisation, and with alkyl chains being optimised only in their all-trans conformers, to limit the total number of optimisations required. These constraints resulted in a total of 73 structures being optimised across the 15 dyes, arising from between 1 and 16 conformers/tautomers for each dye. All of these DFT-optimised structures are shown in the ESI† along with their atomic coordinates.
Each DFT-optimised structure has an associated energy and quadrupole tensor. For each optimised structure, a set of visible transitions was calculated using TD-DFT and a surface tensor was calculated as described in the Experimental section (values listed in Table S2 in the ESI†). Prior to the calculation of any properties for each dye, the relative populations, Pi, of the n conformers (optimised structures) were determined by assuming a Boltzmann distribution according to eqn (12), where gi is the degeneracy of conformer i and Ei and is the energy of conformer i relative to the lowest energy conformer.
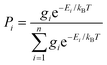 | (12) |
| Dye | λ calc/nm | λ corr/nm | Δ/nm |
|---|---|---|---|
| 1 | 433 | 469 | 4 |
| 2 | 519 | 584 | 31 |
| 3 | 610 | 705 | 10 |
| 4 | 365 | 378 | 11 |
| 5 | 466 | 513 | 30 |
| 6 | 548 | 622 | −32 |
| 7 | 550 | 625 | −30 |
| 8 | 578 | 662 | 9 |
| 389 | 409 | −10 | |
| 9 | 578 | 662 | 7 |
| 389 | 410 | −13 | |
| 10 | 493 | 549 | 42 |
| 335 | 338 | −7 | |
| 11 | 330 | 331 | −14 |
| 12 | 320 | 318 | — |
| 13 | 429 | 463 | −33 |
| 14 | 467 | 514 | −2 |
| 346 | 353 | 4 | |
| 15 | 477 | 528 | −2 |
| 354 | 363 | 3 |
Fig. 6 shows a plot of the calculated wavelengths against the experimental wavelengths, along with a linear fit that shows a good correlation (R2 = 0.97). The calculated values are consistently at shorter wavelengths than those determined experimentally, which is consistent with reported comparisons between calculated and experimental absorption wavelengths of anthraquinone dyes using the same functional as used here.67 In addition, the calculations we report here were carried out without a solvent field, in order to make the method as general as possible, but this approach is likely to underestimate the wavelengths because red-shifts in the absorption bands of dyes are commonly reported on going from non-polar isotropic solvents to cyanobiphenyl-based hosts,27,74–77 indicating that solvent effects are relatively strong in such guest–host mixtures. Applying a linear correction to the calculated wavelengths gives corrected wavelengths according to λcorr = (λcalc − 81.79)/0.7492 (derived from the fit shown in Fig. 6). Table 2 lists these values along with their respective differences from the experimental values, showing a reasonably close match, with an RMS difference of 19 nm (as illustrated also by the spread of data around the fit in Fig. 6).
 | ||
| Fig. 6 Calculated wavelengths, λcalc, (Table 2) plotted against experimental wavelengths, λexp, (Table 1) along with a linear fit to the data. Dye 12 is omitted because λexp is below the short-wavelength cut-off due to host absorption. | ||
The strong correlation in Fig. 6 demonstrates the ability of this simple computational approach to predict trends in the experimental absorption wavelengths of dyes without any correction, and the fit demonstrates that a simple linear correction can yield satisfactory quantitative predictions of the experimental absorption wavelengths for dyes in guest–host mixtures. We note that more sophisticated computational approaches for calculating dye absorption wavelengths, spectra and colours are possible,78 such as those including solvent and vibronic effects; the approach we demonstrate here has the benefits of simplicity and general applicability.
Surface tensor model
The surface tensor model is based on readily calculated molecular surfaces, but is also reliant on the use of an appropriate value of the orienting strength of the host, ε, in eqn (7), which is typically fitted to provide an optimum match between calculated and experimental data.35,43,56,79–81 The premise of the work reported here is to present and assess a method for calculating order parameters of hypothetical structures, thus precluding a value of ε being fitted to experimental data from the dyes being studied. An alternative approach is to use a value of ε that has been shown to be appropriate for nematic hosts in general, although such a value would inevitably be more appropriate for some hosts than others, and any systematic discrepancy between calculated and experimental order parameters would primarily be attributed to the value used for ε. Hence, it is desirable to be able to derive a value of ε that is specific to the host being studied without relying on experimental data from a range of dyes within that host.In order to achieve such an approach, we derived values of ε for 5CB at a range of temperatures by fitting previously reported experimental data from pure 5CB (effectively fitting for a “guest” 5CB molecule in a 5CB “host”), making the ε values independent of the dyes studied. A 5CB molecule was DFT-optimised as its all-trans conformer and its surface tensor calculated to yield values of T2,0 and T2,2, consistent with the approach used for the dye molecules and enabling the orientational order parameter, Szz (D20,0), of 5CB to be calculated using eqn (10) then eqn (5) and (6). The optimised structure of 5CB and the surface tensor values are given in the ESI.† Values of ε were then obtained by fitting the calculated orientational order parameter at a specific temperature to the respective experimental order parameter of 5CB we recently reported from X-ray diffraction experiments at a range of temperatures.69Fig. 7 shows a plot of these fitted ε values against the reduced temperature (T/TNI), along with an empirical fit, which provides a general expression that enables a value of ε to be determined for 5CB at any reduced temperature in this range. The approach we demonstrate here is general, and it can readily be applied to derive ε values for any single-component host, using reported orientational order parameters. Multicomponent hosts may require a modified approach, which could be based on the same principles.
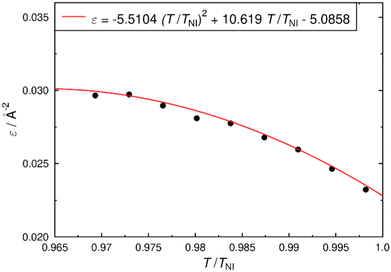 | ||
| Fig. 7 Plot of fitted ε values against the reduced temperature of 5CB, along with an empirical quadratic fit to the data. | ||
For the dyes, a molecular surface and a diagonalised surface tensor was calculated for each optimised conformer in accordance with the method described in the Experimental section, yielding values of T2,0 and T2,2, which are listed in the ESI† (Table S2). An orientational energy expression for each conformer was then obtained according to eqn (10) using the value of ε = 0.030 Å−2 for 5CB at 298 K from the fit in Fig. 7. The orientational order parameters, Szz (D20,0) and  ,32,82 of the individual conformers of the dyes were then obtained using eqn (5) and (6), and the dichroic order parameter Si, of each of the i transitions contributing to the absorption band was calculated by using eqn (4) and the respective TDM angles in the surface tensor (molecular) frame, βTDM and αTDM, for each transition. Where the absorption spectrum showed distinct long- and short-wavelength bands (as listed in Tables 1 and 2), a separate dichroic ratio was calculated for each band, as described below. The specific transitions and angles used for each band are listed in full in Table S2 in the ESI.†
,32,82 of the individual conformers of the dyes were then obtained using eqn (5) and (6), and the dichroic order parameter Si, of each of the i transitions contributing to the absorption band was calculated by using eqn (4) and the respective TDM angles in the surface tensor (molecular) frame, βTDM and αTDM, for each transition. Where the absorption spectrum showed distinct long- and short-wavelength bands (as listed in Tables 1 and 2), a separate dichroic ratio was calculated for each band, as described below. The specific transitions and angles used for each band are listed in full in Table S2 in the ESI.†
A calculated dichroic ratio, Rcalc, was obtained for each absorption band using eqn (13), where m is the total number of transitions contributing to the band, calculated for all transitions across all conformers, and fi is the calculated oscillator strength of transition i, assumed here to be proportional to the absorption coefficient.
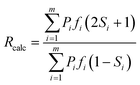 | (13) |
An assumption inherent to this method is that contributions from the transitions are wavelength-independent across the width of each band, and the independence of the experimental dichroic ratios versus wavelength across the bands (Fig. S1 in the ESI†) suggests that this approximation is valid. The calculated dichroic order parameter of each absorption band, Scalc, was then determined from the calculated dichroic ratio using eqn (1), and these values are listed in Table 3 along with the differences between the calculated and experimental values.
| Dye | S calc | Δ |
|---|---|---|
| a Long-wavelength band. b Short-wavelength band. | ||
| 1 | 0.74 | 0.10 |
| 2 | 0.61 | 0.07 |
| 3 | 0.57 | 0.08 |
| 4 | 0.70 | 0.08 |
| 5 | 0.71 | 0.05 |
| 6 | 0.18 | −0.14 |
| 7 | 0.08 | −0.04 |
| 8 | 0.16a | −0.17 |
| 0.20b | 0.24 | |
| 9 | 0.26a | −0.09 |
| 0.14b | 0.20 | |
| 10 | −0.23a | −0.01 |
| 0.64 | 0.17 | |
| 11 | −0.29 | −0.08 |
| 12 | 0.30 | −0.05 |
| 13 | 0.33 | 0.01 |
| 14 | 0.44a | −0.02 |
| 0.39b | 0.02 | |
| 15 | 0.43a | 0.03 |
| 0.35b | 0.03 | |
The values of Scalc are plotted against the experimental values in Fig. 8, along with a linear fit that shows a good correlation (R2 = 0.87). The correlation indicates that the method is generally successful in calculating the trend in the experimental dichroic order parameters, and the RMS difference of 0.106 from the experimental values demonstrates the capability of the method to calculate absolute values.
 | ||
| Fig. 8 Plot of dichroic order parameters calculated using the surface tensor model against experimental values, along with a linear fit to the data (solid red line); bars correspond to the maximum and minimum experimental values given in Table S1 (ESI†). The dashed green line corresponds to Scalc = Sexp. | ||
The largest differences between the calculated and experimental dichroic order parameters occur for the 1,4-disubstituted anthraquinone dyes, 8 and 9, which are amongst the least rod-like of the structures studied here. These dyes also contain the flexible C–NH-phenyl linking group that we have previously shown can cause significant differences between dichroic order parameters calculated from single (static) structures and those based on calculations that include the effects of flexibility.28 This combination of flexibility and being non-rod-like means that, relative to more rigid and rod-like species, variations in molecular structure are more likely to affect the overall molecular shape and hence both the molecular alignments within the host and the TDM alignments within the molecule.
Splitting the results between anthraquinone and azo dyes gives RMS differences of 0.125 and 0.031, respectively, suggesting that the method performs significantly better for azo dyes than for anthraquinone dyes. This may again be attributed in part to the relative flexibilities of the dyes studied here: many of the anthraquinone dyes contain flexible alkyl chains, whereas none are present in the azo dyes studied here, and the flexibility of the linking groups on the anthraquinone core have been calculated to have an influence on the dichroic order parameter of dyes containing these groups.28
The method we report here accounts for a degree of flexibility within the dyes by calculating transitions for a range of conformers, but these structures are limited to those at local energy minima. More sophisticated computational approaches to the effects of flexibility might be taken, but the approach we demonstrate is relatively straightforward and has general applicability.
Combined surface tensor and quadrupole model
In principle, the surface tensor and quadrupole models discussed in the introduction may be combined in the order parameter calculations by adding the orientational energy arising from the quadrupole interactions, given by eqn (11), to the orientational energy arising from the surface interactions, given by eqn (10). However, such an addition requires these two energy terms to be expressed relative to a common molecular frame, i.e. with the same Euler angles, β and γ, relative to the laboratory frame, whereas the general individual expressions presented in the introduction give these energies relative to different molecular frames defined by the eigenvectors of the diagonalised quadrupole and surface tensors, respectively. The molecular frames defined by these two tensors will typically lie at different angles relative to the molecule, and so their respective Euler angles relative to the laboratory frame will not generally be coincident, preventing a simple addition of the terms. To perform such an addition, the quadrupole energy must be expressed in the surface tensor frame (or vice versa), which may be achieved through the closure relation of Wigner functions, as given by general eqn (14).83 This expression enables functions of Euler angles, α′′, β′′, γ′′, between two sets of axes (e.g. the laboratory frame and the quadrupole frame) to be expressed in terms of two sets of Euler angles: one set, α, β, γ, between the initial frame and an intermediate frame (e.g. the laboratory frame and the surface tensor frame) and another set, α′, β′, γ′, between the intermediate frame and the final frame (e.g. the surface tensor frame and the quadrupole frame).84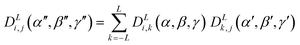 | (14) |
 | (15) |
A method has been proposed to determine FZZ values from reported experimental dielectric permittivities,62 but assumptions in the method have been reported to result in significant errors,37 and our initial tests indicated that the values determined for the systems reported here were largely dependent on the somewhat arbitrary choice of the radius of the necessarily spherical solute cavity. Using the sum of eqn (10) and (15) to give the orientational energy term and fitting FZZ concurrently with ε to match the calculated and experimental order parameters of 5CB at a range of temperatures, analogous to the method used to obtain ε for the surface tensor model alone, is not possible because FZZ and ε are independent unknown parameters. We therefore decided to use a fixed value of FZZ derived from experimental data reported for 5CB and fit a value of ε to match the calculated and experimental order parameters at a set of specific temperatures. Experimental values of FZZ for 5CB have been reported across a range temperatures from NMR studies of D2 in partially deuterated 5CB,56 and Fig. 9 (top) shows these values along with a linear fit, which provides a general expression that enables a value of FZZ to be determined for 5CB at any reduced temperature in this range. It has been established that larger solutes in nematic liquid crystals experience smaller values of FZZ than those obtained from small solutes such as D2, with reported scaling factors being ca. 40% for benzene derivatives50 and ca. 20% for benzoquinone,85 both of which are smaller than any of the molecules used in the work we report here. Hence, the values of FZZ determined from the linear fit were scaled to 20% before being used in eqn (15). Fig. 9 (bottom) shows the values of ε that were then obtained by fitting to the experimental order parameter of 5CB from X-ray diffraction experiments69 at the appropriate temperature. The empirical fit shown in Fig. 9 (bottom) provides an expression that enables a value of ε to be determined for 5CB by this method at any reduced temperature in this range, in which a specific pair of ε and FZZ values define the orienting strength of the 5CB host at a given temperature. At a given temperature, the calculated value of ε for 5CB from this method is higher than that obtained from the surface model alone (Fig. 7) because the reported positive electric field gradient (FZZ) for 5CB combined with the calculated negative principal molecular quadrupole moment along the long axis of 5CB86 (given also in the ESI†) results in the quadrupole effect tending to align the long axis of 5CB away from the director, such that the orienting strength from the surface effect (ε) for 5CB increases to maintain the match with the experimental order parameter.
 | ||
| Fig. 9 Plot of reported experimental FZZ values from D2 in partially deuterated 5CB56 against the reduced temperature of 5CB, along with a linear fit to the data (top). Plot of fitted ε values (obtained from the combined surface tensor and quadrupole model, and with experimental FZZ values scaled to 20%) against the reduced temperature of 5CB, along with an empirical quadratic fit to the data (bottom). | ||
Hence, we used the 20%-scaled value of FZZ = 1.173 × 1017 V m−2 and ε = 0.0319 Å−2 determined for 5CB at 298 K from the fits in Fig. 9 for the guest–host calculations, enabling the dichroic order parameters to be calculated using the same method as that used for the surface tensor alone, but using a summation of eqn (10) and (15) to determine the orientational energy of each conformer with the combined model. Similar to the approach taken using the surface tensor method alone, the minimum value of U(β,γ) arising from the combined surface tensor and quadrupole contributions was added to the DFT-calculated energy of each conformer and used to produce the values of Ei used in eqn (12) to calculate the relative populations of the conformers. The calculated dichroic order parameters are listed in Table 4, along with the differences between the calculated and experimental values. These calculated values are plotted against the experimental values in Fig. 10 along with a linear fit that shows a good correlation (R2 = 0.88). This correlation is slightly better than that obtained using the surface tensor alone (R2 = 0.87), and the RMS difference of 0.114 using the surface and quadrupole model is slightly worse than that of 0.106 obtained using the surface tensor model alone. The slight differences between the two models may not simply be attributed to using a two-parameter model because the values of ε and FZZ were obtained by fitting experimental data from the host alone, and then fixed in the dichroic order parameter calculations for both models. From this analysis, the inclusion of quadrupole coupling provides a slightly better correlation to a linear fit but the overall difference from the experimental dichroic ratios is slightly worse for the combined model. Further tests, given in the ESI† (Fig. S2), showed that this was a general effect: the greater the value of FZZ (scaling from 0% to 100% of the reported experimental FZZ) the larger the RMS difference with the experimental dichroic order parameter values, although the linear fits gave better correlations; and this same effect was observed either on using specific pairs of ε and FZZ values for 5CB obtained from fitting, or from keeping ε fixed at 0.030 Å−2 (as for the surface tensor model alone) and scaling only FZZ. Hence, the surface tensor model alone provides a good overall fit to the experimental data, indicating that the orienting potential experienced by the dyes in the host is dominated by the interactions modelled by this approach.
| Dye | S calc | Δ |
|---|---|---|
| a Long-wavelength band. b Short-wavelength band. | ||
| 1 | 0.77 | 0.13 |
| 2 | 0.64 | 0.10 |
| 3 | 0.60 | 0.11 |
| 4 | 0.74 | 0.12 |
| 5 | 0.74 | 0.08 |
| 6 | 0.20 | −0.12 |
| 7 | 0.07 | −0.05 |
| 8 | 0.17a | −0.16 |
| 0.19b | 0.23 | |
| 9 | 0.27a | −0.08 |
| 0.13b | 0.19 | |
| 10 | −0.26a | −0.04 |
| 0.68b | 0.21 | |
| 11 | −0.30 | −0.09 |
| 12 | 0.32 | −0.03 |
| 13 | 0.36 | 0.04 |
| 14 | 0.48a | 0.02 |
| 0.42b | 0.05 | |
| 15 | 0.47a | 0.07 |
| 0.37b | 0.05 | |
 | ||
| Fig. 10 Plot of dichroic order parameters calculated using the combined surface tensor and quadrupole model against experimental values, along with a linear fit to the data; bars correspond to the maximum and minimum experimental values given in Table S1 (ESI†). The dashed green line corresponds to Scalc = Sexp. | ||
In comparison with the surface tensor model alone, the combined model gives a better match with the experimental dichroic order parameter for six bands and a worse match for fourteen bands, although the differences between the two models are small. As with the surface tensor model alone, the combined model gives some of the largest differences between calculated and experimental dichroic order parameters for dyes 8 and 9, and it performs better for azo dyes than anthraquinone dyes. Both of these similarities are consistent with the effects of molecular flexibility discussed above for the surface tensor model alone.
The ways in which the surface tensor and quadrupole methods model the molecular alignment, and their relative influences on the calculated dichroic ratio values, can be illustrated by considering dyes 6 and 11, via the plots shown in Fig. 11 and 12, respectively, along with the schematic diagram of the Euler angles shown in Fig. 2. The top row in Fig. 11 shows the orientational energy profile of dye 6 as determined by the surface tensor model alone (left), and by the combined surface tensor and quadrupole model along with their individual contributions to the combined model. In the case of dye 6, the surface tensor model alone gives a minimum energy at β = 0 that is independent of γ in this uniaxial phase, and an increase in U for β > 0 that depends strongly on the value of γ, indicating that the orienting potential along the host director depends strongly on the position of the molecular x and y axes around the principal molecular alignment axis, z, i.e. that dye 6 is calculated to exhibit a high degree of surface biaxiality. This effect can also be illustrated by the schematic sequence in the second row of Fig. 11, where the disc-like ellipsoid is defined by the square roots of the Cartesian components of the surface tensor (Tzz, Tyy, Txx) with origin at the centre of mass of dye 6, and where the red line shows the principal surface tensor axis (z) that gives the preferred molecular alignment along the host director. Starting at β = 0° and γ = 0° and rotating to β = 90° while keeping γ = 0° gives only a small increase in U because a small surface area is maintained along the host director when γ = 0°. Then keeping β = 90° and rotating to γ = 90° gives a large increase in U because this rotation gives a large surface area along the host director when γ = 90°. Finally, keeping γ = 90° and rotating to β = 0° gives a large decrease in U because of the return to a small surface area along the host director when γ = 0°. The surface tensor contribution to the combined model has a similar dependence on angle as the surface tensor model alone but the magnitudes of the changes are greater because of the larger value of the surface orienting potential, ε, in this model. The quadrupole contribution to the combined model has a dependence of U on angle that is broadly similar to that of the surface tensor contribution, although the biaxiality is relatively less pronounced. The schematic sequence in the third row of Fig. 11 has lines with colours giving the signs and lengths scaled to the relative magnitudes of the Cartesian components of the quadrupole tensor (Qzz, Qyy, Qxx) of dye 6. In this case, the principal quadrupole axis (z) is aligned with the principal surface tensor axis and Qzz is positive (shown in red), giving a favourable interaction, and a negative Qxx (shown in blue) of almost similar magnitude at a perpendicular reinforces the effect and results in essentially the same preferred molecular alignment axis from both models. Rotating to β = 90° while keeping γ = 0° gives an increase in U because the Qzz interaction is now unfavourable, and then rotating to γ = 90° gives a further increase in U because both Qzz and Qxx interactions are unfavourable. The schematic sequence in the fourth row of Fig. 11 shows a double-headed arrow for the transition dipole moment axis of dye 6, which is closely aligned with the surface molecular alignment axis (i.e. βTDM is small). The net effect is stronger molecular alignment in the combined model, resulting principally from the stronger surface contribution, and a calculated dichroic order parameter that is slightly higher and slightly closer to the experimental value.
Fig. 12 shows equivalent plots and schematic sequences for dye 11, which illustrates a slightly different case. For dye 11, the surface tensor alone and its contribution to the combined model have broadly similar characteristics to those of dye 6, although the surface tensor ellipsoid is clearly more rod-like and less disc-like than that of dye 6, which results in a much stronger dependence of U on β when γ = 0° for dye 11. The quadrupole tensor for dye 11 is quite different from that of dye 6: the principal quadrupole axis of dye 11 is near-perpendicular to the anthraquinone plane and the associated Qzz value is negative. Starting at β = 0° and γ = 0° gives a favourable interaction with the negative Qzz (shown in blue) in this negative FZZ host, but an unfavourable interaction with a positive Qxx (shown in red) of relatively large magnitude that lies close to the anthraquinone plane and close to its long axis. Rotating to β = 90° while keeping γ = 0° gives a decrease in U because both Qzz and Qxx interactions are now favourable, such that this is the preferred quadrupole alignment: the quinoidal group lies near-perpendicular to its orientation at the preferred surface molecular alignment because the in-plane quadrupole component of greatest magnitude (Qxx) is positive and lies near-perpendicular to the in-plane principal surface tensor axis. Rotating then to γ = 90° gives a large increase in U because both the Qzz and Qxx interactions are now unfavourable. The transition dipole moment of dye 11 lies near-perpendicular to the surface alignment axis, resulting in the negative dichroic order parameter, but close to the preferred quadrupole alignment axis that lies close to the anthraquinone plane. The net effect is stronger molecular and perpendicular TDM alignment in the combined model, and a calculated negative dichroic order parameter that is slightly more negative and slightly further from the experimental value.
These two examples are relatively simple cases to discuss and illustrate, with dye 6 being considered here in terms of a single calculated structure and transition, and dye 11 as two relatively similar calculated structures each with a single relevant transition, and where the surface tensor, quadrupole and TDM axes are close to being either parallel or perpendicular to each other in each dye (ESI,† including Table S2). More generally, multiple structures may need to be considered for each dye, with contributions scaled according to their relative energies, and multiple transitions for each band, scaled according to their oscillator strengths, as we have done here for other dyes where appropriate (as given in the ESI†). Moreover, structures that give significant angles between different calculated molecular tensor frames and/or TDM axes, especially allied with biaxiality in differently oriented molecular frames, are difficult to discuss and relate to calculated dichroic ratios as done above for dyes 6 and 11.
Conclusions
A general mean-field approach to calculating dichroic order parameters of dyes in guest–host systems has been presented that may be used with any expression for the orientational energy of a dye molecule. The method enables rapid quantitative calculation of dichroic order parameters with the time scale largely dictated by the length of time taken to run the DFT and TD-DFT calculations required, which is currently on the order of minutes or hours on a current desktop workstation, depending on the level of theory employed. The method requires no experimental data from the dyes, and it relies only on empirical fits to experimental data from the host to assess absolute values (as done here), or typical values of host parameters to assess trends between dyes. The general approach presented here therefore constitutes a practical method for screening hypothetical dye structures prior to synthesis.Both the surface tensor and combined surface tensor and quadrupole methods used to determine the orientational energies provide encouraging results in terms of the quantitative prediction of the experimental dichroic order parameters, resulting in RMS differences of ca. 0.1 and correlation trends of ca. 0.9. Furthermore, these values are in the context of a purposefully chosen wide range of dye structures and positive and negative dichroic order parameters to provide a rigorous test of the methods. The surface tensor approach alone provided a very good model. The combined model including a quadrupole contribution gave a small improvement on that model for a minority of dyes but not for the whole set of dyes, suggesting that the shapes of the dyes studied here dominate their alignment in a nematic host. Nevertheless, there may be systems where a combined model is appropriate, and the work reported here demonstrates a general approach for combining two model orienting potentials to calculate dichroic order parameters of dyes in guest–host systems.
For dye molecules to be of practical use in devices, they must have a high degree of molecular alignment, and therefore they must have highly anisotropic molecular shapes. Such molecules will have highly anisotropic surface tensor eigenvalues, resulting in high energy barriers to molecular rotation arising from molecular shape that are likely to be very large in comparison with the orientational energies from quadrupole interactions. Furthermore, such molecules are typically rod-like with visible TDM vectors oriented along the long axis of the molecule, and in such cases one of the axes of the quadrupole tensor is likely to align approximately with the principal surface axis of the molecule. As a general design principle, it would seem favourable to align the quadrupole axes and maximise the anisotropy of the quadrupole tensor so that any contribution reinforces the molecular alignment given by the principal surface axis.
The methods presented here would benefit from further application to molecules of different dye classes and to different hosts, but this initial work indicates that the method may be widely applicable. Synthetic research into guest–host systems may benefit from screening potential dye molecules using the type of approach described here in order to select and then target molecules with the most promising calculated alignment properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by The Engineering and Physical Sciences Research Council (EPSRC) under grant EP/M020584/1 for the development of dyes for liquid crystal applications. Data from this article are available by request from the University of York Data Catalogue: DOI: 10.15124/b0ec889e-945a-4f66-88aa-169740cfc151.References
- T. Uchida, H. Seki, C. Shishido and M. Wada, Proc. SID, 1981, 22, 41–46 Search PubMed.
- D. L. White and G. N. Taylor, J. Appl. Phys., 1974, 45, 4718–4723 CrossRef CAS.
- H. S. Cole and R. A. Kashnow, Appl. Phys. Lett., 1977, 30, 619–621 CrossRef CAS.
- A. B. Ebru, M. Maxim, H. Børre, G. Anatoliy and L. W. John, Jpn. J. Appl. Phys., 2006, 45, 4146 CrossRef.
- H. Sun, Z. Xie, C. Ju, X. Hu, D. Yuan, W. Zhao, L. Shui and G. Zhou, Polymers, 2019, 11, 694 CrossRef CAS PubMed.
- E. Peeters, J. Lub, J. A. M. Steenbakkers and D. J. Broer, Adv. Mater., 2006, 18, 2412–2417 CrossRef CAS.
- R. Piñol, J. Lub, M. P. García, E. Peeters, J. L. Serrano, D. Broer and T. Sierra, Chem. Mater., 2008, 20, 6076–6086 CrossRef.
- J. B. Chang, J. W. Namgoong, S. H. Kim, S. H. Park, B. H. Hwang and J. P. Kim, Dyes Pigm., 2015, 121, 30–37 CrossRef CAS.
- M. G. Debije, Adv. Funct. Mater., 2010, 20, 1498–1502 CrossRef CAS.
- M. Carrasco-Orozco, W. C. Tsoi, M. O'Neill, M. P. Aldred, P. Vlachos and S. M. Kelly, Adv. Mater., 2006, 18, 1754–1758 CrossRef CAS.
- C. Carrasco-Vela, X. Quintana, E. Oton, M. A. Geday and J. M. Oton, Opto-Electron. Rev., 2011, 19, 496–500 Search PubMed.
- L. De Sio, L. Ricciardi, S. Serak, M. La Deda, N. Tabiryan and C. Umeton, J. Mater. Chem., 2012, 22, 6669–6673 RSC.
- H. Seki, C. Shishido, S. Yasui and T. Uchida, Jpn. J. Appl. Phys., Part 1, 1982, 21, 191–192 CrossRef CAS.
- M. Matsui, S. Okada, M. Kadowaki and M. Yamada, Liq. Cryst., 2002, 29, 707–712 CrossRef CAS.
- B. Bahadur, in Liquid Crystals: Applications and Uses, ed. B. Bahadur, World Scientific Publishing Co. Pte. Ltd., Singapore, 1992, vol. 3, ch. 11, pp. 65–208 Search PubMed.
- M. G. Pellatt, I. H. C. Roe and J. Constant, Mol. Cryst. Liq. Cryst., 1980, 59, 299–316 CrossRef CAS.
- F. C. Saunders, K. J. Harrison, E. P. Raynes and D. J. Thompson, IEEE Trans. Electron Devices, 1983, 30, 499–503 Search PubMed.
- G. Pelzl, H. Zaschke and D. Demus, Displays, 1985, 6, 141–147 CrossRef CAS.
- A. Isenberg, B. Krücke, G. Pelzl, H. Zaschke and D. Demus, Cryst. Res. Technol., 1983, 18, 1059–1068 CrossRef CAS.
- D. Bauman, E. Mykowska and E. Wolarz, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1998, 321, 333–347 CrossRef.
- E. Wolarz, H. Moryson and D. Bauman, Displays, 1992, 13, 171–178 CrossRef CAS.
- D. Bauman and H. G. Kuball, Chem. Phys., 1993, 176, 221–231 CrossRef CAS.
- T. Martyński, E. Mykowska, R. Stolarski and D. Bauman, Dyes Pigm., 1994, 25, 115–129 CrossRef.
- S. Kumar, Chem. Soc. Rev., 2006, 35, 83–109 RSC.
- M. T. Sims, L. C. Abbott, S. J. Cowling, J. W. Goodby and J. N. Moore, Chem. – Eur. J., 2015, 21, 10123–10130 CrossRef CAS PubMed.
- M. T. Sims, L. C. Abbott, S. J. Cowling, J. W. Goodby and J. N. Moore, J. Phys. Chem. C, 2016, 120, 11151–11162 CrossRef CAS.
- M. T. Sims, L. C. Abbott, S. J. Cowling, J. W. Goodby and J. N. Moore, Phys. Chem. Chem. Phys., 2016, 18, 20651–20663 RSC.
- M. T. Sims, L. C. Abbott, S. J. Cowling, J. W. Goodby and J. N. Moore, Phys. Chem. Chem. Phys., 2017, 19, 813–827 RSC.
- M. T. Sims, R. J. Mandle, J. W. Goodby and J. N. Moore, Liq. Cryst., 2017, 44, 2029–2045 CAS.
- G. R. Luckhurst and C. Zannoni, Nature, 1977, 267, 412–414 CrossRef CAS.
- G. R. Luckhurst, in Physical Properties of Liquid Crystals: Nematics., eds. D. A. Dunmur, A. Fukuda and G. R. Luckhurst, IET, London, 2001, pp. 57–88 Search PubMed.
- G. R. Luckhurst, in Biaxial Nematic Liquid Crystals, ed. G. R. Luckhurst and T. J. Sluckin, Wiley, United Kingdom, 2015, pp. 25–54 Search PubMed.
- A. J. van der Est, M. Y. Kok and E. E. Burnell, Mol. Phys., 1987, 60, 397–413 CrossRef CAS.
- D. S. Zimmerman and E. E. Burnell, Mol. Phys., 1990, 69, 1059–1071 CrossRef.
- D. S. Zimmerman and E. E. Burnell, Mol. Phys., 1993, 78, 687–702 CrossRef.
- A. Ferrarini, G. J. Moro, P. L. Nordio and G. R. Luckhurst, Mol. Phys., 1992, 77, 1–15 CrossRef.
- E. E. Burnell, L. C. ter Beek and Z. Sun, J. Chem. Phys., 2008, 128, 164901 CrossRef PubMed.
- A. Ferrarini, G. R. Luckhurst, P. L. Nordio and S. J. Roskilly, J. Chem. Phys., 1994, 100, 1460–1469 CrossRef CAS.
- A. Ferrarini and G. J. Moro, in NMR of Ordered Liquids, ed. E. E. Burnell and C. A. de Lange, Springer, New York, 1997, pp. 241–258 Search PubMed.
- H. Kamberaj, R. J. Low and M. P. Neal, Mol. Phys., 2006, 104, 335–357 CrossRef CAS.
- G. Celebre, G. De Luca and A. Ferrarini, Mol. Phys., 1997, 92, 1039–1050 CAS.
- A. Ferrarini, F. Janssen, G. J. Moro and P. L. Nordio, Liq. Cryst., 1999, 26, 201–210 CrossRef CAS.
- E. E. Burnell and C. A. de Lange, Chem. Rev., 1998, 98, 2359–2387 CrossRef CAS PubMed.
- E. E. Burnell, Z. Ahmed, C. Welch, G. H. Mehl and R. Y. Dong, Chem. Phys. Lett., 2016, 659, 48–54 CrossRef CAS.
- E. E. Burnell, C. A. de Lange and J. G. Snijders, Phys. Rev. A, 1982, 25, 2339–2350 CrossRef CAS.
- P. Diehl, S. Sýkora, W. Niederberger and E. E. Burnell, J. Magn. Reson. (1969), 1974, 14, 260–269 CrossRef CAS.
- E. E. Burnell and C. A. de Lange, eMagRes, John Wiley & Sons, Ltd, 2016, pp. 901–912 DOI:10.1002/9780470034590.emrstm1477.
- A. Saupe, Mol. Cryst., 1966, 1, 527–540 CrossRef CAS.
- R. T. Syvitski and E. E. Burnell, Chem. Phys. Lett., 1997, 281, 199–206 CrossRef CAS.
- R. T. Syvitski and E. E. Burnell, J. Chem. Phys., 2000, 113, 3452–3465 CrossRef CAS.
- Z. Danilović and E. E. Burnell, J. Chem. Phys., 2009, 130, 154506 CrossRef PubMed.
- D. J. Photinos, C. D. Poon, E. T. Samulski and H. Toriumi, J. Phys. Chem., 1992, 96, 8176–8180 CrossRef CAS.
- D. J. Photinos and E. T. Samulski, J. Chem. Phys., 1993, 98, 10009–10016 CrossRef CAS.
- A. F. Terzis and D. J. Photinos, Mol. Phys., 1994, 83, 847–865 CrossRef CAS.
- G. N. Patey, E. E. Burnell, J. G. Snijders and C. A. de Lange, Chem. Phys. Lett., 1983, 99, 271–274 CrossRef CAS.
- A. Weaver, A. J. van der Est, J. C. T. Rendell, G. S. Bates, G. L. Hoatson and E. E. Burnell, Liq. Cryst., 1987, 2, 633–642 CrossRef CAS.
- L. C. ter Beek and E. E. Burnell, Chem. Phys. Lett., 2006, 426, 96–99 CrossRef CAS.
- A. di Matteo, A. Ferrarini and G. J. Moro, J. Phys. Chem. B, 2000, 104, 7764–7773 CrossRef CAS.
- A. di Matteo and A. Ferrarini, J. Phys. Chem. B, 2001, 105, 2837–2849 CrossRef CAS.
- G. Celebre and A. Ionescu, J. Phys. Chem. B, 2010, 114, 228–234 CrossRef CAS PubMed.
- G. Celebre and A. Ionescu, J. Phys. Chem. B, 2010, 114, 235–241 CrossRef CAS PubMed.
- G. Celebre, J. Phys. Chem. B, 2007, 111, 2565–2572 CrossRef CAS PubMed.
- S. J. Cowling, C. Ellis and J. W. Goodby, Liq. Cryst., 2011, 38, 1683–1698 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- D. Jacquemin, E. A. Perpète, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 CrossRef CAS PubMed.
- M. F. Sanner, A. J. Olson and J. C. Spehner, Biopolymers, 1996, 38, 305–320 CrossRef CAS PubMed.
- M. T. Sims, L. C. Abbott, R. M. Richardson, J. W. Goodby and J. N. Moore, Liq. Cryst., 2019, 46, 11–24 CrossRef CAS.
- L. C. Abbott, S. N. Batchelor and J. N. Moore, J. Phys. Chem. A, 2013, 117, 1853–1871 CrossRef CAS PubMed.
- L. C. Abbott, S. N. Batchelor, J. Oakes, B. C. Gilbert, A. C. Whitwood, J. R. Lindsay Smith and J. N. Moore, J. Phys. Chem. A, 2005, 109, 2894–2905 CrossRef CAS PubMed.
- L. C. Abbott, S. N. Batchelor, J. Oakes, J. R. Lindsay Smith and J. N. Moore, J. Phys. Chem. A, 2004, 108, 10208–10218 CrossRef CAS.
- L. C. Abbott, S. N. Batchelor, L. Jansen, J. Oakes, J. R. Lindsay Smith and J. N. Moore, New J. Chem., 2004, 28, 815–821 RSC.
- J. Griffiths and K.-C. Feng, J. Mater. Chem., 1999, 9, 2333–2338 RSC.
- A. Ghanadzadeh Gilani, M. Moghadam, M. S. Zakerhamidi and E. Moradi, Dyes Pigm., 2012, 92, 1320–1330 CrossRef CAS.
- A. G. Gilani, M. Salmanpour and T. Ghorbanpour, J. Mol. Liq., 2013, 179, 118–123 CrossRef CAS.
- A. Ghanadzadeh, A. Zeini, A. Kashef and M. Moghadam, Spectrochim. Acta, Part A, 2009, 73, 324–329 CrossRef CAS PubMed.
- C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- D. S. Zimmerman, Y. Z. Li and E. E. Burnell, Mol. Cryst. Liq. Cryst., 1991, 203, 61–75 CrossRef CAS.
- T. Chandrakumar and E. E. Burnell, Mol. Phys., 1997, 90, 303–314 CrossRef.
- Z. Danilovic and E. E. Burnell, J. Chem. Phys., 2009, 130, 154506 CrossRef PubMed.
- C. Zannoni, in Nuclear Magnetic Resonance of Liquid Crystals, ed. J. W. Emsley, D. Reidel Publishing Company, Dordrecht, 1985, pp. 1–34 Search PubMed.
- E. P. Wigner, Group Theory and its Application to the Quantum Mehcanics of Atomic Spectra, Academic press, New York, 1959 Search PubMed.
- C. Zannoni, in Molecular Physics of Liquid Crystals, ed. G. R. Luckhurst and G. W. Gray, Academic Press, London, 1979, pp. 51–84 Search PubMed.
- G. Celebre and G. De Luca, Chem. Phys. Lett., 2003, 368, 359–364 CrossRef CAS.
- A. Pizzirusso, M. B. Di Cicco, G. Tiberio, L. Muccioli, R. Berardi and C. Zannoni, J. Phys. Chem. B, 2012, 116, 3760–3771 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00178d |
| ‡ Current address: Department of Applied Sciences, Faculty of Health and Life Sciences, Northumbria University, Newcastle Upon Tyne, NE1 8ST, UK. |
| § Current address: School of Physics and Astronomy, University of Leeds, Leeds, LS2 9JT, UK. |
| This journal is © the Owner Societies 2023 |