Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simulation of the cyclic voltammetric response of an outer-sphere redox species with inclusion of electrical double layer structure and ohmic potential drop†
Katherine J.
Levey
 ab,
Martin A.
Edwards
ab,
Martin A.
Edwards
 c,
Henry S.
White
c,
Henry S.
White
 *d and
Julie V.
Macpherson
*d and
Julie V.
Macpherson
 *ab
*ab
aDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK. E-mail: j.macpherson@warwick.ac.uk
bCentre for Diamond Science and Technology, University of Warwick, Coventry, CV4 7AL, UK
cDepartment of Chemistry & Biochemistry, University of Arkansas, Fayetteville, AR 72701, USA
dDepartment of Chemistry, University of Utah, 315 South 1400 East, Salt Lake City, UT 84112, USA. E-mail: white@chemistry.utah.edu
First published on 20th February 2023
Abstract
A finite-element model has been developed to simulate the cyclic voltammetric (CV) response of a planar electrode for a 1e outer-sphere redox process, which fully accounts for cell electrostatics, including ohmic potential drop, ion migration, and the structure of the potential-dependent electric double layer. Both reversible and quasi-reversible redox reactions are treated. The simulations compute the time-dependent electric potential and ion distributions across the entire cell during a voltammetric scan. In this way, it is possible to obtain the interdependent faradaic and non-faradaic contributions to a CV and rigorously include all effects of the electric potential distribution on the rate of electron transfer and the local concentrations of the redox species Oz and Rz−1. Importantly, we demonstrate that the driving force for electron transfer can be different to the applied potential when electrostatic interactions are included. We also show that the concentrations of Oz and Rz−1 at the plane of electron transfer (PET) significantly depart from those predicted by the Nernst equation, even when the system is characterised by fast electron transfer/diffusion control. A mechanistic rationalisation is also presented as to why the electric double layer has a negligible effect on the CV response of such reversible systems. In contrast, for quasi-reversible electron transfer the concentrations of redox species at the PET are shown to play an important role in determining CV wave shape, an effect also dependant on the charge of the redox species and the formal electrode potential of the redox couple. Failure to consider electrostatic effects could lead to incorrect interpretation of electron-transfer kinetics from the CV response. Simulated CVs at scan rates between 0.1 and 1000 V s−1 are found to be in good agreement with experimental data for the reduction of 1.0 mM Ru(NH3)63+ at a 2 mm diameter gold disk electrode in 1.0 M potassium nitrate.
Introduction
In electrochemical measurements of faradaic currents, e.g. voltammetry, chronoamperometry, etc., the distribution of the electric potential throughout the cell plays a critical role in determining the interdependent ohmic potential drop, ion migration, and electric double layer (EDL) structure. It is well established that these electrostatic effects can significantly impact the current response as a function of applied potential or time, leading to incorrect interpretation of electron-transfer kinetics and mass-transfer phenomena.1–5 Several studies have addressed the impact of ohmic potential drop and the EDL structure on faradaic reactions at microelectrodes and nanoelectrodes.4,6–11 However, a comprehensive and rigorous description of the role of cell electrostatics on the response of conventionally sized electrodes used in electroanalysis (i.e. ∼mm radius) has not been reported.Scanning the applied electrode potential during a CV experiment leads to a time-dependent EDL structure and a capacitive, non-faradaic voltammetric current. Most often, in the simplest treatments of experimental data, this non-faradaic process is considered as being independent of the faradaic (electron-transfer) reaction, based on the assumptions that (1) the EDL does not affect redox ion transport or electron-transfer kinetics, and (2) the faradaic generation and depletion of redox ions does not influence the EDL structure.12 However, neither assumption is generally correct, as has been shown in experiments when the size of the concentration depletion layer associated with the faradaic process is comparable in size with the EDL.13 As early as 1933, Frumkin and co-workers recognised the general importance of the EDL on electron-transfer kinetics,14 demonstrating that both the concentration of redox species at the plane of electron-transfer (PET) and the driving force for electron transfer are functions of the potential distribution within the EDL. Here, the PET corresponds to the location of the redox species in solution when it undergoes an electron-transfer reaction. For outer-sphere reactions, this is generally considered approximately equal to the width of the outer-Helmholtz layer.
The ohmic potential drop in the bulk solution that results from the flux of net charge through a solution of finite conductivity also impacts the structure of the EDL, which, in turn, influences the CV response. In particular, the ohmic potential drop reduces the driving force for electron transfer at the electrode surface and gives rise to well-known resistive peak splitting in the CV response.13 Savéant and colleagues proposed that correct analysis of the voltammetric data for ohmic potential drop should account for the interdependence of the faradaic and non-faradaic currents.15 These authors developed a time-dependent electrical circuit analysis approach using resistors and capacitors to account for the solution resistance and electrode capacitance, and applied their analysis to fast-scan cyclic voltammetry at disk ultramicroelectrodes.9,15 This approach was further developed by Amatore and co-workers,16,17 as well as more recently by Lopes and colleagues.18
A more explicit treatment of the influence of the EDL on a faradaic reaction was presented by Amatore and Lefrou, who approximated the EDL structure at a microelectrode using the equilibrium Gouy–Chapman Stern model.8 These authors showed that the shape of the CV was distorted due to the EDL at very high scan rates (105–106 V s−1), conditions where the thicknesses of the EDL and diffusion layer are comparable. However, this model does not account for the influence of the faradic reaction on the ion and electric potential distributions within the EDL, or the coupling of the EDL and ohmic potential drop distribution. A more direct and rigorous method for simulating the non-equilibrium ion and electric potential distributions in the EDL is obtained by simultaneously solving the Poisson (P) equation and the Nernst–Planck (NP) equations. The former equation defines the relationship between local electric potential and charge distributions, whilst the latter describes the diffusion and potential-dependent migration of redox species and supporting electrolyte ions.
The PNP model has been used successfully to model the steady-state CV response of nanoelectrodes,1,2,19,20 and in nanogap thin-layer cells where the separation distance between two electrodes is comparable to the size of the EDL.21–24 Streeter and Compton employed the PNP model to analyse the chronoamperometry response at a hemispherical microelectrode.11 The PNP model has also been used to compute the capacitive current at a planar electrode in the absence of any faradaic reaction.25,26 While significant work has been devoted to modelling the CV response of small electrode systems and non-faradaic currents, a comprehensive treatment of the faradaic and non-faradaic response at larger electrodes (i.e. ≥mm) that includes the EDL structure, ion migration, and ohmic potential drop has not yet been reported.
In this paper, we present a model that describes the CV response for outer-sphere electron transfer reactions at planar electrodes that includes a complete description of the potential and time-dependent distributions of redox species, supporting electrolyte ions, and electric potential across the entire cell. The model uses a commercially available finite-element modelling package that is relatively simple to implement and provides a user-friendly interface to probe how electrostatic phenomena influence the local ion environment at the electrode–electrolyte interface. The Butler–Volmer equation is incorporated into the model in order to assess the impact of finite electron-transfer kinetics. Ohmic potential drop compensation (feedback loop) is also simulated to mimic its use in experiments. Our simulations provide insights into the coupled nature of the faradaic and non-faradaic charging currents and highlight the potential pitfalls of performing kinetic analysis using CV without considering the influence of electrostatics. Finally, simulated CVs using this electrostatic model are compared to experiments and to the simulated CV response obtained in the absence of electrostatic considerations.
Model
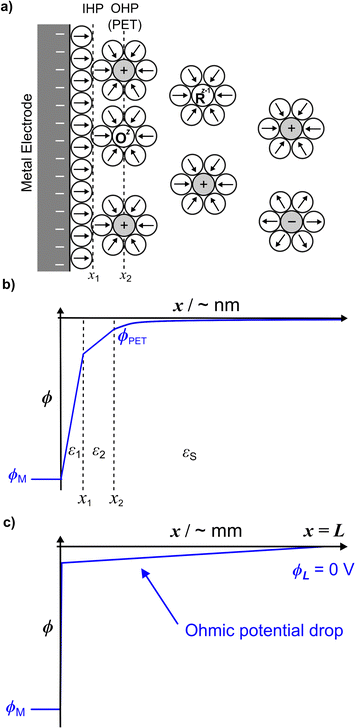
Fig. 1a shows a schematic of the electrode–electrolyte EDL structure used in our model. As commonly accepted, we assume a Helmholtz region comprising an inner Helmholtz plane (IHP) and an outer Helmholtz plane (OHP).27 The region defined by the IHP extends to a thickness x1 = 0.29 nm, which is roughly the diameter of a water molecule based on a hard sphere model.28 The OHP is located at a distance x2 = 0.59 nm from the electrode surface.27,28 We assume that the OHP represents the distance of closest approach of solvated redox species and electrolyte ions. The dielectric constant of the inner and outer layers, shown in Fig. 1b, are set equal to ε1 = 6 and ε2 = 30, respectively, based on reported values.19,27,29 The dielectric constant of water, εS, is assumed to be 80 at T = 293.15 K.30 Beyond x2, the supporting electrolyte ions and redox species are distributed in a manner determined by both the charge on the electrode and the faradaic reaction. We assume that no potential drop occurs within the electrode phase, corresponding to a metal electrode, denoted as ‘M’. At equilibrium, and in the absence of faradaic reactions, the above description reduces to the Gouy–Chapman Stern (GCS) model.13 The finite-element model numerically solves differential equations describing the electric potential (ϕ) and concentration distributions, in which all ions and molecules are treated as point charges in a continuum solvent. As we are modelling a planar disk electrode, the distributions of ϕ and concentrations are a function of the coordinate normal to the electrode, which we denote as x.To briefly introduce the electrostatic phenomena discussed in this article, Fig. 1b shows an example of a simulated ϕ vs. x distribution across the electrode–electrolyte interface, plotted on a nanometre length scale for E = −0.3 V (ϕM) and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 supporting electrolyte concentration, Celec = 1.0 M. This plot corresponds to conditions where no redox process is occurring.
1 supporting electrolyte concentration, Celec = 1.0 M. This plot corresponds to conditions where no redox process is occurring.
We assume a rectangular prism of width L to model the electrochemical cell, where the working and counter electrodes are of equal area, and the reference and counter electrodes are located at the outer boundary of the cell (x = L = 2.5 mm). The assumption of a rectangular cell with planar transport between the electrodes allows for a one-dimensional numerical simulation, as discussed below and in SI 1, ESI.† The choice of L = 2.5 mm is somewhat arbitrary but is sufficiently large to include all of the EDL structure while maintaining semi-infinite boundary conditions for modelling voltammetry at scan rates > = 0.1 V s−1. The choice of L impacts the ohmic potential drop (“iRu drop”, where i is current and Ru is solution resistance), as Ru is proportional to L for the rectangular cell. In our simulations, the iRu drop is computed from the solution of the PNP equations, as opposed to assuming a value of a circuit element Ru based on the cell geometry and solution conductivity. As large values of iRu can significantly impact the driving force for electron transfer (vide infra), the shape of the voltammetric response is dependent on L. The small value of L = 2.5 mm used in the model is representative of the distance between the working and reference electrodes in a real experiment, necessary to minimize ohmic potential drop effects but without the reference electrode interfering with the transport of the redox species to the working electrode. Fig. 1c schematically shows the linear change in ϕ with x across the entire 2.5 mm cell resulting from ohmic potential drop due to finite current passing.
The electrode potential and the formal redox potential of the outer-sphere redox couple, E0′, are referenced versus the reference potential, ϕref, which is set equal to the solution potential, ϕL, at x = L. Thus, ϕL = ϕref. In computing the EDL structure, the potential of zero charge (pzc) of the working electrode must also be defined, as the value of the pzc relative to E0′ influences the voltammetric shape. We assume that the working electrode is a homogeneous surface with a well-defined pzc. For all simulations in the main text, we set pzc = ϕref = 0 V, although we note for experimental work we use a polycrystalline gold electrode that exhibits a range of pzc across different crystal orientations.31 The chosen value of pzc relative to E0′ has a significant effect on the voltammetric response when the electron-transfer kinetics are quasi-reversible, as discussed later and shown in SI 2, ESI.†
We consider a 1e transfer reaction of an outer-sphere redox couple where the oxidised (O) and reduced (R) species have the charge z and z − 1 respectively, eqn (1).
| Oz + e ⇌ Rz−1 | (1) |
The flux (Ji) of the redox species (Oz/Rz−1) and supporting electrolyte ions normal to the electrode surface are assumed to obey the Nernst–Planck equation,
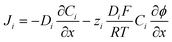 | (2) |
As ions cannot approach the electrode closer than the x2 in our model, the change in ϕ is linear between the electrode and x1 and also between x1 and x2, as governed by the Laplace equation (eqn (3)) and shown in Fig. 1b.
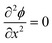 | (3) |
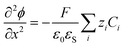 | (4) |
Conservation of mass requires that the flux of Oz and Rz−1 are equal and opposite at the electrode surface. Thus, at the PET we have
| JO = −JR = kbCR|x=PET − kfCO|x=PET | (5) |
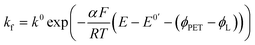 | (6) |
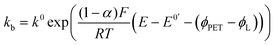 | (7) |
Eqn (2)–(7) were solved numerically using COMSOL Multiphysics (Version 5.6) to simulate the time-dependent potential and ion distributions across the entire cell during the CV experiment. This model specifically includes both the EDL structure and bulk solution and is detailed in SI 1, ESI,† along with a description of the mesh, boundary conditions and numerical parameters.
During voltammetric experiments, the total measured current (iT) is the sum of the combined faradaic (iF) and non-faradaic, double-layer charging (iC) currents, eqn (8).
| iT = iF + iC | (8) |
| iF = −nFAJO | (9) |
The non-faradaic current, eqn (10), is calculated from the rate of change of the charge density (σM) on the electrode with respect to time. Assuming E is scanned at a constant scan rate, ν, eqn (10) can also be written in terms of the change in σM with respect to E.
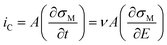 | (10) |
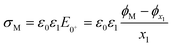 | (11) |
The finite-element model described above, in which the coupled PNP equations are numerically solved, is referred to in the discussion below as the electrostatic model. For comparison, a second model was implemented where we assume mass transfer occurs only by diffusion, and all electrostatic phenomena, i.e. EDL structure, migration, and ohmic potential drop are ignored.11,39 This model corresponds to the classical description of the CV response at a planar electrode and does not include non-faradaic currents. We refer to this as the diffusion model, which is solved in COMSOL by replacing the Nernst–Planck equation, eqn (2), with Fick's first law and fixing ϕ = 0 V throughout the electrolyte. In this limiting case, all of the applied E drives the reaction at the PET, i.e. ϕM − ϕPET = E as ϕPET − ϕL = 0. Butler–Volmer kinetics are still implemented, eqn (6) and (7), but now without the ϕPET − ϕL term.
The models can be applied to the reduction or oxidation of any outer-sphere redox reaction, where mass transport is one-dimensional and planar. This includes the simulation of CVs at a planar disk electrode and microelectrodes operating at very high scan rates.15 The voltammetric responses are reported as current densities (j) vs. E. For those wishing to extend the model to microelectrodes at lower scan rates, or other electrode geometries, the COMSOL-generated model reports are provided as separate ESI† and can be suitably adapted.
Material and methods
Solutions
Doubly distilled water from a Milli-Q purification system (Millipore Corp.) with a resistivity of 18.2 MΩ cm was used to prepare all solutions. Potassium nitrate (KNO3, ≥99.0%, Honeywell) and hexaammineruthenium(III) chloride (Ru(NH3)6Cl3, 99%, Strem Chemicals) were used as received. Ambient temperature was measured at 20 °C.Electrochemical
A three-electrode cell containing a 2 mm diameter gold (Au) disk working electrode (CHI101, CH Instruments), a silver–silver chloride (Ag/AgCl, 3 M KCl) reference electrode (REF321, Radiometer Analytical), and a platinum (Pt) coil counter electrode, were employed throughout. The Au disk is sealed in Kel-F®, exposing the Au surface in an insulating plane. The Au electrode was polished with alumina (0.05 μm, Buehler) on a polishing pad (MicroCloth PSA, Buehler). The electrode was thoroughly rinsed before use. Voltammetric measurements were conducted using an AutoLab potentiostat (PGSTAT128N, Metrohm, Barendrecht, Netherlands). To maintain consistency between experiments and finite-element method simulations the same linear waveform is used (as shown in Fig. S1, ESI†). In experiments we achieved this by using the true linear analogue scan generator (SCAN250) that adopts an analogue instead of a digital staircase signal (the latter as employed by most potentiostats),40,41 coupled with ultra-fast sampling (ADC10M). For ν < 100 V s−1, the potentiostat bandwidth was set to the “high stability” mode (10 kHz), whilst for ν > 100 V s−1, the bandwidth was set to “high-speed” (100 kHz) which prevents the instrument bandwidth from being slower than the response time constant of the cell. Ohmic potential drop compensation was not implemented experimentally. Prior to experiments, the electrolyte solution was bubbled for ∼20 minutes with Ar to purge dissolved oxygen.Results and discussions
The 1e reduction of Ru(NH3)63+, eqn (12), in a 1.0 M KNO3 supporting electrolyte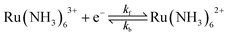 | (12) |
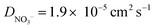 ) were taken from ref. 44. The solution initially contains 1.0 mM Ru(NH3)6(Cl)3 with 1.0 M KNO3 as the supporting electrolyte. Note whilst the counter ion to Ru(NH3)63+ in experiments is Cl−, for simplicity we assume this to be NO3−, instead of adding a second non-electroactive anion species to the model.
) were taken from ref. 44. The solution initially contains 1.0 mM Ru(NH3)6(Cl)3 with 1.0 M KNO3 as the supporting electrolyte. Note whilst the counter ion to Ru(NH3)63+ in experiments is Cl−, for simplicity we assume this to be NO3−, instead of adding a second non-electroactive anion species to the model.
In Fig. 2a and b the simulated voltammetric response of the diffusion model (dashed line) is compared to that obtained based on the electrostatic model (solid). In all simulations presented herein, the potential is initially scanned in the positive direction, starting at E = 0 V, to record the non-faradaic current prior to scanning in the region where Ru(NH3)63+ is reduced. Both the diffusion and electrostatic models give a similar response at the moderate scan rate (Fig. 2a) of 1 V s−1. The separation between the two peaks (ΔEp) in the CV is 56 mV for the diffusion model (in agreement with analytical theory for a reversible reaction, ΔEp = 2.218RT/nF = 56 mV, assuming T = 293 K)45 and 60 mV for the electrostatic model. We note that the small difference in ΔEp values for the two models would be difficult to discern in conventional voltammetric experiments.
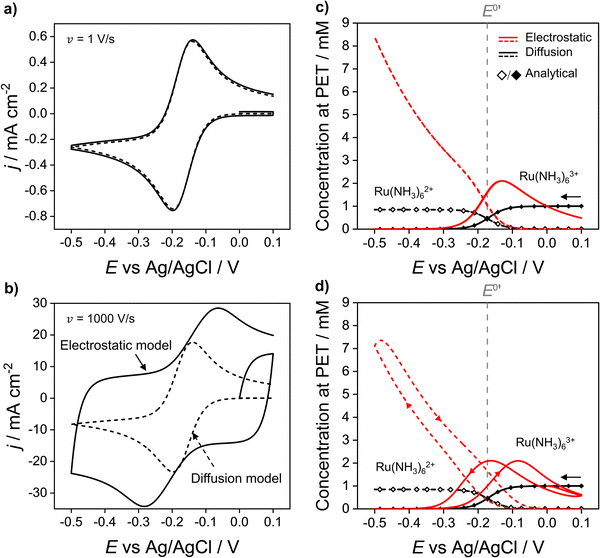 | ||
| Fig. 2 Simulated voltammetric response of 1.0 mM Ru(NH3)63+ in an aqueous solution containing 1.0 M KNO3 corresponding to the electrostatic (solid line) and diffusion (dashed) models at scan rates of (a) 1 and (b) 1000 V s−1. Simulation parameters: x1 = 0.29 nm, x2 = 0.59 nm, ε1 = 6, ε2 = 30, εS = 80, E0′ = −0.173 V (vs. Ag/AgCl), pzc = 0 V, k0 = 13.5 cm s−1, α = 0.45,42DRu(III) = 7.5 × 10−6 cm2 s−1 and DRu(II) = 10.4 × 10−6 cm2 s−1, T = 293.15 K. Simulated concentrations of Ru(NH3)63+ (solid) and Ru(NH3)62+ (dashed) at the PET for the electrostatic (red) and diffusion models (black) at (c) ν = 1 and (d) 1000 V s−1. Points (the open diamond/black diamond symbols) are calculated from the analytical expressions for a reversible redox couple, eqn (13) and (14). | ||
When the scan rate is increased to 1000 V s−1 (Fig. 2b), large non-faradaic charging currents and an increased ΔEp (= 220 mV) are visible in the CV based on the electrostatic model.46,47 In contrast, ΔEp for the diffusion model is still only 59 mV, i.e. very close to that expected for a reversible redox couple (Fig. S6, SI 3, ESI† also shows the CV response using the diffusion model for scan rates of 0.1, 1, 10, 100, 1000 V s−1). The origins of the increased ΔEp observed in the CV response based on the electrostatic model are discussed in detail below.
Redox concentrations and electric potential at the PET during the CV scan
Fig. 2c and d show the simulated concentrations of Ru(NH3)63+ (solid lines) and Ru(NH3)62+ (dashed lines) at the PET during the voltammetric cycle for 1 and 1000 V s−1 respectively. For a very fast redox reaction, such as the reduction of Ru(NH3)63+, and in the absence of electrostatic effects, the surface concentrations are governed by the Nernst equation. Eqn (13) and (14) are analytical expressions for the concentrations of Ru(NH3)63+ and Ru(NH3)62+ at the PET under Nernstian (i.e. reversible) conditions,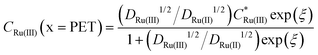 | (13) |
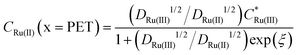 | (14) |
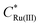 is the initial bulk concentration of the oxidised species. The ratio DRu(III)1/2/DRu(II)1/2 is equal to 0.85, using the values for D previously presented. Derivations of these equations are provided in SI 4, ESI.†
is the initial bulk concentration of the oxidised species. The ratio DRu(III)1/2/DRu(II)1/2 is equal to 0.85, using the values for D previously presented. Derivations of these equations are provided in SI 4, ESI.†
Fig. 2c and d show that at both 1 and 1000 V s−1, the concentrations of Ru(NH3)63+ and Ru(NH3)62+ at the PET, simulated from the diffusion model (black lines) are in excellent agreement with the values computed assuming nernstian behaviour, (black points). For E > E0′, where the equilibrium position of eqn (12) lies far to the left side, the concentration of Ru(NH3)63+ at the PET approaches 1.0 mM and the concentration of Ru(NH3)62+ ∼ 0 mM. Conversely, when E < E0′, the concentration of Ru(NH3)63+ ∼ 0 mM and Ru(NH3)62+ ∼ 0.85 mM, the latter is reflective of the difference in the diffusion coefficients for Ru(NH3)63+ and Ru(NH3)62+, as noted above.
The simulated values for the local concentrations of Ru(NH3)63+ and Ru(NH3)62+ at the PET, computed using the electrostatic model (red lines Fig. 2c and d), are very different to those obtained using the diffusion model, regardless of scan rate. For E > E0′ and E > pzc (= 0 V), the concentration of Ru(NH3)63+ is less than 1.0 mM, due to electrostatic repulsion between the positively charged electrode and positively charged redox species. The concentration of Ru(NH3)63+ increases as E is scanned in the negative direction past the pzc, before rapidly decreasing again at E < E0′ due to conversion to Ru(NH3)62+. In this region, the concentration of Ru(NH3)62+ rises steeply reaching a value of ∼8.4 mM at −0.5 V (Fig. 2c), well above the concentration of 0.85 mM predicted by the diffusion model. This increase is due to the electrostatic attraction of Ru(NH3)62+ to the negatively charged electrode.
We note that the concentrations of both redox species at the PET plotted as a function of E in Fig. 2c for the electrostatic model at 1 V s−1 correspond to both the forward and reverse scans of the voltammogram. That is, at 1 V s−1, no observable hysteresis (within the width of the line) is seen between the forward or reverse scans, indicating that the EDL structure reorganizes fast on time scales corresponding to ν = 1 V s−1. This finding is consistent with the CV having a characteristic nernstian-like shape with a peak splitting of 60 mV, Fig. 2a. However, the concentrations of Ru(NH3)63+ and Ru(NH3)62+ at the PET (Fig. 2c) deviate very sharply from nernstian values. This apparent paradox in the behaviour of the electrostatic model is addressed in detail below.
At 1000 V s−1 (Fig. 2d) the electrostatic model (red) shows a significant hysteresis between the forward and reverse scan directions. The hysteresis at 1000 V s−1 can be understood by considering how ϕ varies as a function of E and x. ϕM − ϕPETvs. E plots at 1 V s−1 in the absence and presence Ru(NH3)63+ are shown in Fig. 3a and b, respectively and at 1000 V s−1 in Fig. 3d and e respectively. The corresponding voltammograms are presented in Fig. 2a and b.
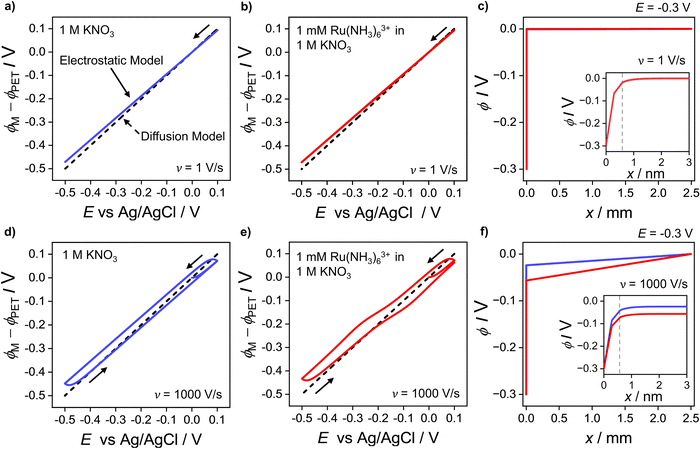 | ||
| Fig. 3 Plot of the simulated potential drop across the compact layer ϕM − ϕPET at (a–c) 1 V s−1 and (d–f) 1000 V s−1. The blue solid curves in (a and d) correspond to ϕM − ϕPET in the absence of the redox species in the 1.0 M KNO3 solution. The red solid curves in (b and e) correspond to ϕM − ϕPET in the presence of 1.0 mM Ru(NH3)63+ and 1.0 M KNO3. The diffusion model response (dashed line), i.e. ϕPET = 0 V is also shown on each plot. Simulated electric potential distributions across the entire cell, i.e. ϕ vs. x, at E = −0.3 V, in the presence (red) and absence (blue) of Ru(NH3)63+ during the negative-going voltammetric scan at 1 V s−1 and 1000 V s−1 are shown in (c and f), respectively. Note that the blue and red lines in (c) are indistinguishable from each other and thus only the red line is apparent. The inset shows ϕ vs. x within 3 nm of the electrode, including inside the compact double layer, 0 < x < x2. The location of the PET at x2 is given by the vertical dashed grey line. All other parameters are as listed in the caption of Fig. 2. | ||
In Fig. 3a, b, d and e for the diffusion model, the plot of ϕM − ϕPETvs. E is a straight line (black dashed line), with unity slope, which is independent of scan rate or the presence/absence of the redox species. This indicates that for all applied electrode potentials, E = ϕM − ϕPET, which is a consequence of setting ϕ = 0 V throughout the electrolyte in this model. For the electrostatic model at 1 V s−1 (Fig. 3a and b), no hysteresis is observed (within the width of the line) between the forward and reverse scans. The diffusion and electrostatic model lines cross at the pzc (E = 0 V), with ϕM − ϕPETvs. E (electrostatic) having a gradient slightly less than 1 in both the absence (Fig. 3a, blue line) and presence of the redox reaction (Fig. 3b, red line). The separation between the diffusion and electrostatic model lines is indicative of a small non-negligible electrical potential difference, ϕPET − ϕL. This term includes contributions from both the potential drop in the EDL beyond x2 and the ohmic potential drop, i.e. the linear potential drop from just outside of the EDL to the reference electrode (ϕL). The electric potential distributions across the entire cell (from working to reference electrode over a distance of 2.5 mm), at E = −0.3 V (1 V s−1), are shown in Fig. 3c, computed in the presence and absence of Ru(NH3)63+. They are essentially identical (within the width of the lines). The inset of Fig. 3c shows the electric potential distribution profile across the EDL, i.e. the first 3 nm of the electrode–electrolyte interface. From x = 3 nm to x = L, the potential decreases from ∼3 mV to 0 mV. It is this small ohmic potential drop which is the cause of the very slight ΔEp increase from 56 (diffusion) to 60 mV (electrostatic model) for the CV in Fig. 2a.
In contrast, ϕM − ϕPETvs. E for the electrostatic model at 1000 V s−1, which is shown in Fig. 3d and e, displays a large hysteresis between the forward and reverse scans and a shape that is dependent on whether Ru(NH3)63+ is present (red line, Fig. 3e) or absent (blue line, Fig. 3d). The hysteresis in both cases indicates that ions do not move quickly enough to re-establish the EDL structure on the time scale corresponding to 1000 V s−1. When Ru(NH3)63+ is present in solution, the plot of ϕM − ϕPETvs. E is nonlinear near E0′ (Fig. 3e), which is a consequence of the ohmic potential drop reducing the driving force for both the reduction of Ru(NH3)63+ (where ϕM − ϕPET < E0′) and oxidation of Ru(NH3)62+ (where ϕM − ϕPET > E0′). The nonlinearity is most apparent at potentials where the faradaic current (and thus iRu) is most rapidly changing. The ohmic potential drop significantly contributes to the large ΔEp (= 220 mV) observed at 1000 V s−1 (Fig. 2c). The impact of the non-faradaic current on ΔEp is discussed in more detail below. If left unaccounted for, this large ΔEp could be incorrectly attributed to sluggish electron-transfer kinetics.
The ohmic potential drop at 1000 V s−1 can be observed more clearly in Fig. 3f, where ϕ is plotted across the entire 2.5 mm wide cell at E = −0.3 V on the negative-going scan, in the presence (red line) and absence (blue line) of the redox couple. The inset of Fig. 3f shows the electric potential distribution profile across the EDL, i.e. the first 3 nm of the electrode–electrolyte interface. There is a clear linear drop in the potential across the solution from just outside of the EDL to the reference electrode, of 24 mV or 57 mV, in the absence or presence of the redox couple, respectively. The higher currents in the presence of the redox couple result in a concurrent larger reduction in ϕM − ϕPET, due to the increasing ϕPET − ϕL contribution. Note, increasing the width of the cell in the simulation would result in a larger Ru and thus a larger reduction in ϕM − ϕPET.
Effect of supporting electrolyte charge
The simulations presented above correspond to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte. However, the model can easily be adapted to consider other electrolytes such as Na2SO4, a 1
1 electrolyte. However, the model can easily be adapted to consider other electrolytes such as Na2SO4, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 electrolyte, as shown in Fig. 4, which compares the simulated voltammetric response of 1.0 mM Ru(NH3)63+ in 1.0 M of a 1
2 electrolyte, as shown in Fig. 4, which compares the simulated voltammetric response of 1.0 mM Ru(NH3)63+ in 1.0 M of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (black) or 1
1 (black) or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (blue) supporting electrolyte, at 1000 V s−1. Fig. 4a shows that the use of a 1
2 (blue) supporting electrolyte, at 1000 V s−1. Fig. 4a shows that the use of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 electrolyte results in a decrease in ΔEp from 220 mV to 120 mV, due to the higher solution conductivity and thus lower ohmic potential drop. Simulations also predict a reduction in the width of the EDL when using the 1
2 electrolyte results in a decrease in ΔEp from 220 mV to 120 mV, due to the higher solution conductivity and thus lower ohmic potential drop. Simulations also predict a reduction in the width of the EDL when using the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 electrolyte, consistent with the Debye length being smaller due to use of a more highly charged electrolyte. Differences in supporting electrolyte charge also lead to variations in the concentrations of redox species at the PET, as shown in Fig. 4b. These differences are seen most clearly for the Ru(NH3)62+ species at the high negative overpotentials, where a lower (but still enhanced) concentration of Ru(NH3)62+ is seen for the 1
2 electrolyte, consistent with the Debye length being smaller due to use of a more highly charged electrolyte. Differences in supporting electrolyte charge also lead to variations in the concentrations of redox species at the PET, as shown in Fig. 4b. These differences are seen most clearly for the Ru(NH3)62+ species at the high negative overpotentials, where a lower (but still enhanced) concentration of Ru(NH3)62+ is seen for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 electrolyte compared to 1
2 electrolyte compared to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This is a consequence of the 1
1. This is a consequence of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 electrolyte more effectively screening the charge on the electrode.
2 electrolyte more effectively screening the charge on the electrode.
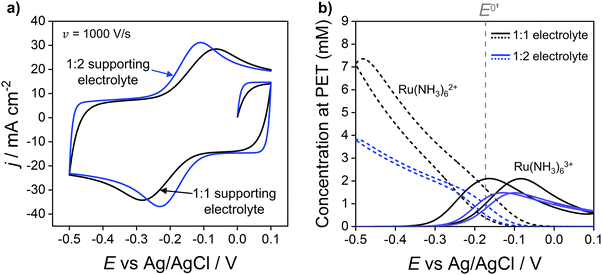 | ||
Fig. 4 (a) Simulated voltammetric response of 1.0 mM Ru(NH3)63+ in 1.0 M of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (black) or 1 1 (black) or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio (blue) supporting electrolyte. The influence of electrostatics is included, and the scan rate is 1000 V s−1. (b) Corresponding simulated concentrations of Ru(NH3)63+(solid) and Ru(NH3)62+ (dashed) at the PET. The diffusion coefficients of the 1 2 ratio (blue) supporting electrolyte. The influence of electrostatics is included, and the scan rate is 1000 V s−1. (b) Corresponding simulated concentrations of Ru(NH3)63+(solid) and Ru(NH3)62+ (dashed) at the PET. The diffusion coefficients of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 supporting electrolyte are set equal to those used for KNO3, i.e., D+ = DK+ = 2.0 × 10−5 cm−2 s−1 and D2− = DNO3− = 1.9 × 10−5 cm−2 s−1, to allow comparison of the effect of electrolyte charge. All other parameters are as listed in the caption to Fig. 2. 2 supporting electrolyte are set equal to those used for KNO3, i.e., D+ = DK+ = 2.0 × 10−5 cm−2 s−1 and D2− = DNO3− = 1.9 × 10−5 cm−2 s−1, to allow comparison of the effect of electrolyte charge. All other parameters are as listed in the caption to Fig. 2. | ||
Contributions of jF and jC to ΔEp
In the previous sections, we demonstrated that the driving force for electron transfer, ϕM − ϕPET in the CV experiment has a dependence on scan rate and solution resistance (Ru). We now consider in more detail the effect of the interdependence of the faradaic and non-faradaic currents on the CV response at 1000 V s−1, where the differences between the diffusion and electrostatic models are greatest. Fig. 5a shows the faradaic (jF) and non-faradaic (jC) components of the total CV response (jT) based on the electrostatic model. Note, while jT cannot be separated into the faradaic and charging currents in a real experiment, this is readily performed in the simulations based on eqn (9) and (10).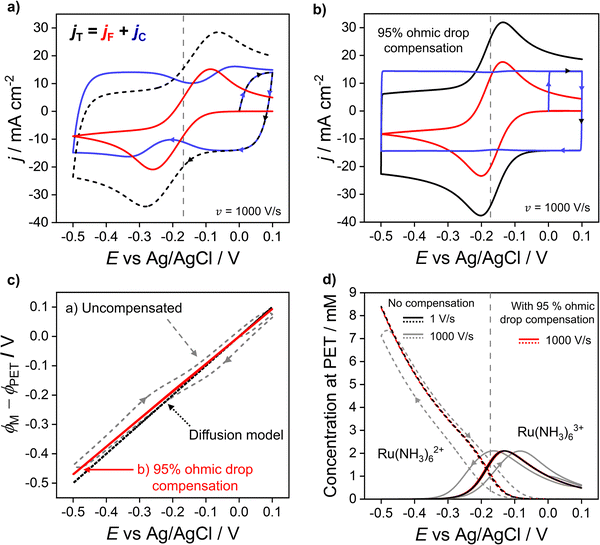 | ||
| Fig. 5 Simulated voltammetric response at 1000 V s−1 (a) without and (b) with ohmic drop compensation. The faradic (red) and non-faradaic (blue) contributions to the total current density (black) during voltammetry of 1.0 mM Ru(NH3)63+ in 1.0 M KNO3 are shown. (c) Driving force for electron transfer for the uncompensated (grey dashed) and 95% compensated (red solid) CVs, and the diffusion model (black dotted). (d) Simulated concentrations of Ru(NH3)62+ (dashed) and Ru(NH3)63+ (solid) at the PET for the uncompensated response at 1 V s−1 (black) and 1000 V s−1 (grey) alongside the 95% compensated response (red) at 1000 V s−1. Ru = 53 Ω assuming A = 0.0314 cm2 and all other parameters as listed in Fig. 2. | ||
In Fig. 5a, ΔEp based solely on jF (solid red curve) is 174 mV, which is ∼50 mV smaller than the observed ΔEp of 220 mV based on the total CV response (jT, dashed curve). The origin of this difference is due to the variation in jC with E (solid blue curve), which displays minima just prior to potentials corresponding to the peak jF currents in the negative and positive scan directions. This can be understood by considering eqn (10) and Gauss's law, eqn (11), which relate jC to the rate of change of electric potential gradient at the electrode surface, ∂[(ϕM − ϕx1)/x1]/∂t. As a faradaic process changes the overall EDL structure, this results in the potential gradient at the electrode surface also changing. In particular, as the faradaic current rises steeply with time, prior to the voltammetric peak, the large ohmic potential drop at 1000 V s−1 (vide supra, Fig. 3f) results in a decreasing proportion of the applied potential contributing to the potential gradient in the compact layer (ϕM − ϕx1)/x1, i.e. the surface charge changes more slowly, which causes the corresponding dip in jC.
In Fig. S7a, SI 5, ESI,† simulations of the CV response without the faradaic reaction, i.e. jC, are shown at scan rates between 0.1 and 1000 V s−1 in 1.0 M KNO3. As seen in Fig. S7a (ESI†), the CV responses are featureless with no potential dependent characteristics. These results and those shown in Fig. 5 showcase the interdependence of jC and jF and reinforce the conclusion that the total CV response cannot be accurately understood without consideration of how the faradaic and non-faradaic responses are intrinsically linked.
Simulation of solution ohmic potential compensation
Experimentally, ohmic potential drop can be compensated using a positive feedback circuit in the potentiostat.41,48 The uncompensated resistance of the solution between the working and reference electrodes is typically measured at a potential where no redox process is occurring, using techniques such as small amplitude impedance.49 That resistance is then multiplied by the voltammetric current to obtain the ohmic potential drop during the CV scan. Most often, Ru is assumed to be constant and the value of iRu is added to the instantaneous applied potential (E + iRu) to reduce the ohmic potential drop.49 Here, we simulate the experimental ohmic potential drop compensation technique. Full details of the implementation are in SI 6, ESI.†In keeping with the experimental protocol, the solution resistance was determined with the solution in its initial state (at E = 0 V, no diffuse layer formed). This was calculated analytically as Ru = L/γA assuming a bulk conductivity, γ, throughout the bulk domain, see eqn (S29) and (S30) (ESI†) for calculation. For A = 0.0314 cm2, L = 2.5 mm, and a 1.0 M KNO3 solution, this gives Ru = 53 Ω. A fraction, f, of iRu is fed back into the potentiostat control loop (described in detail in Section SI 6, ESI†) so that a corrected potential is applied to the working electrode. The positive feedback mechanism in both the experiment and the simulation cannot correct for more than ∼95% (f = 0.95) of the ohmic potential drop without causing instabilities in the circuit.16 Instabilities arise due to a lag in the time between the current measurement and compensation components and manifests as a ringing/oscillating after the switching potential. Ringing due to overcompensation is seen both in experiments and our simulations (see SI 6, Fig. S9c, ESI,†) when >95% compensation is used.50
The total (black), faradaic (red), and non-faradaic (blue) current responses for 95% ohmic potential drop compensated CVs are presented in Fig. 5b (parameters as Fig. 4a) for the 1000 V s−1 CV. Ohmic potential drop compensation results in ΔEp for the faradaic and total current responses decreasing dramatically to 64 and 67 mV, respectively. The decreased ΔEp is, however, still slightly greater than the 59 mV predicted in the diffusion model. Hence care should still be taken if attempting to extract kinetic information. Ohmic potential drop compensation also results in the dip in the non-faradaic current (blue) being dramatically reduced.
The effect of ohmic potential drop compensation on the interfacial potential ϕM − ϕPETvs. E values is shown in Fig. 5c. Compensation leads to the electric potential difference applied between the electrode and PET (ϕM − ϕPET) being close to the full driving force and matching that observed at 1 V s−1 (also shown in Fig. 3b) where there is minimal ohmic potential drop. Moreover, the interfacial potential changes almost linearly with E (contrasting with the uncompensated data). This causes the EDL capacitor to charge at a uniform rate during potential cycling, leading to the elimination of dips in jC. The concentration of Ru(NH3)63+/2+ at the PET is shown in Fig. 5d. At 1000 V s−1, ohmic potential drop compensation has led to hysteresis between the forward and reverse scans being significantly reduced. The surface concentrations at 1000 V s−1 with ohmic potential drop compensation also closely follow those at 1 V s−1 without correction (Fig. 2c, reproduced as black lines in Fig. 5d), further confirming ohmic potential drop as being responsible for the hysteresis observed.
Effect of charge of Oz and Rz−1
We now address how the magnitude and sign of the charge of the redox species (z and z − 1 for the oxidised and reduced forms, respectively) affects the voltammetric response. In Fig. 6, simulations based on the electrostatic model of the Ru(NH3)63+/2+ couple (black) are compared against redox couples with charges equal to 1+/0 (red), 0/1− (blue) and 2−/3− (green). Experimentally these could be couples such ferrocenemethanol (FcMeOH+/0), ferrocenecarboxylic acid (FcCOOH0/−) and hexachloroiridate (IrCl62−/3−) respectively. While these couples all have different physical parameters, e.g. E0′, Di, k0 compared to the Ru(NH3)63+/2+ systems,13 the same parameters listed for Fig. 2a are used for all redox couples in order to examine the effect of charge. The CVs are shown in Fig. 6a and the corresponding concentrations of each redox couple at the PET are shown in Fig. 6b.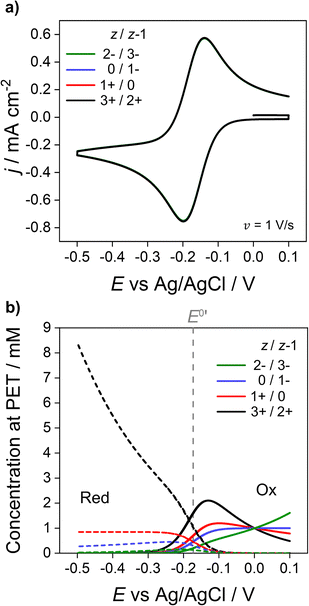 | ||
| Fig. 6 Simulated (a) voltammetric response of 1e redox couples of different charge z/z − 1 (= 3+/2+ (black), 1+/0 (red), 0/1− (blue), 2−/3− (green)) and (b) concentration at the PET of the oxidised (solid) and reduced (dotted) forms of the redox couple. All other parameters are listed in Fig. 2. | ||
As shown in Fig. 6a, CV responses at 1 V s−1 are independent of the charge of the redox species. In each case, the response has essentially the same shape as the diffusion model (nernstian) indicating that the ohmic potential drop is small. In contrast, the surface concentrations at the PET are strongly dependent on the magnitude and sign of the charge of the redox species. For example, for z = 0 (red dotted line), the concentration of the reduced species (dotted lines) remains constant at the nernstian value of 0.85 mM given by eqn (14). When the reduced species is an anion (1− or 3− charge, blue and green lines respectively), its concentration is decreased well below 0.85 mM at E < E0′, a consequence of electrostatic repulsion between the anion and negatively charged electrode.
Effect of electron-transfer kinetics
Throughout the previous sections, we have considered redox systems defined by very fast electron-transfer kinetics (k0 = 13.5 cm s−1).13 We now consider how the inclusion of electrostatics affects the CV behaviour of quasi-reversible systems defined by much smaller k0 values, eqn (6) and (7), Butler–Volmer kinetic equations. In Fig. 7, k0 is reduced by ∼3 orders of magnitude to 0.01 cm s−1 with z/z − 1 varied as per the previous section. Even at the moderate scan rate of 1 V s−1 (Fig. 7), ΔEp of the voltammetric response shows a dependence on the charge identity of the different redox ion pairs, which is not observed in Fig. 6a for very fast kinetics k0 = 13.5 cm s−1. The CV of the negatively charged redox couple 2−/3− (green line) is most influenced, having a ΔEp of 228 mV versus 87 mV for the 3+/2+ ion couple (black line) and exhibiting a pronounced asymmetric waveshape. In contrast, ΔEp for the diffusion model (dashed line), which is independent of the redox species charge, is 128 mV, compared to 56 mV when k0 = 13.5 cm s−1. Interestingly, the 3+/2+ ion couple (black) simulated using the electrostatic model has a smaller ΔEp than that predicted by the diffusion model. Experimentally, this decreased ΔEp would lead to an overestimation of the electron-transfer rate constant using kinetic methods based on ΔEp values.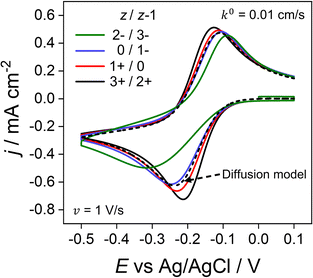 | ||
| Fig. 7 Simulated voltammetric response for O/R redox couples with varying charges and quasi-reversible electron-transfer kinetics. The electron transfer rate constant of k0 = 0.01 cm s−1 used in this simulation is smaller than the value of 13.5 cm s−1 used elsewhere in this work. Charges (z/z − 1) include the redox couple used throughout this work 3+/2+ (black) in addition to 1+/0 (red), 0/1− (blue) and 2−/3− (green) at 1 V s−1. All other parameters are as listed in the caption to Fig. 2. | ||
The disparity in the results between the two models can be understood by considering eqn (5), which describes the flux (Ji) of O/R to/from the electrode surface, i.e. the rate of the electron-transfer reaction, as a function of the concentrations of the redox species at the PET and rate constants for electron transfer (kf and kb). For large k0, Fig. 6b shows that the concentrations of O/R at the PET are non-nernstian. However, here the current is limited by transport and the concentrations of O/R at the PET have no impact on CV waveshape (Fig. 6a and vide infra). In contrast, for a quasi-reversible electron transfer system, the current is partially determined by heterogeneous electron-transfer kinetics, and the concentrations of O/R at the PET now play a role.
The simulations presented in Fig. 7 assume a pzc located at E = 0 V and E0′ = −0.173 V (vs. Ag/AgCl). Thus, the electrode is always negatively charged in the potential range where the faradaic response appears (approx. 0.0 to −0.5 V). In the case of the 2 +/3+ system, the concentration of O and R at the PET are higher than that predicted using the diffusion model due to the electrostatic attraction of these cations to the electrode. This results in slightly higher currents and a smaller ΔEp relative to the CV in the absence of electrostatic effects. Conversely, O and R for the 2−/3− redox system are both repelled from the electrode, resulting in slightly lower currents and a larger ΔEp. Clearly, without consideration of the electrostatic effects, the analysis of the CV response for quasi-reversible reactions at moderate scan rates leads to significant underestimation or overestimation of k0, depending on the charge of the redox species and the value of E0′ relative to the pzc.
Comparison to experiment
We now compare the simulations from the electrostatic model with experimental CV data for the 1e reduction of Ru(NH3)63+ (eqn (12)). Experimental CVs were obtained using a polycrystalline Au macroscale (diameter = 2 mm) disk electrode in a solution containing 1.0 mM Ru(NH3)63+ and 1.0 M KNO3 at scan rates of 0.1 to 1000 V s−1, Fig. 8. Neither the experimental nor simulated CVs are compensated for ohmic potential drop. When increasing the scan rate from 0.1 V s−1 to 1000 V s−1, the experimental ΔEp increases from 60 to 210 mV (black line). The red line data shows the corresponding electrostatic simulations for the different scan rates. The diffusion model CVs (Fig. S6 in SI 3, ESI†) only show an increase in ΔEp from 56 to 59 mV. Thus, the large ΔEp observed in the experiment is not due to slow heterogeneous kinetics but is associated with ohmic potential drop in solution and the non-constant non-faradaic current (jC) as discussed in the context of Fig. 5.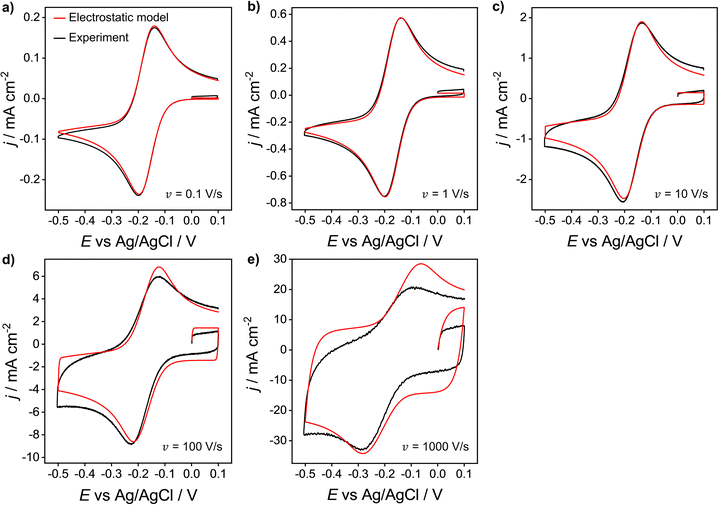 | ||
| Fig. 8 Experimental (black) and simulated (red) voltammetric response of 1.0 mM Ru(NH3)63+ at a Au 2 mm planar disk electrode for scan rates: (a) 0.1, (b) 1, (c) 10, (d) 100 and (e) 1000 V s−1. Supporting electrolyte: 1.0 M KNO3. All other parameters are as listed in the caption of Fig. 2. | ||
It is clear that the electrostatic model is considerably better at simulating the experimental data. The agreement between simulated and experimental CVs becomes significantly poorer for scan rates above 100 V s−1, where charging currents become more dominant. Specifically, the simulation overestimates the capacitive current of the experimental CV in the non-faradaic regions (i.e. 0.0 to 0.1 V) and predicts higher anodic currents. This finding could suggest that the interfacial structure is more complex than the EDL model assumed in our simulations, Fig. 1.
The simulated charging currents in the absence of the redox couple (see ESI†, Fig. S7a) correspond to a background capacitance of ∼14.2 μF cm−2 (at E = 0.1 V), consistent with the range of typical values (10 to 20 μF cm−2) reported in the literature for Au electrodes.51–53 Interestingly, the experimental responses (recorded in 1.0 M KNO3) show a marked decrease in capacitance (calculated using the geometric area) with an increase in scan rate (see Fig. S7b, ESI†). This contrasts with the model (Fig. S7a, ESI†), which predicts a scan rate-independent response at potentials away from the switching potentials. The experimental data suggests a non-perfect Kel-F® insulator to electrode seal on the Au electrode, allowing electrolyte ions to leak into the very thin gap and contact with the sidewalls of the electrode. As the gap region is narrow and very resistive, larger ohmic potential drops are expected in this region at higher scan rates, thereby reducing charging of the electrode sidewall and the observed capacitance.
Why does the EDL have no effect on the CV response of reversible redox couples?
Fig. 2a and 6a show examples of CV responses that have a nernstian-like shape at 1 V s−1, despite the finding that the concentrations of Oz and Rz−1 at the PET (Fig. 2b and 6b) are very different from values predicted by the Nernst equation. This result is surprising, as the analytical description of the nernstian voltammetric waveshape explicitly assumes that the redox surface concentrations are governed by the Nernst equation.13These conflicting results can be readily understood by first noting that, for a nernstian response, equilibrium at the electrode surface can be expressed in terms of the electrochemical potentials of O, R, and the electrons in the metal. Assuming a reversible 1e redox reaction,
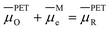 | (15) |
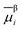 of species i in phase β is defined in terms of the standard chemical potential of i, μ0,βi, the activity of i, aβi, and the electric potential, ϕβ.
of species i in phase β is defined in terms of the standard chemical potential of i, μ0,βi, the activity of i, aβi, and the electric potential, ϕβ.![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) βi = μ0,βi + RT βi = μ0,βi + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aβi + ziFϕβ aβi + ziFϕβ | (16) |
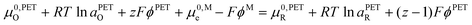 | (17) |
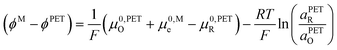 | (18) |
This surprising conclusion can be reconciled by noting that at slow to moderate scan rates, O and R at the PET are in equilibrium with O and R in solution just outside of the EDL (e.g. 10 times the inverse Debye length (κ−1) = 3 nm in 1.0 M KNO3 solution, a position indicated in the equations below by the symbol “S”). This equilibrium condition is stated by eqn (19) and (20).
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) PETO = PETO = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) SO SO | (19) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) PETR = PETR = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) SR SR | (20) |
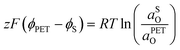 | (21) |
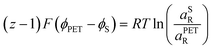 | (22) |
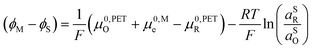 | (23) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 0,PETO/R =
0,PETO/R = ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) 0,SO/R we can rewrite eqn (23) as (24)
0,SO/R we can rewrite eqn (23) as (24)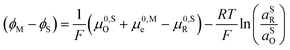 | (24) |
Fig. 9 shows the simulated spatial distributions of Ru(NH3)63+ and Ru(NH3)62+ plotted on scales of 0 to 100 μm (Fig. 9a) and 0 to 3 nm from the electrode surface (Fig. 9b) during a CV at 1 V s−1. The profiles were computed at E = −0.5 V on the cathodic scan (significantly more negative than the E0′ of −0.173 V) in a solution containing 1.0 mM Ru(NH3)63+ and 1.0 M KNO3. These conditions correspond to those in Fig. 2a and c, which show the CV response and concentrations of Ru(NH3)63+ and Ru(NH3)62+ at the PET. Additional plots showing the concentration distributions at different potentials throughout the voltammetric scan are shown in Fig. S10, SI 7, ESI.†
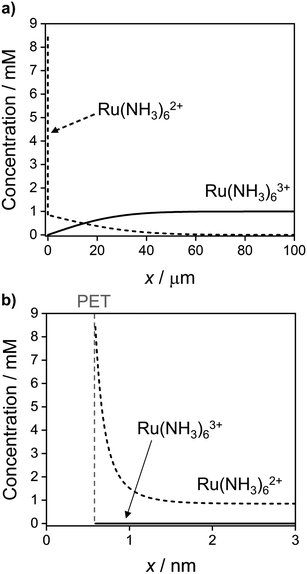 | ||
| Fig. 9 Simulated concentration distribution across the solution of Ru(NH3)63+ (solid) and Ru(NH3)62+ (dashed) redox species at E = −0.5 V on the cathodic sweep at 1 V s−1 on the (a) ∼ μm length scale of the diffuse layer and (b) ∼ nm length scale of the EDL. All other parameters are as listed in the caption to Fig. 2. See Fig. S10, SI 7, ESI† for further examples taken at other potentials during the voltammetric sweep. | ||
In Fig. 9a, the concentration profiles show that at −0.5 V, Ru(NH3)63+ is depleted and Ru(NH3)62+ is generated in the solution over a distance of ∼40 μm from the electrode surface. For a nernstian response, the concentration of Ru(NH3)63+ at the PET should approach zero, while that for Ru(NH3)62+ is equal to 0.85 mM (Fig. 2b, diffusion model). We find that the concentration of Ru(NH3)62+ is indeed 0.85 mM at x = 3 nm, Fig. 9b, but increases sharply to 8.4 mM at the PET, due to electrostatic attractions between Ru(NH3)62+ and the negatively charged electrode.
We note that if an equilibrium exists between O/R at the PET and at a distance of 3 nm from the PET, the concentrations of Ru(NH3)62+ at these two points can be related using the Boltzmann equation, expressed as:
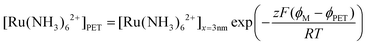 | (25) |
Equilibrium between the redox couple at the PET and just outside of the EDL (x = 3 nm) is maintained by the transport of O and R between these two regions, which can be estimated to occur on a time scale, Δt = (Δx2/2D) where Δx is the width of the EDL. Taking D = 10−5 cm2 s−1 and Δx = 3 nm (3 × 10−7 cm), yields Δt = 4.5 × 10−9 s. Thus, for a fast electron-transfer redox couple, equilibrium between the electrode and solution is maintained for scan rates below ν ∼ RT/FΔt ∼ 5.6 MV s−1. In general, non-nernstian behaviour (ΔEp > ∼56 mV) is observed at much lower scan rates due to uncompensated ohmic potential drop and a potential-dependent capacitive current, as indicated in the results shown throughout this paper. However, using a high level of resistance compensation, reversible CVs for the oxidation of anthracene at 2 MV s−1 have been reported.50,54 Our simulations suggest that such high scan rates are near the theoretical upper limit of where EDL effects on the response of iRu compensated CVs can be ignored for reversible electron-transfer redox reactions.
Conclusions
A general electrostatic finite-element model has been developed to simulate the interplay between ohmic potential drop, ion migration and the EDL on the CV response for a 1e outer-sphere redox process, under both reversible and kinetically controlled electron transfer. The simulation model is based on a complete and rigorous description of ion/molecule transport and electrostatics within the entire electrochemical cell, allowing simultaneous calculation of both the faradaic and non-faradaic currents at a planar electrode. Simulations of the CV response for Ru(NH3)63+ reduction are found to be in good agreement with experimental results. The model can be readily adapted for other electrode geometries and redox reactions and allows modifications to the assumed structure of the compact region of the EDL.Surprisingly, in the case of reversible electron-transfer kinetics, the simulations predict that the concentrations of redox species at the PET are influenced by the EDL structure and are thus dependent upon the charge of the redox species. However, the concentrations at the PET have no effect on the CV response for a reversible redox system when equilibrium between O and R at the PET and just outside of the EDL is established by rapid transport. In contrast, under conditions of quasi-reversible kinetics (small k0 or fast scan rates), the concentrations of redox species at the PET play an important role in determining the CV waveshape, which is shown to depend on the charge on the ion and E0′ relative to the pzc. Without consideration of such electrostatic effects, the analysis of the CV response would lead to significant underestimation/overestimation of k0.
Data availability
All raw data used in the preparation of this manuscript can be found at https://wrap.warwick.ac.uk/171860.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge the Centre for Doctoral Training in Diamond Science and Technology (EP/L015315/1) for funding for KJL. JVM acknowledges support from the Engineered Diamond Technologies Prosperity Partnership (EP/V056778/1). Work at the University of Utah was supported by the Office of Naval Research (award N00014-22-1-2425). MAE acknowledges support by the Australian Research Council Discovery Grant DP210102698.References
- C. P. Smith and H. S. White, Anal. Chem., 1993, 65, 3343–3353 CrossRef CAS.
- R. He, S. Chen, F. Yang and B. Wu, J. Phys. Chem. B, 2006, 110, 3262–3270 CrossRef CAS PubMed.
- S. Yu, L. Yuwen, L. Zhixiu, X. Lu, W. Aili and C. Shengli, J. Phys. Chem. C, 2009, 113, 9878–9883 CrossRef.
- J. D. Norton, H. S. White and S. W. Feldberg, J. Phys. Chem., 1990, 94, 6772–6780 CrossRef CAS.
- J. J. Watkins, J. Chen, H. S. White, H. D. Abruña, E. Maisonhaute and C. Amatore, Anal. Chem., 2003, 75, 3962–3971 CrossRef CAS PubMed.
- C. Amatore, M. R. Deakin and R. M. Wightman, J. Electroanal. Chem. Interfacial Electrochem., 1987, 225, 49–63 CrossRef CAS.
- C. Amatore, B. Fosset, J. Bartelt, M. R. Deakin and R. M. Wightman, J. Electroanal. Chem. Interfacial Electrochem., 1988, 256, 255–268 CrossRef CAS.
- C. Amatore and C. Lefrou, J. Electroanal. Chem. Interfacial Electrochem., 1990, 296, 335–358 CrossRef CAS.
- C. P. Andrieux, P. Hapiot and J. M. Savéant, J. Phys. Chem., 1988, 92, 5987–5992 CrossRef CAS.
- B. D. Pendley, H. D. Abruña, J. D. Norton, W. E. Benson and H. S. White, Anal. Chem., 1991, 63, 2766–2771 CrossRef CAS.
- I. Streeter and R. G. Compton, J. Phys. Chem. C, 2008, 112, 13716–13728 CrossRef CAS.
- E. J. F. Dickinson, J. G. Limon-Petersen, N. V. Rees and R. G. Compton, J. Phys. Chem. C, 2009, 113, 11157–11171 CrossRef CAS.
- A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical Methods: Fundamentals and Applications, Wiley, 3rd edn, 2022 Search PubMed.
- A. Frumkin, Z. Phys. Chem., 1933, 164A, 121–133 CrossRef.
- C. P. Andrieux, D. Garreau, P. Hapiot, J. Pinson and J. M. Savéant, J. Electroanal. Chem. Interfacial Electrochem., 1988, 243, 321–335 CrossRef CAS.
- C. Amatore, C. Lefrou and F. Pflüger, J. Electroanal. Chem., 1989, 270, 43–59 CrossRef CAS.
- C. Amatore, A. Oleinick and I. Svir, Anal. Chem., 2008, 80, 7957–7963 CrossRef CAS PubMed.
- G. Wosiak, D. Coelho, E. B. Carneiro-Neto, E. C. Pereira and M. C. Lopes, Anal. Chem., 2020, 92, 15412–15419 CrossRef CAS PubMed.
- Y. Liu, R. He, Q. Zhang and S. Chen, J. Phys. Chem. C, 2010, 114, 10812–10822 CrossRef CAS.
- J. J. Watkins and H. S. White, Langmuir, 2004, 20, 5474–5483 CrossRef CAS PubMed.
- L. Fan, Y. Liu, J. Xiong, H. S. White and S. Chen, ACS Nano, 2014, 8, 10426–10436 CrossRef CAS PubMed.
- H. S. White and K. McKelvey, Curr. Opin. Electrochem., 2018, 7, 48–53 CrossRef CAS.
- C. Ma, W. Xu, W. R. A. Wichert and P. W. Bohn, ACS Nano, 2016, 10, 3658–3664 CrossRef CAS PubMed.
- S. R. Kwon, K. Fu, D. Han and P. W. Bohn, ACS Nano, 2018, 12, 12923–12931 CrossRef CAS PubMed.
- H. Wang and L. Pilon, Electrochim. Acta, 2012, 64, 130–139 CrossRef CAS.
- H. Wang, A. Thiele and L. Pilon, J. Phys. Chem. C, 2013, 117, 18286–18297 CrossRef CAS.
- J. O. Bockris, M. A. V. Devanathan and K. Müller, Proc. R. Soc. London Ser. A: Math. Phys. Sci., 1963, 274, 55–79 CrossRef CAS.
- W. R. Fawcett, J. Electroanal. Chem., 2001, 500, 264–269 CrossRef CAS.
- Y. Liu and S. Chen, J. Phys. Chem. C, 2012, 116, 13594–13602 CrossRef CAS.
- C. G. Malmberg and A. A. Maryott, J. Res. Natl. Bur. Stand., 1956, 56, 2641 Search PubMed.
- A. Hamelin, T. Vitanov, E. Sevastyanov and A. Popov, J. Electroanal. Chem. Interfacial Electrochem., 1983, 145, 225–264 CrossRef CAS.
- S. W. Feldberg, J. Electroanal. Chem. Interfacial Electrochem., 1986, 198, 1–18 CrossRef CAS.
- C. P. Smith and H. S. White, Anal. Chem., 1992, 64, 2398–2405 CrossRef CAS PubMed.
- M. Ohtani, Electrochem. Commun., 1999, 1, 488–492 CrossRef CAS.
- R. Vasquez, J. Waelder, Y. Liu, H. Bartels and S. Maldonado, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2202395119 CrossRef CAS PubMed.
- K. J. Levey, M. A. Edwards, H. S. White and J. V. Macpherson, Anal. Chem., 2022, 94, 12673–12682 CrossRef CAS PubMed.
- J. Waelder, R. Vasquez, Y. Liu and S. Maldonado, J. Am. Chem. Soc., 2022, 144, 6410–6419 CrossRef CAS PubMed.
- S. L. Wu, M. E. Orazem, B. Tribollet and V. Vivier, Electrochim. Acta, 2014, 131, 3–12 CrossRef CAS.
- Q. Chen, K. McKelvey, M. A. Edwards and H. S. White, J. Phys. Chem. C, 2016, 120, 17251–17260 CrossRef CAS.
- A. W. Bott, Curr. Sep., 1997, 16, 1 Search PubMed.
- A. W. Colburn, K. J. Levey, D. O’Hare and J. V. Macpherson, Phys. Chem. Chem. Phys., 2021, 23, 8100–8117 RSC.
- J. Velmurugan, P. Sun and M. V. Mirkin, J. Phys. Chem. C, 2008, 113, 459–464 CrossRef.
- Y. Wang, J. G. Limon-Petersen and R. G. Compton, J. Electroanal. Chem., 2011, 652, 13–17 CrossRef CAS.
- CRC handbook of chemistry and physics, ed. R. L. David and T. J. Bruno, CRC Press, 97th edn, 2016 Search PubMed.
- R. S. Nicholson and I. Shain, Anal. Chem., 1964, 36, 706–723 CrossRef CAS.
- D. O. Wipf, E. W. Kristensen, M. R. Deakin and R. M. Wightman, Anal. Chem., 1988, 60, 306–310 CrossRef CAS.
- C. P. Andrieux, D. Garreau, P. Hapiot and J. M. Savéant, J. Electroanal. Chem. Interfacial Electrochem., 1988, 248, 447–450 CrossRef CAS.
- J. C. Imbeaux and J. M. Savéant, J. Electroanal. Chem. Interfacial Electrochem., 1970, 28, 325–338 CrossRef.
- Impedance Spectroscopy, ed. J. R. Macdonald, Wiley, 1987 Search PubMed.
- C. Amatore, E. Maisonhaute and G. Simonneau, J. Electroanal. Chem., 2000, 486, 141–155 CrossRef CAS.
- B. Lindholm-Sethson, Langmuir, 1996, 12, 3305–3314 CrossRef CAS.
- R. P. Janek, W. R. Fawcett and A. Ulman, J. Phys. Chem. B, 1997, 101, 8550–8558 CrossRef CAS.
- S. E. Moulton, J. N. Barisci, A. Bath, R. Stella and G. G. Wallace, Electrochim. Acta, 2004, 49, 4223–4230 CrossRef CAS.
- C. Amatore, Y. Bouret, E. Maisonhaute, H. D. Abruña and J. I. Goldsmith, C. R. Chim., 2003, 6, 99–115 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00098b |
| This journal is © the Owner Societies 2023 |