Open Access Article
Open Access ArticlePolarized coherent emission outside high-symmetry points of dye-coupled plasmonic lattices†
Diego
Piccotti
a,
Mirko
Trevisani
 a,
Giuseppe
Pirruccio
a,
Giuseppe
Pirruccio
 b,
Boris
Kalinic
b,
Boris
Kalinic
 a,
Tiziana
Cesca
a,
Tiziana
Cesca
 *a and
Giovanni
Mattei
*a and
Giovanni
Mattei
 a
a
aUniversity of Padova, Department of Physics and Astronomy, NanoStructures Group, via Marzolo 8, I-35131 Padova, Italy. E-mail: tiziana.cesca@unipd.it
bInstituto de Fisica, Universidad Nacional Autonoma de Mexico, Apartado Postal 20-364, Mexico D.F. 01000, Mexico
First published on 6th March 2023
Abstract
Developing intense, coherent and ultra-fast light sources with nanoscale dimensions is a crucial issue for many applications in nanophotonics. To date, plasmonic nanolasers represent one of the most promising nanophotonic devices capable of this remarkable feature. In the present work we report on the emission properties of two-dimensional Au hexagonal nanodome arrays, fabricated by nanosphere lithography, coupled with a dye liquid solution used as the gain medium. Low-threshold stimulated emission at room temperature is demonstrated by spectral and angle-resolved photoluminescence measurements performed as a function of the pump fluence. The emission arises with narrow angular divergence in off-normal direction, out of high-symmetry points of the plasmonic lattice. The polarization properties of the stimulated emission are investigated, revealing a strong linear polarization character controlled by the polarization orientation of the pumping beam, while the first-order temporal coherence properties are measured by using a tilted-mirrors Michelson interferometer. Finally, by comparing the results obtained for the plasmonic Au nanodomes arrays with those of purely dielectric nanoarrays, the role of the plasmonic modes and the photonic lattice modes in the emission process is highlighted.
1. Introduction
Recent years have seen a tremendous burst of the research activity toward the development of intense, coherent and ultra-fast light sources with nanoscale dimensions, namely nanolasers, to be integrated in optical circuits for a variety of applications in nanophotonics, as all-optical information processing, miniaturized smart display technology, or lab-on-a-chip systems.1,2 Conventional laser sources are constrained, both in terms of optical mode size and physical device dimension, by the diffraction limit that hinders device miniaturization below roughly half the operating wavelength. To date, one of the most promising approaches to overcome this limitation and to address most of the technological challenges (low-threshold lasing, room temperature operation, electrical pumping) is given by plasmonic nanolasers, i.e., nanodevices in which the lasing action is obtained by coupling a gain medium with a plasmonic nanostructure acting as a virtual feedback cavity.3–7 The strong electromagnetic field-enhancement and optical confinement below the diffraction limit provided by the plasmonic nanocavity enable low threshold photon amplification and lasing action, and ultra-fast operation at frequencies up to hundreds of GHz.2,8 Since the introduction of the concept of spaser (surface plasmon amplification by stimulated emission of radiation) by Bergman and Stockman in 20039 and the first experimental demonstrations in 2009,10–12 many efforts have been devoted to design novel plasmonic architectures to make plasmonic nanolasers more and more efficient.13 To this regard, the arrangement of plasmonic nanostructures in ordered periodic arrays offers an important way to engineer the plasmonic cavity modes to control lasing threshold, directionality and emission wavelength and different unit cell designs have been explored.14–21While in the vast majority of the works plasmonic nanoarrays with Bravais squared or rectangular lattices are used as feedback cavities, very recently a great interest arose for studying the extremely rich features of hexagonal arrays.22–26 A relatively simple and cost-effective method to produce hexagonal or honeycomb ordered arrays of nanostructures is by nanosphere lithography (NSL).27 NSL is a scalable, high-throughput technique and it can be employed to realize different typologies of two-dimensional plasmonic nanoarrays with proper optical functionalities for different applications, as biosensing,28 third-order optical nonlinearity and second harmonic generation,29,30 to realize chiral metasurfaces31 or to control the radiative properties of quantum emitters.32 In the present work we studied the stimulated emission properties of dye molecules coupled to gold hexagonal nanodome arrays fabricated by nanosphere lithography. Spectral and angle-resolved photoluminescence measurements have been performed to characterize wavelength, threshold and directionality of the lasing emission, while interferometry has been used to determine the first-order temporal coherence properties. The results are compared with those of purely dielectric nanodome arrays made of silica in order to decouple the role of plasmonic and photonic modes on the emission properties.
2. Material and methods
2.1. Samples nanofabrication
Hexagonal nanodome arrays (HNDA) have been realized by nanosphere lithography (NSL) with the multi-step process schematized in Fig. 1a. As the first step, a monolayer of polystyrene (PS) nanoparticles (by MicroParticles GmbH) of 522 nm diameter is self-assembled on a silica glass substrate forming a close-packed hexagonal array. Subsequently (step 2), a reactive ion etching (RIE) treatment in Ar + O2 atmosphere is performed on the PS nanospheres monolayer to reduce the nanospheres diameter (down to about 330 nm) preserving their ordered arrangement. A silica layer (thickness 200 nm) is deposited by magnetron sputtering (step 3) to obtain a continuous, nanostructured film and a more mechanically stable device. Finally (step 4), a 70 nm-thick Au film is sputtered onto the silica layer to form the plasmonic nanodome array. For comparison, a second set of samples have been fabricated by depositing 70 nm of silica, instead of Au, to form a purely dielectric nanodome array.2.2. Morphological and optical characterization
The morphological properties of the synthesized nanoarrays have been characterized after each fabrication step by scanning electron microscopy (SEM) and atomic force microscopy (AFM) measurements. SEM images have been acquired in plane view and in cross-section using a Zeiss Sigma HD field-emission FE-SEM, working in the range 0.2–30 kV and equipped with the InLens secondary electrons detector. AFM measurements have been taken in non-contact mode with a NT-MDT Solver-PRO AFM microscope.The optical band structure of the synthesized nanoarrays along the high-symmetry directions of the first Brillouin zone, Γ–K and Γ–M, has been measured using a home-built specific set-up (Fig. S1 in the ESI†). The measurements have been performed in transmittance in the wavelength range 400–1100 nm. An optical fiber-coupled deuterium–halogen lamp (Ocean Optics DH-2000-BAL) has been used to illuminate the sample with a spot of about 2 mm in diameter. A linear polarizer has been used to select TE or TM polarization orientation of the incident beam. The sample is mounted on a manual goniometer to adjust the azimuthal angle ϕ with respect to the beam direction in order to align the sample with the high-symmetry directions of the nanoarray lattice. The whole sample-holder is put on a motorized goniometer that controls the tilt angle θ. The transmitted beam is then coupled through an optical fiber to a spectrometer (Ocean Optics HR4000).
2.3. FEM simulations
Finite elements method (FEM) electrodynamic simulations of the near-field and far-field optical properties of the nanodome arrays have been carried out using COMSOL Multiphysics.32,33 The periodic array is modeled by considering the hexagonal unit cell extending in the![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) y plane. The boundary conditions in the direction orthogonal to the array plane are Bloch's boundary conditions, enabling to model inclined excitation of the sample. The incident field is described as a plane wave traveling downwards (towards the substrate) with the k vector forming an angle of θ with respect to the ẑ axis (θ is defined as the angle in vacuum and where the refractive index of the medium is different from 1 the corresponding angle is computed using Snell's law.) In the ẑ direction the substrate and the environment are modeled as semi-infinite with interface at z = 0 and using perfectly matched layers (PML). In each unit cell one nanodome is present. The nanodome is modeled as a cylinder of silica of height h = 50 nm and radius Rin = 145 nm over the substrate (silica glass) and placed in the center of the unit cell. A silica hemisphere with the same radius Rin is placed above the cylinder. On this structure, a conformal layer of gold (or silica) of thickness tAu = 70 nm is present, thus having an external radius, at the base of the nanodome, of Rout = 215 nm. For silica, the refractive index n = 1.45 (κ = 0) was used in the simulations, while for Au it was used the experimental dielectric function obtained by ellipsometric measurements performed with a J. A. Woolham V-VASE spectroscopic ellipsometer on a reference thin film deposited on a silica glass substrate with the same conditions used for the samples. The experimental complex refractive index is shown in Fig. S2 of the ESI.† To reconstruct the dispersion relations of the lattice, both wavelength of the incident light λ (in the range 400–900 nm) and incidence angle θ (0°–40° range) have been varied.
y plane. The boundary conditions in the direction orthogonal to the array plane are Bloch's boundary conditions, enabling to model inclined excitation of the sample. The incident field is described as a plane wave traveling downwards (towards the substrate) with the k vector forming an angle of θ with respect to the ẑ axis (θ is defined as the angle in vacuum and where the refractive index of the medium is different from 1 the corresponding angle is computed using Snell's law.) In the ẑ direction the substrate and the environment are modeled as semi-infinite with interface at z = 0 and using perfectly matched layers (PML). In each unit cell one nanodome is present. The nanodome is modeled as a cylinder of silica of height h = 50 nm and radius Rin = 145 nm over the substrate (silica glass) and placed in the center of the unit cell. A silica hemisphere with the same radius Rin is placed above the cylinder. On this structure, a conformal layer of gold (or silica) of thickness tAu = 70 nm is present, thus having an external radius, at the base of the nanodome, of Rout = 215 nm. For silica, the refractive index n = 1.45 (κ = 0) was used in the simulations, while for Au it was used the experimental dielectric function obtained by ellipsometric measurements performed with a J. A. Woolham V-VASE spectroscopic ellipsometer on a reference thin film deposited on a silica glass substrate with the same conditions used for the samples. The experimental complex refractive index is shown in Fig. S2 of the ESI.† To reconstruct the dispersion relations of the lattice, both wavelength of the incident light λ (in the range 400–900 nm) and incidence angle θ (0°–40° range) have been varied.
2.4. Lasing emission measurements
For the lasing emission measurements a solution of Pyridine 2 (Lambdachrome by Lambda Physics) in ethanol, at a concentration of 1 mM, was used as the gain medium. The dye solution was contained in a chamber obtained by attaching a cover-slip glass onto the nanodome arrays samples with a double-sided adhesive tape. The depth of the chamber was about 200 μm. The chamber is placed vertically on the pivot of a motorized rotation stage that controls the collection system. A scheme of the set-up for the lasing emission measurements is reported in the ESI† (Fig. S3). The second harmonic (λ = 532 nm) of a Nd:YAG Q-switched laser (Brilliant, Quantel), with pulse duration of 4 ns and repetition rate of 10 Hz, was used to optically pump the samples. An iris with a diameter of about 3 mm was placed at the output of the laser beam to define the beam spot size. The pump energy on the samples was varied using optical density filters. The luminescent emission was collected as a function of the angle by pumping the samples at an angle of incidence of about 50° with respect to the surface normal (measurements taken at different angles of incidence in the range 0°–50° at steps of 1°, for the same incident fluence, show no dependence of the emission properties on the incidence angle). The collection system is mounted on one arm of the motorized rotation stage and it is composed of a 10× objective coupled through an optical fiber to a spectrometer (Ocean Optics HR4000). An edge filter (cut-on at 550 nm) was placed in front of the objective to prevent stray light from the pump laser to enter the spectrometer. The angular resolution of this system is of about 3°.2.5. Temporal coherence measurements
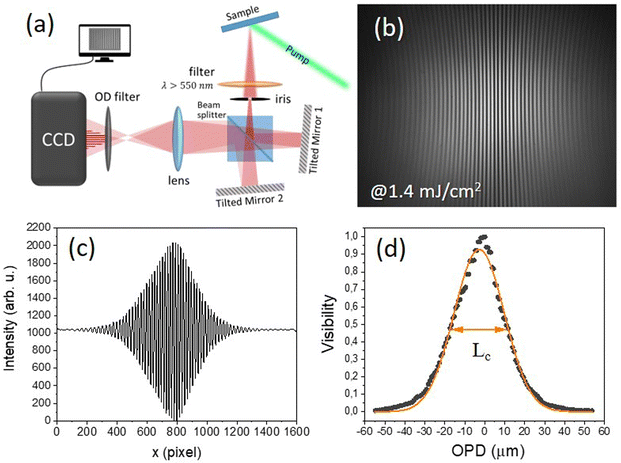
In order to characterize the temporal coherence of the laser emission of our devices, a modified Michelson interferometer, with two tilted mirrors, was set-up. A schematic illustration of the interferometer is shown in Fig. 4(a). The sample is pumped by the second harmonic of the Nd:YAG laser and the emission passes through an iris placed in front of a beam splitter. The beam is then split and directed toward two tilted mirrors, one fixed and the other movable along the beam direction. At the exit of the system a converging lens (focal length f = 40 mm) focuses the two beams onto a CCD camera (BGP-USB-SP503U, by Ophir-Spiricon) where the interference fringes are registered. An edge filter (λ > 550 nm) is placed in front of the iris in order to limit the collection of stray light from the CCD.In a Michelson interferometer, the first-order correlation of the light beams propagating along the two arms is obtained as a function of the optical delay τ. This can be quantified by the first-order correlation function  , where E is the electric field and the symbol 〈·〉 indicates the temporal average.34 The modulus of the first-order correlation function represents the degree of temporal coherence, |g(1)(τ)| ≤ 1. The coherence time, τc, can be defined such that |g(1)(τc)| = 1/2 and correspondingly, the coherence length is obtained as Lc = cτc (c is the speed of light). In an interference experiment the visibility V of the fringes can be calculated and related to the degree of temporal coherence by the relationship:
, where E is the electric field and the symbol 〈·〉 indicates the temporal average.34 The modulus of the first-order correlation function represents the degree of temporal coherence, |g(1)(τ)| ≤ 1. The coherence time, τc, can be defined such that |g(1)(τc)| = 1/2 and correspondingly, the coherence length is obtained as Lc = cτc (c is the speed of light). In an interference experiment the visibility V of the fringes can be calculated and related to the degree of temporal coherence by the relationship:
 | (1) |
In the conventional Michelson interferometer, an optical path difference (OPD) and, consequently, a time delay τ = 2OPD/c, is obtained by moving one of the two mirrors. Then, the fringe visibility V can be plotted as a function of OPD and the coherence length Lc can be determined as the FWHM of the visibility function.
In the tilted-mirror configuration set-up used in the present work, the mirror tilting introduces a continuous increment of OPD along one direction (namely, the x-direction), allowing to obtain the visibility variation as a function of OPD in a single interference pattern. The measured fringes period Λ (i.e., the distance between two interference maxima) is related to OPD and wavelength λ of the radiation through the expression:
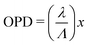 | (2) |
3. Results and discussion
Fig. 1(b) shows a SEM image in plane view of the Au hexagonal nanodome array (Au-HNDA) realized by nanosphere lithography; the unit cell of the hexagonal array is highlighted in the inset. A cross-sectional view of the sample is reported in Fig. 1(c). The images show that ordered arrays over a large area and with a very limited defect density can be realized by nanosphere lithography.To characterize the optical band-structure of the nanoarrays we performed angle-resolved transmission (T) measurements along the high-symmetry direction Γ–M of the system. A sketch of the hexagonal lattice in the reciprocal space is shown in Fig. 1(d), where the first Brillouin zone (red area) and the high-symmetry points, Γ, K and M, are highlighted. Fig. 1(e) shows the extinction map of the Au-HNDA in ethanol (n = 1.36), measured in transmission (extinction is calculated as E = 1 − T) with TM polarization. A comparison of the extinction maps taken with TE and TM polarization in air is reported in Fig. S4 in the ESI.† The large band in the infrared region (at about 1.63 eV) in Fig. 1(e) is the surface plasmon resonance (SPR) band of the Au HNDA. The black lines are the theoretical Rayleigh anomalies (RAs) of the hexagonal lattice (i.e., diffracted modes propagating grazing to the array plane), labeled with their corresponding Miller indexes and calculated according to the grating equation:35
| k‖d = k‖i + G | (3) |
 ,
,  are the components parallel to the lattice plane of the diffracted and incident wavevectors, respectively (ûd and ûi are the unitary vector along respective directions). G = ib1 + jb2 is the reciprocal lattice vector of the hexagonal array, with Miller indexes i and j, and b1 and b2 are the base vectors of the reciprocal lattice; θ is the angle between the direction of the incident beam and the normal to the sample and n is the refractive index of the medium above the nanodome array. In Fig. S5 of the ESI† we reported the extinction map (TM mode, Γ–M direction) of the Au-HNDA obtained by finite elements method (FEM) numerical simulations. The extinction maps of the corresponding silica nanodome array (SiO2-HNDA) have been also determined and reported in the ESI† (Fig. S6(a)). Since the experimental extinction of the sample is dominated by its reflectance, for comparison we reported in Fig. S6(b) (ESI†) the FEM simulated reflectance (R) map. It is important to stress that the highly non-trivial geometry of our system cannot be faithfully reproduced by a simplified perfectly periodic unit cell, such as the one used to compute the simulated extinction. Particularly, finite size effects, structural differences from dome to dome, surface roughness, positional disorder, inhomogeneities within the illumination spot are all limiting factors which cannot be included in the simulations. Nevertheless, the simulated structure allows to capture the major experimental extinction features and trace back the origin of the principal modes. FEM electrodynamic simulations of the HNDA samples have been performed also to investigate the field distribution in the nanoarrays. In Fig. S7 of the ESI† we report the comparison of the maps of field enhancement for the Au and SiO2 nanodome arrays. The maps have been computed at the experimental coupling point where, as discussed in the following, the lasing emission arises (white stars in Fig. 1(e), λ = 723 nm (1.72 eV), emission angle 17°). Owing to the plasmonic properties of the gold thin film, a much stronger field enhancement is demonstrated in close proximity of the Au nanodome with respect to the silica one (it has to be considered the very different color scale in the maps in Fig. S7(b, d and c, e) (ESI†), and the logarithmic scale). As a consequence of this effect, and considering the Lorentz reciprocity theorem, a much higher emission intensity in the direction of illumination is expected for the dye molecules coupled to the Au-HNDA with respect to the SiO2-HNDA.36
are the components parallel to the lattice plane of the diffracted and incident wavevectors, respectively (ûd and ûi are the unitary vector along respective directions). G = ib1 + jb2 is the reciprocal lattice vector of the hexagonal array, with Miller indexes i and j, and b1 and b2 are the base vectors of the reciprocal lattice; θ is the angle between the direction of the incident beam and the normal to the sample and n is the refractive index of the medium above the nanodome array. In Fig. S5 of the ESI† we reported the extinction map (TM mode, Γ–M direction) of the Au-HNDA obtained by finite elements method (FEM) numerical simulations. The extinction maps of the corresponding silica nanodome array (SiO2-HNDA) have been also determined and reported in the ESI† (Fig. S6(a)). Since the experimental extinction of the sample is dominated by its reflectance, for comparison we reported in Fig. S6(b) (ESI†) the FEM simulated reflectance (R) map. It is important to stress that the highly non-trivial geometry of our system cannot be faithfully reproduced by a simplified perfectly periodic unit cell, such as the one used to compute the simulated extinction. Particularly, finite size effects, structural differences from dome to dome, surface roughness, positional disorder, inhomogeneities within the illumination spot are all limiting factors which cannot be included in the simulations. Nevertheless, the simulated structure allows to capture the major experimental extinction features and trace back the origin of the principal modes. FEM electrodynamic simulations of the HNDA samples have been performed also to investigate the field distribution in the nanoarrays. In Fig. S7 of the ESI† we report the comparison of the maps of field enhancement for the Au and SiO2 nanodome arrays. The maps have been computed at the experimental coupling point where, as discussed in the following, the lasing emission arises (white stars in Fig. 1(e), λ = 723 nm (1.72 eV), emission angle 17°). Owing to the plasmonic properties of the gold thin film, a much stronger field enhancement is demonstrated in close proximity of the Au nanodome with respect to the silica one (it has to be considered the very different color scale in the maps in Fig. S7(b, d and c, e) (ESI†), and the logarithmic scale). As a consequence of this effect, and considering the Lorentz reciprocity theorem, a much higher emission intensity in the direction of illumination is expected for the dye molecules coupled to the Au-HNDA with respect to the SiO2-HNDA.36
To characterize the laser emission properties, the sample Au-HNDA is coupled with a solution of Pyridine 2 (Py2) in ethanol and photoluminescence spectra are acquired as a function of the pump fluence. Angle-resolved measurements are taken to study the directional properties of the emission. The red transparent band in Fig. 1(e) represents the emission band of the dye. The normalized absorption and emission spectra of Py2 in ethanol are reported in Fig. S8 of the ESI.† The dye has an emission band at 694 nm (1.79 eV), with a bandwidth of about 150 nm. Fig. 2(a) shows the emission spectrum of the Au-HNDA sample coupled to the solution of Pyridine 2 in ethanol (Au-HDNA + Py2, orange line). The sample has been excited at an angle of 50° with respect to the normal to the surface with a fluence of 1.78 mJ cm−2 and the emission has been collected at an angle of 17° along the Γ–M direction. For comparison, in Fig. 2(a) the emission spectrum of the Pyridine 2 solution alone, taken with the same excitation and collection conditions, is also reported (green line, 10-fold magnification). A narrow peak at about 720 nm (1.72 eV) appears in the spectrum of the Au-HDNA + Py2 sample, which overlaps to the broader fluorescence band of Py2. The trend as a function of the pump fluence of the PL emission of the Au-HDNA + Py2 sample is reported in Fig. 2(b): for pump fluences below 0.8 mJ cm−2, the spectrum is dominated by spontaneous emission (fluorescence) of the dye; at higher pump fluences, the peak at about 720 nm starts to emerge whose amplitude grows quickly as the pump fluence increases, which is distinctive of stimulated emission. To better characterize the evolution of the spectral features as a function of the pump fluence, we performed a multiple Gaussian peak deconvolution of the spectra, from which we obtain one peak centered at 697 nm, with a full width at half maximum, FWHM, of 58 nm and a second peak at 723 nm with FWHM of 12 nm. The spectral position and the FWHM of the peaks remain constant for all the pump fluences, while their amplitude exhibits a very different trend as a function of the pump fluence, as shown in Fig. 2(c): the amplitude of the band at 697 nm (blue squares) grows linearly with the pump fluence, as it occurs for a fluorescent emission, while the trend of the peak at 723 nm (red dots) exhibits steep increase, characteristic of a threshold behavior, indicative of stimulated emission.25 The blue line in the figure is a linear fit of the data, while the red curve is a sigmoidal fit to be used as a guide for the eye. The threshold value can be estimated by the extrapolation to zero of the tangent at the inflection point of the sigmoidal curve (red dashed line), and it resulted Fth = 0.95 mJ cm−2.
Further insights on the emission mechanism can be obtained by studying the directionality of the emission by angle-resolved PL measurements. Fig. 2(d) shows the angular emission map of sample Au-HDNA + Py2 excited above threshold (incidence at 50°) with a pump fluence of 1.4 mJ cm−2. The collection angle is rotated along the Γ–M direction. The white line represents the (−1, −1) Rayleigh anomaly. An intense, sharp spot appears at an energy of 1.72 eV (723 nm), for an angle of about 17°. The angular scan of the emission peak at 1.72 eV is reported in Fig. S9 of the ESI.† By fitting the data with a Gaussian function, we determined the peak angle and the angular divergence of the emission (estimated as the FWHM of the fitting curve), obtaining, respectively, θp = (16.83 ± 0.07)° and Δθ = (3.4 ± 0.1)°. By comparing the results of the angular emission map in Fig. 2(d) and the extinction map in Fig. 1(e), it emerges clearly that stimulated emission is achieved in the region where the plasmon mode, the (−1, −1) lattice mode and the Py2 emission band overlap, giving rise to the peak at 1.72 eV. In this case, the plasmonic nanoarray acts as a cavity, providing a feedback action sufficient to overcome the losses due to the metallic nanostructures and a strong amplification of the emission occurs.
In order to decouple the role of the plasmonic mode in the Au nanodome array from the lattice mode in the emission process, we fabricated and characterized also a totally dielectric nanoarray consisting of an hexagonal nanodome array of silica (SiO2-HNDA). This was obtained with the same fabrication method used to synthesize the Au-HNDA (see Fig. 1(a)) and substituting gold with silica in the final deposition step. Thus, the geometrical parameters are the same as for the Au-HNDA. In Fig. S10 of the ESI† we reported the PL spectra taken as a function of the pump fluence for the sample SiO2-HNDA + Py2. The PL spectra of the solution of Pyridine 2 in ethanol are shown in Fig. 2(e). In this case too, the spectra show the appearance of an amplified emission peak superimposed to the fluorescence band at the same spectral positions as for the Au-HNDA + Py2 sample (Fig. 2(b)), but a much higher pump fluence (about one order of magnitude higher) is needed to excite it and its amplitude results much lower. We have therefore characterized the angular properties of the emission in these samples, as we did for the Au-HNDA + Py2 sample. In Fig. 2(f) we reported the angular emission map of the SiO2-HNDA + Py2 sample. It is worth noting that a much higher pump fluence (15.4 mJ cm−2) was used to excite the sample, that is one order of magnitude higher than the fluence used for the Au-HNDA + Py2 sample (Fig. 2(d)), and the maximum PL emission is about one fifth of the signal measured with the Au-HNDA + Py2 sample. The angular map in Fig. 2(f) shows again the appearance of an intensity spot at the collection angle of 17°, i.e., at the crossing-point between the Py2 emission band and the lattice mode defined by the (−1, −1) Rayleigh anomaly. The Gaussian fit of the angular scan of the emission peak along the Γ–M direction (see Fig. S11 of the ESI†) gives θp = (17.28 ± 0.05)° and Δθ = (3.4 ± 0.1)°, in agreement with the results obtained for the Au-HNDA + Py2 sample. For the sake of completeness, in Fig. S12 of the ESI† we reported also the angular emission map obtained with only the solution of Pyridine 2 dissolved in ethanol (the excitation fluence was 15.4 mJ cm−2, as for the SiO2-HNDA + Py2 sample): no major angular dependence of the emission is observed in this case a part from a minor decrease due to the collection geometry.
In summary, by comparing the results obtained for the plasmonic nanodome array (Au-HNDA) with those of the purely dielectric array (SiO2-HNDA) and the Pyridine 2 solution, it emerges that the spectral position of the stimulated emission peak in the Au-HNDA + Py2 sample seems to be controlled by the amplification of the spontaneous emission in the gain medium (Py2 solution, see Fig. 2(e)), while the directional properties (emission angle and angular divergence) are defined by the coupling of this emission wavelength with the lattice mode of the nanoarray. Moreover, the hybridization of the plasmonic and photonic (lattice) modes in the plasmonic system produces a dramatic decrease (of one order of magnitude) of the threshold to get laser action. Possible mechanisms controlling the nanolasing phenomenon are the Purcell factor enhancement and the resonant scattering of the nanoarray, and to disentangle their role in plasmonic array nanolasers is still an open question in the field.3,5,37 In the present case, by comparing the results obtained for the Au nanodome array (Au-HNDA) with those of the silica nanoarray (SiO2-HNDA) made in the same conditions, and considering that the dye used as the gain medium is expected to have a high quantum efficiency, we believe that the Purcell factor enhancement in these samples may be limited and the dominant mechanism is instead the resonant scattering, so that the hybrid plasmonic-photonic mode in the Au nanodome array acts as an effective cavity and guarantees the necessary feedback to overcome the losses of the system and activate the lasing emission at low threshold.
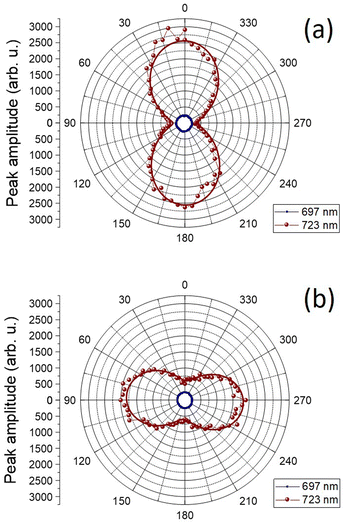
To further characterize the lasing emission properties of the investigated systems, the polarization properties of the emission of the Au-HNDA + Py2 sample have been studied. The results are shown in the polar plots in Fig. 3. In this case, emission spectra have been collected at the angle of maximum emission along the Γ–M direction (17°) as a function of the orientation of a linear polarizer placed in front of the detection system, for TE, vertical (Fig. 3a) and TM, horizontal (Fig. 3b) polarization of the incident beam. A multiple Gaussian peak deconvolution of each spectrum has been done to isolate the contribution and characterize the polarization properties of each peak, i.e., the fluorescence band at 697 nm and the stimulated emission peak at 723 nm. The plots in Fig. 3 highlight that, differently from the fluorescent emission at 697 nm (blue squares), that is not polarized, the stimulated emission peak at 723 nm (red dots) has a clear linear polarization character, oriented along the polarization direction of the pumping beam. The solid lines are best fits to the data according to Malus’ law. The strong polarization character of the stimulated emission observed in the Au-HNDA + Py2 sample is consistent with the results recently reported by Törmä and co-workers25 on the lasing emission in honeycomb plasmonic lattices, where the dependence on the incident polarization (TE or TM) can be understood considering the scattering properties of the Au nanoarray. Moreover, a selective excitation in the gain medium of emitters with transition dipole moment parallel to the incident polarization may occur, as recently demonstrated by Odom and co-workers,38 giving rise to a polarized emission parallel to that of the pumping beam.
Finally, the temporal coherence of the emission of the Au-HNDA + Py2 sample has been studied by using a home-built tilted-mirror Michelson interferometer (Fig. 4(a)). Fig. 4(b) shows the interference pattern acquired by exciting the sample above threshold (at a pump fluence of 1.4 mJ cm−2). A large number of vertical fringes are visible in the image, indicating a good degree of coherence of the emitted radiation. Fig. 4(c) reports the intensity profile as a function of the pixel coordinate (x) normal to the fringes, extracted from the interference pattern. A fast Fourier transform (FFT) filter has been applied to remove possible non-constant background contributions to the recorded intensity. Eqn (2) is used to convert the pixel coordinate x into the optical path difference OPD. Then the visibility V as a function of OPD has been extracted from the intensity profile and plotted in Fig. 4(d). The orange curve in Fig. 4(d) is the Gaussian fit of the visibility data. The coherence length, Lc, is calculated as the FWHM of this fit and it results Lc = 29.66 ± 0.05 μm (corresponding to a coherence time τc = 98.9 ± 0.2 fs). The concept of temporal coherence is intimately connected with monochromaticity: the coherence time can be written as function of the spectral bandwidth as τc = 1/Δν ≅ λ2/(cΔλ).39 To this regard it is worth stressing that in our experiment, in order to maximize the signal-to-noise ratio, no band-pass filter has been inserted to select the emission related to one of the peaks only (a long-pass filter λ > 550 nm is used). As a consequence, above threshold the detected emission is the convolution of the fluorescence band at 697 nm and the stimulated emission peak at 723 nm, which appears as a band centered at 720 nm, with a bandwidth of about 15 nm (Fig. 2(a)). Moreover, this broadening is due to two other different reasons which affect our system: one is correlated to the coupling with a dispersive lattice mode and the other caused by the lattice defects introduced by the self-assembling technique. Considering such a bandwidth value, we can estimate a coherence time of about τcth = 115 fs and, correspondingly, a coherence length Lcth = 35 μm, in agreement with the experimental value obtained by the interference measurements. Interference measurements of the emission of sample Au-HNDA + Py2 have been performed also for excitation below threshold (at 0.4 mJ cm−2). The result of the analysis of the interference pattern is reported in Fig. S13 of the ESI.† A much shorter coherence length is obtained in this case: Lc = 4.43 ± 0.02 μm. The significant increase of the coherence length demonstrated for above-threshold excitation further confirms the stimulated nature of the emission for the Au-HNDA sample.
It is important to stress at this point that for the nanodome arrays investigated in the present work, several aspects have to be taken into account, which affect the bandwidth of the stimulated emission peak, and as a consequence the estimated coherence length. In particular, nanofabrication defects and the possible heterogeneity of the nanodomes due to their surface roughness may give rise to a broadening of the emission features.40 Moreover, the strong overlap of the plasmonic mode to the dispersive lattice modes, which may drain energy, gives rise to a strong absorptive damping and again a reduction of the quality factor of the emission features. This in turn may explain the larger bandwidth of the stimulated emission peak, and thus the smaller coherence length, observed in the present work, with respect to other nanolasing systems in which the nanoarrays are typically fabricated with more sophisticated techniques as electron beam lithography or phase-shifting photolithography.13,25,41 Beside this, a further aspect to be considered is the finite size of the ordered domains that can be obtained by nanosphere lithography, which is of about 50–100 μm, i.e., of the same order of the coherence length that is obtained in these samples. Nonetheless, the possibility to get coherent stimulated emission, the highly directional character (low angular divergence) of the emitted beam, the low lasing-threshold value combined with the cost-effectiveness and high throughput of the fabrication method (NSL) make hexagonal plasmonic nanodome arrays a promising platform for the realization of nanolaser devices. Finally, the presented results allowed to shed some light on the problem of unveiling the dominant mechanism, between Purcell factor or LDOS enhancement and cooperative scattering, in controlling the lasing properties in plasmonic array nanolasers, which is still an open question in this field. In the present case, we observe off-normal stimulated emission at a relatively low threshold for the Au nanodome arrays, which suggests the hybridization of the plasmonic and photonic (lattice) modes and thus a main contribution of the resonant scattering in the plasmonic nanoarray.
4. Conclusions
Plasmonic nanolasers have been realized by coupling two-dimensional Au hexagonal nanodome arrays, fabricated by nanosphere lithography, with a dye liquid solution used as the gain medium. The emission properties of the samples have been investigated at room temperature by spectral and angle-resolved photoluminescence measurements performed as a function of the pump fluence. Stimulated emission has been observed around 720 nm, with a low threshold (about 0.9 mJ cm−2), in off-normal direction (17°) and with an angular divergence of about 3°. Purely dielectric nanoarrays have been also fabricated for comparison, by keeping the same geometry by substituting Au with SiO2. Stimulated emission can be induced in these dielectric nanosystems as well, with analogous directional properties as for the plasmonic nanoarrays, but with a much lower emission intensity and a threshold value more than one order of magnitude higher. Particularly, the comparison of the results obtained for the plasmonic and the dielectric nanosystems and the Pyridine 2 solution shows that the spectral properties of the stimulated emission seem to be controlled by the amplification of the spontaneous emission in the gain medium, while the directional properties are defined by the coupling of this emission with the lattice modes of the nanoarray. Moreover, the hybridization of the plasmonic and photonic (lattice) modes in the plasmonic nanosystem promotes a significant decrease of the threshold for lasing action. The polarization properties of the stimulated emission in the plasmonic nanosystems have been also characterized, demonstrating a strong linear polarization character, which is controlled by the polarization orientation of the pump beam. Finally, by using a tilted mirrors Michelson interferometer, the temporal coherence properties of the stimulated emission have been measured, determining a coherence time of the order of 100 fs, corresponding to a coherence length of about 30 μm. In conclusion, the capability to get polarized and coherent stimulated emission at room temperature, with low threshold and high directionality, combined with the cost-effectiveness and high throughput of the nanofabrication technique, make hexagonal plasmonic nanodome arrays a promising platform for the development of efficient plasmonic nanolasers.Author contributions
DP: methodology, investigation, writing – original draft preparation. MT: investigation, writing – original draft preparation. GP: methodology, investigation, writing – review and editing. BK: investigation. TC: conceptualization, writing – review and editing, supervision, project administration, funding acquisition. GM: conceptualization, writing – review and editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support of the Physics and Astronomy Department through the projects BIRD183751 and PRD-BIRD2022-Cesca is gratefully acknowledged. G. P. was supported by UNAM-PAPIIT IN104522. We thank also Consejo Nacional de Ciencia y Tecnologa for its support through projects 1564464 and 1098652.References
- M. T. Hill and M. C. Gather, Nat. Photonics, 2014, 8, 908–918 CrossRef CAS
.
- R.-M. Ma and R. F. Oulton, Nat. Nanotechnol., 2019, 14, 12–22 CrossRef CAS PubMed
.
- A. F. Koenderink, ACS Nano, 2019, 13, 7377–7382 CrossRef CAS PubMed
.
- H. Wu, Y. Gao, P. Xu, X. Guo, P. Wang, D. Dai and L. Tong, Adv. Opt. Mater., 2019, 1900334 CrossRef
.
- W. Wang, M. Ramezani, A. I. Väkeväinen, P. Törmä, J. G. Rivas and T. W. Odom, Mater. Today, 2018, 21, 303–314 CrossRef
.
- R.-M. Ma, R. F. Oulton, V. J. Sorger and X. Zhang, Laser Photonics Rev., 2013, 7, 1–21 CrossRef CAS
.
- Y. Yin, T. Qiu, J. Li and P. K. Chu, Nano Energy, 2012, 1, 25–41 CrossRef CAS
.
- L. Cui, Y. Zhu, M. Abbasi, A. Ahmadivand, B. Gerislioglu, P. Nordlander and D. Natelson, Nano Lett., 2020, 20, 6067–6075 CrossRef CAS PubMed
.
- D. Bergman and M. Stockman, Phys. Rev. Lett., 2003, 90, 027402 CrossRef PubMed
.
- M. A. Noginov, G. Zhu, A. M. Belgrave, R. Bakker, V. M. Shalaev, E. E. Narimanov, S. Stout, E. Herz, T. Suteewong and U. Wiesner, Nature, 2009, 460, 1110–1112 CrossRef CAS
.
- R. F. Oulton, V. J. Sorger, T. Zentgraf, R.-M. Ma, C. Gladden, L. Dai, G. Bartal and X. Zhang, Nature, 2009, 461, 629–632 CrossRef CAS
.
- M. T. Hill, M. Marell, E. S. P. Leong, B. Smalbrugge, Y. Zhu, M. Sun, P. J. V. Veldhoven, E. J. Geluk, F. Karouta, Y.-S. Oei, R. Nötzel, C.-Z. Ning and M. K. Smit, Opt. Express, 2009, 17, 11107–11112 CrossRef CAS PubMed
.
- D. Wang, W. Wang, M. P. Knudson, G. C. Schatz and T. W. Odom, Chem. Rev., 2018, 118, 2865–2881 CrossRef CAS
.
- J. Y. Suh, C. H. Kim, W. Zhou, M. D. Huntington, D. T. Co, M. R. Wasielewski and T. W. Odom, Nano Lett., 2012, 12, 5769–5774 CrossRef CAS
.
- F. Van Beijnum, P. J. Van Veldhoven, E. J. Geluk, M. J. A. De Dood, W. Gert and M. P. Van Exter, Phys. Rev. Lett., 2013, 110, 206802 CrossRef
.
- X. Meng, J. Liu, A. V. Kildishev and V. M. Shalaev, Laser Photonics Rev., 2014, 8, 896–903 CrossRef CAS
.
- W. Zhou, M. Dridi, J. Y. Suh, C. H. Kim, D. T. Co, M. R. Wasielewski, G. C. Schatz and T. W. Odom, Nat. Nanotechnol., 2013, 8, 506–511 CrossRef CAS PubMed
.
- A. Yang, T. B. Hoang, M. Dridi, C. Deeb, M. H. Mikkelsen, G. C. Schatz and T. W. Odom, Nat. Commun., 2015, 6, 6939 CrossRef CAS PubMed
.
- H.-Y. Wu, L. Liu, M. Lu and B. T. Cunningham, Adv. Opt. Mater., 2016, 4, 708–714 CrossRef CAS
.
- A. H. Schokker and A. F. Koenderink, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155452 CrossRef
.
- T. K. Hakala, H. T. Rekola, A. I. Väkeväinen, J.-P. Martikainen, M. Necada, A. J. Moilanen and P. Törmä, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed
.
- X. G. Juarez, R. Li, J. Guan, T. Reese, R. D. Schaller and T. W. Odom, ACS Photonics, 2022, 9, 52–58 CrossRef CAS
.
- R. Li, M. R. Bourgeois, C. Cherqui, J. Guan, D. Wang, J. Hu, R. D. Schaller, G. C. Schatz and T. W. Odom, Nano Lett., 2019, 19, 6435–6441 CrossRef CAS PubMed
.
- V. T. Tenner, M. J. A. De Dood and M. P. Van Exter, Opt. Lett., 2018, 43, 166–169 CrossRef CAS PubMed
.
- R. Guo, M. Necada, T. Hakala, A. Väkeväinen and P. Törmä, Phys. Rev. Lett., 2019, 122, 013901 CrossRef CAS
.
- D. Becerril, O. Vázquez, D. Piccotti, E. M. Sandoval, T. Cesca, G. Mattei, C. Noguez and G. Pirruccio, Nanoscale Adv., 2020, 2, 1261–1268 RSC
.
- C. L. Haynes and R. P. Van Duyne, J. Phys. Chem. B, 2001, 105, 5599–5611 CrossRef CAS
.
- T. Cesca, N. Michieli, B. Kalinic, I. G. Balasa, R. Rangel-Rojo, J. A. Reyes-Esqueda and G. Mattei, Mater. Sci. Semicond. Process., 2019, 92, 2–9 CrossRef CAS
.
- K. Y. Raygoza-Sánchez, I. Rocha-Mendoza, P. Segovia, A. V. Krasavin, G. Marino, T. Cesca, N. Michieli, G. Mattei, A. V. Zayats and R. Rangel-Rojo, Sci. Rep., 2019, 9, 1–9 CrossRef PubMed
.
- T. Cesca, E. Vianey García-Ramírez, H. Sánchez-Esquivel, N. Michieli, B. Kalinic, J. Manuel Gómez-Cervantes, R. Rangel-Rojo, J. Alejandro Reyes-Esqueda and G. Mattei, RSC Adv., 2017, 7, 17741–17747 RSC
.
- E. Petronijevic, G. Leahu, R. Li Voti, A. Belardini, C. Scian, N. Michieli, T. Cesca, G. Mattei and C. Sibilia, Appl. Phys. Lett., 2019, 114, 053101 CrossRef
.
- N. Michieli, B. Kalinic, C. Scian, T. Cesca and G. Mattei, ACS Photonics, 2018, 5, 2189–2199 CrossRef CAS
.
-
J.-M. Jin, The Finite Element Method in Electromagnetics, Wiley, New York, 2002 Search PubMed
.
-
M. Fox, Quantum Optics. An Introduction, Oxford University Press, 2006 Search PubMed
.
- V. T. Tenner, M. J. A. de Dood and M. P. van Exter, Opt. Express, 2016, 24, 29624 CrossRef CAS PubMed
.
- M. Ramezani, G. Lozano, M. A. Verschuuren and J. Gómez-Rivas, Phys. Rev. B, 2016, 94, 125406 CrossRef
.
- K. Guo and A. F. Koenderink, Phys. Rev. Appl., 2019, 11, 024025 CrossRef CAS
.
- M. P. Knudson, R. Li, D. Wang, W. Wang, R. D. Schaller and T. W. Odom, ACS Nano, 2019, 13, 7435–7441 CrossRef CAS PubMed
.
-
E. Hecht, Optics, Pearson, 5th edn, 2016 Search PubMed
.
- A. H. Schokker and A. F. Koenderink, ACS Photonics, 2015, 2, 1289–1297 CrossRef CAS
.
- T. B. Hoang, G. M. Akselrod, A. Yang, T. W. Odom and M. H. Mikkelsen, Nano Lett., 2017, 17, 6690–6695 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp00068k |
| This journal is © the Owner Societies 2023 |