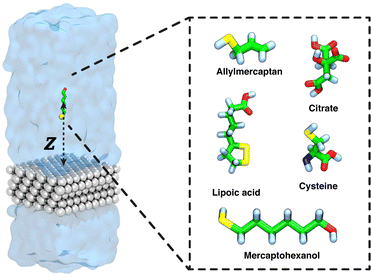
Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics of the physisorption of capping agents on silver nanoparticles†
Matías
Zúñiga-Bustos
 a,
Jeffrey
Comer
a,
Jeffrey
Comer
 *b and
Horacio
Poblete
*b and
Horacio
Poblete
 *cd
*cd
aPrograma Institucional de Fomento a la Investigacion, Desarrollo e Innovacion (PIDi), Universidad Tecnologica Metropolitana, Santiago 8940577, Chile
bDepartment of Anatomy and Physiology, Kansas State University, Manhattan, 66506-580, Kansas, USA. E-mail: jeffcomer@ksu.edu
cCenter for Bioinformatics and Molecular Simulation, Facultad de Ingenieria, Universidad de Talca, 2 Norte 685, Talca, Chile. E-mail: hopoblete@utalca.cl
dMillennium Nucleus of Ion Channel-Associated Diseases (MiNICAD), Talca, Chile
First published on 17th May 2023
Abstract
Nanoscale silver particles have growing applications in biomedical and other technologies due to their unique antibacterial, optical, and electrical properties. The preparation of metal nanoparticles requires the action of a capping agent, such as thiol-containing compounds, to provide colloidal stability, prevent agglomeration, stop uncontrolled growth, and attenuate oxidative damage. However, despite the extensive use of these thiol-based capping agents, the structure of the capping agent layers on the metal surface and the thermodynamics of the formation of these layers remains poorly understood. Here, we leverage molecular dynamics simulations and free energy calculation techniques, to study the behavior of citrate and four thiol-containing capping agents commonly used to protect silver nanoparticles from oxidation. We have studied the single-molecule adsorption of these capping agents to the metal–water interface, their coalescence into clusters, and the formation of complete monolayers covering the metal nanoparticle. At sufficiently high concentrations, we find that allylmercaptan, lipoic acid, and mercaptohexanol spontaneously self-assemble into ordered layers with the thiol group in contact with the metal surface. The high density and ordered structure is presumably responsible for their improved protective characteristics relative to the other compounds studied.
Introduction
Surface stabilization is critical for applications of many engineered nanoparticles. Silver nanoparticles have been one of the most extensively studied nanomaterials for medical and technological applications due to their unique antibacterial,1–3 optical,4,5 electrical,6 and chemical properties.7 Experimentally, the most common synthetic preparation of silver nanoparticles (AgNPs) is based on stabilization by citrate reduction.8–10 The citrate anions reduce the silver ions in a bottom-up synthesis scheme, favoring the nucleation of clusters of silver atoms and stabilizing the colloidal AgNPs.11 Citrate-stabilized AgNPs have served as the cornerstone for developing engineered nanomaterials for a broad range of research and biomedical applications, including biosensors,12–14 surface-enhanced Raman spectroscopy,15 tissue regeneration,16–19 among others.In the context of nanomedicine, AgNPs are immersed in a biological environment. Hence, metal nanoparticles need capping agents to prevent oxidation by radical species. Moreover, it has been found that capping agents can be used to control the final shape and size of the nanoparticles.20,21 Thus, various capping agents and surface modifications (functionalization) have been used to enhance in vivo stability for the duration of their desired function. Citrate is the most commonly used capping agent in the synthesis of silver nanoparticles, due to a its high stabilization effect, as well as the controlled size of the nanoparticles generated.22–24 However, other agents are sometimes used to obtain different surface properties or biological activity. Allylmercaptan is a small naturally occurring organosulfur compound derived from garlic that has been used as a protective agent for silver and gold nanoparticles.25,26 Mercaptohexanol has been used as a capping agent in fluorescent gold nanoparticles for sensing mercury(II) ions.27 The disulfide-containing molecule lipoic acid has been shown to facilitate the covalent protein capping of silver nanoparticles, increasing their oxidative stability in biological environments.28,29 Finally, cysteine has been used as a bio-reducing agent capable of generating silver nanoparticles with homogeneous sizes within a gel matrix.30
Experimentally, Toh et al. demostrated distinct behavior between the two thiol-containing molecules MH and Cys combined with initially citrate-capped nanoparticles. They found that MH formed a dense layer including Ag–S–R and Ag–S–Ag motif, while for Cys, they found merely replacement of the citrate capping agent by Cys.31 Thus, it is necessary investigate the behavior of thiol-containing molecules with different physicochemical properties to understand the link between these properties, the structure of the resulting capping layers, and, the stability and surface chemistry of the capped silver nanoparticles.31
Despite the progress made in development of biomolecule-capped silver nanomaterials, the exact mechanisms involved in the stabilization and the structure of the capping agents at the surface–solvent interface remain poorly understood. It has been shown that thiol-containing molecules, such as mercaptohexanol or cysteine, can replace citrate pre-deposited on the surface of silver nanoparticles, giving different electrochemical and oxidative profiles to the nanoparticle.31 Also, alkanethiols are widely used in silver nanoparticle synthesis.32
The capping molecules are generally covalently linked to the surface (chemisorbed); for example, thiols result in capping moieties including Ag–S covalent bonds. However, the energetic barriers for formation of these covalent linkages are high and, therefore, their formation is quite slow relative to the time scale for physical adsorption. For example, the dissociative adsorption of butanethiol to Ag{111} nanoparticles has been studied.33 The process proceeds by cleavage of the S–H bond (dissociation energy of 0.98 eV) yielding a thiolate, which then forms a covalent bond to the Ag{111} surface. Applying the Arrhenius relation suggests several minutes are required for this chemical reaction at room temperature, (although the presence of solvent and solvent pH affect the barrier) while adsorption and aggregation of the capping molecules occurs on the nanosecond time scale. Therefore, the initial adsorption and organization of the capping molecules are likely dominated by non-covalent interactions and that the final covalently linked structures are similar to those prior to any chemical reactions.
Classical non-reactive molecular dynamics allows us to study the structural arrangements driven by non-covalent interactions of capping agents and their associated thermodynamics on the nano- to microsecond time scale. Molecular simulation yields insight into atomic-scale interactions of surfaces and solutes that are difficult or impossible to access through experiments, yielding insight useful in the rational design of functional nanomaterials. Molecular simulations including polarizable silver surfaces (the AgP model34) and explicit solvent have been used to study the interaction of silver nanosurfaces with proteins,35,36 peptides,34,37–40 collagen-like peptides,41,42 and other small organic molecules. We have previously shown that molecular dynamics simulations, coupled with enhanced sampling methods, can reliably estimate differences in the adsorption affinity of biomolecules.38,43,44
As capping agents for metal nanoparticles, peptides have great promise owing to the ease with which custom sequences can be synthesized and the variety of functional groups available, which at the current time are rivaled by no other class of molecules. Thus, it is important to understand the process of adsorption of small protective agents before designing more complex nanocomplexes using peptides. Rationally modified collagen-like peptides, including the silver-anchor motif CLK, have been demonstrated to form strong complexes with AgNPs and stabilize them in aqueous solution,38,41 while the sequence and length of capping peptides are key factors in controlling production of free radicals.45 Molecular dynamics can be used to elucidate the thermodynamics of recognition of metal nanosurfaces by peptides, and to decompose free energies of adsorption into various contributions, such entropic and enthalpic components,44,46,47 thereby highlighting the roles of different physicochemical effects that control the absorption of small substrates to silver nanostructures.
In the present work, we consider capping of a silver surface by protective agents in three stages (see Fig. 2). We have chosen to focus on the {111} facet of face-centered cubic silver, which is a common exposed crystal plane on Ag nanoparticles.48,49 For the first stage, we perform calculations to determine the thermodynamics of adsorption of a single isolated molecule of the 5 capping agents to the silver–water interface using the enhanced sampling method known as adaptive biasing force (ABF) and decomposing the adsorption free energy into the entropic and enthalpic components. We reveal the thermodynamics of adsorption of citrate (CIT), lipoic acid (LA), allylmercaptan (ALM), mercaptohexanol (MH) and cysteine (CYS), agents which have been previously described experimentally as capping agents on gold and silver nanoparticles.45,50 In the second stage, we study the aggregation of adsorbed molecules at the silver–water interface, performing simulations of many capping molecules at this interface and observe their aggregation and, in some cases, assembly into ordered arrangements. Third, we simulated a complete monolayer of protective agents, calculating the number of molecules per unit area and the type of organization achieved.
Methods
Molecular models and force fields
Molecular dynamics simulations were performed using the polarizable model for Ag{111} surfaces published by Hughes et al.34 and used in studies by us38,41,42 and others.37,39,40 As described below, we constructed silver slabs of distinct dimensions for different types of simulations. In all cases, Ag{111} facets were exposed along the −z and +z directions and the lattice was periodic in the xy-plane, modeling the surface of a nanoparticle with a large diameter compared to the size of the capping molecules. The distance between nearest neighbors in the face-centered cubic silver lattice was 2.9 Å.The surface model of Hughes et al.34 includes a charged particle rigidly bonded to each silver atom to capture atomic polarizability and include image charge effects. It also includes virtual interstitial sites for Ag{111} facets to ensure correct absorption on top of silver atoms and not between them. The charged particles (atom type AGC) carry a charge of 0.308 proton units, while the silver atom centers (type AGS or AGB) carry the opposite charge. The bulk silver atoms (type AGB) serve both as centers of charge and Lennard-Jones interactions, while surface silver atoms (type AGS) have no Lennard-Jones interactions, which are instead assigned the (electrically neutral) virtual interstitial sites (type AGI). Consistent with the prescription of Hughes et al., the silver atom centers and virtual interaction sites (types AGS, AGB, and AGI) were fixed to their initial positions to maintain the ideal fcc structure, while the charged particles (type AGC) were free to rotate at a distance of 0.7 Å from their parent atom (AGS or AGB). The mass of the charged particles was set to 1.0 Da so NAMD would apply rigid bonds. Special Lennard-Jones parameters were used for interactions between silver atoms (or virtual sites) and other atoms, including oxygen atoms in water and capping agent hydroxyl groups, double-bonded carbon atoms of allylmercaptan, the NH3 nitrogen atom of CYS, carbonyl and carboxylate oxygen atoms, polar or thiol hydrogen atoms, and all sulfur atoms, as prescribed by Hughes et al.34
Structures for the capping agents (CIT, LA, ALM, MH) were extracted from the PubChem database,51 while the geometry of the CYS structure was generated from the CHARMM topology files.52 The protonation state of each molecule was estimated using the pKa calculation tool of Marvin Sketch Software.53 CYS adopted its zwitterionic form (with NH3+ and anionic carboxylate groups), while the acid group of LA was deprotonated to a carboxylate anion. Citrate was assigned a singly deprotonated form (total charge of −1), with a central carboxylate and two terminal carboxylic acid groups. The force field parameters and charges of the small molecules were obtained from the ParamChem server (CHARMM General Force Field version 3.0.1).54,55 Parameters for CYS were obtained from the CHARMM36m force field for proteins.52,56–58 Water molecules were placed above and below the Ag{111} surfaces and were represented with the modified TIP3P water model59 conventionally used with the CHARMM force field.
Molecular dynamics parameters
The molecular dynamics simulations were executed in the molecular dynamics software NAMD 2.13.60 We used the Langevin thermostat and Langevin piston barostat,61 to maintain the temperature and pressure at 300 K and 101.325 kPa (1.0 atm), respectively. The particle–mesh Ewald algorithm62 was used to compute the electrostatic interactions. The integration of the equations of motion was performed with a time step of 4 fs.63 Additionally, the length of covalent bonds involving hydrogen atoms were constrained.64,65 Long- and short-range electrostatic interactions were calculated every step. A smooth 8–9 Å cutoff of van der Waals forces was employed. If the system had a charge other than zero, Na+ counterions were added to neutralize this charge.Adsorption calculations
We constructed a silver slab 25 Å × 25 Å in the xy-plane and 5 layers thick in the z-direction. This surface was then solvated with a 25 Å thick layer of TIP3P water above the top silver layer and a 20 Å thick layer below the bottom layer (see Fig. 1), yielding a complete periodic box size of 25 × 25 × 81 Å3. Five systems were created by placing each of the five capping agent molecules at an initial distance of 18 Å from the top layer of silver atoms. All systems were independently subjected to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of energy minimization, followed by 10 ns of equilibration. Starting from the equilibrium configuration so obtained, the potential of mean force (PMF) was calculated using the Adaptive Biasing Force (ABF) method66,67 as implemented in the Colvars module.68 ABF was applied to a single transition coordinate Z, defined as the difference in the z-position of the center of mass of the capping agent molecule and that of the top layer of silver atoms. The ABF calculations were performed in a single-window scheme on the Z on the domain from 3.0 to 25 Å. The ABF simulations were run for a 2 microseconds for each molecule. We used the convention that the potential of mean force is zero for large separations between the surface and solute molecule, which was enforced by shifting each potential of mean force curve so that the average value of the last 0.5 Å of the transition coordinate (24.5–25.0 Å) was zero. To decompose the free energy calculations into enthalpic and entropic contributions, we performed two additional ABF simulations under different temperatures of 280 and 320 K, similar to the approach of Singam et al.44 The following equations were then used to calculate the entropic and enthalpic contributions for each system:44,46,47
000 steps of energy minimization, followed by 10 ns of equilibration. Starting from the equilibrium configuration so obtained, the potential of mean force (PMF) was calculated using the Adaptive Biasing Force (ABF) method66,67 as implemented in the Colvars module.68 ABF was applied to a single transition coordinate Z, defined as the difference in the z-position of the center of mass of the capping agent molecule and that of the top layer of silver atoms. The ABF calculations were performed in a single-window scheme on the Z on the domain from 3.0 to 25 Å. The ABF simulations were run for a 2 microseconds for each molecule. We used the convention that the potential of mean force is zero for large separations between the surface and solute molecule, which was enforced by shifting each potential of mean force curve so that the average value of the last 0.5 Å of the transition coordinate (24.5–25.0 Å) was zero. To decompose the free energy calculations into enthalpic and entropic contributions, we performed two additional ABF simulations under different temperatures of 280 and 320 K, similar to the approach of Singam et al.44 The following equations were then used to calculate the entropic and enthalpic contributions for each system:44,46,47 | (1) |
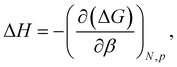 | (2) |
 | (3) |
| ΔH(Z,T) ≈ −ΔG(Z,T) + TΔS(Z,T), | (4) |
Models to study formation of aggregates
To efficiently address the formation of molecular clusters and/or agglomerations of silver-capping agents at concentrations below saturation, it was necessary to increase the size of the silver surface and, proportionally, the number of water molecules. In this case, we used a four-layer slab of silver of with dimensions of 154 × 158 Å2 in the xy-plane. It was solvated with 50 Å of water above the upper layer of silver atoms and 20 Å of water below the bottom layer of silver, reaching a final system size of 154 × 158 × 81 Å3 with a total of approximately 290![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. For each of the six systems, 100 molecules of the given capping agent (CIT, LA, ALM, MH, or CYS) were placed randomly at a distance between 12 and 35 Å from the first layer of Ag{111} atoms using the PackMol software.69,70 All systems were independently subjected to 15
000 atoms. For each of the six systems, 100 molecules of the given capping agent (CIT, LA, ALM, MH, or CYS) were placed randomly at a distance between 12 and 35 Å from the first layer of Ag{111} atoms using the PackMol software.69,70 All systems were independently subjected to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of energy minimization, followed by 300 ns of production simulation. A second replicate simulation of the same length was performed, starting from a new configuration generated by PackMol, for each system to verify that the results were reproducible. Using Colvars,68 a harmonic wall potential was placed at a distance of 40 Å from the upper surface layer of silver atoms to stop the molecules from crossing the periodic boundary and adsorbing to the lower silver surface. The force constant for the wall (upperWallConstant) was 20 kcal mol−1 Å−2. To calculate the free energy of aggregation, we determined the distribution of the capping agent molecules as a function of
000 steps of energy minimization, followed by 300 ns of production simulation. A second replicate simulation of the same length was performed, starting from a new configuration generated by PackMol, for each system to verify that the results were reproducible. Using Colvars,68 a harmonic wall potential was placed at a distance of 40 Å from the upper surface layer of silver atoms to stop the molecules from crossing the periodic boundary and adsorbing to the lower silver surface. The force constant for the wall (upperWallConstant) was 20 kcal mol−1 Å−2. To calculate the free energy of aggregation, we determined the distribution of the capping agent molecules as a function of  the distance from the center of mass of the aggregate in xy plane. With periodic boundary conditions, the center of mass of an arbitrary distribution of molecules cannot be uniquely defined. Hence, we used the following heuristic: for each frame, we determined the capping molecule that had the most neighboring capping molecules within 8 Å (taking into account periodic boundary conditions) and the other capping molecules were wrapped on the periodic boundaries with this molecule at the center. The center of mass of the capping molecules, (x0, y0), was calculated under these wrapping conditions. We also discarded the first portion of the trajectory (250 ns), where the distribution of molecules remained far from equilibrium. The free energies as a function of s, shown in Fig. 5, were calculated as G(s) = −kBT
the distance from the center of mass of the aggregate in xy plane. With periodic boundary conditions, the center of mass of an arbitrary distribution of molecules cannot be uniquely defined. Hence, we used the following heuristic: for each frame, we determined the capping molecule that had the most neighboring capping molecules within 8 Å (taking into account periodic boundary conditions) and the other capping molecules were wrapped on the periodic boundaries with this molecule at the center. The center of mass of the capping molecules, (x0, y0), was calculated under these wrapping conditions. We also discarded the first portion of the trajectory (250 ns), where the distribution of molecules remained far from equilibrium. The free energies as a function of s, shown in Fig. 5, were calculated as G(s) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[ρ(s)/ρ*], where T = 300 K was the temperature, ρ(s) was the areal number density of capping molecules at a distance s averaged over the trajectory and ρ* was the density at large distances from the center.
ln[ρ(s)/ρ*], where T = 300 K was the temperature, ρ(s) was the areal number density of capping molecules at a distance s averaged over the trajectory and ρ* was the density at large distances from the center.
For MH, molecules were only rarely found outside of the central aggregate after 120 ns; hence, there was poor sampling for ρ(s) at large s and ρ* was poorly defined. Hence, in this case, we performed enhanced sampling calculations using ABF. These calculations were performed with 5 replicates, each using a different tagged molecule for the transition coordinate, for a total of 3 μs of simulated time. The geometric (Jacobian) contribution to the free energy, Ggeo(s) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2πs), was subtracted, which gave results consistent to those calculated above from the areal number density ρ(s).
ln(2πs), was subtracted, which gave results consistent to those calculated above from the areal number density ρ(s).
Saturated surface models
In order to explore the structure of complete monolayers of the capping agents at the atomic level and find the maximum density of capping molecules that can coat a silver nanosurface, we performed multiple simulations with increasing numbers of protective agents on the surface. In particular, we used the same silver surface system as in “Adsorption calculations” with dimensions of 25 × 25 × 81 Å3. Thus, we performed molecular simulations 500 ns in length with 5, 10, 15, 20, 25, 30, 35 or 40 capping molecules for each capping agent. For convenience, a harmonic wall was placed at a distance of 30 Å from the upper silver surface, to avoid the diffusion of molecules across to the periodic boundary to the lower face of the silver slab.Results and discussion
Classical molecular dynamics simulation together with the ABF method has helped us understand the process of adsorption and aggregation of capping agents on metallic silver surfaces. Here, we first describe the initial step of adsorption from a dilute solution. Next, we consider agglomeration of the molecules to form extended aggregates. Finally, we investigate the structure of complete monolayers of the capping agents at the interface.First stage: single-molecule adsorption
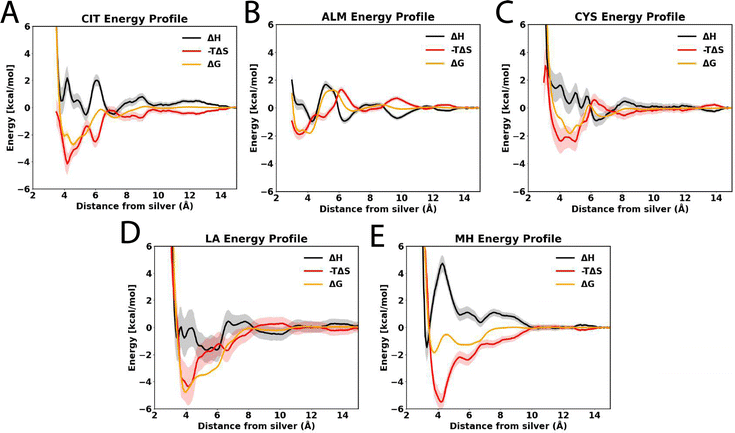
We used molecular dynamics simulations coupled with the ABF method67,71,72 to compute adsorption free energies of citrate (CIT), allylmercaptan (ALM), cysteine (CYS), lipoic acid (LA), and mercaptohexanol (MH) molecules to the interface between Ag{111} and water. Fig. 3 shows the free energy as a function of the distance between the center of mass of the capping agent and the upper layer of silver atoms (Z), as well as a representative conformation adopted by the capping agents when near the global minimum of this function. At large distances (Z > 14 Å), the electrostatic and van der Waals interactions between the substrates and the surface become negligible, and the free energy reaches a plateau, which by convention is anchored to zero. All of the compounds bind with a global minimum free energy below −1.8 kcal mol−1 relative to this plateau. CIT, the most common capping agent used experimentally, shows a global minimum free energy of −2.71 ± 0.18 kcal mol−1 at a distance of Z = 4.6 Å; however, this interaction is expected to be eventually strengthened by coordination interactions73 that are not included in the force field. For all of the sulfur-containing agents, the sulfur atoms make close contact with the surface (Fig. 3C–F) when they are in the configurations associated with minimum free energy. Similar structures are expected after covalent conjugation; for example, for covalent attachment between a cysteine thiolate group and a silver cluster.74 Additionally, The aliphatic chains of LA and MH lie in the plane of the interface, making close contact with the Ag{111} surface. LA, which has a disulfide group, exhibits the strongest affinity (ΔGmin = −4.81 ± 0.12 kcal mol−1) for physical adsorption of the agents considered (Table 1), with both sulfur atoms making close contact with the surface (Fig. 3E).| Capping molecule | Contact area (nm2) | ΔGmin (kcal mol−1) | Z min (Å) |
|---|---|---|---|
| CIT | 0.5 ± 0.1 | −2.71 ± 0.18 | 4.6 |
| ALM | 0.4 ± 0.1 | −1.82 ± 0.03 | 4.1 |
| CYS | 0.3 ± 0.1 | −1.83 ± 0.08 | 4.7 |
| LA | 0.6 ± 0.1 | −4.81 ± 0.12 | 4.0 |
| MH | 0.5 ± 0.2 | −1.86 ± 0.09 | 3.8 |
The thermodynamics of adsorption to the Ag{111} from aqueous solution is strongly controlled by the strength with which water interacts with the silver surface. The density functional theory calculations of the Walsh group34,75 show that water binds much more strongly to silver than graphene and slightly more strongly to silver than gold. Accordingly, in the classical models derived from these calculations, the concentration of water molecules is enhanced at the Ag{111}–water interface, more than four times that in bulk water. As shown in Fig. S1A of the ESI,† the density of the first hydration layer is greater than that of Au{111} or the graphite basal plane. There is also greater orientational order of water at the Ag{111} and Au{111} surfaces than at the graphite surface (Fig. S1B of the ESI†). In several cases, but most prominently for ALM, there is a free energy barrier between the long distance plateau and the global free energy minimum, associated with penetration of the first water layer that covers the silver surface, whose density peaks at Z = 5.8 Å. The free-energy curves in Fig. 3A also exhibit more fine features than similar curves calculated for a graphite surface (Fig. S1C of the ESI†), owing to the complexity of interactions between the polarizable silver surface and polar groups of the molecules.
To reveal thermodynamic contributions to adsorption, we performed free energy calculations for each capping agent at multiple temperatures (280, 300, and 320 K), following the protocol proposed by Singam et al.,44 decomposing the adsorption free energies of the capping agents into their entropic and enthalpic components. Fig. 4 shows the entropic (−TΔS, in red) and enthalpic (ΔH, in black) contributions to the adsorption free energy (ΔG, in orange) at 300 K, calculated from the change in the PMF with the temperature. The compounds evaluated in this investigation showed that the free energy of absorption was mainly driven by the entropy as opposed to enthalpy. In all cases, the enthalpy is unfavorable (ΔH > 0) or only weakly favorable (ΔH > 1 kcal mol−1) near the free energy minimum. This can be understood as follows: the strongest enthalpic interactions with the Ag{111} surface are due to its electrical polarizability and few molecules have a polarizability exceeding that of water (as evidenced by the high dielectric constant of water compared to other materials). Although several of the capping agents have polar groups, they must displace multiple water molecules to occupy the Ag{111} surface and their polar interaction with the surface is invariably weaker than that of the water molecules they displace. This conclusion is supported by the fact that the affinity of water for the Ag{111} surface is stronger (Fig. S1A of the ESI†) than other studied materials such as graphite or Au{111}. However, as we previously observed for graphite,44 releasing water from the interface leads to a considerable gain in entropy since water at the interface has a more restricted spatial and orientational distribution compared to bulk. Indeed, the favorable change in the entropy of the water was the largest contribution to the entropy of adsorption on graphite for the solutes considered and was only partially compensated by the loss of conformational and orientational entropy of the solutes, which are more rigid than the multiple water molecules they replace. As demonstrated by Fig. S1B and C (ESI†), water molecules on the Ag{111} surface are considerably more ordered than those on graphite; hence, there should be an even more favorable gain of entropy when they are released. Hence, it may not be surprising that adsorption to the Ag{111} is entropically driven.
As we previously observed for graphite,44 the minimum values the entropic (−TΔS) and enthalpic (ΔS) contributions to the free energies occur at distinct distances from the surface. For the most flexible molecule, MH, the most favorable entropy occurs at a larger distance from the surface (Z = 4.2 Å) than the most favorable enthalpy (Z = 3.3 Å), which is likely due to steric interactions forcing a more planar geometry, reducing conformational entropy, when the molecule closely approaches the surface (Table 1).
Second stage: aggregation
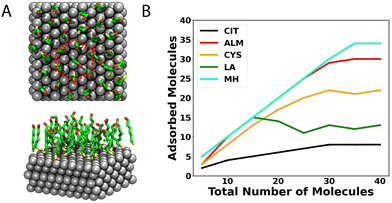
As a second stage of the surface coating process, we simulated silver surfaces loaded with protective agents to observe the formation of aggregates at the silver–water interface. We used classical molecular dynamics to explore the most likely conformations acquired by systems with a large number of molecules (100 molecules). The compactness of the aggregates and degree of ordering depends sensitively on the physicochemical characteristics of each capping agent.Fig. 5 shows the supramolecular organization of the five protective agents considered in this study. It is possible to observe that ALM, LA, and MH form compact aggregates at the silver–water interface. The molecules were initially placed in the solvent some distance from the interface. After 200 ns of simulation, more than 70% of the molecules of ALM, LA, or MH, have adsorbed to the interface and formed multi-molecule aggregates. Likely owing to their relative hydrophobicity, the ALM and MH systems are dominated by one large compact aggregate. The negative charge of LA prevents its aggregates from growing too large and it instead forms a collection of quasi-two-dimensional micelles (Fig. 5A). On the other hand, only about half of the 100 citrate or cysteine molecules adsorb to the surface and any clusters that form are only temporarily bound (Fig. 5C). ALM, LA, and MH agglomerate with the thiol or disulfide groups in contact with the silver surface, similar to the isolated molecules; however, the orientation of the rest of the molecule can differ due to the inter-solute interactions. Notably, while isolated MH molecules typically lie flat parallel to the surface (Fig. 3F), MH molecules within the core of the aggregates orient perpendicular to the interface with their OH groups pointing away from the surface (Fig. 5E).
The middle hydrocarbon portion of MH is hydrophobic and effectively seeks to minimize its water-exposed area. For an isolated molecule, it can do this by lying flat against the silver surface. However, in the MH aggregate, the molecules can reduce exposure of the hydrocarbon region to both water and the polar silver surface by aligning perpendicular to the surface in the interior of the aggregate. This configuration seems to maximize favorable interactions: the hydroxy group of MH makes contact with water, interior hydrocarbon groups are hidden by condensing together, and the thiol group directly contacts the silver surface, for which it has high affinity. At the edges of the aggregate, some of the MH molecules lie flat as they do when isolated at the silver–water interface.
To understand the thermodynamics of the formation of these aggregates at the silver–water interface, we analyzed the distribution of the molecules after the aggregates reached equilibrium (t > 200 ns). As illustrated in Fig. 6A, we calculated the distribution of molecular positions as a function of distance in the xy-plane from the center of mass of the largest aggregate  . From these distributions, we estimated the corresponding free energy profiles as described in Methods. These free energy profiles are shown in Fig. 6B. Due to the fact that the MH aggregate was very cohesive, MH molecules were rarely found outside the aggregate after equilibration and sampling of the position distribution was poor for large distances. Hence, it was necessary to use an enhanced sampling algorithm (ABF) to obtain an accurately anchored free energy curve for MH. While formation of pairs or larger clusters is thermodynamically favorable for all capping agents, free energy plateaus at short distances are visible for ALM and MH, corresponding to the free energy change for transfer of an isolated adsorbed molecule to the aggregate. MH exhibits the greatest tendency to aggregate, with a free energy of −3.2 ± 0.2 kcal mol−1 between the isolated adsorbed phase and aggregate phase.
. From these distributions, we estimated the corresponding free energy profiles as described in Methods. These free energy profiles are shown in Fig. 6B. Due to the fact that the MH aggregate was very cohesive, MH molecules were rarely found outside the aggregate after equilibration and sampling of the position distribution was poor for large distances. Hence, it was necessary to use an enhanced sampling algorithm (ABF) to obtain an accurately anchored free energy curve for MH. While formation of pairs or larger clusters is thermodynamically favorable for all capping agents, free energy plateaus at short distances are visible for ALM and MH, corresponding to the free energy change for transfer of an isolated adsorbed molecule to the aggregate. MH exhibits the greatest tendency to aggregate, with a free energy of −3.2 ± 0.2 kcal mol−1 between the isolated adsorbed phase and aggregate phase.
Furthermore, we have determined the diffusion coefficient of MH molecules under two conditions: when they are in a clustered state and when they are freely diffusing on the silver surface. Fig. S3 of the ESI,† illustrates that MH molecules in a clustered state exhibit reduced diffusion rates due to crowded environment of the cluster, whereas isolated MH molecules at the Ag{111}–water interface exhibit more rapid diffusion. LA exhibits a small free energy barrier near s = 25 Å because this capping agent forms quasi-planar micelles (Fig. 5D) that repel each other electrostatically owing to the negatively charged carboxylates forming the surfaces of these micelles (at neutral or high pH).
Fig. 6C shows the average number of molecules in the largest aggregate at the Ag{111}–water interface for the simulations illustrated in Fig. 5. For MH, nearly all 100 molecules are part of a single disc-like aggregrate (Fig. 5E). Similarly, at the studied concentration, the ALM system contains a dominant large aggregate (Fig. 5B) of about 40 molecules, while the other molecules are mostly adsorbed to the silver surface, but remain independent. Aggregates of LA appear to have a limiting size of about 18 molecules due to electrostatic repulsion of the carboxylate groups (this behavior is likely to be different at low pH). Neither CIT nor CYS form large aggregates at the studied concentrations owing to their relative hydrophilicity and resulting poor cohesion. The evolution of the size of the clusters and number of adsorbed molecules during the simulations is shown in Fig. S2 of the ESI.†
Fig. 6 implies that adsorption of many of the agents is cooperative (especially MH as well as ALM and LA): that is, adsorption of one molecule increases the affinity to adsorb a second. AS we have previously demostrated for organic molecules on graphene,43,44 there likely exist a critical concentration below which there is only a low density of molecules on the surface and above which nearly a complete monolayer is formed. However, predicting this critical concentration (or critical chemical potential) would be quite difficult given the complex structure of the aggregates (for example, the micelle-like aggregates of LA or the orientationally ordered aggregates of MH).
Final stage: highly saturated surfaces
To study the structure of fully saturated surfaces, we prepared simulation systems with different numbers of capping molecules (5–40, in increments of 5 molecules) on the Ag{111} surface model with an area of 6.25 nm2. Molecular dynamics simulations were run under the conditions described above for a total time of 500 ns of production in each system. Table 2 shows the maximum number of adsorbed molecules, total area of coverage, mean number of molecules per nm2, and the area per molecule for each simulated system.| Molecule | Total number | Adsorbed number | Coverage (nm2) | Area/molec. (nm2) |
|---|---|---|---|---|
| CIT | 40 | 8 | 3.85 ± 0.26 | 0.481 ± 0.030 |
| ALM | 40 | 30 | 6.17 ± 0.04 | 0.206 ± 0.001 |
| CYS | 40 | 22 | 5.36 ± 0.12 | 0.243 ± 0.005 |
| LA | 40 | 13 | 4.87 ± 0.21 | 0.375 ± 0.017 |
| MH | 40 | 34 | 6.19 ± 0.02 | 0.182 ± 0.001 |
Fig. 7B shows the mean number of molecules making contact with the Ag{111} surface in equilibrium for simulation systems containing different numbers of molecules. The highest density of molecules occurs for MH (6.19 ± 0.02 nm2), where 34 molecules form a complete ordered monolayer. Fig. 7A shows the associated structure, where the MH molecules are oriented perpendicular to the surface, with the –SH group facing the silver while the –OH group is oriented to the solvent. A hexagonal packing pattern in the xy-plane is evident.
For the case of CIT, the we observe the lowest coverage, achieving a total value of 8 molecules adsorbed on the first layer (3.85 ± 0.26 nm2), and no clear order of the layer is observed. However, as described above, chemisorption not modeled in these simulations may lead to stronger binding and greater coverage.74 On the other hand, this chemisorption should not be too strong, since, after synthesis, citrate is often removed or exchanged with another capping agent.76
On the other hand, the ALM molecule also shows high compactation on top of the surface, showing a coverage area of 6.17 ± 0.04 mol nm−2. However, unlike MH, we do not identify an ordered pattern for ALM on the sulver surface (see Fig. 8A) but rather a mixture of horizontal and vertical molecules. Structurally, the –SH group is always facing the surface, but compared to MH, ALM has a shorter hydrophobic chain and lacks the hydrogen bonding interactions present on the termini of MH.
 | ||
| Fig. 8 Representative configuration the maximum number of adsorbed molecules on the Ag{111} surface. (A) CIT, (B) ALM, (C) CYS, (D) LA, and (E) MH. | ||
Cysteine, in simulations at high concentrations, shows a medium coverage (5.36 ± 0.04 mol nm−2) compared to the other molecules studied here. Like CIT, CYS does not entirely cover the silver surface. The thiol group of CYS shows a strong affinity for the silver surface, which is likely increased by chemical conjugation. Additionally, several articles have proposed cysteine as an anchorage point for conjugating peptides to silver and gold nanoparticles.38,41,42,77,78 In this sense, CYS could be a stable, economical, and biocompatible protective agent for efficient protection during synthesis and for biomedical applications.
Finally, LA, despite having a cyclic disulfide group, which is oriented toward the silver surface, only occupies a coverage area of 4.87 ± 0.04 mol nm−2, which is due to electrostatic repulsion between the carboxylate (COO−) groups at neutral or high pH. Simulations at high concentration show that the S–S group effectively remains near the surface while the carboxylate groups point into the water. As low pH, LA likely can pack more densely and perhaps form a more ordered supramolecular structure.
Conclusion
In the present work, we have used a combination of molecular dynamics simulations and enhanced sampling methods to reveal, at the atomic scale, details of the interaction between silver surfaces and capping agents. First, we find that all the capping agents exhibit affinity for physisorption at the Ag{111}–water interface, which is driven mostly by solvent entropy. Water on the Ag{111} surface is very strongly bound, more so than on the graphite basal plane or Au{111}; therefore, adsorption of a solute necessitates displacing multiple water molecules, incurring a considerable enthalpic penalty. The sulfur-containing groups (thiol and disulfide) show a particularly high affinity for silver. Correspondingly, the most favorable conformation for an isolated molecule of the sulfur-containing capping agents is a planar conformation with the thiol group facing the silver surface. In concentrated solutions, inter-solute interactions lead to agglomeration of some of the capping agents and formation of quasi-planar drop-like structures at the Ag{111}–water interface. Indeed, the supramolecular organization is enhanced as a function of the length of the carbon chain of the capping agent. Mercaptohexanol forms highly cohesive disc-like aggregates in which the internal molecules align vertically and form an ordered lattice. Allylmercaptan also forms aggregates, but they are disordered and the cohesion is weaker. Due to its negative charge at neutral or high pH, lipoic acid (or, more accurately, its lipoate form) associates into quasi-planar micelles of fewer than 20 molecules.On the other hand, cysteine (zwitterionic form) and citrate (doubly-protonated form with charge of −1) exhibit little tendency to aggregate and form ordered patterns.
The study revealed that silver nanoparticles absorb and assemble differently with various thiols-containing molecules, namely MH, LA, ALM, and cysteine. These results indicate that more hydrophobic molecules self-assemble into dense layers on silver, while more hydrophilic molecules, such as zwitterioinc cysteine, exhibit less dense and less structured capping layers, which is consistent with experimental observations.31 This finding underscores the importance of investigating different classes of thiol-containing molecules individually to understand their behavior and how they regulate the properties of the resulting silver nanoparticles. Further research is required to explore the exchange and substitution of citrate with thiol-containing capping agents to understand how they effectively stabilize silver nanoparticles. These findings could have significant implications for the development of silver nanoparticle-based technologies and applications.
A major limitation of this study is that only physical interactions were considered while the capping agents are expected to covalently conjugate with the silver surface. However, under typical synthesis conditions, these chemical reactions are associated with sizable energetic barriers so that physisorption and supramolecular aggregation at the interface likely occurs (on a timescale of nanoseconds) before chemical bonding. Hence, the structures seen in the simulations are likely similar to the structures that persist after chemical conjugation. However, there may be some differences between the physisorbed and chemisorbed structures, such as in the orientation of the citrate molecules relative to the surface.73 Further research including modeling of chemical reactions is required to fully understand the interplay of physical interactions and chemical reactions on the structure of metal surfaces protected by capping agents.
Author contributions
Matias Zuñiga: investigation, execution, writing – review editing. Jeffrey Comer: conceptualization, methodology, software, investigation, writing – original draft writing – review & editing. Horacio Poblete: conceptualization, methodology, investigation, founding acquisition, writing – original draft writing – review & editing, supervision, visualization.Conflicts of interest
There are no conflicts to declare.Acknowledgements
HP acknowledges support from Fondecyt grant no. 1211143, as well as the Millennium Nucleus of Ion Channel-Associated Diseases, which is a Millennium Nucleus of the Millennium Scientific Initiative, National Agency of Research and Development (ANID), Ministry of Science, Technology, Knowledge and Innovation, Chile. We also thanks the Fondo de Equipamiento Científico y Tecnológico (FONDEQUIP) 160063. MZ-B acknowledges the Fondecyt Postdoctoral Fellowship no. 3200252. This material is partially based upon work supported by the US National Science Foundation under grant no. DMR-1945589.Notes and references
- Z.-M. Xiu, Q.-B. Zhang, H. L. Puppala, V. L. Colvin and P. J. Alvarez, Nano Lett., 2012, 12, 4271–4275 CrossRef CAS PubMed.
- S. Tang and J. Zheng, Adv. Healthcare Mater., 2018, 7, 1701503 CrossRef PubMed.
- R. Sood and D. S. Chopra, Appl. Clin. Res., Clin. Trials Regulatory Affairs, 2018, 5, 74–79 CrossRef.
- H. M. Fahmy, A. M. Mosleh, A. Abd Elghany, E. Shams-Eldin, E. S. A. Serea, S. A. Ali and A. E. Shalan, RSC Adv., 2019, 9, 20118–20136 RSC.
- D. D. Evanoff Jr and G. Chumanov, ChemPhysChem, 2005, 6, 1221–1231 CrossRef PubMed.
- I. J. Fernandes, A. F. Aroche, A. Schuck, P. Lamberty, C. R. Peter, W. Hasenkamp and T. L. Rocha, Sci. Rep., 2020, 10, 1–11 CrossRef PubMed.
- A. Roy, O. Bulut, S. Some, A. K. Mandal and M. D. Yilmaz, RSC Adv., 2019, 9, 2673–2702 RSC.
- P. Lee and D. Meisel, J. Phys. Chem., 1982, 86, 3391–3395 CrossRef CAS.
- J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- Z. S. Pillai and P. V. Kamat, J. Phys. Chem. B, 2004, 108, 945–951 CrossRef CAS.
- D. Steinigeweg and S. Schluecker, Chem. Commun., 2012, 48, 8682–8684 RSC.
- Y. Jiang, X. Zhang, L. Pei, S. Yue, L. Ma, L. Zhou, Z. Huang, Y. He and J. Gao, Chem. Eng. J., 2018, 339, 547–556 CrossRef CAS.
- A. J. Haes and R. P. Van Duyne, J. Am. Chem. Soc., 2002, 124, 10596–10604 CrossRef CAS PubMed.
- X. Ren, X. Meng, D. Chen, F. Tang and J. Jiao, Biosens. Bioelectron., 2005, 21, 433–437 CrossRef CAS PubMed.
- K. G. Stamplecoskie, J. C. Scaiano, V. S. Tiwari and H. Anis, J. Phys. Chem. C, 2011, 115, 1403–1409 CrossRef CAS.
- E. I. Alarcon, K. I. Udekwu, C. W. Noel, L. B.-P. Gagnon, P. K. Taylor, B. Vulesevic, M. J. Simpson, S. Gkotzis, M. M. Islam and C.-J. Lee, et al. , Nanoscale, 2015, 7, 18789–18798 RSC.
- S. Mclaughlin, J. Podrebarac, M. Ruel, E. J. Suuronen, B. McNeill and E. I. Alarcon, Front. Mater., 2016, 3, 27 Search PubMed.
- K. Hosoyama, M. Ahumada, C. McTiernan, J. Bejjani, F. Variola, M. Ruel, B. Xu, W. Liang, E. Suuronen and E. Alarcon, RSC Adv., 2017, 7, 47704–47708 RSC.
- S. Allison, M. Ahumada, C. Andronic, B. McNeill, F. Variola, M. Griffith, M. Ruel, V. Hamel, W. Liang and E. J. Suuronen, et al. , J. Mater. Chem. B, 2017, 5, 2402–2406 RSC.
- J. Romann, J. Wei and M.-P. Pileni, J. Phys. Chem. C, 2015, 119, 11094–11099 CrossRef CAS.
- C. R. Bealing, W. J. Baumgardner, J. J. Choi, T. Hanrath and R. G. Hennig, ACS Nano, 2012, 6, 2118–2127 CrossRef CAS PubMed.
- Q. Zhang, N. Li, J. Goebl, Z. Lu and Y. Yin, J. Am. Chem. Soc., 2011, 133, 18931–18939 CrossRef CAS PubMed.
- N. G. Bastús, F. Merkoci, J. Piella and V. Puntes, Chem. Mater., 2014, 26, 2836–2846 CrossRef.
- K. Ranoszek-Soliwoda, E. Tomaszewska, E. Socha, P. Krzyczmonik, A. Ignaczak, P. Orlowski, M. Krzyzowska, G. Celichowski and J. Grobelny, J. Nanopart. Res., 2017, 19, 1–15 CrossRef CAS PubMed.
- C. Battocchio, C. Meneghini, I. Fratoddi, I. Venditti, M. V. Russo, G. Aquilanti, C. Maurizio, F. Bondino, R. Matassa and M. Rossi, et al. , J. Phys. Chem. C, 2012, 116, 19571–19578 CrossRef CAS.
- I. Fratoddi, I. Venditti, C. Battocchio, G. Polzonetti, F. Bondino, M. Malvestuto, E. Piscopiello, L. Tapfer and M. V. Russo, J. Phys. Chem. C, 2011, 115, 15198–15204 CrossRef CAS.
- C.-C. Huang, Z. Yang, K.-H. Lee and H.-T. Chang, Angew. Chem., 2007, 119, 6948–6952 CrossRef.
- A. Sasidharan, J. E. Riviere and N. A. Monteiro-Riviere, J. Mater. Chem. B, 2015, 3, 2075–2082 RSC.
- I. Guzmán-Soto, M. Omole, E. I. Alarcon and C. D. McTiernan, RSC Adv., 2020, 10, 32953–32958 RSC.
- D. V. Vishnevetskii, A. R. Mekhtiev, T. V. Perevozova, A. I. Ivanova, D. V. Averkin, S. D. Khizhnyak and P. M. Pakhomov, Soft Matter, 2022, 18, 3031–3040 RSC.
- H. S. Toh, C. Batchelor-McAuley, K. Tschulik and R. G. Compton, Sci. China: Chem., 2014, 57, 1199–1210 CrossRef CAS.
- M. D. Malinsky, K. L. Kelly, G. C. Schatz and R. P. Van Duyne, J. Am. Chem. Soc., 2001, 123, 1471–1482 CrossRef CAS.
- A. Li, J.-P. Piquemal, J. Richardi and M. Calatayud, Surf. Sci., 2016, 646, 247–252 CrossRef CAS.
- Z. E. Hughes, L. B. Wright and T. R. Walsh, Langmuir, 2013, 29, 13217–13229 CrossRef CAS PubMed.
- E. I. Alarcon, C. J. Bueno-Alejo, C. W. Noel, K. G. Stamplecoskie, N. L. Pacioni, H. Poblete and J. Scaiano, J. Nanopart. Res., 2013, 15, 1–14 CrossRef.
- Z. Tang, J. P. Palafox-Hernandez, W.-C. Law, Z. E. Hughes, M. T. Swihart, P. N. Prasad, M. R. Knecht and T. R. Walsh, ACS Nano, 2013, 7, 9632–9646 CrossRef CAS PubMed.
- J. P. Palafox-Hernandez, Z. Tang, Z. E. Hughes, Y. Li, M. T. Swihart, P. N. Prasad, T. R. Walsh and M. R. Knecht, Chem. Mater., 2014, 26, 4960–4969 CrossRef CAS.
- H. Poblete, A. Agarwal, S. S. Thomas, C. Bohne, J. Phospase, J. Comer and E. I. Alarcon, Langmuir, 2016, 32, 265–273 CrossRef CAS PubMed.
- B. D. Briggs, J. P. Palafox-Hernandez, Y. Li, C.-K. Lim, T. J. Woehl, N. M. Bedford, S. Seifert, M. T. Swihart, P. N. Prasad, T. R. Walsh and M. R. Knecht, Phys. Chem. Chem. Phys., 2016, 18, 30845–30856 RSC.
- N. Soltani and M. R. Gholami, ChemPhysChem, 2017, 18, 526–536 CrossRef CAS PubMed.
- M. Ahumada, E. Jacques, C. Andronic, J. Comer, H. Poblete and E. Alarcon, J. Mater. Chem. B, 2017, 5, 8925–8928 RSC.
- E. Jacques, M. Ahumada, B. Rector, G. Yousefalizadeh, C. Galaz-Araya, R. Recabarren, K. Stamplecoskie, H. Poblete and E. I. Alarcon, Nanoscale, 2018, 10, 15911–15917 RSC.
- J. Comer, R. Chen, H. Poblete, A. Vergara-Jaque and J. E. Riviere, ACS Nano, 2015, 9, 11761–11774 CrossRef CAS PubMed.
- E. Azhagiya Singam, Y. Zhang, G. Magnin, I. Miranda-Carvajal, L. Coates, R. Thakkar, H. Poblete and J. Comer, J. Chem. Theory Comput., 2018, 15, 1302–1316 CrossRef PubMed.
- K. Goel, M. Zuniga-Bustos, C. Lazurko, E. Jacques, C. Galaz-Araya, F. Valenzuela-Henriquez, N. L. Pacioni, J.-F. Couture, H. Poblete and E. I. Alarcon, ACS Appl. Mater. Interfaces, 2019, 11, 17697–17705 CrossRef CAS PubMed.
- D. E. Smith and A. Haymet, J. Chem. Phys., 1993, 98, 6445–6454 CrossRef CAS.
- S. Wan, R. H. Stote and M. Karplus, J. Chem. Phys., 2004, 121, 9539–9548 CrossRef CAS PubMed.
- Y. Sun, Y. Ren, Y. Liu, J. Wen, J. S. Okasinski and D. J. Miller, Nat. Commun., 2012, 3, 971 CrossRef PubMed.
- X. Wang, J. Zhuang, Q. Peng and Y. Li, Nature, 2005, 437, 121–124 CrossRef CAS PubMed.
- S. Monti, V. Carravetta and H. Ågren, Nanoscale, 2016, 8, 12929–12938 RSC.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, Nucleic Acids Res., 2020, 49, D1388–D1395 CrossRef PubMed.
- A. D. MacKerell Jr., D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- B. Cherinka, B. H. Andrews, J. Sanchez-Gallego, J. Brownstein, M. Argudo-Fernandez, M. Blanton, K. Bundy, A. Jones, K. Masters and D. R. Law, et al. , Astronomical J., 2019, 158, 74 CrossRef.
- K. Vanommeslaeghe and A. D. MacKerell Jr, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell Jr, J. Chem. Inf. Model., 2012, 52, 3155–3168 CrossRef CAS PubMed.
- A. MacKerell Jr, M. Feig and C. Brooks III, J. Am. Chem. Soc., 2004, 126, 698–699 CrossRef PubMed.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. MacKerell Jr, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. de Groot, H. Grubmüller and A. MacKerell Jr, Nat. Meth., 2017, 14, 71–73 CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- S. E. Feller, Y. H. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- T. A. Darden, D. M. York and L. G. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- C. W. Hopkins, S. Le Grand, R. C. Walker and A. E. Roitberg, J. Chem. Theory Comput., 2015, 11, 1864–1874 CrossRef CAS PubMed.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- H. C. Andersen, J. Chem. Phys., 1983, 52, 24–34 CAS.
- E. Darve and A. Pohorille, J. Chem. Phys., 2001, 115, 9169–9183 CrossRef CAS.
- J. Comer, J. C. Gumbart, J. Hénin, T. Lelièvre, A. Pohorille and C. Chipot, J. Phys. Chem. B, 2015, 119, 1129–1151 CrossRef CAS PubMed.
- G. Fiorin, M. L. Klein and J. Hénin, Math. Probl. Eng., 2013, 111, 3345–3362 CAS.
- J. M. Martnez and L. Martnez, J. Comput. Chem., 2003, 24, 819–825 CrossRef PubMed.
- L. Martnez, R. Andrade, E. G. Birgin and J. M. Martnez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- E. Darve, D. Rodrguez-Gómez and A. Pohorille, J. Chem. Phys., 2008, 128, 144120 CrossRef PubMed.
- J. Hénin and C. Chipot, J. Chem. Phys., 2004, 121, 2904–2914 CrossRef PubMed.
- T. Ahuja, K. Chaudhari, G. Paramasivam, G. Ragupathy, J. S. Mohanty and T. Pradeep, J. Phys. Chem. C, 2021, 125, 3553–3566 CrossRef CAS.
- A. A. Buglak, R. R. Ramazanov and A. I. Kononov, Amino Acids, 2019, 51, 855–864 CrossRef CAS PubMed.
- Z. E. Hughes, S. M. Tomásio and T. R. Walsh, Nanoscale, 2014, 6, 5438–5448 RSC.
- K. Ranoszek-Soliwoda, E. Tomaszewska, E. Socha, P. Krzyczmonik, A. Ignaczak, P. Orlowski, M. Krzyzowska, G. Celichowski and J. Grobelny, J. Nanopart. Res., 2017, 19, 1–15 CrossRef CAS PubMed.
- L. Hwang, G. Zhao, P. Zhang and N. L. Rosi, Small, 2011, 7, 1939–1942 CrossRef CAS PubMed.
- A. Tofanello, E. G. Miranda, I. W. Dias, A. J. Lanfredi, J. T. Arantes, M. A. Juliano and I. L. Nantes, ACS Omega, 2016, 1, 424–434 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A PDF file containing two figures at https://rsc.org. See DOI: https://doi.org/10.1039/d2cp06002g |
| This journal is © the Owner Societies 2023 |