Vibrational mode-specific quasi-classical trajectory studies for the two-channel HI + C₂H₅ reaction

Abstract

We report a detailed dynamics study on the mode-specificity of the HI + C₂H₅ two-channel reaction (H-abstraction and I-abstraction), through performing quasi-classical trajectory computations on a recently developed high-level ab initio full-dimensional spin–orbit-corrected potential energy surface, by exciting four different vibrational modes of reactants at five collision energies. The effect of the normal-mode excitations on the reactivity, the mechanism, and the post-reaction energy flow is investigated. Both reaction pathways are intensely promoted when the HI-stretching mode is excited while the excitations imposed on C₂H₅ somewhat surprisingly inhibit the dominant H-abstraction reaction pathway. The enhancement effect of the excitation in the HI vibrational mode is found to be much more effective than increasing the translational energy, similar to the HBr + C₂H₅ reaction. Not like the Br-abstraction pathway, however, the I-abstraction reaction pathway could be comparable to the dominant H-abstraction reaction pathway. The dominance of the direct stripping mechanism is indicated in H-abstraction while the direct rebound mechanism is observed in I-abstraction. The H-abstraction is much pickier about the initial attack angle distributions for HI than I-abstraction is, which leads to a decrease in reactivity in the H-abstraction reaction pathway. The dominance of side-on CH₃CH₂ attack in I-abstraction is more obvious than in the case of H-abstraction. In the case of the H-abstraction reaction pathway, the major part of the initial translational energy ends up in translational recoil, while for I-abstraction most energy excites the product C₂H₅I.

---

I. Introduction

Interest in the chemical properties of iodine and its compounds is widely focused on the active participation in atmospheric chemistry.^1–3 The residence time of iodine species in the atmosphere is linked directly to the solar photolysis level but it should be increased by the formation of particles.⁴ Iodine species could affect the trace gas composition of the atmosphere by reacting with primary and secondary pollutants. Their impacts on the ozone cycle and NO_x regimes^5,6 or tropospheric HO_x^7,8 have been significantly studied. Among fission products, iodine-131 whose half-life is equal to 8 days, is recognized as the main radionuclide due to its ability to accumulate in the thyroid gland, thereby increasing the effects of radiation on the human body.⁹ As maybe the simplest compound of iodine, HI is used as a reducing agent, for example, in the reduction of aromatic nitro compounds to anilines.¹⁰ It can also be used in organic and inorganic synthesis as one of the primary sources of iodine. The Cativa process is a major end use of hydroiodic acid, which serves as a co-catalyst for the production of acetic acid by the carbonylation of methanol.^11,12 One important elementary reaction which can reveal the reactivity of iodine and its compounds is the reaction of hydrogen iodide and alkyl radicals. There are at least two reaction pathways in this reaction: H-abstraction which leads to iodine + alkane and I-abstraction which leads to hydrogen + alkyl-iodide.

For the H-abstraction reaction pathway, the investigation started back in 1990 when Seetula et al.¹³ studied the kinetics and thermochemistry of the reactions of HI with five different alkyl radicals including CH₃, C₂H₅, i-C₃H₇, s-C₄H₉, and t-C₄H₉ in a tubular reactor coupled to a photoionization mass spectrometer (between 295 and 648 K). Mečiarová et al.¹⁴ calculated the enthalpy for the reaction pathway HI + CH₃ → I + CH₄ by employing MP2 in conjunction with the cc-pVTZ(-PP) basis set, and predicted the rate constants using the canonical transition state theory with an asymmetrical Eckart tunneling correction. Leplat et al.^15,16 investigated the HI + C₂H₅ → I + C₂H₆ reaction pathway in the temperature range 213–623 K using a Knudsen reactor coupled to a single-photon photoionization mass spectrometer. They also applied ab initio quantum chemistry methods and the canonical transition state theory for the reaction energy profiles and rate constants. However, their experiments and theoretical modelling seem at great odds with each other. In 2019, our group¹⁷ determined benchmark geometries and energies for the stationary points of the backward reaction I + C₂H₆, considering also the H-substitution and the methyl-substitution reaction pathways, by augmenting the CCSD(T)-F12b/aug-cc-pVQZ energies with core–correlation, post-CCSD(T) and spin–orbit corrections. Taking these correction terms into account turns out to be essential to reach subchemical, i.e., 0.5 kcal mol⁻¹, accuracy.

For the I-abstraction reaction pathway, however, as far as we know, only two temperature-dependent rate coefficients are available in the literature, an estimation for flame inhibition modeling from Westbrook,¹⁸k = 5.76 × 10⁻¹⁰ exp(−1760 K/T) cm³ molecule⁻¹ s⁻¹, and an experimental value from Yuan et al.¹⁹ obtained for T = 295–624 K, k = 1.1 × 10⁻¹⁰ exp(−710 K/T) cm³ molecule⁻¹ s⁻¹, and have been employed to investigate the kinetics and mechanism of the pyrolysis of ethyl iodide as an hydrogen atom source.²⁰

Very recently²¹ we reported a high-level ab initio full-dimensional spin–orbit-corrected potential energy surface (PES) built from 10921 geometries and energies at the following composite level of theory: ManyHF-based²² UCCSD(T)-F12a/cc-pVDZ-F12(-PP)²³ + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12(-PP)), where for the I atom, a small-core relativistic effective core potential (ECP)²⁴ is used. The multi-reference computations utilized a minimal active space of 5 electrons on 3 spatial 5p-like orbitals, and the Q Davidson-correction²⁵ estimates higher-order correlation energy effects. The SO computations made use of a spin–orbit pseudopotential in the interacting-states approach,²⁶ where the SO eigenstates were determined by diagonalizing the 6 × 6 SO matrix whose diagonal elements were replaced with the Davidson-corrected MRCI energies. For the fitting of the energy points of the PES we utilized the monomial symmetrization approach (MSA).²⁷ The vibrational ground-state dynamics for the HI + C₂H₅ reaction was also studied in that work.²¹ Following previous mode-specific studies on various polyatomic reactions,^28–36 here we investigate the competition between vibrational and translational excitation in the nine-atomic two-channel HI + C₂H₅ reaction, thereby providing new insights into the dynamics and mechanisms of the title reaction. The HI-stretching mode and three selected vibrational modes of ethyl are excited, one at a time and each with one quantum, at five different collision energies. The effects of the different kinds of excitations on the reactivity, the reaction mechanisms, the alternative product channels, and the post-reaction distribution of energy are monitored.

II. Methodology

A. Quasi-classical trajectory

Quasi-classical trajectory (QCT) simulations are carried out at collision energies (E_coll) of 1, 5, 10, 20, and 40 kcal mol⁻¹ for the HI + C₂H₅ reaction on the full-dimensional spin–orbit-corrected PES recently developed by the present authors.²¹ We pick the HI-stretching and three different ethyl normal mode excitations, each with one quantum [the v_HI HI-stretching (6.73), the v₉ CH₂ wagging (1.09), the v₁ symmetric CH-stretching (9.13), and the v₁₀ asymmetric CH-stretching (9.38) modes with fundamental harmonic energies given in kcal mol⁻¹ in parentheses], and compare the results with those obtained for the ground-state reaction.

The motions corresponding to these normal-mode vibrations of ethyl are represented in Fig. 1. We will also find the similarity of the HI + C₂H₅ reaction with the HBr + C₂H₅ reaction we investigated before.^36,37

Fig. 1 Schematic representation of the normal-mode vibrations of ethyl studied in the present work: v₉ CH₂ wagging, v₁ symmetric CH-stretching, and v₁₀ asymmetric CH-stretching, where v_x [x = 9, 1, 10] refers to the standard Mulliken notations. The imaginary mode of the H-abstraction transition state (v_TS) is also shown.

At the beginning of the trajectories, the initial vibrational excitation energies and the zero-point energies (ZPEs) of HI and C₂H₅ are set by standard normal-mode sampling.³⁸ The spatial orientations of the reactants are randomly sampled. The initial distance between the center of mass of HI and the center of mass of C₂H₅ is (x² + b²)^1/2, where x = 16 bohr (distance along the relative center of mass velocity direction) and the impact parameter (b) is varied between 0 and b_max (where the reaction probability vanishes) with a step size of 0.5 bohr. 1000 trajectories are run at each b value. The trajectories are propagated with a 0.0726 fs time step until the largest interatomic distance becomes larger than the largest initial one by 1 bohr.

Integral cross-sections (σ) for the HI + C₂H₅ reaction are calculated by a b-weighted numerical integration of the P(b) opacity functions at each E_coll. The scattering angle (measured from the direction of the incoming reactant C₂H₅ to the direction of observation of the scattered product C₂H₆/C₂H₅I for the H-abstraction/I-abstraction reactions) distributions are obtained by binning the cosine of the angle (θ) of the relative velocity vectors of the center of masses of the products and those of the reactants into 10 equidistant bins from −1 to 1. The initial attack angle distributions for the reactants are calculated by binning the cosine of the angle (α for HI and β for C₂H₅) of the velocity vector of center of mass of the examined reactant and an interatomic vector that is considered as the I–H bond for HI and the C–C bond for C₂H₅. We also use 10 equidistant bins between −1 to 1 like in the case of scattering angle distributions.

B. Potential energy surface

The schematic energy diagram of the HI + C₂H₅ two-channel reaction is shown in Fig. 2. For comparison, we also show the energy profile of HBr + C₂H₅ in parentheses.³⁶ For the H-abstraction reaction pathway, HI + C₂H₅ releases more energy than HBr + C₂H₅ while for the X-abstraction reaction pathway they absorb similar amount of energy.

Fig. 2 Schematic potential energy diagram of the HX + C₂H₅ (X = I and Br) reaction comparing the classical relative energies obtained on the PES, ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) energies for the geometries optimized on the PES, relative energies for the geometries optimized at UCCSD(T)-F12b/AVDZ (for HX + C₂H₅ → H + C₂H₅X), and the relativistic all-electron CCSDT(Q)/complete-basis-set-quality benchmark relative energies (for HX + C₂H₅ → X + C₂H₆)¹⁷ of the stationary points. The 16.27 kcal mol⁻¹ with a star is the UCCSD(T)-F12b/AVDZ energy calculated using the geometry optimized on the PES. Four single-excited vibrational energy levels of the reactants obtained on the PESs are also shown. All the energies are given in kcal mol⁻¹.

For the H-abstraction reaction pathway, a pre-reaction minimum is located very near to the submerged transition state (TS) and the reaction is exothermic. For the I-abstraction reaction pathway, both the pre-reaction minimum and post-reaction minimum are located below the corresponding reactants and products. We could not locate the TS of the I-abstraction reaction pathway at the UCCSD(T)-F12b/AVDZ level and 16.27 kcal mol⁻¹ with a star shown in Fig. 2 is the UCCSD(T)-F12b/AVDZ energy calculated using the geometry optimized on the PES. Fig. 2 also shows the comparison of the classical relative energies of the stationary points of the HI + C₂H₅ reaction obtained on the analytical PES, the ManyHF-UCCSD(T)-F12a/cc-pVDZ-F12 + SO_corr(MRCI-F12+Q(5,3)/cc-pVDZ-F12) energies computed for the geometries optimized on the PES, and the benchmark results¹⁷ (if not available, then we show the relative energies for the geometries optimized at UCCSD(T)-F12b/AVDZ, in light blue color). The comparison of the former two indicates an excellent fitting behavior for the H-abstraction reaction pathway but just good for the I-abstraction reaction pathway, as the PES was designed for describing the H-abstraction pathway.²¹

III. Results and discussion

A. Reaction probabilities and integral cross-sections

The opacity functions (reaction probabilities as a function of the impact parameter) obtained at different E_coll values are shown in Fig. 3, for both H-abstraction and I-abstraction reaction pathways.

Fig. 3 Reaction probabilities as a function of the b impact parameter for the HI(v_HI = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, and 10] reactions (H-abstraction: three panels on the left, I-abstraction: right panel) at different collision energies. The result of HBr(v_HBr = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, 10] reactions³⁶ (lower panel) are also displayed for comparison.

In the current simulations we only find I-abstraction pathway reaction trajectories when E_coll = 40 kcal mol⁻¹ (except in the case of v_HI = 1 there are a few trajectories when E_coll = 20 kcal mol⁻¹ but too few for analysis in this study). By inspecting the opacity functions shown in the upper panel of Fig. 3, we can observe a significant enhancement for the HI + C₂H₅ reaction when v_HI = 1, especially at low collision energy in the case of the H-abstraction reaction pathway and also for the I-abstraction channel, while the b_max values do not change considerably, and the shape of the opacity functions remains. Only a minor inhabitation effect is seen for the three selected vibrational mode excitations of ethyl for the dominant H-abstraction reaction pathway, just like in the case of HBr + C₂H₅ reaction³⁶ (lower panel).

The sudden vector projection (SVP)^39,40 values, i.e., the overlaps of the vibrational modes of the reactants with the reaction coordinate (imaginary mode) at the H-abstraction transition-state structure are 0.055 (v_HI), 0.096 (v₉), 0.011 (v₁) and 0.000 (v₁₀) using the UCCSD/cc-pVDZ optimized geometries and the corresponding normal-mode vectors of the TS and the two reactants placed far. We noticed that in this system, the vibrational enhancements could not be explained using the SVP, compared to another similar system, Cl + C₂H₆ reaction³¹ we studied, where the vibrational enhancements are consistent with the predictions of the SVP model. The reason is that the imaginary frequency of the H-abstraction transition state in the HI + C₂H₅ reaction is only 114 cm⁻¹ and the mode is twisted, which could not represent the reaction coordinate very well. In addition, the reactivity is inhibited by the mode-specific excitations in C₂H₅, but the SVP model is unable to predict the inhibition effect.

Not like Br-abstraction however, the I-abstraction reaction pathway is comparable to the dominant H-abstraction reaction pathway, especially in the case of v_HI = 1, as shown in the upper-right panel of Fig. 3. By comparing the upper-right panel and the upper-middle-right panel, we see that the reaction probability of I-abstraction is a little higher than that of H-abstraction when b = 0. The contribution (in the form of cross-sections) of the minor reaction pathway to the total reaction when E_coll = 40 kcal mol⁻¹ is listed in Table 1, for both I-abstraction and Br-abstraction cases. As shown in Fig. 2, the I-abstraction reaction has a lower barrier compared to the Br-abstraction reaction (16 to 21 kcal mol⁻¹), thus, it is not a surprise that the contributions of the minor reaction pathway to the total reactivity in HI + C₂H₅ are much larger than those in the case of HBr + C₂H₅.

Table 1 Contributions (in %) of the minor reaction pathway to the total reaction as cross-sections at E_coll = 40 kcal mol⁻¹

Minor reaction pathway	v = 0	v HI/HBr = 1	v 9 = 1	v 1 = 1	v 10 = 1
HI + C2H5 → H + C2H5I	3.8	14.2	5.1	5.2	4.4
HBr + C2H5 → H + C2H5Br^36	0.4	3.0	0.6	0.1	0.5

---

In our previous work on the HBr + C₂H₅ reaction, we found another reaction pathway, hydrogen-exchange (H′Br + C₂H₅ → HBr + C₂H₄H′).³⁶ However, in the present work on the HI + C₂H₅ reaction, none of these trajectories is found. In the case of HBr + C₂H₅, we made a reasonable prediction that the H-exchange reaction barrier is not high, probably less than 5 kcal mol⁻¹.³⁶ Thus, it is quite surprising that we do not see these trajectories in the similar HI + C₂H₅ system. One reason is that the H-exchange reaction pathway in the HBr + C₂H₅ reaction experiences a two-step process, i.e., the hydrogen from HBr transfers to ethyl and the Br atom moves away from ethane (just like the H-abstraction), but the fragments cannot separate, instead Br turns back and abstracts an H atom from ethane and forms HBr. However, in the case of the HI + C₂H₅ reaction, the H-abstraction is more exothermic compared to HBr + C₂H₅ (see Fig. 2); therefore it is harder for the I atom to turn back and form HI. In addition, the electronegativity of the I atom is lower than Br. This could also decrease the probability of forming HI.

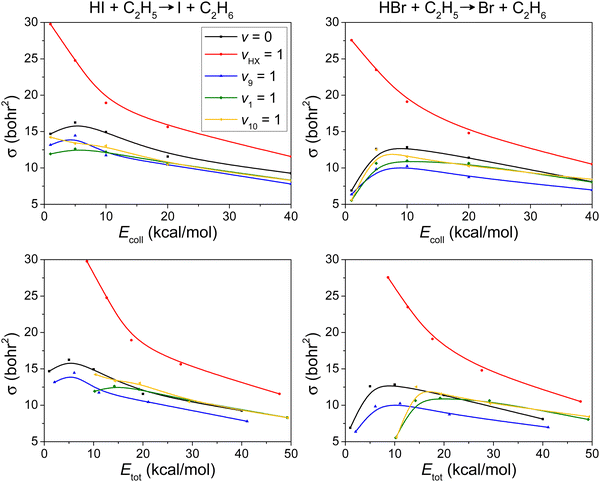
The integral cross-sections (σ) as a function of E_coll for the HI + C₂H₅ → I + C₂H₆ and HBr + C₂H₅ → Br + C₂H₆ reactions, presented in the upper panel of Fig. 4, reflect a substantial jump for v_HI/HBr = 1 and a slight inhibition effect for other mode-specific excitations in C₂H₅. It is interesting to see that v₉ = 1 (CH₂ wagging) inhibits the hydrogen abstraction most efficiently, because this wagging prevents HI/HBr from approaching the CH₂ group.

Fig. 4 Integral cross-sections as a function of collision energy (upper panels) and total energy (lower panels) for the HI/HBr(v_HI/HBr = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, 10] → I/Br + C₂H₆ reactions.

Fig. 3 shows that as E_coll increases, the reaction probability increases but b_max decreases. These two effects compete with each other, which results in the maximum in the excitation functions at around E_coll = 5 kcal mol⁻¹ as shown in Fig. 4. For the v_HX = 1 reaction, however, at low collision energies, HX vibrational excitation effectively enhances the reactivity, which overwhelms the peak that appeared for the ground-state and other excited-state reactions.

We also plot the ICS values as a function of the total initial energy in the lower panels of Fig. 4. This representation allows us to better visualize that vibrational excitation of HI/HBr-stretching wins over the effect of increasing translational energy.

B. Scattering and initial attack angle distributions

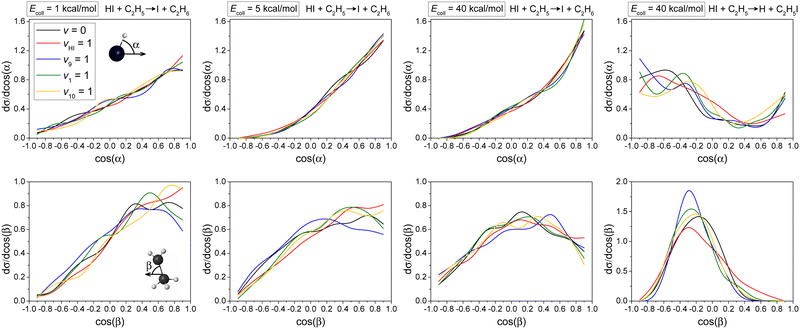
Differential cross-sections showing the scattering angle distributions of the HI + C₂H₅ reaction (H-abstraction: three panels on the left and I-abstraction: right panel) at different E_coll are shown in Fig. 5. The three left panels in Fig. 5 show that the excitation of the HI-stretching mode can clearly promote the forward scattering mechanism, similar to the effect of the high collision energy, indicating the dominance of the direct stripping mechanism in the H-abstraction reaction pathway. In the case of I-abstraction, little mode-specificity and larger statistical errors are observed, due to the fact that fewer I-abstraction reaction trajectories are observed compared to the H-abstraction pathway. But we can still see the clear dominance of backward scattering indicating the direct rebound mechanism for I-abstraction. This is consistent with the smaller b_max in the case of I-abstraction (Fig. 3).

Fig. 5 Normalized scattering angle distributions for the HI(v_HI = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, 10] reaction (H-abstraction: three panels on the left and I-abstraction: right panel) at different collision energies.

Normalized initial attack angle distributions for the HI(v_HI = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, 10] reactions are plotted in Fig. 6. The H-abstraction reaction pathway favors H-side attack over side-on HI and the least-preferred I-side approach, along with increasing collision energy, as expected, because a H–C bond forms in the H-abstraction process, but no clear mode-specificity is observed. In the case of the I-abstraction reaction pathway, it is expected that I-side attack is most favored, because an I–C bond forms in the I-abstraction process, and again no clear mode-specificity is observed. Comparing the two reaction pathways, we see that H-abstraction is much pickier about the initial attack angle distributions for HI than I-abstraction, which leads to a decrease in reactivity for the H-abstraction reaction pathway. This is one reason why the reaction probability of I-abstraction is even a little higher than that of H-abstraction when b = 0 (Fig. 3), even though the I-abstraction pathway is less energy favored (Fig. 2).

Fig. 6 Normalized initial attack angle distributions for the HI(v_HI = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, 10] reactions (H-abstraction: three panels on the left, I-abstraction: right panel). The attack angles are defined at the beginning of each reactive trajectory. α and β are calculated from the velocity vector of center of mass of the examined reactant and an interatomic vector that is considered as the I–H bond for HI and the C–C bond for C₂H₅, respectively.

The H-abstraction reaction pathway favors side-on CH₃CH₂ attack over CH₂-side and the least-preferred CH₃-side approach, especially at high collision energy, without significant mode-specificity. However, the I-abstraction reaction pathway favors side-on CH₃CH₂ attack over head-on CH₃-side or CH₂-side approach. The dominance of side-on CH₃CH₂ attack in I-abstraction is more obvious than in the case of the H-abstraction reaction pathway.

C. The post-reaction distribution of energy

As shown in Fig. 7, at low collision energies, when the HI-stretching mode is excited, the product clearly gains more relative translational energy, similar to the case of the H-abstraction reaction pathway in the HBr + C₂H₅ reaction.³⁶ This is because the vibrational HI-stretching energy transforms to translational energy after the H–I bond is broken. At high collision energies however, this effect is overwhelmed, and no clear mode-specificity is observed.

Fig. 7 Normalized product relative translational energy distributions for the HI(v_HI = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, 10] reactions. (H-abstraction: three panels on the left and I-abstraction: right panel).

In the case of the H-abstraction reaction pathway, the distributions become broader as the E_coll increases, and their maxima are shifted by almost the total increase in the E_coll, indicating that the major part of the initial translational energy ends up in translational recoil in all cases. In the case of the I-abstraction reaction pathway, however, only a small part of the initial translational energy ends up in translational recoil.

The internal energy distributions of the product, ethane for H-abstraction and C₂H₅I for I-abstraction, plotted in the upper panels of Fig. 8, feature clear mode-specificity with maxima shifting toward higher energies with nearly the value of the corresponding vibrational excitation energy.

Fig. 8 Normalized internal energy (E_inte), vibrational energy (E_vib) and rotational energy (E_rot) distributions for the product ethane for the HI(v_HI = 0, 1) + C₂H₅(v_x = 0, 1) [x = 9, 1, 10] reactions. (H-abstraction: three panels on the left and I-abstraction: right panel).

Considering that the ZPE of ethane and C₂H₅I is 47 and 41 kcal mol⁻¹, respectively, only one of the reactive trajectories in our simulations violates the ZPE constraint, in accordance with the middle panels of Fig. 8. The high internal excitation for the ethane product is expected considering the early-barrier, i.e., reactant-like TS with a significantly stretched CH bond, and highly-exothermic nature of the H-abstraction channel. Furthermore, in both reaction pathways, the products are atom + molecule. Since the atom does not have internal energy so all the energy beyond translation becomes the internal energy of the molecular product. In this case, it is a common thing that there is no or negligible ZPE violation (see, for example, ref. 41). The vibrational energy distributions show a red shift compared to the internal energy distributions, due to the fact that some of the vibrational energy is transformed into rotational energy, especially at high E_coll (lower panels). No significant mode-specificity is observed for rotational energy.

IV. Conclusions

The vibrational mode-specific QCT simulations are performed for the HI + C₂H₅ reaction on a recently developed high-level ab initio full-dimensional spin–orbit-corrected PES by exciting four different vibrational modes of the reactants at five collision energies. A significant enhancement for the HI + C₂H₅ reaction when v_HI = 1 is observed, especially for the I-abstraction reaction pathway and at low collision energy for the H-abstraction reaction pathway. The b_max values and the shape of the opacity functions do not change considerably. A minor inhabitation effect is seen for the three selected mode excitations of ethyl for the H-abstraction reaction pathway, just like in the case of the HBr + C₂H₅ reaction.³⁶ The CH₂ wagging (v₉) prevents HI from approaching the CH₂ group, which leads to the most efficient inhabitation effect for H-abstraction. In our previous work on the HBr + C₂H₅ reaction we found another reaction pathway, that is, hydrogen-exchange (H′Br + C₂H₅ → HBr + C₂H₄H′).³⁶ However, in the present work on the HI + C₂H₅ reaction we do not see any of these trajectories. The scattering angle distributions indicate the dominance of the direct stripping mechanism in H-abstraction while the direct rebound mechanism is dominant in I-abstraction. As for the attack angle, the dominance of side-on CH₃CH₂ attack in I-abstraction is more obvious than in the case of the H-abstraction reaction pathway. The translational energy distributions show that the product clearly gains more relative translational energy when the HI-stretching mode is excited, similar to the case in the HBr + C₂H₅ reaction.³⁶ This effect is overwhelmed at high collision energy. As the E_coll increases, the product relative translational energy distributions become broader, and their maxima are shifted by almost the total increase in E_coll, indicating that the major part of the initial translational energy ends up in translational recoil, in the H-abstraction reaction pathway. In the case of I-abstraction, however, only a small part of the initial translational energy ends up in translational recoil. More collision energy is transformed into the vibrational and rotational degrees of freedom of the product at high E_coll, which is more severe in the case of I-abstraction than in the H-abstraction reaction pathway. Only one reactive trajectory violates the ZPE constraint in our simulations. We hope that our work will inspire further experimental and theoretical studies on the mode-specificity of this reaction family, thereby becoming the new benchmark systems of polyatomic reaction dynamics.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research, Development and Innovation Office–NKFIH, K-125317; the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT; project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences. The authors thank Prof. Bin Jiang for sending them their SVP code.

References

1. A. Saiz-Lopez, J. M. C. Plane, G. McFiggans, P. I. Williams, S. M. Ball, M. Bitter, R. L. Jones, C. Hongwei and T. Hoffmann, Atmos. Chem. Phys., 2006, 6, 883.
2. K. Seitz, J. Buxmann, D. Pöhler, T. Sommer, J. Tschritter, T. Neary, C. O'Dowd and U. Platt, Atmos. Chem. Phys., 2010, 10, 2117.
3. C. Fortin, V. Fèvre-Nollet, F. Cousin, P. Lebègue and F. Louis, Atmos. Environ., 2019, 214, 116838.
4. G. McFiggans, H. Coe, R. Burgess, J. Allan, M. Cubison, M. R. Alfarra, R. Saunders, A. Saiz-Lopez, J. M. C. Plane, D. Wevill, L. Carpenter, A. R. Rickard and P. S. Monks, Atmos. Chem. Phys., 2004, 4, 701.
5. A. Saiz-Lopez, J. M. C. Plane, A. R. Baker, L. J. Carpenter, R. von Glasow, J. C. G. Martín, G. McFiggans and R. W. Saunders, Chem. Rev., 2012, 112, 1773.
6. A. Saiz-Lopez, R. P. Fernandez, C. Ordóñez, D. E. Kinnison, J. C. G. Martín, J.-F. Lamarque and S. Tilmes, Atmos. Chem. Phys., 2014, 14, 13119.
7. D. Stone, L. K. Whalley and D. E. Heard, Chem. Soc. Rev., 2012, 41, 6348.
8. D. Stone, T. Sherwen, M. J. Evans, S. Vaughan, T. Ingham, L. K. Whalley, P. M. Edwards, K. A. Read, J. D. Lee, S. J. Moller, L. J. Carpenter, A. C. Lewis and D. E. Heard, Atmos. Chem. Phys., 2018, 18, 3541.
9. I. Korsakissok, A. Mathieu and D. Didier, Atmos. Environ., 2013, 70, 267.
10. J. S. D. Kumar, M. M. Ho and T. Toyokuni, Tetrahedron Lett., 2001, 42, 5601.
11. J. H. Jones, Platin. Met. Rev., 2000, 44, 94.
12. G. J. Sunley and D. J. Watson, Catal. Today, 2000, 58, 293.
13. J. A. Seetula, J. J. Russell and D. Gutman, J. Am. Chem. Soc., 1990, 112, 1347.
14. K. Mečiarová, M. Šulka, S. Canneaux, F. Louis and I. Černušák, Chem. Phys. Lett., 2011, 517, 149.
15. N. Leplat, A. Wokaun and M. J. Rossi, J. Phys. Chem. A, 2013, 117, 11383.
16. N. Leplat, J. Federič, K. Šulková, M. Sudolská, F. Louis, I. Černušák and M. J. Rossi, Z. Phys. Chem., 2015, 229, 1475.
17. D. Papp, B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 396.
18. C. K. Westbrook, Proc. Combust. Inst., 1982, 19, 127.
19. J. Yuan, L. Wells and P. Marshall, J. Phys. Chem. A, 1997, 101, 3542.
20. T. Bentz, M. Szőri, B. Viskolcz and M. Olzmann, Z. Phys. Chem., 2011, 225, 1117.
21. C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 29084.
22. T. Győri and G. Czakó, J. Chem. Phys., 2022, 156, 071101.
23. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113.
24. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
25. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
26. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
27. Z. Xie and J. M. Bowman, J. Chem. Theory Comput., 2010, 6, 26.
28. Z. Chen, J. Chen, R. Chen, T. Xie, X. Wang, S. Liu, G. Wu, D. Dai, X. Yang and D. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9202.
29. Y. Liu, H. Song, D. Xie, J. Li and H. Guo, J. Am. Chem. Soc., 2020, 142, 3331.
30. D. Gao and D. Wang, Phys. Chem. Chem. Phys., 2021, 23, 26911.
31. D. Papp, J. Li, H. Guo and G. Czakó, J. Chem. Phys., 2021, 155, 114303.
32. D. Papp and G. Czakó, J. Chem. Phys., 2021, 155, 154302.
33. S. Mondal, H. Pan and K. Liu, Phys. Chem. Chem. Phys., 2022, 24, 24050.
34. H. Song, W. Xie, C. Zhang and M. Yang, J. Phys. Chem. A, 2022, 126, 663.
35. V. Tajti and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 8166.
36. C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 3083.
37. C. Yin, V. Tajti and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 24784.
38. W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399−407.
39. B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 234104.
40. H. Guo and B. Jiang, Acc. Chem. Res., 2014, 47, 3679.
41. V. Tajti, T. Győri and G. Czakó, J. Chem. Phys., 2021, 155, 124301.

---