Gas phase models of hydride transfer from divalent alkaline earth metals to CO₂ and CH₂O

Abstract

The reactivity of HMg⁺, HMgCl, and HMgCl₂⁻ in hydride transfer reactions with CO₂ and CH₂O were studied by means of the reverse reactions—decarboxylation of HCO₂MgCl_n^+/0/− and deformylation of CH₃OMgCl_n^+/0/− (n = 0–2)—by a combination of quantum chemical computations and mass spectrometry experiments. HCO₂Mg⁺, HCO₂MgCl and HCO₂MgCl₂⁻ display similar energetics for unimolecular carbon dioxide loss; for CH₃OMg⁺, CH₃OMgCl and CH₃OMgCl₂⁻, formaldehyde loss is more favourable for the cationic species than for the anionic one, with the neutral species found in-between. Despite very similar overall thermochemistry for each of the charge states of the CO₂ and CH₂O systems, the intermediate reaction barriers are higher for the CO₂ eliminations due to a more complex and demanding reaction mechanism. Exothermic ligand exchange is observed for CH₃OMg⁺ reacting with CO₂, forming HCO₂Mg⁺ and CH₂O. Both the thermochemistry and the presence of intermediate energy barriers slightly disfavour this type of ligand exchange for CH₃OMgCl and CH₃OMgCl₂⁻. It was also found that CH₃OMg⁺ reacts readily with H₂O to eliminate H₂, whereas quantum chemical computations predict that the corresponding neutral and anionic species suffer unfavourable reaction thermochemistry. A corresponding reaction for the magnesium formate compounds was not observed. Quantum chemical computations were performed to investigate periodic trends in reactivity. The energetic requirements for decarboxylation of HCO₂M⁺, HCO₂MCl and HCO₂MCl₂⁻ increase in the order M = Be, Mg, Ca, Sr and Ba; the only exception is the cationic Be species for which the reaction is more endothermic than for the corresponding Mg species. For deformylation of CH₃OM⁺, CH₃OMCl and CH₃OMCl₂⁻ the trends are more irregular and less pronounced than for the decarboxylation reactions; however, the Be species was found to have higher reaction energies than the Mg species for all the methoxy-compounds irrespective of charge state. The effect on decarboxylation and deformylation upon replacing Cl with F, Br or I was found to be minimal for all aforementioned species. The consequences of these observations on the reverse reactions, hydride transfer to CO₂ and CH₂O, are discussed, and the effects of systematic structural changes on reactivity are rationalized on the basis of thermochemical cycles and well-known periodic trends.

---

Introduction

Main group metal hydrides, MH_n, and metal hydride anions, MH_n+1⁻, are powerful reducing agents that find much use in organic chemistry.¹ Well-known examples are B₂H₆ and AlH₄⁻. Within this group of compounds, we also find MgH₂, which is a stable solid that releases hydrogen upon heating. Since this process is reversible, magnesium hydrides are promising lightweight hydrogen storage materials.^2,3 Mechanically or chemically activated MgH₂ has also been suggested as a potential anode material for use in Li-ion batteries due to their good hydride transfer properties.^4,5 While MgH₂ itself is poorly soluble in organic solvents, derivatives of the type HMgX (X = NR₂, OR, halide, Cp, N-heterocyclic carbenes)—in analogy with the closely related Grignard reagent—often exist in the form of dimers or higher oligomers in such solvents.⁶ These derivatives are effective and selective reducing agents, in particular towards the carbonyl group,^2,7–9 but also towards the CO₂ molecule.^10–12 A β-diketiminato magnesium hydride has even been demonstrated to reductively couple two CO molecules, giving an ene–diolate complex as product.¹³ The same complex has also been found to be reactive towards double and triple carbon–carbon bonds.¹⁴

Because the above-mentioned magnesium hydride derivatives (HMgX) exist as oligomers in solution, they are exceedingly difficult to isolate and characterise. Therefore, in order to study the basic reaction mechanism for hydride reduction, isolating the monomeric species in the gas phase appears to be a particularly attractive strategy. In this respect, OHair and co-workers were pioneers by being able to synthesize and isolate gas phase HMgX₂⁻ by mass spectrometry.¹⁵ These anions were made by decarboxylation of the corresponding formate complex, HCO₂MgX₂⁻, upon collision-induced dissociation (CID). It was also observed that the formate complex could be recreated in the reaction between HMgX₂⁻ and formic acid in the gas phase, upon dehydrogenation:

HMgCl₂⁻ + HCO₂H → HCO₂MgCl₂⁻ + H₂ (1)

It should also be mentioned that more recently, Attygalle and co-workers, using a similar technique, reported the formation of a plethora of metal hydride anions, including AlH₄⁻.¹⁶

In this work, we aim to increase our understanding of the reactions of HMgX species (X = halide) with carbonyl compounds, in particular carbon dioxide and formaldehyde. For practical reasons, the reactions studied will be the reverse of the hydride transfer, i.e., the decarboxylation and deformylation of HCO₂MgX_n^+/0/− and CH₃OMgX_n^+/0/−, respectively (n = 0–2). The essential thermochemical and kinetic information is obtained by quantum chemical computations supplemented by mass spectrometry experiments. Additional work included are possible ligand exchange reactions with CO₂ and H₂O. In addition, quantum chemical computations were performed on the effects of substituting the other alkaline earth metals for Mg.

Methods

Experimental details

The experiments were conducted using a QTOF 2 mass spectrometer (Micromass/Waters) with a quadrupole—time-of-flight geometry, electrospray ionisation (ESI) source and microchannel plate detectors. A collision cell with hexapole ion guide is situated in-between the quadrupole and the TOF unit; a modified collision gas inlet, fitted with a leak-valve, allows greater precision in setting the collision gas pressure compared to the original instrument. The setup has been described in detail previously.^17–20

The ions studied, CH₃OMgCl₂⁻, CH₃OMg⁺, HCO₂MgCl₂⁻ and HCO₂Mg⁺, were produced by ESI using millimolar solutions of MgCl₂, with addition of HCO₂H for the formation of the formate-containing ions. The solvents were either methanol or methanol–water 1 : 1. For specific concentrations, additives and solvent ratios, please see the ESI;† the source conditions used to generate the ions can also be found in the ESI.† All reagents were obtained from commercial suppliers (Sigma-Aldrich, VWR Chemicals) and utilized without further purification.

The quadrupole was used as a mass filter in order to isolate the reactant ions of interest; the selected ions then entered the collision cell, where CID occurred using Ar as the collision gas. The resulting products and surviving reactant ions were then analysed and detected in the TOF unit. The primary products of the CID, as well as being the products of interest, were HMg⁺ (for the positive parent ions) and HMgCl₂⁻ (for the negative parent ions).

For each parent ion, a measurement series comprised 20 measurements at various centre-of-mass (CoM) collision-energies in the approximate range of 50–600 kJ mol⁻¹ (depending upon the ion in question). Data were related to an internal reference in order to ensure comparability between different measurements. Appearance curves were obtained by plotting the phenomenological cross section for formation of HMg⁺ or HMgCl₂⁻ against the CoM collision energy. Five appearance curves were recorded for each ion using different collision gas pressures between 1 × 10⁻⁴ mbar and 5 × 10⁻⁴ mbar.

The appearance curves were analysed using the L-CID software, developed in the group of Chen.²¹ L-CID produces a fit to an experimental appearance curve with the main output being the threshold energy, i.e., the collision energy necessary to induce fragmentation (accounting for thermal shift, kinetic shift, Doppler broadening etc.). The software has previously been used by us to successfully analyse data from the experimental setup in use here;²² a more in depth description of the software, and considerations for its use with the QTOF 2 instrument can be found in that paper. It should be noted that L-CID assumes an instrumental configuration in which the ions are thermalized to the same temperature as the collision gas prior to collision, which is not the case for our setup; as such, a systematic error in the threshold energies is to be expected (depending upon the internal energy distribution of the ions). Furthermore, in order to circumvent the need to know the vibrational frequencies explicitly, L-CID utilizes a single effective frequency, an approximation requiring the ion to be of sufficient size. The ions studied here—with as few as five atoms—are smaller than the smallest test case used in the development of L-CID, the latter being toluene with 15 atoms. Regardless, the obtained threshold energies appear reasonable and internally consistent when compared to the appearance curves from which they were extracted.

Using the threshold energies from five different collision gas pressures, an extrapolation to zero pressure was done in order to compensate for the apparent lowering of a threshold energy caused by the ion experiencing multiple collisions with the gas molecules.

Each experiment was carried out at least twice in order to verify repeatability. To ensure no bias towards the detection of ions with different abundancies, the ability of the mass spectrometer to faithfully reproduce the expected isotope distribution of magnesium chloride clusters was tested before each experiment.

In comparing the results from different experiments, it appears that the greatest uncertainty arising from the process outlined above comes from the extrapolation of threshold energies to zero collision gas pressure. We estimate the final threshold energies to be semi-quantitative in nature and reproducible within ±10–20 kJ mol⁻¹ between experiments.

Computational details

The computational results presented in this work were obtained using the Gaussian-4 (G4) method as implemented in Gaussian 09/16.²³ This is a thermochemical method which utilizes several levels of theory and is estimated to be accurate to within 10–15 kJ mol⁻¹.²⁴ Selected G4 geometries were reoptimized using CCSD(T)/aug-cc-pVTZ, MP2 and a handful of DFT functionals, as presented in Table S3 of the ESI.† CCSD(T)/aug-cc-pVTZ computations were performed in NWChem.²⁵ All minima and transition states were checked for the correct number of imaginary frequencies. Transition states were subjected to an intrinsic reaction coordinate (IRC) computation in order to determine the connected minima. Options selected for the computations can be found in the ESI.†

Results and discussion

Hydride affinities and complexation energies

Before discussing the individual hydride transfer reactions, it is necessary to establish the thermochemistry. In particular, this requires knowledge of the hydride affinities (HA) and complexation energies of the key species involved: CO₂, CH₂O and the relevant Mg(II) complexes. This information was obtained from the quantum chemical computations, using the G4 scheme, and is presented in Fig. 1. The computed values of HA(CO₂) = 254 kJ mol⁻¹ and HA(CH₂O) = 197 kJ mol⁻¹ are higher than the literature estimates of 216 ± 10 kJ mol⁻¹ and 170 ± 4 kJ mol⁻¹, respectively.^26,27,28 The literature values were based on Born–Haber cycles obtained from experimentally determined electron affinities and gas phase enthalpies-of-formation for the species involved. The substantial deviation between the computed and the experimental data is very likely due to the inadequacy of the G4 method in describing the naked hydrogen anion.²⁹ As a result, the electron affinity of H is underestimated by a factor of two, which indicates the magnitude of the error in predicting the above hydride affinities. Besides this, the rest of the computations presented here should be void of this shortcoming and comply with the documented “chemical accuracy” of G4 of approximately ± 10 kJ mol⁻¹.

Fig. 1 Energy diagrams based on the quantum chemical computations (G4, 0 K) indicating the key reaction thermochemistry (in kJ mol⁻¹) for hydride transfer from the Mg(II) species to (a) CO₂ and (b) CH₂O. The ionic species have been investigated experimentally, see below, while the neutral species could only be studied computationally.

As noted above, the gas phase HA of carbon dioxide is higher than that of formaldehyde; however, the gas phase HA of the Mg(II) complexes are significantly higher than the HA of either of the organic substrates. For example, the hydride transfer from HMgCl₂⁻ to CO₂ forming MgCl₂ and HCO₂⁻ is a reaction that is endothermic by (380–254) kJ mol⁻¹ = 126 kJ mol⁻¹. This may at first sight appear counterintuitive, since main group metal hydrides are used as reducing agents in organic chemistry. However, it is important to note that the driving force for the reaction is not necessarily the reduction itself, but the complexation in the resulting product. The possibility to form strong bonds between the oxophilic magnesium centre and the formate or methoxide anions results in reactions that are overall exothermic, as seen in reactions (2)–(7).

It is evident from Fig. 1 that both the HA's and the complexation energies decrease significantly with increasing number of Cl atoms in the Mg(II) complex. Despite this, the energy profiles for the combined hydride transfer and complexation reactions are noticeably similar for all charge states, in both the CO₂ and CH₂O case. Only a small, albeit systematic, difference in the overall reaction energy remains as the effect of the number of chloride ligands, as seen in reactions (2)–(4) and reactions (5)–(7), respectively.

Collision-induced dissociation of HCO₂Mg⁺ and CH₃OMg⁺

Each of the ions HCO₂Mg⁺ and CH₃OMg⁺ were produced by electrospray ionisation and mass selected before being subject to energy variable CID (see the Methods section). At the fairly low collision energies used here, the primary processes are, respectively, decarboxylation and deformylation:

HCO₂Mg⁺ → HMg⁺ + CO₂ (8)

CH₃OMg⁺ → HMg⁺ + CH₂O (9)

The reader should note that reaction (8) is the reverse of reaction (2), while reaction (9) is the reverse of reaction (5).

An example of experimentally recorded appearance curves for reactions (8) and (9) is shown in Fig. 2, collected at a collision gas pressure P_Ar = 5 × 10⁻⁴ mbar. Using the L-CID software,²¹ it is possible to estimate the threshold energies producing the curves to be 163 kJ mol⁻¹ and 104 kJ mol⁻¹, respectively.

Fig. 2 Appearance curves for HMg⁺ upon energy variable CID (P_Ar = 5 × 10⁻⁴ mbar) of HCO₂Mg⁺ (open circles) and CH₃OMg⁺ (closed squares).

To compensate for the CID results being affected by ions experiencing multiple collisions, threshold energies from five different collision gas pressures were extrapolated to produce a threshold energy at P_Ar = 0 mbar (all threshold values and extrapolation parameters can be found in the ESI†). The resulting values were 198 kJ mol⁻¹ for HCO₂Mg⁺ and 136 kJ mol⁻¹ for CH₃OMg⁺.

In addition to HMg⁺, some minor products were also detected upon CID of the reactant ions. For CH₃OMg⁺, loss of elements corresponding to CH₃O^•, giving rise to Mg⁺, was observed above approximately 300 kJ mol⁻¹ (CoM). For HCO₂Mg⁺, we observed small amounts of MgOH⁺, corresponding to loss of CO. However, MgOH⁺ could potentially be formed from the primary product MgH⁺ reacting with restgas H₂O and eliminating H₂; our computations show this reaction to be exothermic at −81 kJ mol⁻¹.

Collision-induced dissociation of HCO₂MgCl₂⁻ and CH₃OMgCl₂⁻

For the anions, HCO₂MgCl₂⁻ and CH₃OMgCl₂⁻, formally derived from each of the two cations discussed above by the addition of two chloride ions, we also observe decarboxylation/deformylation upon CID at low collision energies:

HCO₂MgCl₂⁻ → HMgCl₂⁻ + CO₂ (10)

CH₃OMgCl₂⁻→ HMgCl₂⁻ + CH₂O (11)

Appearance curves for formation of HMgCl₂⁻ from HCO₂MgCl₂⁻ and CH₃OMgCl₂⁻ are shown in Fig. 3 for the collision gas pressure 5 × 10⁻⁴ mbar; the associated threshold energies are 136 and 132 kJ mol⁻¹, respectively. Upon extrapolation to zero collision gas pressure, the threshold energies for reactions (10) and (11) become 189 and 181 kJ mol⁻¹, respectively.

Fig. 3 Appearance curves for HMgCl₂⁻ upon energy variable CID (P_Ar = 5 × 10⁻⁴ mbar) of HCO₂MgCl₂⁻ (open circles) and CH₃OMgCl₂⁻ (closed squares).

For the anionic precursors, formation of Cl⁻ is observed as a secondary reaction-channel in the CID experiments. For HCO₂MgCl₂⁻ the abundance of Cl⁻ was too small to get a good estimate on the threshold energy for its formation. For CH₃OMgCl₂⁻, the abundance of Cl⁻ is lower, albeit comparable, to that of HMgCl₂⁻ and the threshold energy (at zero collision gas pressure) could be estimated to 200 kJ mol⁻¹. In comparing Fig. 2 and 3, we see that for the cations, the methoxide precursor produces a greater abundance of the magnesium hydride product compared to the formate precursor, whereas for the anions, the relationship is reversed. The fact that, for CH₃OMgCl₂⁻, formation of HMgCl₂⁻ is in competition with an easily accessible second reaction channel is the likely explanation as to why. Regardless, the second reaction channel has been explicitly accounted for in the L-CID analysis and should not impact the estimated threshold energies for formation of HMgCl₂⁻.

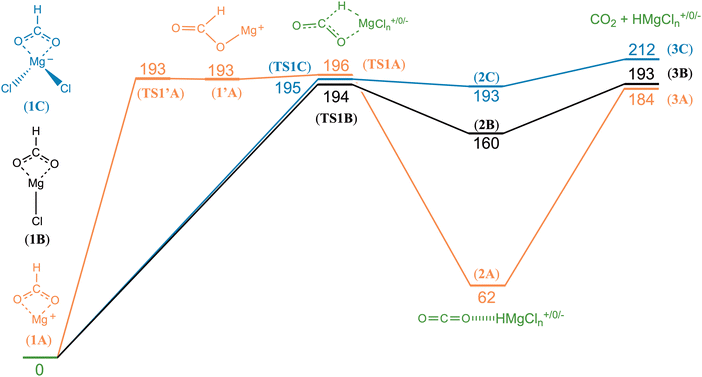
Computational results for decarboxylation of magnesium formate complexes

The potential energy diagrams for decarboxylation of HCO₂Mg⁺, HCO₂MgCl and HCO₂MgCl₂⁻ are displayed in Fig. 4. It can be seen that the three analogous reactions have very similar transition state energies and show a slight increase in the overall reaction energy with increasing number of chloride ligands. The computed transition state energies and reaction energies are so similar that it becomes impossible to decide which of the two reaction steps determines the threshold energy for product formation.

Fig. 4 Potential energy diagram for loss of CO₂ from HCO₂Mg⁺ (orange), HCO₂MgCl (black) and HCO₂MgCl₂⁻ (blue). Based on the quantum chemical computations (G4, 0 K) with relative energies given in kJ mol⁻¹. The reverse reactions equal a hydride transfer coupled with formate complex formation.

There are some distinct differences between the species. On the reactant side, for the cation, a shallow energy minimum is found, featuring the formate entity bound in a monodentate fashion (1′A). No such energy minimum could be located for the neutral or the anion. To which extent this difference is of importance to the overall reaction dynamics is, however, unclear. In any instance, and irrespective of charge state, one of the two Mg–O bonds of the bidentate formate complex must be fully broken in order to reach the transition state of the actual hydrate transfer (TS1A, TS1B or TS1C). The energetic cost of this is approximately the same in all three cases, and consequently, the threshold energy is nearly the same. However, the differences in the binding energies of the product complexes are much more significant. In the cation complex, 2A, there is strong interaction between the cationic magnesium centre, HMg⁺, and one of the electron rich oxygen atoms of CO₂. In contrast, in the anion complex, 2C, there is only a very weak interaction between HMgCl₂⁻ and CO₂. Not surprisingly, the situation for the neutral product complex, 2B, is in-between those of the cationic and the anionic complexes.

Fig. 5 shows the most important binding parameters of the three transition state structures. While the transition state energies are similar, the geometries differ, in particular for the formyl moiety. The geometry is the most reactant-like for the cation in that it has the shortest C–H bond length of the three; the transition state TS1A can therefore be considered to be earlier than TS1B and TS1C with respect to the reaction coordinate 1 → 2; this is consistent with 2A being the most strongly bonded of the product complexes (Hammond's postulate). Thus, the gradual increase in the C–H bond length and the O–C–O bond angle of TS1A, TS1B and TS1C can be said to reflect the trend in the complex energies of 2A, 2B and 2C.

Fig. 5 Transition state geometries for decarboxylation of HCO₂Mg⁺ (TS1A), HCO₂MgCl (TS1B) and HCO₂MgCl₂⁻ (TS1C). Bond lengths are given in pm and bond angles in degrees.

Computational results for deformylation of magnesium methoxide complexes

For the methoxy complexes, the variation in reaction energies for the deformylation reactions, shown in Fig. 6, is slightly more pronounced than for the decarboxylation reactions discussed above (Fig. 4). It is worth noting that while the reaction energies show only a small charge dependence, the energies of the transition states (TS2) and ion–neutral complexes (5) are more strongly dependent upon charge. In any case, for all three charge states (+, 0 and −), the transition state energy is lower than the product energy and the energetic threshold of the reaction is determined by the overall reaction endothermicity.

Fig. 6 Potential energy diagram for loss of CH₂O from CH₃OMg⁺ (orange), CH₃OMgCl (black) and CH₃OMgCl₂⁻ (blue). Based on the quantum chemical computations (G4, 0 K) with relative energies given in kJ mol⁻¹. The reverse reactions equal a hydride transfer coupled with methoxy complex formation.

In contrast to the decarboxylation reactions, for the deformylation reactions the route from the reactant towards the transition state is a direct hydride transfer without the need to first break an additional Mg–O bond; as a result of this, the assumptions inherent to the Hammond postulate are fulfilled. Therefore, we expect increasing endothermicity of the elementary reaction step 4 → 5 to correlate with a higher barrier; we also expect the position of the transition state to be further along the reaction path (i.e. the geometry of the transition state to be less like the reactant). Inspection of Fig. 6 and the transition state geometries in Fig. 7 reveals this to be the case.

Fig. 7 Transition state geometries for decarboxylation of CH₃OMg⁺ (TS2A), CH₃OMgCl (TS2B) and CH₃OMgCl₂⁻ (TS2C). Bond lengths are given in pm and bond angles in degrees.

Comparison of experimental and computational results

The experimental threshold energies—198 kJ mol⁻¹ for loss of carbon dioxide from HCO₂Mg⁺ and 136 kJ mol⁻¹ for loss of formaldehyde from CH₃OMg⁺—can be compared to the rate determining energies from the G4 (0 K) computations. For the former reaction, the relevant computed energy is 196 kJ mol⁻¹ (corresponding to the height of TS1A); for the latter reaction, the computational threshold energy is 164 kJ mol⁻¹ (the overall reaction energy of 4A → 6A).

For loss of carbon dioxide from HCO₂MgCl₂⁻, and loss of formaldehyde from CH₃OMgCl₂⁻, the experimental threshold energies are 189 and 181 kJ mol⁻¹, respectively; the corresponding values from our computations (G4, 0 K) are 212 and 211 kJ mol⁻¹, respectively. The G4 data for reaction (10) are in good qualitative accord with the B3LYP/6-31+G(d) model of Khairallah and O'Hair.¹⁵

Typically, G4 energies are accurate within ±10–15 kJ mol⁻¹.²⁴ Our experimental threshold energies are reproducible within ±10–20 kJ mol⁻¹ (±2 estimated standard deviations), with the extrapolation to zero pressure constituting the highest uncertainty factor. In this respect, the experimental and computed data are not significantly different, although a nominal difference of up to 30 kJ mol⁻¹ may appear high. It is also relevant that DFT methods appear to give lower estimates for reaction energies, by 10–20 kJ mol⁻¹ (see ESI†), compared to the explicitly correlated method used here.

Computational results for other ligands and metals

Additional computations were performed in order to investigate how different charge states, ligands and metals impact the overall reaction energy and transition states of the reactions presented in Fig. 4 and 6. In order to include also the heavier elements, these computations were done using B3LYP/LANL2DZ. This compromise clearly affects the quality of computed energies, and we note that this rather rudimentary basis set give both higher reaction energies and higher transition state energies compared to the more accurate G4 data—compare values from Tables 1 and 2 (M = Mg and X = Cl) to the results in Fig. 4 and 6. On the other hand, the charge dependence (corresponding to the number of anionic ligands) is the same, and we therefore assume that also the periodic trends to be discussed below are correctly reproduced using B3LYP/LANL2DZ.

Table 1 The effect on computed transition state energy, E(TS), and reaction energy, , for decarboxylation and deformylation of magnesium formate and -methoxy complexes, upon substituting F, Br or I for Cl. Energies in kJ mol⁻¹ obtained with B3LYP/LANL2DZ. Note that there is no separate entry for HCO₂Mg⁺ since there is no halide involved

Ligand (X)	HCO2MgX → CO2 + HMgX		HCO2MgX2^− → CO2 + HMgX2^−		CH3OMgX → CH2O + HMgX		CH3OMgX2^− → CH2O + HMgX2^−
	E(TS)		E(TS)	ΔEr°	E(TS)		E(TS)
F	204	216	234	261	197	233	226	249
Cl	204	215	225	246	200	237	231	245
Br	204	214	222	238	202	239	229	242
I	205	214	220	234	204	241	227	240

---

Table 2 Computed transition state energy, E(TS), and reaction energy, , for decarboxylation of HCO₂M⁺, HCO₂MCl and HCO₂MCl₂⁻. M = Be, Mg, Ca, Sr and Ba. Energies in kJ mol⁻¹ obtained with B3LYP/LANL2DZ

Metal (M)	HCO2M^+ → CO2 + HM^+		HCO2MCl → CO2 + HMCl		HCO2MCl2^− → CO2 + HMCl2^−
	E(TS)		E(TS)		E(TS)
Be	187	215	185	172	205	224
Mg	201	195	204	215	225	246
Ca	208	240	220	257	251	281
Sr	216	252	231	279	261	292
Ba	229	274	Not found	298	273	306

---

Table 1 shows how the nature of the halide ligand (X) affects the overall reaction energy, and the energy of the transition state, upon decarboxylation of HCO₂MgX_n^+/0/− and deformylation of CH₃OMgX_n^+/0/− (n = 1, 2). For comparison, in these computations, the decarboxylation of HCO₂Mg⁺ have E(TS) = 201 kJ mol⁻¹ and , while the deformylation of CH₃OMg⁺ have E(TS) = 151 kJ mol⁻¹ and . From the G4-computations (Fig. 4 and 6) we saw that both the reaction energy and the transition state energy tends to increase with the number of Cl-ligands on Mg; the exception is the transition state for decarboxylation of HCO₂Mg⁺ which is higher, not lower, than the transition states of the neutral and anionic species. It appears from the data in Table 1 that the general trend holds true also upon substituting F, Br or I for Cl; that is, the reaction energy and transition state energy increases with increasing number of ligands. It is quite interesting to see that, for the neutral formate- and methoxy complexes, the transition state energies and reaction energies are surprisingly similar for all four halides in Table 1. At variance, for n = 2 (the anions), both the transition state energies and the reaction energies tend to decrease going down in the group.

Table 2 shows the effect of different alkaline earth metals on the decarboxylation reactions at various charge states of the HCO₂MCl_n^+/0/− complexes. The clear trend is that decarboxylation becomes less and less favourable going down in the group of the alkaline earth metals (Be, Mg, Ca, Sr and Ba); both the transition state energies and the reaction energies are affected in the same way, with exception of the reaction energy for decarboxylation of HCO₂Be⁺ which is actually larger than that of HCO₂Mg⁺. Some insight into the observed trend can be found by decomposing the reaction into five steps, with their associated energies (IE = ionisation energy, EA = electron affinity, PA = proton affinity), as follows:

HCO₂M⁺ → HCO₂⁻ + M²⁺ −ΔE_complex (12)

H⁻ → H⁺ + 2e⁻ EA(H) + IE(H) (13)

HCO₂⁻ → H⁻ + CO₂ HA(CO₂) (14)

M + H⁺ → HM⁺ −PA(M) (15)

M²⁺ + 2e⁻ → M −(IE₁(M) + IE₂(M)) (16)

Thus, the total reaction,

HCO₂M⁺ → HM⁺ + CO₂ (17)

has a reaction energy of

Since the contributions from reactions (13) and (14) are constant in the series, the variation in the overall reaction energy, 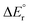, is governed by the contribution from the complexation energy (reaction (12)) minus the combined contributions from the metal's proton affinity and two ionisation energies (reactions (15) and (16)). These contributions show clear trends when going down the periodic table: both the complexation energy and the ionisation energy decrease in magnitude while the proton affinity increases in magnitude (Table 3). As noted above, is found to increase with increasing atomic number of the metal, with the exception of beryllium in the cationic complex; this irregularity can be traced to the very high complexation energy of Be²⁺.

Table 3 Computed trends in complexation energy (ΔE_complex), sum of first and second ionisation energy (IE₁(M) + IE₂(M)), proton affinity (PA(M)) and total reaction energy for the decarboxylation of HCO₂M⁺ with M = Be, Mg, Ca, Sr and Ba (reactions (12)–(18)). Energies in kJ mol⁻¹ obtained with B3LYP/LANL2DZ

	Be	Mg	Ca	Sr	Ba
ΔEcomplex (M(II) + HCO2^− → HCO2M^+)	−1965	−1487	−1209	−1126	−1042
IE1(M) + IE2(M) (M(0) → M(II))	2671	2153	1757	1634	1481
PA(M(0) + H^+ → HM^+)	710	769	843	870	917
	215	196	240	252	274

---

It is evident from Table 3 that the complexation energy for formate to M²⁺ decreases in magnitude with M = Be, Mg, Ca, Sr, Ba. In addition, it seen in Fig. 1a that the complexation energy of formate to Mg significantly decreases in magnitude upon addition of one or two chloride ligands to the metal: ΔE_complex = −338 kJ mol⁻¹ for the latter case. We must therefore consider the possibility that for HCO₂MCl₂⁻, loss of formate can become competitive with the decarboxylation reaction when going down the alkaline earth metal group. However, computed reaction energies for loss of HCO₂⁻ from HCO₂MCl₂⁻ with M = Be, Mg, Ca, Sr and Ba shows this not to be the case (see ESI,† Table S6).

The effect of different alkaline earth metals on the deformylation reactions of CH₃OMCl_n^+/0/− is shown in Table 4 (M = Be, Mg, Ca, Sr and Ba, n = 0–2). Also in this case we observe increasing reaction energies when going down the group of alkaline earth metals, with the exception of beryllium, which now show a higher reaction energy for all three charge states. However, the increase in reaction energy is less pronounced compared to the decarboxylation reactions in Table 2.

Table 4 Computed transition state energy, E(TS), and reaction energy, , for deformylation of CH₃OM⁺, CH₃OMCl and CH₃OMCl₂⁻. M = Be, Mg, Ca, Sr and Ba. Energies in kJ mol⁻¹ obtained with B3LYP/LANL2DZ

Metal (M)	CH3OM^+ → CH2O + HM^+		CH3OMCl → CH2O + HMCl		CH3OMCl2^− → CH2O + HMCl2^−
	E(TS)		E(TS)		E(TS)
Be	149	330	277	290	272	265
Mg	151	221	200	237	231	245
Ca	145	235	174	238	208	248
Sr	143	231	172	247	203	249
Ba	155	248	181	259	206	256

---

If one compares the overall reaction energies for decarboxylation of HCO₂M⁺ (Table 2) and deformylation of CH₃OM⁺ (Table 4), it can be seen that for M = Be and Mg, decarboxylation is easier by 115 and 26 kJ mol⁻¹, respectively. However, for Ca, Sr and Ba, deformylation is the more facile reaction by 5, 21 and 26 kJ mol⁻¹, respectively. In terms of Lewis hard/soft acid/base theory, we note that the Lewis acid, M, becomes increasingly soft when going down the group; consequently, the magnitude of the complexation energy decreases more quickly for the harder of the Lewis bases, CH₃O⁻ (Table S7 in ESI†), compared to the softer of the Lewis bases, HCO₂⁻.

Ligand exchange reactions

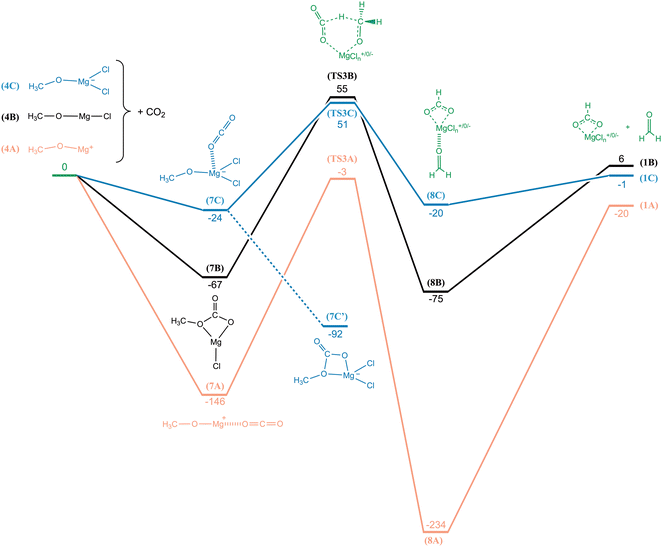
The reactions occurring when CH₃OMg⁺ and CH₃OMgCl₂⁻ collide with CO₂ were investigated, briefly, in mass spectrometry experiments. The anion was found to have an efficient complexation reaction wherein it simply adds CO₂ (ESI,† Fig. S1) and likely forms a stable carbonate-type intermediate (7C′, Fig. 9). For the cation, a ligand exchange reaction was observed instead:

CH₃OMg⁺ + CO₂ → HCO₂Mg⁺ + CH₂O (19)

The experimental result is displayed in the mass spectrum of Fig. 8a. The ligand exchange reaction is slow, resulting in a rather low product ion signal at m/z 69. The identity of the product was verified by repeating the measurement using two different isotopic labelling schemes (Fig. 8b and c), resulting in the expected mass shift, m/z 69 → 70, for the product.

Fig. 8 Mass spectra observed in isotopic reactions: (a) for CH₃OMg⁺ (m/z 55) + CO₂ (E_CoM = 46 kJ mol⁻¹, P_CO2 = 2.94 × 10⁻⁴ mbar), (b) for CH₃OMg⁺ + ¹³CO₂ (E_CoM = 48 kJ mol⁻¹, P_¹³CO2 = 2.62 × 10⁻⁴ mbar), and (c) for CD₃OMg⁺ (m/z 58) + CO₂ (E_CoM = 48 kJ mol⁻¹, P_CO2 = 2.62 × 10⁻⁴ mbar). Note that the intensity of the reactant peaks have been scaled down by a factor of 50.

To rationalize the outcome of these observations, we surveyed the potential energy surfaces using the G4 method. The potential energy curves for CH₃OMg⁺, CH₃OMgCl and CH₃OMgCl₂⁻ reacting with CO₂ is shown in Fig. 9. For CH₃OMg⁺ we find a transition state geometry (TS3A, −3 kJ mol⁻¹) involving a carbon-to-carbon hydride transfer, analogous to the Meerwein–Ponndorf–Verley mechanism.^30–32 This energy barrier—just below the energy of the reactants—explains the low reactivity observed in the measurement. Overall, the reaction is slightly exothermic with the products HCO₂Mg⁺ + CH₂O at −20 kJ mol⁻¹ relative to the reactants. The reactions of the neutral and the anion, CH₃OMgCl and CH₃OMgCl₂⁻, are almost thermoneutral; however, their transition states, TS3B and TS3C, give rise to substantial energy barriers of 55 and 51 kJ mol⁻¹, respectively, which explains why the latter reaction was not observed in our experiments. In all three reactions, the rate determining step is found to be the hydride transfer from the leaving formaldehyde unit to the entering CO₂ unit. The reactant side intermediate for the neutral, 7B, has a covalently bonded CO₂ group and is structurally different from the complexes 7A and 7C. In order for the neutral reaction to reach TS3B, one C–O bond must first be broken before the hydride transfer can occur; this provides the rationale as to why the neutral reaction has a higher barrier (relative to the reactant side intermediate) than the anion reaction, even though the product complex of the former (8B) is lower in energy.

Fig. 9 Potential energy curves for the reaction of CO₂ with CH₃OMg⁺ (orange), CH₃OMgCl (black) and CH₃OMgCl₂⁻ (blue). Based on the quantum chemical computations (G4, 0 K) with relative energies given in kJ mol⁻¹. Dashed lines indicate a reaction step which is presumed to have a non-existent or negligible barrier.

In Fig. 8a, there is a small peak at m/z 71 corresponding to the product CH₃O₂Mg⁺. The formation of this product from a reaction with CO₂ would necessitate the transfer of an oxygen atom to the reactant ion:

CH₃OMg⁺ + CO₂ → CH₃O₂Mg⁺ + CO (20)

Alternatively, the product could arise from a reaction with trace amounts of water vapour present in the collision cell:

CH₃OMg⁺ + H₂O → CH₃O₂Mg⁺ + H₂ (21)

Given the low abundance of rest gas H₂O compared to the ≈3 × 10⁻⁴ mbar of CO₂ used for the measurements in Fig. 8, reaction (21) would have to be significantly more efficient than reaction (19) in order to produce a product of comparable abundance. Separate measurements with water vapour as the collision gas show that CH₃OMg⁺ reacts readily with H₂O to produce the CH₃O₂Mg⁺ ion (ESI,† Fig. S2); CH₃OMgCl₂⁻ does not react in this way, but instead incorporates H₂O and ejects CH₃OH (ESI,† Fig. S3).

Isotope labelling of the carbon atom in carbon dioxide will not affect the mass of the product in reaction (20), nor would it affect a reaction of CH₃OMg⁺ with rest gas H₂O (reaction (21)); in agreement, no shift in the position of the peak can be seen in Fig. 8b. In contrast, Fig. 8c shows a shift in peak position by m/z +2 when starting from the isotopically labelled reactant CD₃OMg⁺. The increase in product mass by just two mass units rules out reaction (20), while for reaction (21) it would mean that the leaving hydrogen molecule comprises one hydrogen atom from CD₃OMg⁺ and one from H₂O.

The reaction between CH₃OMg⁺ and H₂O was investigated computationally (G4); the potential energy curve, along with complementary results for CH₃OMgCl and CH₃OMgCl₂⁻, is shown in Fig. 10. For the cation, we see a submerged barrier at −36 kJ mol⁻¹ and the overall reaction is exothermic at −141 kJ mol⁻¹. In comparing to the energetics of the CO₂/CH₂O ligand exchange reaction in Fig. 9 (barrier of −3 kJ mol⁻¹ and reaction energy of −20 kJ mol⁻¹), we see a clear indication that CH₃OMg⁺ should indeed react more readily with H₂O (reaction (21)) than with CO₂ (reaction (19)). Fig. 10 also shows that reaction with water is highly unfavourable for the anion, CH₃OMgCl₂⁻, with the transition state TS4C at 110 kJ mol⁻¹ relative to the reactants and an overall endothermic reaction. The reaction of CH₃OMgCl—although nearly thermoneutral—should also be unlikely due to the sizeable barrier of TS4B at 72 kJ mol⁻¹.

Fig. 10 Potential energy curves for the reaction of H₂O with CH₃OMg⁺ (orange), CH₃OMgCl (black) and CH₃OMgCl₂⁻ (green). Based on the quantum chemical computations (G4, 0K) with relative energies given in kJ mol⁻¹. Dashed lines indicate a reaction step which is presumed to have a non-existent or negligible barrier.

The three potential energy curves in Fig. 10 are displaced nearly parallel to each other, as determined by the overall thermochemistry; this reflects the similar reaction mechanisms of the species. For all three reactions, the preparation for H₂ elimination involves the H₂O entity providing a proton and the methoxy entity providing a hydride. It is evident that the cationic route is favoured due to activation by the positive charge, giving rise to the TS of lowest energy. The computationally derived reaction mechanisms thus confirm the validity of reaction (21) with regards to the isotope shifts observed upon exchanging CH₃OMg⁺ with CD₃OMg⁺ (Fig. 8c), i.e., each of the hydrogens in the leaving H₂ originate from a different reactant. It should be noted that the corresponding reaction with methanol has been observed by Khairallah and O'Hair: the isolated HMgCl₂⁻ was found to react readily with the methanol used as electrospray solvent.¹⁵

For the sake of completeness, we performed measurements on the reaction between HCO₂Mg⁺ and H₂O (Fig. S4 in ESI†). The analogue of reaction (21) would be

HCO₂Mg⁺ + H₂O → CHO₃Mg⁺ + H₂ (22)

with a product ion at m/z 85. However, in contrast to reaction (21), no firm evidence for this reaction could be found since there was only a very weak signal at the place of the presumed product (compare Fig. S4 to Fig. S2, in ESI†); instead, the main product was complexation of HCO₂Mg⁺ with H₂O, with what appears to be a subsequent elimination of CO as the second reaction channel. The results of isotopically labelled reactions failed to elucidate the matter (Fig. S5 in ESI†). The idea of a reaction between HCO₂Mg⁺ and H₂O proceeding in a manner analogue to the reaction between CH₃OMg⁺ and H₂O (Fig. 10) appears unfeasible based on two observations. Firstly, the H₂ elimination would require the breaking of one of the Mg–O bonds to allow for rotation of the formate unit to bring the hydride and the proton sufficiently close to each other. Secondly, as noted earlier, the HA of CO₂ is higher than that of CH₂O by 57 kJ mol⁻¹. A transition state geometry was located for reaction (22) using G4, positioned 99 kJ mol⁻¹ above the reactants in energy, which should be compared with the transition state of reaction (21) at −36 kJ mol⁻¹ (Fig. S6 in ESI†).

Conclusion

In this study we have analysed a series of decarboxylation and deformylation reactions by mass spectrometry and quantum chemical computations, finding consistency between experimental observation and theoretical model. The results have provided us with a number of valuable insights into the reverse reactions, i.e., the hydride transfer from selected magnesium hydride species to the prototypical carbonyl compounds, CO₂ and CH₂O, and the subsequent complexation between the oxophilic Mg(II) and the newly-formed anionic ligand, coordinated via the oxygen atom(s). It should be noted that there is a key difference in the reaction mechanisms: the hydride transfer to CO₂ involves a shift of the ligand, from a monodentate coordination to the metal in the pre-reaction complex, to a bidentate coordination upon formation of the product complex, which is not required in the CH₂O case. Consequently, the transition states of the former reaction are likely more destabilized.

In comparing the reaction energies and barriers for the three magnesium hydride species HMg⁺, HMgCl and HMgCl₂⁻ reacting with CO₂, we find that the number of chloride ligands (or equivalently overall electric charge) has a minimal impact, although there is a slight tendency for the anion to be more reactive than the neutral (Fig. 4). For HMg⁺, HMgCl and HMgCl₂⁻ reacting with CH₂O, the variation is somewhat larger with the neutral and the anion having more exothermic reactions compared to the cation, by 35–47 kJ mol⁻¹ (Fig. 6); on the other hand, the reaction barrier is more submerged for the cation (−67 kJ mol⁻¹) compared to the neutral (−33 kJ mol⁻¹) and the anion (−16 kJ mol⁻¹). The trends appear to hold true also when substituting other halides (F, Br and I) for Cl.

For the hydride transfer from HMg⁺, HMgCl or HMgCl₂⁻ to either CO₂ or CH₂O, we find that the reaction energies are surprisingly similar between the two substrate molecules; for instance, for the cation the difference is 20 kJ mol⁻¹ and for the anion it is essentially nil. This is despite the fact that carbon dioxide has a HA that is 57 kJ mol⁻¹ higher than that of formaldehyde. This means that the so-formed CH₃O⁻ ligand binds stronger to the magnesium centre compared to HCO₂⁻ by an amount that almost compensates for the difference in HA. However, in considering not just Mg, but also other alkaline earth metals, we find that the binding strength between the metal and the methoxy ligand, relative to that between the metal and the formate ligand, decreases for the series M = Be, Mg, Ca, Sr and Ba. It was also found that the hydride transfer reactions of HM⁺, HMCl and HMCl₂⁻ become increasingly more exothermic when descending group 2: Mg, Ca, Sr, Ba. However, the case of M = Be is exceptional in that it often results in more exothermic reactions compared to the other metals, mostly owing to the strong oxophilicity of Be; the effect is more pronounced for the cation, and more pronounced for the reaction with formaldehyde.

Our experimental investigation also revealed that in the gas phase, CH₃OMg⁺ reacts directly with CO₂ by ligand switching, and CH₂O is released upon formation of HCO₂Mg⁺. The reaction occurs by direct hydride transfer between the electrophilic carbons of the two ligands in a classical Meerwein–Ponndorf–Verley-type mechanism.^30–32 Both alcohols and formic acid are known to be reactive in carbon-to-carbon hydride transfers in organic chemistry.³³ It was also found that CH₃OMg⁺ appears to be highly reactive with H₂O, producing CH₃O₂Mg⁺ upon release of H₂. Isotope labelling in combination with quantum chemical computations revealed that the formation of the leaving hydrogen molecule uses one hydrogen from each of the reactants. The corresponding reaction was not observed for CH₃OMgCl₂⁻ and our computations indicate unfavourable thermochemistry for the reaction of the anion as well as for the neutral. The barriers are, in all cases, moderate so these results do not rule out such dehydrogenation reactions in the presence of water in solution.

It should be noted that the gas-phase reactivity trends reported here are not directly transferable to the corresponding reactions in solution or on interfaces. In solution, the charged species will be strongly affected by stabilizing interactions with other molecules and ions present; despite this, the data presented here describe the inherent reactivity of the key species. In the future, it will hopefully be possible to study these reactions in solution—experimentally and computationally—in sufficient detail and with sufficient accuracy to make a meaningful comparison.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Norwegian Research Council: through Grant No. 249788. The Chemistry of CO₂ Activation and Fixation; through the Hylleraas Centre for Quantum Molecular Sciences, No. 262695/F50, through the Centre of Excellence program of the Norwegian Research Council; and through the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant No. NN4654K). The authors thank J. Jestilä for performing the CCSD(T) computations used in the method evaluation.

References

1. S. Aldridge and A. J. Downs, Chem. Rev., 2001, 101, 3305–3366.
2. B. Bogdanovic, P. Bons, M. Schwickardi and K. Seevogel, Chem. Ber., 1991, 124, 1041–1050.
3. U. Eberle, M. Felderhoff and F. Schüth, Angew. Chem., Int. Ed., 2009, 48, 6608–6630.
4. S. Brutti, G. Mulas, E. Piciollo, S. Panero and P. Reale, J. Mater. Chem., 2012, 22, 14531–14537.
5. R. Mohtadi and S.-I. Orimo, Nat. Rev. Mater., 2016, 2, 16091.
6. E. N. Koukaras, A. D. Zdetsis and M. M. Sigalas, J. Am. Chem. Soc., 2012, 134, 15914–15922.
7. E. C. Ashby and A. B. Goel, Inorg. Chem., 1977, 16, 2941–2944.
8. D. Mukherjee and J. Okuda, Angew. Chem., Int. Ed., 2018, 57, 1458–1473.
9. M. Arrowsmith, M. S. Hill, D. J. MacDougall and M. F. Mahon, Angew. Chem., Int. Ed., 2009, 48, 4013–4016.
10. S. Schnitzler, T. P. Spaniol and J. Okuda, Inorg. Chem., 2016, 55, 12997–13006.
11. L. E. Lemmerz, A. Wong, G. Ménard, T. P. Spaniol and J. Okuda, Polyhedron, 2020, 178, 114331.
12. H. Schwarz, Coord. Chem. Rev., 2017, 334, 112–123.
13. M. D. Anker, M. S. Hill, J. P. Lowe and M. F. Mahon, Angew. Chem., Int. Ed., 2015, 54, 10009–10011.
14. L. Garcia, M. F. Mahon and M. S. Hill, Organometallics, 2019, 38, 3778–3785.
15. G. N. Khairallah and R. A. J. O’Hair, Int. J. Mass Spectrom., 2006, 254, 145–151.
16. Z. Zheng, J. Pavlov, Y. Wei, Y. Zhang and A. B. Attygalle, ACS Omega, 2018, 3, 3440–3452.
17. P. U. Andersson, M. J. Ryding, O. Sekiguchi and E. Uggerud, Phys. Chem. Chem. Phys., 2008, 10, 6127.
18. M. J. Ryding, A. M. Jonsson, A. S. Zatula, P. U. Andersson and E. Uggerud, Atmos. Chem. Phys., 2012, 12, 2809–2822.
19. M. J. Ryding, K. Ruusuvuori, P. U. Andersson, A. S. Zatula, M. J. McGrath, T. Kurtén, I. K. Ortega, H. Vehkamäki and E. Uggerud, J. Phys. Chem. A, 2012, 116, 4902–4908.
20. A. S. Zatula, P. U. Andersson, M. J. Ryding and E. Uggerud, Phys. Chem. Chem. Phys., 2011, 13, 13287.
21. S. Narancic, A. Bach and P. Chen, J. Phys. Chem. A, 2007, 111, 7006–7013.
22. J. S. Jestilä, Z. Iker, M. J. O. Ryding and E. Uggerud, Org. Biomol. Chem., 2020, 18, 9499–9510.
23. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, 2009.
24. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108.
25. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
26. D. J. Goebbert and P. G. Wenthold, Int. J. Mass Spectrom., 2006, 257, 1–11.
27. D. B. Workman and R. R. Squires, Inorg. Chem., 1988, 27, 1846–1848.
28. R. R. Squires, in Structure/Reactivity and Thermochemistry of Ions, ed. P. Ausloos and S. G. Lias, D. Reidel Publishing Company, 1987, pp. 373–375.
29. B. Chan, Y. Luo and M. Kimura, J. Phys. Chem. A, 2021, 125, 835–842.
30. H. Meerwein and R. Schmidt, Justus Liebigs Ann. Chem., 1925, 444, 221–238.
31. W. Ponndorff, Angew. Chem., 1926, 39, 138–143.
32. A. Verley, Bull. Soc. Chim. Fr., 1925, 37, 537–542.
33. N. C. Deno, H. J. Peterson and G. S. Saines, Chem. Rev., 1960, 60, 7–14.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05964a

---