Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High-energy molecular-frame photoelectron angular distributions: a molecular bond-length ruler
I.
Vela-Peréz
a,
F.
Ota
 b,
A.
Mhamdi
c,
Y.
Tamura
b,
A.
Mhamdi
c,
Y.
Tamura
 b,
J.
Rist
a,
N.
Melzer
b,
J.
Rist
a,
N.
Melzer
 a,
S.
Uerken
a,
G.
Nalin
a,
S.
Uerken
a,
G.
Nalin
 a,
N.
Anders
a,
D.
You
a,
N.
Anders
a,
D.
You
 d,
M.
Kircher
d,
M.
Kircher
 a,
C.
Janke
a,
M.
Waitz
a,
F.
Trinter
a,
C.
Janke
a,
M.
Waitz
a,
F.
Trinter
 *ef,
R.
Guillemin
*ef,
R.
Guillemin
 g,
M. N.
Piancastelli
g,
M. N.
Piancastelli
 g,
M.
Simon
g,
M.
Simon
 g,
V. T.
Davis
g,
V. T.
Davis
 h,
J. B.
Williams
h,
R.
Dörner
a,
K.
Hatada
h,
J. B.
Williams
h,
R.
Dörner
a,
K.
Hatada
 b,
K.
Yamazaki
i,
K.
Fehre
a,
Ph. V.
Demekhin
b,
K.
Yamazaki
i,
K.
Fehre
a,
Ph. V.
Demekhin
 *c,
K.
Ueda
dj,
M. S.
Schöffler
*c,
K.
Ueda
dj,
M. S.
Schöffler
 a and
T.
Jahnke
a and
T.
Jahnke
 *k
*k
aInstitut für Kernphysik, Goethe-Universität, Max-von-Laue-Straße 1, 60438 Frankfurt am Main, Germany
bDepartment of Physics, University of Toyama, Toyama 930-8555, Gofuku 3190, Japan
cInstitut für Physik und CINSaT, Universität Kassel, Heinrich-Plett-Straße 40, 34132 Kassel, Germany. E-mail: demekhin@physik.uni-kassel.de
dInstitute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai 980-8577, Japan
eDeutsches Elektronen-Synchrotron (DESY), Notkestraße 85, 22607 Hamburg, Germany
fMolecular Physics, Fritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: trinter@fhi-berlin.mpg.de
gSorbonne Université CNRS, Laboratoire de Chimie Physique-Matiere et Rayonnement, LCPMR, F-75005, Paris, France
hDepartment of Physics, University of Nevada, Reno, Nevada 89557, USA
iRIKEN Center for Advanced Photonics, RIKEN, 2-1 Hirosawa, Wako, Saitama, 351-0198, Japan
jDepartment of Chemistry, Tohoku University, 6-3 Aramaki Aza-Aoba, Aoba-ku, Sendai 980-8578, Japan
kEuropean XFEL, Holzkoppel 4, 22869 Schenefeld, Germany. E-mail: till.jahnke@xfel.eu
First published on 17th April 2023
Abstract
We present a study on molecular-frame photoelectron angular distributions (MFPADs) of small molecules using circularly polarized synchrotron light. We find that the main forward-scattering peaks of the MFPADs are slightly tilted with respect to the molecular axis. This tilt angle is directly connected to the molecular bond length by a simple, universal formula. We apply the derived formula to several examples of MFPADs of C 1s and O 1s photoelectrons of CO, which have been measured experimentally or obtained by means of ab initio modeling. In addition, we discuss the influence of the back-scattering contribution that is superimposed over the analyzed forward-scattering peak in the case of homo-nuclear diatomic molecules such as N2.
Introduction
Recent developments of X-ray free-electron lasers (XFELs) delivering extremely short X-ray pulses of a few femtoseconds1 and of a mega-electron-volt pulsed electron beam2 at SLAC have paved new pathways to image structural changes of molecules in chemical reactions, for example, employing time-resolved X-ray diffraction3 and ultrafast electron diffraction.4 While catching the motion of the individual atoms, including hydrogen atoms, of single molecules during chemical reactions is of fundamental interest, it still remains a challenge.A couple of decades ago, it was pointed out that core-level photoelectron angular distributions include molecular structure information, which can be accessed if the molecule is either fixed in space or if the photoelectron angular distribution in the molecular frame (MFPAD) is retrieved from a coincidence measurement.5 Accordingly, measuring the MFPAD of an isolated molecule is the gas-phase analog of photoelectron diffraction imaging (PED) routinely used for studying the surface structure.6 Following the spirit of PED, a couple of groups7,8 proposed time-resolved MFPAD measurements using an XFEL light pulse as an ionizing source, as one of the future routes to image the motion of individual atoms in a molecule. Several attempts towards time-resolved MFPAD measurements with XFELs were reported, in which the sample molecules were aligned by employing an impulsive or adiabatic alignment method using optical laser fields.9–12 However, no time-resolved studies of molecular structural changes have been reported, so far, partly due to the complexity of the needed pulse sequence: a first laser pulse is needed to align the molecule, a second laser pulse triggers the photoreaction, and a final XFEL pulse ejects the photoelectron at a particular site in the molecule in order to perform PED.
The first high-repetition-rate XFEL, the European XFEL,13 opened the door to coincidence experiments using COLTRIMS (Cold Target Recoil Ion Momentum Spectroscopy) reaction microscopes (REMI)14 for MFPAD measurements. In a COLTRIMS measurement, the spatial orientation of a molecule can be deduced after triggering a fragmentation of the molecule and detecting the momenta of the fragment ions in coincidence. As the momentum of the ejected photoelectron is recorded in coincidence with the fragment ions, the photoelectron's emission direction with respect to the molecule can be determined. Very recently, Kastirke et al. have reported a first successful implementation of this technique at the soft X-ray beamline of the European XFEL.15–17
To establish MFPAD measurements as a routinely usable tool for molecular structure imaging, however, an important ingredient is still missing, which is a method of extracting the molecular structure directly from the measured MFPAD without the need for a full theoretical modeling of the photoemission process. So far, concepts proposed for achieving this goal focused on polarization-averaged MFPADs (see, e.g., ref. 18 and references therein), i.e., on MFPADs, which have been obtained after integrating over all laboratory-frame orientations of the molecule. The concept relies on two prerequisites: firstly, at sufficiently high photoelectron kinetic energies, for which a single-scattering approximation is valid (say, above 70 eV), forward-scattering peaks observable in polarization-averaged MFPADs coincide with the relative location (from the point of view of the emitter atom) of neighboring atoms.19,20 Secondly, the molecular-frame interference pattern caused by the direct and scattered photoelectron waves can be correlated with the distance between the emitter and the scatterers.21,22 In addition, in the case of homo-nuclear molecules, bond-length information can be obtained exploiting the analogy between Young's double-slit principle and MFPADs (see, e.g., ref. 23).
In the present work, we demonstrate a different approach building on the idea of stereo-atomscope diffraction spectroscopy known in the field of surface-structure determination, in which circularly polarized light is employed as an ionizing source for PED.24,25 If the emitter of a photoelectron and a neighboring atomic scatterer are located within the polarization plane of the ionizing light, the forward-scattering peak belonging to that atomic neighbor shows a distinct angular tilt. Thus, employing the hetero-nuclear diatomic molecule CO as a prototype system, we show that high-energy MFPADs of fixed-in-space molecules provide direct access to structural features such as the molecule's bond length, if circularly polarized light is used for the ionization and the MFPAD is confined to the polarization plane. Such MFPADs are hereafter referred to as CP-MFPADs. Earlier works26–28 on CP-MFPADs showed in principle such an angular tilt as well. However, these studies covered in their discussion other properties of the measured emission distributions and in many cases were performed at low electron kinetic energies. At such energies, the tilt angle is sometimes obscured by higher-order multiple-scattering effects and, accordingly, we focus in the present study on high-energy electrons.
While this paper demonstrates this concept for a simple diatomic molecule, it should be possible to extend it in future work to larger molecules as well. Whenever an atom of the molecule is located together with the emitter atom within the polarization plane, its corresponding forward-scattering peak will show a distance-dependent tilt. As detailed below, COLTRIMS reaction microscopes are particularly suited for such studies, as they enable the experimenters to determine the laboratory-frame molecular orientation in addition to the molecular-frame angular emission distribution of the photoelectron.
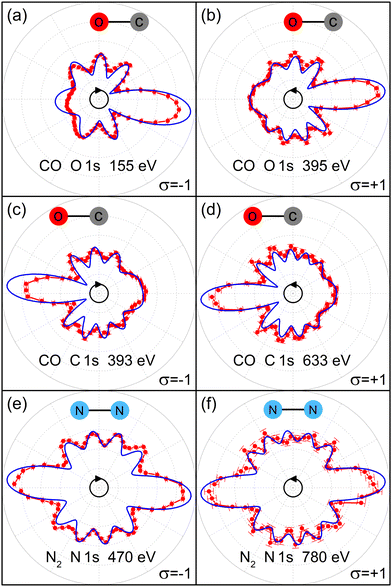
The remaining part of the manuscript is structured as follows: first, we present the experimental C 1s and O 1s CP-MFPADs of CO. We find that the high-energy CP-MFPAD exhibits petal-like features (i.e., a flower shape) with a strong forward-scattering peak in the direction from the emitter to the scatterer. The latter peak is slightly tilted upward or downward, depending on the handedness of the circularly polarized photons. We then show that our ab initio calculations reproduce very well the experimental CP-MFPADs. Finally, we demonstrate that the features of high-energy CP-MFPADs described above can be well captured by a very simple analytic expression, and that the bond length can be directly read off from the tilt angle of the forward-scattering peak without any need for ab initio modeling. For comparison and further insight, we present also the results for the homo-nuclear diatomic molecule N2. It turns out that great care needs to be taken when measuring the MFPADs. As we will show, the resulting error bars for the extraction of the bond length from our routinely measured MFPADs are surprisingly large in some cases and, for example, measuring MFPADs for both light helicities can greatly help to minimize systematic errors.
Experiment
The experiment was performed at Synchrotron SOLEIL (Saint-Aubin, France) using the well-established COLTRIMS technique14 during the 8-bunch mode (pulsed operation) of the synchrotron. A supersonic expansion of CO or N2 gas was skimmed to form a molecular beam that crossed the synchrotron radiation provided by the variable-polarization undulator-based beamline SEXTANTS. Electrons and ions generated by photoionization and subsequent Auger decay were accelerated (in opposite directions) using a static electric field, onto two position- and time-sensitive microchannel-plate detectors (MCPs) using a multi-hit-capable delay-line position readout.29 From the position of the impact on the detectors, the known distance between the ionization region and the MCPs, and the time-of-flight, the particle trajectories inside the spectrometer can be deduced, and from these, the initial momentum vector of each particle can be determined.In more detail, the whole COLTRIMS analyzer consisted of only a single acceleration region (spanning the full region between the two detectors) using a homogeneous electric field with a strength of E = 38.3 V cm−1. The ion arm had a length of 20.6 cm and the ion detector had a diameter of 125 mm. This configuration allowed for the detection of the breakup of the molecules into singly charged ions for a kinetic energy release of up to 30 eV with a full 4π coverage, i.e., independent of the emission direction of the ions in the laboratory frame. Detecting high-energy electrons requires typically the use of either very high electric extraction fields or very high magnetic confinement fields for the electrons. While focusing on the measurement of high-energy electrons, we can exploit the fact that we are mainly interested in their emission distributions within the polarization plane of the ionizing photons (and more specifically in the MFPADs of molecules oriented in parallel to the polarization plane). To achieve this goal, it is therefore not necessary to measure the electrons with full solid-angle coverage, i.e., it is sufficient to detect electrons, which are emitted perpendicularly to the light propagation direction. All possible molecular-frame electron emission angles are then still covered in this measurement as the ions are detected with 4π solid angle (and due to the symmetry features of the circularly polarized light, all molecular orientations within the polarization plane are equivalent). The electron arm had a length of 46.4 cm. The active area of the electron detector had a diameter of 125 mm. With these spectrometer properties and an additional superimposed homogeneous magnetic field with a strength of B = 10 G, we were able to measure electrons of, e.g., Ekin = 633 eV (which corresponds to C 1s electrons of CO at hν = 930 eV) if they are emitted within an angle of 20° relative to the symmetry axis of the COLTRIMS spectrometer. For each ionization event, a core-level photoelectron was detected in coincidence with the two fragment ions resulting from the Coulomb explosion of the molecule after Auger decay. The detection rates throughout our experiment were in the range of 11 kHz on the electron detector and 4.6 kHz on the ion detector. Such rates have been found suitable with respect to coincidence conditions and measurement background in the past. The exact values for the degree of circular polarization of the beamline are not available. Previous studies performed at the same beamline30 suggest, however, that it is very close to 100%.
Details of the calculations
For our ab initio modeling, we employed the following approach: the angular distributions of the C 1s and O 1s photoelectrons of the CO molecule and of the N 1s photoelectrons of the N2 molecule were computed by using the single-center (SC) method and code,31 which provides an accurate description of the partial photoelectron continuum waves in molecules. The calculations were carried out at the equilibrium internuclear geometries of the ground electronic states of CO and N2 in the frozen-core Hartree–Fock approximation. The SC expansions of the occupied orbitals were restricted by partial harmonics with![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c ≤ 99 and for photoelectrons with
c ≤ 99 and for photoelectrons with ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ε ≤ 49.
ε ≤ 49.
Results and discussion
We performed measurements using right circularly and left circularly polarized light at the photon energies of hν = 690 eV and hν = 930 eV for the studies on CO, and hν = 880 eV and hν = 1190 eV for the investigation on N2. The resulting photoelectron kinetic energies are 393 eV and 633 eV for C 1s photoemission of CO, 155 eV and 395 eV for O 1s photoemission of CO, and 470 eV and 780 eV for N 1s photoemission of N2. Fig. 1 depicts the respective experimental CP-MFPADs and those obtained from our ab initio calculations. The experimental data are confined to cases, where the electron emission occurs within the polarization plane within an opening angle of ±15°, and for cases, in which the molecular orientation was parallel to the polarization plane within the same angular range. It should be noted that the tilt-angle effect discussed in the following is not drastically affected by these opening angles, as it scales linearly with that angle. Our modeling nicely reproduces all features observed in the experiment. Looking at the CO results in Fig. 1(a)–(d), we find that the number of petals (resembling a flower shape), which appear as a result of interference between the direct and scattered photoelectron waves, increases as photoelectron energy increases. The same behavior has been seen in studies on polarization-averaged MFPADs.20The most striking feature of all the CP-MFPADs is a very strong forward-scattering peak, which appears in the direction of the scatterer atom that is neighboring the emitter atom: the forward scattering is not located exactly along the molecular axis, but occurs slightly tilted from it in the direction of rotation of the electric-field vector. This upward or downward tilt thus flips if the handedness of the ionizing light is changed from the right (σ = −1) to the left (σ = +1). This tilt is a characteristic feature of the CP-MFPADs, as also of PED on surfaces.24,25 Furthermore, close inspections reveal that the tilt angle decreases with the increase of the photoelectron energy. The results of N2 in Fig. 1(e) and (f) depict these features as well.
In order to gather more detailed information on the findings described above, we performed further ab initio calculations over a wide range of photoelectron energies from 70 eV up to 1000 eV. The results are summarized in Fig. 2. Fig. 2(a), (c), and (e) illustrate that, indeed, the number of petals in the flower shape of the CP-MFPAD increases while the tilt angle of the forward-scattering peak decreases with the increase of the photoelectron kinetic energy. Fig. 2(b), (d), and (f) depict the extracted tilt angle θtilt as a function of photoelectron energy. For the CO molecule [Fig. 2(b) and (d)], we observe monotonic decreases of the tilt angle with the increase of the photoelectron energy. The results for N2 depicted in Fig. 1(f) show that the decrease in the tilt angle is additionally modulated by a damped oscillation.
Aiming at elucidating these characteristic behaviors of the measured and calculated CP-MFPADs, we derive analytic expressions for describing the CP-MFPAD of hetero-nuclear diatomic molecules AB in the high-energy regime. We choose atom A as the photo-absorbing atom that emits a photoelectron. We define the bond-length vector R = rB − rA (along the x axis), the photoelectron wave vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) , and angle θ between them. We assume that CP-MFPADs are measured in the polarization plane of the circular light (x–y plane) and employ the electric-dipole, single-channel, and single-scattering approximations using a site T-matrix expansion.32,33 According to the approach of ref. 18 and 22, the CP-MFPAD is given by the following superposition:
, and angle θ between them. We assume that CP-MFPADs are measured in the polarization plane of the circular light (x–y plane) and employ the electric-dipole, single-channel, and single-scattering approximations using a site T-matrix expansion.32,33 According to the approach of ref. 18 and 22, the CP-MFPAD is given by the following superposition:
IA(k, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) σ) ∝ |BAx(k) + iσBAy(k)|2, σ) ∝ |BAx(k) + iσBAy(k)|2, | (1) |
 | (2) |
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) does not propagate towards the neighboring atom B at θ = 0. Substituting eqn (2) and (3) in eqn (1) and performing necessary simplifications, we arrive at the following compact expression for the CP-MFPAD as a function of the photoelectron emission vector k:
θ) does not propagate towards the neighboring atom B at θ = 0. Substituting eqn (2) and (3) in eqn (1) and performing necessary simplifications, we arrive at the following compact expression for the CP-MFPAD as a function of the photoelectron emission vector k: | (4) |
| Gσ(k,θ) = cos[kR(1 − cosθ) + ϕ(k,θ) − σθ]. | (5) |
The first and the second terms of eqn (4) are the direct wave from the emitter A and the scattering wave from the scatterer B, respectively. The third term represents the interference between the direct and single-scattered waves and depends on the bond length.
Constructive and destructive interference in the differential photoemission intensity (i.e., the fringes in the CP-MFPAD) correspond to the maxima and minima of the fringe function (5). In order to find the angles, at which the maxima and minima appear in Gσ(k,θ), we set dGσ(k,θ)/dθ = 0:
 | (6) |
This condition is satisfied either when the sine function becomes zero, i.e., sin[kR(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) θ) + ϕ(k,θ) − σθ] = 0 or when the second term in braces vanishes, i.e., kR
θ) + ϕ(k,θ) − σθ] = 0 or when the second term in braces vanishes, i.e., kR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + dϕ(k,θ)/dθ − σ = 0. The first condition describes the angles, at which maxima and minima form the flower shape in the CP-MFPAD shown in Fig. 1(a)–(d) and Fig. 2(a), (b). The second condition yields a relationship between kR and the tilt angle θtilt. This relation confirms that the tilt angle decreases with the increase of the photoelectron momentum k (and thus, of the photoelectron kinetic energy), as depicted in Fig. 2(b) and (d) for CO. If |f(k,θ)|θ=0,π ≠ 0, as in this study, dϕ(k,θ)/dθ|θ=0,π = 0 holds.34 We can thus assume that dϕ(k,θ)/dθ is negligible for small tilt angles from the forward and backward directions. From the solution of the second part of eqn (6), we finally obtain the following relationship for the case of hetero-nuclear molecules:
θ + dϕ(k,θ)/dθ − σ = 0. The first condition describes the angles, at which maxima and minima form the flower shape in the CP-MFPAD shown in Fig. 1(a)–(d) and Fig. 2(a), (b). The second condition yields a relationship between kR and the tilt angle θtilt. This relation confirms that the tilt angle decreases with the increase of the photoelectron momentum k (and thus, of the photoelectron kinetic energy), as depicted in Fig. 2(b) and (d) for CO. If |f(k,θ)|θ=0,π ≠ 0, as in this study, dϕ(k,θ)/dθ|θ=0,π = 0 holds.34 We can thus assume that dϕ(k,θ)/dθ is negligible for small tilt angles from the forward and backward directions. From the solution of the second part of eqn (6), we finally obtain the following relationship for the case of hetero-nuclear molecules:
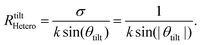 | (7) |
Eqn (7) connects directly the bond length of a molecule and the tilt angle |θtilt| of the forward-scattering peak of the CP-MFPAD, and thus can be thought of as a simple, universal bond-length ruler. As pointed out in an insightful argument by Daimon and coworkers,35 the physics underlying eqn (7) can be understood very intuitively. Upon birth the photoelectron carries one unit of angular momentum, which it inherited from the photon. Classically, an electron moving with a momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) along a straight line thus must follow a path of impact parameter
along a straight line thus must follow a path of impact parameter ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) with respect to the nucleus such that
with respect to the nucleus such that ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ·
·![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) = 1ħ. This straight line defines the tilted symmetry axis of the photoemission. For R ≫ b this results in R = 1/k
= 1ħ. This straight line defines the tilted symmetry axis of the photoemission. For R ≫ b this results in R = 1/k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(θ) and a symmetry axis of the problem, which is tilted by θ with respect to the molecular axis. This simplified classical explanation suggests that the tilt angle should scale linearly with the ellipticity of the ionizing light. Fig. 3 depicts the bond length RtiltHetero estimated from the computed and measured CP-MFPADs using eqn (7). The resulting values are plotted as functions of kReq, where Req = 1.1283 Å and 1.0977 Å for CO and N2, respectively. Note that eqn (7) is derived for hetero-nuclear diatomic molecules, and its application to the homo-nuclear N2 molecule is a rather crude approximation, as we will discuss below. From Fig. 3(a), it is evident that the bond lengths, estimated from both the ab initio modeled and measured CP-MFPADs, agree well with the equilibrium bond length of the neutral ground state of CO (the horizontal dashed line), with a deviation of less than 10%. Please note that the counter-intuitive increase of the relative error with respect to the ab initio modeling for smaller kReq is due to the fact that at lower electron energies higher-order multiple-scattering effects provide a non-negligible contribution to the transition amplitude. On the other hand, the bond lengths of N2 in Fig. 3(b), estimated from the ab initio CP-MFPADs, oscillate as a function of kReq around Req. Those oscillations are damped and drop below 10% for sufficiently high photoelectron energies. The bond length of N2 estimated from the experimental CP-MFPADs is, however, in good agreement with the expected value of Req within the experimental uncertainties.
sin(θ) and a symmetry axis of the problem, which is tilted by θ with respect to the molecular axis. This simplified classical explanation suggests that the tilt angle should scale linearly with the ellipticity of the ionizing light. Fig. 3 depicts the bond length RtiltHetero estimated from the computed and measured CP-MFPADs using eqn (7). The resulting values are plotted as functions of kReq, where Req = 1.1283 Å and 1.0977 Å for CO and N2, respectively. Note that eqn (7) is derived for hetero-nuclear diatomic molecules, and its application to the homo-nuclear N2 molecule is a rather crude approximation, as we will discuss below. From Fig. 3(a), it is evident that the bond lengths, estimated from both the ab initio modeled and measured CP-MFPADs, agree well with the equilibrium bond length of the neutral ground state of CO (the horizontal dashed line), with a deviation of less than 10%. Please note that the counter-intuitive increase of the relative error with respect to the ab initio modeling for smaller kReq is due to the fact that at lower electron energies higher-order multiple-scattering effects provide a non-negligible contribution to the transition amplitude. On the other hand, the bond lengths of N2 in Fig. 3(b), estimated from the ab initio CP-MFPADs, oscillate as a function of kReq around Req. Those oscillations are damped and drop below 10% for sufficiently high photoelectron energies. The bond length of N2 estimated from the experimental CP-MFPADs is, however, in good agreement with the expected value of Req within the experimental uncertainties.
 | ||
Fig. 3 Bond lengths (refer to the left-handed vertical axis), estimated from the tilt angles of the ab initio computed (solid lines with small symbols) and experimentally measured (large symbols with error bars) CP-MFPADs via the derived relation (7) as functions of kReq, and the respective relative errors (broken lines, refer to the right-handed vertical axis). The equilibrium bond lengths RCOeq. = 1.1283 Å and  are indicated by the horizontal dashed lines. are indicated by the horizontal dashed lines. | ||
The large oscillation in RtiltHetero in Fig. 3(b) can be interpreted as follows. In the experiment, one is unable to distinguish photoelectrons originating from the N 1s gerade and ungerade molecular orbitals of N2, which are separated by ∼105 meV36 (or from the degenerate 1s orbitals of the left and right nitrogen atoms). The resultant CP-MFPADs are therefore the sum of the two contributions:
Ī(k,![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) σ) ∝ Ig(k, σ) ∝ Ig(k,![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) σ) + Iu(k, σ) + Iu(k, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) σ) = IA(k, σ) = IA(k,![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) σ) + IA(−k, σ) + IA(−k, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) σ). σ). | (8) |
Here, we used the fact that fA(k,θ) = fB(k,π − θ) for homo-nuclear diatomic molecules. One can see that eqn (8) has a C2 point symmetry, as is evident from Fig. 2(e). The fringe function of eqn (8) can thus be reduced to a superposition of fringe functions of two emitting nitrogen atoms
| Hσ(k,θ) ∝ Gσ(k,θ) + Gσ(k,π − θ), | (9) |
In particular, for high electron energies, θtilt becomes small and, accordingly, its extraction from the experimental data becomes very challenging. Already small systematic errors can prevent the determination of the bond length in such cases. It turned out that performing a set of two measurements using both light helicities as references in the calibration can circumvent these problems to some extent, as the measured MFPADs have to be by definition mirror-symmetric when switching between left- and right-handed polarization. Checking for this mirror symmetry when fine-tuning the calibration parameters of the experiment helped to decrease systematic errors on the required level of detail. While in Fig. 1 all six measured MFPADs agree well with the computed ones, we were not able to extract the offset angle with the required precision in all cases. For N2 at 780 eV, we recorded only one data set with one helicity, and its corresponding data point has a considerably larger error bar. Furthermore, the two measurements performed at the CO C 1s edge are compromised by a small systematic error due to overlapping flight times of the two ionic fragments, which directly (and almost solely) affected the part of the CP-MFPADs, from which θtilt is extracted. We included the lower-energy data point, with an estimate of the error, which is caused by the overlapping flight times. Such experimental difficulties should be considered in future measurements employing the θtilt approach. In the end, we evaluated several methods to extract the tilt angle from the experimental data. For example, the MFPADs can be fitted by a sum over spherical harmonics Yl,m with contributions of up to l = 9. By examining the fitting results, the tilt angle can be directly obtained from the corresponding maximum in the fitting function. However, estimating an error bar for this resulting angle is not straightforward. Instead, we finally determined the angular position of the forward-scattering peak by employing a Gaussian fit to the corresponding region of the measured angular distribution. Unless stated differently, the error bars shown in Fig. 3 are the errors reported by this fitting procedure. Within these error bars both approaches provide the same results.
Conclusions
In summary, we have investigated experimentally and theoretically the CP-MFPADs of core-level photoelectrons emitted from CO and N2 molecules. We showed that (at high photoelectron energies) the tilt angle of the forward-scattering peak appearing in the CP-MFPAD of hetero-nuclear diatomic molecules can be directly connected to the bond length by a simple, universal equation. We applied the derived bond-length ruler formula to several examples of measured and computed CP-MFPADs. The extracted bond lengths agree well with the known bond lengths of CO and N2 in their neutral ground states. The present study illustrates that employing high-energy circularly polarized light, which is available not only at most synchrotron-radiation facilities, but also at XFEL facilities, has many advantages for the extraction of the molecular structure. It allows extraction of molecular bond lengths not only on a qualitative, but also on a quantitative level. We assume that our findings hold not only for the static case, but also for time-resolved MFPAD measurements aiming at catching the motion of individual atoms of molecules undergoing photoreactions, as, e.g., the stretching of chemical bonds. Further studies are required to target the extension of this method to larger molecules. The concept for such an extension is in principle straightforward (as indicated above), but there are still many aspects that need to be addressed when targeting real-life measurement results. Most prominently, the validity of the axial-recoil approximation (i.e., a rapid fragmentation of the molecule as compared to possible rotation or geometrical changes) may not be given in all cases and needs to be confirmed by the measurement, as, e.g., done in ref. 38. However, previous work by Fehre et al.39 demonstrated that it is possible to obtain three-dimensional MFPADs for a molecule as large as methyloxirane. This might be a first indication that the tilt-angle technique will be applicable to larger molecules in the future.As compared to other experimental techniques for molecular structure determination, our bond-length ruler approach provides very easy access to molecular bond lengths. For example, Coulomb explosion imaging requires complex modeling of the charge-up process of the inspected molecule for the extraction of geometrical structures. Despite addressing single molecules in the gas phase, our bond-length ruler avoids the problems caused by randomly oriented samples (or even the need for crystalline samples), which other diffraction methods face. However, its explicit extension to larger molecules remains an intriguing subject for further studies, and our first prototypical demonstration shows that great care needs to be taken when measuring the MFPADs for the bond-length extraction in order to reach a precision in the range of a few percent.
Author contributions
M. S. S., T. J., R. D., P. V. D., and K. U. conceived the present work. I. V.-P., F. O., and A. M. contributed to it equally. The experiment was prepared and carried out by I. V.-P., J. R., N. M., S. U., G. N., N. A., D. Y., M. K., C. J., M. W., F. T., R. G., M. N. P., M. S., V. T. D., J. B. W., R. D., K. U., M. S. S., and T. J. Experimental data analysis was performed by I. V.-P., K. F., and T. J. Ab initio calculations were performed by A. M. and P. V. D. Analytical formulas were derived and employed for the analysis by F. O., Y. T., and K. H. F. O., Y. T., K. H., K. Y., K. U., P. V. D., R. D., M. S. S., and T. J. wrote the paper. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The present work was funded in part by the Deutsche Forschungsgemeinschaft (DFG) Project no. 328961117-SFB 1319 ELCH (extreme light for sensing and driving molecular chirality, subprojects B1 and C1). F. O., K. H., and K. U. acknowledge Cooperative Research Program of “Network Joint Research Center for Materials and Devices”. K. H. acknowledges funding by JSPS KAKENHI under Grant no. 18K05027 and 19KK0139, while K. U. also acknowledges the X-ray Free Electron Laser Utilization Research Project and the X-ray Free Electron Laser Priority Strategy Program of the Ministry of Education, Culture, Sports, Science, and Technology of Japan (MEXT) and the IMRAM program of Tohoku University. D. Y. acknowledges JSPS KAKENHI Grant Number JP19J12870 and a Grant-in-Aid of Tohoku University Institute for Promoting Graduate Degree Programs Division for Interdisciplinary Advanced Research and Education. K. Y. is grateful for the financial support from JSPS KAKENHI Grant Number 19H05628. We acknowledge the SOLEIL synchrotron facility for providing the synchrotron radiation and we would like to thank N. Jaouen and his team for assistance in using beamline SEXTANTS under proposal 20170599. Open Access funding provided by the Max Planck Society.References
- P. Emma, R. Akre, J. Arthur, R. Bionta, C. Bostedt, J. Bozek, A. Brachmann, P. Bucksbaum, R. Coffee, F.-J. Decker, Y. Ding, D. Dowell, S. Edstrom, A. Fisher, J. Frisch, S. Gilevich, J. Hastings, G. Hays, P. Hering, Z. Huang, R. Iverson, H. Loos, M. Messerschmidt, A. Miahnahri, S. Moeller, H.-D. Nuhn, G. Pile, D. Ratner, J. Rzepiela, D. Schultz, T. Smith, P. Stefan, H. Tompkins, J. Turner, J. Welch, W. White, J. Wu, G. Yocky and J. Galayda, Nat. Photonics, 2010, 4, 641–647 CrossRef CAS.
- S. P. Weathersby, G. Brown, M. Centurion, T. F. Chase, R. Coffee, J. Corbett, J. P. Eichner, J. C. Frisch, A. R. Fry, M. Gühr, N. Hartmann, C. Hast, R. Hettel, R. K. Jobe, E. N. Jongewaard, J. R. Lewandowski, R. K. Li, A. M. Lindenberg, I. Makasyuk, J. E. May, D. McCormick, M. N. Nguyen, A. H. Reid, X. Shen, K. Sokolowski-Tinten, T. Vecchione, S. L. Vetter, J. Wu, J. Yang, H. A. Dürr and X. J. Wang, Rev. Sci. Instrum., 2015, 86, 073702 CrossRef CAS PubMed.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. S. Robinson, D. Ratner, T. J. Lane, D. Zhu, J. M. Glownia, M. Kozina, H. T. Lemke, M. Sikorski, Y. Feng, S. Nelson, K. Saita, B. Stankus, T. Northey, J. B. Hastings and P. M. Weber, Phys. Rev. Lett., 2015, 114, 255501 CrossRef CAS PubMed.
- T. J. A. Wolf, D. M. Sanchez, J. Yang, R. M. Parrish, J. P. F. Nunes, M. Centurion, R. Coffee, J. P. Cryan, M. Gühr, K. Hegazy, A. Kirrander, R. K. Li, J. Ruddock, X. Shen, T. Vecchione, S. P. Weathersby, P. M. Weber, K. Wilkin, H. Yong, Q. Zheng, X. J. Wang, M. P. Minitti and T. J. Martínez, Nat. Chem., 2019, 11, 504–509 CrossRef CAS PubMed.
- A. Landers, T. Weber, I. Ali, A. Cassimi, M. Hattass, O. Jagutzki, A. Nauert, T. Osipov, A. Staudte, M. H. Prior, H. Schmidt-Böcking, C. L. Cocke and R. Dörner, Phys. Rev. Lett., 2001, 87, 013002 CrossRef CAS PubMed.
- D. P. Woodruff, Appl. Phys. A, 2008, 92, 439–445 CrossRef CAS.
- F. Krasniqi, B. Najjari, L. Strüder, D. Rolles, A. Voitkiv and J. Ullrich, Phys. Rev. A, 2010, 81, 033411 CrossRef.
- M. Kazama, T. Fujikawa, N. Kishimoto, T. Mizuno, J.-I. Adachi and A. Yagishita, Phys. Rev. A, 2013, 87, 063417 CrossRef.
- A. Rouzée, P. Johnsson, L. Rading, A. Hundertmark, W. Siu, Y. Huismans, S. Düsterer, H. Redlin, F. Tavella, N. Stojanovic, A. Al-Shemmary, F. Lépine, D. M. P. Holland, T. Schlatholter, R. Hoekstra, H. Fukuzawa, K. Ueda and M. J. J. Vrakking, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 164029 CrossRef.
- R. Boll, D. Anielski, C. Bostedt, J. D. Bozek, L. Christensen, R. Coffee, S. De, P. Decleva, S. W. Epp, B. Erk, L. Foucar, F. Krasniqi, J. Küpper, A. Rouzée, B. Rudek, A. Rudenko, S. Schorb, H. Stapelfeldt, M. Stener, S. Stern, S. Techert, S. Trippel, M. J. J. Vrakking, J. Ullrich and D. Rolles, Phys. Rev. A, 2013, 88, 061402(R) CrossRef.
- K. Nakajima, T. Teramoto, H. Akagi, T. Fujikawa, T. Majima, S. Minemoto, K. Ogawa, H. Sakai, T. Togashi, K. Tono, S. Tsuru, K. Wada, M. Yabashi and A. Yagishita, Sci. Rep., 2015, 5, 14065 CrossRef CAS PubMed.
- S. Minemoto, T. Teramoto, H. Akagi, T. Fujikawa, T. Majima, K. Nakajima, K. Niki, S. Owada, H. Sakai, T. Togashi, K. Tono, S. Tsuru, K. Wada, M. Yabashi, S. Yoshida and A. Yagishita, Sci. Rep., 2016, 6, 38654 CrossRef CAS PubMed.
- W. Decking, et al. , Nat. Photonics, 2020, 14, 391–397 CrossRef CAS.
- J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L. P. H. Schmidt and H. Schmidt-Böcking, Rep. Prog. Phys., 2003, 66, 1463 CrossRef CAS.
- G. Kastirke, et al. , Phys. Rev. X, 2020, 10, 021052 CAS.
- G. Kastirke, et al. , Phys. Rev. Lett., 2020, 125, 163201 CrossRef CAS PubMed.
- G. Kastirke, F. Ota, D. V. Rezvan, M. S. Schöffler, M. Weller, J. Rist, R. Boll, N. Anders, T. M. Baumann, S. Eckart, B. Erk, A. De Fanis, K. Fehre, A. Gatton, S. Grundmann, P. Grychtol, A. Hartung, M. Hofmann, M. Ilchen, C. Janke, M. Kircher, M. Kunitski, X. Li, T. Mazza, N. Melzer, J. Montano, V. Music, G. Nalin, Y. Ovcharenko, A. Pier, N. Rennhack, D. E. Rivas, R. Dörner, D. Rolles, A. Rudenko, P. Schmidt, J. Siebert, N. Strenger, D. Trabert, I. Vela-Perez, R. Wagner, T. Weber, J. B. Williams, P. Ziolkowski, L. P. H. Schmidt, A. Czasch, Y. Tamura, N. Hara, K. Yamazaki, K. Hatada, F. Trinter, M. Meyer, K. Ueda, P. V. Demekhin and T. Jahnke, Phys. Chem. Chem. Phys., 2022, 24, 27121–27127 RSC.
- F. Ota, K. Yamazaki, D. Sébilleau, K. Ueda and K. Hatada, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 024003 CrossRef CAS.
- J. B. Williams, C. S. Trevisan, M. S. Schöffler, T. Jahnke, I. Bocharova, H. Kim, B. Ulrich, R. Wallauer, F. Sturm, T. N. Rescigno, A. Belkacem, R. Dörner, T. Weber, C. W. McCurdy and A. L. Landers, Phys. Rev. Lett., 2012, 108, 233002 CrossRef CAS PubMed.
- E. Plésiat, P. Decleva and F. Martín, Phys. Rev. A, 2013, 88, 063409 CrossRef.
- H. Fukuzawa, R. R. Lucchese, X.-J. Liu, K. Sakai, H. Iwayama, K. Nagaya, K. Kreidi, M. S. Schöffler, J. R. Harries, Y. Tamenori, Y. Morishita, I. H. Suzuki, N. Saito and K. Ueda, J. Chem. Phys., 2019, 150, 174306 CrossRef PubMed.
- F. Ota, K. Hatada, D. Sébilleau, K. Ueda and K. Yamazaki, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 084001 CrossRef CAS.
- R. K. Kushawaha, M. Patanen, R. Guillemin, L. Journel, C. Miron, M. Simon, M. N. Piancastelli, C. Skates and P. Decleva, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15201–15206 CrossRef CAS PubMed.
- H. Daimon, S. Imada and S. Suga, Surf. Sci., 2001, 471, 143–150 CrossRef CAS.
- F. Matsui, T. Matsushita and H. Daimon, J. Electron Spectrosc. Relat. Phenom., 2010, 178–179, 221–240 CrossRef CAS.
- T. Jahnke, T. Weber, A. L. Landers, A. Knapp, S. Schössler, J. Nickles, S. Kammer, O. Jagutzki, L. Schmidt, A. Czasch, T. Osipov, E. Arenholz, A. T. Young, R. Díez Muiño, D. Rolles, F. J. García de Abajo, C. S. Fadley, M. A. Van Hove, S. K. Semenov, N. A. Cherepkov, J. Rösch, M. H. Prior, H. Schmidt-Böcking, C. L. Cocke and R. Dörner, Phys. Rev. Lett., 2002, 88, 073002 CrossRef CAS PubMed.
- B. Zimmermann, K. Wang and V. McKoy, Phys. Rev. A, 2003, 67, 042711 CrossRef.
- T. Jahnke, L. Foucar, J. Titze, R. Wallauer, T. Osipov, E. P. Benis, A. Alnaser, O. Jagutzki, W. Arnold, S. K. Semenov, N. A. Cherepkov, L. P. H. Schmidt, A. Czasch, A. Staudte, M. Schöffler, C. L. Cocke, M. H. Prior, H. Schmidt-Böcking and R. Dörner, Phys. Rev. Lett., 2004, 93, 083002 CrossRef CAS PubMed.
- O. Jagutzki, V. Mergel, K. Ullmann-Pfleger, L. Spielberger, U. Spillmann, R. Dörner and H. Schmidt-Böcking, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 477, 244–249 CrossRef CAS.
- M. Tia, M. Pitzer, G. Kastirke, J. Gatzke, H.-K. Kim, F. Trinter, J. Rist, A. Hartung, D. Trabert, J. Siebert, K. Henrichs, J. Becht, S. Zeller, H. Gassert, F. Wiegandt, R. Wallauer, A. Kuhlins, C. Schober, T. Bauer, N. Wechselberger, P. Burzynski, J. Neff, M. Weller, D. Metz, M. Kircher, M. Waitz, J. B. Williams, L. P. H. Schmidt, A. D. Müller, A. Knie, A. Hans, L. B. Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, R. Dörner, T. Jahnke, P. V. Demekhin and M. Schöffler, J. Phys. Chem. Lett., 2017, 8, 2780–2786 CrossRef CAS PubMed.
- P. V. Demekhin, A. Ehresmann and V. L. Sukhorukov, J. Chem. Phys., 2011, 134, 024113 CrossRef PubMed.
- J. S. Faulkner and G. M. Stocks, Phys. Rev. B, 1980, 21, 3222 CrossRef CAS.
- K. Hatada, K. Hayakawa, M. Benfatto and C. R. Natoli, J. Phys.: Condens. Matter, 2010, 22, 185501 CrossRef PubMed.
- O. J. Farrell and B. Ross, Solved Problems in Analysis: As Applied to Gamma, Beta, Legendre and Bessel Functions, Dover Publications, New York, 1971. This can be deduced by employing Eq. (III-27.6) on p. 170 Search PubMed.
- H. Daimon, T. Nakatani, S. Imada, S. Suga, Y. Kagoshima and T. Miyahara, Jpn. J. Appl. Phys., 1993, 32, L1480 CrossRef CAS.
- M. Ehara, H. Nakatsuji, M. Matsumoto, T. Hatamoto, X.-J. Liu, T. Lischke, G. Prümper, T. Tanaka, C. Makochekanwa, M. Hoshino, H. Tanaka, J. R. Harries, Y. Tamenori and K. Ueda, J. Chem. Phys., 2006, 124, 124311 CrossRef CAS PubMed.
- L. I. Schiff, Quantum Mechanics, McGraw-Hill Companies, 3rd edn, 1968, Eq. (38.3) on p. 325 Search PubMed.
- T. Weber, O. Jagutzki, M. Hattass, A. Staudte, A. Nauert, L. Schmidt, M. H. Prior, A. L. Landers, A. Bräuning-Demian, H. Bräuning, C. L. Cocke, T. Osipov, I. Ali, R. Díez Muiño, D. Rolles, F. J. García de Abajo, C. S. Fadley, M. A. Van Hove, A. Cassimi, H. Schmidt-Böcking and R. Dörner, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 3669 CrossRef CAS.
- K. Fehre, et al. , Phys. Rev. Lett., 2021, 127, 103201 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2023 |