Extended-sampling QM/MM simulation of biochemical reactions involving P–N bonds

Abstract

The description of the phosphate group and its reactions with nitrogen species appears to be challenging using semi-empirical quantum chemical methods, and this holds for DFTB3 too. A new parameterization of DFTB3, consisting of a new P–N repulsive function, has been developed to improve its performance for reactions in which a P–N bond is replaced by a P–O bond or vice versa. Extended-sampling QM/MM simulations using the new parameterization of DFTB3 represent biochemical phosphorylation and hydrolysis reactions involving P–N bonds accurately. The parameter set is benchmarked on a reaction modeling the autophosphorylation of histidine, and is applied to study the complex mechanism of the acidic hydrolysis of an anticancer drug, as well as to the autophosphorylation of a genuine histidine kinase protein.

---

1. Introduction

Biomolecules containing phosphorus play key roles in essential biological functions in all kingdoms of life. One such commonly occurring process is the phosphoryl transfer reaction,^1–4 one of the most important chemical processes in biology. Disruptions of the activity of phosphoryl transfer enzymes may cause serious diseases such as cancer, which also makes protein kinases and phosphatases some of the most important drug targets.^5,6

In most cases, a protein or another biomolecule is phosphorylated via an oxygen atom, resulting in an ester or an anhydride species. There are occurrences, however, of phosphorylation taking place via a nitrogen atom,^7–9 thus resulting in a nitrogen ester analog. A prime example is histidine kinase (HK), a key component of the bacterial signal transduction system,¹⁰ involved in histidine phosphorylation.¹¹ Such HKs are found in a large group of bacteria and are involved in a process that does not occur in the human body, making these enzymes suitable targets for the development of drugs against bacterial resistance.

Investigation of the mechanism and energetics of phosphorylation reactions occurring on nitrogen atoms may find an appropriate computational approach very useful, as shown by the prominent example of phosphohistidine (pHis, the product of histidine phosphorylation). As a thermodynamically unstable compound that typically occurs as an intermediate in signal or energy transduction cascades of biochemical reactions, it is extremely difficult to detect pHis in experiments. This makes way for computational studies to investigate possible mechanisms of the phosphoryl transfer reactions involved. Studying such a reaction is always a challenging task due to the highly charged states of the participating compounds and the complex mechanisms involved.¹² Hybrid quantum mechanics–molecular mechanics (QM/MM)^13–15 will be indispensable when studying such biochemical reactions because these take place in strongly polarizable environments, which are one of the factors that control the mechanism and energetics of the reactions.

Numerous QM/MM studies of the phosphoryl transfer mechanism have been carried out.^16–20 The QM region in such a QM/MM simulation will usually constitute of the active site of the enzyme under investigation, and will thus appear relatively small in size. A corresponding QM calculation using a correlated ab initio method or conventional density functional theory (DFT) will be potentially tractable but still computationally extremely demanding, considering that millions of calculations of energy gradients are required for a molecular dynamics (MD) simulation on a temporal scale of nanoseconds. One of the convenient workarounds to this computational bottleneck is the application of computationally efficient semi-empirical QM methods.

The density-functional tight binding to the third order (DFTB3) appears to be particularly useful, which consists of a Taylor-like expansion of the DFT total energy in electron density and a series of well-defined approximations.²¹ These reduce the computational time by a factor of 100 to 1000 with respect to conventional DFT calculations employing triple-zeta basis sets, while keeping the accuracy sufficient for many biochemical applications.^22,23 Combining DFTB3 with QM/MM and enhanced sampling methods, such as metadynamics, constitutes an efficient tool that has been used to investigate the mechanisms of biochemical reactions, e.g., ATP hydrolysis in myosin,²⁴ thiol–disulfide exchange in proteins,²⁵ nucleotide addition in DNA polymerase,²⁶ deprotonation in DNA synthesis,²⁷ and long-range proton transfer in bacteriorhodopsin.²⁸

In DFTB3, the general-purpose parameter set 3OB for organic and biochemical reactions occasionally faces problems with specific isolated chemical species or reactions that differ from everything that was considered during the development of the parameters. While a recent example is the qualitatively wrong energetics of the thiol–disulfide exchange reaction,²⁹ an especially prominent class of reactions that required a correction in the context of DFTB is the hydrolysis of organic phosphates.³⁰ These solutions constitute examples of a more general concept in the semi-empirical realm, known as special reaction parameterization (SRP).^31–36

The aim of this work is to develop a QM/MM methodology to describe the mechanism and energetics of phosphorylation reactions occurring on nitrogen atoms, using an efficient semi-empirical DFT energy function. The aim of this work is to set up a computational scheme to simulate biochemical reactions in which a P–N bond is replaced by a P–O bond, or vice versa. Although this scope may seem very limited, it includes two interesting classes of processes: the phosphorylation of biomolecules via a nitrogen atom, like in histidine, and the hydrolysis of drugs involving an unstable P–N bond. The novel component of the computational scheme will be a specific reparameterization of DFTB3/3OB, as the original parameter set fails to describe said reactions, concentrating on the interactions between phosphorus and nitrogen atoms. This work also includes case studies of three different reactions: First, a model of the phosphorylation of histidine, which will be a part of the parameterization workflow to ensure the correct energetics of the reaction. Second, to showcase the applicability of the computational scheme, the acidic hydrolysis of an anti-cancer drug containing P–N bonds generating the actual active form of the drug. Finally, as a representative of a reaction taking place in a realistic complex biomolecular system, the autophosphorylation of a histidine kianase protein.

2. Methods

2.1 DFTB

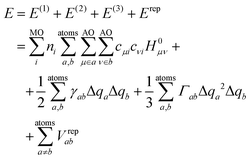
DFTB3 is an approximative DFT method, derived by expanding the DFT total energy functional to the third order in atom-centered charge densities, around a reference charge density of a fictitious union of neutral atoms. The resulting expansion is further approximated by considering the Kohn–Sham orbitals as linear combinations of atomic orbitals |μ〉, which are members of an optimized minimal basis set. The resulting total energy expression consists of two parts, involving a number of parameters to be determined prior to application:
The electronic part E⁽¹⁾ + E⁽²⁾ + E⁽³⁾ involves molecular orbitals 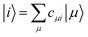with expansion coefficients c_μi, and Mulliken atomic charges 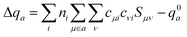with occupation numbers n_i, overlap integrals S_μν = 〈μ|ν〉 and neutral atom charges q⁰_a. The remaining parameters are the charge-independent Hamilton integrals H⁰_μν = 〈μ|H⁰|ν〉^37,38 as well as the chemical hardnesses³⁹ and their charge derivatives^21,40 of the involved chemical elements, appearing in the distance-dependent analytical functions γ and Γ, which describe the interaction of the atom-centered charge densities. The determination of these parameters is relatively straightforward. The interaction between the QM molecule represented by DFTB and any MM environment represented by point charges can be added conveniently at negligible additional computational cost.^41,42

The so-called repulsive part models the zeroth-order contribution to the energy in the density expansion, which corresponds to double-counting terms of DFT and other corrections. Although these can be computed from DFT calculations in principle, an empirical fit to a larger test set is usually performed to achieve a good general accuracy and partially compensate for approximations introduced in the electronic part. Therefore, their determination is usually more involved. The repulsive part is expressed in terms of pair potentials V^rep_ab, which are specific to respective pairs of chemical elements and depend on interatomic distances r_ab but not on atomic charges. Technically, V^rep_ab(r_ab) is represented by a cubic spline, parameterized by fitting to a selected set of reference atomization energies, molecular geometries, and barrier or reaction energies. The spline is preceded by a segment of an exponential function at short interatomic distances, while it converges to zero at a certain (longer) distance.

2.2 Reparameterization of the repulsive potential of DFTB

An SRP of the 3OB parameter set was created in this work, which consisted of a new repulsive function for the P–N atomic pair. The original electronic parameters as well as all repulsive potentials except P–N were kept unchanged. This approach is analogous to that of the previous SRP for phosphate hydrolysis reactions, 3OB/OPhyd,⁴³ which adjusted the P–O repulsive potential while keeping all of the other 3OB parameters intact.

The new P–N repulsive potential was generated by means of the partially automatized procedure erepfit.⁴⁴ As an input, erepfit requires one or several molecular structures containing the bond to be parameterized, in this case P–N, and the corresponding reference energies stemming from higher-level QM calculations. Also, those structures are considered stationary points of energy, so that the vanishing gradients of energy constitute additional input information. Given these conditions, and keeping all of the electronic parameters as well as repulsive parameters other than P–N, the P–N repulsive potential was fitted to minimize the deviation of resulting energies and gradients from the reference data.

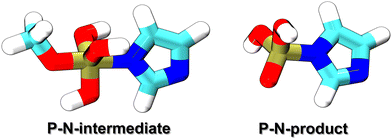
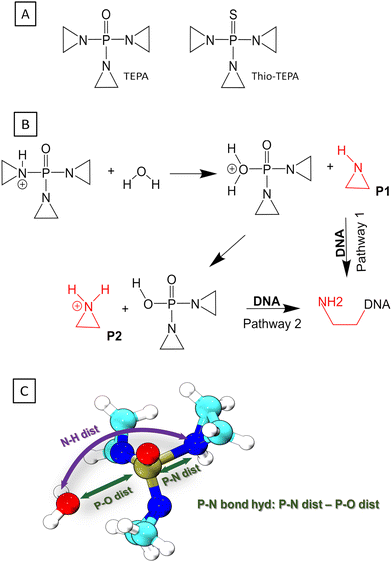
This work considered two molecules containing a P–N bonding pattern that resembles that in relevant biochemical applications, see Fig. 1. P–N-product is a nitrogen analog of a phosphoester, containing a tetravalent phosphorus atom with three P–O bonds and a P–N bond, while P–N-intermediate is a transient species, which involves a pentavalent phosphorus with four P–O bonds and a P–N bond, resembling intermediate or transition states in phosphoryl transfer reactions. In reactions occurring under physiological acidity, the species that our model molecules mimic would occur in deprotonated states, carrying large negative net charges. However, pilot QM calculations performed for these molecules in the gas phase showed extremely difficult SCF convergence. A practical solution of this problem is to consider their fully protonated, electroneutral forms as shown in Fig. 1.

Fig. 1 The molecules considered for the reparameterization of the P–N repulsive potential. P–N-product is a protonated nitrogen analog of phosphoester, while P–N-intermediate is a protonated transition structure leading from an appropriate reactant to P–N-product.

The below described parameterization procedure followed that of 3OB closely.^22,43 The geometries of both P–N-product and P–N-intermediate were energy-minimized at the B3LYP/aug-cc-pVTZ level of theory; see Table S1 (ESI†) for the coordinates. Then, accurate atomization energies E_at were obtained from the composite G3B3 calculations.⁴⁵ All QM calculations were performed with Gaussian 09.⁴⁶ Before conversion to the final third-order spline, the repulsive potential was determined in the form of a fourth-order spline on four consecutive intervals of distances. An additional equation was introduced to make the repulsive potential convex at the P–N distance where the spline starts, to make sure that a well-behaved exponential function can be constructed on shorter distances. An overview of the reference and input data to the parameterization of the P–N repulsive potentials is provided in Table 1.

Table 1 Input data to erepfit used to obtain the P–N repulsive function. The function takes the form of an exponential at P–N distances shorter than 2.7 a.u., while it vanishes at distances beyond 5.0 a.u. During parameterization, the function is represented as a quartic spline, with division points given here, and is converted to a cubic spline afterwards

Molecule	Charge (e)	E at (kcal mol^−1)
a Modified, value from G3B3: 1480 kcal mol^−1.
P–N-product	0	1505^a
P–N-intermediate	0	1947

---

Potential	Division points (a.u.)
P–N	2.7, 3.5, 4.0, 4.5, 5.0

---

Potential	Additional equation
P–N	V′′(1.487 Å) = 0.84 a.u.

---

The repulsive potential was first obtained as described above. Pilot simulations performed in the case study 1 (see below) however revealed incorrect energetics of the reaction involving the replacement of a P–O bond by a P–N bond. Additionally, the P–N repulsive function took a potentially problematic shape with a non-monotonic second derivative, called the sprungschanze (German for “ski-jumping hill”). Note that this occurred in previous DFTB parameterizations repeatedly (e.g., in OPhyd and our DFTB2 parameterization for organic molecules containing halogens).⁴⁷ It turned out that both of these problems could be solved by artificially increasing E_at at the input to erepfit, in a treatment called the overbinding.

On the one hand, the P–N potential became “compatible” with 3OB/OPhyd in the sense that P–O and P–N bonds now have similarly overestimated binding energies, leading to much improved energetics of model reactions (such as those in the Results section). On the other hand, shifting the whole repulsive potential down, to less positive energies, facilitated its convergence to zero largely, making it possible to keep the function convex on the entire distance range. Therefore, several trial rounds of parameterizations were performed, applying overbinding in P–N-product by varying amounts, and checking the energetics of the reaction in case study 1. The final parameterization, yielding the best agreement with the reference energetics, was obtained with E_at = 1505 kcal mol⁻¹ (i.e., increased by 25 kcal mol⁻¹). The unchanged value of E_at for the P–N-intermediate was considered.

2.3 Case studies – simulation details

The metadynamics simulations carried out in this work used one of two possible setups: either a pure QM description of the system, or a QM/MM description with the explicit water in the MM region described with the TIP3P model.⁴⁸ The Lennard-Jones parameters of the atoms in the QM region were taken from the Amber99 force field⁴⁹ (note, these charges are unchanged in the later refined versions, Amber99SB and Amber99SB-ILDN).

The electrostatic interactions in the MM region were treated with the smooth particle–mesh Ewald method,^50,51 with the real-space contribution cut-off at 1 nm. The QM–MM interactions in simulations performed with DFTB+ for the QM region were treated with PME as well;⁵² simulations performed with B3LYP treated the QM–MM electrostatics switched from 1 nm to a cut-off of 1.05 nm because no PME implementation for that case is available in the software used. The Lennard-Jones interactions were always cut-off at 1 nm. There were no counterions in order to avoid any specific interactions between the ions and the highly charged molecules in the QM region, and thus any PME evaluation of forces implicitly involved a uniform neutralizing charge density.

The simulations used the leap-frog integrator with a time step of 1 fs. A constant temperature of 300 K was maintained by means of the Nosé–Hoover thermostat with a time constant of 0.5 ps.^53,54 Each system was first energy-minimised with steepest descents, and then equilibrated for 100 ps at 300 K.

The resulting coordinates and velocities were considered as the initial conditions for QM/MM MD simulations using the metadynamics protocol^55,56 of a length specified below for each case, optionally in the well-tempered⁵⁷ and multiple-walker⁵⁸ variants. The potentials of the mean force (PMF) were obtained from each of the simulations, and they correspond to Helmholtz free energies.

Simulations were performed using a combination of locally modified versions^52,59,60 of Gromacs^61–63 and DFTB+⁶⁴ interfaced with Plumed 2.5.1.⁶⁵ Simulations employing B3LYP were performed with Gromacs interfaced with Orca 4.2.0.^66,67

Imidazole analog of phosphoester. The phosphorylation of imidazole in explicit water was simulated with multiple-walker QM/MM metadynamics. The reactants, a molecule of methylphosphate and a molecule of imidazole, were initially modeled manually and placed in a periodic box sized 3 × 3 × 3 nm³, which was subsequently filled with 872 TIP3P water molecules. The lengths of the bonds being broken (P–O) and created (P–N) were considered as CVs, and 16 metadynamics walkers were employed.

The QM region consisting of the imidazole and methylphosphate molecules, as well as the corresponding products, was treated with the following methods in the three different simulations: (A) DFTB3 with the standard 3OB parameter set, (B) as a reference, the DFT level B3LYP/aug-cc-pVTZ, and (C) DFTB3 with 3OB parameters complemented by OPhyd and the new PNmod.

The metadynamics simulations employing DFTB were run for an accumulated sampling of 25 ns each, and used a constant bias height of 0.2 kJ mol⁻¹. The metadynamics employing B3LYP was much more computationally costly, so that a shorter accumulated simulation time of 372 ps was reached. To make the metadynamics more effective under these circumstances, a higher constant bias height of 1.8 kJ mol⁻¹ was used. The Gaussian bias functions always had a width of 0.02 nm, and were added every 100 steps (0.1 ps). In all the simulations, both CVs (P–N distance and P–O distance) were restrained to values lower than 3.5 Å (“upper wall” of Plumed) with a force constant of 150 000 kJ mol⁻¹ nm⁻², and the angle N–P–O was restrained to 178° with a force constant of 1500 kJ mol⁻¹ rad⁻², to make the sampling of the relevant regions of configuration space more efficient.

Hydrolysis of TEPA. There were two different kinds of multiple-walker QM and QM/MM simulations in the study of hydrolysis of TEPA. The reactants, a protonated molecule of TEPA and a molecule of water, were initially modeled manually and placed in a periodic box sized 3 × 3 × 3 nm³, which was subsequently filled with 874 TIP3P water molecules. As the QM method, DFTB3 was applied with the 3OB parameter set complemented with OPhyd and the new PNmod.

First, the simulations of the first step of the reaction alone, employed 16 walkers and two CVs, the lengths of the bonds being broken (P–N) and created (P–O). One of the simulations, (A) considered the reaction in the gas-phase with the reactants and products treated with the QM and no MM region. The metadynamics of 8 ns added biases of constant height of 0.3 kJ mol⁻¹ and width of 0.02 nm using a bias deposition frequency of 300 steps (0.3 ps). The other simulation (B), considered the reaction in an aqueous environment represented as explicit MM water in a QM/MM setup. The well-tempered metadynamics of 75 ns was run with biases of width 0.02 nm and initial height of 1 kJ mol⁻¹ using a bias deposition frequency of 300 steps (0.3 ps) and a bias factor of 60. In both simulations, the distances P–N and P–O were restrained to values lower than 5 Å (“upper wall”) with a force constant of 150 000 kJ mol⁻¹ nm⁻², and the angle N–P–O was restrained to values higher than 160° (“lower wall”) with a force constant of 1500 kJ mol⁻¹ nm⁻² to focus the sampling into the relevant area of the configurational space. The O–H bond lengths in the water molecule were restrained to 1 Å with a force constant of 150 000 kJ mol⁻¹ nm⁻² to prevent any spurious deprotonation of the water.

Second, the simulations of the entire process – including the proton transfer step following the attachment of the water molecule – used 24 walkers and two different CVs: one is the difference of distances P–N and P–O, called “PN bond hyd” in the following; the other is the N–H distance to describe the transfer of the proton. The first 65 ns of the simulation were carried out with a constant bias height of 1 kJ mol⁻¹ and width of 0.02 nm, and the consecutive 500 ns were run in a well-tempered metadynamics mode with an initial bias height of 2.8 kJ mol⁻¹ and a bias factor of 65 using a bias width of 0.02 nm. The deposition rate was kept at 500 steps (0.5 ps) in both cases. The distances P–N and P–O were restrained to values lower than 5 Å with a force constant of 150 000 kJ mol⁻¹, and the distance N–H (the proton being transferred) was restrained to values lower than 3 Å with a force constant of 1500 kJ mol⁻¹, to improve the sampling of the relevant area of the configurational space. The value of the coordination number (Plumed functionality) of both nitrogens not taking part in the reaction with the hydrogens of the water molecule were restrained to zero with a force constant of 150 000 kJ mol⁻¹ to prevent any spurious proton transfer to the nitrogens.

Autophosphorylation of histidine kinase. The initial structure of the protein was taken from PDB ID 5LFK,⁶⁸ a crystal structure of the hemi-phosphorylated CpxA HK from E. coli. Any missing residues and unresolved loops were modelled using UCSF Chimera⁶⁹ interfaced with MODELLER.⁷⁰ Then, the biomolecular complex was enclosed in a periodic box sized ca. 10 × 10 × 10 nm³, which was filled with water and electro-neutralized by the addition of 16 sodium counterions. First, the system was prepared in an entirely MM representation: The AMBER99SB-ILDN force field was used to describe the protein,⁷¹ while the parametrization of ATP from ref. 72 was employed. The solvent was represented with the TIP3P water model⁴⁸ and Åqvist's parameters for the counterions.⁷³ The electrostatic interactions were treated with PME,^50,51 where the short-range contribution was cut-off at 1 nm, and the Lennard-Jones interactions were cut-off at 1 nm. All of the MD simulations used the leap-frog integrator⁷⁴ with a time step of 1 fs, while all bonds involving hydrogen atoms were constrained with LINCS.⁷⁵ The MM system was energy minimized with steepest descents, and then equilibrated for 10 ns maintaining the temperature of 300 K by means of the Bussi thermostat.⁷⁶

A QM/MM setup was prepared using the final structure from the MM equilibration. The QM region was introduced, consisting of the reaction center and its nearest neighborhood: side chains (starting from Cβ atom) of His248, Glu249, Arg251 and Asn145, the part of the ATP molecule starting from C5 atom, the Mg²⁺ ion as well as ten water molecules. The QM–MM boundary was treated with the link atom scheme, so that a link atom was placed on the Cα–Cβ bond in the side chains in the QM region, and on the C5–C4 bond in the ATP molecule. The QM region was treated with DFTB3/3OB-OPhyd-PNmod. Electronic embedding was employed, which involved our PME implementation.⁵² The MM force field used in the preceding equilibration was kept for the MM region in the QM/MM simulation. The same set of MD simulation parameters were used as in the MM equilibration, and the QM/MM system was equilibrated for a further 1 ns at 300 K.

A PMF was generated by means of a two-dimensional multiple-walker metadynamics simulation employing 48 individual simulations (walkers). The collective variables were the lengths of the bonds being respectively created and broken: Pγ(ATP)–Nε(His248) and Pγ(ATP)–Oβ(ATP). An initial phase of 55 ns was run with biasing Gaussians of 0.02 nm width and a constant height of 0.8 kJ mol⁻¹, while the Gaussian height was reduced to 0.5 kJ mol⁻¹ in the subsequent phase of 23.5 ns. The Gaussians were deposited every 500 steps, and the biases were communicated between the individual walkers every 1000 steps.

During the metadynamics simulations, all of the O–H bonds of QM water molecules were restrained to a length of 0.10 nm with a force constant of 15 000 kJ mol⁻¹ nm⁻². The angle Nδ(His248)–P(γ-phosphate of ATP)–O(β-phosphate of ATP) was restrained to values higher than 160° with a force constant of 1500 kJ mol⁻¹ rad⁻² (‘lower wall’ of PLUMED). The distance P(γ-phosphate of ATP)–Nε(His248) was restrained to values lower than 0.35 nm (‘upper wall’), and the distance P(γ-phosphate of ATP)–O(β-phosphate of ATP) was restrained to values lower than 0.40 nm (‘upper wall’) with a force constant of 15 000 kJ mol⁻¹ nm⁻².

3. Results and discussion

3.1 Characterization of the new P–N repulsive potential

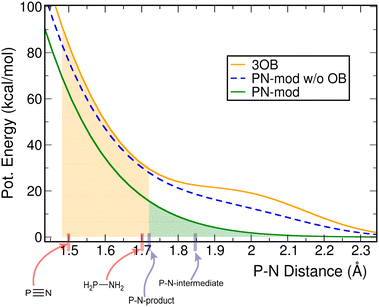
The new P–N repulsive function is presented in Fig. 2, together with the original function from the 3OB parameter set and with our first reparameterization attempt (carried out with the genuine E_at for the P–N-product). The P–N bond lengths in the compounds considered in the different parameterizations are also shown.

Fig. 2 Comparison of the P–N pair repulsive potential in the general-purpose parameter set 3OB (orange), the potential in the SRP generated in this work (green), and a potential obtained from fitting with no overbinding (see the text, broken blue). Colored ticks on the distance axis denote the P–N bond lengths in the molecules used for the parameterizations (red – standard 3OB, blue – this work). Based on this, the shaded regions denote the ranges of distances where a good performance of the respective parameter sets may be expected (orange – standard 3OB, green – the SRP developed in this work).

The parameterization of 3OB considered two small molecules with relatively short P–N bonds of 1.50 and 1.70 Å, respectively. Therefore, a good performance may be expected for similarly simple binding situations and such relatively short P–N bonds. Biochemically relevant reactions involving the P–N bond, however, typically involve more complex binding situations and larger bond lengths; note, the choice of molecules for the parameterization in this work was motivated by the phosphoryl transfer reaction in histidine kinases, and their respective P–N bond lengths are 1.72 and 1.85 Å. Correspondingly, the compounds containing five- and four-fold coordination to phosphorus, including an imidazole moiety, represents those much more closely than the small generic compounds considered in the construction of 3OB.

Owing to the increased E_at for the P–N-product considered in the fitting, the resulting P–N repulsive function is shifted to lower energies in the range of bond lengths of interest: by 14.0 and 16.3 kcal mol⁻¹ for the bond lengths occurring in P–N-product and P–N-intermediate, respectively. On the one hand, this will improve the description of reactions in which a newly formed P–N bond replaces a P–O bond, as the P–O bond itself is subject to overbinding in the 3OB/OPhyd parameter set. On the other hand, in this case, the fitting procedure yielded a function that is convex on the entire range of distances. This avoided a sprungschanze that is visible in the P–N potential in the original 3OB, and to a smaller extent, in the initial reparameterization in this work performed with the genuine E_at for the P–N-product.

3.2 Case study 1: imidazole analog of phosphoester

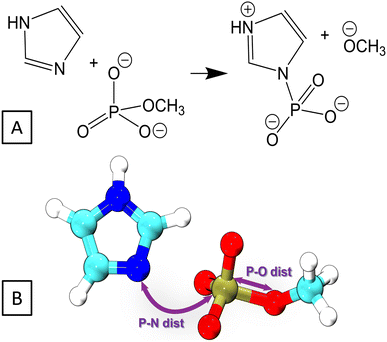
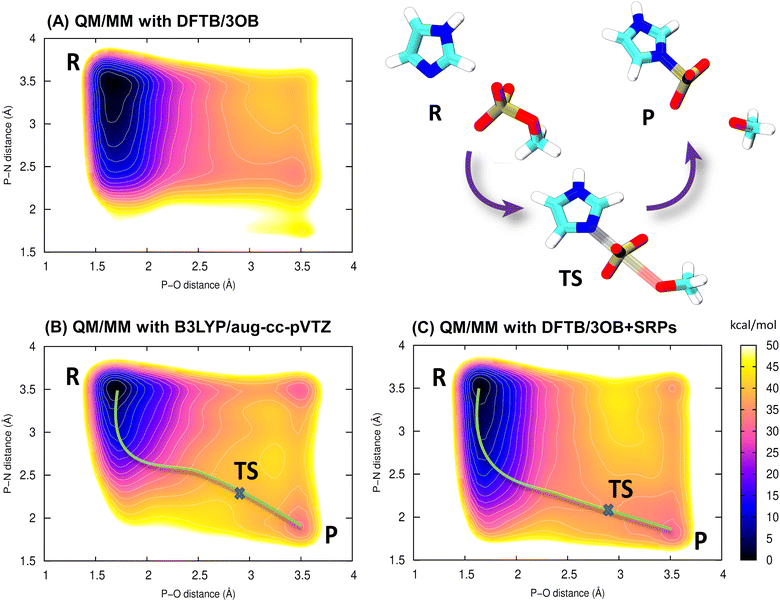
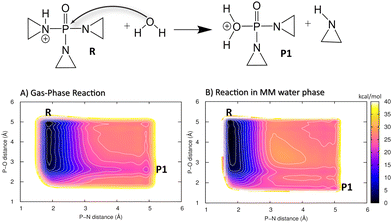
Here, we investigate the phosphoryl transfer reaction in Fig. 3A, which is a roughly simplified model of the chemistry of autophosphorylation reactions in HK. This approach follows several studies carried out to understand in vivo enzymatic catalysis in proteins using small chemical systems in recent decades.^77–79 In our case, the imidazole ring represents the side chain of the histidine residue to be phosphorylated, while the methyl phosphoester is the phosphate donor, simplified in comparison to the genuine donor, ATP; the γ-phosphate group of ATP transfers to histidine in the biochemical phosphorylation. The reaction yields the phosphoimidazole, which is just like the biochemical product, phosphohistidine in HK. We note that the reactant is an ester of phosphoric acid, while ATP, the genuine phosphate donor in the phosphorylation of histidine and other biochemical reaction, is in fact an anhydride. This is the reason why phosphohistidine is a thermodynamically unstable species,^80–82 which occurs in the initial steps of some of the phosphate transfer cascades.⁸¹ Nevertheless, the binding pattern on the phosphorus atom in the reaction investigated here still closely resembles that of the phosphorus atom in the biochemical phosphorylation of histidine.

Fig. 3 (A) The reaction in which phosphoimidazole is formed from imidazole and methylphosphate was considered as a model of histidine phosphorylation. (B) The collective variables employed in the 2D metadynamics simulations of the reaction.

The reaction was simulated by means of 2D QM/MM metadynamics employing the lengths of the bonds being broken and created as CVs, see Fig. 3B. The original parameter set DFTB3/3OB yielded the PMF in Fig. 4A, which does not feature the product state as a minimum of free energy. There is merely a broad low-energy region around the P–N distance of 2.3 Å, indicating a very long P–N distance in comparison with the expected length of 1.7–1.8 Å for a usual P–N bond. Therefore, the reaction energy and the transition path obtained from this free energy plot are also unreliable.

Fig. 4 Potentials of the mean force obtained from the QM/MM metadynamics simulations using the different QM methods: (A) DFTB3 with the standard 3OB parameterization, (B) hybrid DFT at the B3LYP/aug-cc-pVTZ level, and (C) DFTB3/3OB complemented with OPhyd and the new PNmod. The contour lines are spaced by 3 kcal mol⁻¹, and the minimum energy pathways involving the pentavalent phosphorus transition state are marked by a green line.

It may be of interest to compare this behavior with that of DFT-GGA approaches, from which the current parameterizations of DFTB3 descend. A geometry optimization of phosphoimidazole performed on the level PBE/Huzinaga-MINI also resulted in an unusually long P–N bond, see Table S2 (ESI†). This appears to be an interesting correlation with the observation in the DFTB3/3OB simulation above. Still, it should be noted that the choice of molecules to parameterize the P–N interaction in DFTB3/3OB is the likely source of trouble here.

The PMF resulting from the reference simulation, in which the QM region was described with B3LYP/aug-cc-pVTZ, is shown in Fig. 4B. The product minimum appears at the P–N distance of 1.8 Å and the P–O distance of 3.5 Å. The transition state (TS) is a pentavalent phosphorus species,⁸³ somewhat asymmetric with the P–N bonds slightly longer than the P–O bond. This indicates an associative reaction pathway^84,85 as in an S_N2 reaction. The reaction energy is +34 kcal mol⁻¹, and proceeds over a barrier of 40 kcal mol⁻¹. The high positive reaction energy reflects the fact that a relatively stable phosphoester is considered as a phosphate donor. Consequently, the phosphorylation reaction in this artificial molecular complex would not proceed at physiological temperature; the purpose of investigating this reaction is rather to provide a comparison of free energies obtained with the newly parametrized DFTB3/3OB to a higher-level calculation, here, hybrid DFT. In the genuine biochemical phosphorylation reactions, the phosphate donor would be a much less thermodynamically stable species like an anhydride (e.g., ATP), and the phosphohistidine product would be the more stable side in the reaction. On the technical part, the QM/MM simulation considering a hybrid DFT functional for the QM method proved computationally costly, and the accumulated sampling of 372 ps took ca. 3 months of computing time on 192 CPU cores of Intel Xeon 6252 Gold.

Finally, the same reaction was simulated with DFTB3/3OB for the QM method, however now including the newly reparameterized P–N repulsive potential in addition to the OPhyd repulsive potential for P–O. As a matter of fact, this simulation was performed several times, using P–N repulsive potentials obtained with different values of E_at for the P–N-product as described above. The free energy plot in Fig. 4C was obtained with the P–N repulsive yielded by the final round of the parameterization. In this case, the location of the minimum corresponding to the product agrees with the B3LYP reference, as do the reaction energy of +32 kcal mol⁻¹ and reaction barrier of 38 kcal mol⁻¹. Atomic coordinates of representative snapshots corresponding to states R, TS and P may be referred to in Table S3 (ESI†).

Thus, the reparameterization of the P–N repulsive potential brings the performance of DFTB3/3OB to within 2 kcal mol⁻¹ of the B3LYP reference, both in the reaction energy and the energy barriers. Even more importantly, the minimum energy transition pathway proceeds through the correct state involving a pentavalent phosphorus atom. Just like in the reference, the transition region appears broad, and the TS (saddle point) has an asymmetric structure, with the P–O bond being markedly longer than P–N. At this point, it is necessary to notice that our discussion focuses on the pentavalent TS pathway because of its relevance in enzymatic reactions,⁸⁶ although there is also a low-energy trivalent TS visible in the top-right corners of Fig. 4B and C.

3.3 Case study 2: hydrolysis of TEPA

ThioTEPA (N,N′,N′′-triethylenethiophosphoramide)^87,88 and its major metabolite, the oxo analogue TEPA⁸⁹ (see Fig. 5A) are some of the oldest antitumor drugs with continuing clinical use, often applied in high dose combination regimes to treat breast, ovarian, bladder cancers and other solid tumors. They are aromatic nitrogen mustard-based prodrugs for aziridine molecule or aziridinium ions, proposed to induce cancer cell death either by alkylating DNA^90,91 or by the formation of cross-links within DNA.⁹² Although it is known that the aziridine or aziridinium binds to guanine in DNA, the exact mechanism is still not quite clear.

Fig. 5 (A) Structures of ThioTEPA and TEPA. (B) Acidic hydrolysis of TEPA generates aziridine or aziridinium ion, which consequently reacts with a guanine in DNA. Two different pathways postulated: In one, the nucleophilic attack by water breaks one of the P–N bonds, releasing a free aziridine (P1). In the other, an aziridinium ion (P2) forms after consecutive protonation of the aziridine molecule. (C) Collective variables used in the 2D QM/MM metadynamics simulation of the TEPA hydrolysis.

Experimental studies revealed that there are several possible mechanisms for the alkylation of guanine in DNA,^87,93,94 but it still remains unclear which pathway is the most effective. The first step of action is always hydrolysis, which generates the real alkylating agent, aziridine or (since aziridine is a weak base) aziridinium; in ThioTEPA, this follows the initial metabolic activation to TEPA. A previous experimental study showed that TEPA yielded more aziridine than thioTEPA did, and more aziridine was produced at lower pH indicating that acidic hydrolysis dominates,⁹⁵ although several possible pH dependent hydrolysis pathways of TEPA were investigated previously.^96,97

Our current work focuses on the acidic hydrolysis pathway, in which one of the aziridine rings of the TEPA molecule becomes activated as a leaving group by accepting a proton, and then a water molecule carries out a nucleophilic attack on the phosphorus atom of TEPA. This leads to an unstable adduct P1 (see Fig. 5B), in which the oxygen atom of the P–O bond carries a formal positive charge. Consecutive proton transfer from the P–O moiety to the aziridine ring produces another possible nucleophile (aziridinium ion, P2 in Fig. 5B). Earlier computational studies on this particular hydrolysis reaction identified several features of the reaction, the structure of the TS, the reaction energy etc.^96–98 However, the complete mechanism of the hydrolysis has not emerged yet. At the same time, the reaction falls within the area of applicability of PNmod, because a P–N bond is breaking as a P–O bond is forming, and a pentavalent phosphorus TS is likely involved. This makes the acidic hydrolysis of TEPA a good case to show the performance and transferability of the PNmod SRP to other reactions than just phosphorylation via a nitrogen atom.

The two possible pathways involving an aziridine molecule or an aziridinium ion, which would further react with guanine in DNA, were investigated (see Fig. 5B). First, the initial reaction of protonated TEPA with a water molecule, leading to an unprotonated aziridine molecule (P1), was simulated in the gas phase. QM metadynamics was employed, using the distances P–N and P–O as CVs. The QM method was DFTB3 with the 3OB parameter set augmented by the new PN-mod SRP together with the OP-hyd SRP. The resulting PMF shown in Fig. 6A features a broad minimum corresponding to the P–N bond with a length of 1.8 Å. The product P1, involving a neutral aziridine molecule, appears highly thermodynamically unstable, 22 kcal mol⁻¹ above the reactant, while the relevant TS is merely 1 kcal mol⁻¹ higher.

Fig. 6 Top: The nucleophilic attack by a water molecule on the phosphorus atom of TEPA leads to the dissociation of the P–N bond, releasing a free aziridine molecule. Bottom: The potential of the mean force obtained from the 2D metadynamics simulation of the reaction, (A) in the gas phase and (B) in an explicit water environment. The contour lines are spaced by 2 kcal mol⁻¹.

In order to roughly assess the quality of the PMF in Fig. 6A, the energies of species R and P1 as well as that of the corresponding TS were obtained from B3LYP/aug-cc-pVTZ geometry optimizations in the gas phase. The reaction energy was 20.6 kcal mol⁻¹ and the barrier height was 21.2 kcal mol⁻¹, thus the PMF in Fig. 6A seems to agree with this reference well. Although such a comparison of single point energy difference with a free energy difference from a PMF is not rigorous, it still appears to support the quality of the DFTB3/3OB-OPhyd-PNmod description of the reaction.

Interestingly, the reaction energy obtained as the difference of DFTB3/3OB-OPhyd-PNmod single point energies calculated for structures optimized with B3LYP/aug-cc-pVTZ is 16.1 kcal mol⁻¹. From this comparison, the agreement of DFTB3/3OB-OPhyd-PNmod with the reference appears somewhat deteriorated. Importantly, it is restored as soon as the structures of R and P1 are optimized with DFTB, resulting in a reaction energy of 22.6 kcal mol⁻¹. The largest difference between the PES on the B3LYP/aug-cc-pVTZ and DFTB3/3OB-OPhyd-PNmod levels appears in the P1 structure, which is the water adduct involving the P–O⁺ bond (with the oxygen atom carrying a formal positive charge): the bond length is 2.0 and 2.5 Å in the respective optimized structures. (Note that the P1 minimum appears at the P–O distance of 2.5 Å in the PMF in Fig. 6A also.) Considering all this information together with the quite large reaction energies, it can be concluded that DFTB3/3OB-OPhyd-PNmod is adequate for the description of acidic TEPA hydrolysis. The atomic coordinates of the energy-minimized structures discussed above may be referred to in Tables S4 and S5 (ESI†).

After that, the same reaction in an explicit water environment was simulated. This employed a hybrid QM/MM setup in an explicit water environment (QM/MM), while the 2D metadynamics employed the same set of CVs as the gas phase case above. The resulting PMF, shown in Fig. 6B, is very similar to that in the gas phase. The reaction energy and the barrier height remained the same, and the product basin P1 remained high in energy, thermodynamically unfavorable. Still, there is a difference in the structure of the product species: A new state appears on the PMF, corresponding to the P–O⁺ bond being shorter, close to its length in the B3LYP/aug-cc-pVTZ optimization described above. It can be explained as being the consequence of a polarizing effect of the explicit water environment on the charged P–O⁺ bond. Also, the observation of an endergonic reaction in both cases agrees with the previous results produced by others.⁹⁶

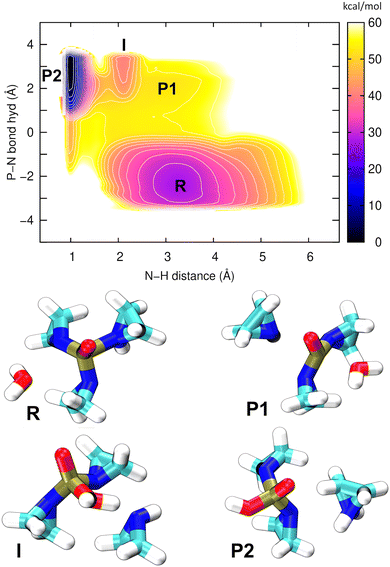
Apparently, down-the-hill energetics leading to a stable product can only be achieved by including the deprotonation of the oxygen moiety to complete the hydrolysis. To this end, the entire process corresponding to the first step of pathway 2 in Fig. 5B was simulated, with aziridinium ion (P2) as the final product. The hybrid QM/MM metadynamics in an explicit water environment used 2 different CVs: “P–N bond hyd” described the replacement of a P–N bond by a P–O bond, while the N–H distance simply described the proton transfer from the oxygen atom to the aziridine molecule. The resulting PMF is shown in Fig. 7.

Fig. 7 Top: The potential of the mean force obtained from the 2D well-tempered metadynamics simulation of acidic hydrolysis of TEPA. The breaking of a P–N bond and making of a P–O bond releases a free aziridine molecule (P1), and the consecutive proton transfer leads to an aziridinium ion (P2). The contour lines are spaced by 3 kcal mol⁻¹. Bottom: The structures corresponding to all of the minima on the PMF.

This single PMF has resolved all of the relevant structural states; atomic coordinates of the representative snapshots may be referred to in Table S6 (ESI†). The final product (aziridinium ion, P2) is now the global minimum on the PMF, lying 30 kcal mol⁻¹ below the reactant (TEPA, R) in terms of free energy, which indicates a strongly exergonic reaction. The first reaction step (R → P1) is rate-determining, with a barrier of ca. 20 kcal mol⁻¹, the same as in our previous simulation above. The nucleophile aziridine (P1), which previously was shown to be unstable, now appears as an intermediate on a possible pathway to the final product P2. Additionally, there is an interesting state “I” located between P1 and P2, which is a strongly hydrogen bridged structure that establishes before the proton transfer has taken place. Overall it is clear that P2 is a far more stable species to serve as a potential alkylating agent.

3.4 Case study 3: autophosphorylation of a trans histidine kinase

HKs are parts of two-component systems, which support signal transduction cascades in certain bacteria. Their participation in the signal transduction relies on a transient phosphorylation of a histidine residue, before the phosphoryl group is further transferred to another protein component, the response regulator. The response of a HK to a stimulus starts with the binding of an ATP molecule and a transition from the inactive to the active conformation, during which the ATP-binding domain approaches the DHp domain carrying a histidine residue to be phosphorylated. The second step, consisting of an actual transfer of a phosphoryl group from the ATP molecule to the histidine residue, represents one of the major applications of the current DFTB3/3OB reparametrization. The HK functional form is dimeric, and depending on the sense of winding of a four-helix bundle in the center of the dimer, the autophosphorylation takes place either in a cis-mechanism, phosphorylating the histidine on the same monomer as the ATP molecule is bound to, or in a trans-mechanism, in which the histidine on the other monomer is phosphorylated. In this particular example, we investigate the autophosphorylation reaction in a HK taking place with a trans-mechanism, namely the CpxA HK from E. coli, PDB ID 5LFK.

The structure of the protein is shown in Fig. 8, and so is a detailed view of the reaction center consisting of the side chains of His248, Glu249, Arg251, Asn145, the ATP molecule with the coordinated Mg²⁺ ion and ten water molecules, which together represent the QM region in the QM/MM simulation. The phosphoryl transfer reaction from the ATP molecule to the side chain of His248 is investigated by way of generating the potentials of the mean force (PMF, representing the free energy surface) of the reaction with QM/MM multiple-walker metadynamics simulation employing DFTB3/3OB-OPhyd-PNmod as the quantum chemical method. Two different collective variables are considered in the metadynamics simulation – the distances P(ATP)–N(His248) and P(ATP)–O(ATP), as indicated in Fig. 8B. The resulting PMF is shown in Fig. 9.

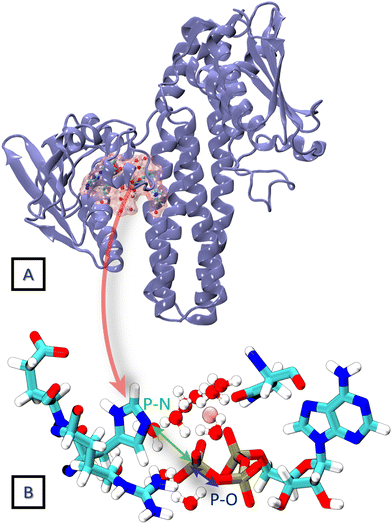Fig. 8 (A) The crystal structure of the trans HK protein, CpxA from E. coli (PDB ID 5LFK). (B) The phosphorylation reaction center constituting the QM region in the 2D QM/MM metadynamics simulation. The distances P–N and P–O are considered as collective variables.

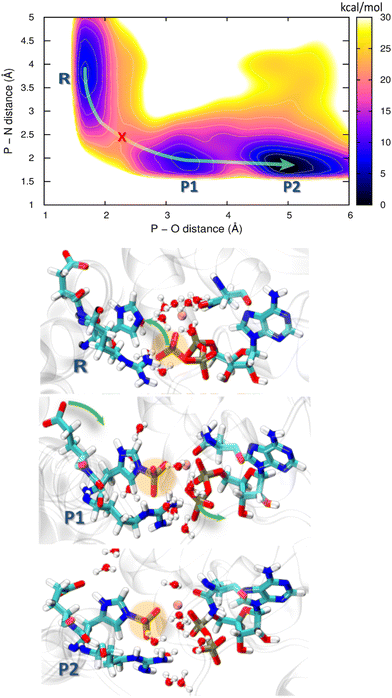Fig. 9 Free energy profile obtained from the 2D QM/MM metadynamics simulations using CVs P–N distance and P–O distance of autophosphorylation reaction for the trans histidine kinase (modelled after pdb id: 5lfk). The green arrow guides through the minimum energy path and the red cross represents the transition state. Representative structures of the corresponding minima are shown below where R is the reactant minimum, P1 is an intermediate product, and P2 is the final product.

Starting from the reactant, an ATP molecule and an unphosphorylated His248 (R), there is a barrier of 15 kcal mol⁻¹ before an intermediate product (P1) is reached, and finally, a stable product (P2) is formed after crossing a lower barrier of 6 kcal mol⁻¹. The phosphoryl transfer proceeds through a pentavalent phosphorus transition state (red cross in the PMF in Fig. 9). His248 and ATP are further apart than in HKs supporting His autophosphorylation in the cis-mechanism,^99,100 which might lead to a higher barrier to autophosphorylation. We recall that the overall barrier height of 18 kcal mol⁻¹ in our study of HK working in the cis-mechanism was in agreement with experimental kinetics, and the barrier to the chemical step – composed of the phosphoryl transfer and the deprotonation of pHis – was 8 kcal mol⁻¹. The current case study of the trans-mechanism only involves the phosphoryl transfer, and this is a likely reason for the higher barrier. The barrier height appears similar to that in a previous study by Marsico, Burastero et al.,¹⁰¹ which however did not resolve the exergonic character of the reaction. Still, an additional flexibility in allowing pHis248 to deprotonate might shift the PMF on the product side to lower energies, also reducing the barrier height.

Both P1 and P2 contain the phosphorylation product – the protonated phosphohistidine 248 (H-pHis248), and the difference is that the resulting ADP molecule rearranges into a stable conformation in P2. Specifically, the β-phosphate leaves the coordination sphere of Mg²⁺, providing additional stabilization as compared to P1. Additional rearrangements in the reaction center are observed during the reaction: In the reactant state, Arg251 forms a salt bridge with the γ-oxygens of the ATP, while it is bridged with the β-oxygens of ADP in both of the product states. Interestingly, Glu249 approaches and forms a hydrogen bridge with H(His248) in the P2 state, indicating that Glu249 could serve as the first proton acceptor (relay) in the proton transfer that would stabilize the final pHis product.

The QM/MM metadynamics simulation presented here is merely a simple ansatz to illustrate the capability of the new parametrization of DFTB3/3OB to describe realistic biomolecular phosphoryl transfer reaction to nitrogen acceptors. Thus, although the obtained reaction energetics and mechanism are likely qualitatively correct, it would be advisable to pass to well-tempered metadynamics when aiming at results of higher accuracy. Additionally, the phosphoryl transfer from ATP to His248 is just the first step of a more complex autophosphorylation reaction. Two more processes will follow immediately, and these could also be simulated with the current methodology: a proton transfer from pHis248H to a suitable nearby base, and furthermore, spatial separation of pHis and ADP, which will remove pHis from the coordination sphere of Mg²⁺, accompanied by the return of β-phosphate into the coordination sphere.

4. Conclusion

The general-purpose parameterization of DFTB3 for organic and biomolecules, 3OB performs poorly for the complex chemistry of phosphate and related species. While the performance for phosphate hydrolysis reactions had been improved by means of the OPhyd SRP previously, the reactions involving making or breaking of a P–N bond were not considered. The current work fills this gap by creating a new SRP, called “PNmod” as a complement to DFTB3/3OB combined with OPhyd.

PNmod consists of a new P–N repulsive potential with the electronic parameters kept intact. The P–N repulsive function introduces an overbinding of P–N bonds and remains convex on the entire range of P–N distances. Used together with DFTB3/3OB and OPhyd in extended-sampling QM/MM simulations, PNmod provides much improved energetics of reactions in which a P–N bond is replaced by a P–O bond or vice versa, which is what appears in phosphorylation and hydrolysis reactions of some biochemically important nitrogen species.

The reaction used to aid parameterization and to benchmark the resulting repulsive potential is phosphorylation of imidazole, a model of the autophosphorylation of histidine taking place in HK proteins. The benchmark used computationally costly extended sampling QM/MM simulations employing hybrid DFT calculations as the reference. DFTB3/3OB-OPhyd-PNmod reproduced the correct reaction mechanism, while both reaction energies and energy barriers are within 2 kcal mol⁻¹ of the reference.

Furthermore, the scope of the use of the new parameterization is demonstrated by a study of the acidic hydrolysis of the anticancer drug TEPA. The previously unclear mechanism of the reaction on the atomic scale was revealed, including the relevant intermediates and the exergonic energy landscape.

Finally, the real process of histidine phosphorylation in a HK protein was investigated. The first step of the autophosphorylation proceeding in the so-called trans-mechanism was uncovered, and the energetics and atomic details were compared to the previous findings for an autophosphorylation proceeding via the cis-mechanism.

The PNmod parameter files can be obtained from the ESI† and, starting later in 2023, from the DFTB website at https://dftb.org/parameters. These files shall be used in combination with the standard 3OB and the special 3OB/OPhyd parameter files. Any recent implementation of DFTB3 can be used, and a particularly practicable way is to follow the protocols in this work, using DFTB+ and Gromacs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to Qiang Cui and Marcus Elstner for their insightful comments and advice. This work was supported by the German Science Foundation (DFG) under project GRK 2450 (Tailored Scale-Bridging Approaches to Computational Nanoscience) and further by the state of Baden-Württemberg through bwHPC and by the DFG through project INST 40/575-1 FUGG (JUSTUS2 cluster).

Notes and references

1. M. Valiev, R. Kawai, J. A. Adams and J. H. Weare, J. Am. Chem. Soc., 2003, 125, 9926–9927.
2. J. R. Knowles, Annu. Rev. Biochem., 1980, 49, 877–919.
3. A. C. Hengge, Adv. Phys. Org. Chem., 2005, 40, 49–108.
4. A. Matte, L. W. Tari and L. T. Delbaere, Structure, 1998, 6, 413–419.
5. P. Cohen, Nat. Rev. Drug Discov., 2002, 1, 309–315.
6. K. Strebhardt, Nat. Rev. Drug. Discov., 2010, 9, 643–660.
7. W. E. Jacobus and A. L. Lehninger, J. Biol. Chem., 1973, 248, 4803–4810.
8. S. Klumpp and J. Krieglstein, Eur. J. Biochem., 2002, 269, 1067–1071.
9. P. Casino, L. Miguel-Romero and A. Marina, Nat. Commun., 2014, 5, 3258.
10. M. C. Pirrung, Chem. Biol., 1999, 6, R167–R175.
11. J. Puttick, E. N. Baker and L. T. Delbaere, Biochim. Biophys. Acta Proteins Proteom., 2008, 1784, 100–105.
12. S. C. Kamerlin, P. K. Sharma, R. B. Prasad and A. Warshel, Q. Rev. Biophys., 2013, 46, 1–132.
13. A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249.
14. M. J. Field, P. A. Bash and M. Karplus, J. Comput. Chem., 1990, 11, 700–733.
15. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
16. M. McCullagh, M. G. Saunders and G. A. Voth, J. Am. Chem. Soc., 2014, 136, 13053–13058.
17. N. Vithani, S. Batra, B. Prakash and N. N. Nair, ACS Catal., 2017, 7, 902–906.
18. N. Vithani, P. K. A. Jagtap, S. K. Verma, R. Tripathi, S. Awasthi, N. N. Nair and B. Prakash, Structure, 2018, 26, 459–466.
19. R. Sun, O. Sode, J. F. Dama and G. A. Voth, J. Chem. Theory Comput., 2017, 13, 2332–2341.
20. R. Tripathi, R. Glaves and D. Marx, Chem. Sci., 2017, 8, 371–380.
21. M. Gaus, Q. Cui and M. Elstner, J. Chem. Theory Comput., 2011, 7, 931–948.
22. M. Gaus, A. Goez and M. Elstner, J. Chem. Theory Comput., 2013, 9, 338–354.
23. M. Gruden, L. Andjeklović, A. K. Jissy, S. Stepanović, M. Zlatar, Q. Cui and M. Elstner, J. Comput. Chem., 2017, 38, 2171–2185.
24. X. Lu, V. Ovchinnikov, D. Demapan, D. Roston and Q. Cui, Biochemistry, 2017, 56, 1482–1497.
25. M. Putzu, F. Gräter, M. Elstner and T. Kubař, Phys. Chem. Chem. Phys., 2018, 20, 16222–16230.
26. D. Roston, D. Demapan and Q. Cui, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 25048–25056.
27. M. T. Gregory, Y. Gao, Q. Cui and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2103990118.
28. D. Maag, T. Mast, M. Elstner, Q. Cui and T. Kubař, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024803118.
29. C. L. Gómez-Flores, D. Maag, M. Kansari, V.-Q. Vuong, S. Irle, F. Gräter, T. Kubař and M. Elstner, J. Chem. Theory Comput., 2022, 18, 1213–1226.
30. Y. Yang, H. Yu, D. York, M. Elstner and Q. Cui, J. Chem. Theory Comput., 2008, 4, 2067–2084.
31. A. Gonzalez-Lafont, T. N. Truong and D. G. Truhlar, J. Phys. Chem., 1991, 95, 4618–4627.
32. P. Imhof, F. Noé, S. Fischer and J. C. Smith, J. Chem. Theory Comput., 2006, 2, 1050–1056.
33. K. Nam, Q. Cui, J. Gao and D. M. York, J. Chem. Theory Comput., 2007, 3, 486–504.
34. J. P. Layfield, M. D. Owens and D. Troya, J. Chem. Phys., 2008, 128, 194302.
35. S. Liang and A. E. Roitberg, J. Chem. Theory Comput., 2013, 9, 4470–4480.
36. Y. Zhou and J. Pu, J. Chem. Theory Comput., 2014, 10, 3038–3054.
37. D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947.
38. G. Seifert, D. Porezag and T. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185–192.
39. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260.
40. Y. Yang, H. Yu, D. York, Q. Cui and M. Elstner, J. Phys. Chem. A, 2007, 111, 10861–10873.
41. W. Han, M. Elstner, K. Jalkanen, T. Frauenheim and S. Suhai, Int. J. Quantum Chem., 2000, 78, 459–479.
42. Q. Cui, M. Elstner, E. Kaxiras, T. Frauenheim and M. Karplus, J. Phys. Chem. B, 2001, 105, 569–585.
43. M. Gaus, X. Lu, M. Elstner and Q. Cui, J. Chem. Theory Comput., 2014, 10, 1518–1537.
44. M. Gaus, C.-P. Chou, H. Witek and M. Elstner, J. Phys. Chem. A, 2009, 113, 11866–11881.
45. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650–7657.
46. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian Inc., Wallingford CT, 2009.
47. T. Kubař, Z. Bodrog, M. Gaus, C. Köhler, B. Aradi, T. Frauenheim and M. Elstner, J. Chem. Theory Comput., 2013, 9, 2939–2949.
48. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
49. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725.
50. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
51. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
52. T. Kubař, K. Welke and G. Groenhof, J. Comput. Chem., 2015, 36, 1978–1989.
53. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
54. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
55. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
56. G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212.
57. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
58. P. Raiteri, A. Laio, F. L. Gervasio, C. Micheletti and M. Parrinello, J. Phys. Chem. B, 2006, 110, 3533–3539.
59. T. Kubař, Gromacs – QM/MM interface for DFTB+, https://github.com/tomaskubar/gromacs-dftbplus, 2022, last accessed 18 March 2022.
60. T. Kubař, DFTB+ – modified QM/MM interface, https://github.com/tomaskubar/dftbplus, 2022, last accessed 18 March 2022.
61. D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
62. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
63. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
64. B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101.
65. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
66. F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78.
67. F. Neese, WIREs Comput. Mol. Sci., 2018, 8, e1327.
68. A. E. Mechaly, S. S. Diaz, N. Sassoon, A. Buschiazzo, J.-M. Betton and P. M. Alzari, Structure, 2017, 25, 939–944.
69. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
70. B. Webb and A. Sali, Curr. Protoc. Bioinf., 2016, 54, 5.6.1–5.6.37.
71. K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins: Struct., Funct., Bioinf., 2010, 78, 1950–1958.
72. K. L. Meagher, L. T. Redman and H. A. Carlson, J. Comput. Chem., 2003, 24, 1016–1025.
73. J. Åqvist, J. Phys. Chem., 1990, 94, 8021–8024.
74. M. A. Cuendet and W. F. van Gunsteren, J. Chem. Phys., 2007, 127, 184102.
75. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
76. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
77. D. Herschlag and W. P. Jencks, J. Am. Chem. Soc., 1987, 109, 4665–4674.
78. D. Herschlag and W. P. Jencks, Biochemistry, 1990, 29, 5172–5179.
79. F. Hollfelder and D. Herschlag, Biochemistry, 1995, 34, 12255–12264.
80. R. Kalagiri, R. L. Stanfield, J. Meisenhelder, J. J. La Clair, S. R. Fuhs, I. A. Wilson and T. Hunter, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2010644118.
81. P. Attwood, M. Piggott, X. Zu and P. Besant, Amino Acids, 2007, 32, 145–156.
82. M. V. Makwana, R. Muimo and R. F. Jackson, Lab. Invest., 2018, 98, 291–303.
83. S. D. Lahiri, G. Zhang, D. Dunaway-Mariano and K. N. Allen, Science, 2003, 299, 2067–2071.
84. J. Yao, X. Wang, H. Luo and P. Gu, Chem. – Eur. J., 2017, 23, 16380–16387.
85. E. Marcos, M. J. Field and R. Crehuet, Proteins: Struct., Funct., Bioinf., 2010, 78, 2405–2411.
86. J. K. Lassila, J. G. Zalatan and D. Herschlag, Annu. Rev. Biochem., 2011, 80, 669–702.
87. M. Van Maanen, C. Smeets and J. Beijnen, Cancer Treat. Rev., 2000, 26, 257–268.
88. S. N. Wolff, R. H. Herzig, J. W. Fay, C. F. LeMaistre, R. A. Brown, D. Frei-Lahr, S. Stranjord, L. Giannone, P. Coccia and J. L. Weick, Semin. Oncol., 1990, 17, 2–6.
89. M. E. de Jonge, S. M. van Dam, M. J. Hillebrand, H. Rosing, A. D. Huitema, S. Rodenhuis and J. H. Beijnen, J. Mass Spectrom., 2004, 39, 262–271.
90. D. Bertram, Trans. R. Soc. Trop. Med. Hyg., 1963, 57, 322–336.
91. B. Chandra Deka and P. K. Bhattacharyya, Clin. Cancer Drugs, 2017, 4, 10–46.
92. E. Cherni, A. I. Adjieufack, B. Champagne, M. Abderrabba, S. Ayadi and V. Liégeois, J. Phys. Chem. A, 2020, 124, 4068–4080.
93. M. J. van Maanen, K. D. Smits, J. M. A. Damen, A. J. Heck and J. H. Beijnen, Int. J. Pharm., 2000, 200, 187–194.
94. M. J. van Maanen, I. M. Tijhof, J. M. A. Damen, C. Versluis, J. J. K. van den Bosch, A. J. Heck, S. Rodenhuis and J. H. Beijnen, Cancer Res., 1999, 59, 4720–4724.
95. S. M. Musser, S. S. Pan, M. J. Egorin, D. J. Kyle and P. S. Callery, Chem. Res. Toxicol., 1992, 5, 95–99.
96. H. Torabifard and A. Fattahi, J. Mol. Model., 2012, 18, 3563–3576.
97. H. Torabifard and A. Fattahi, Struct. Chem., 2013, 24, 1–11.
98. D. Kheffache and O. Ouamerali, J. Mol. Model., 2010, 16, 1383–1390.
99. F. A. Olivieri, O. Burastero, S. I. Drusin, L. A. Defelipe, D. E. Wetzler, A. Turjanski and M. Marti, J. Chem. Inf. Model., 2020, 60, 833–842.
100. M. Kansari, F. Idiris, H. Szurmant, T. Kubař and A. Schug, Mechanism of activation and autophosphorylation of a histidine kinase, 2022.
101. F. Marsico, O. Burastero, L. A. Defelipe, E. D. Lopez, M. Arrar, A. G. Turjanski and M. A. Marti, Biochem. Biophys. Res. Commun., 2018, 498, 305–312.

---

Footnote

† Electronic supplementary information (ESI) available: Parameter files produced and used in this work, in a format readable by the DFTB+ software; cartesian coordinates of molecules used in the parametrization; and cartesian coordinates of significant structural states observed in case studies. See DOI: https://doi.org/10.1039/d2cp05890a

---