A photoelectron spectroscopic investigation of aspirin, paracetamol and ibuprofen in the gas phase

Abstract

We have investigated the electronic structure of isolated molecules of paracetamol, aspirin and ibuprofen using computational methods and benchmarked the results against valence and core photoelectron spectra. Paracetamol, aspirin and ibuprofen exist as multiple conformers, and we have calculated the free energies and populations of the lowest energy conformers. We find generally good agreement with previous experimental and theoretical structural results. The valence band spectrum of gas phase aspirin has not been reported previously, and we report it and assign the features based on calculations. The effect of acetylation on the frontier orbitals of the parent molecule, salicylic acid, is to increase the ionization potential of the highest occupied molecular orbital (HOMO), and to exchange the energetic ordering of the following two orbitals. The acetyl π bond contributes to the next orbital, which is hybridised with ring π orbitals. The core level spectra of all three molecules are reported and compared with calculations and with the spectra of parent molecules (salicylic acid for aspirin, 4-aminophenol for paracetamol). Observed core ionization energies are in agreement with theory. Although all compounds share a benzene ring, and they also have a number of other chromophores in common, the spectroscopic data indicate chemical diversity, suggesting that their modes of bonding under physiological conditions are likely to be diverse.

---

1 Introduction

Among the most commonly used medications, paracetamol, aspirin and ibuprofen are outstanding, and all are on the World Health Organization's list of essential medicines. In order to understand in detail their mechanism of operation, and more importantly to discover improved derivatives, it is essential to understand their electronic structure at the quantum level. Although they operate under physiological conditions, the first step in understanding their detailed electronic structure is investigation of the isolated molecules. In this work we have carried out a theoretical and experimental investigation of the electronic structure of these three drugs, two of which belong to the large class of Non-Steroidal Anti-Inflammatory Drugs (NSAIDs).

These drugs are generally believed to work by binding with cyclooxygenase-1 and cyclooxygenase-2 (COX-1 and COX-2) enzymes,¹ and blocking the production of prostaglandins. While blocking COX-2 is believed to cause the analgesic effect, blocking COX-1 may lead to undesired side effects.² The biochemistry and modelling of the docking process are very complex, and the wide range of NSAIDs and related drugs suggests there is no single binding mechanism to COX-1 and COX-2. As a result, numerical methods are used for each drug or candidate drug,² underlining the importance of understanding the detailed electronic properties.

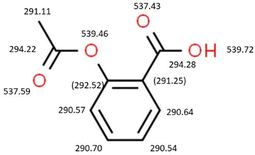
The schematic structures of the molecules are shown in Fig. 1. All contain a di-substituted benzene moiety, have multiple flexible bonds, and aspirin and ibuprofen include carboxylic acid groups, while paracetamol and aspirin both contain acetyl moieties.

Fig. 1 Schematic structures of (a) paracetamol, (b) aspirin and (c) ibuprofen.

Valence band photoelectron spectra and theoretical calculations of the valence structures of paracetamol and ibuprofen were reported by Novak et al.³ To our knowledge, there have been no reports of the valence photoelectron spectrum of aspirin, nor of the core photoelectron spectra of any of these three compounds.

Several theoretical quantum mechanical studies of aspirin reported total energies and conformational structures.^4–6 Cabezas et al.⁶ also reported experimental results of the structure of aspirin in the gas phase using microwave spectroscopy, and observed two conformers. The temperature of their cooled molecular beam was not reported, but they estimated the population ratio of the two rotamers to be 4 : 1, which they stated was consistent with an energy difference of 275 cm⁻¹ (0.68 kcal mol⁻¹). They found that neither conformer was planar, and the structures of the rotamers were characterized by a close approach of the carboxyl or hydroxy oxygen in the carboxylic group to the carbonyl group of the acetyl moiety, as in the Bürgi–Dunitz trajectory.⁷

The optical spectra of paracetamol have been investigated by Beames and Hudson⁸ using resonant two-photon ionization, as well as by Lee et al.⁹ and Sohn et al.¹⁰ using laser hole burning techniques. Beames and Hudson⁸ reported density functional theory (DFT) calculations and interpreted their data in terms of a single conformer. Lee et al.⁹ identified two nearly isoenergetic conformers labelled cis and trans, while Sohn et al.¹⁰ reported four conformers and disagreed with previous interpretations of the data. Varela et al.¹¹ reported microwave spectra and identified four low energy conformers, labelled as trans-E and trans-Z, (for both of which the heavy atoms are planar, with C_s symmetry), and as cis-E and cis-Z (non-planar, C₁ symmetry). In the cis isomers, the acetamino group lies out of the plane of the phenol ring, while E (entgegen) and Z (zusammen) refer to the OH and NH hydrogen orientations being opposed or together. They estimated the population ratio of trans-E to trans-Z conformers to be 5 : 1, corresponding to an energy difference of 300 cm⁻¹ (0.86 kcal mol⁻¹), compared to a calculated value of 109 cm⁻¹ (0.31 kcal mol⁻¹).

The conformational landscape of ibuprofen has been examined by several groups.^12–15 Betz et al.¹⁶ reported a rotational spectroscopy study of the molecule and identified four conformers with similar populations. All showed the same non-planar orientation of the propanoic acid group with respect to the benzene ring, but had different arrangements of the isobutyl group. Aspirin and paracetamol are achiral, while ibuprofen is chiral, and medical formulations are usually a racemic mixture of two enantiomers. In the present study, we used linearly polarized light for ionization, so no effects due to chirality are expected, and calculations were performed for only the S-enantiomer, which is biologically the more active.

Although the conformational structures of the three target molecules in the gas phase have been studied theoretically and experimentally, we are not aware of any core photoelectron studies, nor of any valence photoelectron study of aspirin, which we report and analyse in the present work.

The goals of this study were twofold. Computational simulations of pharmaceutical docking interactions have reached a high level of sophistication, but the size of the systems requires that approximations must be made. Our high-level calculations are compared with experimental data for our three samples. This provides a benchmark for modelling of electronic structure to judge whether the approximations are sufficiently accurate to be reliable. A second, and lesser goal was to investigate whether properties common to the samples under study could be identified, which might lead to insight into the mode of action of the drugs. The quantitative structure-activity relationship approach seeks correlations between properties, such as measured spectra, and chemical activity. For quite some time, relationships have been sought between electronic properties and the activity of bio-active molecules, for example for psychoactive drugs,^17–23 analgesics,^3,24 and amino acids.²⁵ Early claims of correlations of activity with ionization potentials and frontier orbital character have not stood the test of time. Here we investigate qualitatively whether the inclusion of core level spectra, which are sensitive to local chemical environment, permits the identification of relationships.

2 Experimental methods

Paracetamol and aspirin were purchased from Thermo Fisher (Alfa) with purity >98% for paracetamol and purity >99% for aspirin, and used without further purification. Ibuprofen was purchased from abcr GmbH with specified purity >95% and also used without further purification. They were evaporated from a crucible in vacuum at temperatures/background pressures of 381 K/4 × 10⁻⁸ mbar (paracetamol), 307 K/8 × 10⁻⁸ mbar (aspirin) and 322 K/2.8 × 10⁻⁶ mbar (ibuprofen). The background pressure was the lowest for the first compound because a liquid nitrogen trap was available and cooled during the measurement. We note that these temperatures are significantly lower than those used by Novak et al.,³i.e. 170 °C (443 K) for paracetamol, and 105 °C (378 K) for ibuprofen.

The experiments were performed at the gas phase photoemission beamline, synchrotron light source Elettra, Trieste, Italy. The photoemission spectra were measured with a total resolution (photon + analyzer) of 0.2 eV (or better), at photon energy 100 eV (valence), 0.57 eV at photon energy 390 eV (C 1s) and 0.78 eV at photon energy 628 eV (O 1s). The valence band spectrum of the first few bands of aspirin was also measured at 40 eV photon energy with a total resolution of 60 meV (not shown; no further structure was observed). The energy scale of the valence band spectra was calibrated by observing the first ionization potential (IP) of H₂O (present in the residual gas) at 12.62 eV,²⁶ while for core-level photoemission, the spectra were referenced to the following core levels: CO₂, C 1s, 297.66 eV,²⁷ and O 1s, 541.32;^28,29 and N₂, N 1s, 409.9 eV.²⁸ Spectra were measured both with the calibrant and sample present, and with only the sample present.

3 Computational methods

The three drugs share a common feature of flexible structures with rotatable single bonds. The number of conformers existing on a conformational potential energy surface of a flexible compound depends on the number of rotatable bonds and the bond types. For example, sp²–sp² carbon–carbon bonds usually have two minima while the bonds involving sp³ atoms usually have three. Thus, one needs to consider at least 3^N different conformers to ensure all potential energy minima on a given surface are accounted for, under the assumption that each of N rotatable bonds can give rise to two or three local minima. Recently, Wang and Vasilyev developed a robust computer method to generate low energy conformers of large molecules,³⁰ and here we apply it to small molecules. As seen in Fig. 1(a), paracetamol has four rotatable bonds but the bonds for the terminal –CH₃ groups are not included in the rotatable bond list in the above conformational search method. We calculated that the barrier for rotation of the methyl group is 0.2 kcal mol⁻¹, so that at the temperature of the experiment, the methyl group is rotating freely. Nevertheless, the algorithm explores the parameter space including methyl rotations. Thus, one needs to generate at least 27 (3³ = 27) random structures for the conformational search. However, for better conformational sampling, 60 structures were generated.

In the same manner, aspirin (Fig. 1(b)) has five rotatable bonds but only four were used in the search which requires at least 81 (3⁴ = 81) generated structures, with 150 being used in our calculations.

In the case of ibuprofen, we considered only S-ibuprofen as the present results are identical for the R-ibuprofen. Out of eight possible rotatable bonds, five rotatable bonds were used in the search which requires at least 243 (3⁵ = 243) generated structures, while 500 generated structures were used in the calculations. The Boltzmann weights are calculated at room temperature of 293 K and also calculated at the experimental temperatures of paracetamol (381 K), aspirin (307 K) and ibuprofen (322 K).

Based on the optimised geometries of the drugs’ conformers, the valence IPs of the isolated molecules were calculated using the outer valence Green function (OVGF) method with the 6-311++G(d,p) basis set. All optimisation and OVGF calculations were performed using the Gaussian 16 computational chemistry package.³¹ The core electron binding energies (CEBEs) were calculated with the Δ(PW86-PW91/et-pVQZ) + Crel method³² using the Amsterdam Density Functional (ADF) suites of programs.³³ The IP values for unlocalisable core holes are approximated by

CEBE = mKT + shift,

where mKT = meta-Koopmans’ theorem = −ε(SAOP), SAOP = statistical average of the orbital model exchange–correlation potential, and shift = average of (CEBE − mKT) for the localisable core hole.³⁴ For C 1s, the shift was equal to 16.75 eV for aspirin, 16.67 eV for paracetamol, and 16.58 eV for ibuprofen.

4 Results

4.1 Results: conformers

All generated structures were optimised at the B3LYP/6-311G level of theory. The obtained local-minimum structures were re-optimised at the B3PW91/6-31++G(d,p) level of theory, with strain energy cut off (energy difference of a conformer with respect to the global minimum structure) being 3.05 kcal mol⁻¹ for paracetamol, 0.5 kcal mol⁻¹ for ibuprofen and 2.55 kcal mol⁻¹ for aspirin, Table 1. The structures of the lowest energy conformers of paracetamol are in agreement with those reported by Varela et al.¹¹ and Sohn et al.,¹⁰ denoted trans-E and trans-Z for the lowest energy forms, in which the heavy atoms are coplanar, and differ by a rotation of the hydroxyl group. The next lowest energy conformers were labelled cis-E and cis-Z and the heavy atoms are non-coplanar. As well, we found structures in which the methyl group is rotated by 60° with respect to one of these conformers for paracetamol, namely P2 and P4, Table 1, see also ESI,† Fig. S1. As stated above the barrier for rotation is low and at the temperature of this experiment, the methyl group rotates freely. The structures are therefore in agreement with those reported previously.^10,11

Table 1 Selected parameters of the lowest energy conformers of paracetamol, aspirin and ibuprofen, optimized using B3LYP/6-311G after a conformer search. P2 and P4 are paracetamol conformers in which the methyl group is rotated 60° with respect to P1 and P3, respectively. At the temperature of the experiment, the methyl group is freely rotating. The cut off energies are 3.05 kcal mol⁻¹ for paracetamol, 2.55 kcal mol⁻¹ for aspirin and 0.5 kcal mol⁻¹ for ibuprofen

Conformer total energy (Eh)	Strain energy (kcal mol^−1)	Dipole moment (D)	Cluster size	Boltzmann weight (%)		Total number of conformers searched
				293 K	381 K
Paracetamol P1, trans-E	0.000	2.36	15	67.5	37.1	60
P2, trans-E′	0.225	2.43	1	3.1	3.1
P3, trans-Z	0.508	5.35	14	26.3	21.4
P4, trans-Z′	0.728	5.41	2	2.6	3.1
P5, cis-E	3.042	4.52	15	0.36	0.20
P6, cis-Z	3.048	4.41	10	0.24	0.20
−515.4682350 Eh					307 K
Aspirin1	0.00	2.20	23	90.7	75.4	150
Aspirin2	1.30	2.80	18	7.6	21.3
Aspirin3	2.57	4.92	10	0.5	2.9
−648.6650314 Eh					322 K
(S)-Ibuprofen1	0.000	1.515	19	14.9	19.1	500
(S)-Ibuprofen2	0.005	1.517	33	25.7	18.9
(S)-Ibuprofen3	0.023	1.708	22	16.6	18.5
(S)-Ibuprofen4	0.023	1.710	30	22.6	18.3
−656.6823513 Eh

---

The present value of the calculated energy of the second lowest conformer, Table 2, is in accord with published values,^10,11 but for the third and fourth conformers our values are in better agreement with the results of Sohn et al.¹⁰ The calculated values of the dipole moments are in reasonable agreement with the values of Varela et al.¹¹

Table 2 Selected parameters of the lowest energy conformers of paracetamol, aspirin and ibuprofen, re-optimized using the B3PW91/6-311++G(d,p), compared with literature (in parentheses)

Conformer total energy (Eh)	Strain energy (kcal mol^−1)	Dipole moment (D)	Boltzmann weight (%) (293 K)
P1	0.000 (0)^11	2.29 (2.91)^11	65.7
P3	0.415 (0.357,^11 0.31^10)	4.98 (4.64)^11	32.2
P5	2.40 (0.803,^11 3.18^10)	4.39 (4.5)^11	1.07
P6	2.43 (0.815,^11 3.18^10)	4.48 (4.6)^11	1.02
−515.3236052 Eh
Aspirin1	0.000 (0.0)^5,6	2.12 (1.77)^6	79.42
Aspirin2	0.843 (0.97,^6 0.84^5)	2.94 (2.71)^6	18.65
Aspirin3	2.626 (3.06,^6 3.26^5)	4.99	1.745
−648.4824547 Eh
(S)-Ibuprofen1	0.000	1.67	19.49
(S)-Ibuprofen2	0.010	1.68	19.15
(S)-Ibuprofen3	0.022	1.88	18.78
(S)-Ibuprofen4	0.034	1.90	18.37
−656.5056034 Eh

---

The three lowest energy aspirin conformers are shown in Fig. S2 (ESI†). Optimization at the B3PW91/6-31++G(d,p) level of theory yields 11 possible local minimum structures, with the lowest minimum structure corresponding to the Rotamer I found in the microwave (LA-MB-FTMW) spectroscopy study of Cabezas et al.,⁶ and illustrated in their Fig. 1. The second lowest energy structure corresponds to Rotamer II from the study of Cabezas et al.⁶ Note that the structures illustrated in their Table 1 are not labelled as in their Fig. 1, but are reversed. The lowest energy conformers agree quite well with the results of Yurtsever et al.⁵ using second-order Møller–Plesset theory (MP2) and coupled-cluster calculations with singles, doubles and iterative triples (CCSD(T)). The calculated dipole moments of the two lower energy conformers agree with those reported by Cabezas et al.⁶

For aspirin, the first two conformers constitute about 98% of the total population. The rotamer aspirin3 contains an internal hydrogen bond between the carboxylic acid hydrogen and the ether-like oxygen bonded to the acetyl group. Often internal hydrogen bonds are found in the lowest energy conformer^35–38 of a molecule, but in this case the two lowest energy forms do not form an internal hydrogen bond. As noted above, this has been attributed⁷ to the stabilization of the lower energy forms by the Bürgi–Dunitz trajectory.⁶ The conformer pair aspirin1 and aspirin2 both have an s-trans conformation around the acid C–O bond, which may explain why their dipole moments are similar, but they are rather different from the dipole moment of aspirin3 in Table 1.

The four lowest energy S-ibuprofen conformers are shown in Fig. S3 of the ESI,† and selected numerical parameters at the B3LYP/6-31G level of theory are given in Table 1, and in Table 2 after the B3PW91/6-31++G(d,p) re-optimization. Our conformational search at the B3PW91/6-31++G(d,p) level of theory found 18 local minimum structures, with four of them being within 0.03 kcal mol⁻¹ of the global minimum structure. The relative energies of other conformers are near or above 1 kcal mol⁻¹. This is in good agreement with a study by Betz et al.¹⁶ who used microwave spectroscopy (CP-FTMW) and M06-2X/aug-cc-pVTZ calculations. They identified four conformers in their DFT calculations which gave good agreement between experimental and theoretical spectral intensities. Our four lowest energy conformers have essentially the same 3D structures as those reported by Betz et al.¹⁶ Ibuprofen has more rotational degrees of freedom, with low energy differences between the conformers. As a result, more conformers are populated.

4.2 Results: valence ionization

The valence band spectrum of aspirin is shown in Fig. 2, while the valence spectra of paracetamol and ibuprofen are shown in Fig. S4 and S5 (ESI†). The calculated IPs of three conformers of aspirin are given in Table 3, while the calculated values for four conformers of paracetamol and ibuprofen are given in Tables S1 and S2 (ESI†). The outer valence spectra of paracetamol and ibuprofen are in agreement with the previous results of Novak et al.,³ and the present results are compared in the ESI.†

Fig. 2 Outer valence band spectrum of aspirin, measured at 100 eV photon energy with 200 meV spectrometer resolution. Vertical bars indicate the calculated ionization energies of aspirin1. The sharp peak labelled H₂O is due to residual water. Inset: Full valence band measured with 400 meV spectrometer resolution.

Table 3 Theoretical (OVGF) and experimental valence ionization potentials (in eV) of aspirin. Spectroscopic pole strengths (PS) are shown for the conformer aspirin1

Aspirin1	PS	Aspirin2	Aspirin3	Experiment
9.25	0.89	9.31	9.53	9.31
9.57	0.89	9.53	9.49	9.69
10.68	0.89	10.81	10.65	10.40
10.70	0.89	10.96	11.60
11.62	0.88	11.55	11.47	11.20
12.02	0.87	11.91	12.18	11.65
12.43	0.83	12.51	12.69	12.23
12.78	0.89	12.78	12.94	12.56
13.13	0.89	12.96	13.37	13.84
13.58	0.9	13.66	14.28
14.23	0.91	14.38	14.29	14.82
14.28	0.89	14.41	14.83
14.33	0.89	14.54	14.94
15.08	0.89	15.07	15.2	15.49
15.36	0.88	15.31	15.32
15.51	0.88	15.49	15.49
15.9	0.87	16.07	15.98
16.21	0.87	16.17	16.44	16.48
16.54	0.87	16.72	16.87
16.75	0.87	16.87	17.34
17.21	0.88	17.35	17.61
17.58	0.86	17.47	18.17

---

In Table 3, we compare the experimental spectra to the calculations for the conformer aspirin1, since this is predicted to be the dominant conformer. The spectroscopic pole strengths (PS) are shown only for aspirin1 as the PS values for other conformers are all similar and above 0.85. The valence IPs exhibit minimal differences between the conformers of the same molecule. As a result, for the core binding energies, we concentrate on the global minimum energy structure of the first conformer for each molecule in order to reduce computational cost.

The experimental and theoretical HOMO and HOMO−1 energies agree reasonably well, with the theoretical values slightly underestimating the experimental values. The next two ionization energies are predicted to be almost degenerate energetically and appear as a single strong band, whose theoretical energy overestimates. At higher binding energy, theoretically predicted ionic states can be associated with experimental peaks, with positive or negative energy shifts. The strong experimental peak at 14.82 eV is assigned to the three closely spaced states predicted at 14.23–14.33 eV. At further higher binding energy, the high density of states makes exact assignments difficult.

4.3 Results: core level photoelectron spectra

The theoretical and experimental core electron binding energies are summarised in Table 4, and spectra are shown in Fig. 3–6.

Table 4 Experimental and theoretical core 1s binding energies (in eV) and assignments of the ionic states of paracetamol, aspirin and ibuprofen. Values in parentheses refer to unlocalisable core holes, see Section 3. Numbering of C, O, and N atoms follows Fig. 1. The C1s, N1s and O1s assignments are also labelled on the schematic structures. Where not stated otherwise, the estimated relative and absolute errors of the experimental values are ±0.05 and ±0.1 eV, respectively

Core	Paracetamol
	Exp. (4 peaks fit)	Fit (8 peaks)	Theory	Assignment
C 1s	296.3	296.33	—	Shake-up
	293.6	293.62	292.92	C7
	291.7	291.84	291.26	C4
	291.2	291.40	291.15	C1
	290.26	290.24	(290.20)	C2
		290.23	(290.07)	C3
		290.67	290.25	C5
		290.24	290.13	C6
		291.08	(290.36)	C8
N 1s	405.8		406.02
O 1s	536.9		536.57	O2
	539.2		539.22	O1

---

Core	Aspirin
	Exp. (3 peaks fit)	Fit (9 peaks)	Theory	Assignment
C 1s	294.89	294.89	294.28	C9
		294.89	294.22	C7
	292.2	292.23	(292.52)	C2
	290.75	291.33	(291.25)	C1
		290.64	290.57	C3
		290.64	290.70	C4
		290.64	290.54	C5
		290.64	290.64	C6
		290.98	291.11	C8
O 1s	537.7 ± 0.2		537.43	O1
	538.2 ± 0.2		537.59	O4
	539.1 ± 0.2		539.46	O3
	539.9 ± 0.2		539.72	O2

---

Core	Ibuprofen
	Exp. (3 peaks fit)	Fit (13 peaks)	Theory	Assignment
C 1s	294.74	294.74	294.08	C1′
	290.6	291.12	291.06	C2′
		290.80	(290.29)	C1′′
		290.55	(290.27)	C4
		290.54	290.25	C2′′
	290.12	290.24	290.17	C1
		290.24	(290.10)	C2
		290.24	(290.01)	C3′
		290.24	289.99	C6
		290.08	289.93	C5
		289.97	289.93	C3
		289.97	(289.78)	C3′′
		289.97	(289.70)	C4′′
O 1s			537.61	O1
			539.76	O2

---

Fig. 3 C 1s spectrum of paracetamol. Red curve: experimental data. Blue curve: fit of experimental data assuming 8 peaks of equal intensity and width. Green bars: theoretical energies. Blue bars: fitted energies. The labels “3 states” and “4 states” indicate that 3 or 4 nearly degenerate ionic states were fitted at the indicated energies but are not resolved in the figure. Photon energy: 390 eV.

Fig. 4 C 1s spectrum of aspirin. Red curve: experimental data. Blue curve: fit of experimental data, assuming three independent peaks. Green curve: fit of experimental data assuming 9 Gaussian peaks of equal intensity and width. Green bars: theoretical energies. Purple bars: fitted energies assuming 9 Gaussian peaks of equal width and intensity. Photon energy: 390 eV.

Fig. 5 Lower curves: O 1s spectrum of aspirin (red) and its fit (black). Upper curve: O 1s spectrum of salicylic acid.³⁷ Photon energy: 628 eV.

Fig. 6 C 1s spectrum of ibuprofen. Red curve: experimental data. Green curve: fit of experimental data assuming 3 independent Gaussians. Blue curve: fit of experimental data assuming 13 Gaussian peaks of equal intensity and width. The last two curves are offset for clarity. Magenta bars: theoretical energies. Blue bars: energies fitted with 13 equal Gaussians. Photon energy: 390 eV.

For paracetamol, Fig. 3, two distinct peaks labelled B and E, and three minor peaks or shoulders (A, C, D) are visible in the C 1s spectrum. Peak A at 296.33 eV is assigned to a shake-up state associated with the benzene ring. The remainder of the spectrum was fitted with 4 peaks, corresponding to the features B–E, and also with 8 Gaussian functions of equal width and intensity to model the 8 carbon atoms of paracetamol. This procedure is approximate, as peaks may have varying widths and asymmetry and the individual peaks are not resolved. However, the shape of the peak fit and the statistical difference between theoretical and fitted peak energies provide a way of quantifying the comparison of the theoretical spectrum with the density of states observed in the experiment.

The carbonyl C 1s binding energy in paracetamol shows poor agreement between theory and experiment, as the experimental value is 0.7 eV higher than the calculated value. However, the average energy difference between theory and experiment for all other carbon atoms is 0.18 eV, which is quite satisfactory. The binding energies of the N 1s and O 1s core levels are also in good agreement with theory, see Table 4.

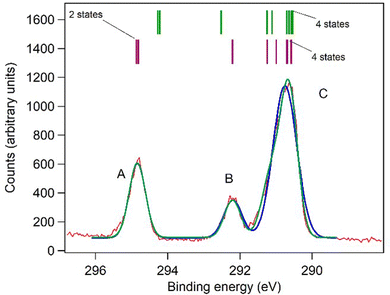
The C 1s spectrum of aspirin (Fig. 4) shows three resolved peaks, A, B and C, and these were fitted by three independent Gaussian functions, as well as by 9 Gaussians of equal width and intensity. The latter gives a slightly better fit. Peak A in Fig. 4 is assigned to ionization of the carboxylic (C9) carbon atom and the carbonyl carbon atom of the acetyl group (C7). Theory predicts that they are energetically very close, although theory also predicts a binding energy that is 0.6 eV lower. Peak B is assigned to the ring carbon atom bonded to the ether-like oxygen atom, and the theoretical binding energy agrees within 0.3 eV with the experimental value. The remaining methyl carbon and five benzene ring carbon atoms have an average energy that is within a few meV of the theoretical average energy and a mean difference of 0.11 eV, which is very satisfactory.

For aspirin, the O 1s spectrum is not fully resolved, see Fig. 5. It was fitted with 4 peaks corresponding to the 4 chemically distinct oxygen atoms, with the constraint that the intensity of each peak did not vary by more than 20% of the mean intensity.

The C 1s spectrum of ibuprofen, Fig. 6, is relatively simple, and shows a peak A assigned to the carboxylic carbon atom (C1′), a weak peak B assigned to the carbon atom C2′ bonded to the carboxylic carbon, and a broad unresolved peak C, assigned to all other carbon atoms. As for the carboxylic acid carbon atom in aspirin, the theory underestimates the binding energy by about 0.6 eV. On the other hand, the energy of C2′ is calculated correctly to within 0.06 meV. For the remaining 11 carbon atoms, the mean energies of the theoretical and fitted experimental band of ionic states are 290.04 and 290.26 eV, respectively. The rms difference between the fitted and theoretical energies is 0.25 eV. The reason for this small discrepancy is clear from the bars indicating theoretical energies in Fig. 6; theory tends to underestimate the spread in energies and, as stated, the average energy is offset by 0.25 eV.

5 Discussion

We expect that the valence electronic structure of salicylic acid and its acetyl derivative aspirin will be closely related. The experimental outer valence ionization potentials (in eV) of salicylic acid were reported by Novak et al.³ (gas phase) and Tseplin et al.³⁹ (solid state); present IP values of aspirin are compared with those of salicylic acid in Table 5. The full list of ionization potentials of salicylic acid^3,39,40 are provided in the ESI,† Table S3. We compare salicylic acid and aspirin in the correlation diagram, Fig. 7, where the calculated charge densities of the orbitals are shown.⁴⁰

Table 5 Summary of experimental and theoretical valence ionization energies for aspirin and salicylic acid in eV

Aspirin [this work] exp. (theory)	Salicylic acid^40 exp. (theory)	Salicylic acid^3 exp. (theory)	Salicylic acid^39 exp.
9.31 (9.25)	8.81 (8.64)	8.8 (8.55)	8.87
9.69 (9.57)	9.75 (9.41)	9.65 (9.38)	9.78
10.40 (10.68, 10.70)	10.73 (11.08)	10.75 (10.95)	10.82
11.20 (11.62)		11.8 (11.70)
11.65 (12.02)	11.96 (11.96)	12.1 (12.1, 12.31)	11.76
12.23 (12.43)	11.96 (12.29)
12.56 (12.78)	11.96 (12.45)		12.07

---

Fig. 7 Correlation diagram and charge density maps for the molecular orbitals of salicylic acid (left)⁴⁰ and aspirin (right). Horizontal lines indicate the ionization potentials. Charge densities are indicated for the relevant ionization energies. The carboxylic moiety is at the top; the hydroxy moiety of salicylic acid and the acetyl moiety of aspirin are on the right.

The agreement of the present experimental results and theoretical results⁴⁰ for salicylic acid with the published^3,39 results is good.

The HOMO of salicylic acid has primarily benzene π character.³⁹ From the correlation diagram, it can be seen that the main effect on this orbital of acetylation is to shift it to higher binding energy. The HOMO−1 and HOMO−2 of salicylic acid exchange energy positions in aspirin, and show some mixing with orbitals localised on the acetyl moiety. The HOMO−3 of aspirin is not easily correlated to salicylic acid orbitals and contains substantial weight of the acetyl group orbitals, and benzene π orbitals. The HOMO−3 of salicylic acid has almost pure π C=O character³⁹ which mixes with the π orbital of the acetyl group to form the orbitals HOMO−4 and HOMO−5 of aspirin.

We turn our attention now to the core level spectra. As expected, the C 1s spectrum of aspirin resembles the spectrum of salicylic acid.³⁷ Peak A in Fig. 4 is due to the two carbon atoms C7 and C9 which are bonded to two oxygen atoms, and the binding energy, 294.89 eV, is only slightly less than that of the carboxylic carbon in salicylic acid, 295.01 eV. Peak B is due to the ring carbon atom C2 bonded to a single oxygen atom and has a binding energy 0.16 eV lower than C2 in salicylic acid. The remaining carbon core levels contribute to the unresolved peak C: for salicylic acid, it was possible to resolve some fine structure, and assign the binding energy of C5. Theory indicates that most of these core levels undergo rather small shifts of 0.2 to 0.03 eV with respect to salicylic acid, except for C1 which is predicted to shift to lower binding energy by 0.6 eV. This may be associated with the rehybridization noted in the valence spectra, where the acetyl moiety causes significant changes in the charge density of the π bond of the carboxylic acid group bonded to C1. In particular, the HOMO−3 of the carboxylic acid group of salicylic acid mixes with the orbitals of the acetyl group of aspirin to form HOMO−4 and HOMO−5.

Comparing the O 1s spectrum of aspirin with the data of Hill et al.³⁷ in Fig. 5, we note that salicylic acid contains an internal hydrogen bond, which is not present in the low-energy conformers of aspirin. The additional acetyl oxygen increases the spectral intensity of the O 1s band at low binding energy, and additional shifts are attributed to the absence of hydrogen bonding. The two O 1s core levels of the carboxyl group, O1 and O2, remain at almost the same binding energy, while the phenolic oxygen becomes the ether-like oxygen O3 in aspirin and the core level shifts 0.5 eV to lower binding energy. This can be attributed to more efficient screening of the core hole by the acetyl group compared with a hydrogen atom, and is commonly observed in compounds such as ethers derived from alcohols.⁴¹ The core level binding energies of the carboxylic oxygen atoms are similar to those of ibuprofen within the experimental error.

For paracetamol, compared with the core level spectra of the parent compound, 4-aminophenol, the N 1s binding energy of 405.8 eV is a little higher than that of 4-aminophenol (405.2 eV),^42,43 as expected due to the presence of the neighbouring, electron-withdrawing acetyl group. As noted above, the planar structure of the heavy atoms in the lowest energy conformers may lead to delocalisation of the nitrogen lone pair into the phenyl π system or the acetyl π bond, and this may further affect the N 1s binding energy. The phenolic oxygen in the hydroxy group of paracetamol is far from the acetyl substituent, and has the same binding energy as 4-aminophenol, 539.2 eV.^42,43 On the other hand, the core level binding energy of the acetyl oxygen in paracetamol, 536.9 eV, is significantly lower than that of the acetyl oxygen of aspirin, 538.2 eV. This can be traced to the presence of the nearest neighbour, which is nitrogen in paracetamol, and less electronegative than the oxygen nearest neighbour in aspirin.

For the C 1s peaks of 4-aminophenol, two peaks at 291.1 and 291.4 eV were reported, but this was a typographical error as the main peak occurred at 290.1 eV, while the second broad peak occurred at 291.4 eV.^42,43 The weaker peak is assigned to the two substituted carbon atoms, while the main peak is attributed to the other four (unsubstituted) ring carbon atoms. The ratio of intensities of the main to the weaker peak was 1.7, fairly close to the expected stoichiometric ratio of 2. For paracetamol, the C 1s peaks are resolved at energies of 291.7, assigned to C4 bonded to nitrogen, and 291.2 eV, assigned to C1, bonded to oxygen. The average energy agrees with that of the unresolved, corresponding peaks of 4-aminophenol. The average C 1s energy of the unsubstituted carbon atoms is 290.26 eV, close to the value of 4-aminophenol.

We note that theory predicts that the C1–C4 1s energy difference should be only 0.11 eV, but is a little larger. The experimental energy of the unsubstituted ring carbon atoms is in good agreement with the present calculated range of values, 290.07–290.25 eV.

Lastly, the ibuprofen C 1s spectrum shows a strongly shifted peak due to the carboxylic acid carbon at an energy similar to that of aspirin. The alkyl substituents of the benzene ring cause only small core level shifts so that fine structure is not resolved, and the spectrum shows an asymmetric, unresolved peak due to the ring and alkyl carbon atoms.

A goal of this investigation was to search for similar spectroscopic and chemical properties that might help to explain similar medicinal effects: as mentioned above, the molecules have several chromophores in common. However, the results underline the diversity of these drugs. Core-level spectroscopy is sensitive to the charge distribution in a molecule, and although all three drugs contain a di-substituted benzene ring, the C 1s spectra of the 6 carbon atoms are all different, indicating different local potentials. Aspirin and paracetamol contain an acetyl group, but the experimental C 1s binding energies of the carbonyl carbon differ by more than 1 eV, again indicating different charge distributions. Only the carboxylic acid groups of aspirin and ibuprofen are spectroscopically very similar.

6 Conclusions

The geometries and energies of the lowest energy conformers of paracetamol, aspirin, and ibuprofen have been calculated and found to be in generally good agreement with previous theoretical and experimental work. We have measured the valence photoelectron spectrum of aspirin, and the core level spectra of aspirin, paracetamol and ibuprofen. The spectra agree well with the present theoretical calculations, and aspirin and paracetamol are clearly related to their parent compounds, salicylic acid and 4-aminophenol, and details of the relationship have been identified. Although the three target compounds share several motifs, their spectroscopic fingerprints indicate dissimilar electronic charge distributions, and therefore diverse chemical interactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully thank our colleagues at Elettra for providing high-quality synchrotron light. This work was carried out during a scientific leave (academic year 2021–2022) and a sabbatical leave (academic year 2022–2023) granted to H. S. from the University of Jordan, Amman, Jordan. H. S. acknowledges the TRIL fellowship awarded by the Abdus Salam International Centre for Theoretical Physics (ICTP), Trieste, Italy. FW acknowledges Dr Ersin Yurtsever (ref. 5) for his generosity in sending us the raw results of his article on aspirin monomer conformation, and Mr Alexander Hill for calculations contributing to Fig. 7. We thank Mr Awad Mohamed for assistance during some of the measurements of one of the compounds.

References

1. J. R. Vane and R. M. Botting, Am. J. Med., 1998, 104, 2S–8S,  DOI:10.1016/S0002-9343(97)00203-9.
2. Y. Shamsudin Khan, H. Gutiérrez-de-Terán, L. Boukharta and J. Åqvist, J. Chem. Inf. Model., 2014, 54, 1488–1499,  DOI:10.1021/ci500151f.
3. I. Novak, L. Klasinc, D. P. Chong and S. P. McGlynn, Spectrochim. Acta, Part A, 2013, 112, 110–115,  DOI:10.1016/j.saa.2013.04.012.
4. R. Glaser, J. Org. Chem., 2001, 66, 771–779,  DOI:10.1021/jo001241s.
5. Z. Yurtsever, B. Erman and E. Yurtsever, Turk. J. Chem., 2012, 36, 383–395,  DOI:10.3906/kim-1112-16.
6. C. Cabezas, J. L. Alonso, J. C. López and S. Mata, Angew. Chem., Int. Ed., 2012, 51, 1375–1378,  DOI:10.1002/anie.201106621.
7. H. B. Bürgi, J. D. Dunitz and E. Shefter, J. Am. Chem. Soc., 1973, 95, 5065–5067,  DOI:10.1021/ja00796a058.
8. J. M. Beames and A. J. Hudson, Phys. Chem. Chem. Phys., 2010, 12, 4157–4164,  10.1039/B923202H.
9. S. J. Lee, A. Min, Y. Kim, A. Ahn, J. Chang, S. H. Lee, M. Y. Choi and S. K. Kim, Phys. Chem. Chem. Phys., 2011, 13, 16537–16541,  10.1039/C1CP21999E.
10. W. Y. Sohn, J. S. Kang, S. Y. Lee and H. Kang, Chem. Phys. Lett., 2013, 581, 36–41,  DOI:10.1016/j.cplett.2013.07.018.
11. M. Varela, C. Cabezas, J. C. López and J. L. Alonso, J. Phys. Chem. A, 2013, 117, 13275–13278,  DOI:10.1021/jp404581z.
12. A. Jubert, M. L. Legarto, N. E. Massa, L. L. Téves and N. B. Okulik, J. Mol. Struct., 2006, 783, 34–51,  DOI:10.1016/j.molstruc.2005.08.018.
13. M. L. Vueba, M. E. Pina and L. A. E. Batista de Carvalho, J. Pharm. Sci., 2008, 97, 845–859,  DOI:10.1002/jps.21007.
14. Z. Fu, X. Li and K. M. Merz Jr., J. Comput. Chem., 2011, 32, 2587–2597,  DOI:10.1002/jcc.21838.
15. L. Liu and H. Gao, Spectrochim. Acta, Part A, 2012, 89, 201–209,  DOI:10.1016/j.saa.2011.12.068.
16. T. Betz, S. Zinn and M. Schnell, Phys. Chem. Chem. Phys., 2015, 17, 4538–4541,  10.1039/C4CP05529B.
17. A. R. Blaazer, P. Smid and C. G. Kruse, ChemMedChem, 2008, 3, 1299–1309,  DOI:10.1002/cmdc.200800133.
18. S. Kang and J. P. Green, Nature, 1970, 226, 645,  DOI:10.1038/226645a0.
19. S. Kang and J. P. Green, Proc. Natl. Acad. Sci. U. S. A., 1970, 67, 62–67 JSTOR, http://www.jstor.org/stable/60110. Accessed 18 Feb. 2023.
20. G. Beuerle, K.-A. Kovar and M. Schulze-Alexandru, Quant. Struct.-Act. Relat., 1997, 16, 447–458,  DOI:10.1002/qsar.19970160603.
21. B. W. Clare, Austr. J. Chem., 1995, 48, 1385–1400,  DOI:10.1071/CH9951385.
22. M. M. Abdou, J. Psychoact. Drugs, 2001, 33, 295–300,  DOI:10.1080/02791072.2001.10400577.
23. L. Klasinc, B. Ruščić, A. Sabljić and N. Trinajstić, J. Am. Chem. Soc., 1979, 101, 7477–7482,  DOI:10.1021/ja00519a005.
24. L. Klasinc, I. Novak, A. Sabljić and S. P. McGlynn, Int. J. Quantum Chem., Quantum Biol. Symp., 1986, 13, 251–260,  DOI:10.1002/qua.560300824.
25. L. Klasinc, J. Electron Spectrosc. Relat. Phenom., 1976, 8, 161–164,  DOI:10.1016/0368-2048(76)80018-7.
26. K. Kimura, S. Katsumata, Y. Achiba, T. Yamazaki and S. Iwata, Handbook of He(I) Photoelectron Spectra of Fundamental Organic Molecules, Japan Scientific Societies Press, Tokyo, Japan, 1981.
27. V. Myrseth, J. D. Bozek, E. Kukk, L. J. Sæthre and T. D. Thomas, J. Electron Spectrosc. Relat. Phenom., 2002, 122, 57–63,  DOI:10.1016/S0368-2048(01)00321-8.
28. T. D. Thomas and R. W. Shaw Jr., J. Electron Spectrosc. Relat. Phenom., 1974, 5, 1081–1094,  DOI:10.1016/0368-2048(74)85066-8.
29. T. Hatamoto, M. Matsumoto, X.-J. Liu, K. Ueda, M. Hoshino, K. Nakagawa, T. Tanaka, H. Tanaka, M. Ehara, R. Tamaki and H. Nakatsuji, J. Electron Spectrosc. Relat. Phenom., 2007, 155, 54–57,  DOI:10.1016/j.elspec.2006.10.002.
30. F. Wang and V. Vasilyev, Int. J. Quantum Chem., 2021, 121, e26765,  DOI:10.1002/qua.26765.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
32. D. P. Chong, Canadian J. Chem., 1996, 74, 1005–1007,  DOI:10.1139/v96-112.
33. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967,  DOI:10.1002/jcc.1056.
34. D. P. Chong, Canadian J. Chem., 2019, 97, 697–703,  DOI:10.1139/cjc-2019-0082.
35. V. Feyer, O. Plekan, R. Richter, M. Coreno, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2008, 112, 7806–7815,  DOI:10.1021/jp803017y.
36. O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K. C. Prince and V. Carravetta, J. Phys. Chem. A, 2007, 111, 10998–11005,  DOI:10.1021/jp075384v.
37. A. Hill, H. Sa’adeh, D. Cameron, F. Wang, A. B. Trofimov, E. Yu. Larionova, R. Richter and K. C. Prince, J. Phys. Chem. A, 2021, 125, 9877–9891,  DOI:10.1021/acs.jpca.1c07523.
38. S. Islam, A. Ganesan, R. Auchettl, O. Plekan, R. G. Acres, F. Wang and K. C. Prince, J. Chem. Phys., 2018, 149, 134312,  DOI:10.1063/1.5048691.
39. E. E. Tseplin, S. N. Tseplina, G. M. Tuĭmedov and O. G. Khvostenko, Opt. Spectrosc., 2009, 106, 334–342,  DOI:10.1134/S0030400X09030047.
40. A. Hill, An XPS study of positional isomers of hydroxybenzoic acids: theory and experiment, Honours Thesis, Swinburne University of Technology, Melbourne, Australia, 2019 (Unpublished).
41. W. L. Jolly, K. D. Bomben and C. J. Eyermann, At. Data Nucl. Data Tables, 1984, 31, 433–493,  DOI:10.1016/0092-640X(84)90011-1.
42. V. Zhaunerchyk, M. Kamińska, M. Mucke, R. J. Squibb, J. H. D. Eland, M. N. Piancastelli, L. J. Frasinski, J. Grilj, M. Koch, B. K. McFarland, E. Sistrunk, M. Gühr, R. N. Coffee, C. Bostedt, J. D. Bozek, P. Salén, P. V. D. Meulen, P. Linusson, R. D. Thomas, M. Larsson, L. Foucar, J. Ullrich, K. Motomura, S. Mondal, K. Ueda, R. Richter, K. C. Prince, O. Takahashi, T. Osipov, L. Fang, B. F. Murphy, N. Berrah and R. Feifel, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 244003,  DOI:10.1088/0953-4075/48/24/244003.
43. M. Mucke, et al., in preparation.

---

Footnote

† Electronic supplementary information (ESI) available: Molecular structures of lowest-energy conformers, valence band spectrum, and theoretical and experimental valence ionization potentials. See DOI: https://doi.org/10.1039/d2cp05810c

---