 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Paddle-wheel mechanism in doped succinonitrile–glutaronitrile plastic electrolyte: a joint magnetic resonance, dielectric, and viscosimetry study of Li ion translational and molecular reorientational dynamics
S.
Lansab
 *a,
B.
Grabe
*a,
B.
Grabe
 b and
R.
Böhmer
b and
R.
Böhmer
 a
a
aFakultät Physik, Technische Universität Dortmund, D-44221 Dortmund, Germany. E-mail: sofiane.lansab@tu-dortmund.de
bFakultät für Chemie und Chemische Biologie, Technische Universität Dortmund, D-44221 Dortmund, Germany
First published on 16th March 2023
Abstract
Mixtures of 60% SN (succinonitrile) and 40% GN (glutaronitrile) doped with LiTFSI or LiPF6 at different concentrations are investigated using dielectric spectroscopy. Room temperature conductivities up to 10−3 S cm−1 are measured along with an overall conductivity enhancement of almost five decades compared to pure SN. Additionally, the dynamics of the methylene (CD2) groups of SN and that of the Li+ ions within the mixture are studied in a wide temperature range using 2H and 7Li NMR relaxometry, respectively. Static-field-gradient proton NMR combined with viscosity measurements probe the molecular diffusion. GN addition and Li doping both enhance the electrical conductivity significantly, while leaving the reorientational motion within the matrix essentially unchanged. The times scales and thus the effective energy barriers characterizing the Li ion motion as well as the molecular reorientations are very similar in the liquid and in the plastic phases, findings that argue in favor of the presence of a paddle-wheel mechanism.
1. Introduction
In recent years, the need for powerful energy-storage solutions has become crucial for a more sustainable future, where fuel-based energy sources cease to be an option and where green energy is expected to play a major role. A transition to such a future requires efficient energy materials, hence the need for better electrolytes. These materials must satisfy several conditions, including electrochemical aspects, such as an ionic conductivity of at least 10−4 S cm−1 and a high electrochemical stability, as well as practical, safety-, and economy-related aspects.Whether used as simple plasticizers among more complex systems or as main matrices, dinitriles such as N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–(CH2)n–C
C–(CH2)n–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N are subject to extensive research and have proven to be suitable electrolytes for Li ion batteries when doped with sufficient amounts of Li salt.1–11 Their relatively high ionic conductivity, even in the absence of a dopant,12 alongside with their low toxicity and low flammability, make them particularly compelling candidates for battery research.
N are subject to extensive research and have proven to be suitable electrolytes for Li ion batteries when doped with sufficient amounts of Li salt.1–11 Their relatively high ionic conductivity, even in the absence of a dopant,12 alongside with their low toxicity and low flammability, make them particularly compelling candidates for battery research.
Since dinitriles are highly polar and can dissolve enormously large amounts of Li salts,13 when doped with Li ions they can reach room-temperature ionic conductivities of up to σ ≈ 10−3 S cm−1.3 On top of that, dinitriles show a large electrochemical stability window (up to 6 V vs. Li+/Li)6 and a better electrode/electrolyte interfacial resistance than conventional inorganic solid-state materials.14 Compared with conventional polymer electrolytes, nitrile-based ion conductors require smaller amounts of doping and are easier to produce.
In that sense, succinonitrile (SN, n = 2) is particularly interesting for pliable or stretchable cells because it exhibits a plastically crystalline phase.15–17 In this phase, its molecular constituents exhibit partial alignment arising from the orientational degrees of freedom that are located on well-defined lattice sites.18 Thus, this electrolyte allows for a large degree of mechanical flexibility and high deformability. Additionally, Angell has shown that the temperature window in which the plastic phase exists, happens to be easily extendable by adding a sufficient amount of glutaronitrile (GN, n = 3).19
Moreover, Geirhos et al.20 reported that the ionic conductivity of LiPF6 doped SN increases by about 3 decades when adding GN. These authors observed a strong coupling between the ionic conductivity of the Li ions and the reorientational motion of the matrix molecules when increasing the GN fraction. These findings were suggested20 to be compatible with the previously discussed “revolving door mechanism”,21,22 also in mixtures of different other nitriles with SN.23 The relevance of this mechanism in a wide range of different solid electrolytes and the exciting prospects this offers for the design of future materials was recently reviewed.24
Additionally, several studies provided valuable information regarding the structure of SN before and after Li ion incorporation.18,25–32 In its plastic phase, SN crystallizes in a cubic structure with a lattice constant of a = 6.341 Å.18 In particular, incorporation of salts such as LiClO4 or lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) does not alter this lattice spacing.27 Furthermore, X-ray absorption spectroscopy at the Cu K-edge reveals that the cations (in CuTFSI doped SN) occupy well-defined sites in the cubic lattice. These are each coordinated by four SN molecules which “persists even in the molten host”.29 Furthermore, a variety of Li-ion solvation structures were identified in SN by means of combining ultrafast vibrational spectroscopy and quantum chemical investigations, where the latter reveal, e.g., for a Li+–SN3 complex “that there are four possible conformations for one Li+ directly binding to 3 SN molecules”.31 Taking the conformational changes into account, for the condensed phases one thus expects a large multiplicity of charge environments at the cationic sites.
Recently, Sasaki et al.33 conducted molecular dynamics simulations of the Li ion transport within an SN matrix: These authors suggested a two-step migration process, where first, in the vicinity of a vacant Li site, a gauche-to-trans isomerization of two SN molecules takes place, followed by a swing motion by one of them “holding Li-ions towards the vacancy”.33
Interestingly, for GN fractions on the order of 15%, Zachariah et al.34 reported a breakdown of the correlation between reorientational motion and doping induced conductivity. Furthermore, these authors ascribed their findings to a conductivity process arising from the self-diffusion of a minority of ionized dinitrile molecules.
Finally, in nitrile materials the mutual distances between the sites participating in the Li ion exchange can be relatively long (≈5 Å for Li(N(SO2F)2)(SN)2),36 while low activation energies against Li hopping have been reported.12,35,36 The ionic transport mechanism causing these low activation energies is not fully understood, and deeper insights regarding the interactions governing the charge dynamics are needed to optimize wider applications. In particular, the relationship between the molecular reorientation of the nitrile molecules and the lithium hopping process requires further clarification.37
In this context, nuclear magnetic resonance (NMR) spectroscopy has established itself as a primary technique for the study of Li electrolytes.38–43 Indeed, it has the advantage of being element specific, allowing for an independent investigation of the reorientational motion of the matrix, here through the nitrile molecules, as well as of the hopping motion of the Li ions that are involved in the conduction process. Therefore, if the Li ions within the SN–GN matrix occupy distinguishable environments, the Li spins resonate at different frequencies which then can be detected using suitable NMR experiments. The resulting distribution of the different resonance frequencies usually provides valuable information about the relevant interactions and thus on the nature of the charge transport process.
Furthermore, with the availability of perdeuterated SN (SN-d4),442H NMR can be exploited to directly probe the matrix dynamics through the reorientational fluctuations of the C–D bonds.45 Additionally, one can use 1H NMR to monitor the dynamic behavior46 specifically of the GN molecules in the same binary system, for instance, by means of NMR diffusometry. This latter method, combined with viscosity measurements, provide deep insights into the type of dynamics occurring within the matrix and help to clarify how the addition of GN contributes to the overall conductivity enhancement.20 Additionally, abrupt viscosity changes are useful to unravel the phase transitions of SN–GN mixtures.
Similarly, dielectric spectroscopy yields helpful information regarding the reorientational dynamics within the matrix. It is sensitive to the molecular (electric) dipole moment which for the dinitriles happens to be large (around 3.9 D for SN and GN).47 The combination of dielectric and NMR spectroscopy as well as the combination of 2H and 7Li NMR thus can elucidate the possible correlation between reorientational motion and ionic charge transport.
Finally, based on the classification of correlated dynamics discussed by Jansen22 and with the information obtained from the present NMR data in combination with dielectric and rheology results, we will provide a clarified picture on how the Li ions and the nitrile molecules dynamically cooperate.
In the present work, we investigate the ionic conductivity and reorientational dynamics of the plastic mixture of 60% SN and 40% GN doped with 1% and 5% of LiTFSI or LiPF6. We use dielectric spectroscopy and viscosimetry as well as 1H, 2H, and 7Li NMR. The dynamics of the Li ions as well as that of the matrix is thoroughly studied via deuterated SN. In addition, detailed comparisons with previous results48–50 obtained for undoped 60SN–40GN mixtures are provided.
2. Experimental details
Protonated GN (stated purity 99%) and protonated SN (99%) as well as LiTFSI (99%), all purchased from Sigma-Aldrich, are used in this work. The deuterated SN (degree of deuteration: 91%) is from the previously used batch.48 LiPF6 (98%) was acquired from ThermoFischer Scientific. All samples were prepared inside a glovebox, where 60% SN and 40% GN were mixed as reported earlier.48 The Li salts were first dried at T = 353 K for a minimum of 8 hours directly before use. Afterwards they were ground to optimize dissolution and added to the nitrile mixtures under heavy stirring. Karl Fischer titration showed water fractions of less than 0.05% for all investigated samples. After several freeze–thaw–pump cycles the NMR samples were flame sealed in glass tubes.The 7Li spectroscopy measurements were carried out using a home-built spectrometer operated at a Larmor frequency of 116.9 MHz. To record 7Li solid-echo spectra, the 90° 7Li pulse was 3 μs long. A Gaussian apodization with a spectral width of 1 kHz was applied. The software package DMFit was used to analyze the spectra.51 For 7Li relaxometry, a saturation recovery pulse sequence followed by Hahn-echo or solid-echo refocusing was used.
NMR deuterium relaxometry and proton diffusion measurements were performed using home-built spectrometers operated at Larmor frequencies of 46.5 MHz for 2H and 87.0 MHz for 1H. Deuteron spin–lattice relaxation times T1 were measured using an inversion recovery pulse sequence augmented by Hahn-echo or solid-echo rephasing. Deuteron spin–spin relaxation times T2 were obtained by employing Hahn-echo or solid-echo pulse sequences. Static field-gradient NMR was used to probe the proton diffusion in the samples. These experiments were conducted in the fringe field of a superconducting magnet employing a constant gradient strength of g = (34.1 ± 0.2) T m−1 as described previously.48
The 7Li diffusion experiments were performed with a Bruker Avance III HD Nanobay 400 MHz spectrometer equipped with a 5 mm RT BBFO smart probe using stimulated echoes including longitudinal eddy current delays with bipolar gradients and spoil pulses.52 The probe's maximum gradient strength of about 0.5 T m−1 was calibrated using doped D2O water (P/N Z10906), containing 1% H2O, 0.1% GdCl3, and 0.1% 13CH3OH. The diffusion coefficients were determined by linearly varying the gradient strength in 16 steps between 10 and 80% of its maximum using gradient pulse lengths δ between 1.6 and 2.8 ms, diffusion delays Δ between 0.3 and 1 s, and a 90° 7Li pulse of 9.0 μs.
Dielectric spectroscopy experiments were carried out in a Novocontrol system in combination with an Alpha impedance analyzer and a Quatro temperature controller. The frequency range from 10−1 to 106 Hz was scanned. The typical temperature stability was ±0.1 K.
Rotational viscosities were recorded in the liquid phase of the samples and in the linear-response regime using an Anton-Paar MCR 502 rheometer and an EVU20 temperature module at a typical temperature stability of ±0.2 K. The sample was placed between two plates separated by d = 0.9 mm. The upper plate rotates with an angular frequency ωrot leading to a shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = ωrotr/d, while the lower plate with a diameter of 2r = 50 mm is fixed.
= ωrotr/d, while the lower plate with a diameter of 2r = 50 mm is fixed.
3. Results and analyses
A. Dielectric spectroscopy
To probe the reorientational motion of the matrix and the conductivity enhancement after doping, we conducted dielectric spectroscopy measurements during cooling on three (SN-d4)0.6(GN)0.4 mixtures: These were doped with 1% LiPF6, 5% LiPF6, or 5% LiTFSI. Ref. 37 presented modulus losses for samples with 5% LiTFSI doping, but neither conductivity nor permittivity were reported, two quantities that we find particularly useful for comparison with our NMR results. Furthermore, although dielectric data for 1% LiPF6 doped SN0.6GN0.4 were presented in ref. 20, here we measured this sample to ensure a better overall comparability of our results also in view of the dependence on the Li salt concentration.The results for the sample with 5% LiTFSI are presented in Fig. 1, where frame (a) shows the real part of the frequency dependent electrical conductivity σ′(ν), focusing on frequencies for which electrode polarization is not relevant. The dc conductivity corresponds to the plateau σdc observed in σ′(ν), which for T = 231 K appears near 10−4 S cm−1. This value indicates an exceptionally high ionic conductivity. For the mixture without Li doping, at the same temperature we observed a dc plateau of about 10−7 S cm−1.48 This difference implies a LiTFSI doping induced conductivity enhancement of at least three decades, in agreement with that reported for similar mixtures doped with various other Li salts.20,34 Towards lower temperatures, the plateau in σ′ shifts to lower values and lower frequencies.
 | ||
| Fig. 1 Frequency-dependent measurements of (a) the electrical conductivity, (b) the real part, and (c) the imaginary part of the complex permittivity of (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI. The temperature range for frame (a) is between 213 and 177 K, while that for frames (b) and (c) is between 162 and 141 K. The crosses in frame (c) show dielectric losses for undoped (SN-d4)0.6(GN)0.4,48 acquired at T = 160 K. In this plot, these data are displayed with a relaxation strength that was rescaled by a factor of 0.22. The solid lines in frame (c) reflect fits using eqn (1) with γ = 0.5 ± 0.1. | ||
Fig. 1b and c show the frequency dependent dielectric constant ε′ and the dielectric loss ε′′, respectively, measured at various temperatures. As the frequency increases, the dielectric constant ε′ displays a steplike decrease from about 50 to 5, while between 162 and 147 K the dielectric loss ε′′ reveals characteristic peaks in the present frequency window that originate from a reorientational relaxation process. These peaks shift to lower frequencies with decreasing temperature.
The decrease seen in the dc conductivity as well as that observed in the dielectric constant while the loss peaks shift towards lower frequencies, are well-known dielectric aspects of liquids and plastic crystals53 and are similar to results obtained for the undoped mixture.48,49
For an analysis of the dielectric spectra, like before,48 we use the Cole–Davidson (CD) function54
 | (1) |
 | (2) |
From Fig. 1c it is obvious that the solid lines calculated using eqn (1) with γ = 0.5 ± 0.1, fit only the high-frequency flanks of the peaks seen in the dielectric loss ε′′. The low-frequency side features an additional contribution that is not observed in the absence of Li ions, but visible (see, e.g., Fig. 2c of ref. 20) even for a doping level of 1%.
B. Lithium NMR spectroscopy
The measurement of the static 7Li (spin I = 3/2) NMR spectra yields information about the environment surrounding the Li ions and the type of interactions involved in spectral broadening. In 7Li NMR, the line shape is often governed by electrical quadrupole interactions and to a lesser extent by magnetic dipole–dipole interactions.38Fig. 2 shows temperature dependent 7Li spectra for (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI. As the temperature increases, a successive line narrowing is observed. The contributions to the spectral shape were assessed for the spectrum recorded at T = 155 K: We fitted this spectrum with a superposition of a Lorentzian line (accounting for 54% of the total intensity) and a Gaussian contribution (accounting for the remaining 46%). The full width at half maximum (FWHM) of the dipolarly broadened central-transition (−1/2 ↔ +1/2) line is Δν1/2 = 6 kHz, while for the quadrupolarly broadened satellite spectrum, one has Δν1/2 = 32 kHz. The broad satellite lineshape indicates that it is caused by a superposition of several NMR lines. These arise from different structural environments in which the Li ions experience quadrupolar interactions of different strengths. | ||
| Fig. 2 7Li solid-echo spectra recorded for (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI. Note that for T ≥ 195 K the spectra were recorded at 155.5 MHz, otherwise at 116.9 MHz. The spectrum obtained at 155 K (the measured spectrum is here shown as dashed line) was fitted with a superposition of a Lorentzian central-transition contribution (filled dashed area) and a Gaussian satellite-transition contribution (filled area without dashes). The sum of the two is represented by the solid purple double line. The inset shows a sketch, inspired by the structures in ref. 31, of a Li ion embedded in a solvation shell that features the partially negatively charged N atoms (blue spheres) of the dinitrile molecules. | ||
Fig. 3 summarizes the temperature dependent line widths, obtained from the solid-echo echo spectra. For their analysis, we use an equation first put forward by Bloembergen, Purcell, and Pound.56,57 In the present context it is exploited with the goal to extract the correlation times describing the translational motion of the Li ions
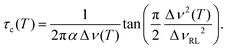 | (3) |
 | ||
| Fig. 3 7Li central-transition line widths determined for (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI at 155.5 MHz (filled symbols) and 116.9 MHz (open symbols). | ||
C. NMR relaxometry
In order to gain a detailed understanding of how the matrix dynamics is affected by adding Li ions, we conducted 2H NMR relaxometry measurements on (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI. In fact, the reorientational motion within the matrix is predominantly due to isomerizations of the nitrile molecules18,59 that are associated with fluctuations of the carbon–deuteron bonds. Thus, 2H NMR directly monitors this reorientational motion within the matrix. In order to be sensitive to the charge carrier motion we exploited also 7Li relaxometry.We recorded the longitudinal magnetization recovery, Mz(t), for the doped and the undoped samples and used the stretched exponential function
| Mz(t) = M0 + (Mi − M0)exp[−(t/T1)μ1], | (4) |
Analogously, spin–spin relaxation times T2 were acquired by varying the pulse separation Δ. The decay of the transverse magnetization Mxy(Δ) was parameterized using
| Mxy(Δ) = M0 exp[−(2Δ/T2)μ2], | (5) |
The spin–lattice and spin–spin relaxation times for 2H as well as the spin–lattice relaxation times for 7Li, measured for (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI, are shown in Fig. 4. The corresponding Kohlrausch exponents were set to μ1 = μ2 = 1 for 2H and 7Li at T > 160 K and at T > 180 K, respectively.
 | ||
| Fig. 4 The temperature dependent deuterium spin–lattice relaxation times T1 (full symbols) and spin–spin relaxation times T2 of (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI are shown. T2 was measured using Hahn-echo (×, for T > 180 K) and solid-echo sequences (+, for T < 210 K). All measurements were recorded during cooling. The solid blue and dashed blue lines are calculated using eqn (7) in conjunction with the spectral density given by eqn (6) and using the fit parameters from ref. 48. Deuterium T1 and T2 data for the undoped mixture48 are shown by the light blue squares and circles, respectively. 7Li spin–lattice relaxation times for the doped mixture are presented as red diamonds. The dash-dotted red line is calculated using eqn (9) and the parameters given in the text. The black dashed line, cf.eqn (8), reflects an apparent energy barrier of 17 kJ mol−1. | ||
For a quantitative analysis, we describe the orientational fluctuation probability of the C–D bond using the Cole–Davidson spectral density60
 | (6) |
 and assuming that the quadrupolar relaxation mechanism dominates, the spin–lattice relaxation of the 2H nuclei can be described as61
and assuming that the quadrupolar relaxation mechanism dominates, the spin–lattice relaxation of the 2H nuclei can be described as61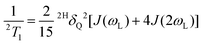 | (7) |
 | (8) |
Analogously, the spin–lattice relaxation rate for 7Li is61
 | (9) |
 .
.
Considering first the deuterium NMR data in Fig. 4, in the extreme-narrowing regime we observe a slight discrepancy between 2T1 and 2T2, similar to the behavior of the undoped mixture.48 As previously reported, this discrepancy can be ascribed to deviations from local cubic ordering in the plastic phase.44 A significant drop in 2T2, but not in 2T1, is observed near 230 K, i.e., close to the temperature at which a related drop was observed for the undoped sample.48 This observation is taken as a hint that the Li-doped sample is characterized by a somewhat lower transition temperature as compared to undoped (SN-d4)0.6(GN)0.4.
To describe the relaxometry data, the blue lines in Fig. 4 were calculated using eqn (6), (7), and (8) in conjunction with γNMR = 0.3 and the time scale parameters found for undoped (SN-d4)0.6(GN)0.4.48 The 2H quadrupolar anisotropy parameter turned out to be 2HδQ = 2π × 125 kHz, similar to the value determined for the undoped mixture.48Eqn (7) provides a good fit for the measured 2T1, with small deviations observed at high temperatures. On the other hand, between 230 and 195 K the 2T2 values deviate significantly from the fit based on eqn (8). Furthermore, 2T2 displays a minimum near 175 K. All these findings agree excellently with those for the undoped sample and imply a complete absence of any kind of hindrance or stimulation of the molecular reorientation dynamics upon doping the matrix with 5% of Li salt.
Taking a closer look at the 7Li spin–lattice relaxation times, these are seen to reveal a minimum near 240 K and to pass continuously through the liquid-to-plastic-crystal transition. The minimal 7T1 is almost two decades longer than the minimal 2T1. This difference for the different probe nuclei is compatible with our finding that the 7Li quadrupolar interaction is significantly smaller than that observed for deuterium. The red line in Fig. 4 was calculated using eqn (6) and (9) in conjunction with γNMR = 0.24. The time scales were calculated using the Vogel-Fulcher parameters reported in ref. 48, with a pre-exponential factor of τ∞ = 9.3 × 10−12 s, a strength parameter Dτ = 2.1, and a divergence temperature T0 = 178 K. These parameters are close to those reported by Davidowski et al.37 for the same sample. The fit shown in Fig. 4 was found to agree well with the data when choosing 7LiδQ = 2π × 32 kHz, a value that is compatible with the width obtained from the 7Li spectrum.
The 7Li spin–lattice relaxation is governed by the quadrupolar interactions of the Li nuclei with their charge environment which is modulated in time. This modulation happens mostly as the ions perform translational motion within the SN–GN matrix and to a lesser extent, see Section 4, below, via conformational changes of adjacent dinitrile molecules.
Thus, by using the condition ω0τc ≈ 0.62 (or slightly different for a Cole–Davidson distribution63), from the motional correlation time, τc at 240 K the Li-ion jump rate is estimated to be about τLi = 12 × 108 s−1. Based on the Einstein–Smoluchowski equation64
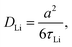 | (10) |
 | ||
| Fig. 5 Arrhenius plot of the temperature dependent 7Li (unfilled red stars) and 1H (unfilled red diamonds) self-diffusion coefficients (scale on the left-hand side) as well as of the temperature dependent fluidity, i.e., of the inverse zero-shear viscosity (triangles, scale on the right-hand side). The unfilled red stars refer to measurements conducted during heating and using PFG NMR. The blue triangles pointing down or up refer to viscosity measurements taken upon cooling or heating, respectively. The half-filled black star refers to the 7Li diffusion coefficient obtained from eqn (10), where τLi was obtained from the 7Li T1 minimum, using 1.8 Å as jump distance. Prior to each diffusion measurement, the samples were given 3 hours to equilibrate. 1H self-diffusion coefficients and fluidities for the same mixture without doping48 are shown by red (+) and blue (×) symbols, respectively. The dashed black lines reflect apparent energy barriers of 32 kJ mol−1. The dash-dotted vertical line highlights the transition temperature from the undoped liquid to the plastically crystalline phase as identified in ref. 48. | ||
Finally, using the Arrhenius law, the activation energy for temperatures above the T1 minimum turned out to be Ea = 17 kJ mol−1, a value within the range of those reported for LiTFSI in GN.65
D. Diffusometry and viscometry
To selectively investigate the diffusion process of the GN molecules after addition of the Li ions, we measured the proton diffusion coefficient D of (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI. In other words, here (since SN contributes only ≤9% of the protons in our samples) we almost exclusively probe the diffusion of the GN molecules within the mixture. For that purpose, like in previous work,48 we use a static field gradient and measure D by means of the stimulated-echo pulse sequence π/2 – tp – π/2 – t – π/2 – tp – acquisition. Not writing out the spin relaxation terms, the resulting NMR signal is given by66 | (11) |
To probe the diffusion process not only of the matrix molecules, but of the charge carriers as well, we conducted temperature dependent 7Li pulsed field gradient (PFG) NMR measurements on fully protonated SN0.6GN0.4 doped with 5% LiTFSI. In this experiment the stimulated-echo pulse sequence is used as well. The field gradient is incremented stepwise, thus causing an attenuation of the echo signal according to the Stejskal–Tanner equation67
 | (12) |
In addition to the diffusion measurements, we conducted temperature dependent zero-shear viscosity measurements on protonated SN0.6GN0.4 doped with 5% LiTFSI. The results for the 1H and the 7Li diffusion coefficients as well as for the fluidity (inverse of viscosity), presumably all referring to the liquid state, are shown in Fig. 5. For comparison, we also include results for undoped samples where some data could also be gathered in the plastic solid.48
From Fig. 5, it is clear that the proton diffusion of the dinitrile molecules slows down only slightly when adding the lithium salt. The measured viscosities confirm this trend, since they are similar to those obtained for the undoped mixture.48
When extrapolated to 294 K, the lithium diffusion coefficients differ by only a factor of 0.6 from those characterizing the dinitrile molecules. Furthermore, near room temperature the (effective) energy barrier of Ea = 32 kJ mol−1 that characterizes the lithium-ion diffusion agrees with the barrier deduced from the proton data.
A similar value can also be deduced for undoped SN0.6GN0.4.48 Evidently, after doping the SN0.6GN0.4 mixture with 5% LiTFSI we do not observe an increase of Ea (cf. the dashed lines in Fig. 5) which reflects the activation barrier that a GN molecule has to overcome in order to undergo translational motion. This confirms that the nitrile diffusion, or at least that of the GN molecules, is barely affected by Li ion doping.
By contrast, based on terahertz time-domain spectroscopy for SN doped with various Li salts (including LiTFSI), Nickel et al.35 observed a significant increase of the activation energy relative to that of pure SN. This increase was explained by “the presence of the effectively motionless ionic impurities”.35
4. Discussion
To allow for deeper insights into possible correlations between the reorientational motion of the nitrile molecules and the overall charge transport, we compare the temperature dependent ionic conductivities (Fig. 6a) with the temperature dependent reorientational relaxation times τ (Fig. 6b) for the three currently investigated samples. | ||
Fig. 6 Arrhenius plot of (a) the temperature dependent ionic conductivity and (b) the correlation time τ of (SN-d4)0.6GN0.4 mixtures doped with 1% LiPF6, 5% LiPF6, and 5% LiTFSI from the present work. The data in frames (a) and (b) for pure SN (▽),1 for SN doped with 1% LiPF6 (☆),23 for (SN-d4)0.6(GN)0.4 (o),48 and for another data set of (SN)0.6(GN)0.4 doped with 1% LiPF620 (represented as magenta crosses ×) are from the literature. Frame (a) also includes the conductivities of (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI as obtained after converting the Li diffusion coefficients (*) and the fluidity (![[pentagon open]](https://www.rsc.org/images/entities/char_e1c1.gif) ): The conversions are based on eqn (13) and (14), respectively, and the parameters given below these equations. The vertical dotted line indicates the transition temperature (T = 240 K) of undoped SN0.6GN0.4.48 Frame (b) includes correlation times from 2H and 7Li relaxometry of (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI, cf.Fig. 4 and from the 7Li line widths Δν1/2 (cf.Fig. 3). NMR time scales from Davidowski et al. for fully protonated samples are included as half-filled symbols.37 The solid line represents a Vogel-Fulcher fit for undoped (SN-d4)0.6GN0.4.48 The shear relaxation times τη are obtained from the Maxwell relation τη = η/G∞, with G∞ set to 0.18 GPa. The translational times τT were obtained from eqn (15) and the hydrodynamic radius given below that equation. ): The conversions are based on eqn (13) and (14), respectively, and the parameters given below these equations. The vertical dotted line indicates the transition temperature (T = 240 K) of undoped SN0.6GN0.4.48 Frame (b) includes correlation times from 2H and 7Li relaxometry of (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI, cf.Fig. 4 and from the 7Li line widths Δν1/2 (cf.Fig. 3). NMR time scales from Davidowski et al. for fully protonated samples are included as half-filled symbols.37 The solid line represents a Vogel-Fulcher fit for undoped (SN-d4)0.6GN0.4.48 The shear relaxation times τη are obtained from the Maxwell relation τη = η/G∞, with G∞ set to 0.18 GPa. The translational times τT were obtained from eqn (15) and the hydrodynamic radius given below that equation. | ||
The conductivities were obtained from the dc plateaus in σ′(ν) (Fig. 1a), while the correlation times were extracted from the dielectric loss peaks (Fig. 1c), i.e., by fits using eqn (1) combined with eqn (2). For comparison, Fig. 6 includes data for pure SN,1 for SN doped with 1% LiPF6,23 and for (SN-d4)0.6(GN)0.4.48 We also added the characteristic timescales obtained from 2H and 7Li NMR relaxometry of (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI, cf.Fig. 4.
Carefully reviewing Fig. 6a, it becomes obvious that the addition of 40% GN to pure SN enhances the conductivity by more than two decades, in accord with previous work.20 Further addition of lithium salt leads to even higher conductivities with an overall enhancement of more than four decades, as compared to pure SN.1 From Fig. 6a one observes similar conductivities no matter whether the samples are doped with LiPF6 or with LiTFSI. In view of the environmental and health issues related to LiPF6 it is clear that LiTFSI provides a safer alternative.
In order to compare the conductivity data obtained from dielectric spectroscopy with those deduced from the Li NMR diffusion coefficients and the viscosities shown in Fig. 5, we use the Nernst–Einstein relation,
 | (13) |
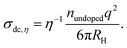 | (14) |
The conductivity obtained from eqn (13) can be understood as arising exclusively from the translational motion of the Li ions within the matrix. Eqn (14), on the other hand, considers a conductivity arising from the fluidity-related displacement of the nitrile molecules. From Fig. 6a one recognizes that the conductivities obtained from the Li diffusion viaeqn (13) and from the viscosity measurements viaeqn (14), nicely agree with each other and with the conductivities that are directly obtained from dielectric spectroscopy. These observations which essentially refer to the liquid phase imply a strongly correlated motion between the Li ions and the dinitrile molecules, a feature which results in a high ionic mobility and a significant conductivity enhancement.
Also referring to the liquid state, Fig. 6b includes viscosity-based timescales τη as assessed from the Maxwell relation, η = G∞τη, where G∞ is the high-frequency shear modulus. The value of G∞ needed to achieve overlap (0.18 GPa) equals the one reported for the undoped mixture,48 reinforcing the argument that the matrix properties are not affected by doping.
Furthermore, the correlation times τNMR from deuteron NMR and the 1H diffusion based translational timescales
| τT = RH2/(9D), | (15) |
Adapting eqn (15), 7Li diffusion-based translational timescales are similarly calculated using RH = 2.0 Å. Based on this value, the translational timescales turn out to agree well with the reorientational dynamics of the liquid matrix. The finding that the Li ion and the nitrile dynamics take place on the same time scale corroborates the scenario of an intimate coupling of the different degrees of freedom.
Additionally, by looking at Fig. 6b it becomes obvious that the reorientational correlation times of all Li doped samples are governed by the same molecular dynamics which agrees with that observed for the undoped SN–GN mixture.48,49 Also the reorientational timescales reported for pure and doped SN crystals are the same.1,20 All these findings clearly show that a few percent of Li doping do not affect the dynamics of the matrix. This supports the notion that, at the current doping levels, Li ion addition does not significantly distort the dinitrile lattice.
It is now important to realize that the 7Li spin–lattice relaxation times vary smoothly across the crystallization transition and that the correlation times in the plastic phase inferred from Δν1/2, using eqn (3) with α = 10, nicely coincide with the reorientational timescales, see Fig. 6b. These findings strongly suggest that the agreement of translational and reorientational timescales, above established for the liquid, persists also in the plastic solid. The relative large value of α deserves a comment: It may be conjectured that this could be a consequence of the circumstance (briefly mentioned in Section 3.C, above) that the frequency of the Li probe can be modulated (1) by active environmental changes stemming from the translation of the Li ions and to some extent also (2) by passive changes stemming from reorientations of adjacent nitrile segments, even if the Li ions would remain immobile.
However, in view of the multiplicity of nitrile configurations that characterizes the cationic solvation shell,31 – and akin to the scenario theoretically treated and experimentally tested in ref. 71 for other solid Li ion conductors – the frequency modulation amplitude associated with the two kinds of situation differs vastly: (1) can be read here to imply that after a Li ion has jumped to another site, the orientations of essentially all its adjacent C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N segments have changed at once. Typically, this will alter the NMR frequency of the Li probe significantly. (2) Conversely, a reorientation of only a single adjacent C
N segments have changed at once. Typically, this will alter the NMR frequency of the Li probe significantly. (2) Conversely, a reorientation of only a single adjacent C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N segment will change the NMR frequency of the Li probe by only a small step, unless the local reorientational motion is by itself highly cooperative. For (SN)0.6(GN)0.4 this appears not to be the case at least down to about 175 K.72
N segment will change the NMR frequency of the Li probe by only a small step, unless the local reorientational motion is by itself highly cooperative. For (SN)0.6(GN)0.4 this appears not to be the case at least down to about 175 K.72
Ionic mobilities that are coupled with reorientational molecular motions were previously variously referred to as being indicative for a revolving-door or a paddle-wheel mechanism.22,23,73 Often these terms are used indistinctively, however, they describe two different processes. Indeed here, the paddle-wheel mechanism implies cooperative dynamics between the reorientational motion of the dinitrile molecules and the hopping motions of the Li ions.22 This leads to very similar time scales and thus effective activation energies for the rotational and translation degrees of freedom. As a prerequisite this mechanism requires the availability of sufficiently large free volume for the molecules to rotate.74 The revolving-door mechanism, can be related to a scenario where the reorienting matrix molecules “react with an evasive motion towards the passage of cations”.22 Applied to the presently considered materials, this would imply just a correlated motion of Li ions and dinitrile molecules in the sense that only the temperature dependence of the corresponding times is the same but not the timescales themselves.
It is a remarkable finding that neither GN addition nor Li doping lead to any kind of hindrance or stimulation of the reorientational motion of the SN molecules. Considering the Li ions within a paddle-wheel scenario, this finding means that the ions occupy the free space between the dinitrile molecules without disturbing their reorientational motions. Furthermore, since the addition of GN does not affect the dynamics of the matrix but leads to higher conductivities, a possible explanation is that in the plastic phase, the addition of GN only affects the vacant space within the lattice of the mixed crystal. This way, the GN molecules would increase the free volume that is effectively available for Li ion migration, thus enhancing the efficiency of the charge transport. This hypothesis, here arrived at on the basis of dielectric spectroscopy, viscometry, and several NMR techniques, corroborates the interpretation of the very efficient charge transport in the nitriles in terms of a paddle-wheel and not just in terms a revolving-door mechanism.20
5. Conclusions
In this work we studied (SN-d4)0.6(GN)0.4 doped with 5% LiTFSI using several experimental methods. For comparison we measured the electrical conductivity also for several other Li-salt doped nitriles. The conductivities deduced from the Li translational diffusion as well as those obtained from the viscosity measurements, agree with those measured using dielectric spectroscopy. A strong correlation of timescales and thus of the effective energy barriers deduced thereof, were found between the reorientational motion of the dinitrile molecules and the translational motion of the Li ions. To describe this correlation – based on the classification of correlated dynamics put forward by Jansen22 and in harmony with the distinction of the terms given above – we identify the mechanism active in our sample as a “paddle-wheel” rather than a “revolving-door” mechanism.Additionally, and independent of the type or of the amount of Li doping as well as of the addition or not of GN molecules, the reorientational dynamics of the nitrile molecules remain unaffected. Based on these findings, one is tempted to argue that volume defects that are present within the SN lattice, directly impact on the efficiency of the Li ion transport mechanism. Future structural investigations should be directed at further elucidating the correlation between the fraction of volume defects within the matrix and the overall efficiency of the paddle-wheel mechanism also when varying the size of the cationic species.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Henrik Scholz (Department of Biochemical and Chemical Engineering, TU Dortmund University) for conducting Karl Fischer titrations and DSC measurements. This work was financially supported by the Deutsche Forschungsgemeinschaft under Project No. 429918288.References
- S. Long, D. R. MacFarlane and M. Forsyth, Fast ion conduction in molecular plastic crystals, Solid State Ionics, 2003, 161, 105–112 CrossRef CAS.
- P.-J. Alarco, Y. Abu-Lebdeh, A. Abouimrane and M. Armand, The plastic-crystalline phase of succinonitrile as a universal matrix for solid-state ionic conductors, Nat. Mater., 2004, 3, 476–481 CrossRef CAS PubMed.
- A. Abouimrane and I. J. Davidson, Solid Electrolyte Based on Succinonitrile and LiBOB: Interface Stability and Application in Lithium Batteries, J. Electrochem. Soc., 2007, 154, A1031–A1034 CrossRef CAS.
- A. Abouimrane, P. S. Whitfield, S. Niketic and I. J. Davidson, Investigation of Li salt doped succinonitrile as potential solid electrolytes for lithium batteries, J. Power Sources, 2007, 174, 883–888 CrossRef CAS.
- L.-Z. Fan, Y.-S. Hu, A. J. Bhattacharyya and J. Maier, Succinonitrile as a Versatile Additive for Polymer Electrolytes, Adv. Funct. Mater., 2007, 17, 2800–2807 CrossRef CAS.
- Y. Abu-Lebdeh and I. Davidson, High-Voltage Electrolytes Based on Adiponitrile for Li-Ion Batteries, J. Electrochem. Soc., 2009, 156, A60–A65 CrossRef CAS.
- N. Voigt and L. van Wüllen, The Effect of Plastic-Crystalline Succinonitrile on the Electrolyte System PEO:LiBF4: Insights from Solid State NMR, Solid State Ionics, 2014, 260, 65–75 CrossRef CAS.
- G. P. Pandey, T. Liu, C. Hancock, Y. Li, X. S. Sun and J. Li, Thermostable gel polymer electrolyte based on succinonitrile and ionic liquid for high-performance solid-state supercapacitors, J. Power Sources, 2016, 328, 510–519 CrossRef CAS.
- D. Farhat, J. Maibach, H. Eriksson, K. Edström, D. Lemordant and F. Ghamouss, Towards high-voltage Li-ion batteries: Reversible cycling of graphite anodes and Li-ion batteries in adiponitrile-based electrolytes, Electrochim. Acta, 2018, 281, 299–311 CrossRef CAS.
- J. Villarreal, R. Orrostieta Chavez, S. A. Chopade, T. P. Lodge and M. Alcoutlabi, The Use of Succinonitrile as an Electrolyte Additive for Composite-Fiber Membranes in Lithium-Ion Batteries, Membranes, 2020, 10, 45–58 CrossRef CAS PubMed.
- J. Möller, V. Van Laack, K. Koschek, P. Bottke and M. Wark, Solid-State NMR Revealing the Impact of Polymer Additives on Li-Ion Motions in Plastic-Crystalline Succinonitrile Electrolytes, J. Phys. Chem. C, 2023, 127, 1464–1474 CrossRef.
- S. Long, D. R. MacFarlane and M. Forsyth, Ionic conduction in doped succinonitrile, Solid State Ionics, 2004, 175, 733–738 CrossRef CAS.
- Y. Ugata, R. Tatara, K. Ueno, K. Dokko and M. Watanabe, Highly concentrated LiN(SO2CF3)2/dinitrile electrolytes: Liquid structures, transport properties, and electrochemistry, J. Chem. Phys., 2020, 152, 104502 CrossRef CAS PubMed.
- H. Zhi, L. Xing, X. Zheng, K. Xu and W. Li, Understanding How Nitriles Stabilize Electrolyte/Electrode Interface at High Voltage, J. Phys. Chem. Lett., 2017, 8, 6048–6052 CrossRef CAS PubMed.
- G. Lee, J. W. Kim, H. Park, J. Y. Lee, H. Lee, C. Song, S. W. Jin, K. Keum, C.-H. Lee and J. S. Ha, Skin-Like, Dynamically Stretchable, Planar Supercapacitors with Buckled Carbon Nanotube/Mn–Mo Mixed Oxide Electrodes and Air-Stable Organic Electrolyte, ACS Nano, 2018, 13, 855–866 CrossRef PubMed.
- P. Lv, Y. Li, Y. Wu, G. Liu, H. Liu, S. Li, C. Tang, J. Mei and Y. Li, Robust Succinonitrile-Based Gel Polymer Electrolyte for Lithium-Ion Batteries Withstanding Mechanical Folding and High Temperature, ACS Appl. Mater. Interfaces, 2018, 10, 25384–25392 CrossRef CAS PubMed.
- P. Lv, J. Yang, G. Liu, H. Liu, S. Li, C. Tang, J. Mei, Y. Li and D. Hui, Flexible solid electrolyte based on UV cured polyurethane acrylate/succinonitrile-lithium salt composite compatibilized by tetrahydrofuran, Composites, Part B, 2017, 120, 35–41 CrossRef CAS.
- P. Derollez, J. Lefebvre, M. Descamps, W. Press and H. Fontaine, Structure of succinonitrile in its plastic phase, J. Phys.: Condens. Matter, 1990, 2, 6893–6903 CrossRef CAS.
- C. A. Angell, Relaxation in liquids, polymers and plastic crystals—strong/fragile patterns and problems, J. Non-Cryst. Solids, 1991, 131–133, 13–31 CrossRef CAS.
- K. Geirhos, P. Lunkenheimer, M. Michl, D. Reuter and A. Loidl, Communication: Conductivity enhancement in plastic-crystalline solid-state electrolytes, J. Chem. Phys., 2015, 143, 081101 CrossRef CAS PubMed.
- E. I. Cooper and C. A. Angell, Ambient temperature plastic crystal fast ion conductors (PLICFICS), Solid State Ionics, 1986, 18–19, 570–576 CrossRef CAS.
- M. Jansen, Volume Effect or Paddle-Wheel Mechanism—Fast Alkali-Metal Ionic Conduction in Solids with Rotationally Disordered Complex Anions, Angew. Chem., Int. Ed. Engl., 1991, 30, 1547–1558 CrossRef.
- D. Reuter, P. Lunkenheimer and A. Loidl, Plastic-crystalline solid-state electrolytes: Ionic conductivity and orientational dynamics in nitrile mixtures, J. Chem. Phys., 2019, 150, 244507 CrossRef CAS PubMed.
- Z. Zhang and L. F. Nazar, Exploiting the paddle-wheel mechanism for the design of fast ion conductors, Nat. Rev. Mater., 2022, 7, 389–405 CrossRef.
- P. Derollez, J. Lefebvre and M. Descamps, Neutron diffuse scattering in the plastic phase of succinonitrile, J. Phys.: Condens. Matter, 1990, 2, 9975–9987 CrossRef CAS.
- G. Cardini, R. Righini and S. Califano, Computer simulation of the dynamics of the plastic phase of succinonitrile, J. Chem. Phys., 1991, 95, 679–685 CrossRef CAS.
- S. Das, S. Mitra, J. Combet, R. Mukhopadhyay and A. J. Bhattacharyya, Study of solvent relaxation of pristine succinonitrile and succinonitrile–salt mixtures using quasielastic neutron scattering, Solid State Ionics, 2015, 279, 72–77 CrossRef CAS.
- L. Van Eijck, A. Best, S. Long, F. Fernandez-Alonso, D. MacFarlane, M. Forsyth and G. Kearley, Localized Relaxational Dynamics of Succinonitrile, J. Phys. Chem. C, 2009, 113, 15007–15013 CrossRef CAS.
- W. V. Edwards, A. Berko, A. N. Blacklocks, S. L. P. Savin and A. V. Chadwick, Ionic Transport and Structure in Doped Plastically Crystalline Solids, Z. Phys. Chem., 2012, 226, 409–420 CrossRef CAS.
- P. S. Whitfield, A. Abouimrane and I. J. Davidson, In-situ XRD study of the succinonitrile–lithium bis(trifluoromethylsulfonyl) imide (LiTFSI) phase diagram, Solid State Ionics, 2010, 181, 740–744 CrossRef CAS.
- Y. Shen, G.-H. Deng, C. Ge, Y. Tian, G. Wu, X. Yang, J. Zheng and K. Yuan, Solvation structure around the Li+ ion in succinonitrile–lithium salt plastic crystalline electrolytes, Phys. Chem. Chem. Phys., 2016, 18, 14867–14873 RSC.
- S. Hore, R. Dinnebier, W. Wen, J. Hanson and J. Maier, Structure of Plastic Crystalline Succinonitrile: High-Resolution in situ Powder Diffraction, Z. Anorg. Allg. Chem., 2009, 635, 88–93 CrossRef CAS.
- R. Sasaki, M. Moriya, Y. Watanabe, K. Nishio, T. Hitosugi and Y. Tateyama, peculiarly fast Li-ion conduction mechanism in a succinonitrile-based molecular crystal electrolyte: a molecular dynamics study, J. Mater. Chem. A, 2021, 9, 14897–14903 RSC.
- M. Zachariah, M. Romanini, P. Tripathi, M. Barrio, J. L. Tamarit and R. Macovez, Self-Diffusion, Phase Behavior, and Li+ Ion Conduction in Succinonitrile-Based Plastic Cocrystals, J. Phys. Chem. C, 2015, 119, 27298–27306 CrossRef CAS.
- D. V. Nickel, H. Bian, J. Zheng and D. M. Mittleman, Terahertz Conductivity and Hindered Molecular Reorientation of Lithium Salt Doped Succinonitrile in its Plastic Crystal Phase, J. Infrared, Millimeter, Terahertz Waves, 2014, 35, 770–779 CrossRef CAS.
- K. Tanaka, Y. Tago, M. Kondo, Y. Watanabe, K. Nishio, T. Hitosugi and M. Moriya, High Li-Ion Conductivity in Li{N(SO2F)2}(NCCH2CH2CN)2 Molecular Crystal, Nano Lett., 2020, 20, 8200–8204 CrossRef CAS PubMed.
- S. K. Davidowski, A. R. Young-Gonzales, R. Richert, J. L. Yarger and C. A. Angell, Relation of Ionic Conductivity to Solvent Rotation Times in Dinitrile Plastic Crystal Solvents, J. Electrochem. Soc., 2020, 167, 070553 CrossRef.
- R. Böhmer, K. R. Jeffrey and M. Vogel, Solid-state lithium NMR with applications to the translational dynamics in ion conductors, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87–174 CrossRef.
- A. Kuhn, M. Kunze, P. Sreeraj, H.-D. Wiemhöfer, V. Thangadurai, M. Wilkening and P. Heitjans, NMR relaxometry as a versatile tool to study Li ion dynamics in potential battery materials, Solid State Nucl. Magn. Reson., 2012, 42, 2–8 CrossRef CAS PubMed.
- C. Vinod Chandran and P. Heitjans, Solid-State NMR Studies of Lithium Ion Dynamics Across Materials Classes, Annu. Rep. NMR Spectrosc., 2016, 89, 1–102 CrossRef.
- O. Pecher, J. Carretero-González, K. J. Griffith and C. P. Grey, Materials’ Methods: NMR in Battery Research, Chem. Mater., 2016, 29, 213–242 CrossRef.
- S. Haber and M. Leskes, What Can We Learn from Solid State NMR on the Electrode–Electrolyte Interface?, Adv. Mater., 2018, 30, 1706496 CrossRef PubMed.
- R. Böhmer, M. Storek and M. Vogel, NMR studies of ionic dynamics in solids, in Modern Methods in Solid-State NMR: A Practitioner's Guide, ed. P. Hodgkinson, Royal Society of Chemistry, 2018, ch. 7, pp. 193–230 Search PubMed.
- A. Golemme, S. Zamir, R. Poupko, H. Zimmermann and Z. Luz, Selfdiffusion in the plastic phase of succinonitrile by 2H NMR quadrupole echo train, Mol. Phys., 1994, 81, 569–678 CrossRef CAS.
- R. Böhmer, G. Diezemann, G. Hinze and E. Rössler, Dynamics of supercooled liquids and glassy solids, Prog. Nucl. Magn. Reson. Spectrosc., 2001, 39, 191–267 CrossRef.
- S. K. Davidowski, J. L. Yarger, R. Richert and C. A. Angell, Reorientation Times for Solid State Electrolyte Solvents and Electrolytes from NMR Spin Lattice Relaxation Studies, J. Phys. Chem. Lett., 2020, 11, 3301–3304 CrossRef CAS PubMed.
- W. J. Orville-Thomas, Tables of Experimental Dipole Moments, J. Mol. Struct., 1977, 36, 165–171 Search PubMed.
- S. Lansab, P. Münzner, H. Zimmermann and R. Böhmer, Deuteron nuclear magnetic resonance and dielectric studies of molecular reorientation and charge transport in succinonitrile-glutaronitrile plastic crystals, J. Non-Cryst. Solids: X, 2022, 14, 100097 CAS.
- T. Bauer, M. Köhler, P. Lunkenheimer, A. Loidl and C. A. Angell, Relaxation Dynamics and Ionic Conductivity in a Fragile Plastic Crystal, J. Chem. Phys., 2010, 133, 144509 CrossRef PubMed.
- M. Götz, T. Bauer, P. Lunkenheimer and A. Loidl, Supercooled-liquid and plastic-crystalline state in succinonitrile-glutaronitrile mixtures, J. Chem. Phys., 2014, 140, 094504 CrossRef PubMed.
- D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J.-O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Modelling one- and two-dimensional solid-state NMR spectra, Magn. Reson. Chem., 2001, 40, 70–76 CrossRef.
- D. H. Wu, A. D. Chen and C. S. Johnson, An Improved Diffusion-Ordered Spectroscopy Experiment Incorporating Bipolar-Gradient Pulses, J. Magn. Reson., 1995, 115, 260–264 CrossRef CAS.
- R. Brand, P. Lunkenheimer and A. Loidl, Relaxation dynamics in plastic crystals, J. Chem. Phys., 2002, 116, 10386–10401 CrossRef CAS.
- C. J. F. Böttcher and P. Bordewijk, Theory of Electric Polarization II: Dielectrics in Time-Dependent Fields, Elsevier, Amsterdam, 1978 Search PubMed.
- F. Kremer and A. Schönhals, Broadband Dielectric Spectroscopy, Springer, Berlin, Heidelberg, 2003 Search PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Relaxation Effects in Nuclear Magnetic Resonance Absorption, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- A. Abragam, The Principles of Nuclear Magnetism, Oxford University Press, Oxford, 1961, p. 456 Search PubMed.
- M. J. Zuriaga, R. Hallsworth, R. L. Armstrong, G. A. Monti and C. A. Martín, An NQR and NMR study of solid trichlorofluoromethane, J. Magn. Reson., 1992, 99, 56–65 CAS.
- M. Bee, R. E. Lechner, J. P. Amoureux and R. Fouret, Temperature dependence of rotational isomerisation and molecular reorientation rates in plastic succinonitrile, J. Phys. C: Solid State Phys., 1983, 16, 4973–4983 CrossRef CAS.
- P. A. Beckmann, Spectral densities and nuclear spin relaxation in solids, Phys. Rep., 1988, 171, 85–128 CrossRef.
- H. W. Spiess, in Rotation of Molecules and Nuclear Spin Relaxation, Dynamic NMR Spectroscopy, Springer, Berlin, 1978 Search PubMed.
- G. Diezemann and H. Sillescu, Dipolar interactions in deuteron spin systems. II. Transverse relaxation, J. Chem. Phys., 1995, 103, 6385–6393 CrossRef CAS.
- H. Nelson, A. Ihrig, R. Kahlau, P. Kibies, S. M. Kast and R. Böhmer, Dielectric and deuteron magnetic resonance studies of guest reorientation and defect dynamics in six clathrate hydrates with ring-type guests, J. Non-Cryst. Solids, 2015, 407, 431–440 CrossRef CAS.
- H. Mehrer, Diffusion in Solids, Springer, Berlin, Heidelberg, 2009 Search PubMed.
- R. Rohan, T.-C. Kuo, J.-H. Lin, Y.-C. Hsu, C.-C. Li and J.-T. Lee, Dinitrile–Mononitrile-Based Electrolyte System for Lithium-Ion Battery Application with the Mechanism of Reductive Decomposition of Mononitriles, J. Phys. Chem. C, 2016, 120, 6450–6458 CrossRef CAS.
- B. Geil, Measurement of translational molecular diffusion using ultrahigh magnetic field gradient NMR, Concepts Magn. Reson., 1998, 10, 299–321 CrossRef CAS.
- E. O. Stejskal and J. E. Tanner, Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Fundamental questions relating to ion conduction in disordered solids, Rep. Prog. Phys., 2009, 72, 046501 CrossRef.
- C. Gainaru, S. Ahlmann, L. S. Röwekamp, K. Moch, S. P. Bierwirth and R. Böhmer, Rheology based estimates of self- and collective diffusivities in viscous liquids, J. Chem. Phys., 2021, 155, 011101 CrossRef CAS PubMed.
- J. T. Edward, Molecular Volumes and Stokes-Einstein Equation, J. Chem. Educ., 1970, 47, 261–270 CrossRef CAS.
- M. Storek, K. R. Jeffrey and R. Böhmer, Local-field approximation of homonuclear dipolar interactions in 7Li-NMR: Density-matrix calculations and random-walk simulations tested by echo experiments on borate glasses, Solid State Nucl. Magn. Reson., 2014, 59–60, 8–19 CrossRef CAS PubMed.
- M. Michl, T. Bauer, P. Lunkenheimer and A. Loidl, Nonlinear dielectric spectroscopy in a fragile plastic crystal, J. Chem. Phys., 2016, 144, 114506 CrossRef CAS PubMed.
- A. Lundén, On the paddle-wheel mechanism for cation conduction in lithium sulphate, Z. Naturforsch., A: Phys. Sci., 1995, 11, 1067–1076 CrossRef.
- Z. Xu and Y. Xia, Progress, challenges and perspectives of computational studies on glassy superionic conductors for solid-state batteries, J. Mater. Chem. A, 2022, 10, 11854–11880 RSC.
| This journal is © the Owner Societies 2023 |
