Molecular dynamics and Raman optical activity spectra reveal nucleotide conformation ratios in solution

Abstract

Nucleotide conformational flexibility affects their biological functions. Although the spectroscopy of Raman optical activity (ROA) is well suited to structural analyses in aqueous solutions, the link between the spectral shape and the nucleotide geometry is not fully understood. We recorded the Raman and ROA spectra of model nucleotides (rAMP, rGMP, rCMP, and dTMP) and interpreted them on the basis of molecular dynamics (MD) combined with density functional theory (DFT). The relation between the sugar puckering, base conformation and spectral intensities is discussed. Hydrogen bonds between the sugar's C3′ hydroxyl and the phosphate groups were found to be important for the sugar puckering. The simulated spectra correlated well with the experimental data and provided an understanding of the dependence of the spectral shapes on conformational dynamics. Most of the strongest spectral bands could be assigned to vibrational molecular motions. Decomposition of the experimental spectra into calculated subspectra based on arbitrary maps of free energies provided experimental conformer populations, which could be used to verify and improve the MD predictions. The analyses indicate some flaws of common MD force fields, such as being unable to describe the fine conformer distribution. Also the accuracy of conformer populations obtained from the spectroscopic data depends on the simulations, improvement of which is desirable for gaining a more detailed insight in the future. Improvement of the spectroscopic and computational methodology for nucleotides also provides opportunities for its application to larger nucleic acids.

---

1. Introduction

Nucleotides may fulfill various biological functions depending on their structure.^1–3 Their structural variations affect the conformation and impact nucleotide recognition in living cells, ligand binding, and enzymatic activity. For example, adenosine diphosphate and triphosphate are involved in muscle work and act as an energy pool in many enzymatic processes. Remdesivir, a drug recommended for the treatment of the COVID-19 flu, is metabolized to an adenosine analogue as the active form.⁴ Cyclic adenosine monophosphate serves as a messenger as it controls and mediates activities of peptide hormones. Other nucleotides and oligonucleotides have been widely applied as therapeutic agents, where their biological activity could be manipulated by their chemical modifications.⁵

Apart from the more usual NMR,⁶ solutions’ properties of nucleotides can be conveniently studied using chiroptical spectroscopies, where the spectra are very sensitive to geometry variations. As a standard in the past, electronic circular dichroism (ECD) provides useful information, although the bands corresponding to electronic transitions are not well resolved and are difficult to interpret.⁷ The ECD signal also primarily arises from the nitrogenous base which does not reflect much conformation of the ribose or deoxyribose residues.⁷ Vibrational optical activity (VOA) techniques including vibrational circular dichroism (VCD) and Raman optical activity (ROA) in principle provide more numerous and more resolved bands than ECD. These come from all molecular parts and are better linked to a local molecular structure.⁸

However, although VCD is very sensitive to the structure of oligonucleotides^9–11 and nucleic acids,^12–14 the signal of mononucleotides is rather weak.¹⁵ The aqueous environment and strong water absorption also cause problems for VCD. ROA pursued in the current study is measurable more easily, and a wider region of wavenumbers includes more bands providing information on the conformation of the glycosidic bond, sugar, and the phosphate group. Unlike the one-photon techniques (ECD and VCD), ROA spectroscopy detects a small difference in the scattering of the left and right circularly polarized light. Its reported applications include aqueous solutions of nucleosides, nucleic acids, whole viruses, and other biosystems.^16–18

For some time, interpretation of ROA experiments relied on characteristic spectral markers of similar compounds^19,20 or statistical methods.²¹ Later, it was completed by more universal quantum mechanical computations.^22–24 However, as for oligopeptides and proteins,^25,26 the computations are complicated by nucleotides’ flexibility and polarity. In addition, while protein ROA essentially stems from the peptide backbone,²⁷ more diverse chemical groups are involved in nucleotides. Spectral intensities of aromatic base, sugar, and phosphate may be calculated with different precision and the resultant spectrum is distorted. Below, we need to address this problem specifically for the P=O stretching frequency. For the solvent, simplified dielectric solvent models^28,29 provide only limited accuracy^30,31 and computations explicitly involving the solvent–solute interactions are preferred. For the description of the molecular dynamics, ab initio molecular dynamics and time-dependent approaches^32,33 may be technically superior, but they are currently computationally too demanding for our systems.

In the present study, we are therefore using a combination of (classical) molecular dynamics (MD) and density functional theory (DFT), where solute–solvent clusters are extracted from MD trajectories. Using DFT, after a minimal optimization of geometries, spectral intensities are calculated and many clusters are averaged.^31,34 The spectral analysis can be significantly enhanced by the decomposition of the experimental spectra into the simulated conformer sub-spectra.^35,36 Instead of fitting the conformer populations directly, we use an intermediate fit using an arbitrary energy surface³⁷ that makes it possible to process a large number of clusters (∼1000) at once. The information about conformer populations can also be used to verify and improve MD force fields, although their development goes beyond the topic of this work. Overall, in spite of the approximations involved, the MD/DFT simulations provide an in-depth understanding of the observed Raman and ROA spectral features and they enable us to link spectral intensities to molecular vibrations and thus make the VOA spectroscopy even more useful in understanding the behavior of nucleotides and nucleic acids.

2. Methods

2.1 Spectral measurement

Deoxythymidine 5′-monophosphate disodium salt (dTMP, ≥95%), cytidine 5′-monophosphate disodium salt (rCMP, ≥99%), adenosine 5′-monophosphate (rAMP, ≥97%) and guanosine 5′-monophosphate disodium salt (rGMP, ≥99%) (Fig. 1) were purchased from Sigma-Aldrich and dissolved in deionized water to a concentration of 0.05 mol L⁻¹. This concentration, relatively low for ROA spectroscopy, was used to avoid nucleotide stacking. Solutions’ pH was adjusted to 8 with NaOH to ensure fully deprotonated phosphate groups. Raman and ROA spectra were recorded at 25 °C on a spectrometer located at the Palacký University Olomouc.³⁸ The experiments were performed using scattered circular polarization (SCP) modulation and backscattering geometry (180°). The spectra were recorded in a fused silica cell of 4 mm optical path length (3 mm width), 70 μL sample volume, in a range of 50–4500 cm⁻¹, using 532 nm excitation wavelength, 0.5 s illumination time cycles, and 8 cm⁻¹ resolution. Laser power for the sample was 800 mW and the spectra were recorded for about 30 h. From the Raman spectra, the solvent (H₂O) signal was subtracted, and minor baseline corrections were made.

Fig. 1 Investigated nucleotides, characteristic torsion angles γ, χ, and τ₀ − τ₄ are indicated for dTMP or rCMP, and sugar puckering was defined in a standard way¹ as P = (τ₂ + τ₄ −τ₁ − τ₃)/(3.078 × τ₀) with the amplitude of τ_m = τ₁/cos(P).

2.2 Molecular dynamics (MD)

All MD simulations were carried out within the Amber18 program.³⁹ For rGMP, four different force fields were tested: GAFF,⁴⁰ GAFF2,⁴¹ RNA.OL3,⁴² and DNA.Bsc1.⁴³ GAFF2 was then used as a default. The TIP3P force field⁴⁴ was applied for water. Atomic partial charges were obtained using a standard electrostatic field fitting procedure,⁴⁵ based on ab initio calculations performed at the B3LYP⁴⁶/6-31++G(d,p)/CPCM⁴⁷ level of theory. For all quantum chemistry, we used the Gaussian 16 program.⁴⁸ The nucleotides, sodium counterions, and water were kept in 40³ ų cubic boxes, an NVT dynamics was run at the temperature of 300 K, using 1 fs integration time step, Langevin thermostat with 2 ps⁻¹ collision frequency, particle mesh Ewald method, and 8 Å Lennard-Jones cutoff. After 1 ns equilibration, production runs at least 7 ns long followed, the trajectories were analyzed using the cpptraj module of Amber18, and intramolecular H-bonds were counted using 3 Å distance between heavy atoms and 135° angle cutoffs. In addition to unrestricted MD, dependencies of the free energy on two torsion angles were obtained using the weighted histogram analysis method (WHAM).⁴⁹ In this case, angles χ and γ were incremented by 36°, harmonic force constants of 3 kcal mol⁻¹ rad² were applied, and 1 ns trajectories were investigated.

2.3 Simulated Raman and ROA spectra

The spectra were computed for MD snapshot geometries by default for every 10 ps. From the free dynamics, the spectra of 100–700 snapshots were averaged as specified below, waters farther than 3.6 Å from the nucleotides were deleted, and the remaining clusters partially optimized in normal mode coordinates^50,51 at the B3PW91⁵²/6-31++G**/CPCM level. At the same level, harmonic Raman and ROA intensities were calculated, with polarizability derivatives related to the water molecules set to zero. The B3PW91 functional provided reasonable results for ROA earlier^27,53 and in trial computations gave almost same results as the more common B3LYP functional (Fig. S1, ESI†). The intensities were convoluted with Lorentzian bands of 10 cm⁻¹ full width at half-height. The calculated frequency of the phosphate symmetric stretching band was significantly lower than observed. Therefore, the P=O bond force constants were scaled to match the experiment, using a protocol previously used for the C=O bonds.⁵⁴ For comparison with the experiment, resultant frequencies were scaled by 0.98.

2.4 Spectral fitting and decomposition algorithm

The frequency scaling enabled us to directly decompose an experimental spectrum S into subspectra S_i of many snapshots,where ν is the frequency. In the decomposition, the coefficients c_i were expressed using arbitrary free energy maps as described in ref. 37, and current implementation is schematically overviewed in Fig. 2. The χ and γ angles (Fig. 1) served as the arbitrary variables, and we set the coefficients to c_i = exp(−ΔG_i/kT), where kT is the Boltzmann temperature quantum, and , where g₁ = 1, g₂(x) = sin(x), g₃(x) = cos(x), g₄(x) = sin(2x), g₅(x) = cos(2x), etc. By default, we used m = 5. Then we minimized the error as a function of the coefficients d_ab, and the integration ran from 200 to 1800 cm⁻¹. Integrating the resultant probability p(χ,γ) = exp(−ΔG/kT) over the relevant coordinates, we could determine the relative populations of conformers I–VI defined below.

Fig. 2 The process of fitting an experimental spectrum with MD snapshot spectra, for two-dimensional arbitrary maps.

The algorithm described above requires geometries with evenly spaced coordinates.³⁷ Differently populated parts of the (χ,γ) coordinate plane would contribute differently to the error. The MD snapshots, however, are concentrated around energy-favored coordinates. Therefore, 400 intermediate (arbitrary) spectra (S_i) were calculated and used in the decomposition instead. Each intermediate spectrum corresponded to a point (χ_i,γ_i) on a grid in the plane (angle increment δ = 18°, 20 × 20 points). If some MD geometries in the (χ_i − δ/2,χ_i + δ/2) × (γ_i - δ/2,γ_i + δ/2) square were available, the arbitrary spectrum was calculated as an average of these clusters. Otherwise, MD geometry and spectrum closest to (χ_i,γ_i) were taken.

For the decomposition, MD snapshots (typically more than 1000) were taken from the WHAM computations covering a large portion of the conformational space. For the fitting, explicit water molecules were not included in computations of the spectra, which cause only minor differences in Raman and ROA spectral intensities (Fig. S2, ESI†). Raman bands that could be unambiguously assigned were shifted to the experimental positions, and frequencies between them interpolated. Note that although for an ideal case, true maps of free energies are obtained using this procedure,³⁷ given the approximation used we take them as intermediate constructs of the fitting procedure corresponding to the exact dependencies only approximately.

3. Results and discussion

3.1 Effect of the force fields on rGMP geometry and spectra

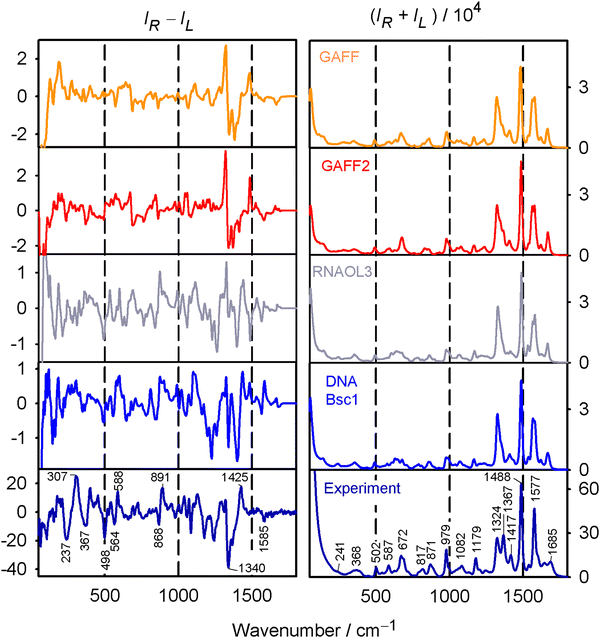
The rGMP conformation was rather sensitive to the force field variant used; distributions of sugar puckering, χ angle, and puckering amplitude obtained with the GAFF, GAFF2, RNA.OL3 and DNA.Bsc1 force field are plotted in Fig. 3. GAFF and GAFF2 both favor the anti conformer (χ ∼ 180°), in line with NMR observations.⁵⁵ However, they give different sugar puckerings, where for GAFF, all values are rather equally possible, while GAFF2 prefers the C3′-endo pucker with P ∼ 0°. The RNA.OL3 and DNA.Bsc1 results are similar, and both force fields favor the syn conformer (χ ∼ 60°) and C2′-endo pucker (P ∼ 180°). As discussed elsewhere⁵⁶ the χ angle affects the occurrences of intramolecular hydrogen bonds. For example, for GAFF, the C'OH⋯OP hydrogen bond was present in 25% of the snapshots analyzed, while GAFF2 gave 70%. The puckering amplitude (τ_m) occurs most often around 33° for GAFF; for the other three force fields, the amplitude is higher (∼39°) and its distribution is narrower. In Table S1 (ESI†) are provided some hints of the differences between the four force fields; supposedly variations of the torsion angle parameters affect the conformer ratios most strongly.

Fig. 3 Calculated probabilities p of puckering P, torsion angle χ, and amplitude τ_m for rGMPs and GAFF, GAFF2, RNA.OL3 and DNA.Bsc1 force fields.

The geometry variations are reflected in the average spectra calculated using the four force fields. In the Raman (Fig. 4, right) spectra, the variations are rather subtle. For example, the experimentally observable doublet 1324/1367 cm⁻¹ is best reproduced with the GAFF2 force field, although the calculated splitting is still limited. ROA spectra (Fig. 4, left) differ much more and no force field gives satisfactory agreement with the experiment. GAFF and GAFF2 give well the 1340 cm⁻¹ experimental negative band and the trends in the signal below 300 cm⁻¹; the ±868/891 cm⁻¹ bands are reasonably obtained only by RNA.Ol3, for the ±564/588 cm⁻¹ couplet, DNA.Bsc1 works best, etc. The reasonable agreement of the computed Raman spectra and a worse one for ROA suggest that no force field gives very realistic conformer distribution of rGMP. We choose the GAFF2 force field as an advanced alternative of GAFF as a default. The RNA.Ol3 and DNA.Bsc1 force fields might be biased towards canonical nucleic acid geometries.

Fig. 4 Calculated and experimental Raman (I_R+ I_L) and ROA (I_R − I_L) spectra of rGMP. Calculated averages from 100 snapshots obtained with four force fields (GAFF, GAFF2, RNA.OL3 and DNA.Bsc1) are shown, with explicit water molecules, and frequencies are scaled by 0.98.

3.2 Nucleotide conformers

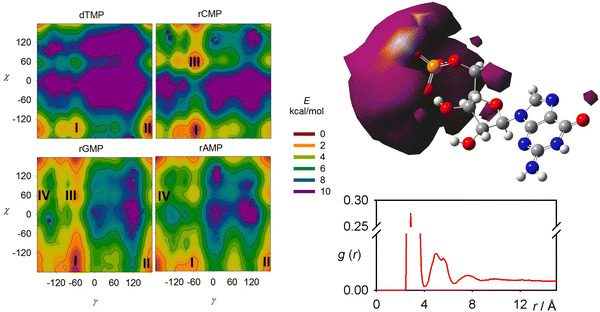
The pyrimidine nucleotides (dTMP, rCMP) behave slightly differently from those derived from purine (rGMP, rAMP). The calculated dependencies of the free energy on the γ and χ angles are plotted in Fig. 5, left, and the parameters for selected energy minima are listed in Table S2 (ESI†). The χ torsion angle determines the position of the base to the sugar and most often adopts two values, syn (χ ∼ 80°) and anti (χ ∼ 180°); the angle γ adopts about three values (g⁺/g⁻/t ∼ 60°/−60°/± 180°).^57,58 Perhaps contra-intuitively, the smaller pyrimidine residues in dTMP and rCMP make larger areas energetically forbidden (e.g., with E > 10 kcal mol⁻¹) in these plots. For dTMP, the most favored conformer II is anti/t, for rCMP, it is anti/g⁻ (I), both in agreement with the crystal structure.⁵⁹ The anti/g⁻ most populated conformer I of rGMP is consistent with ref. 55, and the preference of rAMP for anti/t (I) corresponds to the X-ray.⁵⁹ Nevertheless, the simulations strongly suggest that for all nucleotides, multiple conformers/conformer classes are present in solutions.

Fig. 5 (left) Dependence of the free energy on the torsion angles χ and γ (in degrees) as obtained from the metadynamics, (right) 3-D distribution of the sodium counterions around rGMP and the corresponding radial distribution function related to P and Na atoms. The purple surface encloses the region with elevated Na⁺ concentration.

An average distribution of the sodium ions around the molecule and the radial distribution function related to sodium and phosphorus as obtained by MD is for rGMP documented in Fig. 5, right. The probability to encounter a sodium molecule in the vicinity of the phosphate group is higher than elsewhere, and some ions are momentarily bonded to it. However, such vicinity involves relatively small volume, and most sodium atoms freely float in the solution. In our (40 Å)³ box, only about 6% of the sodium atoms stayed closer than 4 Å to phosphorus. This justifies the approach used in the calculation of the nucleotide spectra where sodium atoms were included in MD and were then only included implicitly in DFT, as a part of the dielectric environment.

3.3 Intramolecular hydrogen bonds

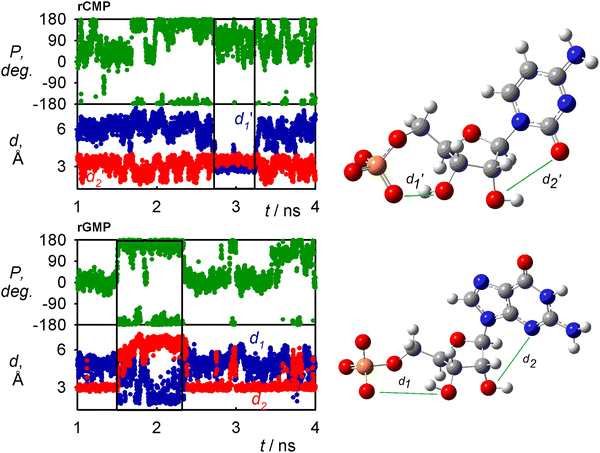
The nucleotide conformation is also given by a fine equilibrium between intra and inter-molecular hydrogen bonds. The occurrence of snapshots where internal hydrogen bonds are formed as obtained by MD is for GAFF2 summarized in Table 1. The H-bonds somewhat correlate with the conformation of the sugar, which is shown for rGMP and rCMP in Fig. 6 where H-bond distances and sugar puckering as functions of time are plotted. Time dependencies of other coordinates for all four nucleotides are shown in Fig. S3 (ESI†). The C1′-exo (P ∼ 110°) conformation of rCMP appears during the C3′O⋯OP H-bonding, but the correlation is not particularly strong. It is stronger for rGMP, where the C3′O⋯OP interaction (small d₁) stabilizes the sugar in the C2′-endo (P∼180°) form; at the same time, H-bonding between C2′OH and the base is broken (increase of d₂).

Table 1 Percentages of MD snapshots with detected intramolecular hydrogen bonds

H-bond	dTMP	rCMP	rGMP	rAMP
C3′OH⋯OP	74	44	45	4
C2′OH⋯OC3′	—	11	3	3
C3′OH⋯OC2′	—	6	—	2
C2′OH⋯OC6′	—	4	—	—
C2′OH⋯N3	—	—	11	9
None	26	35	41	82

---

Fig. 6 Time dependence of the C3′O⋯OP (d₁,d₁′) and C2′O⋯N3/OC3′ (d₂,d₂′) distances (left) and sugar pucker (right), for rCMP and rGMP. The C2′O H-bonding with the base (small d₂, d₂′) in rGMP stabilizes C2′-endo (P ∼ 180°), and for rCMP, the correlation is not so tight.

A very frequent (74%, Table 1) H-bonding between the PO and C3′ hydroxyl groups of dTMP results in the “east type” sugar conformations with P ∼ 100°.¹ In rAMP, the C2′OH⋯N3 H-bond occurs in 9% of the snapshots, and the overall low percentage of intramolecular hydrogen bonds makes possible an even distribution of the C2′-endo and C3′-endo conformations. Other relations among the principle coordinates (pseudorotation angle P, angles χ, γ, β) can be seen in conformer populations recalculated to the free energy maps in Fig. S4 (ESI†). As in Fig. 5 for χ and γ, the maps also confirm that the nucleotides have many degrees of freedom, but the coordinates are correlated, and a limited number of distinct conformers exist in solutions.

3.4 Spectral fitting and conformer ratios

The experimental Raman and ROA spectra of all four nucleotides are compared to the simulated ones in Fig. 7. A plain average from the GAFF2 MD snapshots is shown along with the fit where the calculated frequencies were scaled. Assignments of the main Raman and ROA bands are summarized in Table S3 (ESI†). For rGMP, the calculated spectra from 700 snapshots (Fig. 7) are reasonably close to those obtained with 100 snapshots (Fig. 4), which shows that little improvement would be achieved with longer MD/more geometries. This is also indicated by Fig. S5 (ESI†), top, where for rGMP, spectra generated from 7 ns, and 1 μs MD runs differ by less than ∼15% in maximal intensities. For rAMP, similarly as for rGMP, 100 snapshots averaging produced quite similar spectra as for the 700 snapshots (Fig. S5, ESI†, bottom).

Fig. 7 Raman (I_R+ I_L) and ROA (I_R − I_L) spectra of studied nucleotides, plain average from 700 MD snapshots (blue), a fit (red), and experiment (black). The calculated spectra were normalized to the strongest Raman band, and similarity indices⁶⁰ between scaled calculated and experimental spectra, , are indicated for the integrals within 200–1900 cm⁻¹.

The plain snapshot averaging (blue in Fig. 7) well-reproduces the main Raman features and also Raman spectra differences among the four nucleotides. This is also reflected in the high values of the similarity indices⁶⁰ (>0.85), which are equal to one for identical spectra. A band-to-band assignment is nevertheless problematic in the region around 1300 cm⁻¹ with a large number of vibrational modes, most frequently related to CH bending (Table S3, ESI†). As expected for the vibrational optical activity,⁶¹ the similarity indices are much lower for ROA (0.42–0.60), although the main ROA spectral features are reproduced by the computations as well. As discussed in detail for rGMP (Fig. 4), inconsistencies occur in particular below 1300 cm⁻¹; for dTMP, for example, ROA below 150 cm⁻¹ is negative, while the simulation gives a bisignate pattern, and the experimental positive band at 1228 cm⁻¹ is not reproduced, etc. Overall, however, the accuracy is reasonable and corresponds to that achieved for similarly complex (flexible and polar) molecules.^34,62 Interesting is also the large low-frequency ROA, close to the 50 cm⁻¹ instrumental limit, where the parent Raman spectra are virtually featureless and start to diverge towards the Rayleigh line. Similar ROA bands were previously observed for sugars,⁶³ peptides⁶⁴ and chiral liquids,⁶⁵ and seem to provide interesting, although still relatively unexplored, possibility to expand ROA structural studies.

The fitted ROA spectra (red in Fig. 7) are closer to the experiment than the plain average. This is not always true for the Raman spectra, indicating some benefits of the explicit water model used for the MD averaged (blue) spectra. The conformer populations obtained from MD and from the fit of the Raman and ROA spectra with calculated subspectra are listed in Table 2. As discussed before, Raman spectra are rather independent of the conformation, and conformer populations derived from them may be less reliable than for ROA.^36,63 The limited sensitivity of Raman intensities can be also seen in Fig. S6 (ESI†), where calculated spectra of individual conformers are compared. Nevertheless, the Raman results significantly differ from the ROA populations only for rAMP. For dTMP, there is a large discrepancy between the MD and ROA I : II conformer ratios (8 : 92 vs. 54 : 46), suggesting that the GAFF2 force field may not be appropriate for this molecule. For rCMP, the experimental conformer ratios almost copy the MD results, within the expected accuracy of the fitting/decomposition process (∼10–20%).^35,36,66 A large difference also appears for conformers of rGMP, e.g., 68% of I with WHAM, while both Raman and ROA give 6%. For rAMP, the ROA and MD conformer populations are closer.

Table 2 Conformer populations obtained from WHAM (%), and decomposition of Raman and ROA spectra, see also Fig. 5 and Table S2 (ESI) for the conformer definition

Conformer	γ/°	χ/°	Populations (%)
			MD, WHAM	Fit, Raman	Fit, ROA
dTMP
I	−57	−147	8	54	54
II	177	−149	92	46	46
rCMP
I	−57	179	75	82	69
III	−57	63	25	18	31
rGMP
I	−61	−177	68	6	6
II	−177	179	24	60	59
III	−59	61	6	2	4
IV	−177	63	2	32	31
rAMP
I	−179	179	16	47	29
II	−65	179	79	33	66
IV	179	67	5	20	5

---

Although the arbitrary dependencies of the free energies on the (γ,χ) angles obtained during the spectral fitting are hampered by the computational errors, some similarities with those obtained by WHAM indicate that they are partially realistic (Fig. S7, ESI†). The free energy maps obtained from ROA spectra are closer to the MD/WHAM results, confirming that the conformational predictions based on ROA are more reliable than for Raman spectra. As follows also from Table 2, in some cases, the MD and spectra-derived conformer populations differ a lot, and the energy minima obtained by the two approaches do not have the same coordinates. Overall, the spectral analysis in light of the theoretical simulations suggests rather inadequate conformer distribution obtained from MD, and although the accuracy of the numbers obtained from the fitting is also limited, it provides enormous potential to study potential energy surfaces of molecules in solutions.

3.5 Spectra and local molecular structure

Similarly as for nucleosides,¹⁶ the nucleotide ROA spectrum can be roughly divided in regions sensitive to coupling of the sugar ring and the base (∼1200–1600 cm⁻¹), sugar puckering (∼900–1200 cm⁻¹), and sugar and base deformations (<900 cm⁻¹). The (PO₃)²⁻ group stretching contributes to the signal around 1150 cm⁻¹, with weak ROA. Conformation of the glycosidic bond itself is reflected by many ROA bands; its effect on the strongest bands for rGMP in the 1300–1500 cm⁻¹ region is shown in Fig. 8. The comparison with the experiment suggests that the syn conformer with a positive signal around 1380 cm⁻¹ is significantly present in the sample, but not dominant, in accordance with the MD and spectra analyses (Table 2). Similar comparison can be done in other spectral regions and for other nucleotides (Fig. S8, ESI†), which on one side documents the enormous sensitivity of ROA to the conformation and on the other one also shows the limits of the contemporary methodology. In particular, better precision of the simulation would be desirable to increase the effective spatial resolution of this kind of spectroscopy.

Fig. 8 Calculated ROA spectra of the four rGMP conformers (MD average, frequency multiplied by 0.98) and the experiment.

To understand the nucleotide spectral origin more deeply, in a computer experiment, the intensity tensors (polarizability derivatives)⁶⁷ for different molecular parts were set to zero. Thus approximate contributions of nucleotides’ chromophores and interactions to Raman and ROA signals could be estimated for rGMP, as shown in Fig. 9. From the left side of the figure, we see that in the entire spectral region, the signal of the aromatic base dominates in the Raman spectrum, except for the phosphate band at 1007 cm⁻¹. In spite of its inherent achirality (planarity), the base also provides large ROA contributions. However, the ROA signal becomes much bigger when interaction between the chromophores is enabled by including polarizabilities from the base and sugar, or from the phosphate and sugar (right side of the figure). In particular, the base–sugar interaction gives rise to strong positive and negative bands around 1350 cm⁻¹. These bands are caused by the base and sugar CH bending modes, and their coupling also explains the ROA sensitivity to the variation of the χ angle (Fig. 8).

Fig. 9 Raman and ROA spectral contributions calculated for rGMP, and average from 700 MD snapshots. Except for the indicated molecular parts, atomic polarizabilities were set to zero, and Raman spectra below 1320 cm⁻¹ are multiplied by 5 for better visibility.

We did not attempt to analyze the lowest-frequency (<100 cm⁻¹) ROA signal, because of its complexity and extensive computer demands needed.⁶⁵ Nevertheless, the experimental spectra plotted in the full range (Fig. S9, ESI†) also show in this region significant differences between the nucleotides; this signal is particularly strong for rAMP, stronger than in any other wavenumber region. Also the CH stretching Raman and ROA bands (∼2900 cm⁻¹) provide so far limited information, as they are weak and prone to error in experiment, and eventual simulation would require rather expensive computations involving anharmonic corrections.³⁸ As explained before,⁶³ ROA in the OH/NH stretching region (>3000 cm⁻¹) cannot be measured reliably, due to the large Raman scattering of water. Maybe in the future, it can provide some information about the molecular hydration shell.

4. Conclusions

We measured and analyzed the Raman and ROA spectra of four common nucleotides to investigate the link of the spectral shapes to the geometry, and to probe the quality of the molecular dynamics force fields and spectral simulation techniques. The results appeared helpful in the effort to better understand the nucleotide conformational behavior and to develop the spectroscopy of vibrational optical activity as a universal tool in molecular structural studies.

An analysis of molecular dynamics trajectories revealed that sugar puckering was strongly dependent on intramolecular H-bonding, which differed in different nucleotides. In dTMP, H-bonding between the PO and C3′ hydroxyl groups stabilized the sugar-pucker in C1′-exo conformation. The H-bonding was less extended in rAMP where it allowed for an equilibrium of the C2′-endo and C3′-endo sugar conformation.

The conformer distribution obtained from molecular dynamics combined with DFT provided a reasonable basis to interpret the experimental spectra. Raman and ROA bands were assigned, which was useful for monitoring the conformation of the base and sugar puckering. The phosphate group gave a rather weak ROA signal. The decomposition of the experimental spectra into the theoretical ones indicated further potential of the optical spectroscopy, where in principle the true molecular potential energy surface can be obtained. However, the procedure currently has a drawback of the limited precision of the molecular dynamics and DFT computations. Nevertheless, Raman optical activity already appears as a useful tool for the study of the solution structure of nucleic acid components.

Author contributions

V. S., M. S. P. K. and J. K. were involved in data acquisition, analysis, computations, and data analysis. J. K. and P. B. were involved in conceptualization, methodology and software development. All authors participated in writing and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Grant Agency (22-04669S) and the Ministry of Education (CZ.02.1.01/0.0/0.0/16_019/0000729 and LM2018140) of the Czech Republic.

References

1. C. Altona and M. Sundaralingam, J. Am. Chem. Soc., 1972, 94, 8205–8212.
2. M. Evich, A. M. Spring-Connell and M. W. Germann, Heterocycl. Commun., 2017, 23, 155–165.
3. L. M. Alvarez-Salas, Curr. Top. Med. Chem., 2008, 8, 1379–1404.
4. S. M. Hashemian, T. Farhadi and A. A. Velayati, Drug Des. Devel. Ther., 2020, 14, 3215–3222.
5. T. C. Roberts, R. Langer and M. J. A. Wood, Nat. Rev. Drug Discov., 2020, 19, 673–694.
6. M. Ebrahimi, P. Rossi, C. Rogers and G. S. Harbison, J. Magn. Reson., 2001, 150, 1–9.
7. C. A. Sprecher and W. C. Johnson Jr., Biopolymers, 1977, 16, 2243–2264.
8. L. Nafie, Vibrational optical activity: Principles and applications, Wiley, Chichester, 2011.
9. S. S. Birke, M. Moses, M. Gulotta, B. Kagarlovsky, D. Jao and M. Diem, Biophys. J., 1993, 65, 1262–1271.
10. V. Andrushchenko, D. Tsankov, M. Krasteva, H. Wieser and P. Bouř, J. Am. Chem. Soc., 2011, 133, 15055–15064.
11. V. Andrushchenko and P. Bouř, Chirality, 2010, 22, E96–E114.
12. L. Wang and T. A. Keiderling, Biochemistry, 1992, 31, 10265–10271.
13. L. J. Wang, P. Pančoška and T. A. Keiderling, Biochemistry, 1994, 33, 8428–8435.
14. A. M. Polyanichko, V. V. Andrushchenko, E. V. Chikhirzhina, V. I. Vorobev and H. Wieser, Nucleic Acids Res., 2004, 32, 989–996.
15. A. Annamalai and T. A. Keiderling, J. Am. Chem. Soc., 1987, 109, 3125–3132.
16. A. F. Bell, L. Hecht and L. D. Barron, J. Chem. Soc., Faraday Trans., 1997, 93, 553–562.
17. A. F. Bell, L. Hecht and L. D. Barron, J. Am. Chem. Soc., 1998, 120, 5820–5821.
18. E. W. Blanch, L. Hecht, C. D. Syme, V. Volpetti, G. P. Lomonossoff, K. Nielsen and L. D. Barron, J. Gen. Virol., 2002, 83, 2593–2600.
19. A. J. Hobro, M. Rouhi, E. W. Blanch and G. L. Conn, Nucleic Acids Res., 2007, 35, 1169–1177.
20. L. D. Barron, E. W. Blanch, I. H. McColl, C. D. Syme, L. Hecht and K. Nielsen, Spectrosc. Int. J., 2003, 17, 101–126.
21. F. J. Zhu, N. W. Isaacs, L. Hecht and L. D. Barron, Structure, 2005, 13, 1409–1419.
22. P. L. Polavarapu, T. M. Black, L. D. Barron and L. Hecht, J. Am. Chem. Soc., 1993, 115, 7736–7742.
23. T. Helgaker, K. Ruud, K. L. Bak, P. Joergensen and J. Olsen, Faraday Discuss., 1994, 99, 165–180.
24. K. Ruud, T. Helgaker and P. Bouř, J. Phys. Chem. A, 2002, 106, 7448–7455.
25. C. Herrmann, K. Ruud and M. Reiher, Chem. Phys. Chem., 2006, 7, 2189–2196.
26. J. Hudecová, J. Horníček, M. Buděšínský, J. Šebestík, M. Šafařík, G. Zhang, T. A. Keiderling and P. Bouř, Chem. Phys. Chem., 2012, 13, 2748–2760.
27. J. Kessler, J. Kapitán and P. Bouř, J. Phys. Chem. Lett., 2015, 6, 3314–3319.
28. B. Roux and T. Simonson, Biophys. Chem., 1999, 78, 1–20.
29. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
30. P. Bouř, D. Michalík and J. Kapitán, J. Chem. Phys., 2005, 122, 144501.
31. K. H. Hopmann, K. Ruud, M. Pecul, A. Kudelski, M. Dračínský and P. Bouř, J. Phys. Chem. B, 2011, 115, 4128–4137.
32. M. Brehm and M. Thomas, J. Phys. Chem. Lett., 2017, 8, 3409–3414.
33. A. Baiardi, J. Bloino and V. Barone, J. Chem. Theory Comput., 2018, 14, 6370–6390.
34. J. R. Cheeseman, M. S. Shaik, P. L. A. Popelier and E. W. Blanch, J. Am. Chem. Soc., 2011, 133, 4991–4997.
35. M. Buděšínský, P. Daněček, L. Bednárová, J. Kapitán, V. Baumruk and P. Bouř, J. Phys. Chem. A, 2008, 112, 8633–8640.
36. J. Jungwirth, J. Šebestík, M. Šafařík, J. Kapitán and P. Bouř, J. Phys. Chem. B, 2017, 121, 8956–8964.
37. V. Parchaňský, J. Kapitán, J. Kaminský, J. Šebestík and P. Bouř, J. Phys. Chem. Lett., 2013, 4, 2763–2768.
38. P. Michal, R. Čelechovský, M. Dudka, J. Kapitán, M. Vůjtek, M. Berešová, J. Šebestík, K. Thangavel and P. Bouř, J. Phys. Chem. B, 2019, 123, 2147–2156.
39. D. A. Case, I. T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, J. K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
40. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
41. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
42. M. Zgarbová, M. Otyepka, J. Šponer, A. Mládek, P. Banáš, T. E. Cheatham, III and P. Jurečka, J. Chem. Theory Comput., 2011, 7, 2886–2902.
43. I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Nat. Methods, 2016, 13, 55–58.
44. W. L. Jorgensen, J. Chandrasekhar and J. D. Madura, J. Chem. Phys., 1983, 79, 926–935.
45. W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollman, J. Am. Chem. Soc., 1993, 115, 9620–9631.
46. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
47. Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77.
48. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Gaussian, Inc., Wallingford, CT, 2016.
49. S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021.
50. P. Bouř and T. A. Keiderling, J. Chem. Phys., 2002, 117, 4126–4132.
51. J. Hudecová, K. H. Hopmann and P. Bouř, J. Phys. Chem. B, 2012, 116, 336–342.
52. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
53. J. Kessler, S. Yamamoto and P. Bouř, Phys. Chem. Chem. Phys., 2017, 19, 13614–13621.
54. A. Kurochka, J. Průša, J. Kessler, J. Kapitán and P. Bouř, Phys. Chem. Chem. Phys., 2021, 16635–16645.
55. F. E. Evans and R. H. Sarma, J. Biol. Chem., 1975, 250, 1290–1296.
56. N. Foloppe, B. Hartmann, L. Nilsson and A. D. MacKerell, Biophys. J., 2002, 82, 1554–1569.
57. J. Šponer, P. Banáš, P. Jurečka, M. Zgarbová, P. Kührová, M. Havrila, M. Krepl, P. Stadlbauer and M. Otyepka, J. Phys. Chem. Lett., 2014, 5, 1771–1782.
58. W. Saenger, Principles of Nucleic Acid Structure, Springer-Verlag, New York, 1984.
59. M. Sundaralingam, Ann. N. Y. Acad. Sci., 1975, 255, 3–42.
60. E. Debie, E. De Gussem, R. K. Dukor, W. Herrebout, L. A. Nafie and P. Bultinck, Chem. Phys. Chem., 2011, 12, 1542–1549.
61. P. L. Polavarapu and E. Santoro, Nat. Prod. Rep., 2020, 37, 1661–1699.
62. V. Palivec, V. Kopecký, P. Jungwirth, P. Bouř, J. Kaminský and H. Martinez-Seara, Phys. Chem. Chem. Phys., 2020, 22, 1983–1993.
63. V. Palivec, P. Michal, J. Kapitán, H. Martinez-Seara and P. Bouř, Chem. Phys. Chem., 2020, 21, 1272–1279.
64. S. Yamamoto, S. Ishiro, J. Kessler and P. Bouř, Phys. Chem. Chem. Phys., 2021, 23, 26501–26509.
65. P. Michal, J. Kapitán, J. Kessler and P. Bouř, Phys. Chem. Chem. Phys., 2022, 24, 19722–19733.
66. J. Šugar and P. Bouř, J. Raman Spectr., 2016, 47, 1298–1303.
67. L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, UK, 2004.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05756e

---