Open Access Article
Open Access ArticleAnion and ether group influence in protic guanidinium ionic liquids†
Daniel
Rauber
 *a,
Frederik
Philippi
*a,
Frederik
Philippi
 b,
Julian
Becker
b,
Julian
Becker
 b,
Josef
Zapp
c,
Bernd
Morgenstern
a,
Björn
Kuttich
d,
Tobias
Kraus
b,
Josef
Zapp
c,
Bernd
Morgenstern
a,
Björn
Kuttich
d,
Tobias
Kraus
 ad,
Rolf
Hempelmann
ad,
Rolf
Hempelmann
 a,
Patricia
Hunt
a,
Patricia
Hunt
 be,
Tom
Welton
be,
Tom
Welton
 b and
Christopher W. M.
Kay
*af
b and
Christopher W. M.
Kay
*af
aDepartment of Chemistry, Saarland University, Campus B 2.2, 66123 Saarbrücken, Germany. E-mail: daniel.rauber@uni-saarland.de
bDepartment of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, London W12 0BZ, UK
cPharmaceutical Biology, Saarland University, Campus B 2.3, 66123 Saarbrücken, Germany
dINM-Leibniz Institute for New Materials, Campus D2.2, 66123 Saarbrücken, Germany
eSchool of Chemical and Physical Sciences, Victoria University of Wellington, New Zealand
fLondon Centre for Nanotechnology, University College London, 17-19 Gordon Street, London WC1H 0AH, UK. E-mail: c.kay@ucl.ac.uk
First published on 3rd February 2023
Abstract
Ionic liquids are attractive liquid materials for many advanced applications. For targeted design, in-depth knowledge about their structure–property-relations is urgently needed. We prepared a set of novel protic ionic liquids (PILs) with a guanidinium cation with either an ether or alkyl side chain and different anions. While being a promising cation class, the available data is insufficient to guide design. We measured thermal and transport properties, nuclear magnetic resonance (NMR) spectra as well as liquid and crystalline structures supported by ab initio computations and were able to obtain a detailed insight into the influence of the anion and the ether substitution on the physical and spectroscopic properties. For the PILs, hydrogen bonding is the main interaction between cation and anion and the H-bond strength is inversely related to the proton affinity of the constituting acid and correlated to the increase of 1H and 15N chemical shifts. Using anions from acids with lower proton affinity leads to proton localization on the cation as evident from NMR spectra and self-diffusion coefficients. In contrast, proton exchange was evident in ionic liquids with triflate and trifluoroacetate anions. Using imide-type anions and ether side groups decreases glass transitions as well as fragility, and accelerated dynamics significantly. In case of the ether guanidinium ionic liquids, the conformation of the side chain adopts a curled structure as the result of dispersion interactions, while the alkyl chains prefer a linear arrangement.
Introduction
Ionic liquids are a unique and versatile class of liquid materials. Such low temperature ionic fluids can be considered as the link between molecular liquids and conventional (high temperature) molten salts, resulting in a unique combination of beneficial properties. These characteristics commonly include and combine negligible volatility, intrinsic ionic conductivity and high electrochemical stability. Due to this singular combination of features ionic liquids are of much interest for fundamental research1 as well as practical applications, ranging from additives used in low amount to large scale processes in industry.2 Exemplary uses of ionic liquids include electrochemical energy storage and conversion devices,3,4 lubrication,5 or their utilization in the exploitation of sustainable resources.6 For the enhancement or optimization of existing technologies by the implementation of ionic liquids as well as for the development of new applications utilizing the characteristics of ionic liquids, knowledge about the fluids' property combination is important to find the representative to best suit a given application. Therefore, studies about the structure–property relationships in the ionic liquids are needed to gain insight into the influence of molecular structure, conformations and underlying intermolecular forces and how they influence the macroscopic properties.Sophisticated investigations on the interrelations of structure and properties of ionic liquids are required as the amount of possible ionic liquids has been estimated to exceed those of molecular solvents by several orders of magnitude.7 Detailed knowledge about structure–property relations is even more required as the intermolecular interactions in ionic liquids are multifaceted and intricate. These microscopic interactions include van der Waals and Coulombic forces as well as hydrogen bonds which differ in their strength and directionalty. In addition to electrostatic forces the flexibility of the ions, geometric factors and the formation of aggregates on different spatial and time scales also influence structure and dynamics of ionic liquids.
In practice, the main limitations of bulk ionic liquids are their melting point and viscosity as they are usually desired to be in liquid state and highly fluid. These characteristics are required frequently in electrochemical devices, such as rechargeable batteries3 or supercapacitors,8 to allow for operation in broad temperature ranges and with fast charging and discharging rates. Both the solidification temperature and the transport properties are strongly influenced by the choice of ion, particularly ions with high conformational flexibility, i.e. low energy barriers between different conformers of minimum energy are used to optimize these characteristics.9,10 Ether groups are commonly applied in the side chains of the organic cations in ionic liquids or flexible anions such as those of the imide-type that can exist in cis and trans configuration of the C–S⋯C–S dihedral angle.9,11
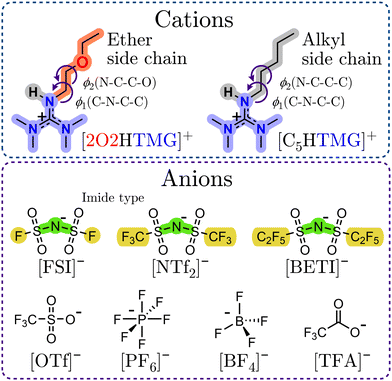
Besides the investigation of the influence of functional groups, it is also possible to alter the properties of ionic liquids by changing the type of cation. However, literature investigations on ionic liquid properties are mainly limited to a few established, often commercially available representatives, almost exclusively with imidazolium, pyridinium, ammonium and phosphonium cations. Accordingly, the investigation of other cation-types can broaden the spectrum of possible properties and applications. In this contribution we report the synthesis and properties of novel guanidinium ionic liquids based on the tetramethylguanidinium (TMG) cation with an ether group in the 2-ethoxy-ethyl (2O2) side group. To investigate the influence of the ether group in the side chain we also included samples with a pentyl side group (C5), where the oxygen atom is replaced by a methylene unit. The molecular structures and abbreviations are given in Fig. 1.
These investigated protic ionic liquids (PILs) derive from the superbase 1,1,3,3-tetramethylguanidine (pKa ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [HHTMG]+
[HHTMG]+ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = 13.6 in aqueous solution12) and are obtained by proton transfer from the corresponding free acid of the desired anion to the free base. Compared to aprotic ionic liquids (AILs), which are often formed by anion metathesis, the protic counterparts have the advantage that they are conventionally obtained by a simple, high-yield single step from acids and bases rather than an alkylation and subsequent anion exchange, giving a more economic and ecological synthesis protocol.
= 13.6 in aqueous solution12) and are obtained by proton transfer from the corresponding free acid of the desired anion to the free base. Compared to aprotic ionic liquids (AILs), which are often formed by anion metathesis, the protic counterparts have the advantage that they are conventionally obtained by a simple, high-yield single step from acids and bases rather than an alkylation and subsequent anion exchange, giving a more economic and ecological synthesis protocol.
The guanidinium cations have a delocalized π-electron system, similar to the imidazolium and pyridinium cations, with the difference that the resonance system in the guanidinum has a Y-shape (Y-aromaticity13), while in the other two a cyclic π-system is found. Guanidinium ionic liquids have already been shown to exhibit beneficial thermal and transport properties,14 are suitable as electrolytes in electrochemical devices,15 as efficient reaction media16 or in gas capture technologies.17
To investigate the anion influence we chose a range of different widely used ions with various structures. In particular we examined the imide-type ions bis(fluorosulfonyl)imide [FSI]−, bis(trifluoromethylsulfonyl)imide [NTf2]−, bis(pentafluoroethylsulfonyl)imide [BETI]−, the octahedral hexafluorophosphate [PF6]− and tetrahedral tetrafluoroborate [BF4]− as well as the non-flexible, non-spherical ions trifluoromethanesulfonate/triflate [OTf]− and trifluoroacetate [TFA]−. All of these anions stem from strong acids with very low pKa-values18 (pKa ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [HNTf2]
[HNTf2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = −10, pKa
= −10, pKa ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [HOTf]
[HOTf]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = −7 and pKa
= −7 and pKa ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [HTFA]
[HTFA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = 0.5) giving ionic liquids with large ΔpKa between the constituting acid and base.19 These large differences in the pKa values have been reported to yield ionic liquids with complete proton transfer from acid HA to base B forming the ionic liquids [HB]+[A]− according to HA + B ⇌ [HB]+[A]− with an equilibrium far on the right side20,21 rather than forming an mixture of molecular and ionic components (as seen in so called pseudo-protic ionic liquids22). The equilibrium of PIL formation significantly influences the resulting properties, such as thermal stabilities and transport properties as the precursors are neutral molecules, thus volatile, more mobile and non-conductive.20,22 Due to the reversibility of the proton transfer, the PILs subclass is also of great interest for applications where fast proton transfer is desired. Therefore, the type of proton transfer, either by vehicle or Grotthuß mechanism, in PILs is always of great concern.22,23 In addition, many PILs have been proven to incorporate hydrogen bonds between the cation's acidic proton and the anion, which again has implications on the observed properties of these ionic liquids.19,24–26
= 0.5) giving ionic liquids with large ΔpKa between the constituting acid and base.19 These large differences in the pKa values have been reported to yield ionic liquids with complete proton transfer from acid HA to base B forming the ionic liquids [HB]+[A]− according to HA + B ⇌ [HB]+[A]− with an equilibrium far on the right side20,21 rather than forming an mixture of molecular and ionic components (as seen in so called pseudo-protic ionic liquids22). The equilibrium of PIL formation significantly influences the resulting properties, such as thermal stabilities and transport properties as the precursors are neutral molecules, thus volatile, more mobile and non-conductive.20,22 Due to the reversibility of the proton transfer, the PILs subclass is also of great interest for applications where fast proton transfer is desired. Therefore, the type of proton transfer, either by vehicle or Grotthuß mechanism, in PILs is always of great concern.22,23 In addition, many PILs have been proven to incorporate hydrogen bonds between the cation's acidic proton and the anion, which again has implications on the observed properties of these ionic liquids.19,24–26
Materials and methods
Additional details about the synthesis of the ionic liquids including reagents used and NMR signals of the samples used in this work are given in the ESI† (Section S1). Purity of the samples was confirmed by multinuclear NMR spectroscopy. All samples were dried in high vacuum prior to each physicochemical measurement and further handled using Schlenk techniques, glove box and NMR ports to avoid contact with atmospheric moisture.Physicochemical properties
Thermal and transport properties were measured under inert gas conditions with the details given in previous works.9,27 Thermal transitions were obtained by differential scanning calorimetry (DSC) in sealed aluminum crucibles on a DSC 1 STARe device (Mettler Toledo, Germany) with liquid nitrogen cooling. Slow scanning rates of ±1 K min−1 were used to avoid glass formation by quenching of the samples rather than crystallization to ensure determination of all thermal events.28 Dynamic decomposition temperatures were determined by thermogravimetric analysis (TGA) using a TGA/DSC 1 STARe instrument (Mettler Toledo, Germany) with +10 K min−1 heating rate under constant nitrogen flow. Decomposition temperatures Td are given as onset temperatures.Dynamic viscosity was measured using a Physica MCR301 rheometer (Anton Paar, Austria) with cone plate geometry. The CP50-1 cone had 49.95 mm diameter and a distance of the cone tip to the plate of 0.101 mm. The rheometer was located on a vibration-isolated table. After reaching temperature equilibrium, the viscosity was measured in 30 linear steps for shear rates ranging from 5 to 80 s−1 with 15 s time per measuring point. As there was no time- or shear-dependent behavior observable (Newtonian fluid behavior), the measurements per T-point were averaged. The temperature-dependent viscosity curves were constructed by repeating this protocol in steps of 5 K from 298.15 K to 403.15 K. Temperature stability during the measurements was better than ±0.01 K. Uncertainty of the viscosity values is ±1.5% as estimated from commercial (T-dependent) viscosity standards, multiple measurements and literature values for ionic liquids.29 The specific conductivity was measured with a SP-150 potentiostat (Biologic, France) using a commercial conductivity probe (WTW, Germany) with 0.5 cm−1 nominal cell constant. The sealed conductivity probe was immersed in a Proline RP 1845 thermostat bath (LAUDA, Germany) for temperature control. The conductivity probe consisted of two rectangular (freshly platinized) platinum electrodes fused in glass. The actual cell constant was determined with commercial conductivity standards of different nominal conductivity. T stability of the heat bath was within ±0.01 K. Uncertainty of the specific conductivity values is approximately ±2%, estimated from commercial conductivity standards and multiple measurements. The molar conductivity was calculated from the specific conductivity using the density ρ and molar mass M according to eqn (1).
 | (1) |
NMR spectroscopic measurements
All samples for the investigations of the neat ionic liquids were measured in the inserts of coaxial tubes (inner diameter ≈1 mm) to ensure temperature stability and to minimize convection by the narrow geometry. The dried samples were placed in the tubes under argon atmosphere, evacuated and flame sealed to avoid uptake of atmospheric moisture. For the measurements of the 1H chemical shifts the inserts of the coaxial tubes were placed in an outer tube containing CDCl3 which served as reference. For the 15N measurements the bulk ionic liquids were flame sealed in an NMR tube containing a sealed capillary with (CD3)2SO. δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1H) are referred to tetramethylsilane (TMS) and δ(
1H) are referred to tetramethylsilane (TMS) and δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15N) to nitromethane (90% in CDCl3). The individual self-diffusion coefficients were determined using NMR spectroscopy with a pulsed field gradient stimulated echo (PFGSTE) pulse sequence including bipolar gradients and longitudinal eddy current delay.27,30 The self-diffusion measurements were conducted on an Avance Neo 500 (Bruker, USA) equipped with Prodigy TCI cryo probe head and BCU II temperature unit. The 1H signals were used to determine the self-diffusion coefficients of the acidic proton Ds,H and the cation Ds+ by the separated resonances and the 19F signals to calculate the anion self-diffusion coefficients Ds−. The temperature control unit of the spectrometer was calibrated with methanol and ethylene glycol.31 The gradient of the spectrometer was calibrated and checked with pure water from a Milli-Q ultrapure water system (Merck, Germany) using literature values of the diffusion.32 After temperature equilibration, the pulse widths and longitudinal relaxation time T1 were determined; parameters for the diffusion time Δ and gradient duration δ were optimized to yield a signal attenuation of 95% compared to the initial measurement when applying gradient strengths of 2 to 95% of the maximum gradient strength (65.7 G cm−1). With these parameters a series of 16 measurements, each 16 scans with linear increase of the gradient strength were recorded. The self-diffusion coefficients Ds,i were determined using the Stejskal–Tanner eqn (2)
15N) to nitromethane (90% in CDCl3). The individual self-diffusion coefficients were determined using NMR spectroscopy with a pulsed field gradient stimulated echo (PFGSTE) pulse sequence including bipolar gradients and longitudinal eddy current delay.27,30 The self-diffusion measurements were conducted on an Avance Neo 500 (Bruker, USA) equipped with Prodigy TCI cryo probe head and BCU II temperature unit. The 1H signals were used to determine the self-diffusion coefficients of the acidic proton Ds,H and the cation Ds+ by the separated resonances and the 19F signals to calculate the anion self-diffusion coefficients Ds−. The temperature control unit of the spectrometer was calibrated with methanol and ethylene glycol.31 The gradient of the spectrometer was calibrated and checked with pure water from a Milli-Q ultrapure water system (Merck, Germany) using literature values of the diffusion.32 After temperature equilibration, the pulse widths and longitudinal relaxation time T1 were determined; parameters for the diffusion time Δ and gradient duration δ were optimized to yield a signal attenuation of 95% compared to the initial measurement when applying gradient strengths of 2 to 95% of the maximum gradient strength (65.7 G cm−1). With these parameters a series of 16 measurements, each 16 scans with linear increase of the gradient strength were recorded. The self-diffusion coefficients Ds,i were determined using the Stejskal–Tanner eqn (2) | (2) |
Fitting of the transport properties
The T-dependent transport properties were fitted using the empirical Vogel–Fulcher–Tammann eqn (3) | (3) |
Small angle X-ray scattering
For the small angle X-ray scattering (SAXS) experiments, the dried ionic liquid samples were filled into thin walled capillaries made of borosilicate that were then closed immediately by flame sealing. The samples were measured using a Xeuss 2.0 device (Xenocs, France) with a Genix 3D X-ray source generating X-rays at the copper Kα-line with a wavelength λ = 1.54 Å. The scattered photons were recorded by a Pilatus 3R 1 M and a Pilatus 100 K detector (Dectris, Switzerland). The scattering intensity was recorded in the range from q = 0.02 Å−1 to q = 3.02 Å−1 with the scattering vector q = |![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) | = 4π
| = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)λ−1 and the scattering angle 2θ. The obtained two dimensional isotropic scattering patterns were radially averaged into the one dimensional scattering curves and the peak positions analyzed using Lorentzian functions.
sin(θ)λ−1 and the scattering angle 2θ. The obtained two dimensional isotropic scattering patterns were radially averaged into the one dimensional scattering curves and the peak positions analyzed using Lorentzian functions.
Crystal structure analysis
Suitable single crystals for X-ray crystallography were obtained by crystallization of the [PF6]− samples from the supercooled melt. The data set for [2O2HTMG][PF6] was collected using a D8 Venture diffractometer (Bruker, Germany) at 133 K with a microfocus sealed tube and a Photon II detector. For [C5HTMG][PF6] the data set was collected at 152 K on an Apex II (Bruker, Germany) with focus sealed tube and CCD detector. Monochromated MoKα (λ = 0.71073 Å) was used for both samples. Data was corrected for absorption effects using the multi-scan method. The structure was solved by direct methods using SHELXT36 and refined by full matrix least squares calculations on F2 (SHELXL201837) in the graphical user interface Shelxle.38 Further details on the refinement method are given in the ESI.† Crystal structures are available from the Cambridge Crystallographic Data Centre under deposition number 2157466 ([2O2HTMG][PF6]) and 2157463 ([C5HTMG][PF6]).Computations
Ab initio calculations were performed using the Gaussian software package, Revision E.01.39 No symmetry was applied for the calculations. A pruned integration grid with 99 radial shells and 590 angular points per shell was used. SCF convergence criteria were 10−10 RMS change and 10−8 maximum change in the density matrix. For MP2 calculations, the SCF convergence was tightened to 10−11 RMS change and 10−9 maximum change in the density matrix. Most calculations were performed at the B3LYP-GD3BJ/6-311+G(d,p) level of theory. Potential energy surfaces PES were obtained from frozen core MP2 single point calculations, i.e. at the MP2/cc-pVTZ//B3LYP-GD3BJ/6-311+G(d,p) level of theory.40,41 Volumes were calculated using Multiwfn as described in the ESI.† Minima on the PES were validated via absence of imaginary normal modes during vibrational frequency analysis. Intramolecular symmetry adapted perturbation theory (SAPT) calculations on the different cation conformers using the cc-pVTZ basis set were carried out with the Psi4 program (version 1.3.3).42 Density fitting was employed to decrease computation times.The ABCluster program (version 2.0)43,44 was used to create ion pair input geometries in which the two ions occupy two corners of a 2 × 2 × 2 cube and are randomly oriented towards each other. Ten ion pairs were constructed for each stable conformer of the isolated cation resulting in a total of 30 ion pair input structures for each ionic liquid. For the [NTf2]− ionic liquid cis and trans anion conformers were each combined with each stable cation conformer to yield five ion pairs per cation conformer. The ion pairs were fully optimized according to the methods described above.
Intermolecular interactions in the ion pairs were studied via a combination of natural bonding orbitals (NBOs) as implemented in the NBO software (version 6.0),45 Bader's quantum theory of atoms in molecules (QTAIM) using the AIMAll software (version 19.10.12),46 and the non-covalent interaction (NCI) framework as implemented in the NCIPLOT4 software.47 0.005 a.u. and 0.5 cut-offs on the electron density and the reduced electron density gradient were applied during the NCI analysis. VMD (version 1.9.3)48 was used to visualize NCI plots.
Results and discussion
Thermal transitions and density
One of the most interesting characteristics of ionic liquids is their tendency to be in a liquid state at temperatures far lower than those of other ionic compounds. This enables the use of ionic liquids in a bulk state even below ambient temperature, offering a broad spectrum of potential applications. Since ionic liquids show negligible vapor pressure, their upper thermal limit is usually determined by their decomposition. Thermal transitions and stability are thus key questions when investigating new ionic liquids. The thermal transition temperatures of the protic guanidinium ionic liquids in this work are summarized in Table 1.| Ionic liquid | T c/°C | T g/°C | T cc/°C | T m/°C | T d/°C | ρ 25°C/g mL−1 |
|---|---|---|---|---|---|---|
| a Measured in supercooled state. | ||||||
| [2O2HTMG][FSI] | — | −92 | — | — | 283 | 1.2890 |
| [2O2HTMG][NTf2] | — | −88 | — | — | 340 | 1.3663 |
| [2O2HTMG][BETI] | — | −76 | — | — | 347 | 1.4399 |
| [2O2HTMG][OTf] | — | −69 | — | — | 323 | 1.2415 |
| [2O2HTMG][PF6] | — | −67 | −27 | 49 | 337 | 1.2993a |
| [2O2HTMG][BF4] | — | −68 | — | — | 303 | 1.1663 |
| [2O2HTMG][TFA] | — | −69 | −37 | 28 | 183 | 1.1575a |
| [C5HTMG][NTf2] | — | −82 | — | — | 354 | 1.3239 |
| [C5HTMG][PF6] | 31 | — | — | 79 | 338 | — |
Most of the samples formed glasses (Tg) upon cooling under the experimental conditions. The only exceptions were the sample [2O2HTMG][TFA] and ionic liquids with the hexafluorophosphate anion, [2O2HTMG][PF6] and [C5HTMG][PF6]. The first two formed glasses upon cooling and subsequently underwent a glass transition, cold crystallization (Tcc) and melting (Tm) upon reheating. The protic alkylated ionic liquid [C5HTMG][PF6] showed a crystallization upon cooling (Tc) followed by a melting upon heating, a behavior similar to most solid compounds but with a comparably large difference between Tc and Tm, thus this ionic liquid exhibited pronounced supercooling. Due to the high melting point of the hexafluorophosphate ionic liquid with the pentyl group, the transport properties of this sample were not measured further. The glass transition temperatures of the ionic liquids with the [2O2HTMG]+ cation increase with molecular weight [FSI]− < [NTf2]− < [BETI]− for the imide ionic liquids, while the glass transition of the other ether containing ionic liquids is approximately the same [OTf]− ≈ [PF6]− ≈ [BF4]− ≈ [TFA]−. Replacing the ether side chain in the guanidinium cation with an alkyl chain of the same length increases the value of Tg for the [NTf2]− anion and leads to a change in the behavior of the thermal transitions for the [PF6]− anion with the absence of disordered crystalline phases.
The investigated samples in this set display the three thermal behaviors for the heating and cooling curves that are commonly found for ionic liquids.28 The first type includes only Tg with complete absence of crystalline phases, the second type glass transition upon cooling with subsequent cold crystallization upon heating followed by Tm, and for the third type crystallization upon cooling and melting upon heating are found. The absence of crystalline phases in the DSC traces and pronounced supercooling is characteristic for the ionic liquid class. These phenomena are related to the intended destabilization of the crystalline lattice and affect both thermal behavior and dynamic properties. The lowering of the Gibbs energy for the crystalline state is achieved by size, charge delocalization and conformational flexibility of the ions constituting the ionic liquid. These combined effects lead to low values for the melting enthalpy while at the same time the melting entropy obtains comparably large values. For most ionic liquids in this set no formation of crystalline phases is observed, which indicates an entropic favoring of the liquid state. The trend for glass formation for these guanidinium ionic liquids could be rationalized by high configurational and conformational flexibility of the ions. Therefore, the glass transitions of the ether cations combined with the flexible imide-type anions [FSI]−, [NTf2]− and [BETI]−, which have a contribution of different conformations (cis and trans, separated by low energy barriers),9 are below those of the rigid anions [OTf]−, [PF6]−, [BF4]− and [TFA]−.
Similar to ionic liquids with other cations, the glass transition temperature decreases when a methylene group in a hydrocarbon side chain is replaced by an ether group, as seen when comparing Tg of [2O2HTMG][NTf2] and [C5HTMG][NTf2].9,49 The glass transition temperatures of the guanidinium ionic liquids for a particular anion are quite low. For instance, the Tg value of [2O2HTMG][NTf2] is even slightly lower than for the comparable imidazolium ionic liquid 1-(2-ethoxy-ethyl)-3-methyl-imidazolium bis(trifluoromethanesulfonyl)imide, [2O2C1im][NTf2] which was reported to be −86 °C.50 The side-chain configurations of the ether groups furthermore results in additional contribution of configurational entropy as the result of more diffuse cation–anion arrangements. This in turn increases the entropy difference between crystalline and liquid state, thus lowering the Tg values of ionic liquids upon ether substitution compared to the samples with hydrocarbon groups while the influence of increased side-chain flexibility had only a minor influence.9,49 In addition to the entropic effects favoring glass formation and lowering Tg, one could assume an enthalpic contribution of the cation conformation change upon ether substitution, where the curling of the ether chain shields the positively charged cation center, thereby lowering the lattice enthalpy of the crystal.49 A similar reasoning can also be used to explain the higher Tm of [C5HTMG][PF6], compared to the ether substituted [2O2HTMG][PF6] and the finding that the latter forms a glass when cooled from the melt.
Results of the thermogravimetric analysis are given in Table 1. It should be noted that we give the decomposition temperatures Td as onset of the mass loss in the TGA trace (ESI,† Fig. S1). Therefore, we do not differentiate in decomposition via chemical breakdown, transfer of the acidic proton on the anion with evaporation of the neutral molecules, or evaporation as ion pair. This differentiation could be done by TGA coupled with other techniques, such as mass spectrometry and is beyond the scope of this work. The dynamic decomposition temperatures increase in the order [TFA]− < [FSI] < [BF4]− < [OTf]− < [PF6]− < [NTf2]− < [BETI]− with a difference of 200 °C between the sample of the lowest and the highest stability. Replacing the 2-ethoxy-ethyl group by a pentyl group gives slightly higher Td values for ionic liquids with the same anion. The thermal stabilities of the guanidinium ionic liquids show a clear trend related to the type of anion used. Similar Td values and trends were also found for imidazolium51 and ammonium based ionic liquids with ether and alkylated side chains.49 For instance, the thermal stabilities for the tris(2-methoxy-ethyl)methylammonium [N(2O1)31]+ and tributylmethylammonium cation [N4441]+ with the [NTf2]− anion are 338 °C and 390 °C.49 A similar dependence of the Td values on the anion is given in the literature for ionic liquids resulting from the super-strong base 1,8-diazabicyclo-[5,4,0]-undec-7-ene (DBU). For the samples with the [TFA]− anion a nearly identical Td value of 183 °C was reported, while the imide-type anions reached higher decomposition temperatures (Td(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [HDBU][BETI]) = 431 °C).20
[HDBU][BETI]) = 431 °C).20
The density of the ionic liquids increases with the presence of heavier elements in the anion. Substituting the pentyl side chain in [C5HTMG][NTf2] with the ether chain leads to an increase in density which is higher than to be expected from the difference in molecular weight of the methylene group and oxygen ether group. The higher density of the ether substituted [NTf2]− ionic liquid compared to the alkylated analogue can be rationalized by a change of the preferred cation conformation by a curling of the ether side chain towards the positively charged cation center. This altered coordination of ether side chains compared to alkyl ones leads to a more compact structure with better packing and higher densities, which was also found for other ionic liquids with ether substituents, such as imidazolium,50 phosphonium,9,27 or ammonium9,49,52 cations. The temperature-dependent density for all ionic liquids in this set could be well fitted by a simple linear fit (see ESI,† Section S3).
Viscosity
Viscosity is another key property for the application of ionic liquids limiting, for instance, heat transfer or the transport of dissolved species and thus reaction rates. Therefore, the search for low viscosity ionic liquids and the investigation of the underlying mechanism that governs viscosity in ionic fluids is important for their successful implementation. Furthermore, the viscosity as macroscopic property gives some insight into the underlying interactions and dynamics on molecular scale. For instance, the viscosity values of ionic liquids are approximately two to three orders of magnitude higher than those of molecular liquids due to the inherent presence of the strong, long-range Coulombic interactions. The data for the temperature-dependent viscosity of the investigated ionic liquids is given in Table 2 and the plots are shown in Fig. 2.| Ionic liquid | η 25°C/mPa s | η 0/10−1 mPa s | B η /K | T 0,η/K | δ η |
|---|---|---|---|---|---|
| [2O2HTMG][FSI] | 50.7 | 2.381 | 675.6 | 172.0 | 3.93 |
| [2O2HTMG][NTf2] | 58.5 | 2.045 | 670.7 | 179.6 | 3.73 |
| [2O2HTMG][BETI] | 116.4 | 1.681 | 728.0 | 186.8 | 3.90 |
| [2O2HTMG][OTf] | 172.1 | 1.730 | 757.1 | 188.5 | 4.02 |
| [2O2HTMG][PF6] | 505.1 | 1.629 | 821.7 | 195.9 | 4.19 |
| [2O2HTMG][BF4] | 264.5 | 1.658 | 759.1 | 195.2 | 3.89 |
| [2O2HTMG][TFA] | 137.0 | 2.070 | 664.9 | 195.8 | 3.40 |
| [C5HTMG][NTf2] | 92.4 | 1.523 | 777.2 | 176.7 | 4.40 |
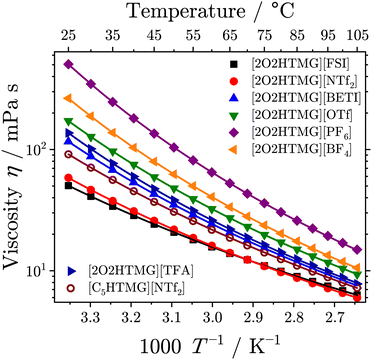 | ||
| Fig. 2 Temperature-dependent viscosity of the investigated protic guanidinium ionic liquids. Drawn lines are the VFT fits following eqn (3). | ||
The viscosities of the [2O2HTMG]+ ionic liquids at 25 °C increases in the order [FSI]− < [NTf2]− < [BETI]− < [TFA]− < [OTf]− < [BF4]− < [PF6]−. Sorting for the anion type shows that the lowest viscosities are found for the flexible imide-type anions; the non-flexible anions give higher viscosity values and the highest values are found for the anions with highest symmetry (tetrahedral and octahedral). The trend in the viscosity values resembles the trend found for the glass transitions, where the imide-type anions have significantly lower values than the ionic liquids with other anions. Such relations are a common finding in the field of ionic liquids9,49 and can, for instance, be rationalized by the Adam–Gibbs model that relates the kinetics of glass forming liquids to thermodynamics.53 Comparing the viscosity of the [NTf2]− ionic liquids with alkyl and ether chains shows that the sample with the [C5HTMG]+ cation has a 1.6 fold higher value than found for the [2O2HTMG]+ cation. A decreasing viscosity for ionic liquids with ether side-chains of the same length as hydrocarbon chains is a general finding.9,49,50,52 However, the decrease in viscosity upon ether substitution is more pronounced for the guanidinium cations. For instance, the pair [C5C1im][NTf2]/[2O2C1im][NTf2] with imidazolium based cations has only a 1.3 fold increase in viscosity when the oxygen-ether in the imidazolium cation is replaced by an methylene group.50 The viscosity of the ether–guanidinium cations at 25 °C are also similar to other ether-subsituted cations with the same cation. For instance, some example viscosities of ionic liquids with the [NTf2]− anion are 46 mPa s for [2O2C1im][NTf2],50 58 mPa s for the ether substituted trimethylammonium [N1112O2][NTf2]52 or 45 mPa s for the trimethylphosphonium cation with attached ether containing side chain [P1112O2][NTf2].54 For comparable ether-subsituted imidazolium ionic liquids with the tetrahedral [BF4]− anion (η25°C ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [2O2C1im][BF4]
[2O2C1im][BF4]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = 103 mPa s)55 and the non-flexible, triflate (η25°C
= 103 mPa s)55 and the non-flexible, triflate (η25°C ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [2O1C2im][OTf]
[2O1C2im][OTf]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = 73 mPa s),56 the viscosity was reported to be lower.
= 73 mPa s),56 the viscosity was reported to be lower.
The T-dependence of the ionic liquids' viscosity revealed a clear deviation from Arrhenius behavior. Therefore, the VFT-eqn (3) was used for the fitting of the viscosity values, as is commonly done for the ionic liquid transport properties.34 The order of the viscosity values remained unchanged over the whole temperature range, however [FSI]− and [NTf2]− change their position at approximately 72 °C. A similar behavior for T-dependent viscosity of these two imide type anions was also found for ammonium ionic liquids with and without ether-substituents.49 From the VFT-fitting the Angell-strength factor of viscosity δη, which is used to quantify the deviation from the Arrhenius type behavior, could be determined. While so-called strong liquids give straight lines in the Angell plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η vs. T/Tg, the fragile glass formers show curvatures, increasing with the liquid's fragility. Small values of the strength parameter δY of a particular transport quantity Y indicate highly fragile liquids, whereas large values correspond to so-called strong liquids. All ether-substituted guanidinium ionic liquids in this set have δη values in a comparatively narrow range, ranging from 3.40 for [2O2TMG][TFA] to 4.02 for [C5HTMG][NTf2]. Therefore, these ionic liquids can be classified as highly fragile liquids. For imidazolium ionic liquids with the 1-butyl-3-methylimidazolium cation ([C4C1im]+) δη values of 4.65 for the [NTf2]−,57 5.92 for the [BF4]−58 and 6.96 for the [PF6]59 anion were reported. For ammonium ionic liquids with threefold ether-substitution δη values in the very similar range from 3.21 to 4.26 were reported.49 However, the difference in the Angell strength factor between [2O2HTMG][NTf2] and [C5HTMG][NTf2] is striking. This agrees with literature reports about increasing Angell's strength factors upon substitution of methylene groups in alkyl chains with ether oxygens.49,52 The reason for this may lie in the formation of a nanostructure with the segregation into polar domains of ionic groups and non-polar domains consisting of hydrocarbon chains.60 This hypothesis of the different orientation of the side chain and domain formation will find further proof in the X-ray experiments discussed below. The nanostructural organization of longer alkyl chains might reduce the dynamic heterogeneities in ionic liquids, which is believed to be responsible for the high fragility of ionic liquids.61,62
η vs. T/Tg, the fragile glass formers show curvatures, increasing with the liquid's fragility. Small values of the strength parameter δY of a particular transport quantity Y indicate highly fragile liquids, whereas large values correspond to so-called strong liquids. All ether-substituted guanidinium ionic liquids in this set have δη values in a comparatively narrow range, ranging from 3.40 for [2O2TMG][TFA] to 4.02 for [C5HTMG][NTf2]. Therefore, these ionic liquids can be classified as highly fragile liquids. For imidazolium ionic liquids with the 1-butyl-3-methylimidazolium cation ([C4C1im]+) δη values of 4.65 for the [NTf2]−,57 5.92 for the [BF4]−58 and 6.96 for the [PF6]59 anion were reported. For ammonium ionic liquids with threefold ether-substitution δη values in the very similar range from 3.21 to 4.26 were reported.49 However, the difference in the Angell strength factor between [2O2HTMG][NTf2] and [C5HTMG][NTf2] is striking. This agrees with literature reports about increasing Angell's strength factors upon substitution of methylene groups in alkyl chains with ether oxygens.49,52 The reason for this may lie in the formation of a nanostructure with the segregation into polar domains of ionic groups and non-polar domains consisting of hydrocarbon chains.60 This hypothesis of the different orientation of the side chain and domain formation will find further proof in the X-ray experiments discussed below. The nanostructural organization of longer alkyl chains might reduce the dynamic heterogeneities in ionic liquids, which is believed to be responsible for the high fragility of ionic liquids.61,62
Conductivity
Since ionic liquids are highly attractive electrolytes in the field of electrochemical storage and conversion devices their conductivity is one of their most interesting properties. The experimental values of the molar conductivity ΛM and VFT fitting parameters are given in Table 3 and the T-dependent values are plotted in Fig. 3a. Experimental values for the specific conductivity are given in the ESI† (Section S5).| Ionic liquid | Λ 25°CM/S cm2 mol−1 | Λ 0,M/S cm2 mol−1 | B Λ M /K | T 0,ΛM/K | δ Λ M |
|---|---|---|---|---|---|
| [2O2HTMG][FSI] | 1.166 | 235.6 | −739.9 | 158.9 | 4.63 |
| [2O2HTMG][NTf2] | 0.820 | 219.5 | −708.1 | 171.5 | 4.00 |
| [2O2HTMG][BETI] | 0.407 | 246.6 | −802.0 | 174.3 | 4.31 |
| [2O2HTMG][OTf] | 0.282 | 233.7 | −789.2 | 180.6 | 4.35 |
| [2O2HTMG][PF6] | 0.142 | 269.9 | −773.1 | 195.8 | 3.92 |
| [2O2HTMG][BF4] | 0.262 | 256.0 | −699.4 | 196.5 | 3.38 |
| [2O2HTMG][TFA] | 0.214 | 198.5 | −863.2 | 171.7 | 5.47 |
| [C5HTMG][NTf2] | 0.585 | 225.7 | −741.9 | 173.6 | 4.30 |
The values of the molar conductivity for the ether containing samples at 25 °C show the reverse order as found for the viscosity, with the difference that the samples with [TFA]− and [BF4]− are interchanged. Comparing the alkyl substituted [C5HTMG][NTf2] with the ether substituted [2O2TMG][NTf2] revealed a significantly increased molar conductivity for the ether ionic liquid. Similar to the viscosity, the molar conductivities show a clear deviation from Arrhenius type behavior (Fig. 3a), but could be fitted well with the VFT eqn (3). Furthermore, the values for Angell's strength factor δΛM are very similar to the values found for the viscosity, having values from 3.92 to 5.47. The greatest difference between the δη and δΛM is found for [2O2HTMG][TFA]. This might stem from the more pronounced back reaction towards the neutral precursors at elevated temperatures (endothermal reaction as reverse reaction of the exothermal protonation of the base) effectively lowering the concentration of ions but increasing conductivity in an intricate way.20 The reciprocal correlation is not surprising as it is well known that the two transport properties are related to each other by the Walden relation (eqn (4))
| ΛM ∝ (η−1)t | (4) |
Nuclear magnetic resonance spectroscopy
| Ionic liquid | δ(1H), bulka/ppm | δ(1H), CDCl3/ppm | δ(1H), (CD3)2SO/ppm | δ(15N) bulk/ppm |
|---|---|---|---|---|
| a Chemical shift of the pure substance referred to external CDCl3. | ||||
| [2O2HTMG][FSI] | 5.81 | 5.77 | 7.51 | −296.7 |
| [2O2HTMG][NTf2] | 5.93 | 5.96 | 7.50 | −296.1 |
| [2O2HTMG][BETI] | 5.88 | 6.02 | 7.51 | −296.1 |
| [2O2HTMG][OTf] | 6.82 | 6.96 | 7.50 | −295.2 |
| [2O2HTMG][PF6] | 5.51 | 5.52 | 7.50 | −298.3 |
| [2O2HTMG][BF4] | 6.08 | 6.17 | 7.49 | −298.0 |
| [2O2HTMG][TFA] | 8.82 | 9.47 | 7.66 | −289.7 |
| [C5HTMG][NTf2] | 5.92 | 5.93 | 7.55 | −288.9 |
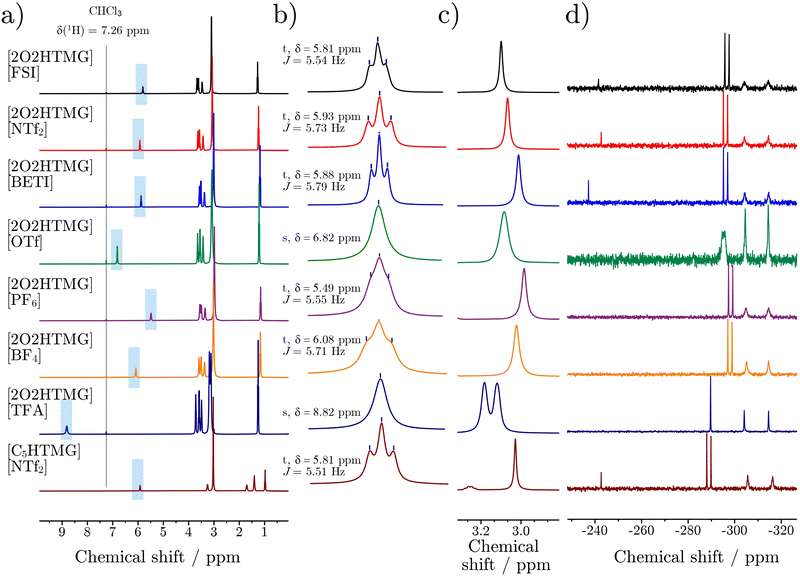
The 1H-NMR spectra of the pure compounds show that the signal of the acidic proton has a strong dependence on the type of acid used for the preparation of the ionic liquid ranging from 5.51 ppm for [2O2HTMG][PF6] to 8.82 ppm for [2O2HTMG][TFA], Fig. 4(b). Replacing the ether side chain with a hydrocarbon chain shows nearly identical 1H chemical shifts of the acidic proton as seen for the couple [2O2HTMG][NTf2]/[C5HTMG][NTf2]. This indicates that the differences in δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1H) result from the type of counteranion, rather than the substitution pattern. Similar dependencies on the strength of the acid used – and thus the anion type – are also reported for ionic liquids based on ammonium65 and amidinium20 cations. It is thereby noteworthy that the 1H chemical shifts of these cations only reach values down to ≈7 ppm for these cation classes samples, although similar anions were chosen.20,65 The increased upfield shift of the guanidinium ionic liquids are the result of the higher base strength of guanidines compared to amines or amidines. Literature reports correlate the 1H-chemical shifts of the ionic liquid's acidic proton to the strength of the constituting acid and the difference in the pKa values of the acid and base forming the protic ionic liquid. Exemplary pKa values of the corresponding acids are given as pKa(
1H) result from the type of counteranion, rather than the substitution pattern. Similar dependencies on the strength of the acid used – and thus the anion type – are also reported for ionic liquids based on ammonium65 and amidinium20 cations. It is thereby noteworthy that the 1H chemical shifts of these cations only reach values down to ≈7 ppm for these cation classes samples, although similar anions were chosen.20,65 The increased upfield shift of the guanidinium ionic liquids are the result of the higher base strength of guanidines compared to amines or amidines. Literature reports correlate the 1H-chemical shifts of the ionic liquid's acidic proton to the strength of the constituting acid and the difference in the pKa values of the acid and base forming the protic ionic liquid. Exemplary pKa values of the corresponding acids are given as pKa(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HNTf2) = −10.0, pKa(
HNTf2) = −10.0, pKa(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HOTf) = −7.0 and pKa(
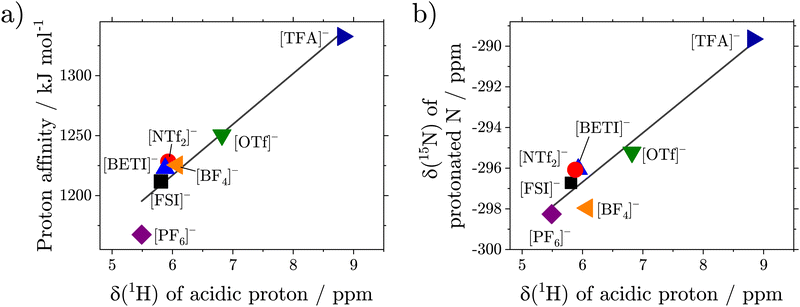
HOTf) = −7.0 and pKa(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HTFA) = 0.5.19 A higher acid strength therefore means a weaker interaction of the cation with the anion by a H-bond. However, pKa values are only strictly defined in aqueous media. We therefore used the proton affinity of the acids in the gas phase, calculated ab initio, as a measure for the acid strength, see ESI.† As shown in Fig. 5(a) there is a linear correlation between the proton affinity of the constituting acids and the chemical shift of the acidic proton.
HTFA) = 0.5.19 A higher acid strength therefore means a weaker interaction of the cation with the anion by a H-bond. However, pKa values are only strictly defined in aqueous media. We therefore used the proton affinity of the acids in the gas phase, calculated ab initio, as a measure for the acid strength, see ESI.† As shown in Fig. 5(a) there is a linear correlation between the proton affinity of the constituting acids and the chemical shift of the acidic proton.
Higher chemical shifts also correlate with an increase in bond length and thus weakening of the N–H bond by stronger interaction with the anion. The formation of hydrogen bonds in the guanidinium ionic liquids is also found in the crystal structure of the samples with the [PF6]− anions stemming from the acid with the highest proton affinity. The correlation of the acidic proton's 1H chemical shifts in bulk to the interaction with the anion influencing the hydrogen bond is also supported by the measurements of the ionic liquids in deuterated solvents. In the non-polar solvent CDCl3, which promotes the formation of ion pairs,68,69 the observed chemical shifts are similar to those in the bulk. On the other hand, the δ(1H) values of the acidic proton in DMSO-d6, which is known for its efficient shielding and separation of the ions,69,70 are only in a narrow range from 7.49 to 7.66 ppm. In addition to the chemical shifts of the acidic proton, to obtain information about the hydrogen bonding between cation and anion, the multiplicity of the signal itself gives further information about the localization of the proton. For all samples, besides [2O2HTMG][OTf] and [2O2HTMG][TFA], the signal of the acidic proton appeared as a triplet, while the two mentioned exceptions showed a singlet (Fig. 4b). This means that the rate constant for the exchange kex of this proton must be significantly larger than the coupling constant with the protons at the side chain (kex ≫ 3JHH ≈ 5.5–5.8 Hz).65 This finding can be explained by a hopping of the proton from cation to anion (forming the neutral precursors), making it an exchangeable proton, although these ionic liquids are formed by super-strong bases and strong acids. Further support of this interpretation will be delivered by the self-diffusion coefficient of the acidic proton in comparison to the ones of cation and anion, Table 5. Another hint supporting the presence of transient proton back transfer is the splitting of the N(CH3)2 groups (located at 3.18 and 3.12 ppm; Δν = 25.9 Hz at 298 K), only found in the [TFA]− sample which also shows the highest interaction with the anion. The observation of the methyl groups as two singlet signals is the result from slow molecular rotation around the C–NH(2O2) bond, so that two signals corresponding to rotamers are found. In substituted (non-protonated) tetramethyl guanidines the N(CH3)2 groups are also observed as individual 1H resonances due to the rigid double bond preventing the rotation.14 For [2O2HTMG][TFA] the slow rotation around the C–NH(2O2) bond is unlikely to be the result of overall slow dynamics as this sample is not the one with the highest viscosity. The observation of rotamers in the 1H-NMR could rather be interpreted as the result of strong hydrogen bonding, locating the anion and hampering the rotation around the N–C bond. Alternatively, this could be rationalized by higher contribution of the neutral precursor species, where the rotation of the N–C double bond is also restricted.
| Ionic liquid | D s+/10−12 m2 s−1 | D s,H/10−12 m2 s−1 | D s−/10−12 m2 s−1 | D s +/Ds− | Λ M,NE | H R −1 | Δ NE | ΔW |
|---|---|---|---|---|---|---|---|---|
| [2O2HTMG][FSI] | 21.2 | 21.1 | 26.3 | 0.81 | 1.781 | 0.65 | 0.35 | 0.59 |
| [2O2HTMG][NTf2] | 18.0 | 18.0 | 17.5 | 1.03 | 1.334 | 0.61 | 0.39 | 0.48 |
| [2O2HTMG][BETI] | 9.54 | 9.51 | 7.95 | 1.20 | 0.657 | 0.62 | 0.38 | 0.47 |
| [2O2HTMG][OTf] | 6.43 | 6.61 | 6.47 | 0.99 | 0.485 | 0.58 | 0.42 | 0.49 |
| [2O2HTMG][PF6] | 2.51 | 2.51 | 2.67 | 0.94 | 0.195 | 0.73 | 0.27 | 0.72 |
| [2O2HTMG][BF4] | 4.21 | 4.19 | 5.33 | 0.79 | 0.358 | 0.73 | 0.27 | 0.69 |
| [2O2HTMG][TFA] | 6.71 | 7.20 | 7.17 | 0.94 | 0.521 | 0.41 | 0.59 | 0.29 |
| [C5HTMG][NTf2] | 12.0 | 12.0 | 11.8 | 1.01 | 0.900 | 0.65 | 0.35 | 0.53 |
Additional insight into the hydrogen bonding via the acidic proton can be obtained from the 15N NMR spectra, Fig. 4(d). The δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15N) values of the N atom where the acidic proton is attached, show a dependency similar to δ(
15N) values of the N atom where the acidic proton is attached, show a dependency similar to δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1H) on the strength of the acid used to form the ionic liquid with the [2O2HTMG]+ cation. The δ(
1H) on the strength of the acid used to form the ionic liquid with the [2O2HTMG]+ cation. The δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15N) range from −298.3 ppm for the [PF6]− sample to −289.7 ppm for the ionic liquids with the [TFA]− anion. For stronger acids the weaker interaction of the anion with the cation leads to shielding of the N–H nuclei as observed by the upfield shift of δ(
15N) range from −298.3 ppm for the [PF6]− sample to −289.7 ppm for the ionic liquids with the [TFA]− anion. For stronger acids the weaker interaction of the anion with the cation leads to shielding of the N–H nuclei as observed by the upfield shift of δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15N), thus in the same direction as the δ(
15N), thus in the same direction as the δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1H) with a good correlation, Fig. 5(b). However, the 15N chemical shifts cover a wider ppm range, so are potentially more sensitive to obtain information on cation–anion interactions. The different electronic structure of [C5HTMG][NTf2] affects the quite sensitive δ(
1H) with a good correlation, Fig. 5(b). However, the 15N chemical shifts cover a wider ppm range, so are potentially more sensitive to obtain information on cation–anion interactions. The different electronic structure of [C5HTMG][NTf2] affects the quite sensitive δ(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15N) values in the form of a stronger downfield shift, so that this sample is not suitable to be compared to the ether substituted ionic liquids. Furthermore, the multiplicity of the protonated nitrogen in the 15N NMR spectra without decoupling reveals coupling between the 15N and 1H nuclei, yielding a clear doublet (with coupling constant 1JNH ≈ 92 Hz) for all samples besides [2O2HTMG][OTf] and [2O2HTMG][TFA]. The trifluoroacetate ionic liquid shows a singlet, while the triflate marks an intermediate case where a broadened peak is observed. This suggests that only in the [TFA]− ionic liquid the exchange of the acidic proton is fast compared to the N–H coupling constant (kex ≫ 1JNH), while for the samples with doublets this exchange is slow (kex ≪ 1JNH). The triflate sample represents the intermediate case, where the peak is broadened by the proton exchange, somehow similar to coalescence triggered by temperature. For protic ionic liquids with the diethylmethyl-ammonium cation doublets are also found for strong acids, including the [OTf]− anion, the nitrate [NO3]− anion being the intermediate case, while for [TFA]− a singlet is also reported.65 This clearly shows that the difference in acid and base strength, ΔpKa, is not suitable by itself to adequately explain the exchange rate of the acidic proton, as guanidines are far stronger bases than amines, but the latter show a slower hydrogen exchange with the same anion, [OTf]−. In addition, the exchange of the labile acidic proton is observed by two-dimensional NMR spectroscopy. For all the protic ionic liquids, again besides the triflate and trifluoroacetate, the 1H–1H Correlated Spectroscopy (COSY), 1H–13C Heteronuclear Multiple Bond Correlation (HMBC) and 1H–15N Heteronuclear Single Quantum coherence (HSQC) experiments showed correlations between the acidic proton and the different adjacent nuclei, see ESI.†
15N) values in the form of a stronger downfield shift, so that this sample is not suitable to be compared to the ether substituted ionic liquids. Furthermore, the multiplicity of the protonated nitrogen in the 15N NMR spectra without decoupling reveals coupling between the 15N and 1H nuclei, yielding a clear doublet (with coupling constant 1JNH ≈ 92 Hz) for all samples besides [2O2HTMG][OTf] and [2O2HTMG][TFA]. The trifluoroacetate ionic liquid shows a singlet, while the triflate marks an intermediate case where a broadened peak is observed. This suggests that only in the [TFA]− ionic liquid the exchange of the acidic proton is fast compared to the N–H coupling constant (kex ≫ 1JNH), while for the samples with doublets this exchange is slow (kex ≪ 1JNH). The triflate sample represents the intermediate case, where the peak is broadened by the proton exchange, somehow similar to coalescence triggered by temperature. For protic ionic liquids with the diethylmethyl-ammonium cation doublets are also found for strong acids, including the [OTf]− anion, the nitrate [NO3]− anion being the intermediate case, while for [TFA]− a singlet is also reported.65 This clearly shows that the difference in acid and base strength, ΔpKa, is not suitable by itself to adequately explain the exchange rate of the acidic proton, as guanidines are far stronger bases than amines, but the latter show a slower hydrogen exchange with the same anion, [OTf]−. In addition, the exchange of the labile acidic proton is observed by two-dimensional NMR spectroscopy. For all the protic ionic liquids, again besides the triflate and trifluoroacetate, the 1H–1H Correlated Spectroscopy (COSY), 1H–13C Heteronuclear Multiple Bond Correlation (HMBC) and 1H–15N Heteronuclear Single Quantum coherence (HSQC) experiments showed correlations between the acidic proton and the different adjacent nuclei, see ESI.†
Contrary to the situation in the 1H, where only the [TFA]− sample showed a slow rotation around the C–NH(2O2) bond, in all 15N NMR spectra the signals of the N(CH3)2 groups are split into two singlets (located at approximately −304 and −315 ppm) indicating rotamers. The splitting of the N(CH3)2 groups means that the rate of the rotation is slower than the frequency difference Δν ≈ 520 Hz between the two peaks. The broad peaks however indicate that these guanidinium ionic liquids are close to the coalescence temperature in the 15N spectra, while the coalescence T is already reached for the 1H spectra, so that the 15N experiments are capable of resolving faster processes. Further studies dealing with the rotational barrier in these samples will be conducted in the future.
Self-diffusion coefficients
The microscopic self-diffusion Ds coefficients of ionic liquids give more detailed insight on transport phenomena than the macroscopic properties viscosity and conductivity. Modern high-resolution NMR spectrometers allow for the determination of the self-diffusion coefficients of individual species. In case of the protic ionic liquids it is possible to determine the self-diffusion coefficient of the cation Ds+ by using the separated signals of the carbon-bonded protons and the one of the acidic proton Ds,H from the proton attached the nitrogen atom. The results are summarized in Table 5.For the values of the diffusion coefficients, trends similar to the macroscopic transport properties are found, e.g. samples with low viscosity show fast self-diffusion and vice versa, and the dynamics are significantly accelerated upon ether substitution in the side chain. For all samples the Ds+ and Ds,H are identical within experimental error (below 0.4% difference), with the exception of [2O2HTMG][OTf] and [2O2HTMG][TFA] were the self-diffusion of the acidic protons are 1.03 and 1.07 times as high as the values of the cation. For the ionic liquids where the self-diffusion coefficients of the protons are identical, an acidic proton that is tightly bound to the cation can be assumed, while for faster diffusion of the N–H proton, an exchange of this nucleus is evident. This also correlates perfectly with the observations from the coupling patterns observed in the one-dimensional 1H and 15N spectra, Fig. 4, as well as absence of correlations in the two-dimensional spectra for the ionic liquids with the [OTf]− and [TFA]− anions.
For most samples the anion diffuses faster than the cation, with the exception of the comparatively large anions [NTf2]− and [BETI]−. The slower diffusion of the anions can be rationalized by their higher mass, as only the aforementioned heavier imides have higher mass than the guanidinium cations. From the Nernst–Einstein eqn (5) the molar conductivity ΛM,NE can be calculated from the self-diffusion coefficients of the ionic species
 | (5) |
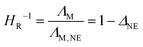 | (6) |
Due to the shown correlation with the proton affinities, Fig. 5a) this also means that ‘stronger’ acids lead to protic ionic liquids with higher HR−1 values. Similar ionicity values and trends are also found for other types of ionic liquids with the same anion trends.27,49,71 This means that [BF4]−, [PF6]− and the imide type anions have higher ionicities than the ones based on sulfonic acid and carboxylic acid derivatives. Only the [TFA]− sample has an ionicity value that is lower than the ones reported for aprotic counterparts,27,49,71 but similar to those for other protic ionic liquids.14 This again shows that especially the trifluoroacetate ionic liquid differs from the other protic guanidinium ionic liquids which have properties similar to aprotic ionic liquids (due to the localization of the proton at the cation). Replacing the oxygen atom in the side chain with a methylene group slightly increases the reciprocal Haven ratio, a trend that was also found for other cation classes.49,52 Possible rationalizations for this correlation could be the transfer of the proton from the cation to the anion that is most pronounced for the [TFA]− sample and to a lesser degree for the [OTf]− sample, so that there is a certain fraction of molecular species decreasing the HR−1 values, while for the ‘strong’ acids this reaction is negligible at the investigated temperature. However, the proposal that molecular species formed in these ionic liquids could not explain why the values of the reciprocal Haven ratio are also not equal to unity for the samples where a localization of the acidic proton is found in the NMR spectra (and the Ds+ and Ds,H values are identical). Furthermore, similar trends are also observed for aprotic ionic liquids, where a proton back transfer is intrinsically impossible. Therefore, a better explanation – in agreement with the other NMR measurements – would be the interaction of the cation with the anion via the hydrogen bond at the acidic proton. This acidic proton is clearly located on the cation if sufficiently strong acids are used, but the interaction with the anion could be interpreted as the formation of ion aggregates. This interaction is then in reverse proportionality to the proton affinity, meaning that ‘stronger’ acids lead to weaker cation–anion interactions which increases the ionicity values. For the acids with the higher proton affinity, such as trifluoroacetic acid or the intermediate case of trifluoromethane sulfonic acid the acidic proton seems to be in fast exchange with the anion, thus less located at the cation. The participation of neutralized species then leads to an decrease of the HR−1 values. This would then be somehow similar to so-called pseudo ionic liquids, consisting for instance of amines and carboxylic acids where there are incomplete proton transfers and large fractions of neutral species. These mixtures of neutral and ionic species result in fluids with very low HR−1 values22,65,66 and physicochemical properties significantly different from ionic liquids, such as volatility.20 However, it seems that in contrast to pseudo ionic liquids the sample [2O2HTMG][TFA] still has a comparably high ionicity, high decomposition temperature and low volatility, so it can somehow be considered as an intermediate case between a permanent proton transfer and significant amount of neutral species. This could be beneficial for applications where proton conduction at higher temperatures is demanded, for instance by combination with acids to achieve proton hopping mechanisms.74 Another possible rationalization correlating reciprocal Haven ratios with decreasing proton affinity could be given when velocity cross-correlations are considered.64,73 The deviations between ΛM,NE and ΛM are smaller, when the anti-correlations between oppositely charged species ions are lower, thus when the motion of cation and anion is more correlated.14 This would be the case if there is a directed interaction of sufficient strength between cation and an anion, which is the case of hydrogen bonding here. Indications for hydrogen bonding are also found in the liquid and crystal structure as well as in the computations given below. Furthermore, the velocity cross-correlation could also explain the similar values and trends of the ionicity values found for aprotic ionic liquids,10,27,49,54 but with the need to rationalize cation–anion interactions without a dominant hydrogen bond.
A further frequently used method to determine the ionicity values in the literature is the deviation from the so-called 'ideal line' in the Walden plot (Fig. 3b) which is the bisection when the logarithm of the fluidity (reciprocal viscosity) in centipoise is plotted against the logarithm of the molar conductivity given in S cm2 mol−1. The ‘ideal line’ was assumed to represent a 0.01 M aqueous KCl solution where negligible interactions between the ions were assumed.72 Values that are closer to the bisection are regarded as being closer to the ideal electrolyte behavior, thus have higher ionicity.75 The ionicity from the Walden plot ΔW can be calculated from the experimental data by the equation:
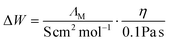 | (7) |
Small angle X-ray scattering
The liquid structure of ionic liquids can be investigated experimentally using small angle X-ray scattering (SAXS). For the ionic liquids, commonly up to three maxima of the scattering vector q (‘peaks’) are found in the scattering patterns.78 At high q values of 1.3 to 1.7 Å−1 the so called ‘adjacency peak’ is found, which is attributed to various inter- and intramolecular correlations between neighboring atoms. Consequently, the adjacency correlations are found for both ionic and molecular liquids. At lower q values of approximately 0.7 to 1.2 Å−1 the ‘charge peak’ is observed. This charge peak results from the arrangement of cations and anions in shells around oppositely charged ions. The charge separation is inherently present in ionic liquids and hence this peak is a characteristic feature of these (and conventional molten salts at high temperature). It should be noted that, due to cancellations of peaks and antipeaks, this peak is sometimes not observed in the SAXS patters, which does not mean that there is no organization into ion shells.78 For ionic liquids with sufficiently long hydrocarbon chains a third peak, termed ‘polarity peak’ is observed at q values below 0.6 Å−1. This peak results from the nanostructural segregation of the liquid into polar, ionic and non-polar, hydrocarbon domains, similar to microscopic demixing of lipophobic and lipophilic liquids.The obtained maxima of the scattering vector q and the resulting real space distances are given in Table 6 and the experimental SAXS patters are given in the ESI,† Section S8.
| Peak positions | Real space distance | ||||||
|---|---|---|---|---|---|---|---|
| Ionic liquid | Polarity/Å−1 | Charge/Å−1 | Adjacency/Å−1 | Polarity/Å | Charge/Å | Adjacency/Å | r + + r−/Å |
| [2O2HTMG][FSI] | — | 1.06 | 1.57 | — | 5.95 | 4.01 | 7.27 |
| [2O2HTMG][NTf2] | — | 0.84 | 1.28 | — | 7.47 | 4.92 | 7.72 |
| [2O2HTMG][BETI] | — | 0.78 | 1.20 | — | 8.04 | 5.24 | 8.06 |
| [2O2HTMG][OTf] | — | 1.02 | 1.34 | — | 6.15 | 4.67 | 7.06 |
| [2O2HTMG][PF6] | — | 1.14 | 1.55 | — | 5.52 | 4.06 | 6.92 |
| [2O2HTMG][BF4] | — | 1.24 | 1.65 | — | 5.07 | 3.82 | 6.62 |
| [2O2HTMG][TFA] | — | 1.12 | 1.44 | — | 5.59 | 4.35 | 6.91 |
| [C5HTMG][NTf2] | 0.52 | 0.80 | 1.32 | 12.0 | 7.83 | 4.76 | 7.78 |
For all samples with the ether side chain only the ‘charge’ and ‘adjacency’ peak are distinguishable in the SAXS pattern, consequently [C5HTMG][NTf2] is the only sample where a ‘polarity peak’, albeit weak, is observed. The ionic liquids with the imide-type anions were the only samples that showed clearly separated peaks, whereas the other scattering patterns show broad, merging peaks. Broader peaks than the alkylated counterparts are frequently reported for ionic liquids with ether groups79–81 and are the result of the more diffuse cation–anion arrangements stemming from the charge shielding of the cation core by the more polar functional groups.49 We fitted the peaks with Lorentzian functions for a quantitative comparison of their positions. The cation–anion distance for [C5HTMG][NTf2] is noticeably shorter than for the sample with the ether chain, [2O2HTMG][NTf2], despite the nearly equal ion size. All ‘polarity’ peaks are at q values that are similar to or lower than the cation–anion distances for comparable aprotic ionic liquids. For ionic liquids with the slightly smaller [C4C1im]+ cation, for instance, values for the cation–anion distance of 7.4 Å for the [NTf2]−,82 6.5 Å for the [PF6]−83 and 4.3 Å for the [BF4]− anion84 are reported. Furthermore, the polarity peak of [C5HTMG][NTf2] is comparable to the literature value for [C5C1im][NTf2] which has the same side-chain length and non-polar domains of 11.0 Å size.82 The cation–anion distances thereby increased with ion sizes. We furthermore compared the experimental cation–anion distances in the liquid state which includes interaction and packing effects (perturbed system), with an ion distance to be expected from the individual ion radii, as obtained from ab initio calculations, where no perturbations are present. Plotting the cation–anion distance versus the sum of the ab initio radii yields a good linear correlation, see ESI,† with good agreement for the larger anions [NTf2]− and [BETI]− but increasing differences with decreasing size of the anions. This can be explained by the assumption of an unperturbed system and the closer packing of the smaller anions and consequently the possibility for better interactions with the cation via a hydrogen bond, which would decrease the cation–anion distance even further. This postulation is also supported by the single crystal structure, where clear hydrogen bonds between the cations and even the most weakly interacting anions, the hexafluorophosphates, are found. Furthermore, the distance between the charge centers of the cations and anions (approximated as the carbon of the guanidinium and phosphorous of the anion) in the single crystal is in similar range, but smaller than the distances in the liquid state, being 5.15 Å for [2O2HTMG][PF6] and 5.16 Å for [C5HTMG][PF6]. The difference in the cation–anion distance for the ether- and alkyl-substituted [NTf2]− ionic liquid is the result of an altered cation conformation. Ether-substituents attached to ionic liquids are reported to show a curled structure, where the side chain is bent with the oxygen atom interacting with the positive cation core, while non-functionalized alkyl chains of sufficient length assume a stretched, linear configuration. This leads to more space demanding cation conformations for the ether samples, expanding cation–anion distances compared to the alkylated samples. In addition, the linear alkyl chain configurations are beneficial for interaction between the hydrocarbon chains to align in non-polar domains, which results in the observed nanosegregation, manifested as the ‘polarity peak’.
Crystal structures
Single crystal X-ray crystallography of ionic liquids is a valuable tool to obtain experimental information about minimum energy structures, which allows us to draw conclusions about preferred conformations and interactions between the ions. In addition, it allows cross-checking the results obtained by ab initio calculations and gives insights into the liquid state, as similar interactions and arrangements are present.60 As the sample [C5HTMG][NTf2], which we chose for a comparison with the properties of the ether substituted [2O2HTMG]+ ionic liquids, showed no melting point in the DSC we decided to include the alkylated cation with the [PF6]−, from which suitable crystals for X-ray diffraction could be obtained. The asymmetric units of the two guanidinium ionic liquids with the [PF6]− anions are shown in Fig. 7.As expected from the proposed interactions of the anion with the acidic proton, as seen from the NMR measurements, a hydrogen bond between the ions at this position is also seen in the single-crystal structure. For the case of the [PF6]−, the H-bond is from the protonated nitrogen to a fluorine atom of the anion. For the ether-substituted sample the N⋯F distance is 2.893 ± 0.015 Å and the hydrogen bond angle is 133.0 ± 1.9° for the nearest fluorine atom. For the alkylated sample a N⋯F distance of 2.929 ± 0.002 Å and a bond angle 159.5 ± 3° for the hydrogen bond are found. The hydrogen bonds in these samples show quite similar properties, which demonstrates that the conformation and electronic structure of the attached side chain has only minor influence on the dominant cation–anion interactions. These hydrogen bonds can be classified as ionic hydrogen bonds of moderate strength using geometric properties, where donor-acceptor distances between 2.5 and 3.2 Å and bond angles higher than 130° are common.24 Although the side chain composition has only a minor influence on the hydrogen bonding as the main interactions within a particular cation–anion pair, the replacement of the alkyl side chain by an ether chain of the same length has a marked impact on the thermal and dynamic properties of ionic liquids. The conformation of the side chain towards the cation as a result of the ether functionalization can be described by the first two dihedral angles from the cation center, which is the carbon atom of the guanidinium moiety. In case of the [2O2HTMG][PF6] the dihedral angles are 288.9 ± 0.3° for ϕ1 (C–N–C–C) and 60.1 ± 0.2° for ϕ2 (N–C–C–O). For the alkylated counterpart the ϕ1 (C–N–C–C) torsional angle is 228.2 ± 0.4° and the ϕ2 (N–C–C–C) one is 183.3 ± 0.4°. Consequently, the ether substituted sample shows a bending of the ether group towards the positive cation center, while the pentyl group of the alkylated sample has a linear geometry pointing away from the guanidinium unit. Curled structures for ionic liquid cations with ether groups in the side chain and linear conformations for alkylated counterpart of the same chain length, have also been reported for other cation classes.49
Calculations on isolated cations
Most cations and anions used in ionic liquids can assume more than one conformation, and the accessible conformational space can be calculated ab initio. Here, we used model cations with the side chain shortened by one methylene unit to save computational time without changing the central motif (2-(2-methoxy-ethyl)-1,1,3,3-tetramethyl guanidinium [2O1HTMG]+ as model for the ether cation and 2-butyl-1,1,3,3-tetramethyl guanidinium [C4HTMG]+ for the alkylated cation). We chose to investigate the two dihedral angles which define the orientation of the side chain relative to the guanidinium center, cf.Fig. 1 and the previous section. Both the C–N–C–C and N–C–C–X (X = CH2 or O) dihedral angles were scanned, Fig. 8.Here, we use 15 kJ mol−1 to define the thermally accessible region of the potential energy surface (short dashed lines in Fig. 8). For [C4HTMG]+ (Fig. 8a), three basins are observed, each containing two or three minima separated by shallow barriers. In contrast, the thermally accessible region is considerably smaller for the ether functionalized [2O1HTMG]+ cation: The conformers with the N–C–C–O dihedral taking values around 180° are higher than 15 kJ mol−1 in energy relative to the global minimum. Thus, for the ether functionalized cation, those conformations are preferred in which the side chain (with the ether group) is oriented towards the polar core of the cation. Pictures of the conformations taken for the ether cations are drawn in Fig. 8(c), those for the cation with alkyl chain can be found in the Fig. S7 of the ESI.†
Curling of ether side chains towards the positively charged region of molecular cations is a well-known phenomenon in ionic liquids.9,49,81,85–87 Several effects lead to the curling. We have previously demonstrated for ether-functionalized ammonium cations that hydrogen bonding and nonspecific effects (electrostatic, induction, dispersion) contribute approximately equally to the stabilization of the curled structure.49 In contrast, in this work we mainly found non-specific interactions change with the degree of ether chain curling in guanidinium cations, with hydrogen bonding playing a much smaller role. While no intra-molecular hydrogen bonding interactions were observed in the curled lowest energy conformer of the isolated [2O1HTMG]+ cation, only weak intra-molecular hydrogen bonding is present in the higher energy conformers (see Section S10.3.2 of the ESI†). Thus, stabilization of the curled cation conformer must be due to a combination of non-specific interactions, in this case electrostatic (−13 kJ mol−1), dispersive (−14 kJ mol−1) and induction effects (−11 kJ mol−1) are contributing almost equally to the curling of the cation as suggested by intramolecular SAPT analysis. Cation geometries with an extended ether side chain experience less stabilization through dispersion (−8 to −10 kJ mol−1) and electrostatics (−10 to −12 kJ mol−1) while the induction component is quantitatively insensitive to a change in cation geometry (see Section S10.3.2 of the ESI†).
Computations on cation–anion pairs
The side chains in ether functionalized cations compete with the anions for coordination of the cation charged region due to curling. A (small) shielding effect of the ether side chain in the curled conformation is visible in the ESP histogram, see Fig. S10 of the ESI.† Thus, reduced electrostatic cation–anion interactions are expected for ILs in which the ether chain curling is preserved in the liquid bulk. Our experimental results suggest pronounced interactions between the protic guanidinium cations and some of the anions, especially the trifluoroacetate anion. Thus, we paired [TFA]− and [NTf2]− anions with the [2O1HTMG]+ cation for ion pair calculations in order to study the effect of a strongly and a weakly hydrogen bond accepting anion on the intermolecular interactions present and on the curling of the cation. Both anions are capable of forming hydrogen bonds to the most acidic proton on the cation as well to the alkyl periphery (see Section S10.4 in the ESI†). The number of weak hydrogen bonding contacts with the cation periphery is much larger for the [NTf2]− anion due to its size and the increased number of potential hydrogen bond acceptor atoms. We observed a tendency for the ether side chain (in the curled conformation) being replaced by both anions. In other words, intramolecular interactions in the cations were suppressed by intermolecular interactions with the anions.In both cases, the lowest energy ion pair exhibits a primary hydrogen bonding interaction between the cation N–H group and the anion oxygen ([TFA]−)/nitrogen ([NTf2]−) atom forcing the cation ether chain to exist in an extended conformation (see Fig. S11 and S12 in the ESI†). The cation–anion hydrogen bond in the [2O1HTMG][TFA] ion pair is much stronger (ρBCP = 0.0602 a.u.) than in the [NTf2]− analogue (ρBCP = 0.0347 a.u.) and shows an increased covalent character (see Section S10.4 Fig. S14 of the ESI†). This increased covalency is in line with the observation of a singlet resonance for the most acidic proton in the 1H NMR spectrum of [2O2HTMG][TFA], which is due to a temporary proton transfer from the cation to the anion (Fig. 4). The strong hydrogen bonding interaction with an increased covalent contribution can be understood as a step preceding and enabling the proton transfer event. However, in the gas phase, a proton transfer in the lowest energy [2O1HTMG][TFA] ion pair to form the corresponding guanidine and trifluoroacetic acid is not accessible (see Fig. S15 of the ESI†).
The replacement of the ether side chain in the curled cation conformer with an anion might be due to the absence of other counterions in our ion pair structures, hence it would be interesting to perform bulk (molecular dynamics) simulations in the future to investigate the competition between cation–anion hydrogen bonding and ether group curling. Furthermore, it is likely that the shielding effect – and thus the ionic liquid transport properties – can be significantly improved by introducing more ether side chains into the cation.
Our experimental results suggest pronounced interactions between the protic guanidinium cations and some of the anions, especially the trifluoroacetate anion. Ion pair calculations show that trifluoroacetate is indeed capable of forming a strong hydrogen bond to the most acidic proton in the protic guanidinium cation, see ESI.† The much larger [NTf2]− anion also forms several hydrogen bonds, yet not as strong as the trifluoroacetate-based ion pair.
Conclusions
We synthesized a series of novel protic ionic liquids based on the tetramethyl guanidinium cation, which is a derivative of the strong organic base guanidine, with an ether side chain and various anions. By measuring their thermal and transport properties, NMR spectra and structures in liquid and crystal state, supported by ab initio calculations we were able to gain in-depth understanding of the structure–property relations in this sparsely investigated ionic liquid class. The hydrogen bonding between the acidic proton of the cation and the anion is the main interaction between the oppositely charged ions and can be classified as moderately strong.24 The proton affinity of the acid used in the formation of the protic ionic liquid correlates to the chemical shifts in the 1H and 15N NMR spectra. For the acids with high proton affinities a clear localization of the acidic proton at the cation is found, while for the corresponding bases from acids with lower proton affinities, namely the triflate [OTf]− and the trifluoroacetate [TFA]−, an exchange of the N–H proton is observed. This lability of the acidic proton is evident from the coupling patterns of the NMR spectra and the self-diffusion coefficients of the cation's acidic and non-acidic protons which are different in case of the [OTf]− and [TFA]− samples. The glass transition temperatures and fragilities of the ionic liquids decreased and the dynamics were significantly accelerated for the flexible imide-type anions as well as where an ether group was incorporated in the side chain. Regarding faster transport processes of the ionic liquids, ether substitution was shown to relate to the altered cation conformation. For the cations with an ether group, curling of the side chain towards the positively charged cation center was observed, marking a minimum on the potential energy surface. In contrast, the cations with alkyl side group adopted linear geometries. Contrary to other cation classes, intramolecular hydrogen bonding was found less important for the curling of the cation ether side chain. Non-specific electrostatics and dispersion interactions are strongly dependent on the ether side chain conformation and are the driving force for stabilisation of the curled cation structure.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Instrumentation and technical assistance for this work were provided by the Service Center NMR at Saarland University, with financial support from Saarland University and German Research Foundation DFG (project number 4772985087). Instrumentation and technical assistance for this work were provided by the Service Center X-ray Diffraction, with financial support from Saarland University and German Science Foundation (project number INST 256/506-1). This work is funded by the Imperial President's PhD Scholarship.Notes and references
- F. Philippi and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 6993–7021 RSC.
- A. J. Greer, J. Jacquemin and C. Hardacre, Molecules, 2020, 25, 5207 CrossRef CAS PubMed.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS PubMed.
- T. Rüther, A. I. Bhatt, A. S. Best, K. R. Harris and A. F. Hollenkamp, Batteries Supercaps, 2020, 1–36 Search PubMed.
- Y. Zhou and J. Qu, ACS Appl. Mater. Interfaces, 2017, 9, 3209–3222 CrossRef CAS PubMed.
- A. Brandt, J. Gräsvik, J. P. Hallett and T. Welton, Green Chem., 2013, 15, 550–583 RSC.
- S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, J. Chem. Sci., 2021, 12, 6820–6843 CAS.
- S. Pan, M. Yao, J. Zhang, B. Li, C. Xing, X. Song, P. Su and H. Zhang, Frontiers Chemistry, 2020, 8, 1–18 CrossRef PubMed.
- F. Philippi, D. Pugh, D. Rauber, T. Welton and P. A. Hunt, J. Chem. Sci., 2020, 11, 6405–6422 CAS.
- F. Philippi, D. Rauber, B. Kuttich, T. Kraus, C. W. M. Kay, R. Hempelmann, P. A. Hunt and T. Welton, Phys. Chem. Chem. Phys., 2020, 22, 23038–23056 RSC.
- M. Deetlefs, C. Hardacre, M. Nieuwenhuyzen, A. A. Padua, O. Sheppard and A. K. Soper, J. Phys. Chem. B, 2006, 110, 12055–12061 CrossRef CAS PubMed.
- K. Abdur-Rashid, T. P. Fong, B. Greaves, D. G. Gusev, J. G. Hinman, S. E. Landau, A. J. Lough and R. H. Morris, J. Am. Chem. Soc., 2000, 122, 9155–9171 CrossRef CAS.
- I. Rozas, G. Sánchez-Sanz, I. Alkorta and J. Elguero, J. Phys. Org. Chem., 2013, 26, 378–385 CrossRef CAS.
- D. Rauber, F. Philippi, J. Zapp, G. Kickelbick, H. Natter and R. Hempelmann, RSC Adv., 2018, 8, 41639–41650 RSC.
- S. Fang, L. Yang, J. Wang, M. Li, K. Tachibana and K. Kamijima, Electrochim. Acta, 2009, 54, 4269–4273 CrossRef CAS.
- S. Li, Y. Lin, H. Xie, S. Zhang and J. Xu, Org. Lett., 2006, 8, 391–394 CrossRef CAS PubMed.
- X. Lu, J. Yu, J. Wu, Y. Guo, H. Xie and W. Fang, J. Phys. Chem. B, 2015, 119, 8054–8062 CrossRef CAS PubMed.
- A. Kütt, T. Rodima, J. Saame, E. Raamat, V. Mäemets, I. Kaljurand, I. A. Koppel, R. Y. Garlyauskayte, Y. L. Yagupolskii, L. M. Yagupolskii, E. Bernhardt, H. Willner and I. Leito, J. Org. Chem., 2011, 76, 391–395 CrossRef PubMed.
- M. S. Miran, H. Kinoshita, T. Yasuda, M. A. B. H. Susan and M. Watanabe, Chem. Commun., 2011, 47, 12676 RSC.
- M. S. Miran, H. Kinoshita, T. Yasuda, M. A. B. H. Susan and M. Watanabe, Phys. Chem. Chem. Phys., 2012, 14, 5178–5186 RSC.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed.
- H. Watanabe, T. Umecky, N. Arai, A. Nazet, T. Takamuku, K. R. Harris, Y. Kameda, R. Buchner and Y. Umebayashi, J. Phys. Chem. B, 2019, 123, 6244–6252 CrossRef CAS PubMed.
- J. Ingenmey, S. Gehrke and B. Kirchner, ChemSusChem, 2018, 11, 1900–1910 CrossRef CAS PubMed.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Chem. Soc. Rev., 2015, 44, 1257–1288 RSC.
- A. Mariani, M. Bonomo, X. Gao, B. Centrella, A. Nucara, R. Buscaino, A. Barge, N. Barbero, L. Gontrani and S. Passerini, J. Mol. Liq., 2021, 324, 115069 CrossRef CAS.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734 CrossRef PubMed.
- F. Philippi, D. Rauber, J. Zapp and R. Hempelmann, Phys. Chem. Chem. Phys., 2017, 19, 23015–23023 RSC.
- E. Gomez, N. Calvar and A. Domiguez, Ionic Liquids – Current State of the Art, InTech, 2015, pp. 199–208 Search PubMed.
- K. R. Harris and M. Kanakubo, Phys. Chem. Chem. Phys., 2015, 17, 23977–23993 RSC.
- D. Wu, A. Chen and C. Johnson, J. Magn. Reson., Ser. A, 1995, 115, 260–264 CrossRef CAS.
- C. Ammann, P. Meier and A. Merbach, J. Magn. Reson. (1969), 1982, 46, 319–321 CrossRef CAS.
- A. J. Easteal, W. E. Price and L. A. Woolf, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 1091–1097 RSC.
- K. R. Harris and M. Kanakubo, J. Chem. Eng. Data, 2021, 66, 4618–4628 CrossRef CAS.
- C. Schreiner, S. Zugmann, R. Hartl and H. J. Gores, J. Chem. Eng. Data, 2010, 55, 4372–4377 CrossRef CAS.
- P. Sippel, P. Lunkenheimer, S. Krohns, E. Thoms and A. Loidl, Sci. Rep., 2015, 5, 13922 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct, Chem., 2015, 71, 3–8 Search PubMed.
- C. B. Hübschle, G. M. Sheldrick and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 1281–1284 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.09, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010 RSC.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2013, https://nbo6.chem.wisc.edu/ Search PubMed.
- T. A. Keith, TK Gristmill Software, Overland Park KS, USA, 2019, http://aim.tkgristmill.com Search PubMed.
- R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J. P. Piquemal, Y. Maday and J. Contreras-Garcĺa, J. Chem. Theory Comput., 2020, 16, 4150–4158 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- D. Rauber, F. Philippi, B. Kuttich, J. Becker, T. Kraus, P. Hunt, T. Welton, R. Hempelmann and C. W. Kay, Phys. Chem. Chem. Phys., 2021, 23, 21042–21064 RSC.
- S. I. Lall-Ramnarine, M. Zhao, C. Rodriguez, R. Fernandez, N. Zmich, E. D. Fernandez, S. B. Dhiman, E. W. Castner and J. F. Wishart, J. Electrochem. Soc., 2017, 164, H5247–H5262 CrossRef CAS.
- Z. Xue, L. Qin, J. Jiang, T. Mu and G. Gao, Phys. Chem. Chem. Phys., 2018, 20, 8382–8402 RSC.
- D. Rauber, A. Hofmann, F. Philippi, C. W. M. Kay, T. Zinkevich, T. Hanemann and R. Hempelmann, J. Appl. Sci., 2021, 11, 5679 CrossRef CAS.
- S. Cheng, M. Musiał, Z. Wojnarowska and M. Paluch, J. Chem. Phys., 2020, 152, 091101 CrossRef CAS PubMed.
- F. Philippi, D. Rauber, J. Zapp, C. Präsang, D. Scheschkewitz and R. Hempelmann, Chem. Phys. Chem., 2019, 20, 443–455 CrossRef CAS PubMed.
- Z. J. Chen, T. Xue and J.-M. Lee, RSC Adv., 2012, 2, 10564 RSC.
- J. Wei, D. Lu, C. Jiang, D. Fang and X. Hu, J. Mol. Liq., 2020, 313, 113538 CrossRef CAS.
- K. R. Harris, M. Kanakubo and L. A. Woolf, J. Chem. Eng. Data, 2007, 52, 1080–1085 CrossRef CAS.
- K. R. Harris, M. Kanakubo and L. A. Woolf, J. Chem. Eng. Data, 2007, 52, 2425–2430 CrossRef CAS.
- K. R. Harris, L. A. Woolf and M. Kanakubo, J. Chem. Eng. Data, 2005, 50, 1777–1782 CrossRef CAS.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
- S. M. Urahata and M. C. C. Ribeiro, J. Phys. Chem. Lett., 2010, 1, 1738–1742 CrossRef CAS.
- Y.-L. Wang, B. Li, S. Sarman, F. Mocci, Z.-Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877 CrossRef CAS PubMed.
- K. R. Harris, J. Mol. Liq., 2016, 222, 520–534 CrossRef CAS.
- K. R. Harris and M. Kanakubo, J. Chem. Eng. Data, 2016, 61, 2399–2411 CrossRef CAS.
- S. K. Davidowski, F. Thompson, W. Huang, M. Hasani, S. A. Amin, C. A. Angell and J. L. Yarger, J. Phys. Chem. B, 2016, 120, 4279–4285 CrossRef CAS PubMed.
- P. Judeinstein, C. Iojoiu, J.-Y. Sanchez and B. Ancian, J. Phys. Chem. B, 2008, 112, 3680–3683 CrossRef CAS PubMed.
- K. Chen, Y. Wang, J. Yao and H. Li, J. Phys. Chem. B, 2018, 122, 309–315 CrossRef CAS PubMed.
- M. Lozynski, J. Pernak, Z. Gdaniec, B. Gorska and F. Béguin, Phys. Chem. Chem. Phys., 2017, 19, 25033–25043 RSC.
- S. R. P. Bandlamudi and K. M. Benjamin, J. Chem. Phys., 2018, 148, 201101 CrossRef PubMed.
- R. Matsumoto, M. W. Thompson and P. T. Cummings, J. Phys. Chem. B, 2019, 123, 9944–9955 CrossRef CAS PubMed.
- O. Nordness and J. F. Brennecke, Chem. Rev., 2020, 120, 12873–12902 CrossRef CAS PubMed.
- K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649 RSC.
- K. R. Harris, J. Phys. Chem. B, 2010, 114, 9572–9577 CrossRef CAS PubMed.
- H. Zhu, U. A. Rana, V. Ranganathan, L. Jin, L. A. O'Dell, D. R. MacFarlane and M. Forsyth, J. Mater. Chem. A, 2014, 2, 681–691 RSC.
- D. R. MacFarlane, M. Forsyth, E. I. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962 RSC.
- K. R. Harris, J. Phys. Chem. B, 2019, 123, 7014–7023 CrossRef CAS PubMed.
- C. Schreiner, S. Zugmann, R. Hartl and H. J. Gores, J. Chem. Eng. Data, 2010, 55, 1784–1788 CrossRef CAS.
- J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740 CrossRef CAS PubMed.
- W. D. Amith, J. C. Araque and C. J. Margulis, J. Ionic Liquids, 2022, 2, 100012 CrossRef.
- A. Triolo, O. Russina, R. Caminiti, H. Shirota, H. Y. Lee, C. S. Santos, N. S. Murthy and E. W. Castner, Chem. Commun., 2012, 48, 4959–4961 RSC.
- H. K. Kashyap, C. S. Santos, R. P. Daly, J. J. Hettige, N. S. Murthy, H. Shirota, E. W. Castner and C. J. Margulis, J. Phys. Chem. B, 2013, 117, 1130–1135 CrossRef CAS PubMed.
- O. Russina, A. Triolo, L. Gontrani, R. Caminiti, D. Xiao, L. G. Hines Jr, R. A. Bartsch, E. L. Quitevis, N. Pleckhova and K. R. Seddon, J. Phys.: Condens. Matter, 2009, 21, 424121 CrossRef.
- A. Triolo, A. Mandanici, O. Russina, V. Rodriguez-Mora, M. Cutroni, C. Hardacre, M. Nieuwenhuyzen, H. J. Bleif, L. Keller and M. A. Ramos, J. Phys. Chem. B, 2006, 110, 21357–21364 CrossRef CAS PubMed.
- O. Russina, B. Fazio, G. Di Marco, R. Caminiti and A. Triolo, The Structure of Ionic Liquids, Springer International Publishing Switzerland, 2014, pp. 39–61 Search PubMed.
- K. Shimizu, C. E. S. Bernardes, A. Triolo and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2013, 15, 16256 RSC.
- H. J. Zeng, M. A. Johnson, J. D. Ramdihal, R. A. Sumner, C. Rodriguez, S. I. Lall-Ramnarine and J. F. Wishart, J. Phys. Chem. A, 2019, 123, 8370–8376 CrossRef CAS PubMed.
- K. Yoshii, T. Uto, N. Tachikawa and Y. Katayama, Phys. Chem. Chem. Phys., 2020, 22, 19480–19491 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis details for the ionic liquids and NMR resonances; experimental values for density, viscosity and conductivity; TGA curves; potential energy surface for [C4HTMG][NTf2]; 2D-NMR spectra; crystal structures of [2O2HTMG][PF6] and [C5HTMG][PF6]; ESP histograms including numerical data; H-bonding; NCI analysis; Gaussian log files for PES minima; ion volumes; xyz files of ion pair complexes and the structures used for proton affinity calculations. CCDC 2157463 and 2157466. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2cp05724g |
| This journal is © the Owner Societies 2023 |